Момент инерции — формулы определения, единицы измерения
Основные понятия и суть
Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.
Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате.
Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r
- mi — масса в точке;
- rj — расстояние от точки до координаты.
То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.
youtube.com/embed/S5u33knDwIA»> Вычисление параметра
Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r
Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.
Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.
Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей.
Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Методика решения
Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения.
- Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
- Формула нахождения момента для материальной точки I = m*r2.
Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O.
Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования.
- прямая пропорциональность массе;
- соответствие квадрату размера;
- изменение с учетом оси вращения.
Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.
Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.
Моменты простейших объектов
Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта.
- Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r
- Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.
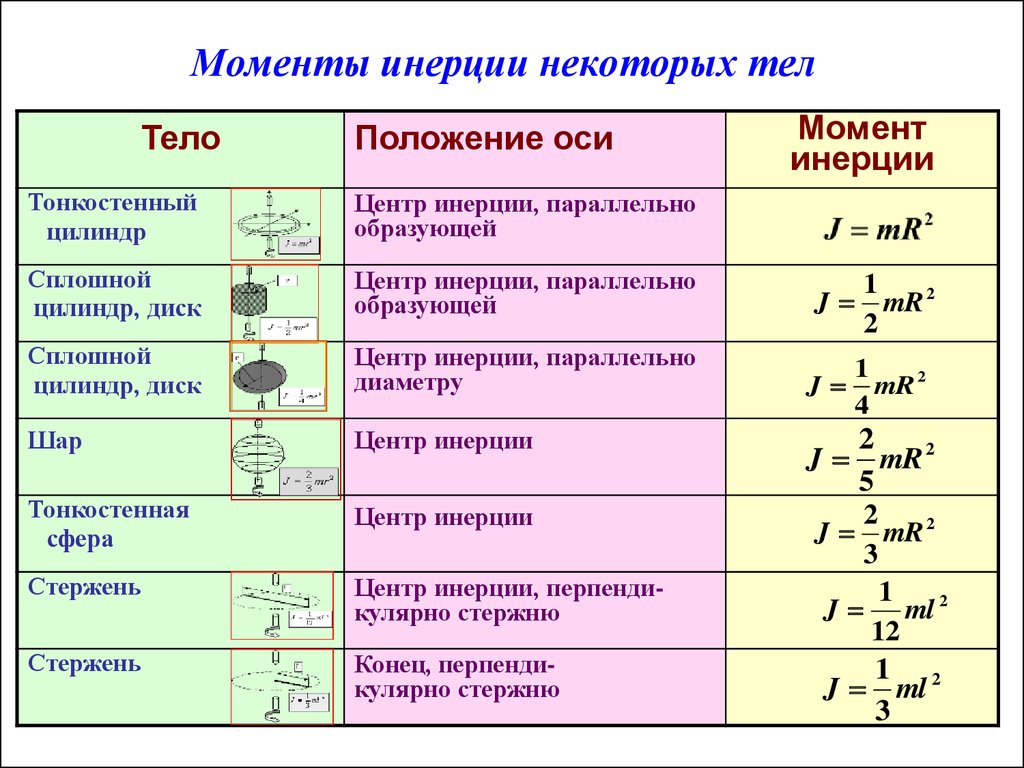
- Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца. Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r2 / 2.
- Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси.
- Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.
- Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.
- Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.
Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r
При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.
Теорема Гюйгенса — Штейнера
Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей.
Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:
- Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2)/ m.
- Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2.
Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.
Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю.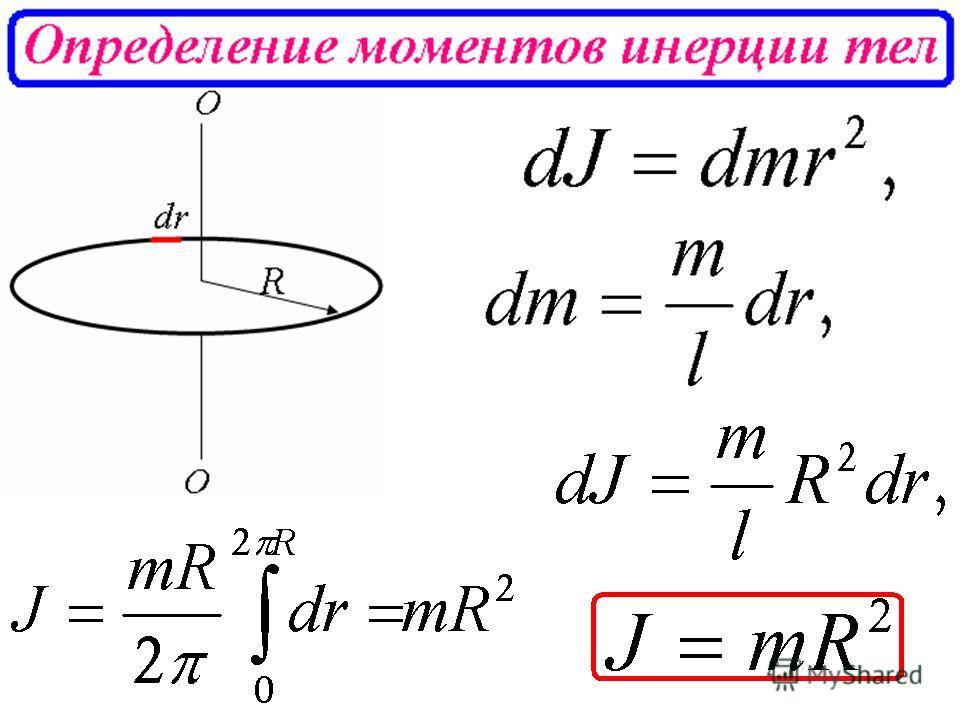
Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.
Находится ri’2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’2 = (xi — Oц)2 + yi2. Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.
Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2.
Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.
Пример задачи
Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.
Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md2. Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.
Момент вращения относительно диска определяется с помощью выражения I1 = m* d2 / 2.
Для решения задачи она будет выглядеть Io = m* d2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.
МЕХАНИКА ТВЕРДОГО ТЕЛА — Студопедия
Поделись
| Момент инерции, Единицы измерения |
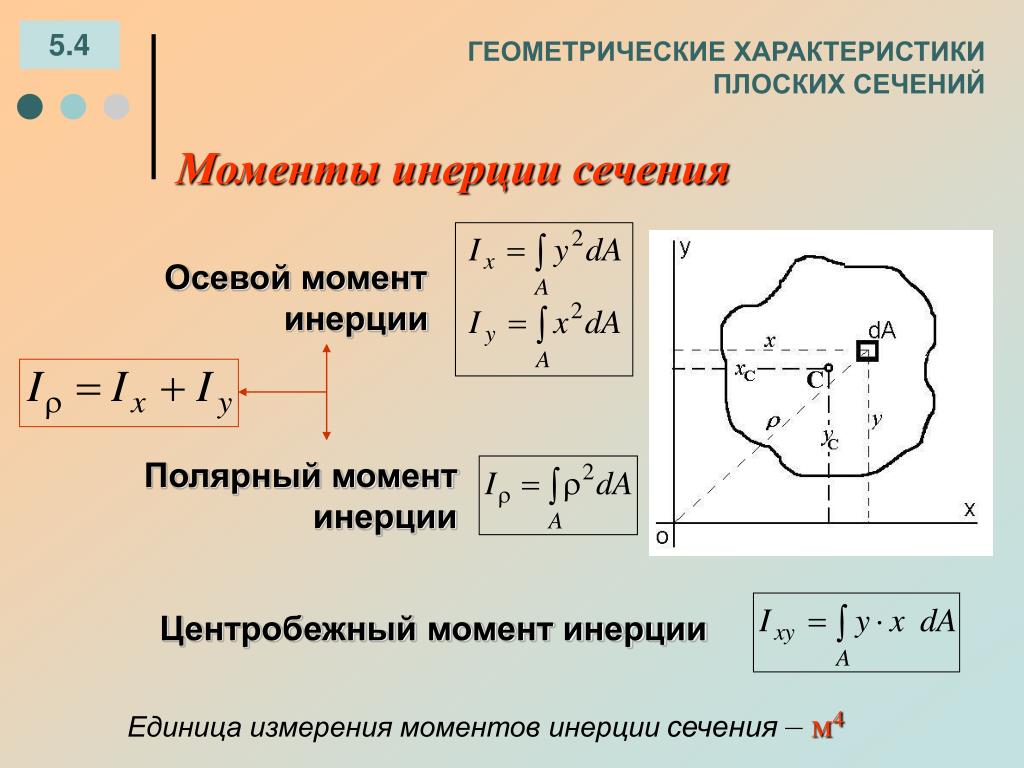
Физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси.
Суммирование производится по всем элементарным массам , на которые можно разбить тело.
Момент инерции – величина аддитивная: момент инерции тела равен сумме моментов инерции его частей
Момент инерции материальной точки рассчитывается как
В случае непрерывного распределения масс момент инерции рассчитывается как интеграл по объему.
Здесь — плотность тела в данной точке; — масса малого элемента тела объемом , отстоящего относительно оси вращения на расстоянии .
|
| МОМЕНТЫ ИНЕРЦИИ ОДНОРОДНЫХ ТЕЛ |
| МОМЕНТ СИЛЫ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА |
| Момент силы относительно неподвижной точки О | Физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку А приложения силы, на силу . — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к | ||||
| Модуль вектора момента силы Единицы измерения | |||||
| Уравнение динамики вращательного движения твердого тела | |||||
Момент сил твердого тела относительно оси равен произведению момента инерции относительно той же оси на угловое ускорение.
Выведем эту формулу
,
но для вращательного движения
тогда или
Вывод сделан для материальной точки и для случая, когда угол (см. выражение для модуля момента силы)
| |||||
| Момент импульса |
| Момент импульса материальной точки относительно неподвижной точки О | Физическая величина, определяемая векторным произведением радиуса-вектора материальной точки, проведенного из точки О, на импульс этой материальной точки. псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к | |
| Модуль вектора момента импульса | ||
| Момент импульса абсолютно твердого тела относительно неподвижной оси z | ||
| Единицы измерения | ||
| Еще одна форма записи уравнения динамики вращательного движения твердого тела | ||
| Закон сохранения момента импульса – фундаментальный закон природы В замкнутой системе момент внешних сил и , тогда |
Что такое единица момента инерции в физике?
Главная » Механика » Что такое единица момента инерции в физике?Изображение, сделанное с помощью холста
Первый закон движения Ньютона познакомил нас с понятием инерции.
Инерция тела — это его неспособность самостоятельно изменять состояние покоя или линейного равномерного движения.
Теперь вопрос заключается в том, есть ли у нас подобная концепция, когда речь идет о вращающихся телах, и ответ: да, у нас есть инерция вращения. Давайте сначала 94$
Единица момента инерции выражается в миллиметрах $(мм)$ в данном случае площади момента инерции.
Момент инерции, с которым мы работаем в механике, это момент инерции массы.
Единица момента инерции в системе МКС
Единица момента инерции в системе МКС кг.м 2
Что такое единица момента инерции в системе СИ?
Единица момента инерции является производной единицей измерения. В Международной системе (СИ) масса $m$ измеряется в килограммах, а расстояние $r$ измеряется в метрах, при этом $I$ (момент инерции) имеет размерность килограмм-метр в квадрате.
Итак, единица момента инерции в системе СИ равна кг.м 2 . Это то же самое, что и система единиц МКС.
Единица момента инерции в системе СГС
В системе СГС единица измерения равна г.см 2
Это связано с тем, что в системе единиц СГС единицей массы является грамм, а для измерения длины в качестве единицы используется сантиметр.
Преобразование между единицами
Ниже приведена таблица преобразования единиц момента инерции:
| Единица | кг. м 2 | г.см 2 | фунтов m ft 2 | lb m in 2 |
kg. m 2 | 1 | 1×10 7 | 2.37×10 | 3.42×10 3 |
| g.cm 2 | 1×10 -7 | 1 | 2,37×10 -6 | 3.42×10 -4 |
| lb m ft 2 | 4.21×10 -2 | 4.21×10 5 | 1 | 1.44×10 2 |
| lb m in 2 | 2.93×10 -4 | 2.93×10 3 | 6,94×10 -3 | 1 |
Часто задаваемые вопросы
Является ли момент инерции скалярным или векторным?
Момент инерции является скалярной величиной.
В его формулу входят масса и расстояние в квадрате. Мы знаем, что масса скалярна, как и расстояние, и даже сам квадрат расстояния не имеет направления. Произведение обеих этих скалярных величин, т. Е. Квадрат массы на время, дает скалярную величину.
От каких факторов зависит момент инерции?
Момент инерции зависит от следующих факторов,
1. Плотность материала
2. Форма и размеры тела
3. Ось вращения
4. Распределение массы (распределение массы) относительно ось
В чем именно разница между моментом инерции и моментом инерции площади?
Момент инерции, как и инерция, представляет собой сопротивление вращению вокруг оси, тогда как
момент инерции площади является мерой сопротивления формы изгибу вокруг определенной оси.
Влияет ли момент инерции на угловой момент?
Да, угловой момент $(L)$ пропорционален угловой скорости $(\omega)$
В механике вращения угловое ускорение пропорционально моменту инерции тела.
Момент инерции можно рассматривать как способность выдерживать крутящий момент. Угловой момент твердого тела равен просто $\omega$, где $\omega$ — угловая скорость в радианах в секунду.
Случайный преобразователь | Преобразователь момента инерции Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. From: kilogram meter²kilogram centimeter²kilogram millimeter²gram centimeter²gram millimeter²kilogram-force meter second²ounce inch²ounce-force inch second²pound foot²pound-force foot second²pound inch²pound-force inch second²slug foot² To: kilogram meter²kilogram centimeter²kilogram millimeter²gram centimeter²gram millimeter²kilogram-force meter секунда²унция дюйм²унция-сила дюйм секунда²фунт-фут²фунт-сила-фут секунда²фунт дюйм²фунт-сила дюйм секунд²слаг-фут² Электрический зарядЗнаете ли вы назначение статических разрядников на крыльях самолета? Если вы раньше их не замечали, нажмите или коснитесь, чтобы узнать, как они помогают обеспечить надежную работу бортового навигационного и коммуникационного оборудования! Маховик имеет высокий момент инерции, что обеспечивает сопротивление изменению скорости вращения. Обзор Спорт Высокий момент инерции Низкий момент инерции ОбзорМомент инерции, также иногда обозначаемый как MOI, представляет собой свойство тела сопротивляться изменению вращательного движения. Чем выше момент инерции — тем больше это сопротивление. Его часто сравнивают с массой для линейного движения, потому что масса показывает, насколько тело сопротивляется изменению при линейном движении. В то время как при прямолинейном движении распределение веса не влияет на это сопротивление, распределение веса вдоль вращающегося тела играет роль в величине момента инерции. Этот центробежный регулятор использует момент инерции для управления скоростью двигателя, уменьшая количество топлива, когда скорость достигает установленного предела. Двигатель вращает два шара сверху, и по мере увеличения скорости они раздвигаются, увеличивая момент инерции устройства. Когда момент инерции достигает заданного значения, уменьшают подачу топлива. Для расчета момента инерции для обычных геометрических фигур с постоянной плотностью по всему объекту можно использовать формулы. Исчисление используется в более сложных вычислениях. Два объекта с одинаковой массой могут иметь разный момент инерции в зависимости от распределения веса внутри объекта. Например, формула для момента инерции I , твердого шара однородной плотности: I = 2 mr ²/5 Здесь м — масса, r — радиус. Если у нас есть два шара одинакового веса, один с радиусом в два раза больше другого, то момент инерции большего шара будет в 2²=4 раза больше. Здесь радиус указывает расстояние между центром вращения и точкой объекта, наиболее удаленной от центра вращения. Если у нас есть цилиндр с массой м , что равно массе шара сверху, а длина L равна радиусу шара сверху, то его момент инерции I равен: I = mr ²/3 , если цилиндр вращается вокруг своего конца, и: I = mr ²/12 , если он вращается вокруг своего центра (вдоль). В спорте Спортсмены часто увеличивают или уменьшают момент инерции для улучшения результатов. Высокий момент инерции помогает поддерживать текущую скорость вращения или сохранять равновесие, если скорость вращения равна нулю. С другой стороны, низкий момент инерции позволяет легче изменять скорость вращения, поэтому уменьшение момента инерции уменьшает количество энергии, необходимой для увеличения или уменьшения скорости вращения. Высокий момент инерцииСерфер вытянул руки, чтобы увеличить момент инерции и сохранить равновесие на доске для серфинга. В некоторых ситуациях важно сохранить вращение, несмотря на силы, действующие на тело, чтобы предотвратить это вращение. В качестве альтернативы они могут увеличить радиус от центра вращения до самой дальней точки своего тела, находящейся вдали от центра вращения. Для этого они могут вытягивать руки или ноги или даже, например, держать длинные стержни. Спортсмену, например, водолазу, может понадобиться увеличить момент инерции перед входом в воду. Вес распределяется на более длинную штангу, чтобы обеспечить лучший баланс и безопасность спортсмена. Однако всегда полезно тренироваться с партнером, который при необходимости может поддержать спортсмена. Как мы видели выше, больший момент инерции означает не только сохранение имеющейся скорости вращения для движущегося тела, но и сохранение нулевой скорости для невращающегося тела. Это полезно не только в том случае, если человек хочет сохранить вращение, но и если он хочет сохранить равновесие, не вращаясь. Например, акробаты, которые ходят по канату, часто носят с собой длинный стержень, который помогает им оставаться на канате, а не «раскручиваться» и падать вниз. Поднятие тяжестей также часто использует момент инерции для равновесия. Вес распределяется по длинной штанге, чтобы спортсменам было безопаснее поднимать ее во время упражнений в жиме лежа. Если вместо этого поднять меньший предмет того же веса, например, мешок с песком или гирю, то даже небольшой толчок под углом может привести к вращению этого предмета. В результате спортсмен может потерять контроль и упасть. Вот почему гири никогда не используются для жима лежа — они могут серьезно повредить или даже убить человека, который их использует. Даже утяжелители, прикрепленные к штанге, иногда представляют опасность для здоровья спортсмена — большое количество массы, сосредоточенной на концах штанги, может привести к вращению штанги и повредить запястья спортсмена. Чтобы предотвратить это, штанги, предназначенные для подъема сверхтяжелых весов, также известные как олимпийские штанги, имеют механизм, который позволяет весу вращаться вокруг штанги, не заставляя всю штангу вращаться вместе с ней. У этой гири очень большой момент инерции. При работе с ним необходимо соблюдать осторожность, потому что это может быть очень опасно, если спортсмен потеряет над ним контроль. Рекомендуется перемещать его плавными движениями и держать как можно дальше от других частей тела, чтобы он не повредил спортсмену, если он потеряет контроль. Работа с гирями и другими подобными предметами обычно осуществляется за счет увеличения момента инерции за счет смещения центра вращения, часто к телу человека. Например, при раскачивании гири обычно не используется запястье или даже локоть в качестве центра вращения, а вместо этого вращается вся рука или даже все тело, иначе это может быть очень опасно, как описано выше. Низкий момент инерцииФигурист сводит руки к туловищу, чтобы увеличить момент инерции. Как только она это сделает, скорость ее вращения увеличится. В спорте часто необходимо ускорить или замедлить угловое движение, затрачивая как можно меньше энергии. В некоторых случаях важен общий момент инерции тела спортсмена. В этой ситуации спортсмены уменьшают свой момент инерции, приближая конечности к телу во время вращения. Это помогает им вращаться быстрее. Такие приемы используются в фигурном катании, прыжках в воду, танцах, гимнастике. Вам не нужно заниматься одним из этих видов спорта, чтобы испытать этот эффект. Просто попробуйте покрутиться на офисном стуле, вытянув руки и ноги, а затем подтяните их к телу — когда вы это сделаете, ваша скорость вращения увеличится. Момент инерции важен при использовании спортивного или игрового оборудования для качелей. Оборудование с более низким моментом инерции позволяет игрокам качаться быстрее и, таким образом, дает им больше времени для ожидания и наблюдения за игрой, прежде чем совершить качание. В других видах спорта спортсмены вращают только части своего тела, например, руку или только запястье, часто удерживая снаряжение, такое как бейсбольная бита или клюшка для гольфа. Однако важно отметить, что когда скорость качания одинакова для двух бит, одна с более низким и одна с более высоким моментом инерции, удар с той же скоростью с последней заставит мяч двигаться быстрее , хотя для раскачивания биты с высоким моментом инерции требуется больше энергии, чем для раскачивания битой с более низким моментом инерции. Производители клюшек для гольфа и теннисных ракеток отображают информацию о моменте инерции клюшек и ракеток, однако производители бейсбольных бит не предоставляют эту информацию потребителям. Непонятно, почему так происходит, но это может быть связано с разными маркетинговыми стратегиями производителей. В любом случае, если эта информация не отображается, важно опробовать оборудование в магазине, возможно, в сравнении с другим подобным оборудованием, чтобы выбрать наиболее подходящее. Список литературы Эта статья была написана Kateryna Yuri . Вы можете быть заинтересованы в других преобразователях в группе механиков:Угловой преобразователь угловой конвертер с частотой. . Преобразователь Преобразователь плотности Преобразователь энергии и работы Преобразователь силы Преобразователь длины и расстояния массовый преобразователь Moment of Force Converter Power Converter Давление, напряжение, преобразователь модуля Young Конкретный объемный преобразователь Преобразование крутящего момента Объем и обычный измерение кулинарного измерения и общие измерения повара Преобразователь линейной скорости и скорости Компактный калькулятор Полный калькулятор Определения единиц измерения У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков. |
Это позволяет накапливать энергию, вырабатываемую вращением маховика.
Вторая формула выводится из первой — здесь радиус от центра вращения до самой дальней точки равен половине длины цилиндра, но поскольку этот радиус возведен в квадрат, 1/2 L (или r ) становится 1/4 L ² (или r ²). В любом случае мы видим, что даже смещение центра вращения изменяет момент инерции, но эта величина также различна для двух объектов разной формы, цилиндра и шара. Момент инерции влияет на работоспособность в спорте и механике, поэтому его часто изменяют, изменяя массу или длину объекта или тела человека.
На самом деле момент инерции настолько важен, что некоторые теории предлагают сопоставлять спортивное снаряжение по его моменту инерции, если в одном и том же виде спорта используется более одного предмета снаряжения. Это иногда делается, например, в гольфе, где некоторые считают, что игроку в гольф помогает улучшить свой замах, если все его клюшки имеют одинаковый момент инерции. В других видах спорта спортсмены варьируют оборудование в зависимости от его момента инерции, в зависимости от эффекта, которого они хотят достичь, например, в зависимости от того, насколько быстро они хотят качаться. Они также могут выбрать оборудование с большим моментом инерции, чтобы улучшить свою мышечную силу, не увеличивая массу оборудования. Например, момент инерции влияет на то, какую скорость может придать мячу бейсбольная клюшка.
Например, акробат, гимнаст, танцор, ныряльщик или фигурист может захотеть поддерживать вращение с постоянной скоростью в течение определенного промежутка времени. В этом случае они могут захотеть иметь больший момент инерции. Чтобы увеличить его, они могут увеличить вес своего тела. Это можно сделать, удерживая дополнительные веса, которые они могут сбросить, как только им больше не требуется высокий момент инерции. Это не всегда разумное решение, тем более, что гири могут полететь в неправильном направлении и нанести ущерб или травму. Два человека также могут взяться за руки, чтобы увеличить суммарный момент инерции во время вращения, а затем отпустить друг друга. Этот прием часто используется в фигурном катании.
При вращении в воздухе ныряльщик дожидается, пока он окажется лицом в правильном направлении для входа в воду, а затем выпрямляет руки и ноги, чтобы остановить вращение и одновременно увеличить момент инерции. Это помогает сохранить нулевую скорость вращения, и спортсмен входит в воду под правильным углом. Эта техника также используется фигуристами, танцорами и гимнастами, чтобы приземлиться без травм или упасть после вращения в воздухе.
Для этого спортсмен либо выбирает спортивный снаряд с меньшим моментом инерции, либо уменьшает момент инерции собственного тела.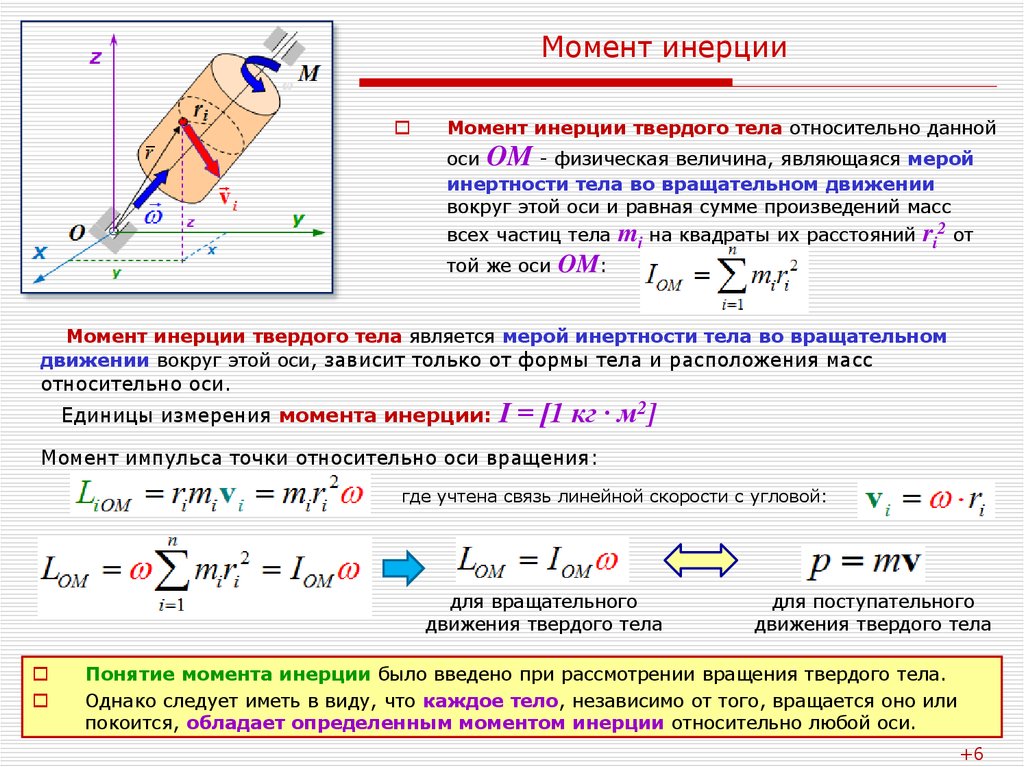
В этом случае вес распределяется по бите или клюшке таким образом, чтобы минимизировать момент инерции. Это важно и для мечей, как настоящих, так и деревянных тренировочных, а также для любого другого спортивного инвентаря, который спортсмен размахивает или вращает, например шары для боулинга. Момент инерции также влияет на то, насколько тяжелым ощущается спортивное снаряжение для спортсмена — чем меньше момент инерции, тем легче оно ощущается. Меньший момент инерции обычно означает более быстрые замахи, что позволяет спортсмену начать замах позже. Это полезно при игре против соперника, потому что ему труднее предсказать ход. Это также дает дополнительное время, чтобы предсказать траекторию мяча, прежде чем совершить замах, что полезно, например, в теннисе и бейсболе.
Таким образом, оборудование с более низким моментом инерции не всегда является решением — иногда для достижения лучших результатов спортсмен не может полагаться на оборудование с более низким моментом инерции, а вместо этого должен увеличивать мышечную силу и скорость и использовать оборудование с более высоким моментом инерции. .
