Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр Калькулятор
✖Масса тела – это количество вещества в теле независимо от его объема или действующих на него сил.ⓘ Масса тела [M] | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Длина стержня — это размер стержня от одного конца до другого конца (длина стержня). | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Момент инерции — это мера сопротивления тела угловому ускорению относительно данной оси. |
Грамм квадратный сантиметрГрамм квадратный миллиметрКилограмм квадратный сантиметрКилограмм квадратный метрКилограмм квадратный миллиметрКилограмм-сила, метр в квадрате, секундаУнция квадратный дюймУнция-сила, дюйм в квадрате, секундаФунт квадратный футфунт квадратный дюймФунт-сила-фут-квадрат-секундаФунт-сила, дюйм в квадрате, секундаСлаг Квадратный фут |
⎘ копия |
👎
Формула
сбросить
👍
Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.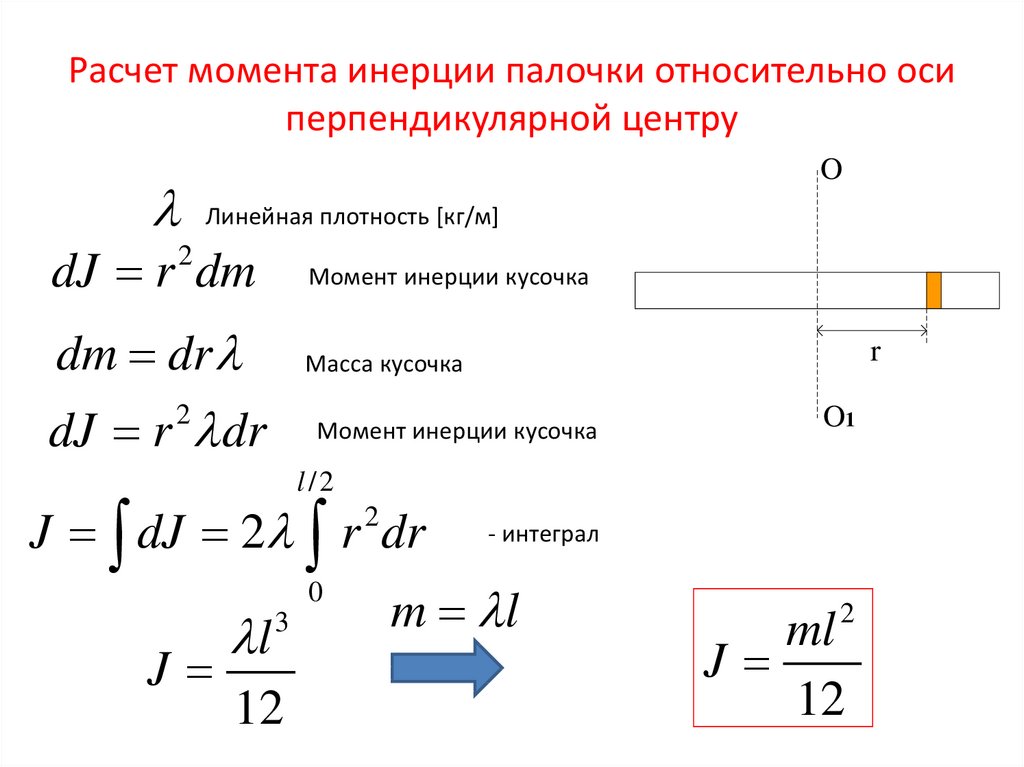 2))/12
2))/12
Почему важен момент инерции?
Это неотъемлемое свойство материи. При вращательном движении момент инерции тела является мерой его инерции. Чем больше момент инерции, тем больше крутящий момент, необходимый для создания в нем заданного углового ускорения.
Share
Copied!
§ 3. Вычисление момента инерции . Том 1. Механика, излучение и теплота
Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси z имеет вид
или
(19.4)
Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси (xi2+yi2). Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.
В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3).
Фиг. 19.3. Прямой стержень, вращающийся вокруг оси, проходящей через один из его концов.
Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния х (в этом случае все у — нулевые). Под суммой, разумеется, я имею в виду интеграл от x2, умноженный на «элементики» массы. Если мы разделим стержень на кусочки длиной
и
(19.5)
Размерность момента инерции всегда равна массе, умноженной на квадрат длины, так что единственная существенная величина, которую мы вычислили, это множитель 1/3.
А чему будет равен момент инерции I, если ось вращения проходит через середину стержня? Чтобы найти его, нам снова нужно взять интеграл, но уже в пределах от —1/2L до +1/2L.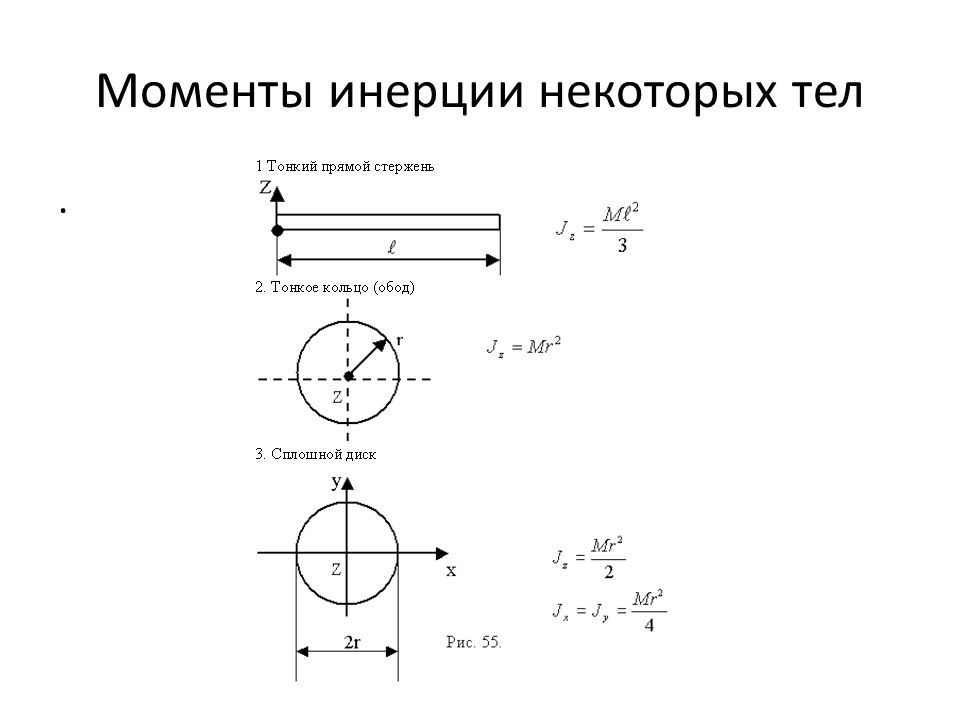
(19.6)
Таким образом, стержень гораздо легче крутить за середину, чем за конец.
Можно, конечно, продолжить вычисление моментов инерции других интересующих нас тел. Но поскольку такие расчеты требуют большого опыта в вычислении интегралов (что очень важно само по себе), они как таковые не представляют для нас большого интереса. Впрочем, здесь имеются некоторые очень интересные и полезные теоремы. Пусть имеется какое-то тело и мы хотим узнать его момент инерции относительно какой-то оси. Это означает, что мы хотим найти его инертность при вращении вокруг этой оси. Если мы будем двигать тело за стержень, подпирающий его центр масс так, чтобы оно не поворачивалось при вращении вокруг оси (в этом случае на него не действуют никакие моменты сил инерции, поэтому тело не будет поворачиваться, когда мы начнем двигать его), то для того, чтобы повернуть его, понадобится точно такая же сила, как если бы вся масса была сосредоточена в центре масс и момент инерции был бы просто равен  м., где Rц.м.— расстояние от центра масс до оси вращения. Однако формула эта, разумеется, неверна. Она не дает правильного момента инерции тела. Ведь в действительности при повороте тело вращается. Крутится не только центр масс (что давало бы величину I1), само тело тоже должно поворачиваться относительно центра масс. Таким образом, к моменту инерции I1 нужно добавить I
м., где Rц.м.— расстояние от центра масс до оси вращения. Однако формула эта, разумеется, неверна. Она не дает правильного момента инерции тела. Ведь в действительности при повороте тело вращается. Крутится не только центр масс (что давало бы величину I1), само тело тоже должно поворачиваться относительно центра масс. Таким образом, к моменту инерции I1 нужно добавить I
(19.7)
Эта теорема называется теоремой о параллельном переносе оси. Доказывается она очень легко. Момент инерции относительно любой оси равен сумме масс, умноженных на сумму квадратов х и у, т. е. I=?mi(x2i+y2i). Мы сейчас сосредоточим наше внимание на х, однако все в точности можно повторить и для у. Пусть координата х есть расстояние данной частной точки от начала координат; посмотрим, однако, как все изменится, если мы будем измерять расстояние  Чтобы это выяснить, мы должны написать
Чтобы это выяснить, мы должны написать
Возводя это выражение в квадрат, находим
Что получится, если умножить его на mi и просуммировать по всем i? Вынося постоянные величины за знак суммирования, находим
Третью сумму подсчитать легко; это просто МХ2ц.м.. Второй член состоит из двух сомножителей, один из которых ?mixi; он равен x’-координате центра масс. Но это должно быть равно нулю, ведь х‘ отсчитывается от центра масс, а в этой системе координат среднее положение всех частиц, взвешенное их массами, равно нулю. Первый же член, очевидно, представляет собой часть х от Iц. Таким образом, мы и приходим к формуле (19.7).
Давайте проверим формулу (19.7) на одном примере. Просто проверим, будет ли она применима для стержня. Мы уже нашли, что момент инерции стержня относительно его конца должен быть равен ML2/3. А центр масс стержня, разумеется, находится на расстоянии L/2. Таким образом, мы должны получить, что МL2/3=МL2/12+М(L/2)2. Так как одна четвертая+одна двенадцатая=одной третьей, то мы не сделали никакой грубой ошибки.
Таким образом, мы должны получить, что МL2/3=МL2/12+М(L/2)2. Так как одна четвертая+одна двенадцатая=одной третьей, то мы не сделали никакой грубой ошибки.
Кстати, чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл. Можно просто предположить, что он равен величине ML2, умноженной на некоторый неизвестный коэффициент ?. После этого можно использовать рассуждения о двух половинках и для момента инерции (19.6) получить коэффициент 1/4?. Используя теперь теорему о параллельном переносе оси, докажем, что ?=1/4?+1/4, откуда ?=1/3. Всегда можно найти какой-нибудь окольный путь!
При применении теоремы о параллельных осях важно помнить, что ось Iцдолжна быть параллельна оси, относительно которой мы хотим вычислять момент инерции.
Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью z, направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у. Доказывается это совсем просто. Заметим, что
Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью z, направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у. Доказывается это совсем просто. Заметим, что
(поскольку все zi=0). Аналогично,
но
Момент инерции однородной прямоугольной пластинки, например с массой М, шириной w и длиной L относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто
поскольку момент инерции относительно оси, лежащей в плоскости пластинки и параллельной ее длине, равен Mw2/12, т. е. точно такой же, как и для стержня длиной w, а момент инерции относительно другой оси в той же плоскости равен ML2/12, такой же, как и для стержня длиной L.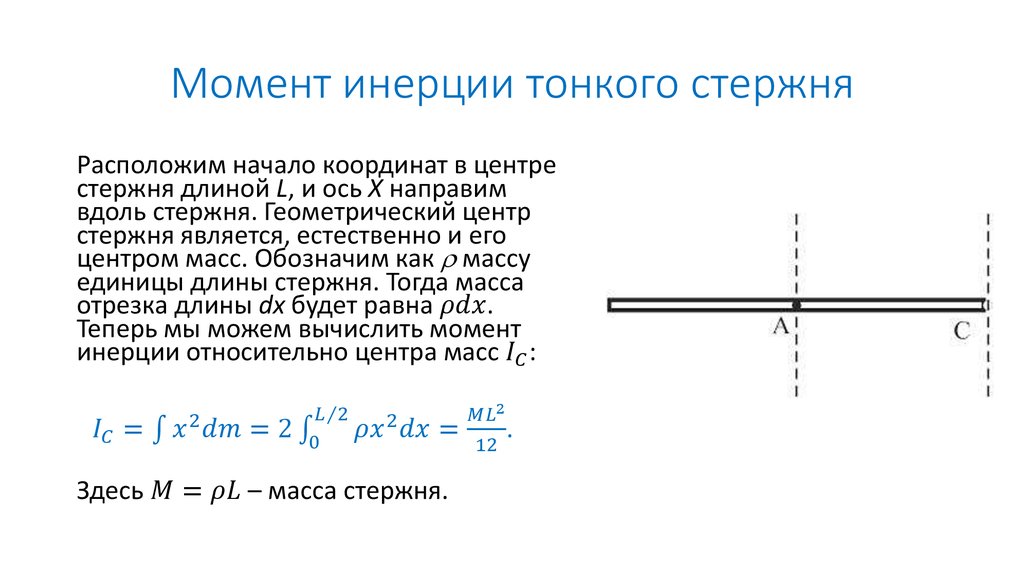
Итак, перечислим свойства момента инерции относительно данной оси, которую мы назовем осью z:
1. Момент инерции равен
2. Если предмет состоит из нескольких частей, причем момент инерции каждой из них известен, то полный момент инерции равен сумме моментов инерции этих частей.
3. Момент инерции относительно любой данной оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение полной массы на квадрат расстояния данной оси от центра масс.
4. Момент инерции плоской фигуры относительно оси, перпендикулярной к ее плоскости, равен сумме моментов инерции относительно любых двух других взаимно перпендикулярных осей, лежащих в плоскости фигуры и пересекающихся с перпендикулярной осью.
Таблица 19.1 простые примеры моментов инерции
В табл. 19.1 приведены моменты инерции некоторых элементарных фигур, имеющих однородную плотность масс, а в табл. 19.2 — моменты инерции некоторых фигур, которые могут быть получены из табл.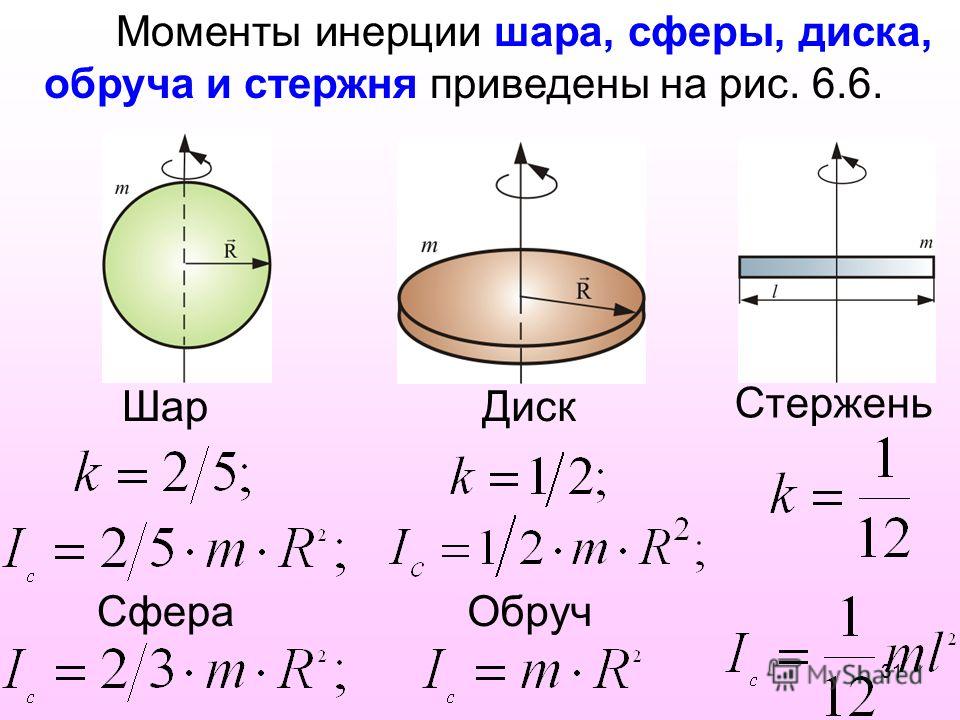 2$, как указано здесь. 93$.
2$, как указано здесь. 93$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. 2/12$ и c.o.m находится в центре тяжести?
также, если 2 стержня образуют крест, то для расчета момента инерции относительно точки их пересечения было бы правильно суммировать отдельные моменты инерции формы стержней?? 92$, а также для $B$ и $C$, так что общий момент инерции равен:
2/12$ и c.o.m находится в центре тяжести?
также, если 2 стержня образуют крест, то для расчета момента инерции относительно точки их пересечения было бы правильно суммировать отдельные моменты инерции формы стержней?? 92$, а также для $B$ и $C$, так что общий момент инерции равен:$$ I = I_A + I_B + I_C $$
Итак, просто рассчитайте отдельные моменты инерции для всех объектов в вашей системе, затем добавьте их вместе. В вашем конкретном случае объекты идентичны, поэтому общая сумма равна моменту инерции одного стержня, умноженному на три.
$\endgroup$
1
$\begingroup$
Момент инерции определяется относительно точки вращения, которая в данном случае является центром равностороннего треугольника. Затем вы можете умножить этот результат на 3.
$\endgroup$
$\begingroup$
Ответ @DrChuck правильный.


 ⓘ Длина стержня [Lrod]
ⓘ Длина стержня [Lrod]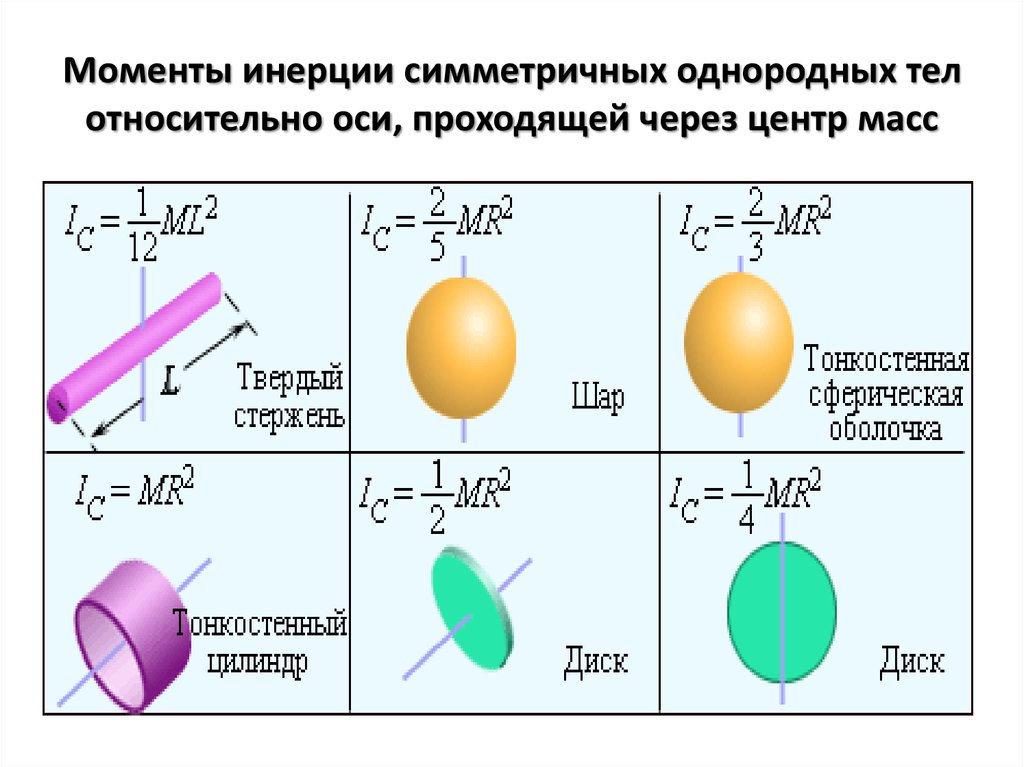 ⓘ Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр [I]
ⓘ Момент инерции стержня относительно перпендикулярной оси, проходящей через его центр [I]