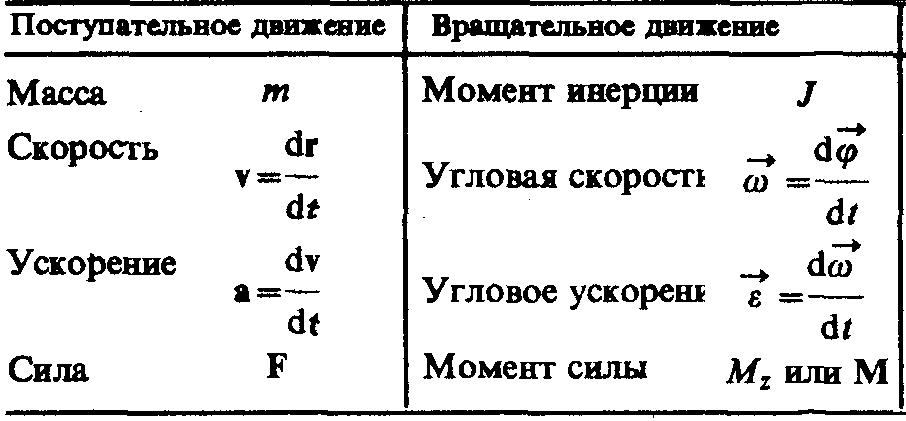
III Момент инерции и момент силы. Момент импульса системы, закон сохранения момента импульса замкнутой системы
Моментом инерции твёрдого тела относительно оси называется сумма произведений массы каждой материальной точки тела на квадрат её расстояния до оси.
Момент силы относительно оси называется скалярная физическая величина, численно равная проекции на эту ось момента силы относительно произвольной точки взятой на данной оси.
Моментом импульса относительно оси называется скалярная величина, численно равная проекции на эту ось момента импульса, относительно произвольной точки, взятой на этой оси.
Момент считается положительным, если, глядя с конца оси, мы видим поворот против часовой стрелки.
Парой сил называются две силы равные по модулю и противоположные по направлению, силы, приложенные к телу.
Рассмотрим возможные случаи приложения сил:
1. Действие всех сил эквивалентно одной
равнодействующей — поступательное
движение.
Действие всех сил эквивалентно одной
равнодействующей — поступательное
движение.
2. Действие всех сил эквивалентно паре сил — вращательное движение.
3. Действие всех сил эквивалентно совокупности равнодействующих и паре сил – сложное движение.
Найдём момент импульса твёрдого тела.
Из основного уравнения динамики для вращательного движения.
, если
— закон сохранения момента импульса для твердого тела. Если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения.
Изменяя момент инерции можно изменить угловую скорость вращающегося тела.
Кинетическая энергия вращающегося тела.
— кинетическая энергия вращающегося тела.
В
случае плоского движения необходимо
кроме вращательного движения учитывать
поступательное движение.
— кинетическая энергия плоского движения.
— скорость центра масс тела.
— момент инерции тела относительно оси проходящей через центр масс тела.
План лекции
Мгновенные оси вращения. Главные оси вращения
Условие равновесия твёрдого тела. Виды равновесия
Мгновенные оси вращения. Главные оси вращения
Плоское движение твердого тела можно представить как сумму двух движений: поступательного, со скоростью , и вращательного с угловой скоростью(цилиндр катится по плоскости без скольжения).
Систему отчета связанную с плоскостью назовем неподвижной.
Движение
можно представить, как вращение с
угловой скоростьюв
системе отсчета, которая движется
относительно неподвижной системы,
поступательно со скоростью,
тогда скорость произвольной точки тела
при сложном движении.
Рассмотрим куб.
Элементарные перемещения твердого тела при плоском движении всегда можно представить, как поворот вокруг неподвижной оси называемой мгновенной осью вращения. Мгновенная ось вращения перемещается по боковой поверхности цилиндра со скоростью равной скорости поступательного движения его оси.
Ось, положения которой остается в пространстве неизменной при вращении вокруг нее тела в отсутствии внешних сил называется свободной осью тела.
Для тела любой формы и с произвольным распределением массы существует три взаимноперпендикулярных и проходящих через центр масс тел оси, которые могут служить свободными осями. Они называются главными осями инерции тела.
1. Моменты инерции относительно главной оси называют главными моментами инерции. В общем случае: .
2. В случае осевой
симметрии: .
В случае осевой
симметрии: .
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 9 из 25Следующая ⇒
В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические величины — момент сил и момент инерции, физический смысл которых раскроем ниже. Пусть некоторое тело под действием силы , приложенной в точке А, приходит во вращение вокруг оси ОО’ (рисунок 5.1). Рисунок 5.1 – К выводу понятия момента силы
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль (5.
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
(5.2) Единица момента силы — ньютон-метр (Н.м). Направление вектора момента силы находиться с помощью правила правого винта. Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая Момент инерции материальной точки относительно оси вращения — произведение массы этой точки на квадрат расстояния от оси: (5.3)
Момент инерции тела относительно оси вращения — сумма моментов инерции материальных точек, из которых состоит это тело: (5. В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием: , (5.5) где r — расстояние от оси вращения до элемента массой dm. Если тело однородно и его плотность ρ = m/V, то момент инерции тела (5.6) Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему. Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему. Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню, (5.7) Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
(5.8) Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр, (5.
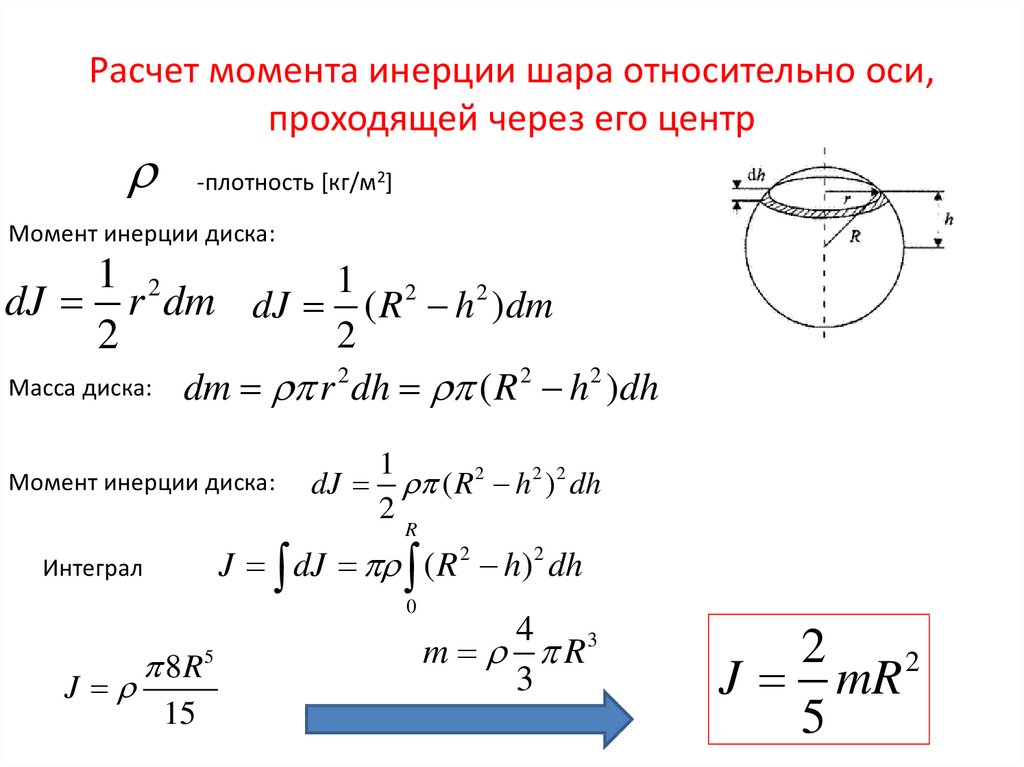
Момент инерции шара относительно диаметра
(5.10) Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Пусть масса диска – m, а его радиус – R. Площадь кольца (рисунок 5.2), заключенного между r и , равна . Рисунок 5.2 – К выводу момента инерции диска
Площадь диска . При постоянной толщине кольца,
откуда или . Тогда момент инерции диска,
(5.11)
Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Рисунок 5.3 – Моменты инерции IC некоторых однородных твердых тел.
Теорема Штейнера Приведенные выше формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции.
(5.12)
где m — масса тела, d — расстояние от центра масс до выбранной оси вращения. Единица момента инерции — килограмм-метр в квадрате (кг . м2). Так, момент инерции однородного стержня длиной l относительно оси, проходящей через его конец, по теореме Штейнера равен
(5.13)
⇐ Предыдущая45678910111213Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Момент инерции
Момент инерцииМасса m помещена на стержень длины r и имеет пренебрежимо малую массу и вынуждена вращаться вокруг неподвижной оси. Если масса выходит из горизонтальной ориентации, это можно описать либо с точки зрения силы и ускорения с помощью второго закона Ньютона для линейного движения, либо как чистое вращение вокруг оси с помощью второго закона Ньютона для вращения. Это обеспечивает настройку для сравнения линейных и вращательных величин для одной и той же системы. Этот процесс приводит к выражению для момента инерции точечной массы. | INDEX Moment of Inertia Concepts Moment of Inertia Примеры | ||||||||||||||||||||||||||||||||||||||||
|


 Все правила по сольфеджио
Все правила по сольфеджио
 1)
1) 4)
4) 9)
9) Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и величины md2:
Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и величины md2: su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)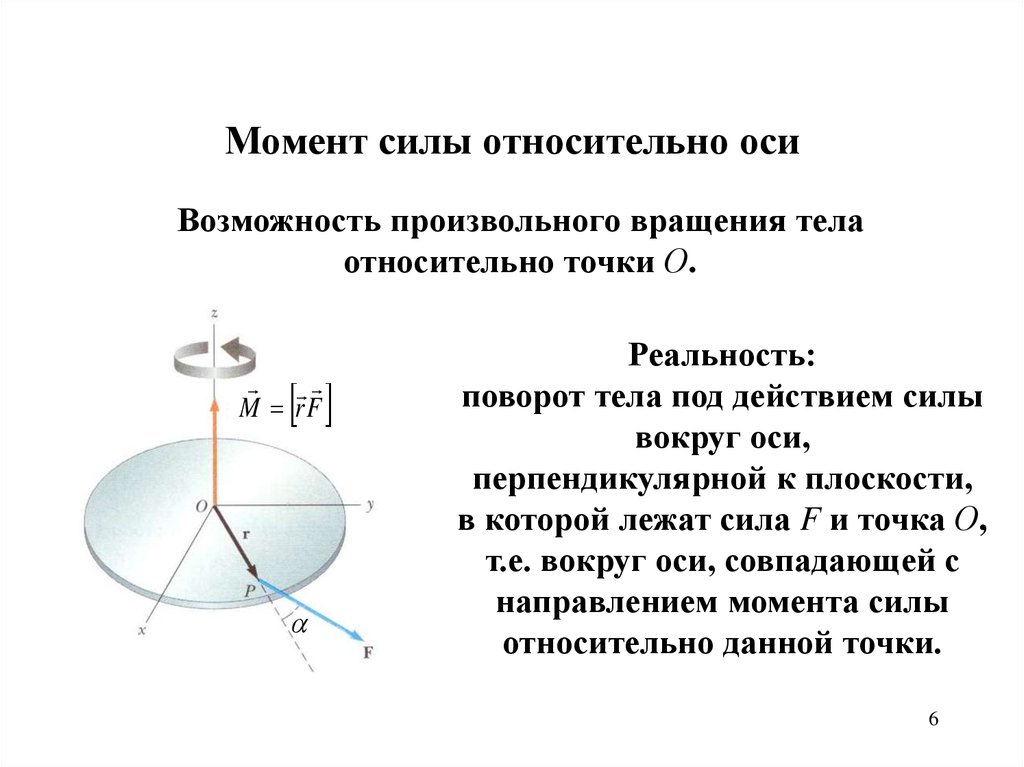
 Момент инерции точечной массы определяется выражением I = mr 2 , но стержень нужно рассматривать как бесконечное число точечных масс, и каждую нужно умножить на квадрат расстояния от оси. Полученная бесконечная сумма называется интегралом. Общий вид момента инерции
это:
Момент инерции точечной массы определяется выражением I = mr 2 , но стержень нужно рассматривать как бесконечное число точечных масс, и каждую нужно умножить на квадрат расстояния от оси. Полученная бесконечная сумма называется интегралом. Общий вид момента инерции
это: Чтобы выполнить интеграл, необходимо выразить все в интеграле через одну переменную, в данном случае переменную длины r. Так как общая
длина L имеет массу M, тогда M/L
отношение массы к длине и масса
элемент может быть выражен, как показано.
Интегрируя от -L/2 до +L/2 от
центр включает в себя весь стержень. Интеграл
имеет полиномиальный тип:
Чтобы выполнить интеграл, необходимо выразить все в интеграле через одну переменную, в данном случае переменную длины r. Так как общая
длина L имеет массу M, тогда M/L
отношение массы к длине и масса
элемент может быть выражен, как показано.
Интегрируя от -L/2 до +L/2 от
центр включает в себя весь стержень. Интеграл
имеет полиномиальный тип: