Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
- Подробности
- Просмотров: 507
«Физика — 10 класс»
При решении задач на эту тему следует иметь в виду, что моменты силы, инерции и импульса зависят от выбора оси вращения. Кроме этого, нужно обращать внимание на то, что моменты импульса всех тел записываются относительно одной и той же системы отсчёта.
Задача 1.
На блок радиусом r и массой m1 намотана нить, к концу которой привязан груз массой m2 (рис. 6.12).
Груз отпускают, и он движется вниз, раскручивая нить. Определите ускорение груза. Массой нити можно пренебречь.
Р е ш е н и е.
Обозначим на рисунке силы, действующие на блок и груз.
На блок действуют сила тяжести m1
На груз действуют сила тяжести m2 и сила натяжения ‘.
Согласно второму закону Ньютона в проекции на ось Y для груза запишем:
m2a = m2g — T’. (1)
Согласно основному закону динамики вращательного движения для блока запишем:
Iε = Tr. (2)
Момент инерции блока Связь углового и линейного ускорений а = εr.
Так как по условию задачи нить невесома, то Т = Т’.
Преобразуем уравнение (2): тогда
Подставив это выражение в уравнение (1), получим
Окончательно
Задача 2.
Скамья Жуковского радиусом 1 м со стоящим в центре человеком вращается, делая 2 об/с. Человек переходит на край скамьи. Определите изменение угловой скорости вращения скамьи. Масса человека 50 кг, момент инерции скамьи 30 кг • м
Р е ш е н и е.
Так как внешние силы — сила тяжести и сила реакции опоры, направленные параллельно оси вращения, не могут изменить момент импульса системы тел «скамья—человек», то согласно закону сохранения импульса
I1ω1 = I2ω2. (1)
Когда человек находится в центре скамьи, то момент инерции системы равен только моменту инерции скамьи: I1 = Iск
После того как человек перешёл на край скамьи, момент инерции системы стал равен I2 = Iск + mr2.
Угловая скорость связана с числом оборотов в секунду соотношением ω1 = 2πn.
Подставив найденные выражения в уравнение (1), получим Iск2πn = (Iск + mr2)ω2. Тогда
Изменение угловой скорости
Задача 3.
На наклонную плоскость вкатывается колесо, двигавшееся по горизонтальной поверхности со скоростью 4 м/с. Вся масса колеса сосредоточена в ободе. Определите максимальную высоту, на которую поднимется колесо. Работой силы трения можно пренебречь.
Р е ш е н и е.
Выберем нулевой уровень отсчёта потенциальной энергии так, как показано на рисунке 6.13. Учтём, что момент инерции колеса-обруча I = mR2, а угловая скорость вращения ω = υ/R. Механическая энергия колеса на горизонтальной поверхности равна сумме кинетических энергий поступательного и вращательного движений колеса:
На максимальной высоте механическая энергия равна потенциальной энергии Е2 = mgh. Согласно закону сохранения механической энергии получим Е1 = Е2, или mυ2 = mgh, откуда h = υ2/g = 1,6 м.
Задача 4.
Сплошной цилиндр раскрутили до угловой скорости ω и положили на пол к стенке. Коэффициент трения между стенкой, полом и цилиндром μ, радиус цилиндра R. Определите, сколько оборотов сделает цилиндр до остановки.
Р е ш е н и е.
Решаем задачу, используя теорему об изменении кинетической энергии. При этом учтём, что ось вращения цилиндра неподвижна, момент инерции цилиндра относительно этой оси равен соответственно кинетическая энергия цилиндра вначале равна
Изменение кинетической энергии равно алгебраической сумме работ сил, действующих на него:
На цилиндр (рис. 6.14) действуют силы тяжести m реакции опоры 1, 2 и силы трения тр1, тр2.
Так как перемещается относительно стенок угла только точка приложения сил трения, то работу совершают только силы трения. В связи с этим справедливо уравнение
Работы сил трения равны Aтp1 = -Fтp12πRn; Aтp2 = -Fтp12πRn, где n — число полных оборотов цилиндра до остановки, а силы трения определяются силами реакции опоры стенок на цилиндр: Fтp1 = μN1; Fтp2 = μN2.
Найдём силы реакции опоры.
По условию задачи цилиндр только вращается, его центр тяжести не движется, следовательно, векторная сумма сил, действующих на него, равна нулю:
m + 1 + 2 + тp1 + тp2 = 0.
В проекциях на оси ОХ и OY имеем
N1 + Fтp2 — mg = 0. (3)
Подставив в уравнения (2) и (3) выражения для сил трения, получим
μN1 — N2 = 0; (4)
N1 + μN2 — mg = 0. (5)
Решая систему уравнений (4) и (5), найдём силы реакции опоры:
Тогда число оборотов до остановки цилиндра
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику — момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.
Вращение и момент инерции
Инерции момент проще всего ввести для материальной точки. Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:
I = M*R2.
Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:
I = ∫m(r2*dm).
Через объем и плотность это равенство записывается в таком виде:
I = ∫V(ρ*r2*dV).
Его часто применяют для вычисления значений I конкретных геометрических объектов.
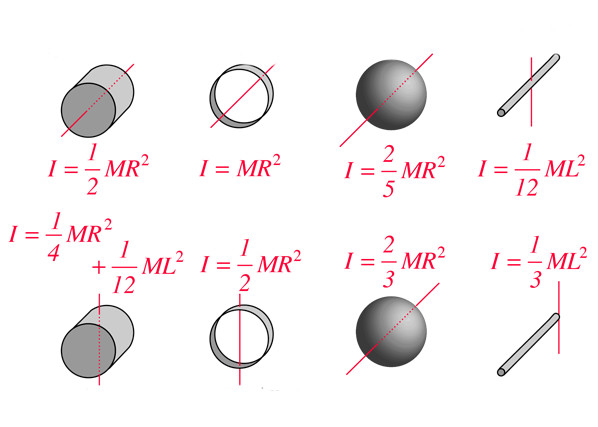
Физический смысл инерции момента I заключается в том, что он определяет, насколько «сложно» данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.
Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, — это закон сохранения момента импульса. Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.
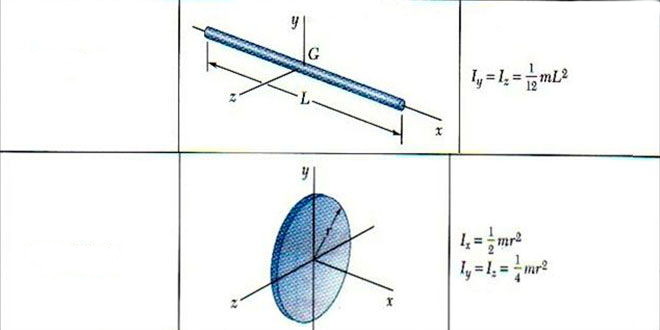
Тонкий стержень и оси вращения
Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной. Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.
Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.
Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O1, вторая — через конец стержня, обозначим ее O2. Относительно них и вычислим величину I.
Момент инерции относительно O1
В первую очередь выпишем общую формулу. Имеем:
I = ∫V(ρ*r2*dV).
Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.
Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:
I = ∫L(ρ*S*l2*dl).
Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O1 проходит через середину стержня, то пределы интегрирования будут следующими:
I = ∫-L/2L/2(ρ*S*l2*dl).
Результатом вычисления этого интеграла является следующая формула:
I = M*L2/12.
Таким образом, момент инерции тонкого стержня определяется его массой и длиной.
Инерции момент относительно O2
Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.
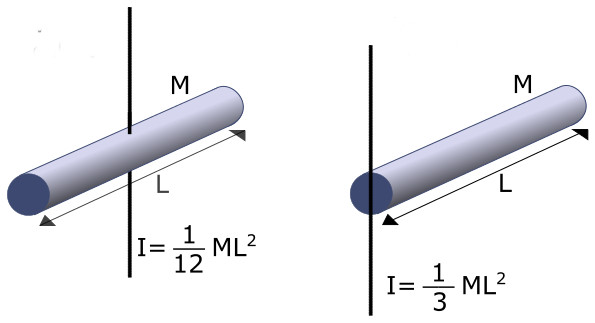
Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:
I = I0 + M*h2.
Здесь I0 — момент инерции стержня относительно оси O, h — дистанция между осями.
Эту формулу можно с успехом применить для нашего случая. Поскольку I0 мы рассчитали в предыдущем пункте статьи относительно оси O1, и расстояние между O1 и O2 составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:
I = I0 + M*h2 = M*L2/12 + M*L2/4 = M*L2/3.
Таким образом, для стержня величина I относительно оси O2 в 4 раза больше, чем относительно оси O1. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O2 следует приложить в 4 раза больший крутящий момент, чем в случае оси O1.
Пример задачи
Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?
Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O1 и заданной в задаче равно:
h = 0,25 — 0,2 = 0,05 м.
Тогда получаем момент инерции стержня (однородного):
I = I0 + M*h2 = 5*0,52/12 + 5*0,052 = 0,117 кг*м2.
В СИ момент инерции стержня измеряется в указанных единицах.
Тела, совершающие круговые движения, в физике принято описывать с помощью формул, включающих в себя угловую скорость и угловое ускорение, а также такие величины, как моменты вращения, сил и инерции. Рассмотрим подробнее эти понятия в статье.
Эту физическую величину также называют моментом импульса. Слово «момент» означает, что при определении соответствующей характеристики учитывается положение оси вращения. Так, момент импульса частицы массой m, которая вращается со скоростью v вокруг оси O и находится от последней на расстоянии r, описывается следующей формулой:
L¯ = r¯*m*v¯ = r¯*p¯, где p¯ — импульс частицы.
Знак «¯» указывает на векторный характер соответствующей величины. Направление вектора момента вращения L¯ определяется по правилу правой руки (четыре пальца направлены от конца вектора r¯ к концу p¯, и отставленный большой палец показывает, куда будет направлен L¯). Направления всех названных векторов можно посмотреть на главном фото статьи.
При решении практических задач пользуются формулой для момента импульса в форме скалярной. Кроме того, линейную скорость заменяют угловой. В этом случае формула для L будет выглядеть так:
L = m*r2*ω, где ω = v*r — угловая скорость.
Величина m*r2 обозначается буквой I и называется моментом инерции. Она характеризует инерционные свойства системы вращения. В общем виде выражение для L записывается так:
L = I*ω.
Эта формула справедлива не только для вращающейся частицы массой m, но и для любого тела произвольной формы, которое совершает круговые перемещения относительно некоторой оси.
Момент инерции I
В общем случае введенная в предыдущем пункте величина I рассчитывается по формуле:
I = ∑i(mi*ri2).
Здесь i указывает на номер элемента с массой mi, расположенном от оси вращения на расстоянии ri. Это выражение позволяет произвести расчет для неоднородного тела произвольной формы. Для большинства идеальных объемных геометрических фигур этот расчет уже произведен, и полученные значения момента инерции внесены в соответствующую таблицу. Например, для однородного диска, который совершает круговые движения вокруг оси, перпендикулярной его плоскости и проходящей через центр масс, I = m*r2/2.
Чтобы понять физический смысл момента инерции вращения I, следует ответить на вопрос, относительно какой оси легче раскрутить швабру: той, которая проходит вдоль швабры или той, которая ей перпендикулярна? Во втором случае придется приложить больше усилий, поскольку момент инерции для этого положения швабры имеет большую величину.

Закон сохранения величины L
Изменение момента вращения во времени описывается приведенной ниже формулой:
dL/dt = M, где M = r*F.
Здесь M — это момент результирующей внешней силы F, приложенной к плечу r относительно оси вращения.
Формула показывает, если M=0, тогда изменение момента импульса L не будет происходить, то есть он будет оставаться сколь угодно длительное время неизменным независимо от внутренних изменений в системе. Этот случай записывают в виде выражения:
I1*ω1 = I2*ω2.
То есть любые изменения внутри системы момента I будут приводить к изменениям угловой скорости ω таким образом, что их произведение будет оставаться постоянным.

Примером проявления этого закона является спортсмен в фигурном катании, который, выбрасывая руки и прижимая их к телу, меняет свой I, что отражается на изменении его скорости вращения ω.
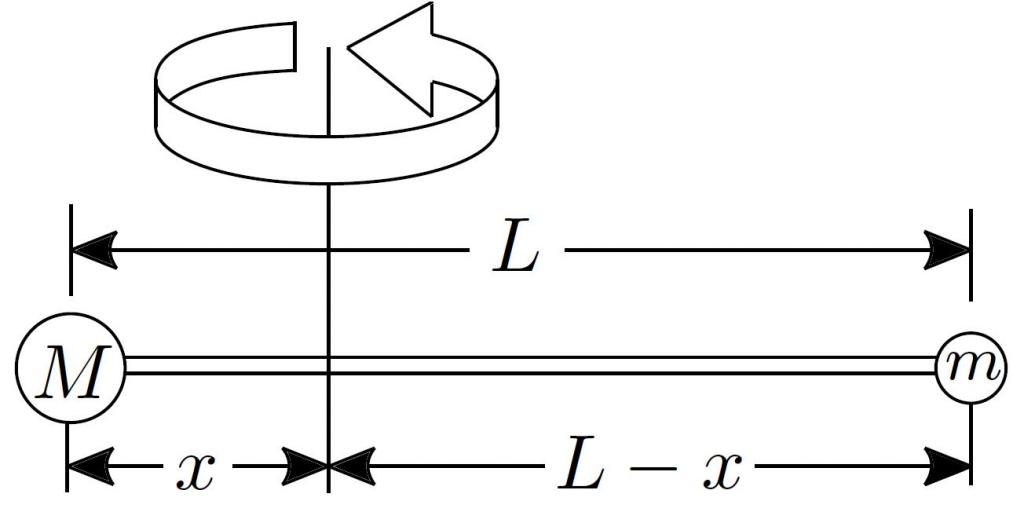
Задача на вращение Земли вокруг Солнца
Решим одну интересную задачу: используя приведенные выше формулы, необходимо рассчитать момент вращения нашей планеты по своей орбите.

Поскольку притяжением остальных планет можно пренебречь, а также учитывая, что момент гравитационной силы, действующей со стороны Солнца на Землю, равен нулю (плечо r=0), то L=const. Для вычисления L воспользуемся следующими выражениями:
L = I*ω; I = m*r2; ω = 2*pi/T.
Здесь мы приняли, что Землю можно считать материальной точкой с массой m=5,972*1024 кг, поскольку ее размеры намного меньше расстояния до Солнца r=149,6 млн км. T = 365,256 дня — период обращения планеты вокруг своей звезды (1 год). Подставляя все данные в выражение выше, получаем :
L = I*ω = 5,972*1024*(149,6*109)2*2*3,14/(365,256*24*3600) = 2,66*1040 кг*м2/с.
Рассчитанное значение момента импульса является гигантским, что обусловлено большой массой планеты, высокой скоростью ее вращения по орбите и огромным астрономическим расстоянием.
Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.
Общие сведения о физической величине
Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.
Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:
Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы
I = m * r².
Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).
Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:
I = ∫m(r² * dm) = ρ * ∫V(r² * dV).
Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.
Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.
Величина I для тел разной формы
При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:
стержень: I = 1 / 12 * M * L²;
цилиндр: I = 1 / 2 * M * R²;
сфера: I = 2 / 5 * M * R².
Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.
Теорема Штейнера и формула
Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:
I = IO + M * h3.
Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r0 + h.
Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:
I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.
Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.
Уравнение моментов
В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:
M = I * α.
Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:
M = F * d.
Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.
Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.
Пример решения задачи
Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.
Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:
I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².
Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:
M = F * d = 10 * 0,3 = 3 Н*м.
Теперь можно определить ускорение:
α = M/I = 3/0,09125 ≈ 32,9 рад/с².
Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.
Источник
При решении задач на динамику твердого тела, как правило, необходимо применять основное уравнение динамики вращательного движения. Часто в подобных задачах твердое тело приводится в движение силами натяжения нитей, к которым подвешены грузы, поэтому необходимо также записывать уравнения движения (второй закон Ньютона) для грузов. Условие, связывающее два типа движения, как правило, заключается в отсутствии проскальзывания нити, что позволяет получить кинематическую связь между линейным ускорением груза и угловым ускорением твердого тела. Рассмотрим конкретные примеры.
 |
Задача 1. Два тела, массы которых 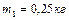 и
и 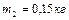 , связаны нитью, переброшенной через блок. Блок массой
, связаны нитью, переброшенной через блок. Блок массой 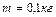 укреплен на краю горизонтального стола, по поверхности которого скользит тело массой
укреплен на краю горизонтального стола, по поверхности которого скользит тело массой 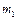 . Коэффициент трения тела
. Коэффициент трения тела 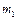 о поверхность стола
о поверхность стола 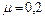 . С каким ускорением движутся тела и каковы силы натяжения нити по обе стороны от блока? Массу блока можно считать равномерно распределенной по ободу, трением в подшипниках оси блока пренебречь.
. С каким ускорением движутся тела и каковы силы натяжения нити по обе стороны от блока? Массу блока можно считать равномерно распределенной по ободу, трением в подшипниках оси блока пренебречь.
Решение
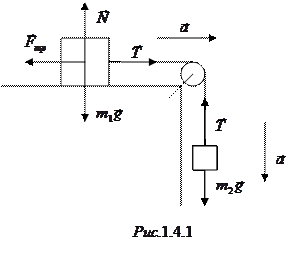
Применим для грузов второй закон Ньютона, а для блока – основное уравнение динамики вращательного движения. Силы, действующие на грузы, показаны на рис.1.4.1.
Для груза 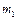 второй закон Ньютона в проекциях на горизонтальное и вертикальное направления принимает вид
второй закон Ньютона в проекциях на горизонтальное и вертикальное направления принимает вид
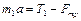 ,
, 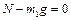 , (1.4.1)
, (1.4.1)
а по определению сила трения скольжения
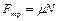 .
.
Для груза 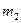 уравнение вертикального движения
уравнение вертикального движения
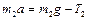 . (1.4.2)
. (1.4.2)
Наконец, уравнение вращательного движения блока
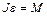 , (1.4.3)
, (1.4.3)
где 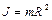 — момент инерции блока (обруча),
— момент инерции блока (обруча), 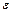 — угловое ускорение блока,
— угловое ускорение блока, 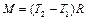 — результирующий момент сил натяжения, действующий на блок.
— результирующий момент сил натяжения, действующий на блок.
При отсутствии скольжения нити по блоку его угловое ускорение связано с линейным ускорением грузов по формуле 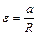 . С учетом приведенных соотношений уравнение (1.4.3) принимает вид
. С учетом приведенных соотношений уравнение (1.4.3) принимает вид
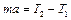 . (1.4.4)
. (1.4.4)
Исключая из (1.4.1) силы трения и реакции опоры, получаем
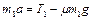 . (1.4.5)
. (1.4.5)
Наконец, складывая уравнения (1.4.2), (1.4.4), (1.4.5), получаем
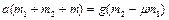 ,
,
откуда находим
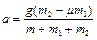 . (1.4.6)
. (1.4.6)
Подставляя числовые значения, получаем
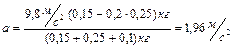 .
.
Подставляя (1.4.6) в (1.4.2) и (1.4.5), находим силы натяжения:
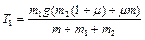 ,
,
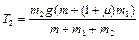 .
.
Вычисления приводят к результатам:
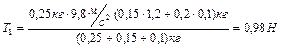 ,
, 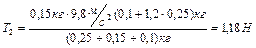 .
.
Задача 2. В однородном диске массой 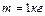 и радиусом
и радиусом 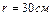 вырезано круглое отверстие диаметром
вырезано круглое отверстие диаметром 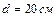 , центр которого находится на расстоянии
, центр которого находится на расстоянии 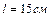 от оси диска. Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
от оси диска. Найти момент инерции полученного тела относительно оси, проходящей перпендикулярно плоскости диска через его центр.
Решение
Данное тело можно представить как совокупность сплошного диска, изготовленного из материала с некоторой плотностью, и другого диска из материала с такой же по величине, но противоположной по знаку плотностью, расположенного в отверстии первого диска. Тогда результирующий момент инерции этой системы можно найти, вычитая из момента инерции первого диска момент инерции второго диска.
Для первого диска
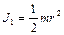 ,
,
а для второго по теореме Штейнера
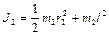 ,
,
где 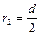 , а массу второго диска можно определить из условия пропорциональности массы и площади:
, а массу второго диска можно определить из условия пропорциональности массы и площади: 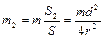 .
.
Тогда 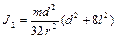 , следовательно,
, следовательно,
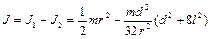 .
.
Выполняя вычисления, находим
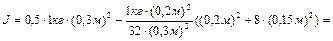 .
.
 |
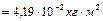 .
.Задача 3. Однородный тонкий стержень массой 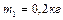 и
и
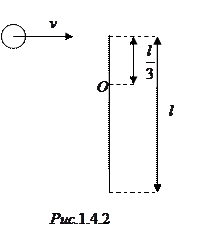
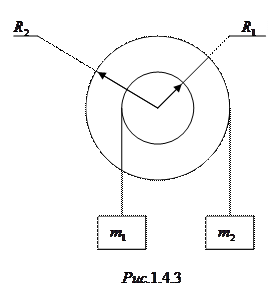
длиной 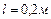 может свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис.1.4.2). В верхний конец стержня попадает пластилиновый шарик массой
может свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис.1.4.2). В верхний конец стержня попадает пластилиновый шарик массой 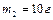 , движущийся со скоростью
, движущийся со скоростью 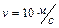 , и прилипает к стержню. Определить угловую скорость стержня и линейную скорость нижнего конца стержня сразу после удара, если расстояние от верхнего конца стержня до точки О равно
, и прилипает к стержню. Определить угловую скорость стержня и линейную скорость нижнего конца стержня сразу после удара, если расстояние от верхнего конца стержня до точки О равно 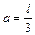 .
.
Решение
Для определения угловой скорости вращения стержня воспользуемся законом сохранения момента импульса. Рассматривая шарик как материальную точку, получаем:
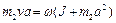 , (1.4.7)
, (1.4.7)
где момент инерции стержня относительно точки О по теореме Штейнера равен
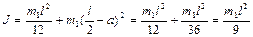 . (1.4.8)
. (1.4.8)
Из (1.4.7) и (1.4.8) находим угловую скорость стержня сразу после удара
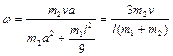 .
.
Вычисления дают
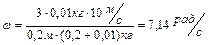 .
.
Для определения линейной скорости нижнего конца стержня воспользуемся связью линейной и угловой скорости: 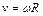 , где радиус окружности равен
, где радиус окружности равен 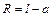 . Получаем
. Получаем
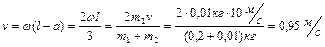 .
.
 |
Задача 4. На ступенчатый цилиндрический блок намотаны в противоположных направлениях две нити с подвешенными к ним грузами массами
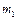 и
и 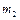 (рис.1.4.3). Найти ускорения грузов и силы натяжения нитей. Момент инерции блока
(рис.1.4.3). Найти ускорения грузов и силы натяжения нитей. Момент инерции блока 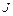 , радиусы соответствующих участков блока
, радиусы соответствующих участков блока 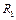 и
и 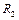 .
.Решение
Запишем второй закон Ньютона для грузов в проекции на вертикальное направление
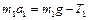 ,
, 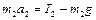 , (1.4.9)
, (1.4.9)
где 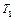 и
и 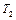 — силы натяжения нитей.
— силы натяжения нитей.
Уравнение вращательного движения блока
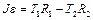 . (1.4.10)
. (1.4.10)
В силу отсутствия проскальзывания нитей по блоку можно записать
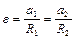 . (1.4.11)
. (1.4.11)
Из (1.4.9) – (1.4.11) следует
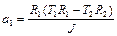 ,
, 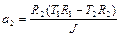 . (1.4.12)
. (1.4.12)
Подставляя в уравнения движения грузов, получаем систему уравнений для определения сил натяжения нитей
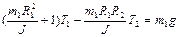 ,
,
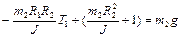 . (1.4.13)
. (1.4.13)
Решая систему (1.4.13), находим
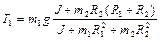 ,
, 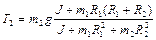 .
.
Подстановка полученных результатов в (1.4.12) дает
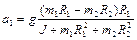 ,
, 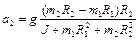 .
.
Задача 5. Два диска с моментами инерции 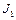 и
и 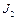 вращаются с угловыми скоростями
вращаются с угловыми скоростями 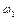 и
и 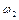 вокруг одной и той же оси без трения. Диски пришли в соприкосновение друг с другом. Из-за возникшего между дисками трения через некоторое время проскальзывание одного диска по другому прекращается. Какова станет тогда угловая скорость вращения дисков? Какое количество теплоты выделится?
вокруг одной и той же оси без трения. Диски пришли в соприкосновение друг с другом. Из-за возникшего между дисками трения через некоторое время проскальзывание одного диска по другому прекращается. Какова станет тогда угловая скорость вращения дисков? Какое количество теплоты выделится?
Решение
Применим закон сохранения момента импульса. Получаем
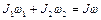 ,
,
где 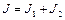 — момент инерции системы,
— момент инерции системы, 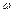 — угловая скорость системы после прекращения проскальзывания. В результате находим
— угловая скорость системы после прекращения проскальзывания. В результате находим
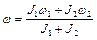 .
.
Для определения количества теплоты, выделившегося в результате взаимодействия дисков, воспользуемся законом сохранения энергии, согласно которому
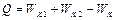 ,
,
где 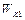 и
и 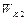 — кинетические энергии дисков до взаимодействия,
— кинетические энергии дисков до взаимодействия, 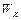 — кинетическая энергия системы после взаимодействия. Поскольку
— кинетическая энергия системы после взаимодействия. Поскольку
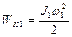 ,
, 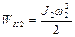 ,
, 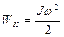 ,
,
получаем
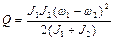 .
.
Задача 6. Тонкий обруч радиуса 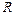 раскрутили вокруг его оси до угловой скорости
раскрутили вокруг его оси до угловой скорости 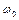 и положили плашмя на горизонтальный стол. Через какое время обруч остановится, если коэффициент трения между столом и обручем равен
и положили плашмя на горизонтальный стол. Через какое время обруч остановится, если коэффициент трения между столом и обручем равен 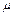 ? Сколько оборотов сделает обруч до полной остановки?
? Сколько оборотов сделает обруч до полной остановки?
Решение
Так как действующая на обруч сила трения постоянна, то вращение обруча будет равнозамедленным, и мы можем применить уравнения равнозамедленного вращения
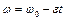 ,
, 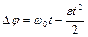 .
.
Если обруч сделает до остановки 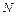 оборотов, то угол поворота составит
оборотов, то угол поворота составит 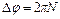 . В момент остановки обруча угловая скорость
. В момент остановки обруча угловая скорость 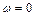 , следовательно,
, следовательно,
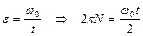 . (1.4.14)
. (1.4.14)
Воспользуемся законом сохранения энергии, согласно которому работа силы трения равна изменению кинетической энергии обруча
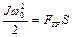 . (1.4.15)
. (1.4.15)
Здесь 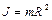 — момент инерции обруча,
— момент инерции обруча, 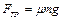 — сила трения и
— сила трения и 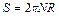 — путь, пройденный каждой точкой обруча до его остановки.
— путь, пройденный каждой точкой обруча до его остановки.
Решая систему уравнений (1.4.14), (1.4.15) с учетом выписанных соотношений для пути, силы трения и момента инерции, получаем
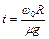 ,
, 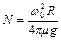 .
.
Примеры решения задач
Пример
1. Найти
момент инерции тонкого однородного
диска массой 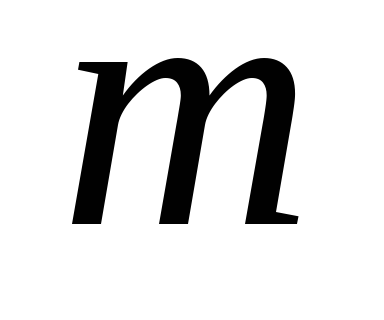 и радиуса
и радиуса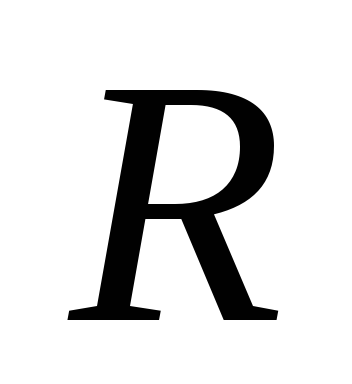 относительно: а) оси симметрии,
перпендикулярной к плоскости диска; б)
оси, совпадающей с диаметром диска.
относительно: а) оси симметрии,
перпендикулярной к плоскости диска; б)
оси, совпадающей с диаметром диска.
Р
е ш е н и е. а)Выберем
на диске цилиндрический слой радиуса 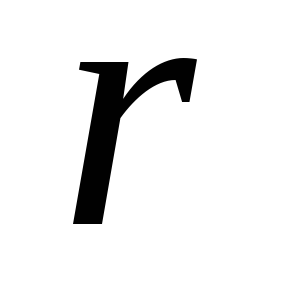 и шириной
и шириной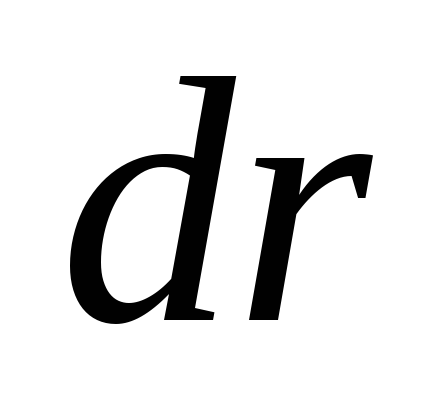 (см.
рис. 3а). Так как все элементы цилиндрического
слоя находятся на одном расстоянии
от центра кольца, его момент инерции
равен
(см.
рис. 3а). Так как все элементы цилиндрического
слоя находятся на одном расстоянии
от центра кольца, его момент инерции
равен
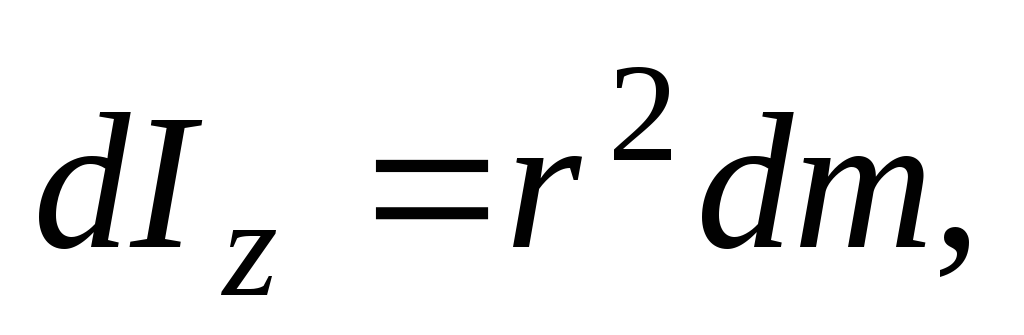 (14)
(14)
где 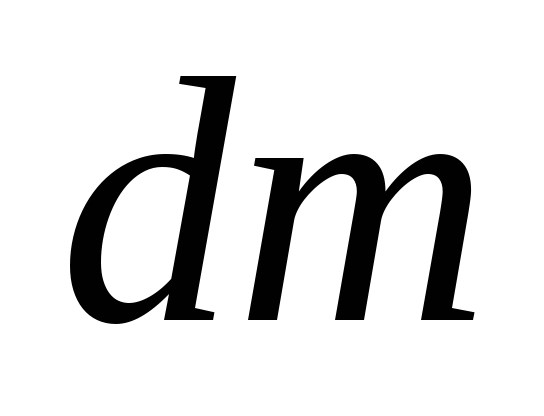 – масса кольца, которую можно найти,
определив поверхностную плотность
материала диска
– масса кольца, которую можно найти,
определив поверхностную плотность
материала диска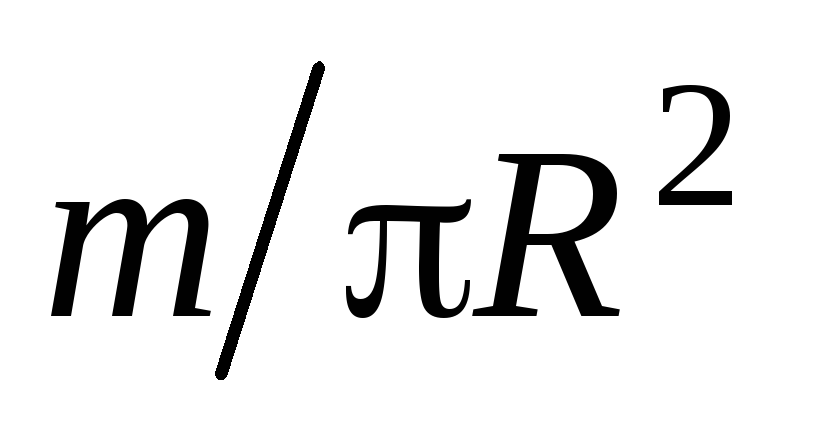 и умножив ее на площадь поверхности
кольца
и умножив ее на площадь поверхности
кольца т.е.
т.е.
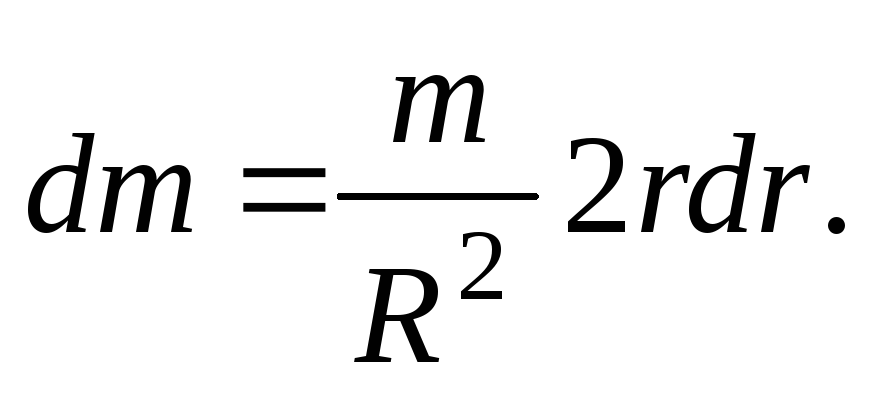
П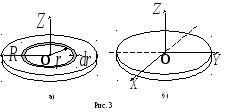 одставляя
это значение в (14) интегрируя по
одставляя
это значение в (14) интегрируя по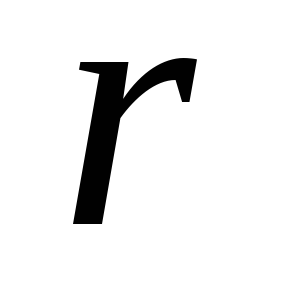 в пределах от 0 до
в пределах от 0 до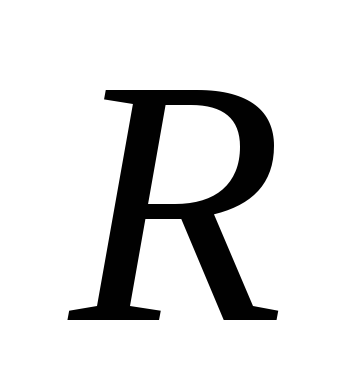 ,
найдем момент инерции диска относительно
оси симметрии
,
найдем момент инерции диска относительно
оси симметрии
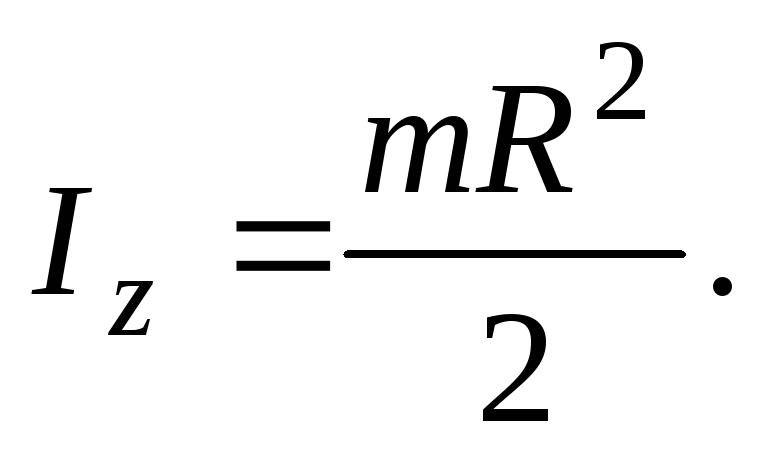 (15)
(15)
б)
Для нахождения момента инерции диска
относительно диаметра, например оси 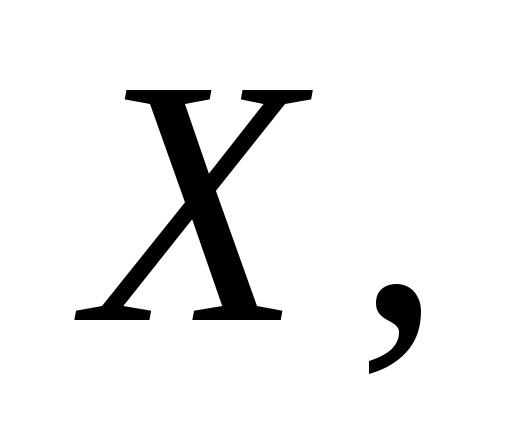 воспользуемся соотношением (6). Проведем
три взаимно перпендикулярные оси
воспользуемся соотношением (6). Проведем
три взаимно перпендикулярные оси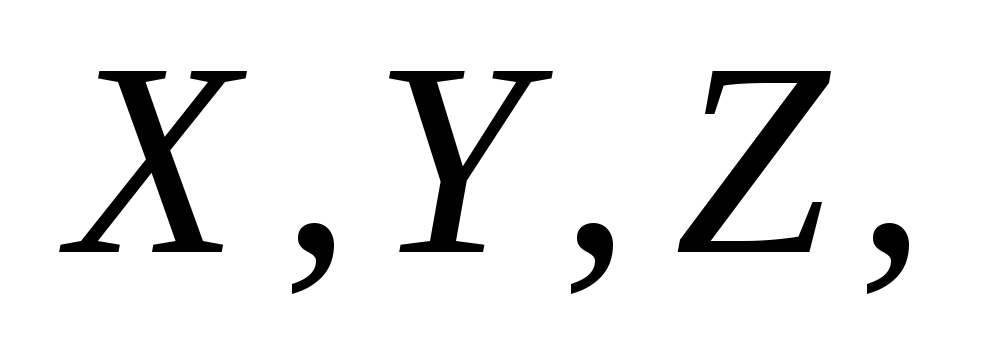 пересекающиеся в центре диска (рис. 3б).
Очевидно, что
пересекающиеся в центре диска (рис. 3б).
Очевидно, что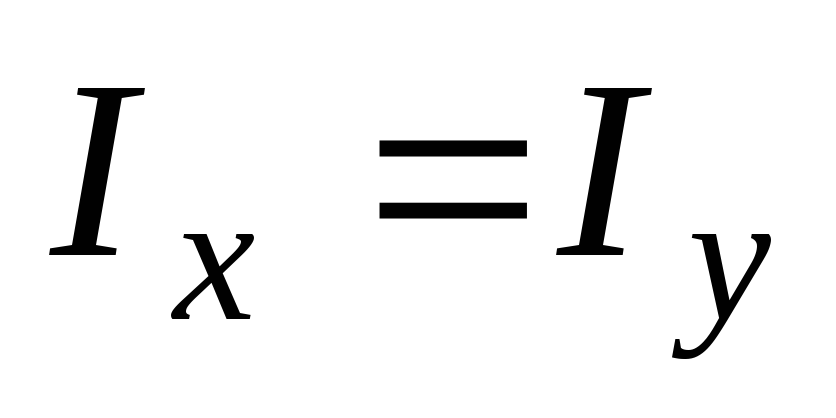 ,
тогда из уравнения (6) следует
,
тогда из уравнения (6) следует
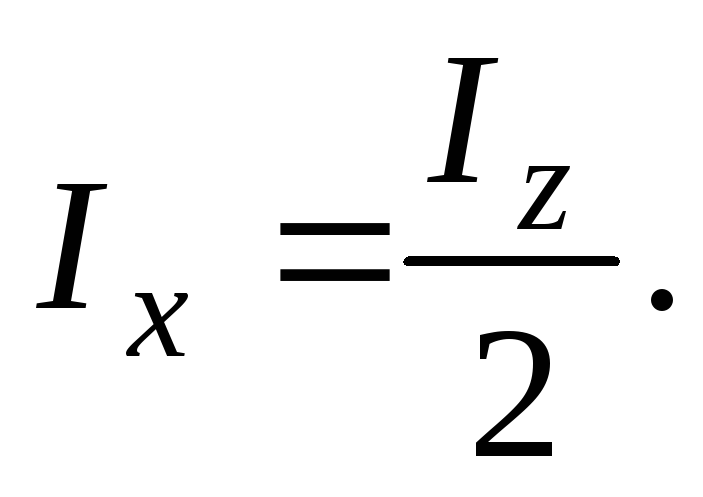
Подставляя
в это выражение значение 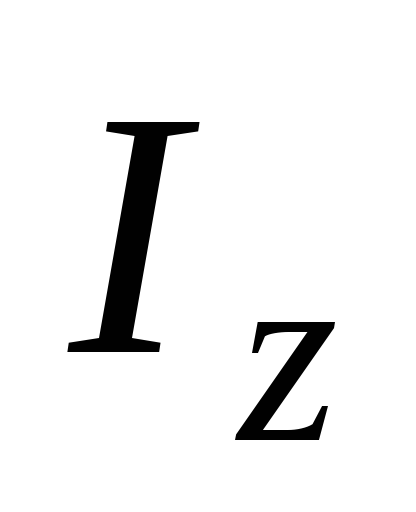 из уравнения (15), найдем момент инерции
диска относительно диаметра
из уравнения (15), найдем момент инерции
диска относительно диаметра
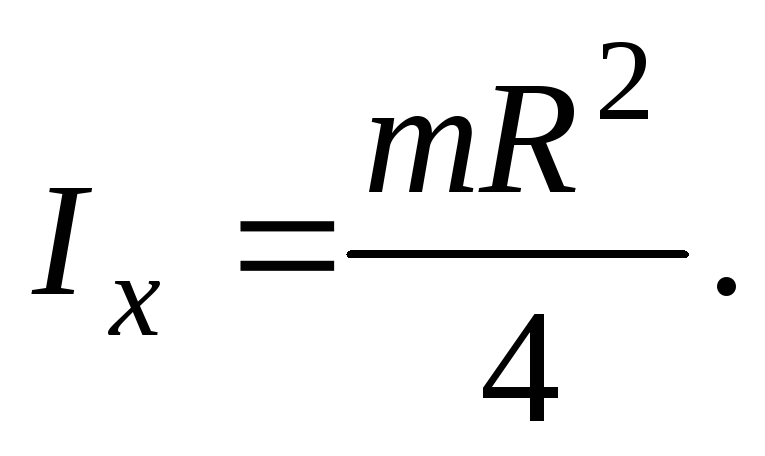
Пример
2. Найти
момент инерции однородного шара массы 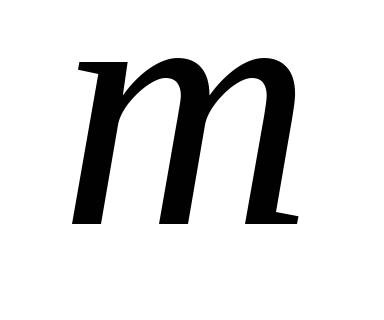 и радиуса
и радиуса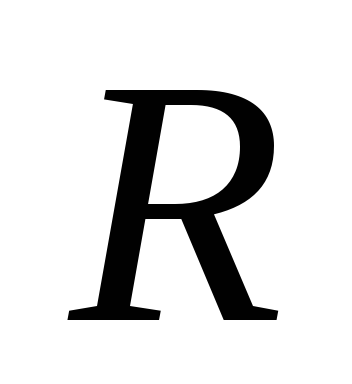 относительно оси, совпадающей с центром
шара.
относительно оси, совпадающей с центром
шара.
Р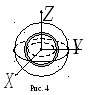 е ш е н и е. Вычисление момента инерции
шара прямым методом, т.е. с использованием
уравнения (1) довольно трудоемкая
математическая задача, поэтому для
нахождения этого момента инерции
воспользуемся соотношением (5). Проведем
три взаимно перпендикулярные оси
е ш е н и е. Вычисление момента инерции
шара прямым методом, т.е. с использованием
уравнения (1) довольно трудоемкая
математическая задача, поэтому для
нахождения этого момента инерции
воспользуемся соотношением (5). Проведем
три взаимно перпендикулярные оси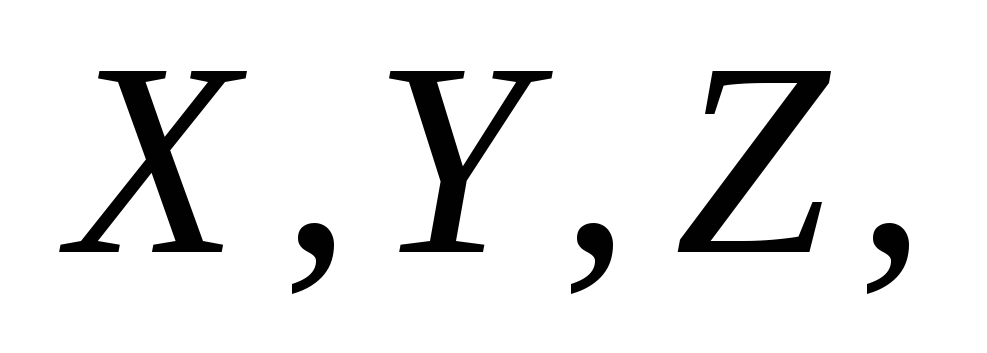 пересекающиеся в центре шара (см. рис.
4). Очевидно, что
пересекающиеся в центре шара (см. рис.
4). Очевидно, что
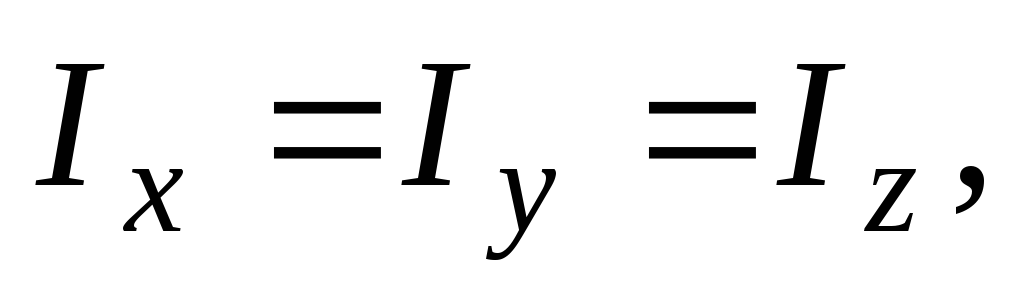
поэтому соотношение (5) перепишем в виде
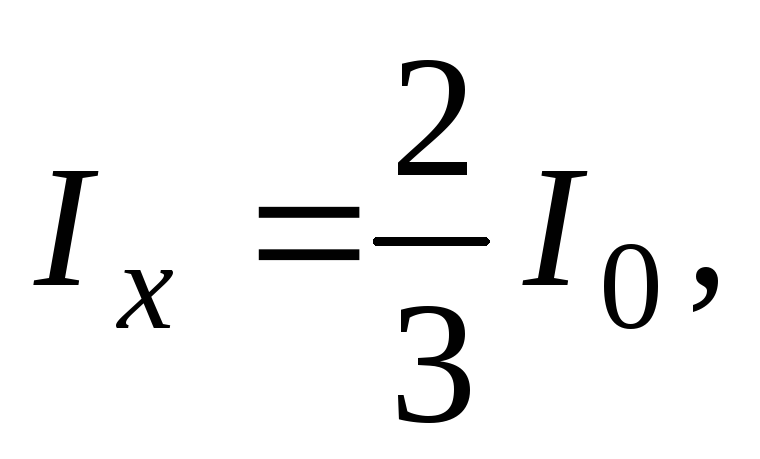 (16)
(16)
где 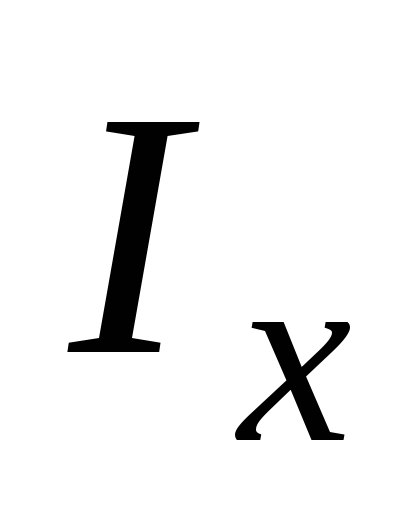 – искомый момент инерции,
– искомый момент инерции,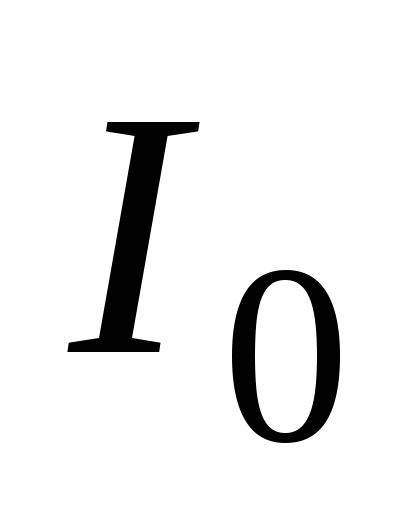 – момент инерции шара относительно
центра шара.
– момент инерции шара относительно
центра шара.
Для
нахождения момента инерции 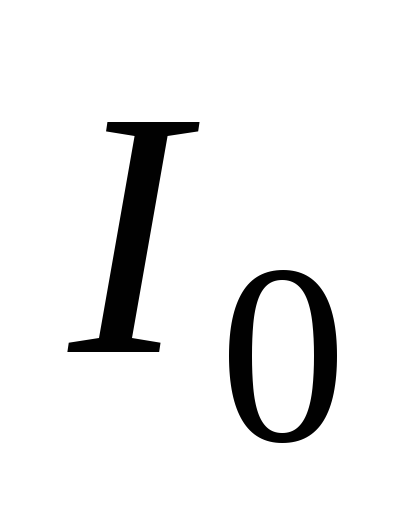 выберем тонкий сферический слой радиуса
выберем тонкий сферический слой радиуса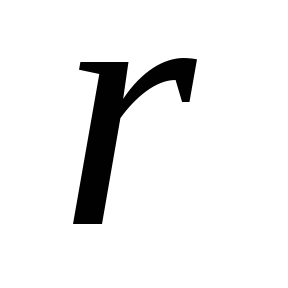 и толщиной
и толщиной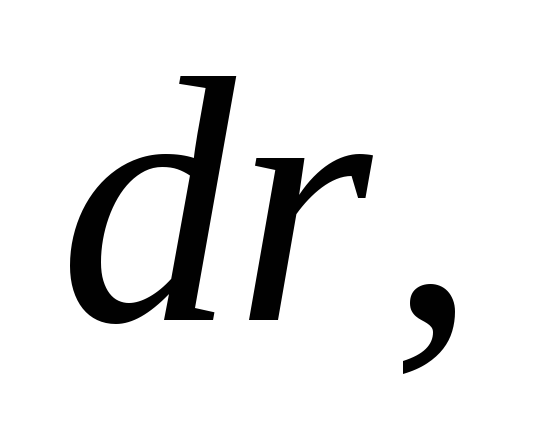 центр
которого совпадает с центром шара (на
рис. 4 он выделен цветом). Все элементы
этого слоя находятся на одинаковом
расстоянии от центра шара, поэтому его
момент инерции относительно центра
шара равен
центр
которого совпадает с центром шара (на
рис. 4 он выделен цветом). Все элементы
этого слоя находятся на одинаковом
расстоянии от центра шара, поэтому его
момент инерции относительно центра
шара равен
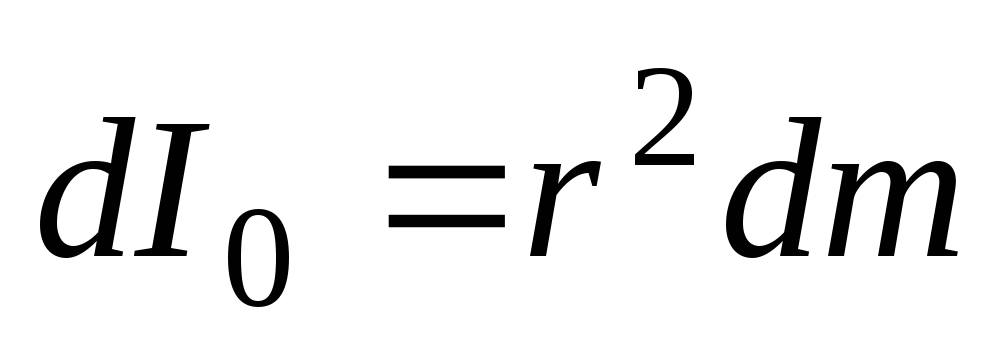 .
(17)
.
(17)
Объемная
плотность шара равна 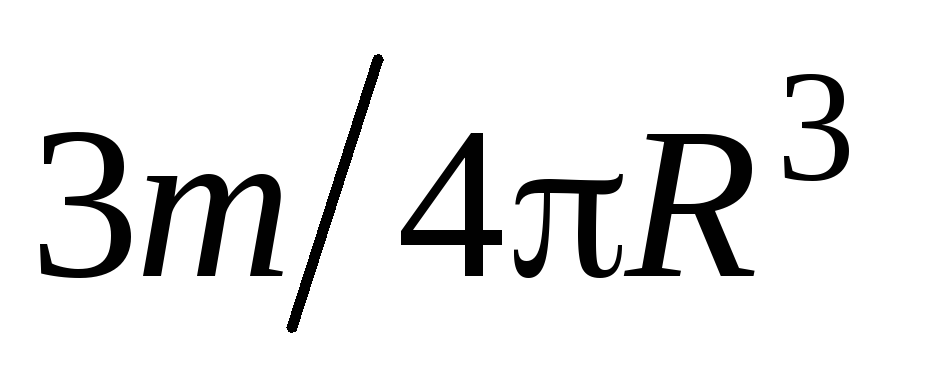 ,
умножая ее на объем тонкого сферического
слоя
,
умножая ее на объем тонкого сферического
слоя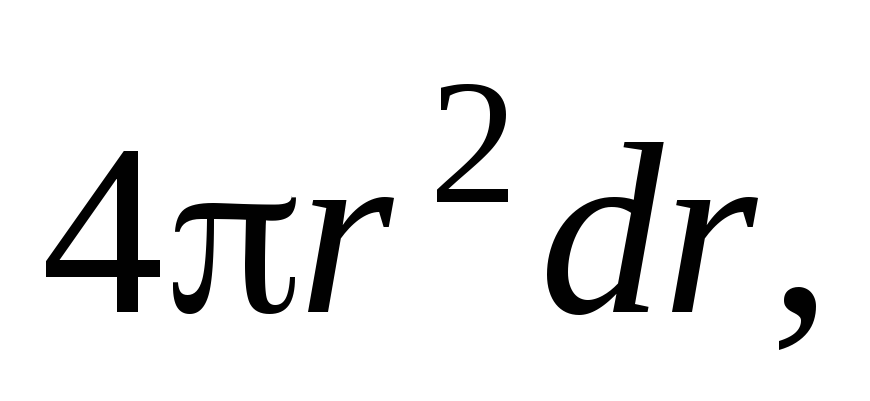 найдем массу сферического слоя
найдем массу сферического слоя
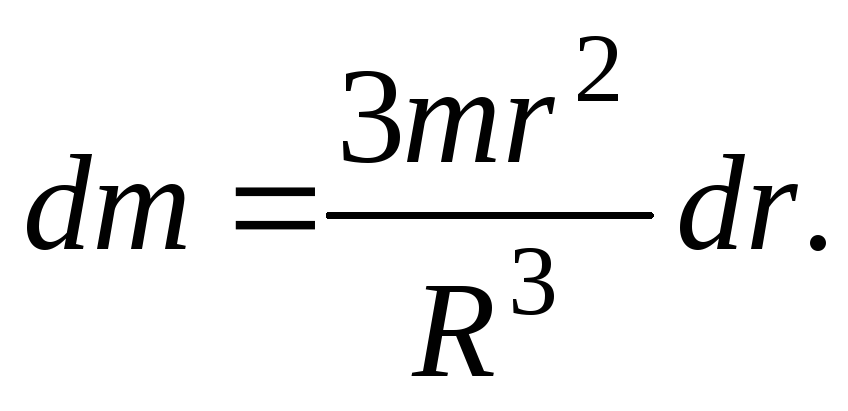
Подставляя
это выражение в (17) и интегрируя в пределах
от 0 до 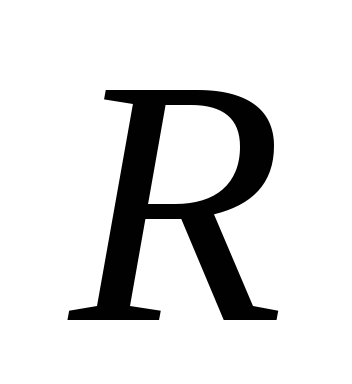 ,
найдем момент инерции шара относительно
центра
,
найдем момент инерции шара относительно
центра
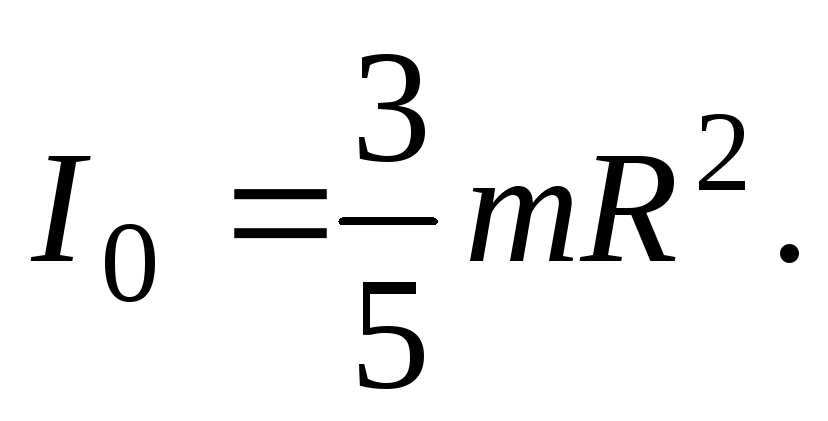
С учетом этого из уравнения (16) находим искомый момент инерции шара
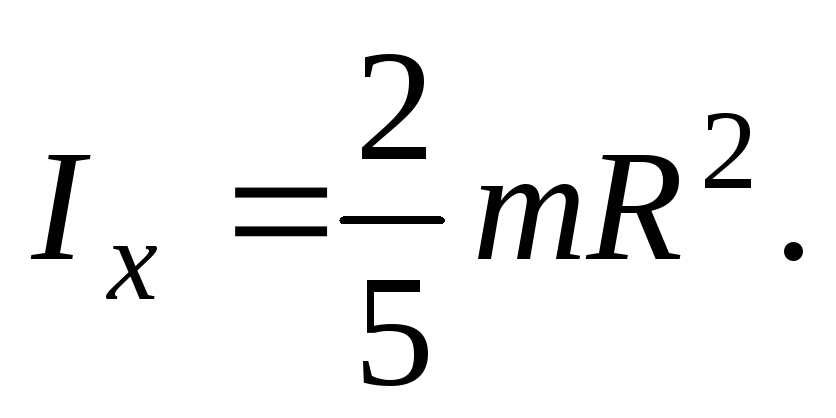
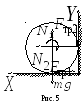 Пример
3. Однородный
цилиндр радиуса
Пример
3. Однородный
цилиндр радиуса 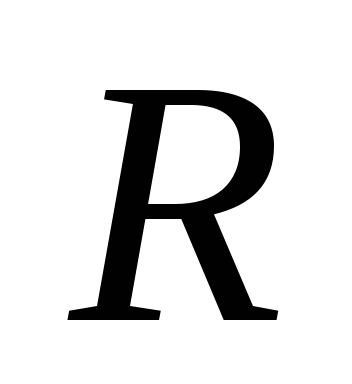 раскрутили вокруг его оси до угловой
скорости
раскрутили вокруг его оси до угловой
скорости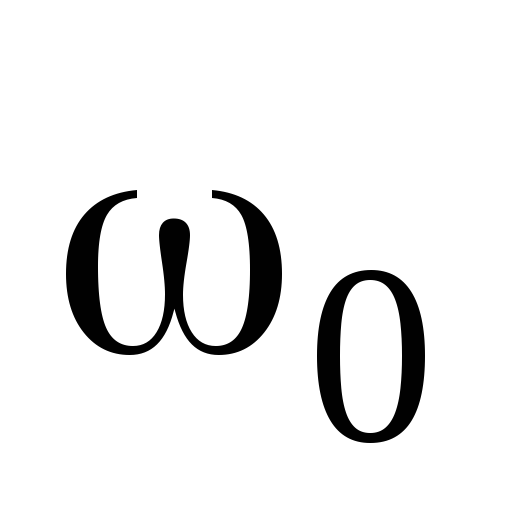 и поместили затем в угол (рис.5) Коэффициент
трения между стенками угла и цилиндром
равен
и поместили затем в угол (рис.5) Коэффициент
трения между стенками угла и цилиндром
равен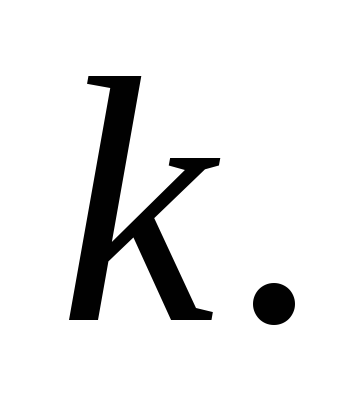 Сколько оборотов сделает цилиндр до
остановки?
Сколько оборотов сделает цилиндр до
остановки?
Р е ш е н и е. Расставим силы, действующие на цилиндр. Запишем уравнение, описывающее выражение цилиндра относительно его оси
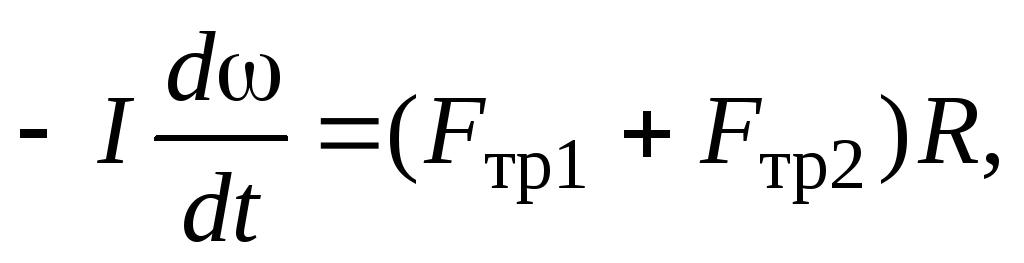 (18)
(18)
где 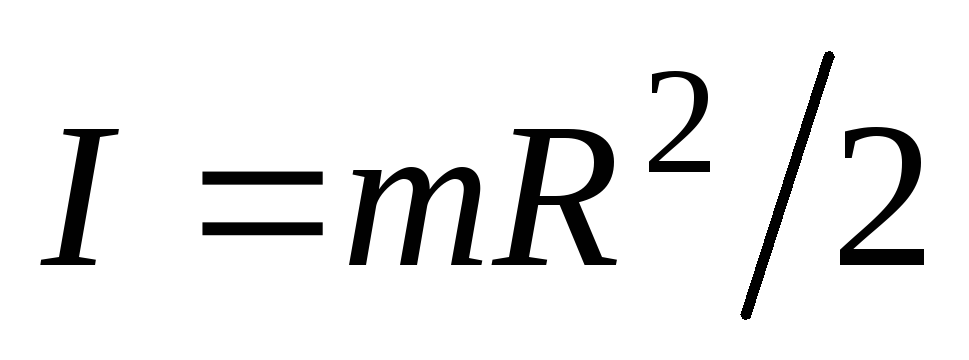 – момент инерции цилиндра относительно
этой оси. Знак “–” в левой части этого
уравнения обусловлен тем, что при
замедленном движении модуль углового
ускорения
– момент инерции цилиндра относительно
этой оси. Знак “–” в левой части этого
уравнения обусловлен тем, что при
замедленном движении модуль углового
ускорения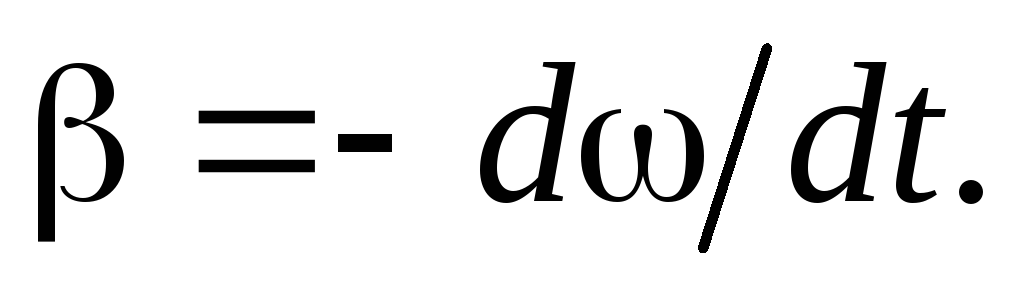 Так как нам необходимо найти число
оборотов, которое сделает цилиндр до
остановки, исключим из уравнения (18)
время. Для этого умножим и разделим
левую часть уравнения (18) на
Так как нам необходимо найти число
оборотов, которое сделает цилиндр до
остановки, исключим из уравнения (18)
время. Для этого умножим и разделим
левую часть уравнения (18) на
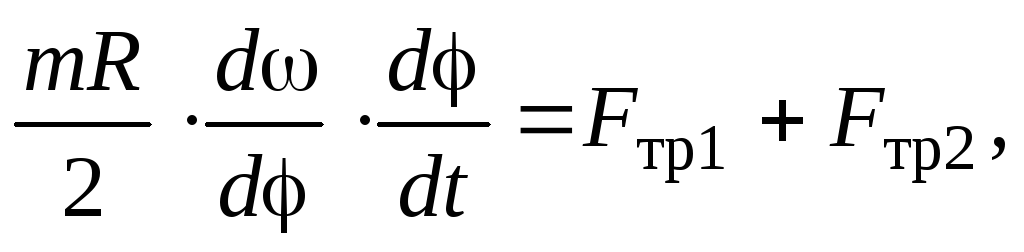
где 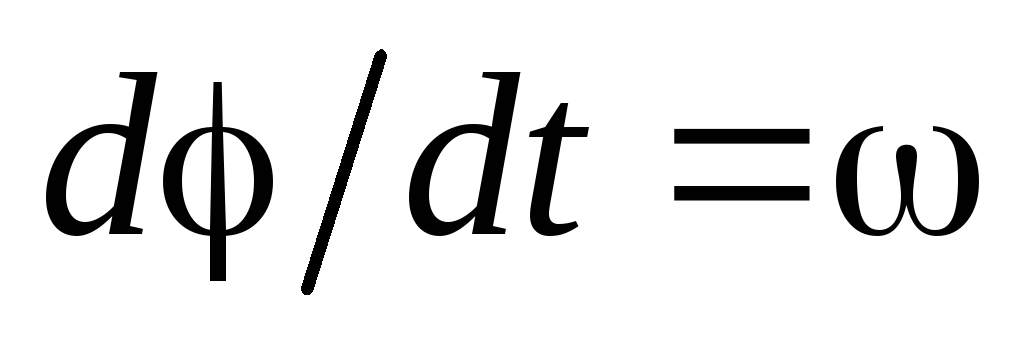 – угловая скорость вращения цилиндра
в некоторый момент времени. После
преобразований получим
– угловая скорость вращения цилиндра
в некоторый момент времени. После
преобразований получим
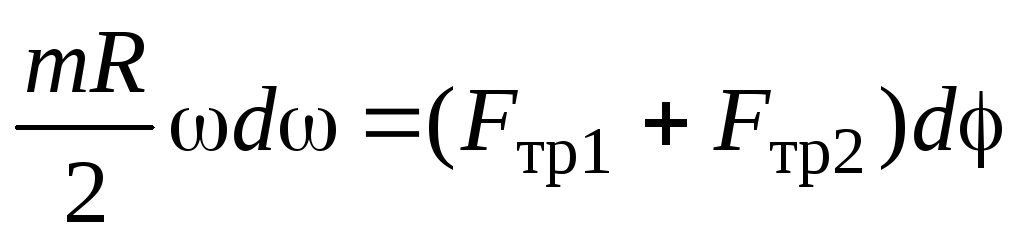 .
(19)
.
(19)
Прежде чем решать это уравнение, найдем выражения для сил трения. Так как центр цилиндра покоится,
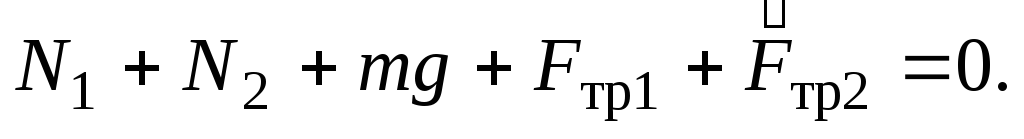
Запишем
это уравнение в проекциях на оси 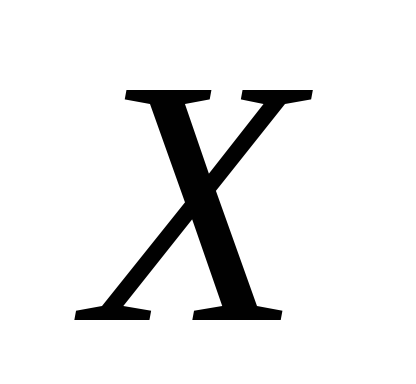 и
и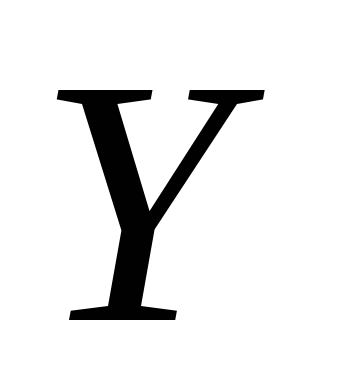 (см. рис. 5)
(см. рис. 5)
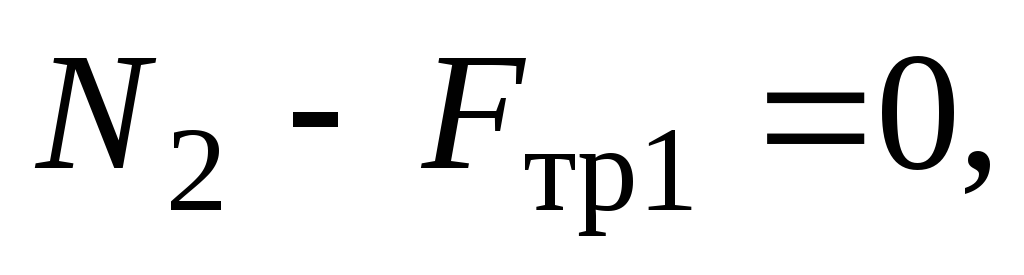
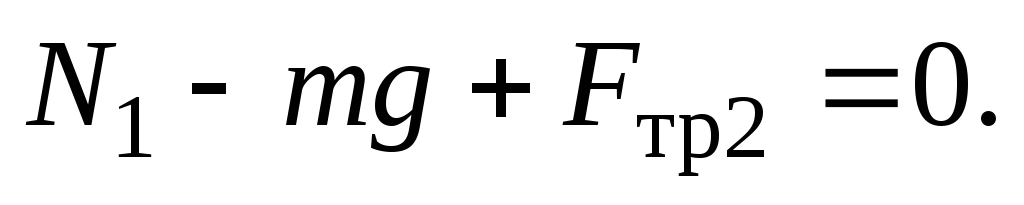
Решая
эту систему уравнений, учитывая, что 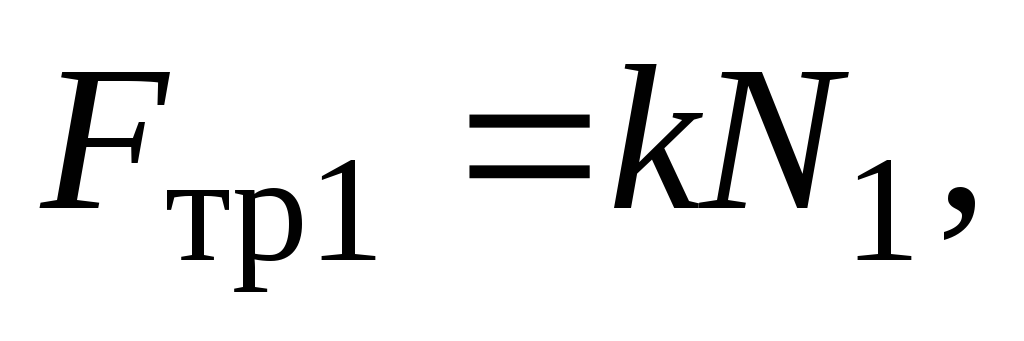 а
а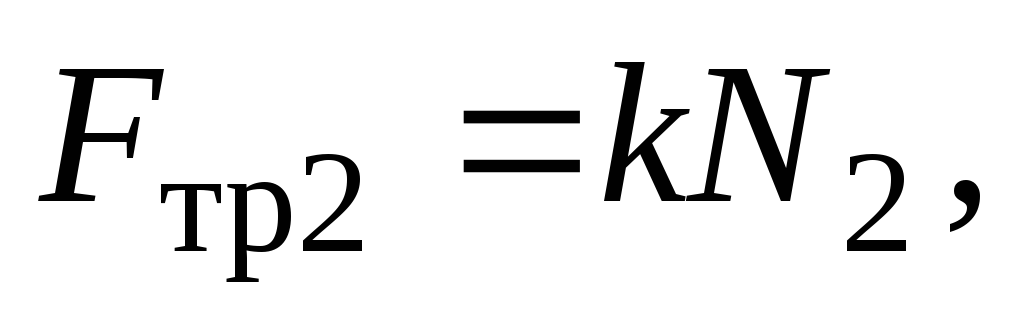 получим
выражения для сил трения
получим
выражения для сил трения
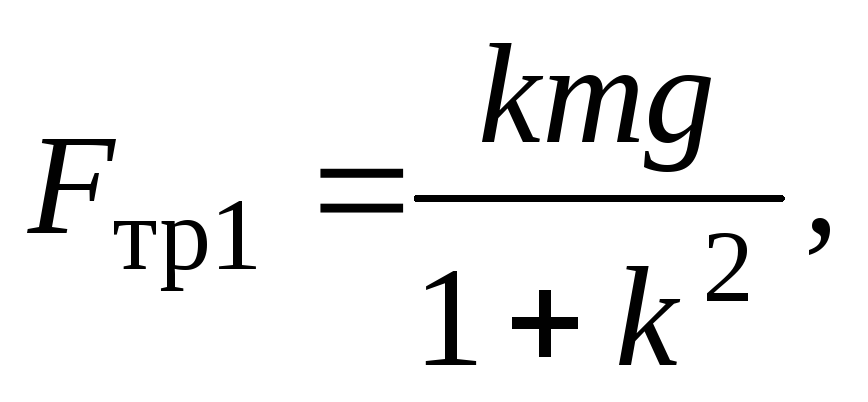
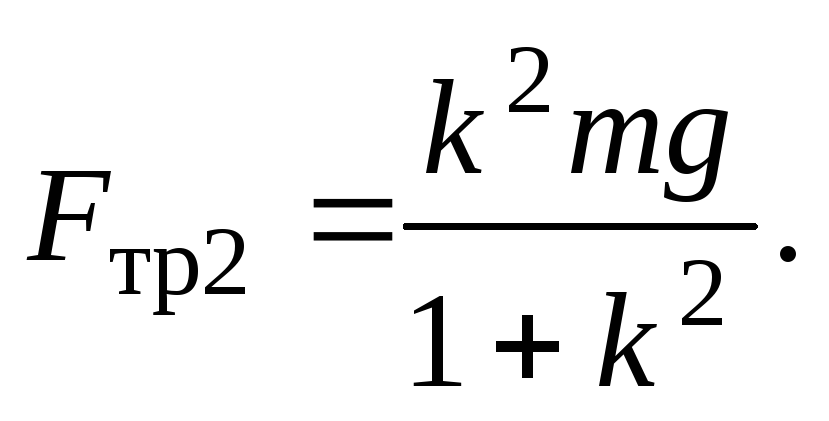
Подставляя эти
выражения в уравнение (19) и интегрируя
левую часть этого уравнения в пределах
от 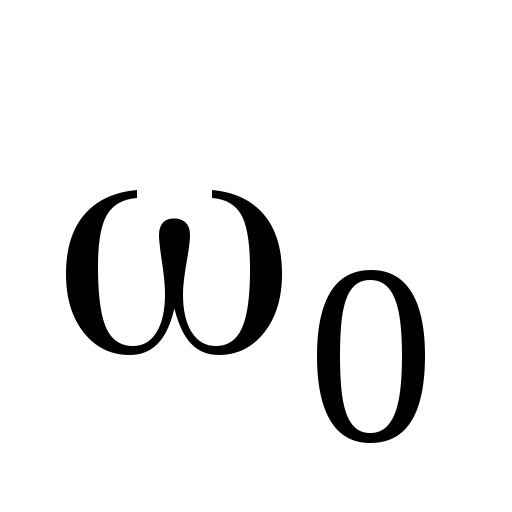 до 0, а правую часть в пределах от 0 до
до 0, а правую часть в пределах от 0 до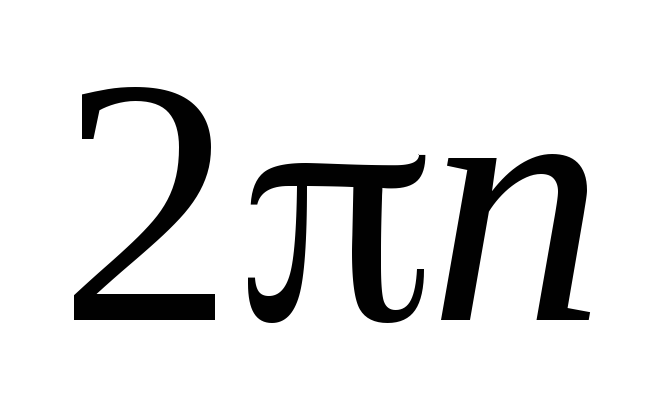 ,
найдем число оборотов
,
найдем число оборотов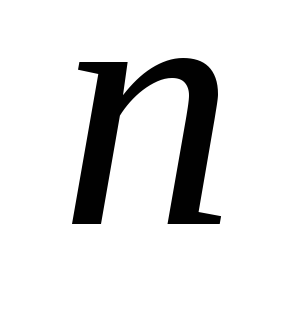 ,
которое сделает цилиндр до остановки
,
которое сделает цилиндр до остановки
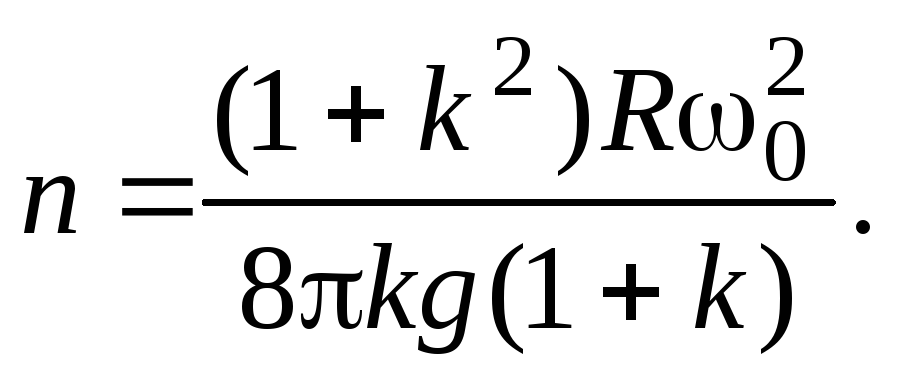
Пример
4. Однородный
шар скатывается без скольжения по
наклонной плоскости, составляющей угол  с горизонтом. Найти ускорение
с горизонтом. Найти ускорение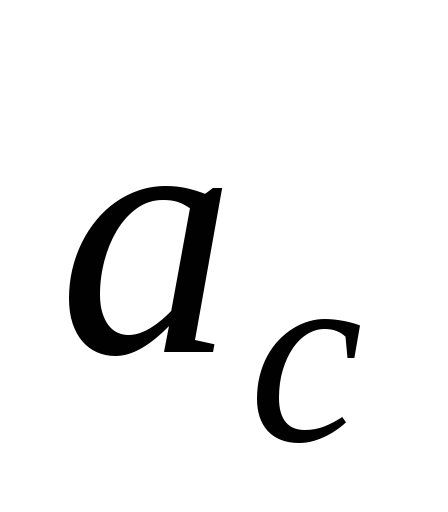 центра шара и кинетическую энергию шара
через время
центра шара и кинетическую энергию шара
через время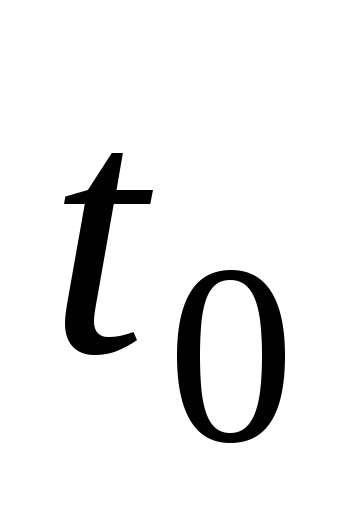 после начала движения.
после начала движения.
Р е ш е н и е. Решим задачу двумя способами.
а) Шар совершает
плоское движение. Свяжем подвижную
систему отсчета с центром шара. Эта
система движется поступательно
относительно наклонной плоскости, а
шар в этой системе вращается вокруг
оси, проходящей через его центр. Расставим
силы, действующие на шар в
процессе движения (см. рис.6). Запишем
теорему о движении центра масс в проекции
на ось 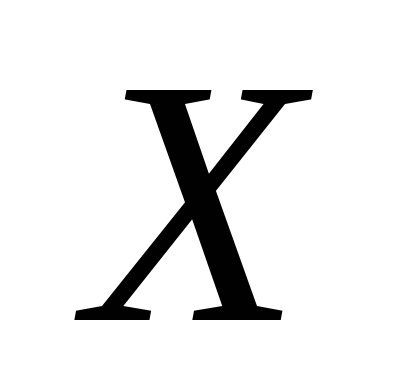 (см.
рис.6)
(см.
рис.6)
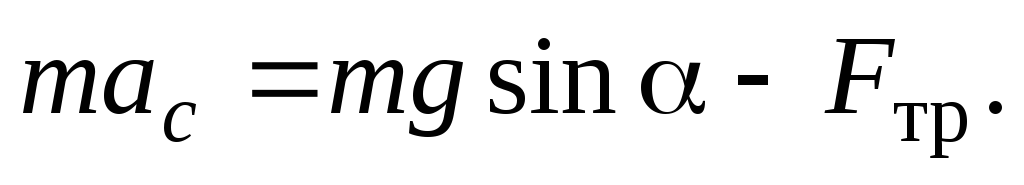 (20)
(20)
У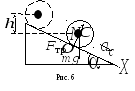 равнение
вращательного движения шара вокруг
оси, проходящей через центр масс имеет
вид
равнение
вращательного движения шара вокруг
оси, проходящей через центр масс имеет
вид
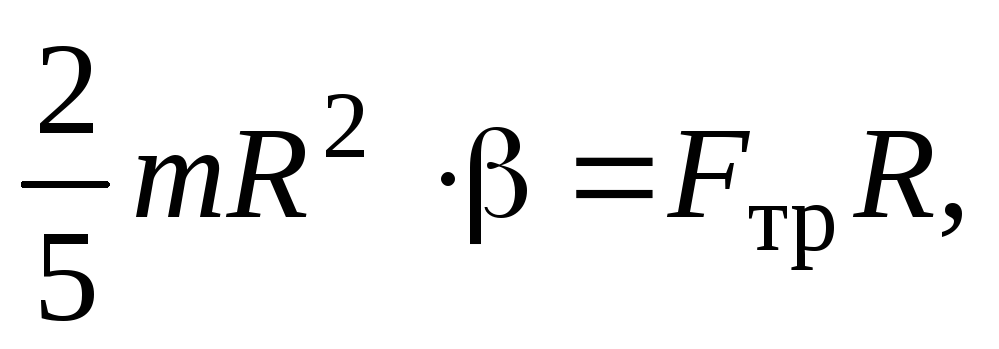 (21)
(21)
где 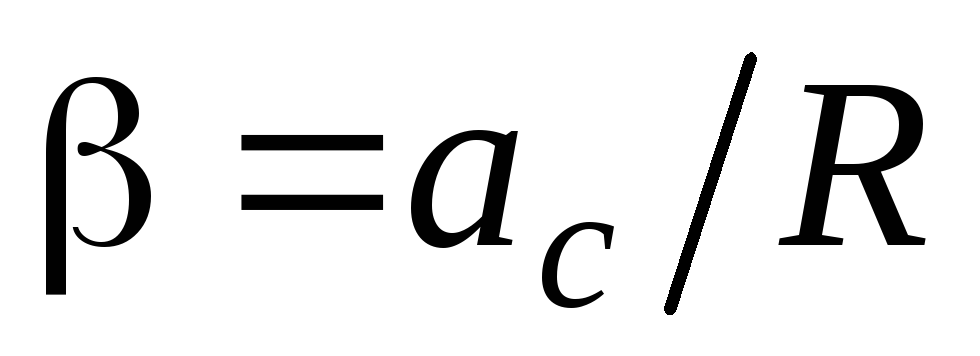 – угловое ускорение шара,
– угловое ускорение шара,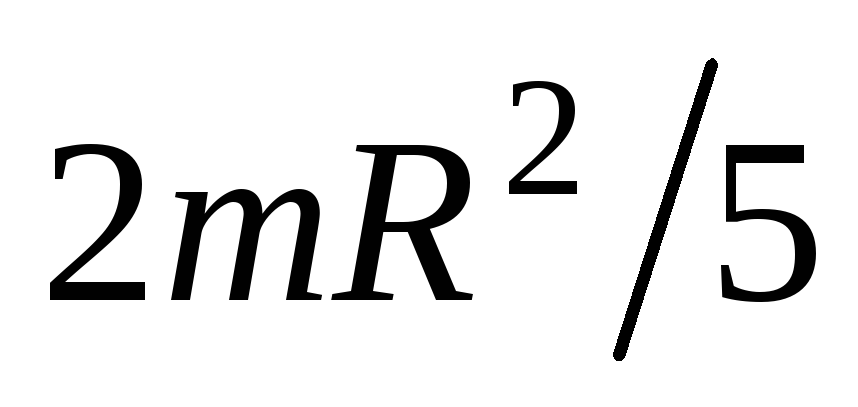 – момент инерции шара относительно оси
вращения. Решая совместно уравнения
(20) и (21), найдем ускорение центра шара
– момент инерции шара относительно оси
вращения. Решая совместно уравнения
(20) и (21), найдем ускорение центра шара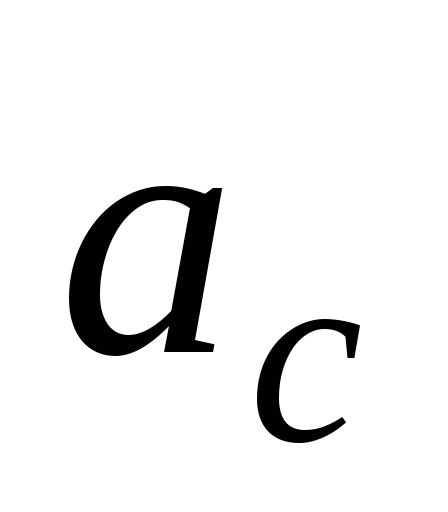 и его угловое ускорение
и его угловое ускорение
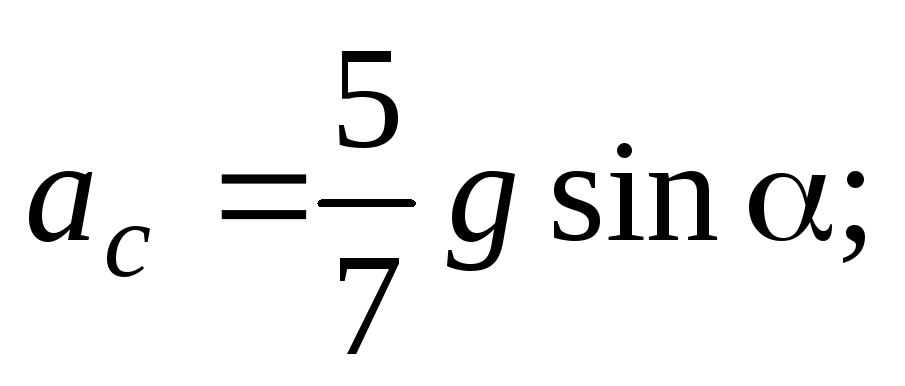
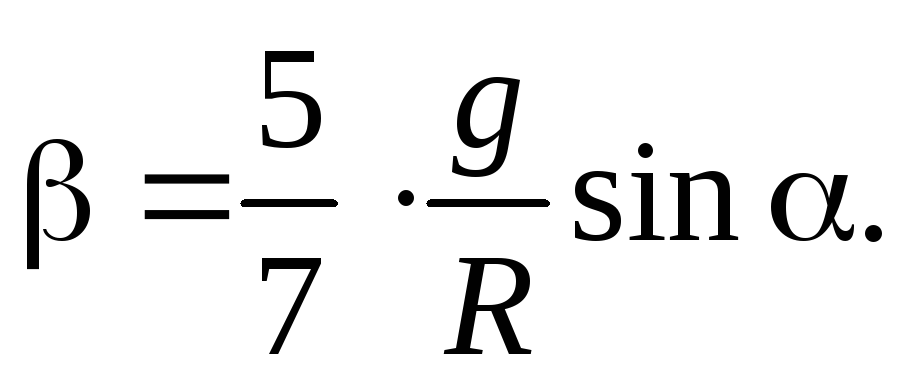 (22)
(22)
Используя формулу
(13) для кинетической энергии тела,
совершающего плоское движение, и
учитывая, что в интересующий нас момент
времени 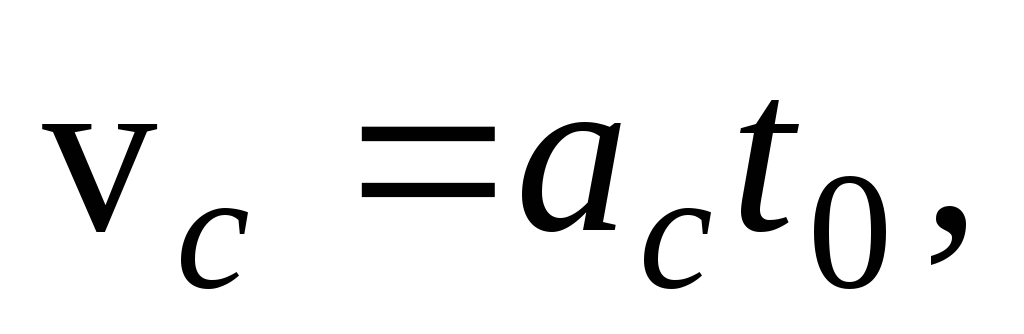 и
и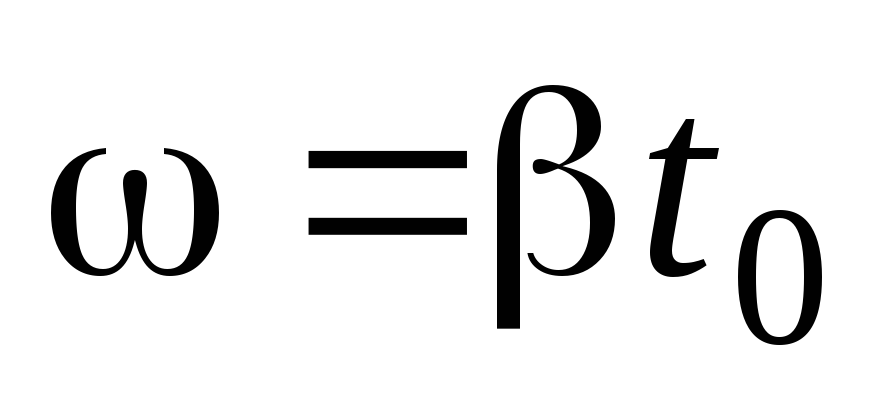 (т.к.
(т.к.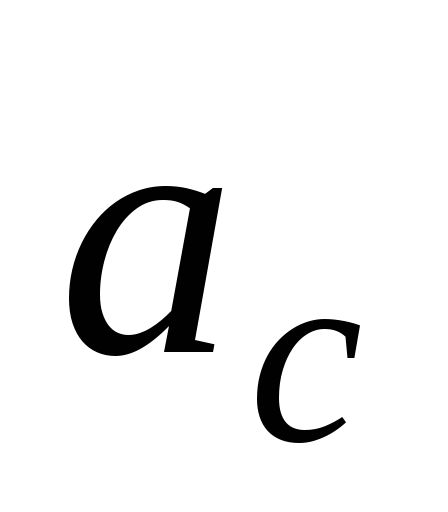 и
и постоянные), найдем кинетическую энергию
шара через время
постоянные), найдем кинетическую энергию
шара через время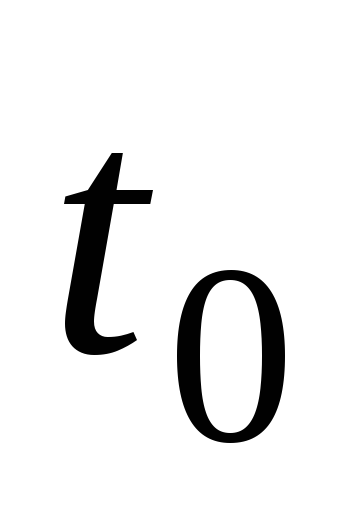 после начала движения
после начала движения
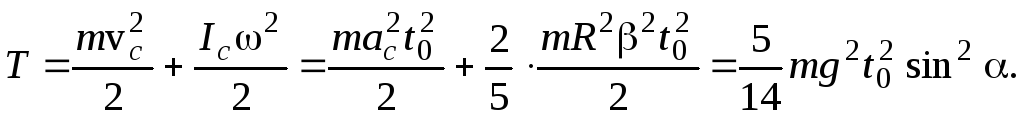
б) Так как шар
катится без проскальзывания, точка
соприкосновения шара 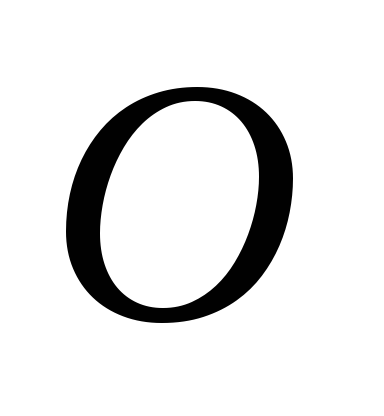 с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точку
с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точку является мгновенной осью вращения.
Относительно этой оси шар совершает
вращательное движение, поэтому для
описания движения достаточно записать
уравнение (12) в виде
является мгновенной осью вращения.
Относительно этой оси шар совершает
вращательное движение, поэтому для
описания движения достаточно записать
уравнение (12) в виде
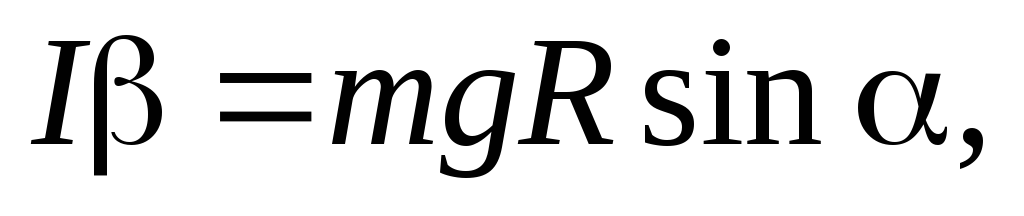 (23)
(23)
где 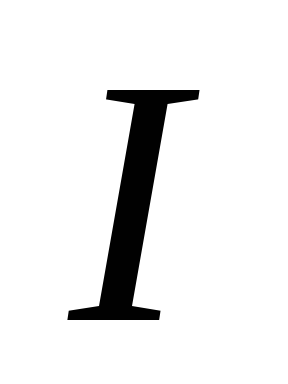 – момент инерции шара относительно
мгновенной оси вращения. Согласно
теореме Штейнера момент инерции
– момент инерции шара относительно
мгновенной оси вращения. Согласно
теореме Штейнера момент инерции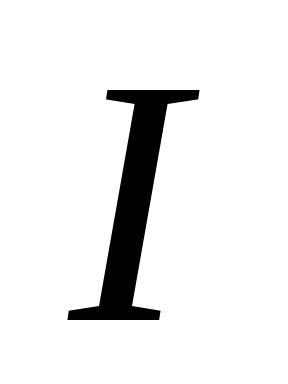 равен
равен
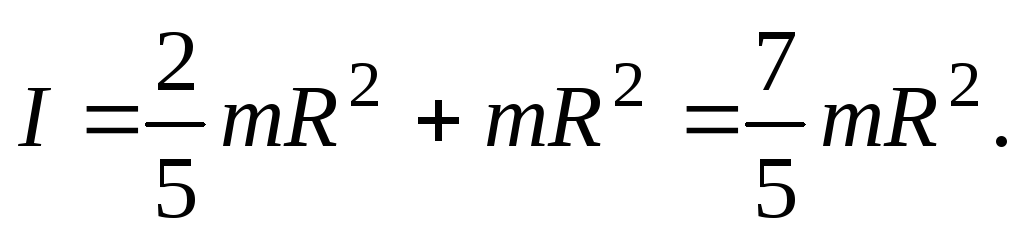
Подставляя это
выражение в уравнение (23), находим
ускорение центра шара 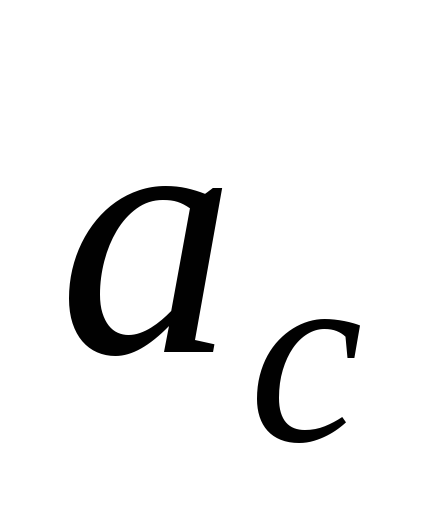 и его угловое ускорение
и его угловое ускорение (см. уравнения (22)).
(см. уравнения (22)).
Кинетическая энергия шара, в этом случае, определяется только вращательным движением
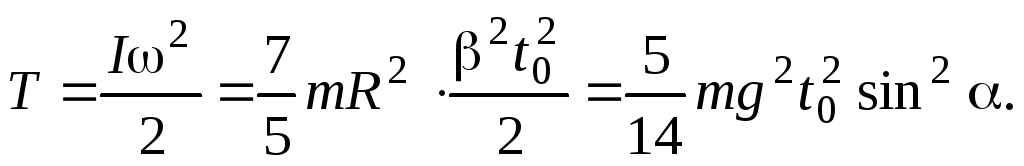
Заметим, что при
любом способе решения, кинетическую
энергию шара можно найти из закона
сохранения энергии (сила трения работы
не совершает, т.к. эта сила – сила трения
покоя). Пусть за время 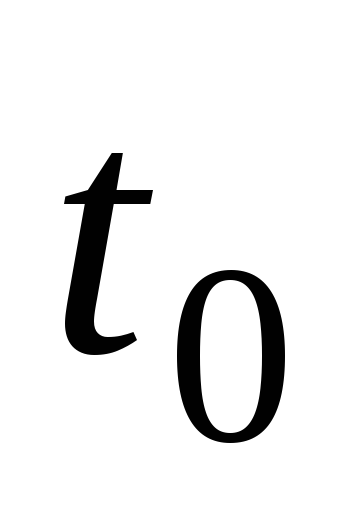 высота центра шара изменилась на
высота центра шара изменилась на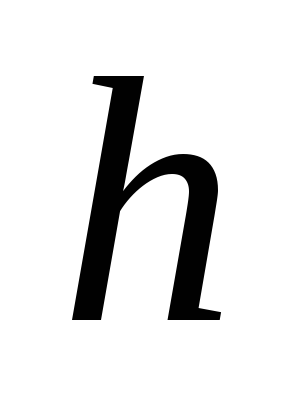 (см. рис.6), тогда
(см. рис.6), тогда
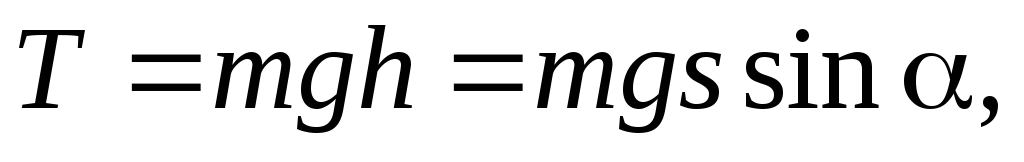 (24)
(24)
где 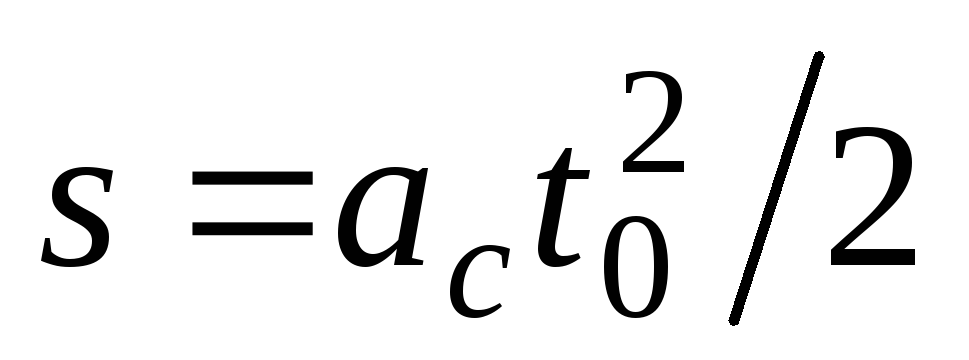 – расстояние, пройденное центром шара
за время
– расстояние, пройденное центром шара
за время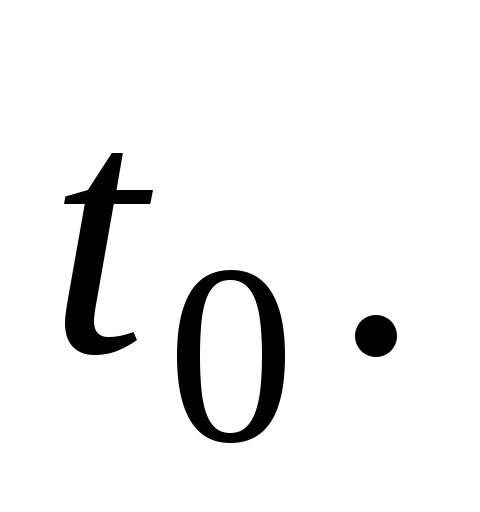 Подставляя
в (24) выражение для
Подставляя
в (24) выражение для и
и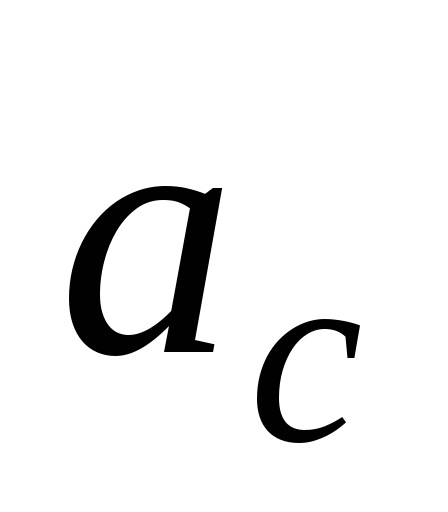 ,
находим кинетическую энергию шара
,
находим кинетическую энергию шара
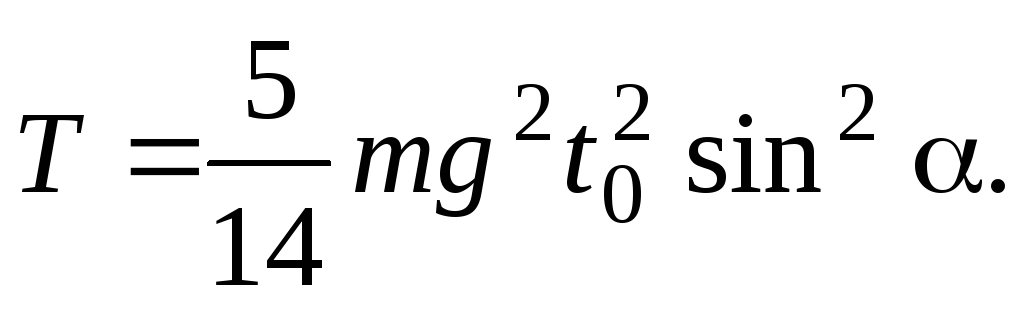
Пример
5. Однородный
стержень длины 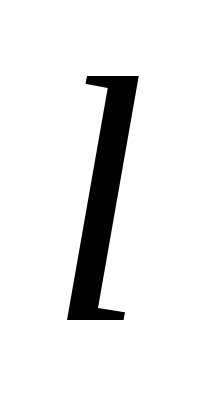 может вращаться вокруг горизонтальной
оси, перпендикулярной к стержню и
проходящей через один из его концов
(рис. 7). Систему равномерно вращают с
угловой скоростью
может вращаться вокруг горизонтальной
оси, перпендикулярной к стержню и
проходящей через один из его концов
(рис. 7). Систему равномерно вращают с
угловой скоростью вокруг вертикальной оси. Пренебрегая
трением, найти угол
вокруг вертикальной оси. Пренебрегая
трением, найти угол между стержнем и вертикалью.
между стержнем и вертикалью.
Р е ш е н и е. Решим задачу двумя способами. Первое решение приведем в инерциальной системе отсчета, т.е. в системе, в которой стержень вращается. Второе решение – в неинерциальной системе отсчета, жестко связанной со стержнем.
а) Система отсчета,
в которой будем решать задачу, на рис.
7 не показана. Решение задачи относительно
вертикальной оси вращения не даст
желаемого результата, т.к. моменты сил,
действующих на стержень (сила тяжести
и сила реакции в точке 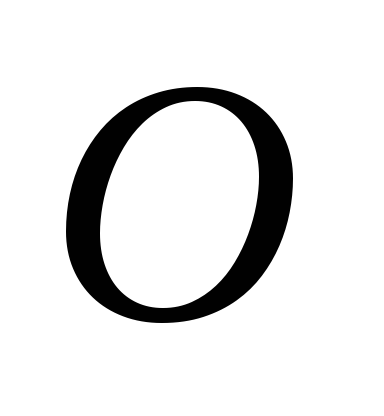 ),
относительно этой оси равны нулю, и
величина момента импульса остается
постоянной.
),
относительно этой оси равны нулю, и
величина момента импульса остается
постоянной.
Поэтому
будем решать задачу относительно точки 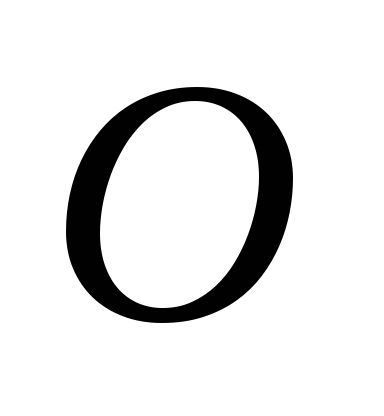 подвеса стержня. Напомним, что уравнение
моментов относительно точки имеет вид
подвеса стержня. Напомним, что уравнение
моментов относительно точки имеет вид
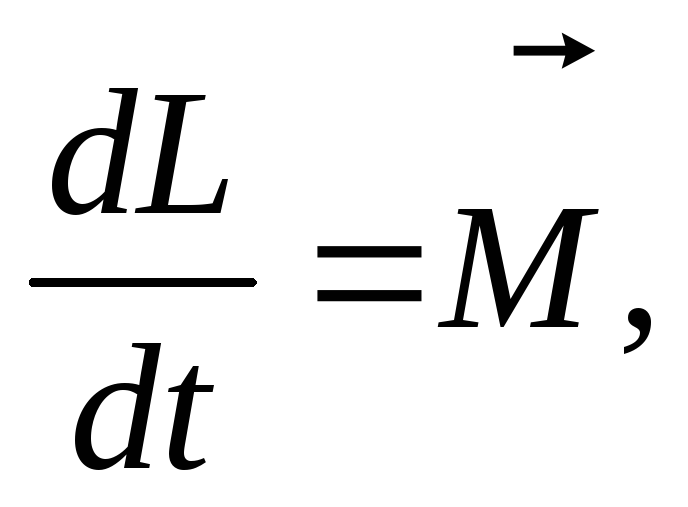
откуда видно, что
направление изменения момента импульса 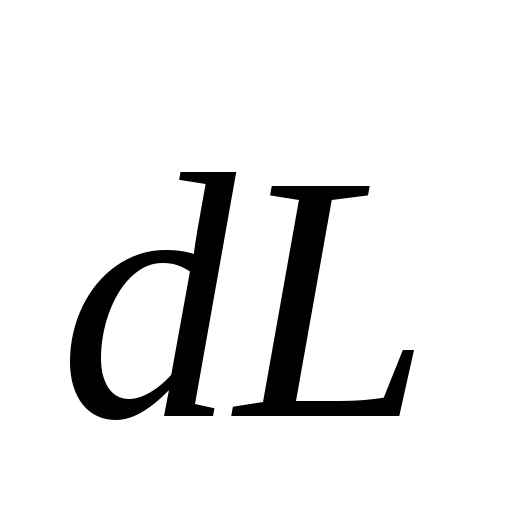 совпадает по направлению с направлением
момента сил
совпадает по направлению с направлением
момента сил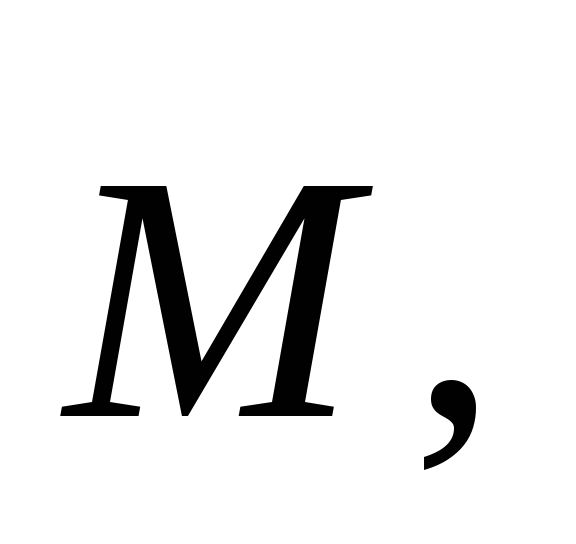 действующих на стержень, поэтому в
дальнейшем это уравнение будем записывать
для модулей
действующих на стержень, поэтому в
дальнейшем это уравнение будем записывать
для модулей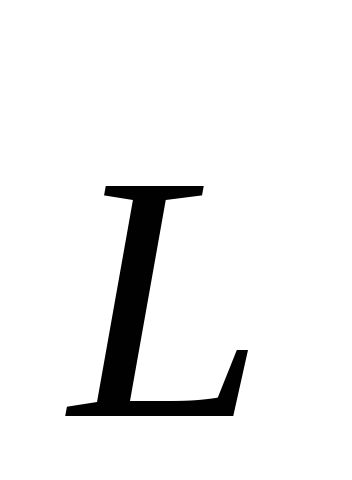 и
и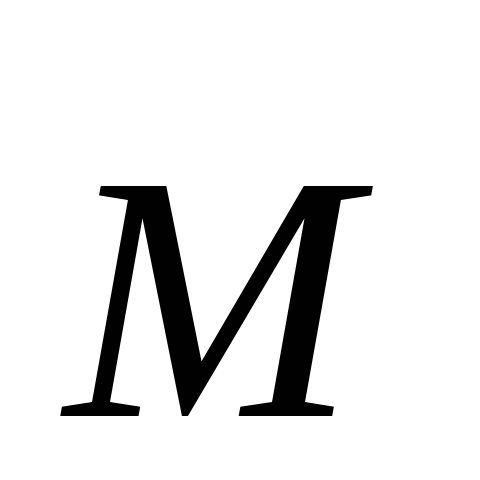
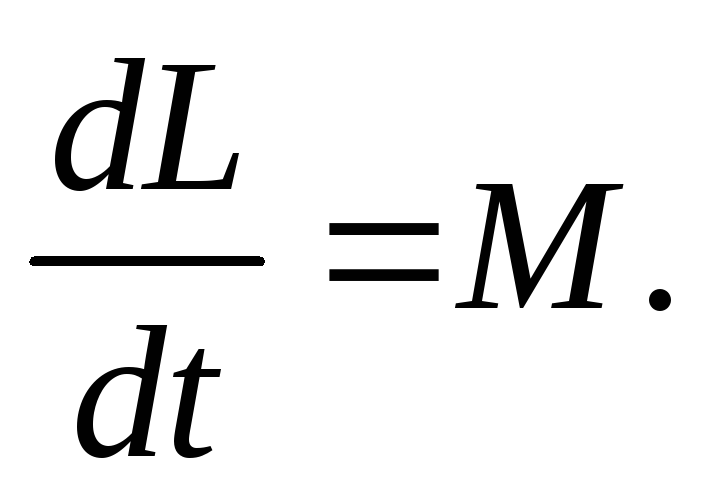 (25)
(25)
Момент силы реакции
в точке 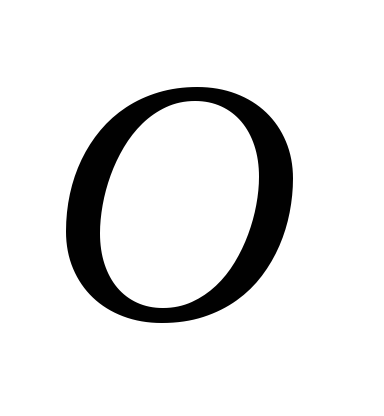 равен нулю, т.к. плечо этой силы равно
нулю. Направление момента силы тяжести
показано на рис.7, а величина равна
равен нулю, т.к. плечо этой силы равно
нулю. Направление момента силы тяжести
показано на рис.7, а величина равна
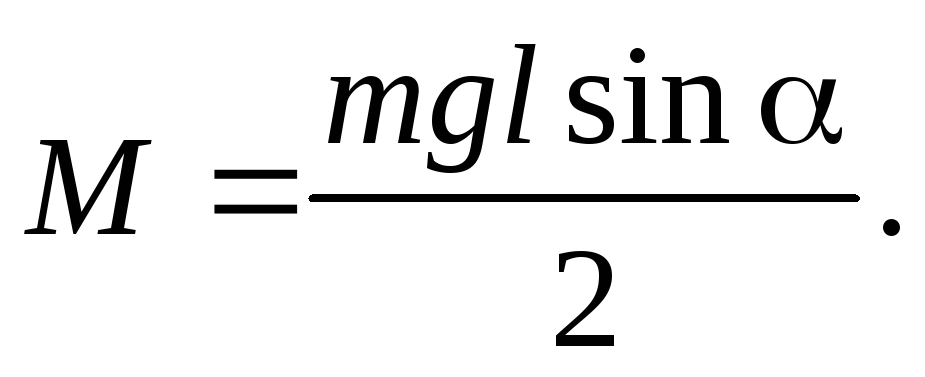 (26)
(26)
Найдем величину
и направление момента импульса 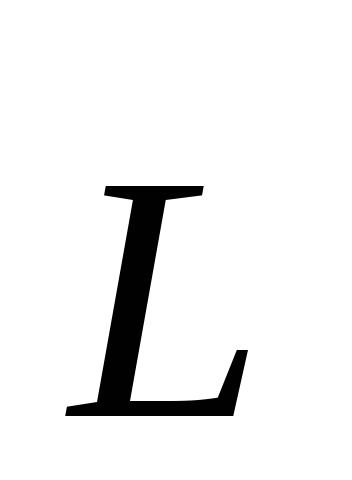 стержня относительно точки
стержня относительно точки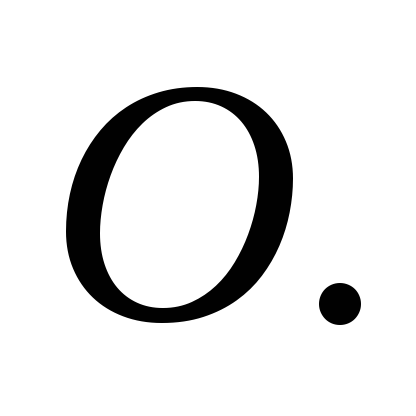 Для этого выделим на стержне небольшой
участок длиной
Для этого выделим на стержне небольшой
участок длиной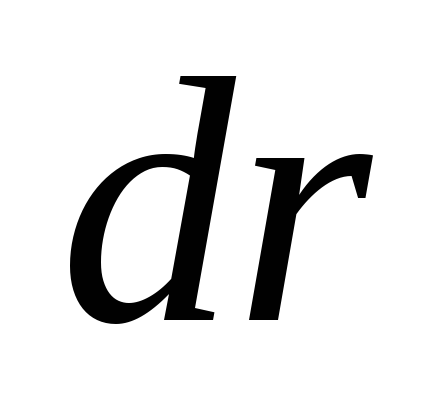 и массой
и массой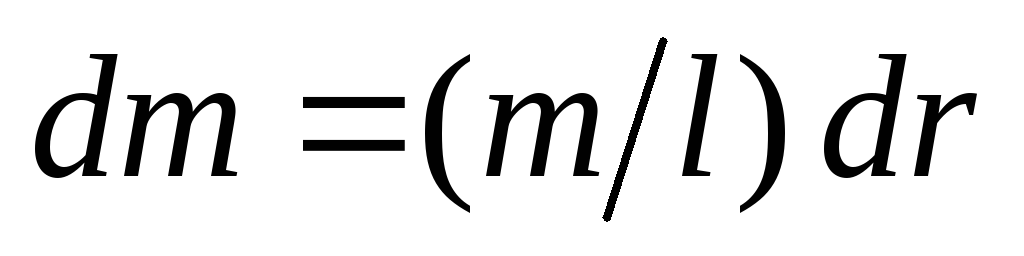 положение которого относительно точки
положение которого относительно точки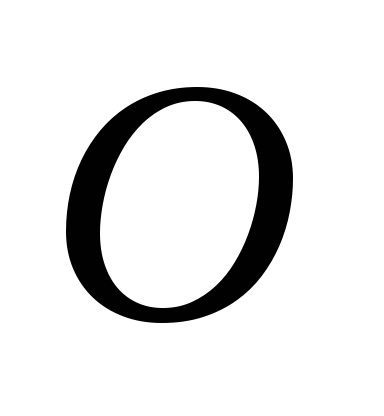 зададим радиус-вектором
зададим радиус-вектором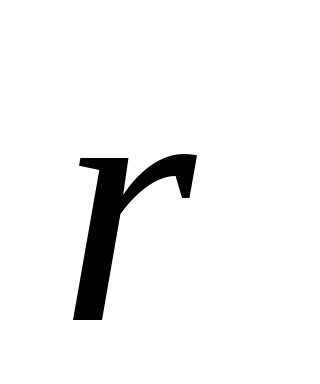 (см.
рис. 7). Обозначим величину момента
импульса этого участка как
(см.
рис. 7). Обозначим величину момента
импульса этого участка как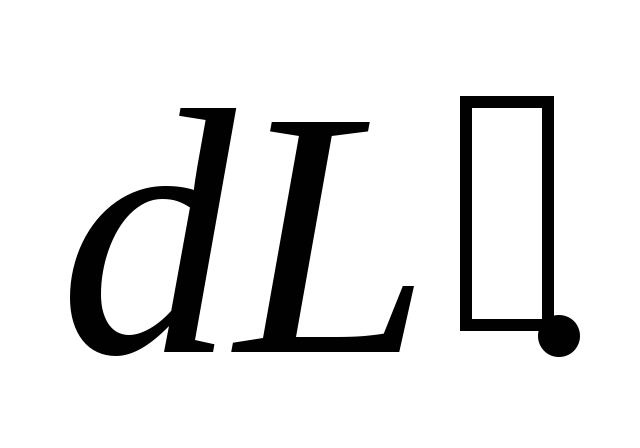 Так как стержень вращается вокруг
вертикальной оси, так как показано на
рисунке, скорость
Так как стержень вращается вокруг
вертикальной оси, так как показано на
рисунке, скорость этого участка будет направлена за
плоскость рисунка, поэтому как следует
из определения момента импульса
этого участка будет направлена за
плоскость рисунка, поэтому как следует
из определения момента импульса
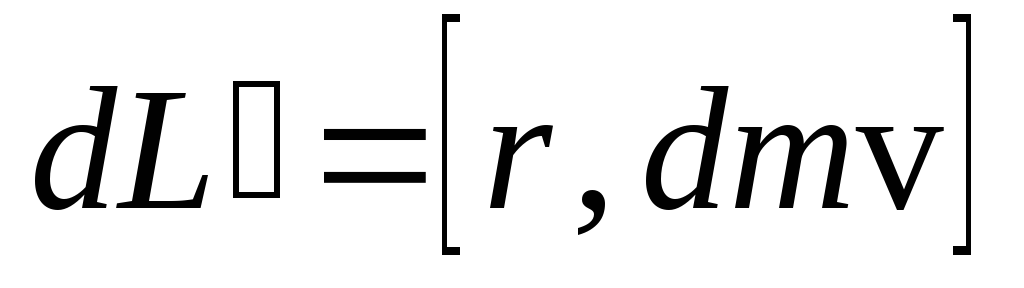 ,
,
он будет направлен
перпендикулярно стержню, как показано
на рис. 7. Очевидно, что направления всех
моментов импульса остальных участков
стержня будут иметь такое же направление,
поэтому результирующий момент импульса
будет также перпендикулярен стержню.
Учитывая, что векторы 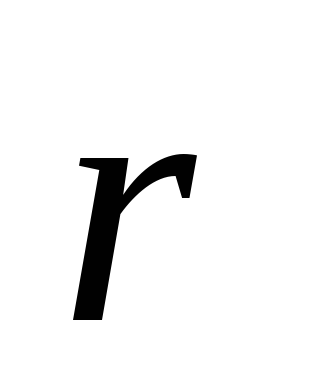 и
и взаимно перпендикулярны, величина
взаимно перпендикулярны, величина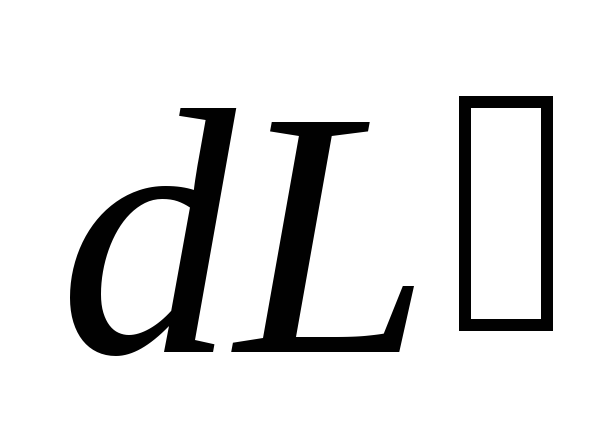 равна
равна
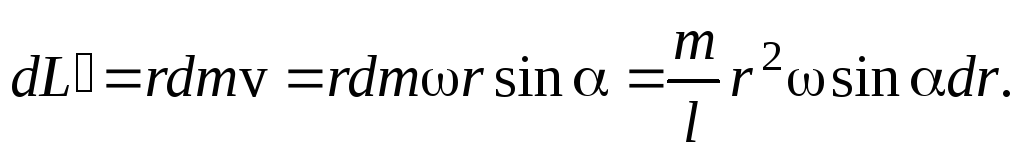
Интегрируя это уравнение
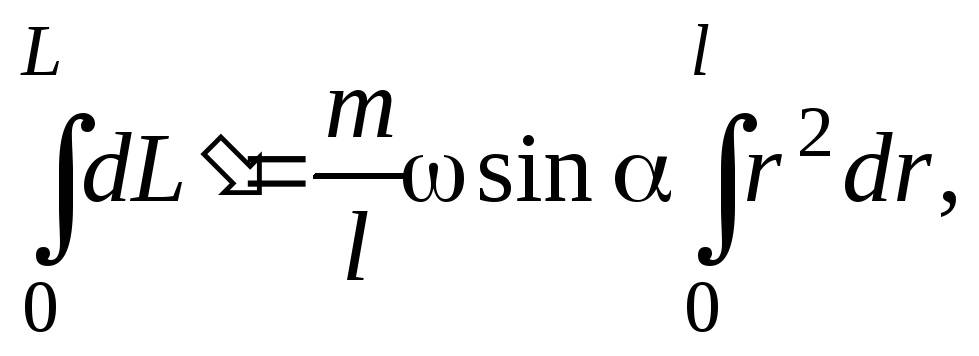
найдем величину
момента импульса стержня относительно
точки 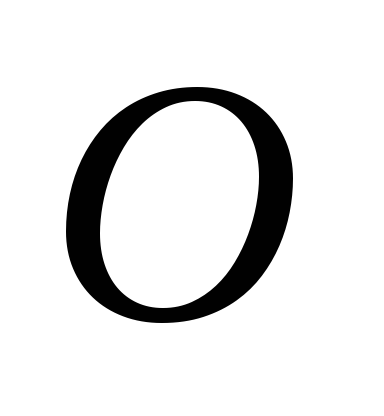
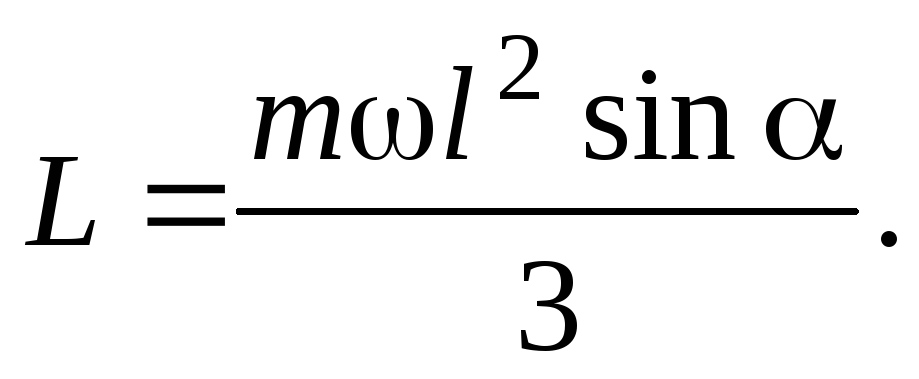
Момент
импульса поворачивается вместе со
стержнем, и за время 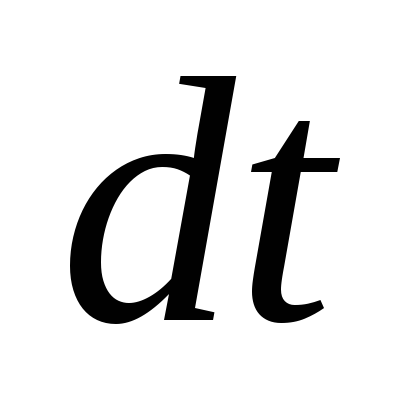 повернется на некоторый угол
повернется на некоторый угол ,
получив приращение
,
получив приращение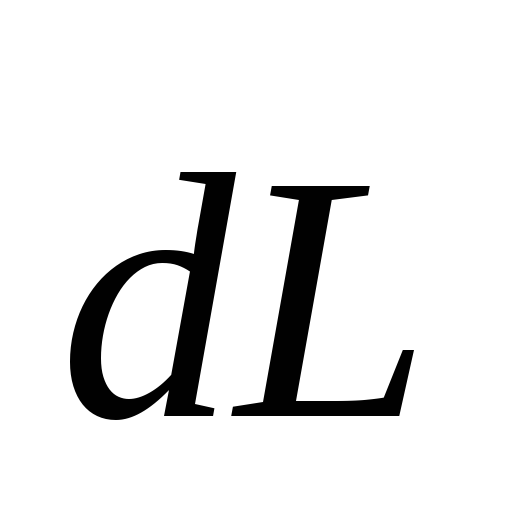 (см. рис.8).
Найдем величину этого приращения
(см. рис.8).
Найдем величину этого приращения
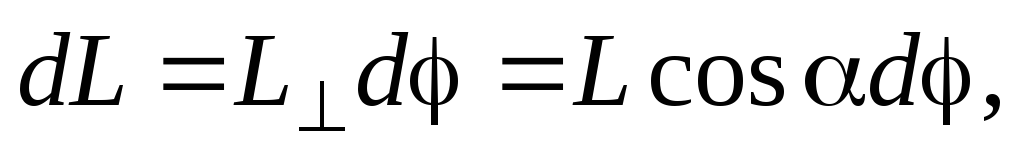
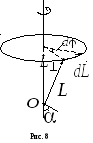
или
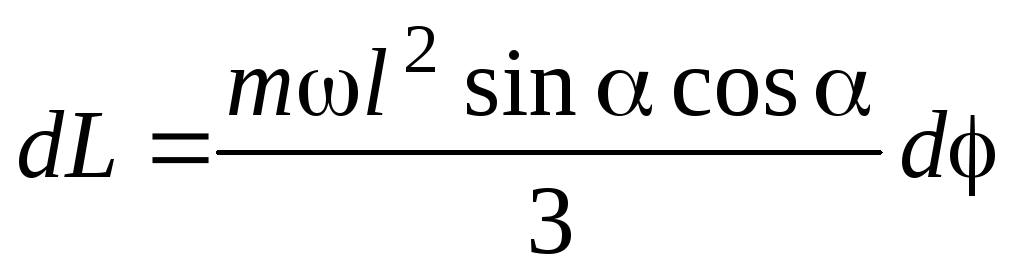 .
(27)
.
(27)
Подставляя уравнение (26) и (27) в уравнением моментов (25), получим
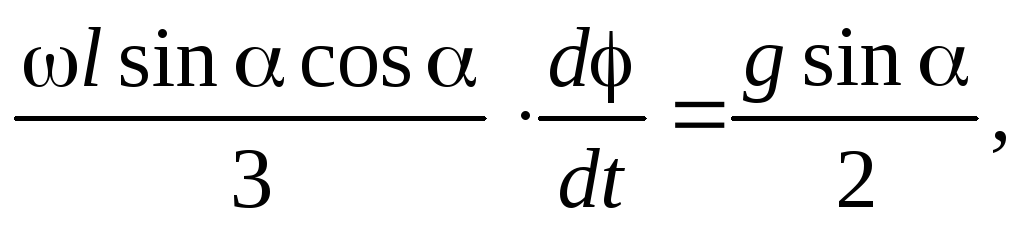
где  .
Преобразуем это уравнение к виду
.
Преобразуем это уравнение к виду
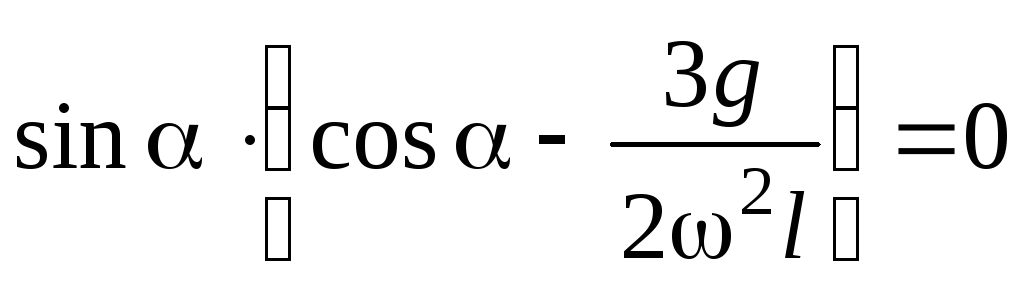 .
(28)
.
(28)
Если величина
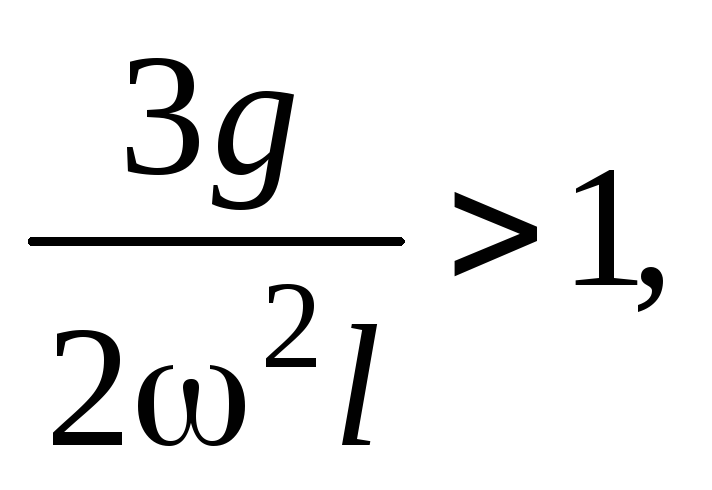
уравнение (28) имеет
одно решение 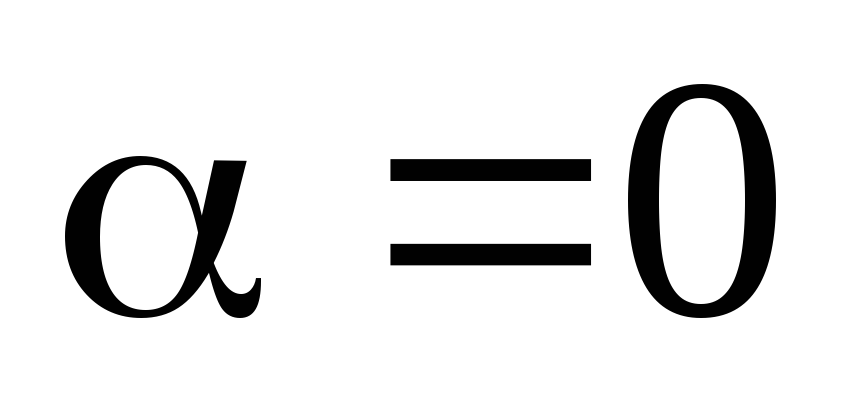 ,
и это положение устойчивое, т.е. стержень
будет занимать вертикальное положение
и будет вращаться вокруг собственной
оси.
,
и это положение устойчивое, т.е. стержень
будет занимать вертикальное положение
и будет вращаться вокруг собственной
оси.
Если 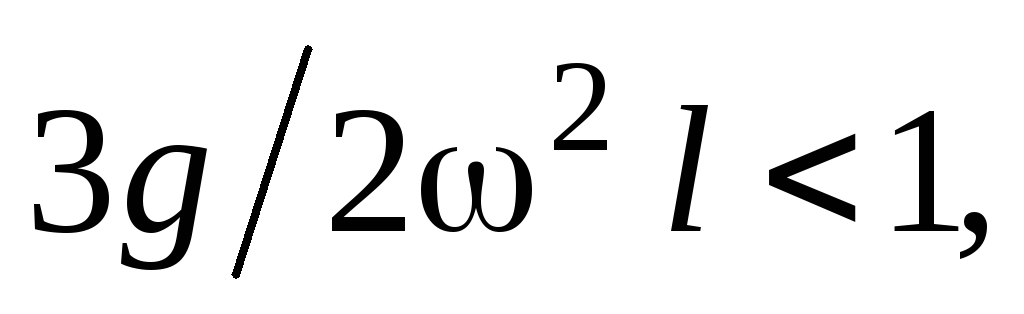 то уравнение (28) будет иметь два решение
то уравнение (28) будет иметь два решение
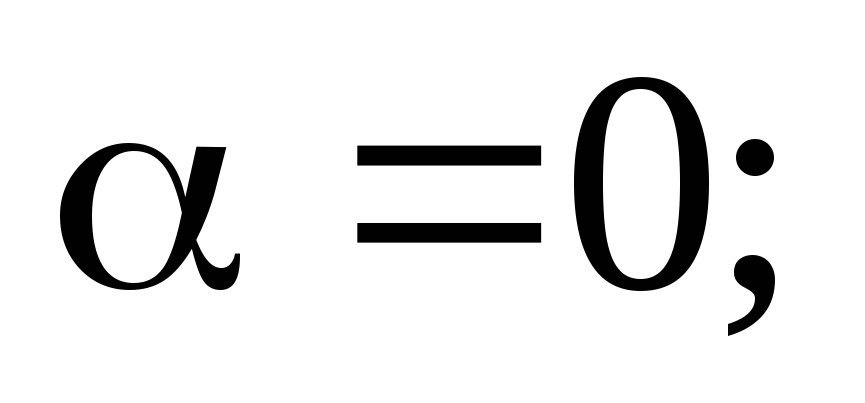 и
и 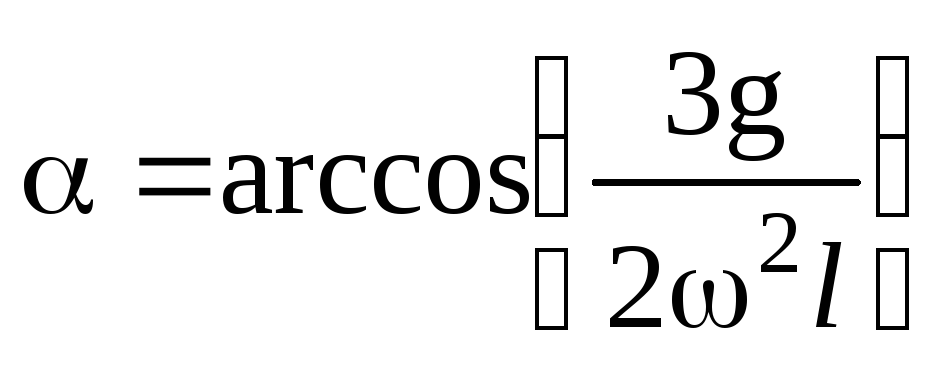 ,
,
причем можно показать, что первое решение перестает быть устойчивым, и стержень отклонится на угол, определяемый вторым решением.
б) Решим теперь задачу в неинерциальной системе отсчета, жестко связанной со стержнем. В этой системе отсчета на стержень, кроме сил взаимодействия действует центробежная сила инерции. Так как стержень находится в равновесии, сумма моментов сил, действующих на стержень, должна равняться нулю, т.е.
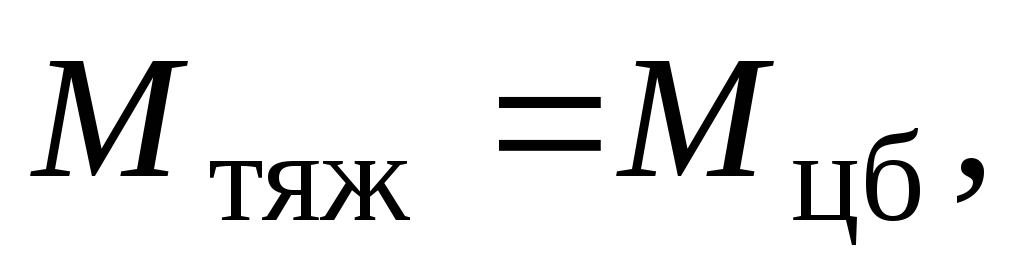
где 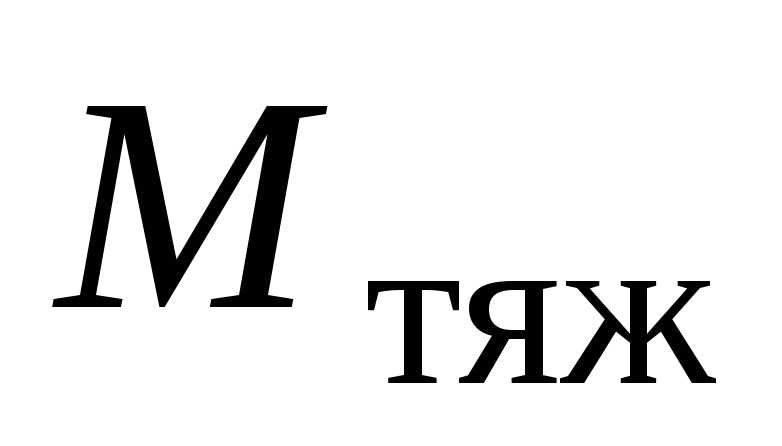 – величина момента силы тяжести,
– величина момента силы тяжести,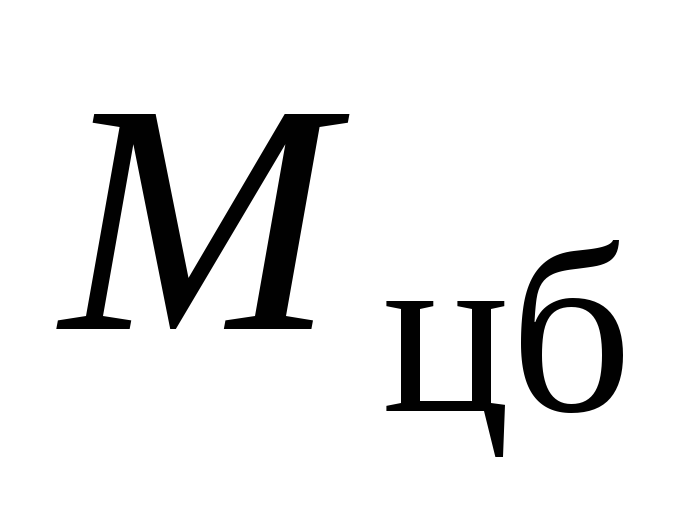 – величина момента центробежной силы
инерции относительно точки
– величина момента центробежной силы
инерции относительно точки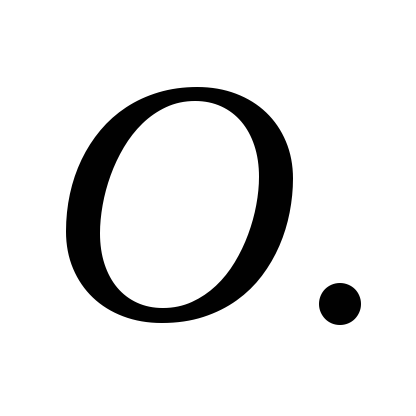 Величина момента силы тяжести определяется
уравнением (26).
Для нахождения момента центробежной
силы инерции воспользуемся рис. 7, считая,
что стержень покоится.
Величина момента силы тяжести определяется
уравнением (26).
Для нахождения момента центробежной
силы инерции воспользуемся рис. 7, считая,
что стержень покоится.
На выделенный участок стержня действует центробежная сила инерции
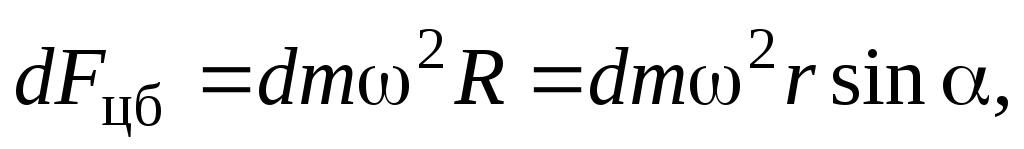
величина момента
которой, относительно точки 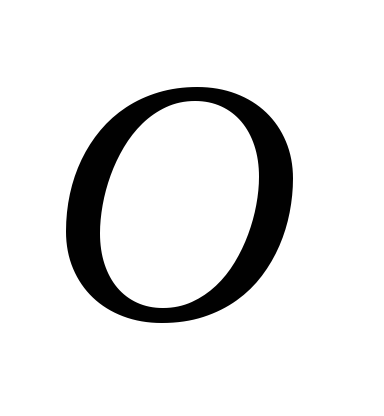 равна
равна
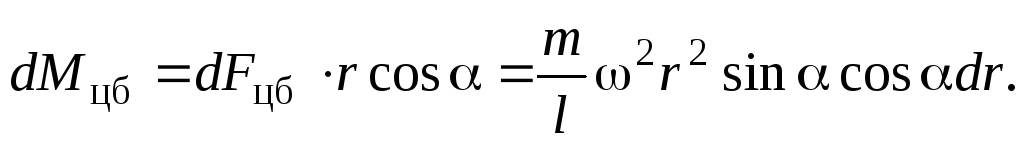
Интегрируя это выражение по всей длине стержня, получим
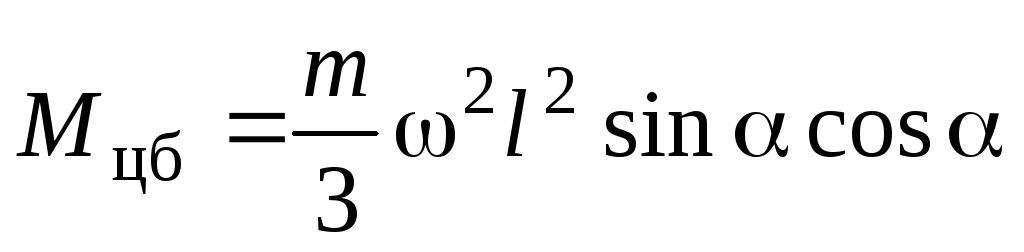 .
.
Подставляя это выражение и соотношение (26) в уравнение моментов (25), получим уравнение
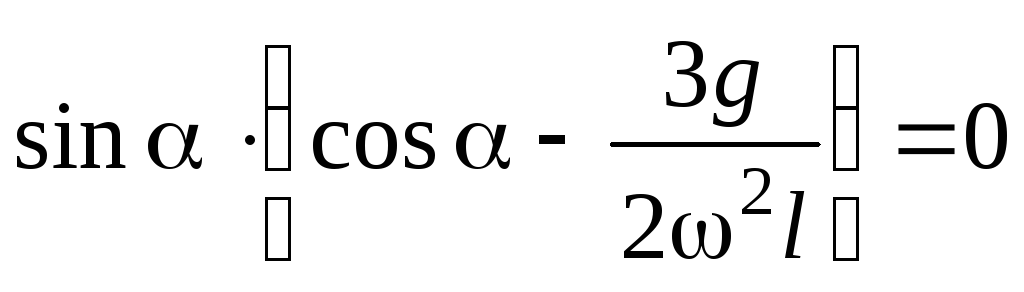 ,
,
в точности совпадающее с уравнением (28).
Надо заметить, что решение этой задачи в неинерциальной системе отсчета много проще, чем в инерциальной.
Пример
6. Однородная
тонкая квадратная пластинка массы 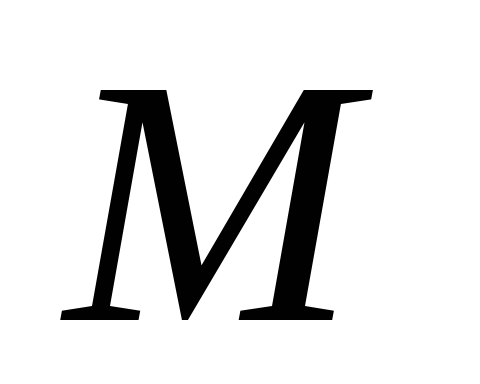 может свободно вращаться вокруг
неподвижной вертикальной оси, совпадающей
с одной из ее сторон. В центр пластины
по нормали к ней упруго ударяется шарик
массы
может свободно вращаться вокруг
неподвижной вертикальной оси, совпадающей
с одной из ее сторон. В центр пластины
по нормали к ней упруго ударяется шарик
массы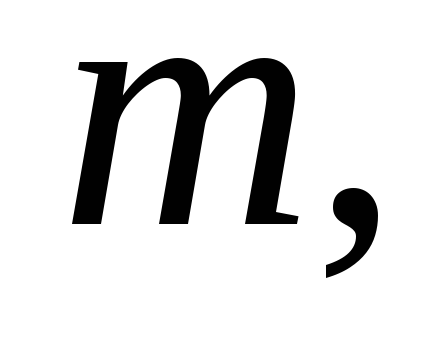 летевший со скоростью
летевший со скоростью Найти величину скорости шарика
Найти величину скорости шарика сразу после удара.
сразу после удара.
Р е ш е н и е. Система “пластина-шарик” незамкнута, так как для удержания оси пластины в неподвижном состоянии к ней необходимо приложить внешние силу. Однако надо заметить, что момент этих внешних сил относительно оси равны нулю, т.к. они приложены непосредственно к оси.
Для
решения задачи воспользуемся законами
сохранения энергии (удар упругий) и
законом сохранения момента импульса
(сумма момента внешних сил относительно
оси равен нулю). Будем считать, что длина
стороны пластины равна 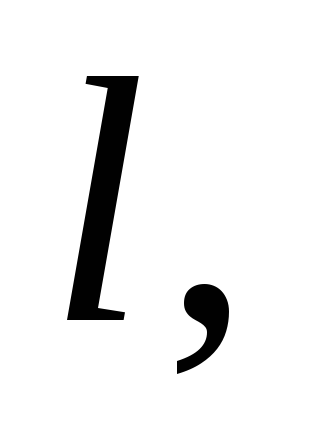 и шарик после удара будет лететь в
прежнем направлении, тогда
и шарик после удара будет лететь в
прежнем направлении, тогда
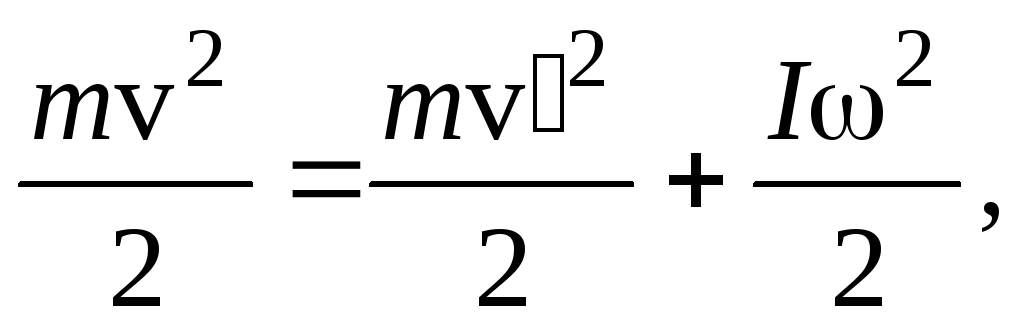
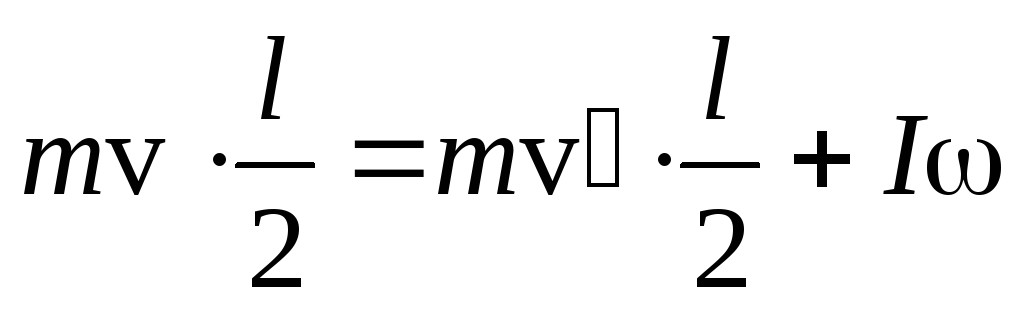 ,
,
где 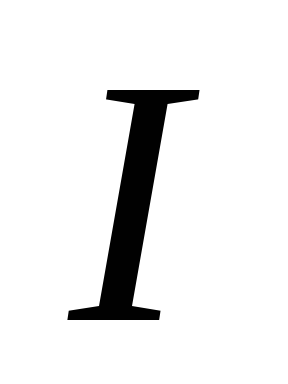 – момент инерции пластины относительно
оси,
– момент инерции пластины относительно
оси, – угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.
– угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.
Для простоты решения этой системы перепишем ее в виде
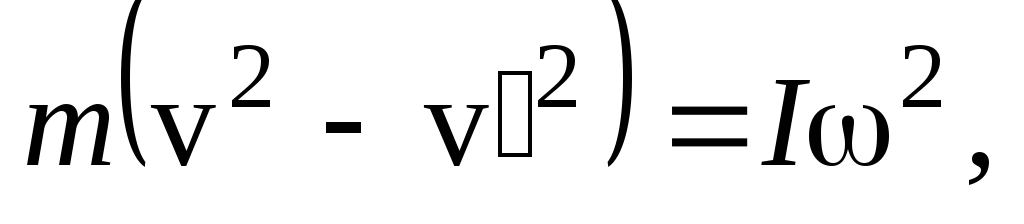
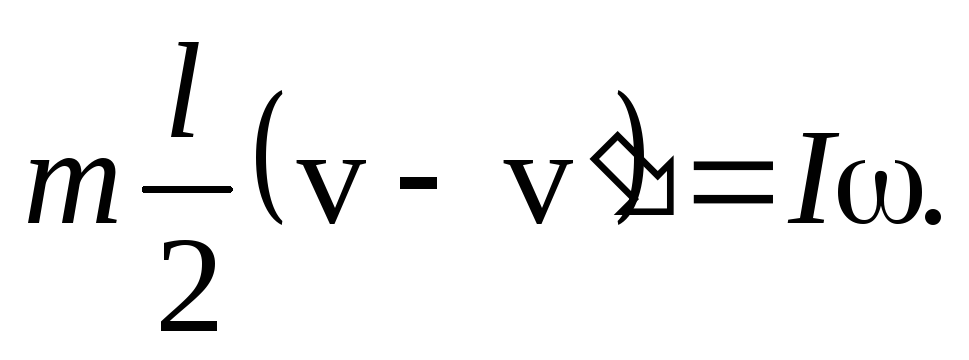 (29)
(29)
Разделив первое уравнение не второе, получим
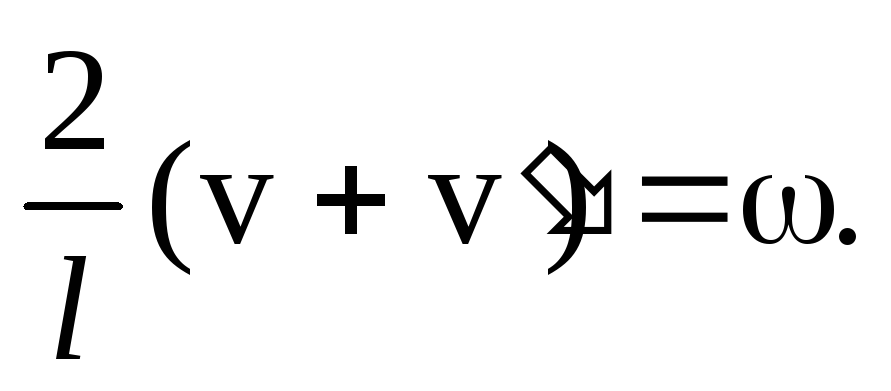 (30)
(30)
Решая
совместно уравнения (29) и(30) и учитывая,
что момент инерции пластины относительно
оси, совпадающей с одной из ее сторон
равен 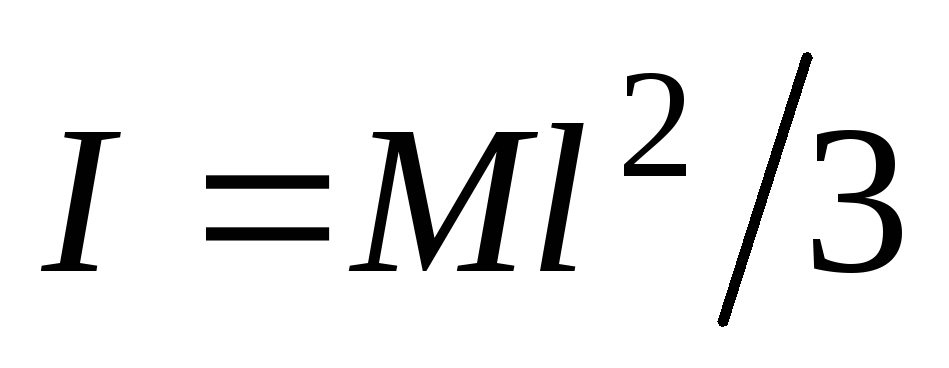 (докажите это самостоятельно), найдем
скорость шарика после удара
(докажите это самостоятельно), найдем
скорость шарика после удара
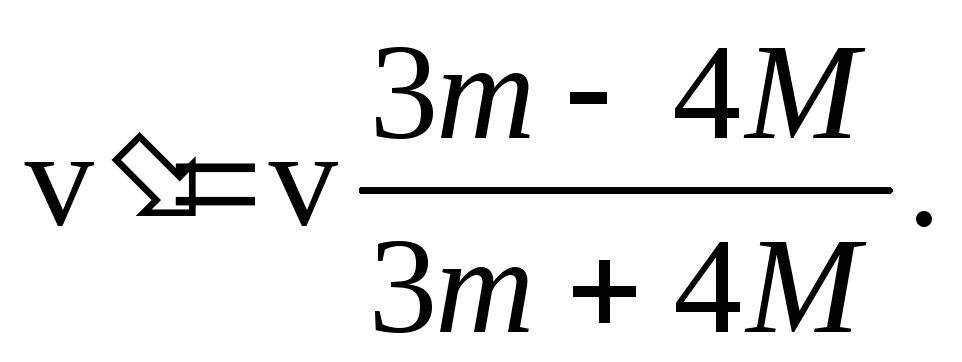
Заметим,
что если 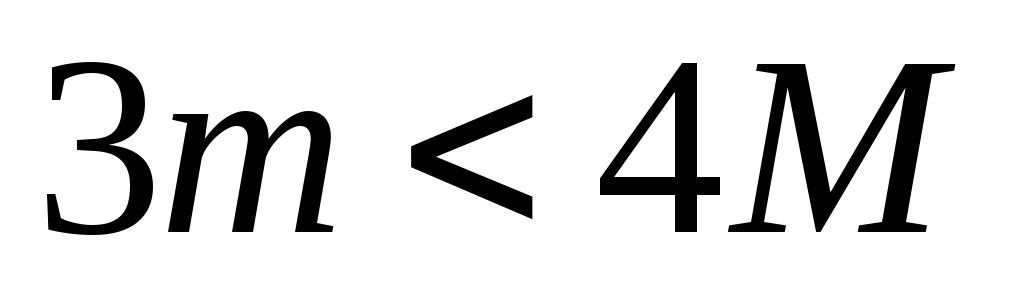 ,
скорость шарика после удара становится
отрицательной. Это означает, что при
,
скорость шарика после удара становится
отрицательной. Это означает, что при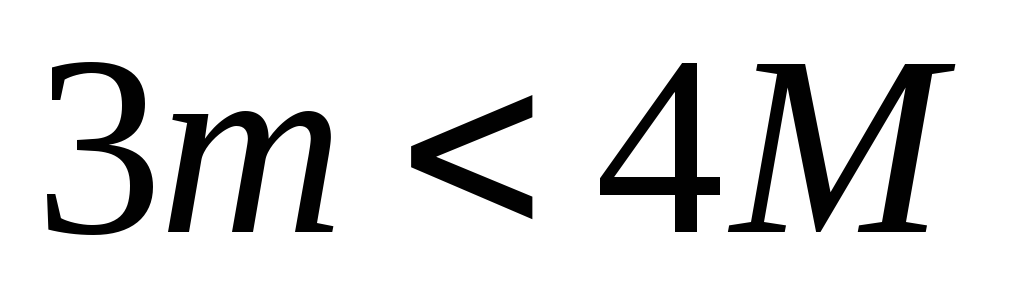 шарик полетит в обратную сторону.
шарик полетит в обратную сторону.
Пример
7. Однородный
диск радиуса 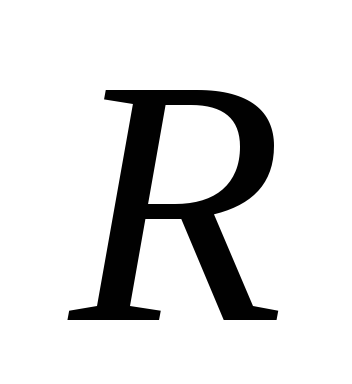 и массы
и массы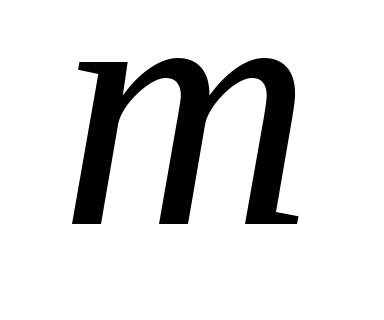 лежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концу
лежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концу которой приложили постоянную горизонтальную
силу
которой приложили постоянную горизонтальную
силу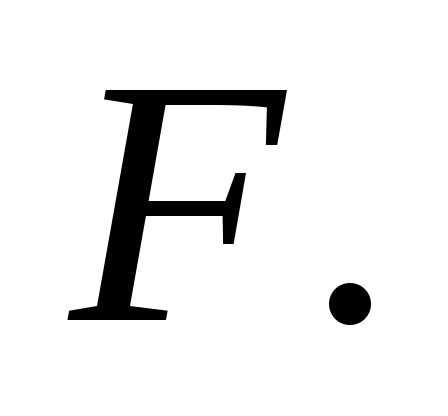 После начала движения диска точка
После начала движения диска точка переместилась на расстояние
переместилась на расстояние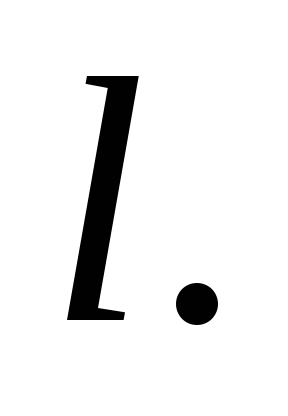 Найти угловую скорость диска к этому
моменту времени.
Найти угловую скорость диска к этому
моменту времени.
Р
е ш е н и е. Под действием силы 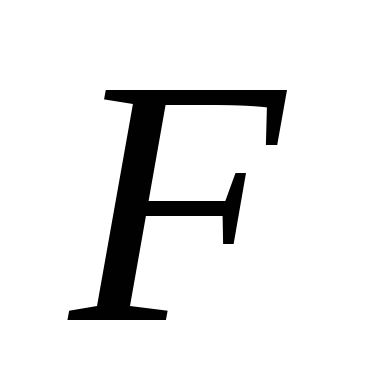 диск будет совершать плоское движение.
Свяжем подвижную систему отсчета с
центром масс диска. Величину ускорения
центра масс
диск будет совершать плоское движение.
Свяжем подвижную систему отсчета с
центром масс диска. Величину ускорения
центра масс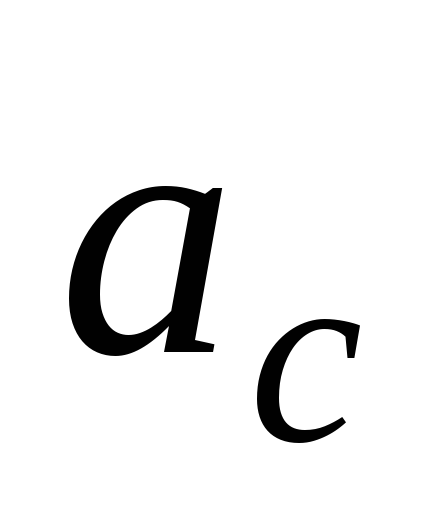 найдем из второго закона Ньютона,
записанного в проекции на направление
движения
найдем из второго закона Ньютона,
записанного в проекции на направление
движения
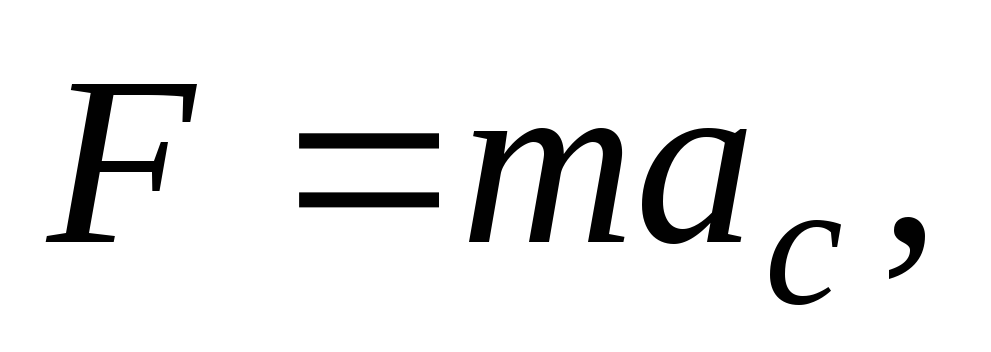

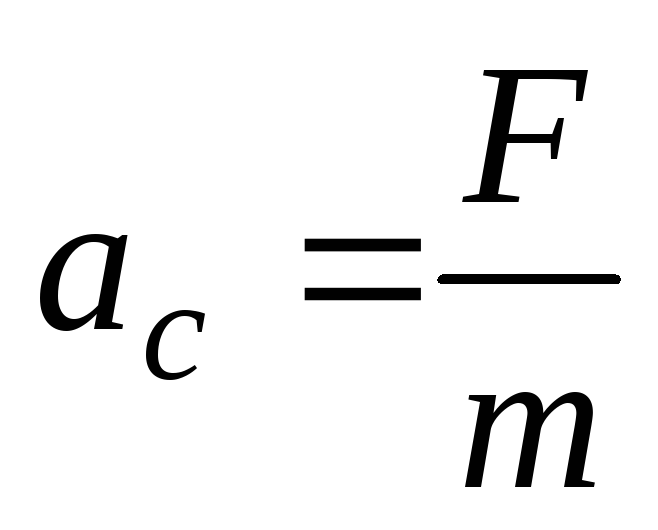 .
(31)
.
(31)
В
системе отсчета, связанной с центром
масс, диск вращается с угловым ускорением  ,
которое найдем из уравнения вращательного
движения диска
,
которое найдем из уравнения вращательного
движения диска
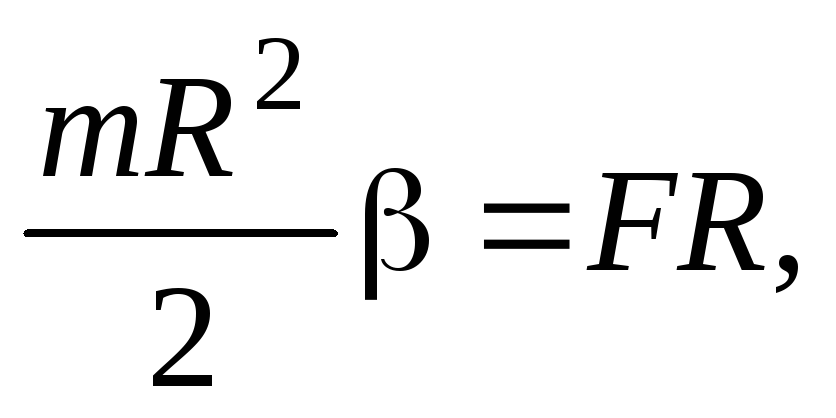

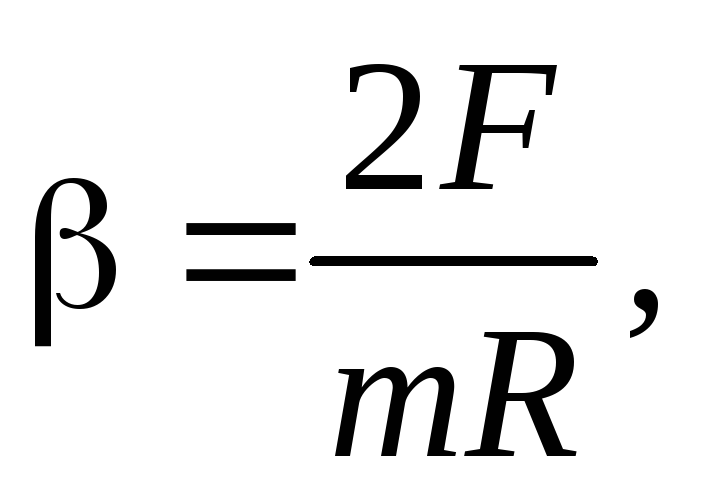 (32)
(32)
где 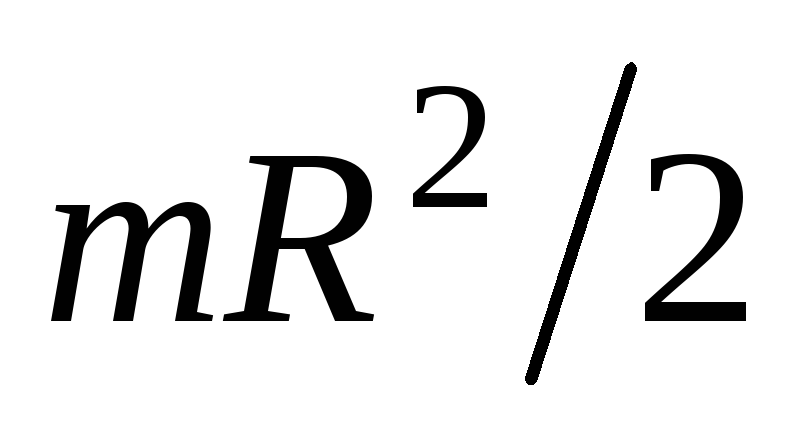 – момент инерции диска, относительно
оси вращения.
– момент инерции диска, относительно
оси вращения.
Найдем
величины скорости 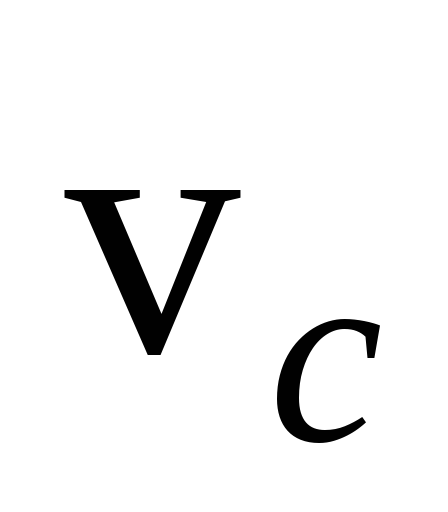 центра масс диска и угловой скорости
его вращения к моменту времени
центра масс диска и угловой скорости
его вращения к моменту времени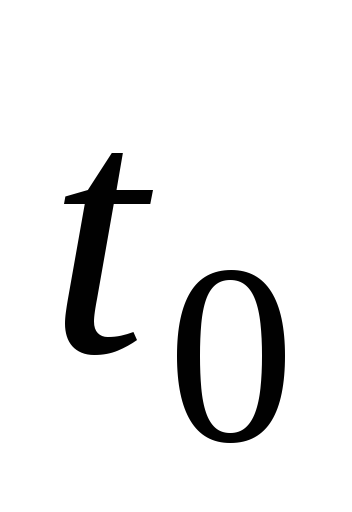 ,
когда точка приложения силы
,
когда точка приложения силы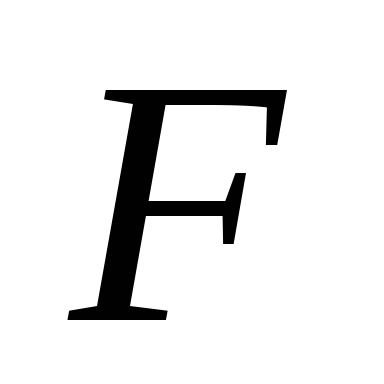 совершит перемещение
совершит перемещение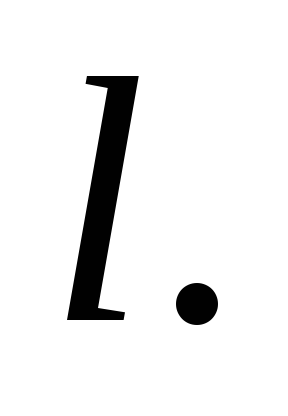 Так как в начальный момент времени диск
покоился, а величины ускорений
Так как в начальный момент времени диск
покоился, а величины ускорений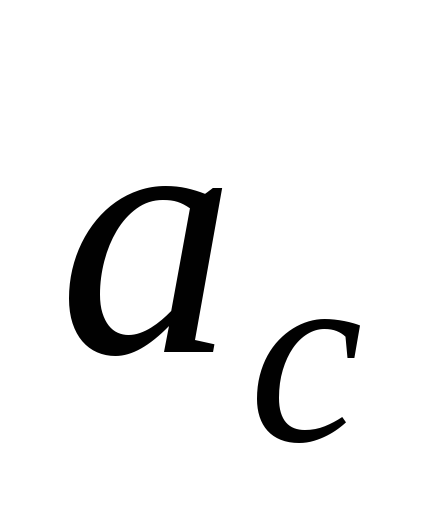 и
и не меняются с течением времени (см.
уравнения (31) и (32)), получим
не меняются с течением времени (см.
уравнения (31) и (32)), получим
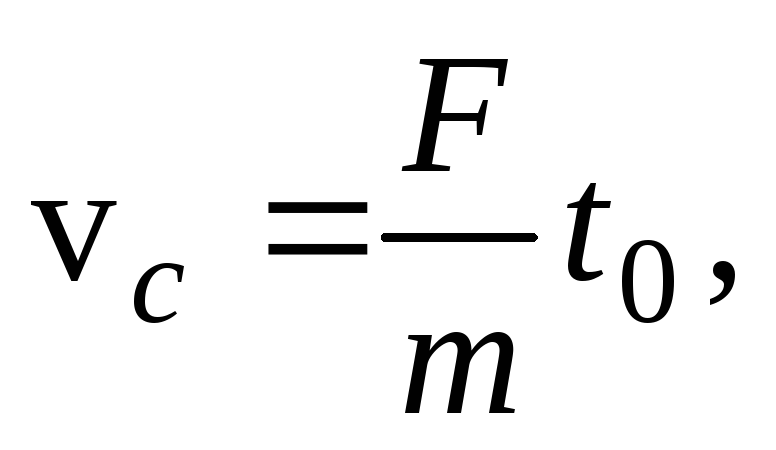
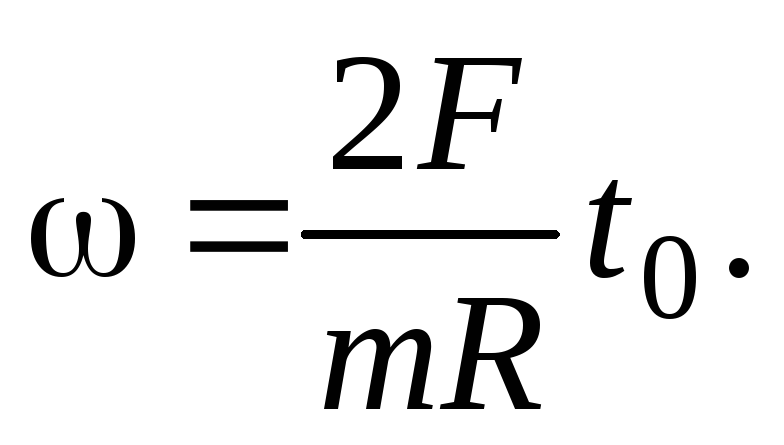
Исключая
из этих уравнений время 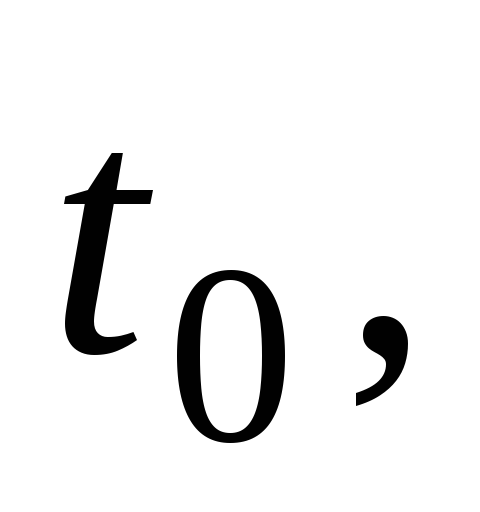 найдем связь между скоростью центра
масс и угловой скоростью вращения диска
найдем связь между скоростью центра
масс и угловой скоростью вращения диска
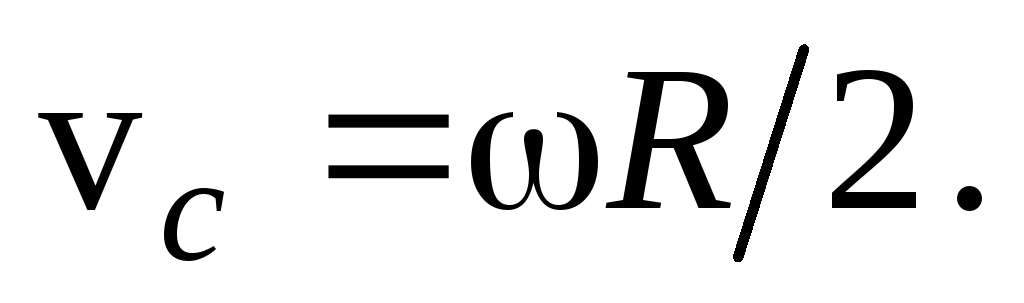 (33)
(33)
Запишем теорему об изменении кинетической энергии для диска
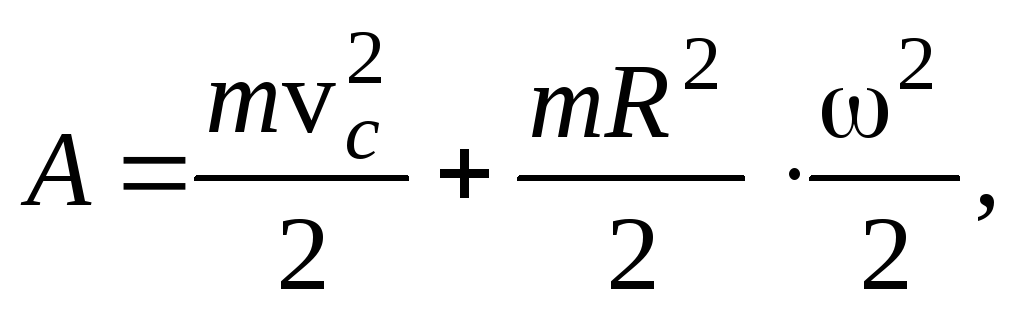 (34)
(34)
где  – работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная сила
– работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная сила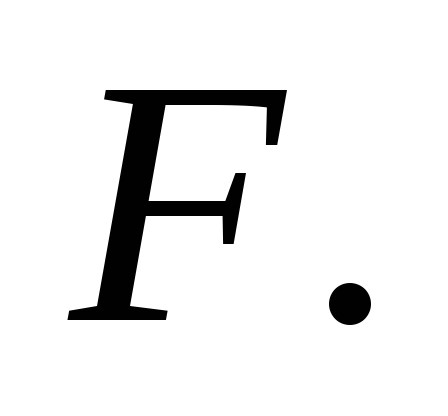 По определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом
По определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом
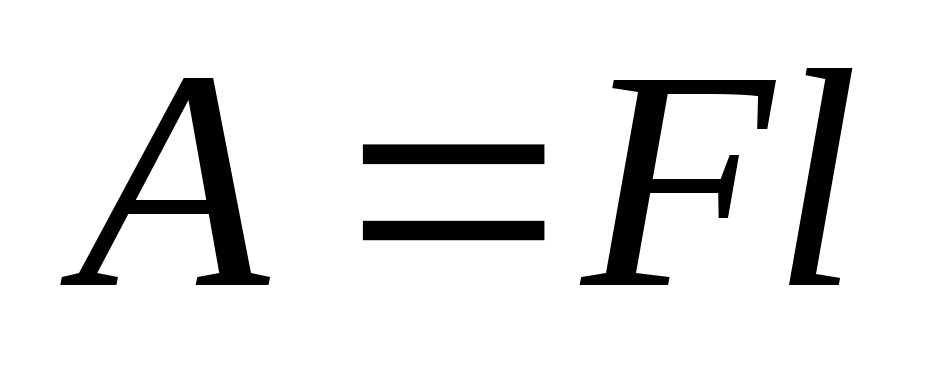 .
(35)
.
(35)
Подставляя
выражения (33) и (35) в уравнение (34), найдем
величину угловой скорости диска к
моменту времени, когда точка приложения
силы совершит перемещение 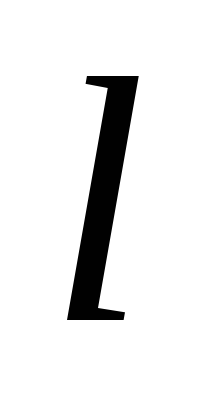
Расчет момента инерции | Онлайн калькулятор
При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.
Момент инерции треугольника
Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
Ix0 = b×h 3 / 36;
Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
Ix1 = b×h 3 / 12;
Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
Ix2 = b×h 3 / 4.
Момент инерции кольца относительно главной центральной оси:
Ix = π×D 4/64 – π×d 4/64;
Полярный момент инерции кольца:
Ip = π×D 4/32 – π×d 4/32.
Момент инерции прямоугольника относительно главных центральных осей:
Ix = (b×h 3 – b1×h2 3)/12;
Iy = (h×b 3 – h2×b1 3)/12.
Моменты инерции двутавра относительно главных центральных осей:
Ix = (B×H 3 – (B – s)×(H – 2t) 3) / 12;
Iy = (2t×B3 + (H – 2t)×s3) / 12.
Моменты инерции уголка относительно центральных осей:
Ix = (d×(H – y)3 + B×y3 – (B – d)×(y – d)3) / 3;
Iy = (d×(B – x)3 + H×x3 – (H – d)×(x – d)3) / 3,
где x и y – расстояния от наружных сторон уголка до центральных осей Y и X соответственно.
Моменты инерции швеллера относительно главных центральных осей:
Ix = (B×H 3 – (B – s)×(H-2d)3) / 12;
Iy = (H×x 3 – (H – 2d)×(x – s)3 + d×(B – x) 3)/3,
где x – расстояния от наружной сторон швеллера до центральной оси Y.
Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.
Момент инерции , в физике, количественная мера инерции вращения тела, т. Е. Оппозиция, которую тело демонстрирует скорости вращения вокруг оси, измененной приложением крутящего момента (сила поворота). Ось может быть внутренней или внешней и может быть или не быть фиксированной. Момент инерции ( I ), однако, всегда задается относительно этой оси и определяется как сумма произведений, полученных умножением массы каждой частицы вещества в данном теле на квадрат его расстояния от ось.При расчете момента импульса для твердого тела момент инерции аналогичен массе в линейном импульсе. Для линейного импульса импульс p равен массе м, в раз превышающей скорость v ; тогда как для углового момента угловой момент L равен моменту инерции I раз угловой скорости ω.
На рисунке показаны два стальных шарика, которые приварены к стержню AB , который прикреплен к стержню OQ при C .Пренебрегая массой AB и предполагая, что все частицы массой м каждого шара сконцентрированы на расстоянии r от OQ , момент инерции задается как I = 2 mr 2
Encyclopædia Britannica, Inc.Единица момента инерции является составной единицей измерения. В Международной системе (СИ) м выражается в килограммах, а r в метрах, а I (момент инерции) имеет размерный квадрат килограмм-метр.В обычной системе США м в слизняках (1 пуля = 32,2 фунта) и м в футах, при этом I выражены в единицах квадратных футов.
Момент инерции любого тела, имеющего форму, которая может быть описана математической формулой, обычно рассчитывается интегральным исчислением. Момент инерции диска на рисунке около OQ можно было бы аппроксимировать, разрезав его на несколько тонких концентрических колец, найдя их массы, умножив массы на квадраты их расстояний от OQ и сложив их товары.Используя интегральное исчисление, процесс суммирования выполняется автоматически; ответ: I = ( mR 2 ) / 2. (См механика; крутящий момент.)
Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской. Подпишитесь сегодняДля тела с математически неописуемой формой момент инерции можно получить экспериментальным путем. В одной из экспериментальных процедур используется связь между периодом (временем) колебания крутильного маятника и моментом инерции взвешенной массы.Если диск на рисунке подвешен к проводу OC , зафиксированному на O , он будет колебаться около OC , если его повернуть и отпустить. Время одного полного колебания будет зависеть от жесткости проволоки и момента инерции диска; чем больше инерция, тем дольше время.
Момент инерции ( я {\ displaystyle I} ), также называемый « угловой массы » (кг · м 2 ), [1] — это инерция вращающегося тела относительно его вращения.
Это сопротивление вращающегося тела угловому ускорению или замедлению, равное произведению массы на квадрат его перпендикулярного расстояния от оси вращения.
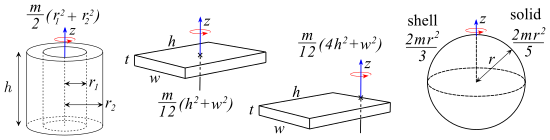
Моменты инерции для нескольких объектов [изменить | изменить источник]
- × Аткинсон П. (2012). Теория управления с обратной связью для инженеров . Springer Science & Business Media. п. 50. ISBN 978-1-4684-7453-4 .
Студенту рекомендуется рассматривать момент инерции как эквивалент «угловой массы»; Уравнения в механике вращения, как правило, аналогичны уравнениям в механике поступательного движения. Где бы ни возникало уравнение в поступательной механике с массой м , в механике вращения существует эквивалентное уравнение с моментом инерции J .Единицами момента инерции являются килограммы метров 2 (сокращение кг м 2 ).
Разница между инерцией и моментом инерции
Ключевая разница: Инерция может быть описана как свойство или тенденция объекта, который сопротивляется любым изменениям его состояния движения. Момент инерции — это измерение сопротивления объекта изменению его вращения.
Инерция может быть описана как свойство или тенденция объекта, который противостоит любым изменениям его состояния движения. Таким образом, тело остается в покое или продолжает свое движение, если на него не действует внешняя сила.Латинский корень для инерции — это тот же корень для «инертного», что означает отсутствие способности двигаться. Галилей, ученый семнадцатого века, разработал концепцию инерции, заявив, что движущийся объект имеет тенденцию останавливаться из-за силы трения. Позже Ньютон сформулировал законы движения. Первый закон движения Ньютона фокусируется на инерции. Он описывается как — «В отсутствие внешних сил движение по прямой и с постоянной скоростью продолжается бесконечно».
Момент инерции — это измерение сопротивления объекта изменению его вращения.Момент инерции выражается относительно выбранной оси вращения. Это также известно как инерция вращения. Это зависит от трех сил — массы объекта, формы и относительной точки вращения. Он представлен символом I. Можно также определить момент инерции как способность противостоять крутящей силе или крутящему моменту. Момент инерции зависит от формы объекта, и, следовательно, зависимость можно легко увидеть в различных формулах. Ниже приведены несколько примеров формул, используемых при расчете момента инерции:
Для однородного диска с радиусом r и массой m момент инерции = 1/2 (m x r²).
Для твердой сферы I = 2/5 (m x r²).
Точечная частица массой m на орбите на расстоянии r от объекта, момент инерции = (m x r²).
Сравнение инерции и момента инерции:
Инерция | Момент инерции | |
Определение | Инерция может быть описана как свойство или тенденция объекта, который противостоит любым изменениям его состояния движения. | Момент инерции — это измерение сопротивления объекта изменению его вращения. Момент инерции выражается относительно выбранной оси вращения. |
Структурная жесткость: момент инерции
Я получил вопрос от Маноя об основах жесткости. Поскольку пост о структурной жесткости ( липких медведей! ) настолько популярен, я подумал, что было бы неплохо поделиться другой историей о жесткости, которую я часто использую… пещерные люди!

Вопрос может показаться простым, но я уверен, что в этом посте будет много интересных идей, о которых вы, возможно, никогда не слышали! В конце концов, кому не нравится хорошая история, которая объясняет вещи простым способом?
Всегда рассказывайте историю…
Я буквально ненавидел занятия по прочности материалов.Они были скучными, вещи казались непрактичными, и были дифференциальные уравнения и интеграция … и не намного!
В течение многих лет я презирал эти курсы. Пока мне действительно не нужно было использовать некоторые знания из этой области. Конечно, я не изучал силу материалов, будучи студентом (кстати, A’s BTW). Так как я думал, что это «теоретическая корма», я просто сделал минимум, чтобы получить «А» без каких-либо усилий, чтобы понять это. Ба! Я даже выучил некоторые дифференциальные уравнения наизусть, так как мне было лень учиться их решать!
Итак, когда пришла необходимость использовать знания … пришло время действительно изучить этот материал.К счастью, у меня всегда была хорошая интуиция, чтобы понять что-то в стиле фанк-детски. С этим умением я смог рассказать себе истории о вещах, которые помогли мне понять все это. Позже я с удивлением обнаружил, что люди обычно так не учатся. Поэтому я начал использовать эти истории на курсах Uni, которые я проводил.
Я твердо верю, что до тех пор, пока вы не сможете объяснить своей бабушке, как что-то работает в технике, вы сами этого недостаточно понимаете! Для этого и нужны истории!
Я знал, что у большинства студентов будут серьезные проблемы с прочностью материалов, поэтому большинство моих занятий начинаются с «всего, что вам нужно знать о прочности материалов за 45 минут или меньше».Это история пещерных людей!
Однажды во Франции…
Наше племя пещерных людей живет во Франции. Это важный факт, так как общеизвестно, что во Франции деревья не круглые! Как вы знаете, типичное сечение французского дерева прямоугольное. Это важно и пригодится!

Представьте, что наше небольшое примитивное племя столкнулось с самой первой инженерной проблемой: они хотят пересечь реку!
Поскольку вокруг много деревьев, все, что им нужно сделать, — это срубить одно, протолкнуть его через реку и пересечь его.
Конечно, срезать более тонкое дерево — значит меньше работать… и вот как мы обнаружили первую проблему оптимизации!
Больше нечего делать, наше небольшое племя решило провести несколько тестов, просто чтобы посмотреть, что произойдет.
Пещерные инженеры науки!
Первое наблюдение примитивно просто. Чем толще дерево, тем оно сильнее. Удивительно, но результаты не так уж последовательны, но через несколько лет пещерные люди могут более или менее «угадать», является ли поперечное сечение достаточным или нет.Созданы первые инженерные таблицы:

Это простая площадь поперечного сечения! Чем больше у вас есть, тем лучше!
Несчастные случаи в службе развития
Теоретически, история могла бы закончиться здесь, если бы не тот факт, что кто-то сделал что-то глупое. Вместо того, чтобы поставить прямоугольное поперечное сечение «плоским как всегда», кто-то поставил дерево в вертикальное положение… и вместимость оказалась вне графика!

То же поперечное сечение, но расположенное в другом направлении, дало кардинально разные результаты.
Первое, что легко заметить, это то, что «плоский как всегда» ствол отклоняется гораздо больше, чем «вертикальный» ствол при той же нагрузке пещерного человека (давайте назовем его Тьфу!).
Здесь следует сделать один очень важный вывод: прогиб не зависит от поперечного сечения! Есть «что-то еще»!

Назовите свое направление!
Чтобы заглянуть глубже в это фантастическое открытие, нам нужно сделать несколько предположений.Мы немного безнадежны, когда дело доходит до определения «позиции» дерева. Использование «плоско как всегда» и «вертикально» имеет большое значение для французского дерева… но для неправильной формы такое описание не сработает!
Также мы не можем использовать «top», «bottom», «right» и «left» для описания этой позиции. Это просто доказать:

Это заставило пещерных людей использовать ось. Было легко экспериментально проверить, в каком направлении дерево сгибалось больше всего, а в каком направлении ствол дерева отклонялся меньше всего.Удивительно, но эти направления всегда были перпендикулярны друг другу.

Примечание: направление нагрузки (и направление деформации) перпендикулярно оси! Это означает, что если нагрузка действует вниз, деформация будет направлена против горизонтальной оси. Так же, как я нарисовал выше.
Вначале это может немного смущать, но через некоторое время это становится естественным. 🙂
Благодаря этому открытию, вместо того, чтобы идти с «вершиной» или «вертикально», направление нагрузки (или направление отклонения, если хотите) будет определяться относительно оси.Это идеально, так как поперечное сечение всегда имеет «самое сильное» и «самое слабое» направление. Это не изменится, если вы повернете это поперечное сечение! Также, чтобы избежать путаницы, мы всегда будем размещать оси так, чтобы они пересекались в центре тяжести нашего поперечного сечения.

Также можно заметить, что багажник в вертикальном положении немного качается при загрузке. Возможно, в реальном смысле не колеблется, но, по крайней мере, кажется нестабильным. Это проблема стабильности: каждое поперечное сечение хочет согнуться против самой слабой оси.Если вы согнете его против сильной оси, он попытается повернуть, чтобы изменить место приложения нагрузки. Это называется боковое скручивание при кручении, и это тема для совершенно другой истории!
Где сила спрятана в дереве?
С заданной осью есть только одна часть головоломки, которую нам не хватает. То есть: в чем разница между сильной и слабой осью?
Давайте еще раз посмотрим:

Если бы мы выглядели достаточно долго, это определенно поразило бы нас! Дерево ближе к слабой оси и более «далеко» от сильной оси.По сути, это единственное и самое важное отличие.
Если материал поперечного сечения находится «далеко» от оси этого поперечного сечения, поперечное сечение будет «более прочным» или более жестким. Если материал находится близко к оси, это будет относительно «слабая» ось.
Это явление описывается параметром момент инерции.
Если подумать, это имеет смысл. В конце концов, именно поэтому мы делаем I-секции правильными?

История продолжается…
Если честно, в этой истории есть кое-что еще, но мы дошли до того, что я могу просто ответить на вопрос Маноя.Я уверен, что рано или поздно я вернусь к этому!
Ответить на оригинальный вопрос
Плоская панель имеет очень маленький момент инерции . Проще говоря, у него есть материал очень близко к оси, относительно которой вы будете сгибать его. Изогнутая панель имеет гораздо больший момент инерции на той же оси. Вот почему он ведет себя гораздо жестче!

Конечно, момент инерции влияет гораздо больше, чем прогиб при изгибе.То есть если секция имеет более высокий момент инерции, она также с меньшей вероятностью прогибается.
В целом люди относятся к моменту инерции как к жесткости. Чтобы быть справедливым, жесткость — это более широкий термин, но обычно момент инерции где-то есть!
Я надеюсь, вы нашли это полезным!
Хотите узнать больше?
Прежде всего, если у вас есть вопрос, связанный с ВЭД или конструкционной сталью, не стесняйтесь отправить его мне по адресу: enterfea @ enterfea.ком. Вы также можете оставить его в комментариях ниже или отправить через Linkedin. Таким образом, я смогу ответить на ваш вопрос, так же, как и на вопрос, который я получил от Маноя!
Знание жесткости — отличный шаг к использованию ВЭД. Это потому, что жесткость является одним из фундаментальных понятий, которые вам необходимо понять, чтобы освоить метод конечных элементов. Если вам нравится FEA, вы можете узнать некоторые полезные вещи из моего бесплатного курса по основам FEA.
,
