4.5. Зависимости между моментами инерции при повороте осей. Главные оси и главные моменты инерции. Радиус инерции сечения
Вычислим моменты инерции фигуры
произвольной формы относительно осей,
повернутых относительно заданных осей  и
и на угол
на угол (Рис.4.14)
(Рис.4.14)
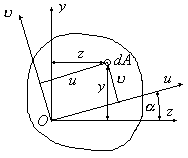
Рис.4.14
Пусть моменты инерции относительно
осей  и
и
 и выразим ее координаты в системе осей
и выразим ее координаты в системе осей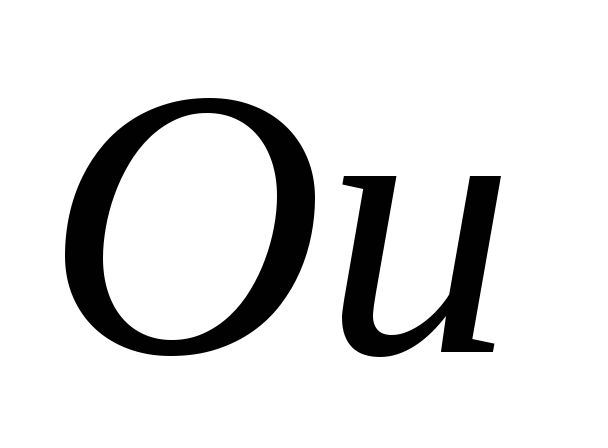 и
и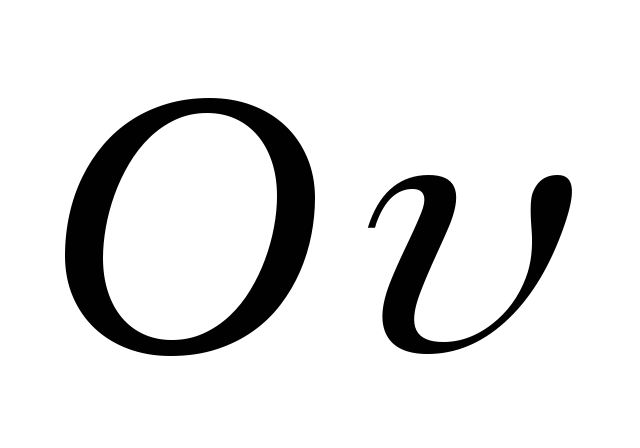 через координаты в прежних осях
через координаты в прежних осях и
и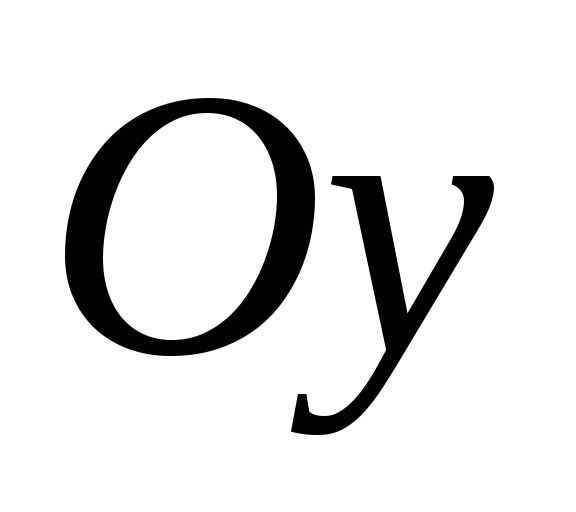 :
:  ,
,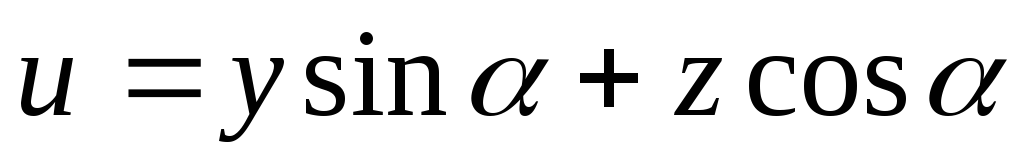
Найдем осевые и центробежный моменты
инерции фигуры относительно повернутых
осей 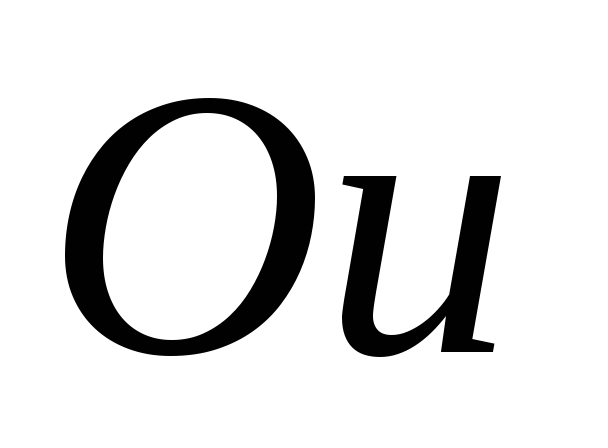 и
и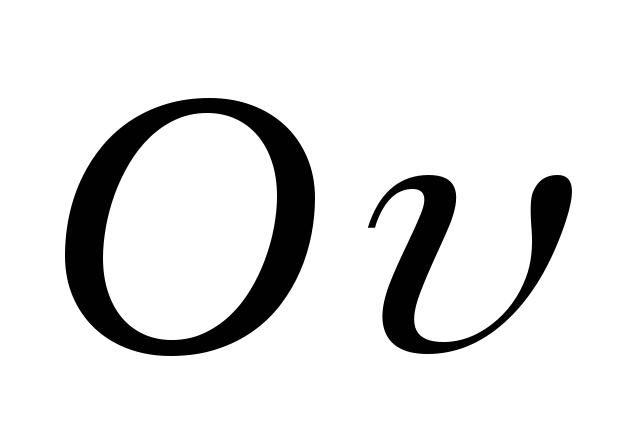 :
:
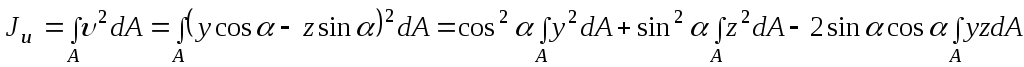 .
(4.28)
.
(4.28)
Принимая во внимание, что
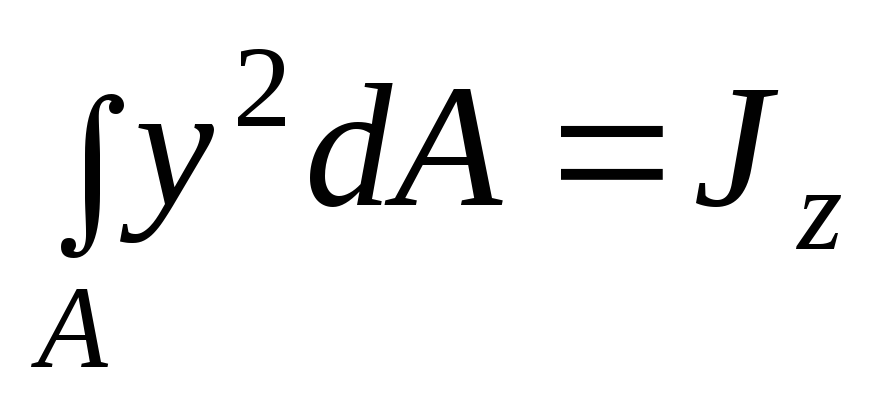
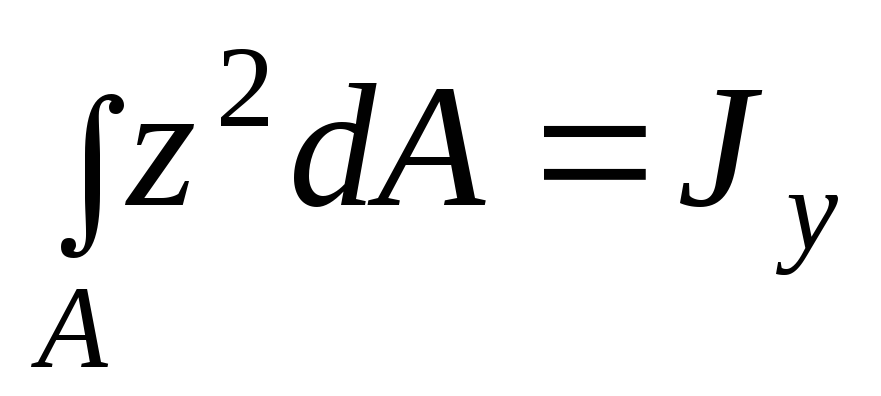 и
и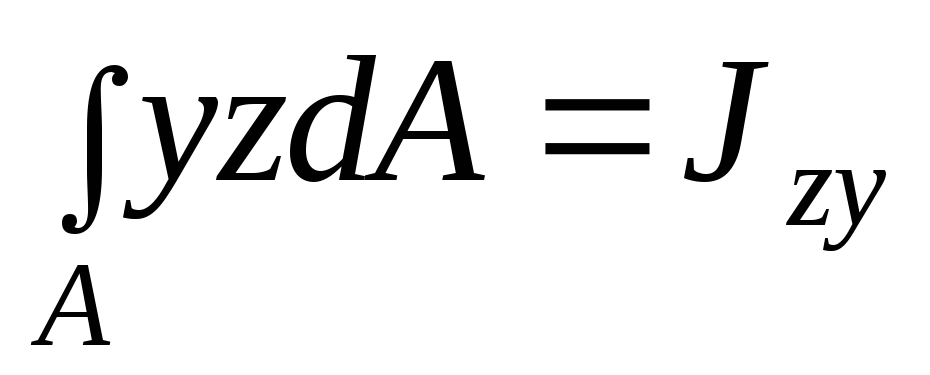 ,
,получим:
 .
(4.28)
.
(4.28)
Таким же образом установим:
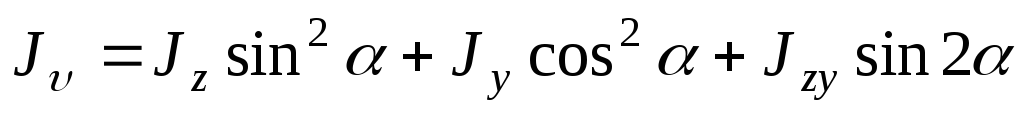 .
(4.29)
.
(4.29)
Центробежный момент инерции принимает вид:

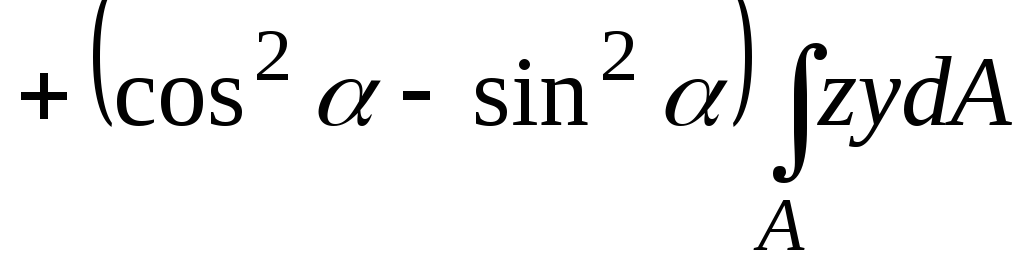
или
 .
(4.30)
.
(4.30)
Выразим осевые моменты через синус и косинус двойного угла. Для этого введем следующие функции:
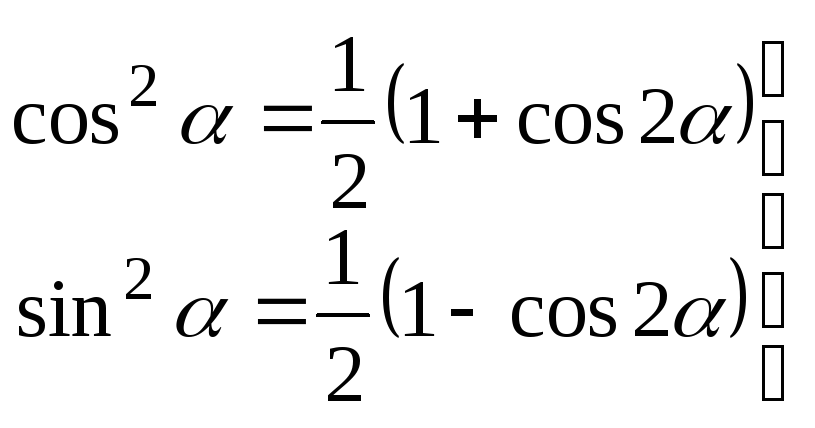 . (4.31)
. (4.31)
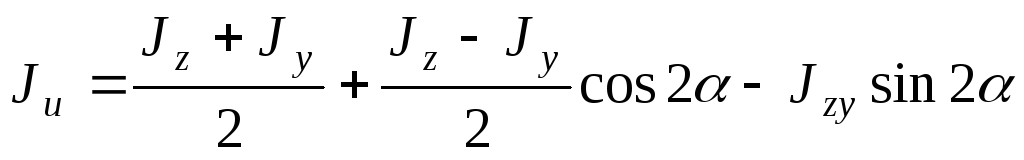 .
(4.32)
.
(4.32)
 .
(4.33)
.
(4.33)
Если сложить выражения для осевых моментов инерции (4.32) и (4.33), то получим:
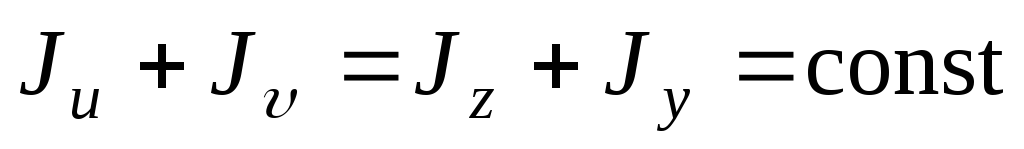 .
(4.34)
.
(4.34)
Условие (4.34) представляет условие инвариантности суммы осевых моментов инерции относительно двух взаимно перпендикулярных осей, т.е.
Исследуем уравнение для момента инерции  на экстремум и найдем такое значение
угла
на экстремум и найдем такое значение
угла ,
при котором момент инерции достигнет
экстремальной величины. Для этого
возьмем первую производную от момента
инерции
,
при котором момент инерции достигнет
экстремальной величины. Для этого
возьмем первую производную от момента
инерции
 (выражение (4.32)) и результат приравняем
нулю. При этом положим
(выражение (4.32)) и результат приравняем
нулю. При этом положим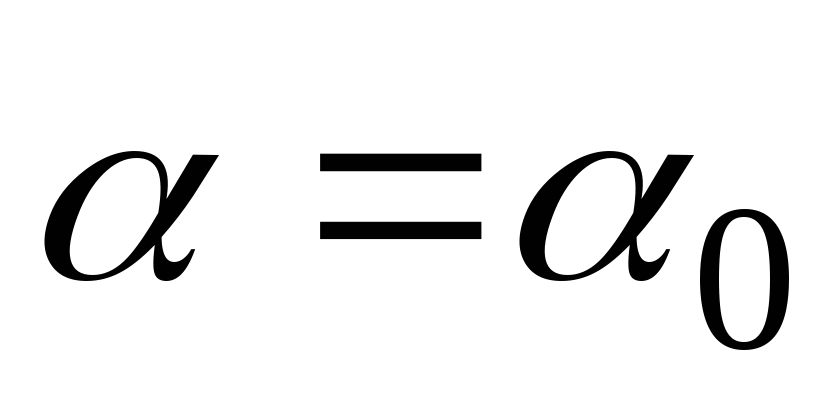 .
. 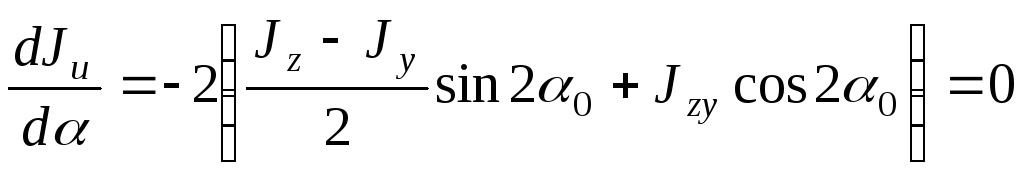 (4.35)
(4.35)
Выражение в скобках представляет собой
центробежный момент инерции относительно
осей, наклоненных к оси 
 .
Относительно этих осей центробежный
момент инерции равен нулю:
.
Относительно этих осей центробежный
момент инерции равен нулю: 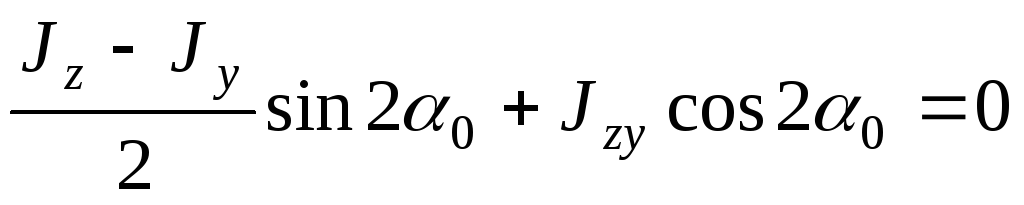 ,
(4.36)
,
(4.36)
а это означает, что новые оси являются главными осями.
Ранее было определено, что главными осями инерции являются оси, относительно которых центробежный момент инерции равен нулю. Сейчас это определение можно расширить – это оси, относительно которых осевые моменты инерции
Найдем положение главных осей инерции. Из выражения (4.36) можно получить:
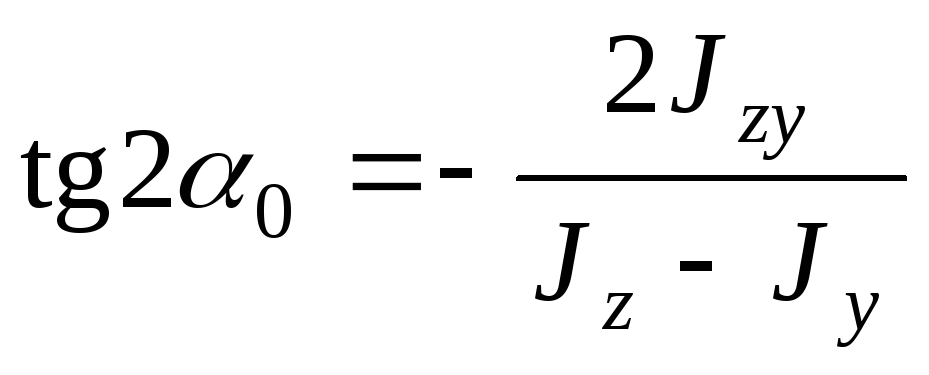 .
(4.37)
.
(4.37)
Полученная формула дает для угла 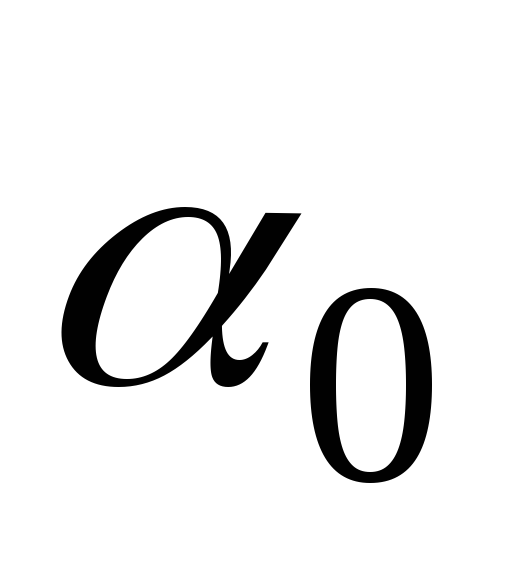 два значения:
два значения: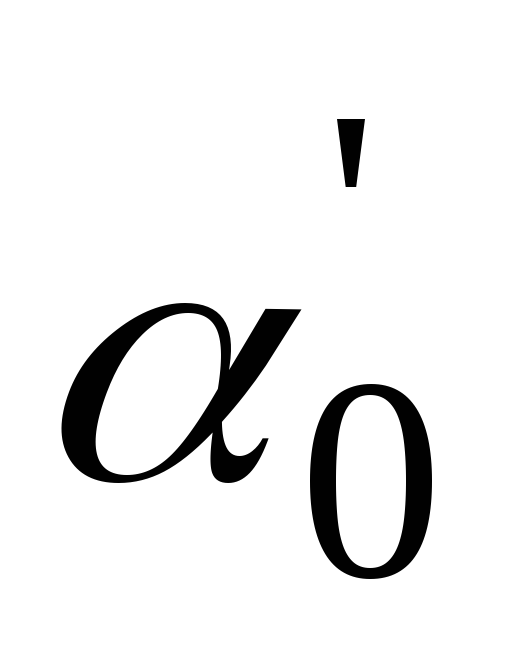 и
и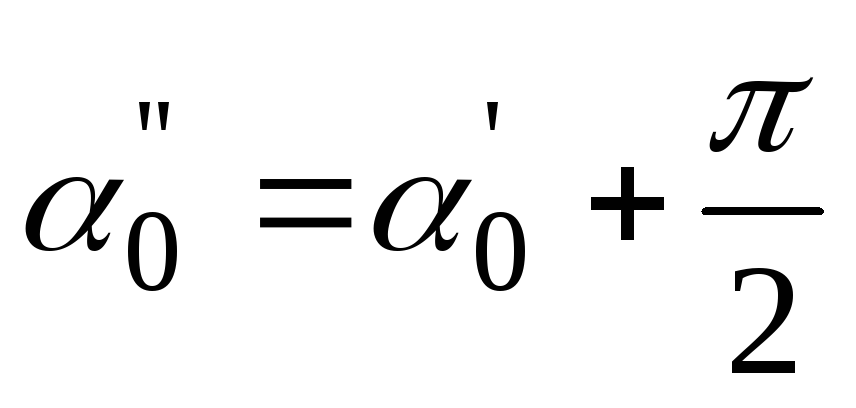
Следовательно, существуют две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Как уже отмечалось выше, такие
оси называются главными осями инерции.
Остается установить, относительно какой
из осей момент инерции достигает
максимального значения, а относительно
какой – минимального значения. Решить
эту задачу можно путем исследования
второй производной от выражения (4.32) по
углу  .
Подставив в выражение для второй
производной значение угла
.
Подставив в выражение для второй
производной значение угла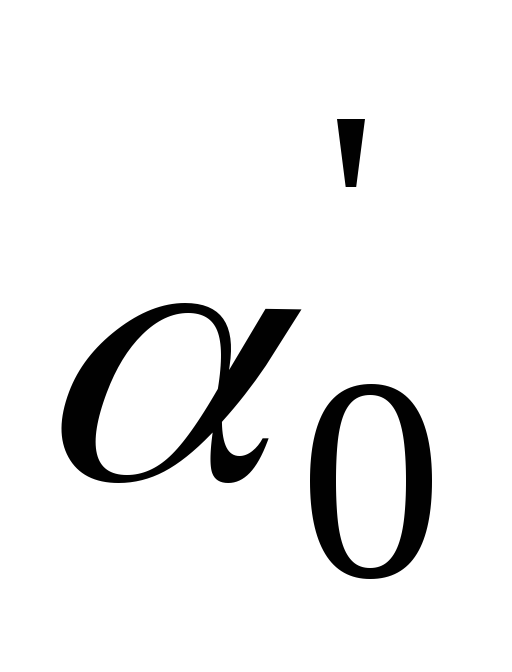
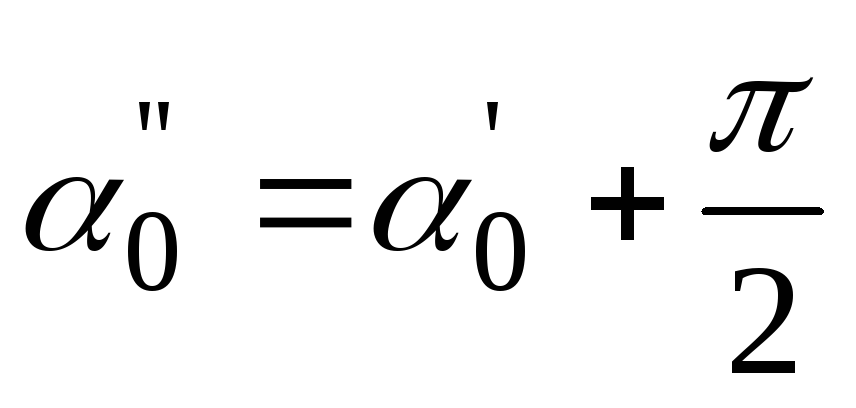 и исследуя знак второй производной,
можно судить о том, какой из углов
соответствует максимальному моменту
инерции, какой – минимальному. Ниже
будут приведены формулы, которые дадут
однозначное значение угла
и исследуя знак второй производной,
можно судить о том, какой из углов
соответствует максимальному моменту
инерции, какой – минимальному. Ниже
будут приведены формулы, которые дадут
однозначное значение угла .
. Найдем экстремальные значения для
моментов инерции. Для этого преобразуем
выражение (4.32) , вынося за скобку  :
:
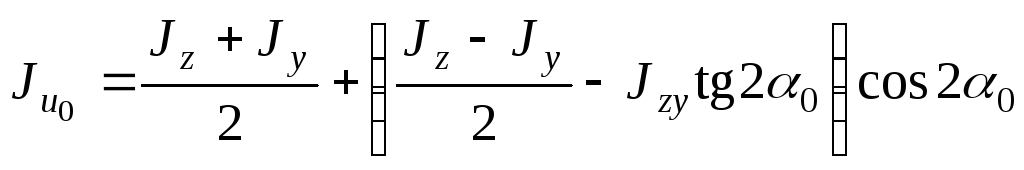
Используем известную из тригонометрии функцию и подставим в нее выражение (4.37), получим:
 .
(4.39)
.
(4.39)
Подставляя в формулу (4.38) выражение
(4.39) и производя необходимые вычисления,
получаем два выражения для экстремальных
моментов инерции, которые не включают
в себя угол наклона осей  :
:
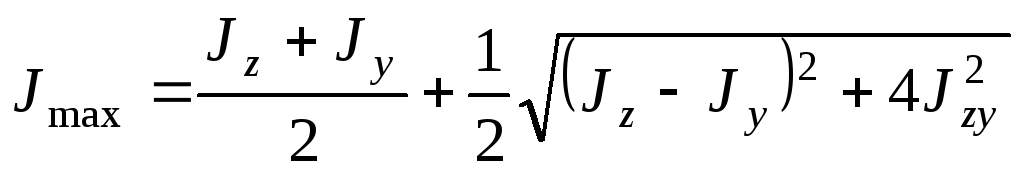
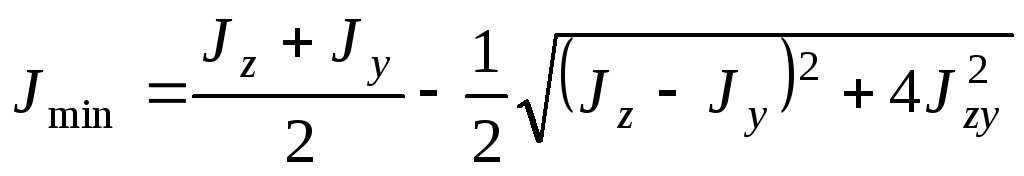 . (4.41)
. (4.41)
Из формул (4.40) и (4.41) видно, что величины
главных моментов инерции определяются
непосредственно через моменты инерции
относительно осей  и
и .
Поэтому их можно определять, не зная
положения самих главных осей.
.
Поэтому их можно определять, не зная
положения самих главных осей.
Зная экстремальные значения моментов
инерции 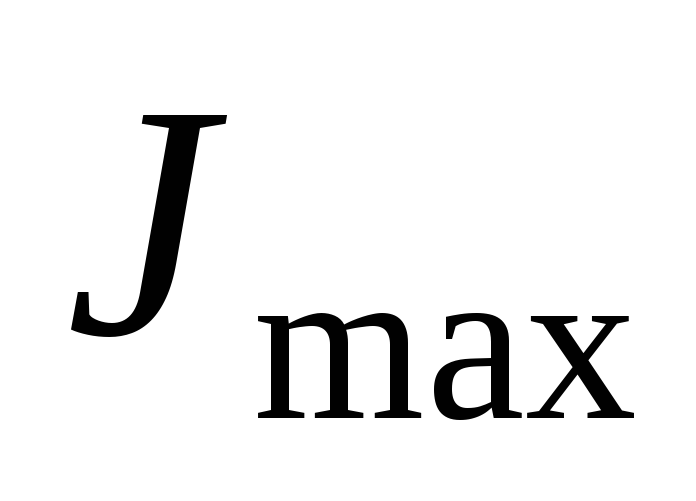 и
и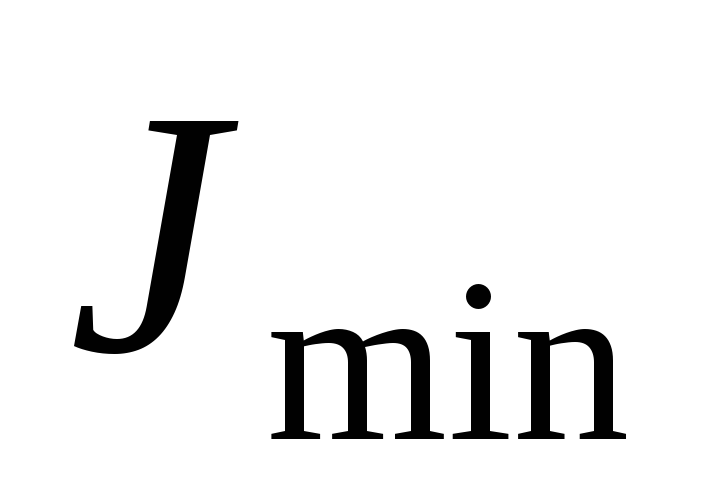 можно помимо формулы (4.37) определять
положение главных осей инерции.
можно помимо формулы (4.37) определять
положение главных осей инерции.
Приведем без вывода формулы, позволяющие
находить углы 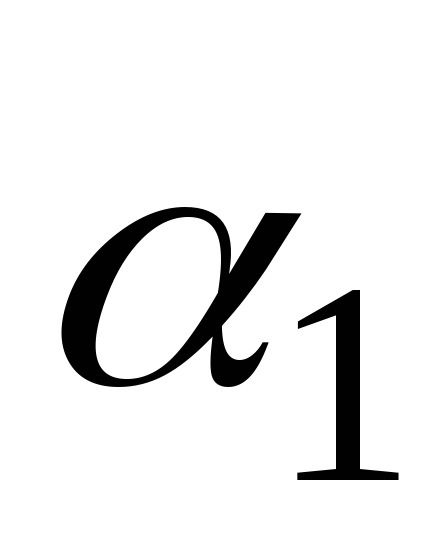 и
и между осью
между осью и главными осями:
и главными осями:
 ;
;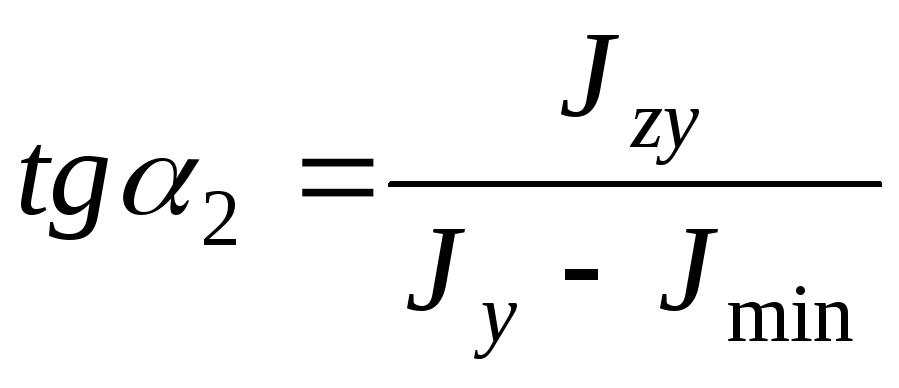 (4.42)
(4.42)
Угол 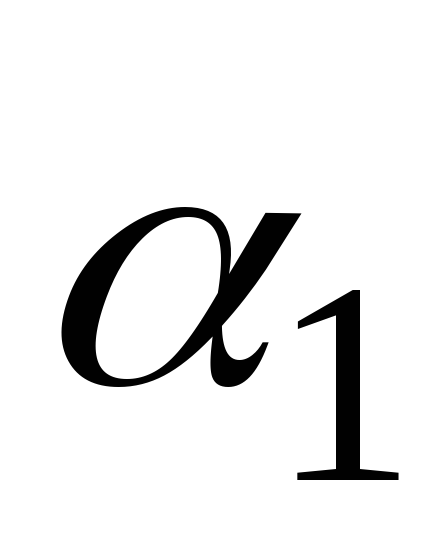 определяет положение оси, относительно
которой момент инерции достигает
максимальной величины (
определяет положение оси, относительно
которой момент инерции достигает
максимальной величины (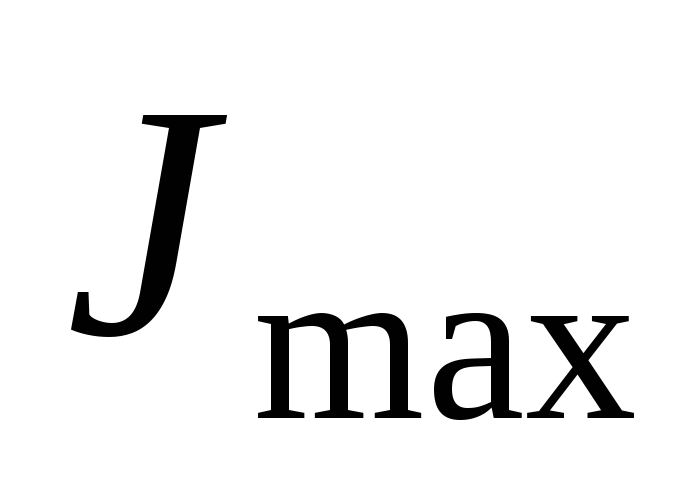 ),
угол
),
угол определяет положение оси, относительно
которой момент инерции достигает
минимальной величины (
определяет положение оси, относительно
которой момент инерции достигает
минимальной величины ( ).
).
Введем еще одну геометрическую
характеристику, которая называется
радиусом инерции сечения. Обозначается
эта характеристика буквой  и может быть вычислена относительно
осей
и может быть вычислена относительно
осей и
и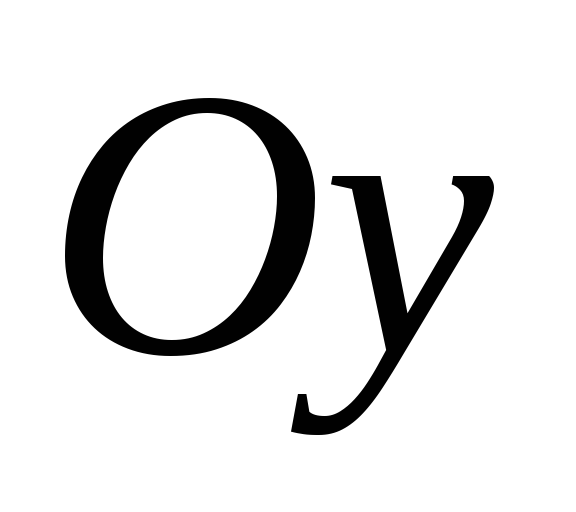 следующим образом:
следующим образом:
 ;
;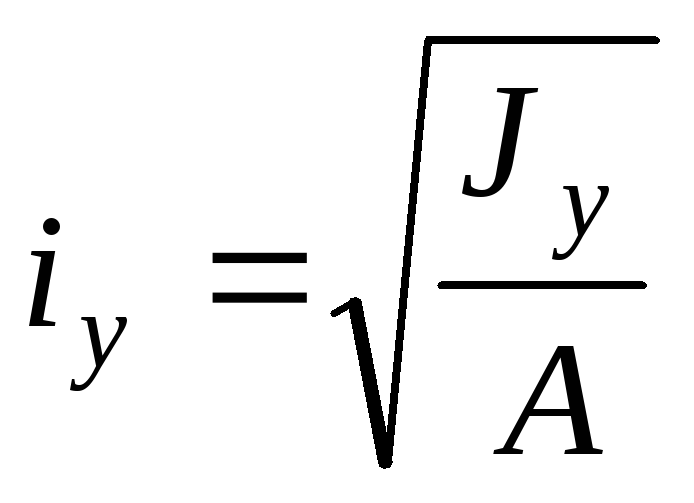 (4.43)
(4.43)
Радиус инерции находит широкое применение в задачах сопротивления материалов и его применение будет рассмотрено в следующих разделах курса.
Рассмотрим несколько примеров расчетов конструкций с учетом поворота осей и с использованием радиуса инерции сечения.
Пример 4.7. Моменты инерции сечения
прямоугольной формы относительно
главных осей равны соответственно см4,
см4, см4.
При повороте на 450моменты инерции
относительно новых осей оказались
одинаковыми. Чему равна их величина?
см4.
При повороте на 450моменты инерции
относительно новых осей оказались
одинаковыми. Чему равна их величина?
Решение:
Для решения задачи воспользуемся выражением (4.28) с учетом того, что центробежный момент инерции относительно главных осей равен нулю:
 .
(а)
.
(а)
Подставим в формулу (а) численные значения для моментов инерции и угла поворота осей:
 см4.
см4.
Пример
4.8. У которой
из фигур (Рис.4.15), имеющих одинаковую
площадь, радиус инерции относительно
оси 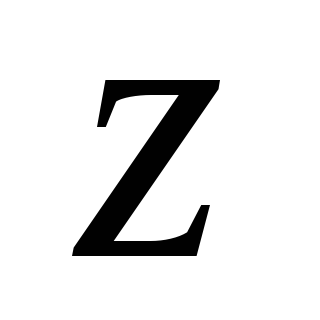 ,
будет
наибольшим?
Определить
наибольший радиус инерции сечения
относительно оси
,
будет
наибольшим?
Определить
наибольший радиус инерции сечения
относительно оси 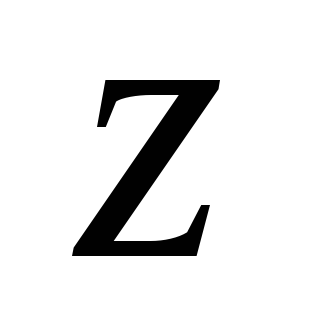 .
.
Решение:
1. Найдем площадь каждой из фигур и
размеры сечений. Площадь фигур равняется
для третьей фигуры 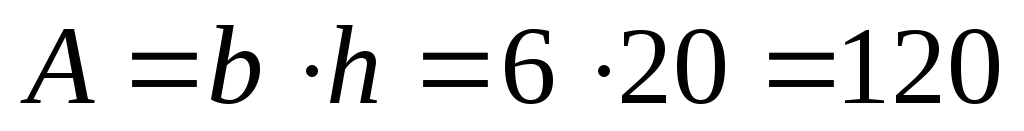 см2.
см2.
Диаметр первого сечения найдем из выражения:
 см.
см.
Размер стороны квадрата:
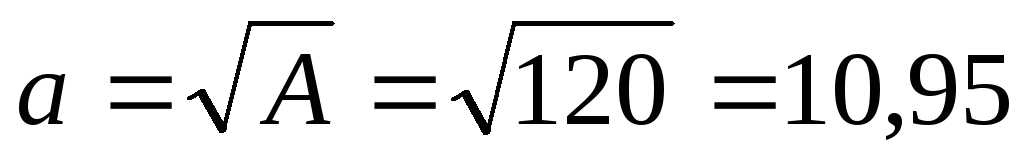 см.
см.
Основание треугольника:
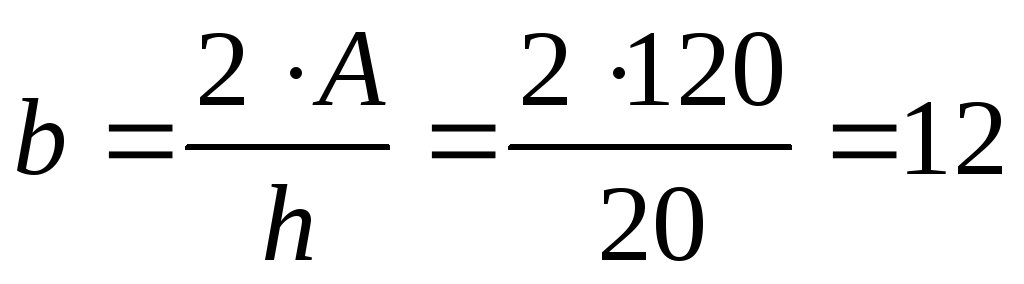 см.
см.

Рис.4.15
2. Находим моменты и радиусы инерции
каждого из сечений относительно
центральной оси  .
.
Для сечения круглой формы:
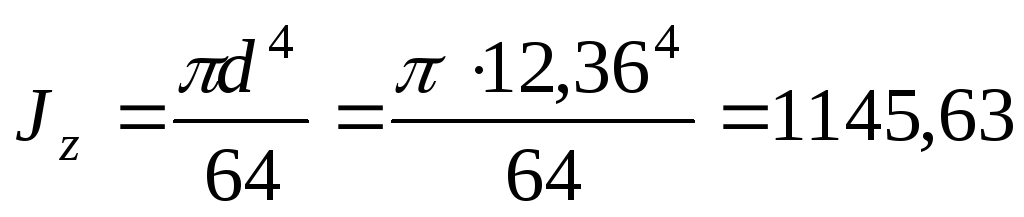 см4;
см4; см.
см.
Для сечения квадратной формы:
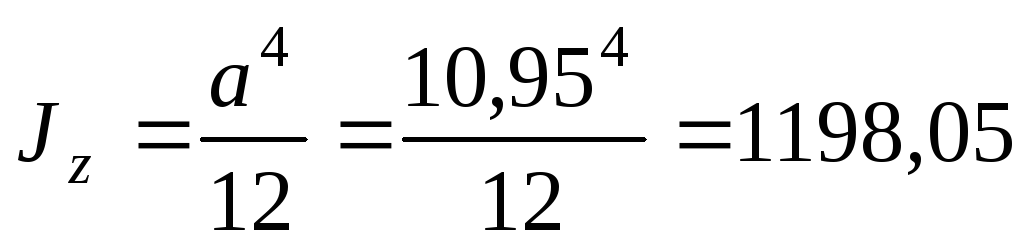 см4;
см4;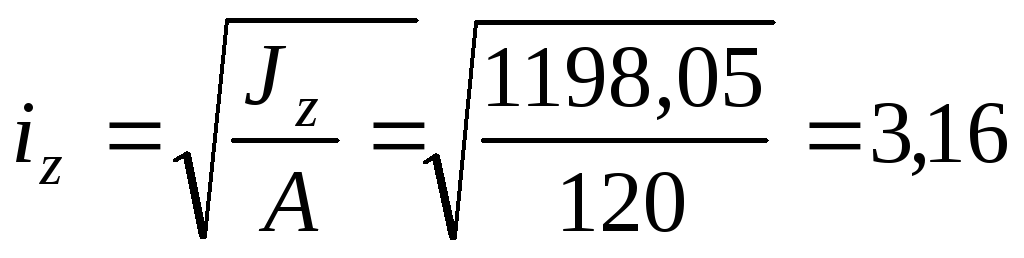 см.
см.
Для сечения прямоугольной формы:
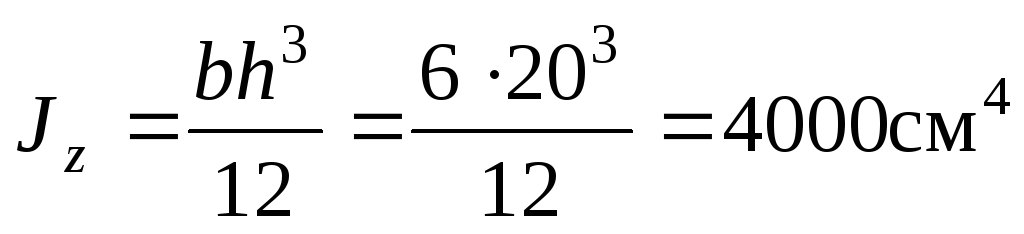 ;
;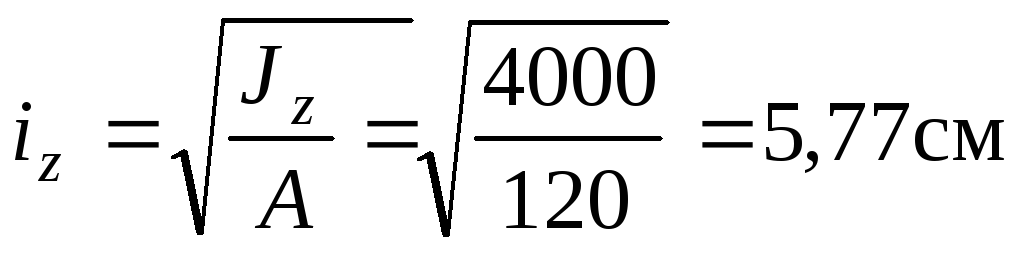
Для сечения треугольной формы:
 см4;
см4;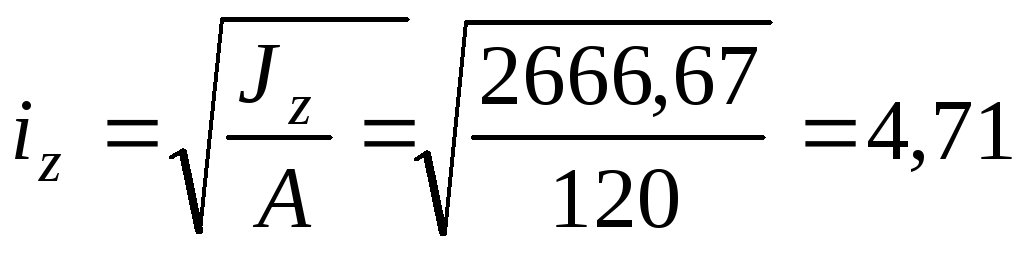 см.
см.
Наибольший радиус инерции оказался у
сечения прямоугольной формы и равен он  см.
см.
Момент инерции при повороте осей координат (сопромат)
Пусть нам известны собственные моменты инерции , и относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси и , повернутые относительно осей x и y на угол (рис. 4.3, б). Будем считать этот угол положительным при повороте осей координат против хода часовой стрелки.
Моменты инерции поперечного сечения при повороте осей координат определяются по формулам:
;
.
Из формул моментов инерции при повороте осей координат видно, что сумма собственных осевых моментов инерции не изменяется при повороте координатных осей:
Две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда из третьей формулы моментов инерции при повороте осей координат легко можно определить направление этих осей:
Из полученного выражения найдем два значения угла , которые отличаются друг от друга на угол , которые определяют положение двух главных центральных осей.
24.Зависимость между моментами инерции при повороте осей. Главные оси и главные моменты инерции.
Найдем
зависимость межу моментами инерции
относительно осей 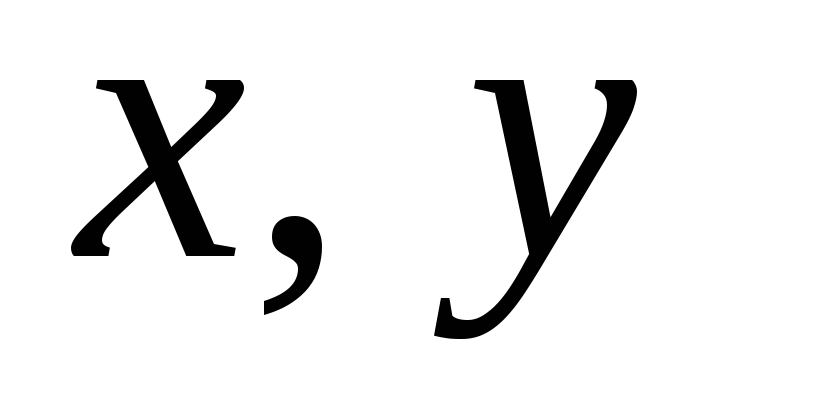 и моментами инерции относительно осей
и моментами инерции относительно осей ,
повернутых на угол
,
повернутых на угол (рис. 3.11). Пусть
(рис. 3.11). Пусть и положительный угол
и положительный угол отсчитывается от оси
отсчитывается от оси против часовой стрелки.
против часовой стрелки.
Рис. 3.11. Поворот осей координат
Для
решения поставленной задачи найдем
зависимость между координатами бесконечно
малой площадки  в
исходных и повернутых осях
в
исходных и повернутых осях
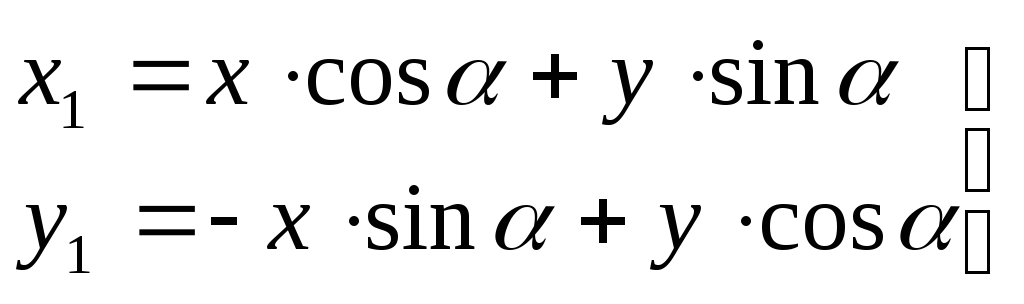 (3.27)
(3.27)
Теперь
определим моменты инерции относительно
осей 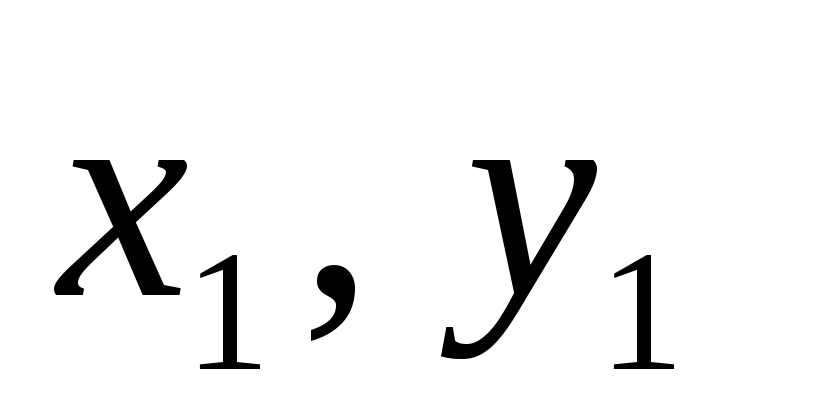
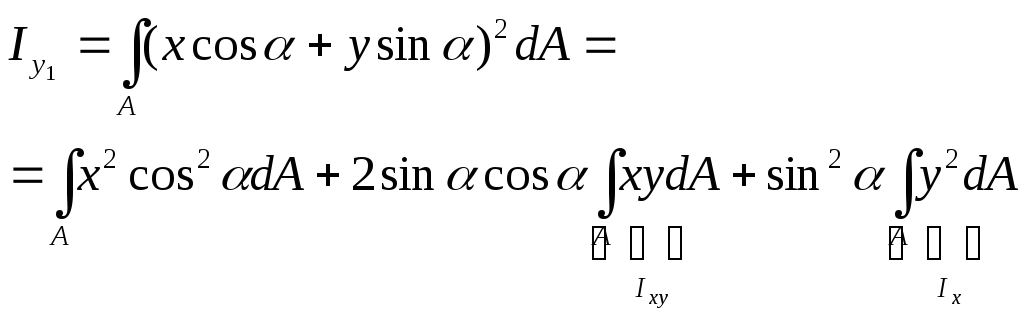
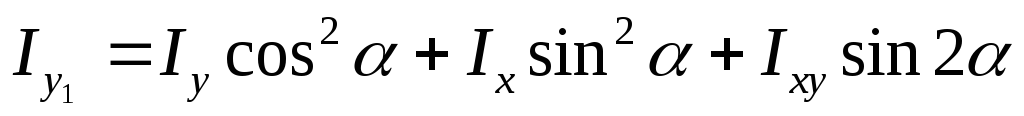 . (3.28)
. (3.28)
Аналогично

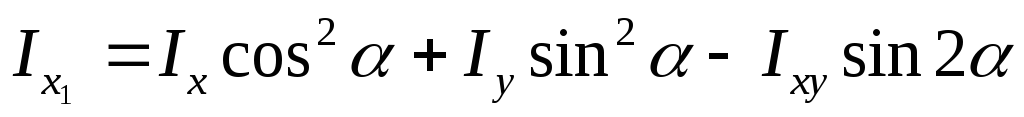 . (3.29)
. (3.29)
Для центробежного момента
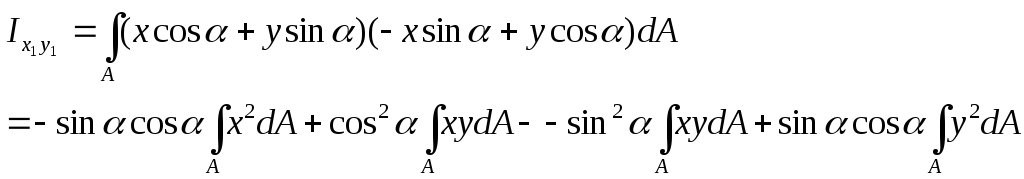
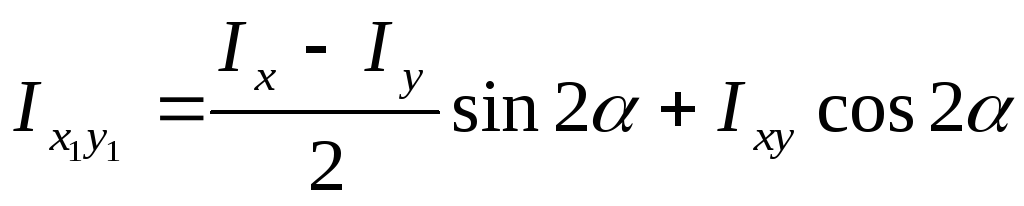 . (3.30)
. (3.30)
Складывая (3.28) и (3.29), получаем
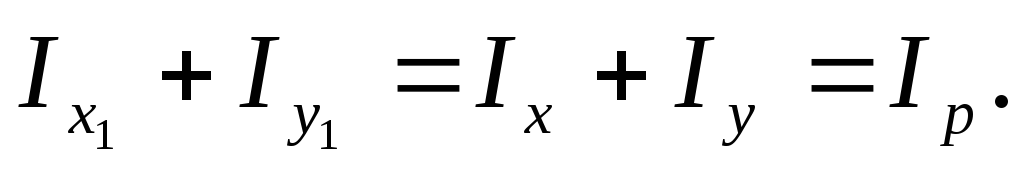 (3.31)
(3.31)
Вычитая (3.28) из (3.29), получаем
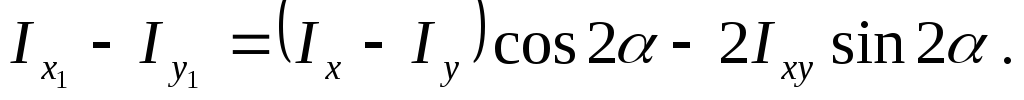 (3.32)
(3.32)
Формула (3.31) показывает, что сумма моментов инерции относительно любых взаимно перпендикулярных осей не меняется при их повороте.
Формула
(3.32) может быть использована для вычисления
центробежного момента инерции относительно
осей 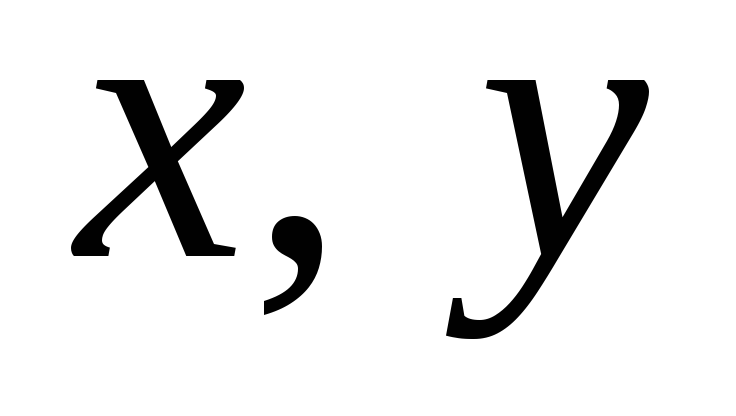 по известным осевым моментам инерции
относительно осей
по известным осевым моментам инерции
относительно осей и
и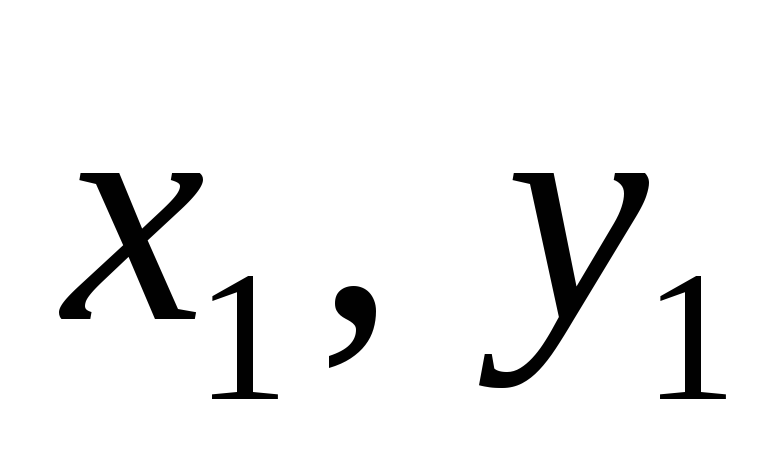 .
.
Главные оси инерции и главные моменты инерции
При
изменении угла  (рис. 3.10)
моменты инерции (3.280 – (3.31) изменяются.
Найдем значение угла, при котором
(рис. 3.10)
моменты инерции (3.280 – (3.31) изменяются.
Найдем значение угла, при котором 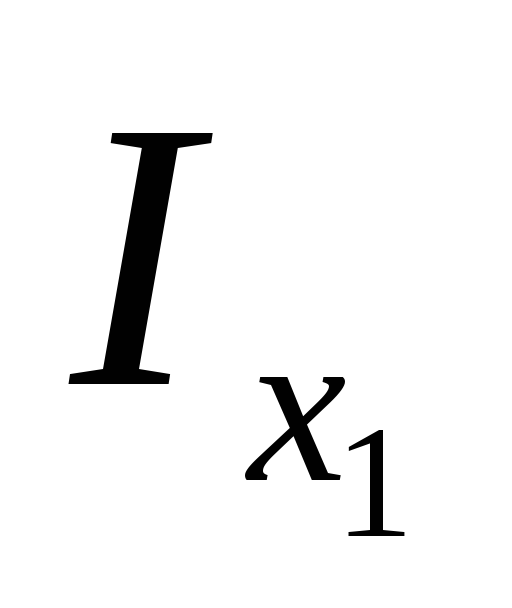 и
и 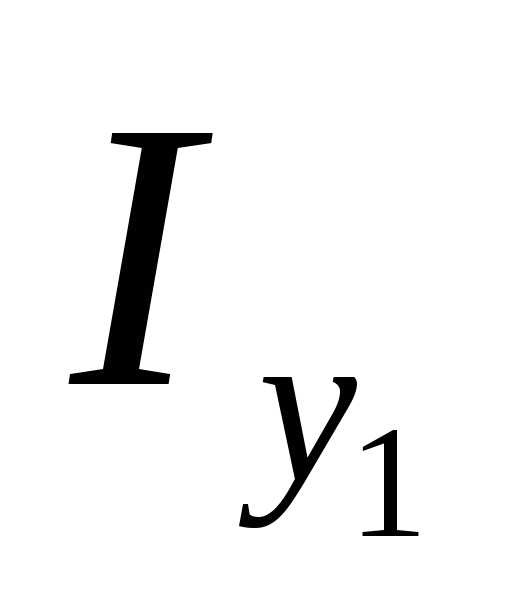 имеют экстремальное значение. Для этого
возьмем от
имеют экстремальное значение. Для этого
возьмем от 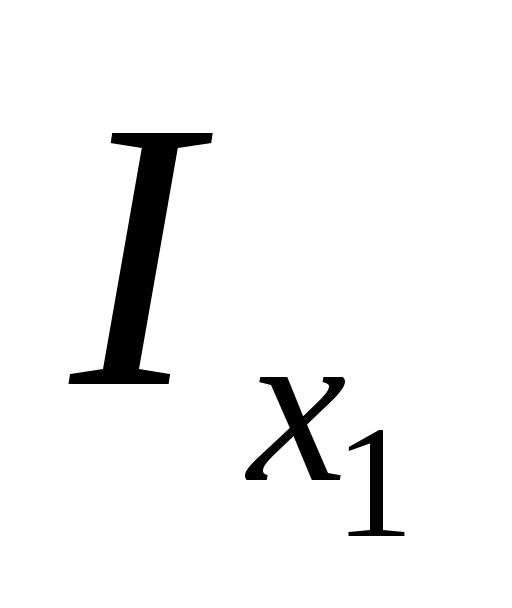 и
и 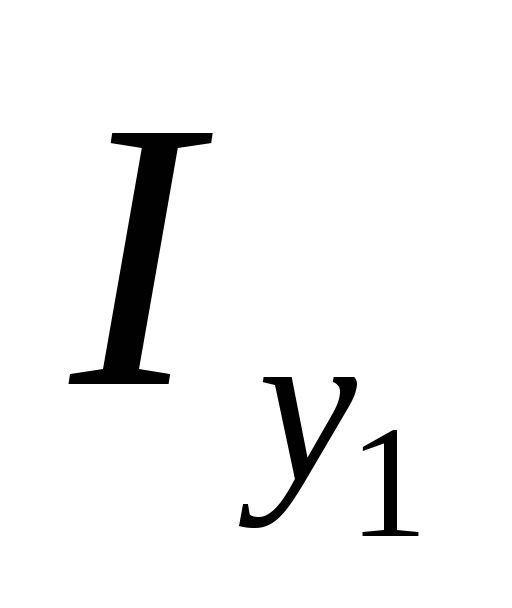 первую производную по
первую производную по и приравниваем ее нулю:
и приравниваем ее нулю:

или

откуда
 (3.33)
(3.33)
Эта формула определяет положение двух осей, относительно которых осевой момент инерции максимален, а относительно другой минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции.
Значения
главных моментов инерции найдем из
формул (3.28) и (3.29, подставив в них 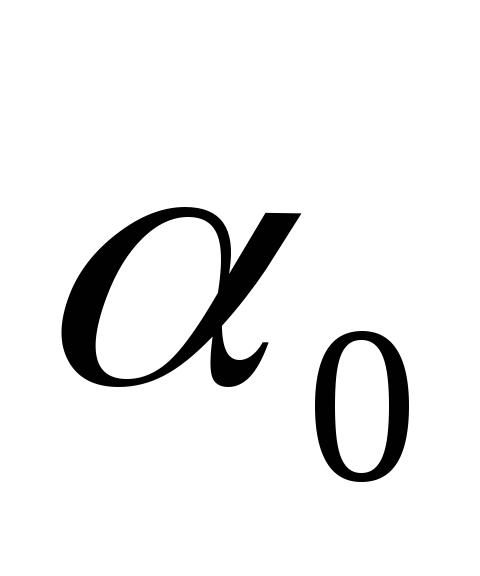 из формулы (3.33), при этом используем
известные формулы тригонометрии для
функций двойных углов. После преобразования
получим формулу для определения главных
моментов инерции:
из формулы (3.33), при этом используем
известные формулы тригонометрии для
функций двойных углов. После преобразования
получим формулу для определения главных
моментов инерции:
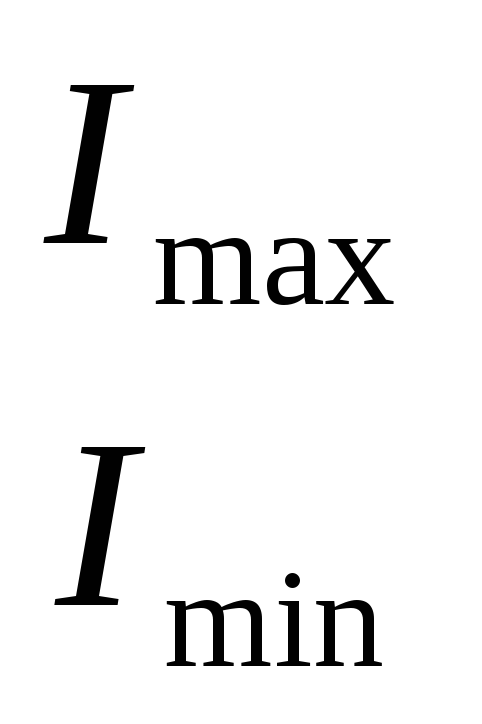 =
= (3.34)
(3.34)
Покажем
теперь, что относительно главных осей
центробежный момент инерции равен нулю.
Действительно, приравнивая  по формуле (3.30) нулю, получаем
по формуле (3.30) нулю, получаем
 ,
,
откуда
для  вновь получается формула (3.33)
вновь получается формула (3.33)
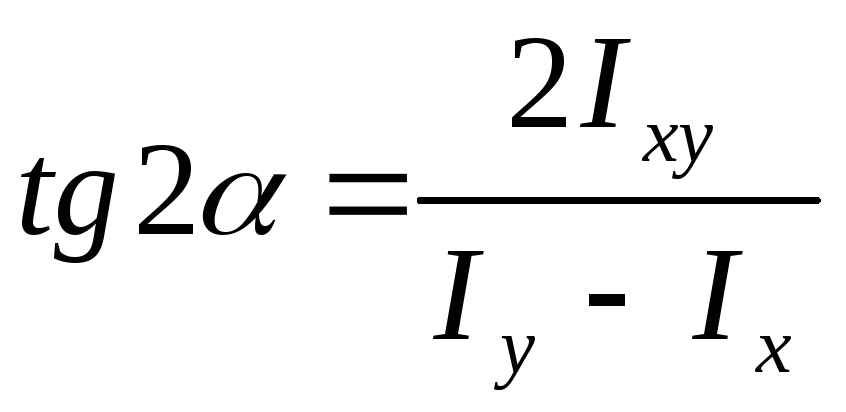 .
.
Таким образом, главными осями называют оси, обладающие следующими свойствами:
Центробежный момент инерции относительно этих осей равен нулю.
Моменты инерции относительно главных осей имеют экстремальные значения (относительно одной – максимум, относительно другой – минимум).
Главные оси, приходящие через центр тяжести сечения, называются главными центральными осями.
Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Это следует из того обстоятельства, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.
25.Вычисление главных центральных осевых моментов инерции простых сечений.
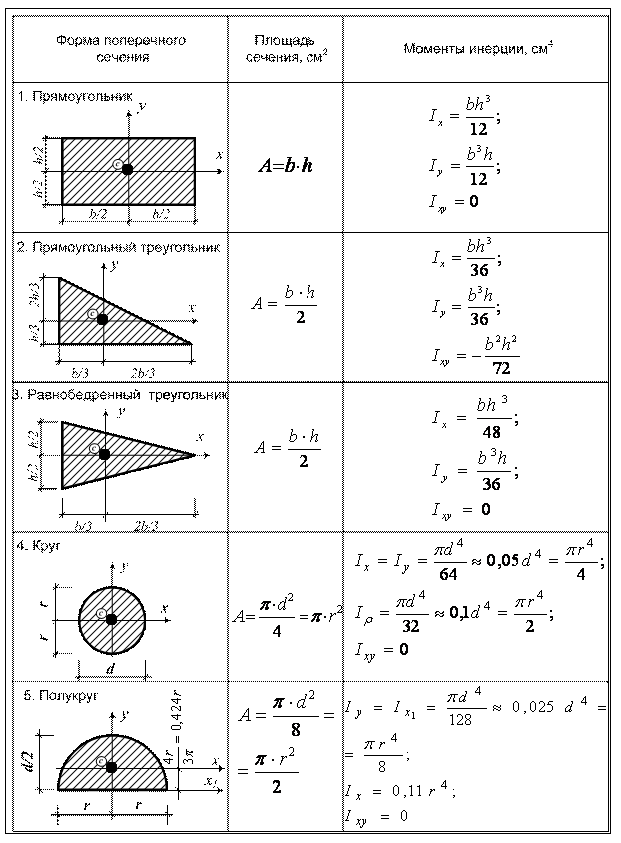
26.Вычисление главных центральных осевых моментов инерции сложных сечений.
При отсутствии у заданного сечения оси симметрии задача решается в следующей порядке последовательности:
1. Сечение разбиваем на простые фигуры и проводим их вертикальные и горизонтальные центральные оси.
2. Проводим произвольные оси Z’ и Y’, параллельные центральным осям простых фигур.
3. Определяем координаты центра тяжести заданного сечения zС и yС относительно осей Z’ и Y’ по формулам (5.3).
4. Откладываем расстояния zС и yС с учетом знаков от осей Z’ и Y’ и проводим центральные оси всего сечения Z и Y, параллельные осям Z’ и Y’.
5. Определяем осевые и центробежные моменты инерции всего сечения относительно осей Z и Y по формулам (5.9).
6. Определяем величины главных центральных (экстремальных) моментов инерции всего сечения по формуле:
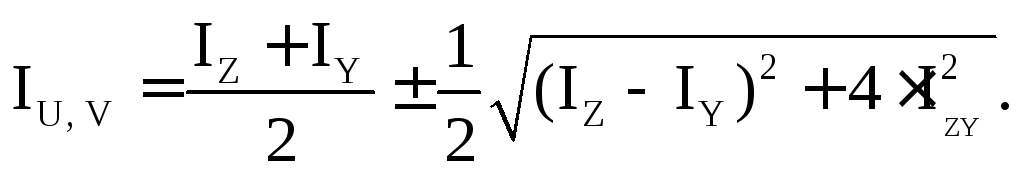 (5.21)
(5.21)
7. Определяем положение главных центральных осей:
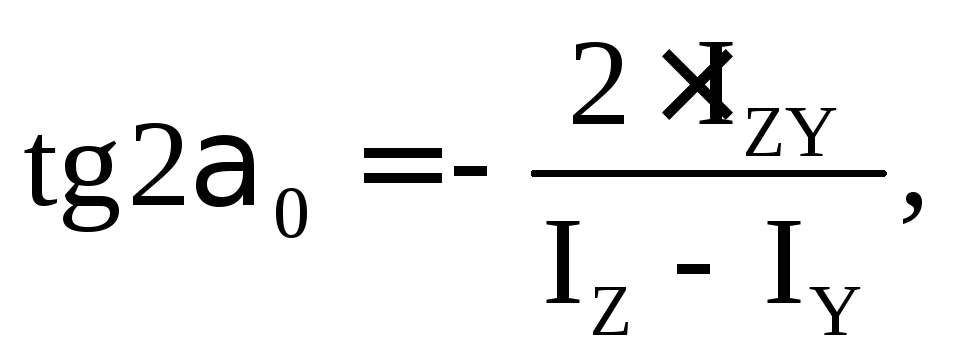 (5.22)
(5.22)
где – угол, на который нужно повернуть осиZ и Y, чтобы они стали главными.
Угол 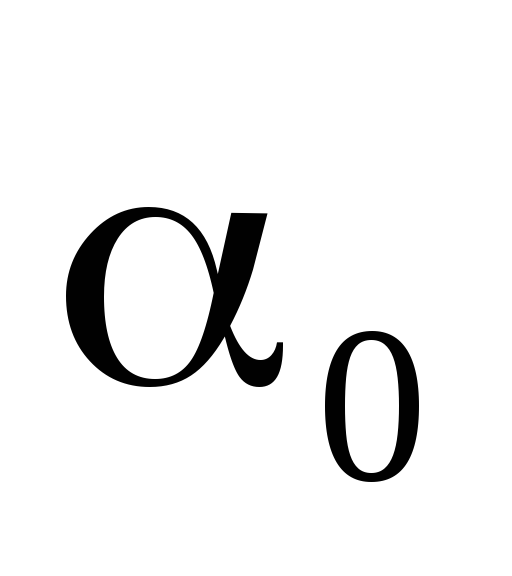 нужно отложить против хода часовой
стрелки, если он имеет знак «плюс»
и по ходу часовой стрелки – если знак
«минус».
нужно отложить против хода часовой
стрелки, если он имеет знак «плюс»
и по ходу часовой стрелки – если знак
«минус».
27.Крутящийся момент и его определение. Построение эпюры крутящего момента. Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.
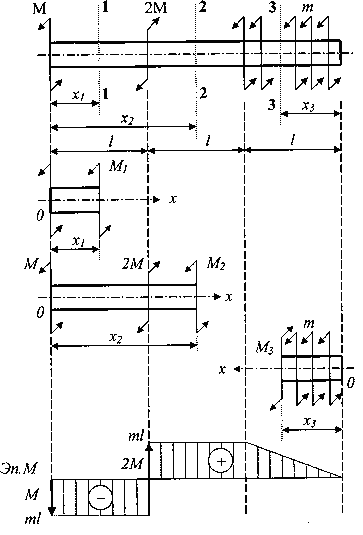
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m, рис.2.
Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
а) расчетная схема, б) первый участок, левая часть в) второй участок, левая часть г) третий участок, правая часть, д) эпюра внутренних крутящих моментов
Рис. 2. Построение эпюры внутренних крутящих моментов:
В исходных сечениях No 1,2 и 3 задаются положительными значениями внутренних крутящих моментов М1, М2, М3. Пусть М=ml.
Для первого участка (рис.2 б):

Для второго участка (рис.2 в):
Для третьего участка (рис.2 г):

Границы измерения параметра х3 в следующей системе координат:
Тогда:

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис.2 д).
Зависимость между моментами инерции при повороте осей
новых осях через
координаты в старых осях, угол  при повороте осей против часовой стрелки:
при повороте осей против часовой стрелки:
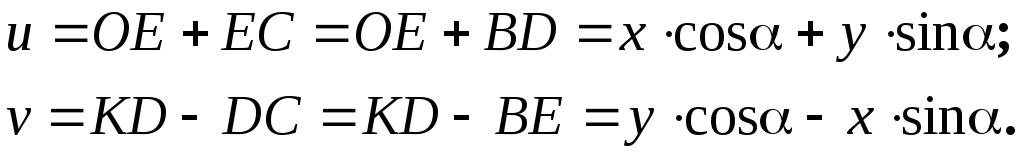
Найдем момент
инерции относительно оси  :
:

Учитывая, что 
Окончательно получим
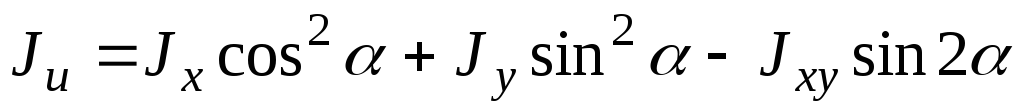 (2.11)
(2.11)
Аналогично можно установить, что
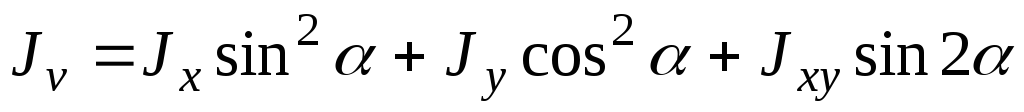 (2.11а)
(2.11а)
Для центробежного момента инерции получим
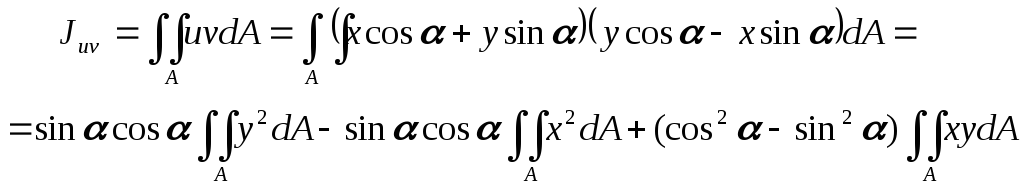
Учитывая, что 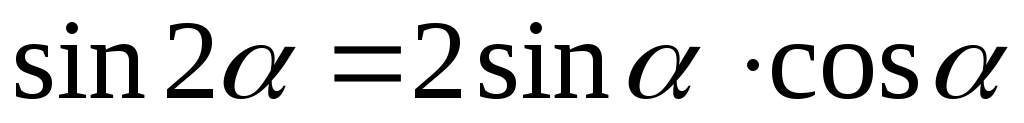 и
и 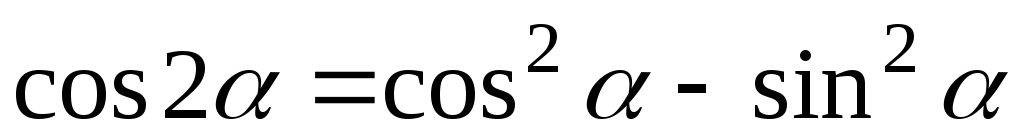 ,
получим
,
получим
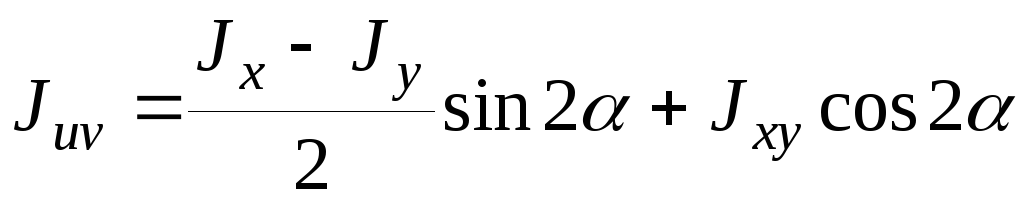 (2.12)
(2.12)
Сложим выражения (2.11) и (2.11а), получим

Сумма моментов инерции относительно любых взаимно перпендикулярных осей у и х не меняются при их повороте. Это показано и соотношением (2.8).
Главные оси инерции и главные моменты инерции
В предыдущем
разделе было показано, что величины
моментов инерции меняются
при повороте осей.
Можно найти такое значение угла  ,
при котором момент инерции достигает экстремального значения. Для определения экстремума
приравняем нулю первую производную от
(2.11) и положим
,
при котором момент инерции достигает экстремального значения. Для определения экстремума
приравняем нулю первую производную от
(2.11) и положим 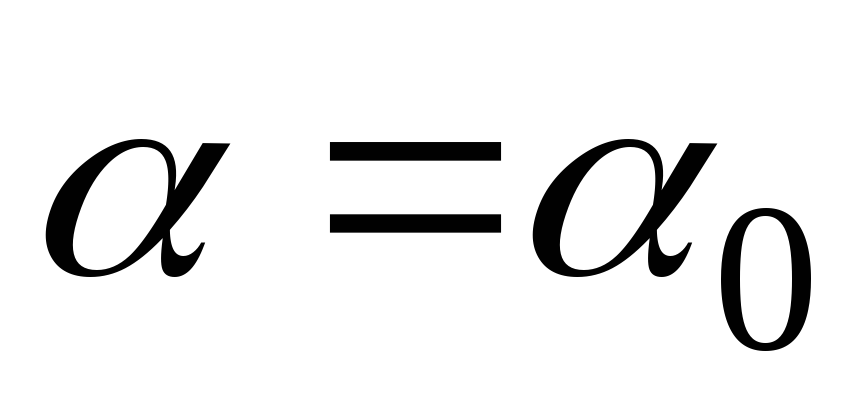 :
:
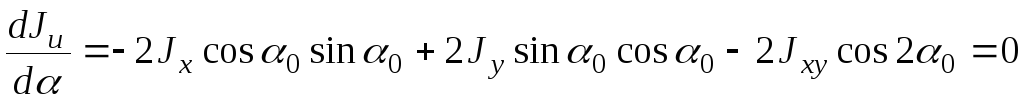
или

откуда
 (2.13)
(2.13)
Полученная формула
дает для угла  два значения, отличающиеся на 90.
Следовательно, существует две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Такие оси называют главными
осями инерции,
их будем обозначать
два значения, отличающиеся на 90.
Следовательно, существует две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Такие оси называют главными
осями инерции,
их будем обозначать  и
и  ,
а моменты относительно этих осей – главные
моменты инерции.
,
а моменты относительно этих осей – главные
моменты инерции.
При положительном
значении угла 0, для определения
по нему положения одной из главных осей
инерции, ось х следует повернуть на угол 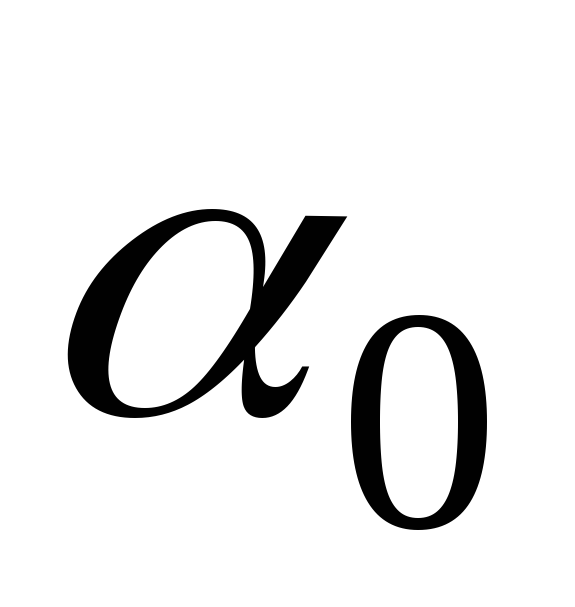 против
вращения часовой стрелки.
против
вращения часовой стрелки.
Рис. 2.7 | Одна из главных осей инерции является осью максимум (относительно нее осевой момент инерции сечения максимален), а другая – осью минимум. Ось максимум всегда сос-тавляет меньший угол с той |
из осей (х или у), относительно которой осевой момент инерции имеет большее значение (рис. 2.7).
Для отыскания главных моментов инерции есть два способа.
I способ: По формулам из тригонометрии используя выражения (2.11) и (2.13), после некоторых преобразований, найдем
 (2.14)
(2.14)
II способ:
Вычислим по (2.13) угол  и с учетом его знака проводим главные
оси ОХ0 и ОY0.
В формулы (2.11) и (2.11а) подставляем
и с учетом его знака проводим главные
оси ОХ0 и ОY0.
В формулы (2.11) и (2.11а) подставляем 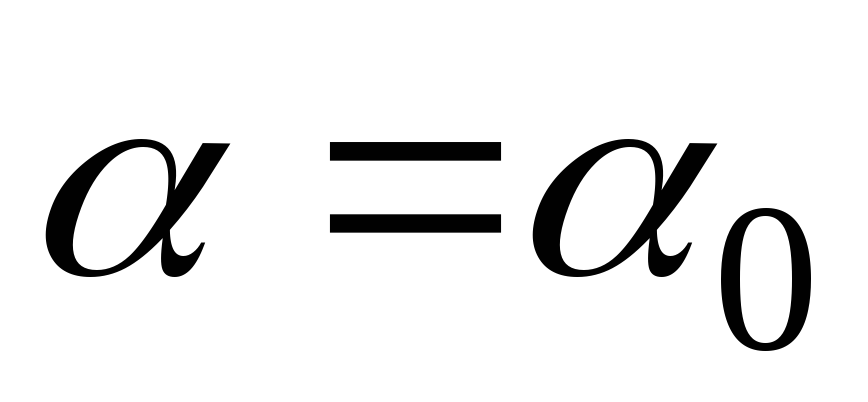 и вычисляем
и вычисляем 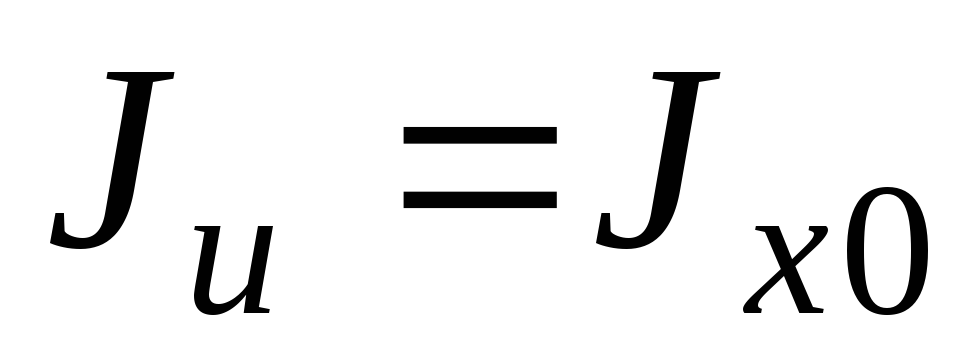 и
и 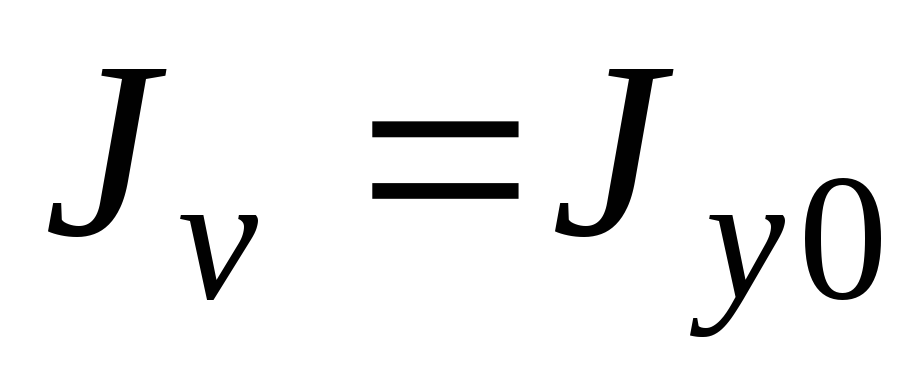 .
По числовым значениям
.
По числовым значениям 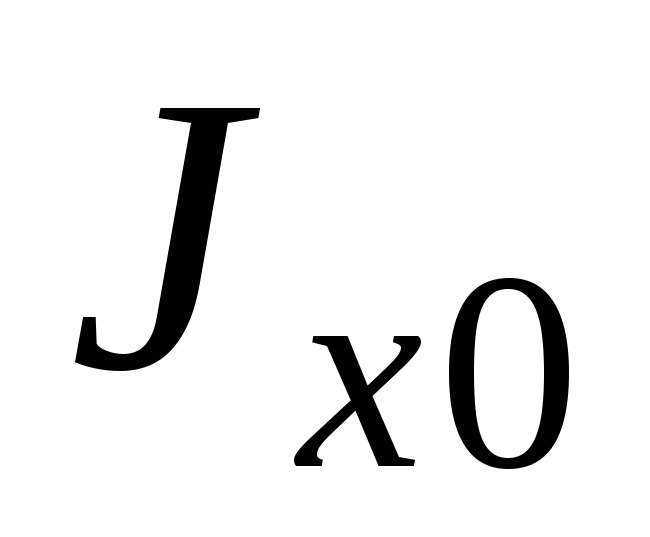 и
и  сразу видно, какая ось максимум, а какая
минимум. Полученные так
сразу видно, какая ось максимум, а какая
минимум. Полученные так 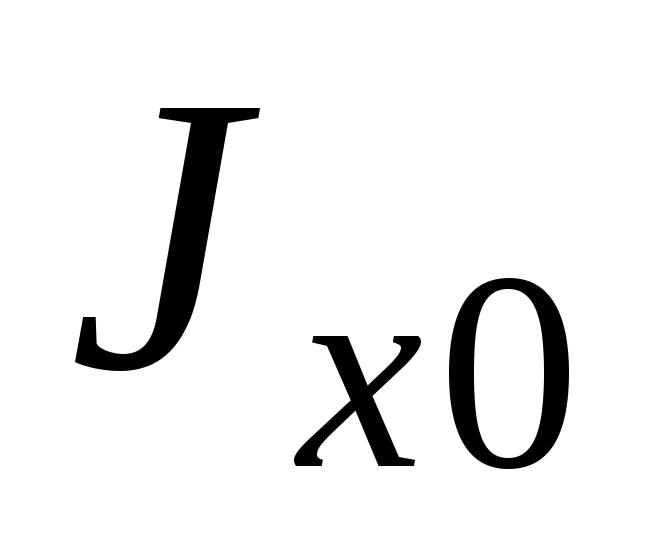 и
и  численно равны
численно равны 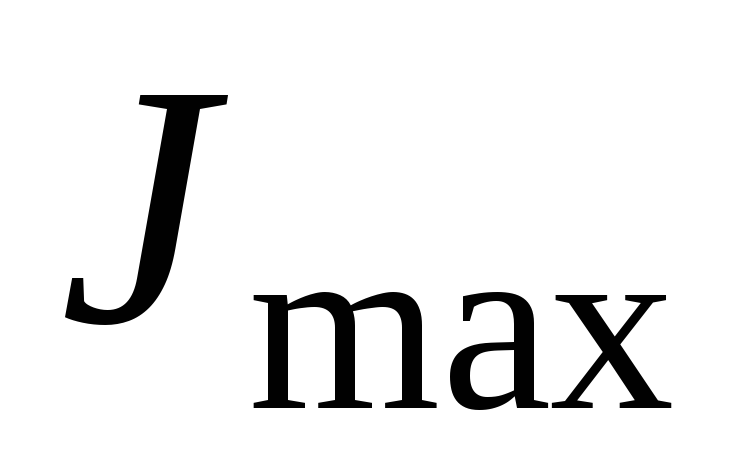 и
и  ,
определяемым по формуле (2.14).
,
определяемым по формуле (2.14).
Интересно отметить,
что центробежный момент инерции
относительно главных осей инерции равен
нулю. Для этого в формулу (2.12) вместо  подставим значение
подставим значение 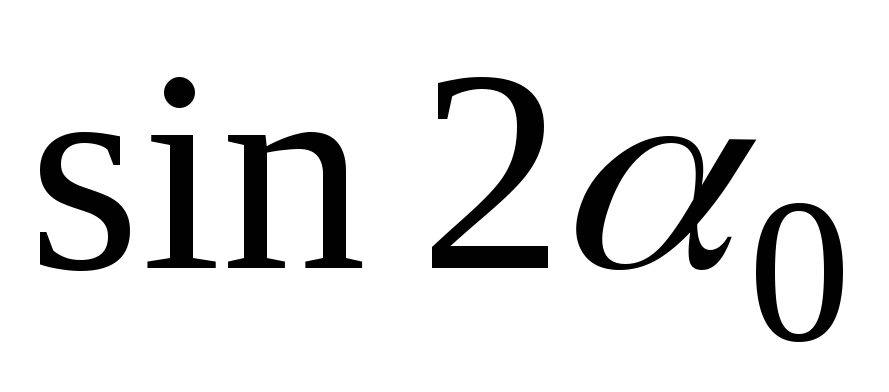 ,
определяемого из формулы (2.13) и т.к.
,
определяемого из формулы (2.13) и т.к. 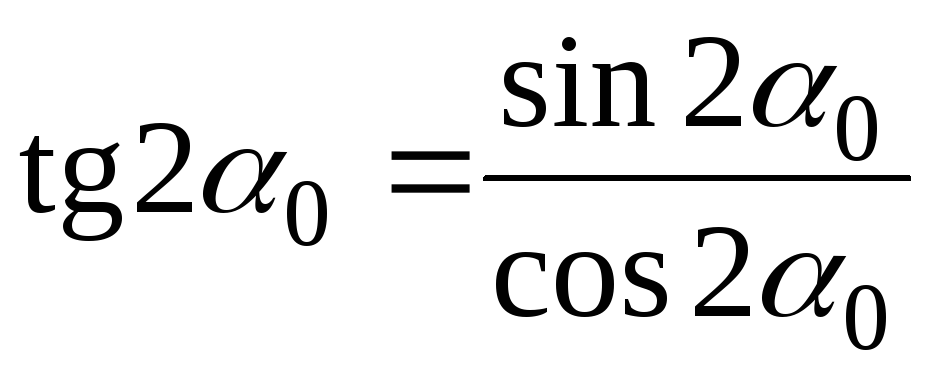 ;
;
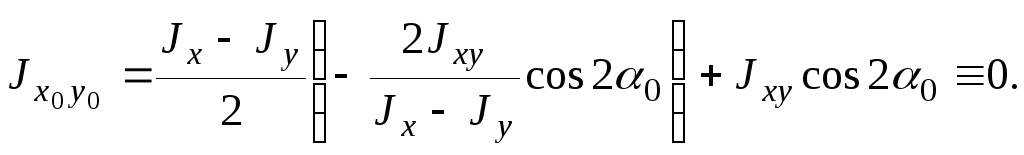
Условие равенства нулю центробежного момента инерции часто используют для определения положения главных осей инерции – если одна из осей фигуры совпадает с осью симметрии этой фигуры, то эти оси будут главные, т.к. центробежный момент относительно таких осей равен нулю. Таким образом, для симметричных фигур главные оси устанавливаются без вычислений.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
Эллипс инерции
Введем новую геометрическую характеристику, которую назовем радиусом инерции.
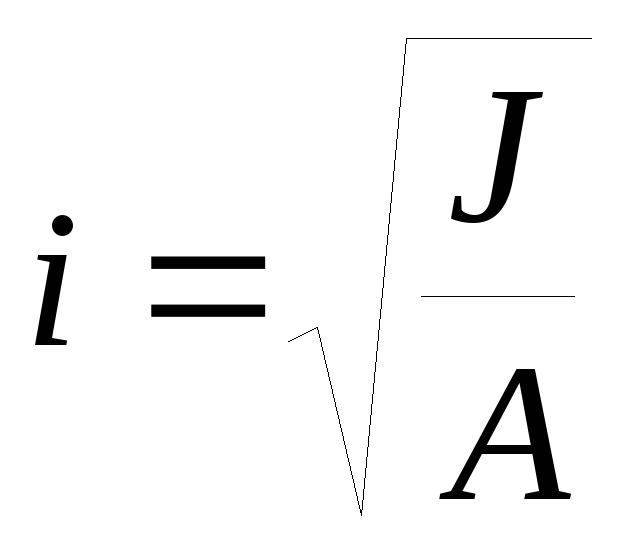 (2.15)
(2.15)
Предположим, что
для какой-либо фигуры оси  и
и  являются главными центральными осями.
Запишем выражение момента инерции
относительно оси
являются главными центральными осями.
Запишем выражение момента инерции
относительно оси  ,
наклонной к оси
,
наклонной к оси  на угол
на угол  .
На основании (2.11) получим
.
На основании (2.11) получим
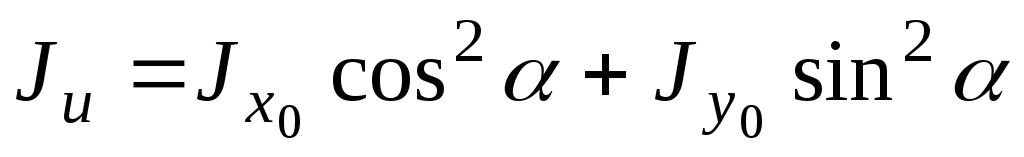 ,
т.к.
,
т.к.  .
.
Разделив все на А, получим
 (2.16)
(2.16)
обозначенное на
рис. 2.8 величиной  равно:
равно:
 (2.17)
(2.17)
Сравнивая полученную
зависимость с выражением (2.16) видим, что
величина  численно равна радиусу инерции
относительно наклонной оси
численно равна радиусу инерции
относительно наклонной оси  .
Установленное свойство эллипса инерции
позволяет графически определить момент
инерции относительно любой оси, проходящей
через начало координат. Для этого
достаточно провести касательную к
эллипсу параллельно этой оси и замерить
кратчайшее расстояние между касательной
и осью. Это расстояние
.
Установленное свойство эллипса инерции
позволяет графически определить момент
инерции относительно любой оси, проходящей
через начало координат. Для этого
достаточно провести касательную к
эллипсу параллельно этой оси и замерить
кратчайшее расстояние между касательной
и осью. Это расстояние 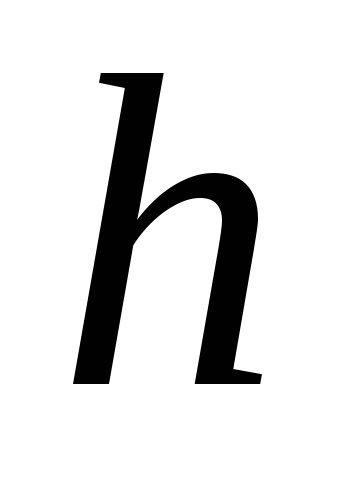 будет равно радиусу инерции для
рассматриваемой оси. Момент инерции
определяется так:
будет равно радиусу инерции для
рассматриваемой оси. Момент инерции
определяется так:
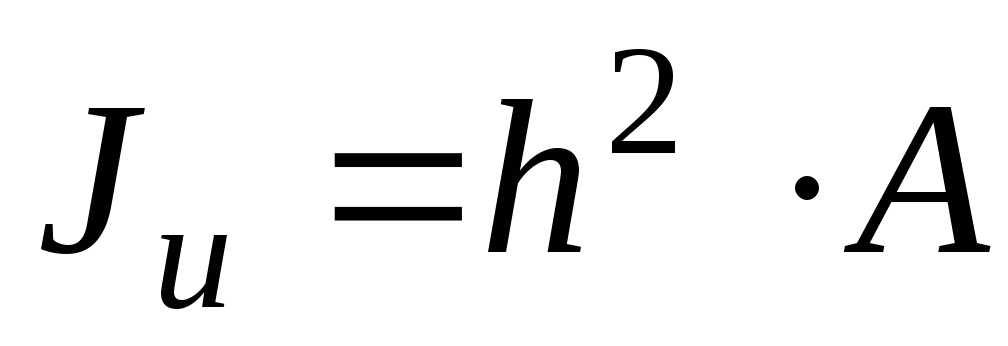
Зависимость между моментами инерции при повороте осей
новых осях через
координаты в старых осях, угол  при повороте осей против часовой стрелки:
при повороте осей против часовой стрелки:
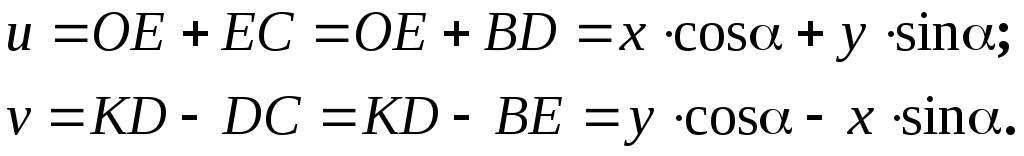
Найдем момент
инерции относительно оси  :
:

Учитывая, что 
Окончательно получим
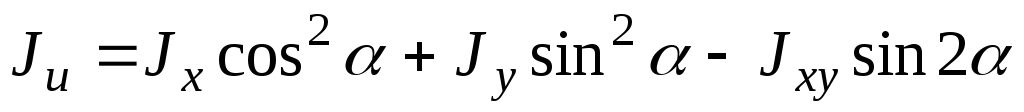 (2.11)
(2.11)
Аналогично можно установить, что
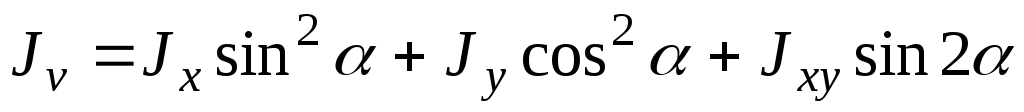 (2.11а)
(2.11а)
Для центробежного момента инерции получим
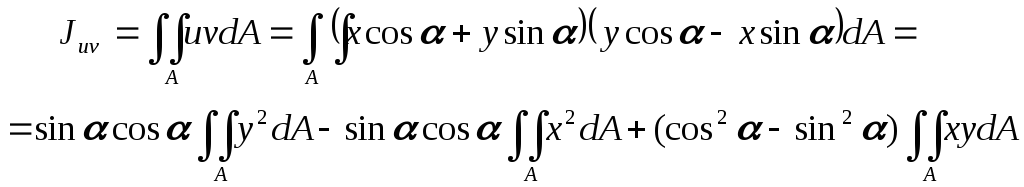
Учитывая, что 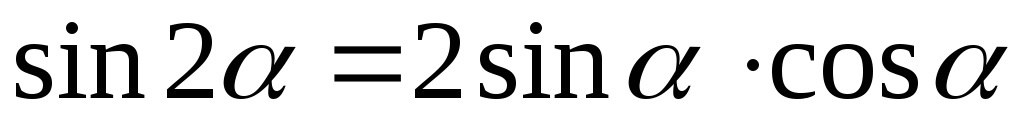 и
и  ,
получим
,
получим
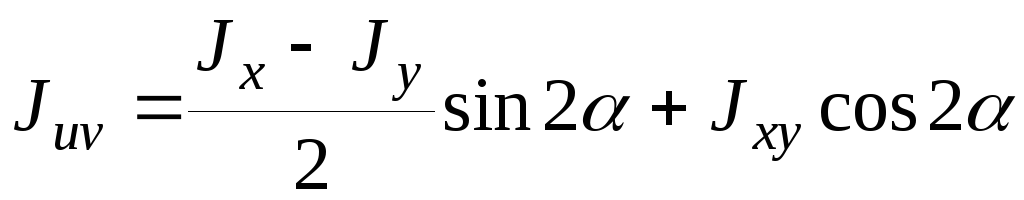 (2.12)
(2.12)
Сложим выражения (2.11) и (2.11а), получим
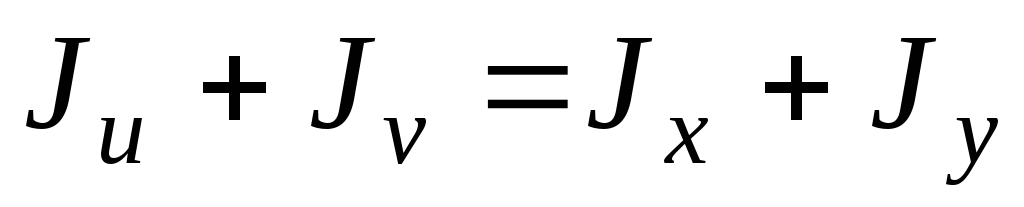
Сумма моментов инерции относительно любых взаимно перпендикулярных осей у и х не меняются при их повороте. Это показано и соотношением (2.8).
Главные оси инерции и главные моменты инерции
В предыдущем
разделе было показано, что величины
моментов инерции меняются
при повороте осей.
Можно найти такое значение угла 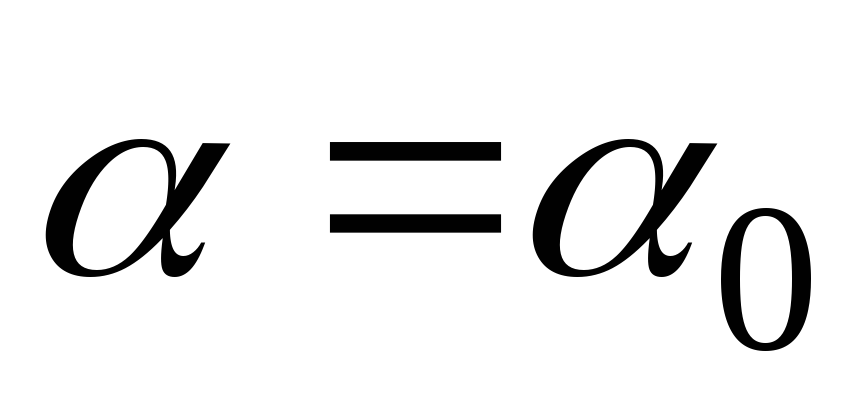 ,
при котором момент инерции достигает экстремального значения. Для определения экстремума
приравняем нулю первую производную от
(2.11) и положим
,
при котором момент инерции достигает экстремального значения. Для определения экстремума
приравняем нулю первую производную от
(2.11) и положим 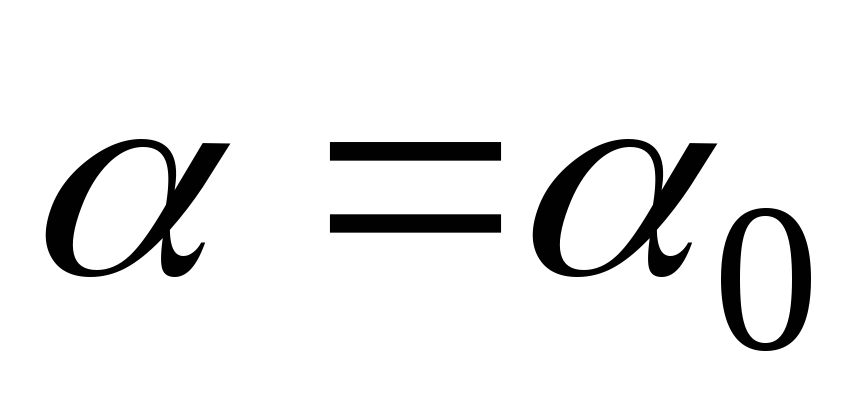 :
:
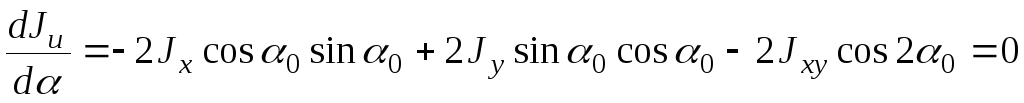
или
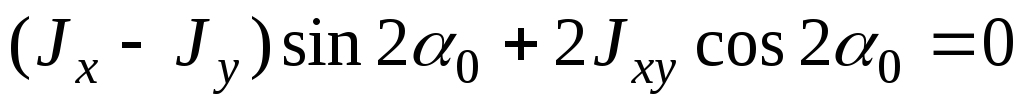
откуда
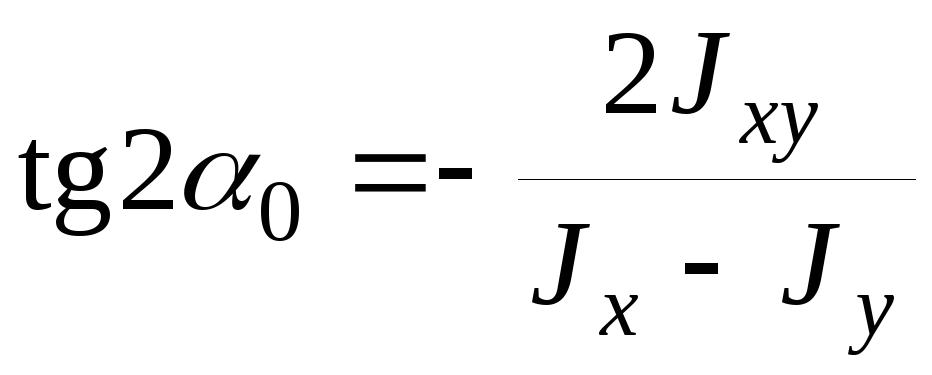 (2.13)
(2.13)
Полученная формула
дает для угла 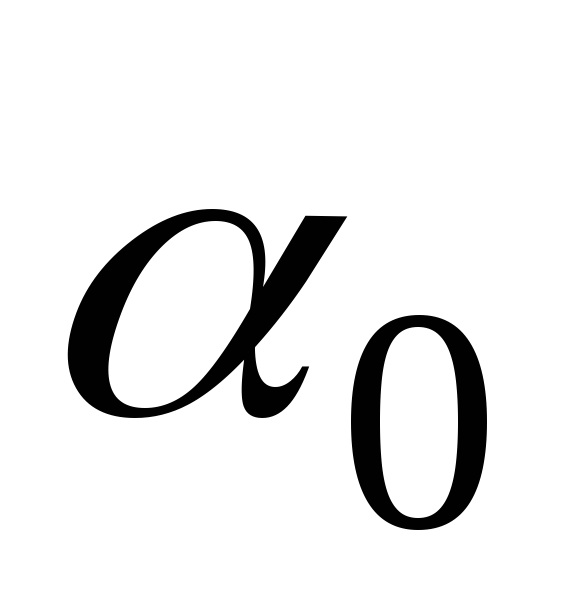 два значения, отличающиеся на 90.
Следовательно, существует две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Такие оси называют главными
осями инерции,
их будем обозначать
два значения, отличающиеся на 90.
Следовательно, существует две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Такие оси называют главными
осями инерции,
их будем обозначать 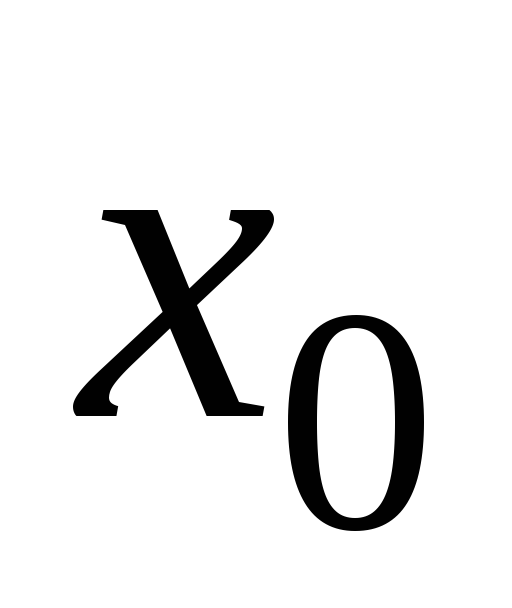 и
и 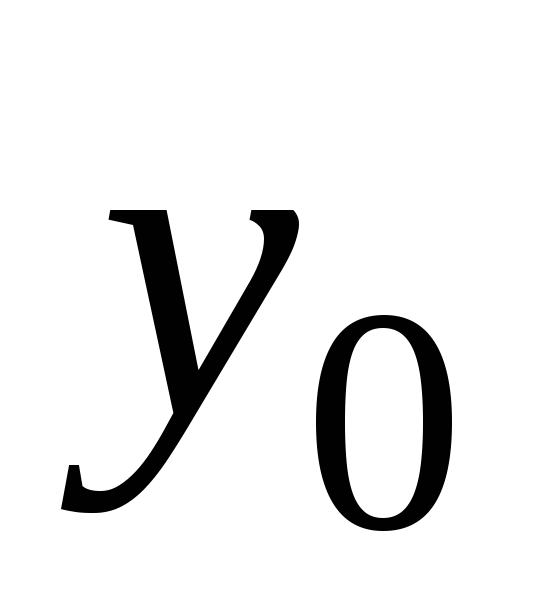 ,
а моменты относительно этих осей – главные
моменты инерции.
,
а моменты относительно этих осей – главные
моменты инерции.
При положительном
значении угла 0, для определения
по нему положения одной из главных осей
инерции, ось х следует повернуть на угол 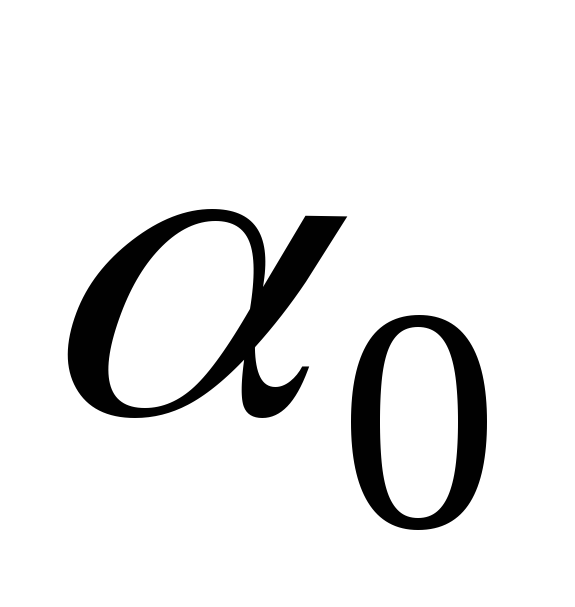 против
вращения часовой стрелки.
против
вращения часовой стрелки.
Рис. 2.7 | Одна из главных осей инерции является осью максимум (относительно нее осевой момент инерции сечения максимален), а другая – осью минимум. Ось максимум всегда сос-тавляет меньший угол с той |
из осей (х или у), относительно которой осевой момент инерции имеет большее значение (рис. 2.7).
Для отыскания главных моментов инерции есть два способа.
I способ: По формулам из тригонометрии используя выражения (2.11) и (2.13), после некоторых преобразований, найдем
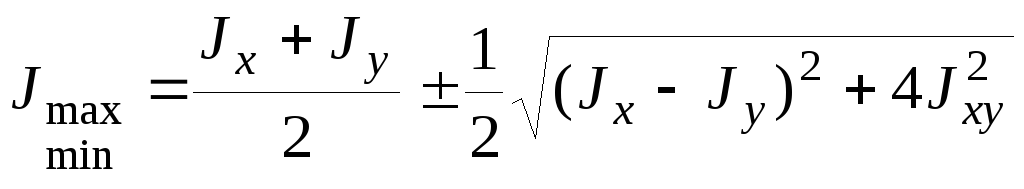 (2.14)
(2.14)
II способ:
Вычислим по (2.13) угол  и с учетом его знака проводим главные
оси ОХ0 и ОY0.
В формулы (2.11) и (2.11а) подставляем
и с учетом его знака проводим главные
оси ОХ0 и ОY0.
В формулы (2.11) и (2.11а) подставляем  и вычисляем
и вычисляем 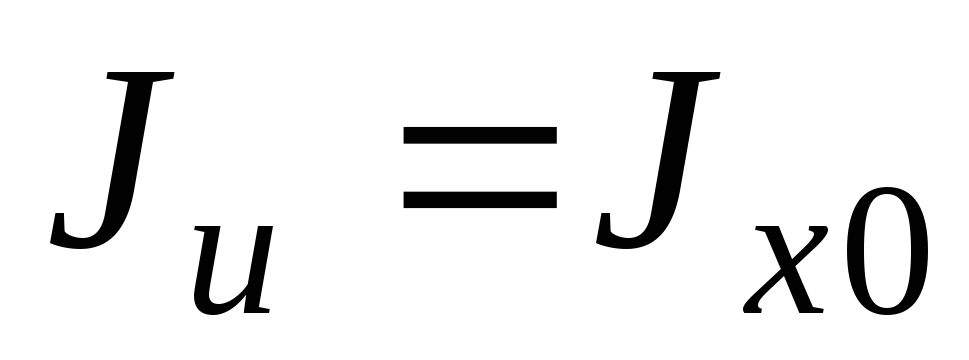 и
и  .
По числовым значениям
.
По числовым значениям 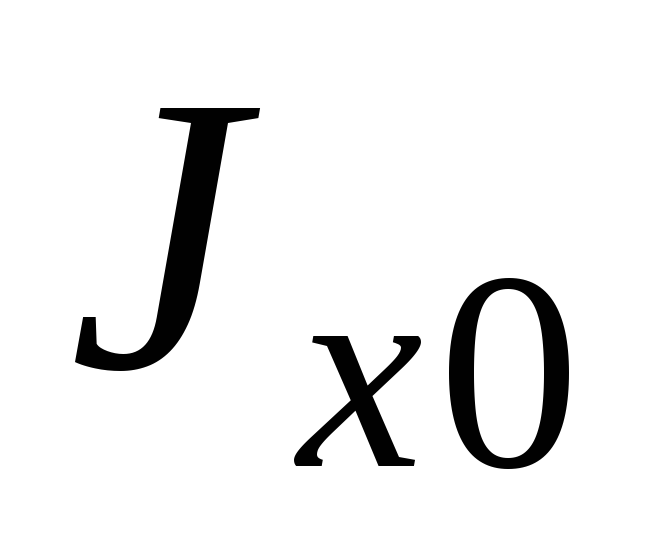 и
и  сразу видно, какая ось максимум, а какая
минимум. Полученные так
сразу видно, какая ось максимум, а какая
минимум. Полученные так 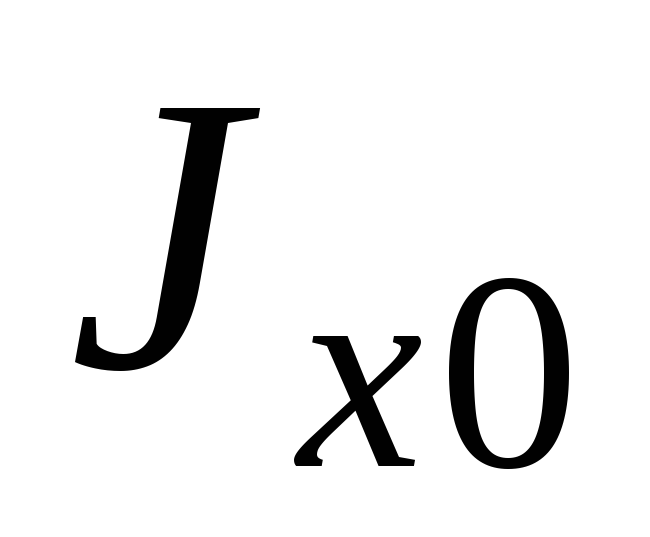 и
и 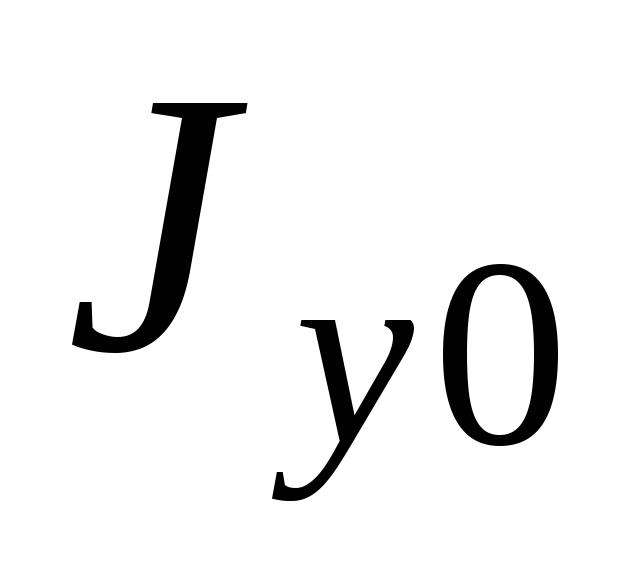 численно равны
численно равны 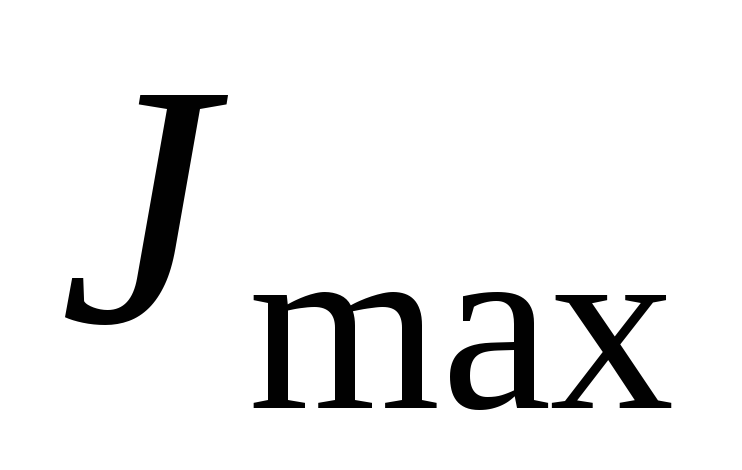 и
и  ,
определяемым по формуле (2.14).
,
определяемым по формуле (2.14).
Интересно отметить,
что центробежный момент инерции
относительно главных осей инерции равен
нулю. Для этого в формулу (2.12) вместо  подставим значение
подставим значение 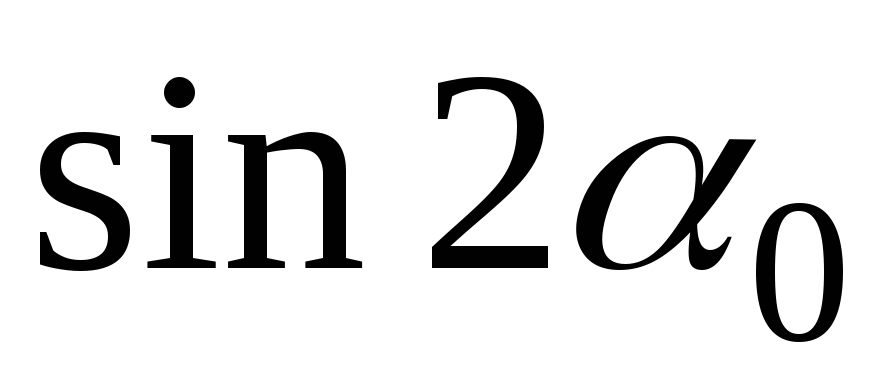 ,
определяемого из формулы (2.13) и т.к.
,
определяемого из формулы (2.13) и т.к. 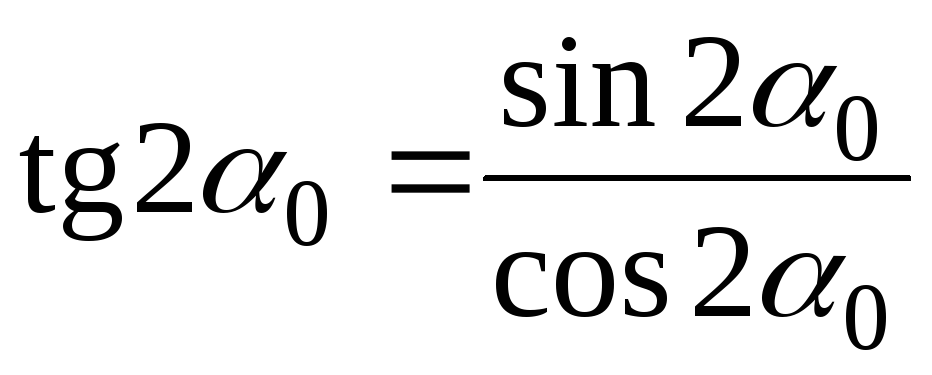 ;
;
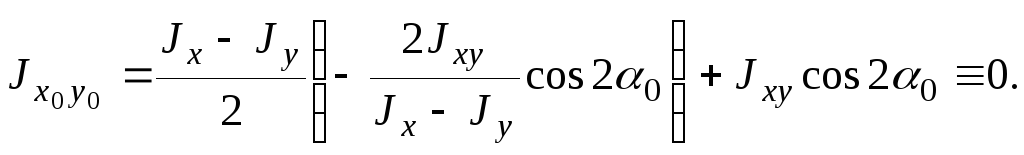
Условие равенства нулю центробежного момента инерции часто используют для определения положения главных осей инерции – если одна из осей фигуры совпадает с осью симметрии этой фигуры, то эти оси будут главные, т.к. центробежный момент относительно таких осей равен нулю. Таким образом, для симметричных фигур главные оси устанавливаются без вычислений.
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
Эллипс инерции
Введем новую геометрическую характеристику, которую назовем радиусом инерции.
 (2.15)
(2.15)
Предположим, что
для какой-либо фигуры оси  и
и  являются главными центральными осями.
Запишем выражение момента инерции
относительно оси
являются главными центральными осями.
Запишем выражение момента инерции
относительно оси 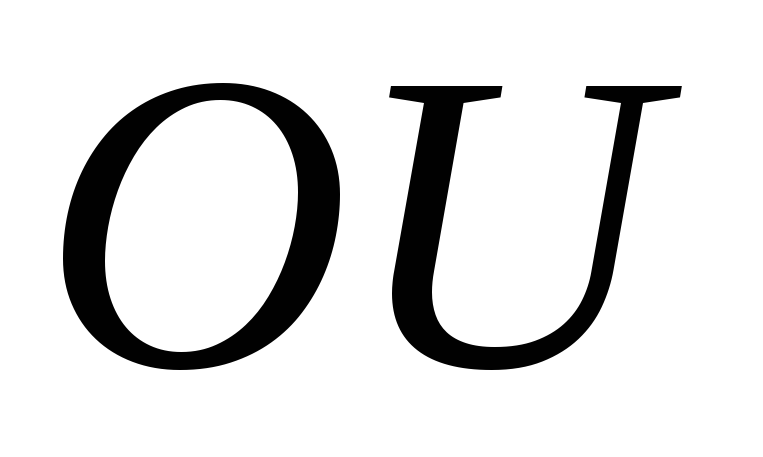 ,
наклонной к оси
,
наклонной к оси 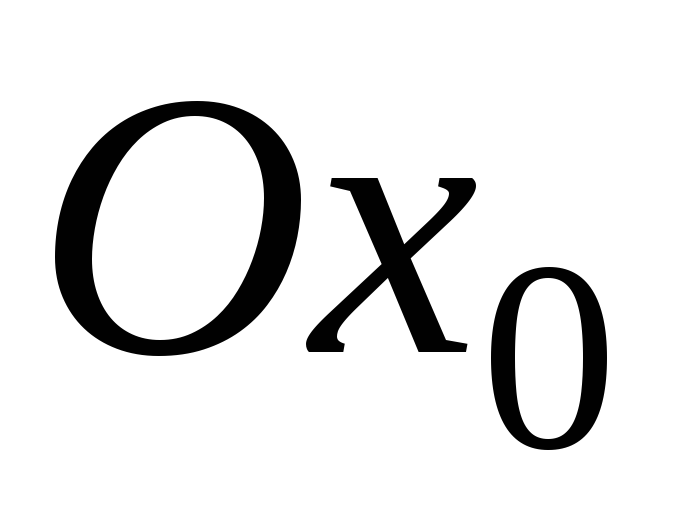 на угол
на угол  .
На основании (2.11) получим
.
На основании (2.11) получим
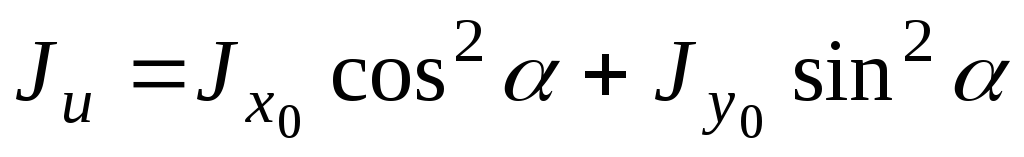 ,
т.к.
.
,
т.к.
.
Разделив все на А, получим
 (2.16)
(2.16)
обозначенное на
рис. 2.8 величиной  равно:
равно:
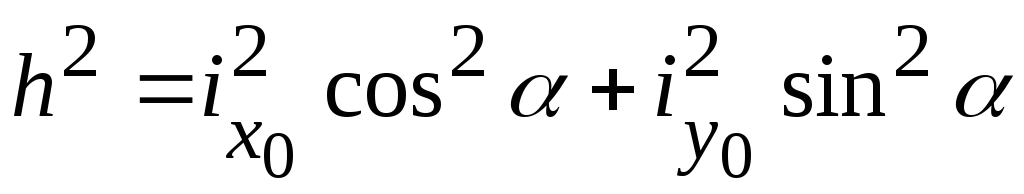 (2.17)
(2.17)
Сравнивая полученную
зависимость с выражением (2.16) видим, что
величина 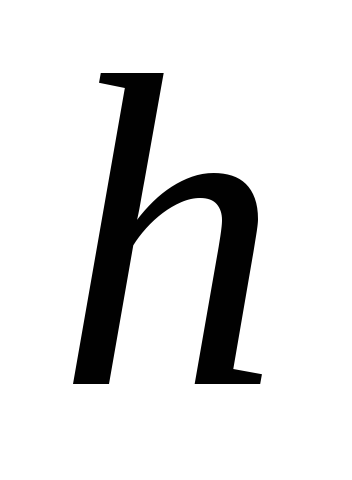 численно равна радиусу инерции
относительно наклонной оси
численно равна радиусу инерции
относительно наклонной оси 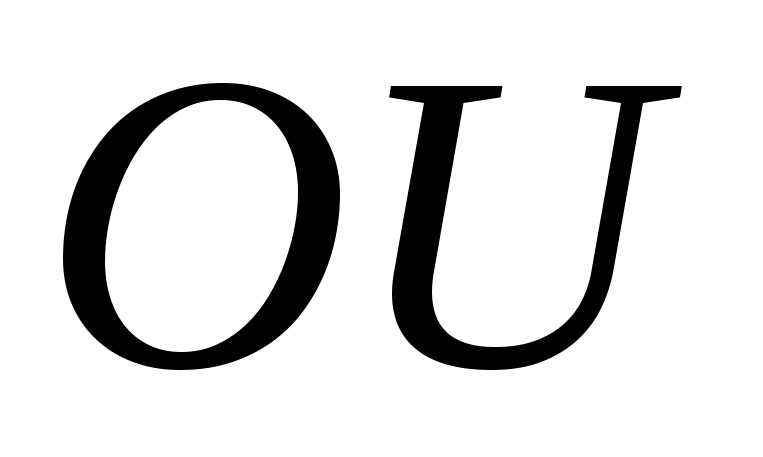 .
Установленное свойство эллипса инерции
позволяет графически определить момент
инерции относительно любой оси, проходящей
через начало координат. Для этого
достаточно провести касательную к
эллипсу параллельно этой оси и замерить
кратчайшее расстояние между касательной
и осью. Это расстояние
.
Установленное свойство эллипса инерции
позволяет графически определить момент
инерции относительно любой оси, проходящей
через начало координат. Для этого
достаточно провести касательную к
эллипсу параллельно этой оси и замерить
кратчайшее расстояние между касательной
и осью. Это расстояние  будет равно радиусу инерции для
рассматриваемой оси. Момент инерции
определяется так:
будет равно радиусу инерции для
рассматриваемой оси. Момент инерции
определяется так:
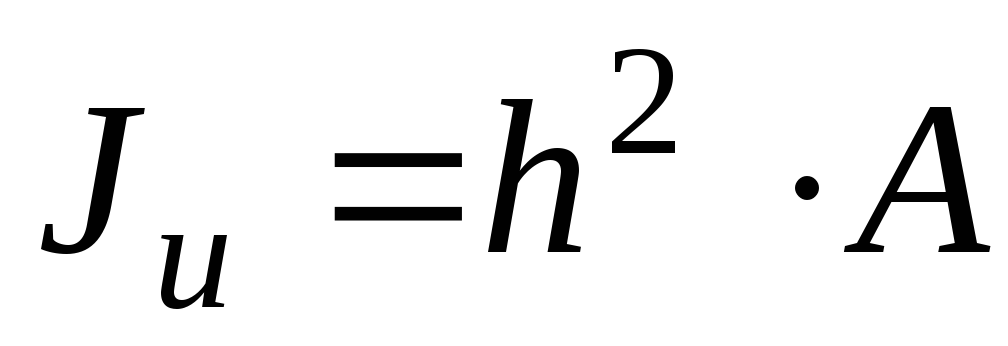
Зависимость между моментами инерции сечения при повороте осей. Главные оси и главные моменты инерции
Пусть заданы моменты инерции . Требуется найти, относительно осей, повернутых к заданным на угол(рис. 4.5).
Рис. 4.5
Выберем произвольную площадку и выразим ее координаты в новых осяхичерез старые.
Проектируем замкнутый четырехугольник на осии. Так как проекция ломаной линии равна проекции замыкающей, находим:
.
В выражениях исключаем итогда
,
откуда
(4.5)
Рассмотрим первые два уравнения из 4.5, складывая их почленно, получим:
.
Таким образом, при повороте осей сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной. Заметим, что , где— расстояние от элементарной площадки до точки 0.
Таким образом
, (4.6)
где — полярный момент инерции.
При помощи выражения 4.6 легко найти осевые моменты инерции для круга.
.
С изменением каждая из величинименяется, а сумма их остается постоянной. Следовательно, существует такой угол, при котором один из элементов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.
Дифференцируя первое выражение из 4.5 по , и приравнивая производную нулю, найдем
(4.7)
При этом значение один из осевых моментов достигает максимального значения, другой — минимального, а центробежный равен 0.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями.
Найдем величины главных моментов инерции. Для этого первые две формулы из 4.5 приведем к виду
.
Учитывая, что
,
.
Исключаем при помощи 4.7 угол , получим для определения значений главных моментов инерции.
. (4.8)
Глава 5. Изгиб
5.1. Основные понятия
Под изгибом понимается такой вид нагружения стержня, когда в его поперечных сечениях возникают изгибающие моменты. Если изгибающий момент является единственным силовым фактором, то изгиб называется чистым. Большей частью в поперечных сечениях бруса наряду с изгибающими моментами возникают и поперечные силы. В этом случае изгиб называют поперечным. В дальнейшем встретимся с более сложными видами изгиба.
Брус, работающий на изгиб, обычно называют балкой. Кроме балок на изгиб работают элементы рам. Рамой называется конструкция, состоящая из стержней, элементы которой работают преимущественно на изгиб.
Ранее мы уже познакомились с внутренними силовыми факторами , возникающими при изгибе, и строили их эпюры. Теперь перейдем к исследованию напряжений, возникающих при изгибе.
5.2. Дифференциальные зависимости между и
Изгибающий момент , поперечная силаи интенсивность внешней нагрузкисвязаны между собой определенной зависимостью. Вырежем из балки, загруженной распределенной нагрузкой, изменяющейся по какому—либо закону (рис. 5.1,а), элемент длиной(рис. 5.1,б).
Рис. 5.1
Нагрузку считают положительной, если она направлена вверх; на протяжении длины ее считают равномерно распределенной.
Составим два уравнения равновесия элемента:
.
.
В первом уравнении произведением как величиной второго порядка малости по сравнению с остальными слагаемыми можно пренебречь.
После элементарных преобразований из приведенных выше уравнений находим
. (5.1)
. (5.2)
Из двух полученных дифференциальных зависимостей вытекает третья:
. (5.3)
Зависимости (5.1) и (5.2) часто используются при проверке правильности построения эпюр моментов и поперечных сил.
Изменение моментов инерции при повороте осей.
Р ассмотрим
изменение моментов инерции при повороте
осей координат. Положим, даны моменты
инерции некоторого сечения относительно
осейx и y (не обязательно центральных).
Требуется определитьJu, Jv, Juv—
моменты инерции относительно осейu,v,
повернутых на угола. Так проекцияОАВС равна проекции замыкающей:
ассмотрим
изменение моментов инерции при повороте
осей координат. Положим, даны моменты
инерции некоторого сечения относительно
осейx и y (не обязательно центральных).
Требуется определитьJu, Jv, Juv—
моменты инерции относительно осейu,v,
повернутых на угола. Так проекцияОАВС равна проекции замыкающей:
u=y sin а + x cos a (1)
v=y cos a – x sin a (2)
Исключим u,vв выражениях моментов инерции:
Ju = ∫v2dF; Jv= ∫u2dF; Juv= ∫uvdF. Подставив в выражения (1) и (2) получим:
Ju=Jxcos2a – Jxysin 2a + Jy sin2 a
Jv=Jxsin2a + Jxysin 2a + Jy cos2 a (3)
Juv=Jxycos2a + sin 2a(Jx-Jy)/2
Ju +Jv=Jx +Jy=∫F(y2+x2)dF => Сумма осевых моментов инерции относительно 2х взаимно перпенд. Осей не зависит от углаа. Заметим, чтоx2+y2=p2. p— расстояние от начала координат до элементарной площадки. Т.о.Jx +Jy=Jp.(4)
Jp=∫F p2dF –полярный момент, не зависит от поворотах,у
2)Т. Кастелиано.
Частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению этой силы.
Рассмотрим стержень, нагруженный произвольной системой сил и закрепленный как показано на рис.

Пусть потенциальная
энергия деформации, накопленная в объеме
тела в результате работы внешних сил,
равна U.
Силе Fn дадим приращение d
Fn.
Тогда потенциальная энергия U
получит приращение  и примет видU+
и примет видU+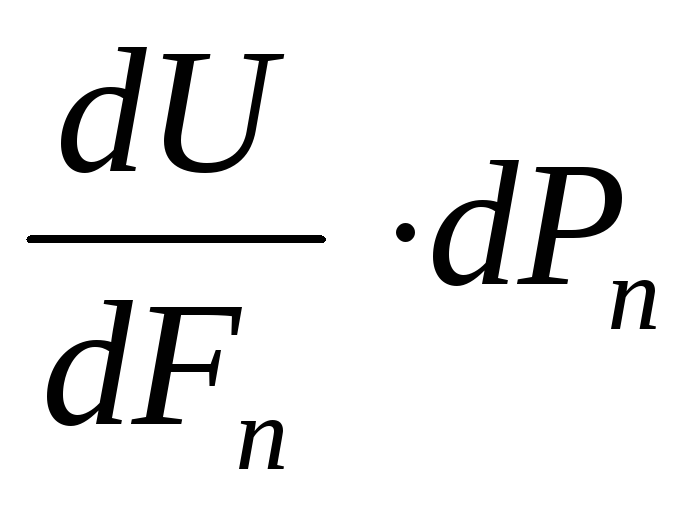 .(5.4)
.(5.4)
Изменим теперь порядок приложения сил. Приложим сначала к упругому телу силу dPn. В точке приложения этой силы возникнет соответственно малое перемещение, проекция которого на направление силы dPn равна. dδn. Тогда работа силы dPn оказывается равной dPn· dδn /2. Теперь приложим всю систему внешних сил. При отсутствии силы dPn потенциальная энергия системы снова приняла бы значение U. Но теперь эта энергия изменится на величину дополнительной работы dPn·δn которую совершит сила dPn на перемещении δn, вызванном всей системой внешних сил. Величина δn опять представляет собой проекцию полного перемещения на направление силы Рn.
В итоге при обратной последовательности приложения сил выражение для потенциальной энергии получаем в виде
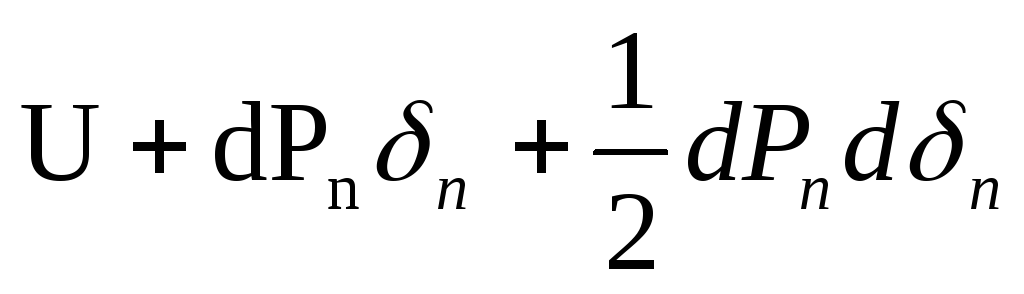 (5.5)
(5.5)
Приравниваем это выражение выражению (5.4) и, отбрасывая произведение dPn· dδn /2 как величину высшего порядка малости, находим
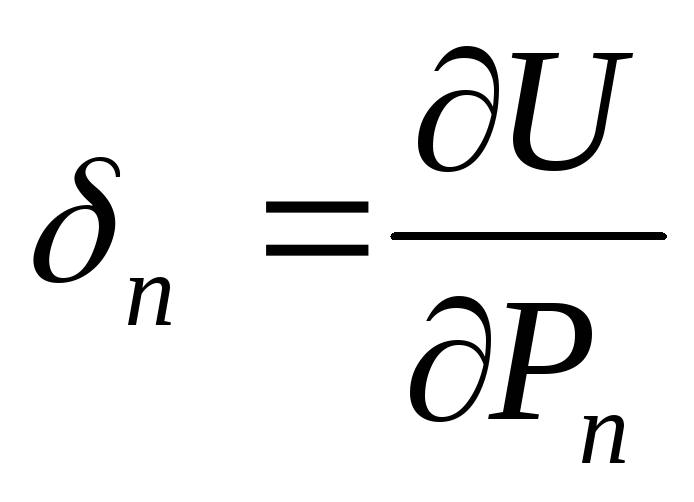 (5.6)
(5.6)
Билет 23
Кому-то не повезло
Билет 24
1) Кручение стержня прямоугольного поперечного сечения (определение напряжений и перемещений). Кручение бруса прямоугольного сечения, напряжения в поперечном сечении
П ри
этом нарушается закон плоских сечений,
сечения некруглой формы при кручении
искривляются – депланация поперечного
сечения.
ри
этом нарушается закон плоских сечений,
сечения некруглой формы при кручении
искривляются – депланация поперечного
сечения.
Э пюры
касательных напряжений прямоугольного
сечения.
пюры
касательных напряжений прямоугольного
сечения.
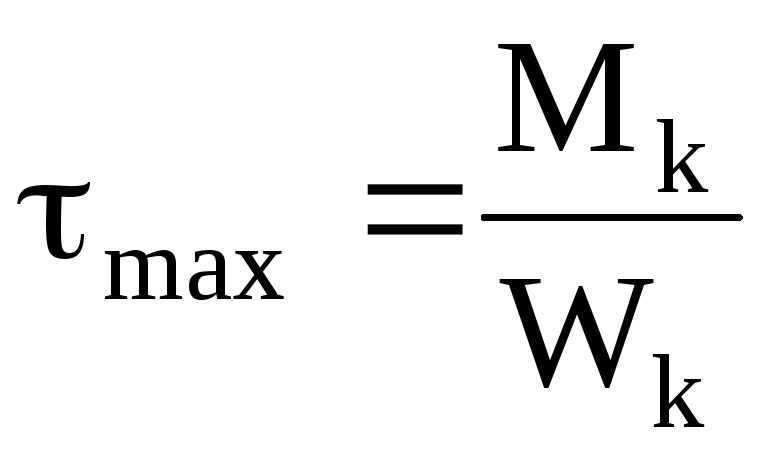 ;
;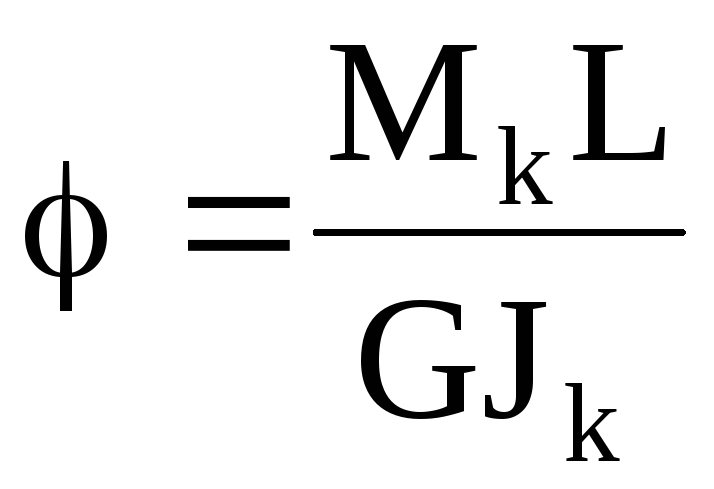 ,
Jk и Wk — условно называют моментом
инерции и моментом сопротивления при
кручении. Wk=hb2,
,
Jk и Wk — условно называют моментом
инерции и моментом сопротивления при
кручении. Wk=hb2,
Jk= hb3, Максимальные касательные напряженияmax будут посредине длинной стороны, напряжения по середине короткой стороны:=max, коэффициенты:,,приводятся в справочниках в зависимости от отношения h/b (например, при h/b=2,=0,246;=0,229;=0,795.
При расчете бруса на кручение (вала) требуется решить две основные задачи. Вопервых, необходимо определить напряжения, возникающие в брусе, и, вовторых, надо найти угловые перемещения сечений бруса в зависимости от величин внешних моментов.