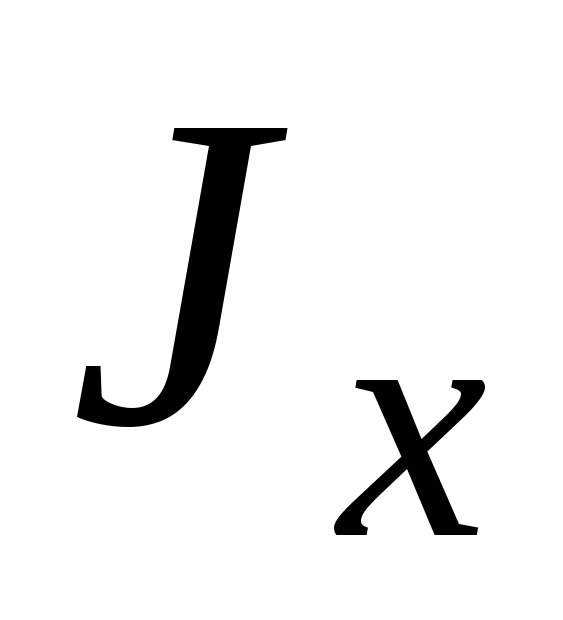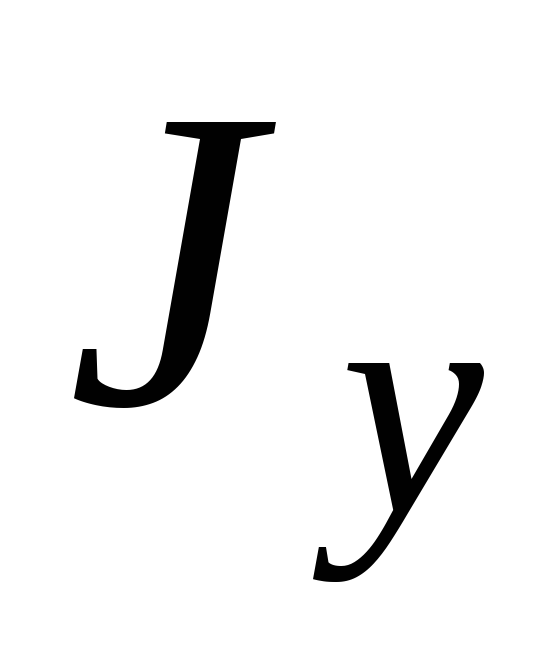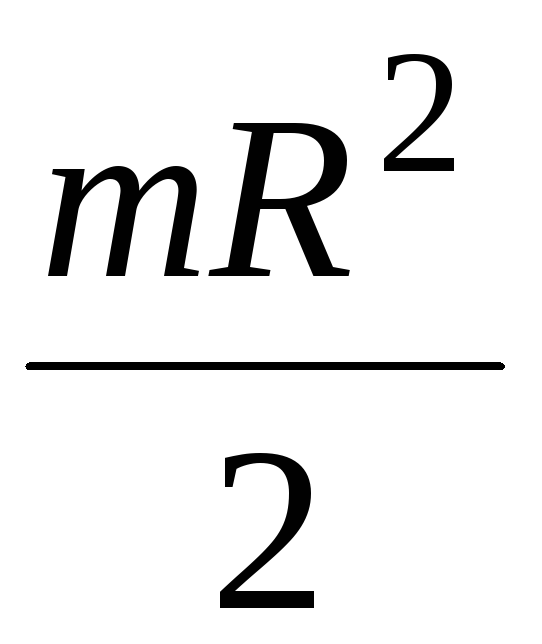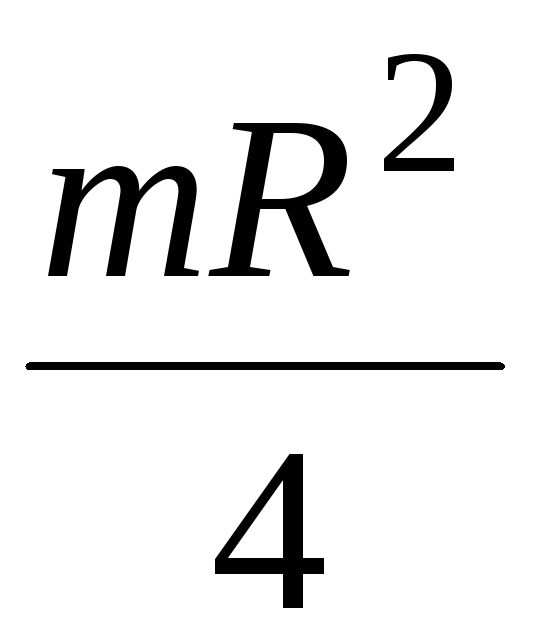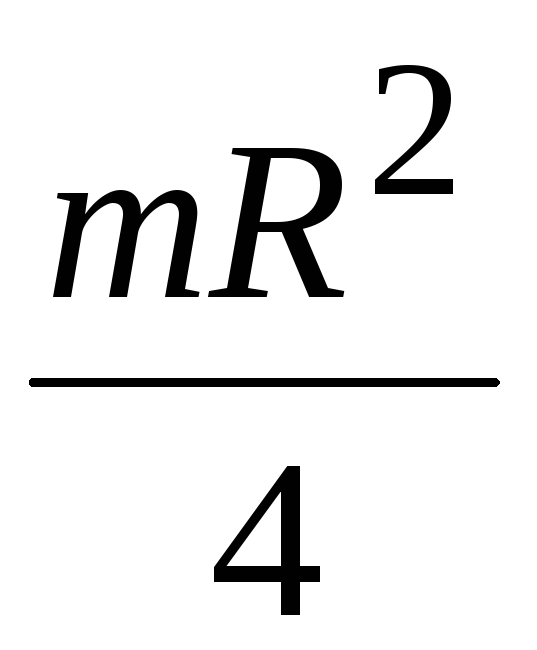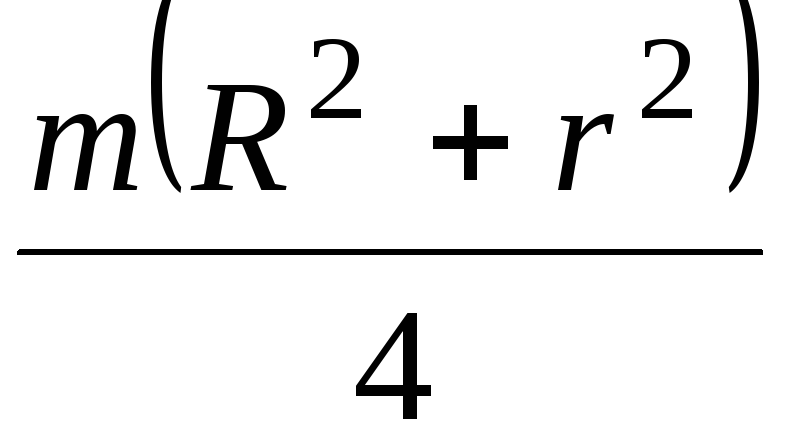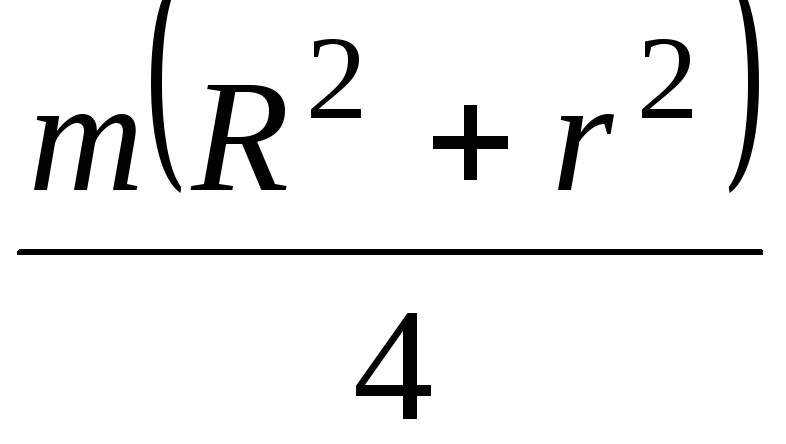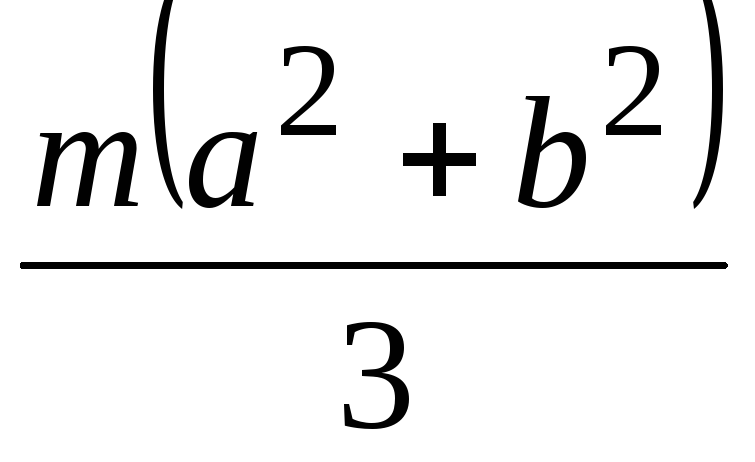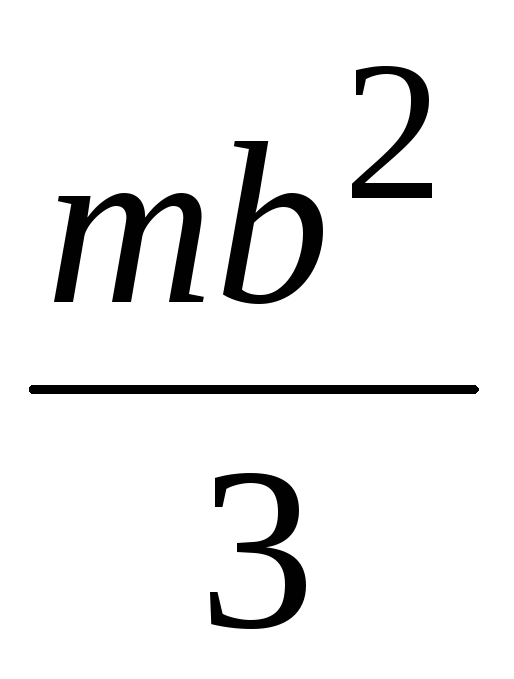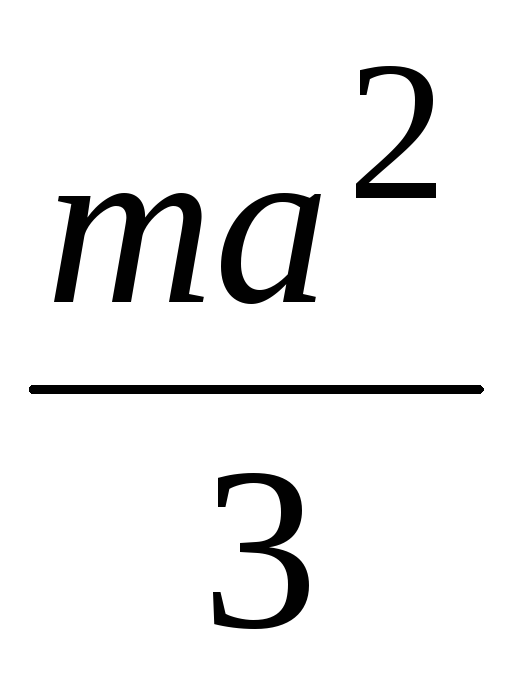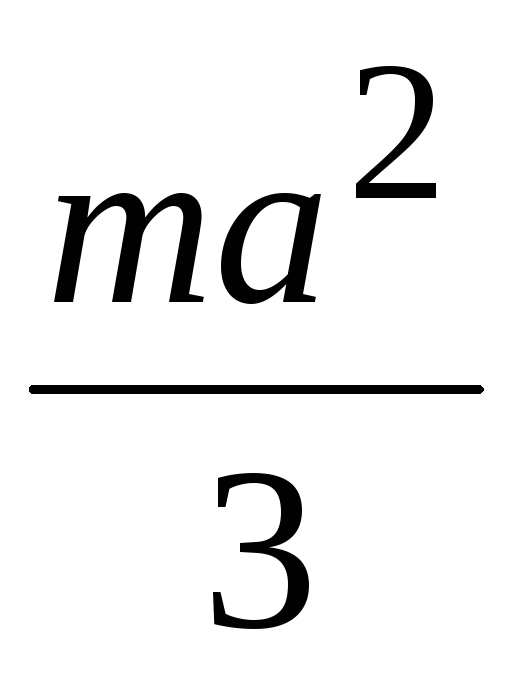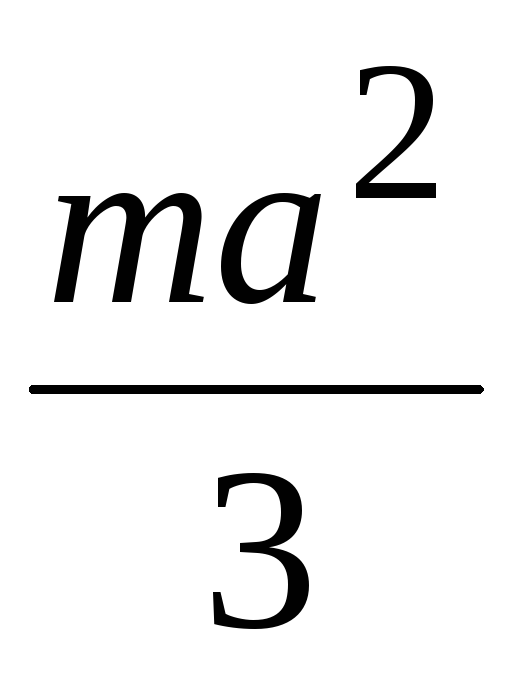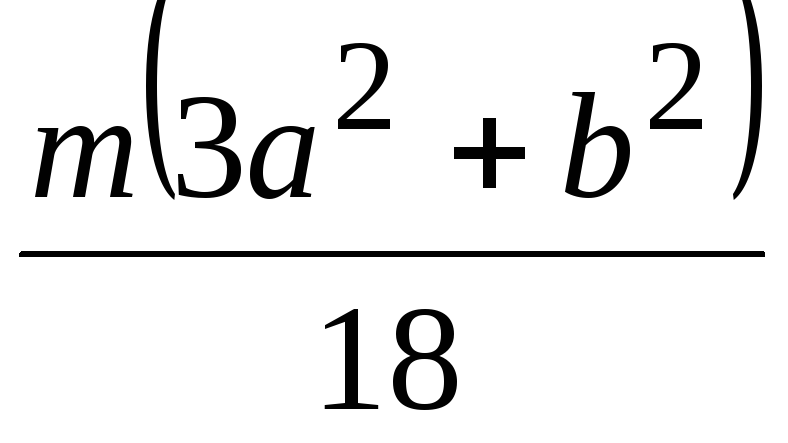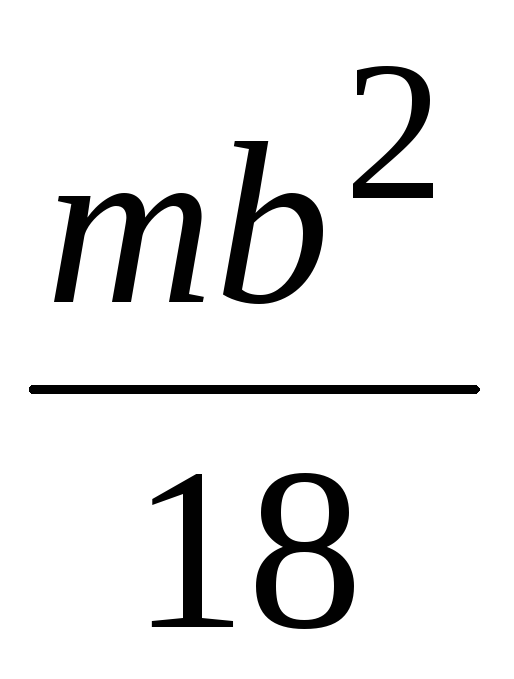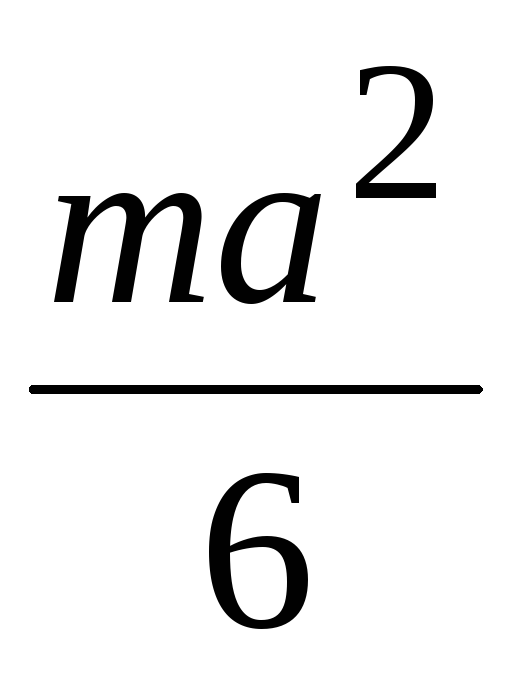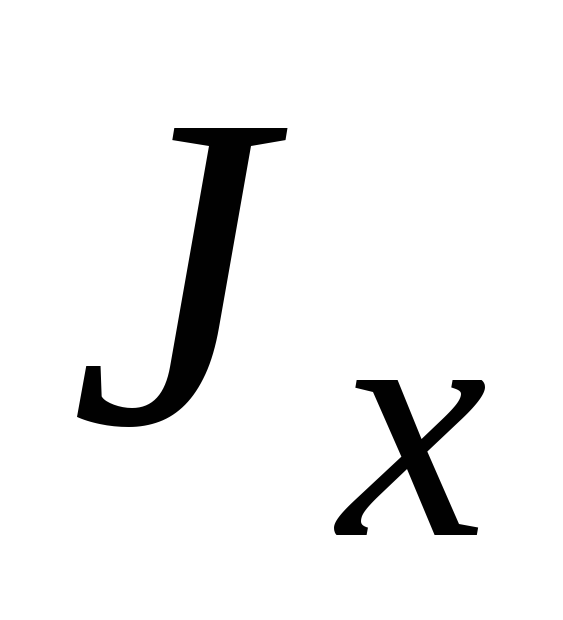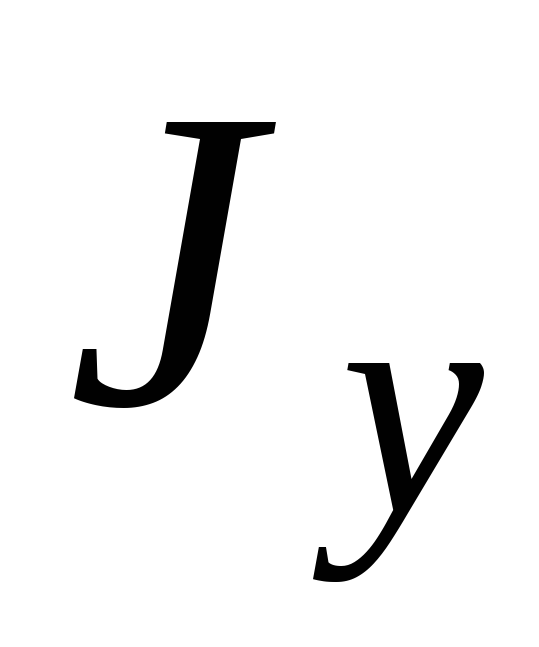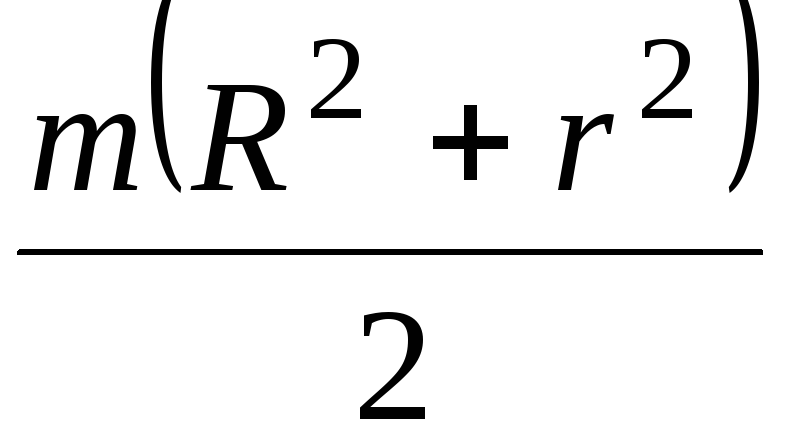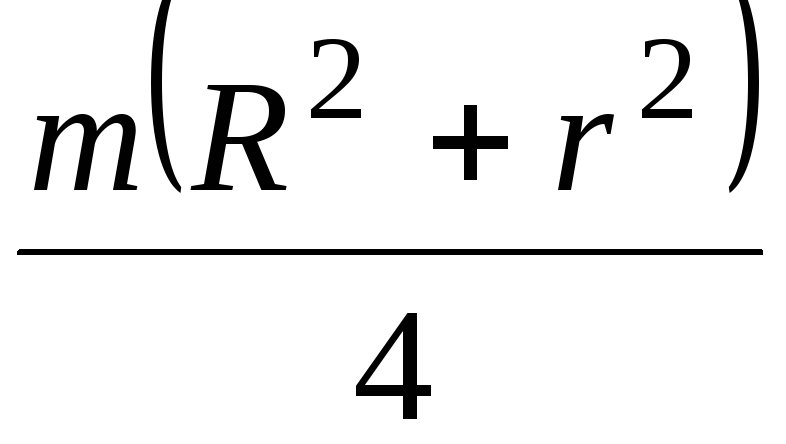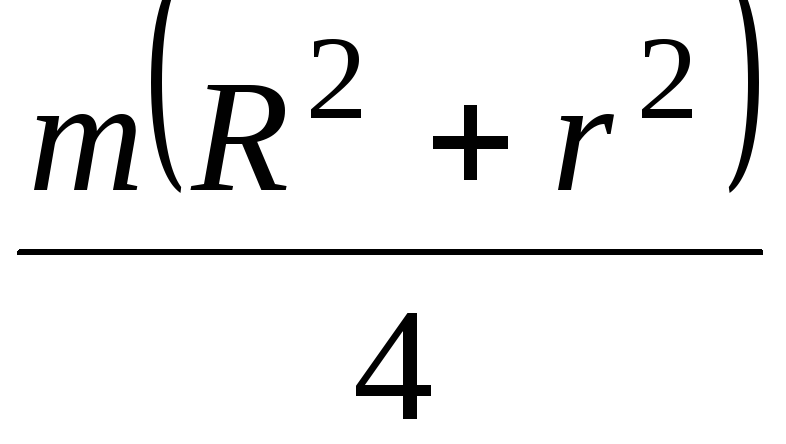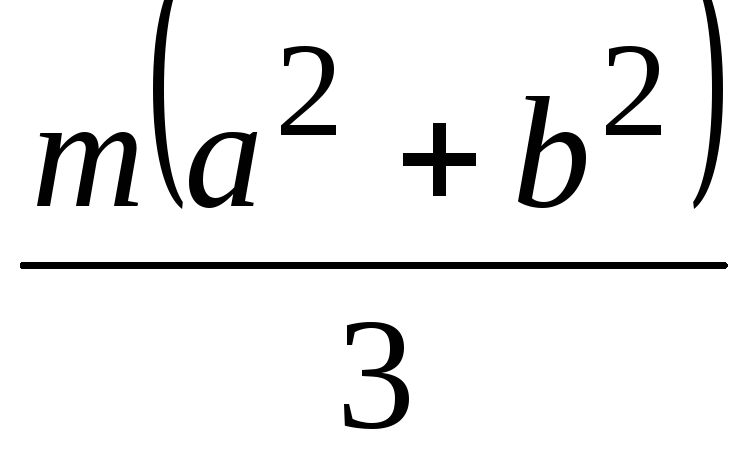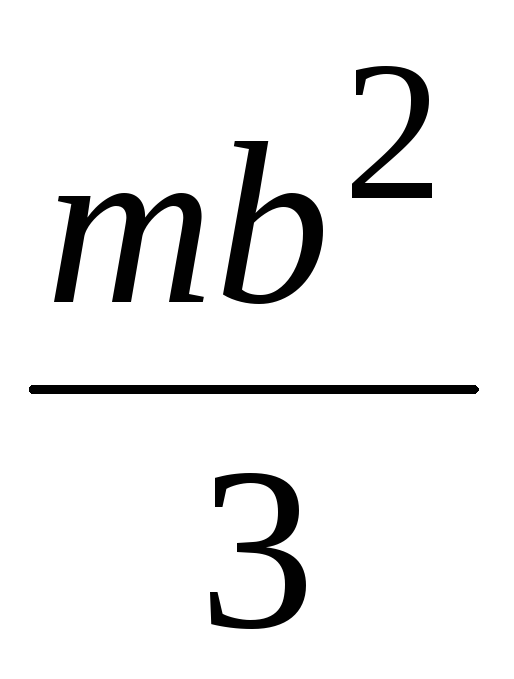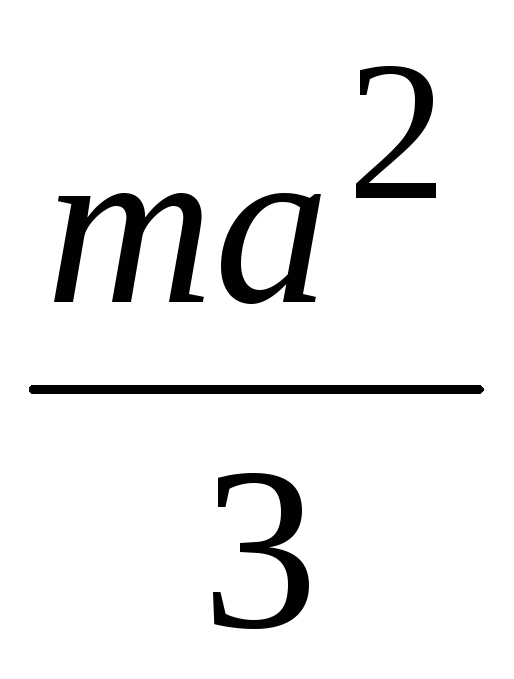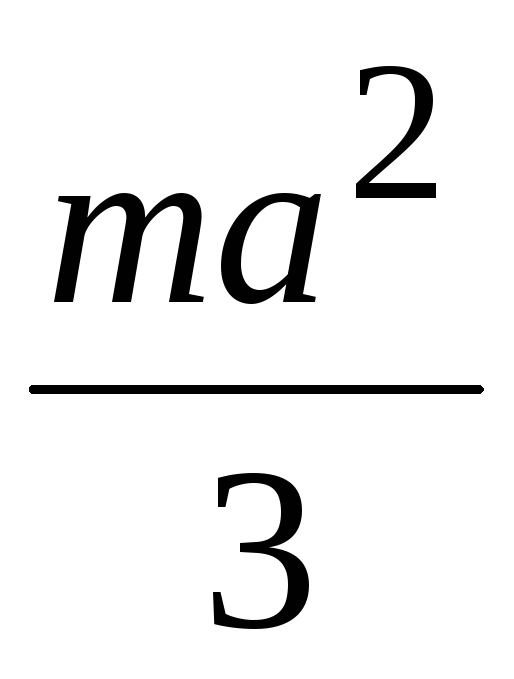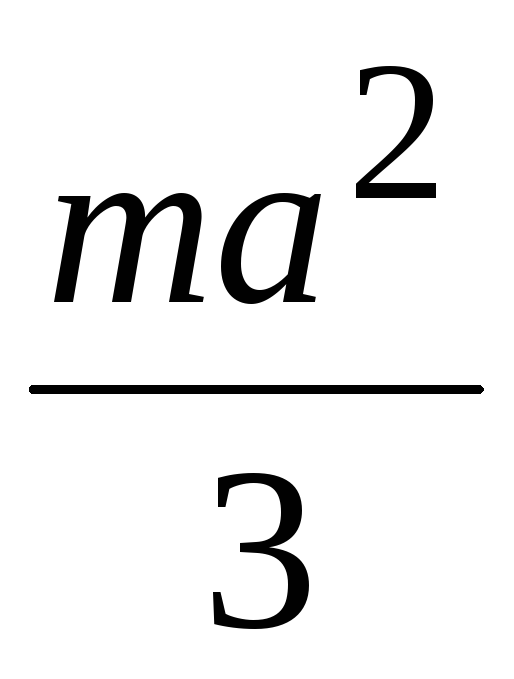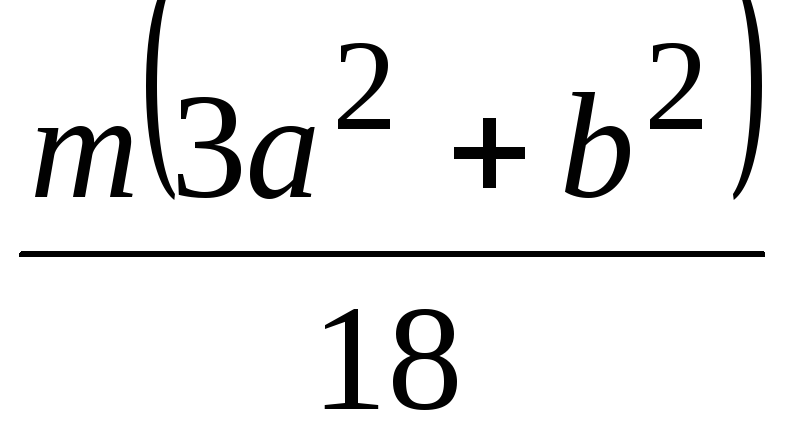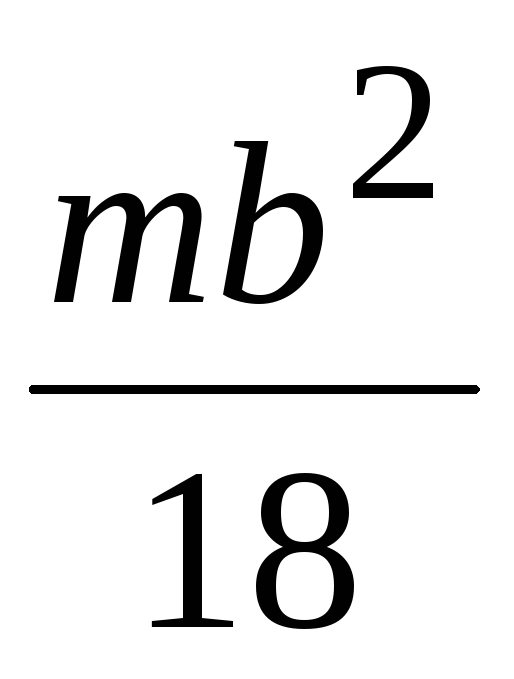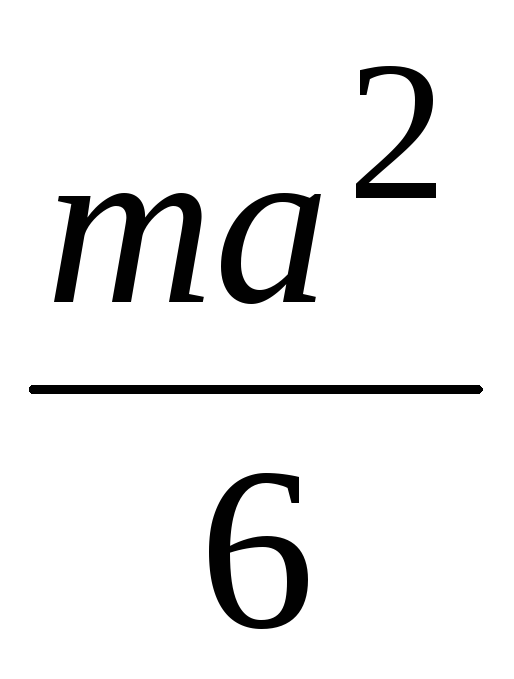Момент инерции твёрдого тела.
Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:
где — масса 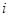 -й частицы тела,
-й частицы тела, 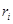 — ее расстояние от заданного центра или оси.
— ее расстояние от заданного центра или оси.
Предположим, что масса выделенной частицы тела , расстояние от нее до начала координат (т. о) 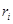 , а координаты, соответственно,
, а координаты, соответственно, 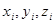 (рис. 58).
(рис. 58).
Момент инерции относительно т. О по определению равен
(250)
(рис. 58)
а относительно координатных осей:
(251)
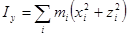 (252)
(252)
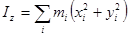 (253)
(253)
Сравнивая (230), (231), (232) и (233), получим связь момента инерции тела относительно начала координат с моментами инерции относительно координатных осей:
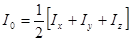 (254)
(254)
Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде
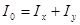
Примеры расчёта сил инерции.
Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящий через его центр масс.
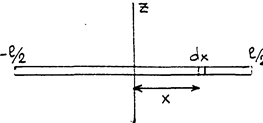
(рис. 59)
Если стержень имеет массу 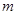 и длину
и длину 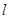 , а ось
, а ось 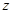
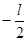 и . Выделим в стержне на расстоянии от оси малый его участок длины . Его момент инерции относительно
и . Выделим в стержне на расстоянии от оси малый его участок длины . Его момент инерции относительно 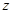 равен:
равен:
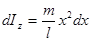 (256)
(256)
Интегрируя (236), получим:
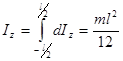
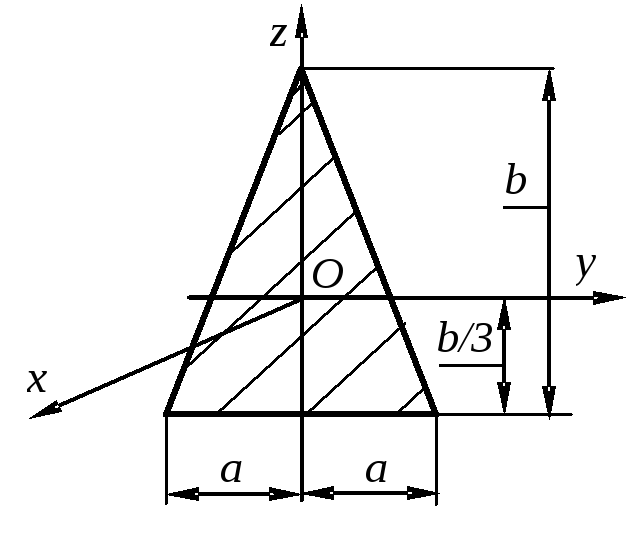
Момент инерции тонкой пластины прямоугольной формы относительно одной из её сторон.
(рис. 60)
Размеры тонкой пластины массы 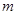 приведены на рис. 60, выделим в пластине на расстоянии от оси
приведены на рис. 60, выделим в пластине на расстоянии от оси 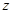 узкий слой ширины и запишем его момент инерции:
узкий слой ширины и запишем его момент инерции:
(258)
Интегрируя (258), получаем:
(259)
Момент инерции однородного шара относительно его центра.
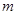 , а радиус . Выделим в шаре тонкий сферический слой радиуса , толщины , момент инерции которого относительно центра шара равен
, а радиус . Выделим в шаре тонкий сферический слой радиуса , толщины , момент инерции которого относительно центра шара равен
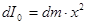 (260)
(260)
где:
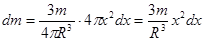
Интегрируя (260), получим искомый результат:
 (261)
(261)
Теорема Штейнера.
Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера:
Момент инерции тела относительно произвольной оси 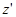 равен сумме момента инерции относительно оси
равен сумме момента инерции относительно оси 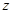 , параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:
, параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:
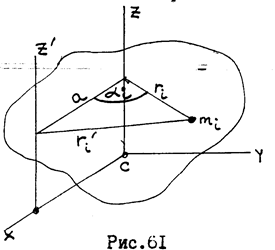

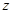 , параллельную заданной оси
, параллельную заданной оси 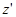 (рис. 61). Расстояние между осями равно
(рис. 61). Расстояние между осями равно 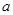 . Выберем частицу тела массы , настояние от нее до осей
. Выберем частицу тела массы , настояние от нее до осей 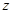 и
и 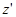
Момент инерции тела относительно 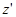 по определению:
по определению:
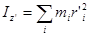 (262)
(262)
Из геометрических соображений:
Первое слагаемое в правой части дает момент инерции тела относительно 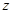 :
:
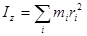 (263)
(263)
Поскольку a=const, второе слагаемое принимает вид (Ma
В последнем слагаемом:
следовательно, по определению центра масс:
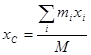
последнее слагаемое обращается в нуль, поэтому:
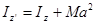
что и требовалось доказать.
Кинетическая энергия твёрдого тела для различных типов движения.
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
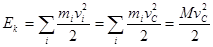
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
(265)
ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА
В любой момент времени плоское движение можно представить, как вращение вокруг мгновенного центра вращения, пусть О -мгновенный центр вращения, а т. С — центр с масс тела. Тогда:
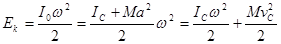 (266)
(266)
где: 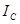 и
и 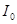 — моменты инерции тела относительно осей, проходящих через центр масс и мгновенный центр вращения,
— моменты инерции тела относительно осей, проходящих через центр масс и мгновенный центр вращения, 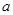
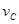 . — скорость центра масс поступательной части движения),
. — скорость центра масс поступательной части движения), 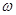 (омега) — угловая скорость вращения вокруг оси, проходящей через центр масс.
(омега) — угловая скорость вращения вокруг оси, проходящей через центр масс.
2. Вращательное движение
СВОБОДНЫЕ ОСИ ВРАЩЕНИЯ
Момент импульса тела в произвольном случае его вращения не совпадает по направлению с вектором угловой скорости вращения. Тем не менее, существует такие оси, при вращении вокруг которых момент импульса и угловая скорость по направлению совпадают. Такие оси называются главными осями инерции (свободными осями вращения). Таких осей в каждом теле три, все они взаимноперпендикулярны и проходят через центр масс тела, поэтому их удобно принимать в качестве системы отсчета для каждой из этих осей
, , 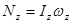 .
.
В случае произвольного по форме тела легко показать, что и 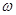 (омега) не совпадает по направлению (рис. 62).
(омега) не совпадает по направлению (рис. 62).
Кинетическая энергия тела при таком вращении может быть представлена суммой энергий вращения вокруг трех главных осей:
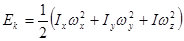
или:
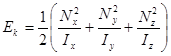
или:
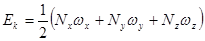
или:
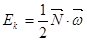
Направление векторов и 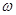 можно указать заданием направляющих косинусов, например:
можно указать заданием направляющих косинусов, например:
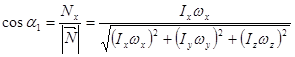
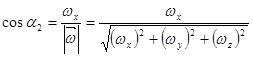
очевидно, что направления и 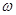 совпадают в том случае, если:
совпадают в том случае, если:
(267)
Твердое тело, отвечающее условию (267), называется шаровым волчком. Твердое тело, у которого 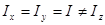 , называется симметричным волчком с осью симметрии
, называется симметричным волчком с осью симметрии 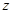 .
.
Твердое тело, у которого все три главных момента инерции различны, называет несимметричным волчком 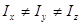 .
.
СВОБОДНОЕ ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
Свободным называют такое вращение тела, при котором сумма моментов внешних сил, приложенных к телу, равна нулю:
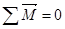
Отсюда следует, что при свободном вращении:
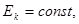
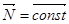
Рассмотрим свободное вращение симметричного волчка с осью симметрии 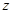 .Кинетическая энергия для него равна:
.Кинетическая энергия для него равна:
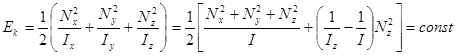
В этом выражении первое слагаемое постоянно, следовательно, постоянно и второе, т.е.:
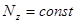 (268)
(268)
Учитывая, что 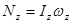 получаем:
получаем:
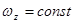 (269)
(269)
Написав выражение для кинетической энергии в виде:
делаем вывод, что:
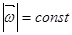 (270)
(270)
наконец, кинетическую энергию представим в виде:
(271)
где a — угол между векторами и 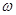 .Из (271) следует, что,
.Из (271) следует, что,
(272)
Учитывая (269), (270), (271) ,(272) свободное вращение тела можем представить как вращение оси симметрии тела вокруг неподвижного направления . При этом относительное расположение 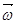 , и
, и 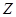 со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью
со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью 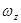 , a сама ось описывает коническую поверхность, вращаясь вокруг неподвижного направления с угловой скоростью прецессии .
, a сама ось описывает коническую поверхность, вращаясь вокруг неподвижного направления с угловой скоростью прецессии .

(рис. 63)
Т. o . для вращающегося тела можно выделить три оси — момента импульса., угловой скорости и оси симметрии. Существенно, что относительное расположение этих осей зависит от величины угловой скорости вращения тела вокруг оси симметрии 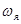 . Несложно доказать, что при очень быстром вращении тела
. Несложно доказать, что при очень быстром вращении тела 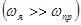 все три направления практически сливаются в одно. Эта особенность быстро вращающихся тел лежит в основе элементарной теории гироскопов.
все три направления практически сливаются в одно. Эта особенность быстро вращающихся тел лежит в основе элементарной теории гироскопов.
Гироскопы.
Рассмотрим быстро вращающийся относительно оси симметрии массивный диск (рис.64). При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии.
Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов:
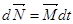
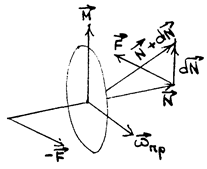
рис. 64)
Через промежуток времени момент импульса изменит свое направление и станет равным 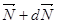 Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента — в вертикальной.
Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента — в вертикальной.
Уравнение моментов в скалярном виде в этом случае представляют следующим образом:
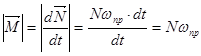
С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так:
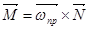 (273)
(273)
Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.
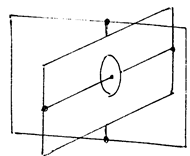
Рис.65
Для определения угловой скорости прецессии удобно пользоваться следующими соображениями. Масштаб измерения можно выбрать таким, что конец вектора совпадает с концом оси гироскопа (рис. 66).
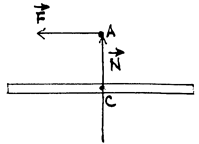
(рис. 66)
При действии на конец оси (в т. А) силы 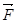 ее момент вызовет прецессионное вращение. По уравнению моментов
ее момент вызовет прецессионное вращение. По уравнению моментов
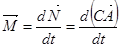
Но 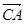 можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:
можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:
(274)
14.8. Прецессия волчка.
Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания 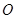 неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр
неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр 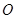 .
.
при указанном направлении вращения момент силы тяжести вызывает прецессию в направлении, указанном на рисунке. Угловую скорость прецессии
(рис. 67)
можно определить, пользуясь (274):
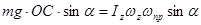
т.е.
(275)
Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.
Гидростатика.
Гидромеханика изучает свойства покоя и движения жидкостей и газов. Гидростатика изучает только свойства покоя жидкостей и газов.
Основные соотношения гидромеханики получены для идеальной жидкости, т.е. для абсолютно несжимаемой и невязкой жидкости.
Основной задачей гидростатики является нахождение распределений давления и плотности по объему жидкости или газа (в случае идеальной жидкости — только давления).
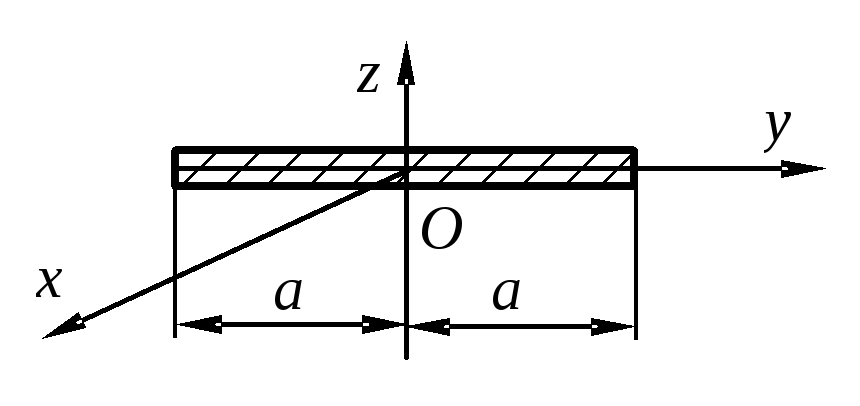
Осевые моменты инерции однородных пластинок
Форма пластинки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
4.3. Пример выполнения задания
4.3.1. Условие примера
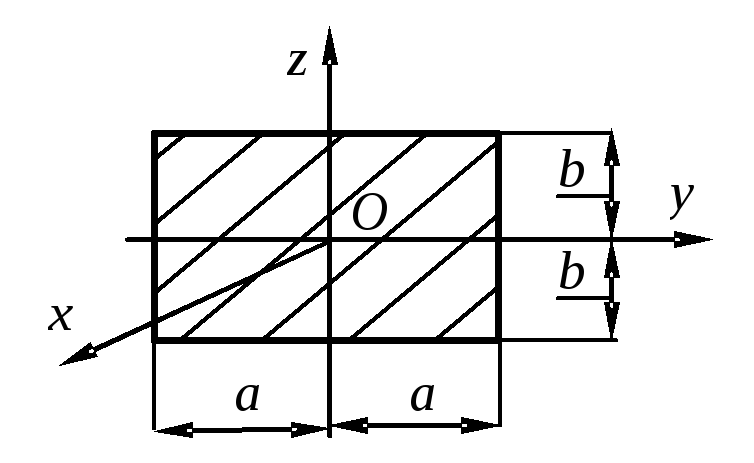
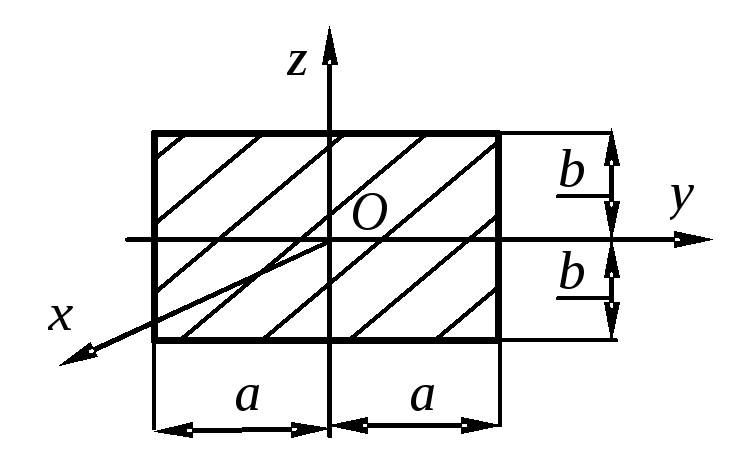
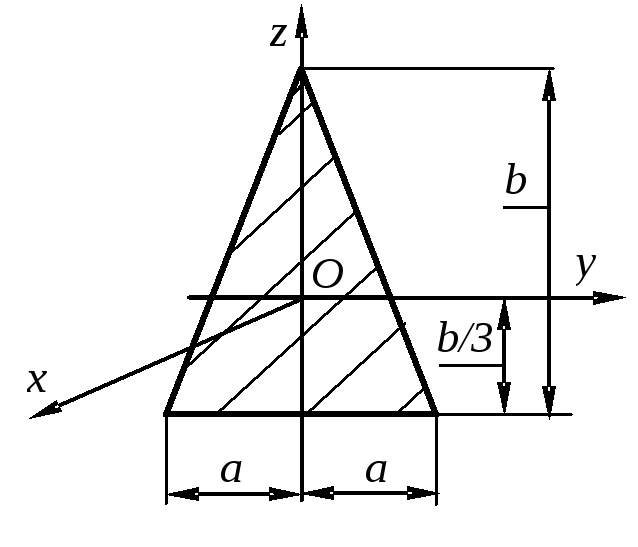
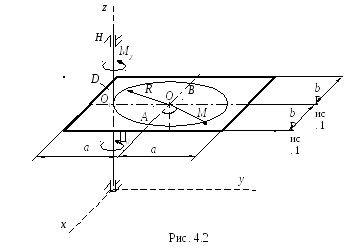
Тело D, имеющее
форму прямоугольной пластины, показанной
на рис. 4.2, массой 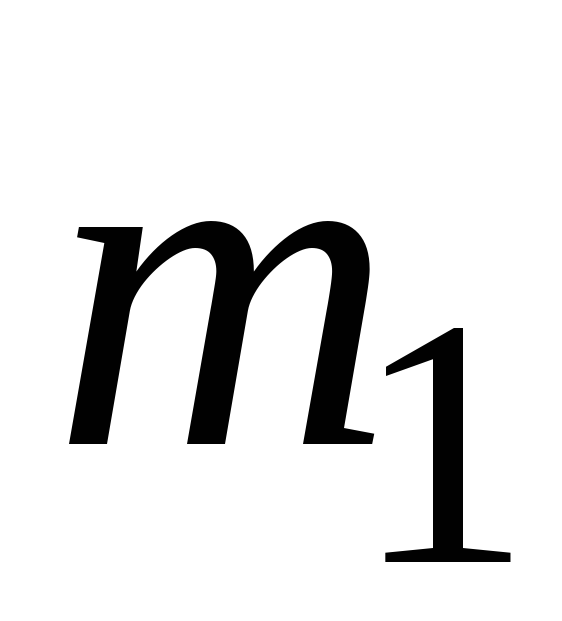 =20
кг вращается вокруг вертикальной осиz
с угловой скоростью
=20
кг вращается вокруг вертикальной осиz
с угловой скоростью 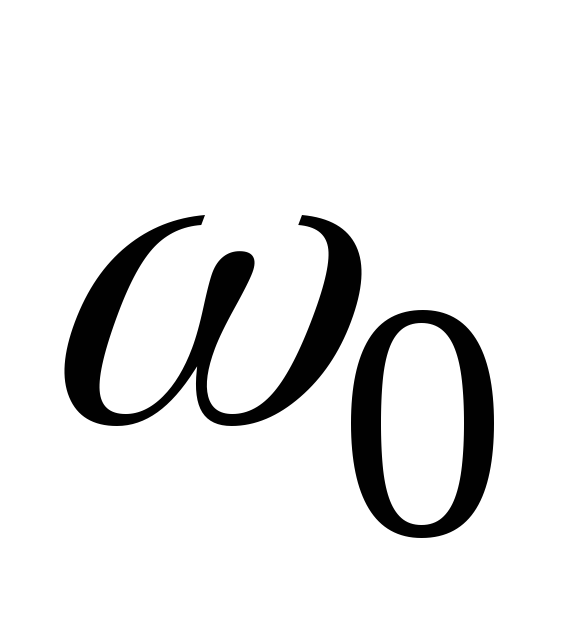 =2
с-1.
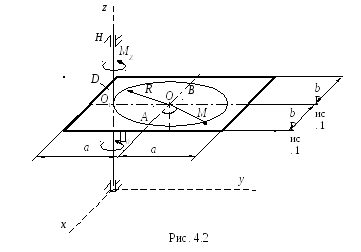
При этом в точке M желоба AB тела D на расстоянии AM=
=2
с-1.
При этом в точке M желоба AB тела D на расстоянии AM=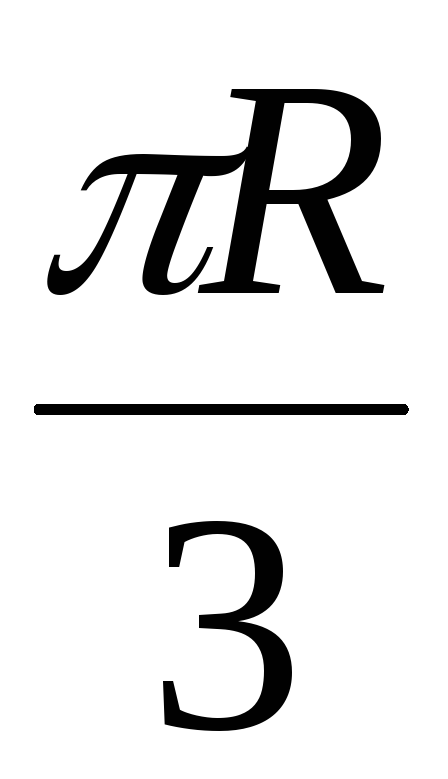 от точкиA,
отсчитываемом вдоль желоба, закреплена
материальная точка K массой
от точкиA,
отсчитываемом вдоль желоба, закреплена
материальная точка K массой 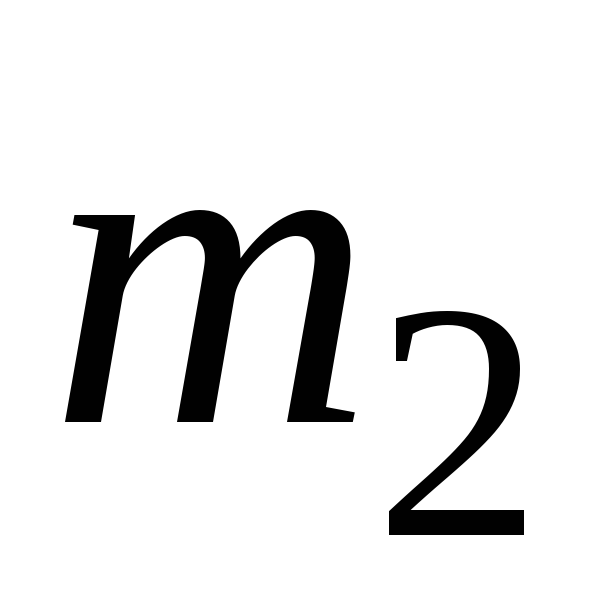 =8
кг. В момент времени
=8
кг. В момент времени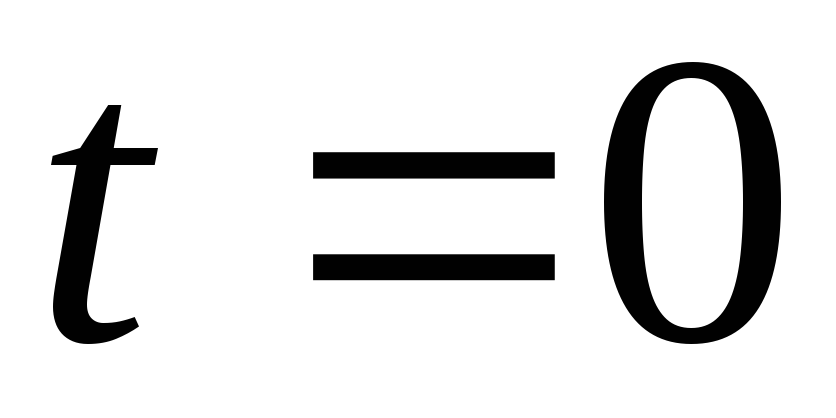 на систему начинает действовать пара
сил с моментом
на систему начинает действовать пара
сил с моментом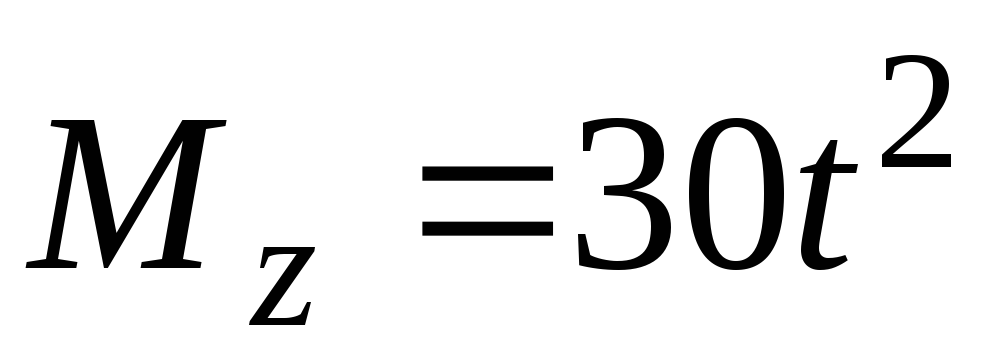 Нм. Приt=t1=4с действие
пары сил прекращается; одновременно
точка K начинает относительное движение по
желобу согласно закону
Нм. Приt=t1=4с действие
пары сил прекращается; одновременно
точка K начинает относительное движение по
желобу согласно закону 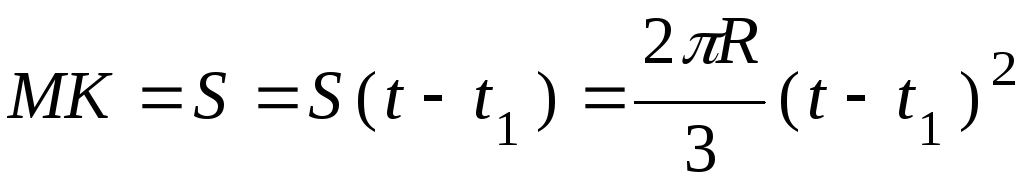 м.
м.
Определить угловые
скорости тела D соответственно в моменты времени 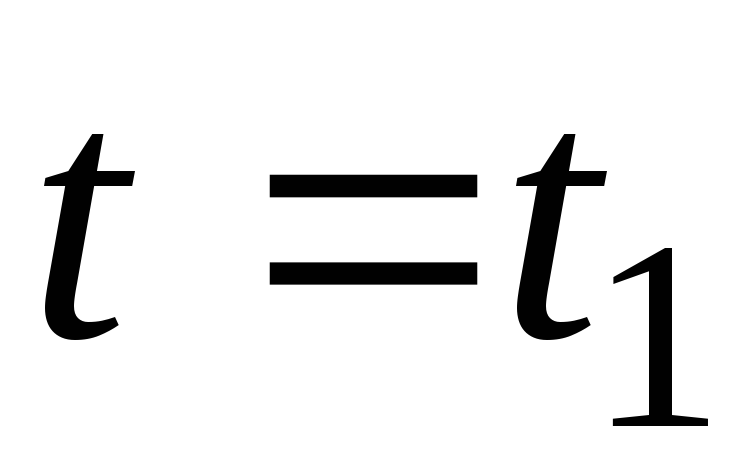 и t=t2=5
с, если R=0,6
м, a=1,2
м; b=0,9
м
и t=t2=5
с, если R=0,6
м, a=1,2
м; b=0,9
м
4.3.2. Решение примера
Запишем равенство, выражающее теорему об изменении кинетического момента механической системы относительно оси z
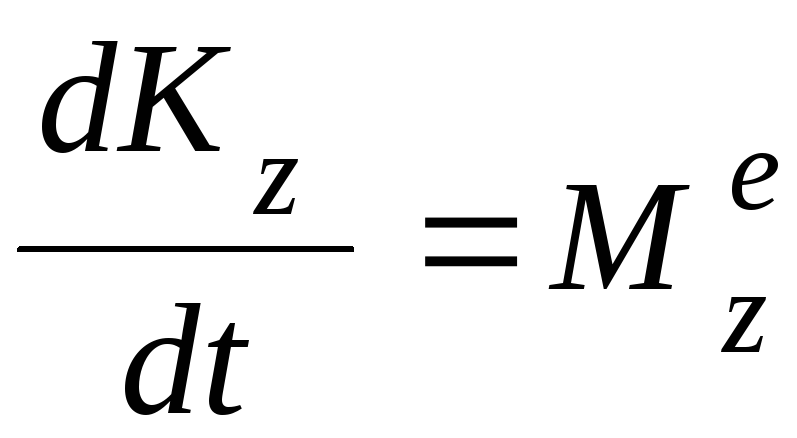 , (4.1)
, (4.1)
где 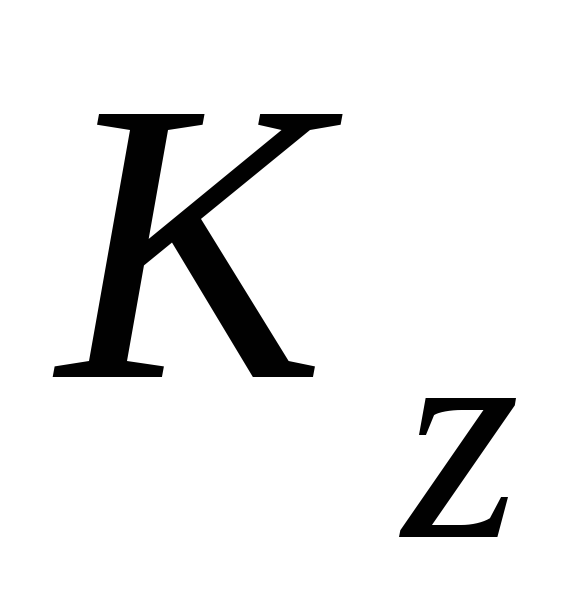 — кинетический момент механической
системы, состоящей в данном случае из
кинетического момента телаD и кинетического момента точки К,
относительно оси z;
— кинетический момент механической
системы, состоящей в данном случае из
кинетического момента телаD и кинетического момента точки К,
относительно оси z;
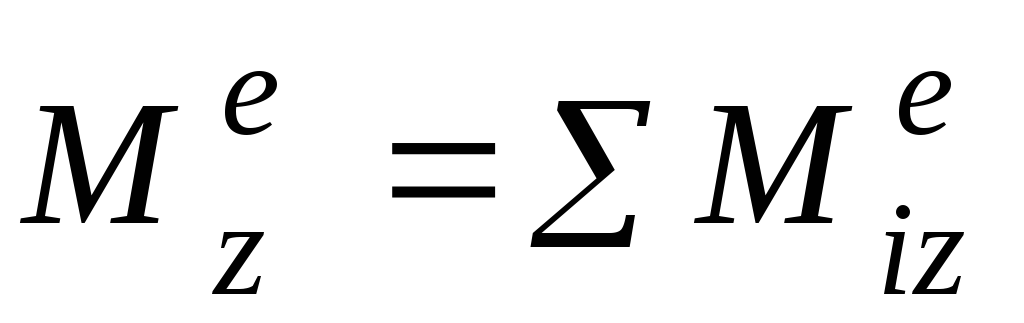 — главный момент
внешних сил, приложенных к системе,
относительно оси z.
— главный момент
внешних сил, приложенных к системе,
относительно оси z.
Рассмотрим движение системы в отрезке времени [0;t1].
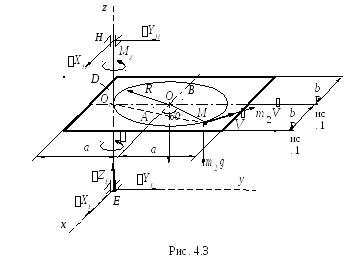
В произвольный
момент времени на систему действуют
внешние силы 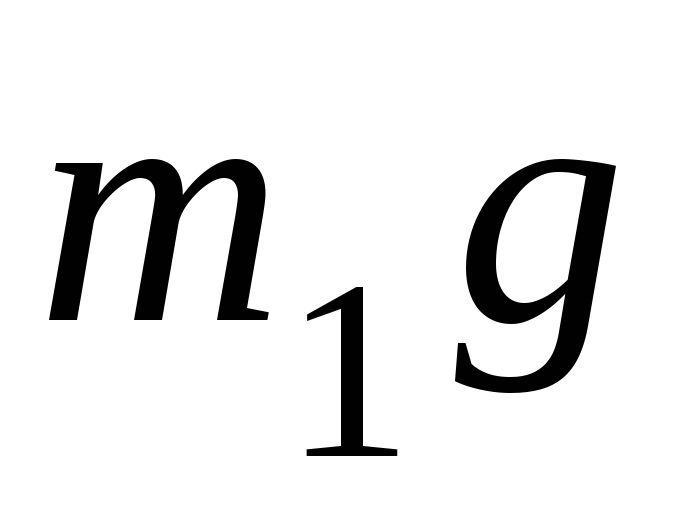 ,
,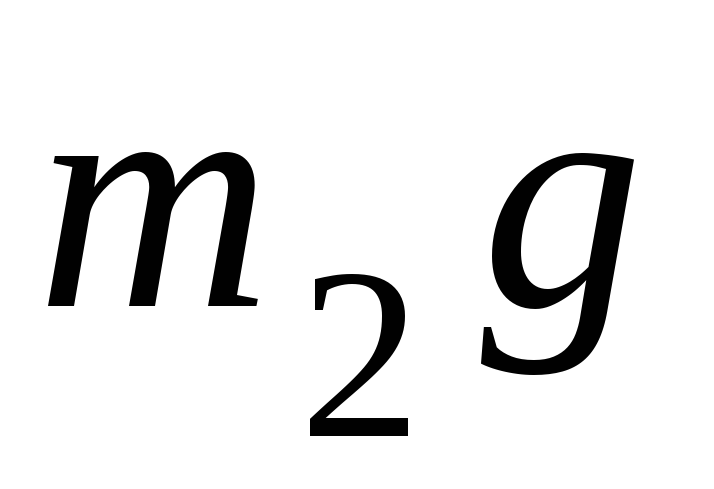 ,
,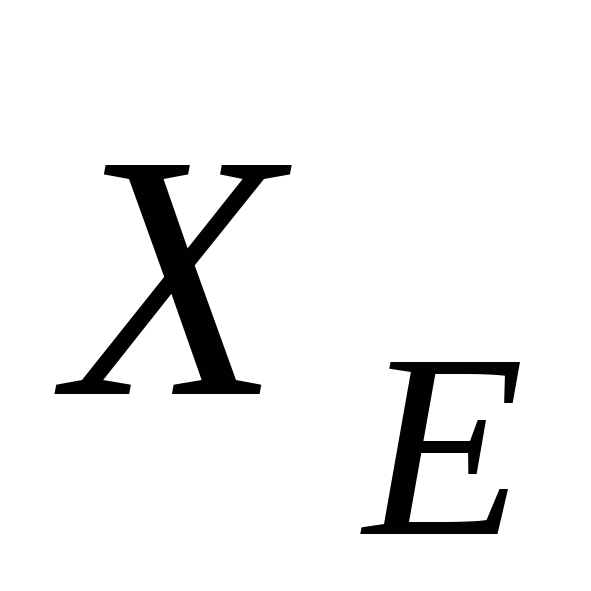 ,
,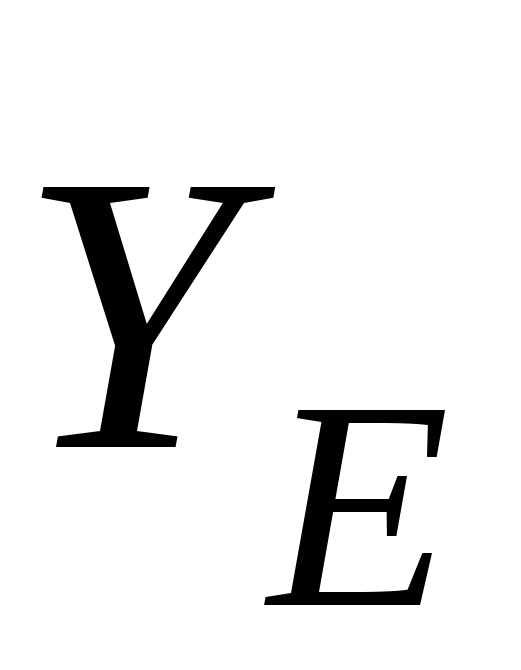 ,
,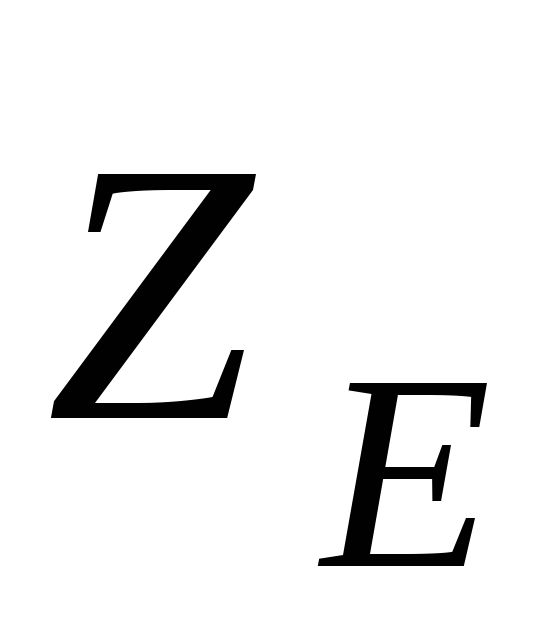 ,
,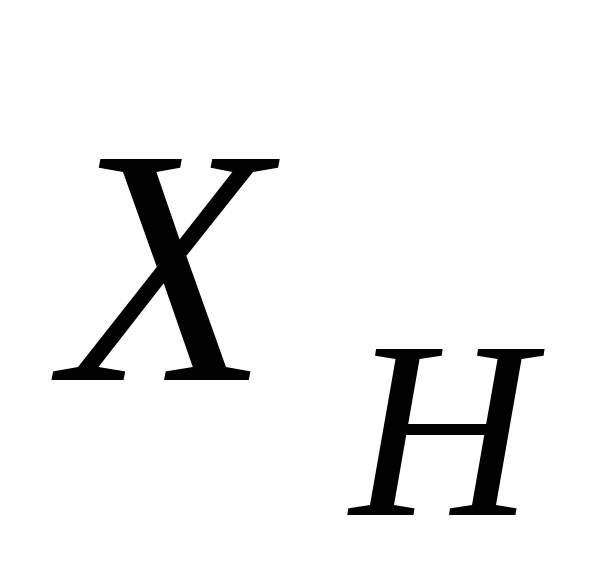 ,
,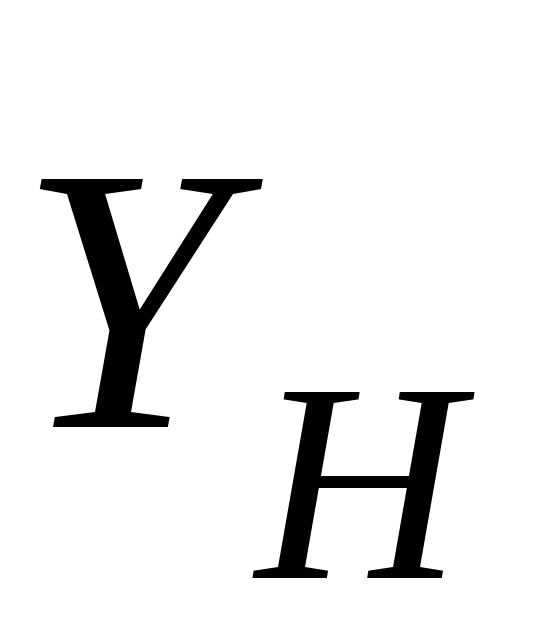 ,
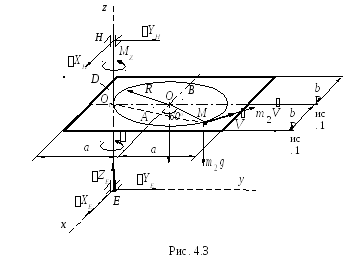
,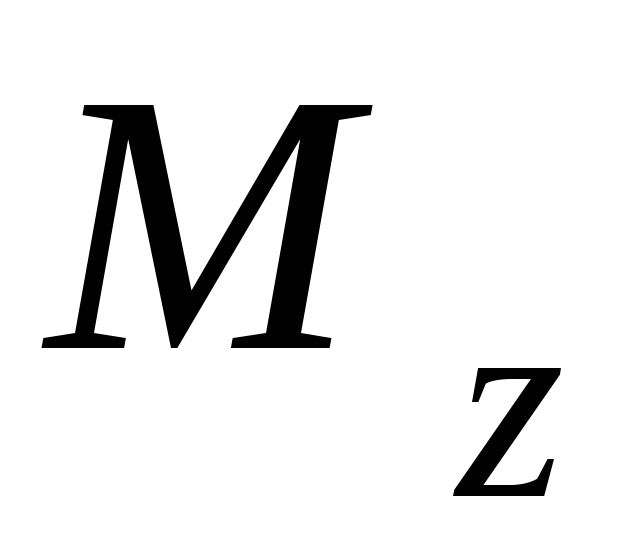 (рис. 4.3), главный момент которых
относительно осиz равен вращающему моменту
(рис. 4.3), главный момент которых
относительно осиz равен вращающему моменту 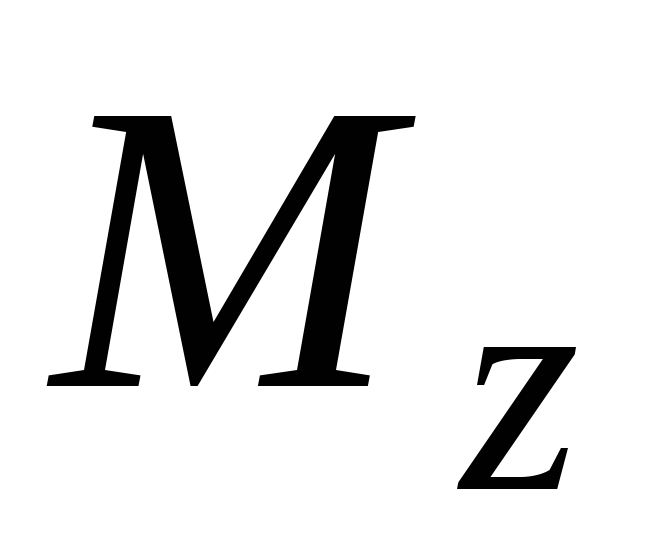 ,
то есть
,
то есть
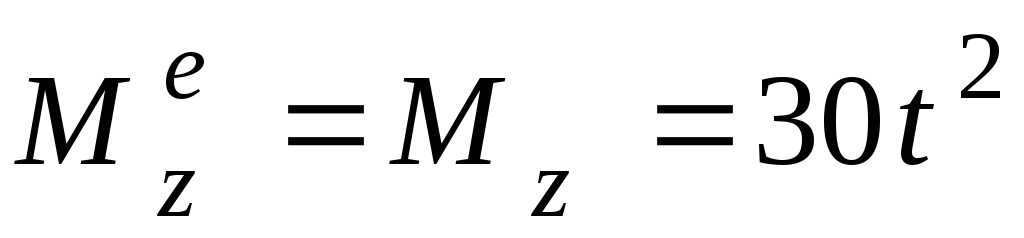 . (4.2)
. (4.2)
Кинетический момент данной системы равен сумме
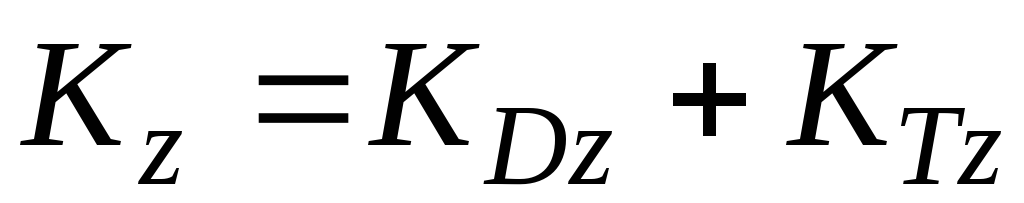 ,
,
где 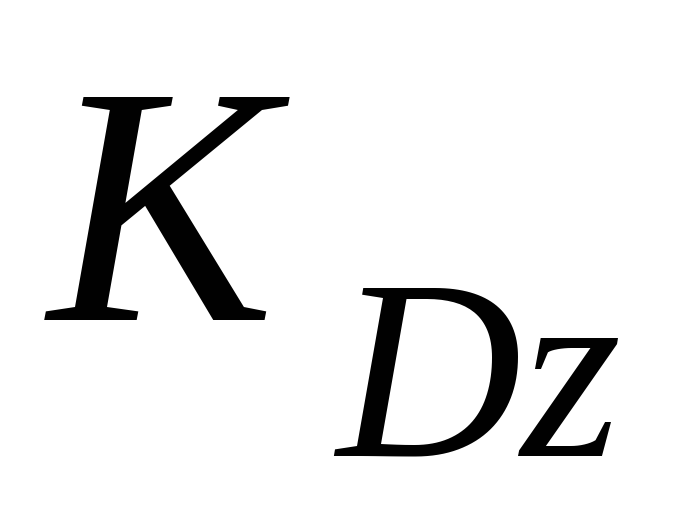
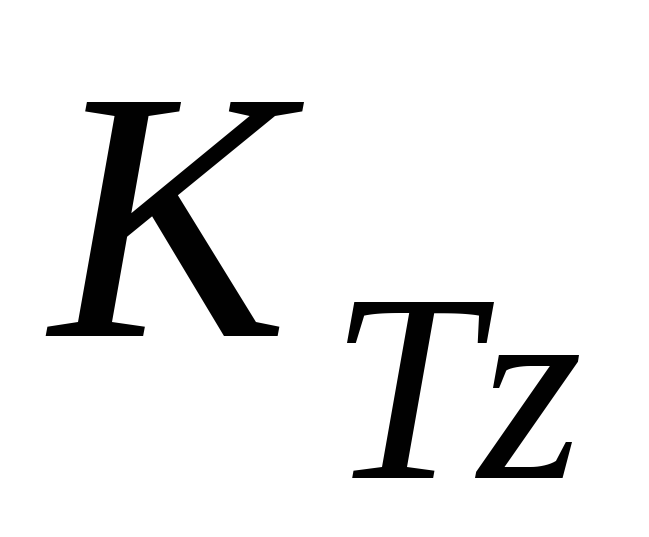 — кинетические моменты телаD и точки K относительно оси z.
— кинетические моменты телаD и точки K относительно оси z.
Тело D вращается относительно неподвижной оси, поэтому
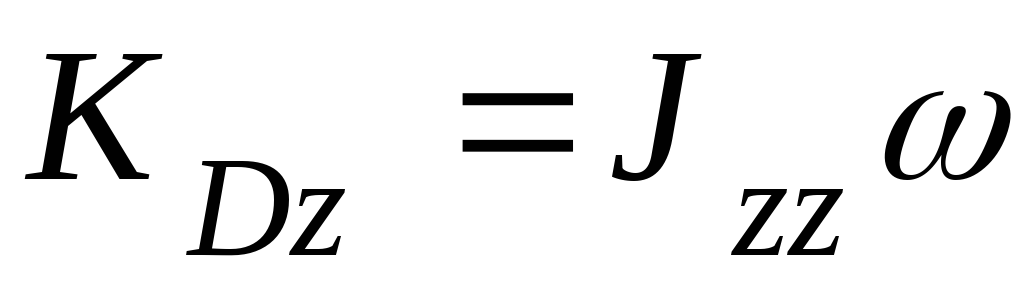 .
.
Здесь  — угловая скорость тела,
а
— угловая скорость тела,
а 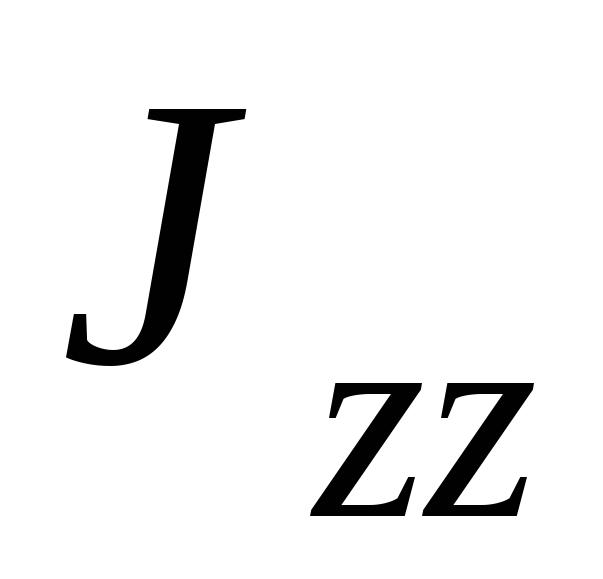 — его момент инерции относительно оси z.
— его момент инерции относительно оси z.
Момент инерции 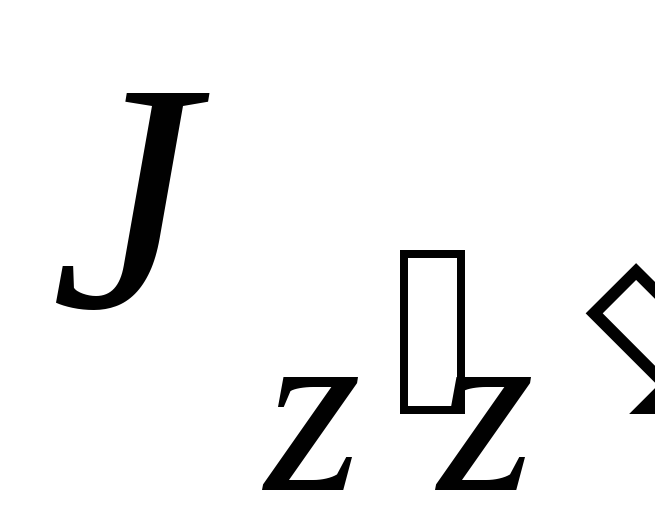 тела относительно оси
тела относительно оси 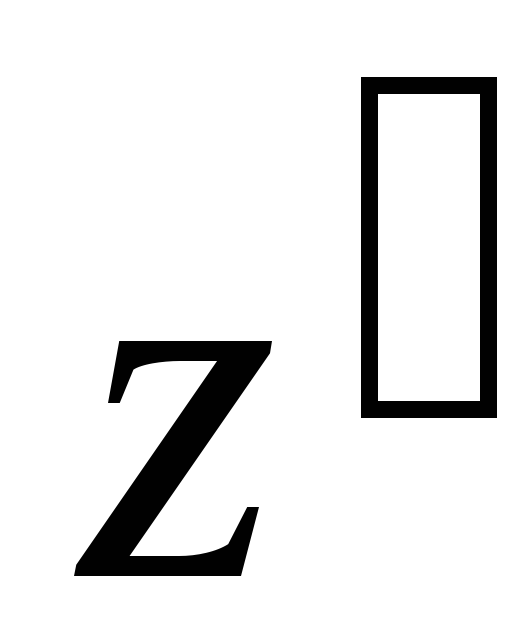 ,
параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл.
4.2)
,
параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл.
4.2)
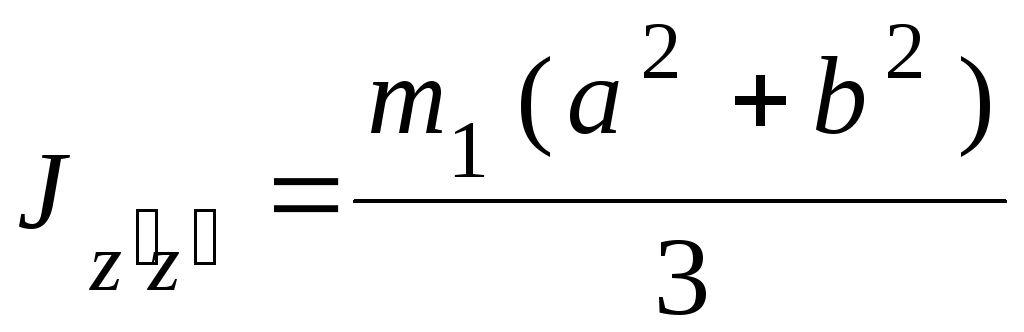 .
.
По теореме Штейнера
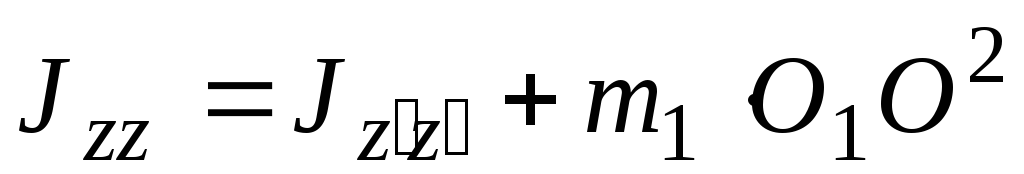 .
.
Таким образом
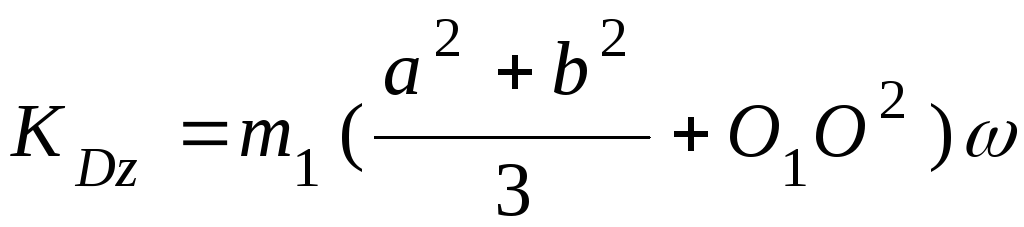 .
.
Кинетический момент материальной точки K, закрепленной в точке М желоба
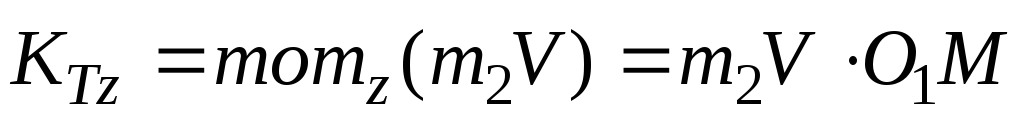 .
.
Скорость точки К
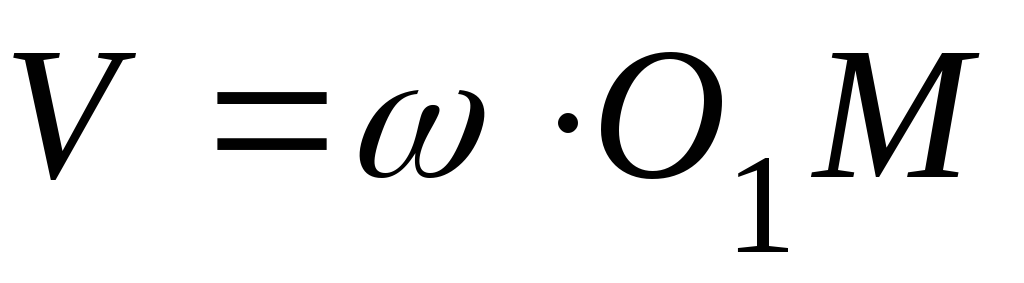 .
.
Очевидно, что 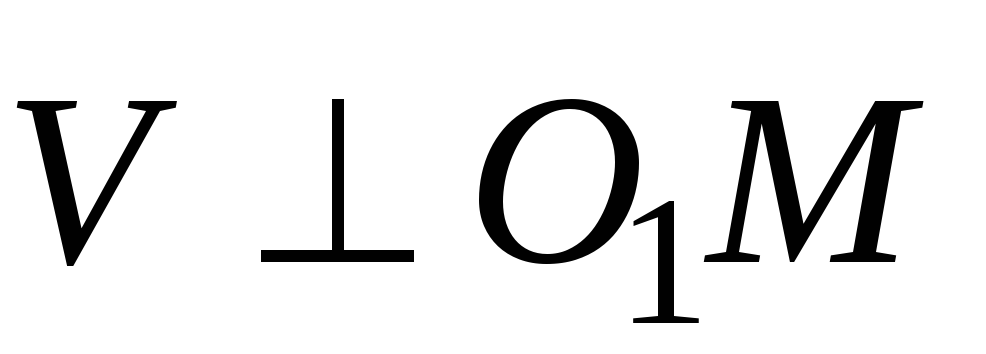 .
.
Согласно условию
задачи длина дуги окружности 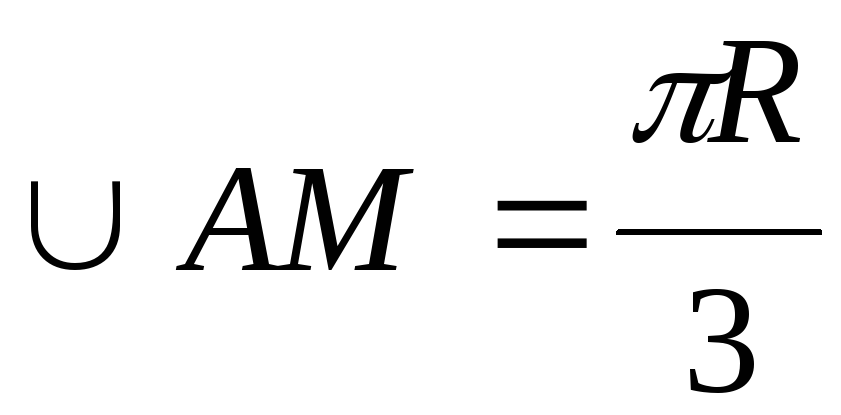 ,
тогда центральный угол
,
тогда центральный угол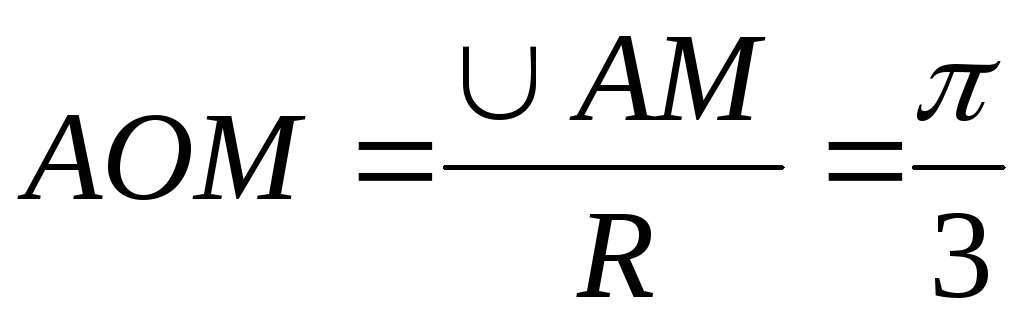 .
Следовательно, в равнобедренном
треугольникеОМО1
.
Следовательно, в равнобедренном
треугольникеОМО1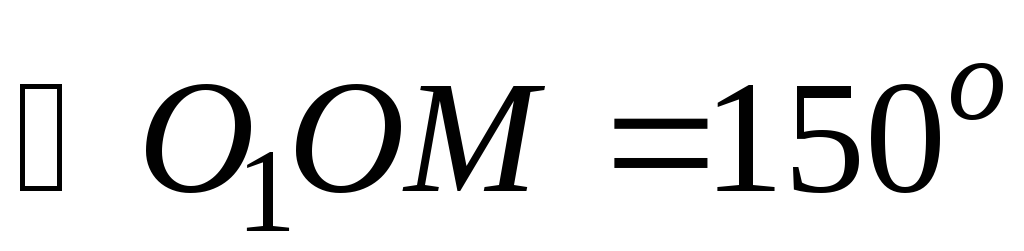 и
и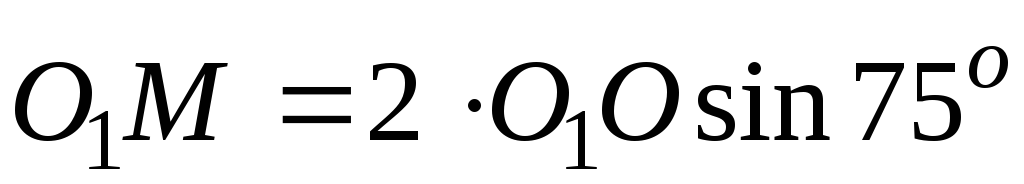 .
.
Имеем
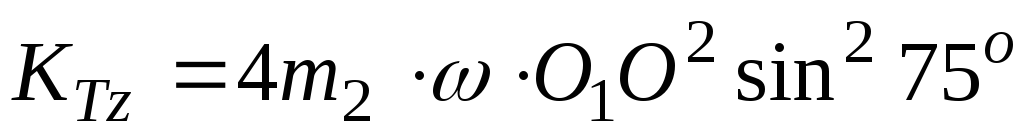 .
.
Окончательное выражение кинетического момента системы относительно оси z следующее
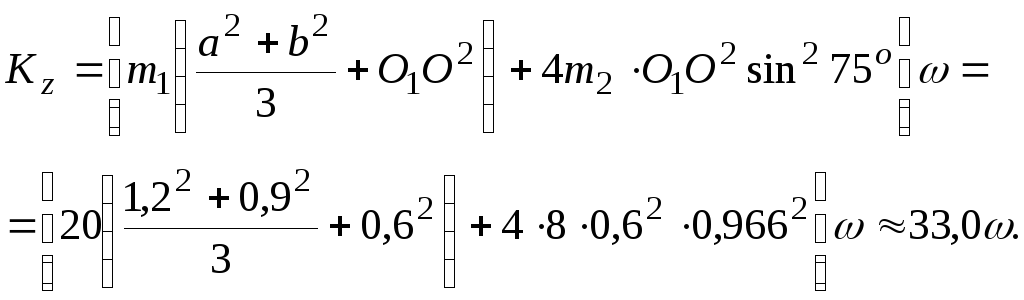 (4.3)
(4.3)
Подставляя выражения (4.2) и (4.3) в равенство (4.1), имеем
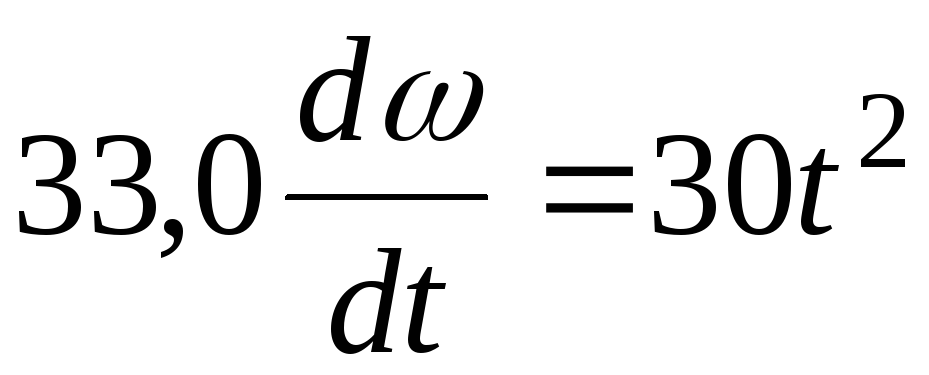 ,
,
откуда
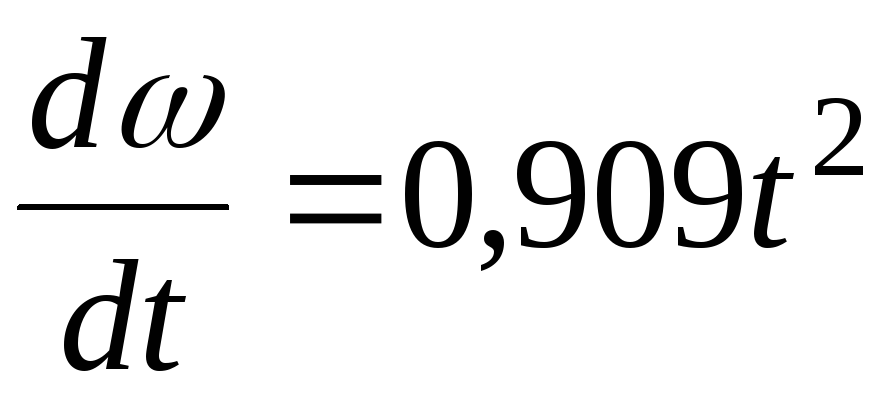 .
.
Разделяем в последнем уравнении переменные и интегрируем левую и правую части уравнения:
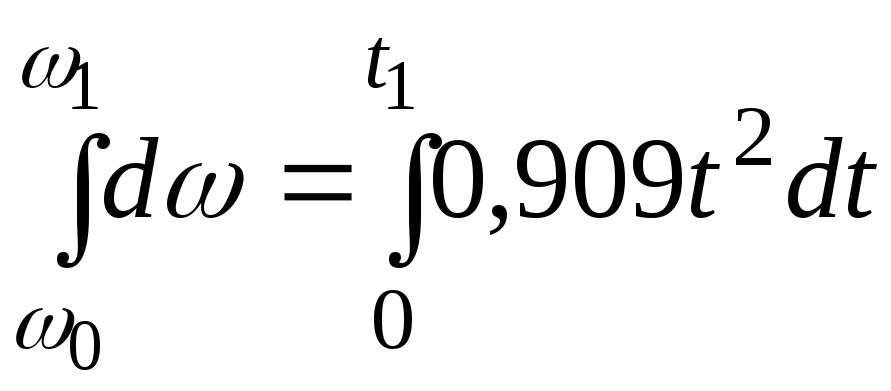 .
.
Тогда
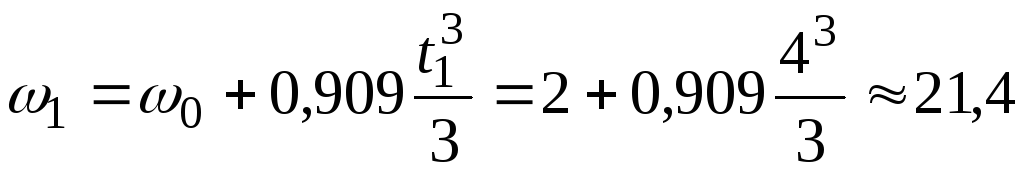 с-1.
с-1.
В момент времени t1 из выражения (4.3) имеем
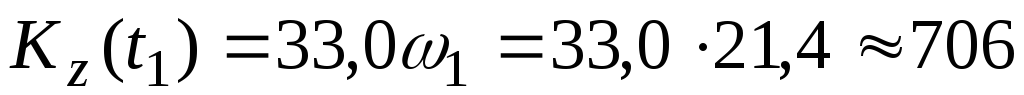 Нмс.
Нмс.
Рассмотрим теперь
движение системы в отрезке времени 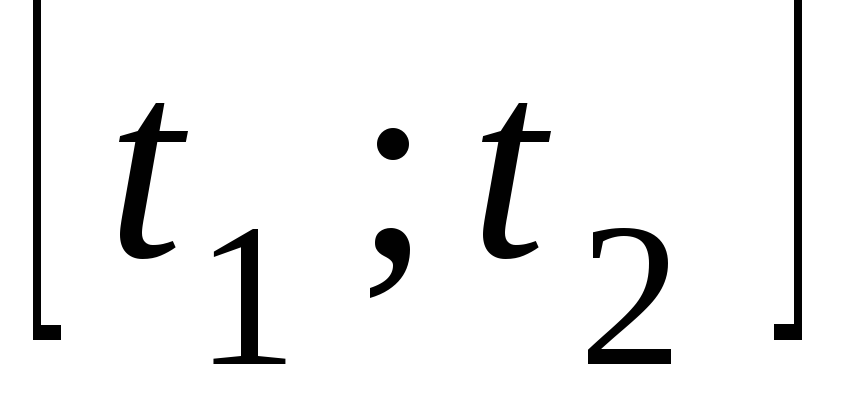 .
.
После прекращения
действия момента 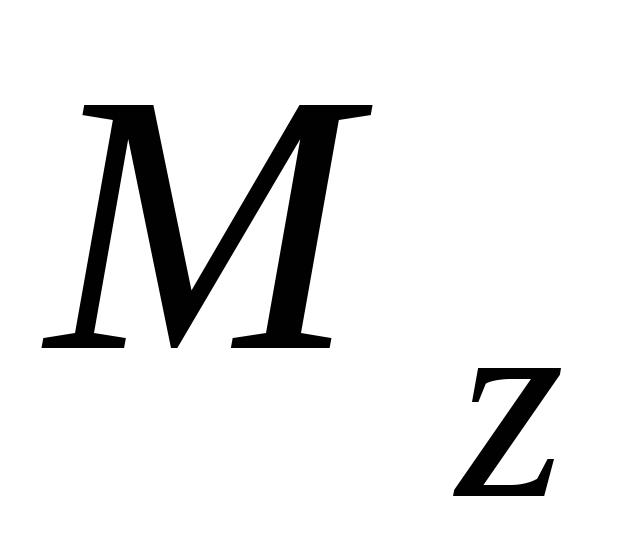 на телоD,
главный момент внешних сил относительно
оси z
на телоD,
главный момент внешних сил относительно
оси z 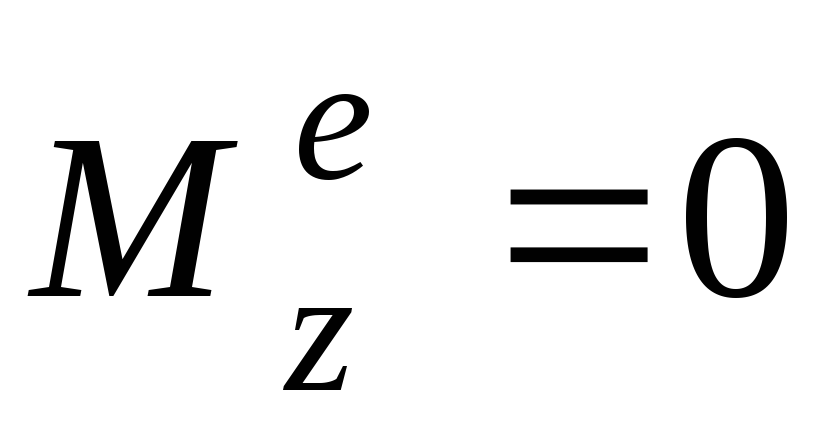 (см. рис. 4.4).
(см. рис. 4.4).
Тогда равенство (4.1) примет вид
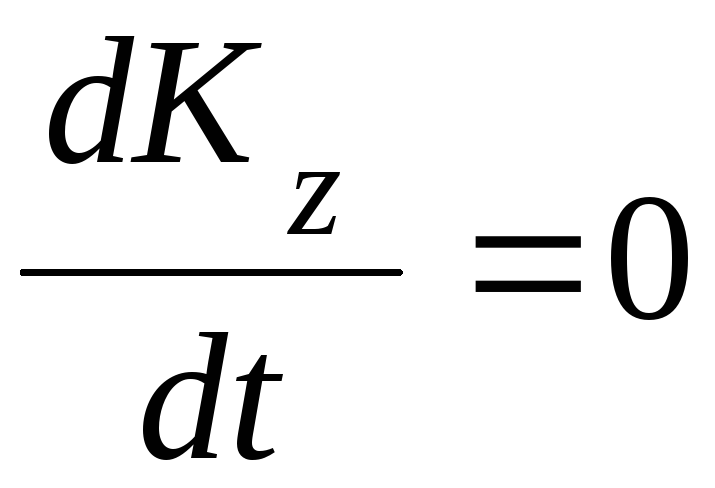 ,
,
то есть 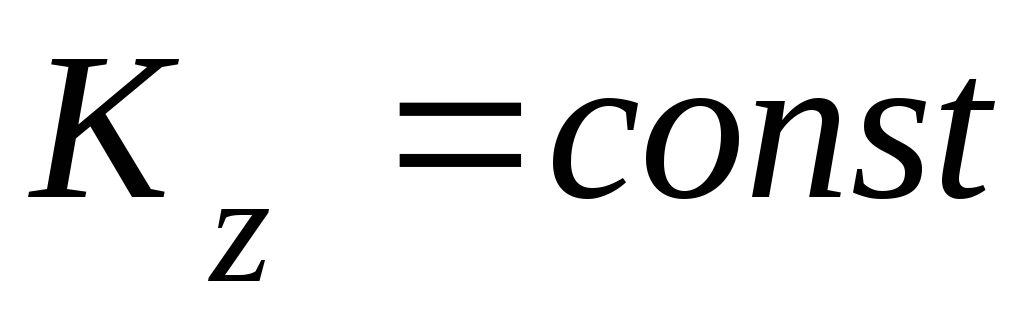 .
.
Это означает, что кинетические моменты системы относительно оси в начале t1 и в конце t2 отрезка времени [t1; t2] равны
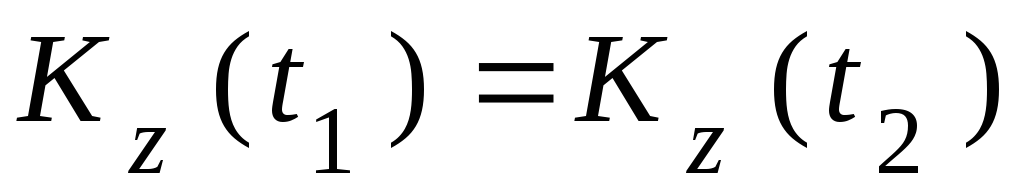 .
.

В момент времени t2 тело D вращается с угловой скоростью 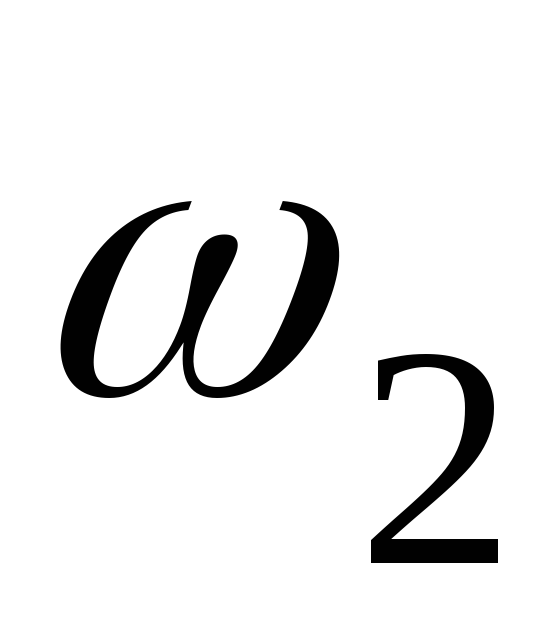 (см. рис. 4.4). При этом точкаК, совершая
сложное движение, оказывается в точке В желоба. Действительно, центральный угол
(см. рис. 4.4). При этом точкаК, совершая
сложное движение, оказывается в точке В желоба. Действительно, центральный угол
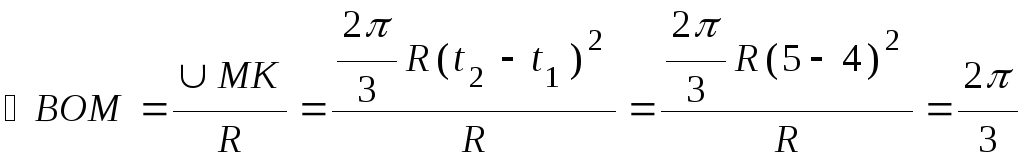 .
.
Кинетический
момент системы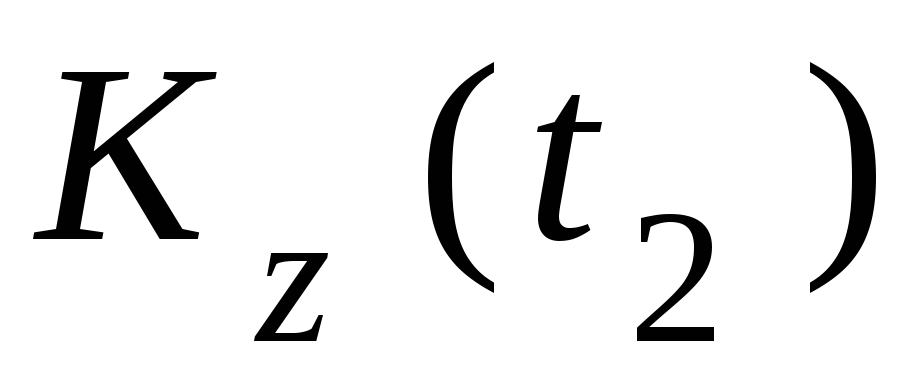 относительно оси в конце t2 отрезка времени [t1; t2]
также равен сумме кинетических моментов
тела
относительно оси в конце t2 отрезка времени [t1; t2]
также равен сумме кинетических моментов
тела 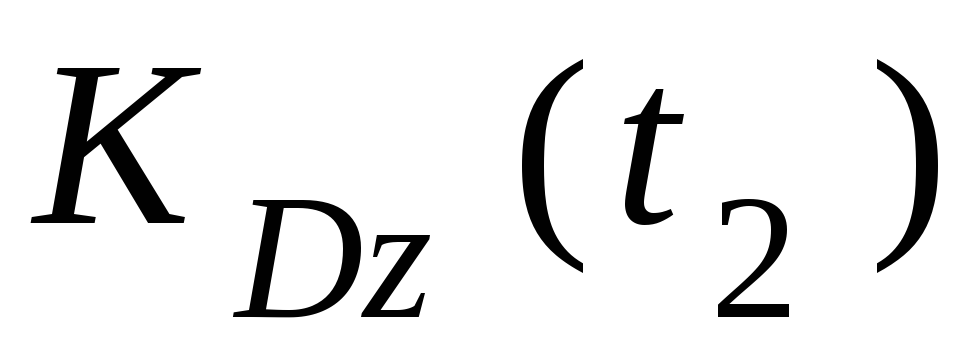 и точки
и точки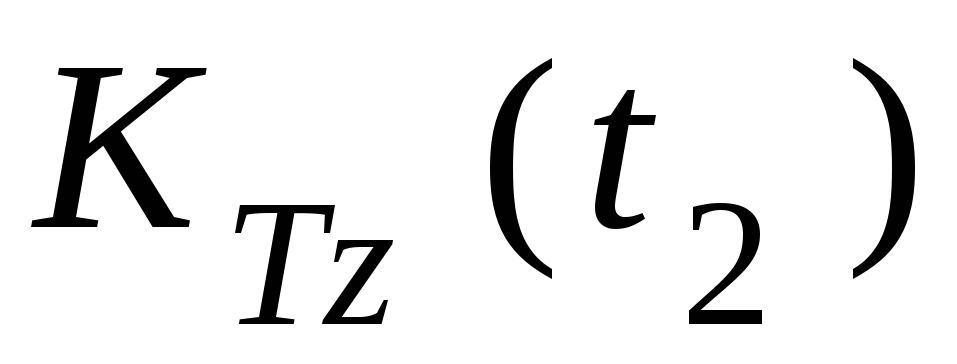 :
:
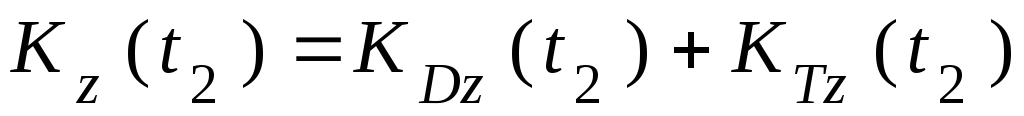 .
.
Очевидно, что
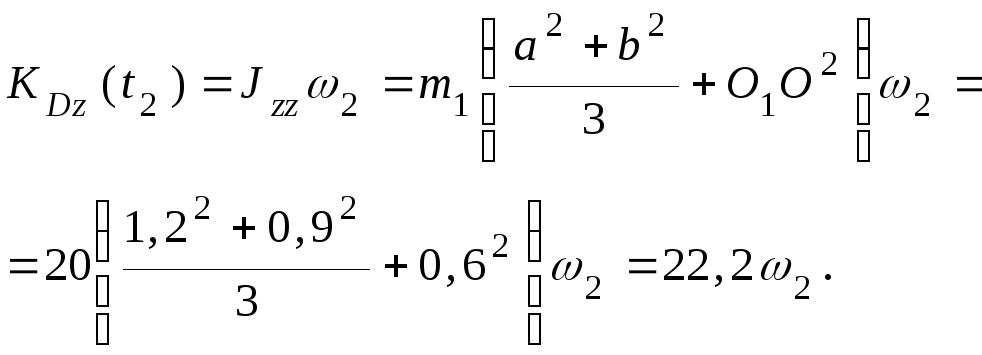
По теореме о сложении скоростей:
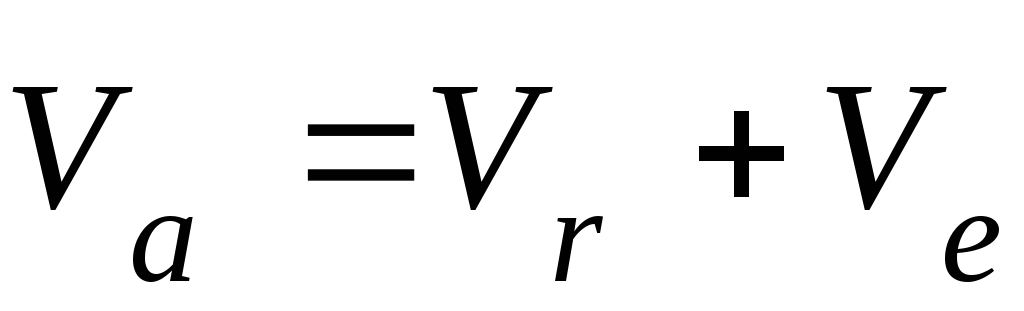 ,
,
где 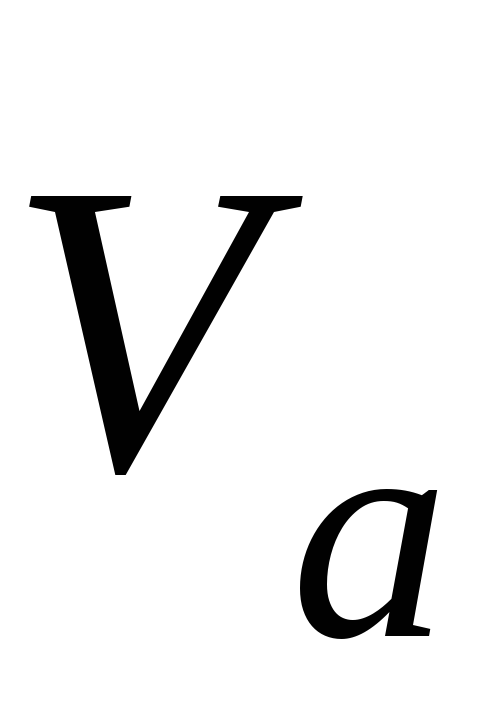 ,
,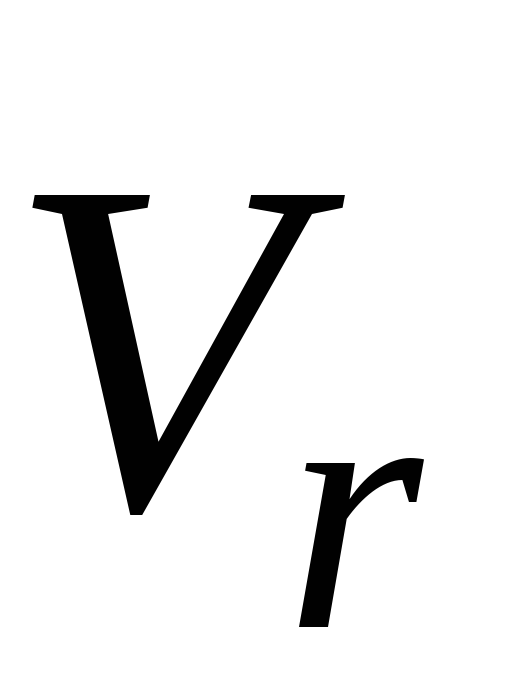 ,
,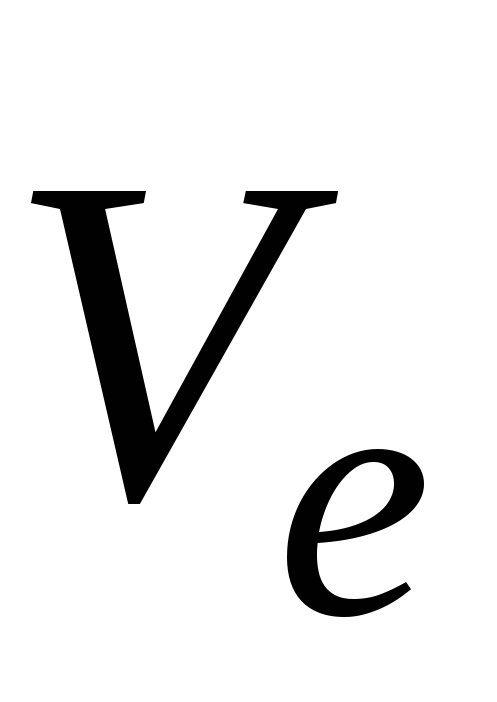 — абсолютная, относительная и переносная
скорости точки.
— абсолютная, относительная и переносная
скорости точки.
Умножая обе части этого равенства на m2, получаем:
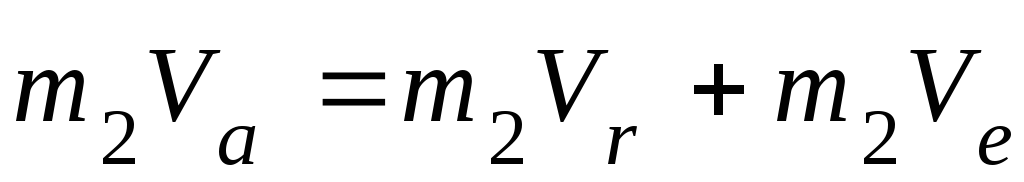 .
.
Следовательно,
кинетический момент точки К в конце отрезка времени t2 равен сумме
моментов векторов 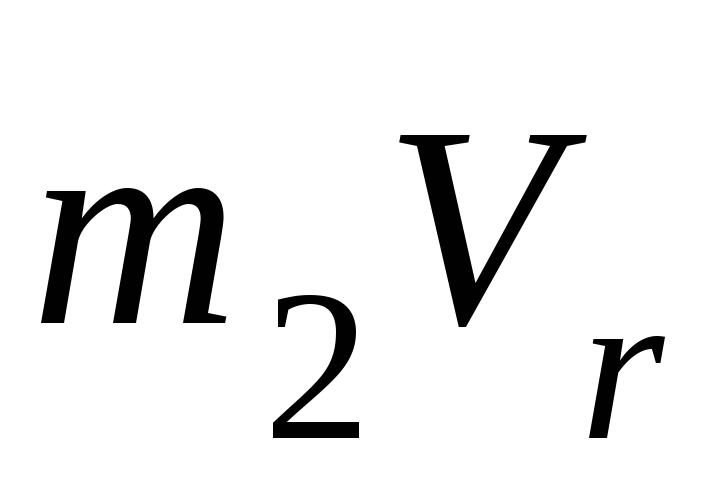 и
и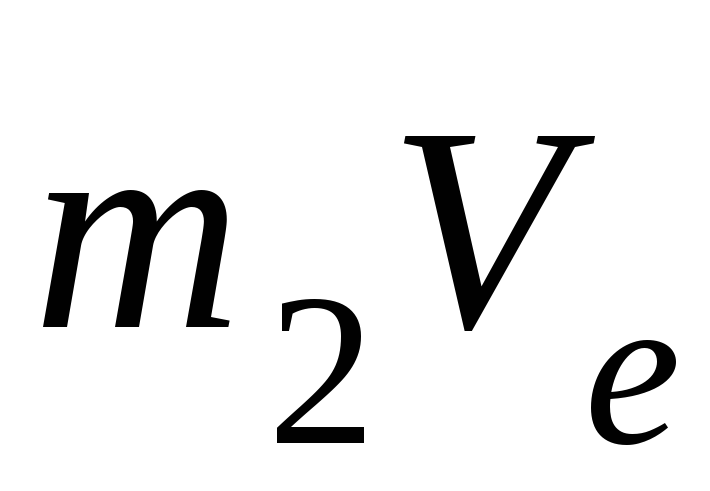 относительно осиz
относительно осиz
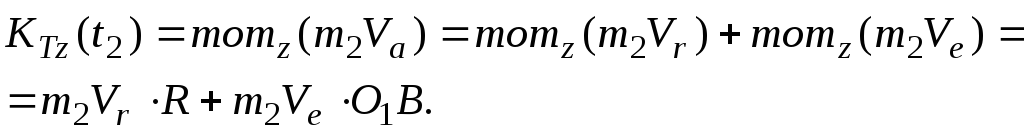
Относительная скорость точки К
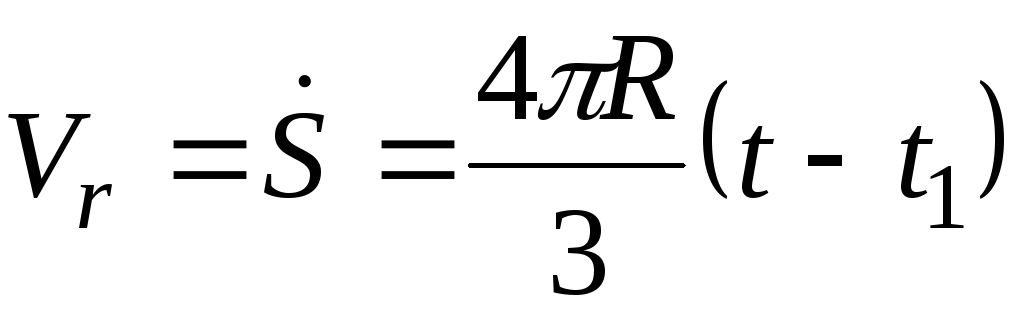 .
.
При t=t2=5 c найдем величину относительной скорости точки К
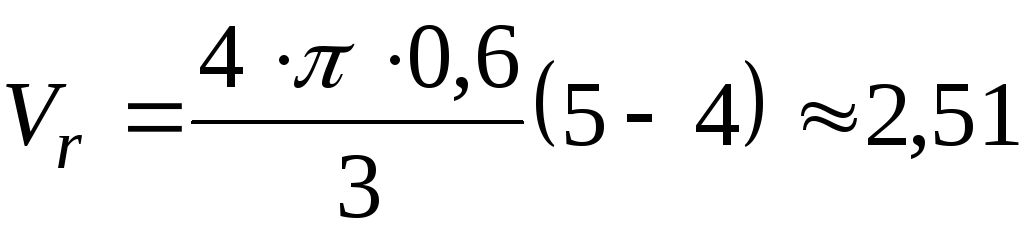 м/с.
м/с.
Переносная скорость точки К
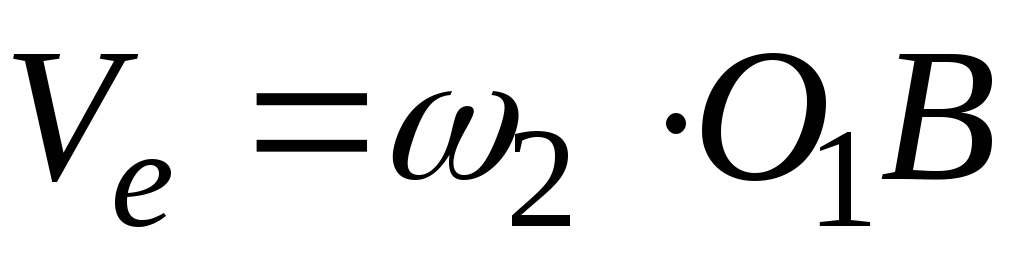 .
.
Из прямоугольного треугольника О1ОВ по теореме Пифагора имеем:
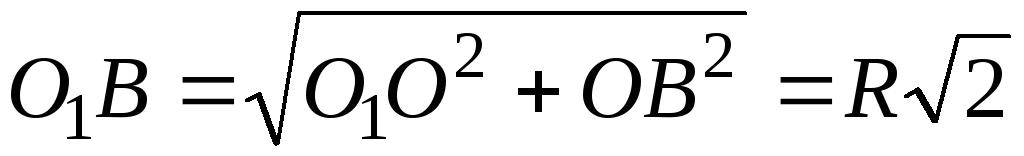 .
.
Окончательно получаем
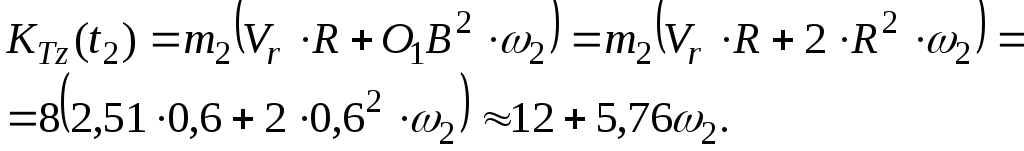
Тогда
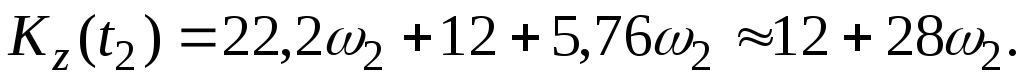
Приравнивая 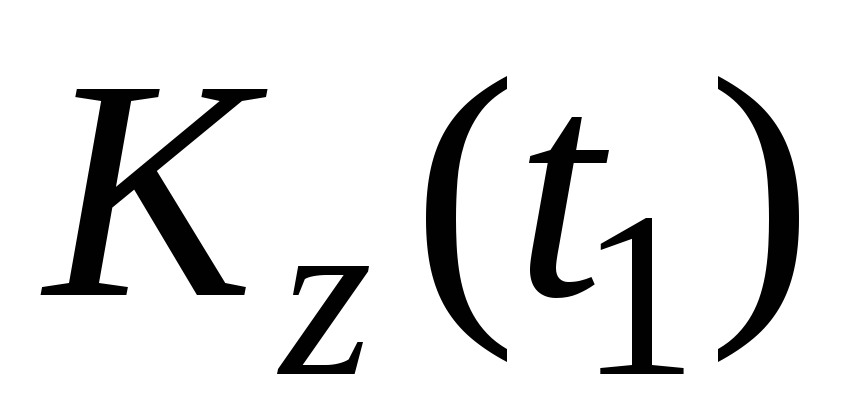 и
и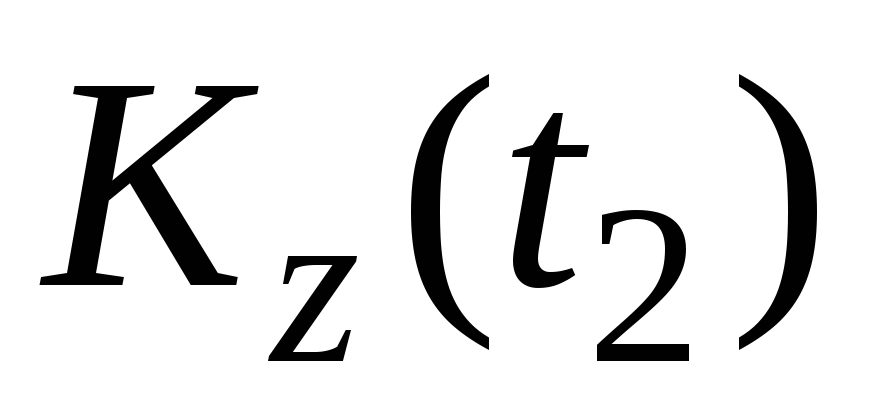 :
:
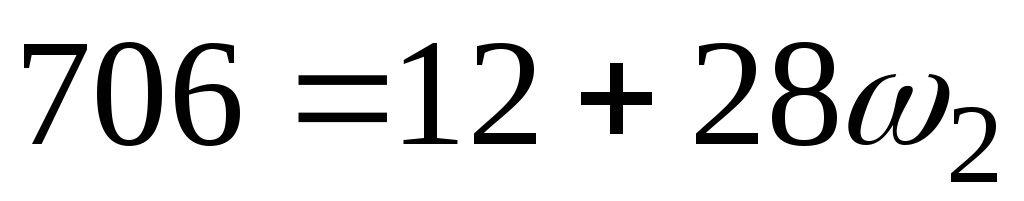 ,
,
находим
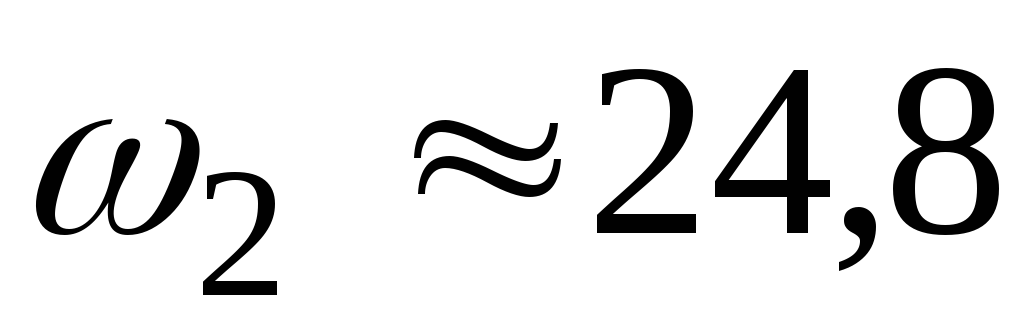 с-1.
с-1.
Краткие теоретические сведения
При
условии малых колебаний, т.е. 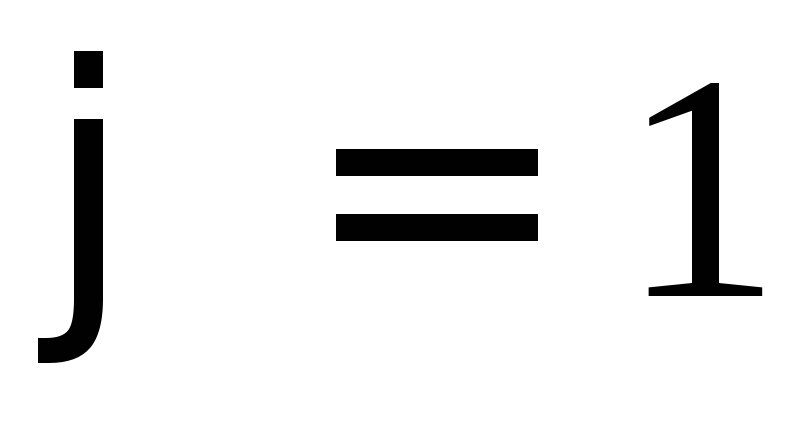 рад, колебания диска можно считать
гармоническими с периодом
рад, колебания диска можно считать
гармоническими с периодом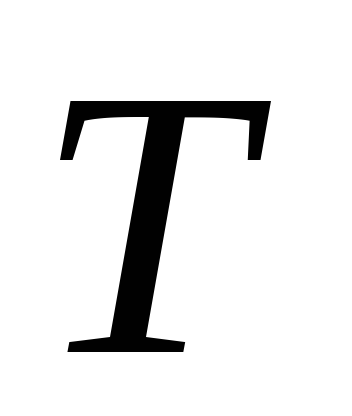 :
:
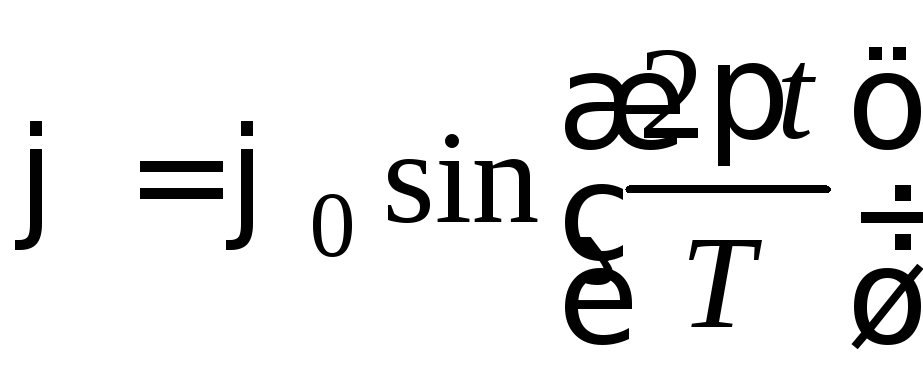 (1)
(1)
Пусть диск поднялся на максимальную высоту
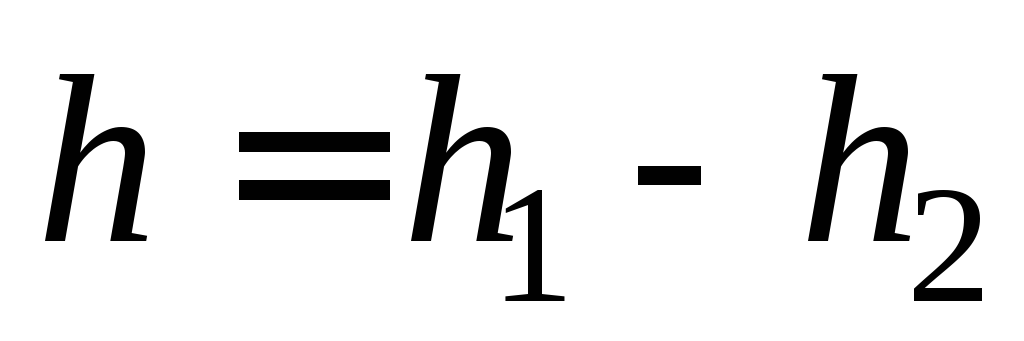 .
.
Тогда приращение потенциальной энергии равно:
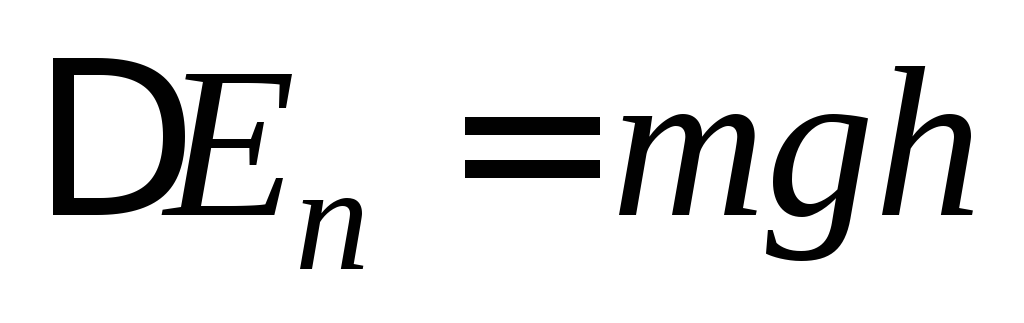
При последующем вращении диска потенциальная энергия переходит в кинетическую энергию вращательного движения
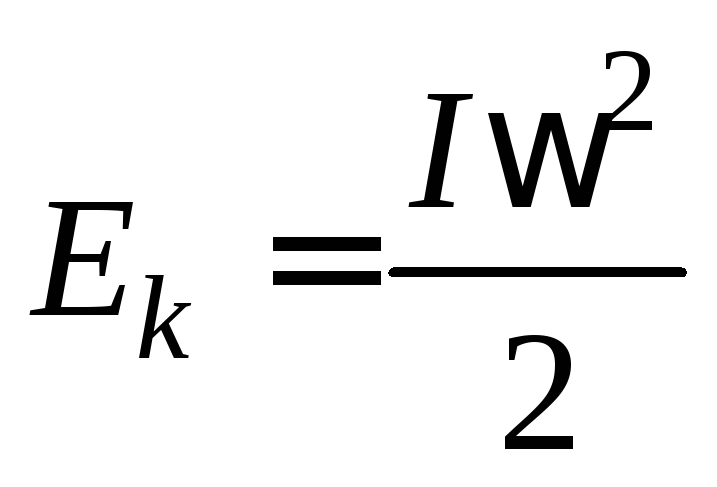 ,
,
где 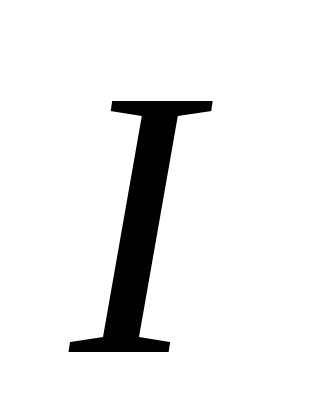 – момент инерции тела относительно оси
вращения,– угловая
скорость вращения.
– момент инерции тела относительно оси
вращения,– угловая
скорость вращения.
В момент прохождения положения равновесия кинетическая энергия принимает максимальное значение, и, пренебрегая трением, можно записать закон сохранения энергии:
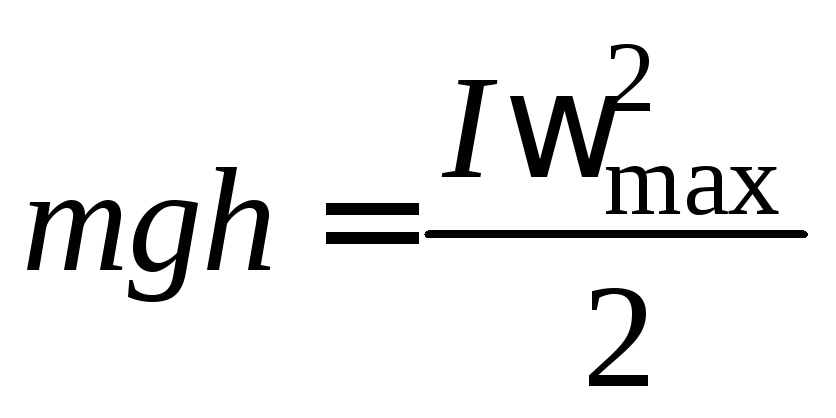 . (2)
. (2)
Угловую
скорость диска можно найти, взяв
производную от из (1):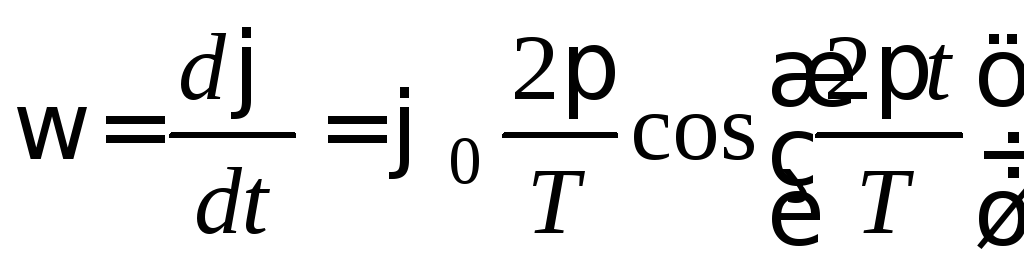
тогда 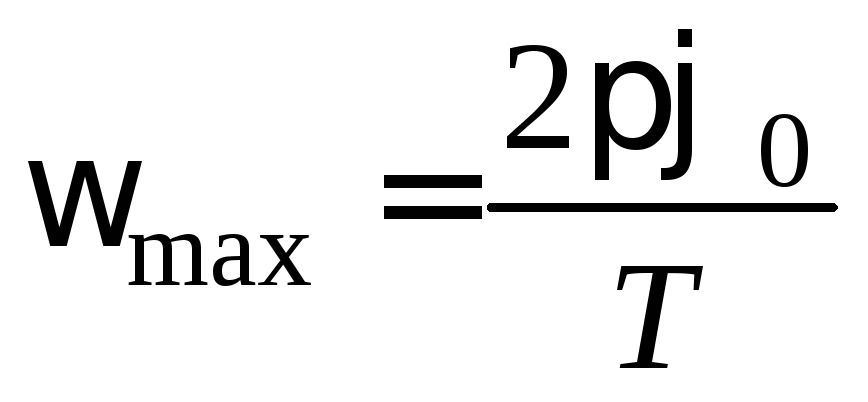 . (3)
. (3)
Величину h можно найти,
считая, что при повороте диска на малый
угол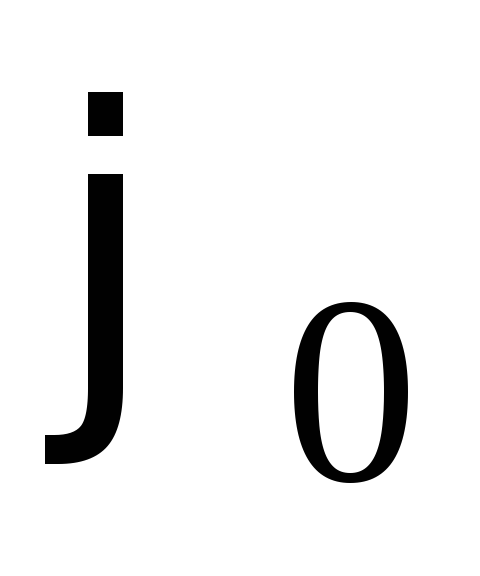 можно приблизительно считать, что
можно приблизительно считать, что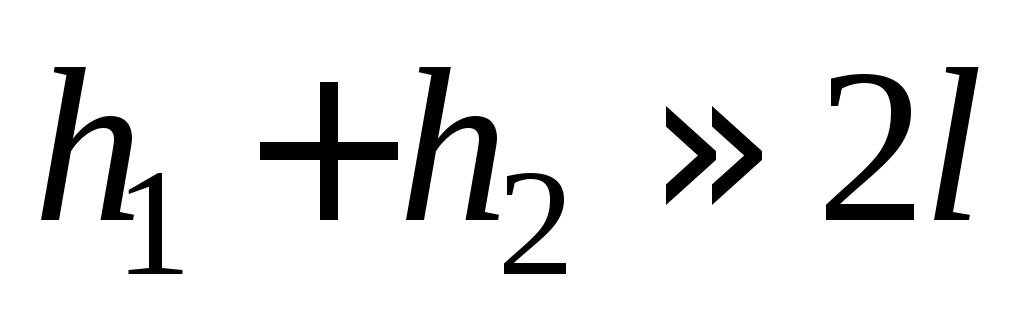 .
Тогда
.
Тогда
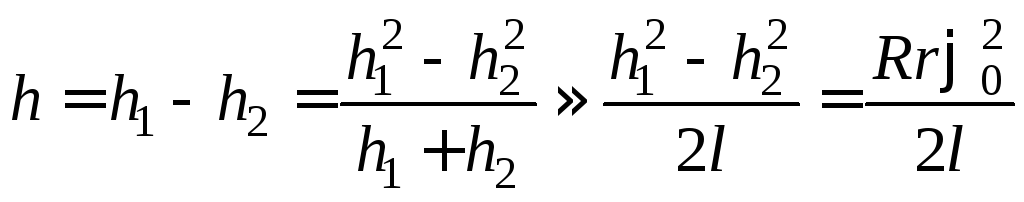 , (4)
, (4)
где учтено, что (см. рис.1)
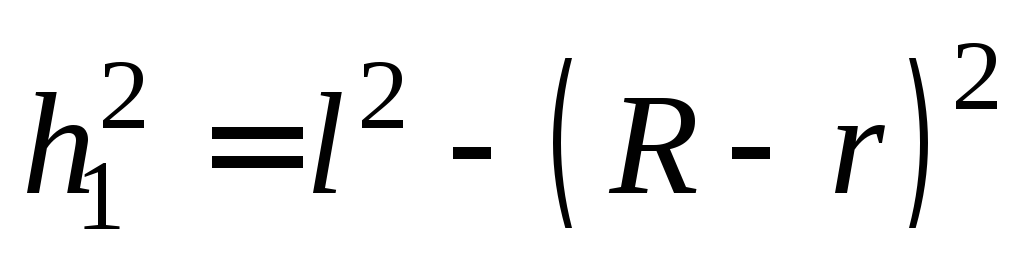 ,
, 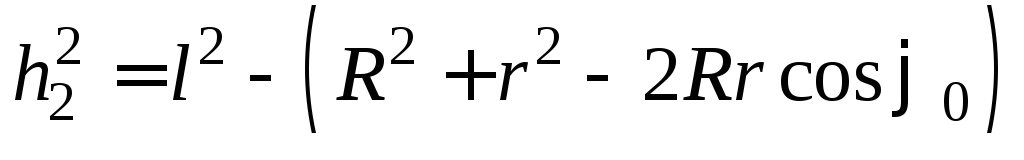 ,
,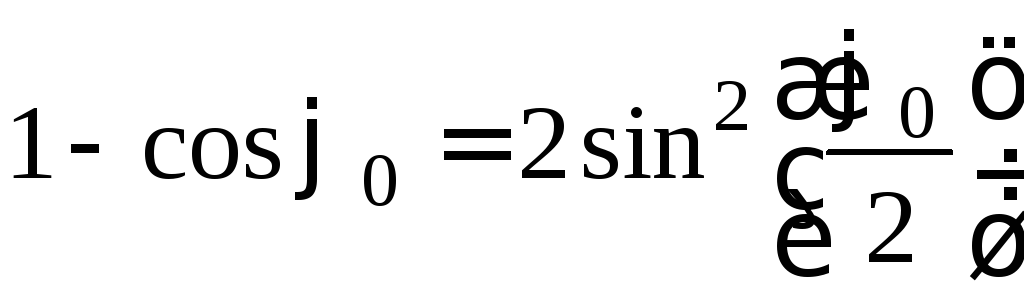 , а также, что вследствие малости угла
, а также, что вследствие малости угла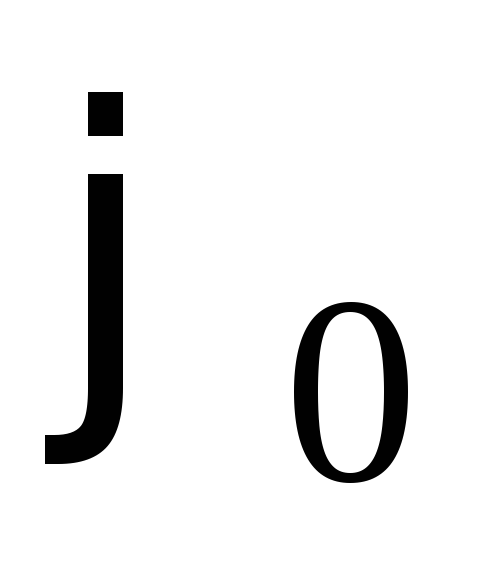 ,синус можно заменить значением самого
угла в радианах.
,синус можно заменить значением самого
угла в радианах.
В
результате подстановки (4) и (3) в (2),
получим расчётную формулу для момента
инерции маятника массой 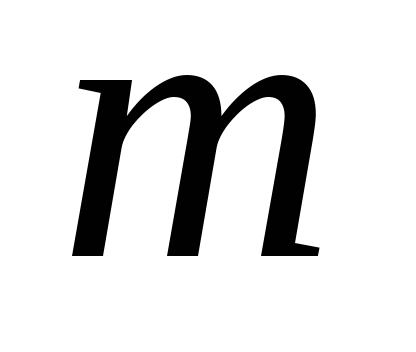 :
:
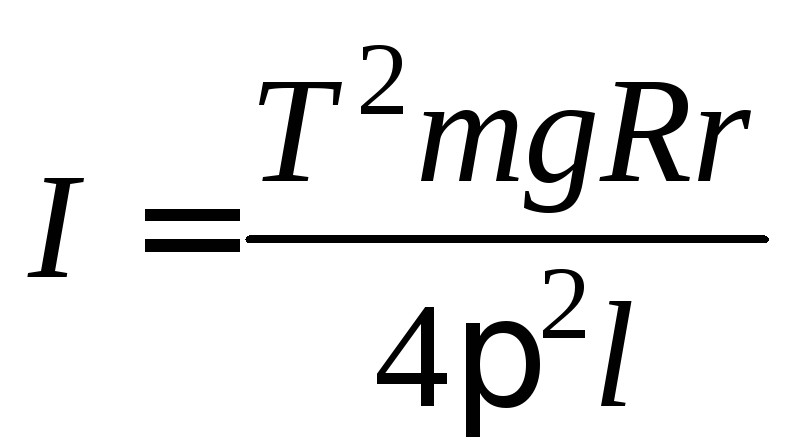 (5)
(5)
По зависимости (5) можно рассчитать момент инерции как нагруженного исследуемой пластиной, так и ненагруженного диска В. Тогда, вследствие аддитивности, момент инерции исследуемого тела (пластины) легко определяется по формуле:
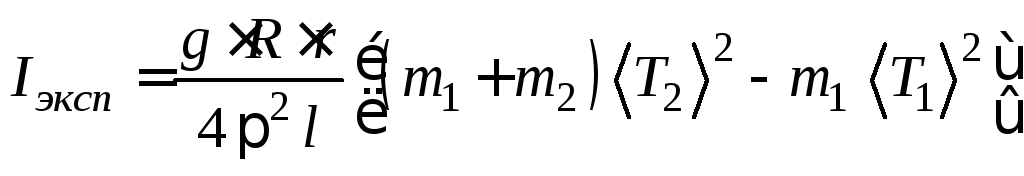 (6)
(6)
где 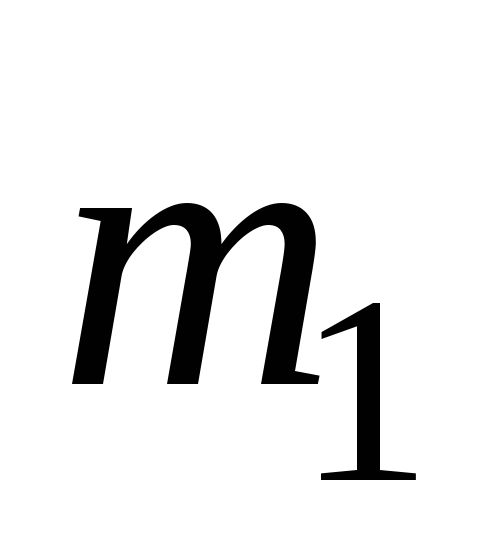 и
и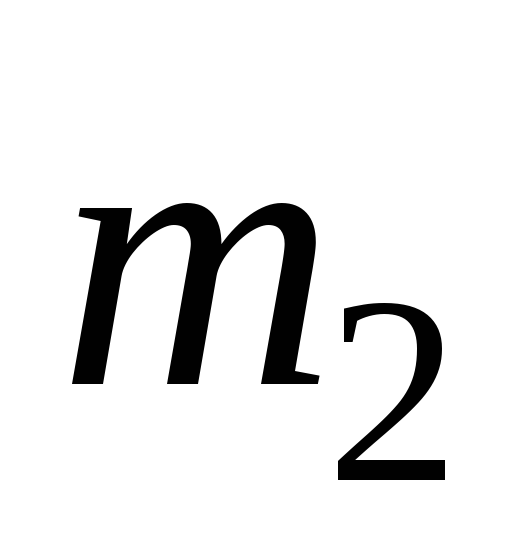 – массы ненагруженного диска и
исследуемой пластины соответственно,
а
– массы ненагруженного диска и
исследуемой пластины соответственно,
а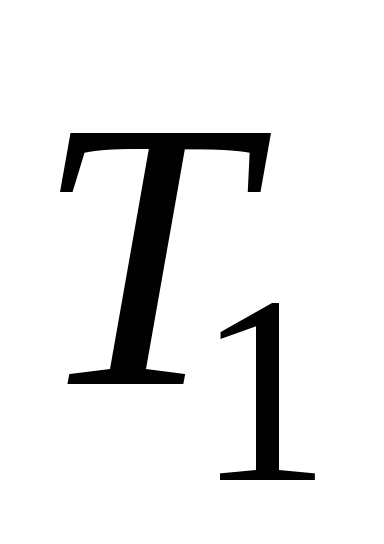 и
и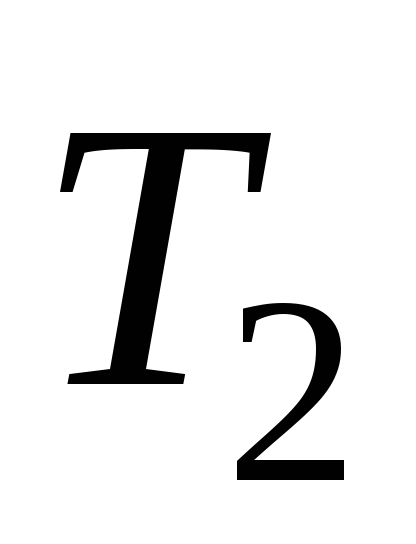 – период колебаний ненагруженного и
нагруженного диска соответственно.
– период колебаний ненагруженного и
нагруженного диска соответственно.
Момент инерции есть мера инертности тела при его вращательном движении. Это значит, что чем больше момент инерции, тем больший момент сил необходимо приложить к телу, чтобы заставить тело вращаться, если оно покоилось, или остановить, если вращалось.
Момент
инерции материальной точки: 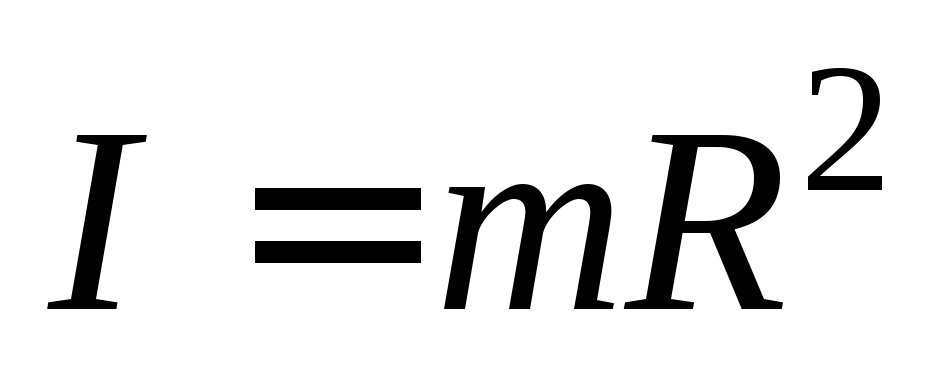 ,
где
,
где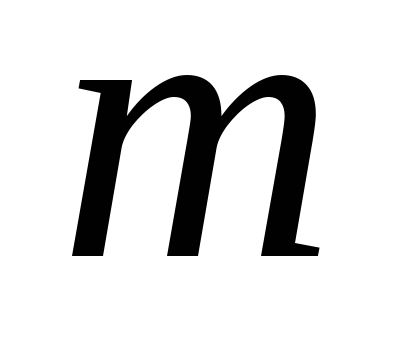 – масса точки, а R– расстояние от нее до оси вращения.
Момент инерции– величина аддитивная,
т.е. момент инерции системы материальных
точек или твердого тела определяется
как сумма моментов инерции частей, из
которых состоит система или тело, т.е.
– масса точки, а R– расстояние от нее до оси вращения.
Момент инерции– величина аддитивная,
т.е. момент инерции системы материальных
точек или твердого тела определяется
как сумма моментов инерции частей, из
которых состоит система или тело, т.е.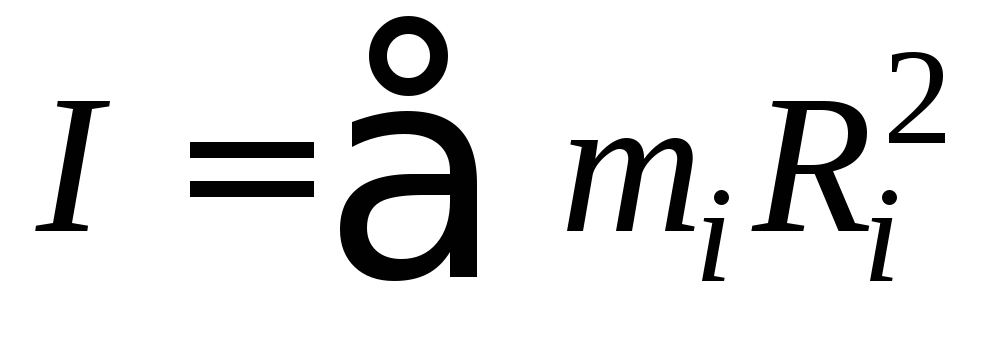 или
или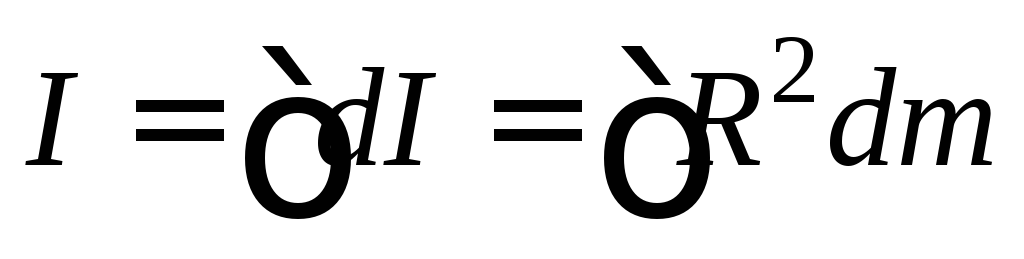 (*)
(*)
Момент инерции зависит от формы и размеров тела или системы, а также от положения и ориентации в пространстве оси, относительно которой определяется момент инерции.
Например,
если известен момент инерции тела
относительно оси, проходящей через его
центр масс, то относительно любой другой
оси его можно рассчитать с помощью теоремы Штейнера: момент
инерции тела относительно произвольной
оси О 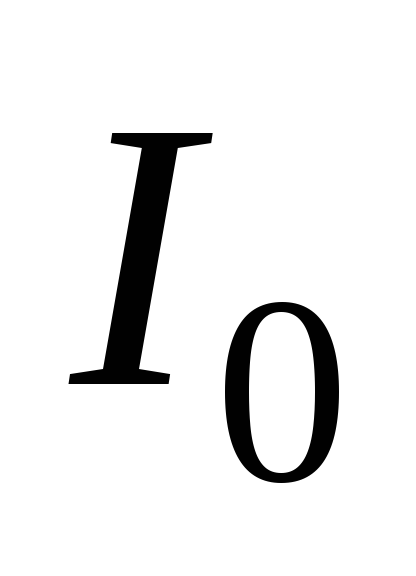 равен сумме момента инерции этого тела
относительно оси, параллельной данной
и проходящей через центр масс С
равен сумме момента инерции этого тела
относительно оси, параллельной данной
и проходящей через центр масс С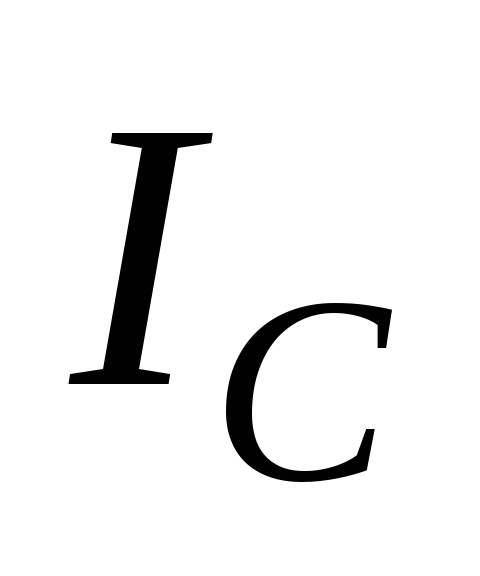 ,
и произведения массы тела на квадрат
расстояния между осями (ОС =d) ,
т.е.
,
и произведения массы тела на квадрат
расстояния между осями (ОС =d) ,
т.е.
IО = IС + m d2.
Моменты инерции тел относительно оси, проходящей через центр масс IСможно определить, пользуясь определением (*) и разбивая тело на элементы
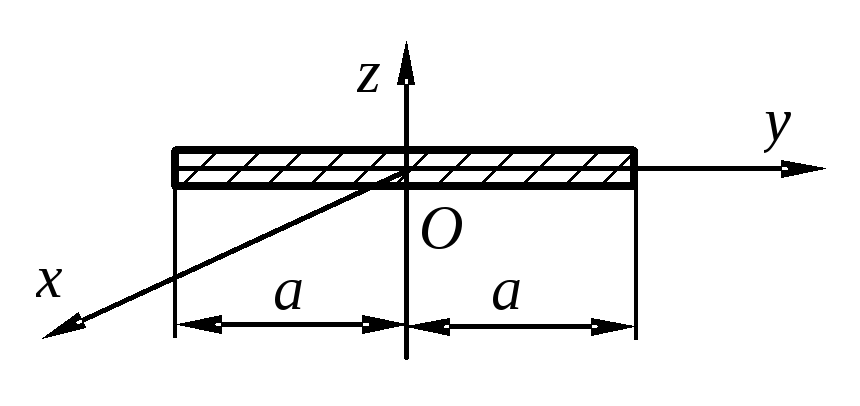
1. Момент инерции плоской прямоугольной пластины относительно оси, проходящей через центр масс перпендикулярно ее плоскости.
М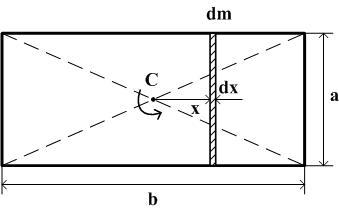 омент
инерции выделенного элемента (в виде
стержня массойdm, длинойa и толщинойdx как
показано на рисунке) по теореме Штейнера:
омент
инерции выделенного элемента (в виде
стержня массойdm, длинойa и толщинойdx как
показано на рисунке) по теореме Штейнера:
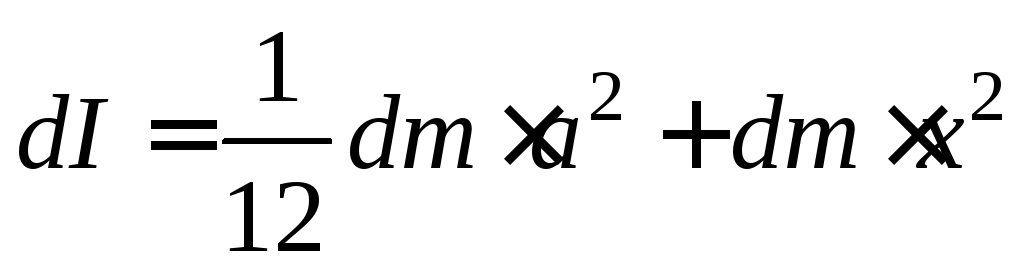
Из
геометрических соображений 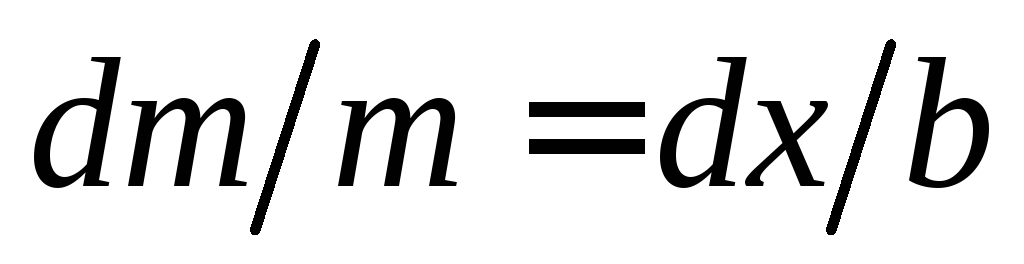 ,откуда
,откуда 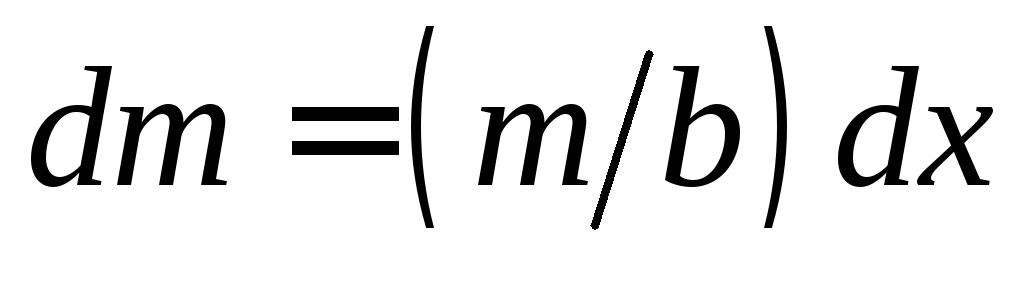 ,тогда
,тогда
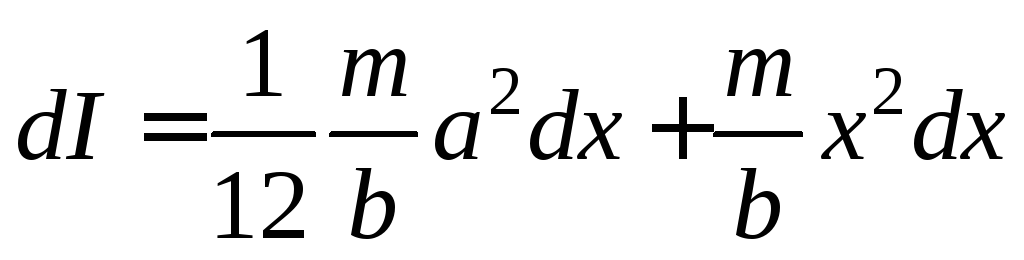
Тогда момент инерции пластины:
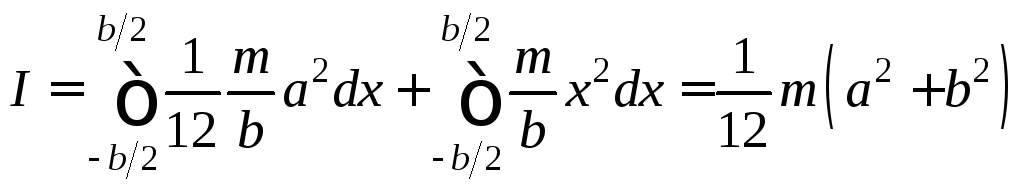
Момент инерции и момент сопротивления
05-12-2012: Адольф СталинБыло бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно
05-12-2012: Доктор Лом
В принципе, что такое момент инерции и откуда он взялся, достаточно подробно объяснено в статье «Основы сопромата, расчетные формулы», здесь лишь повторюсь: «W — это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы». Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям. Момент инерции необходимо знать для определения углов поворота поперечного сечения и прогиба (смещения) центра тяжести поперечного сечения, так как максимальные деформации возникают в самом верхнем и в самом нижнем слое изгибаемой конструкции, то определить момент инерции можно, умножив момент сопротивления на расстояние от центра тяжести сечения до верхнего или нижнего слоя, поэтому для прямоугольных сечений I=Wh/2. При определении момента инерции сечений сложных геометрических форм сначала сложная фигура разбивается на простейшие, затем определяются площади сечения этих фигур и моменты инерции простейших фигур, затем площади простейших фигур умножаются на квадрат расстояния от общего центра тяжести сечения до центра тяжести простейшей фигуры. Момент инерции простейшей фигуры в составе сложного сечения равен моменту инерции фигуры + квадрат расстояния умноженный на площадь. Затем полученные моменты инерции суммируются и получается момент инерции сложного сечения. Но это максимально упрощенные формулировки (хотя, соглашусь, все равно выглядит достаточно мудрено). Со временем напишу отдельную статью.
05-12-2012: Гиви
В принципе все предельно ясно, но здесь проще www.kataltim.ru
20-04-2013: Petr
Не нужно полностью доверять поданной в сайтах информации. Её никто по-хорошему не проверяет. И ссылки на неё не даются. Так в Таблице 1. «Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм» для тонкостенной трубы дается определение, что отношение диаметра к толщине оболочки должно быть больше 10. По другим источникам — должно быть больше 20!!! (Н.М. Беляев. Сопротивление материалов. М.1996. стр.160. или Н.И.Безухов. Основы теории упругости, пластичности и ползучести.М.1961.стр.390)
21-04-2013: Доктор Лом
Верно. Доверять нельзя. Но логическое мышление пока никто не отменял. Самый правильный вариант — рассчитывать момент инерции или момент сопротивления для любой трубы по формулам, приведенным для обычной трубы (на 1 пункт выше). Формулы, приводимые для тонкостенной трубы, в любом случае будут приближенными и годятся только для первичного расчета и об этом забывать нельзя.
Впрочем параметры максимально допустимой толщины стенки исправил.
25-06-2013: Саня
требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву «Ш». не получается найти какую либо информацию. буду признателен за какую нибудь информацию
25-06-2013: Доктор Лом
Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона» (http://doctorlom.com/item249.html)
там в частности определяется момент инерции тоже не совсем простого сечения.
03-11-2014: Радик
Вот здесь http://otvet.mail.ru/question/33111076
дана другая формула для момента сопротивления трубы, а именно: W=(D^3-d^3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).
04-11-2014: Доктор Лом
Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.
04-11-2014: Радик
Спасибо, док!
11-11-2014: Ильгам
Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.
11-11-2014: Доктор Лом
Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).
04-01-2015: Valerij
Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).
05-01-2015: Доктор Лом
Для определения момента инерции вам нужно вычесть из момента инерции трубы момент инерции вашего отверстия. Для этого нужно определить площадь сечения отверстия и затем умножить ее на квадрат расстояния до центра трубы плюс собственный момент инерции отверстия. Больше подробностей в статье «Моменты инерции поперечных сечений».
Если расчет не требует особой точности и диаметр отверстия в 5 и более раз меньше диаметра трубы (вроде ваш случай, если 32.39 — это наружный диаметр), то сегмент отверстия можно привести к прямоугольнику. Если отверстие не сквозное, то следует дополнительно определить положение центра тяжести трубы с отверстием для того, чтобы потом вычислить новое значение момента сопротивления.
Но и это еще не все. Вам следует учесть, что возле отверстий возникают значительные локальные напряжения.
09-10-2015: Борис
Неравноплечий уголок.При вычислении Wy не y,а H-y
09-10-2015: Доктор Лом
Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.
09-10-2015: Борс
Для треугольников при вычислении Wzп h в квадрате.
09-10-2015: Борис
Пардон,Wz
09-10-2015: Доктор Лом
Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.
28-04-2016: Jama
Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!
28-04-2016: Доктор Лом
Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).
29-08-2016: Максим
Здравствуйте ! Имеется швеллер № 12. В верхний пояс будут вкручиваться саморезы и винты для крепления кровли. Как учесть ослабление швеллера, т.е как определить W ослабленного сечения.
29-08-2016: Доктор Лом
Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.
21-03-2017: игорь
здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.
21-03-2017: Доктор Лом
Игорь, я отправил вам письмо.
30-08-2017: Али
Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.
31-08-2017: Доктор Лом
Посмотрите статью «Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.13330.2011», там все достаточно подробно расписано.
13-11-2017: Абдуахад
Здравствуйте пожалуйста подскажите почему Ql^2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял
Осевые моменты инерции однородных пластинок
Форма пластинки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
4.3. Пример выполнения задания
4.3.1. Условие примера
Тело D, имеющее
форму прямоугольной пластины, показанной
на рис. 4.2, массой 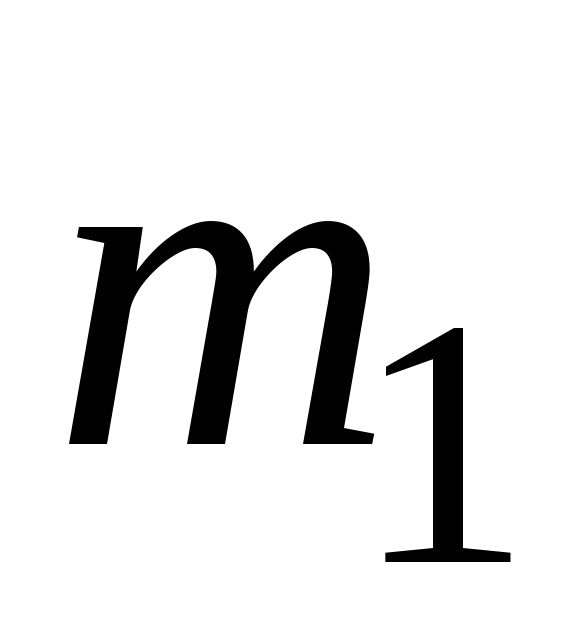 =20
кг вращается вокруг вертикальной осиz
с угловой скоростью
=20
кг вращается вокруг вертикальной осиz
с угловой скоростью 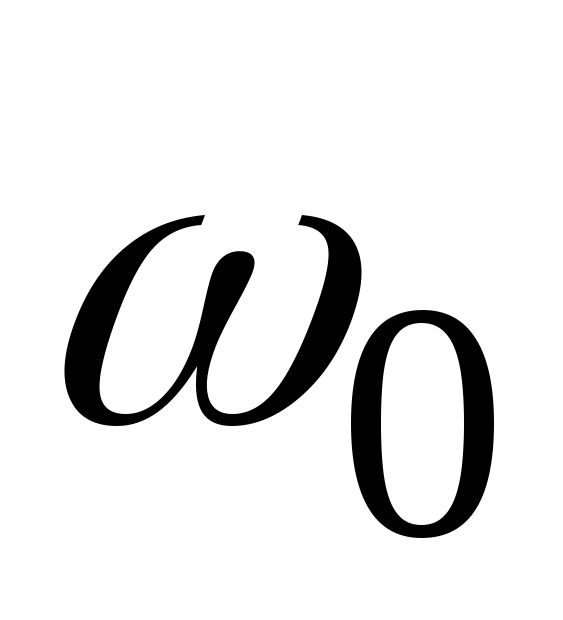 =2
с-1.
При этом в точке M желоба AB тела D на расстоянии AM=
=2
с-1.
При этом в точке M желоба AB тела D на расстоянии AM=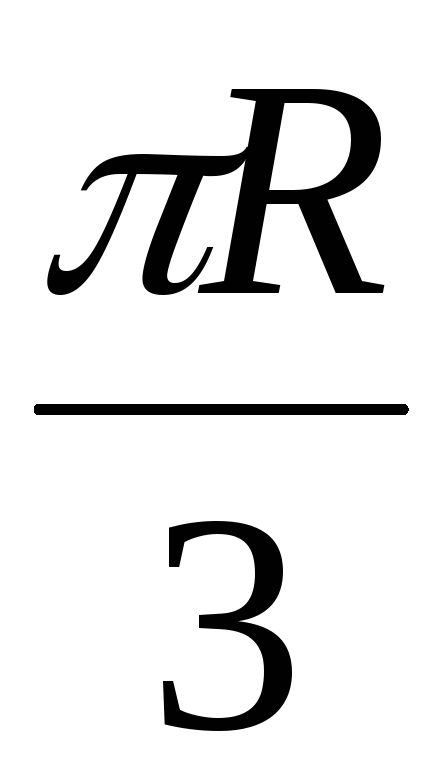 от точкиA,
отсчитываемом вдоль желоба, закреплена
материальная точка K массой
от точкиA,
отсчитываемом вдоль желоба, закреплена
материальная точка K массой 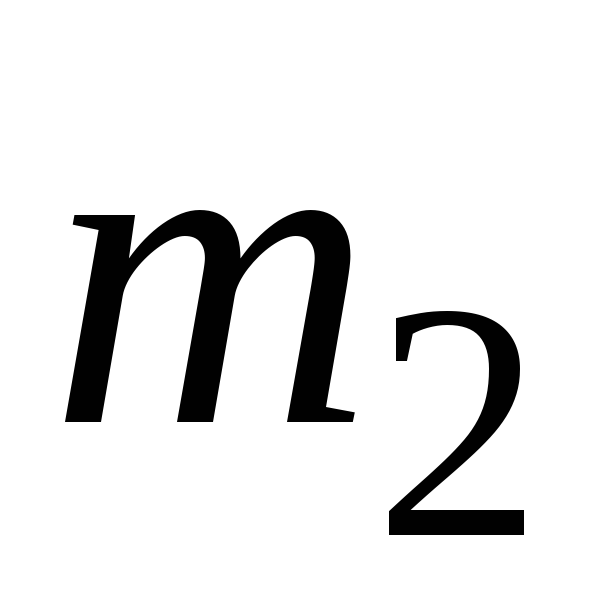 =8
кг. В момент времени
=8
кг. В момент времени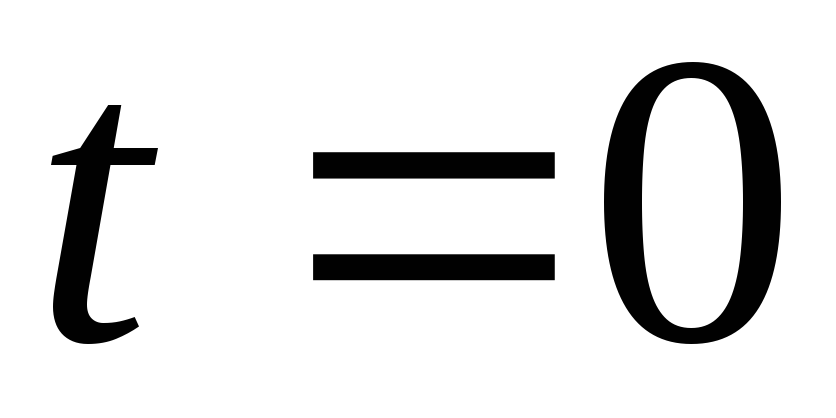 на систему начинает действовать пара
сил с моментом
на систему начинает действовать пара
сил с моментом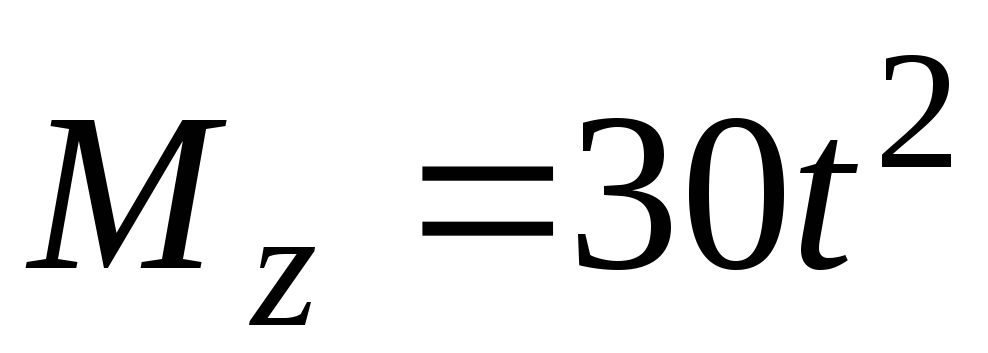 Нм. Приt=t1=4с действие
пары сил прекращается; одновременно
точка K начинает относительное движение по
желобу согласно закону
Нм. Приt=t1=4с действие
пары сил прекращается; одновременно
точка K начинает относительное движение по
желобу согласно закону 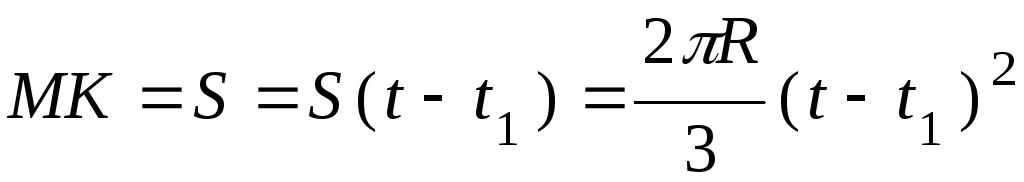 м.
м.
Определить угловые
скорости тела D соответственно в моменты времени 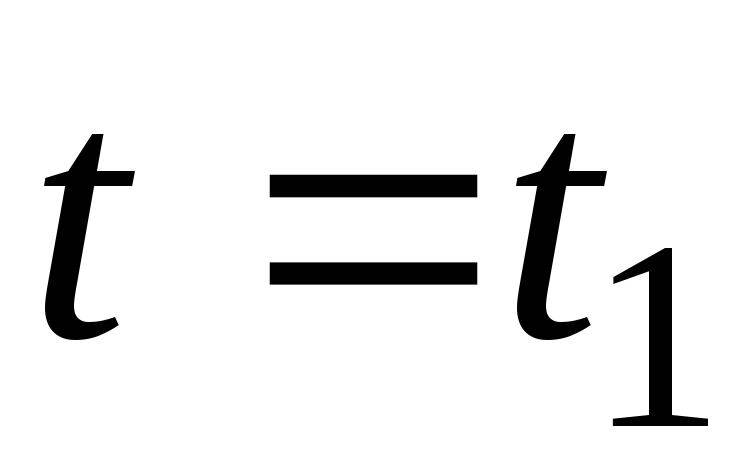 и t=t2=5
с, если R=0,6
м, a=1,2
м; b=0,9
м
и t=t2=5
с, если R=0,6
м, a=1,2
м; b=0,9
м
4.3.2. Решение примера
Запишем равенство, выражающее теорему об изменении кинетического момента механической системы относительно оси z
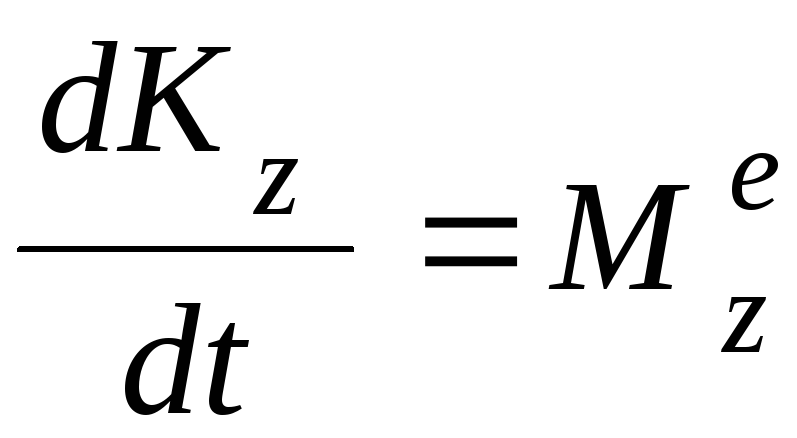 , (4.1)
, (4.1)
где 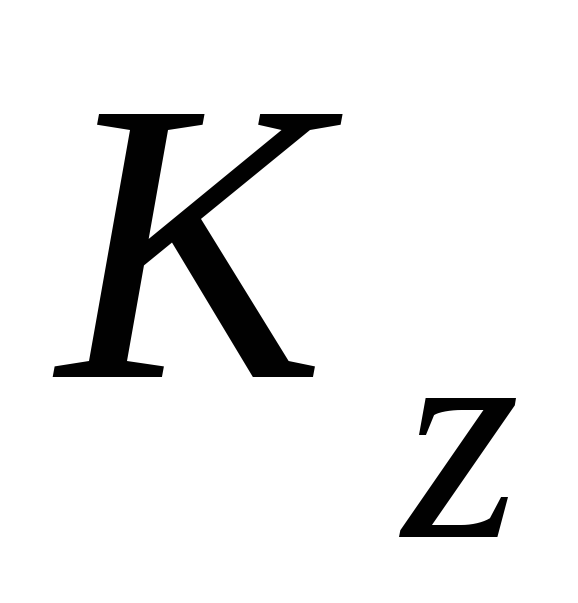 — кинетический момент механической
системы, состоящей в данном случае из
кинетического момента телаD и кинетического момента точки К,
относительно оси z;
— кинетический момент механической
системы, состоящей в данном случае из
кинетического момента телаD и кинетического момента точки К,
относительно оси z;
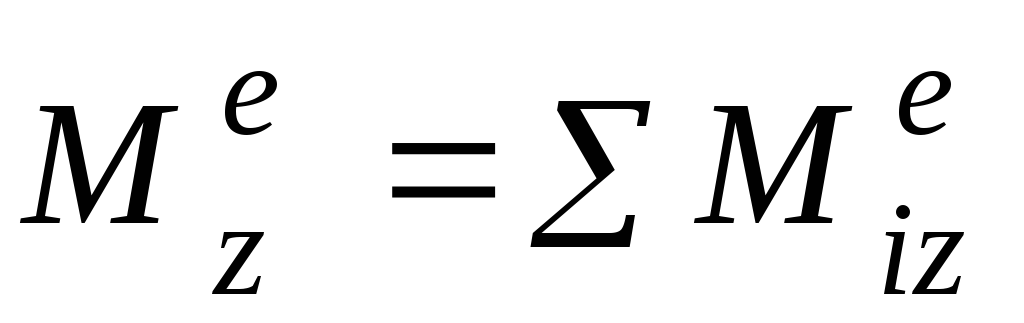 — главный момент
внешних сил, приложенных к системе,
относительно оси z.
— главный момент
внешних сил, приложенных к системе,
относительно оси z.
Рассмотрим движение системы в отрезке времени [0;t1].
В произвольный
момент времени на систему действуют
внешние силы 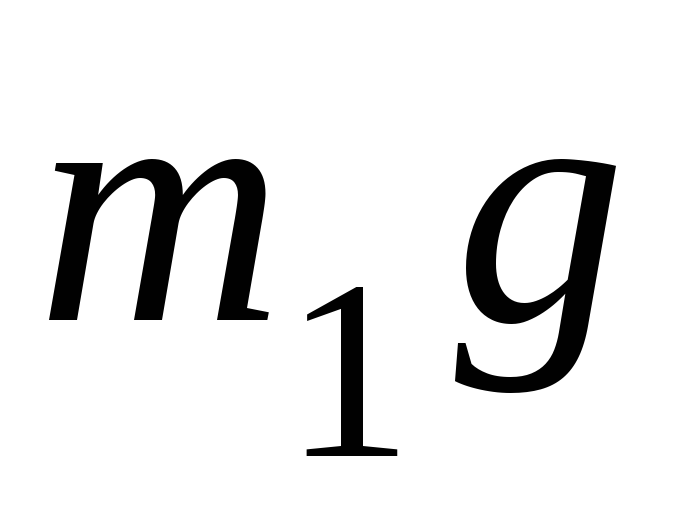 ,
,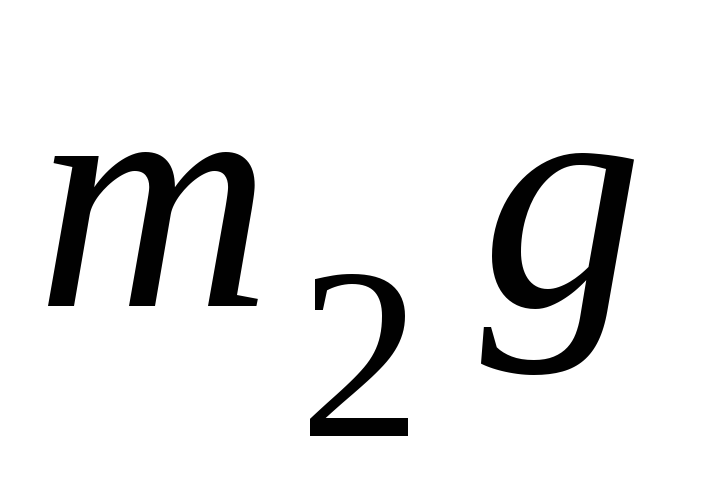 ,
,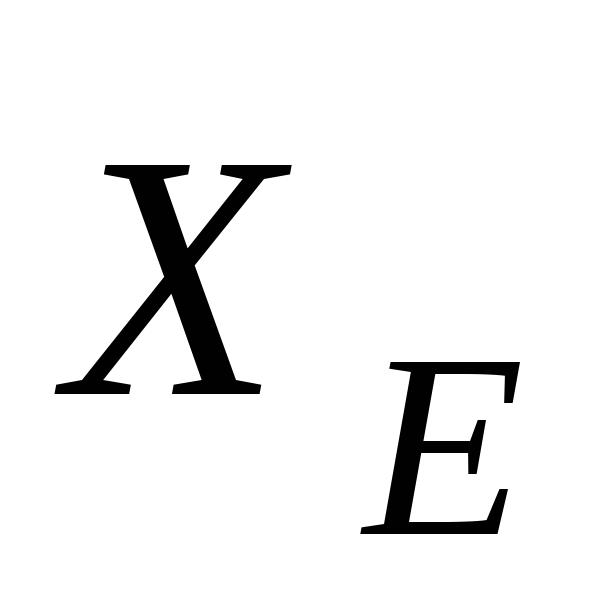 ,
,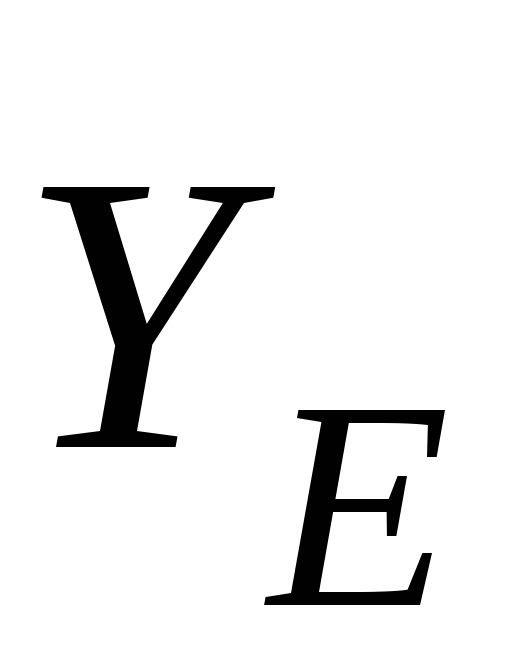 ,
,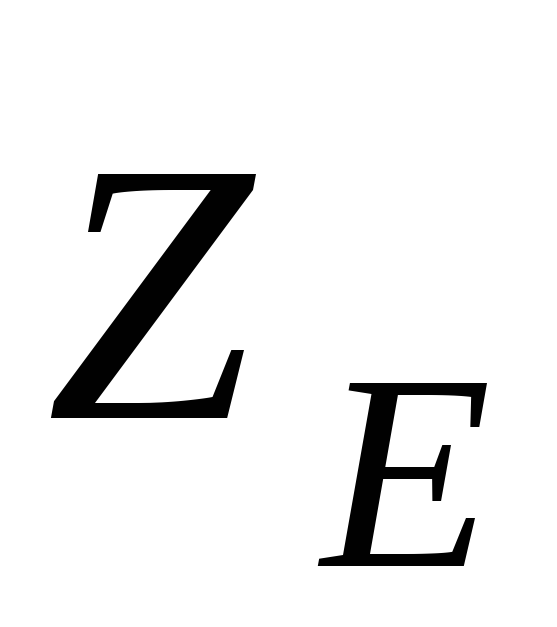 ,
,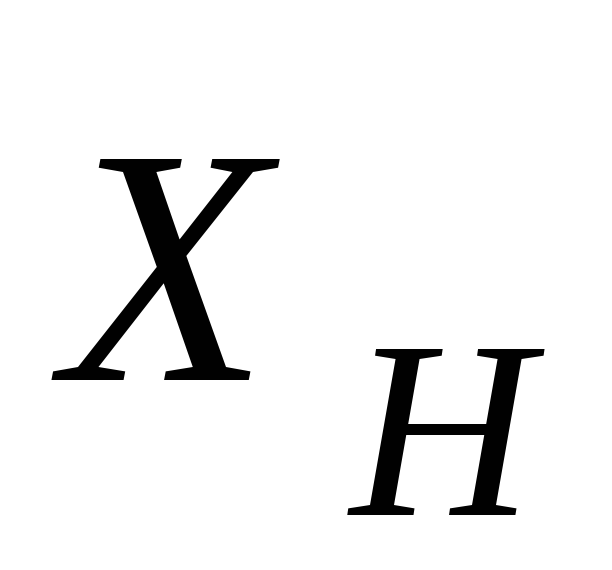 ,
,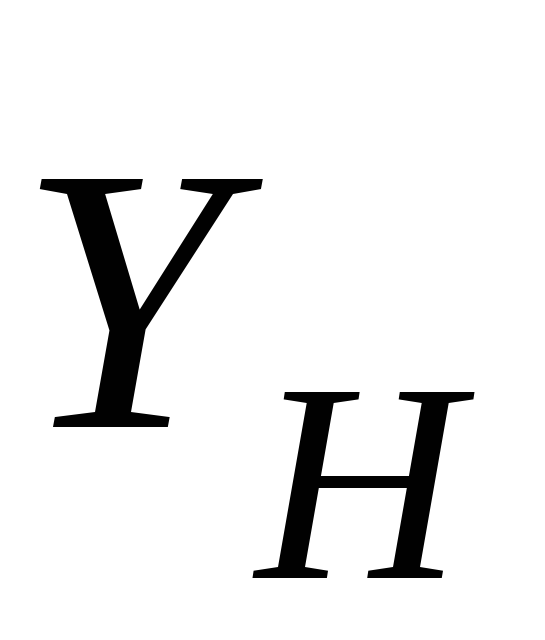 ,
,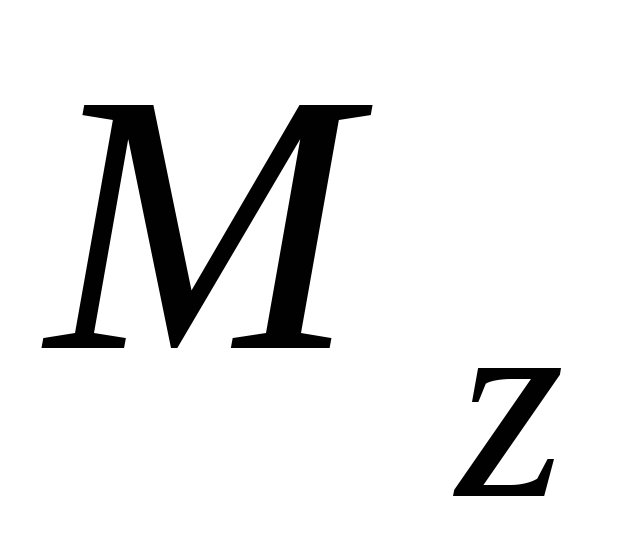 (рис. 4.3), главный момент которых
относительно осиz равен вращающему моменту
(рис. 4.3), главный момент которых
относительно осиz равен вращающему моменту 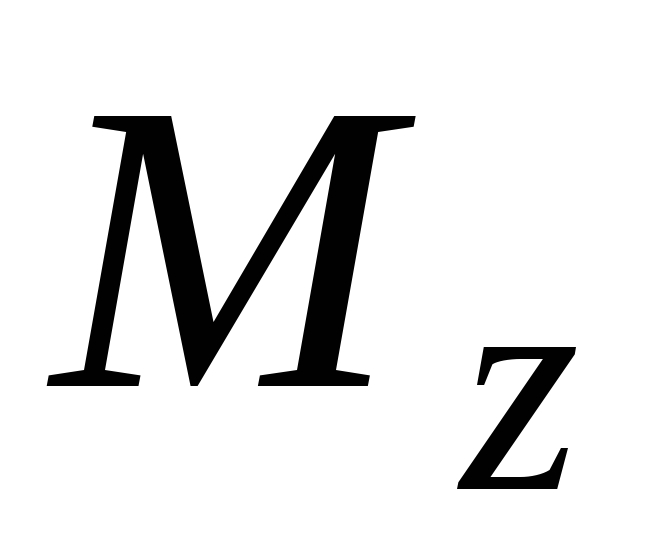 ,
то есть
,
то есть
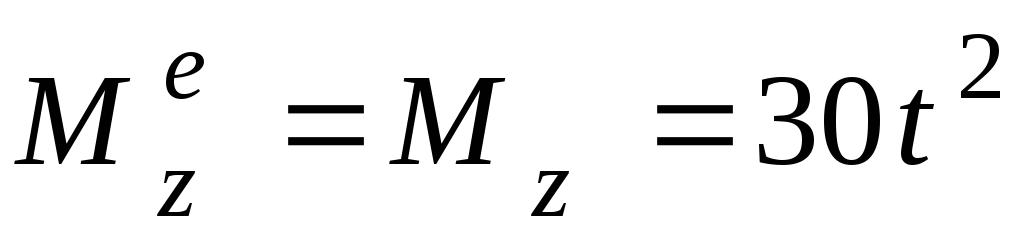 . (4.2)
. (4.2)
Кинетический момент данной системы равен сумме
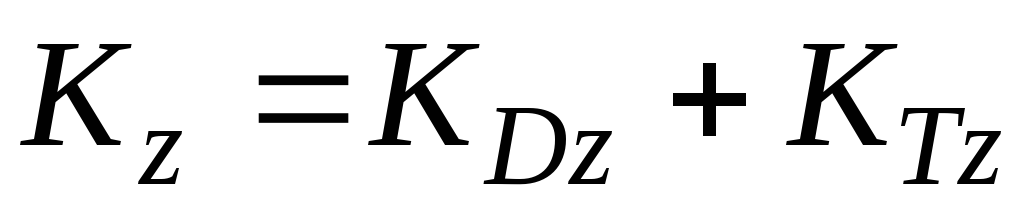 ,
,
где 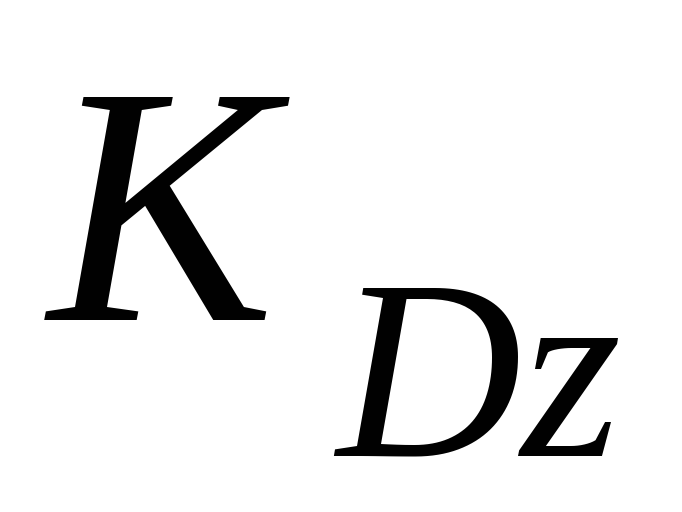
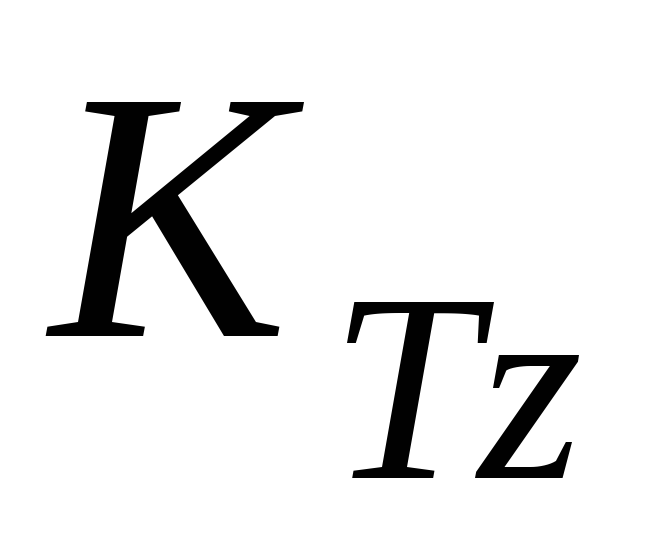 — кинетические моменты телаD и точки K относительно оси z.
— кинетические моменты телаD и точки K относительно оси z.
Тело D вращается относительно неподвижной оси, поэтому
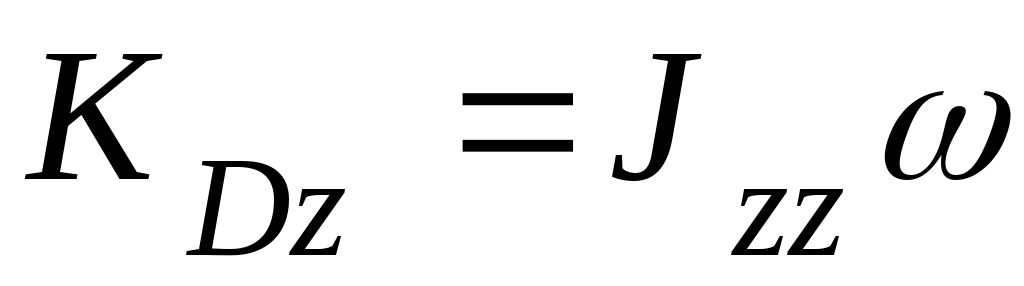 .
.
Здесь  — угловая скорость тела,
а
— угловая скорость тела,
а 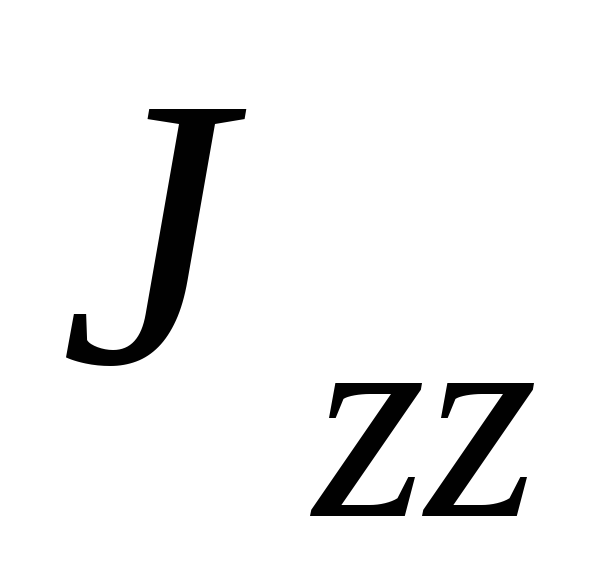 — его момент инерции относительно оси z.
— его момент инерции относительно оси z.
Момент инерции 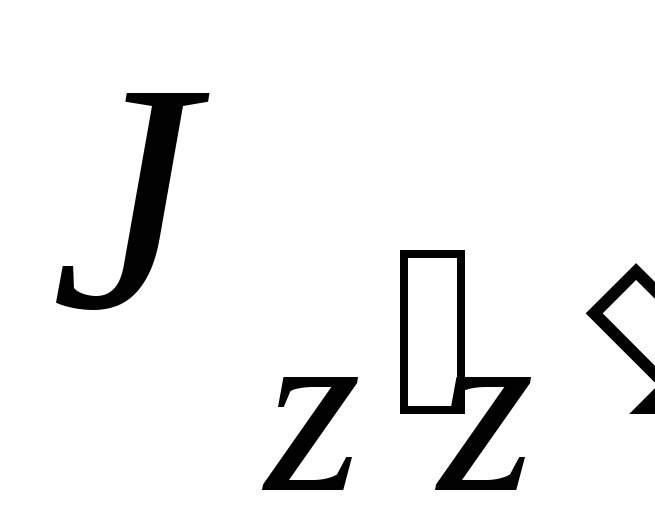 тела относительно оси
тела относительно оси 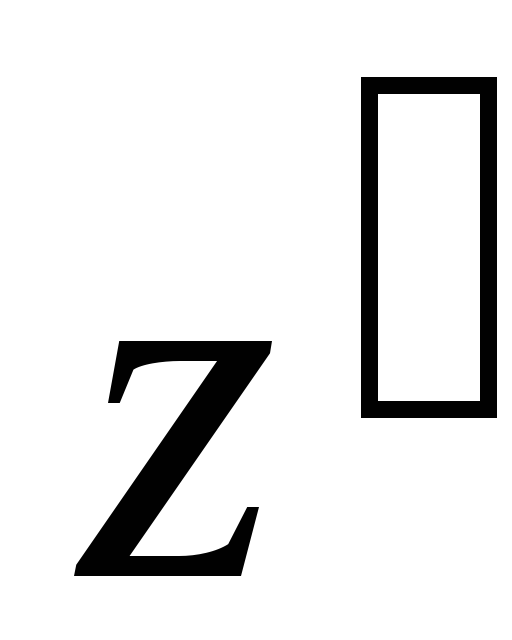 ,
параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл.
4.2)
,
параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл.
4.2)
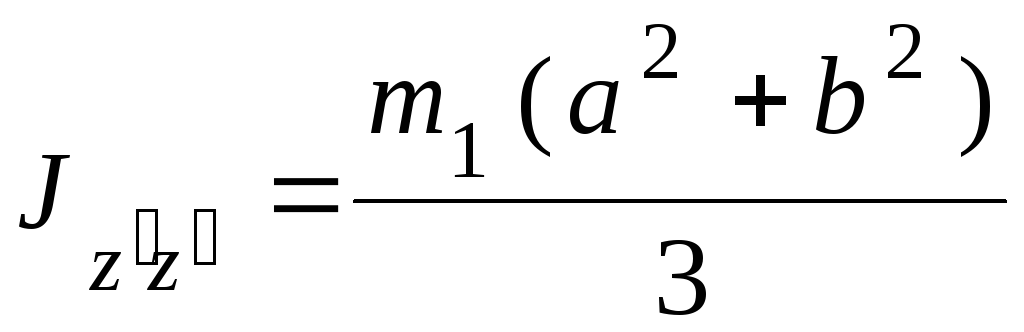 .
.
По теореме Штейнера
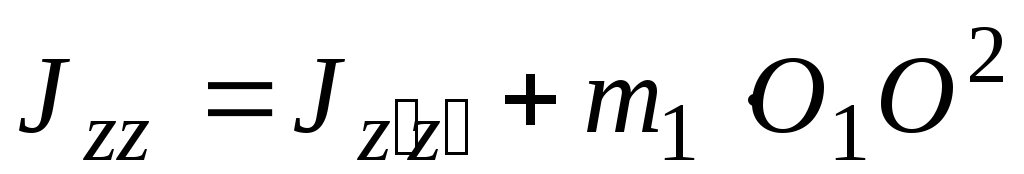 .
.
Таким образом
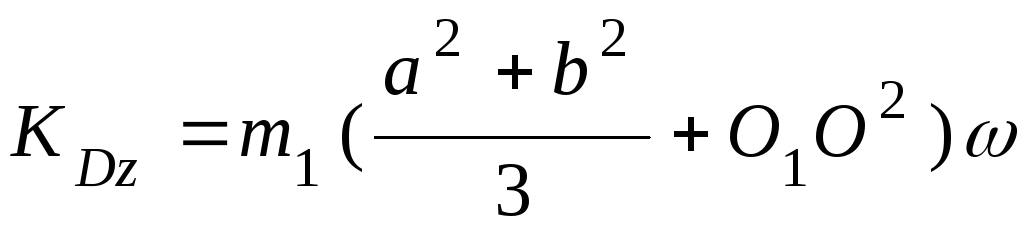 .
.
Кинетический момент материальной точки K, закрепленной в точке М желоба
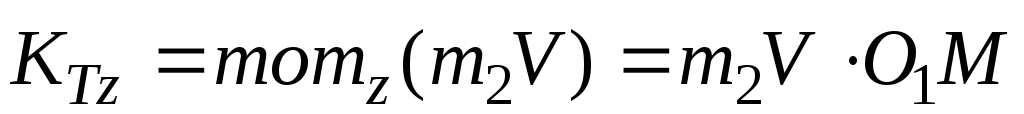 .
.
Скорость точки К
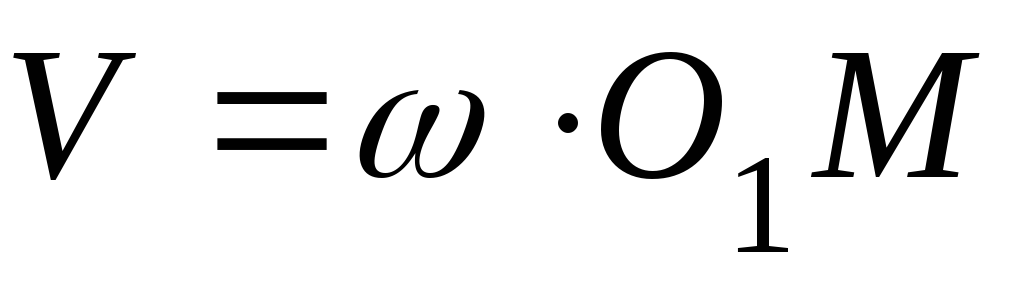 .
.
Очевидно, что 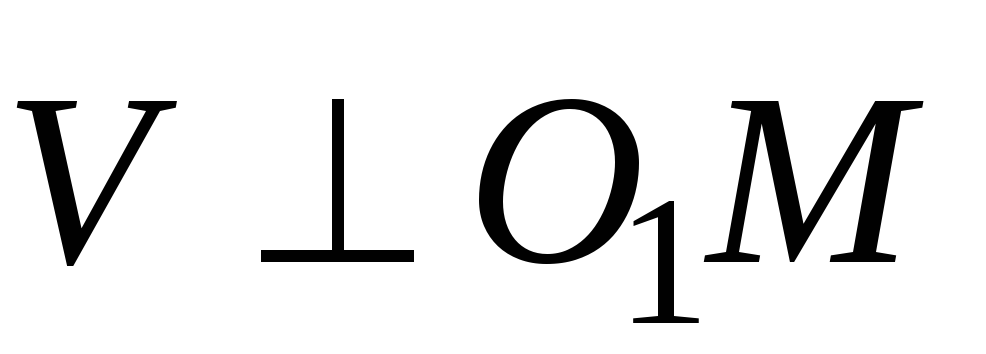 .
.
Согласно условию
задачи длина дуги окружности 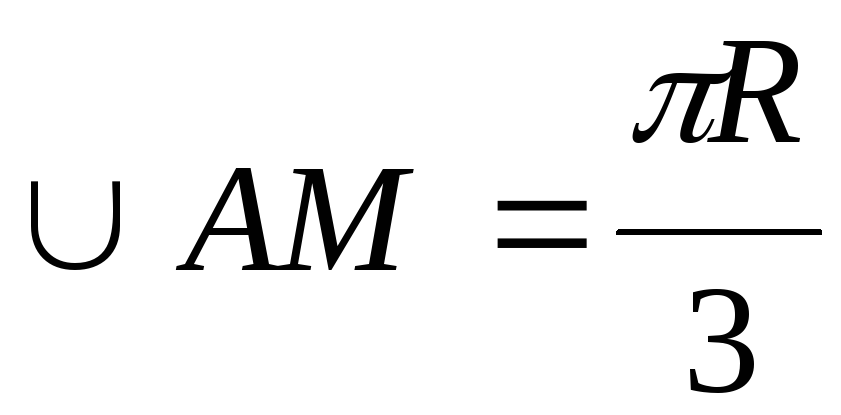 ,
тогда центральный угол
,
тогда центральный угол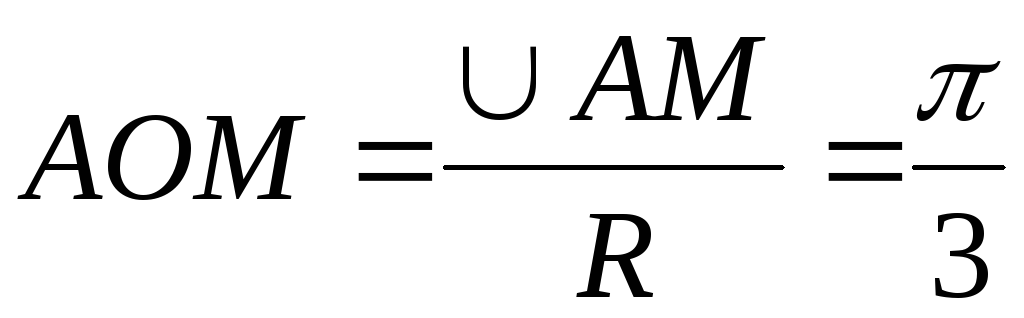 .
Следовательно, в равнобедренном
треугольникеОМО1
.
Следовательно, в равнобедренном
треугольникеОМО1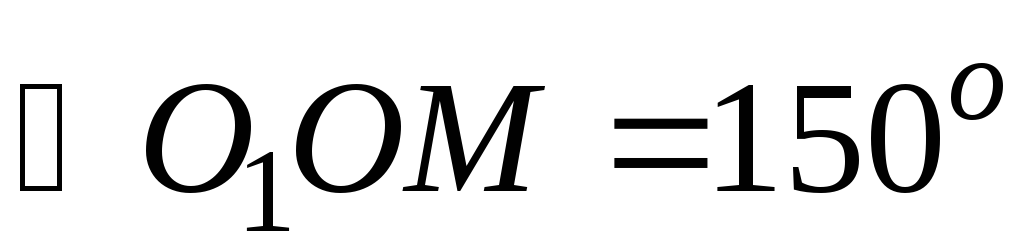 и
и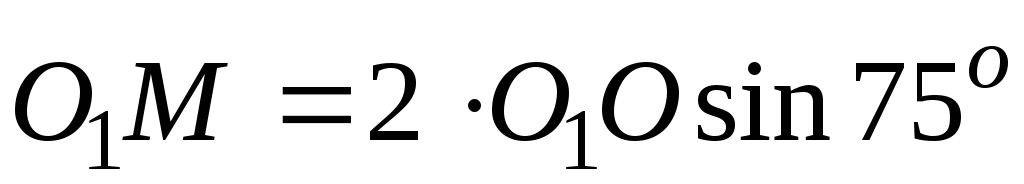 .
.
Имеем
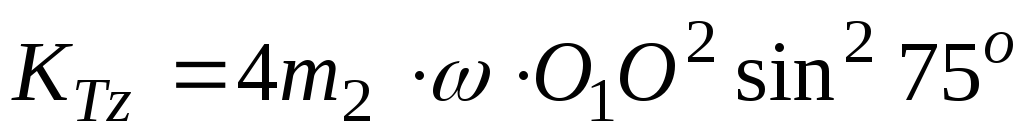 .
.
Окончательное выражение кинетического момента системы относительно оси z следующее
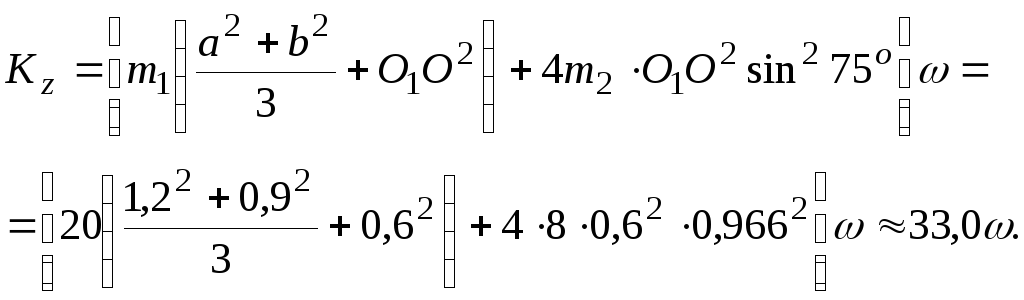 (4.3)
(4.3)
Подставляя выражения (4.2) и (4.3) в равенство (4.1), имеем
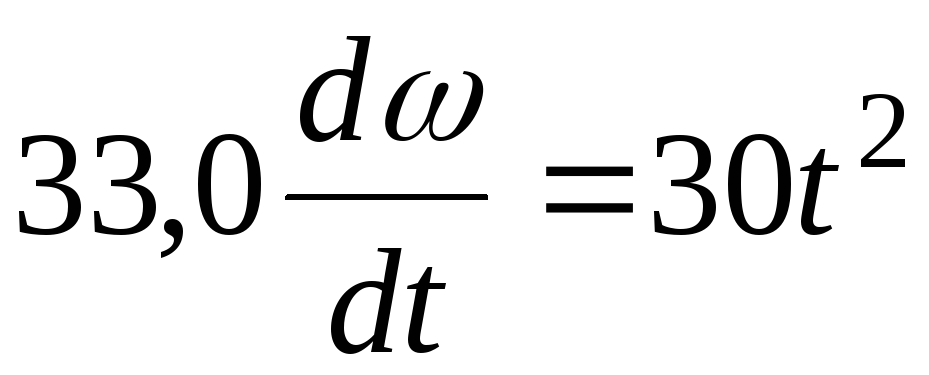 ,
,
откуда
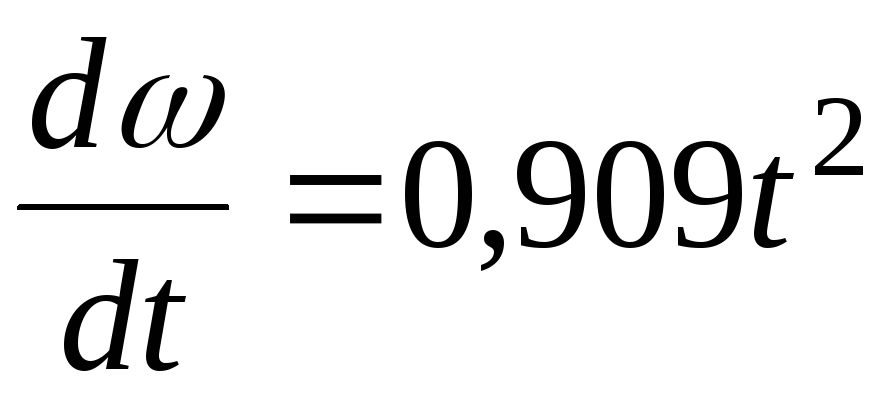 .
.
Разделяем в последнем уравнении переменные и интегрируем левую и правую части уравнения:
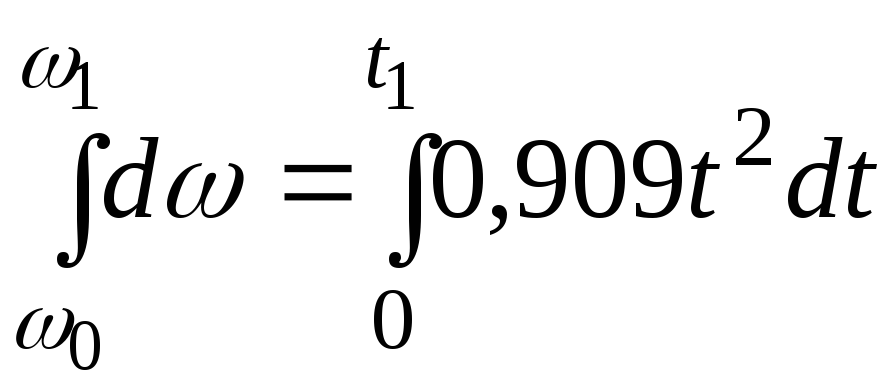 .
.
Тогда
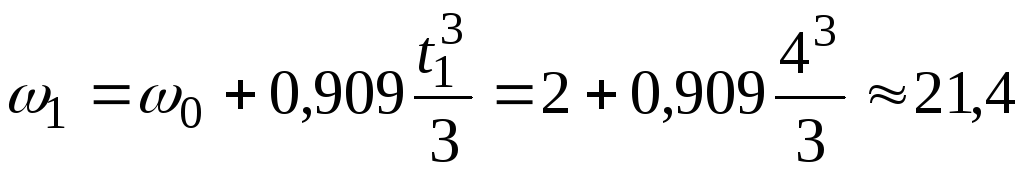 с-1.
с-1.
В момент времени t1 из выражения (4.3) имеем
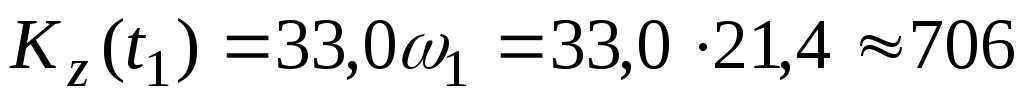 Нмс.
Нмс.
Рассмотрим теперь
движение системы в отрезке времени 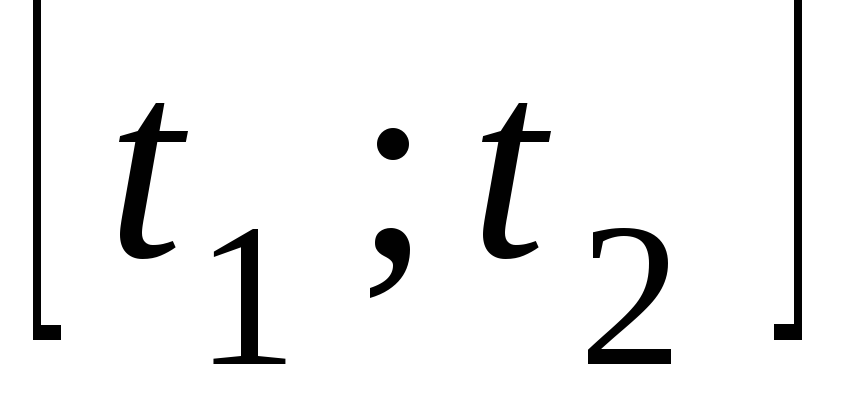 .
.
После прекращения
действия момента 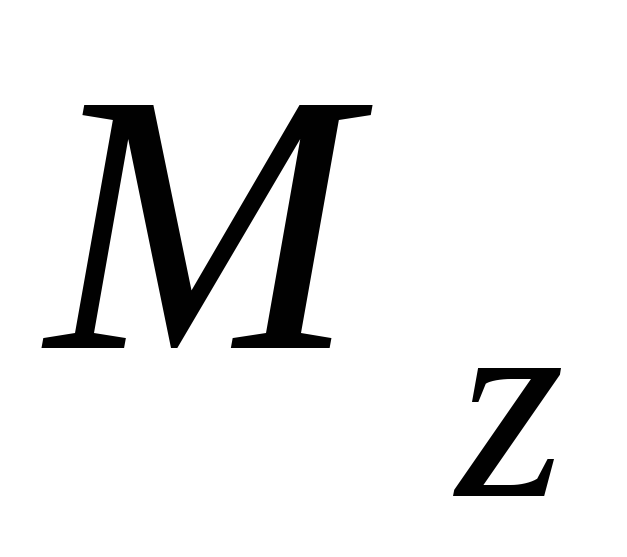 на телоD,
главный момент внешних сил относительно
оси z
на телоD,
главный момент внешних сил относительно
оси z 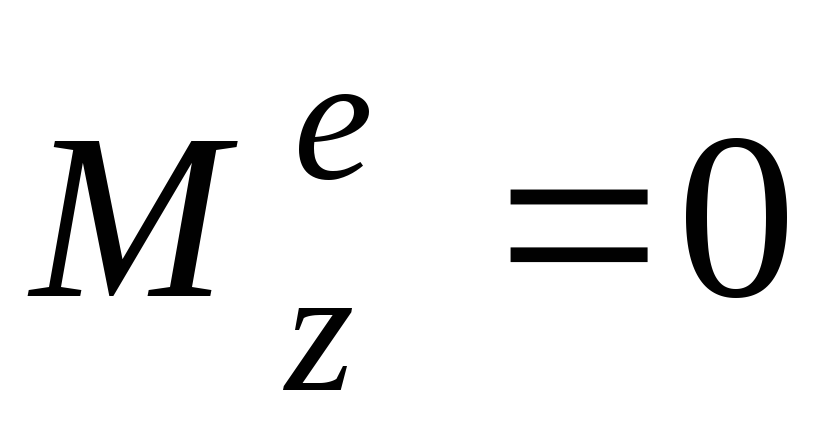 (см. рис. 4.4).
(см. рис. 4.4).
Тогда равенство (4.1) примет вид
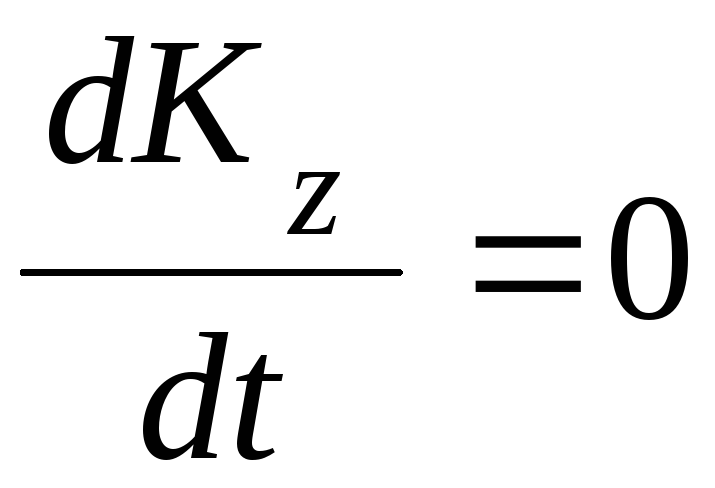 ,
,
то есть 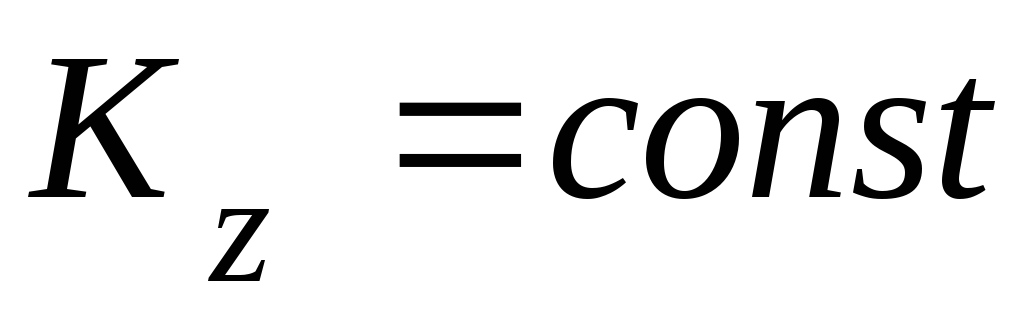 .
.
Это означает, что кинетические моменты системы относительно оси в начале t1 и в конце t2 отрезка времени [t1; t2] равны
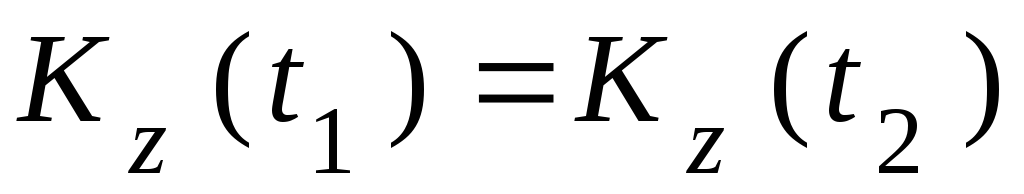 .
.

В момент времени t2 тело D вращается с угловой скоростью 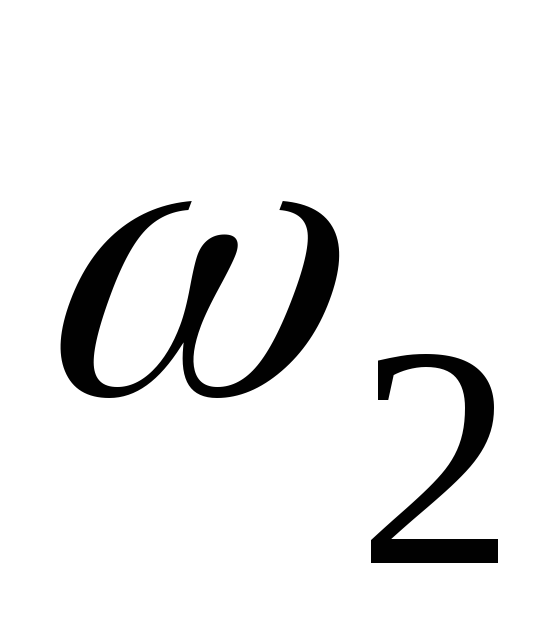 (см. рис. 4.4). При этом точкаК, совершая
сложное движение, оказывается в точке В желоба. Действительно, центральный угол
(см. рис. 4.4). При этом точкаК, совершая
сложное движение, оказывается в точке В желоба. Действительно, центральный угол
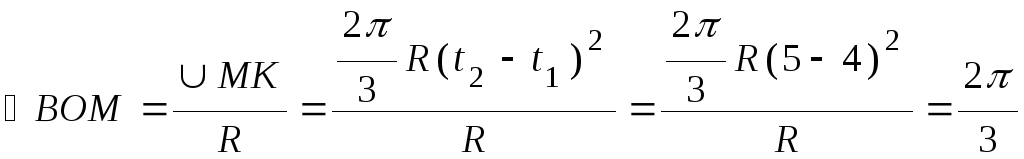 .
.
Кинетический
момент системы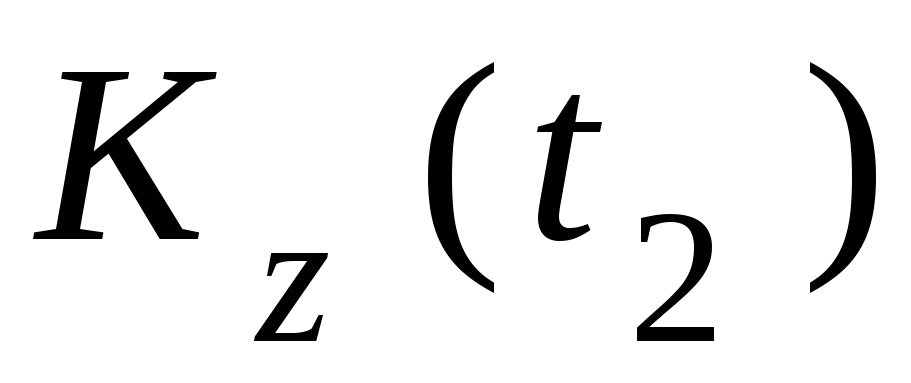 относительно оси в конце t2 отрезка времени [t1; t2]
также равен сумме кинетических моментов
тела
относительно оси в конце t2 отрезка времени [t1; t2]
также равен сумме кинетических моментов
тела 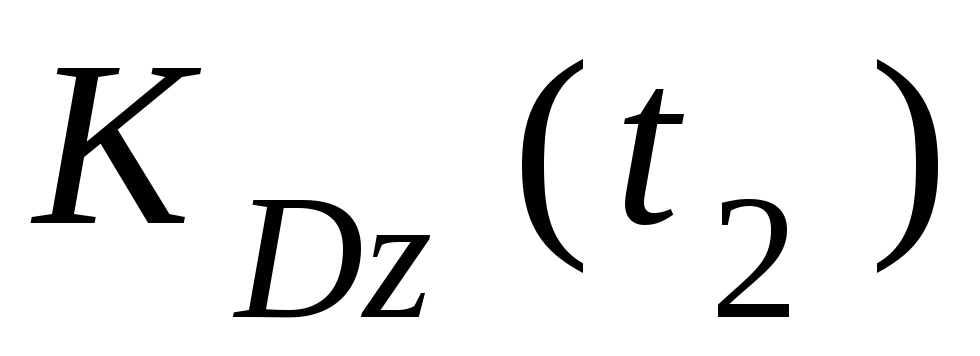 и точки
и точки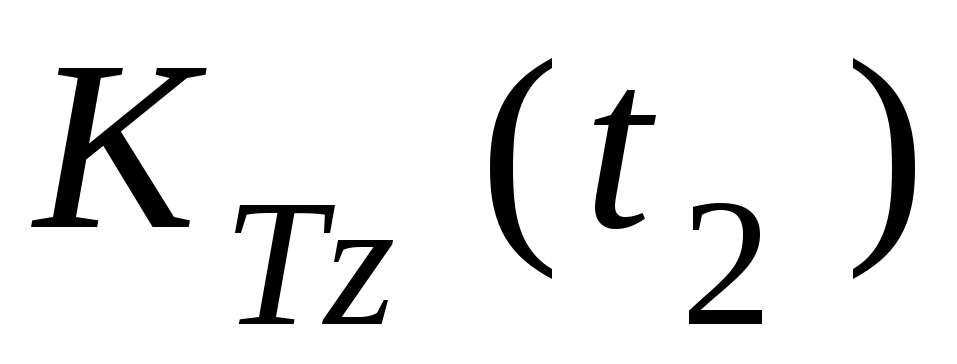 :
:
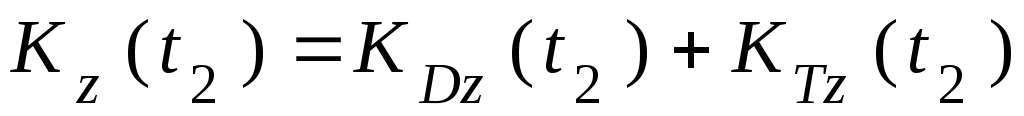 .
.
Очевидно, что
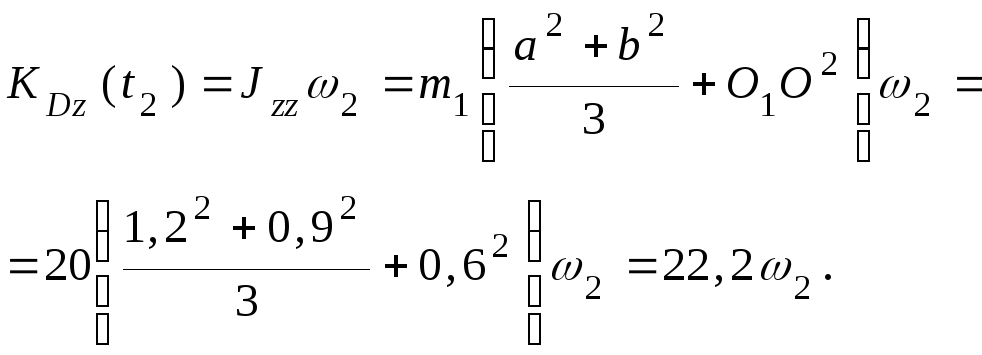
По теореме о сложении скоростей:
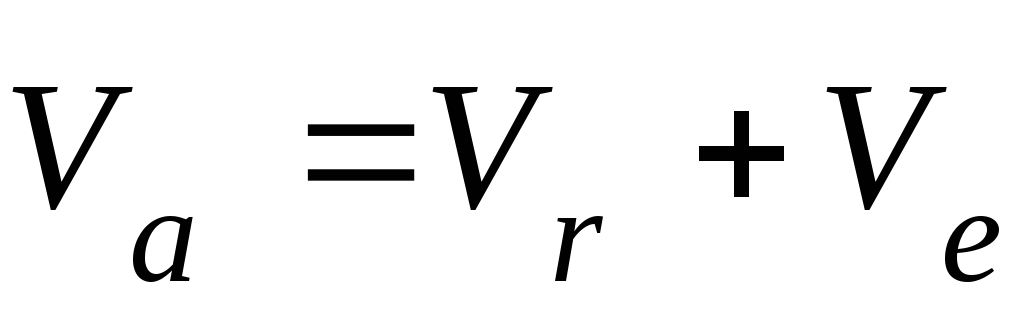 ,
,
где 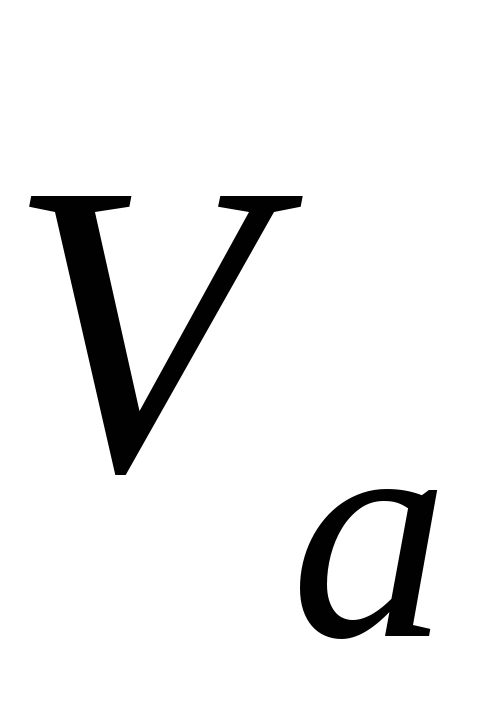 ,
,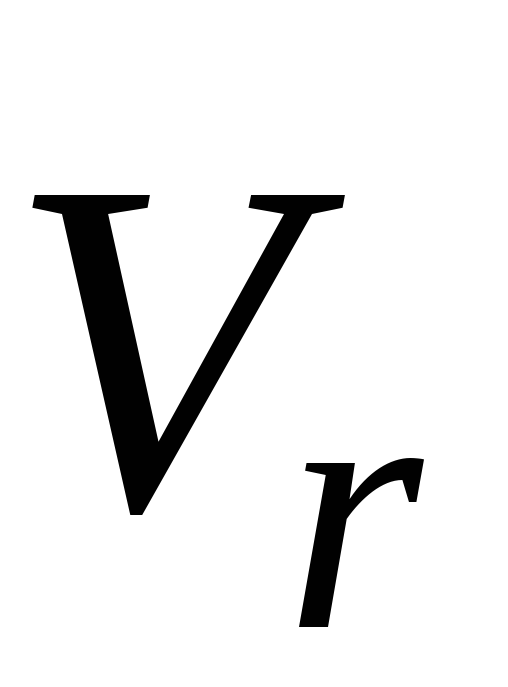 ,
,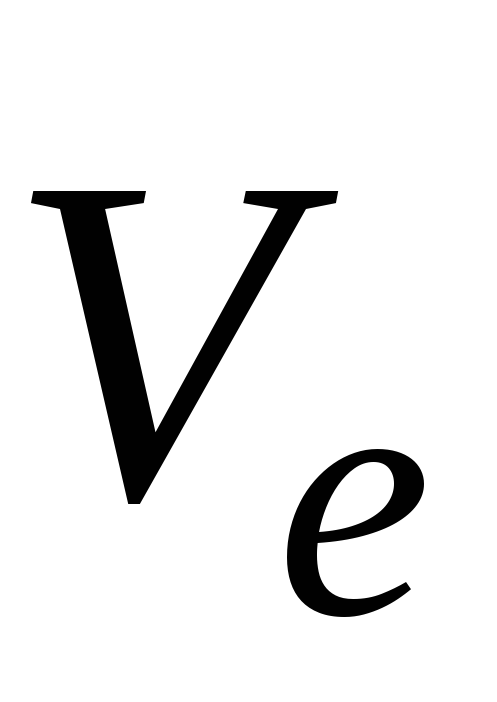 — абсолютная, относительная и переносная
скорости точки.
— абсолютная, относительная и переносная
скорости точки.
Умножая обе части этого равенства на m2, получаем:
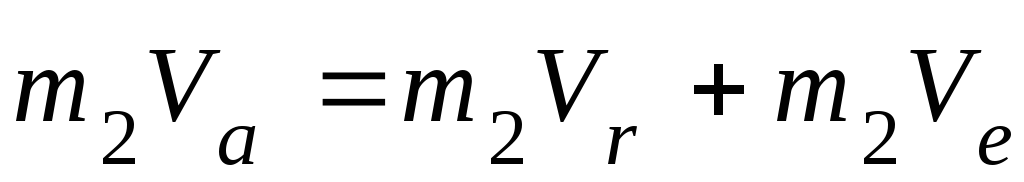 .
.
Следовательно,
кинетический момент точки К в конце отрезка времени t2 равен сумме
моментов векторов 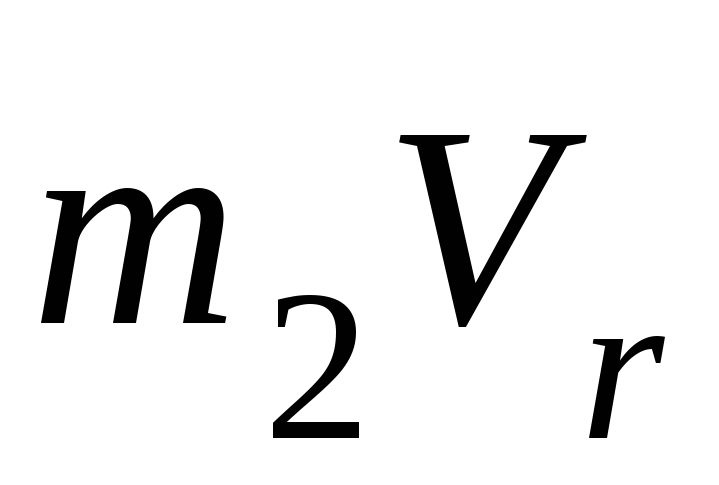 и
и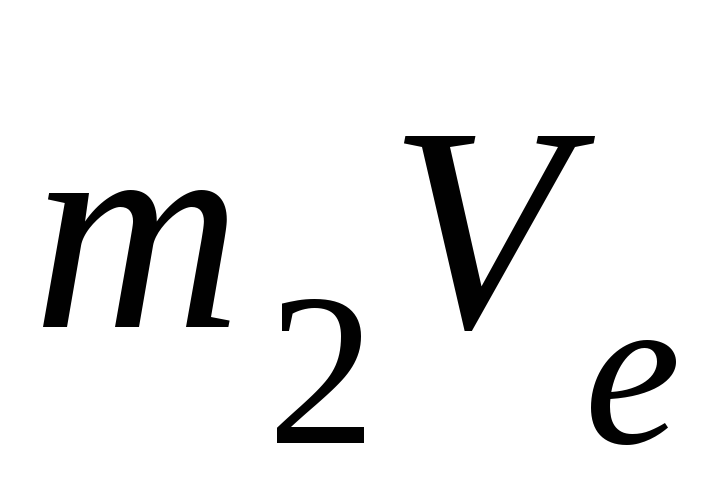 относительно осиz
относительно осиz
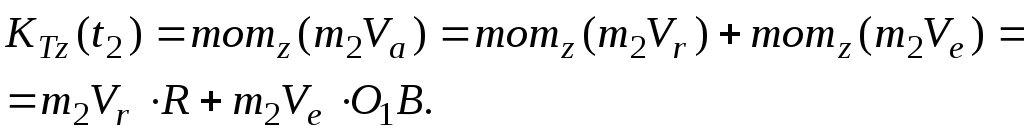
Относительная скорость точки К
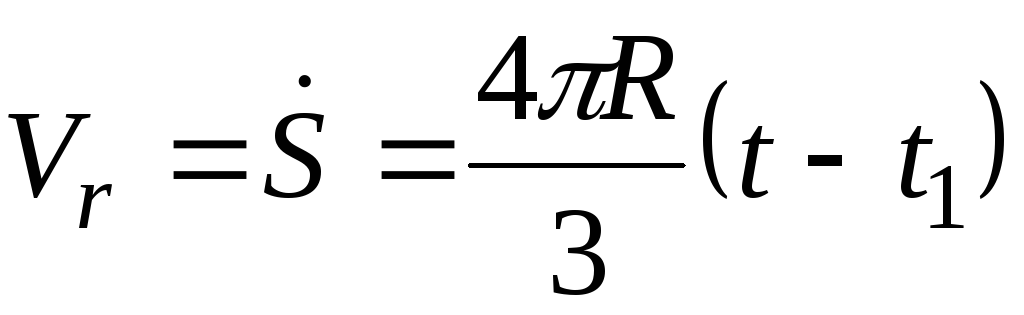 .
.
При t=t2=5 c найдем величину относительной скорости точки К
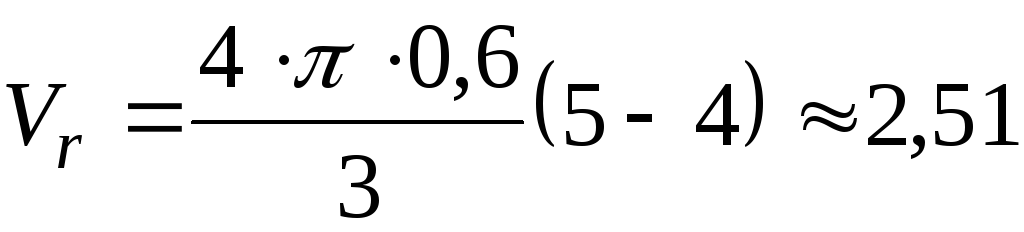 м/с.
м/с.
Переносная скорость точки К
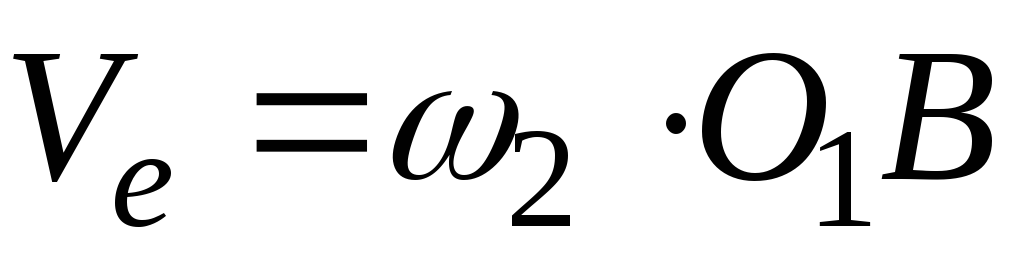 .
.
Из прямоугольного треугольника О1ОВ по теореме Пифагора имеем:
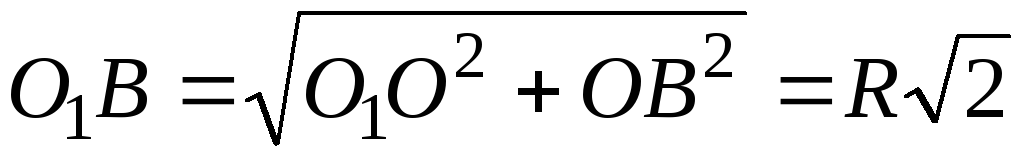 .
.
Окончательно получаем
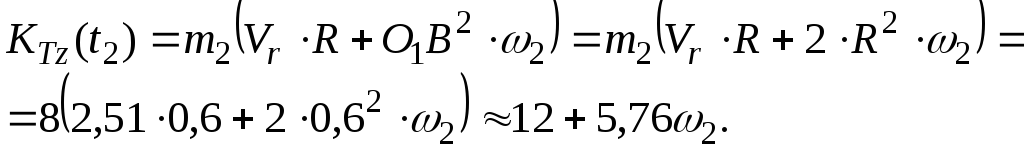
Тогда
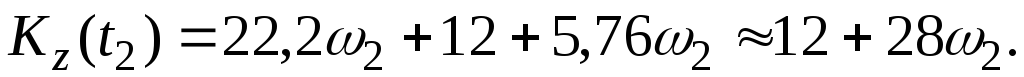
Приравнивая 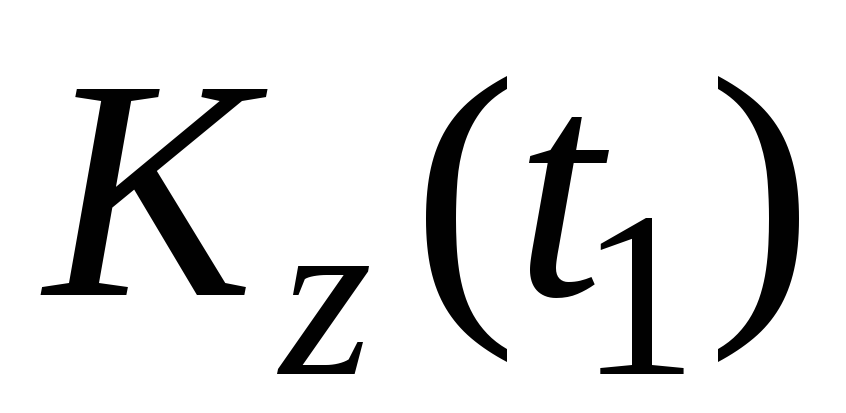 и
и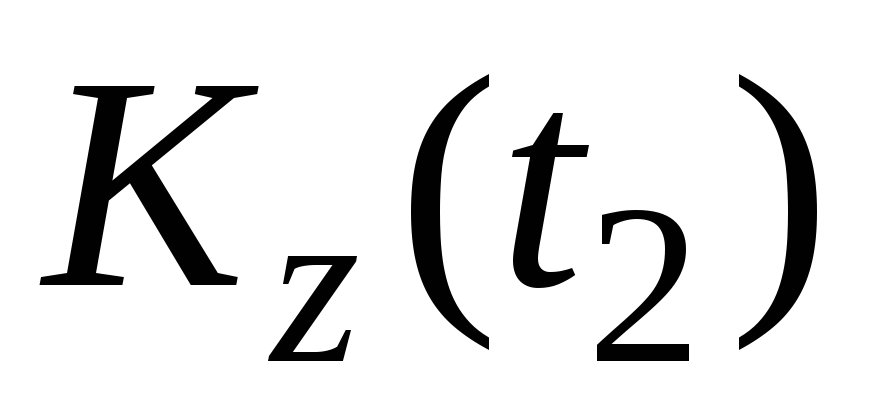 :
:
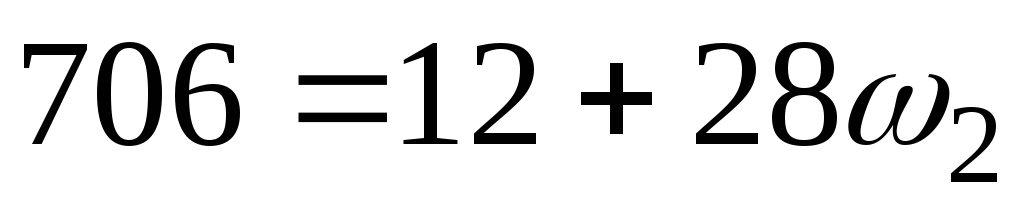 ,
,
находим
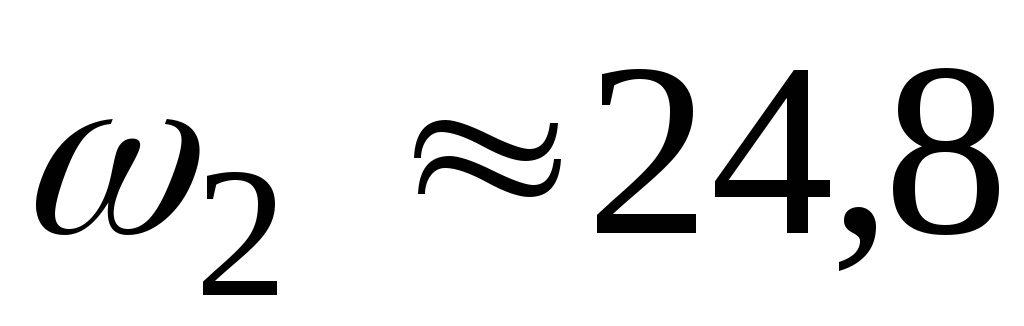 с-1.
с-1.
V Вычисление моментов инерции пластины
Известно из
механики, что момент инерции материальной
точки 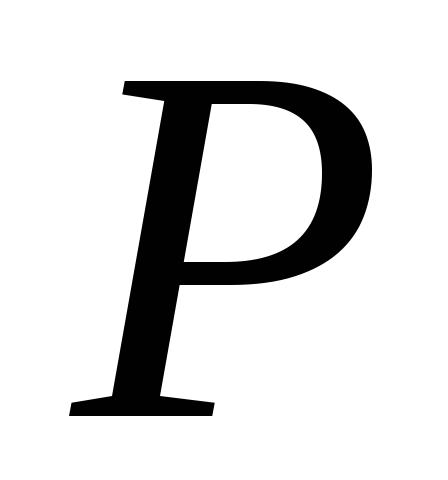 относительно оси
относительно оси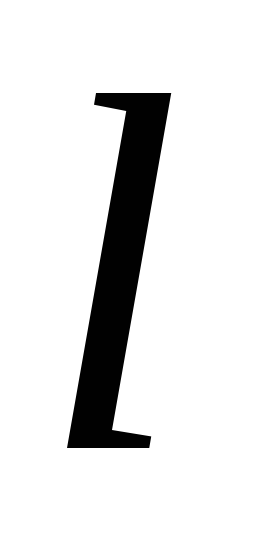 (или точкиО)
равен произведению массы точки на
квадрат расстояния от
(или точкиО)
равен произведению массы точки на
квадрат расстояния от 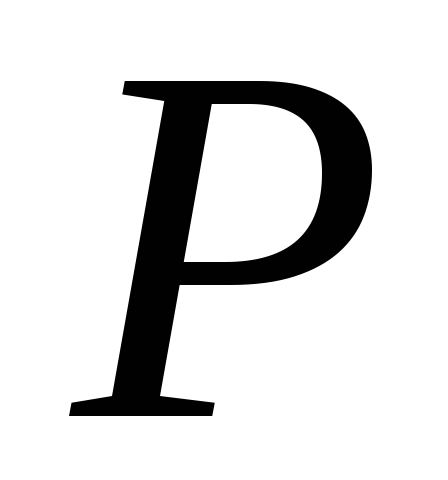 до
до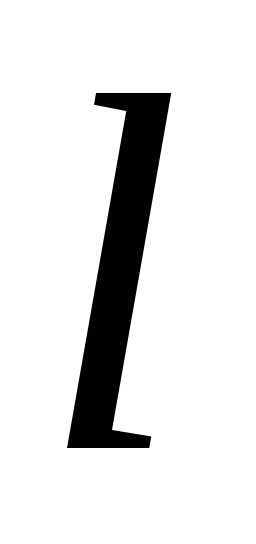 (или доО).
Кроме того, момент инерции системы
материальных точек равен сумме моментов
инерции этих точек.
(или доО).
Кроме того, момент инерции системы
материальных точек равен сумме моментов
инерции этих точек.
Пусть теперь в
области 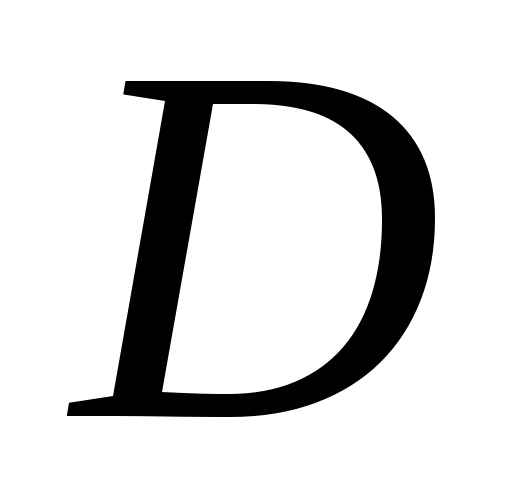 имеем распределение массы с поверхностной
плотностью
имеем распределение массы с поверхностной
плотностью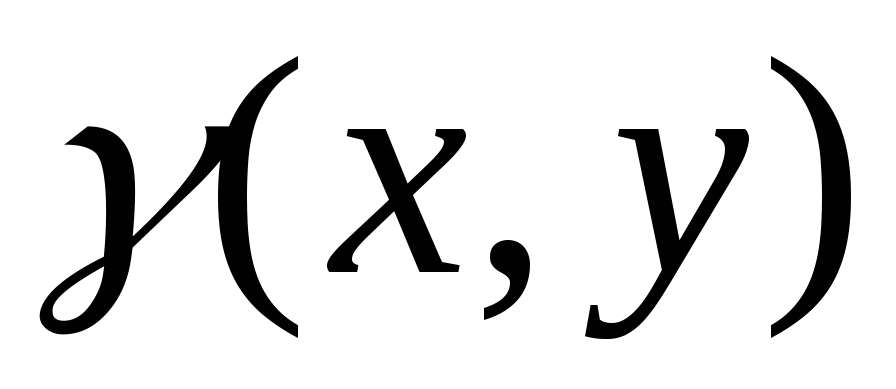 .
Чтобы найти момент инерции
.
Чтобы найти момент инерции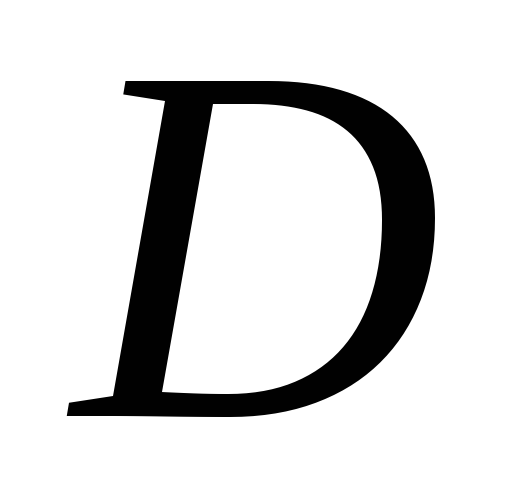 относительно, например, оси
относительно, например, оси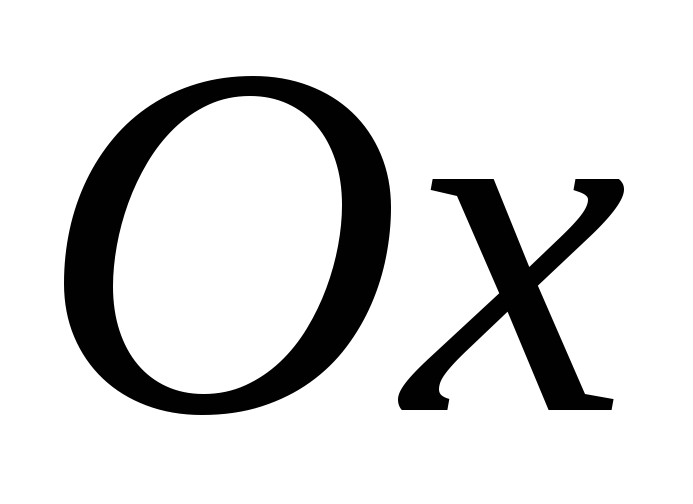 ,
как и в предыдущем пункте, разобьём
,
как и в предыдущем пункте, разобьём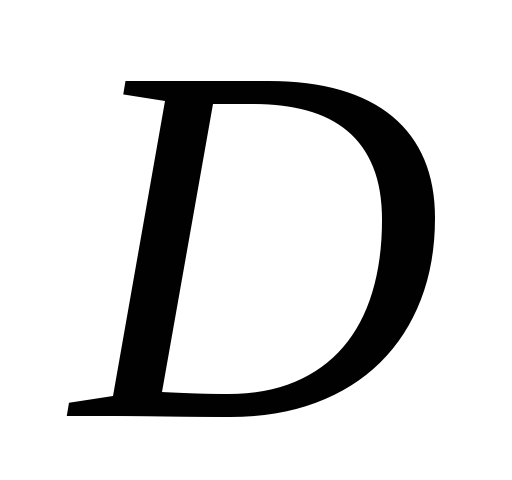 на части, выберем в каждой части
на части, выберем в каждой части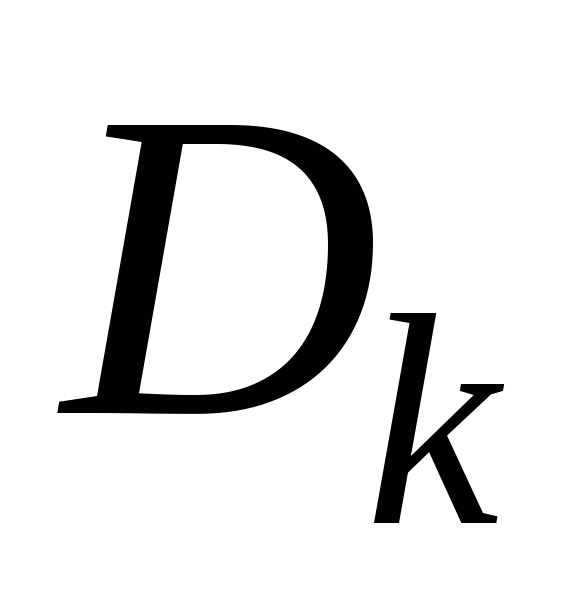 точку
точку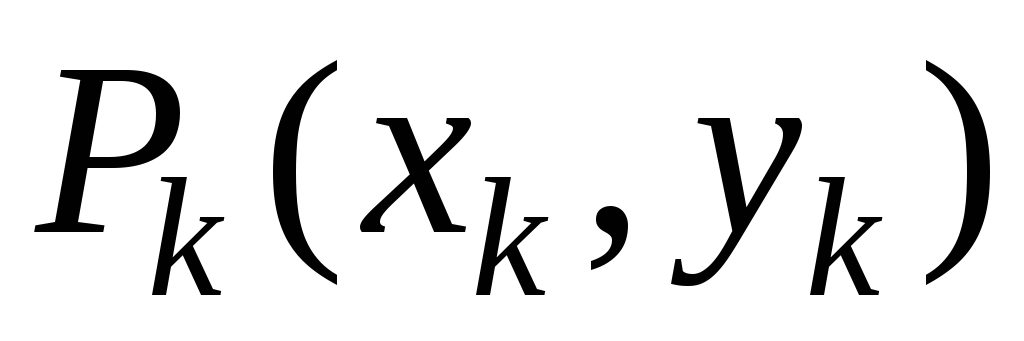 и сосредоточим всю массу
и сосредоточим всю массу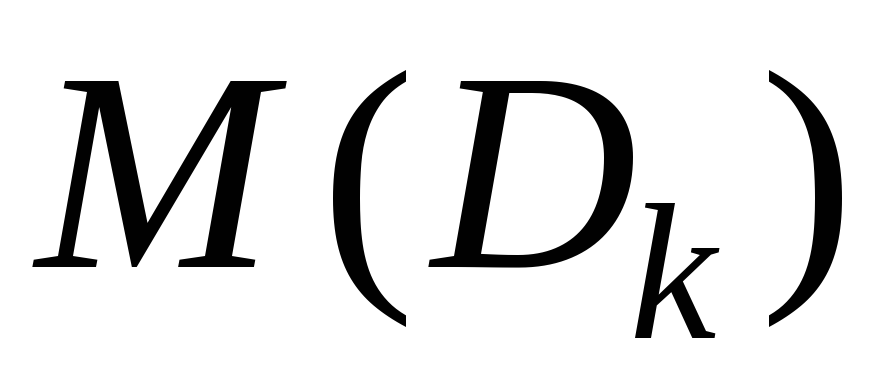 в этой точке. Получим систему материальных
точек, и момент инерции этой системы
даст приближённое значение для искомого
момента инерции
в этой точке. Получим систему материальных
точек, и момент инерции этой системы
даст приближённое значение для искомого
момента инерции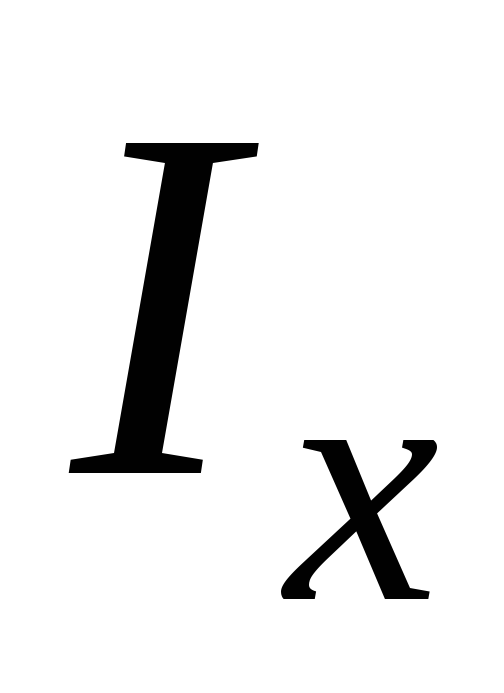 области
области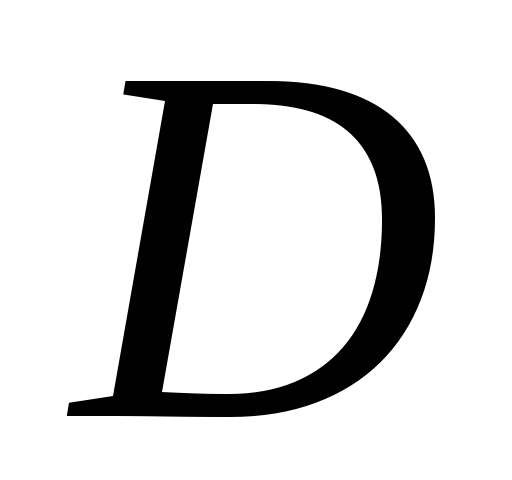 :
:
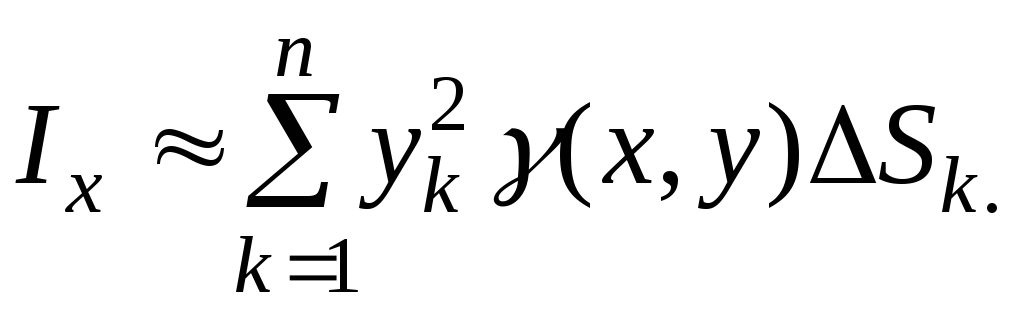
Точное значение получим в виде интеграла:
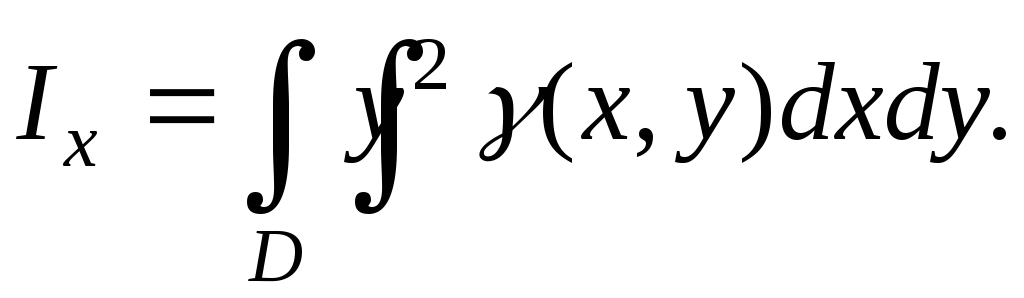
Аналогично для
момента инерции относительно оси 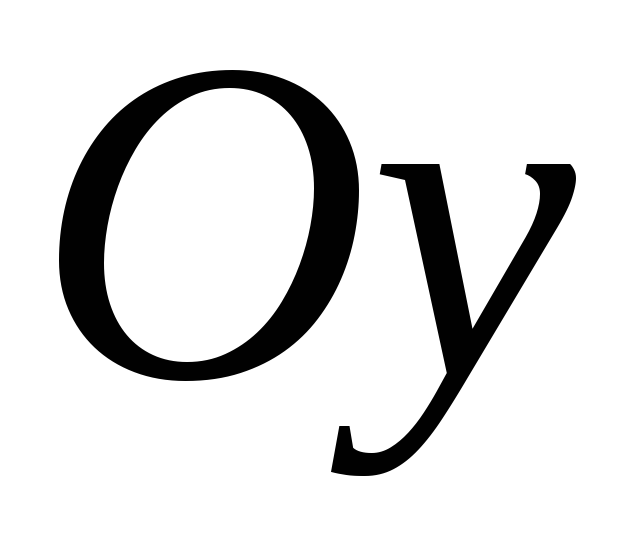 :
:
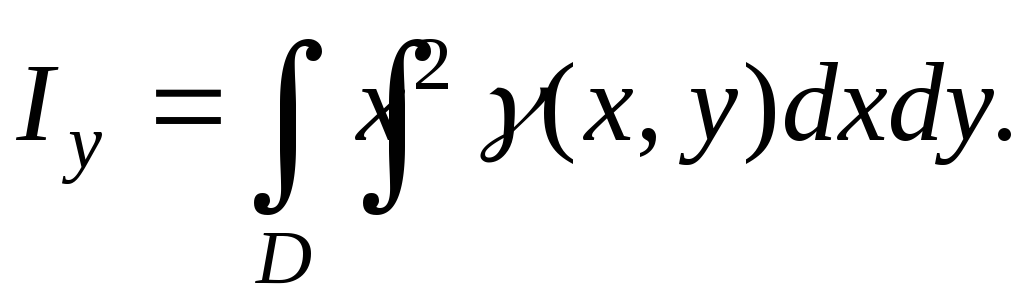
Нетрудно догадаться,
что момент инерции 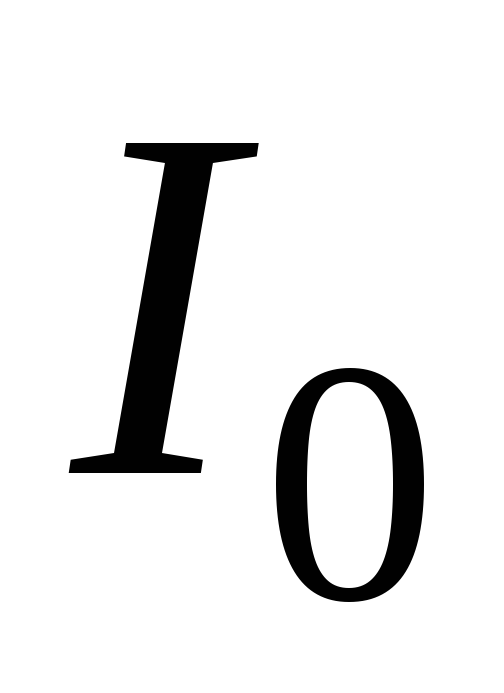 области
области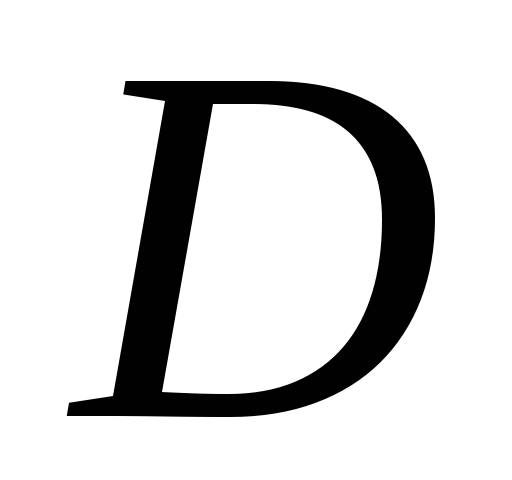 относительно начала координат можно
найти по формуле
относительно начала координат можно
найти по формуле
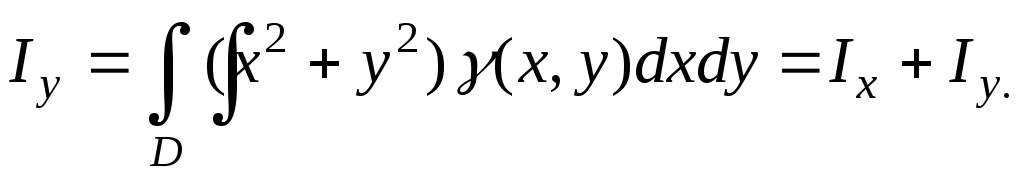
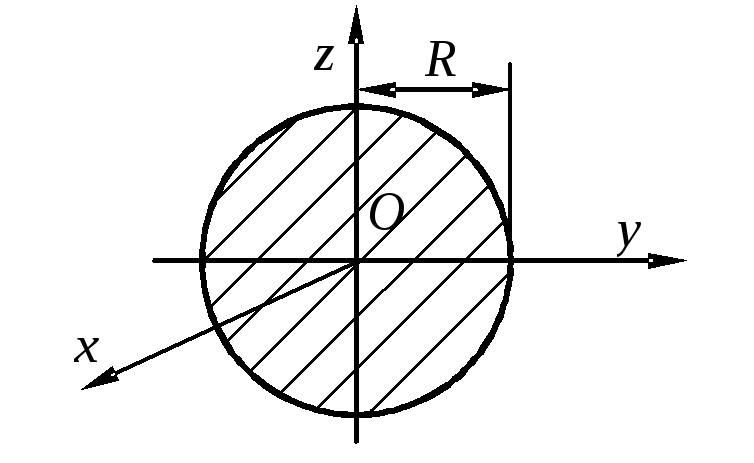
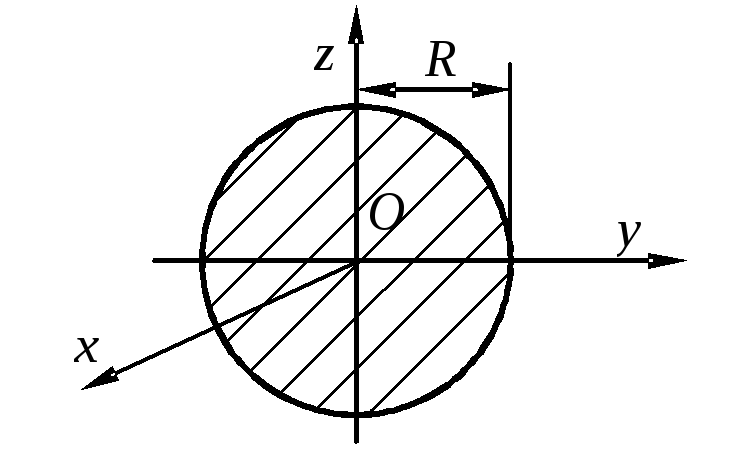
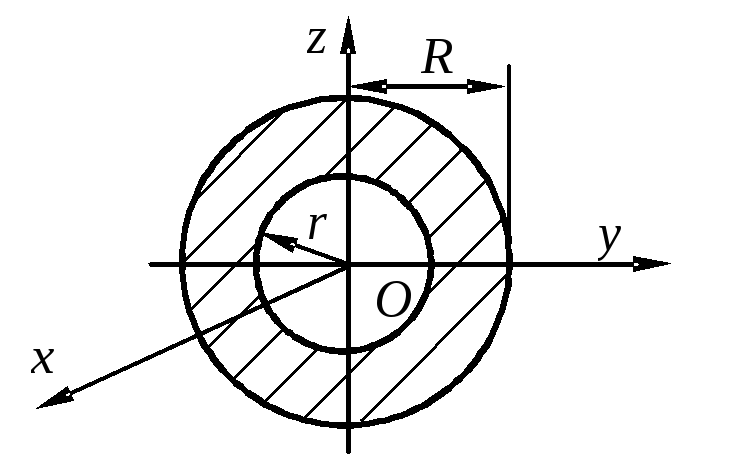
Пример 6. Найти момент инерции однородного круга
радиуса  отно-сительно фиксированного диаметра.
отно-сительно фиксированного диаметра.
Решение. Пусть центр круга – в начале координат,
а фиксированный диаметр лежит на оси 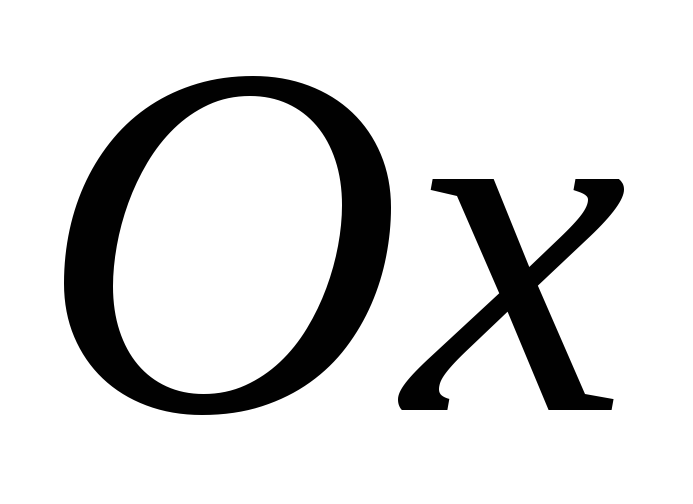 .
Однородность означает, что
.
Однородность означает, что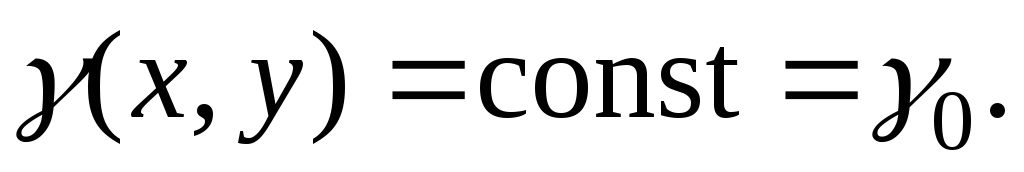 .
.
Искомый момент инерции:
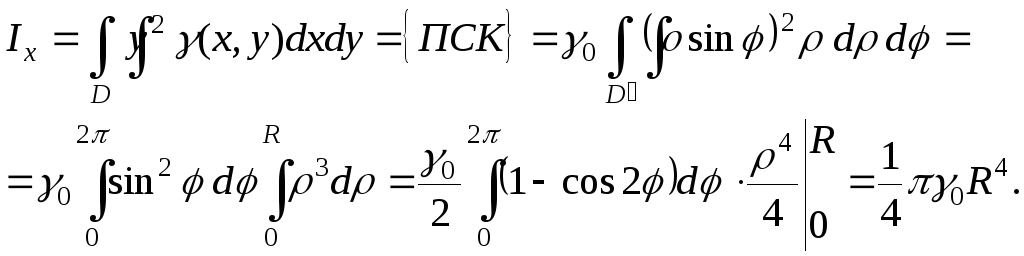
VI Вычисление площади поверхности
Прежде всего, требуется определить само понятие площади поверхности. В своё время математики показали, что невозможно определить это понятие путём вписывания и описывания многогранных поверхностей (так это было сделано при определении площади плоской фигуры и объёма тела). Был предположен другой подход.
Будем обозначать
поверхность символом 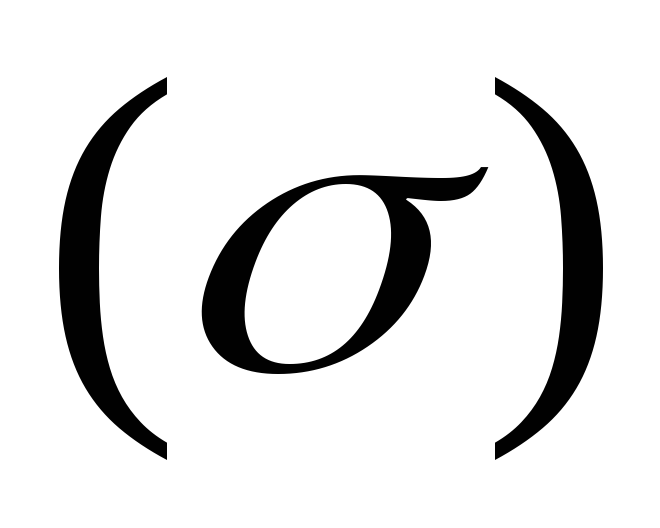 ,
а её площадь –
,
а её площадь – .
Такую же систему обозначений примем и
для части поверхности
.
Такую же систему обозначений примем и
для части поверхности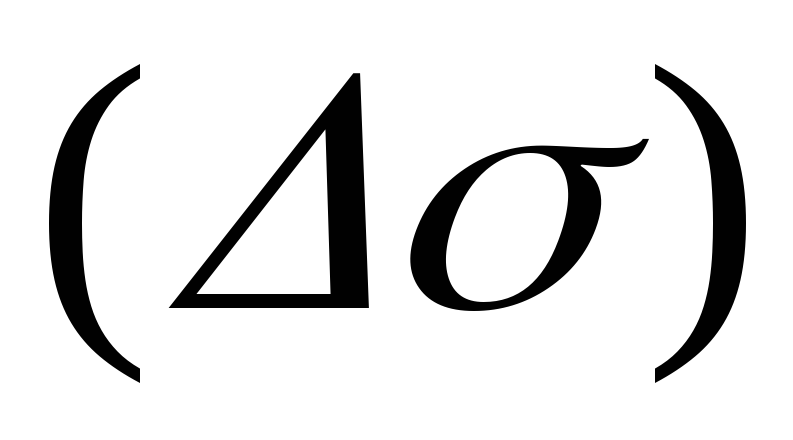 и для плоских фигур.
и для плоских фигур.
Разобьём 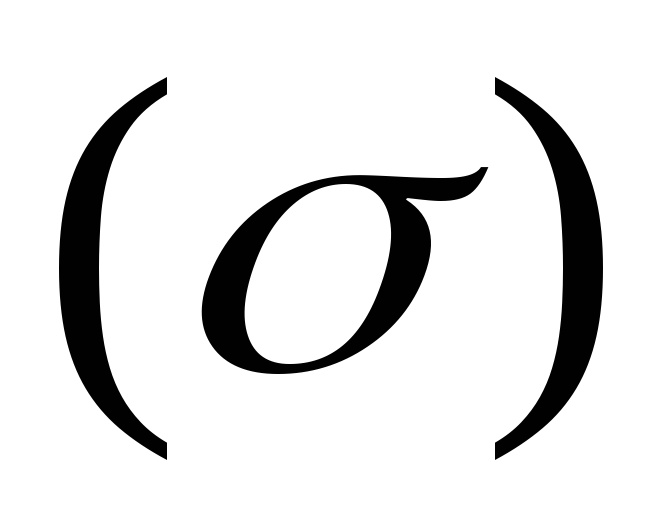 на
на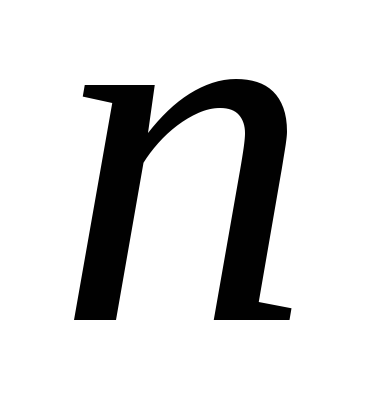 частей
частей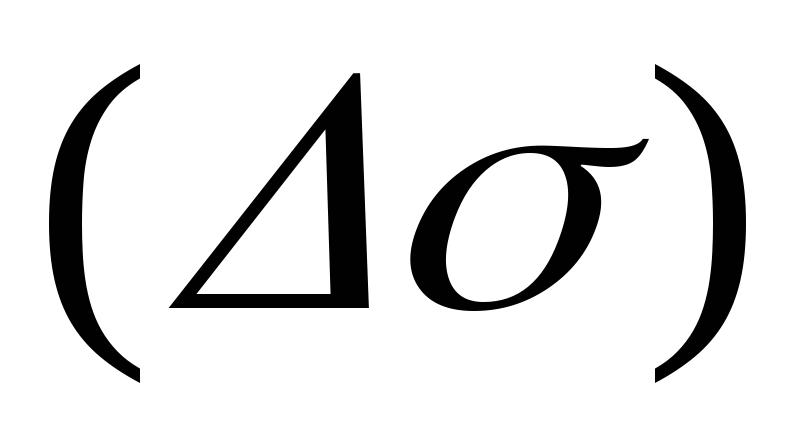 и в каждой из них выберем точку
и в каждой из них выберем точку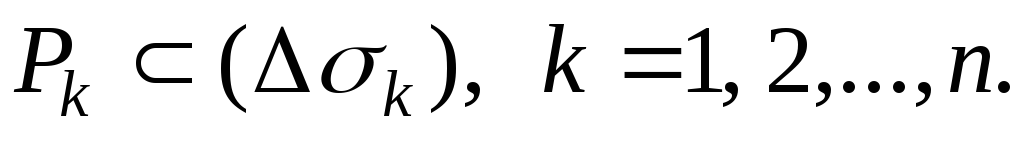 Через выбранную точку проведем касательную
плоскость к поверхности и спроектируем
Через выбранную точку проведем касательную
плоскость к поверхности и спроектируем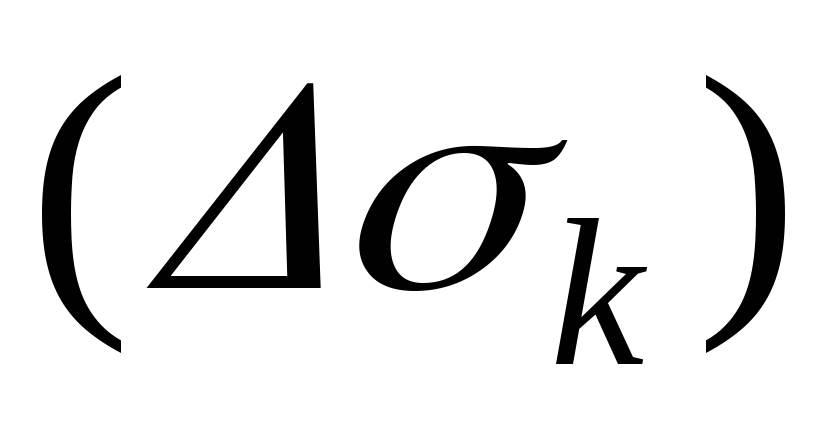 на эту плоскость. Обозначим
на эту плоскость. Обозначим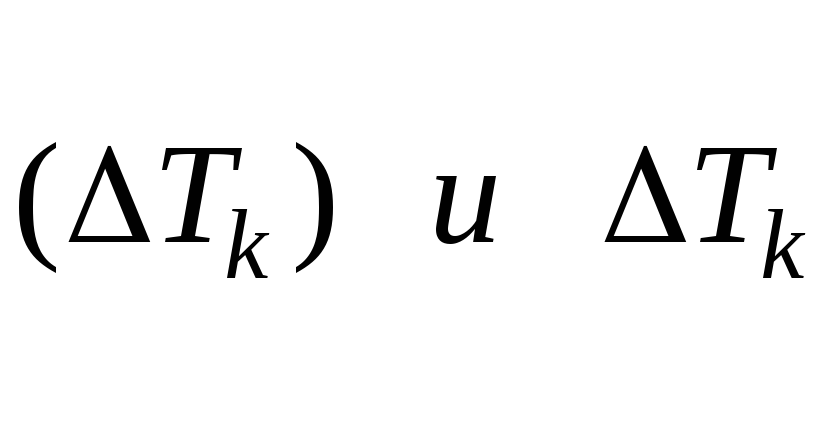 полученную проекцию и её площадь. Пусть,
кроме того,
полученную проекцию и её площадь. Пусть,
кроме того,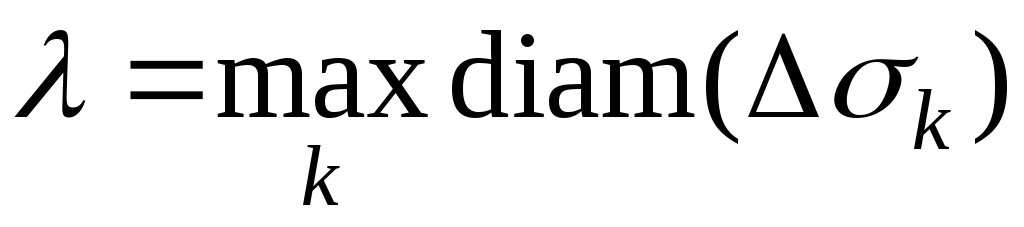 .
.
Определение. Конечный предел вида
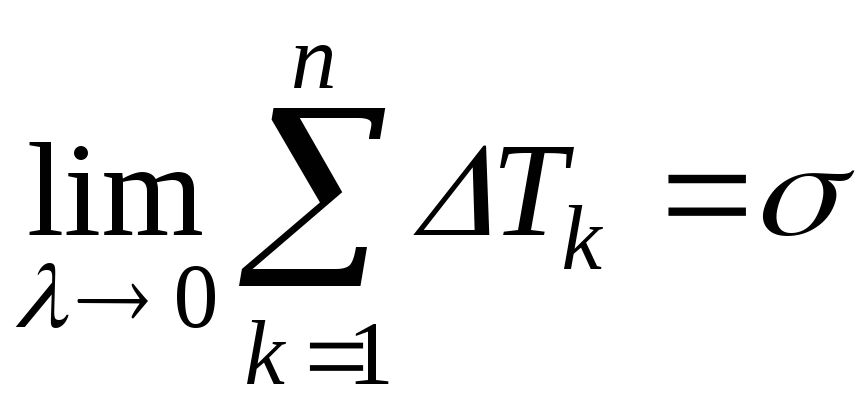
называют площадью
поверхности 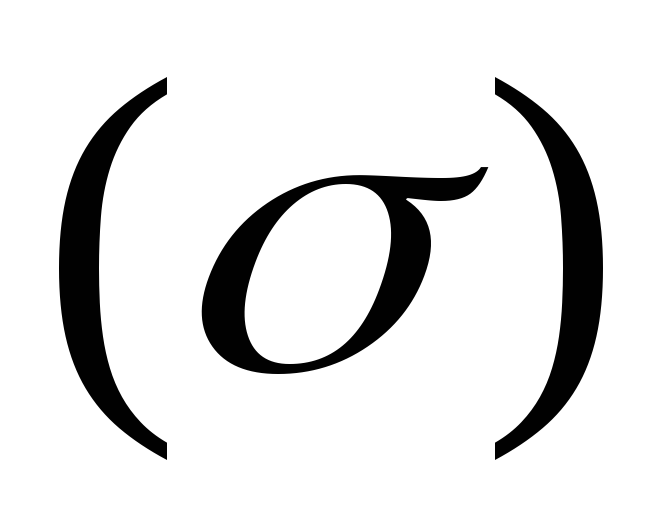 .
.
Можно показать,
что если поверхность 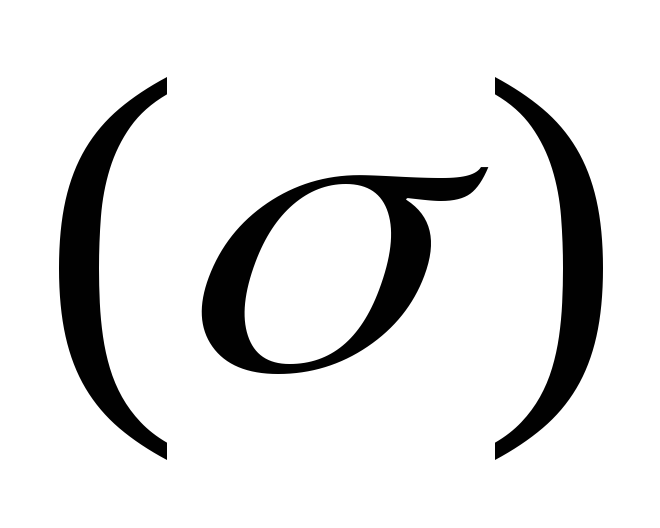 не имеет особых точек (т.е. в каждой её
точке можно провести касательную
плоскость), то данный предел существует
и не зависит от разбиения
не имеет особых точек (т.е. в каждой её
точке можно провести касательную
плоскость), то данный предел существует
и не зависит от разбиения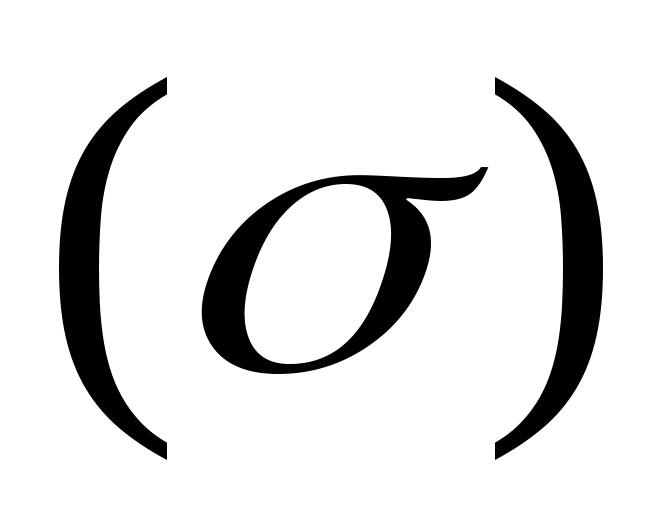 на части
на части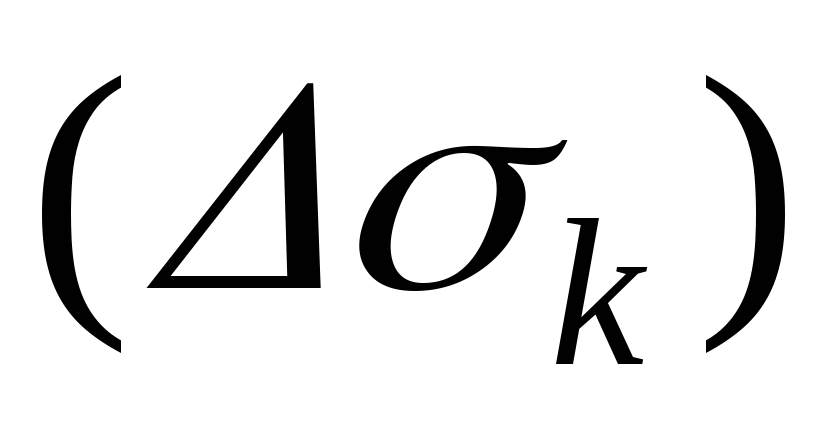 и от выбора точек
и от выбора точек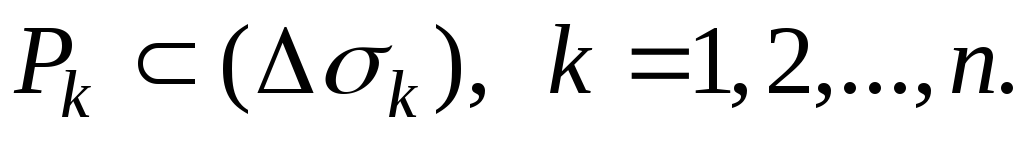 .
.
Напомним, что,
если поверхность 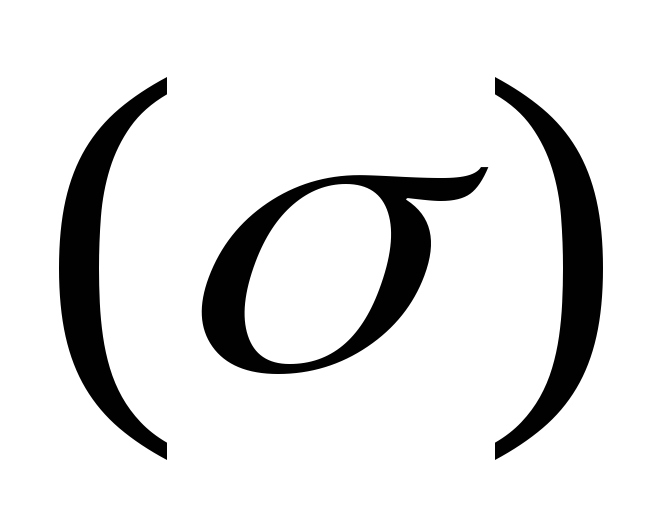 задана явным уравнением
задана явным уравнением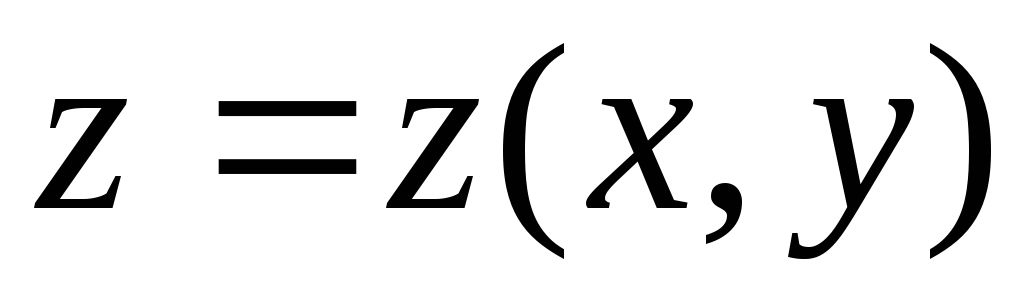 ,
причем
,
причем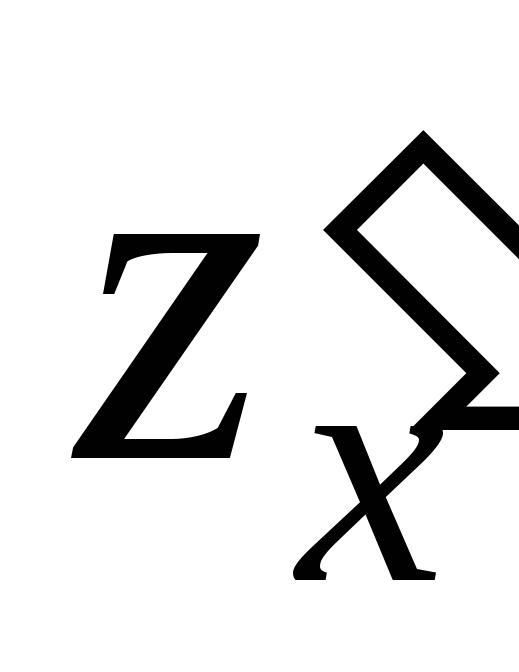 и
и существуют в точке
существуют в точке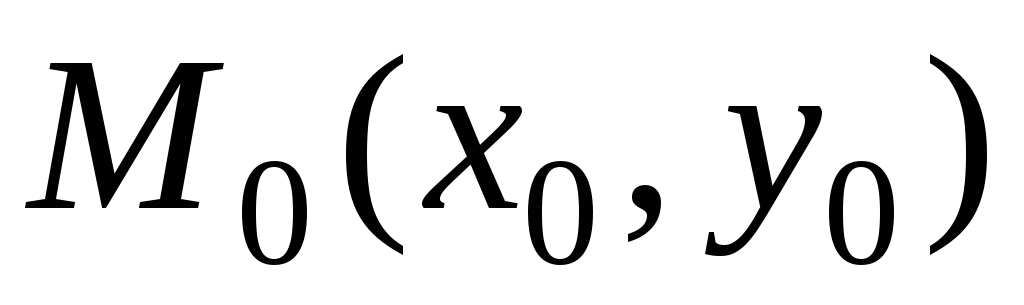 ,
то существует и касательная плоскость
в точке
,
то существует и касательная плоскость
в точке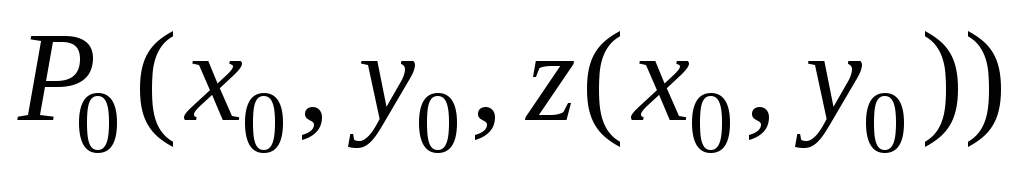 ,
и её нормальный вектор имеет вид
,
и её нормальный вектор имеет вид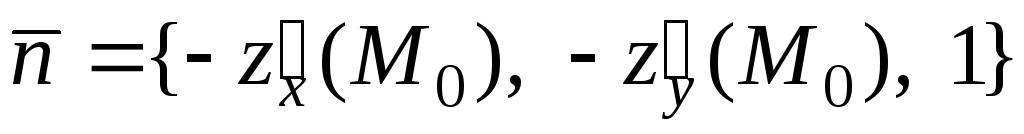 .
Заметим, что этот вектор образует острый
угол с осью
.
Заметим, что этот вектор образует острый
угол с осью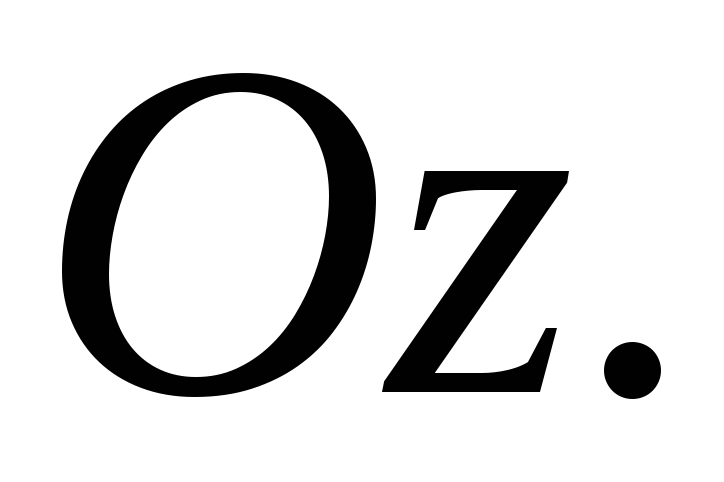
Теорема. Пусть поверхность 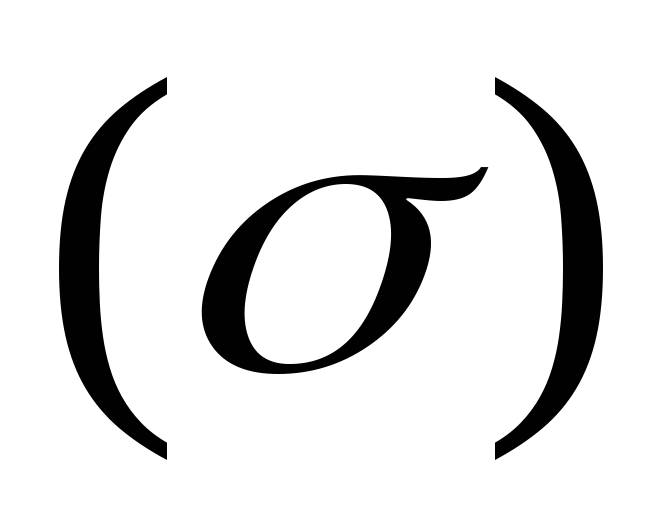 задана уравнением
задана уравнением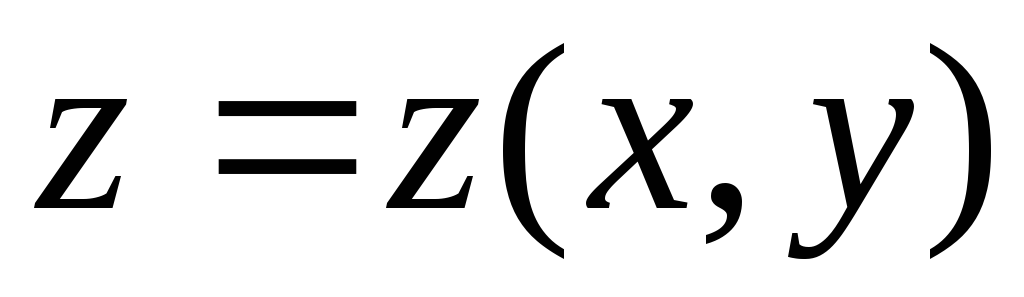 ,
,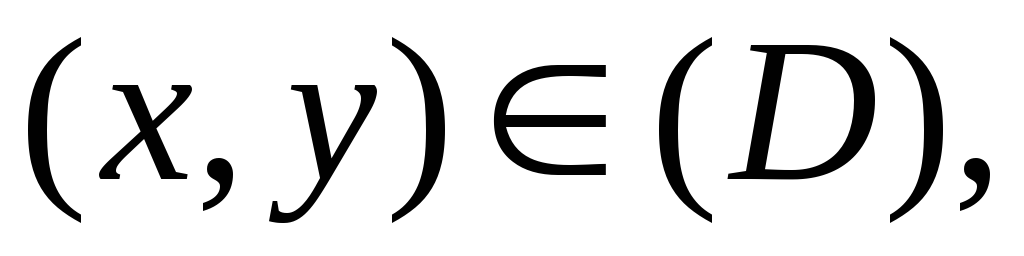 причем частные производные
причем частные производные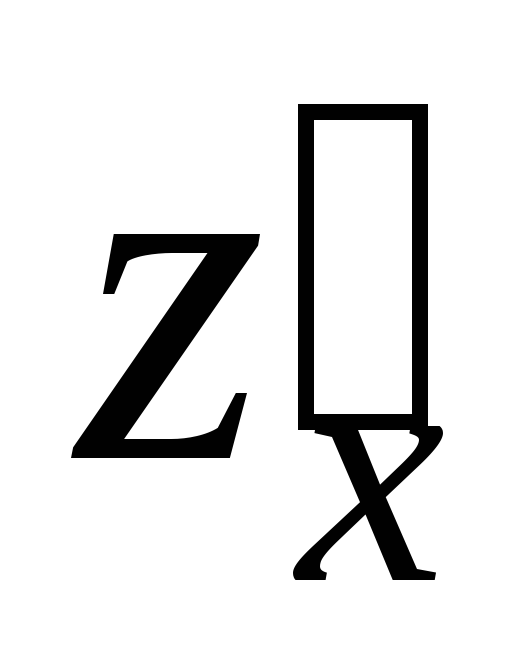 и
и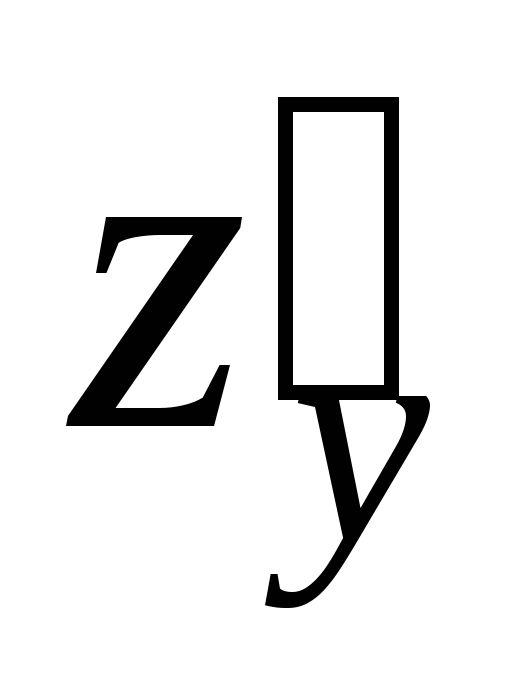 непрерывны в
непрерывны в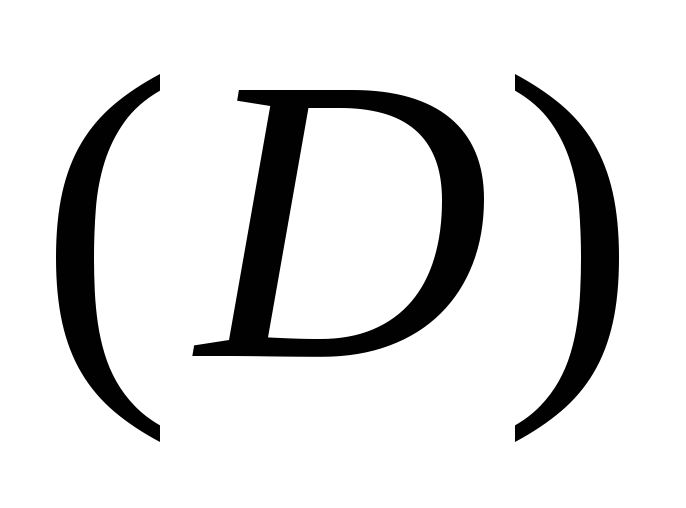 .
Тогда площадь данной поверхности можно
вычислить по формуле
.
Тогда площадь данной поверхности можно
вычислить по формуле
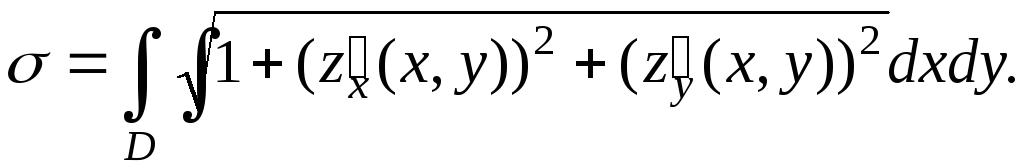
Идея
доказательства. Разобьём
область 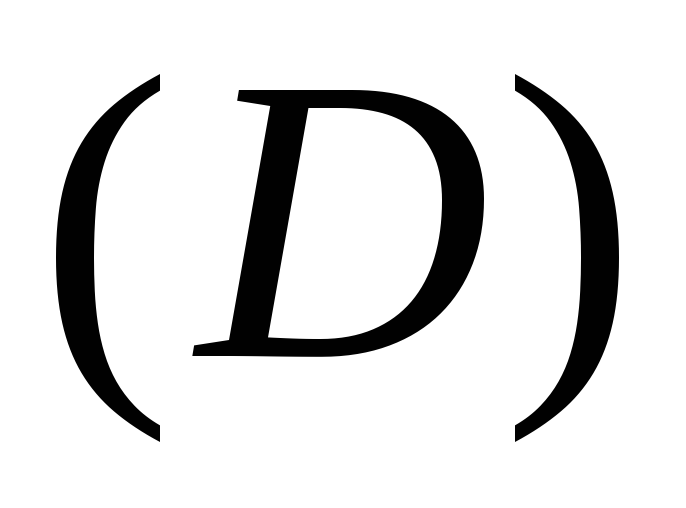 (проекцию
(проекцию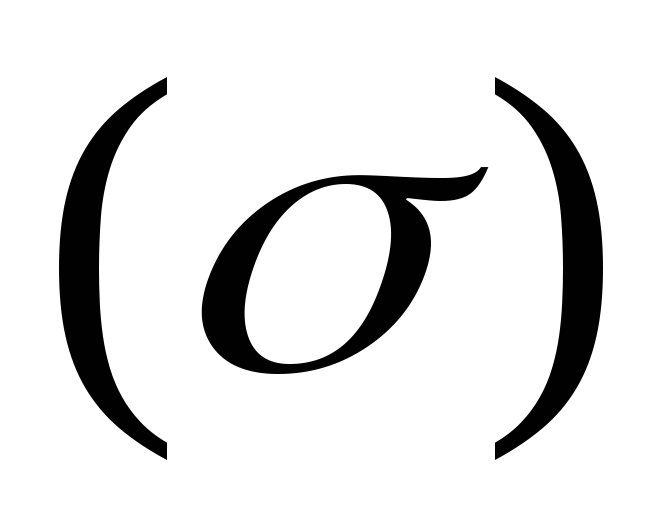 на плоскость
на плоскость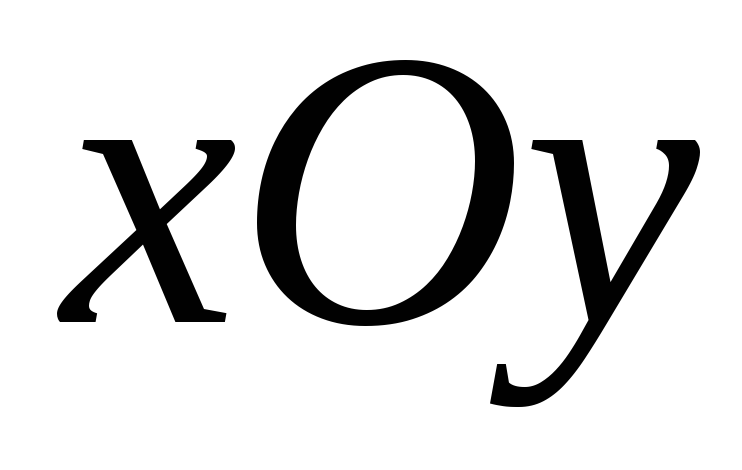 )
на
)
на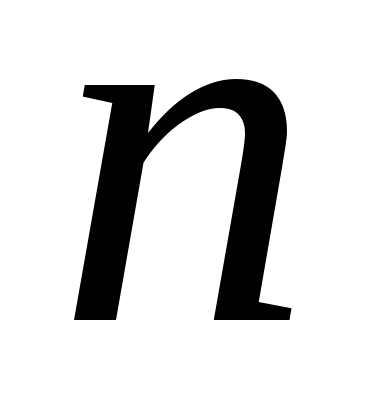 частей
частей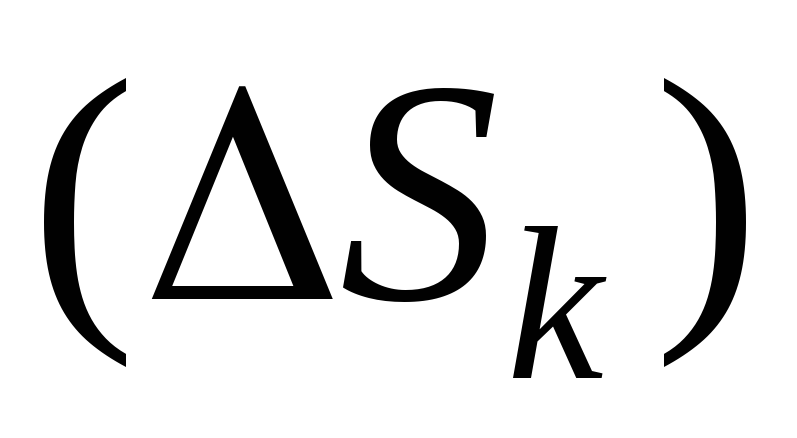 и через их границы проведем цилиндрические
поверхности с образующими параллельными
оси
и через их границы проведем цилиндрические
поверхности с образующими параллельными
оси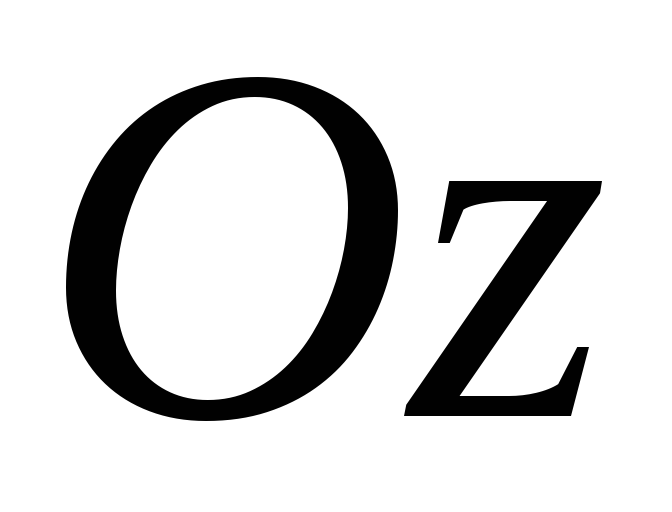 .
Тогда и поверхность
.
Тогда и поверхность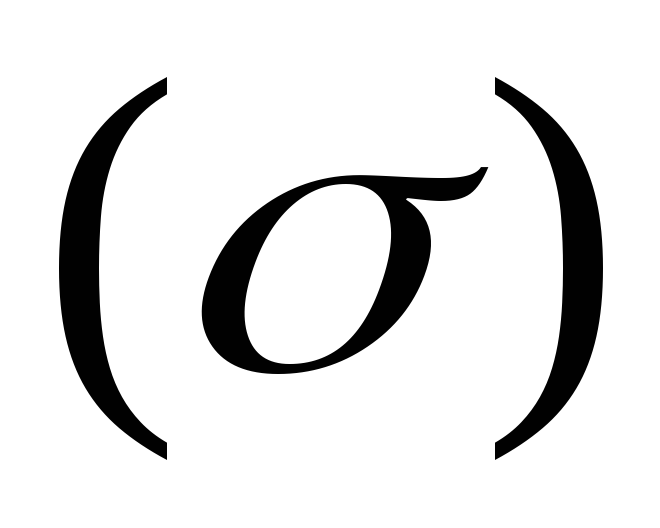 разобьётся на
разобьётся на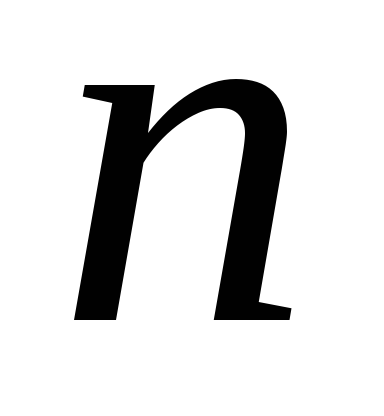 частей
частей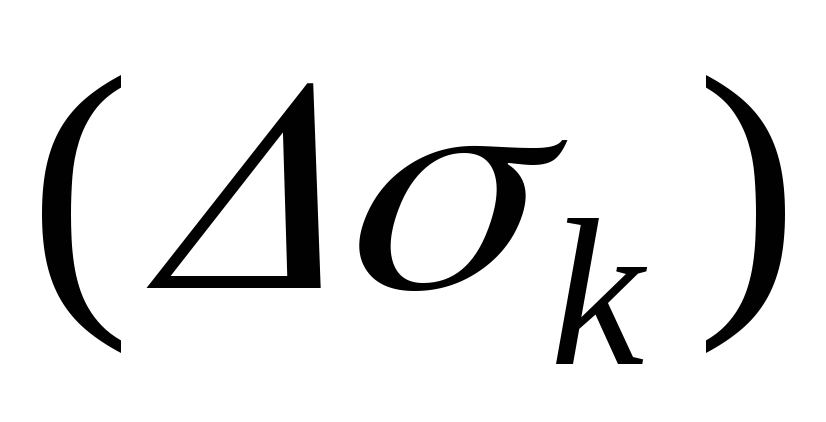 .
В каждой такой части выберем точку
.
В каждой такой части выберем точку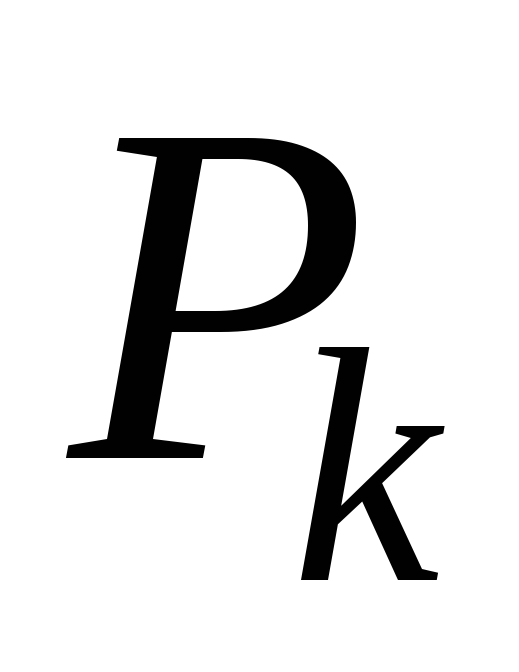 ,
проведем касательную плоскость
,
проведем касательную плоскость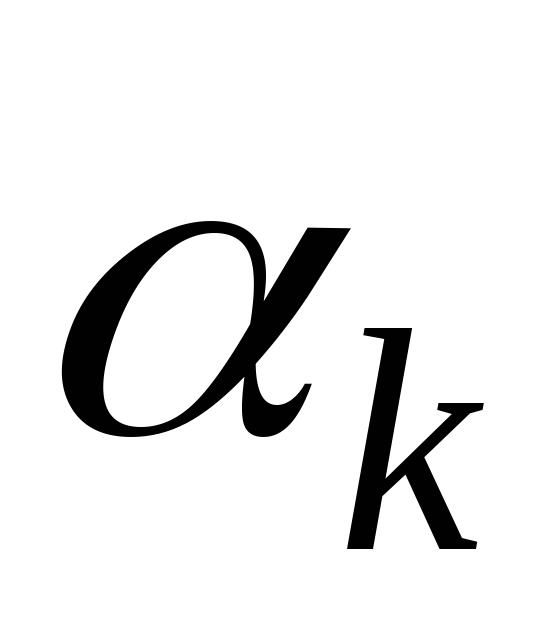 с нормальным век- тором
с нормальным век- тором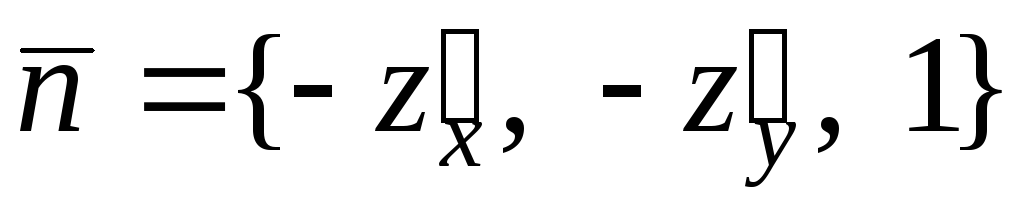 .
Данный вектор составляет с осью
.
Данный вектор составляет с осью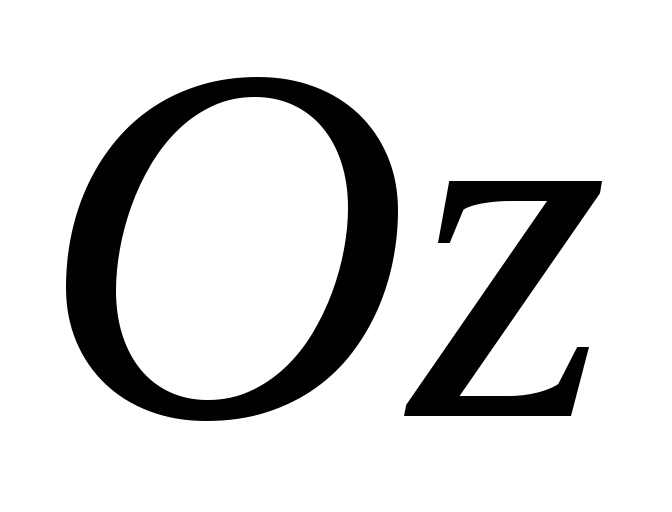 угол
угол такой, что
такой, что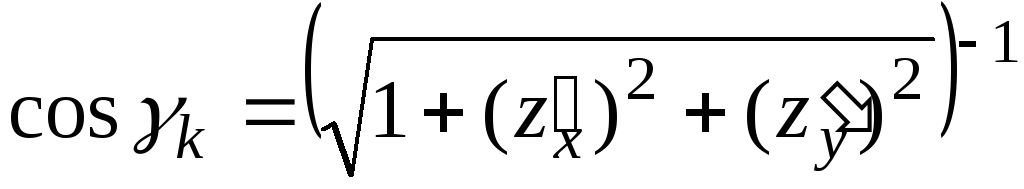 .Тот
же самый угол
.Тот
же самый угол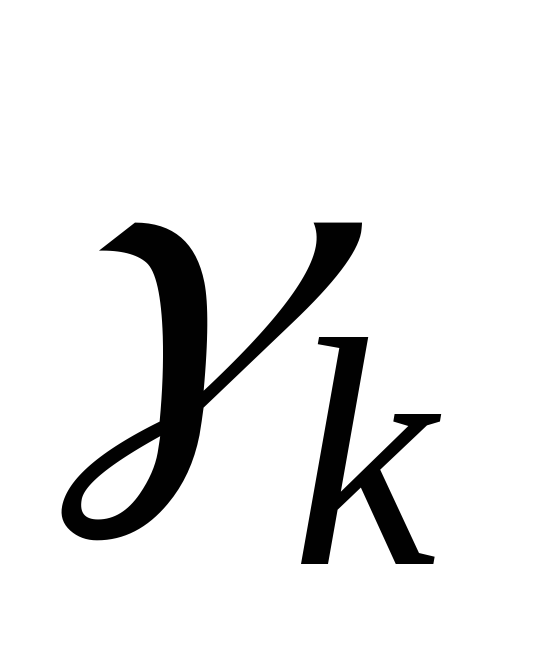 составляет касательная плоскость
составляет касательная плоскость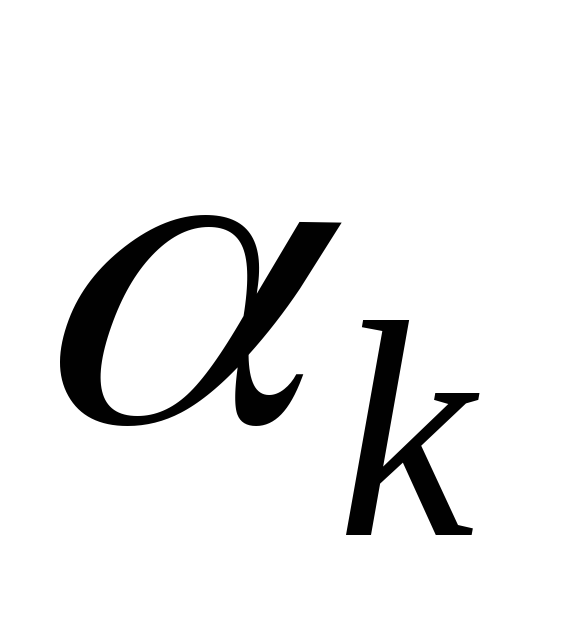 с координатной плоскостью
с координатной плоскостью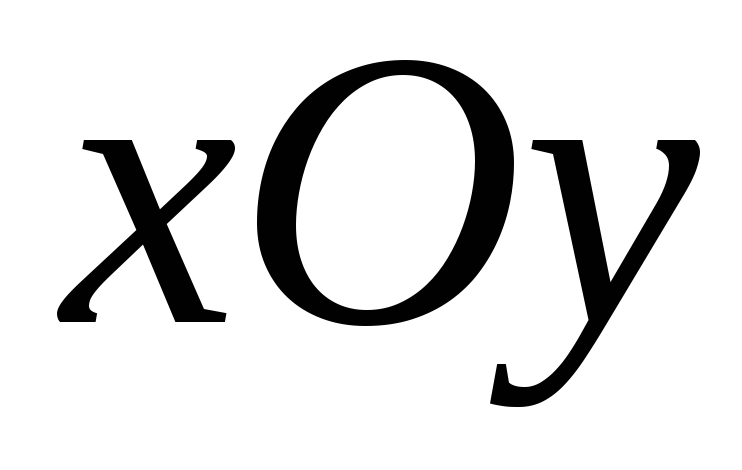
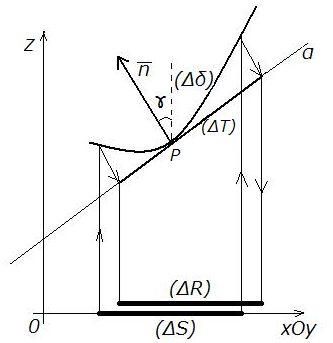
Пусть 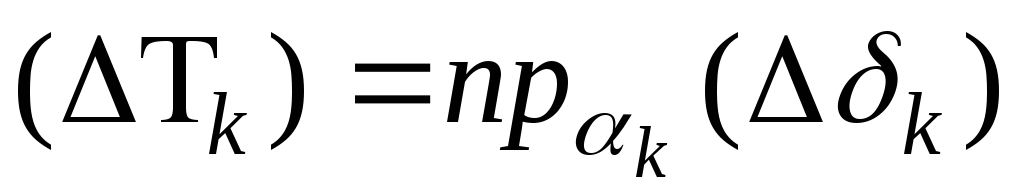 и
и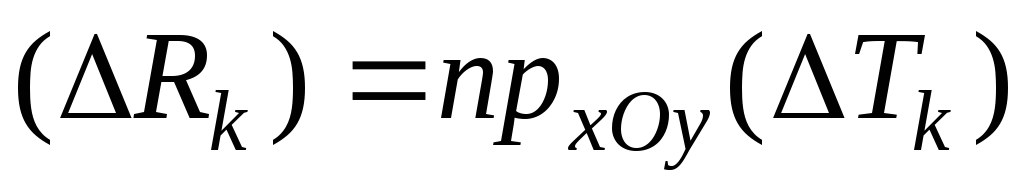 .
Можно показать, что
.
Можно показать, что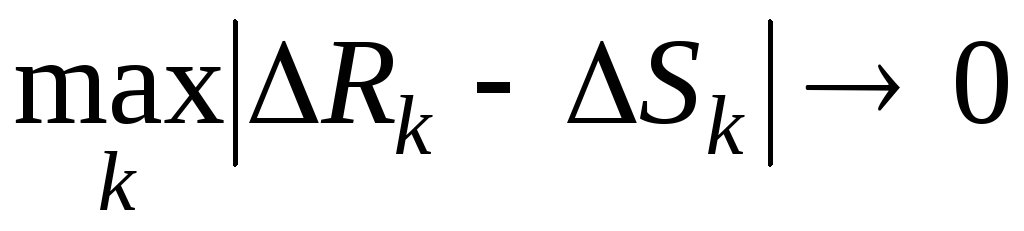 при
при .
Это означает,
.
Это означает,
что
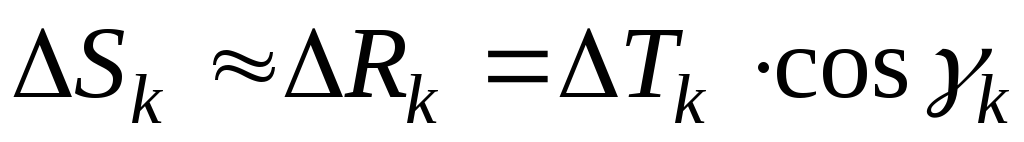 .
.
Отсюда
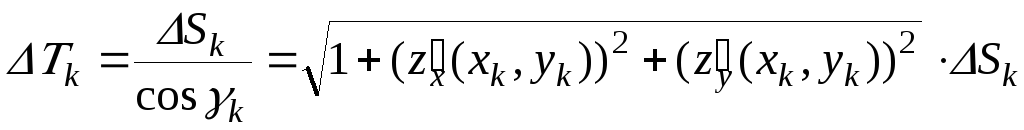 .
.
Но тогда сумма 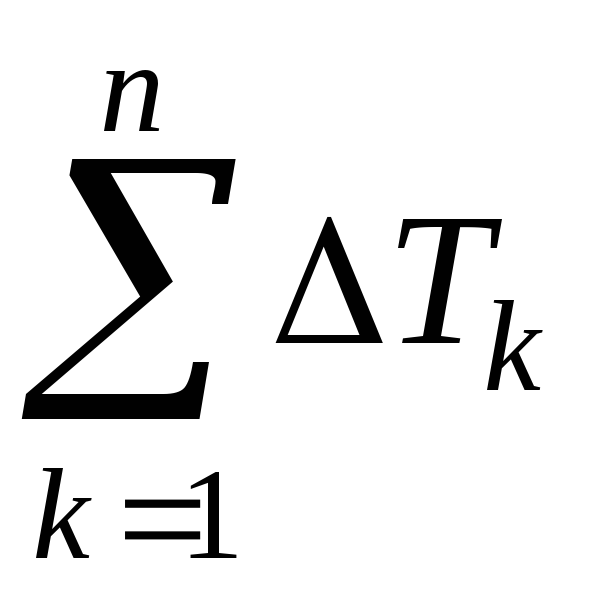 — это интегральная сумма, которая в
пределе и даёт интеграл из формулировки
теоремы.
— это интегральная сумма, которая в
пределе и даёт интеграл из формулировки
теоремы.
Пример 7. Найти площадь части поверхности 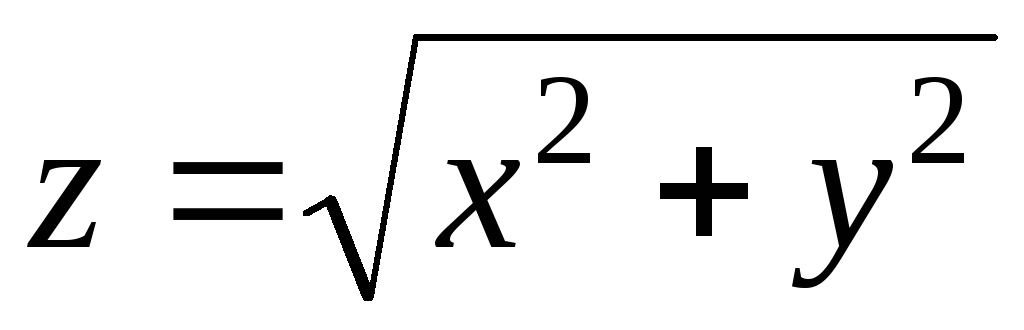 ,
распо-
,
распо-
ложенную внутри
цилиндра 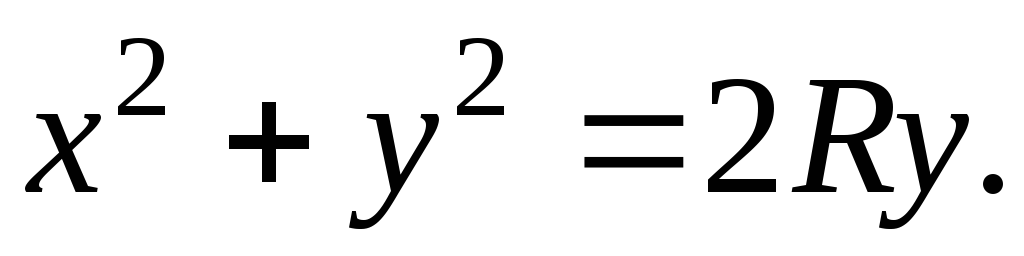
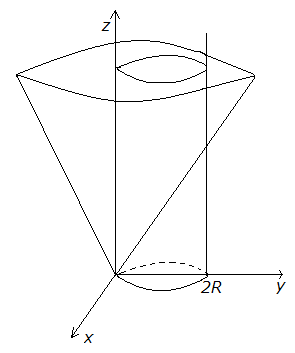
Решение. Очевидно, проекцией части конуса,
расположенной в цилиндре, есть “основание“
цилиндра – круг радиуса  с центром
с центром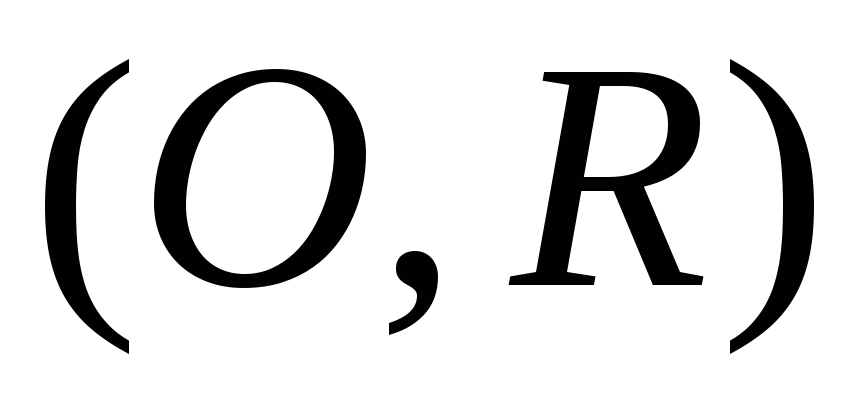 .
Предварительные вычисления:
.
Предварительные вычисления:
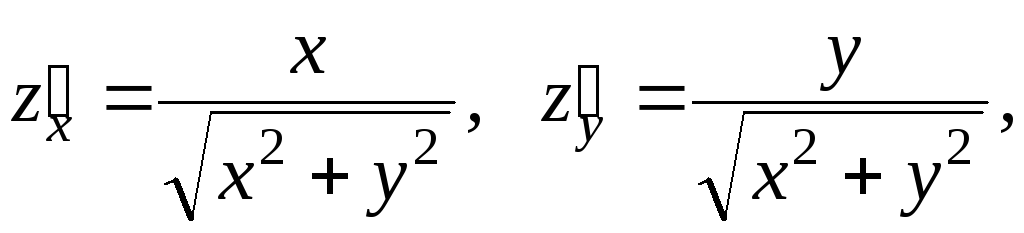
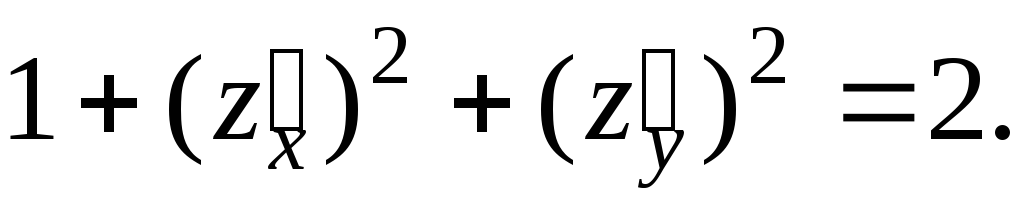
Имеем для  :
:
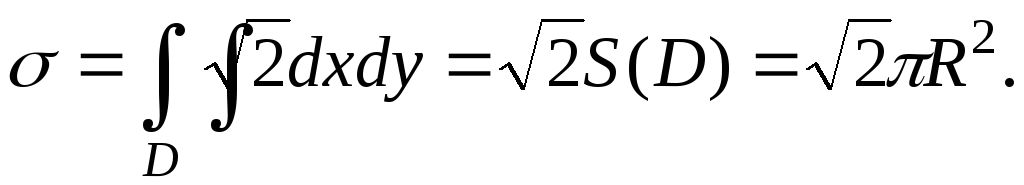
Задачи (для самостоятельного решения)
1. Вычислить объём тела, ограниченного поверхностями
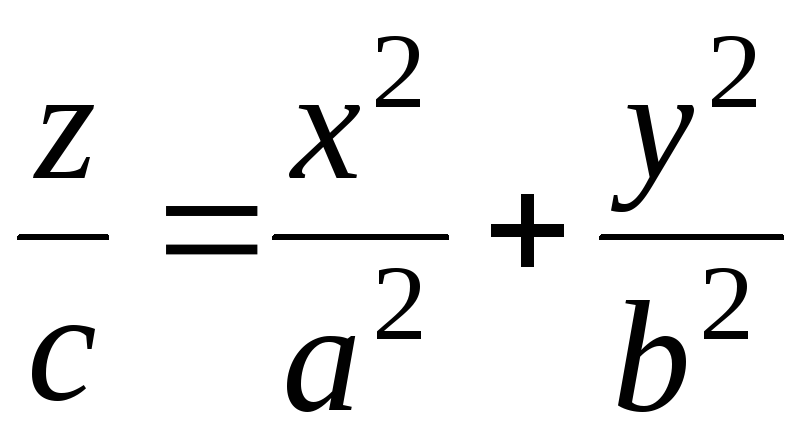 и
и 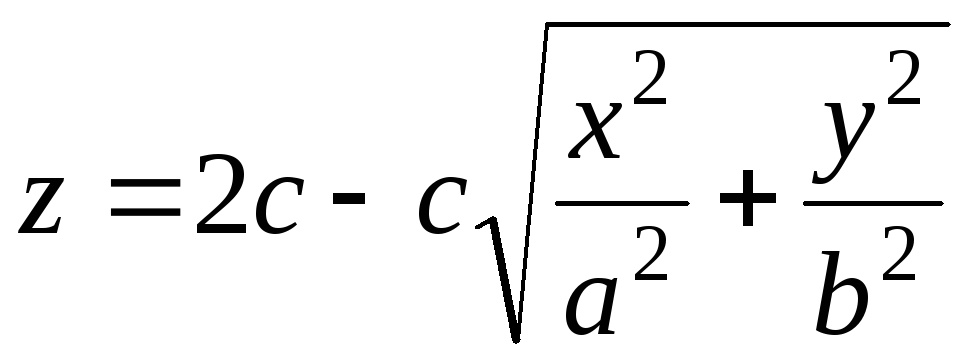 .
.
2. Найти положение
центра масс однородного полукольца 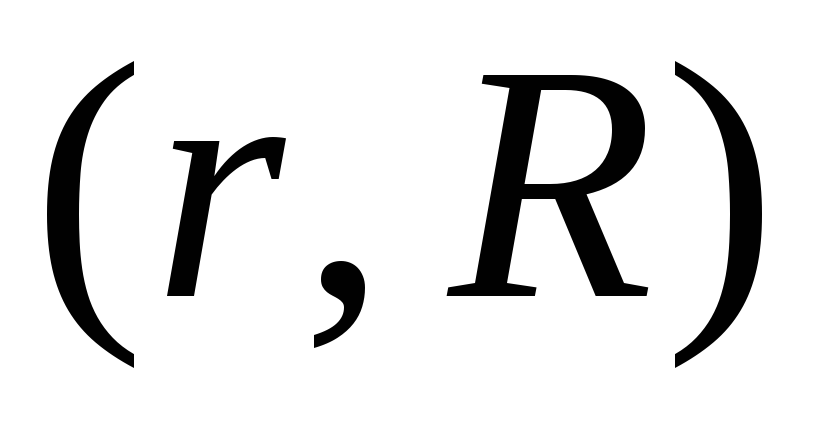 .
.
3. Поверхностная
плотность в каждой точке 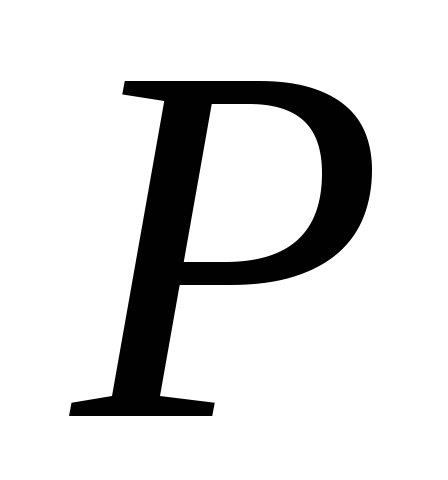 круга
круга пропор-циональна расстоянию от
пропор-циональна расстоянию от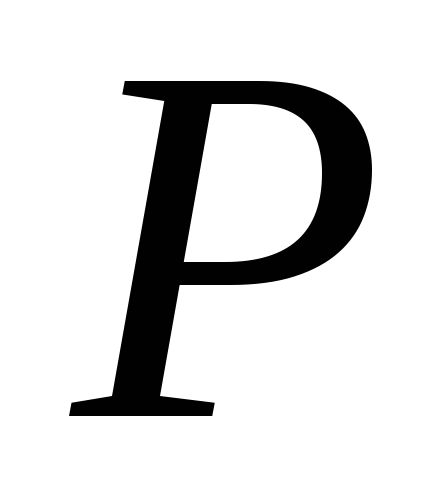 до некоторого фиксированного диаметра.
Найти момент инерции круга относительно
конца этого диаметра.
до некоторого фиксированного диаметра.
Найти момент инерции круга относительно
конца этого диаметра.
4. Найти площадь
части сферы 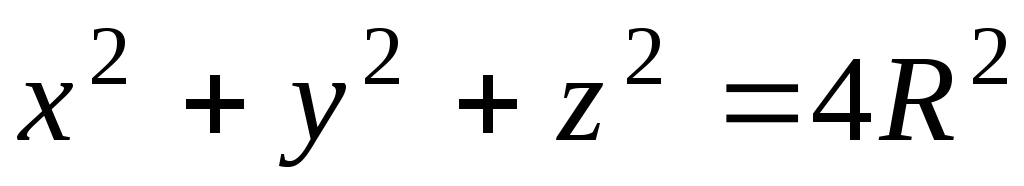 ,
расположенной внутри цилиндра
,
расположенной внутри цилиндра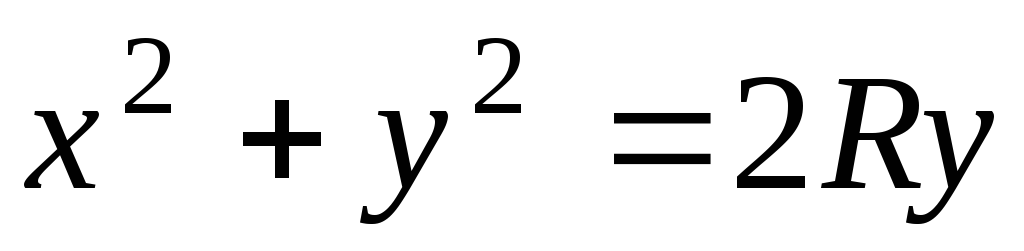 .
.