15.Момент инерции материальной точки.
Величина
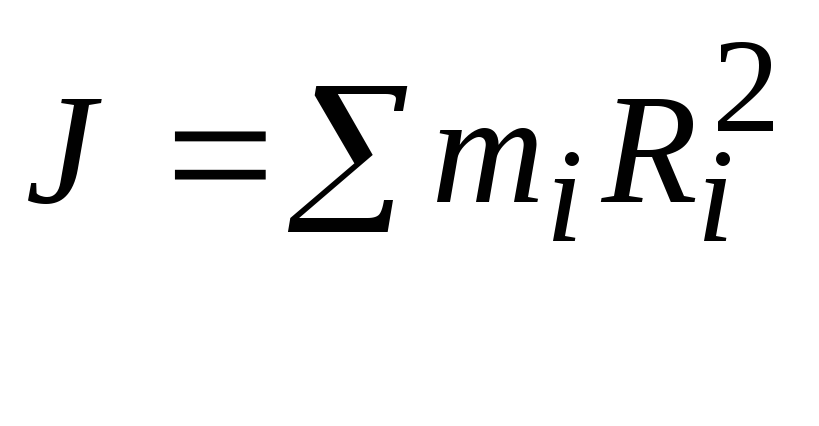
является моментом инерции тела относительно оси вращения.
Из этого выражения следует, что момент инерции вычисляется путем суммирования по всем частицам тела. В случае непрерывного распределения массы тела по его объему естественно перейти от суммирования к интегрированию, вводя плотность тела. Если тело однородно, то плотность определяется отношением массы к объему тела:
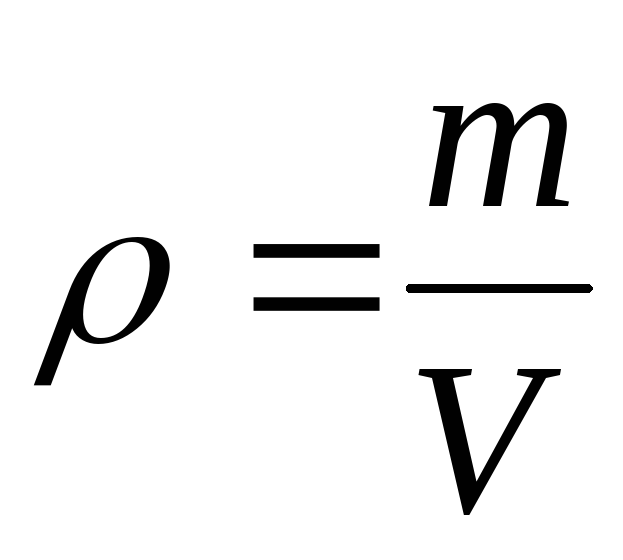 .
.
Для тела с неравномерно распределенной массой плотность тела в некоторой точке определяется производной
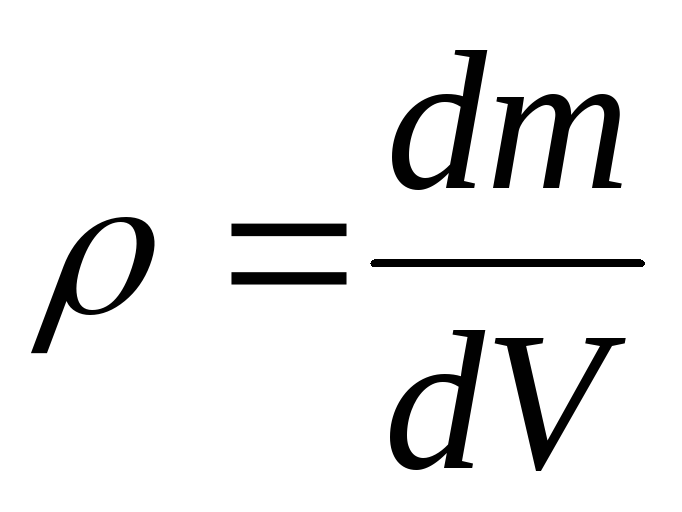 .
.
Момент инерции представим в виде:
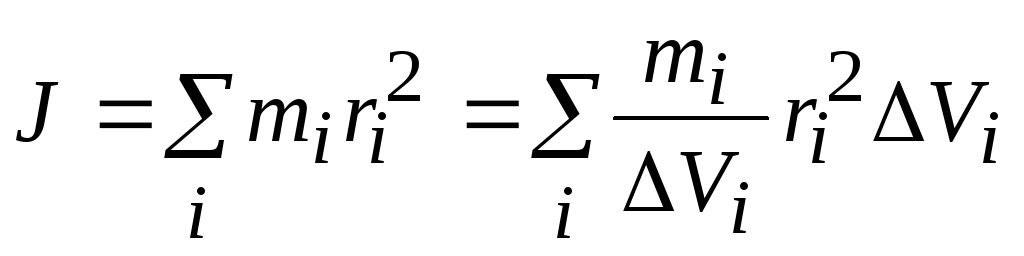 ,
,
где V — микроскопический объем, занимаемый точечной массой.
Поскольку твердое тело состоит из большого числа частиц, практически непрерывно заполняющих весь занимаемый телом объем, в выражении (1.94) микроскопический объем можно считать бесконечно малым, в то же время полагая, что точечная масса «размазана» по этому объему. Фактически мы производим сейчас переход от модели точечного распределения масс к модели сплошной среды, какой в действительности и является твердое тело благодаря большой его плотности. Произведенный переход позволяет в формуле (2.94) заменить суммирование по отдельным частицам интегрированием по всему объему тела:
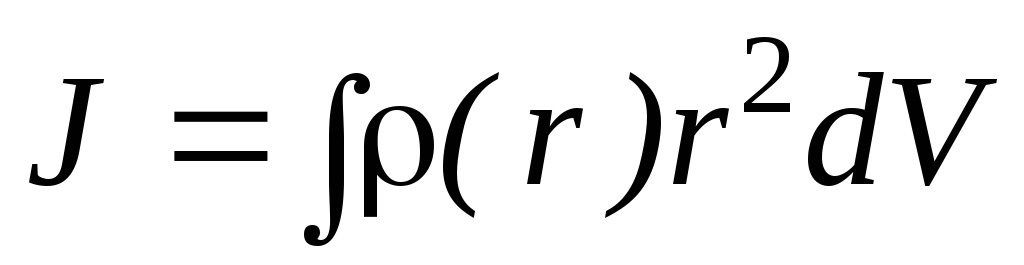 .
.
16.Момент инерции тела. Теорема Штейнера.
См. билеты номер 12 и 15.
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями:
J=J0+ma2.
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
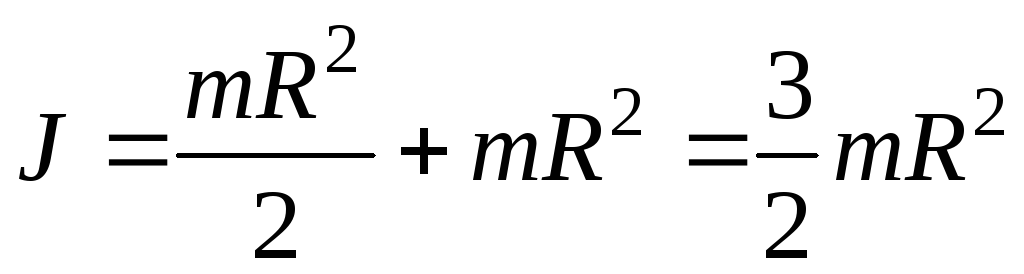
19.Момент инерции тонкого диска.
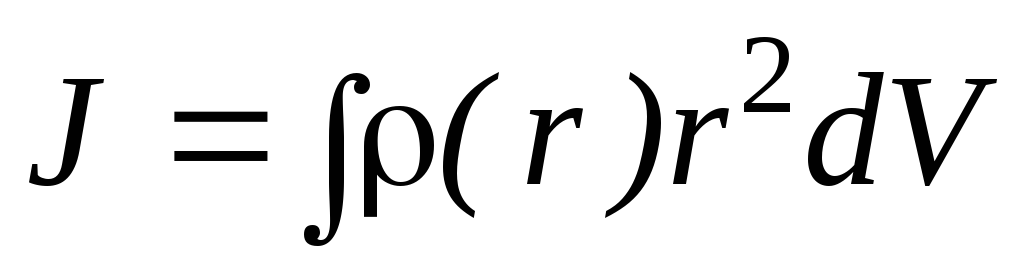 .
.
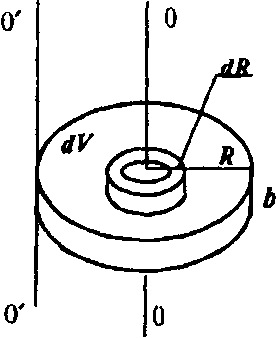
Рис. Вычисление момента инерции однородного диска
Вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.).
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
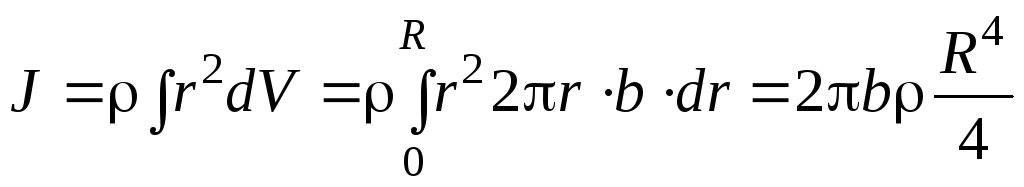 ,
,
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим:
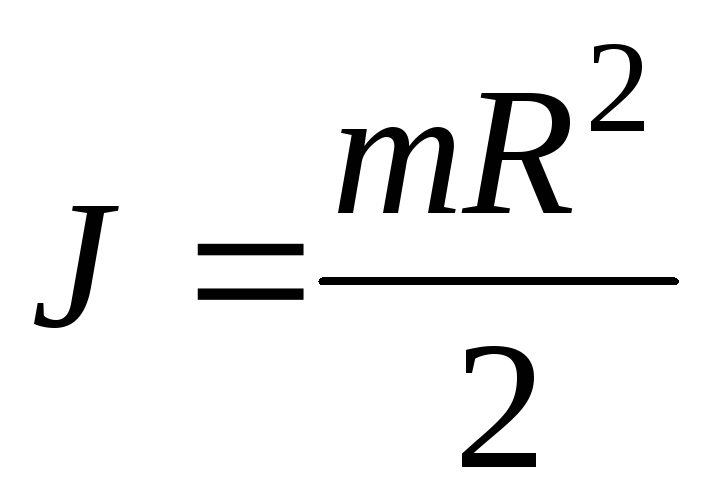 .
.
21.Поле. Силовое поле. Работа и кинетическая энергия
Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F=0.
В
отсутствие внешних сил сохраняется еще
одна скалярная величина. Если умножить
уравнение 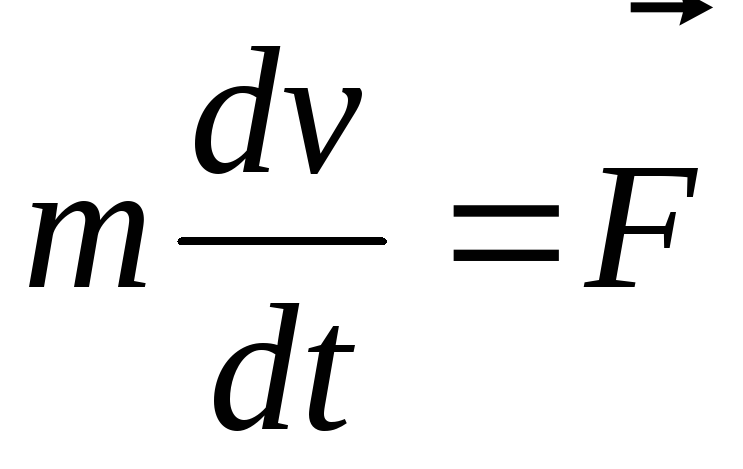
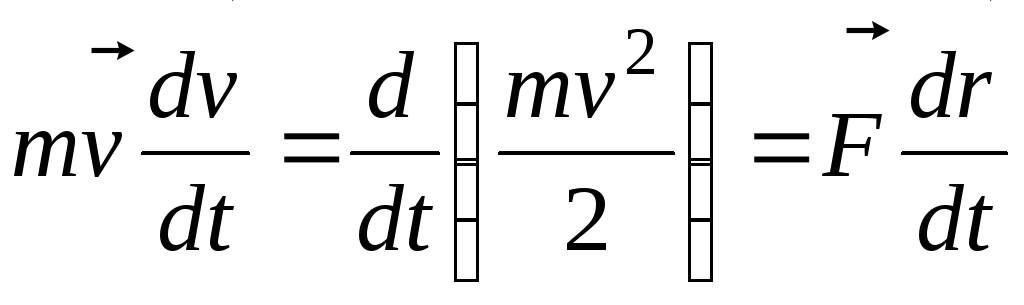 .
.
Пусть F = 0. Тогда
постоянной во время движения является
величина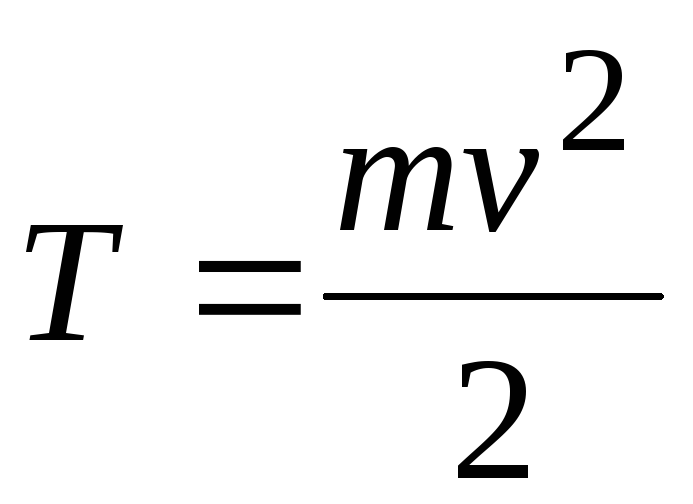
Она называется кинетической энергией частицы. При отсутствии внешних сил, т. е. в замкнутой системе, сохраняется кинетическая энергия как в случае одного тела, так и для системы тел. Когда на частицу действует внешняя сила
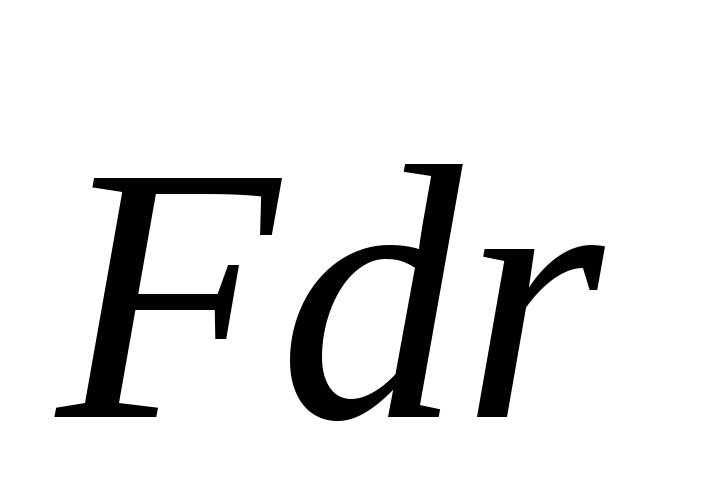 .
Величина dA =
.
Величина dA = 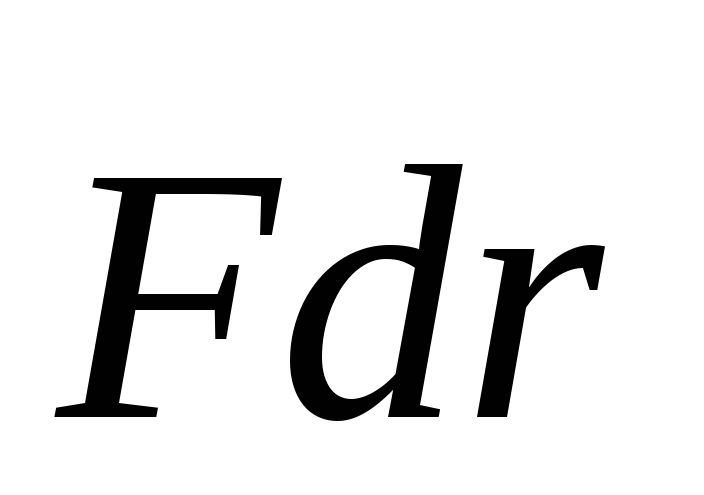 — это работа, совершаемая силой F на
пути dr .
— это работа, совершаемая силой F на
пути dr . Проинтегрируем
соотношение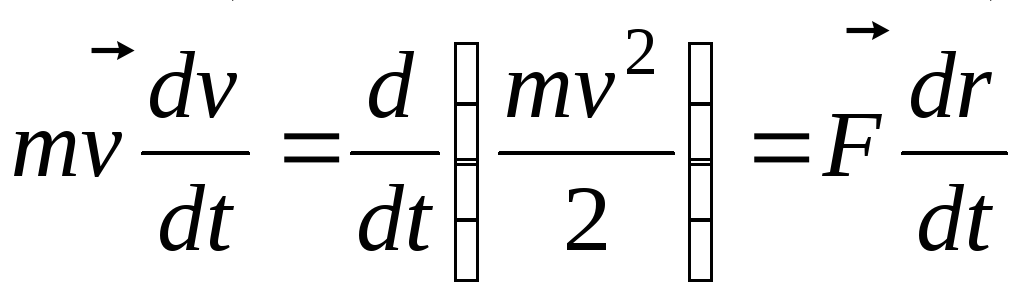 вдоль
некоторой траектории от точки 1 до точки
2:
вдоль
некоторой траектории от точки 1 до точки
2: 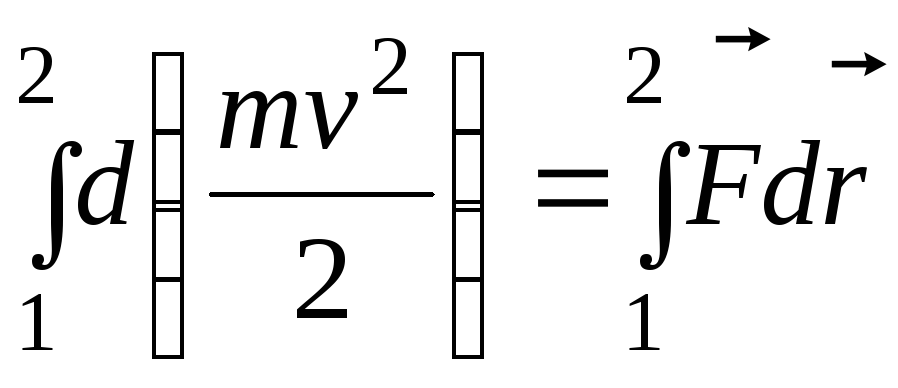
Левая
часть представляет собой приращение
кинетической энергии на пути между
точками 1 и 2, а величина 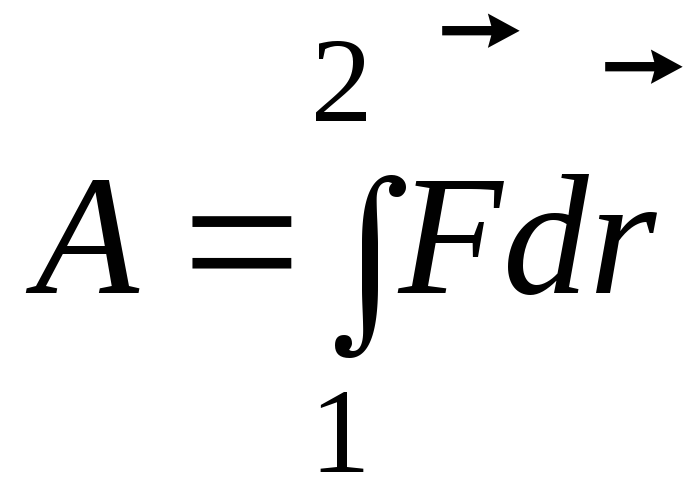 есть работа силы на пути 1—2.
есть работа силы на пути 1—2.
Таким
образом, работа сил, действующих на
частицу, расходуется на изменение ее
кинетической энергии: 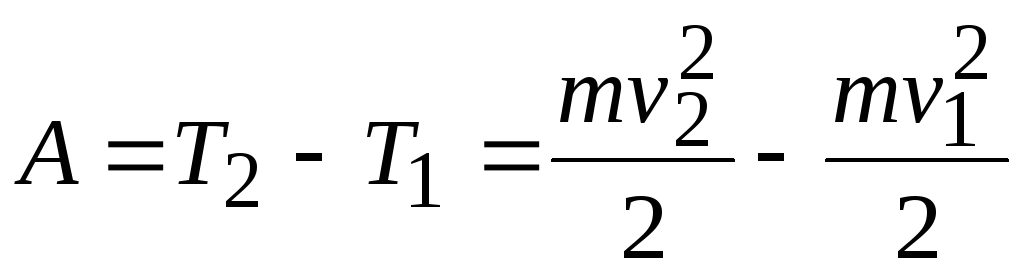
Соответственно, изменение кинетической энергии частицы служит мерой работы, произведенной над частицей.
Если частица в каждой точке пространства подвержена действию других тел, то говорят, что эта частица находится в поле сил. В случае силового поля действие силы распределено по всему пространству. Рассмотрим такое поле сил, действие которого на частицу зависит только от положения частицы в пространстве. Такое поле можно описать с помощью некоторой скалярной функции φ(
 ,
,
где постоянная определяется свойствами частицы, взаимодействующей с полем сил.
Подставим
соотношение,в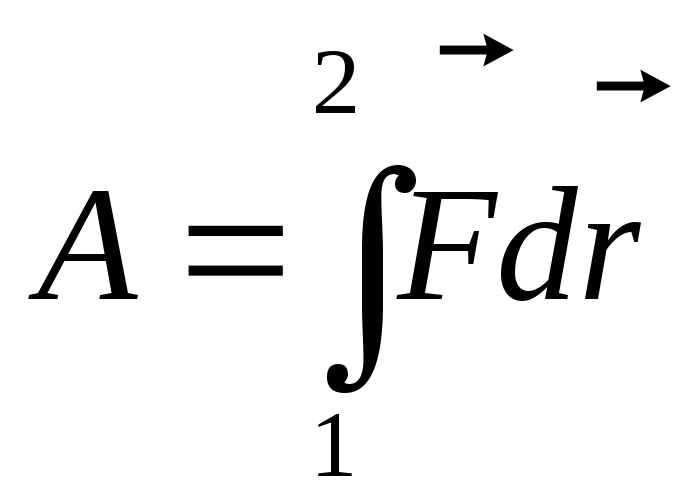 и опять проинтегрируем вдоль траектории
от точки 1 до точки 2. Получим : T2 — T1 +const(φ2 — φ1)
= О,
и опять проинтегрируем вдоль траектории
от точки 1 до точки 2. Получим : T2 — T1 +const(φ2 — φ1)
= О,
т.е. величина T2 +const·φ2 = T1 +const·φ1
остается постоянной при движении вдоль траектории. Таким образом, для частицы в потенциальном поле внешней силы сохраняется, т. е. является интегралом движения, величина
Величина U = const·φ(r) называется потенциальной энергией частицы в поле φ(r), а выражение представляет собой полную механическую энергию частицы E = T + U.
Мощность
Важнейшей инженерной динамической характеристикой является мощность, определяющая работу, совершаемую силой в единицу времени
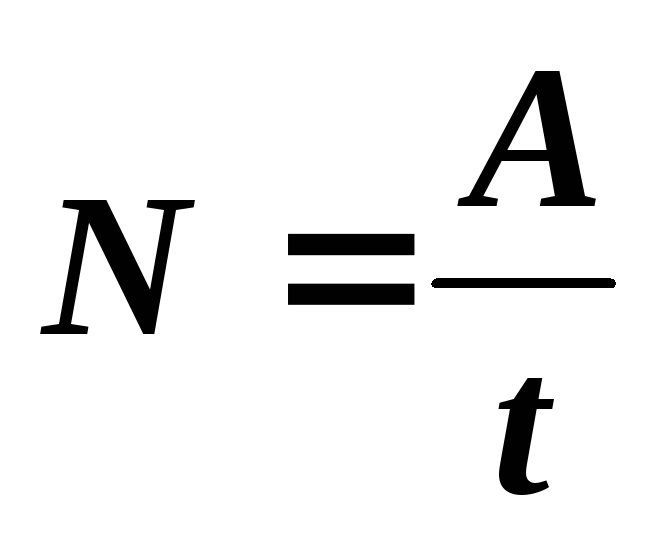
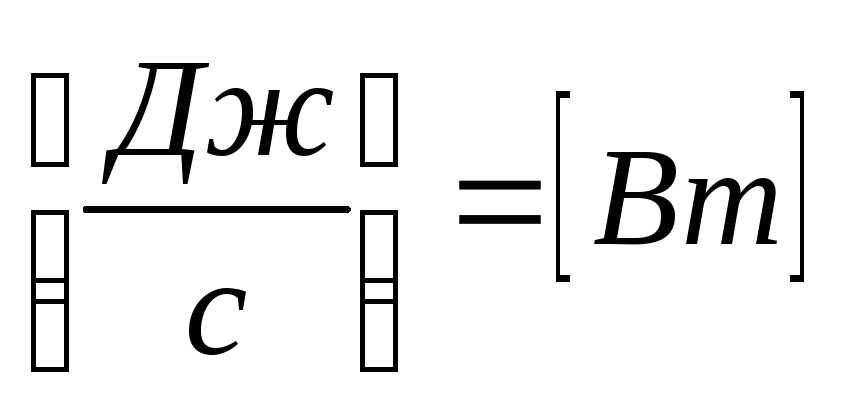 .
(53)
.
(53)Уравнение (53) справедливо для работы, совершаемой равномерно во времени. В общем случае
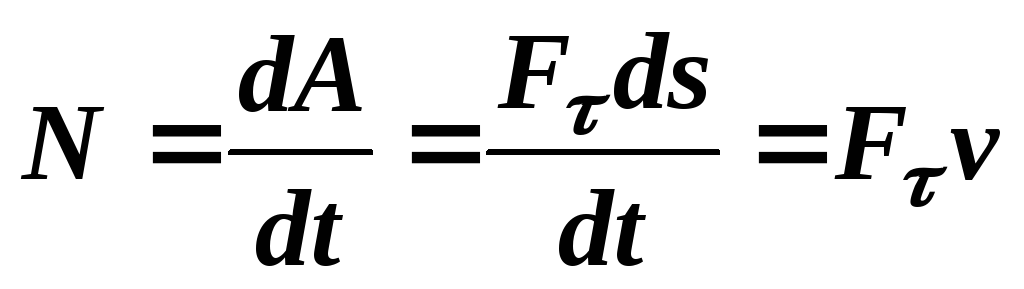 .
(54)
.
(54)
Динамика механической системы Основные определения
Механической системой называется такая совокупность материальных точек или тел, в которой положение или движение каждой точки (или тела) зависит от положения и движения всех остальных.
Любое твердое тело является механической системой.
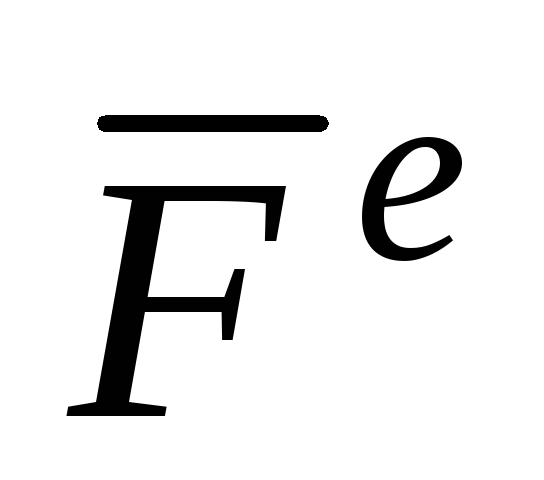 )
– это такие силы, с которыми тела, не
входящие в данную систему, действуют
на тела системы.
)
– это такие силы, с которыми тела, не
входящие в данную систему, действуют
на тела системы. Внутренние
силы системы
(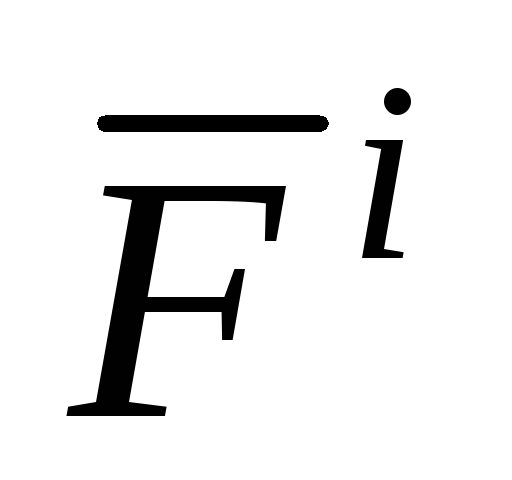 )
– это силы, с которыми тела данной
системы действуют друг на друга.
)
– это силы, с которыми тела данной
системы действуют друг на друга.
Свойства внутренних сил системы: В соответствии с третьим законом Ньютона геометрическая сумма всех внутренних сил системы всегда равна нулю, аналогично геометрическая сумма моментов всех внутренних сил системы равна нулю.
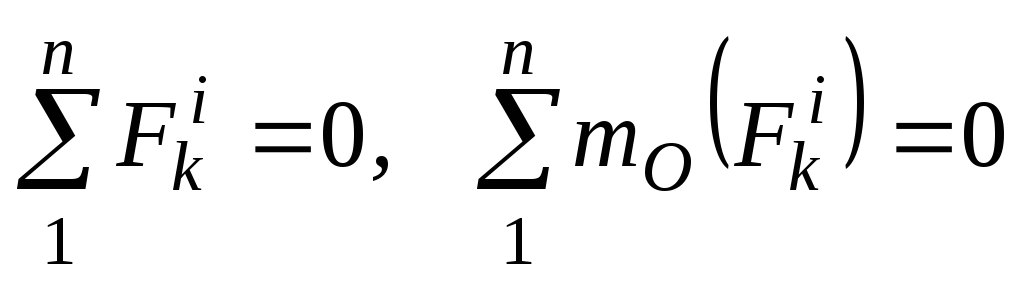
Центр масс системы – это такая точка, которая определяется уравнением
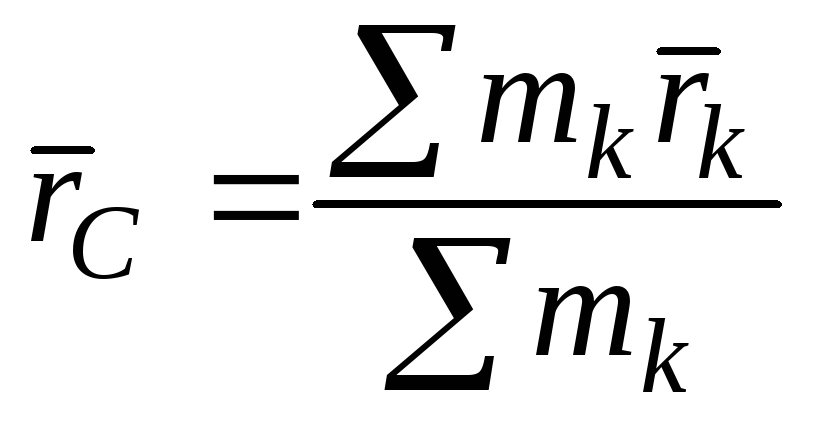 (56)
(56)
При решении задач удобно пользоваться аналитическими выражениями для нахождения центра масс
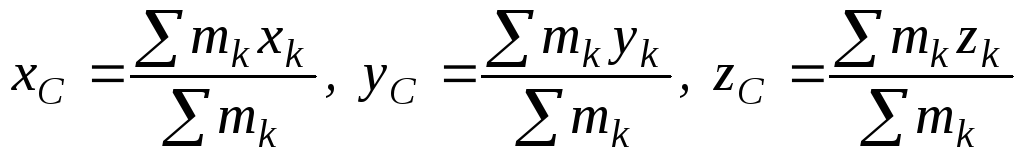 ,
(57)
,
(57)
где xC, yC, zC – координаты центра масс системы;
xk, yk, zk, mk – координаты и масса каждой точки системы;
rC, rk – радиус-вектор, проведенный соответственно в центр масс системы и каждую ее точку.
Масса системы определяется как арифметическая сумма масс всех ее точек
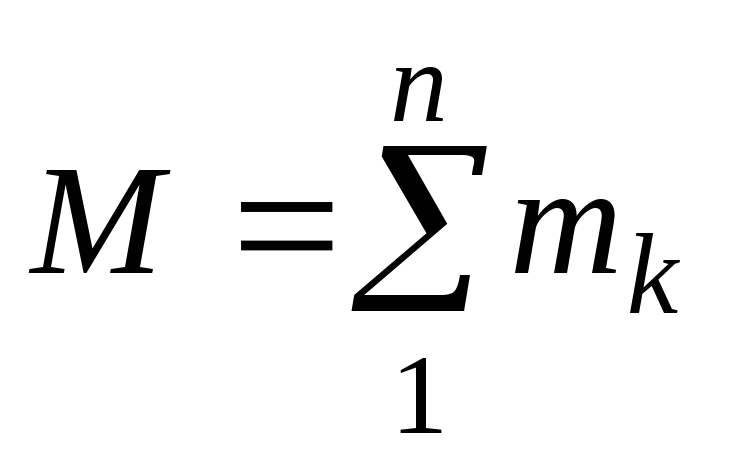 .
(58)
.
(58)
Момент инерции механической системы.
При изучении произвольного (не поступательного) движения механической системы знание массы системы и ее центра не достаточно. Необходимо знать характер распределения масс. Такая характеристика называется моментом инерции системы.
Моментом инерции системы относительно некоторого центра называется сумма произведений масс точек на квадрат их расстояния до данного центра
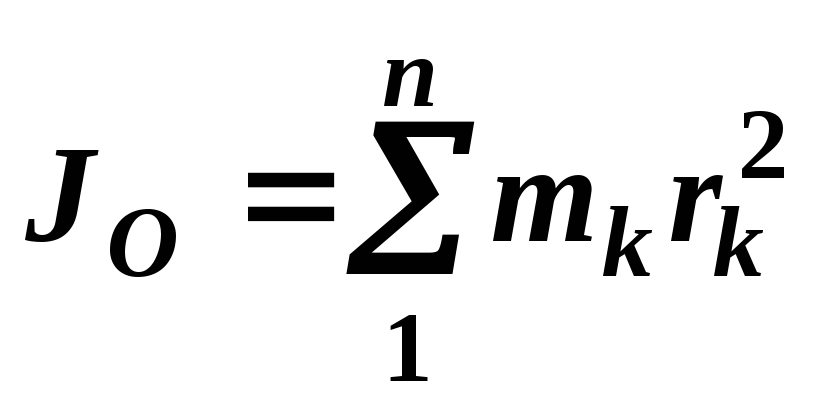 .
(59)
.
(59)
Чаще в технике используется понятие момента инерции тела относительно оси.
Моментом инерции системы относительно осиназывается арифметическая сумма произведений масс точек на квадрат их расстояний до одной оси.
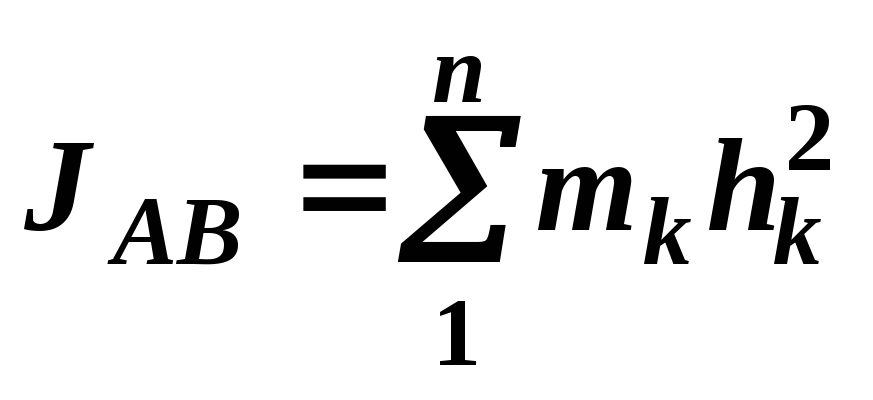
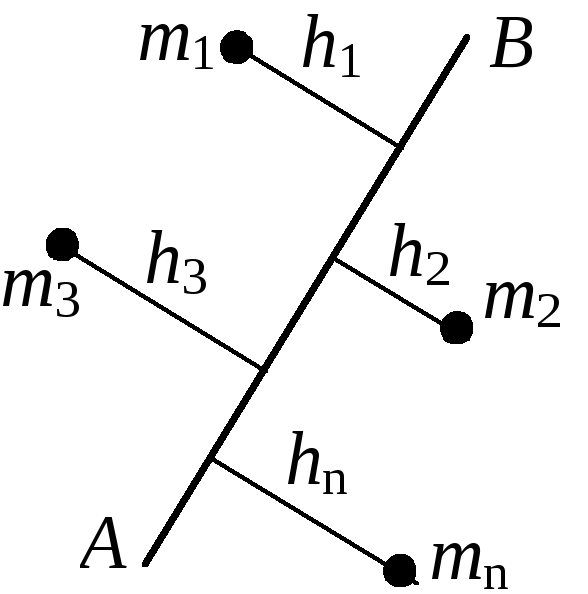 (60)
(60)
Момент инерции тела относительно координатных осей можно вычислить по следующим формулам:
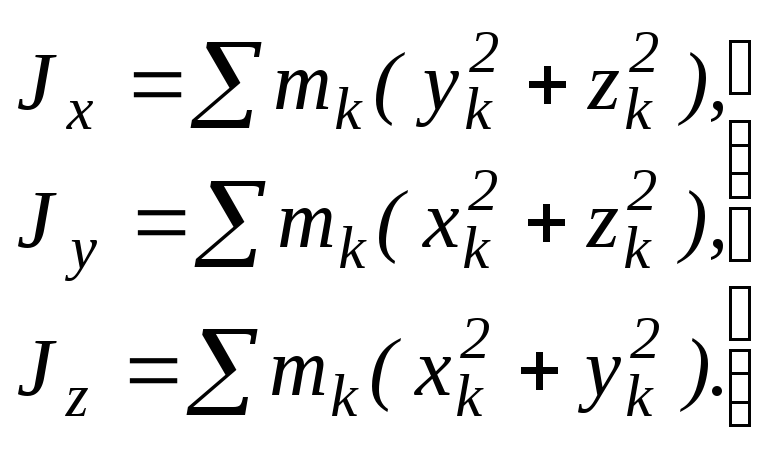 (61)
(61)
Центральным моментом инерции механической системы называется момент инерции относительно любой оси, проходящей через центр масс системы.
Значения центральных моментов инерции некоторых простейших однородных тел приводятся в справочниках.
Теорема Гюйгенса:Момент инерции тела относительно любой оси, параллельной центральной оси, равен сумме центрального момента инерции и произведения массы системы на квадрат расстояния между осями
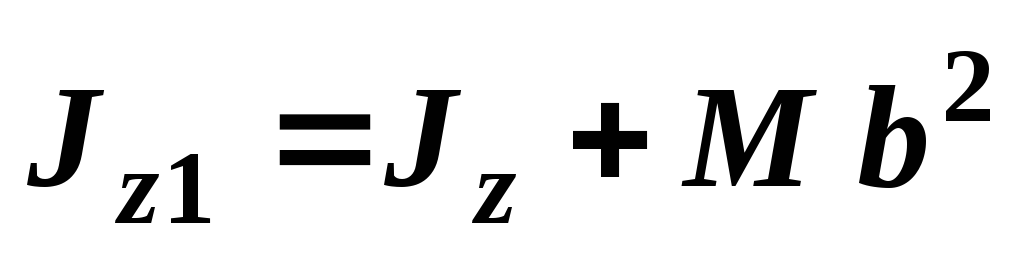 .
(62)
.
(62)
Дифференциальные уравнения движения
механической системы
Для каждой материальной точки, входящей в данную систему, на основе второго закона Ньютона можно записать следующие ОУД
(63)
где 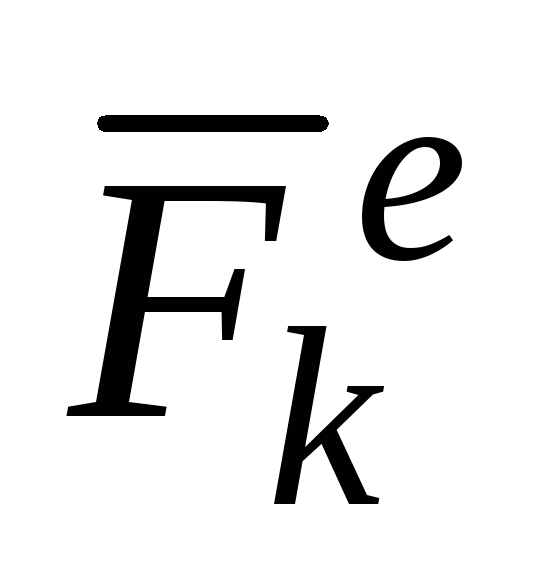
равнодействующая всех внешних сил,
приложенных к k-точке;
равнодействующая всех внешних сил,
приложенных к k-точке;
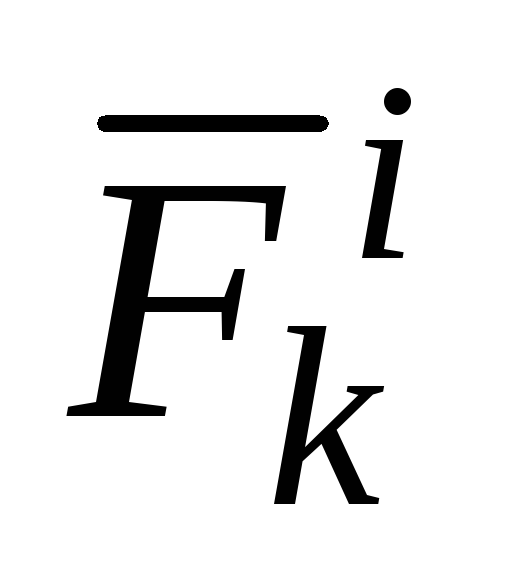 равнодействующая
всех внутренних сил приложенных к k-точке.
равнодействующая
всех внутренних сил приложенных к k-точке.
В общем случае для инженерных задач система дифференциальных уравнений (63) является нелинейной и ее аналитическое решение практически невозможно. Исследование таких систем выполняется численными методами с помощью ЭВМ.
Общие теоремы динамики механической системы
Разработаны некоторые общие приемы изучения движения механической системы, которые позволяют получить важные характеристики движения без интегрирования (63).
Теорема о движении центра масс механической системы
Перепишем уравнение (56) в следующем виде
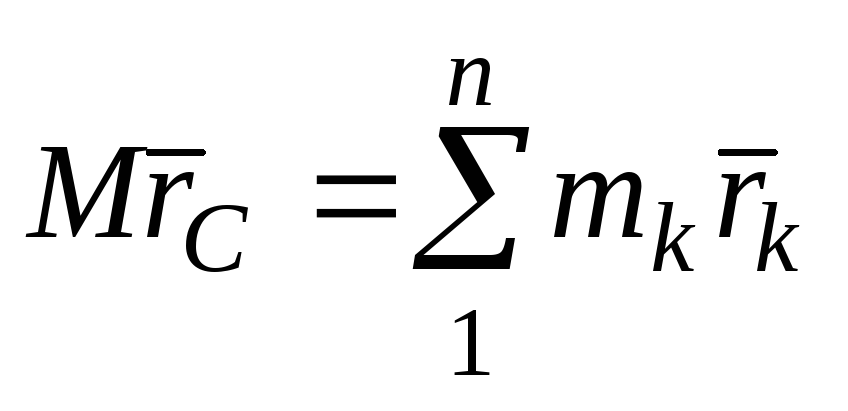 (64)
(64)
и вычислим вторую производную
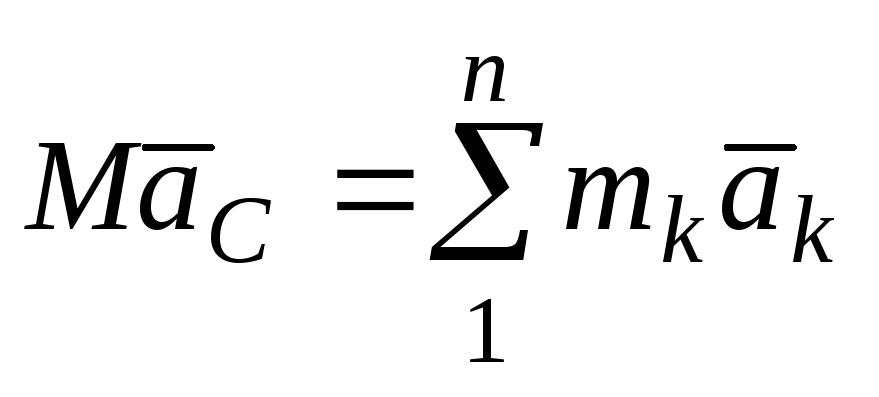 .
(65)
.
(65)
В левой части (65) произведение массы системы на ускорение центра масс. Для выяснения физического смысла правой части уравнения просуммируем почленно все уравнения (63) для материальных точек системы
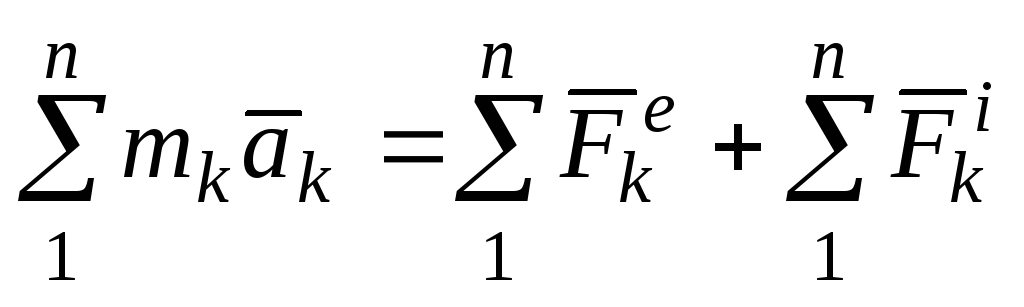 .
(66)
.
(66)
Решая совместно (65) и (66) и учитывая, что сумма всех внутренних сил системы равна нулю, получим
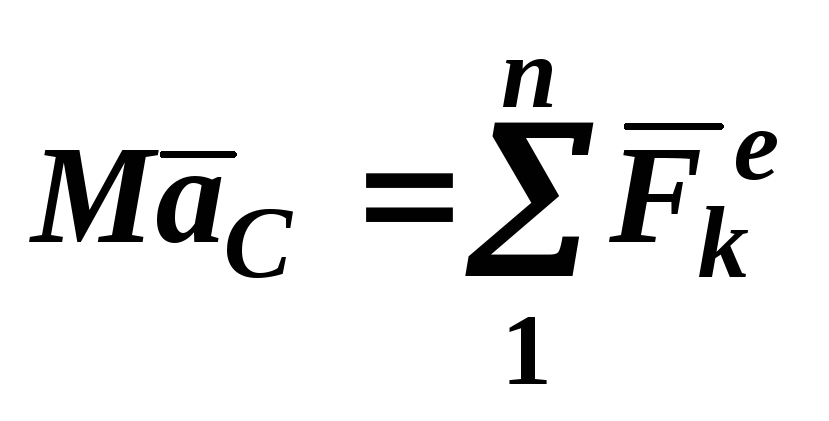 .
(67)
.
(67)
Уравнение (67) выражает следующую теорему.
Теорема: Центр масс механической системы движется как материальная точка, наделенная массой всей системы, в предположении, что все внешние силы приложены в центре масс системы.
При решении задач необходимо спроектировать (67) на координатные оси
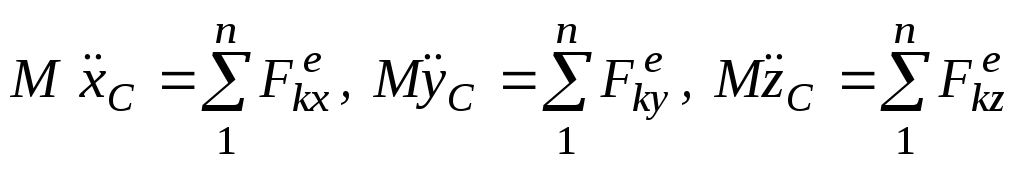 .
(68)
.
(68)
Из рассмотрения уравнений (67) и (68) вытекает закон сохранения движения центра масс системы: Если сумма всех внешних сил системы равняется нулю, то центр масс ее движется с постоянной по величине и направлению скоростью или покоится
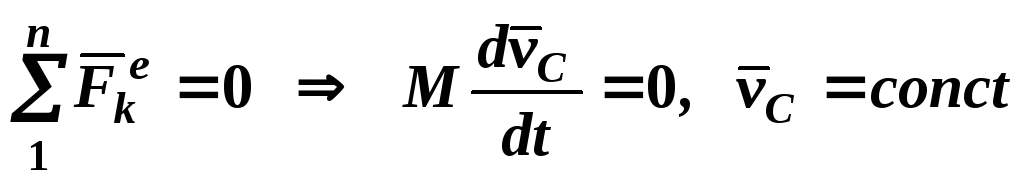 .
(69)
.
(69)
Другими словами, скорость центра масс нельзя изменить действием внутренних сил системы.
Частным случаем выполнения закона (69) является равенство нулю суммы проекций сил на одну из координатных осей, в этом случае центр масс вдоль этой оси не перемещается или движется с постоянной скоростью.
Момент инерции материальной точки, системы материальных точек, твердого тела. Теорема Штейнера. Основной закон динамики вращательного движения.
Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: — масса i-й точки, — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
Моментом инерции системы материальных точек (или тела) относительно полюса (точки) называют алгебраическую сумму произведений масс м.т., из которых состоит тело, на квадрат расстояния их до полюса 0.
При непрерывном распределении массы по объему тела момент инерции относительно полюса
— момент инерции твердого тела относительно оси.
Теорема Штейнера:
Момент инерции твёрдого тела вокруг произвольной оси равен моменту инерции тела вокруг оси, проходящей через центр массы данного тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями.
Основной закон динамики вращательного движения.
Момент силы— векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр.
Основным законом динамики вращательного движения является связь момента силы М с моментом инерции и угловым ускорением β:
Работа постоянной и переменной силы. Элементарная работа внешних сил при вращении твердого тела.
A = |F|·|S|·cosa = (F·S)
Работа постоянной силы равняется скалярному произведению силы на перемещение.
Единица измерения работы — Джоуль. 1 Дж = 1 Н·м.
Работа переменной силы
Пусть тело движется прямолинейно с равномерной силой под углом £ к направлению перемещения и проходит расстояние S/ Работой силы F называется скалярная физическая величина, равная скалярному произведению вектора силы на вектора перемещения. A=F·s·cos £. А=0, если F=0, S=0, £=90º. Если сила непостоянная (изменяется), то для нахождения работы следует разбивать траекторию на отдельные участки. Разбиение можно производить до тех пор, пока движение не станет прямолинейным, а сила постоянной │dr│=ds.. Работа, совершенная силой на данном участке определяется по представленной формуле dA=F· dS· cos £= = │F│·│dr│· cos £=(F;dr)=Ft·dS A=F·S· cos £=Ft·S . Таким образом работа переменной силы на участке траектории равна сумме элементарных работ на отдельных малых участках пути A=SdA=SFt·dS= =S(F·dr).
Момент инерции материальной точки. — Студопедия.Нет
Величина
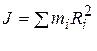
является моментом инерции тела относительно оси вращения.
Из этого выражения следует, что момент инерции вычисляется путем суммирования по всем частицам тела. В случае непрерывного распределения массы тела по его объему естественно перейти от суммирования к интегрированию, вводя плотность тела. Если тело однородно, то плотность определяется отношением массы к объему тела:
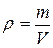 .
.
Для тела с неравномерно распределенной массой плотность тела в некоторой точке определяется производной
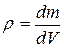 .
.
Момент инерции представим в виде:
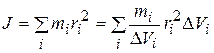 ,
,
где DV — микроскопический объем, занимаемый точечной массой.
Поскольку твердое тело состоит из большого числа частиц, практически непрерывно заполняющих весь занимаемый телом объем, в выражении (1.94) микроскопический объем можно считать бесконечно малым, в то же время полагая, что точечная масса «размазана» по этому объему. Фактически мы производим сейчас переход от модели точечного распределения масс к модели сплошной среды, какой в действительности и является твердое тело благодаря большой его плотности. Произведенный переход позволяет в формуле (2.94) заменить суммирование по отдельным частицам интегрированием по всему объему тела:
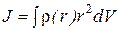 .
.
16.Момент инерции тела. Теорема Штейнера.
См. билеты номер 12 и 15.
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями:
J=Jс+ma^2.
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
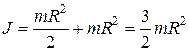
Определение момента инерции тонкого стержня
Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых 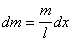 . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции
. Если выбранный элемент находится на расстоянии x от оси, то его момент инерции 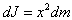 , т.е.
, т.е. 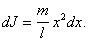
Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим
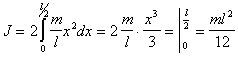 (п.1)
(п.1)
Момент инерции тонкого диска.
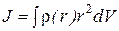 .
.
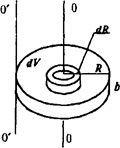
Вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.).
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
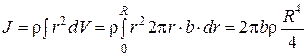 ,
,
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим: 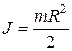 .
.
Момент инерции шара.
Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).
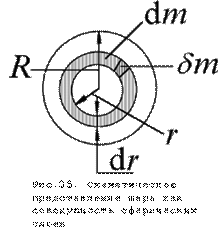
Рассмотрим малый элемент сферического слоя delta m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя —delta Jx, delta Jy, delta Jz, равны 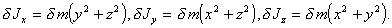
Т. е. можно записать 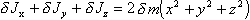 (п.26)
(п.26)
Так как для элементов сферического слоя x2+y2+z2=r2 то 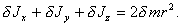
После интегрирования по всему объему слоя получим 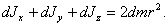 (п.27)
(п.27)
Так как, в силу симметрии для сферического слоя dJx=dJy=dJz=dJ , а 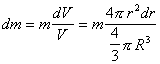 , то
, то 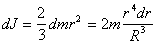
Интегрируя по всему объему шара, получаем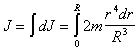
Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен 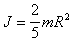 (п.28)
(п.28)
21.Поле. Силовое поле. Работа и кинетическая энергия
Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F=0.
В отсутствие внешних сил сохраняется еще одна скалярная величина. Если умножить уравнение 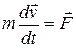 одновременно слева и справа на вектор скорости, в левой части окажется производная от полного дифференциала, и уравнение примет вид
одновременно слева и справа на вектор скорости, в левой части окажется производная от полного дифференциала, и уравнение примет вид
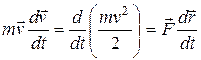 .
.
Пусть F = 0. Тогда постоянной во время движения является величина 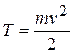
Она называется кинетической энергией частицы. При отсутствии внешних сил, т. е. в замкнутой системе, сохраняется кинетическая энергия как в случае одного тела, так и для системы тел. Когда на частицу действует внешняя сила F, кинетическая энергия не остается постоянной. В этом случае приращение кинетической энергии за время dt равно скалярному произведению 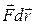 . Величина dA =
. Величина dA = 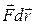 — это работа, совершаемая силой F на пути dr .
— это работа, совершаемая силой F на пути dr .
Проинтегрируем соотношение 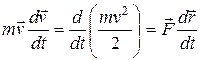 вдоль некоторой траектории от точки 1 до точки 2:
вдоль некоторой траектории от точки 1 до точки 2: 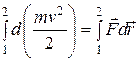
Левая часть представляет собой приращение кинетической энергии на пути между точками 1 и 2, а величина 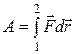 есть работа силы на пути 1—2.
есть работа силы на пути 1—2.
Таким образом, работа сил, действующих на частицу, расходуется на изменение ее кинетической энергии: 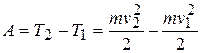
Соответственно, изменение кинетической энергии частицы служит мерой работы, произведенной над частицей.
Если частица в каждой точке пространства подвержена действию других тел, то говорят, что эта частица находится в поле сил. В случае силового поля действие силы распределено по всему пространству. Рассмотрим такое поле сил, действие которого на частицу зависит только от положения частицы в пространстве. Такое поле можно описать с помощью некоторой скалярной функции φ(r), зависящей, а соответствии со сказанным, только от координат. Это случай специального, но часто встречаемого в природе потенциального поля, а функция φ(r), характеризующая поле, является потенциалом поля. Сила связана с потенциалом в каждой точке соотношением
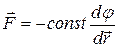 ,
,
где постоянная определяется свойствами частицы, взаимодействующей с полем сил.
Подставим соотношение 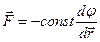 ,в
,в 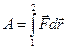 и опять проинтегрируем вдоль траектории от точки 1 до точки 2. Получим : T 2— T 1+const(φ2 — φ1) = О,
и опять проинтегрируем вдоль траектории от точки 1 до точки 2. Получим : T 2— T 1+const(φ2 — φ1) = О,
т.е. величина T 2+const ·φ2 = T 1+const ·φ1
остается постоянной при движении вдоль траектории. Таким образом, для частицы в потенциальном поле внешней силы сохраняется, т. е. является интегралом движения, величина E = T+const·φ(r).
Величина U = const·φ(r) называется потенциальной энергией частицы в поле φ(r), а выражение представляет собой полную механическую энергию частицы E = T + U.
Работа и энергия.
Работа равнодействующей силы на элементарное перемещение частицы ведет к приращению ее кинетической энергии (теорема о кинетической энергии): 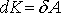
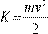
В случае конечного перемещения частицы, будем иметь 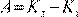
 ,
,
т.е. работа равнодействующей силы, действующей на частицу, независимо от природы этой силы, равна приращению кинетической энергии частицы. Если работа положительна, то кинетическая энергия частицы возрастает. Силы сопротивления уменьшают кинетическую энергию частицы.
Рассмотрим механическую систему, состоящую из n частиц, которые имеют кинетические энергии 
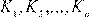
 .
.
Кинетическая энергия i-той частицы равна работе равнодействующей силы, действующей на эту частицу: 
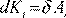
 . Полная работа сил, действующих на систему, будет
. Полная работа сил, действующих на систему, будет
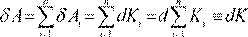 ,
,
где величина 
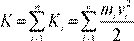
 есть сумма кинетических энергий составляющих систему частиц, и называется кинетической энергией системы. Следовательно, полная работа сил, действующих в системе, равна приращению ее кинетической энергии.
есть сумма кинетических энергий составляющих систему частиц, и называется кинетической энергией системы. Следовательно, полная работа сил, действующих в системе, равна приращению ее кинетической энергии.
Диссипативные силы, их работа.
Действующие в системе силы мы разделяем на внешние и внутренние, а по характеру совершаемой ими работы — на консервативные и неконсервативные силы. Работу консервативных сил всегда можно представить в виде убыли скалярной функции — потенциальной энергии, зависящей от координат.
К классу неконсервативных сил относятся диссипативные силы.
Диссипативные силы – это силы трения и сопротивления. Выяснение физической природы диссипативных сил выходит за рамки механики. Отметим только, что это сложно устроенные силы электромагнитной природы. Так что, здесь мы ограничимся изложением экспериментально полученных законов трения.
В отличие от сил упругости, кулоновских сил и сил всемирного тяготения, которые зависят только от взаимного положения взаимодействующих частиц, силы трения зависят от относительных скоростей диссипативно взаимодействующих тел. Любую силу диссипативного взаимодействия можно представить в виде 
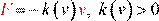
 ,
,
где 

 – относительная скорость взаимодействующих тел, а
– относительная скорость взаимодействующих тел, а 
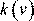
 – положительная функция. Диссипативная сила всегда направлена обратно относительному движению тел.
– положительная функция. Диссипативная сила всегда направлена обратно относительному движению тел.
Диссипативные силы также можно делить на внешние и внутренние. Например, в случае движения автомобиля, силы, действующие на него со стороны воздуха и покрытия дороги, это внешние диссипативные силы, а силы трения, действующие во внутренних узлах автомобиля — внутренние диссипативные силы.
Работа внешних диссипативных сил, в зависимости от выбранной системы отсчета, может быть как положительной, так и отрицательной.
Независимо от выбора системы отсчета, работа внутренних диссипативных сил всегда отрицательна.
Полная работа, совершенная в системе диссипативными силами, есть сумма работ всех парных сил диссипативного взаимодействия: 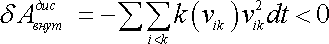
Заметим, что в разных системах отсчета результаты, полученные для работы внутренних диссипативных сил, совпадают 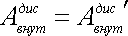
Кинетическая энергия
Про тела, которые могут совершать работу, говорят, что они обладают энергией. Энергией называют скалярную физическую величину, показывающую, какую работу может совершить тело. Энергия равна той максимальной работе, которую тело может совершить в данных условиях. Механическая работа является мерой изменения энергии в различных процессах. Поэтому энергию и работу выражают в одних и тех же единицах (в СИ — в джоулях). В более общем смысле энергия — это единая мера разных форм движения материи, а также мера перехода движения материи из одной формы в другую. Для характеристики конкретных форм движения материи используют понятия о соответствующих видах энергии: механической, внутренней, электромагнитной и т. д. Механическая энергия является характеристикой движения и взаимодействия тел. Она зависит от скоростей и взаимного расположения тел.
Кинетическая энергия
Рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v1 до v2.
Как было отмечено в §17, работу постоянной силы вычисляют по формуле А=Fscosa. Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то cosa=1 и А=Fs. По второму закону Ньютона F=ma. В § 2 было показано, что для прямолинейного равноускоренного движения справедлива формула
v2=vo2+2as.
Из этой формулы при vо=v1 и v=v2 Следует, что
s=(v22-v12)/2a.
Подставив значения F и s в формулу работы, получим
А=mv22/2-mv12/2 (3.12).
Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины mv22/2.
Выше отмечалось, что механическая работа есть мера изменения энергии. Следовательно, в правой части формулы (3.12) стоит разность двух значений энергии данного тела. Это значит, что величина mv22/2 представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается Wк. Следовательно,
Wк=mv22/2. (3.13)
С учетом (3.13) формулу (3,12) можно записать в виде
А=Wk2-Wk1=DWk, (3.14)
т.е. работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела.
Когда направление силы совпадает с направлением перемещения тела, работа силы положительна (т.е. A>0). Из формулы (3.14) видно, что в этом случае Wk2-Wk1>0, т.е. Wk2>Wk1. Следовательно, когда сила совершает положительную работу, кинетическая энергия тела увеличивается. Когда же направление силы противоположно направлению перемещения, то A<0 и Wk2-Wk1<0, т.е. Wk2<Wk1. Следовательно, когда сила совершает отрицательную работу, кинетическая энергия тела уменьшается.
Потенциальная энергия
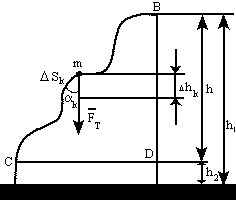 Определим работу, совершаемую силой тяжести Fт при переносе материальной точки массой m по криволинейной траектории ВС из одной точки В поля тяготения Земли в другую точку С (рис 31). Для этого разобьем траекторию движения тела на сколь угодно малые участки Dsk, каждый из которых можно считать прямолинейным.
Определим работу, совершаемую силой тяжести Fт при переносе материальной точки массой m по криволинейной траектории ВС из одной точки В поля тяготения Земли в другую точку С (рис 31). Для этого разобьем траекторию движения тела на сколь угодно малые участки Dsk, каждый из которых можно считать прямолинейным.
На произвольно выбранном таком участке сила тяжести Fт составляет с перемещением Dsk угол ak. Поэтому на данном участке работа силы тяжести
DAk=Fт·Dsk·cos(ak). (3.15)
Спроецируем участок Dsk на вертикаль BD. Его проекция
Dhk=Dsk·cos(ak). (3.16)
Из (3.15) и (3.16) имеем DAk=Fт·Dhk. Очевидно, что работа ABC силы тяжести Fт на всем пути ВС равна сумме элементарных работ Dhk на всех участках Dsk этого пути:
ABC=Fт(h1-h2)=mgh1-mgh2 (3.17)
Из последней формулы видно, что работа силы тяжести при переносе материальной точки массой m в поле тяготения Земли равна разности двух значений некоторой величины mgh. Поскольку работа есть мера изменения энергии, то в правой части формулы (3.17) стоит разность двух значений энергии этого тела. Это значит, что величина mgh представляет собой энергию, обусловленную положением тела в поле тяготения Земли.
Энергию, обусловленную взаимным расположением взаимодействующих между собой тел (или частей одного тела), называют потенциальной и обозначают Wп. Следовательно, для тела, находящегося в поле тяготения Земли,
Wп=mgh. (3.18)
С учетом (3.18) формулу (3.17) можно записать в виде
ABC=Wп1-Wп2=-(Wп2-Wп1)=-DWп (3.19)
т. е. работа силы тяжести равна изменению потенциальной энер-гии тела, взятому с противоположным знаком.
Из рис. видно, что работа ABD, совершаемая силой тяжести при перемещении материальной точки массой m из точки B в точку D по вертикали ВD, составляет ABC=mgh1-mgh2. Следовательно, ABD=ABC. Таким образом, работа силы тяжести не зависит от траектории движения тела, а определяется лишь положением в поле тяготения Земли начальной и конечной точек перемещения тела.
В § 12 отмечалось, что силы, работа которых не зависит от траектории движения тела, называют консервативными, а поле таких сил называется потенциальным. Сила тяжести является консервативной, а поле тяготения — потенциальным. Из формулы (3.19) следует, что работа консервативных сил равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Следует отметить, что тела имеют потенциальную энергии не только вследствие их притяжения к Земле. В § 10 было показано, что в результате упругой деформации тело тоже приобретает потенциальную энергию. Если, например, сжимается или растягивается упругая пружина, то ее потенциальная энергия вычисляется по формуле Wп=kх2/2, где k — жесткость пружины, x — ее удлинение, т.е. смещение точки приложения силы упругости.
Работа силы упругости определяется по формуле
A=Wп1-Wп2= kх12/2- kх22/2=-DWп (3.20)
Сумму кинетической и потенциальной энергии тела называют полной механической энергией этого тела и обозначают W.
W=Wп+Wk (3.21)
Момент инерции — это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
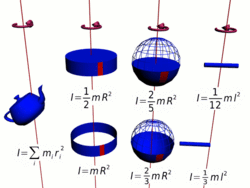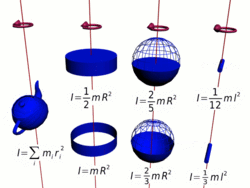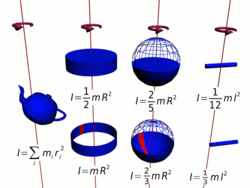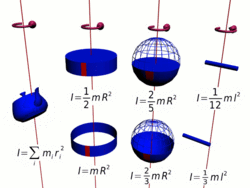 Осевые моменты инерции некоторых тел.
Осевые моменты инерции некоторых тел.Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

