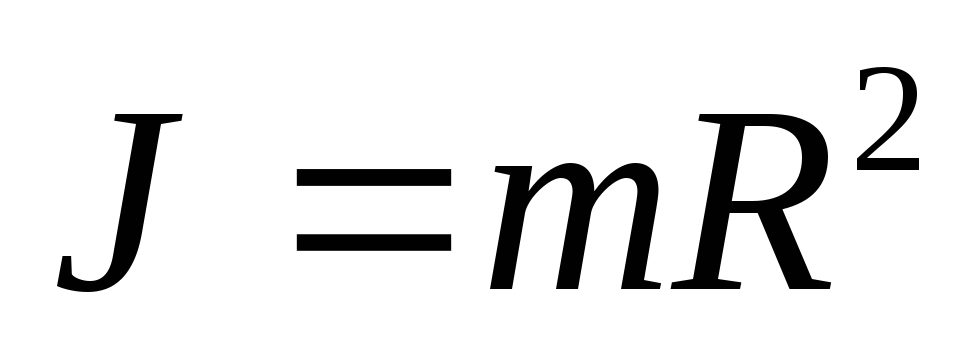относительно оси вращения, материальной точки и твердых тел
В статье узнаете что такое момент инерции, как влияет ось вращения, а также момент вращения для материальной точки, множества частиц и для твердых тел.
Момент инерции, обозначенный буквой I, является физической величиной, характерной для вращательного движения тела. Это значение предполагает постоянное значение для данного тела и конкретной оси его вращения. Величина момента инерции зависит от веса тела, положения оси вращения, вокруг которой вращается тело и распределения его массы. Поэтому можно написать, что момент инерции тела информирует нас о том, как масса вращающегося тела распределяется вокруг фиксированной оси его вращения. Чем выше значение момента инерции, тем сложнее установить или изменить вращательное движение данного тела (например, уменьшить или увеличить его угловую скорость).
Момент инерции тела относительно оси вращения

На следующем рисунке показано, как выбор оси вращения тела влияет на значение момента его инерции и, следовательно, на легкость/сложность его вращения. На рисунках а) и б) показан однородный цилиндр с радиусом r и высотой h, который вращается вокруг продольной оси (рисунок а) и вокруг оси, перпендикулярной цилиндру, проходящему через его центр (рисунок б).
Ролик с радиусом r и высотой h вращается вокруг продольной оси (рисунок а) и оси, перпендикулярной цилиндру, проходящему через его центр (рисунок б)). Вес ролика в случае а) гораздо более сфокусирован вблизи его оси вращения, чем в случае б), поэтому цилиндр с рисунка а) вращать легче, чем ролик с рисунка б).
В обоих случаях мы имеем дело с одним и тем же телом, но в первом случае (рис. А) легче вращать ролик. Причиной такой ситуации является различное распределение веса цилиндра вокруг его оси вращения: при вращении цилиндра вокруг продольной оси масса ролика более сфокусирована вблизи оси вращения, чем во второй. В результате получается меньшее значение момента инерции цилиндра из рисунка а), а не цилиндра из рисунка б).
Если вы не хотите читать всю информацию советуем вам посмотреть видео про момент силы, в котором вы узнаете абсолютно все:
Момент инерции материальной точки

Чтобы вычислить момент инерции и вращение отдельной частицы вокруг заданной оси вращения, используем следующее выражение:
где m — масса частицы, r — расстояние частицы от оси вращения.
Момента инерции измеряется в кг ⋅ м2 в системе СИ.
Момент инерции сложного тела с частицами
Момент инерции тела, состоящего из n частиц, равен сумме моментов инерции каждой частицы относительно данной оси вращения.

Например, для тела, состоящего из четырех частиц, имеем:

где m1, m2, m3 и m4 — массы частиц, которые составляют тела, r1, r2, r3 и r4, расстояние от оси вращения соответственно частиц с массами m1, m2, m3 и m4.
Момент инерции твердого тела
Когда тело состоит из очень многих частиц, расположенных близко друг к другу, сумма моментов инерции в приведенном выше уравнении заменяется интегралом. Если расширенное тело разделено на бесконечно малые элементы с массой dm, удаленной от оси вращения на величину r, момент инерции I будет равен:

На следующем рисунке показаны выбранные расширенные тела с их моментами инерции, рассчитанными для осей вращения, указанных на чертежах.
Момент инерции обода

Момент инерции обода будет равен I=mr2
Момент инерции шара

Момент инерции шара будет равен I=2/5mr2
Момент инерции сферы

Момент инерции сферы будет равен I=2/3mr2
Момент инерции к оси цилиндра

Момент инерции к оси цилиндра будет равен I=1/2mr2
Момент инерции к оси через центр цилиндра

Момент инерции к оси цилиндра, проходящей через центр цилиндра будет равен I=1/4mr2+1/12mh2
Момент инерции к оси перпендикулярной поверхности пластины

Момент инерции к оси перпендикулярной поверхности пластины, которая проходит через ее центр будет равен I=1/12m(x2+y2)
Важное примечание:
при вводе значения момента инерции I для данного тела не забывайте всегда указывать ось вращения, для которой было рассчитано значение I.
15.. Момент инерции материальной точки. Момент инерции тела. Теорема Штейнера.
Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси.Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
J=J_C+md^2
J_C — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.
16. Момент импульса материальной точки. Момент импульса твердого тела относительно неподвижной оси вращения.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам ~\mathbf r и ~\mathbf p. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
17.Основное уравнение динамики вращательного движения.
Основое уравнение динамики вращательного движения материальной точки — угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
Момент инерции материальной точки и твердого тела. Теорема Штейнера-Гюйгенса.
Момент инерцииматериальной точки относительно оси вращения — произведение массы этой точки на квадрат расстояния от оси.
При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения.
Момент инерции твердого тела — это величина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:
Единица момента инерции — килограмм-метр в квадрате.
Теорема Штейнера
Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R — расстояние между осями.
Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции телаотносительно некоторой оси
15. вопрос момент инерции однородного цилиндра или диска (вывод).
20 Применение закона сохранения импульса для абсолютно упругого и абсолютно неупругого взаимодействия.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m << M почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M – во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
| Рисунок 1.21.2. Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
| Модель. Упругие и неупругие соударения |
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
| Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние |
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При
Первое из этих равенств означает, что векторы скоростей , и образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами и равен 90°.
| Модель. Соударения упругих шаров |
|
21.Закон сохранения полной механической энергии
Превращение одного вида механической энергии в другой
А как вы считаете, обладает ли эта несущаяся вниз стихия энергией? Никто не будет спорить с тем, что да. А вот какой энергией будет обладать вода – кинетической или потенциальной? И вот тут оказывается, что ни первый, ни второй варианты ответа не будут верны. А верным окажется ответ – падающая вниз вода обладает обоими видами энергии. То есть, одно и то же тело может обладать обоими видами энергии. Их сумму называют полной механической энергией тела: E=E_к+E_п. Более того, вода в данном случае не только обладает обоими видами энергии, но их величина меняется по ходу движения воды. Когда наша вода находится в верхней точке водопада и еще не начала падать, то она обладает максимальным значением потенциальной энергии. Кинетическая же энергия в данном случае равна нулю. Когда вода начинает падать вниз, у нее появляется кинетическая энергия движения. По ходу движения вниз потенциальная энергия уменьшается, так как уменьшается высота, а кинетическая, наоборот, возрастает, так как увеличивается скорость падения воды. То есть, происходит превращение одного вида энергии в другой. При этом полная механическая энергия сохраняется. В этом и заключается закон сохранения и превращения энергии.
Закон сохранения полной механической энергии
Закон сохранения полной механической энергии гласит: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной. Когда же присутствует, например, трение скольжения, тело вынуждено тратить часть энергии на его преодоление, и энергия, естественно будет уменьшаться. Поэтому в реальности, при передаче энергии практически всегда существуют потери, которые приходится учитывать.
Закон сохранения энергии можно представить в виде формулы. Если мы обозначим начальную и конечную энергию тела как E_1 и E_2, то закон сохранения энергии можно выразить так: E_1=E_2. В начальный момент времени тело имело скорость v_1 и высоту h_1:
E_1=(mv_1^2)/2+mgh_1.
В конечный момент времени со скоростью v_2 на высоте h_2 энергия
E_2=(mv_2^2)/2+mgh_2.
В соответствии с законом сохранения энергии:
(mv_1^2)/2+mgh_1=(mv_2^2)/2+mgh_2.
Если мы знаем начальные значения скорости и энергии, то мы можем высчитать конечную скорость на высоте h, или, наоборот, найти высоту, на которой тело будет иметь заданную скорость. При этом масса тела не имеет значения, так как она сократится из уравнения.
Энергия также может передаваться от одного тела к другому. Так, например, при выпуске стрелы из лука потенциальная энергия тетивы, превращается в кинетическую энергию летящей стрелы.
23.Потенциальная энергия поля силы тяжести
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по модулю и направлению сила тяжести Работа этой силы равна изменению некоторой физической величины mgh (где h – высота, отсчитываемая от некоторого нулевого уровня), взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести:
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. В то же время она равна работе внешних сил на перемещение тела с нулевого уровня на требуемую высоту. Потенциальная энергия Eр зависит от выбора нулевого уровня отсчета. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
|
17. Момент инерции тела и его физический смысл. Примеры вычисления момента инерции твердых тел. Теорема Штейнера .
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица
измерения СИ: кг·м². 
Обозначение: I или J.
2. Физический смысл момента инерции. Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил, приложенных к телу. Сравните. Вращательное движение. Поступательное движение. Момент инерции представляет собой меру инерции тела во вращательном движении
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:

Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :
18. Момент импульса твердого тела. Вектор угловой скорости и вектор момента импульса. Гироскопический эффект. Угловая скорость прецессии
Момент
импульса твердого тела относительно
оси есть сумма моментов импульса
отдельных частиц, из которых состоит
тело относительно оси. Учитывая, что  ,
получим
,
получим  .
.
Если
сумма моментов сил, действующих на тело,
вращающееся вокруг неподвижной оси,
равна нулю, то момент импульса сохраняется
(закон сохранения
момента импульса):  .
Производная момента импульса твердого
тела по времени равна сумме моментов
всех сил, действующих на тело:
.
Производная момента импульса твердого
тела по времени равна сумме моментов
всех сил, действующих на тело: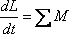 .
.
угловую скорость как вектор, величина которого численно равна угловой скорости, и направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось2, что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») − если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.
Вращающееся тело ( колесо мотоцикла ) стремиться сохранять положение оси вращения в пространстве неизменным .( гироскопический эффект ) Поэтому возможно движение на 2-х колёсах, но не возможно стояние на двух колёсах Этот эфект используется в корабельных и танковых системах наведения орудий. ( корабль качается на волнах, а орудие смотрит в одну точку ) В навигации и др.
Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.
Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве. В примере с волчком этого не произойдет, поскольку в нём вызывающая прецессию сила — гравитация Земли — действует постоянно.
19. Идеальная и вязкая жидкость. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бирнулли.
Идеальной жидкостью назвается воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутреннее трение и теплопроводность. Так как в ней отсуствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.
вязкая жидкость характеризуется наличием сил трения, которые возникают при ее движении. вязкой наз. жидкость, в которой при движении кроме нормальных напряжений наблюдаются и касательные напряжения
Рассматриваемые
в Г. ур-ния относит. равновесия несжимаемой
жидкости в поле сил тяжести (относительно
стенок сосуда, совершающего движение
по нек-рому известному закону, напр.
поступательное или вращательное) дают
возможность решать задачи о форме
свободной поверхности и о плескании
жидкости в движущихся сосудах — в
цистернах для перевозки жидкостей,
топливных баках самолётов и ракет и т.
п., а также в условиях частичной или
полной невесомости на космич. летат.
аппаратах. При определении формы
свободной поверхности жидкости,
заключённой в сосуде, кроме сил
гидростатич. давления, сил
инерции и
силы тяжести необходимо учитывать
поверхностное натяжение жидкости. В
случае вращения сосуда вокруг вертик.
оси с пост. угл. скоростью свободная
поверхность принимает форму параболоида
вращения, а в сосуде, движущемся
параллельно горизонтальной плоскости
поступательно и прямолинейно с пост.
ускорением а,
свободной поверхностью жидкости является
плоскость, наклонённая к горизонтальной
плоскости под углом 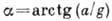
1. Момент инерции материальной точки
 ,
,
где m – масса материальной точки; r – расстояние от точки до оси вращения.
2. Момент инерции системы материальных точек
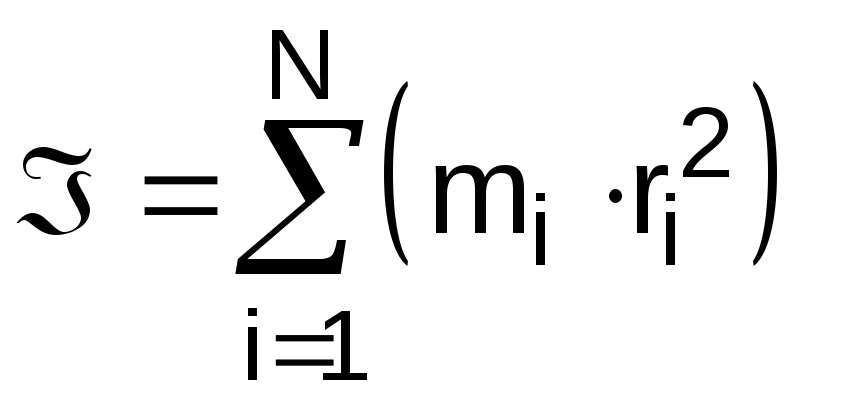 .
.
3. Момент инерции абсолютно твердого тела
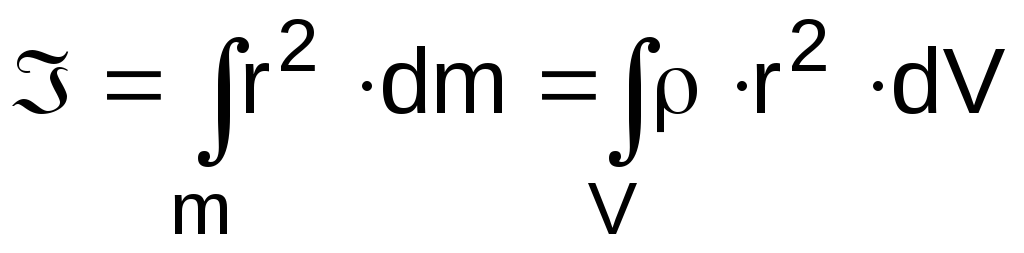 .
.
Сила – это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или деформируется (изменяет свою форму или размеры).
Механика использует различные модели для описания механического движения.
Материальная точка (м.т.)– это тело, обладающее массой, размерами которого в данной задаче можно пренебречь.
Абсолютно твердое тело (а.т.т.) – это тело, которое в процессе движения не деформируется, то есть расстояние между любыми двумя точками в процессе движения остается неизменным.
3.1.2.
Законы движения.
Первый закон ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, воздействие со стороны других тел не заставит ее изменить это состояние.
Те системы отсчета, по отношению к которым выполняется первый закон Ньютона, называются инерциальными системами отсчета (ИСО). Следовательно, первый закон Ньютона утверждает существование ИСО.
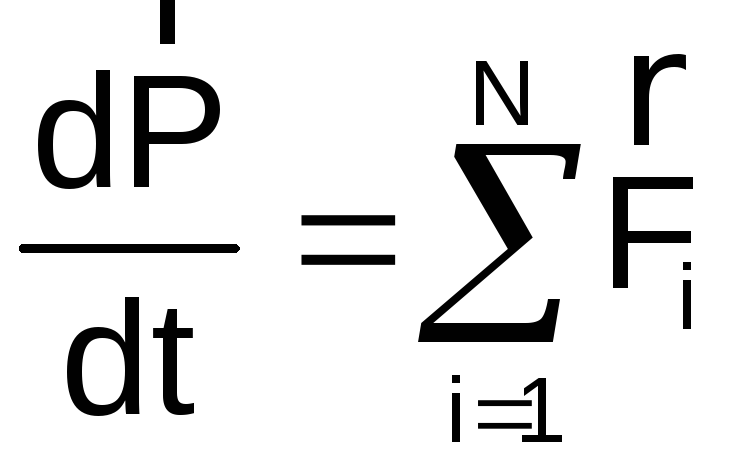
Третий закон Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми материальные точки действуют друг на друга, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки
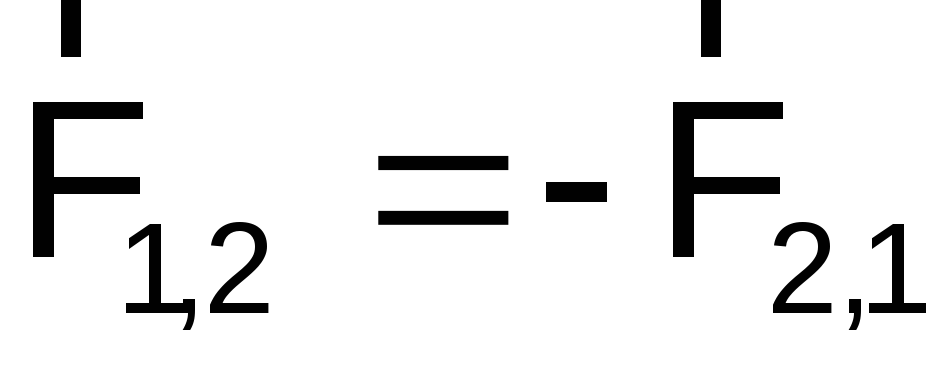 ,
,
здесь 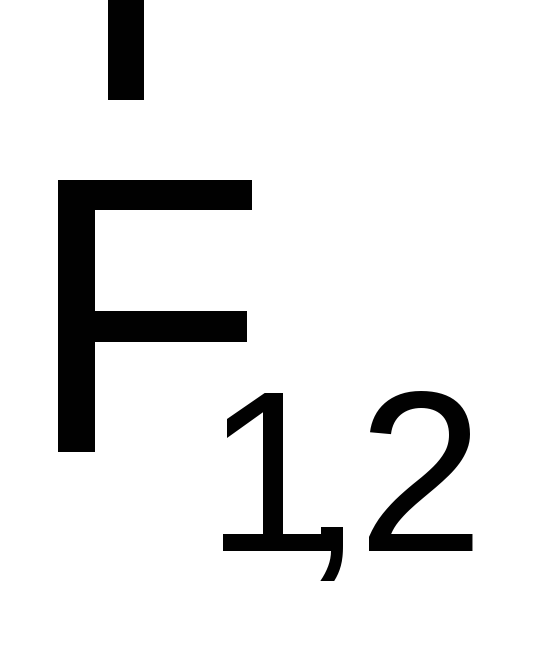 – сила, действующая на первую материальную
точку со стороны второй;
– сила, действующая на первую материальную
точку со стороны второй;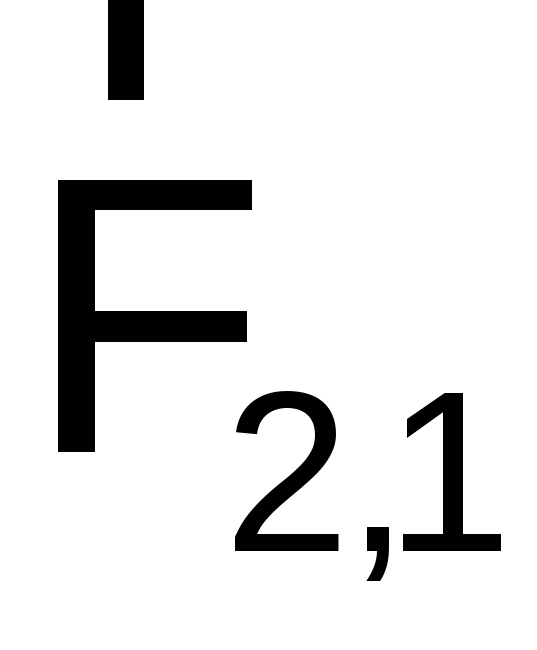 – сила, действующая на вторую материальную
точку со стороны первой. Эти силы
приложены к разным материальным точкам
(телам), всегда действуют парами и
являются силами одной природы.
– сила, действующая на вторую материальную
точку со стороны первой. Эти силы
приложены к разным материальным точкам
(телам), всегда действуют парами и
являются силами одной природы.
Закон всемирного тяготения: между любыми двумя материальными точками (телами) действуют силы взаимного притяжения
 ,
прямо пропорциональные произведению
масс
,
прямо пропорциональные произведению
масс и
и этих точек и обратно пропорциональные
квадрату расстояния
этих точек и обратно пропорциональные
квадрату расстояния между ними. Силы тяготения направлены
вдоль прямой, проходящей через
взаимодействующие материальные точки
(тела).
между ними. Силы тяготения направлены
вдоль прямой, проходящей через
взаимодействующие материальные точки
(тела).
 ,
,
здесь  – гравитационная постоянная.
– гравитационная постоянная.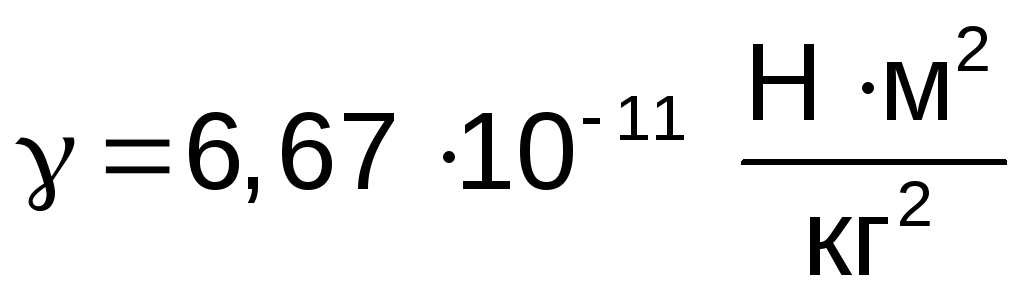 .
.
3.1.3.
Принцип относительности.
Принцип относительности Галилея: внутри равномерно движущейся системы все механические процессы протекают так же, как и внутри покоящейся.
Принцип относительности Галилея-Ньютона:
во всех инерциальных системах отсчета (ИСО) механические процессы протекают одинаково;
никакой механический эксперимент не позволяет нам выделить из совокупности ИСО какую-либо одну преимущественную систему отсчета;
все законы природы одинаковы во всех ИСО (инвариантны относительно перехода из одной ИСО в другую ИСО).
Отсюда следует:
3.1.4.
Пространство и время.
Интуитивные представления о понятиях пространства и времени имеет каждый человек на основании повседневного опыта.
Пространство — это совокупность отношений, выражающих взаимное расположение материальных объектов – расстояния между ними и ориентацию.
Время — это совокупность отношений, выражающих длительность и последовательность событий.
Тем самым пространство — это пространственные отношения между материальными объектами, а время — это временные отношения событий друг к другу.
Наиболее общее свойство пространства и времени — их взаимозависимость. Говорить о пространстве без материальных объектов и о времени без каких-либо процессов не имеет никакого смысла. Не существует пространственных и временных отношений по отдельности – любой процесс в природе происходит в некоторой области пространства, а любой материальный объект как-то меняется со временем. Поэтому имеет смысл говорить лишь о единых пространственно-временных отношениях между событиями. Однако для первого знакомства с их свойствами рассмотрим сначала временные отношения в данной точке пространстве и пространственные отношения в данный момент времени порознь. Такое условное разделение допустимо, пока рассматриваемые нами объекты движутся медленно.
А). Временные отношения в природе
Чтобы описать временные отношения, вводится эталонный процесс, называемый часами. В качестве часов можно использовать любой процесс, в котором периодически повторяется одно и то же состояние материального объекта. Примеры таких процессов хорошо известны из повседневной жизни: пульс у человека, движение Земли вокруг оси (сутки) и вокруг Солнца (год), колебания маятника.
Время одномерно. Это значит, что ответ на вопрос «Когда произошло событие А?» требует измерения и указания лишь одного числа — момента времени события tА. Моменты времени различных событий могут быть упорядочены в соответствии с правилом «раньше – позже», после чего им могут быть сопоставлены геометрические точки на оси времени. За начало отсчета на такой оси можно выбрать произвольный момент времени to. Моменты времени одного и того же события относительны, т.е. зависят от выбора начала отсчета времени, сами по себе они не могут служить объективными характеристиками временных отношений.
В
качестве объективной характеристики
временных отношений принято выбирать
промежуток времени  ,
равный разности между двумя моментами
времени, отвечающими началу и концу
какого-либо процесса. В отличие от них
промежуток времени
,
равный разности между двумя моментами
времени, отвечающими началу и концу
какого-либо процесса. В отличие от них
промежуток времени обладает тем свойством, что его значение
уже не зависит от выбора начала отсчета
времени. Иными словами, в данной точке
пространства промежутки времени
инвариантны, т.е. неизменны по отношению
к выбору начала отсчета времени. В этом
проявляется важнейшее свойство времени
— егооднородность.
обладает тем свойством, что его значение
уже не зависит от выбора начала отсчета
времени. Иными словами, в данной точке
пространства промежутки времени
инвариантны, т.е. неизменны по отношению
к выбору начала отсчета времени. В этом
проявляется важнейшее свойство времени
— егооднородность.
Время изменяется только от прошлого через настоящее к будущему.
15.Кинетическая энергия абсолютно твердого тела, вращающегося вокруг относительно неподвижной оси. Момент инерции. Теорема Штейнера. Моменты инерции тел простейшей геометрической формы.
Кинетическая энергия твёрдого тела, вращающегося относительно неподвижной оси.
Рассмотрим абсолютно твёрдое тело, вращающееся около неподвижной оси, проходящей через тело. Мысленно разобьём это тело на маленькие объёмы с элементарными массами m1, m2,…,mn, находящиеся на расстоянии r1, r2,…, rn, от оси вращения. При вращении твёрдого тела относительно неподвижной оси отдельные его элементарные объёмы опишут окружности различных радиусов ri и имеют различные линейные скорости υi.
Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т1, т2 ,…, тn , находящиеся на расстоянии r1, r2,…, rn от оси.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi опишут окружности различных радиусов ri, и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
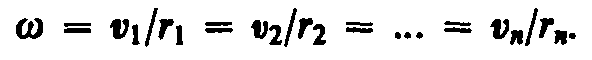 (17.1)
(17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

или

Используя выражение (17.1), получаем

где Jz — момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
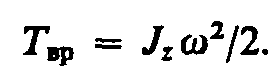 (17.2)
(17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv2/2), следует, что момент инерции — мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

где m — масса катящегося тела; vc — скорость центра масс тела; Jc — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.

Кинетическую энергию вращающегося тела найдём как сумму кинетических энергий его элементарных объёмов.
Tвр=∑ni=1miυi2/2=∑ni=1miω2ri2/2=(ω2∑ni=1miri2)/2=Izω2/2,  гдеIz – момент инерции тела. Вращение твёрдого
тела вокруг неподвижной оси:
гдеIz – момент инерции тела. Вращение твёрдого
тела вокруг неподвижной оси:
Можно показать, что проекция момента импульса на ось “Z” может быть записана таким образом:
где R – расстояние до оси.
Момент инерции
материальной точки относительно
неподвижной оси — скалярная физическая величина,
являющаяся мерой инертности этой точки
при вращательном движении и, равная
произведению её массы на квадрат
расстояния до оси, т.е.  ,
а также
,
а также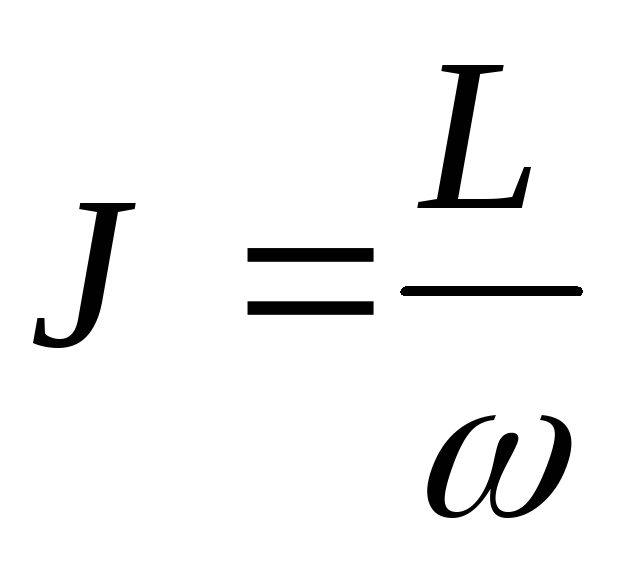 ,
где
,
где —
угловая скорость тела относительно
данной оси.
—
угловая скорость тела относительно
данной оси.
Теорема Штейнера: Момент инерции твердого тела относительно некоторой оси вращения равен сумме момента инерции этого тела относительно оси параллельной данной и проходящей через центр масс тел и произведению массы тела не квадрат расстояния между осями.

Обруч

Цилиндр

Круг

Стержень, ось посередине

Стержень, ось на конце

6. Момент инерции материальной точки и абсолютно твердого тела. Пример расчета момента инерции тела правильной формы. Теорема Штейнера.
Момент инерции – это физическая величина, характеризующаяся распределением массы тела относительно оси вращения и является мерой инертности (это свойство тел, обладающих массой, сохранять свою скорость в отсутствии действия на нее других тел) тела при вращательном движении. Это величина аддитивная.
Если ось вращения не проходит через центр симметрии тела, то для расчета момента инерции применяется теорема Штейнера: момент инерции тела относительно произвольной оси вращения I равен моменту его инерции относительно параллельной оси, проходящей через центр масс тела I0 , сложенному с произведением массы тела на квадрат расстояния между осями.
7. Момент силы относительно точки и относительно оси вращения. Момент импульса. Основной закон динамики вращательного движения.
Момент силы относительно точки О – это векторная физическая величина, равная векторному произведению радиуса R, проведенного от этой точки к точке приложения силы на векторную силу F.
Момент силы относительно оси Z – это скалярная величина, равная проекции на данную ось вектора момента силы относительно какой-либо точки на этой оси.
Момент импульса относительно точки О – векторная физическая величина, равная векторному произведению радиус – вектора r, проведенного от точки О к материальной точке на векторе импульса p.
Момент импульса относительно оси вращения Z – это скалярная величина, равная проекции на ось Z вектора момента импульса относительно какой-либо точки на оси Z.
Основной закон динамики вращательного движения: момент силы абсолютно твердого тела прямо пропорционален моменту сил и обратно пропорционален моменту инерции, расположенного вдоль той же оси вращения.
Обобщенная формулировка основного закона динамики вращательного движения: скорость изменения момента импульса тела относительно оси вращения равна результирующему моменту действующих на тело сил относительно этой же оси.
8. Механическая работа. Мощность. Консервативные и неконсервативные силы.
Работа – это физическая величина, характеризующая процесс превращения одной формы движения (энергии) в другую. Работа совершается силой.
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы.
Мощность – скорость совершения работа (работа за единицу времени).
Консервативные силы – силы, которые приводят к сохранению. Это силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положения тела в пространстве. Работа консервативных сил равна 0. К консервативным силам относятся сила тяжести, сила упругости, сила Архимеда.
К неконсервативным силам относятся силы, работы которых в замкнутой системе не равны 0 – сила тяги, сила трения, сила сопротивления.


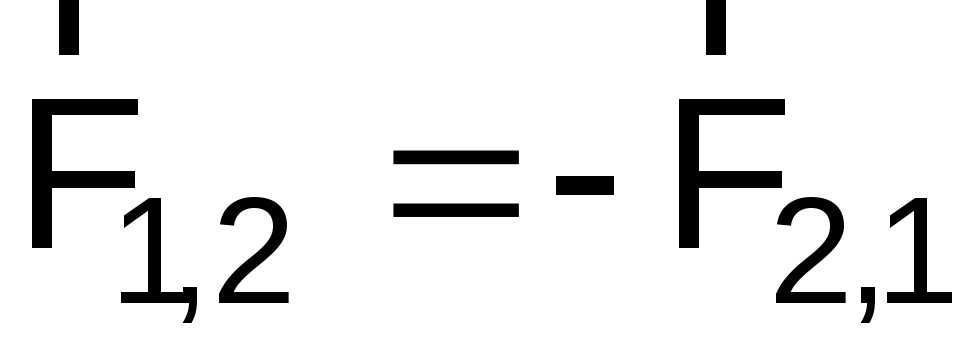 ,
прямо пропорциональные произведению
масс
,
прямо пропорциональные произведению
масс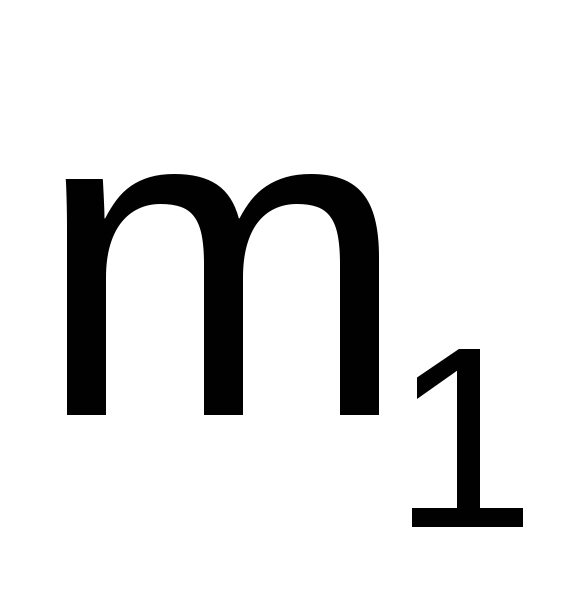 и
и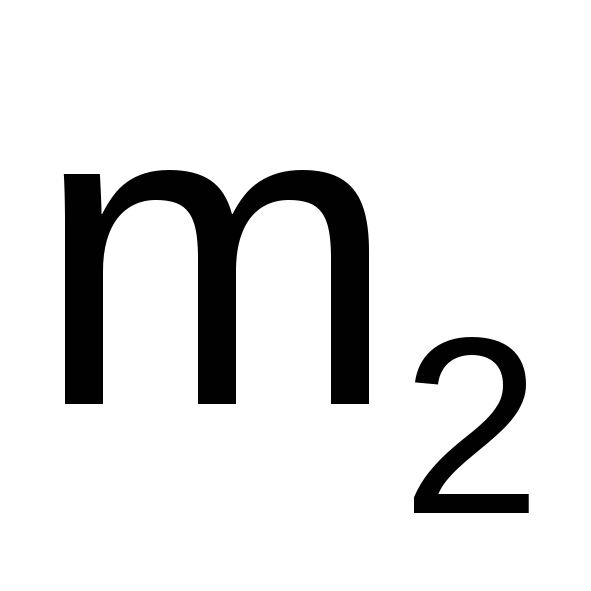 этих точек и обратно пропорциональные
квадрату расстояния
этих точек и обратно пропорциональные
квадрату расстояния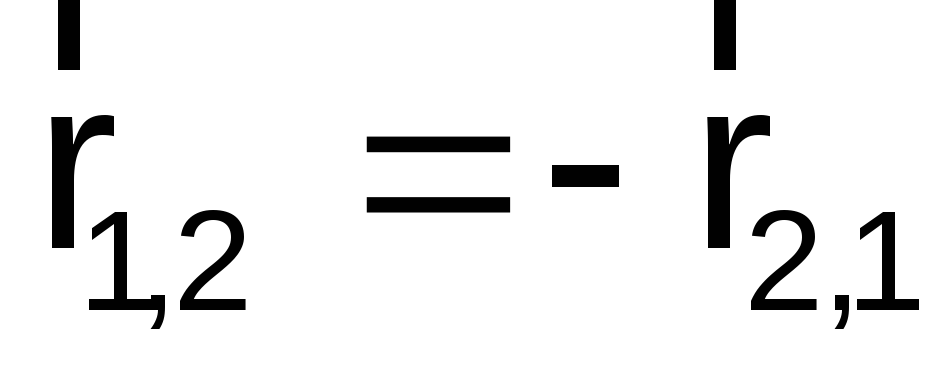 между ними. Силы тяготения направлены
вдоль прямой, проходящей через
взаимодействующие материальные точки
(тела).
между ними. Силы тяготения направлены
вдоль прямой, проходящей через
взаимодействующие материальные точки
(тела).