МОМЕНТ ИНЕРЦИИ — это… Что такое МОМЕНТ ИНЕРЦИИ?
— величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают M. и. осевые и центробежные. Осевым M. и. тела относительно оси z наз. величина, определяемая равенством
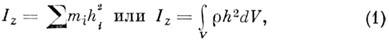
где mi — массы точек тела, hi — их расстояния от оси z, r — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой M. и. можно также выразить через линейную величину rz, наз. радиусом инерции относительно оси z, по ф-ле Iz= Mr2z,. где M — масса тела. Размерность M. и.- L2M; единицы измерения -кг . м 2.
Центробежными M. и. относительно системы прямоуг. осей х, у, z, проведённых в точке О, наз. величины, определяемые равенствами
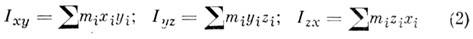
или соответствующими объёмными интегралами. Эти величины являются характеристиками динамич. неуравновешенности тела. Напр., при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в к-рых закреплена ось.
M. и. относительно параллельных осей z и z’ связаны соотношением (теорема Гюйгенса)
где z’ — ось, проходящая через центр массы тела, d — расстояние между осями.
M. и. относительно любой проходящей через начало координат О оси Ol с направляющими косинусами a, b, g находится по ф-ле
Зная шесть величин Ix, Iy, Iz, Ixy, Iyz, Izx, можно последовательно, используя ф-лы (4) и (3), вычислить всю совокупность M. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно перпендикулярные оси, наз. гл. осями инерции, для к-рых
M. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о M. и. широко пользуются при решении мн. задач механики и техники. Лит.: Геpнет M. M., Ратобыльский В. Ф., Определение моментов инерции, M., 1969; Фаворин M. В., Моменты инерции тел. Справочник, M., 1970; см. также лит. при ст. Динамика. С. M. Таре.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
Момент инерции — это… Что такое Момент инерции?
величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z называется величина, определяемая равенством:
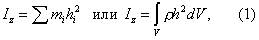где mi — массы точек тела, hi — их расстояния от оси z, ρ — массовая плотность, V — объём тела. Величина Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:
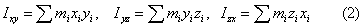
или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси
М. и. относительно параллельных осей z и z’ связаны соотношением
Iz = Iz‘ + М d2 (3)
где z’ — ось, проходящая через центр масс тела, a d — расстояние между осями (теорема Гюйгенса).
М. и. относительно любой, проходящей через начало координат О оси Ol с направляющими косинусами α, β, γ находится по формуле:
lol = Ix α2 + Iy β2 + Iz γ2 — 2Ixy αβ — 2Iyz βγ — 2Izxγα. (4)
Зная шесть величин Ix, Iy, Iz, Ixy, Iyх, Izx, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для которых
М. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники.
Лит.: Краткий физико-технический справочник, под общ. ред. К. П. Яковлева, т. 2, М., 1960, с. 94—101; Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Гернет М. М., Ратобыльский В. Ф., Определение моментов инерции, М., 1969; см. также лит. при ст. Механика.
С. М. Тарг.
МОМЕНТ ИНЕРЦИИ — что такое в Физической энциклопедии
Смотреть что такое МОМЕНТ ИНЕРЦИИ в других словарях:
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ , величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Разли
МОМЕНТ ИНЕРЦИИ
величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и цен
МОМЕНТ ИНЕРЦИИ
тела относительно оси — величина, являющаяся мерой инертности тела во вращат. движении вокруг этой оси. М. и. J равен сумме произведений элементарных м
МОМЕНТ ИНЕРЦИИ
, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной ма
МОМЕНТ ИНЕРЦИИ
величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механик
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ (обозначение I), для вращающегося тела — сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расс
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Разли
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различ
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). П
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различ
МОМЕНТ ИНЕРЦИИ
(Moment d’inertie, Trägheitsmoment, Moment of inertia) — понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же ро
МОМЕНТ ИНЕРЦИИ
— величина, характеризующая распределение масс в теле иявляющаяся наряду с массой мерой инертности тела при непоступат. движении.Различают осевые и цен
МОМЕНТ ИНЕРЦИИ
[moment of inertia, second moment] — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непосту
МОМЕНТ ИНЕРЦИИ
Момент инерции (Moment d‘inertie, Trä gheitsmoment, Moment of inertia) — понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выраж
МОМЕНТ ИНЕРЦИИ
МОМЕНТ ИНЕРЦИИ, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В ме
МОМЕНТ ИНЕРЦИИ СЕКТОРИАЛЬНЫЙ
геометрическая характеристика поперечного сечения открытого тонкостенного стержня, равная сумме произведений элементарных площадок сечений на квадраты
МОМЕНТ ИНЕРЦИИ СЕКТОРИАЛЬНЫЙ
МОМЕНТ ИНЕРЦИИ СЕКТОРИАЛЬНЫЙ - геометрическая характеристика поперечного сечения открытого тонкостенного стержня, равная сумме произведений элементарн
МОМЕНТ ИНЕРЦИИ СЕЧЕНИЯ
геометрическая характеристика поперечного сечения стержня, равная сумме произведений элементарных площадок сечения на квадраты их расстояний до рассмат
МОМЕНТ ИНЕРЦИИ СЕЧЕНИЯ
МОМЕНТ ИНЕРЦИИ СЕЧЕНИЯ - геометрическая характеристика поперечного сечения стержня, равная сумме произведений элементарных площадок сечения на квадрат
момент инерции — это… Что такое момент инерции?
- момент инерции
- [moment of inertia, second moment] — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают моменты инерции осевые и центробежные. Осевым момента инерции тела относительно оси ± Z называется величина, определяемая равенством:
Смотри также:
— Момент
— момент сопротивления сечения
— момент прокатки
— момент количества движения
— диамагнитный момент
— момент силы
— магнитный момент
Энциклопедический словарь по металлургии. — М.: Интермет Инжиниринг. Главный редактор Н.П. Лякишев. 2000.
- second moment
- diamagnetic moment
Смотреть что такое «момент инерции» в других словарях:
Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь
Книги
- Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
- Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
- Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
МОМЕНТ ИНЕРЦИИ — Физический энциклопедический словарь
Величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая равенством:
где mi — массы точек тела, hi — их расстояния от оси z, a r — массовая плотность, V — объём тела. Величина Iz явл. мерой инертности тела при его вращении вокруг оси (см. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ). Осевой М. и. можно также выразить через линейную величину r, наз. радиусом инерции, по формуле
Iz=Mr2,
где М — масса тела.
Размерность М. и.— L2M; а единицы — кг•м2 или г•см2. Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, наз. величины, определяемые равенствами:
или же соответствующими объёмными интегралами. Эти величины явл. характеристиками динамич. неуравновешенности тел. Напр., при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в к-рых закреплена ось. М. п. относительно параллельных осей z и z’ связаны соотношением:
lz=l’z + Md2 (3)
где z’ — ось, проходящая через центр масс тела, а d — расстояние между осями.
М. и. относительно любой проходящей через начало координат О оси О1 с направляющими косинусами a, b, g находится по ф-ле:
IOl=Ixa2+Iyb2+Izg2-2Ixyab-2Iyzbg-2Izxga. (4)
Зная шесть величин Ix, Iy Iz, Iху, Iyz, Izx, можно последовательно, используя ф-лы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести три такие взаимно-перпендикулярные оси, наз. главными осями инерции, для к-рых Ixy=Iyz=Izx=0
Тогда, зная главные оси инерции и М. п. относительно этих осей, можно определить М. и. тела относительно любой оси.
М. п. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники
Источник: Физический энциклопедический словарь на Gufo.me
Значения в других словарях
- Момент инерции — (Moment d’inertie, Trägheitsmoment, Moment of inertia) — понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий. Энциклопедический словарь Брокгауза и Ефрона
- МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Большой энциклопедический словарь
- МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ (обозначение I), для вращающегося тела — сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы привести тело во вращение. Научно-технический словарь
- Момент инерции — Величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. Большая советская энциклопедия
момент инерции — это… Что такое момент инерции?
- момент инерции
3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси.
2.25. Момент инерции — момент инерции (динамический) тела относительно оси, представляющий собой сумму (интегральную) произведений масс его отдельных частей на квадраты их расстояний от оси.
Примечание. Эта величина обозначается буквенным символом I и выражается в кг · м2.
Смотри также родственные термины:
3.18 момент инерции (динамический момент инерции) ротора: Сумма произведений масс всех частиц ротора на квадраты расстояний от оси его вращения.
27. Момент инерции лопасти несущего винта относительно горизонтального и вертикального шарниров
Момент инерции лопасти
Момент инерции массы лопасти несущего винта и других агрегатов, совершающих вместе с лопастью маховое движение:
3.8 момент инерции механизма : Приведенный к валу электродвигателя момент инерции сочлененного с ним механизма.
28. Момент инерции несущего винта
Jω
Суммарный момент инерции массы лопастей и всех кинематически связанных с ним агрегатов, приведенный к оси вращения несущего винта.
Примечание. Кинематически связанные с несущим винтом агрегаты определяются в каждом конкретном случае
Момент инерции поперечного сечения распорного кольца, мм4 (см4)
Iк
74 момент инерции электропривода: Сумма моментов инерции всех движущихся масс электропривода при приведении их к скорости элемента приведения электропривода
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- момент затяжки М
- момент инерции (динамический момент инерции) ротора
Смотреть что такое «момент инерции» в других словарях:
Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь
Книги
- Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
- Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
- Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
Тензор инерции — Википедия
Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с угловой скоростью:
- L→=Jω→{\displaystyle \ {\vec {L}}=J{\vec {\omega }}}
где J{\displaystyle \ J} — тензор инерции, ω→{\displaystyle \ {\vec {\omega }}} — угловая скорость, L→{\displaystyle {\vec {L}}} — момент импульса
- Ekin rot=12 ω→T⋅J⋅ω→{\displaystyle \ E_{kin\ rot}={1 \over 2}\ {\vec {\omega }}^{\,T}\cdot J\cdot {\vec {\omega }}}
- Ekin=Ekin rot+p22m{\displaystyle \ E_{kin}=E_{kin\ rot}+{p^{2} \over 2m}},
в компонентах это выглядит так:
- Li=∑jJijωj{\displaystyle \ L_{i}=\sum _{j}J_{ij}\omega _{j}}
- Ekin rot=12∑ijωiJijωj{\displaystyle \ E_{kin\ rot}={1 \over 2}\sum _{ij}\omega _{i}J_{ij}\omega _{j}}
Используя определение момента импульса системы N материальных точек (перенумерованных в формулах ниже индексом k):
- L→=∑k=1N[ r→k×( mk v→k ) ]{\displaystyle \ {\vec {L}}=\sum _{k=1}^{N}[\ {\vec {r}}_{k}\times (\ m_{k}\ {\vec {v}}_{k}\ )\ ]}
и кинематическое выражение для скорости через угловую скорость:
- v→=[ ω→×r→ ]{\displaystyle \ {\vec {v}}=[\ {\vec {\omega }}\times {\vec {r}}\ ]}
и сравнивая с формулой, выражающей момент импульса через тензор инерции и угловую скорость (первой в этой статье), нетрудно получить явное выражение для тензора инерции:
- Jij=∑k( mk (δijrk2−rikrjk) )){\displaystyle \ J_{ij}=\sum _{k}(\ m_{k}\ (\delta _{ij}r_{k}^{2}-r_{i_{k}}r_{j_{k}})\ ))}
или в непрерывном виде:
- Jij=∫(δijr2−rirj )dm=∫(δijr2−rirj )ρdV{\displaystyle \ J_{ij}=\int (\delta _{ij}r^{2}-r_{i}r_{j}\ )dm=\int (\delta _{ij}r^{2}-r_{i}r_{j}\ )\rho dV},
где r — расстояния от точек до центра, относительно которого вычисляется тензор инерции, а ri — координатные компоненты соответствующих отрезков, i и j — номера координат (от 1 до 3), индекс же k (от 1 до N) в дискретной формуле нумерует точки системы или маленькие части, её составляющие.
Уже из этих формул явно видно, что тензор инерции любого тела зависит от точки, относительно которой он рассчитан. Обычно выделенную роль играет тензор инерции относительно центра масс тела (тогда p в третьей формуле — это просто импульс тела). Также может быть удобно пользоваться моментом инерции, рассчитанным относительно закрепленной (неподвижной) точки тела или точки, находящейся на закреплённой оси вращения. Пересчёт тензора инерции для нового центра, зная его относительно старого, позволяет легко осуществить теорема Штейнера (она же позволяет сделать это и в виде пересчёта, например, формулы кинетической энергии, позволяя, таким образом, оперировать только тензором инерции относительно центра масс).
Из этих же формул видно, что это симметричный тензор, то есть Jij=Jji.
В непрерывном виде формулу можно вывести следующим образом:
- L→=∫(m)[ r→×( v→dm ) ]=ρ∫(V)[ r→×[ ω→×r→ ] ]dV{\displaystyle {\vec {L}}=\int \limits _{(m)}[\ {\vec {r}}\times (\ {\vec {v}}dm\ )\ ]=\rho \int \limits _{(V)}[\ {\vec {r}}\times [\ {\vec {\omega }}\times {\vec {r}}\ ]\ ]dV}
Откуда по формуле Лагранжа получим
- L→=ρ∫(V)[ ω→⋅r2−r→(ω→, r→) ]dV{\displaystyle {\vec {L}}=\rho \int \limits _{(V)}[\ {\vec {\omega }}\cdot r^{2}-{\vec {r}}({\vec {\omega }},\ {\vec {r}})\ ]dV}
Запишем разложение векторов v→{\displaystyle \ {\vec {v}}} и r→{\displaystyle \ {\vec {r}}} в ортонормированном базисе:
- r→=xi→+yj→+zk→{\displaystyle \ {\vec {r}}=x{\vec {i}}+y{\vec {j}}+z{\vec {k}}}
- ω→=ωxi→+ωyj→+ωzk→{\displaystyle \ {\vec {\omega }}=\omega _{x}{\vec {i}}+\omega _{y}{\vec {j}}+\omega _{z}{\vec {k}}}
По свойствам скалярного произведения,
- (ω→, r→)=xωx+yωy+zωz{\displaystyle \ ({\vec {\omega }},\ {\vec {r}})=x\omega _{x}+y\omega _{y}+z\omega _{z}}
С учетом того, что r2=x2+y2+z2{\displaystyle \ r^{2}=x^{2}+y^{2}+z^{2}} можем записать проекции вектора момента импульса на оси:
- Lx=ρ∫(V)(ωx(x2+y2+z2)−x(xωx+yωy+zωz))dV{\displaystyle L_{x}=\rho \int \limits _{(V)}\left(\omega _{x}(x^{2}+y^{2}+z^{2})-x(x\omega _{x}+y\omega _{y}+z\omega _{z})\right)dV}
Или, приведя подобные слагаемые
- Lx=ρ∫(V)(ωx(y2+z2)−ωyxy−ωzxz)dV{\displaystyle L_{x}=\rho \int \limits _{(V)}\left(\omega _{x}(y^{2}+z^{2})-\omega _{y}xy-\omega _{z}xz\right)dV}
Аналогично
- Ly=ρ∫(V)(ωy(x2+z2)−ωxyx−ωzyz)dV{\displaystyle L_{y}=\rho \int \limits _{(V)}\left(\omega _{y}(x^{2}+z^{2})-\omega _{x}yx-\omega _{z}yz\right)dV}
- Lz=ρ∫(V)(ωz(x2+y2)−ωxzx−ωyzy)dV{\displaystyle L_{z}=\rho \int \limits _{(V)}\left(\omega _{z}(x^{2}+y^{2})-\omega _{x}zx-\omega _{y}zy\right)dV}
Введем обозначения:
- Jxx=ρ∫(V)(y2+z2)dV{\displaystyle J_{xx}=\rho \int \limits _{(V)}(y^{2}+z^{2})dV}
- Jyy=ρ∫(V)(x2+z2)dV{\displaystyle J_{yy}=\rho \int \limits _{(V)}(x^{2}+z^{2})dV}
- Jzz=ρ∫(V)(x2+y2)dV{\displaystyle J_{zz}=\rho \int \limits _{(V)}(x^{2}+y^{2})dV}
- Jxy=Jyx=−ρ∫(V)xydV{\displaystyle J_{xy}=J_{yx}=-\rho \int \limits _{(V)}xydV}
- Jxz=Jzx=−ρ∫(V)xzdV{\displaystyle J_{xz}=J_{zx}=-\rho \int \limits _{(V)}xzdV}
- Jyz=Jzy=−ρ∫(V)yzdV{\displaystyle J_{yz}=J_{zy}=-\rho \int \limits _{(V)}yzdV}
Из них можно составить тензор инерции в матричном виде:
- J=|JxxJxyJxzJyxJyyJyzJzxJzyJzz|{\displaystyle J={\begin{vmatrix}J_{xx}&J_{xy}&J_{xz}\\J_{yx}&J_{yy}&J_{yz}\\J_{zx}&J_{zy}&J_{zz}\\\end{vmatrix}}}
Легко проверить, что согласно нашим обозначениям, верна тензорная связь:
- {Lx=Jxxωx+Jxyωy+JxzωzLy=Jyxωx+Jyyωy+JyzωzLz=Jzxωx+Jzyωy+Jzzωz{\displaystyle \left\{{\begin{aligned}L_{x}=J_{xx}\omega _{x}+J_{xy}\omega _{y}+J_{xz}\omega _{z}\\L_{y}=J_{yx}\omega _{x}+J_{yy}\omega _{y}+J_{yz}\omega _{z}\\L_{z}=J_{zx}\omega _{x}+J_{zy}\omega _{y}+J_{zz}\omega _{z}\\\end{aligned}}\right.}
Как и любой симметричный тензор, тензор инерции может быть диагонализован, то есть можно найти три ортогональные оси координат (собственные оси, орты которых являются собственными векторами и образуют собственный базис тензора инерции) — жестко связанные, конечно, с твёрдым телом, — в которых матрица тензора инерции диагональна, и её собственные числа (собственные числа тензора инерции) определяют главные моменты инерции тела[1].
Нетрудно видеть, что главные моменты инерции совпадают с осевыми моментами инерции относительно главных осей:
- Jxx=∫(y2+z2)dm=∫ryz2dm{\displaystyle \ J_{xx}=\int (y^{2}+z^{2})dm=\int r_{yz}^{2}dm},
- Jyy=∫(x2+z2)dm=∫rxz2dm{\displaystyle \ J_{yy}=\int (x^{2}+z^{2})dm=\int r_{xz}^{2}dm},
- Jzz=∫(x2+y2)dm=∫rxy2dm{\displaystyle \ J_{zz}=\int (x^{2}+y^{2})dm=\int r_{xy}^{2}dm},
(внимание: x, y и z в этих формулах подразумевают именно главные оси, если мы хотим совпадения с главными моментами).
- Все формулы этой статьи предполагали использование ортонормированного базиса, поэтому используются только нижние тензорные индексы, так как в этом случае между верхними и нижними индексами нет разницы.
- Тензор инерции можно считать обобщением понятия момента инерции относительно оси; связь этих величин — см. в статье Момент инерции (там собственные числа тензора инерции обозначены как JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}}). При чтении статьи по ссылке следует иметь в виду некоторое различие обозначений, так, в той статье Jxy,Jyz,Jzx{\displaystyle J_{xy},J_{yz},J_{zx}} обозначены не соответствующие компоненты тензора инерции, а центробежные моменты инерции, которые совпадают по модулю с соответствующими компонентами тензора, но имеют противоположный знак.
Иногда термин тензор инерции применяется к математически аналогичным конструкциям, не имеющим прямого механического смысла, например, если ρ в формулах — не плотность массы, а плотность других величин, например, плотность статистического распределения; да и пространство, в котором происходит расчет может быть в принципе любым, хотя при этом наиболее осмыслен случай одинаковой природы всех осей (то есть одинаковых единиц измерения по ним). Это применение термина представляет собой прямую геометрическую аналогию, так же, как применение таких терминов, как центр масс или центр тяжести в подобном контексте.
В случае применения термина тензор инерции к плотностям распределений, особенно если он считается относительно «центра тяжести», речь идет по сути о матрице ковариации, причем задача нахождения её собственных векторов и собственных чисел также может обсуждаться в терминах «главных осей» и «главных моментов», что соответствует не только аналогии с моментом инерции, но и вполне строгой терминологии вторых моментов многомерного распределения (многомерной случайной величины) в статистике (и суть, и терминология здесь могут быть очень близки). При этом, в двумерном случае тензор инерции и матрица ковариации в собственных осях полностью совпадают — с точностью до перестановки осей, а в случаях большей размерности речь идет не о совпадающих, а только о близко связанных формально и по смыслу матрицах, диагонализующихся при этом в одном и том же базисе (имеющих одни и те же собственные оси).
