6.5. Момент инерции сплошного шара
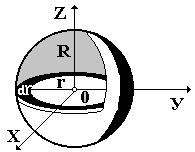
Рис. 6.3
Сплошной однородный шар можно представить как сумму бесконечно тонких сферических слоев с массами dm = mdV/V (рис. 6.3). Объем сферического слоя dV представим в виде: dV = 4r2dr, где r – радиус сферического слоя. Объем шара V = 4/3R3, где R – радиус шара. Если шар полый, то момент инерции сферического слоя относительно его центра масс (точка С) Ic = mR2, но , где
из-за симметрии Ix = Iy = Iz. Момент
инерции сферического слоя относительно
диаметра
, где
из-за симметрии Ix = Iy = Iz. Момент
инерции сферического слоя относительно
диаметра 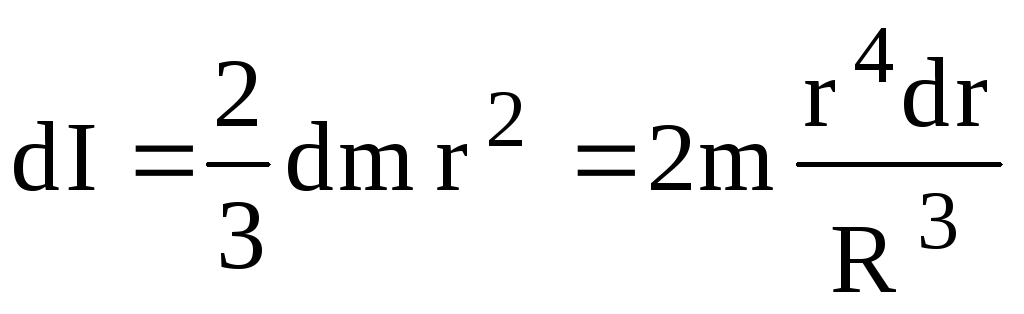 .
. Тогда момент инерции шара
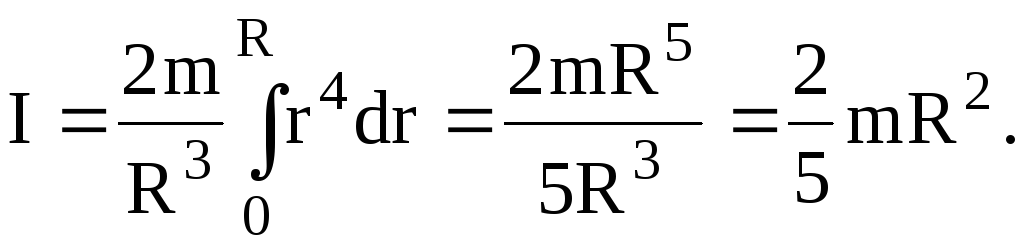
6.5.1. Примеры моментов инерции некоторых тел
4. Тонкое кольцо радиусом R
и шириной d.
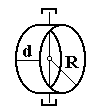
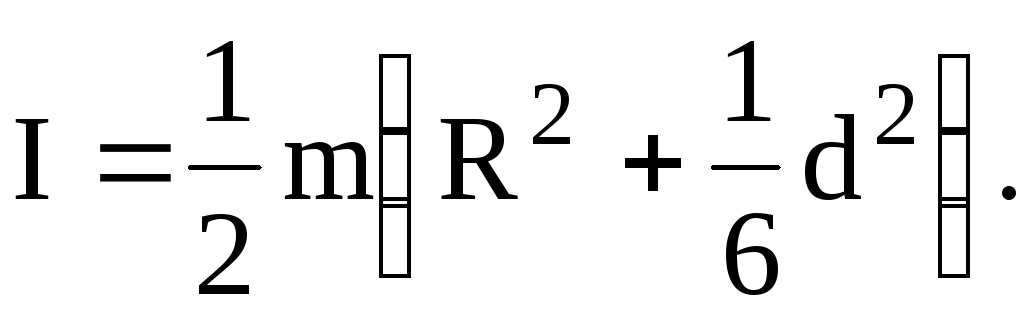
3. Полый цилиндр с внутренним r и внешним R радиусами
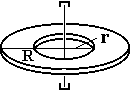
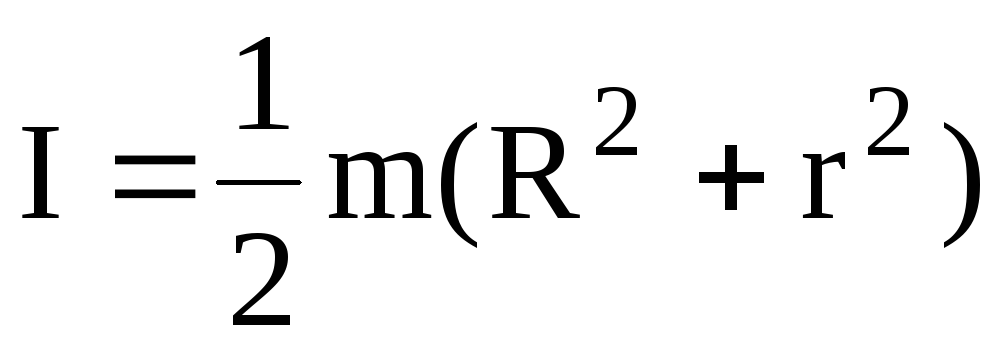 .
.
2. Тонкое кольцо
радиуса R
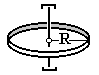
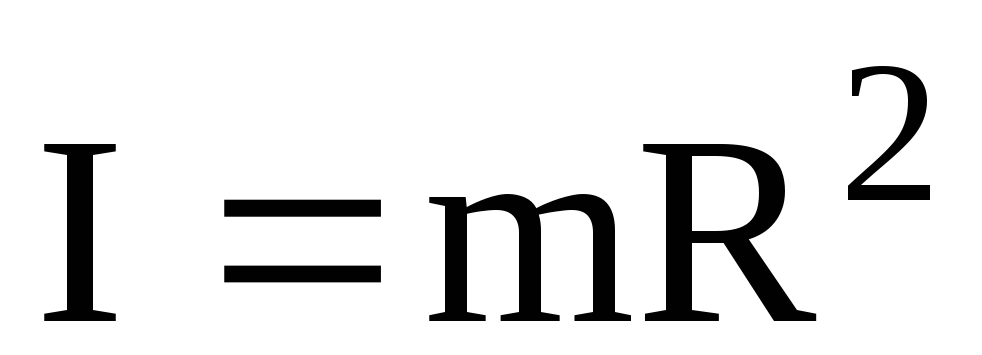
1. Сплошной

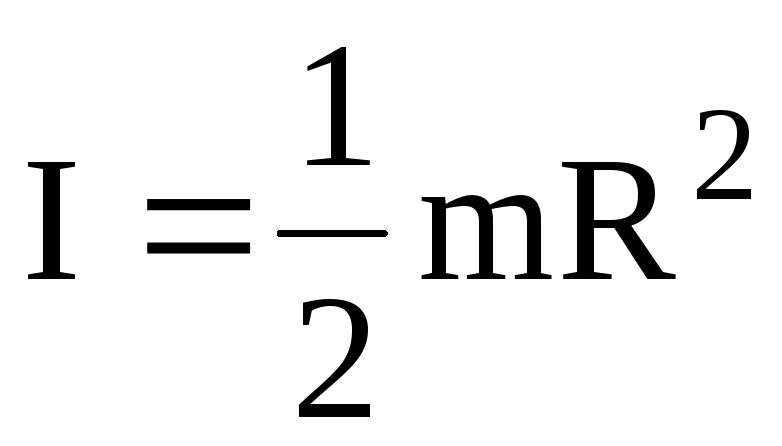
5. Тонкий параллелепипед
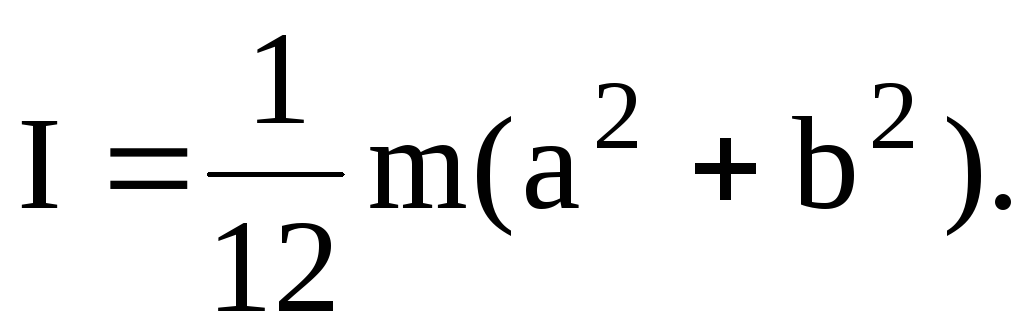
при вращательном движении
Если
произвольная м. т. вращается по окружности
и на нее действует сила  (рис.
6.4), то при повороте на некоторый угол
совершается элементарная работа
(рис.
6.4), то при повороте на некоторый угол
совершается элементарная работа
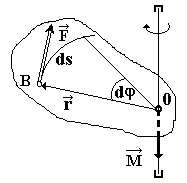
Рис. 6.4
А = F ds, где ds = r d.Тогда А = (r F) d = M d. (6.8)
Полученное выражение остается справедливым и случае системы м.т. (твердых тел), совершающих вращательное движение относительно оси Z при = сonst. В этом случае момент внутренних сил равен нулю и работа не совершается. Для нахождения полной работы необходимо вычислить интеграл:
 ,
(6.9)
,
(6.9)
где = 2 1.
Если действующая сила является потенциальной, то А = dWp ,
где dWp бесконечно малое изменение потенциальной энергии тела при повороте на малый угол dj, т. е.
dWp = Mzd или Mz = dWp/d .
6.7. Кинетическая энергия тела, совершающего
вращательное движение
Кинетическая
энергия м. т. Wk = mv2 / 2 . Тогда для системы м. т. или тела 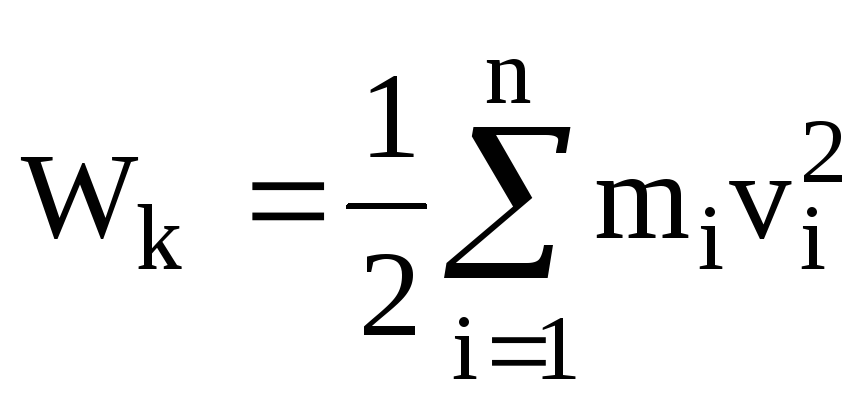 .
Используя связь линейной скорости с
угловой в видеvi = ri,
получим
.
Используя связь линейной скорости с
угловой в видеvi = ri,
получим 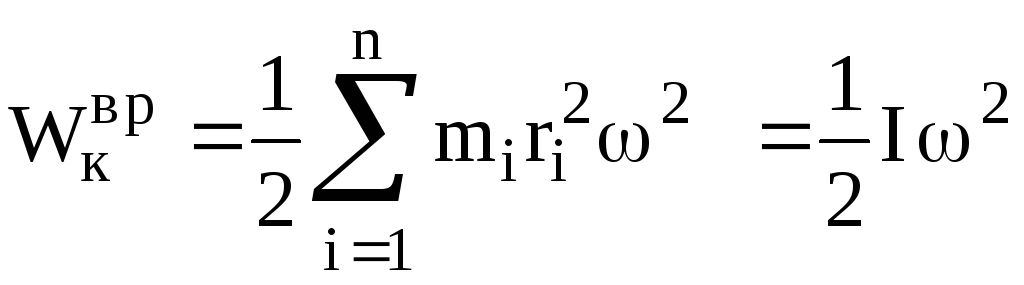 .
(6.10)
.
(6.10)
Замечание: При плоском движении тел (например, цилиндр скатывается по наклонной плоскости, рис. 6.5) полная скорость
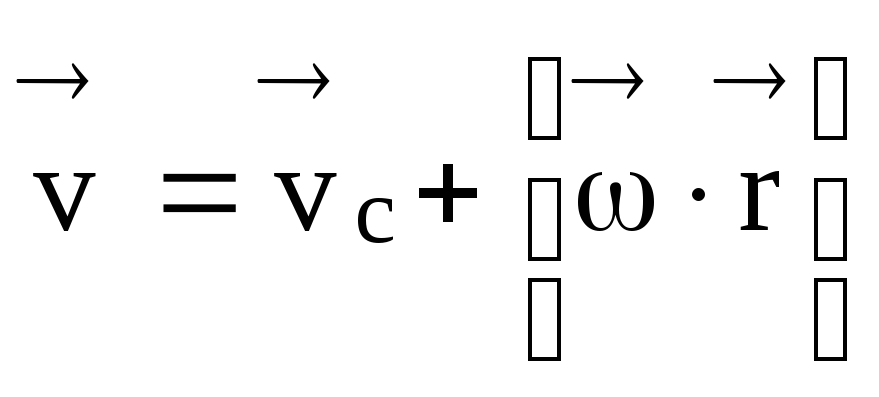
где С центр инерции.
Полная кинетическая энергия тела равна сумме кинетической энергии поступательного движения его центра масс (центра инерции) и кинетической энергии вращательного движения тела относительно точки С, т. е.
. (6.12)
Замечание: При скатывании тела (без проскальзывания)
на него действует сила трения покоя 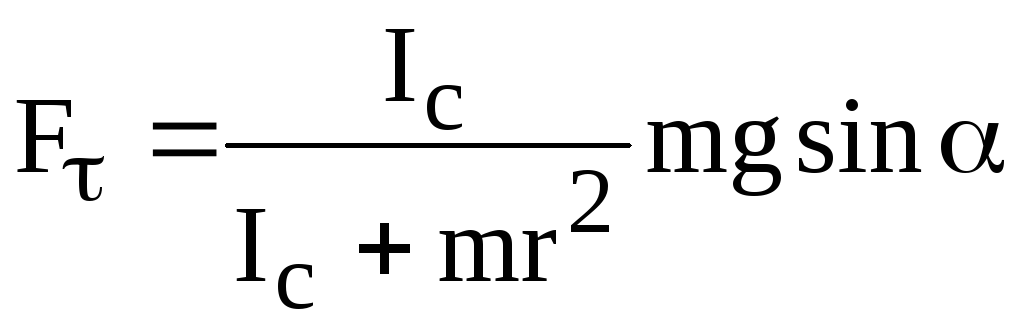 (рис. 6.5).
(рис. 6.5).
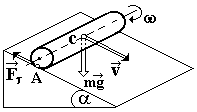
Рис. 6.5
Несмотря на наличие диссипативной силы (сила трения покоя) можно применять законы сохранения, так как сила трения покоя приложена к точкам (А) тела, которые лежат на мгновенной оси вращения. Скорость таких точек равна нулю. Поэтому сила трения сцепления работы не совершает и не влияет на величину полной кинетической энергии.Роль силы трения сцепления заключается в том, чтобы привести тело во вращательное движение для обеспечения чистого качения. При этом работа силы тяжести приводит к увеличению кинетической энергии как поступательного, так и вращательного движений.Вычисление момента инерции однородного шара
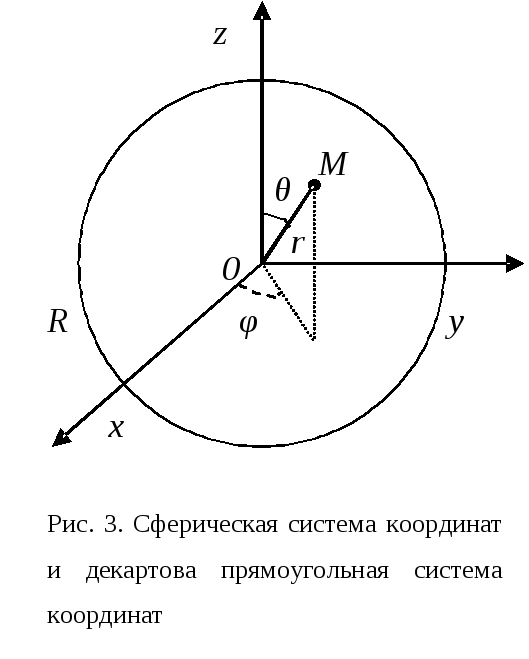 Рассчитаем
момент инерции шара радиусаR и плотности ρ относительно
оси, проходящей через его центр. Введем
декартову прямоугольную систему
координат с началом в центре шара (рис.
18). Пусть осью вращения является ось OZ. Разобьем мысленно шар на малые объемы
Рассчитаем
момент инерции шара радиусаR и плотности ρ относительно
оси, проходящей через его центр. Введем
декартову прямоугольную систему
координат с началом в центре шара (рис.
18). Пусть осью вращения является ось OZ. Разобьем мысленно шар на малые объемы 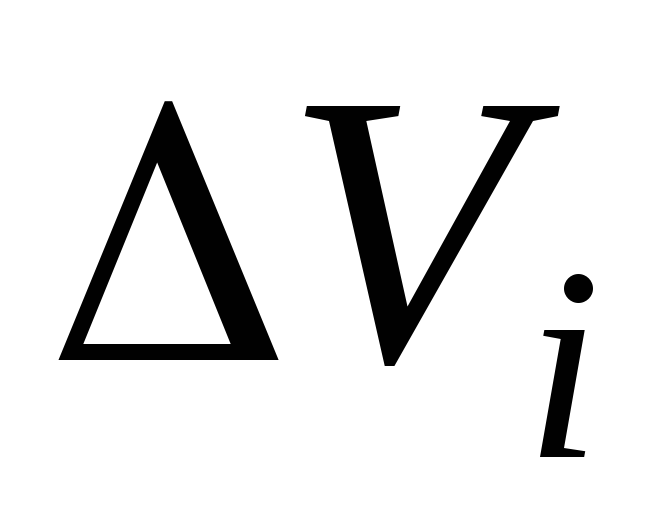
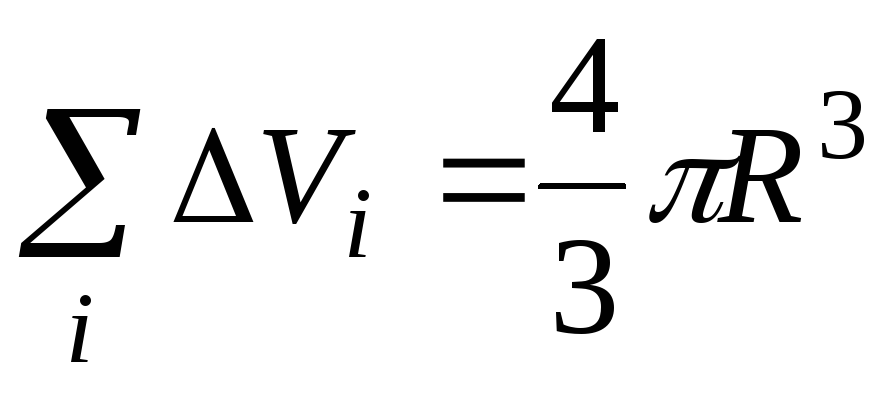 ,
а сумма масс
,
а сумма масс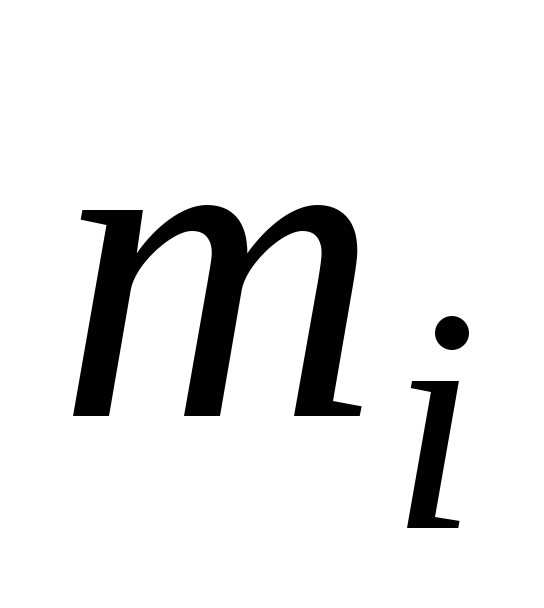 равна его массе. Будем считать их
материальными точками. Момент инерции
системы материальных точек относительно
осиOZ равен сумме
моментов:
равна его массе. Будем считать их
материальными точками. Момент инерции
системы материальных точек относительно
осиOZ равен сумме
моментов: 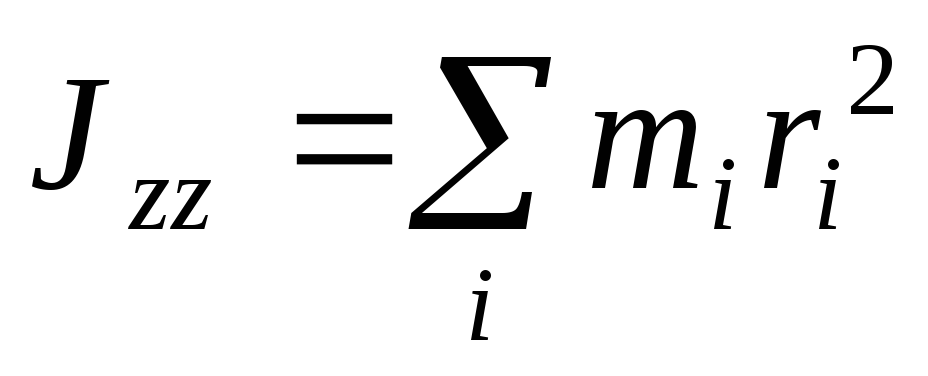 . (25)
. (25)
Шар
однороден, это значит ρ=const,
поэтому 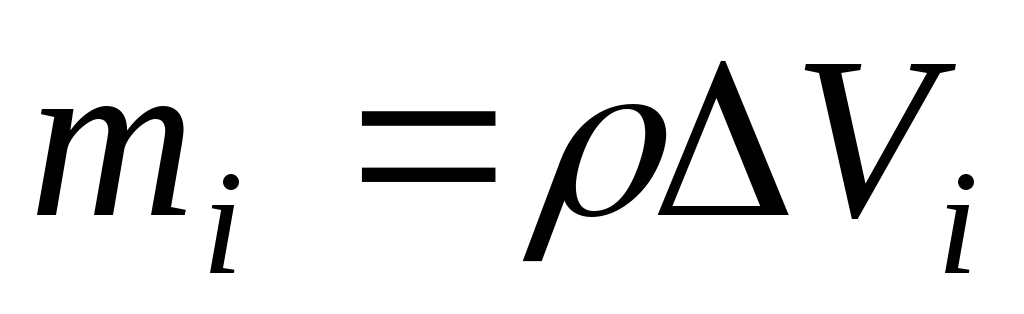 .
Тогда формула (25)
запишется в виде:
.
Тогда формула (25)
запишется в виде:
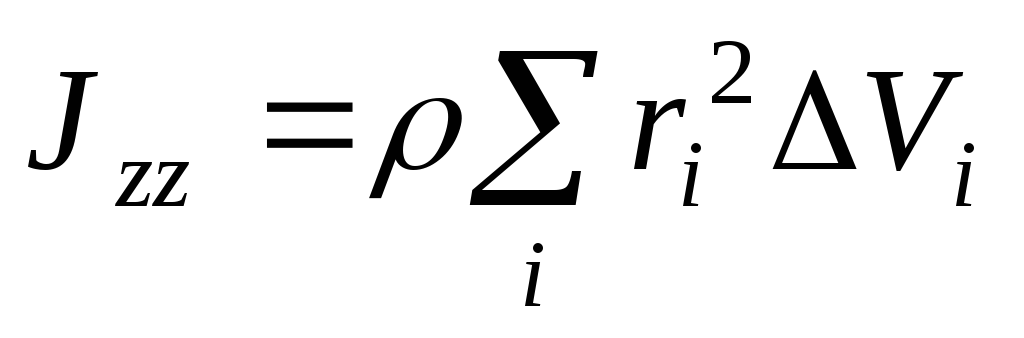 . (26)
. (26)
Если
элементы объема уменьшать так, что 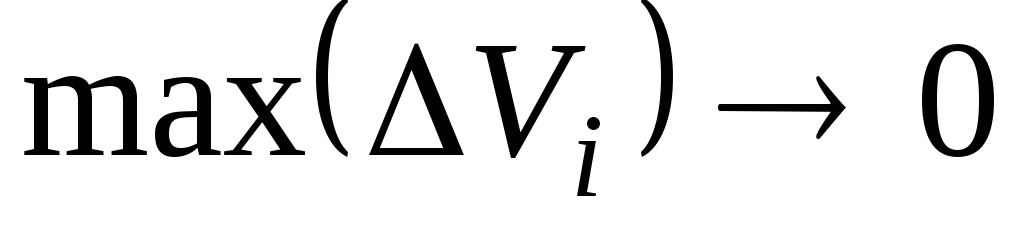 ,
то пределом суммы (26) будет интеграл
,
то пределом суммы (26) будет интеграл
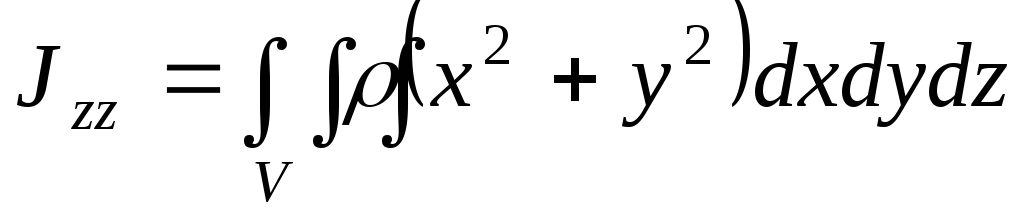 . (27)
. (27)
Введем
сферическую систему координат  .
Положение произвольной точкиM в ней характеризуется тремя числами:
.
Положение произвольной точкиM в ней характеризуется тремя числами: 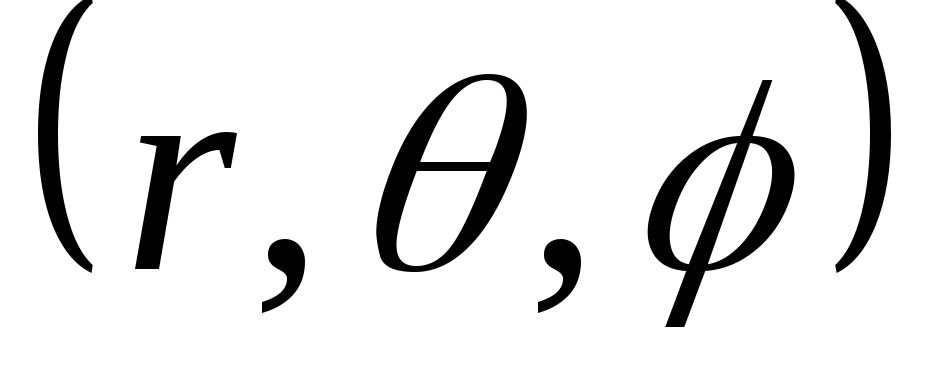
 (28)
(28)
Связь
между декартовыми координатами любой
точки пространства M(x, y, z) и сферическими M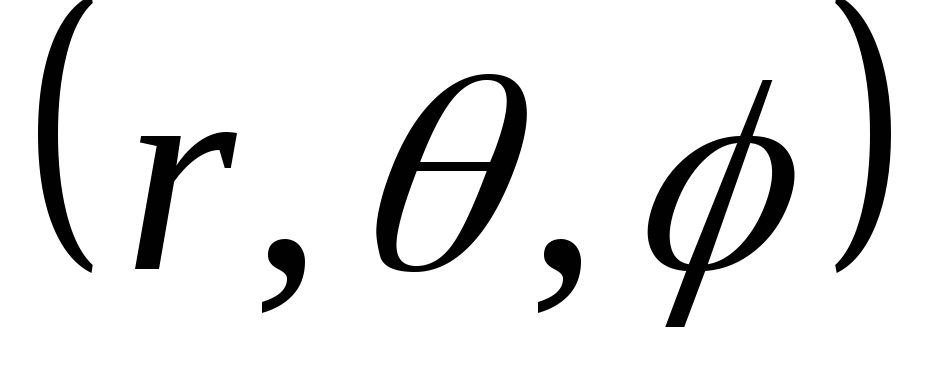 этой же точки имеет вид:
этой же точки имеет вид:
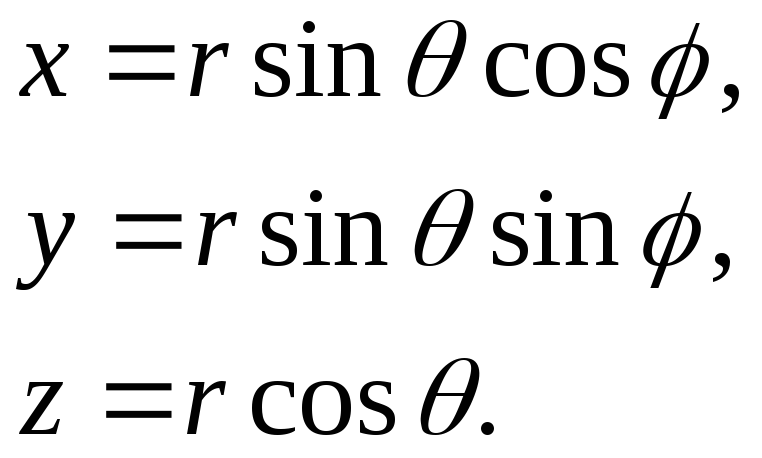
Элемент
объема в сферических координатах 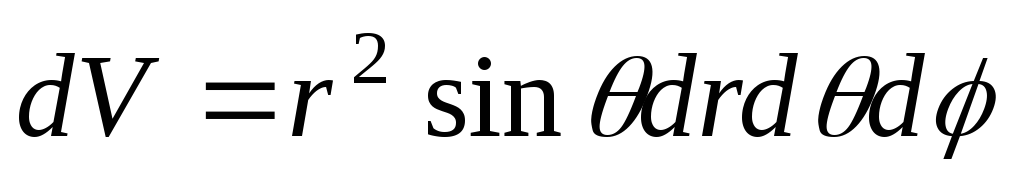 .
Квадрат расстояния от произвольной
точкиM до оси вращения равен:
.
Квадрат расстояния от произвольной
точкиM до оси вращения равен:
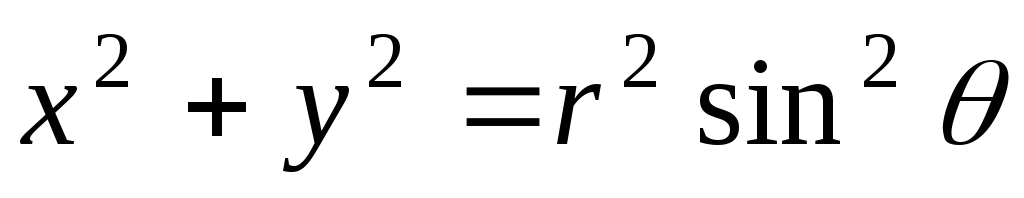 . (30)
. (30)
Формула (27) для момента инерции в сферических координатах примет вид:
 . (31)
. (31)
Вычисление начнем с интеграла
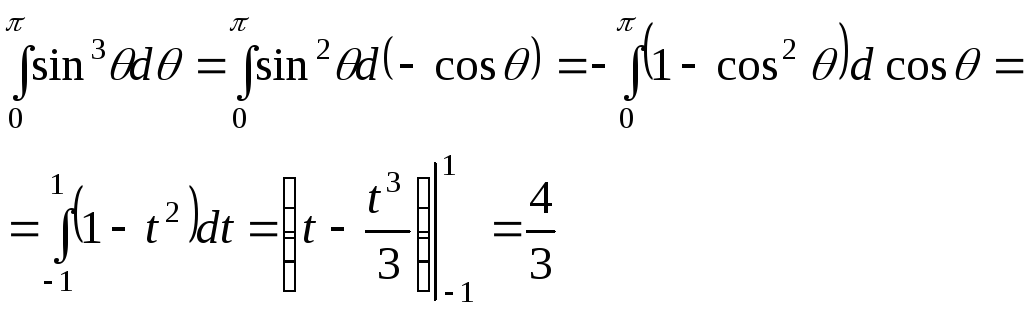 (32)
(32)
Вычислим интеграл
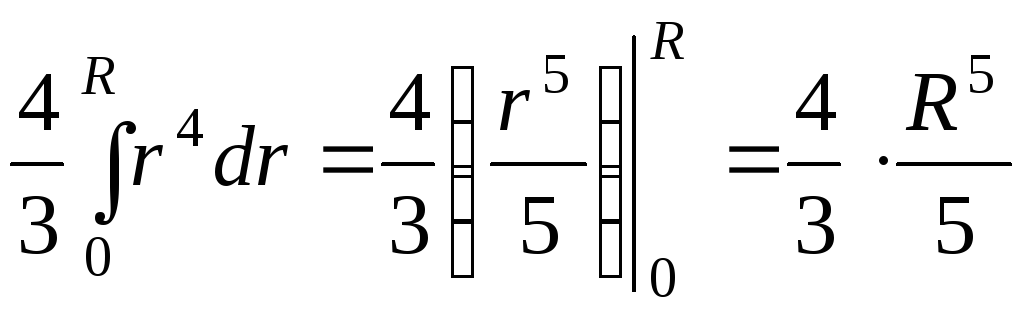 . (33)
. (33)
И, наконец, найдем последний интеграл:
 . (34)
. (34)
Масса
шара равна  .
(35)
.
(35)
Тогда момент инерции шара относительно оси OZ запишется в виде:
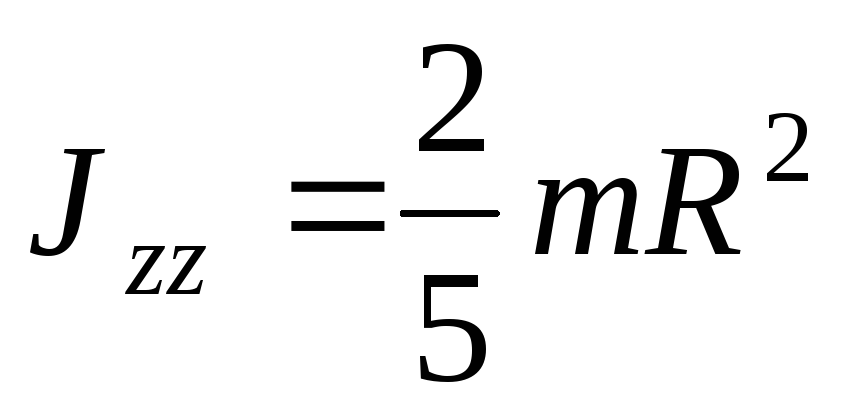 . (36)
. (36)
Аналогично можно рассчитать моменты инерции относительно осей OX и OY.
Ход работы
Определите диапазон углов, в пределах которого справедлива формула (10) и период колебаний не зависит от амплитуды. Измерьте период колебаний маятника для 10 различных значений максимального угла отклонения, в пределах от 150до00,постепенно уменьшая угол отклонения, до тех пор, пока измеряемые периоды колебаний престанут отличаться друг от друга в пределах случайных ошибок эксперимента. Результаты занесите в таблицу 1. Сделайте вывод, в каком диапазоне амплитудных углов колебания можно считать изохронными, то есть не зависящими от амплитуды, с точностью до0,1; 0,5; 1%.
Таблица 1
θ | θ1 | θ2 | θ3 | … | θ10 |
T(θ) | T(θ1) | T(θ2) | T(θ3) | … | T(θ10) |
Определите добротность маятника.
Рассчитайте, при какой длине нити закрепленный на ней груз можно считать материальной точкой. Для этого измерьте при помощи штангенциркуля радиус шара, найдите массу шара и рассчитайте, в каких пределах длины нити момент инерции однородного шара будет составлять 5% от момента инерции МТ, закрепленной на невесомой нити длиныl. Используйте формулу (13)
Исследуйте зависимость периода колебаний Tи квадрата периодаT2от длины нитиl. Результаты занесите в таблицу.
Постройте график экспериментальной
зависимости 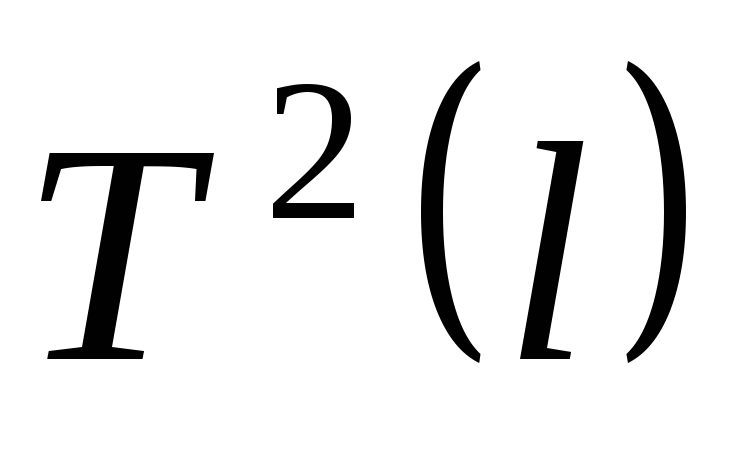 .
.
Обработка результатов
Рассчитайте затухание маятника.
Оцените влияние затухания на период колебаний.
Методом наименьших квадратов найдите тангенс угла наклона зависимости
 и оцените погрешность метода.
и оцените погрешность метода.По тангенсу угла наклона зависимости
 рассчитайтеg
— ускорение свободного падения.
рассчитайтеg
— ускорение свободного падения.
Контрольные вопросы
Что такое амплитуда, частота, фаза колебаний?
Как будут зависеть от времени кинетическая и потенциальная энергия математического маятника?
Какие функции являются решениями уравнения (9)? Проверить.
Как будут связаны между собой смещение, скорость и ускорение при гармоническом колебании?
Постройте график зависимости скорости осциллятора от его смещения при гармоническом колебании.
Что такое нелинейные колебания?
Что такое затухающие колебания? Запишите уравнение затухающих колебаний.
Начертите график зависимости затухающих колебаний от времени.
Рассчитайте логарифмический декремент затухания маятника.
Получите формулы для частоты и периода колебаний при наличии затухания.
Получите уравнение (14) для математического маятника, пользуясь законом сохранения энергии.
Убедитесь, что функция (18) является решением уравнения (17).
Литература: [1] — §34, [2] — § 39-41, [11] – глава 7.
Динамика вращательного движения твердого тела Кинетическая энергия вращения твёрдого тела. Момент инерции твердого тела
Рассмотрим твёрдое тело, которое может вращаться вокруг неподвижной вертикальной оси. Чтобы удержать ось от перемещений в пространстве, заключим её в подшипники. Опирающийся па нижний подшипник фланец Фл , предотвращает передвижение оси в вертикальном направлении .

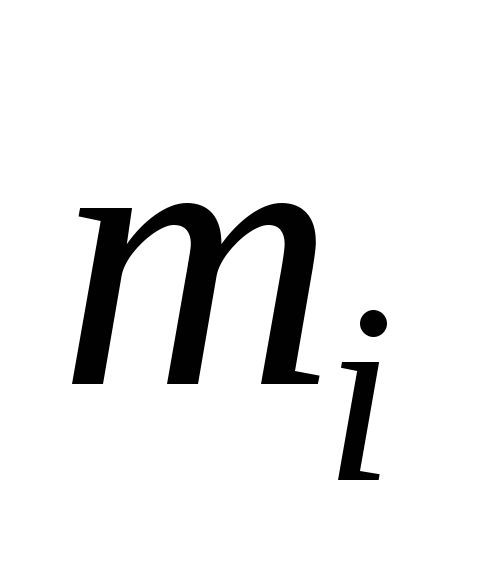 равна
равна 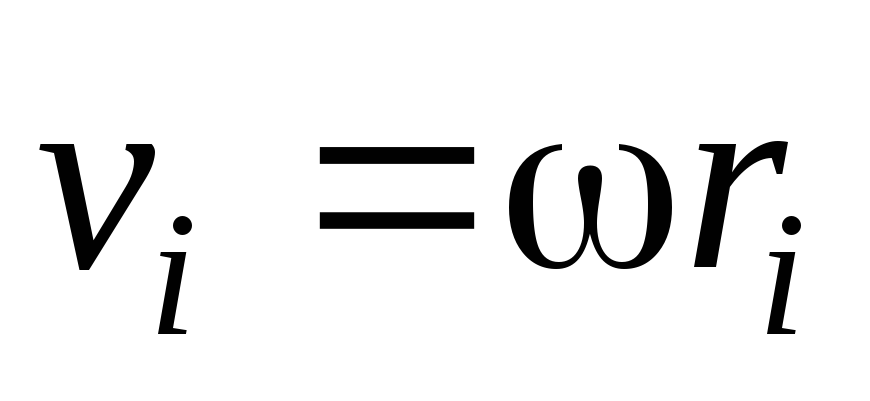 ,
где
,
где 
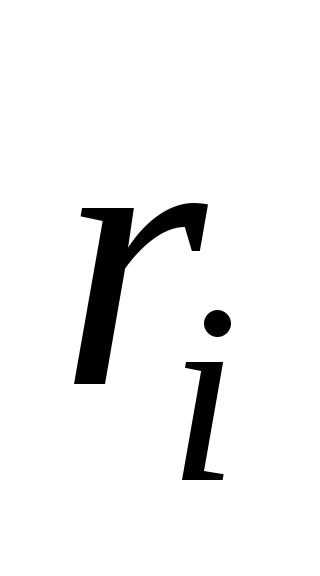 -расстояние
массы
-расстояние
массы 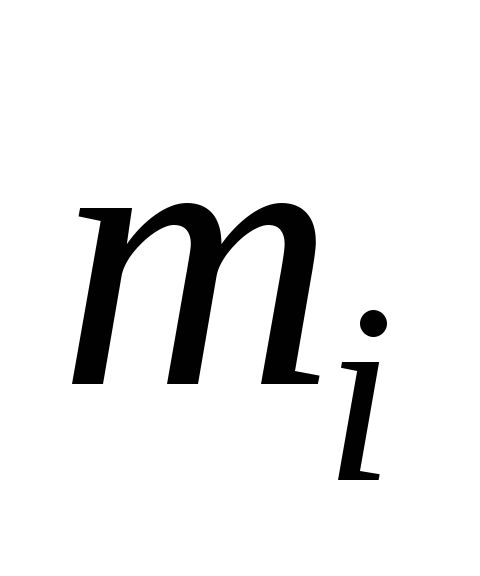 от оси вращения. Следовательно, для
кинетической энергии элементарной
массы получается выражение
от оси вращения. Следовательно, для
кинетической энергии элементарной
массы получается выражение 
Кинетическая энергия вращающегося твёрдого тела складывается из кинетических энергий его частей.
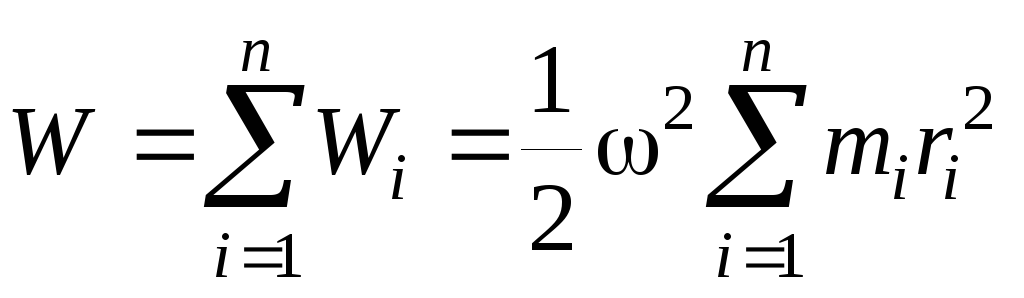
Сумму, входящую в правую часть этого соотношения назовём моментом инерции I тела относительно оси вращения
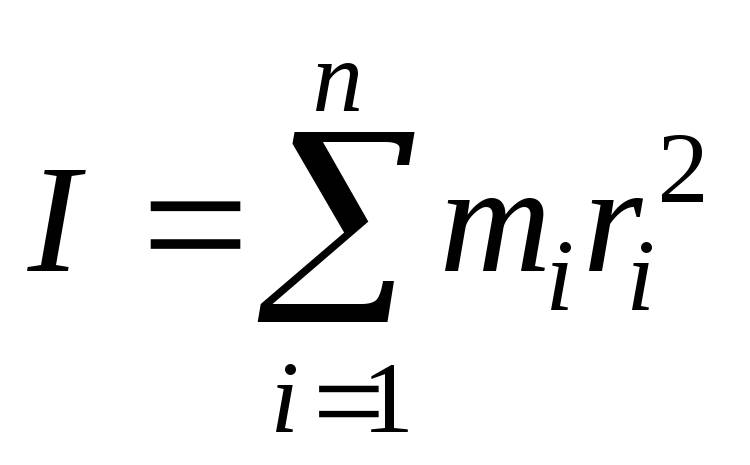 — момент инерции
твёрдого тела.
— момент инерции
твёрдого тела.
Слагаемые этой суммы представляют момент инерции материальной точки относительно оси вращения
 — момент
инерции материальной
— момент
инерции материальной
точки относительно оси вращения.
Размерность
момента инерции [ I ]= 1 кг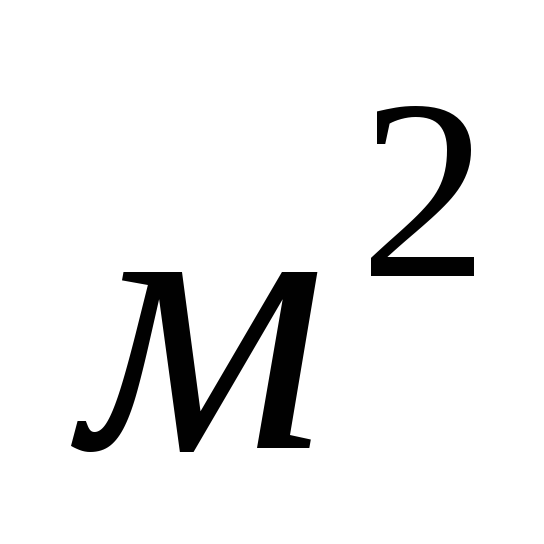
Таким образом, кинетическая энергия тела вращающегося вокруг неподвижной оси, равна
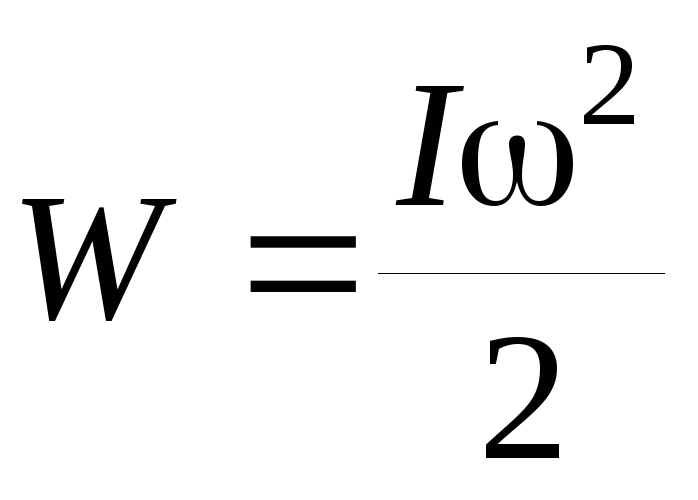 — кинетическая
энергия вращающегося
— кинетическая
энергия вращающегося
твёрдого тела.
Вычисление моментов инерции некоторых тел правильной формы Согласно определению момент инерции твёрдого тела равен
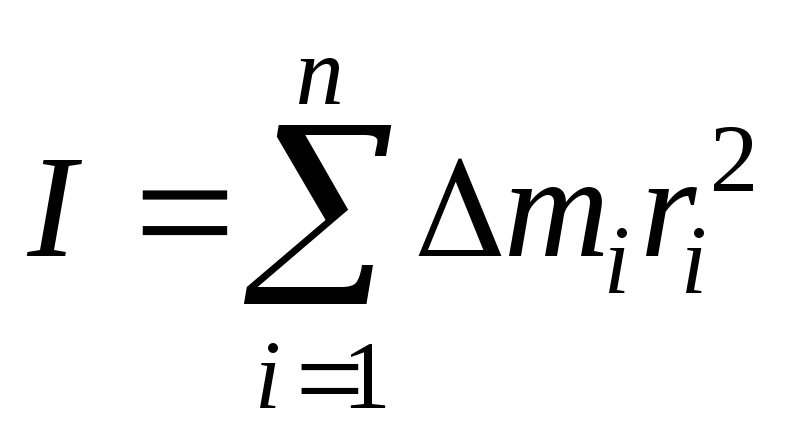 ,
,
где
символом  обозначена элементарная масса
обозначена элементарная масса  .
Элементарная масса
.
Элементарная масса 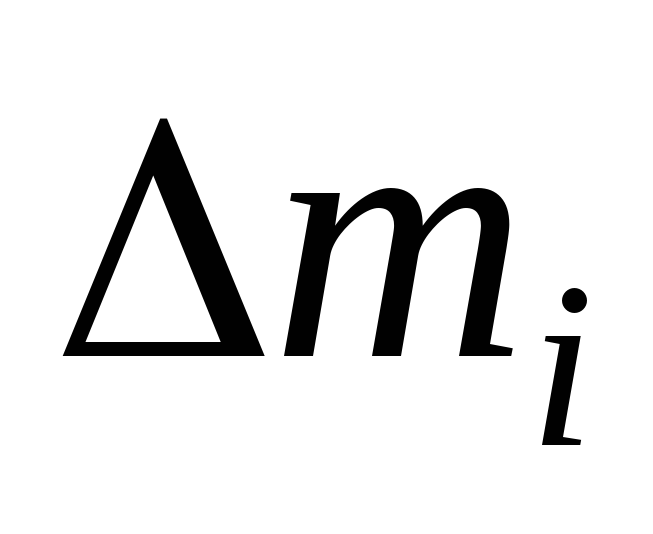 равна произведению плотности тела
равна произведению плотности тела 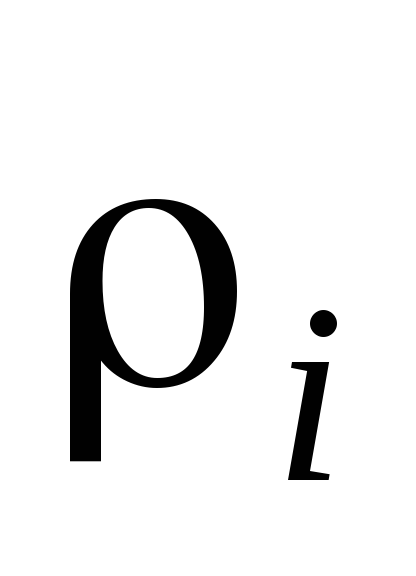 в данной точке на соответствующий
элементарный объём
в данной точке на соответствующий
элементарный объём 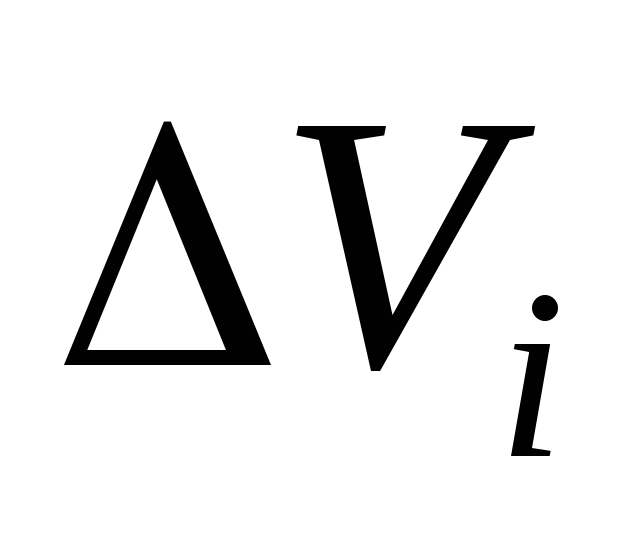
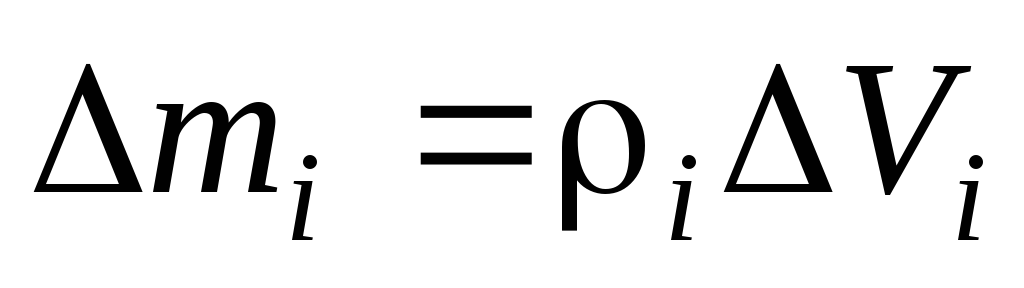 .
.
Следовательно, момент инерции можно представить в виде
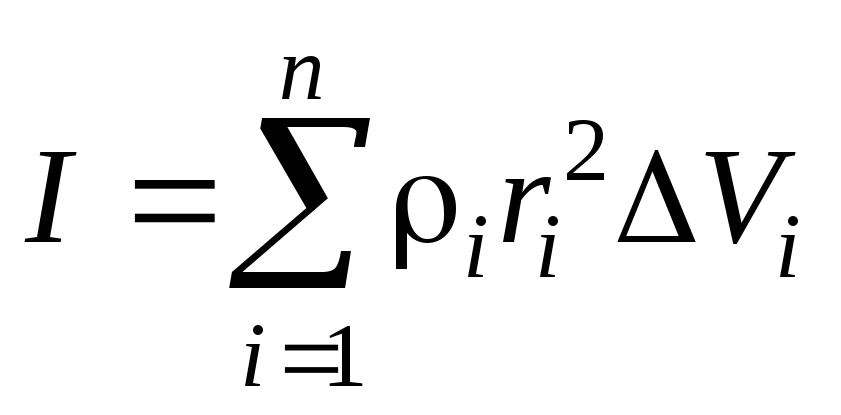 .
.
Это значение момента инерции является приближенным . Точное значение I получается при замене суммирования на интегрирование, т.е.
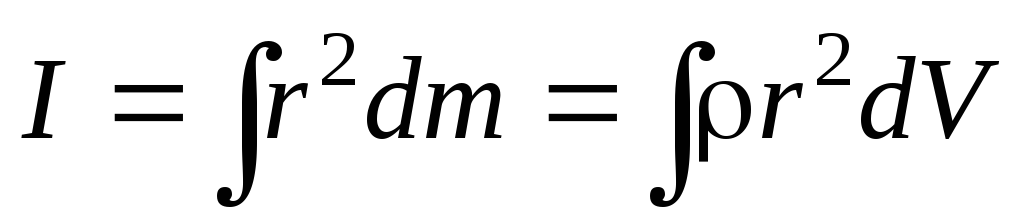 .
.
Эти интегралы берутся по всему объёму тела .
Пример 1: Вычисление момента инерции тонкого стержня массы m и длинной l, вращающегося вокруг оси перпендикулярной стержню и проходящей через центр масс.
Б
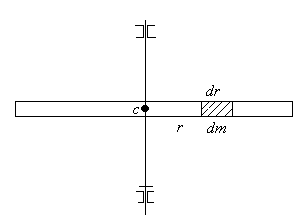
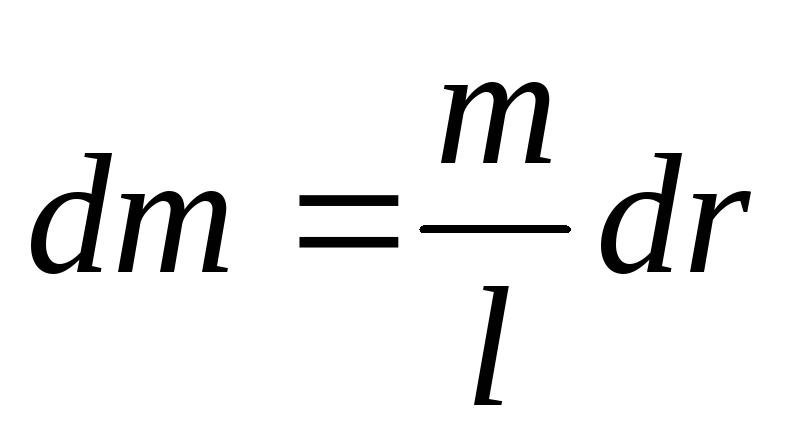
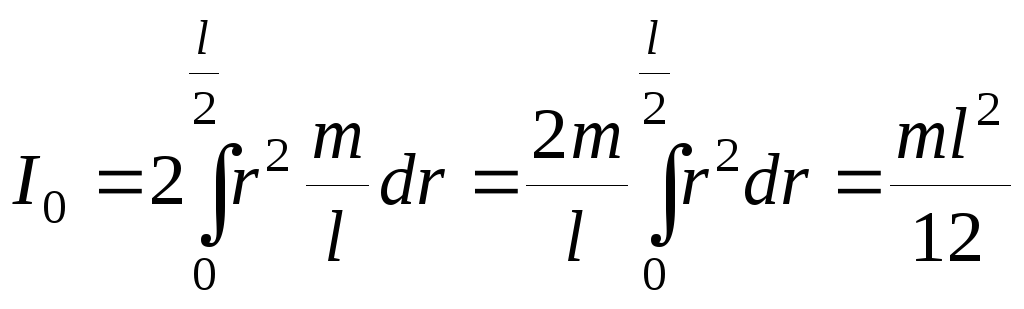
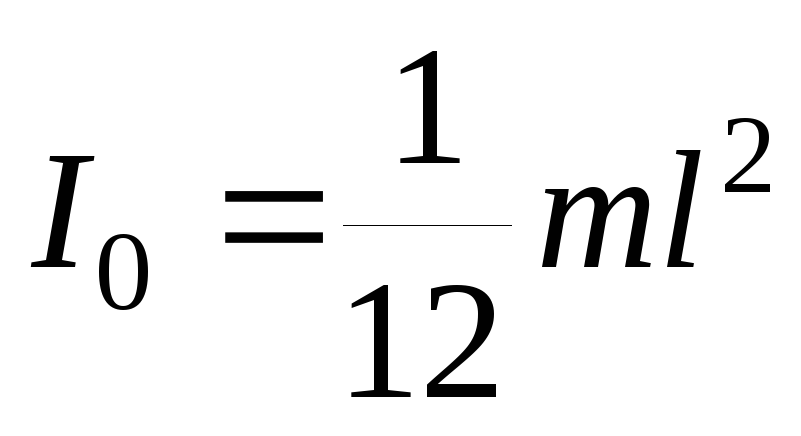
Другие примеры значений моментов инерции для некоторых тел правильной формы приведём без вычислений .
Пример 2: Полый тонкостенный цилиндр, тонкое кольцо :
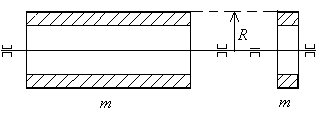
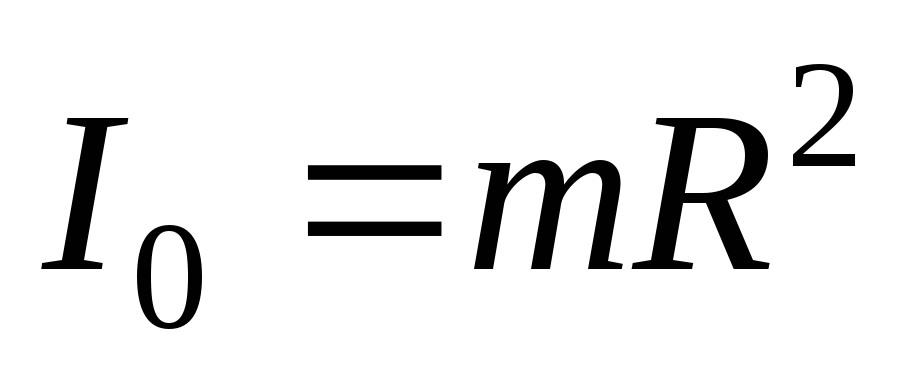 — момент
инерции цилиндра или
— момент
инерции цилиндра или
тонкого кольца
Пример 3: Сплошной цилиндр, диск.
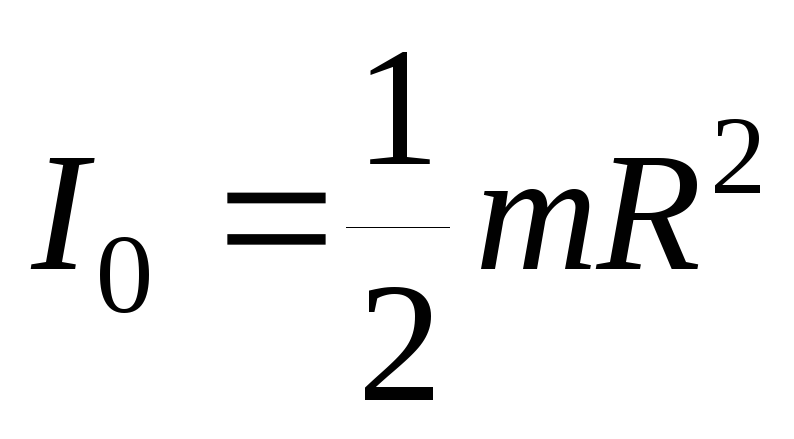
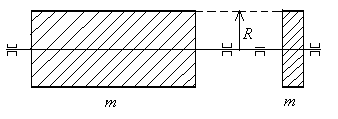
цилиндра или диска
Пример 4: Сплошной шар .
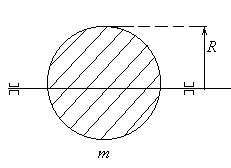
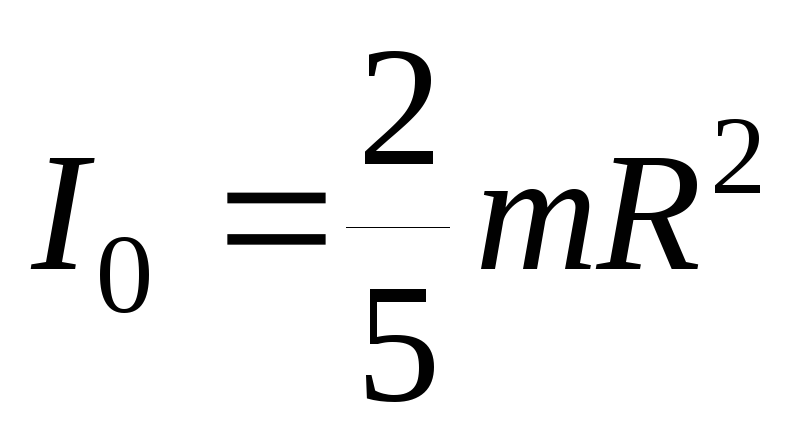 — момент
инерции шара.
— момент
инерции шара.
Заметим, что во всех приведённых примерах, тела предполагаются однородными, и вычисляются моменты инерции относительно центральных осей,
т.е. осей проходящих через центр масс.
Момент инерции, теория и примеры задач
Определение момента инерции
Момент инерции тела по отношению к оси вращения – это мера инертности тела во вращении вокруг этой оси.
Если тело является непрерывным, то суммирование (1) можно свести к интегрированию, если перейти к бесконечно малым элементам тела (dm):
где интегрирование производят по всему объему тела. Величина r – функция положения материальной точки в пространстве; – плотность тела; dV – элементарный объем тела.
Единицей измерения момента инерции в международной системе единиц является:
Теорема Штейнера
Теорема Штейнера позволяет найти момент инерции тела относительно любой оси вращения, если известен момент инерции рассматриваемого тела относительно оси, которая проходит через центр масс этого тела и оси параллельны. Математическая запись теоремы Штейнера:
где J – момент инерции тела относительно произвольной оси вращения; – момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны.
Получается, что момент инерции тела по отношению к оси, которая проходит через его центр масс всегда меньше, чем относительно любой другой оси, параллельной первой.
Некоторые выражения для вычисления моментов инерции тела
Если осями вращения служат оси прямоугольной декартовой системы координат, то для непрерывного тела моменты инерции можно вычислить как:
где m – масса тела; V – объем тела; – координаты бесконечно малого элемента тела.
Если тело является однородным, то момент инерции по отношению к оси является прямо пропорциональным плотности тела и зависит от формы, размеров тела, то того как тело размещено по отношению к оси вращения.
Моменты инерции, которые находят как:
называют центробежными моментами инерции по отношению к осям прямоугольной декартовой системы координат.
Если тело является набором материальных точек, то есть не является непрерывным, то в выражениях (4-9) вместо интегрирования переходят к суммированию.
Примеры решения задач
Момент инерции твердого тела
Определение и общие сведения о моменте инерции твердого тела
Это скалярная (в общем случае тензорная) величина.
где – массы материальных точек, на которые разбивают тело; на квадраты расстояний от материальной точки до оси вращения.
Для непрерывного однородного тела, вращающегося около оси, момент инерции чаще определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Тензор инерции
Совокупность величин:
называют тензором инерции. Диагональные элементы тензора: . Тензор инерции является симметричным.
Пусть все недиагональные элементы тензора равны нулю, не равны нулю только диагональные составляющие. Тогда тензор запишем как:
В таком случае оси тела совпадают с осями координат и являются главными осями инерции. Величины:
называют главными моментами инерции. Тензор в виде (4) приведен у диагональному виду. Моменты инерции, находящиеся вне главной диагонали матрицы (3) называются центробежными. Если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции равны нулю.
Если главные оси проведены через центр масс тела, то они называются центральными главными осями, а тензор центральным тензором.
Главные оси не всегда для тела не всегда легко отыскать. Но иногда достаточно использовать соображения симметрии. Так, в шаре относительно любой точки главные оси можно найти так. Одна из главных осей проходит через центр шара, две другие ориентированы произвольно в плоскости, которая перпендикулярна первой оси.
Составляющие момента инерции сплошного тела относительно осей декартовой системы координат определены как:
где – координаты элемента массы тела (), которая обладает объемом .
Момент инерции твердого тела зависит от формы тела и распределения ассы в теле относительно оси вращения.
Величины, равные:
называют радиусами инерции тела по отношению к соответствующим осям системы координат.
Теорема Штейнера
В некоторых случаях вычисление момента инерции существенно облегчает знание теоремы Штейнера (иногда ее называют теоремой Гюйгенса): Момент инерции тела (J) относительно произвольной оси равен моменту инерции относительно оси, которая проведена через центр масс рассматриваемого тела (), плюс произведение массы тела (m) на расстояние между осями в квадрате, при условии, если оси параллельны:
Примеры решения задач
6. Элементы механики твердого тела
11
Механика твердого тела
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Лекция 6
Момент инерции материальной точки
Момент инерции м. т. и тел является скалярной величиной и широко применяется не только в физике, но и ряде других дисциплин: теоретическая, прикладная механика и т. д.
Моментом инерции м. т. относительно полюса называют скалярную величину, равную произведению массы этой точки на квадрат расстояния до полюса.
Момент инерции м. т. можно найти по формуле
I0 = m R2, (6.1)
где m – масса м. т.; R – расстояние до полюса 0.
Единицей измерения момента инерции в СИ является килограмм, умноженный на метр в квадрате (кгм2).
Момент инерции системы материальных точек
Тело можно представить состоящим из большого числа м.т., поэтому момент инерции системы м. т.
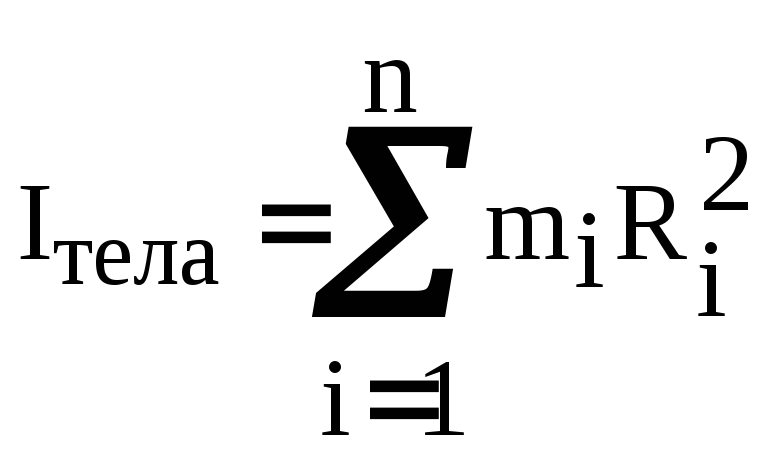 , (6.2)
, (6.2)
где mi – масса i-й м. т.; Ri – ее расстояние до полюса 0.
Моментом инерции системы м. т. или тела относительно полюса (точки) называют алгебраическую сумму произведений масс м. т., из которых состоит тело, на квадрат расстояния их до полюса 0.
При непрерывном распределении массы по объему тела момент инерции относительно полюса находится по формуле
 (6.3)
(6.3)
В случае момента инерции относительно полюса массу dm умножают на квадрат расстояния до неподвижной точки (полюса), а в случае момента инерции относительно оси – до неподвижной оси.
В декартовой системе координат сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающих в одной точке 0, равна удвоенному моменту инерции этого тела относительно этого же начала:
Ix + Iy+ Iz = 2I0 .(6.4)
6.3. Теорема Штейнера
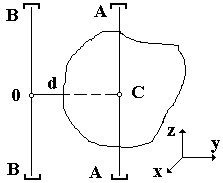
Рис. 6.1
Для установления связи (рис. 5.1) между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера (Штейнера – Гюйгенса):I = Ic + md2. (6.5)
Момент инерции тела относительно произвольной оси равен моменту инерции относительно оси, параллельной данной, проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между осями.
6.4. Момент инерции однородного стержня
Моменты инерции различных тел можно найти по формуле I = mR2,
где m – коэффициент пропорциональности, который зависит от формы тела и его расположения относительно оси вращения.
Найдем момент инерции однородного стержня относительно оси, проходящей через один из его концов, перпендикулярно продольной геометрической оси симметрии (рис. 6.2). Пусть ось вращения ВВ проходит через правый конец стержня (т. Г), тогда I = mmL2, где L — длина стержня.
Согласно
теореме Штейнера, имеем 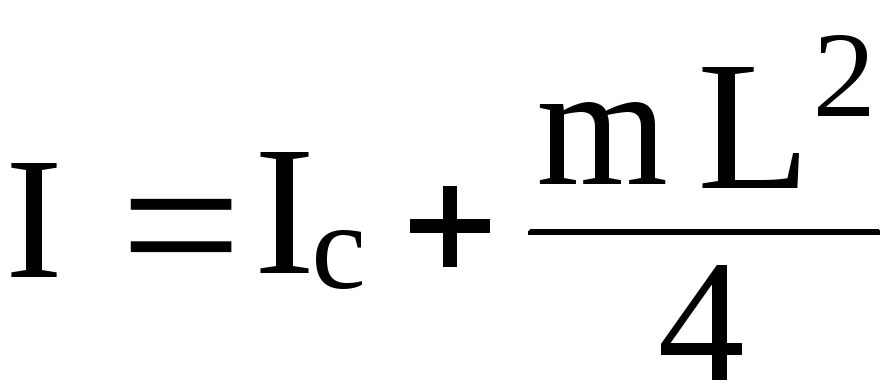 .
.
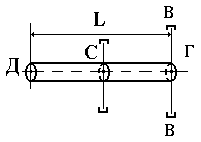
Рис. 6.2
Величину момента инерции Ic относительно оси, проходящей через центр масс (точка С), представим как сумму моментов инерции двух стержней с длинами ДС = СГ = L/2 и массой каждого, равной m/2 стержня, т. е. 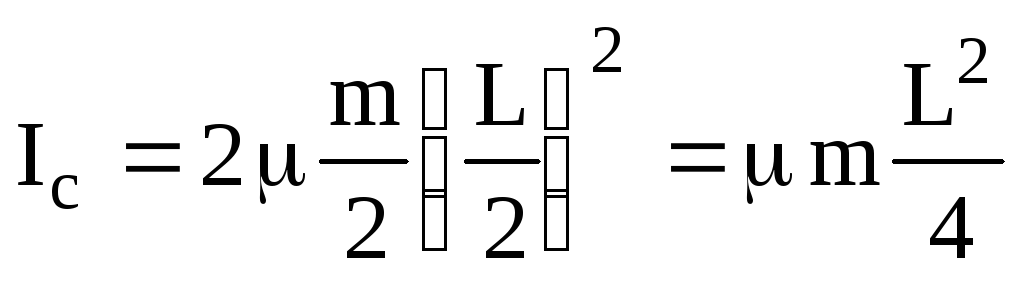 .
.
Подставим
значения момента инерции I и Ic в формулу теоремы Штейнера – Гюйгенса
и найдем :  .
.
После преобразования получим, что m = 1 / 3.
Следовательно,
момент инерции стержня относительно
оси, проходящей через центр масс, 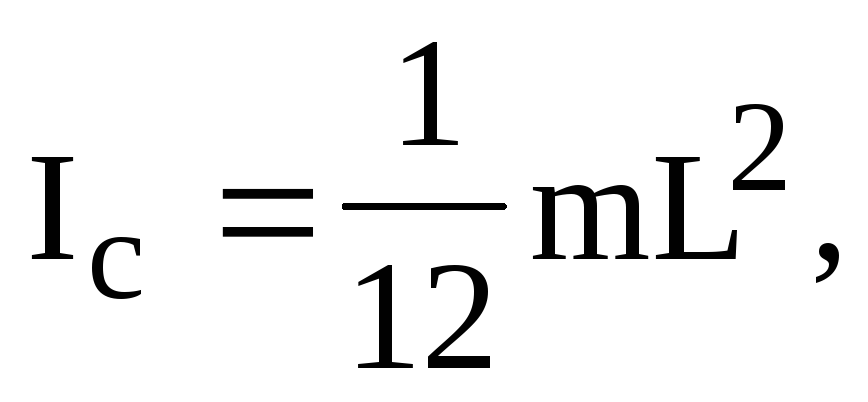 (6.6)
(6.6)
относительно
оси ВВ, 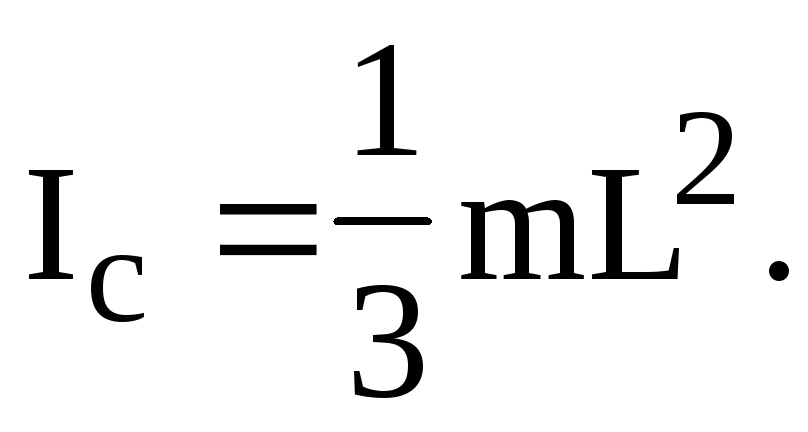 (6.7)
(6.7)
Момент инерции тела, теория и примеры
Определение момента инерции
Это скалярная (в общем случае тензорная) физическая величина, которая равна произведению масс материальных точек () на которые следует провести разбиение рассматриваемого тела, на квадраты расстояний () от них до оси вращения:
В том случае, если тело можно считать непрерывным, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как , тогда J тела, вращающегося около оси:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Для однородного тела выражение (2) можно представить как:
Момент инерции в международной системе единиц измеряется в :
Величина J входит в основные законы, при помощи которых описывают вращение твердого тела.
В общем случае величина момента инерции зависит от направления оси вращения, а так как в процессе движения вектор обычно изменяет свое направление относительно тела, то момент инерции следует рассматривать как функцию времени. Исключением является момент инерции тела, вращающегося вокруг неподвижной оси. В таком случае момент инерции остается постоянным.
Теорема Штейнера
Теорема Штейнера дает возможность вычислить момент инерции тела относительно произвольной оси вращения, когда является известным момент инерции рассматриваемого тела по отношению к оси, проходящей через центр масс этого тела и эти оси являются параллельными. В математическом виде теорема Штейнера представляется как:
где – момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны. Из выражения (4) следует, что:
Некоторые выражения для вычисления моментов инерции тела
При вращении вокруг оси материальная точка имеет момент инерции равный:
где m – масса точки; r – расстояние от точки до оси вращения.
Для однородного тонкого стержня массой m и длиной l J относительно оси, проходящей через его центр масс (ось перпендикулярна стержню), равен:
Тонкое кольцо, с массой вращающееся около оси, которая проходит через его центр, перпендикулярно плоскости кольца, то момент инерции вычисляется как:
где R – радиус кольца.
Круглый однородный диск, радиуса R и массы m имеет J относительно оси, проходящей через его центр и перпендикулярной плоскости диска, равный:
Для однородного шара
где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.
Если осями вращения являются оси прямоугольной декартовой системы координат, то для непрерывного тела моменты инерции можно вычислить как:
где – координаты бесконечно малого элемента тела.


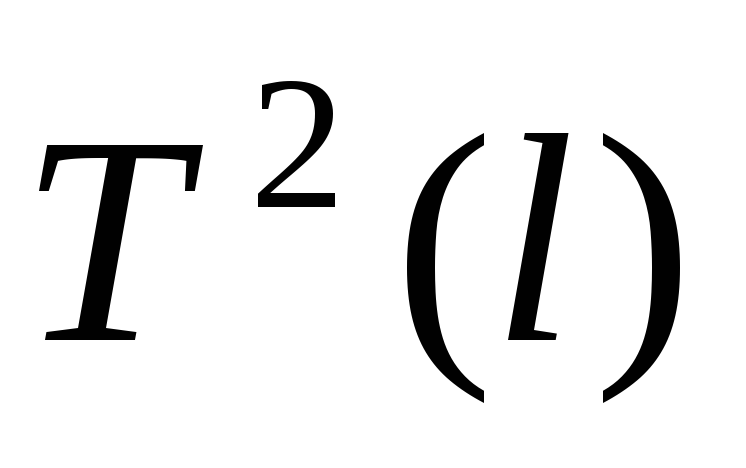 и оцените погрешность метода.
и оцените погрешность метода. рассчитайтеg
— ускорение свободного падения.
рассчитайтеg
— ускорение свободного падения.