12Момент импульса и момент силы относительно точки и оси. Уравнение моментов.
Момента импульса механической системы относительно некоторой точки О как векторную сумму моментов импульса ее отдельных частиц: L=(сумм)i Li, где все векторы определены относительно одной и той же точки О заданной системы отсчета. Момент импульса системы – величина аддитивная: момент
импульса системы равен векторной сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют ли они между собой. Момент импульса системы может изменяться только под
действием суммарного момента всех внешних сил.
Моментом импульса механической системы относительно оси называется проекция на эту ось вектора момента импульса системы относительно любой точки, выбранной на данной оси.
Моментом силы F относительно некоторой точки О называется физическая величина, численно равная векторному произведению радиус-вектора
Модуль момента силы равен M = lF, где l = rsina – плечо вектора силы F относительно точки О.
Уравнение моментов. Найдем скорость изменения момента импульса тела.
dL/dt = ([dri/dt·pi] + [ri·dpi/dt]). (7.4)
Первое слагаемое в выражении (7.4) равняется нулю, поскольку производная от радиуса по времени, являющаяся скоростью iой
dpi/dt = Fi + Fik*, где Fi и Fik* — соответственно сумма внешних и внутренних силы, действующие на iый элемент тела.
Подставив это выражение в (7.4), получим, что скорость изменения момента импульса равняется сумме моментов внешних Mi и внутренних Mik* сил. Причем, последний из них равен нулю. Таким образом,
dL/dt = (Mi + Mi*) = Mi = M. (7.5)
Следовательно, скорость изменения момента импульса вращающегося тела равняется суммарному моменту внешних сил, действующих на него.
Уравнение (7.5) называется уравнением вращательного движения в форме моментов (уравнением моментов).
13 Момент инерции твердого тела.

14Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси.
Рассмотрим
произвольное тело, ось вращения которого
закреплена в неподвижных подшипниках.
Разобьём тело на элементарные массы 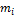 ,
модуль момента импульса которых
,
модуль момента импульса которых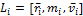
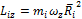 .
Момент импульса всего тела относительно
осиOZ
.
Момент импульса всего тела относительно
осиOZ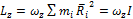 . Момент
инерции твёрдого тела — сумма произведений элементарных масс
на квадрат их расстояния до произвольно
выбранной оси. Момент инерции зависит
от выбора оси и распределения массы
тела. Воспользуемся уравнением моментов
. Момент
инерции твёрдого тела — сумма произведений элементарных масс
на квадрат их расстояния до произвольно
выбранной оси. Момент инерции зависит
от выбора оси и распределения массы
тела. Воспользуемся уравнением моментов 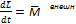 .
Спроецируем это уравнение на ось OZ
и подставим в полученную формулу для
.
Спроецируем это уравнение на ось OZ
и подставим в полученную формулу для 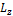 :
: 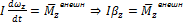 — основное
уравнение динамики вращательного
движения,
— основное
уравнение динамики вращательного
движения, 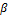 – угловое ускорение тела.
– угловое ускорение тела.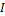 является
аналогом
является
аналогом 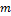 и
характеризует инертность тела по
отношению к вращению. Если суммарный
момент внешних сил = 0, а в пределах тела
происходит перемещение масс, то проекция
момента импульса сохраняется
и
характеризует инертность тела по
отношению к вращению. Если суммарный
момент внешних сил = 0, а в пределах тела
происходит перемещение масс, то проекция
момента импульса сохраняется 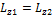 .
если распределение массы несимметрично
относительно оси вращения, то момент
импульса тела будет образовывать
некоторый угол с.
при вращении тела
.
если распределение массы несимметрично
относительно оси вращения, то момент
импульса тела будет образовывать
некоторый угол с.
при вращении тела 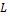 вращается,
образуя некоторый конус. Если распределение
масс симметрично,
вращается,
образуя некоторый конус. Если распределение
масс симметрично, 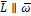 ,
,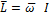 вместо
вместо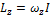 .
.
6. Момент импульса относительно неподвижной точки.
Моментом импульса материальной точки аотносительно неподвижной точки 0 называется физическая величина, равная векторному произведению
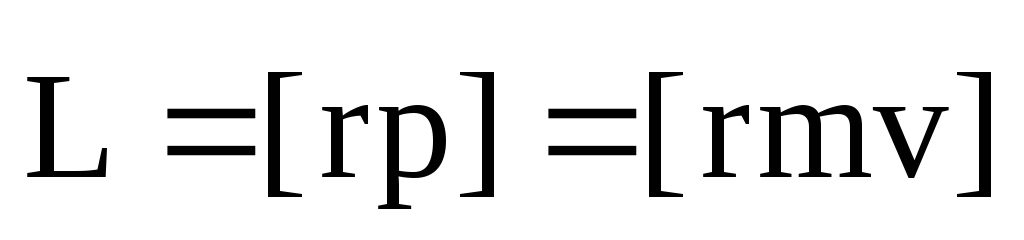 ,
(20)
,
(20)
где  — радиус-вектор проведенный из точки 0
в точку а,
— радиус-вектор проведенный из точки 0
в точку а,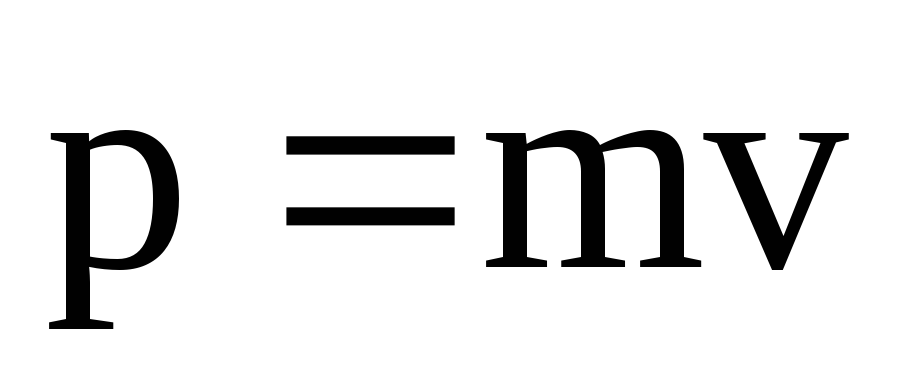

Рис.9.
Направление вектора  совпадает с направлением поступательного
движения правого винта при его вращении
от
совпадает с направлением поступательного
движения правого винта при его вращении
от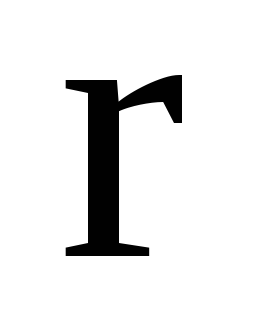 к
к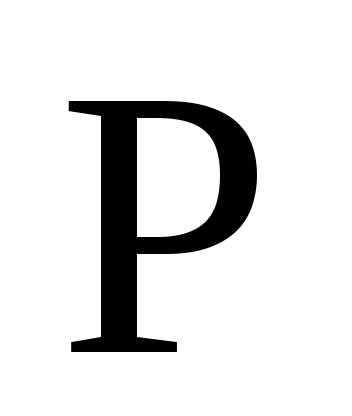 .
Модуль вектора момента импульса
.
Модуль вектора момента импульса
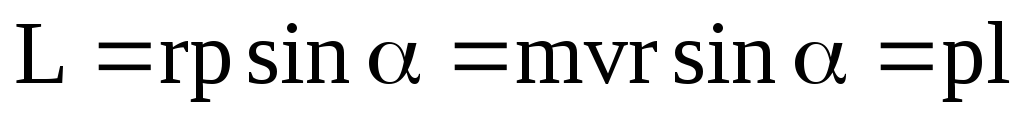 (21)
(21)
где  — угол между векторами
— угол между векторами и
и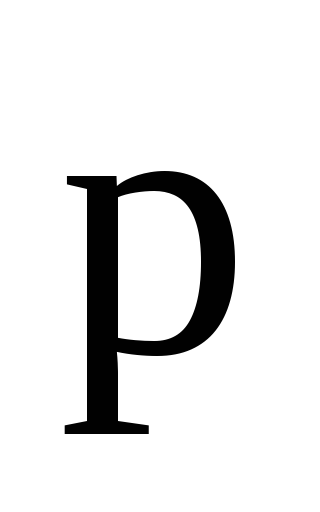 ,
,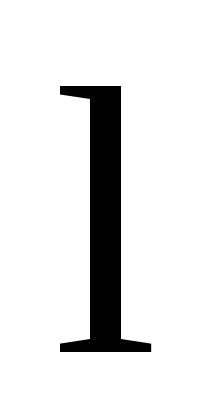 — плечо вектора
— плечо вектора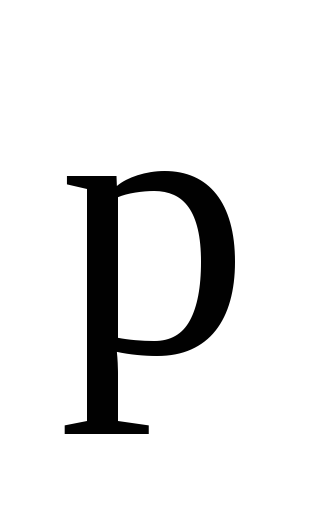 относительно точки 0. Моментом импульса
системы материальных точек относительно
неподвижной точки 0 называется векторная
сумма моментов импульсов всех материальных
точек системы относительно той же точки
0
относительно точки 0. Моментом импульса
системы материальных точек относительно
неподвижной точки 0 называется векторная
сумма моментов импульсов всех материальных
точек системы относительно той же точки
0
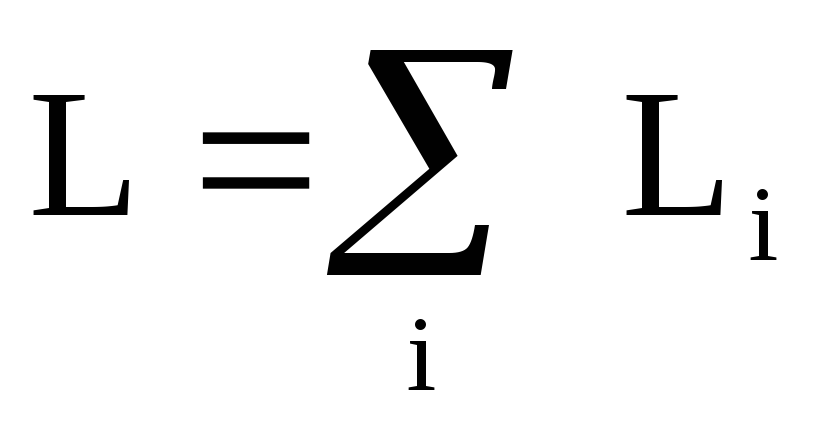 (22)
(22)
7. Момент импульса относительно неподвижной осиz.
Моментом импульса материальной точки аотносительно неподвижной осиzназывается скалярная величина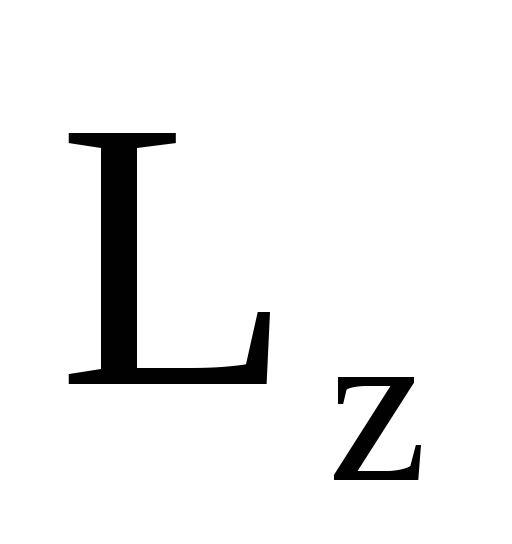 ,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки 0 данной
оси. Значение момента импульса не зависит
от положения точки 0 на осиz.
,
равная проекции на эту ось вектора
момента импульса, определенного
относительно произвольной точки 0 данной
оси. Значение момента импульса не зависит
от положения точки 0 на осиz.
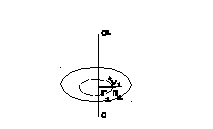
Рис.10.
Рассмотрим вращение твердого тела
вокруг неподвижной оси z(О-О1). Каждая точка твердого тела
описывает горизонтальную окружность
радиуса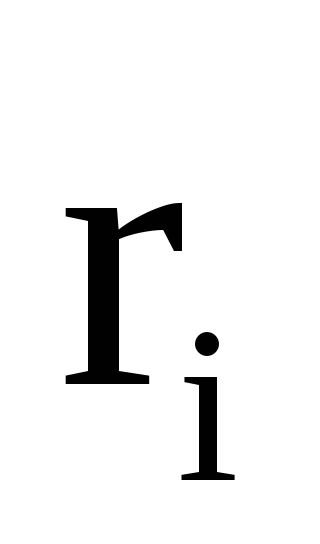 со скоростью
со скоростью .
Скорость
.
Скорость .и
импульс
.и
импульс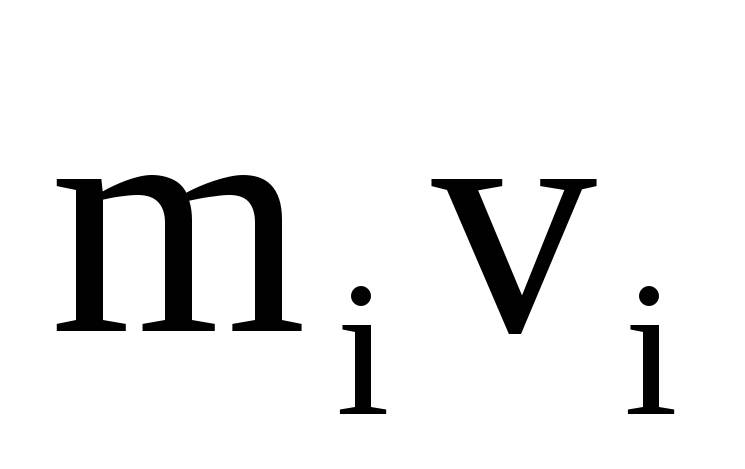 перпендикулярны этому радиусу,
поэтомурадиус является плечом вектора
перпендикулярны этому радиусу,
поэтомурадиус является плечом вектора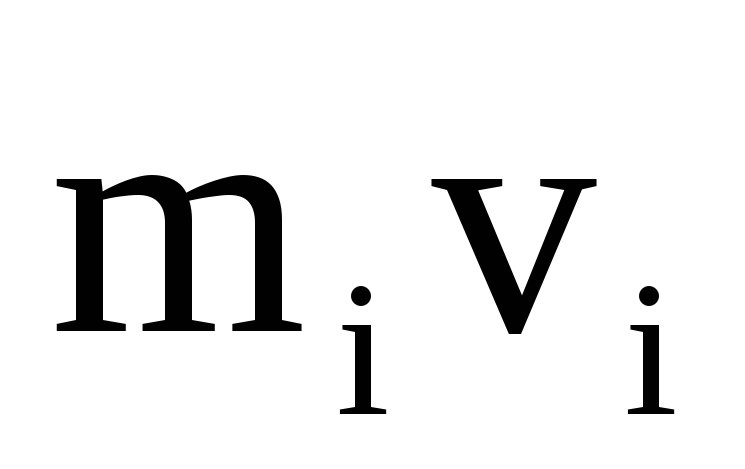
 =900).
Момент импульса каждой точки твердого
тела относительно осиzравен
=900).
Момент импульса каждой точки твердого
тела относительно осиzравен 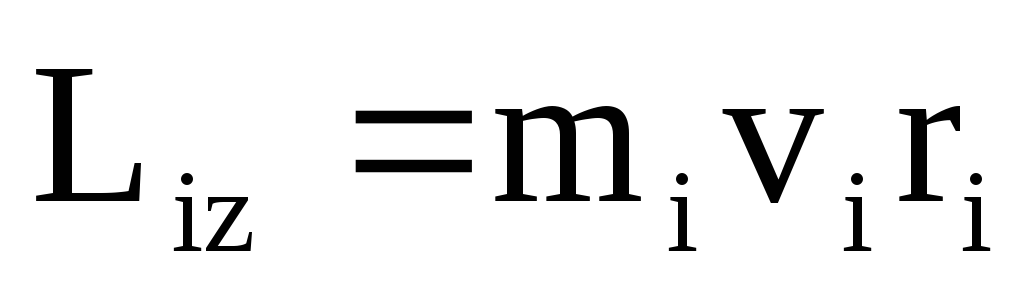 (23)
(23)
и направлен по оси в сторону, определяемую правилом правого винта. Моменты импульса всех точек твердого тела будут сонаправлены, поэтому момент импульса твердого тела относительно оси есть сумма моментов импульсов отдельных частиц
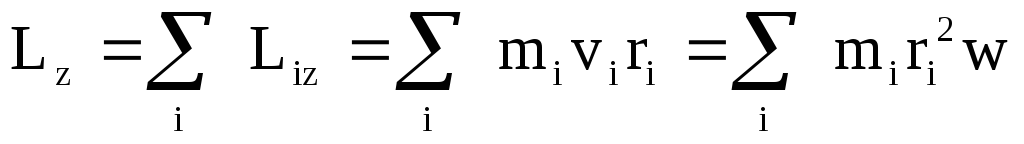
то есть все точки твердого тела вращаются с одинаковой угловой скоростью, то wможно вынести за знак суммы
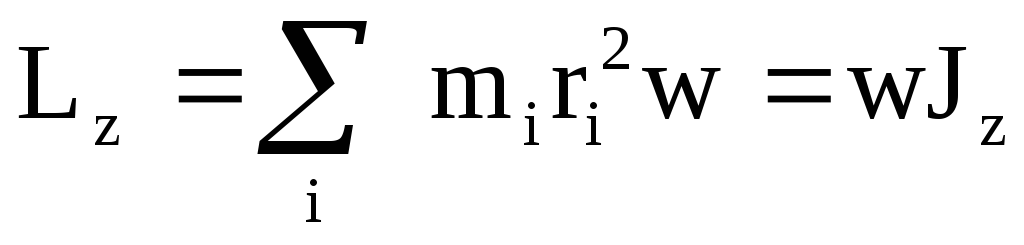 ,
,
то есть
.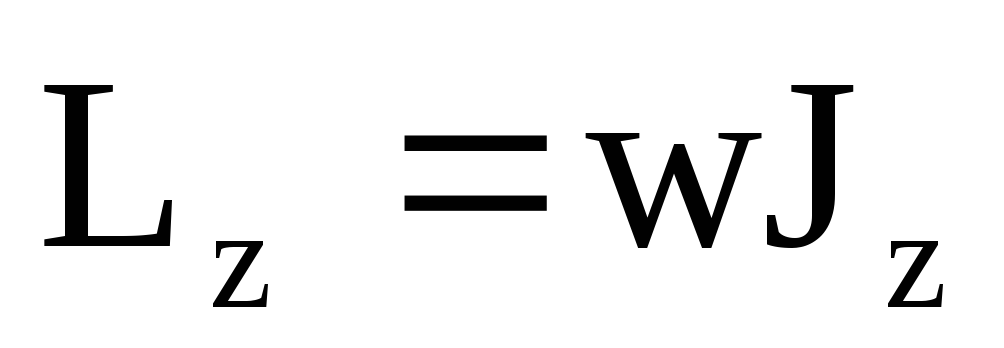 .
.
Момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.
Лекция 6. Уравнения динамики вращательного движения.
1. Закон сохранения момента импульса.
Продифференцируем момент импульса  по времени
по времени
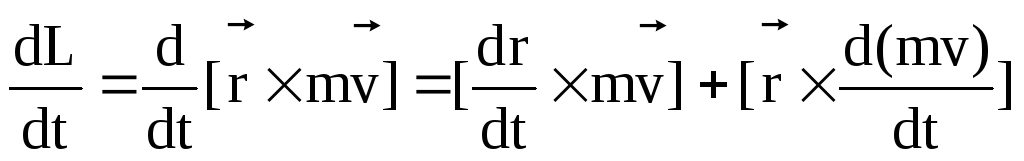 .
.
Величина 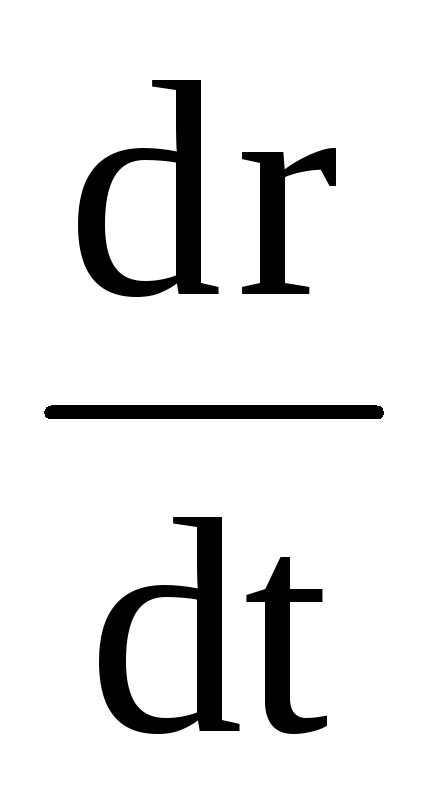 есть скорость материальной точки,
связанная с ее импульсом соотношением
есть скорость материальной точки,
связанная с ее импульсом соотношением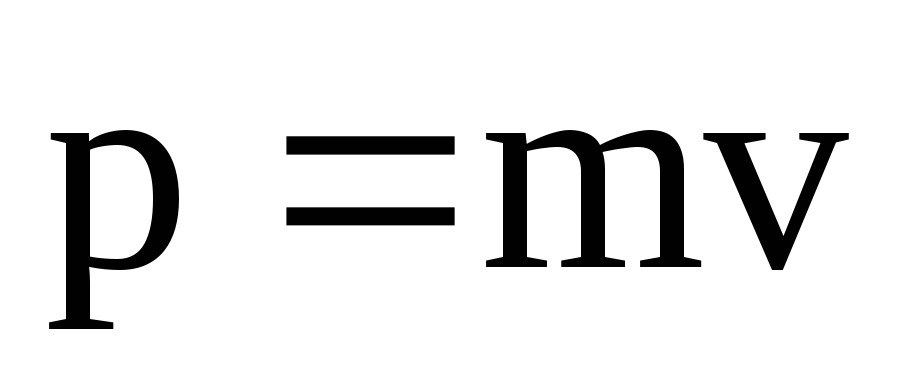 .
Поэтому первое слагаемое
.
Поэтому первое слагаемое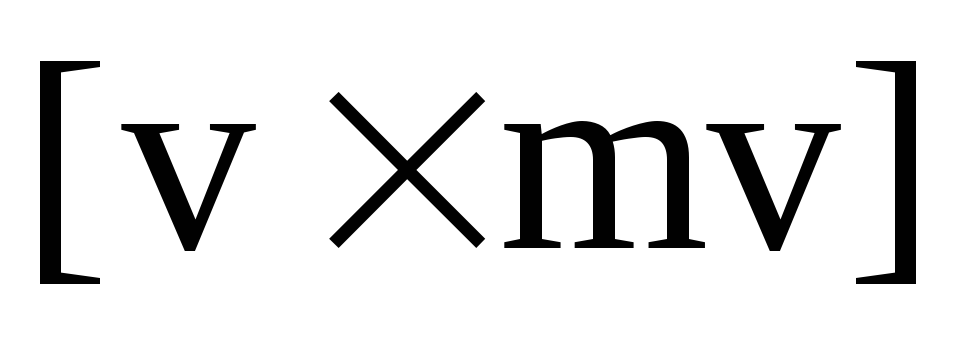 равно нулю как векторное произведение
коллинеарных векторов
равно нулю как векторное произведение
коллинеарных векторов и
и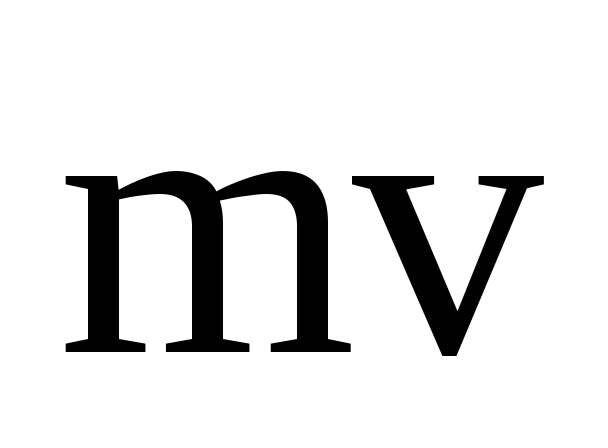 ,
(
,
(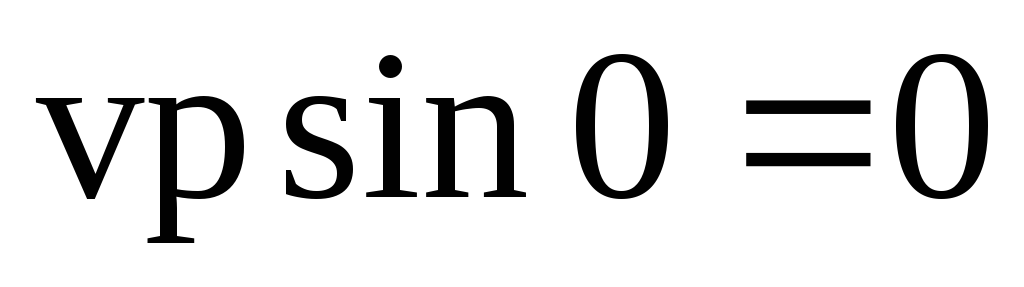 )
Второе слагаемое можно преобразовать
с помощью уравнения Ньютона
)
Второе слагаемое можно преобразовать
с помощью уравнения Ньютона
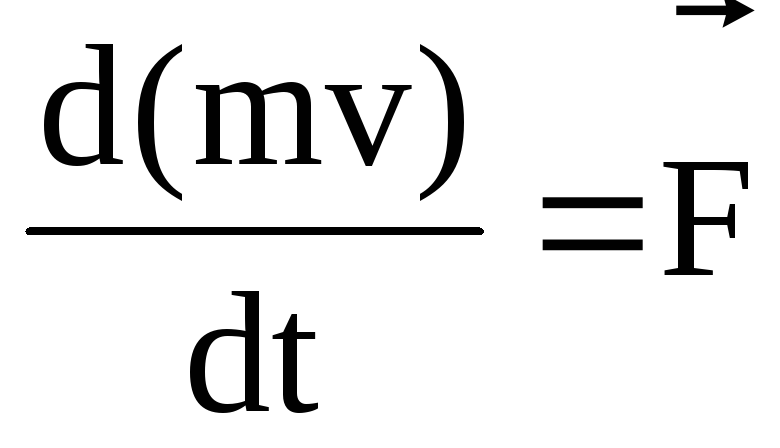 .
.
Тогда
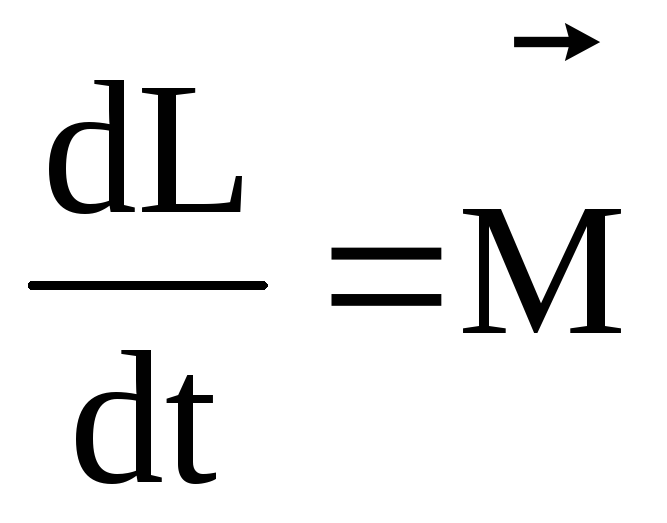 .
(1)
.
(1)
Это уравнение моментов относительно неподвижной точки. Производная по времени момента импульса материальной точки (относительно неподвижной точки) равна моменту силы относительно этой же точки.
Уравнение моментов (1) можно обобщить на случай произвольной системы материальных точек. Пусть система состоит из nматериальных точек вращающихся вокруг центра 0.
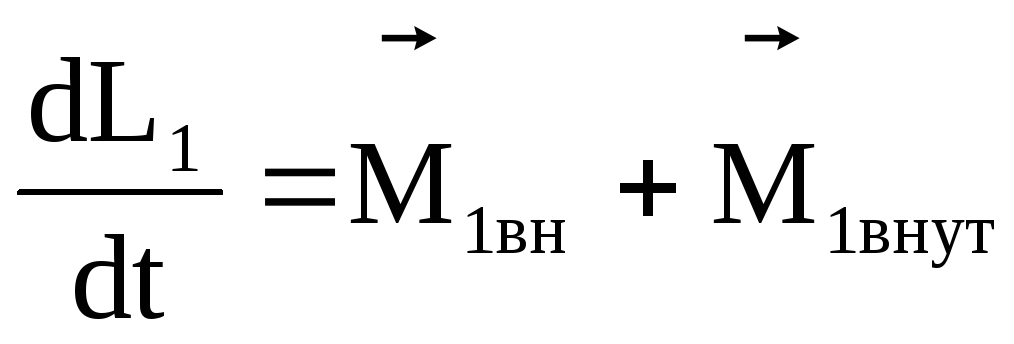
+
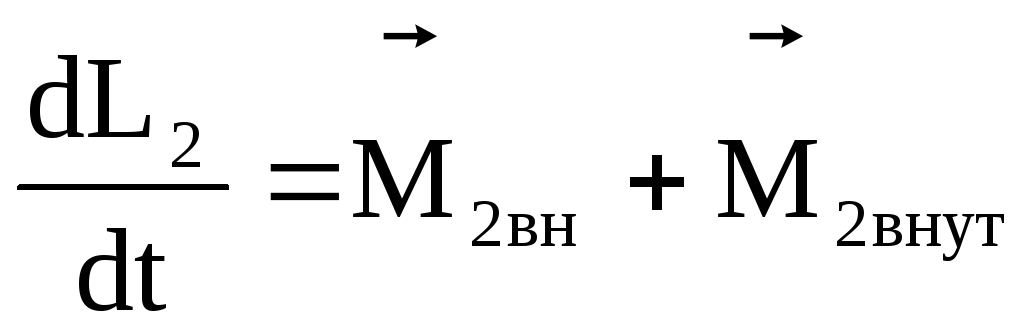
+
…………………….
+
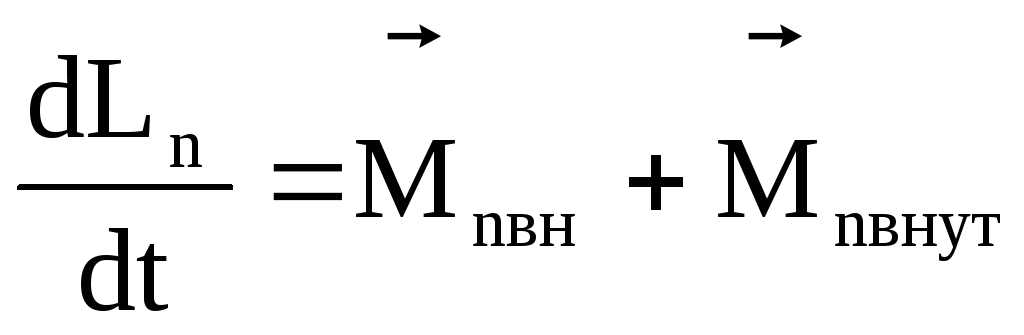
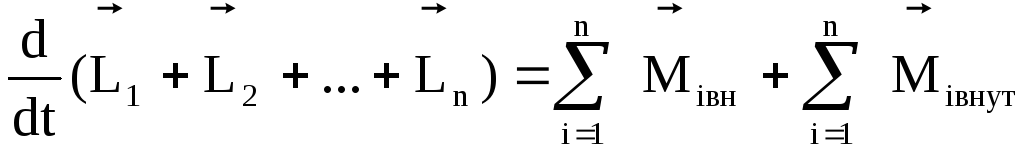
где 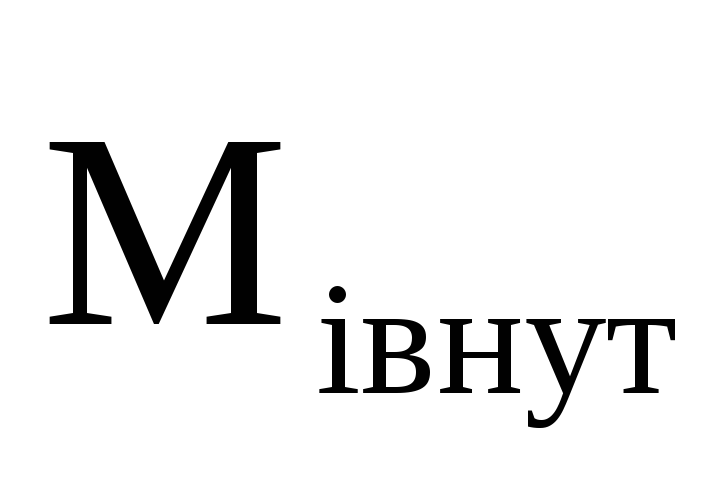 — момент внутренних сил,
— момент внутренних сил,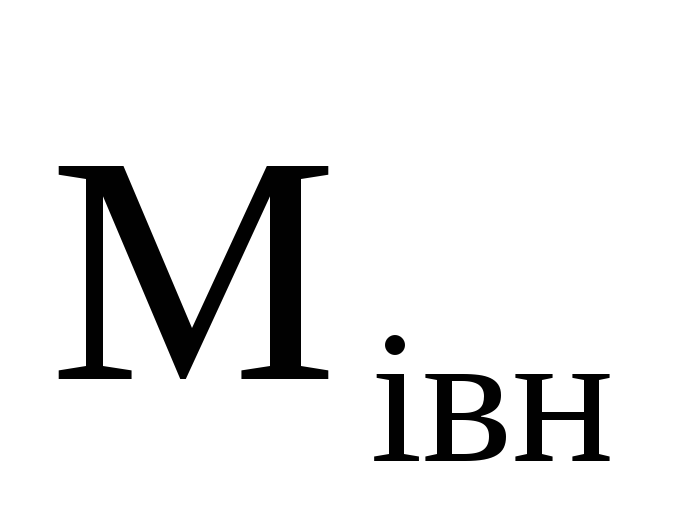 — момент внешних сил.
— момент внешних сил.
По третьему закону Ньютона 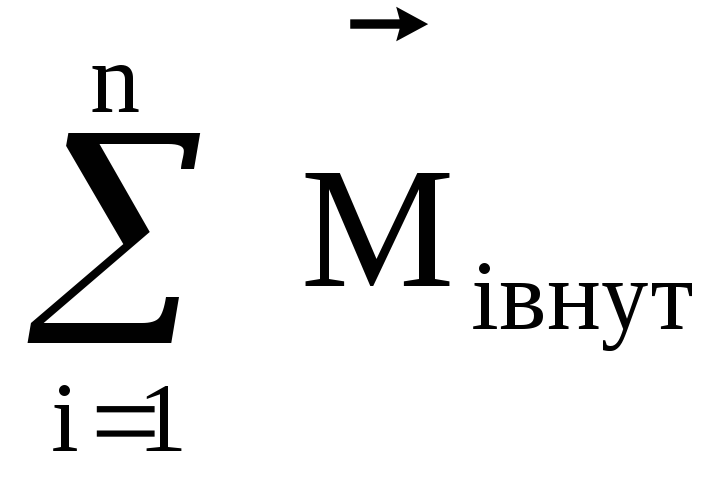 = 0, так как внутренние силы входят
попарно, сила с которой одно тело
действует на другое равно и противоположно
направлена сила с которой второе тело
действует на первое. Полный момент этих
сил равен нулю (см. рис.)
= 0, так как внутренние силы входят
попарно, сила с которой одно тело
действует на другое равно и противоположно
направлена сила с которой второе тело
действует на первое. Полный момент этих
сил равен нулю (см. рис.)
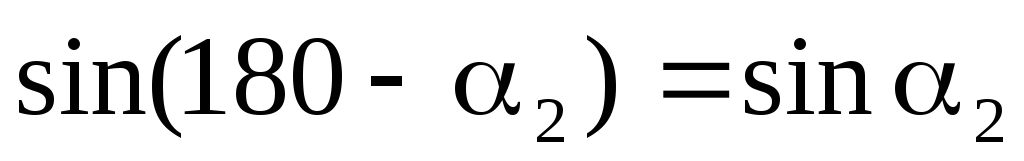 ,
,
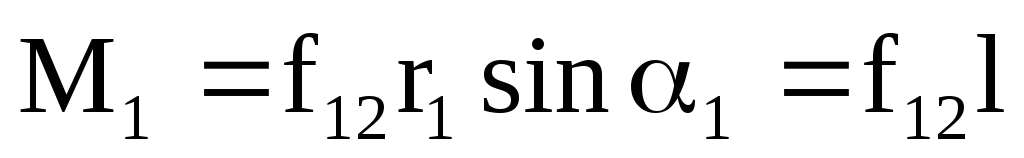
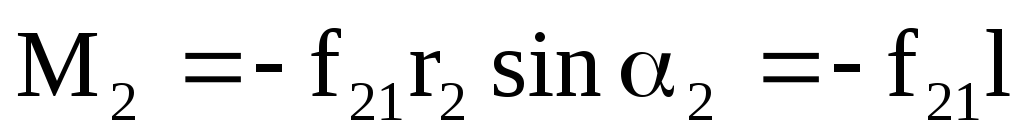
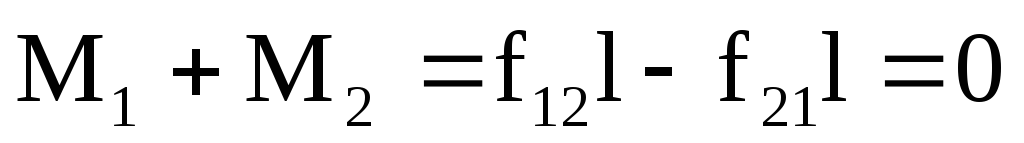

Исходя из этого уравнение примет вид
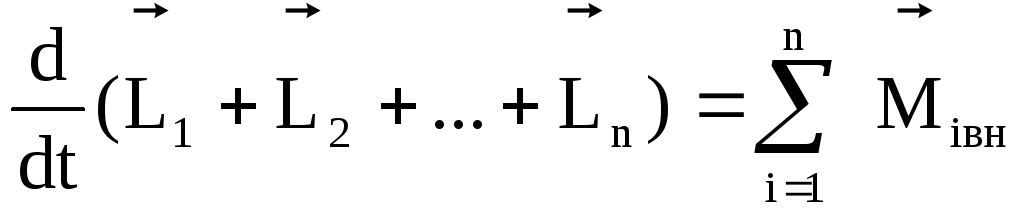 ,
,
где 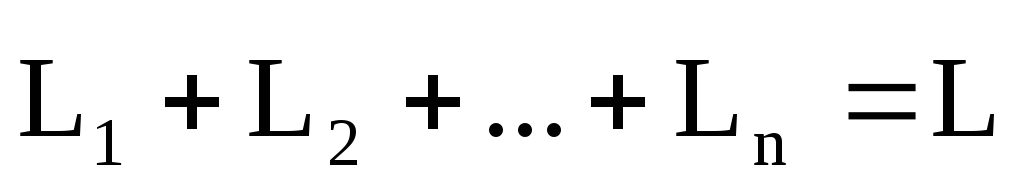 — момент импульса системы материальных
точек.
— момент импульса системы материальных
точек.
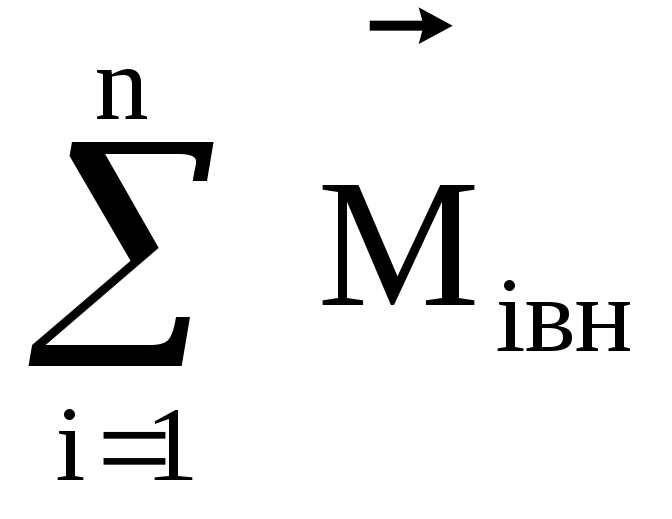 =
= — момент всех сил действующих на систему
материальных точек.
— момент всех сил действующих на систему
материальных точек.
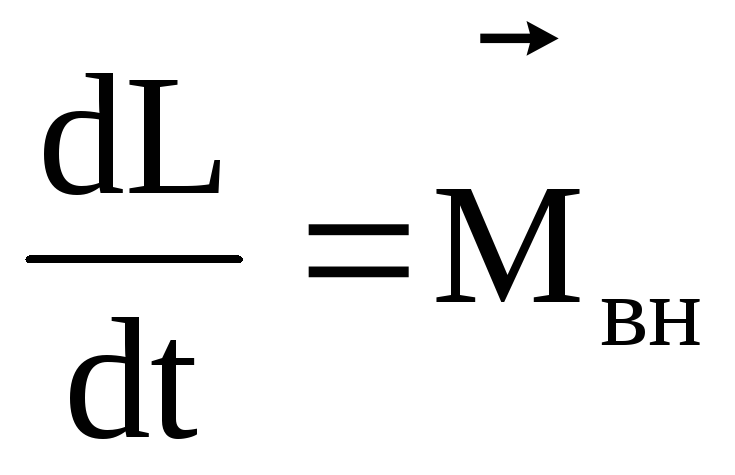 (2)
(2)
Основной закон динамики вращательного движения для системы материальных точек. Производная по времени от момента импульса системы материальных точек относительно неподвижной точки равна геометрической сумме моментов всех внешних сил относительно этой точки.
Если момент всех внешних сил относительно неподвижной точки равен нулю, то момент импульса системы относительно той же неподвижной точки остается постоянным во времени.
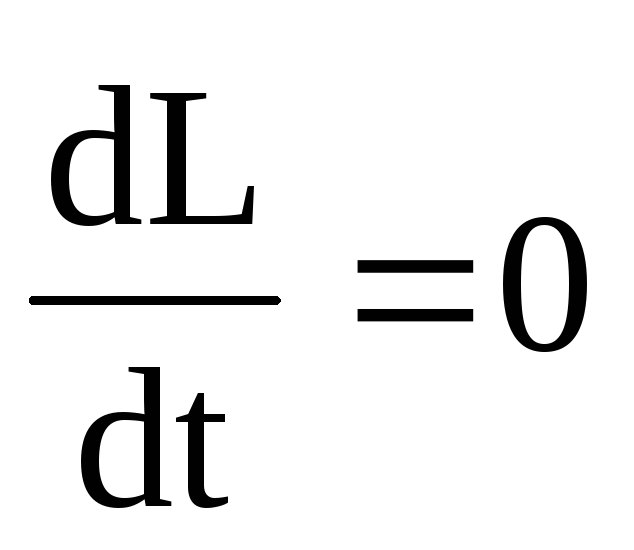 и
и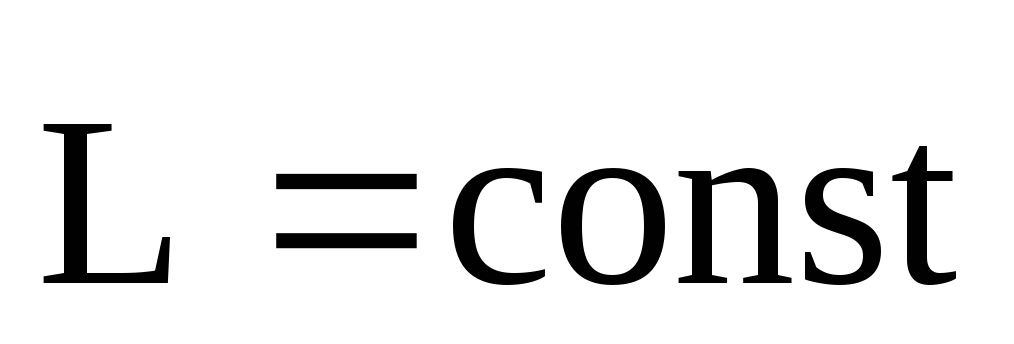 или
или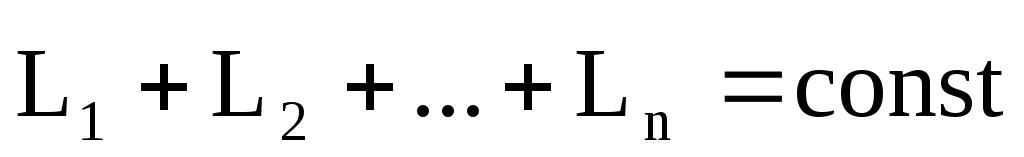 (3)
(3)
Выражение (3) – математическая запись закона сохранения момента импульса. Если мы продифференцируем по времени момент импульса относительно неподвижной оси, то получим уравнение моментов относительно неподвижной оси
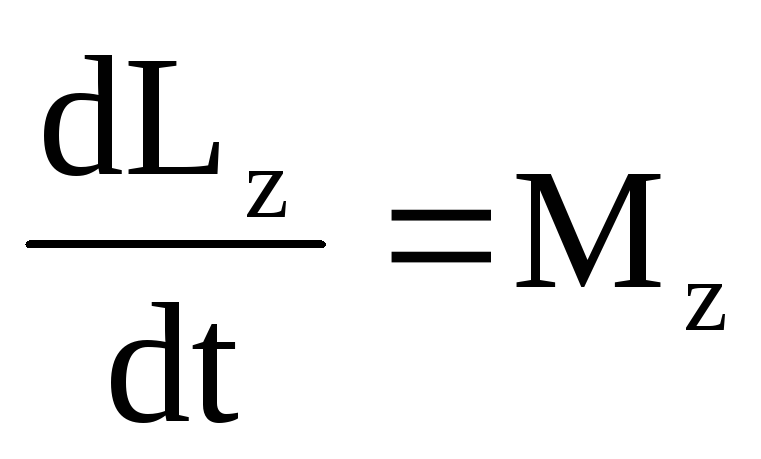 (4)
(4)
Как было показано ранее, момент импульса твердого тела относительно оси вращения равен
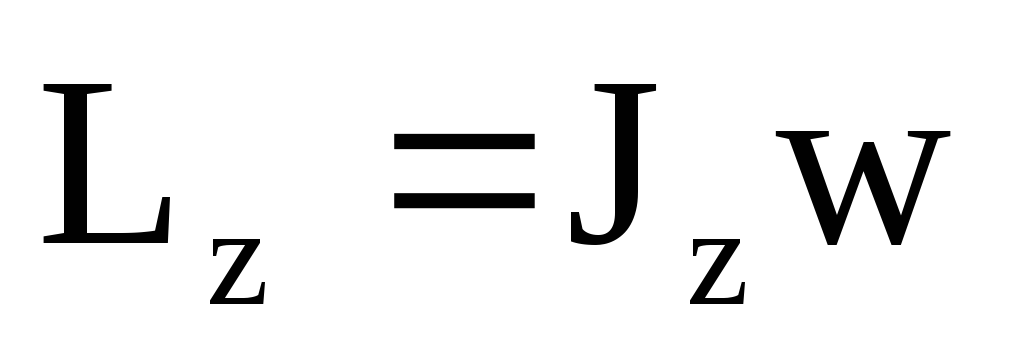 .
.
Если момент инерции 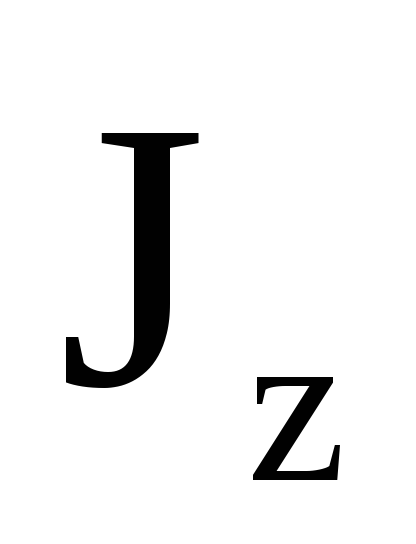 при
вращении остается постоянным, то
при
вращении остается постоянным, то
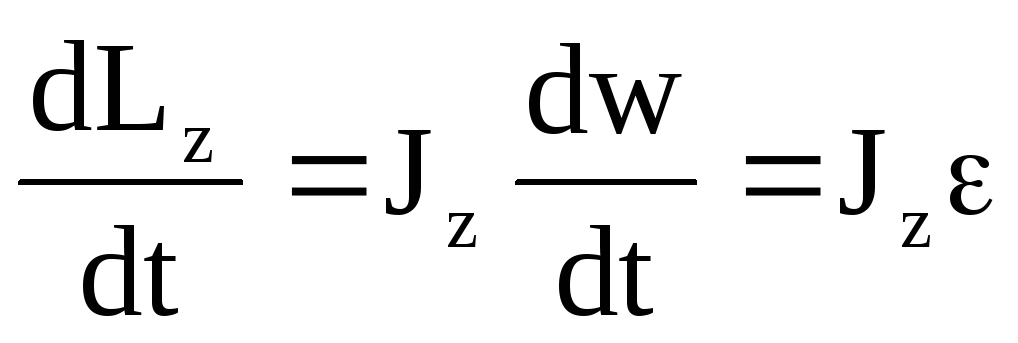 ,
,
где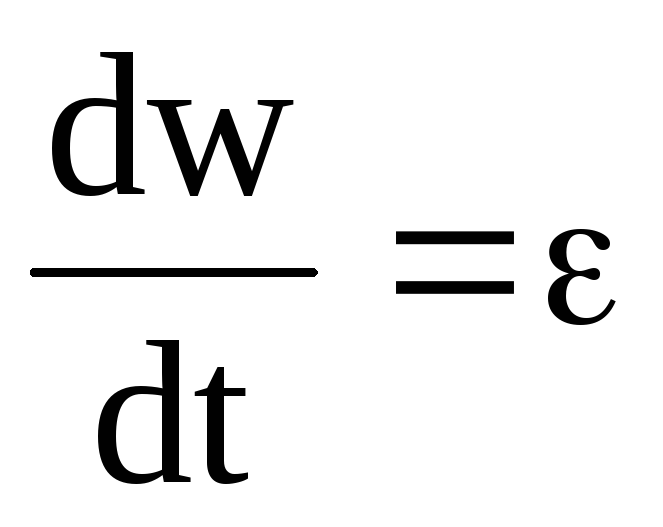 — угловое ускорение. Тогда
— угловое ускорение. Тогда
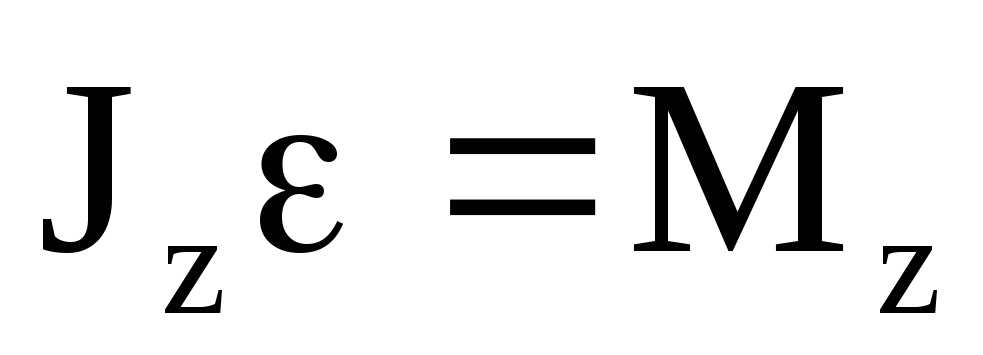 (5).
(5).
Произведение момента инерции твердого тела относительно оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.
Уравнение (5) – основное уравнение динамики вращательного движения вокруг неподвижной оси. Оно напоминает уравнение Ньютона для поступательного движения.
Роль массы mиграет момент инерцииJ, роль скоростиv– угловая скоростьw, роль с илыF– момент силыM, роль импульсаp– момент импульсаL. Момент импульсаLчасто называют вращательным импульсом системы.
Если момент внешних сил Mzотносительно оси вращения равен нулю, то вращательный импульс сохраняется:
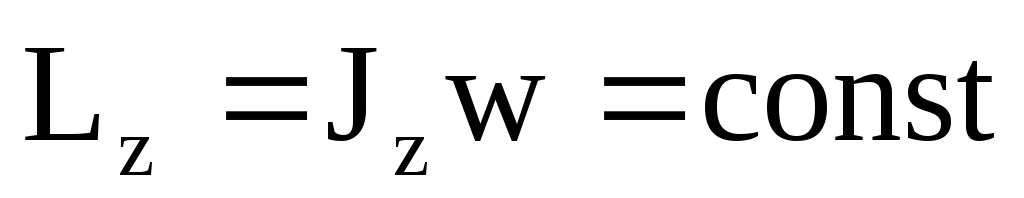 (6)
(6)
Продемонстрировать закон сохранения импульса можно с помощью скамьи Жуковского. Скамья Жуковского представляет собой стул, сиденье которого имеет форму диска. Диск может свободно вращаться вокруг вертикальной оси на шариковых подшипниках.
Человек, оттолкнувшись ногой от пола, приводит скамью во вращение. Вместе со скамьей будет вращаться и он сам. Во время вращения момент импульса системы скамья плюс человек будет оставаться постоянным, какие бы внутренние движения не совершались в системе.
Если человек разведет руки в стороны, то он увеличит момент инерции системы J, а потому угловая скорость вращенияwдолжна уменьшиться, чтобы оставался неизменным вращательный импульсL=Jw(см рис 1а и 1б)
Рис.1а. L=J1w1Рис.1бL=J2w2
J1w1=J2w2(J2>J1,w2<w1)
Если человек, стоя на неподвижной скамье Жуковского, начинает делать конические движения над головой, скамья начинает вращаться в другую сторону (рис.2).
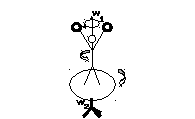
Общий момент импульса системы остается равным нулю.
Когда винт судна начинает вращаться, по закону сохранения момента импульса системы, корпус судна должен вращаться в противоположную сторону. В обычных условиях это не страшно, но в критических ситуациях (сильная боковая волна, легкое судно) может привести к опрокидыванию судна. Эта же ситуация всегда реализуется и для вертолетов. Чтобы этого не происходило, на хвосте устанавливается другой винт для гашения вращения.
В заключении сопоставим основные величины и уравнения определяющие вращение тела им его поступательное движение.
Поступательное движение | Вращательное движение |
Масса m Скорость v = dr/dt Ускорение a = dv/dt Сила F Импульс p = mv Основное уравнение динамики F = ma F = dp/dt Работа dA = F ds Кинетическая энергия mv2/2 | Момент инерции J Угловая скорость w = dφ/dt Угловое ускорение ε = dw/dt Момент силы M = Fr Момент импульса L = Jw Основное уравнение динамики M = Jε M = dL/dt Работа вращения dA = Mdφ Кинетическая энергия вращения Jw2/2 |
Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов.
Моме́нт
и́мпульса (кинетический момент, угловой
момент, орбитальный момент, момент
количества движения) характеризует
количество вращательного движения.
Величина, зависящая от того, сколько
массы вращается, как она распределена
относительно оси вращения и с какой
скоростью происходит вращение. 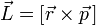 Единицы измерения СИ —
м2·кг·с−1 // джоуль-секунда; Дж·с. СГС
— см2·г·с−1
Единицы измерения СИ —
м2·кг·с−1 // джоуль-секунда; Дж·с. СГС
— см2·г·с−1
Момент
силы (синонимы: крутящий момент,
вращательный момент, вертящий момент,
вращающий момент) — векторная физическая
величина, равная произведению
радиус-вектора, проведенного от оси
вращения к точке приложения силы, на
вектор этой силы. Характеризует
вращательное действие силы на твёрдое
тело.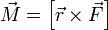 Единицы измерения СИ
— Ньютон-метр
Единицы измерения СИ
— Ньютон-метр
Уравнение моментов. Закон сохранения момента импульса.
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем.
П
 роизводная
момента импульса по времени есть момент
силы:
роизводная
момента импульса по времени есть момент
силы: 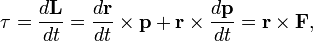 Таким
образом, требование замкнутости системы
может быть ослаблено до требования
равенства нулю главного (суммарного)
момента внешних сил: Математически закон сохранения момента
импульса следует из изотропии пространства
Таким
образом, требование замкнутости системы
может быть ослаблено до требования
равенства нулю главного (суммарного)
момента внешних сил: Математически закон сохранения момента
импульса следует из изотропии пространства

Момент импульса и момент силы относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.
Моме́нт
и́мпульса (кинетический момент, угловой
момент, орбитальный момент, момент
количества движения) характеризует
количество вращательного движения.
Величина, зависящая от того, сколько
массы вращается, как она распределена
относительно оси вращения и с какой
скоростью происходит вращение. 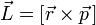 Единицы
измерения СИ —
м2·кг·с−1//
джоуль-секунда; Дж·с. СГС
— см2·г·с−1
Единицы
измерения СИ —
м2·кг·с−1//
джоуль-секунда; Дж·с. СГС
— см2·г·с−1
Момент
силы (синонимы: крутящий момент,
вращательный момент, вертящий момент,
вращающий момент) — векторная физическая
величина, равная произведению
радиус-вектора, проведенного от оси
вращения к точке приложения силы, на
вектор этой силы. Характеризует
вращательное действие силы на твёрдое
тело. 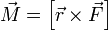 Единицы измерения СИ
— Ньютон-метр.
Единицы измерения СИ
— Ньютон-метр. 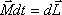 Это
выражение носит название основного
уравнения динамики вращательного
движения и формулируется следующим
образом: изменение момента количества
движения твердого тела
Это
выражение носит название основного
уравнения динамики вращательного
движения и формулируется следующим
образом: изменение момента количества
движения твердого тела 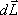 , равно импульсу момента
, равно импульсу момента 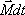 всех внешних сил, действующих на это
тело.
всех внешних сил, действующих на это
тело.
Инерция при вращательном движении. Момент инерции. Кинетическая энергия твердого тела при вращательном движении.
Момент
инерции — скалярная физическая величина,
мера инертности тела во вращательном
движении вокруг оси, подобно тому, как
масса тела является мерой его инертности
в поступательном движении. Характеризуется
распределением масс в теле: момент
инерции равен сумме произведений
элементарных масс на квадрат их расстояний
до базового множества (точки, прямой
или плоскости). Обозначение: I или J. 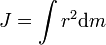 Единицы измерения СИ
— кг·м². СГС — г·cм²
Единицы измерения СИ
— кг·м². СГС — г·cм²
Кинетическая
энергия вращательного движения —
энергия тела, связанная с его вращением.
Кинетические энергии различных частиц
различны, так как различны их линейные
скорости. Чтобы рассчитать полную
энергию вращательного движения твердого
тела, необходимо просуммировать энергии
всех его элементов: Основные кинематические
характеристики вращательного движения
тела — его угловая скорость (ω) и угловое
ускорение. Основные динамические
характеристики вращательного движения
— момент импульса относительно оси
вращения z: Kz
= Izω и
кинетическая энергия 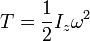 ,
, 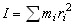 —
момент инерции где Iz — момент инерции
тела относительно оси вращения.
—
момент инерции где Iz — момент инерции
тела относительно оси вращения.
4.2. Момент импульса
П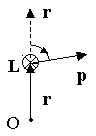 усть
дана материальная точка, имеющая импульср. Пусть её положение
относительно точки О определяется
радиусом-векторомr. Движение такой точки характеризуют
моментом импульсаL.
усть
дана материальная точка, имеющая импульср. Пусть её положение
относительно точки О определяется
радиусом-векторомr. Движение такой точки характеризуют
моментом импульсаL.
Моментом импульса материальной точки относительно точки О называется векторная величина, равная векторному произведению радиуса-вектораr и вектора импульсаp:
L=[r,p].
Модуль момента импульса L=rpsin, где — угол между векторамиr и р. Направление вектора момента импульса определяется по правилу правого винта.
Размерность момента импульса [L]=кг.м2/с.
М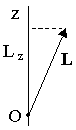 омент
импульса тела относительно точки равен
векторной сумме моментов импульсов
частиц тела относительно той же точки
омент
импульса тела относительно точки равен
векторной сумме моментов импульсов
частиц тела относительно той же точки
L=L1+L2+…+LN.
Проекция вектора момента импульса относительно точки О на ось z, проходящую через эту точку, называетсямоментом импульса относительно оси:
Lz=[r,p]z.
Момент импульса относительно оси является скалярной величиной.
Момент импульса тела относительно оси z равен проекции момента импульса тела относительно точки О на осьz, проходящую через эту точку.
4.3. Связь момента силы и момента импульса
Момент импульса и момент силы связаны между собой. Найдём выражение, связывающее их.
Возьмём производную по времени от выражения, определяющего момент импульса:
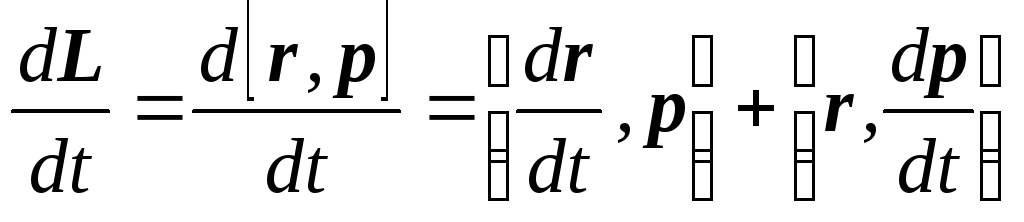
Член 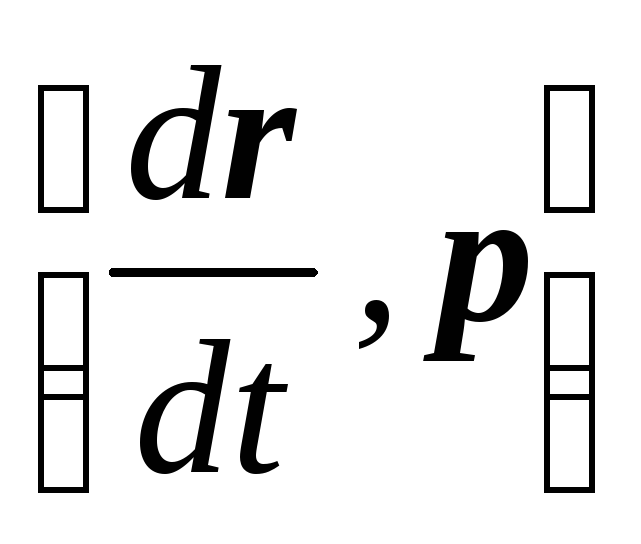 равен нулю, так как угол между вектором
скоростиdr/dtи
вектором импульсар равен нулю.
равен нулю, так как угол между вектором
скоростиdr/dtи
вектором импульсар равен нулю.
Производная импульса по времени, имеющаяся во втором члене полученного выражения, равна силе (второй закон Ньютона). Поэтому можем записать полученное выражение в следующей форме:
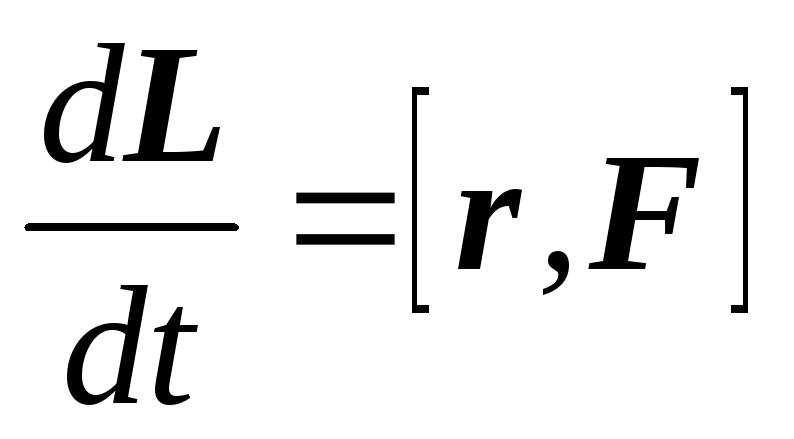 .
.
Но [r,F] есть по определениюмомент силыF относительно той же точки О. Поэтому
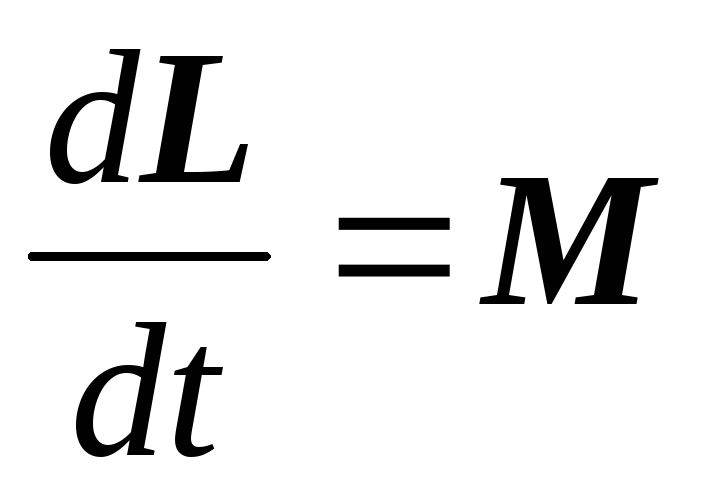
т.е. скорость изменения момента импульса частицы равна моменту силы, действующему на эту частицу.
Проекция последнего уравнения на ось zвыражает связь момента импульса относительно осиzи момента силы относительно той же оси.
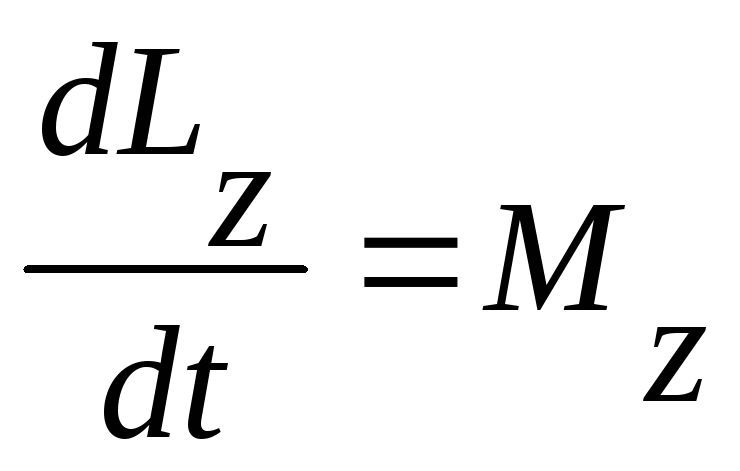 .
.
4.4. Основной закон динамики вращательного движения
Пусть твёрдое тело вращается относительно неподвижной оси z.
Выразим момент импульса твёрдого тела относительно оси вращения. Для этого представим твёрдое тело как совокупность элементарных масс. Момент импульса одной элементарной массы относительно осиz
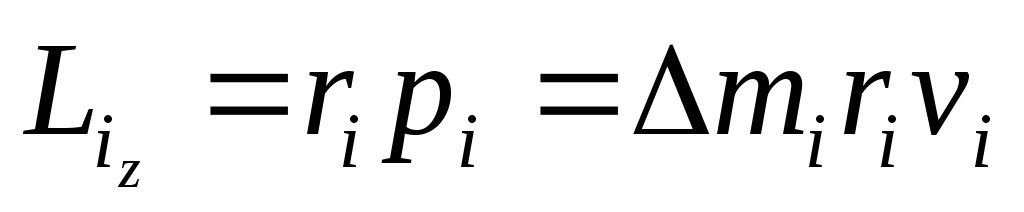
Момент импульса всего тела равен сумме моментов импульсов всех элементарных масс
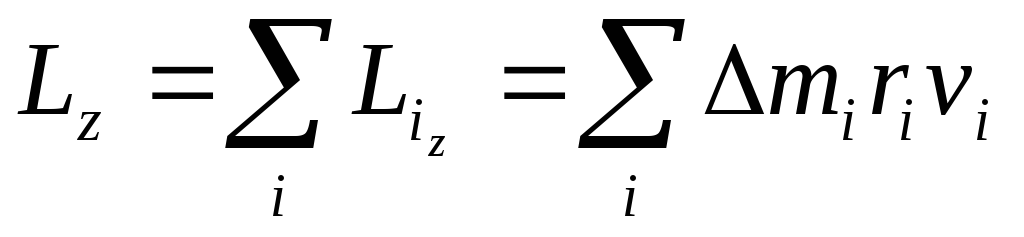
Скорость vу разных элементарных масс различна, а угловая скорость одинакова.
Поскольку v=r,
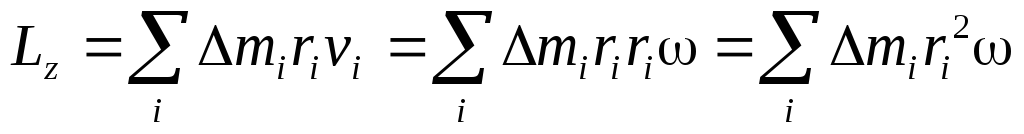
Поскольку угловая скорость со одинакова для всех элементарных масс, её можно вынести за знак суммы
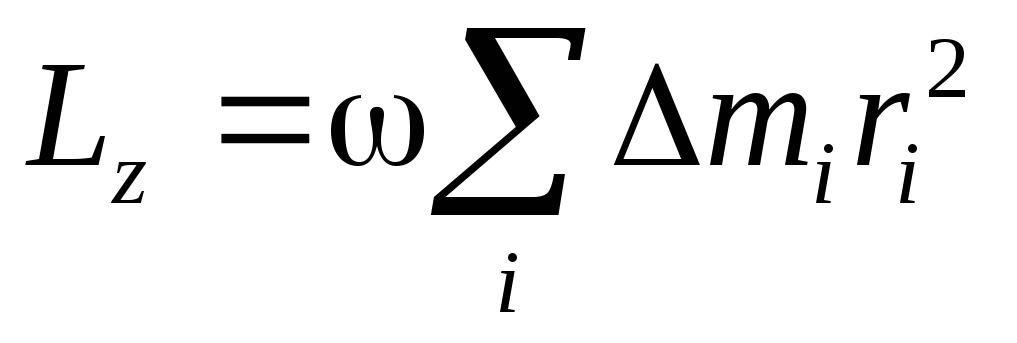
Введём обозначение 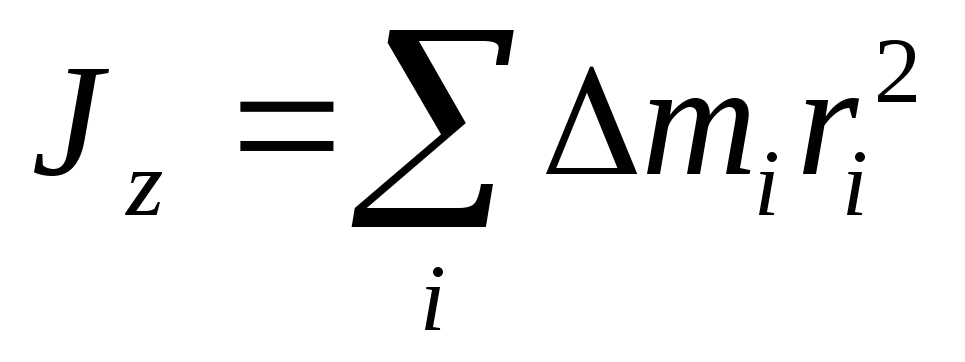 .
С учётом этого
.
С учётом этого
Lz=Jz..
Ранее мы получили, что момент импульса и момент силы связаны следующим образом:
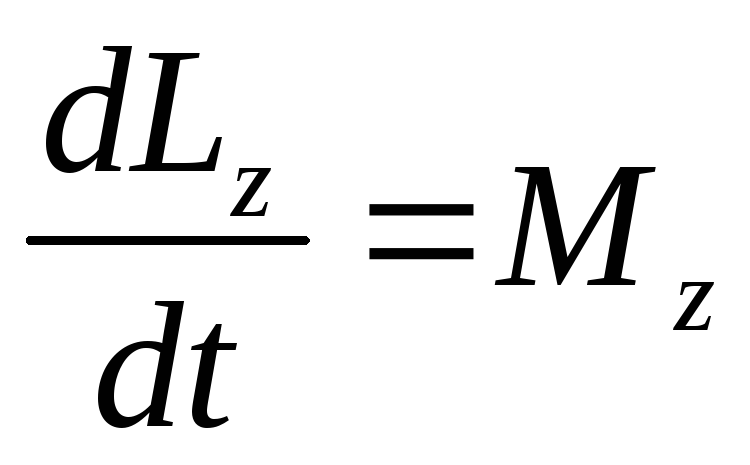 .
.
Заменив Lz наJzωи с учётом того, чтоJz с течением времени не изменяется, получаем
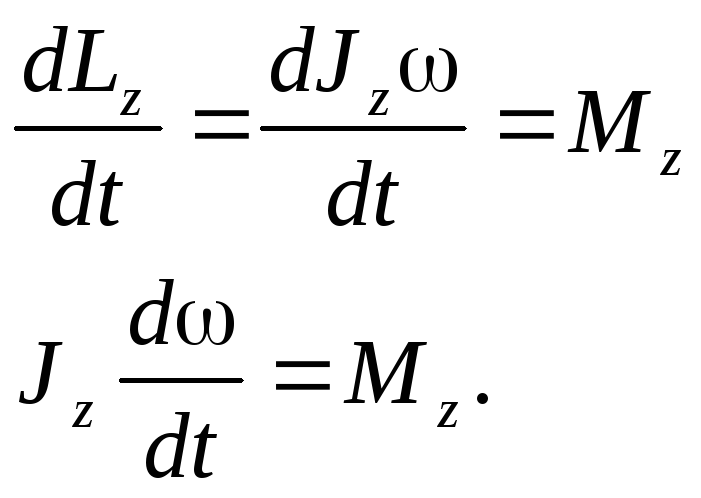
Учитывая, что производная угловой скорости по времени равна угловому ускорению , получаем
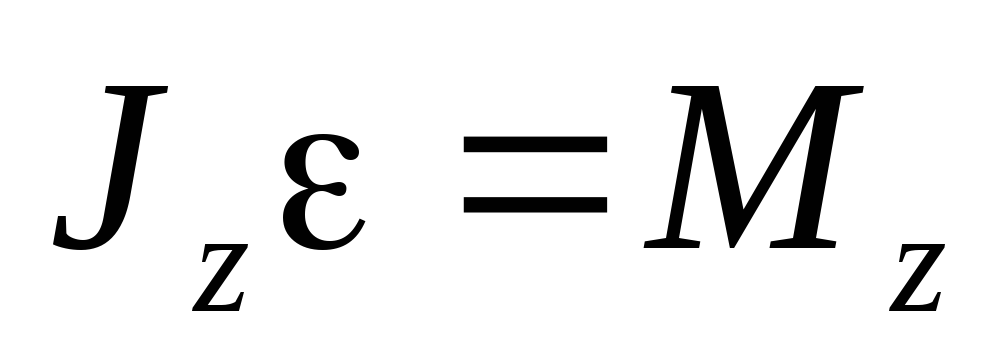 .
.
Полученное выражение — основной закон динамики вращательного движения, связывающий между собой меру внешнего воздействия — момент силы Mz с результатом внешнего воздействия — угловым ускорением.
Коэффициент Jz, стоящий в этом уравнении, зависит от массы тела и от того, как она распределена по объёму тела (это видно из определения величиныJz).
Чем меньше Jz, тем большее угловое ускорение получит тело при воздействии момента силыMz. Это говорит о том, что коэффициентJz. характеризует инертность вращающегося тела. ПоэтомуJz называют моментом инерции тела относительно осиz.
Знание величины момента инерции тела необходимо для описания вращательного движения. Поэтому обсудим более подробно, что такое момент инерции и как его вычислить.
4.2. Момент импульса частицы. Момент силы.
Кроме энергии и импульса существует
ещё Одина физическая величина. С которой
связан закон сохранения — это момент
импульса. Моментом импульса частицы 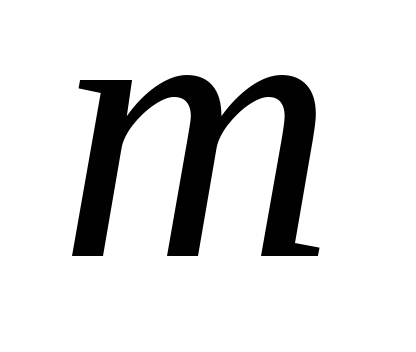 относительно точки О называется вектор
относительно точки О называется вектор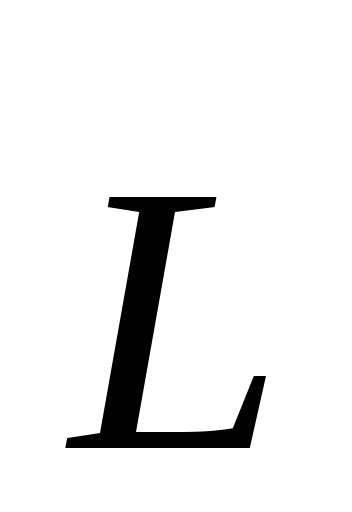 равный
равный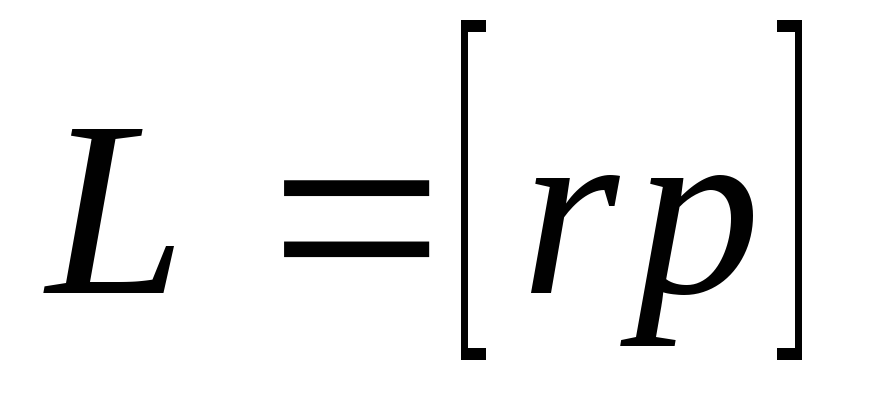 ,
,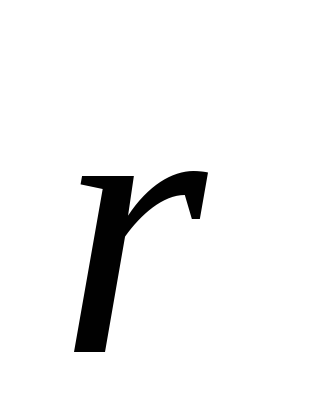 -радиус;
-импульс.
-радиус;
-импульс.
Т.е. 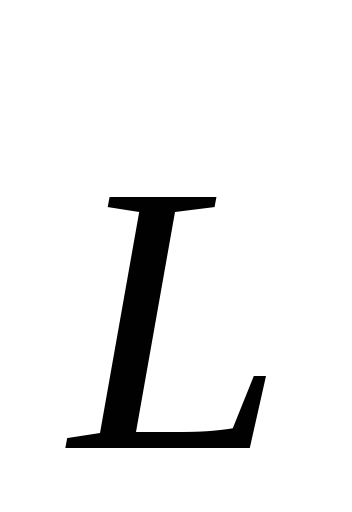 является ??? вектором. Его направление
выбрано так, что вращение вокруг О в
направлении
является ??? вектором. Его направление
выбрано так, что вращение вокруг О в
направлении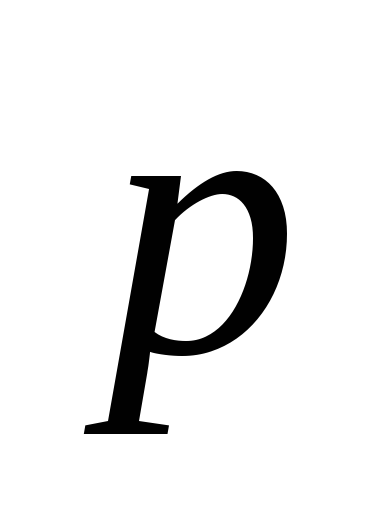 и вектор
и вектор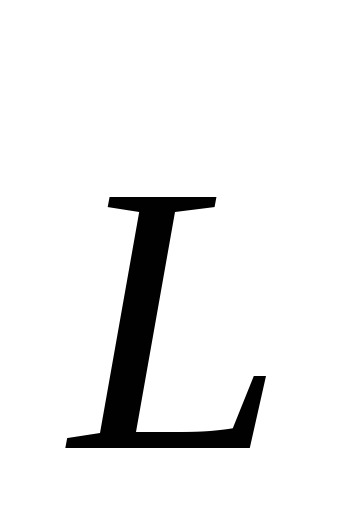 образует правовинтовую систему. Модуль
образует правовинтовую систему. Модуль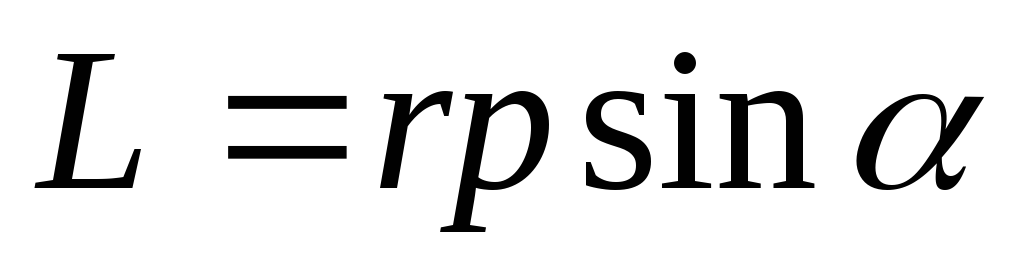
 угол
между
угол
между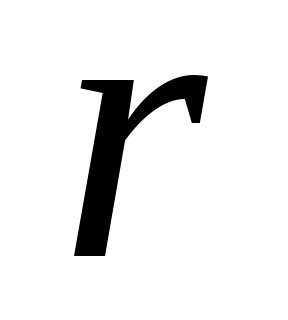 и
и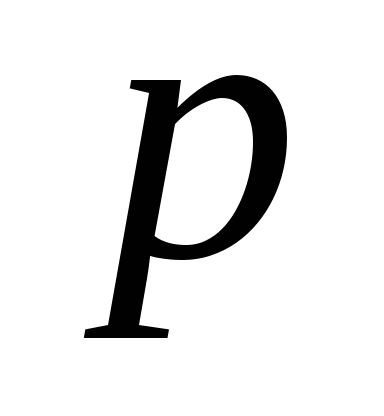
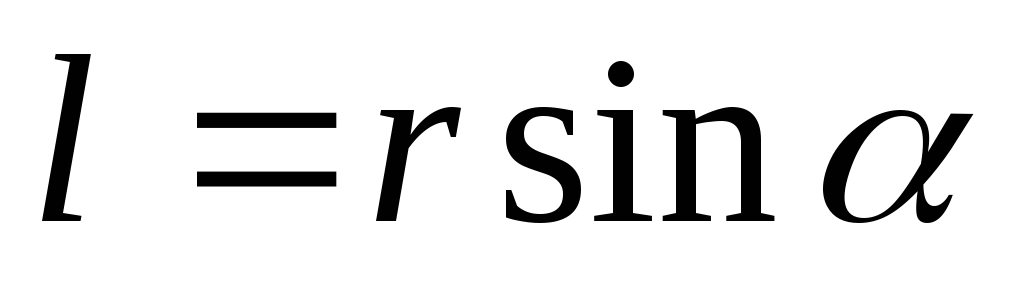 плечо вектора
плечо вектора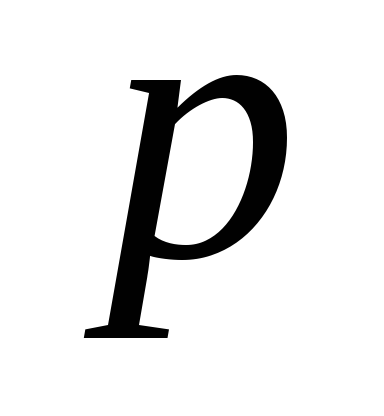 относительно О.
относительно О.
Найдем с какой величиной связано
изменение вектора 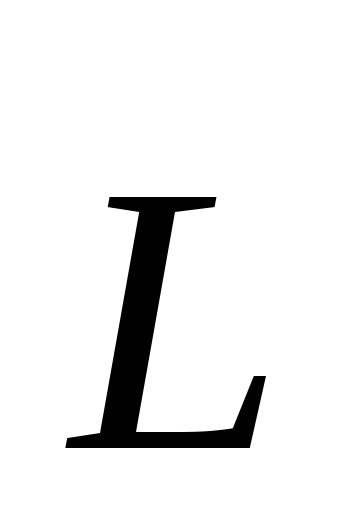 во времени:
во времени:
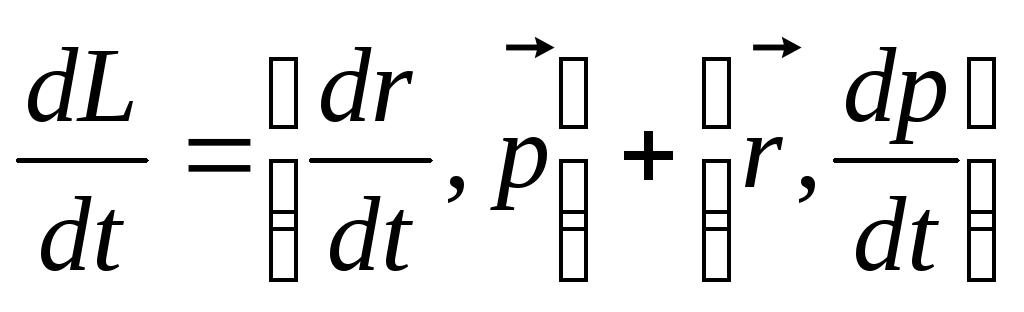
 .
.
Т .к
т.о неподвижна, то
.к
т.о неподвижна, то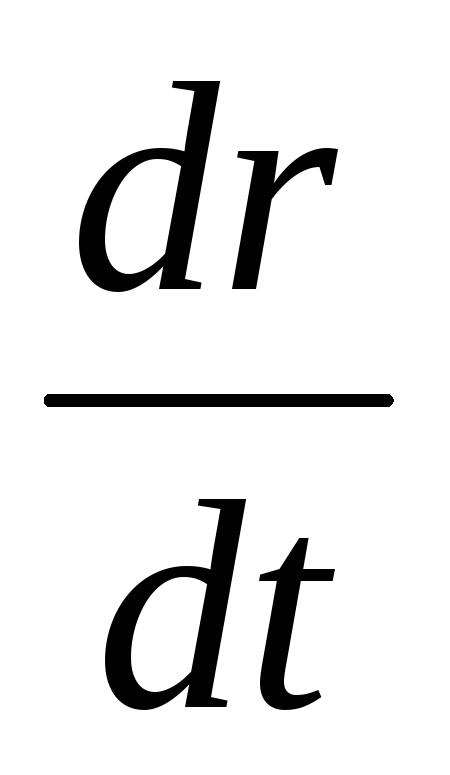 равно скорости частицы, т.е. совпадает
с
равно скорости частицы, т.е. совпадает
с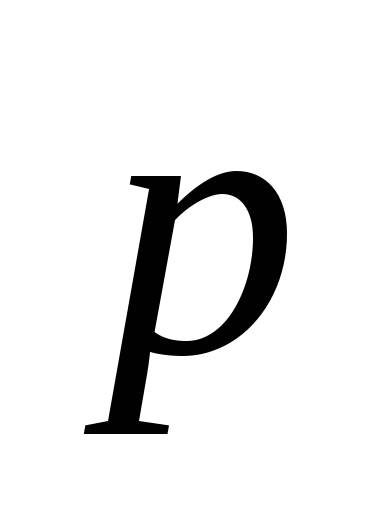 ,
т.е.
,
т.е.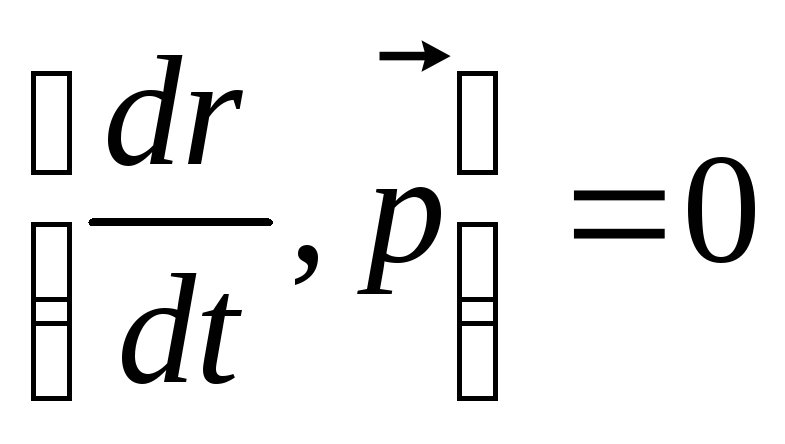 .
Далее
.
Далее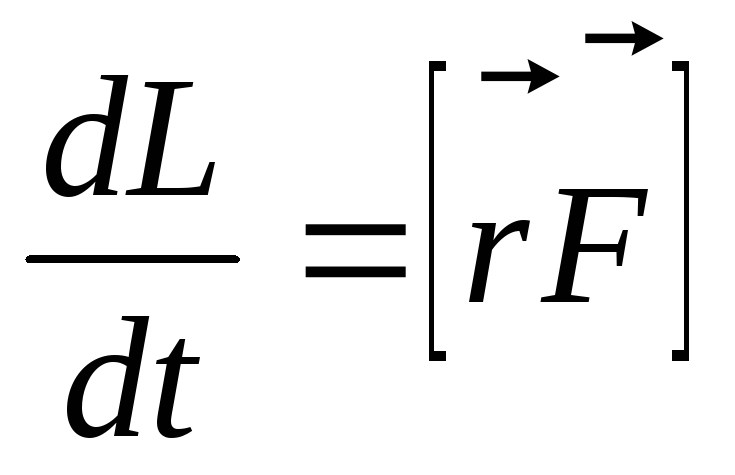 — второй закон Ньютона и
— второй закон Ньютона и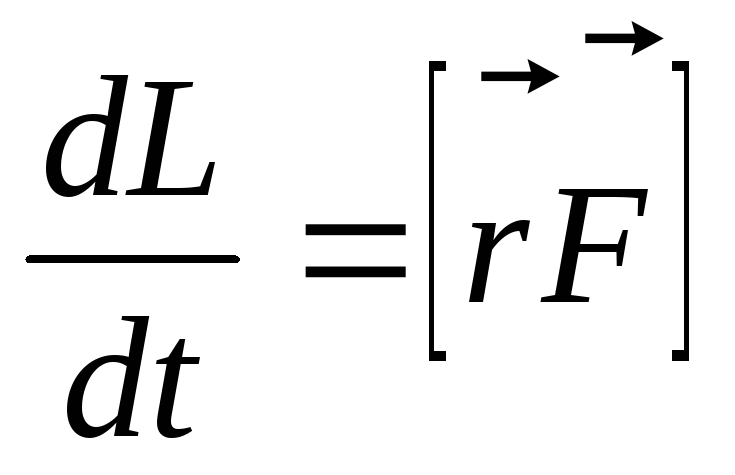 ;
Величина
;
Величина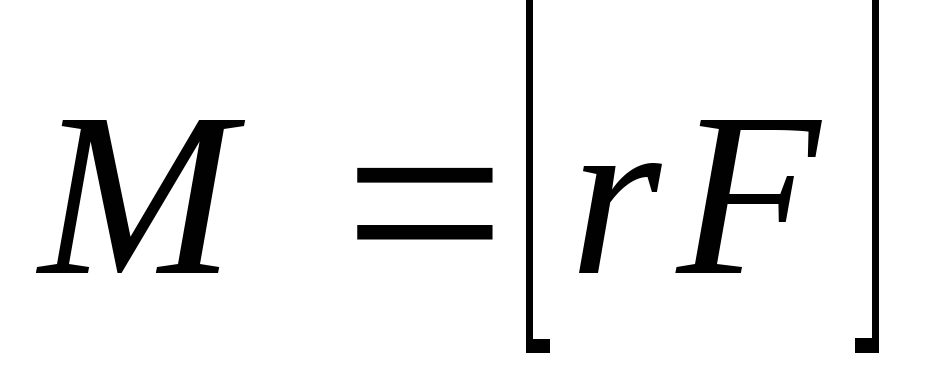 —момент
силы аксиальный вектор.
—момент
силы аксиальный вектор.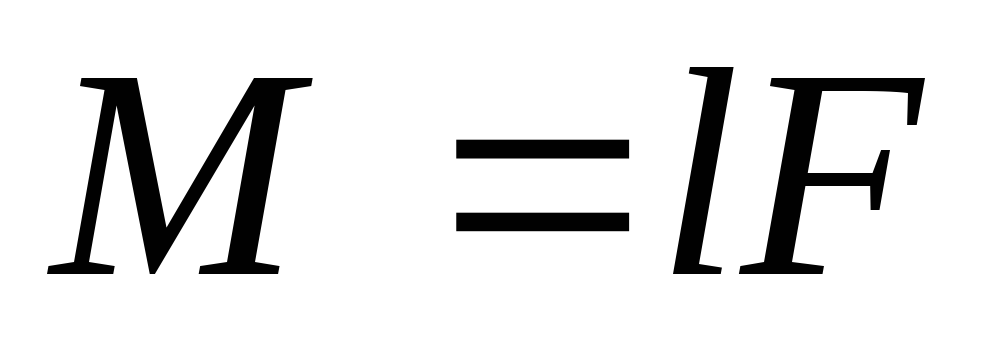 ,
,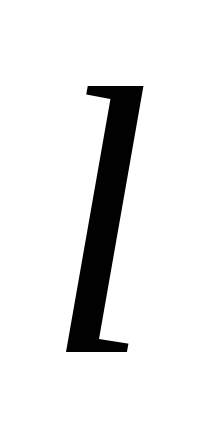 —плечо
силы
—плечо
силы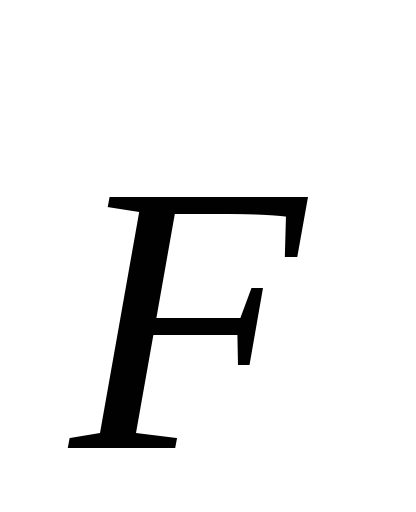 относительно т.О.
относительно т.О.
Т.о производная по 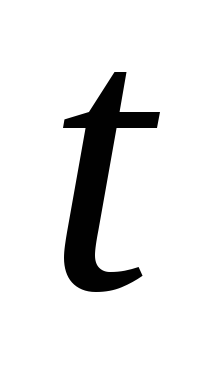 момента импульса
момента импульса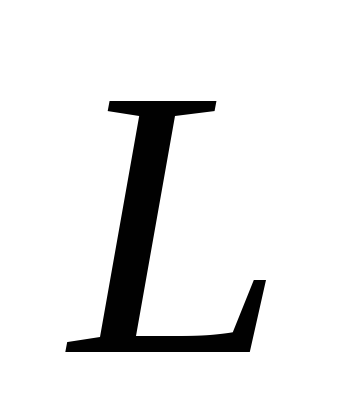 частицы, относительно некоторой т.О
выбранной системы отсчета равна моменту
равнодействующей силы
частицы, относительно некоторой т.О
выбранной системы отсчета равна моменту
равнодействующей силы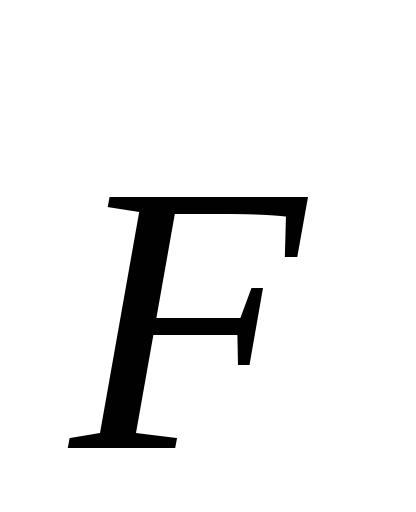 относительно этой точки
относительно этой точки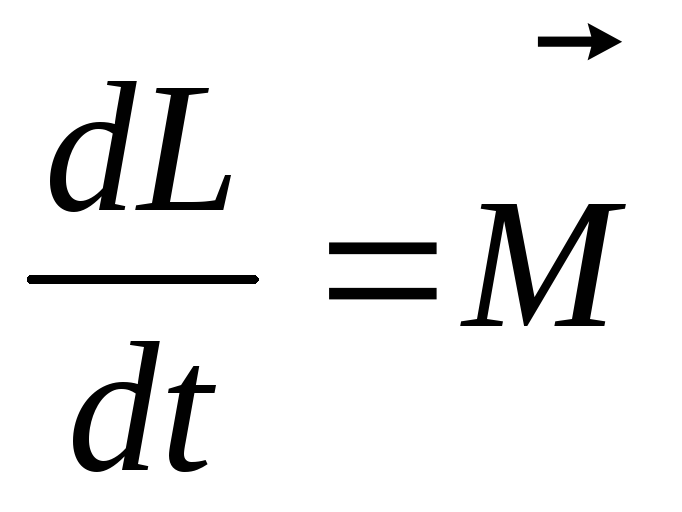 .
Это уравнение называют уравнением
моментов.
.
Это уравнение называют уравнением
моментов.
Если система отсчета является
неинерциальной, то в момент силы 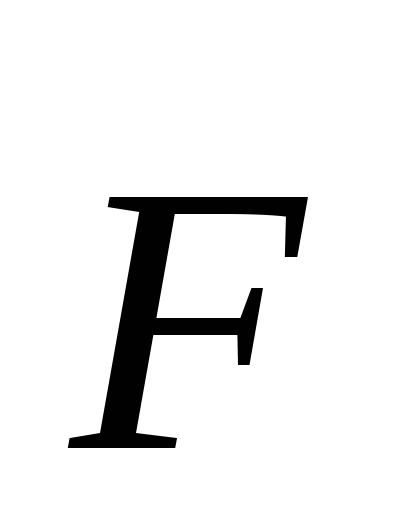 включает в себя как момент сил
взаимодействия, так и момент сил инерции
(относительно той же т.О). Из уравнения
моментов следует что если
включает в себя как момент сил
взаимодействия, так и момент сил инерции
(относительно той же т.О). Из уравнения
моментов следует что если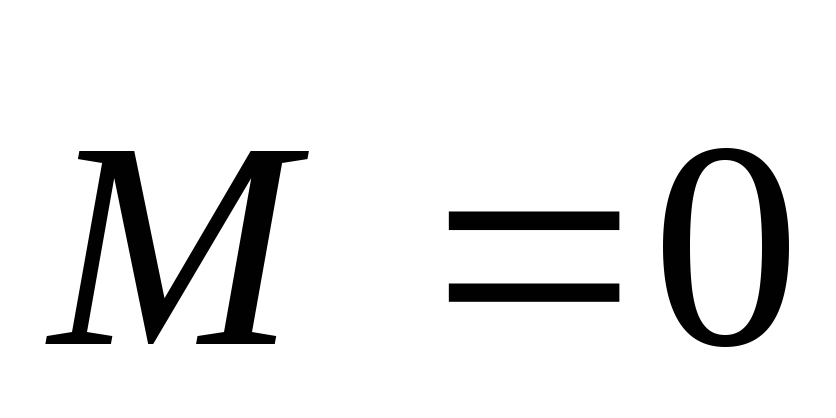 ,
то
,
то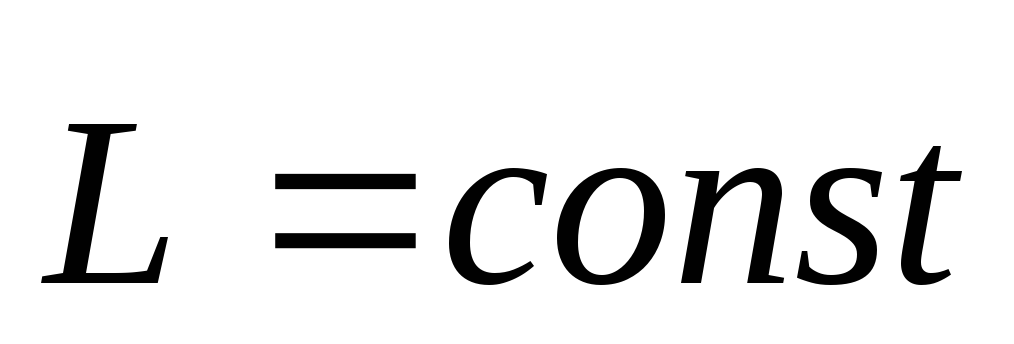 —равномерное
вращательное движение. Т.е. если момент
всех сил относительно т.О системы отсчета
равен О, в течение интересующего нас
—равномерное
вращательное движение. Т.е. если момент
всех сил относительно т.О системы отсчета
равен О, в течение интересующего нас ,
то момент импульса частицы относительно
этой точки остается постоянным.
,
то момент импульса частицы относительно
этой точки остается постоянным.
Уравнение моментов позволяет найти 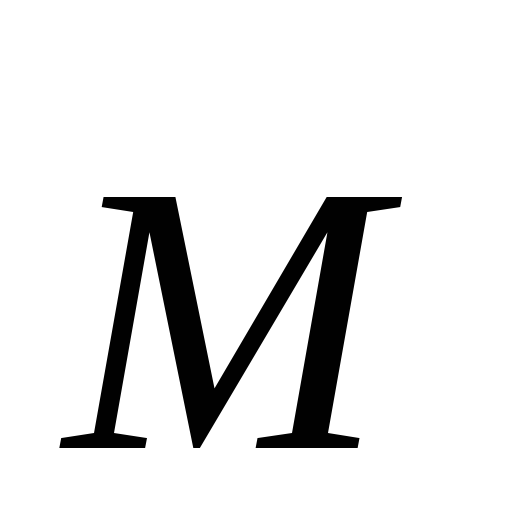 точки относительно О в любой момент
времени если известна
точки относительно О в любой момент
времени если известна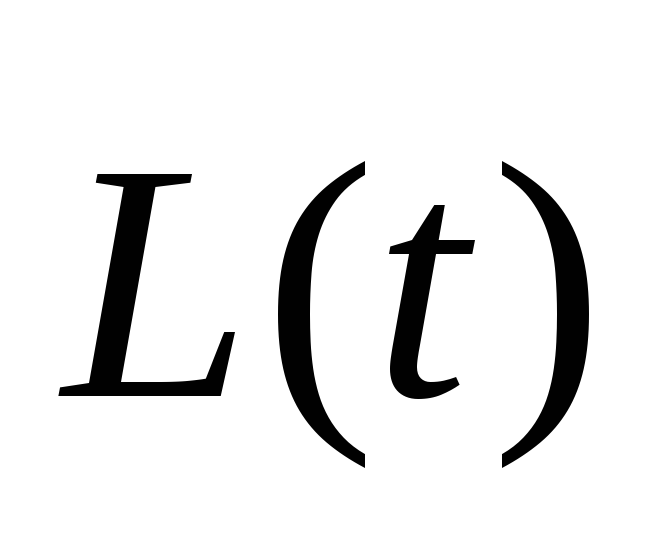 частицы относительно точки. Для этого
достаточно продифференцировать уравнение
частицы относительно точки. Для этого
достаточно продифференцировать уравнение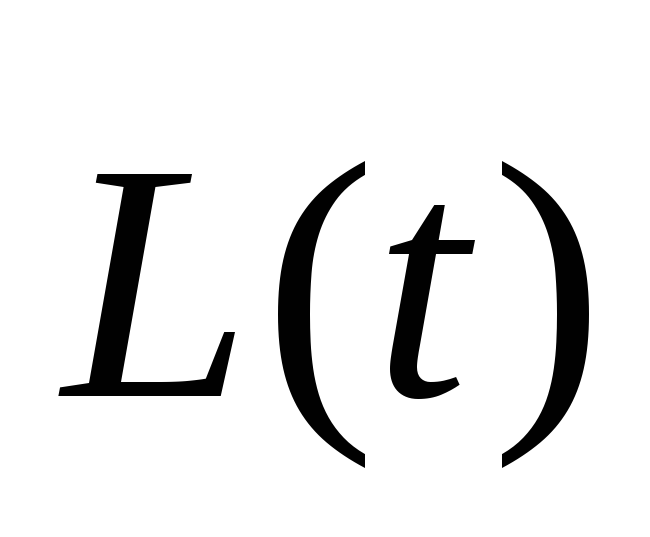 .
Кроме этого, если известна зависимость
.
Кроме этого, если известна зависимость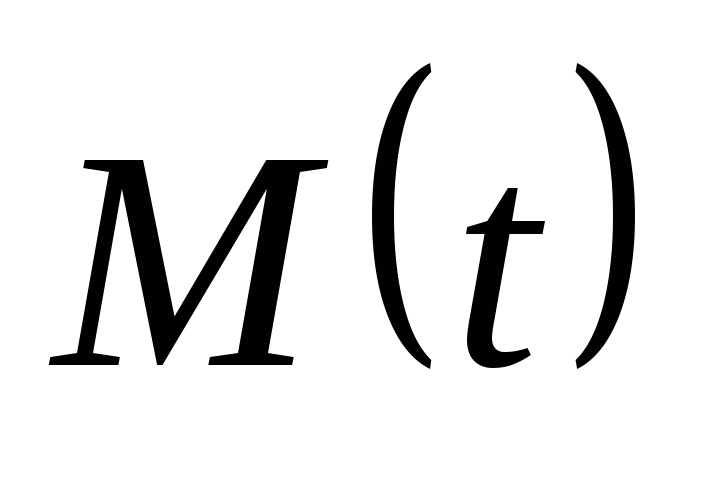 ,
то можно найти приращение момента
импульса частицы относительно т.О за
любой промежуток времени. Для этого
необходимо проинтегрировать уравнение
,
то можно найти приращение момента
импульса частицы относительно т.О за
любой промежуток времени. Для этого
необходимо проинтегрировать уравнение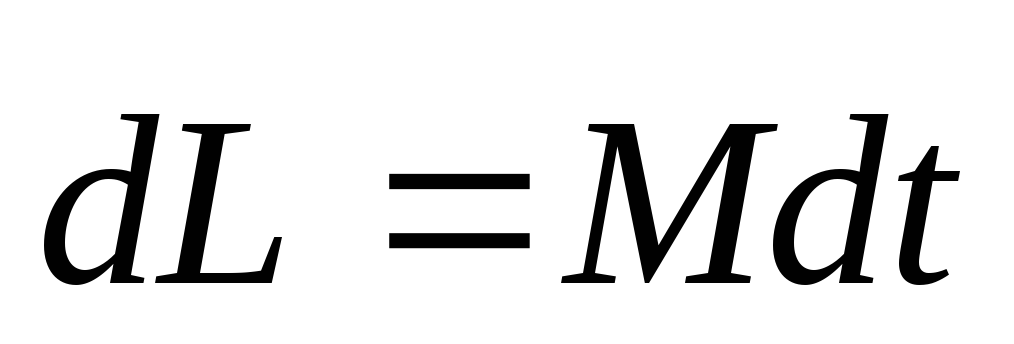 ,
тогда
,
тогда
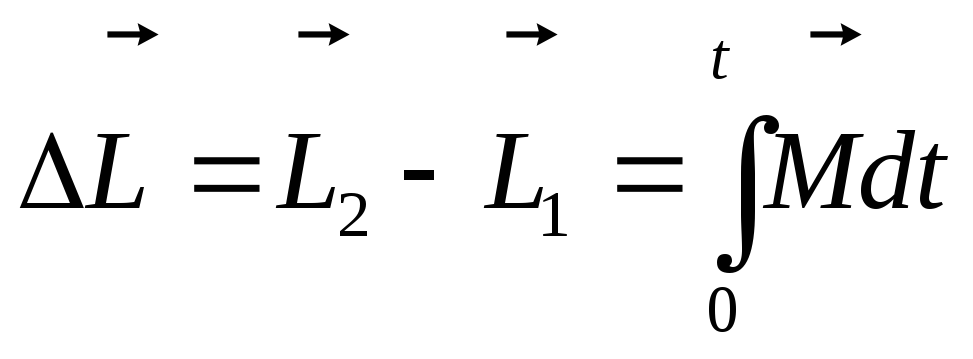
Выражение 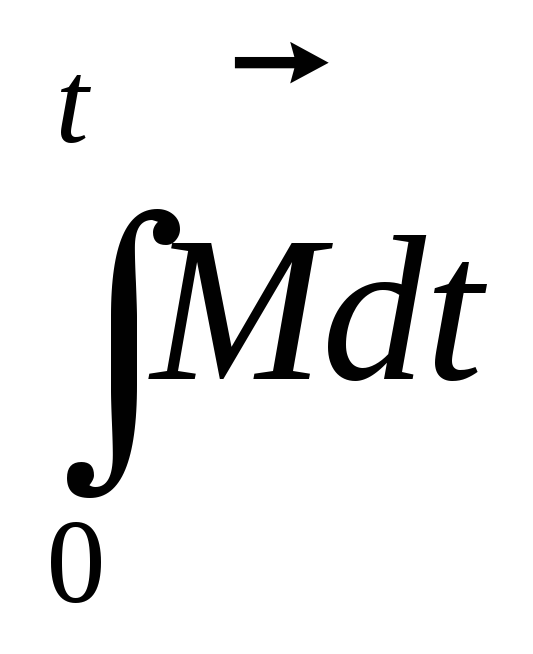 —импульс
момента силы подобно
—импульс
момента силы подобно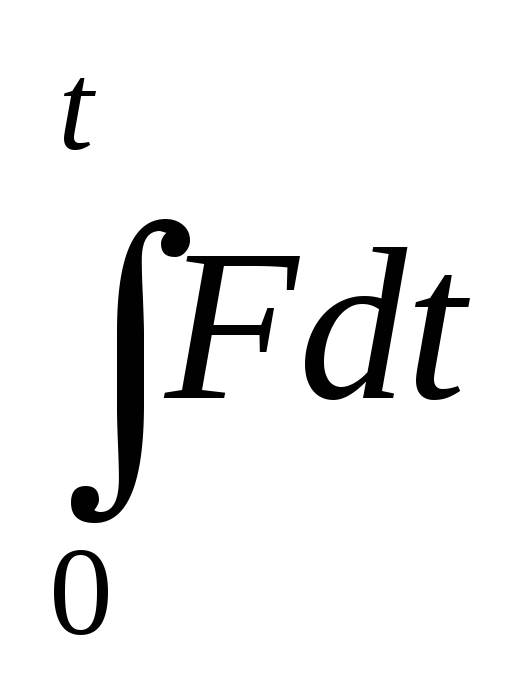 ,
т.е. приращение момента импульса частицы
за любой промежуток времени равно
импульсу момента силы за э
,
т.е. приращение момента импульса частицы
за любой промежуток времени равно
импульсу момента силы за э
то время.
4.3. Момент импульса и момент силы относительно оси.
В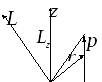
 озьмем
в интересующей нас системе отсчета
произвольную неподвижную ось
озьмем
в интересующей нас системе отсчета
произвольную неподвижную ось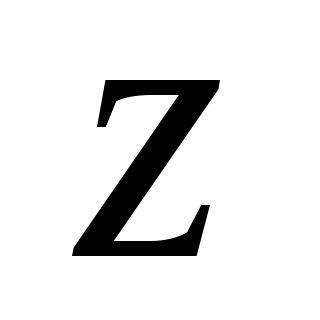 .
Пусть относительно некоторой т.О оси
.
Пусть относительно некоторой т.О оси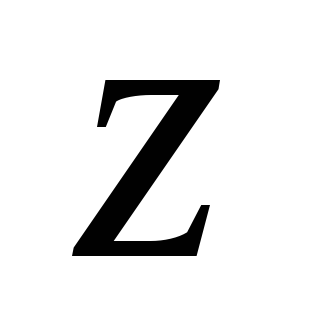 момент импульса частицы равен
момент импульса частицы равен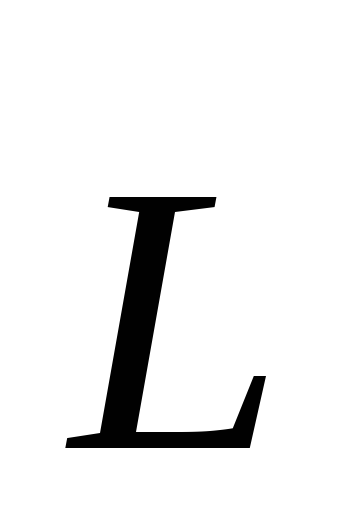 ,
а момент сил
,
а момент сил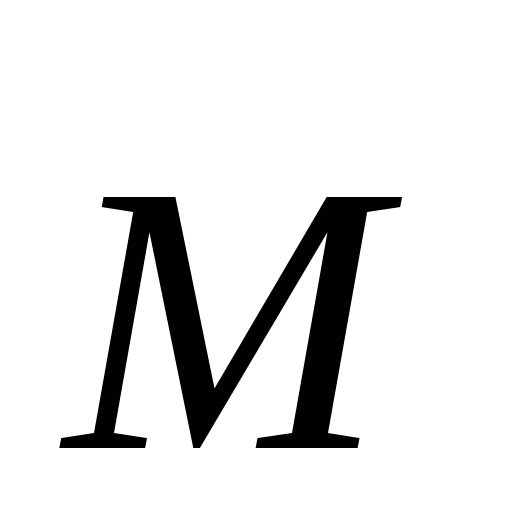 .
Момент импульса относительно оси
.
Момент импульса относительно оси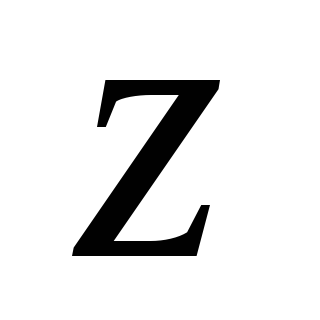 называется проекция на эту ось вектора
называется проекция на эту ось вектора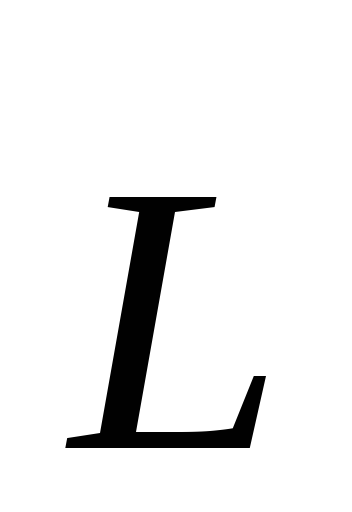 ,
определенного относительно произвольной
точки О данной оси. Аналогично вводится
понятие момента силы относительно оси
,
определенного относительно произвольной
точки О данной оси. Аналогично вводится
понятие момента силы относительно оси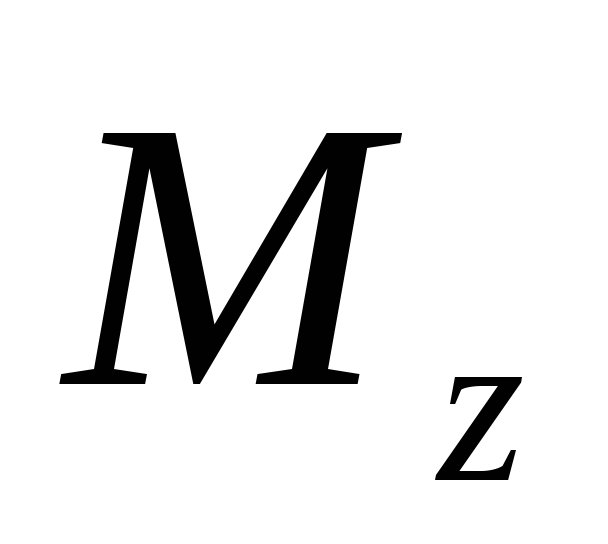 .
Уравнение момента относительно оси
.
Уравнение момента относительно оси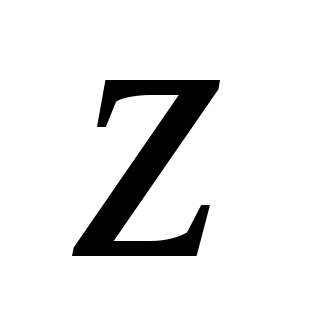
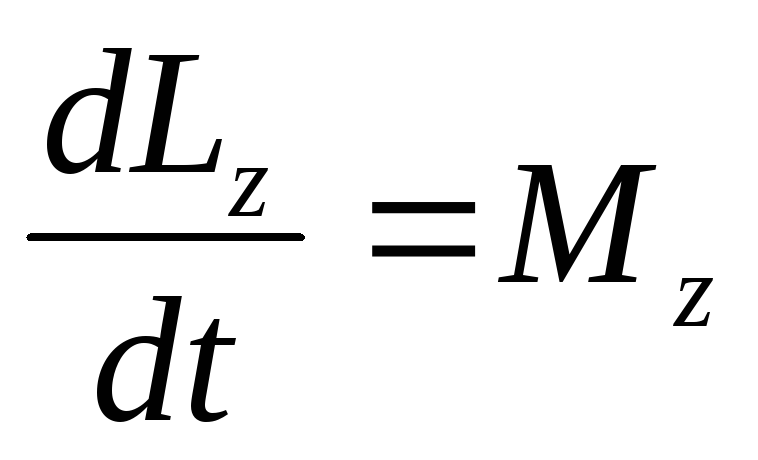 т.е. производная от
т.е. производная от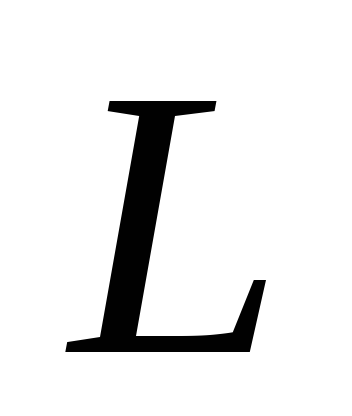 относительно
относительно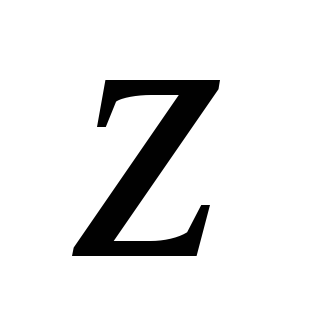 равна
равна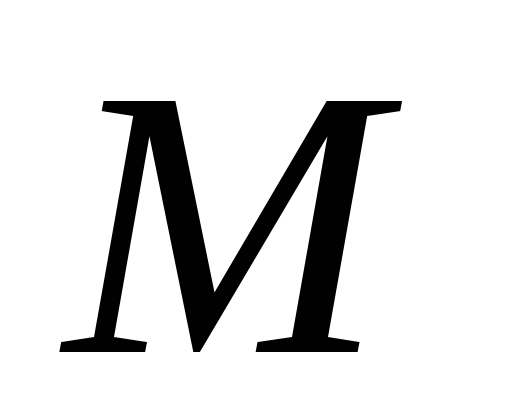 относительно
этой оси. В частности при
относительно
этой оси. В частности при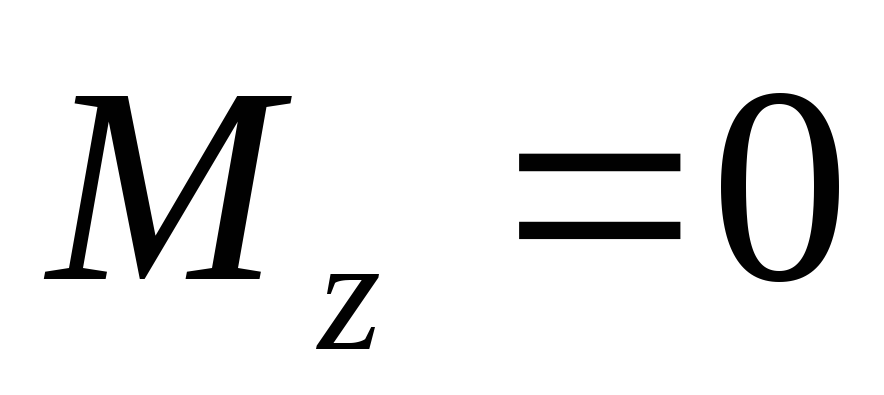
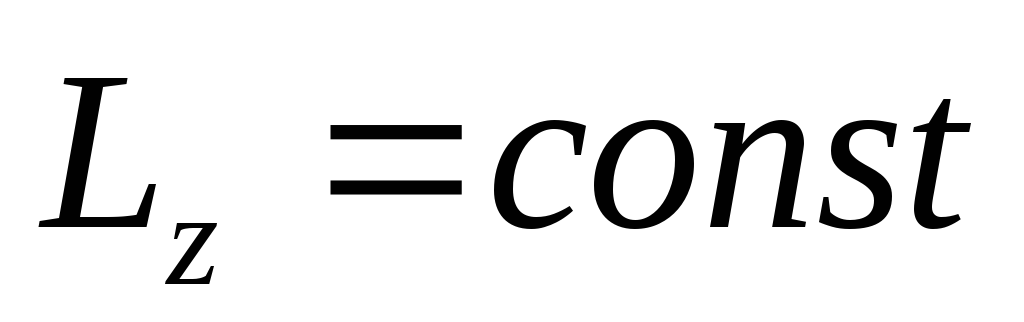 .
Т.е. если момент илы относительно
некоторой оси
.
Т.е. если момент илы относительно
некоторой оси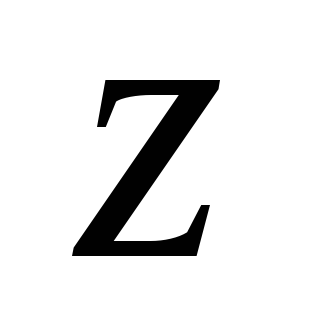 равен 0, то
равен 0, то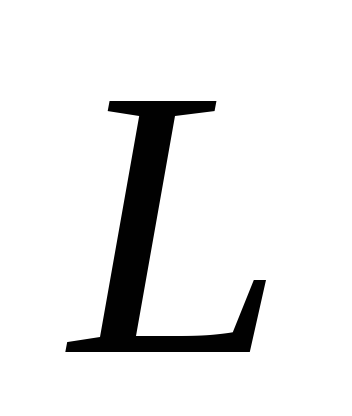 относительно этой оси остаеся постоянным.
При этом вектор
относительно этой оси остаеся постоянным.
При этом вектор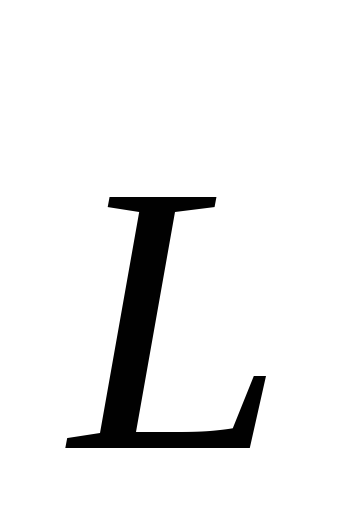 меняется.
меняется.
4.4. Закон сохранения момента импульса системы.
Рассмотрим систему состоящую из 2 частиц,
на которые действуют также силы  и
и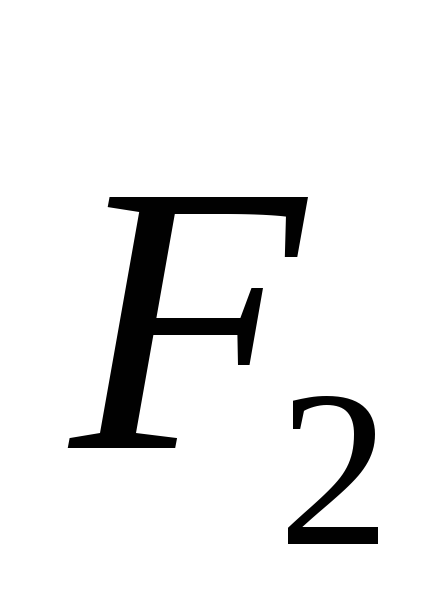 .
Момент импульса является аддитивной
величиной. Для системы равен векторной
сумме моментов импульса отдельных
частиц относительно одной и той же точки
.
Момент импульса является аддитивной
величиной. Для системы равен векторной
сумме моментов импульса отдельных
частиц относительно одной и той же точки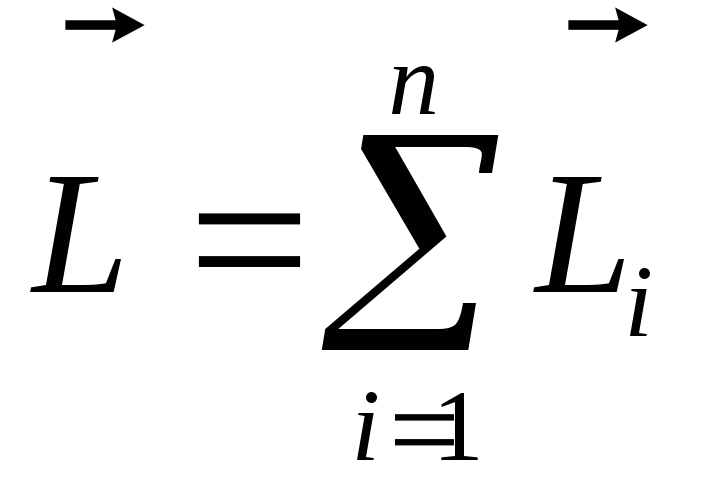 .
.
Нам известно, что 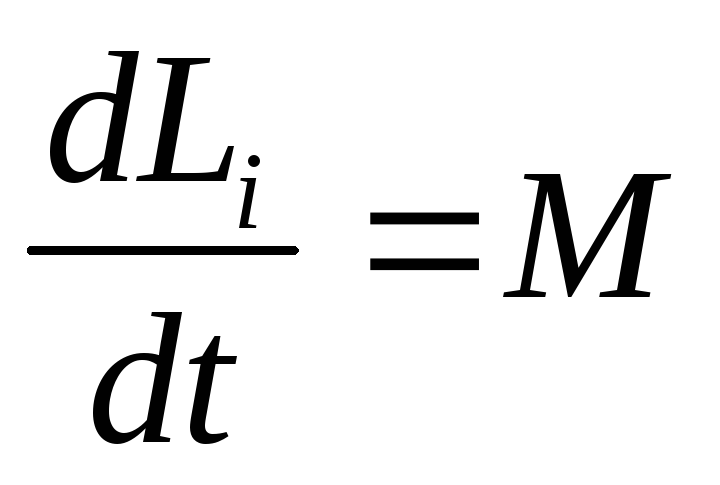 —моменту
всех сил, действующих на частицу, а
изменение момента системы
—моменту
всех сил, действующих на частицу, а
изменение момента системы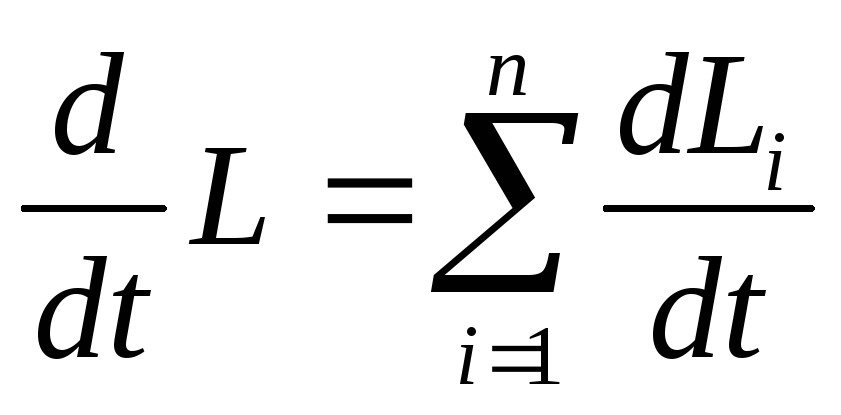 ,
тогда
,
тогда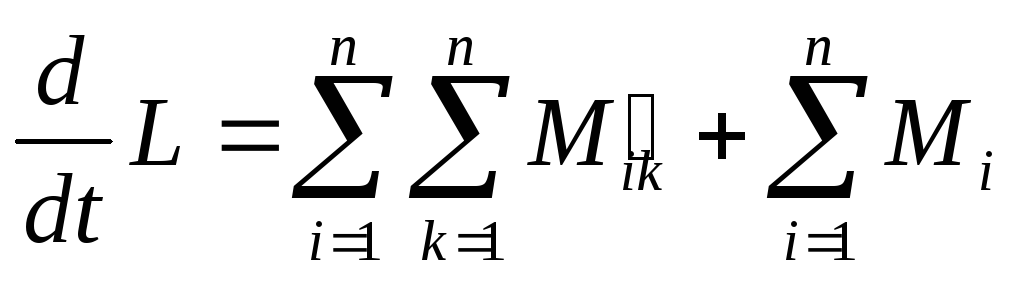 ;
;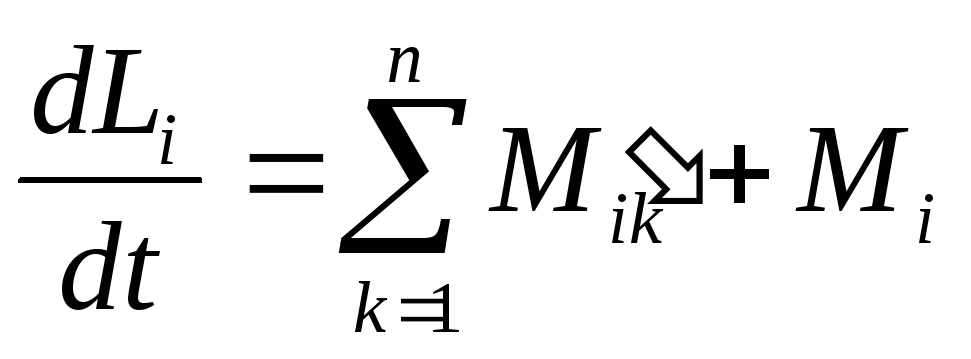 ;
;
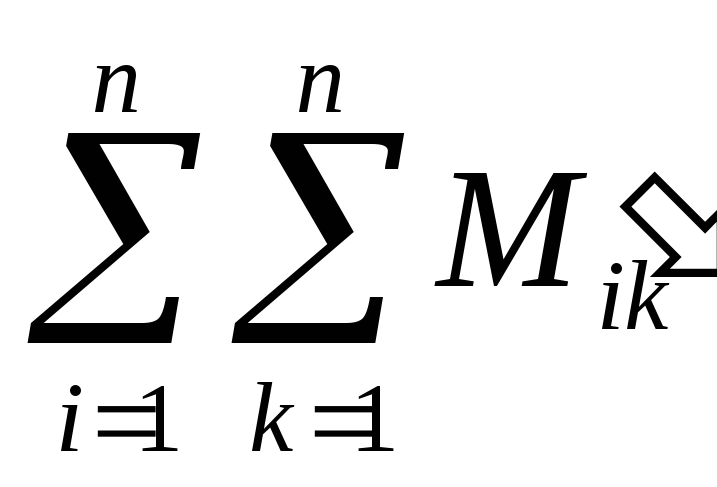 —
суммарный момент всех внутренних сил
действующих на частицы.
—
суммарный момент всех внутренних сил
действующих на частицы.
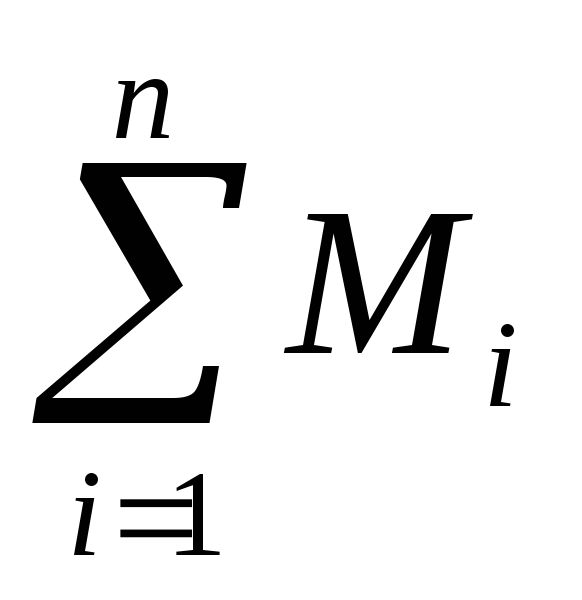 —
суммарный момент всех внешних сил
действующих на частицы.
—
суммарный момент всех внешних сил
действующих на частицы.
Значит для двух частиц:
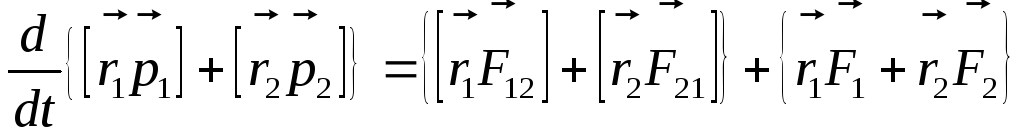 .
.
Суммарный момент внутренних сил
относительно любой точки равен 0. силы
взаимодействия между частицами 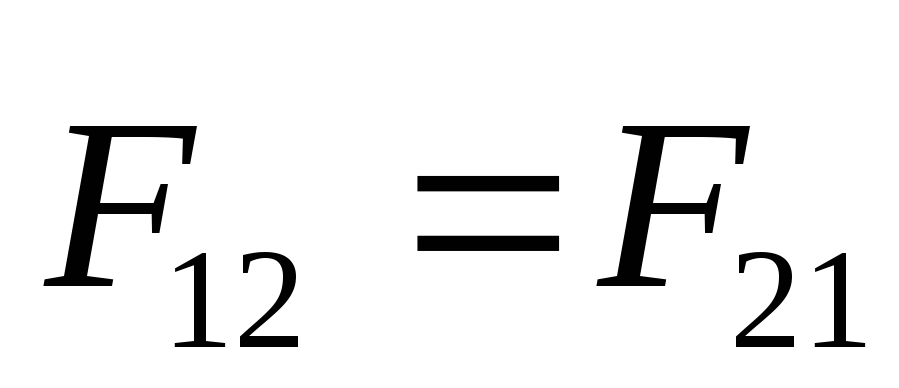 по 3му закону Ньютона
действуют по одной прямой, значит имеют
одинаковое плечо, поэтому момент каждой
пары внутренних сил равен 0.
по 3му закону Ньютона
действуют по одной прямой, значит имеют
одинаковое плечо, поэтому момент каждой
пары внутренних сил равен 0.
Т.о. 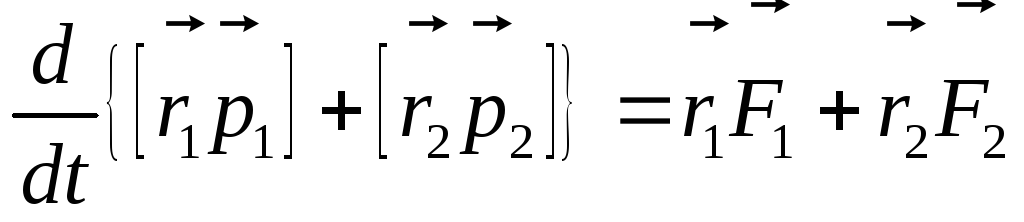 ;
т.е. системы изменяются под действием
внешних сил
;
т.е. системы изменяются под действием
внешних сил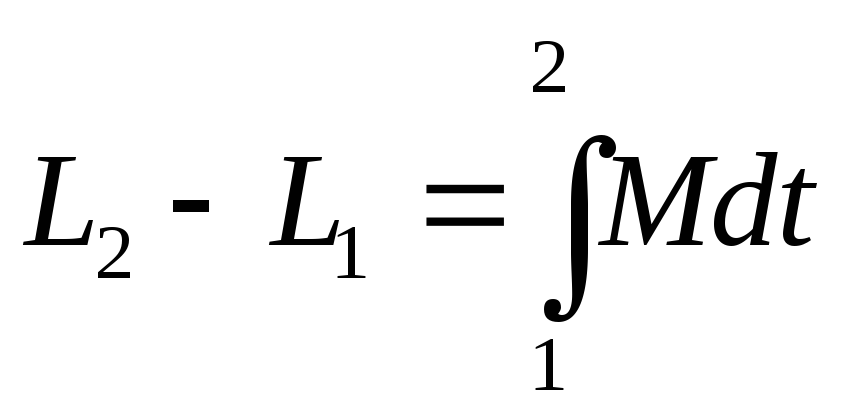 .
Если внешние силы отсутствуют
.
Если внешние силы отсутствуют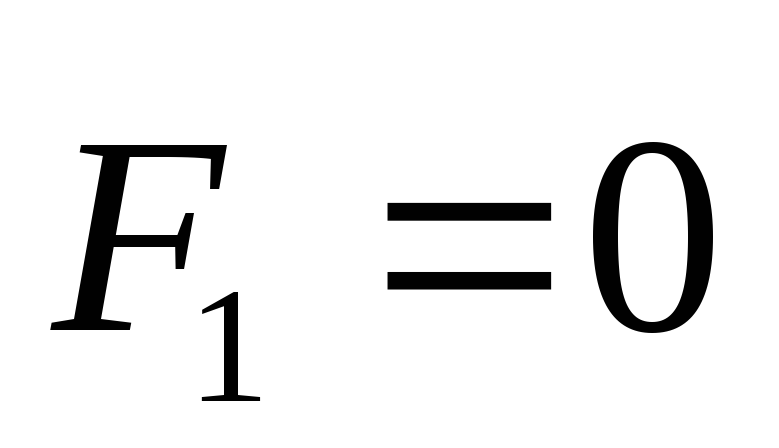 ,
,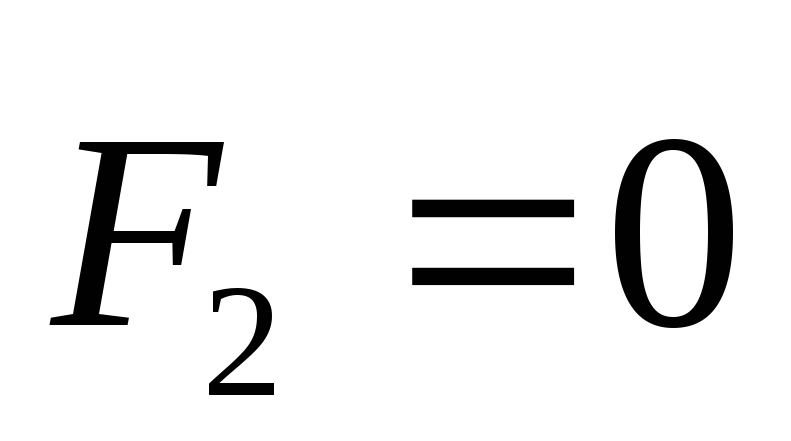 ,
то
,
то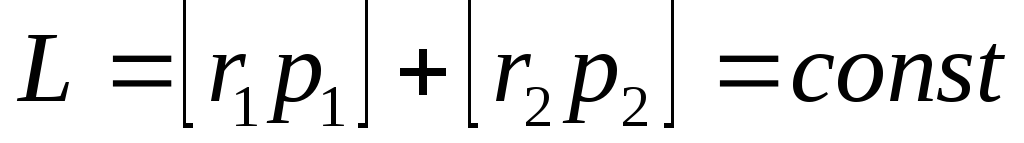 ,
является аддитивным сохраняющейся
величиной. Т.е. момент импульса замкнутой
системы частиц остается постоянным, не
меняется со временем. Это справедливо
относительно любой точки инерциальной
системы отсчета:
,
является аддитивным сохраняющейся
величиной. Т.е. момент импульса замкнутой
системы частиц остается постоянным, не
меняется со временем. Это справедливо
относительно любой точки инерциальной
системы отсчета: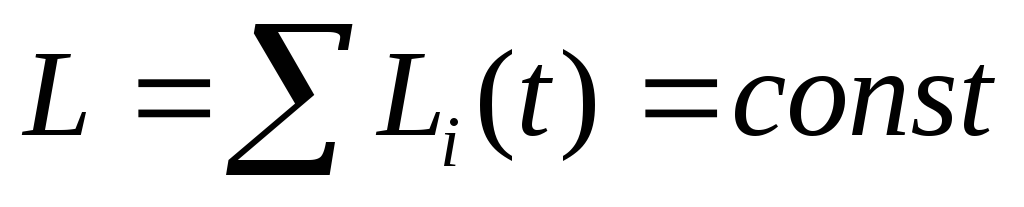 т.е. моменты импульса отдельных частей
т.е. моменты импульса отдельных частей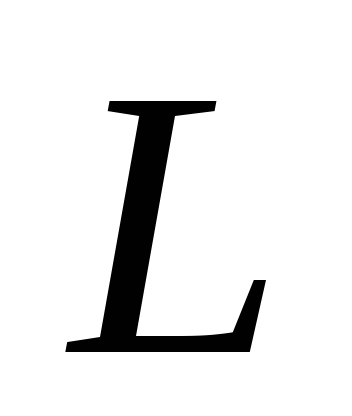 одной части системы происходят за счет
убыли
одной части системы происходят за счет
убыли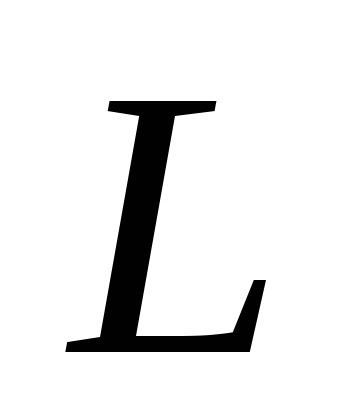 другой части (относительно одной точки).
другой части (относительно одной точки).
Закон справедлив и в неинерциальной системе отсчета в тех случаях когда суммарный момент всех внешних сил, включая силы инерции равен нулю.
З акон
играет такую же роль как закон сохранения
энергии импульса. Он позволяет решать
разные задачи, не рассматривая детально
внутренние процессы. Пример: разгоняют????
акон
играет такую же роль как закон сохранения
энергии импульса. Он позволяет решать
разные задачи, не рассматривая детально
внутренние процессы. Пример: разгоняют????
Момент импульса 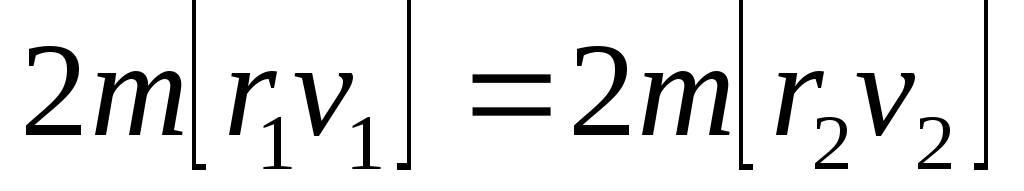 ;
;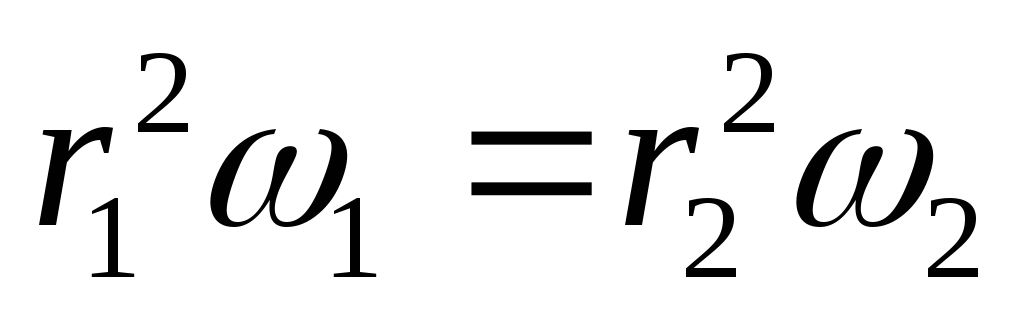 т.е.
т.е.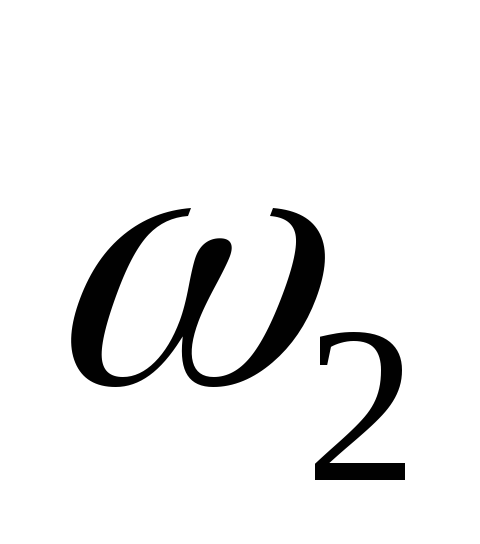 уменьшается как
уменьшается как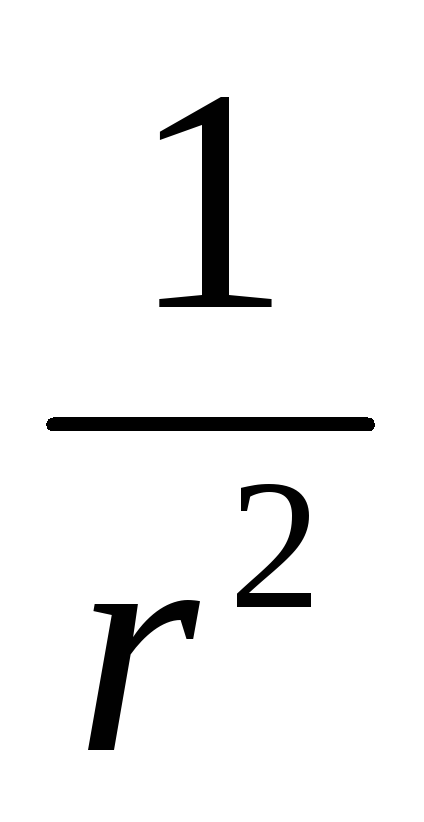 .
Этот эффект широко используют гимнасты,
фигуристы и т.д. здесь мы интересуемся
силами взаимодействия и т.д. у незамкнутых
систем может сохраняться не сам
.
Этот эффект широко используют гимнасты,
фигуристы и т.д. здесь мы интересуемся
силами взаимодействия и т.д. у незамкнутых
систем может сохраняться не сам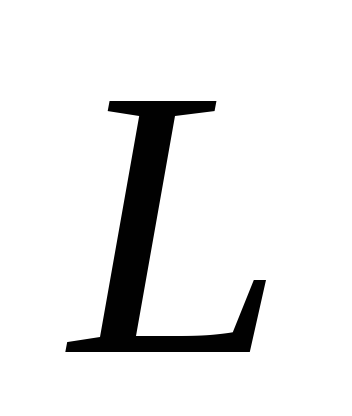 ,
а его проекция на некоторую неподвижную
ось
,
а его проекция на некоторую неподвижную
ось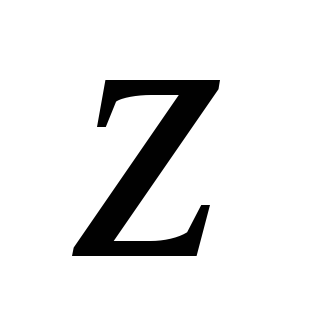 .
Это бывает, когда
.
Это бывает, когда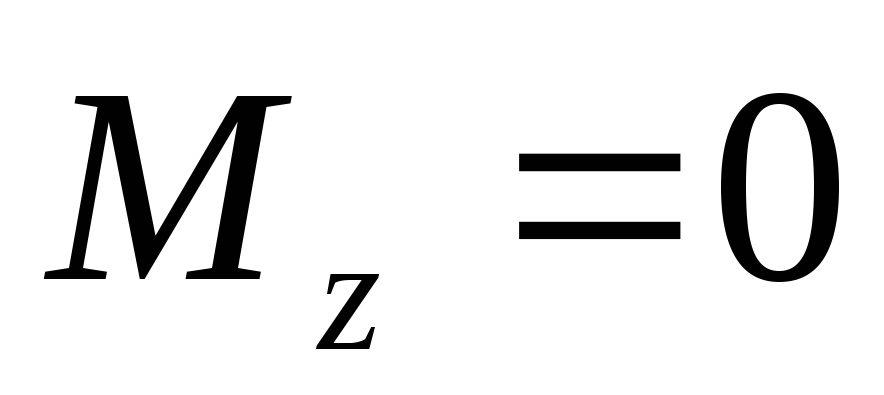 всех внешних сил.
всех внешних сил.
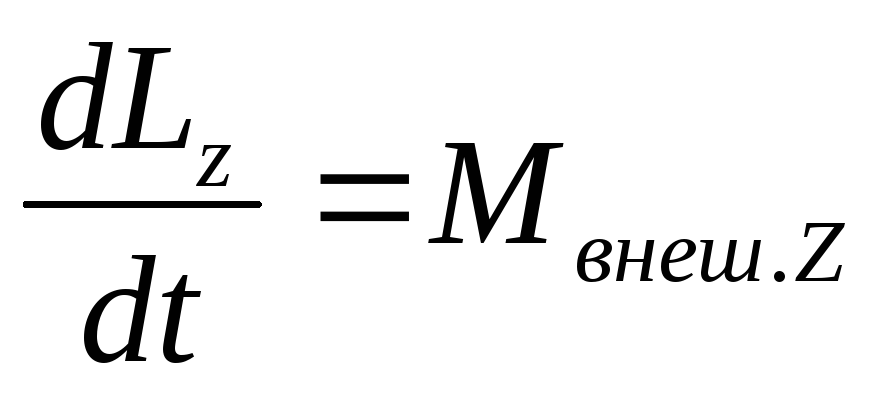 ;
;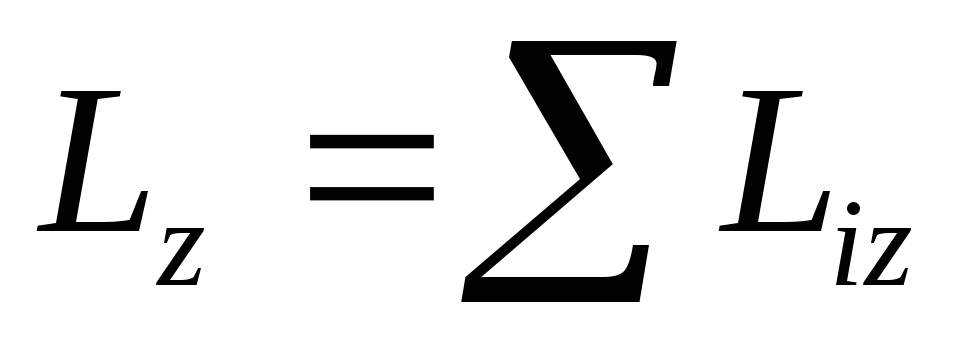 ;
;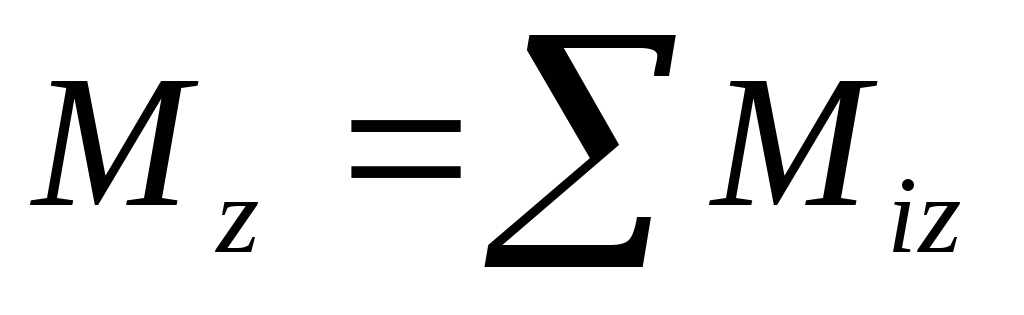
В физике понятие момента импульса расширяют на немеханические системы (с электромагнитным излучением, в атомах, ядра и др.) где не действуют законы Ньютона. Здесь закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельныйпринцип, является обобщением опытных фактов и является одним из фундаментальных законов наряду с законами сохранения энергии и импульса.
Лекция 8 «Механика твёрдого тела»
План лекции:
Момент силы и момент импульса относительно неподвижного центра и неподвижной оси.
Уравнение моментов для материальной точки и системы материальных точек.
Закон сохранения момента импульса.
Прежде чем приступить к изучению движения твёрдых тел, необходимо познакомиться с рядом новых физических понятий и характеристик движения.
Момент силы и момент импульса относительно неподвижного центра и неподвижной оси
Рассмотрим движение материальной точки mпод действием силы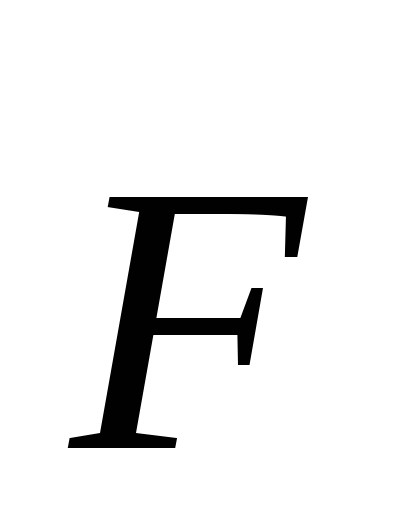 .
Положение этой частицы будем задавать
относительно начала неподвижной системы
координат радиус-вектором
.
Положение этой частицы будем задавать
относительно начала неподвижной системы
координат радиус-вектором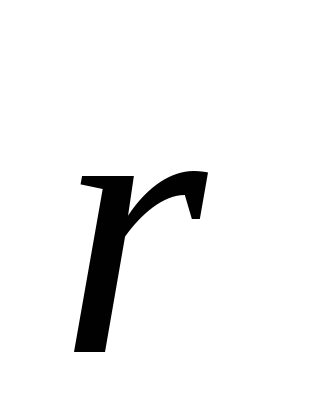 (рис. 8.1).
(рис. 8.1).

Рис. 8.1
По определению, моментом силы 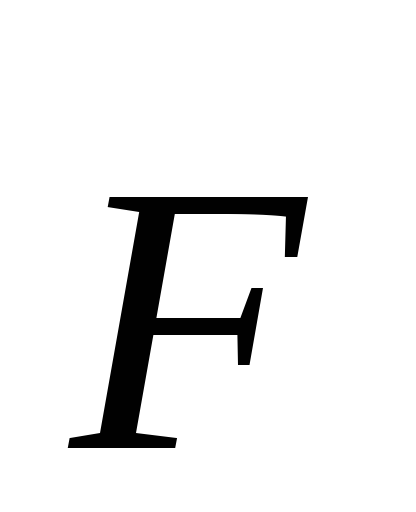 относительно неподвижного центра0 называется следующее векторное
произведение:
относительно неподвижного центра0 называется следующее векторное
произведение:
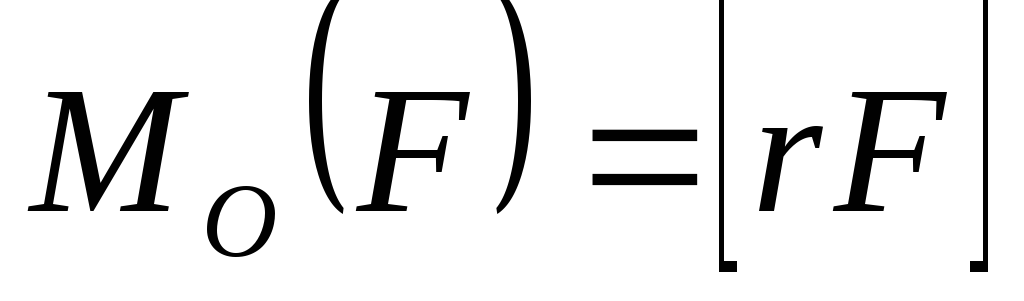 . (8.1)
. (8.1)
Вектор момента силы перпендикулярен
плоскости, образованной векторами 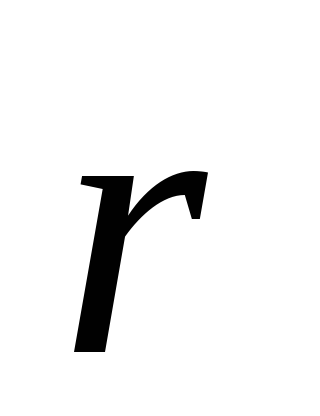 и
и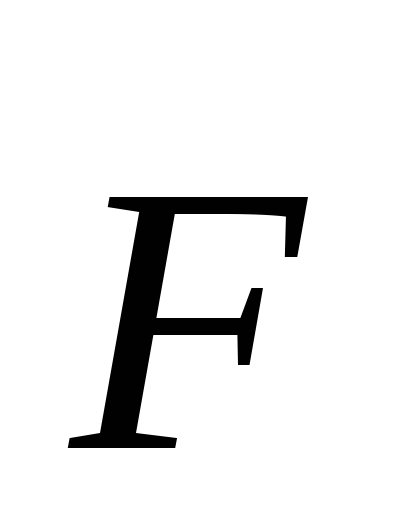 .
Направление этого вектора связано с
направлениями перемножаемых векторов
«правилом правого винта».
.
Направление этого вектора связано с
направлениями перемножаемых векторов
«правилом правого винта».
Проекция вектора момента силы на
какую-либо ось называется моментом силы
относительно этой оси. Рассмотрим,
например, момент силы 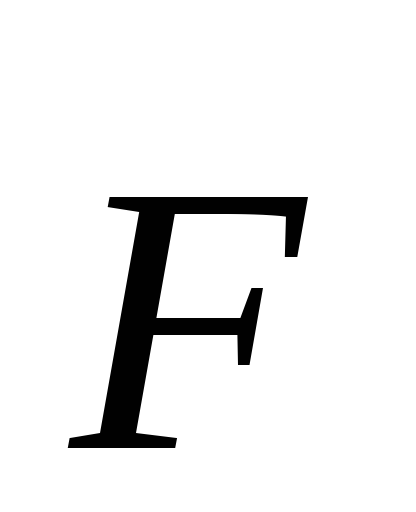 относительно осиz(рис. 8.2). Разложим
силу
относительно осиz(рис. 8.2). Разложим
силу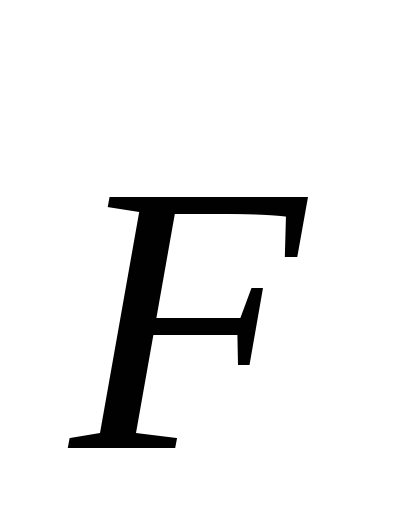 на три составляющие:
на три составляющие:
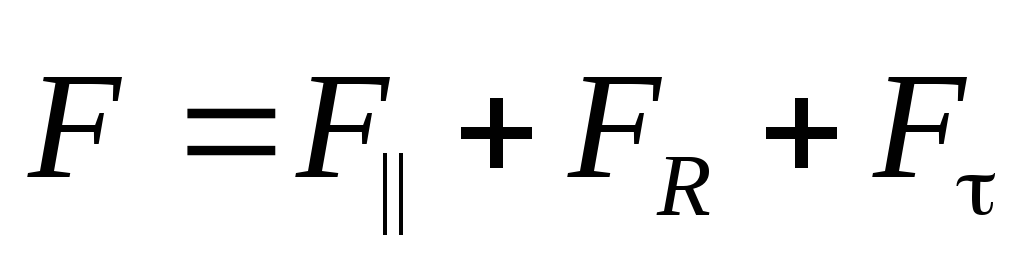
здесь: 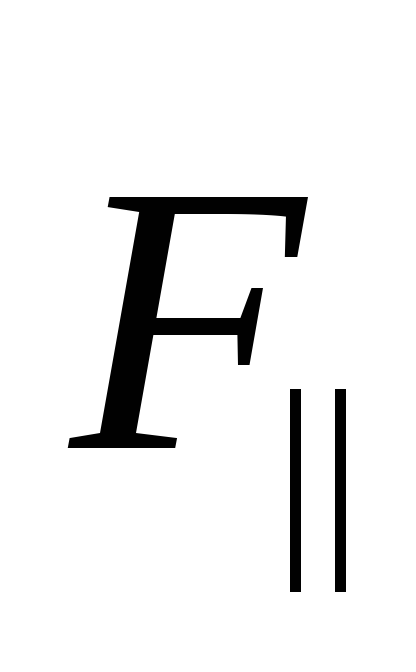 — составляющая, параллельная осиz;
— составляющая, параллельная осиz;
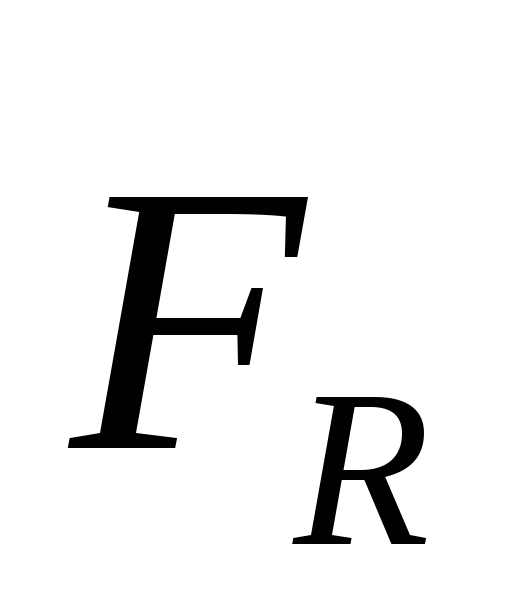 — составляющая, перпендикулярная осиzи действующая вдоль прямой,
проходящей черезz;
— составляющая, перпендикулярная осиzи действующая вдоль прямой,
проходящей черезz;
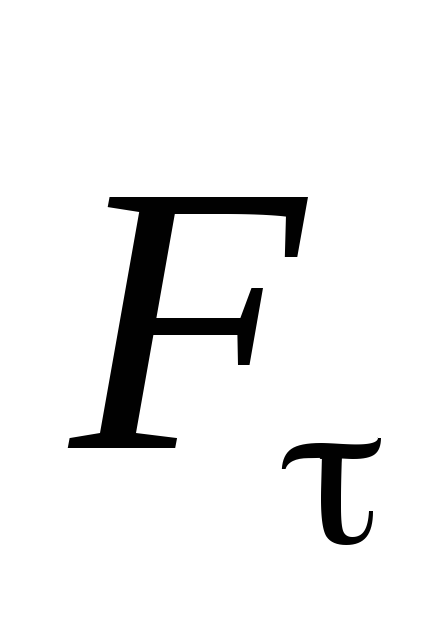 — составляющая, перпендикулярная
плоскости, проходящей через ось и точку
приложения силы.
— составляющая, перпендикулярная
плоскости, проходящей через ось и точку
приложения силы.
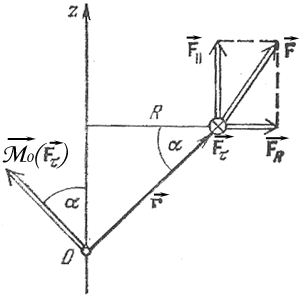
Рис. 8.2
Момент силы 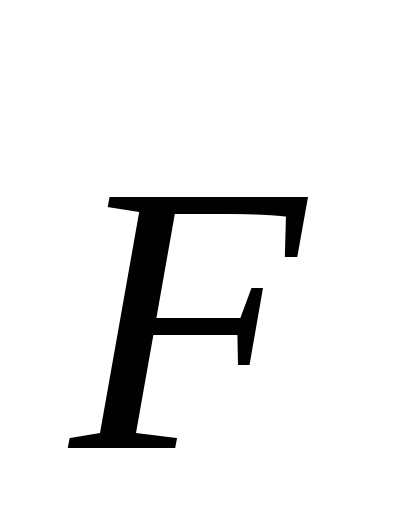 относительно центра 0 можно представить
теперь суммой моментов её составляющих
относительного того же центра.
Действительно, умножим векторно
предыдущее разложение на радиус-вектор
относительно центра 0 можно представить
теперь суммой моментов её составляющих
относительного того же центра.
Действительно, умножим векторно
предыдущее разложение на радиус-вектор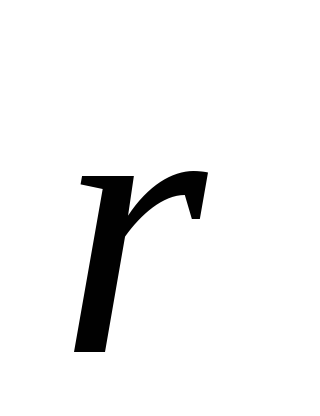 :
:
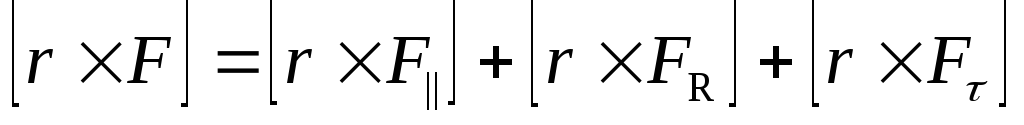 .
.
В этом равенстве все слагаемые — моменты соответствующих сил:
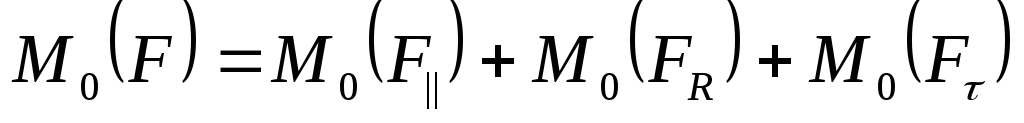 .
.
Спроецируем это уравнение на ось Z
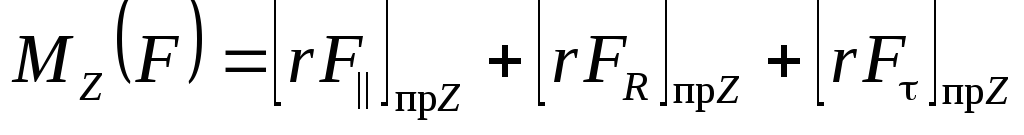 .
.
Первые слагаемые равны нулю, так как
векторы 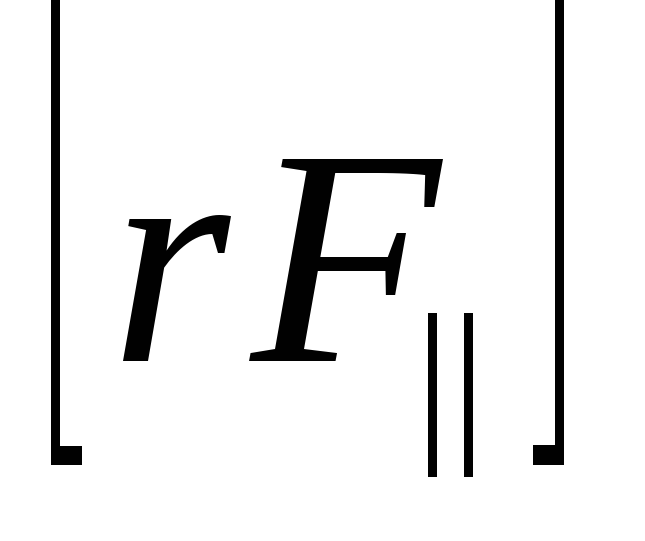 и
и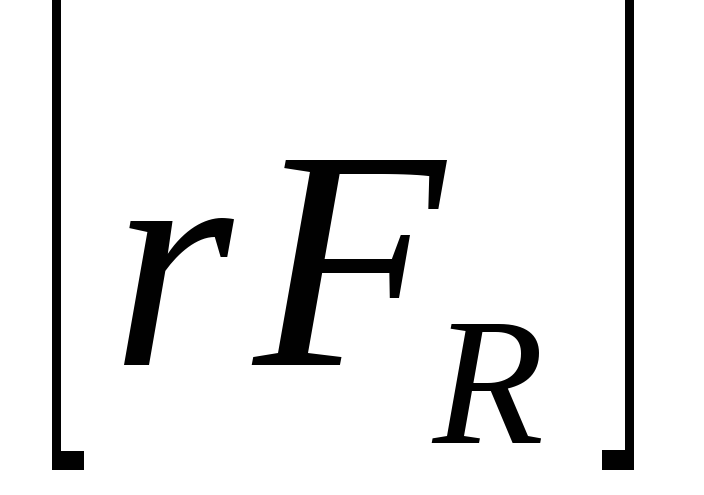 перпендикулярны осиZ, поэтому их
проекции наZравны нулю.
перпендикулярны осиZ, поэтому их
проекции наZравны нулю.
Таким образом, момент силы 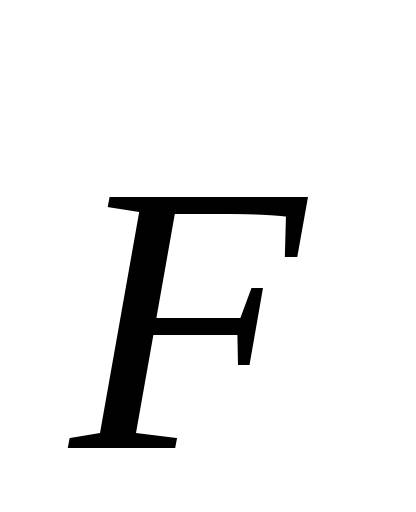 относительно осиZравен проекции
на эту ось момента силы
относительно осиZравен проекции
на эту ось момента силы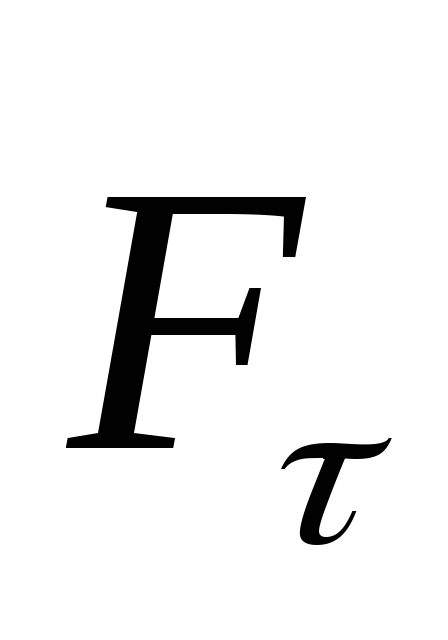 относительно центра 0.
относительно центра 0.
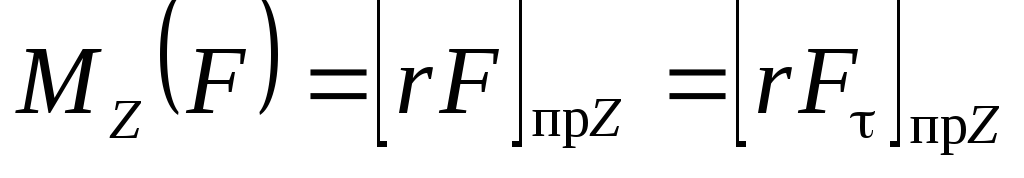
Момент силы 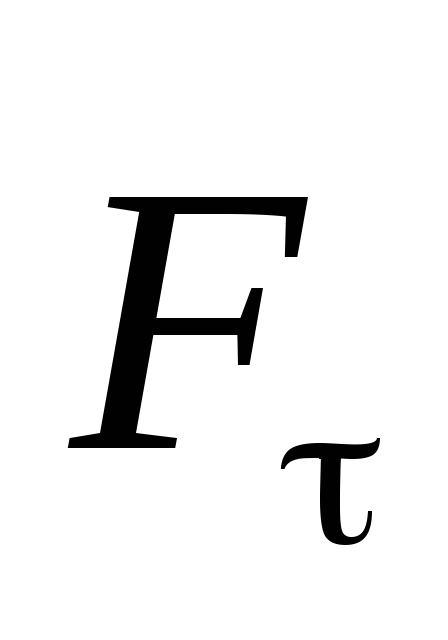 относительно неподвижного центра 0:
относительно неподвижного центра 0:
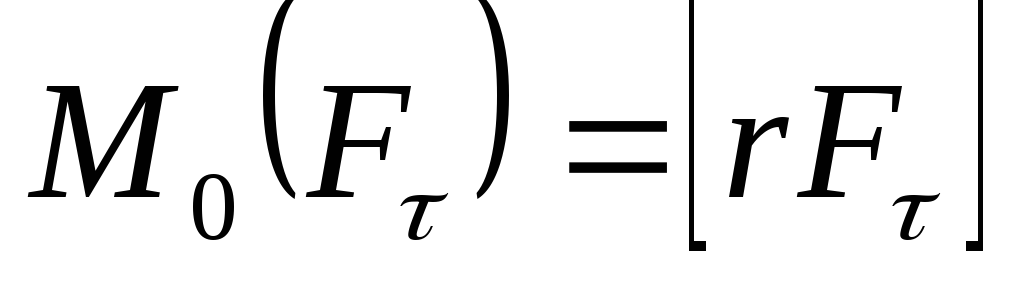
образует с осью Z угол (см. рис. 8.2), поэтому его проекцию на эту ось следует записать так:
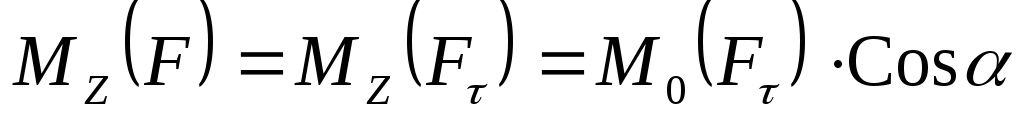 .
.
Здесь 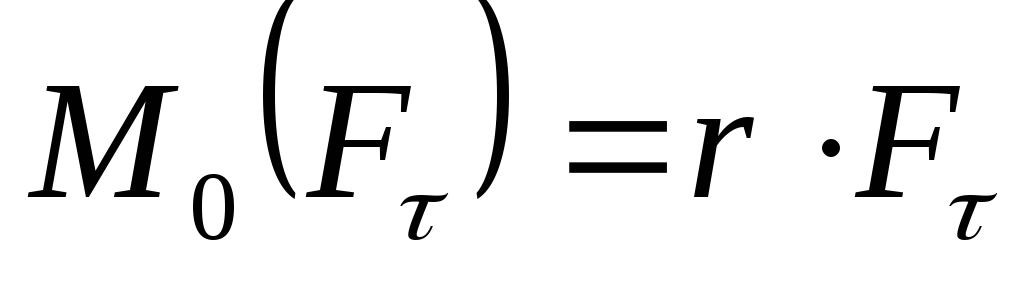 ,
поэтому
,
поэтому
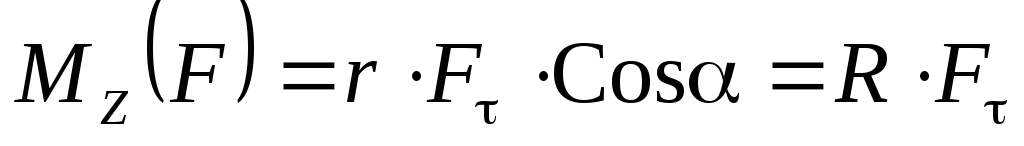 . (8.2)
. (8.2)
Здесь R=rСos–кратчайшее расстояние от оси вращения до точки приложения силы называется плечом силы.
Как и следовало ожидать, момент силы 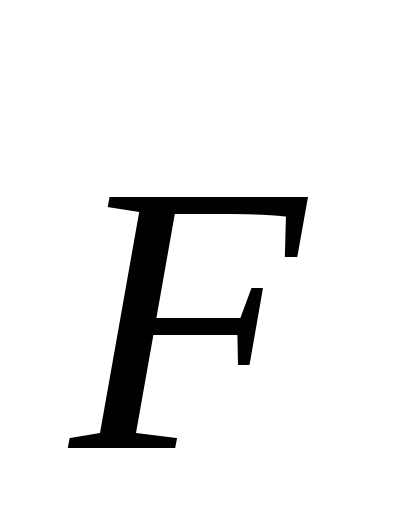 относительно осиZзависит от величины
её составляющейF.
Две другие составляющие —и
относительно осиZзависит от величины
её составляющейF.
Две другие составляющие —и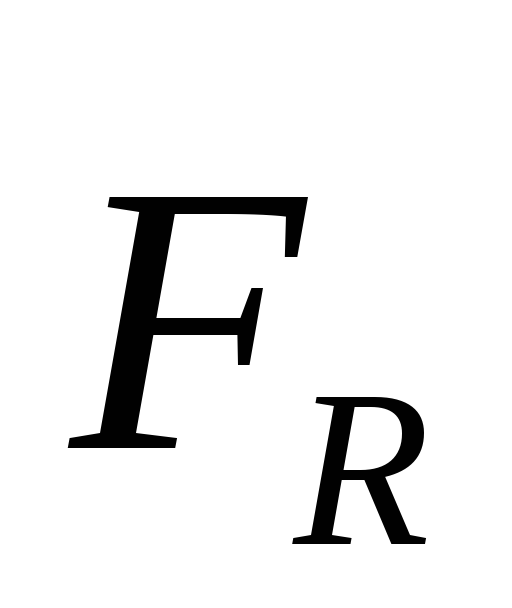 — вообще не создают момента относительно
осиZ.
— вообще не создают момента относительно
осиZ.
Другой важной характеристикой
вращательного движения частицы является моментимпульсаотносительно
неподвижного центра «0».Это тоже
векторная величина. Она равна векторному
произведению радиус-вектора частицы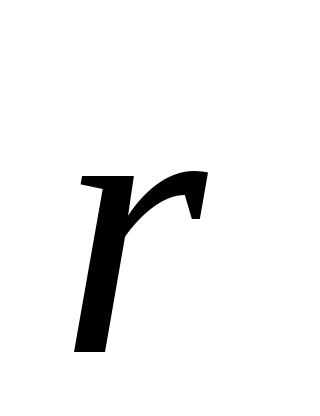 на её импульс
на её импульс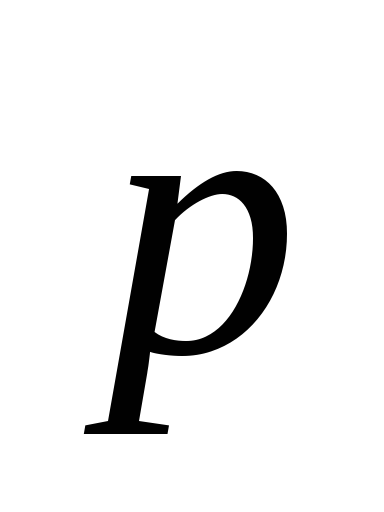 =
=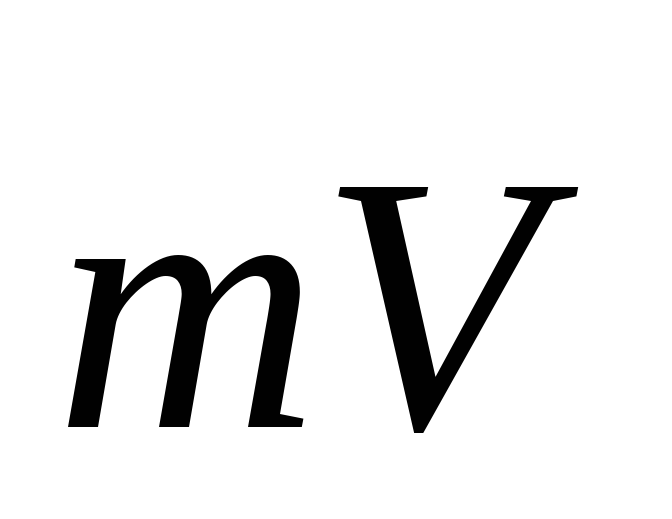 (рис. 8.3).
(рис. 8.3).
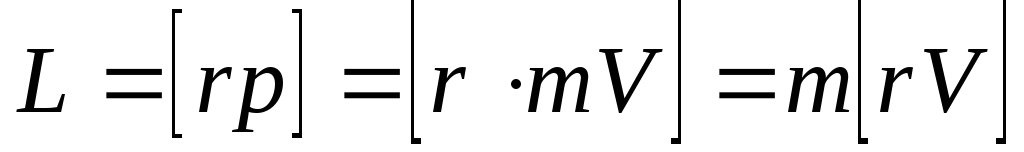 . (8.3)
. (8.3)
Модуль момента импульса равен:
L=rmVSin=rpSin,
где — угол между векторами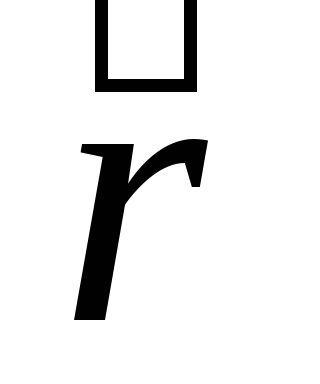 и
и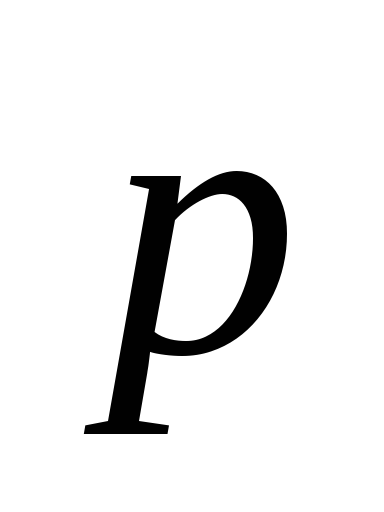 .
.

Рис. 8.3
Моментом импульса системы материальных точек называется векторная сумма их моментов импульса:
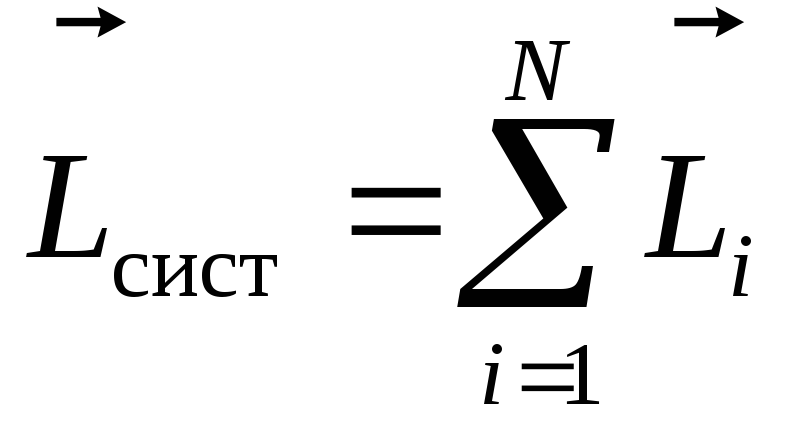 .
.
Проекция вектора момента импульса на некоторую ось OZ называется моментом импульса частицы (или системы) относительно этой оси:
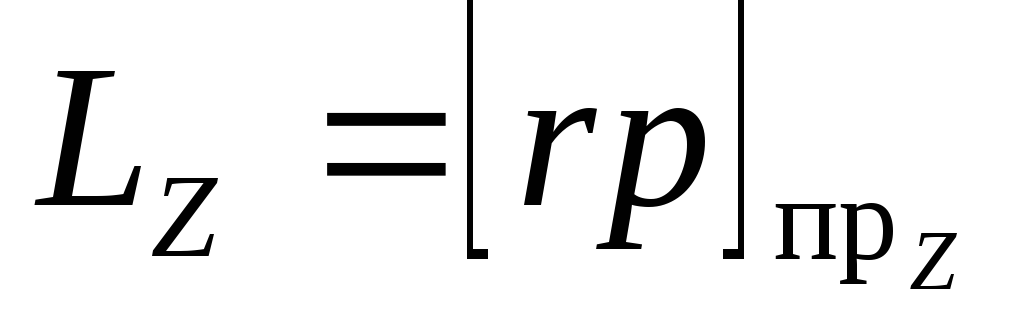 .
.
Введение понятий «момент силы» и «момент импульса» обусловлено тем, что эти величины связаны друг с другом. В механике эта связь устанавливается «уравнением моментов».
Уравнение моментов для материальной точки и системы материальных точек
Рассмотрим систему двух взаимодействующих
частиц (рис. 8.4). На этом рисунке 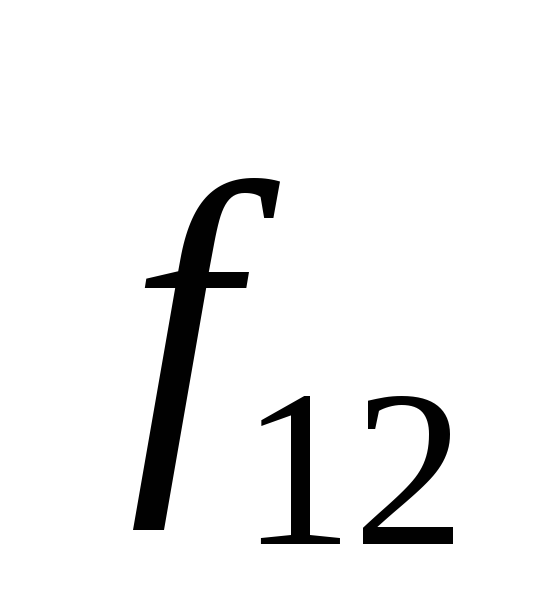 и
и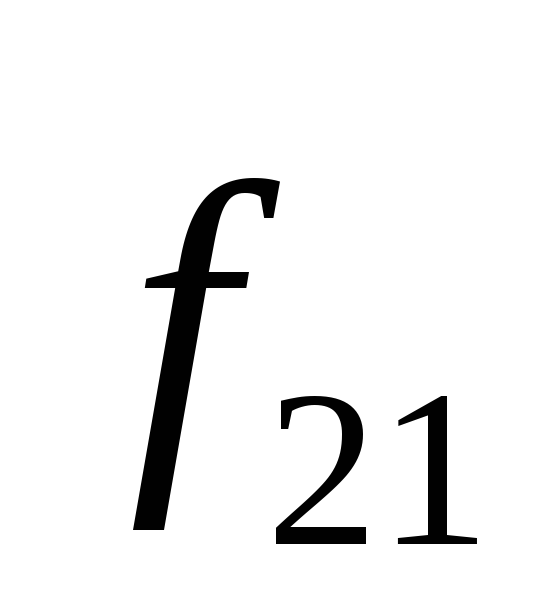 — внутренние силы взаимодействия частиц
друг с другом:
— внутренние силы взаимодействия частиц
друг с другом: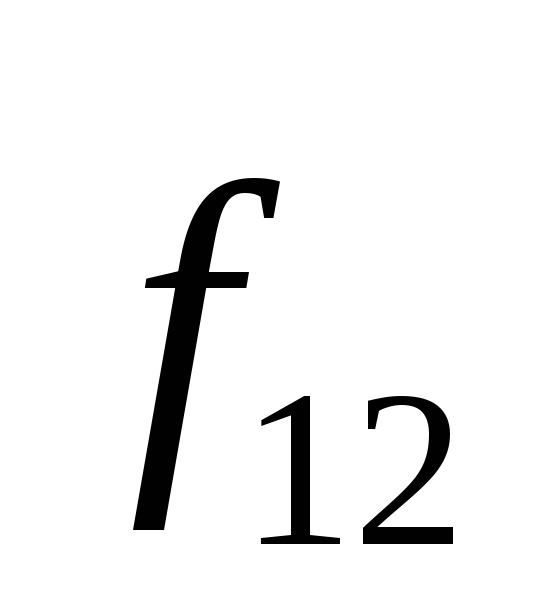 = –
= –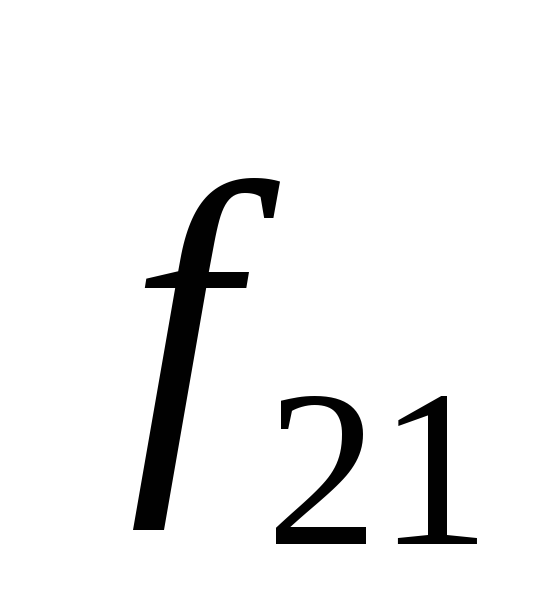 .
.

Рис. 8.4
 и
и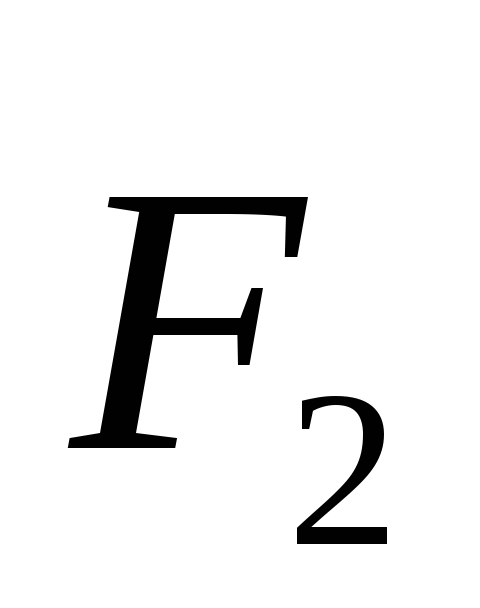 — внешние силы, действующие на частицыm1иm2,и
— внешние силы, действующие на частицыm1иm2,и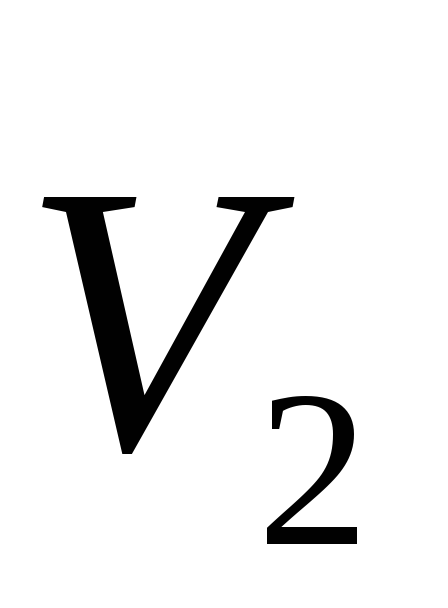 — скорости частиц.
— скорости частиц.
Запишем уравнения их движения (уравнения второго закона Ньютона):
 +
+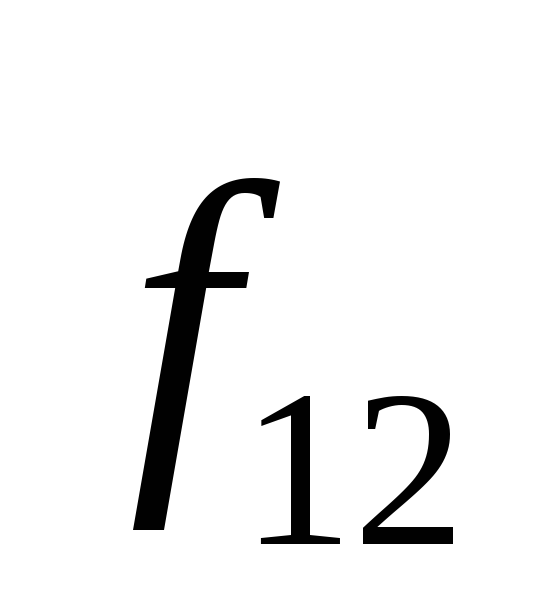 =
=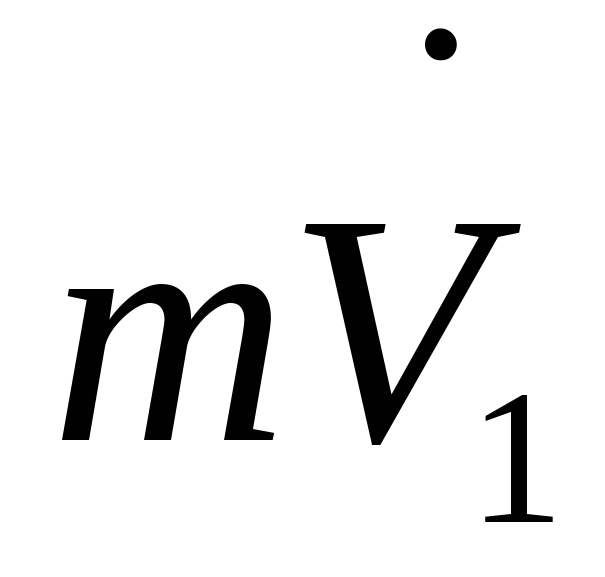 ;
;
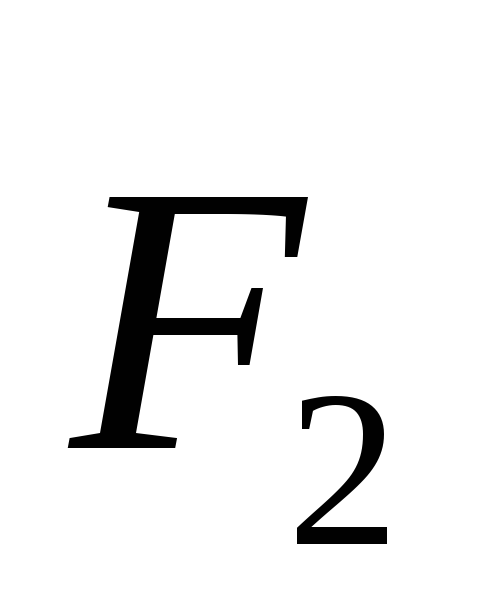 +
+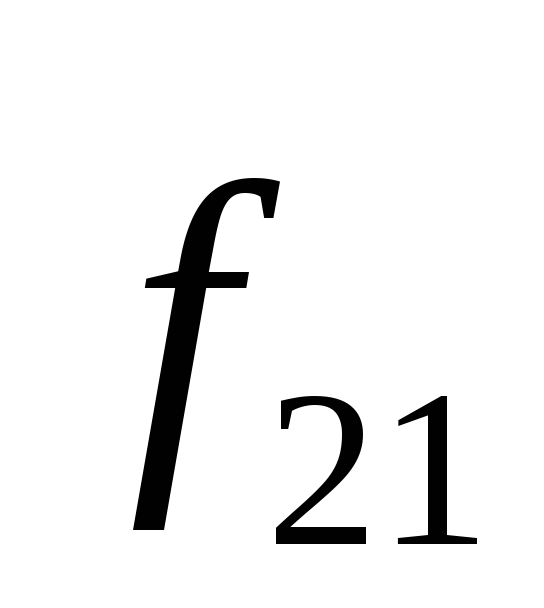 =
=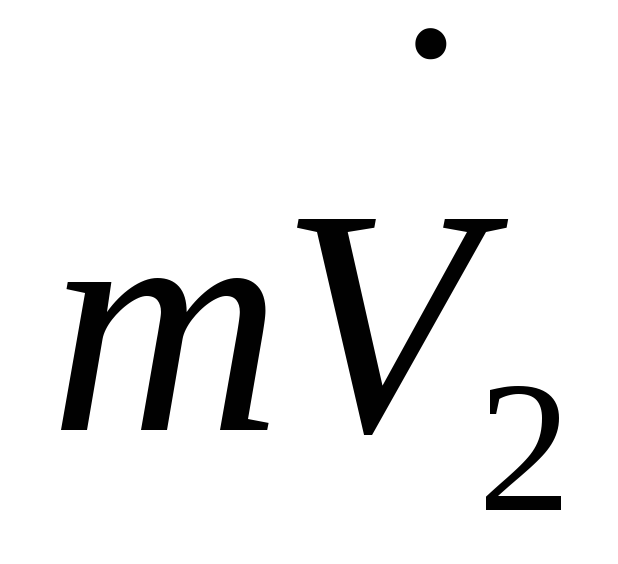 .
.
Умножим векторно первое уравнение на
радиус-вектор первой частицы 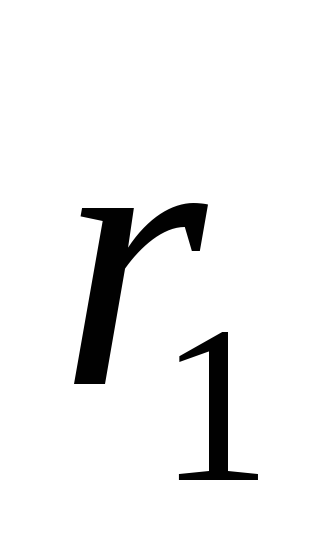 ,
а второе — на
,
а второе — на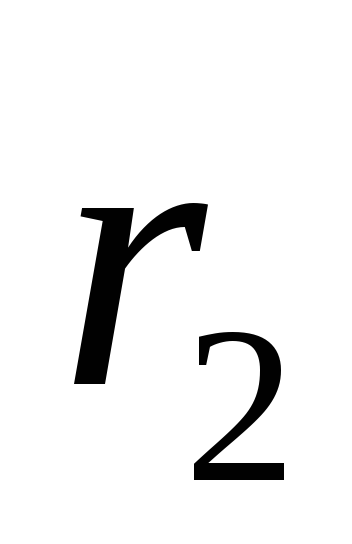 .
.
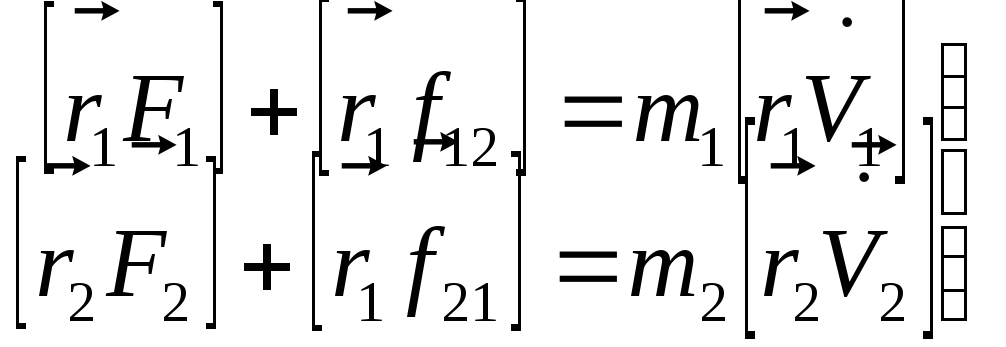 . (8.3)
. (8.3)
Заметим, что 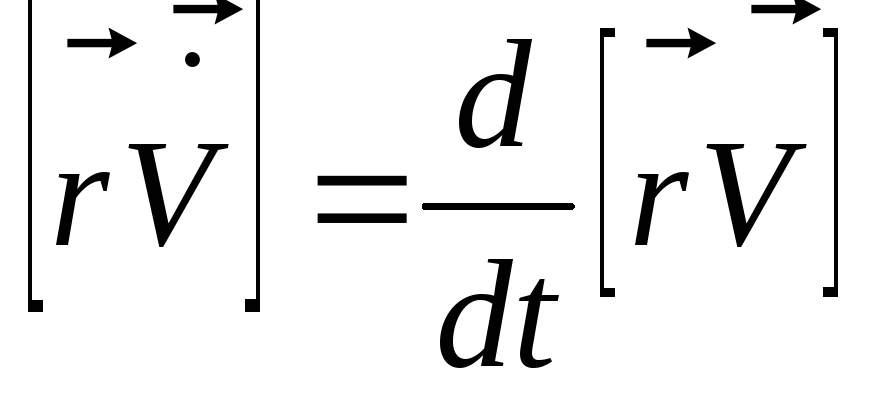 .
Действительно,
.
Действительно,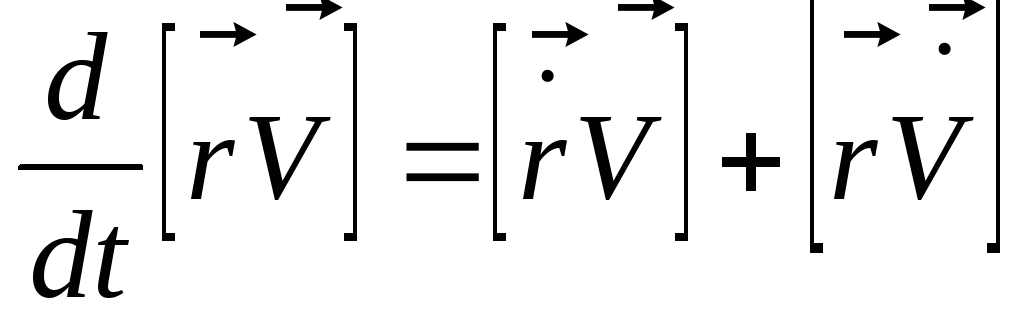 .
Первое слагаемое справа равно нулю, так
как
.
Первое слагаемое справа равно нулю, так
как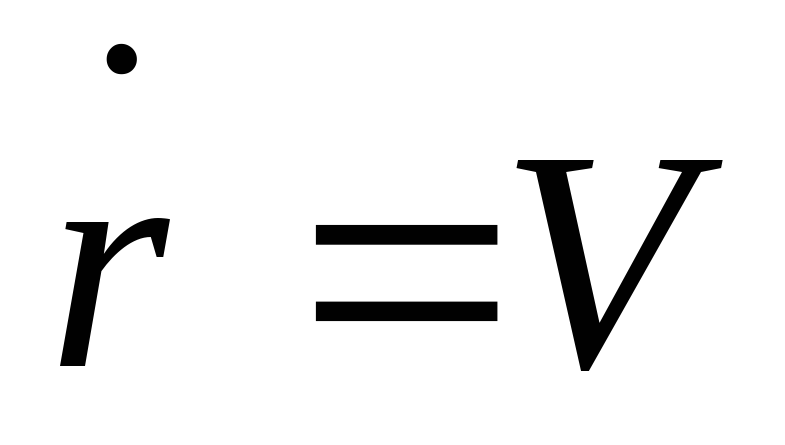 .
Следовательно, здесь векторно умножаются
совпадающие векторы. Такое произведение
равняется нулю.
.
Следовательно, здесь векторно умножаются
совпадающие векторы. Такое произведение
равняется нулю.
Перепишем уравнения системы (8.3), учтя
ещё, что 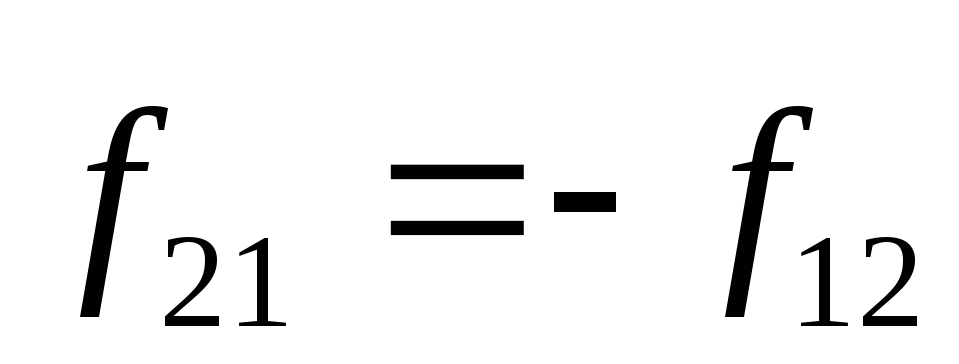 :
:
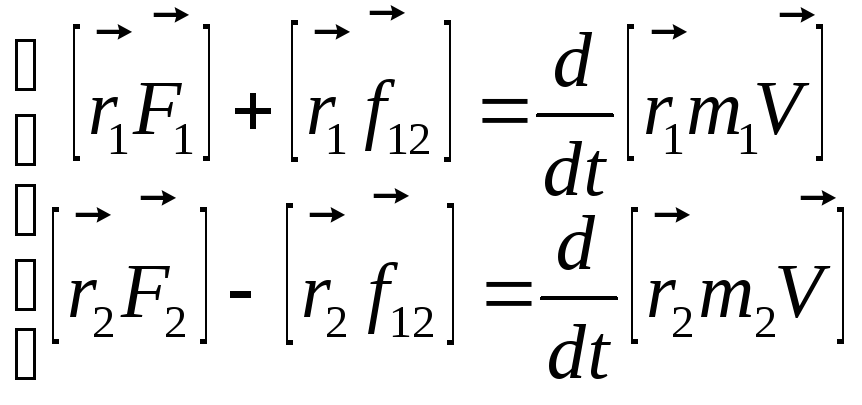 .
.
Сложим эти уравнения:
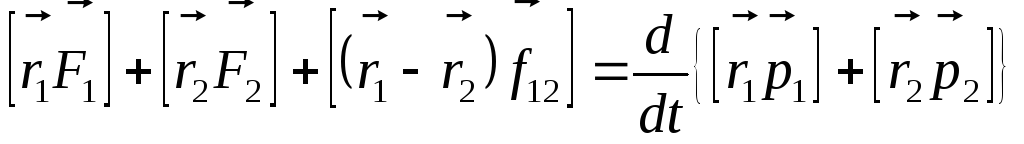 .
.
Векторы 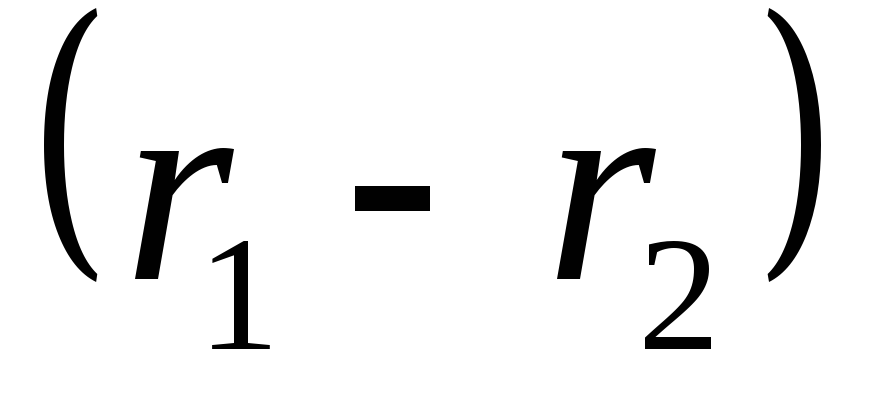 и
и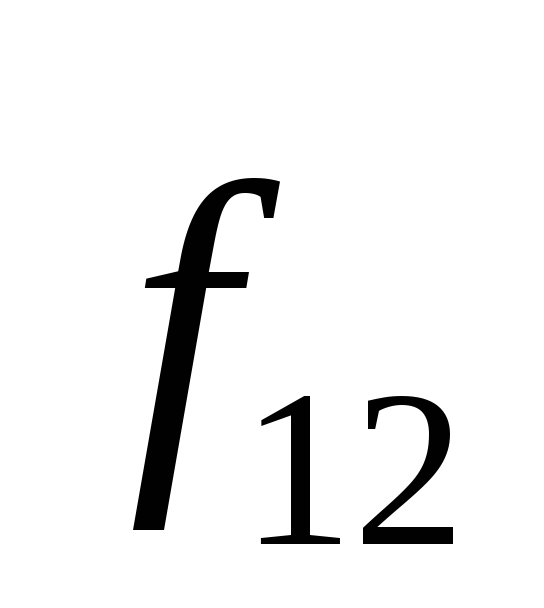 коллинеарны (см. рис. 8.4), поэтому их
векторное произведение равно нулю.
коллинеарны (см. рис. 8.4), поэтому их
векторное произведение равно нулю.
Окончательно это уравнение можно записать в таком виде:
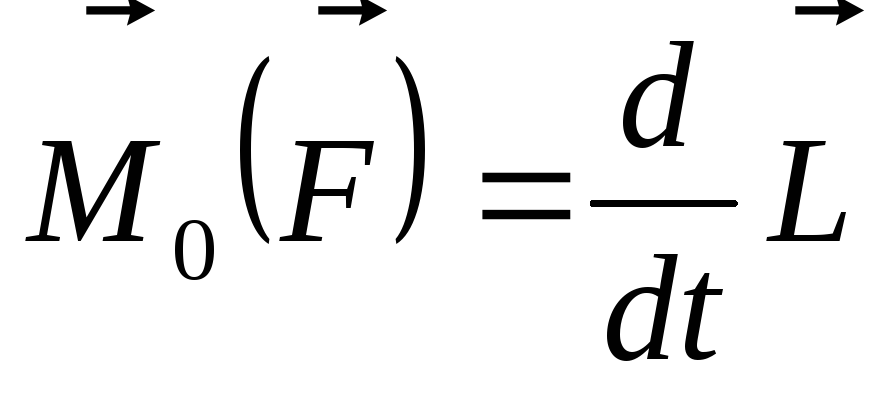 . (8.4)
. (8.4)
Здесь: 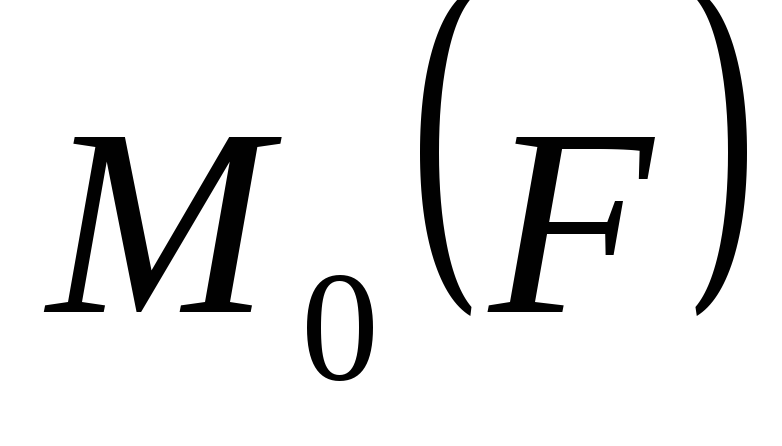 — векторная сумма моментов всех внешних
сил относительно центра 0;
— векторная сумма моментов всех внешних
сил относительно центра 0;
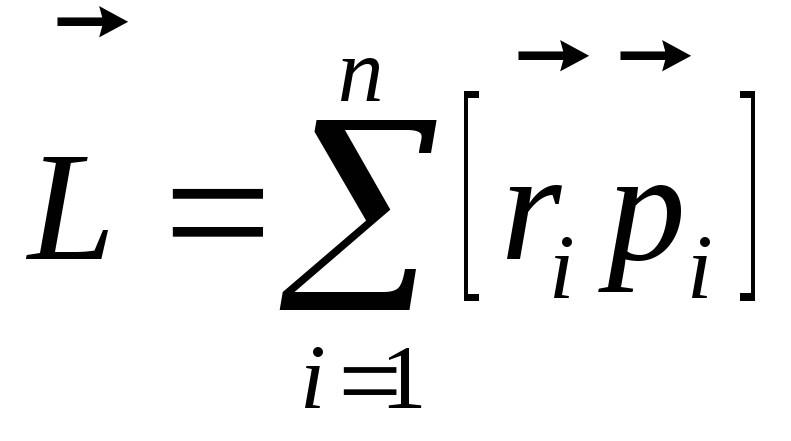 — момент импульса силы относительно
того же центра.
— момент импульса силы относительно
того же центра.
Это уравнение получило название уравнения моментов относительно неподвижного центра: производная по времени момента импульса системы материальных точек относительно произвольного неподвижного центра равна геометрической сумме моментов всех внешних сил относительно того же центра.
Уравнение моментов показывает, что
изменение момента импульса системы
может произойти только в результате
действия момента внешних сил. Если
внешние силы отсутствуют или их вращающий
момент равен нулю 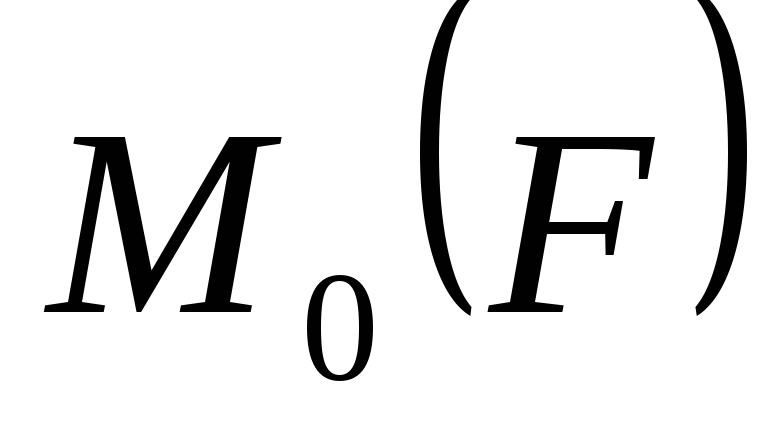 = 0, то момент импульса системы остаётся
неизменным во времени:
= 0, то момент импульса системы остаётся
неизменным во времени:
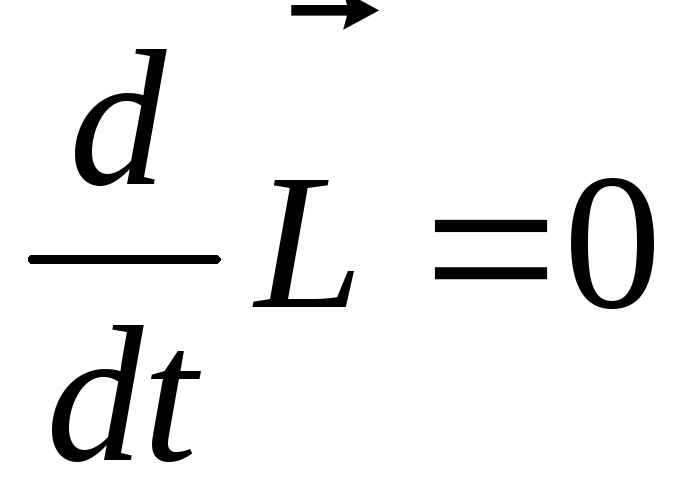 ,
то есть
,
то есть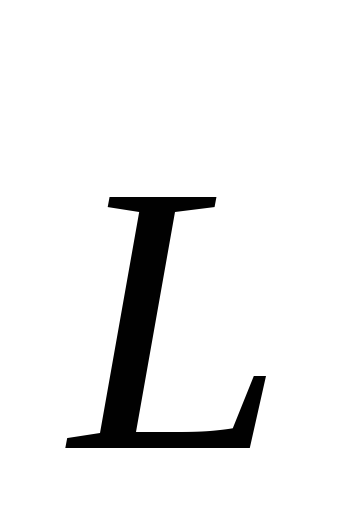 =сonst.
=сonst.
Спроецировав уравнение (8.4) на произвольную ось Z, получим уравнение моментов относительно этой оси:
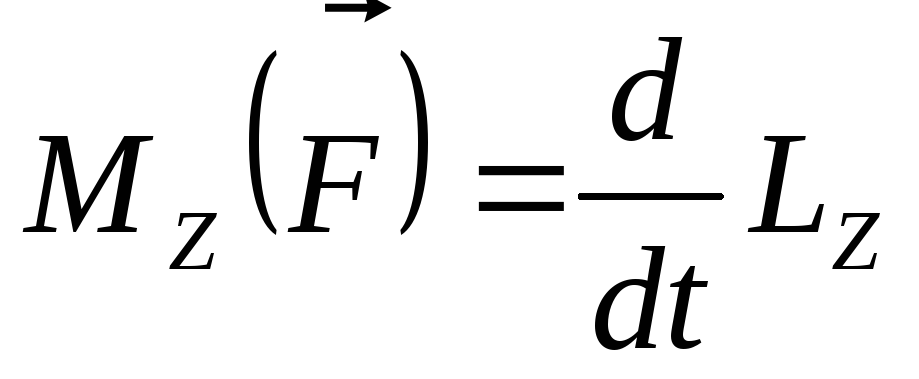 .
.
Производная по времени момента импульса системы относительно оси Z равна сумме моментов внешних сил относительно этой оси.
Если сумма моментов внешних сил относительно оси равна нулю, то момент импульса системы относительно этой оси будет оставаться постоянным.
Момент импульса
1. Момент импульса частицы
Пусть частица движется по некоторой траектории и в данный момент
времени
ее радиус-вектор равен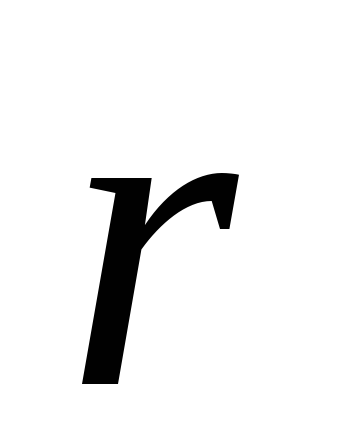 ,
а импульс
,
а импульс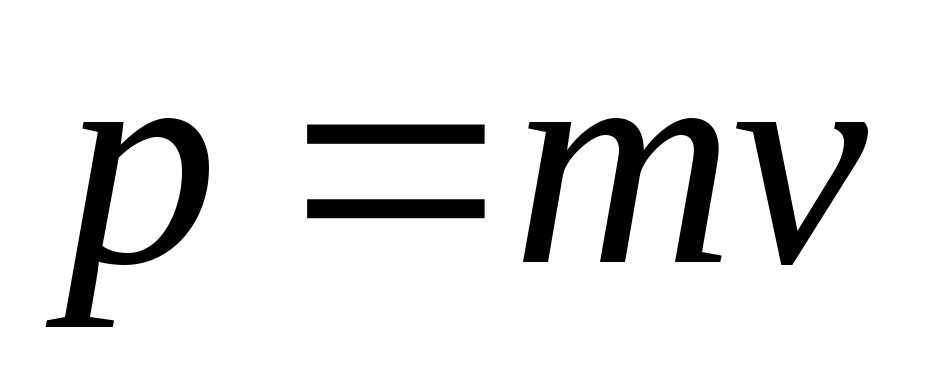 .
Кроме импульса, существует еще одна
векторная характеристика движения
(динамическая переменная) — момент
импульса.Моментом
импульса частицы относительно точки (центра) О
называется
.
Кроме импульса, существует еще одна
векторная характеристика движения
(динамическая переменная) — момент
импульса.Моментом
импульса частицы относительно точки (центра) О
называется
векторное произведение радиус-вектора на импульс частицы:
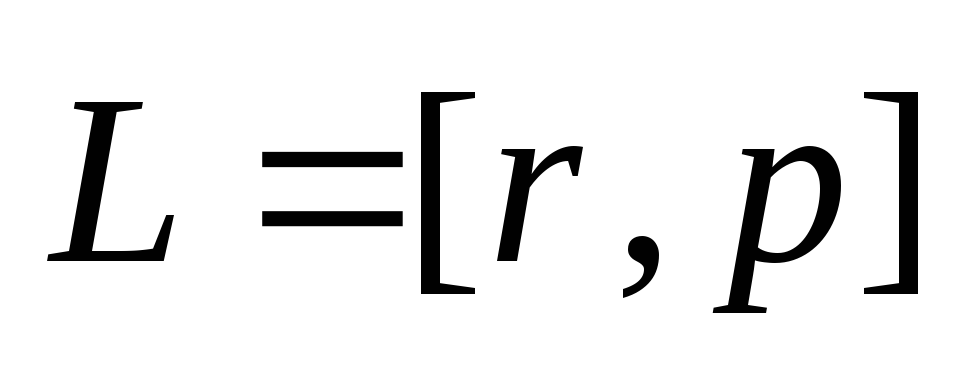 .
.
Согласно
определению, 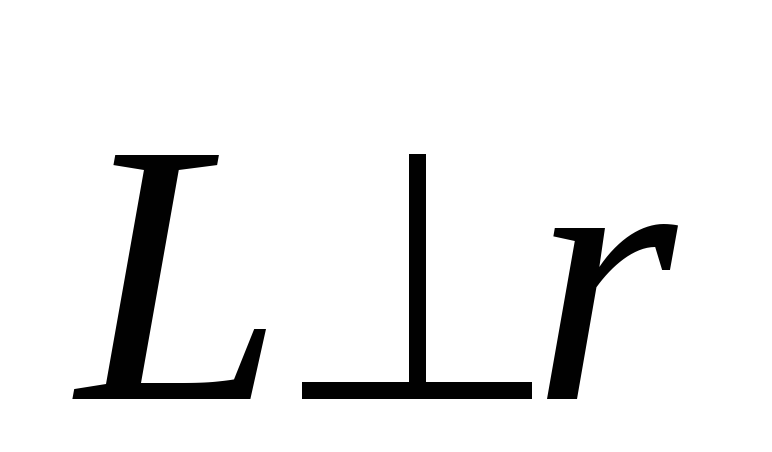 и
и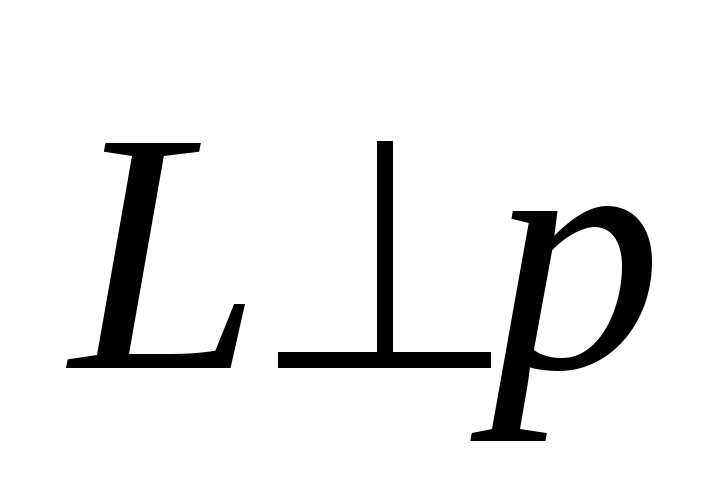 ,
а его направление определяется по
правилу правого винта.
,
а его направление определяется по
правилу правого винта.
Заметим,
что величина 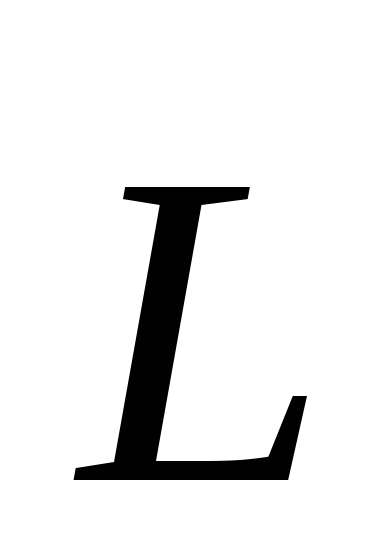 зависит от выбора точки О; вообще говоря,
зависит от выбора точки О; вообще говоря,
ее можно выбрать где угодно, но обычно выбирают на оси вращения (если таковая имеется в наличии).
2. Закон изменения момента импульса. Момент силы
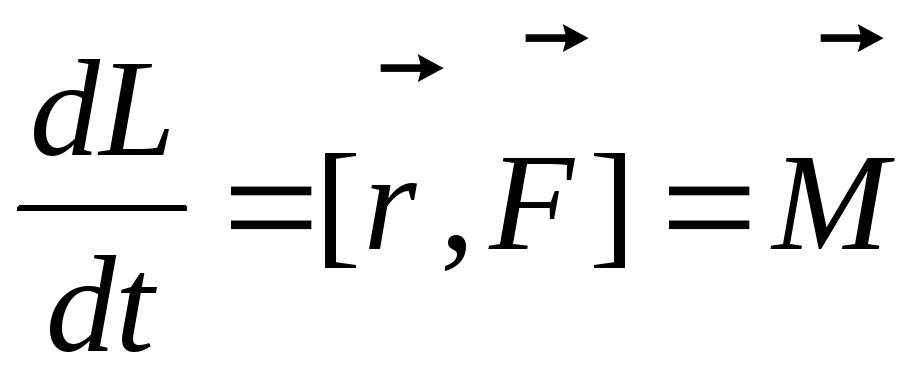 .
.
Вектор, равный векторному произведению радиус-вектора на силу,
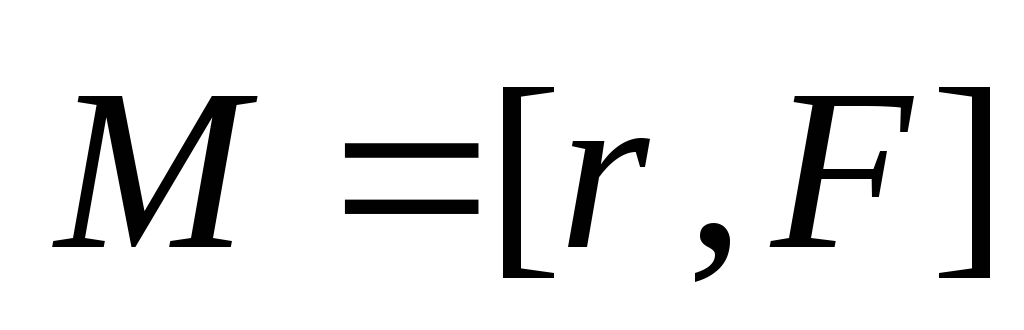 называется моментом
силы.
называется моментом
силы.
Скорость изменения момента импульса частицы относительно некоторой точки равна моменту силы относительно той же точки.
Кратчайшее расстояние от точки О до линии действия силы l=r sin
называется плечом силы. Отсюда следует, что точку приложения силы
(если, конечно, речь идет о твердом теле) можно сдвигать вдоль линии
действия
силы — при этом ни l, ни 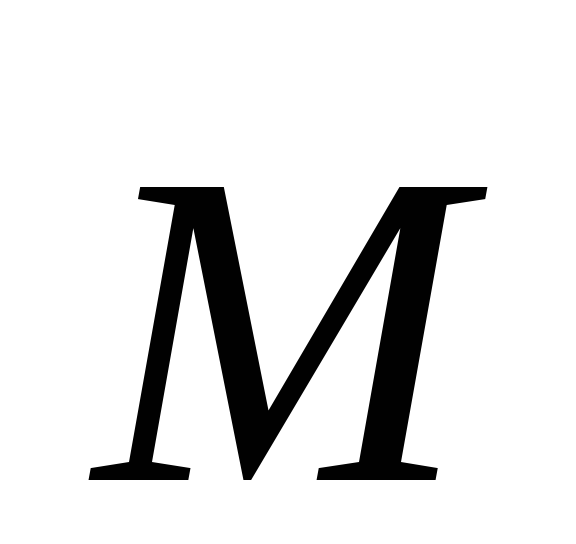 не изменятся.
не изменятся.
3. Момент импульса относительно оси
В дальнейшем нам придется столкнуться с проекцией момента импульса
на некоторую фиксированную (закрепленную) ось (например, ось z).
Эта величина называется моментом импульса относительно оси. Пусть частица массы m движется по окружности радиуса R вокруг этой оси.
Выберем
точку О, относительно которой определяются
вектора 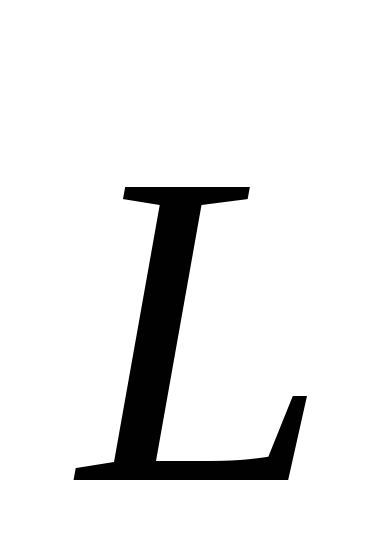 и
и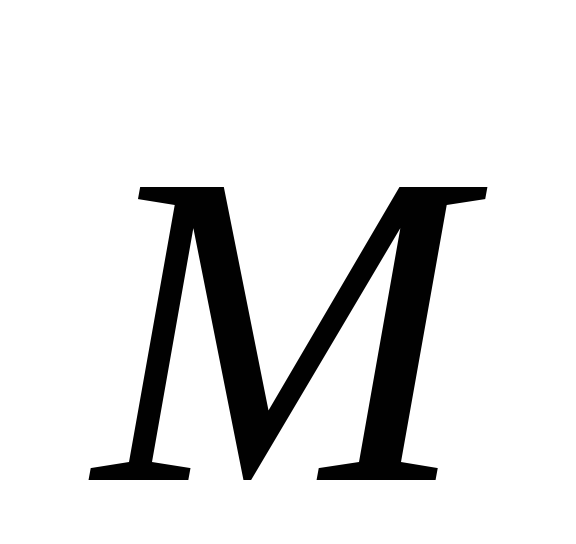 ,
на оси z. Тогда
,
на оси z. Тогда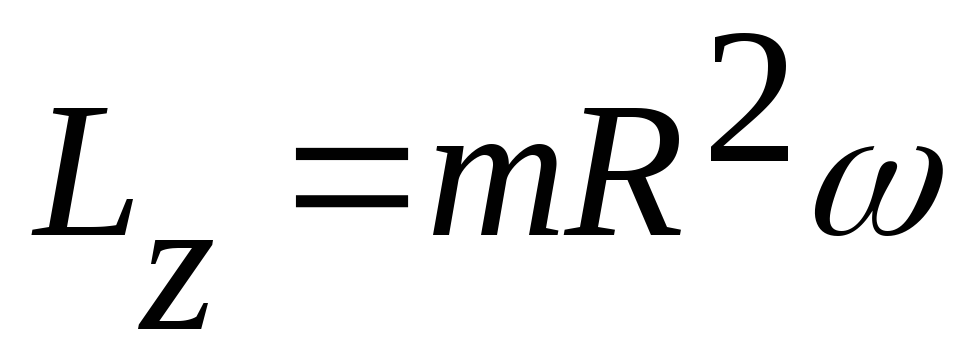 .
Величина
.
Величина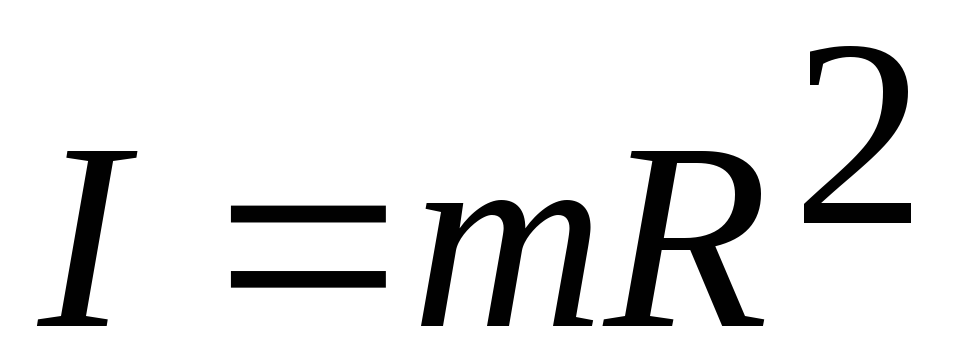 называетсямоментом
инерции частицы относительно оси.Таким образом,
называетсямоментом
инерции частицы относительно оси.Таким образом,
Lz=I,
т.е. момент импульса относительно оси равен произведению момента
инерции на угловую скорость вращения.
Закон изменения момента импульса относительно оси:
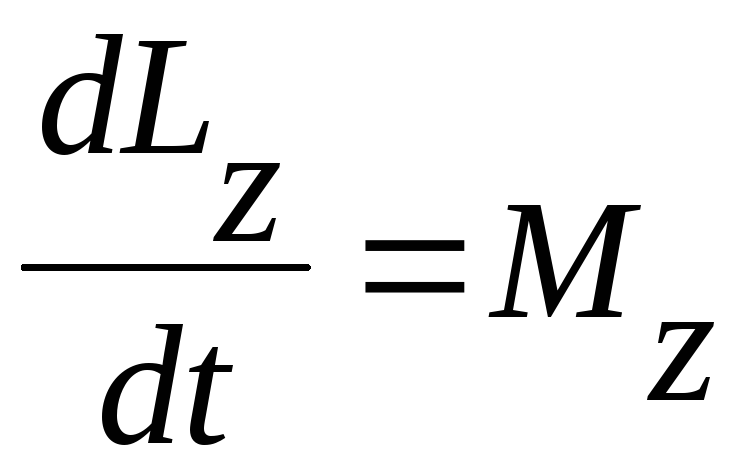 ,
,
где Mz — проекция момента силы на ту же ось (или момент силы относительно оси).
Динамика системы частиц. Законы сохранения
Законы изменения и сохранения полного импульса системы частиц
В этой главе объектом изучения будет не одна частица, а система частиц. Система частиц может представлять собой любое агрегатное состояние вещества — газ, жидкость или твердое тело.
Систему всегда можно разбить на столь малые участки (линейные, плоские или объемные) с массой mi, что их размерами можно пренебречь и рассматривать эти участки как частицы (материальные точки).
Положение
каждой из этих частиц задается
радиус-вектором 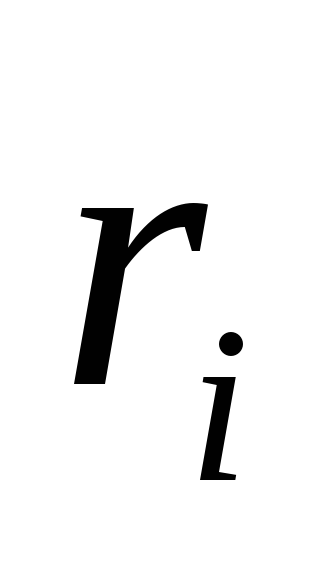 .
.
Масса
всей системы определяется как m=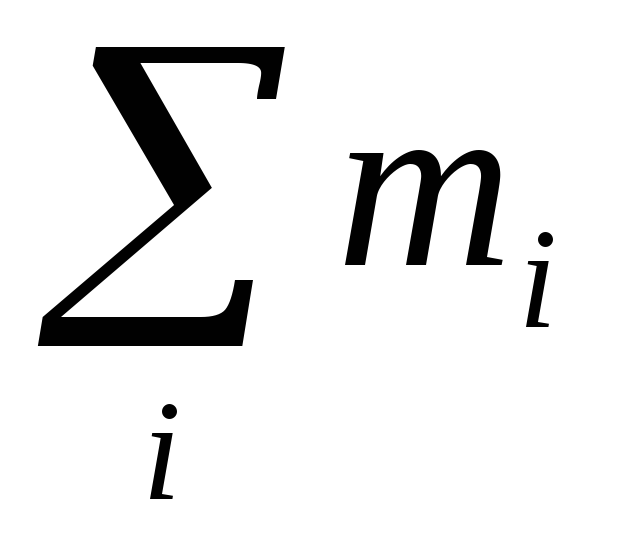 .
Если
– плотность системы (тела), а dV – объем
маленького участка, то его масса dm=dV,
а масса всей системы m=
.
Если
– плотность системы (тела), а dV – объем
маленького участка, то его масса dm=dV,
а масса всей системы m=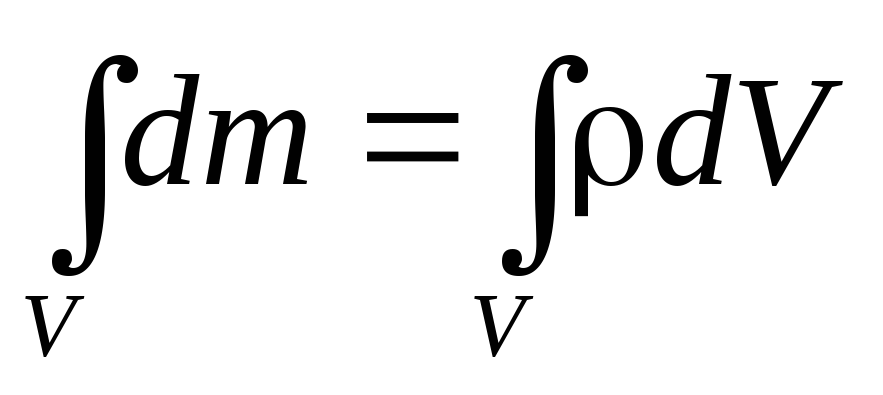 где интеграл берется по всему объему
системы.
где интеграл берется по всему объему
системы.
На
i-ую частицу системы, вообще говоря,
действуют как внешняя
сила 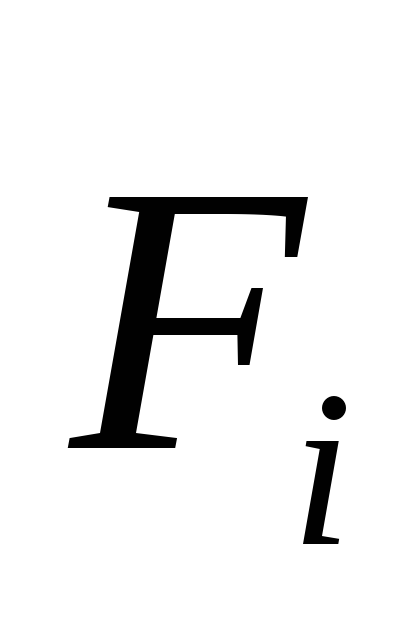 со стороны окружающих систему тел или
полей, так и сумма внутренних
сил
со стороны окружающих систему тел или
полей, так и сумма внутренних
сил 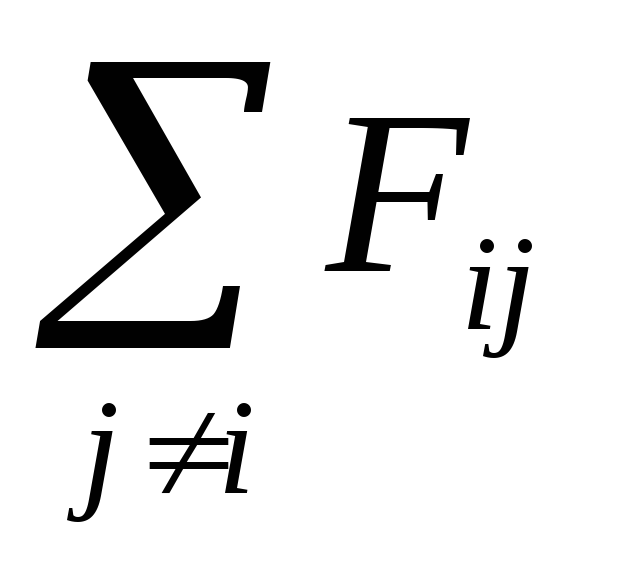 со стороны всех остальных частиц
системы. Поэтому закон движения i-ой
частицы запишется в виде
со стороны всех остальных частиц
системы. Поэтому закон движения i-ой
частицы запишется в виде
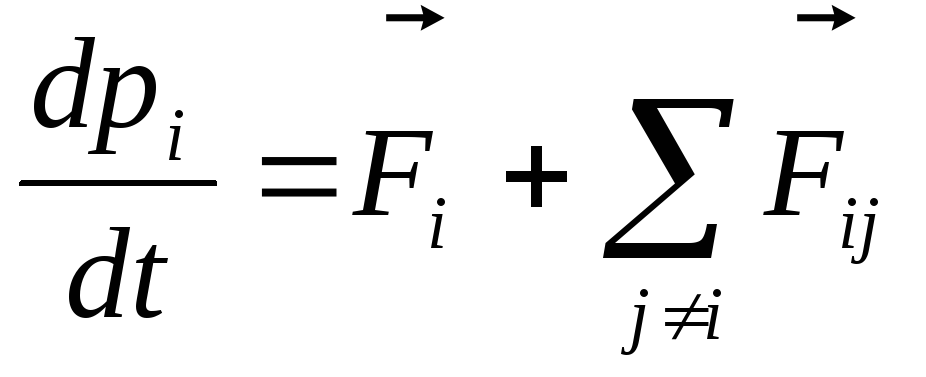
Таких
уравнений будет столько же, сколько
всего частиц в системе. Суммируя эти
уравнения для всех частиц системы и учитывая, что в силу
третьего закона Ньютона 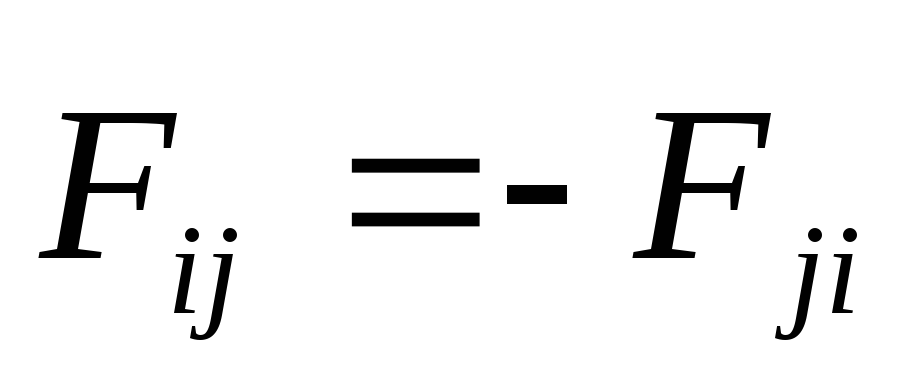 ,
сумма всех внутренних сил, действующих
на все частицы системы обращается в
нуль, получаем
,
сумма всех внутренних сил, действующих
на все частицы системы обращается в
нуль, получаем
Таким образом, закон движения системы частиц или закон изменения полного импульса системы читается так:
Производная по времени (скорость изменения) полного импульса системы частиц равна результирующей внешних сил:
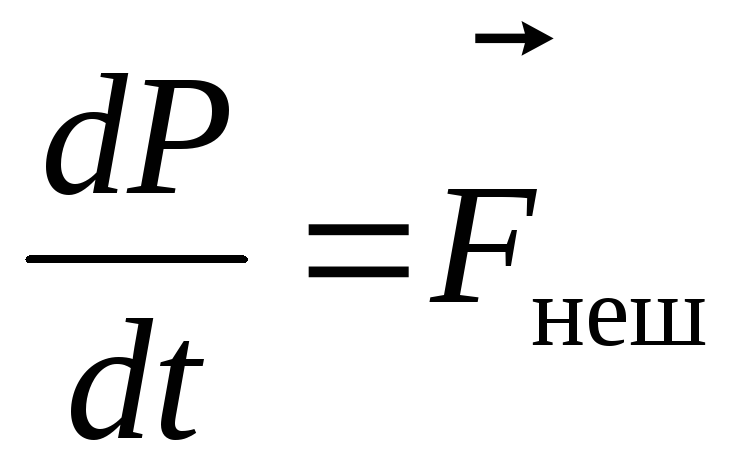
Уравнение
можно записать и прочитать по-иному,
если ввести еще одно понятие – импульс
силы за время dt: это 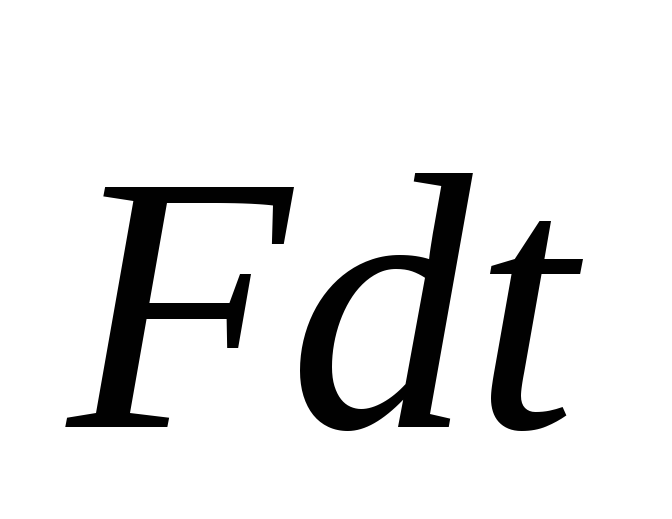 .
.
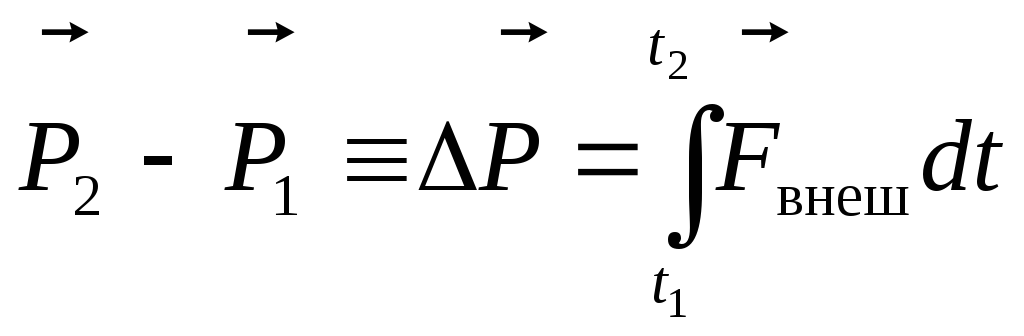
т.е. изменение (приращение) полного импульса системы за время t=t2 – t1 равно импульсу внешних сил за то же время.
Если
все внешние силы, действующие на систему,
уравновешиваются, т.е. 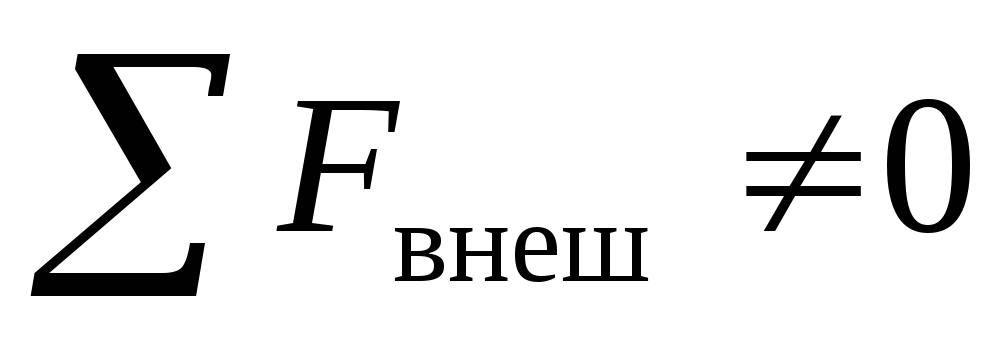 то система называется замкнутой.
Для нее
то система называется замкнутой.
Для нее 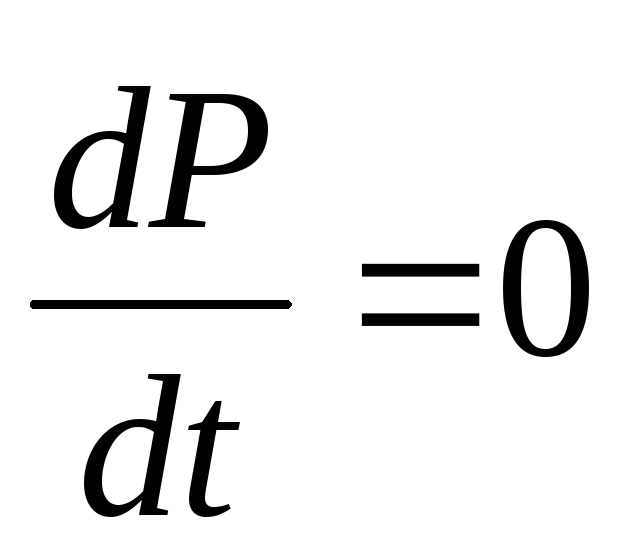 или
или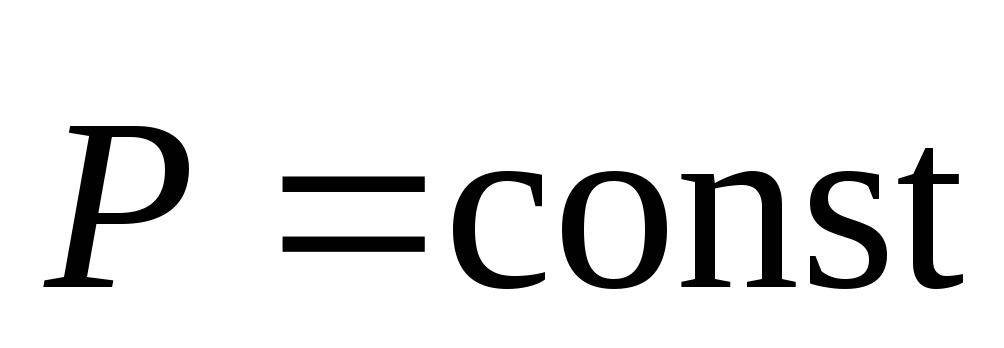 –полный
импульс замкнутой системы сохраняется.
Это – закон
сохранения импульса.
–полный
импульс замкнутой системы сохраняется.
Это – закон
сохранения импульса.
Часто 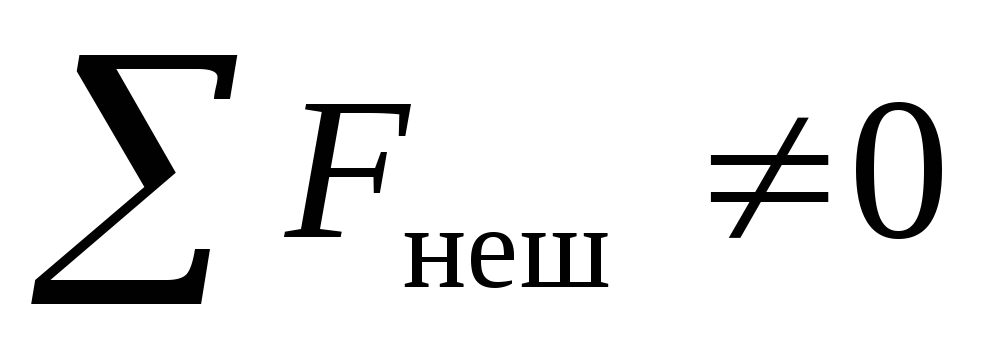 ,
но действие сил длится столь малое
времяt0,
что импульс не успевает заметно
измениться:
,
но действие сил длится столь малое
времяt0,
что импульс не успевает заметно
измениться: 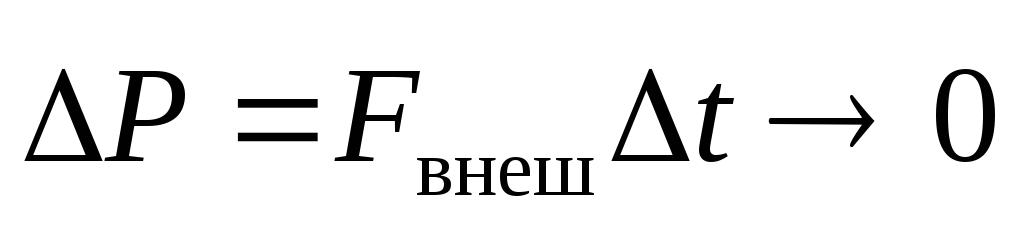 .
В этих случаях (быстрое столкновение,
взрыв и т.п.) также можно применять закон
сохранения импульса:
.
В этих случаях (быстрое столкновение,
взрыв и т.п.) также можно применять закон
сохранения импульса:
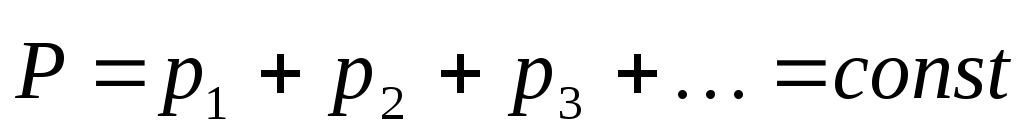
Заметим
также, что возможны случаи, когда 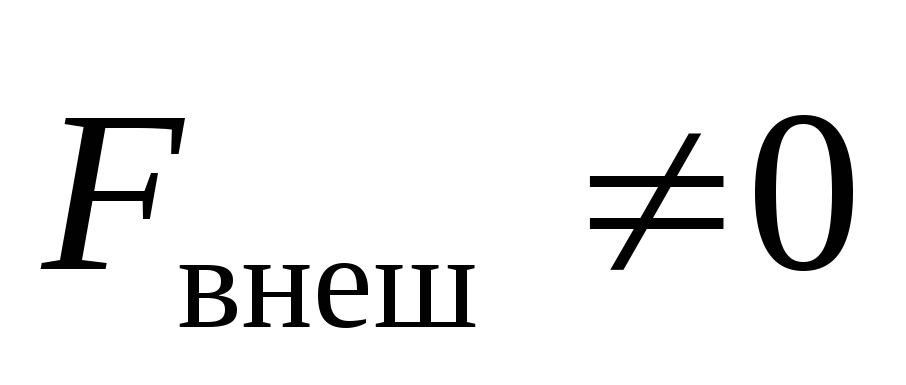 ,
но
,
но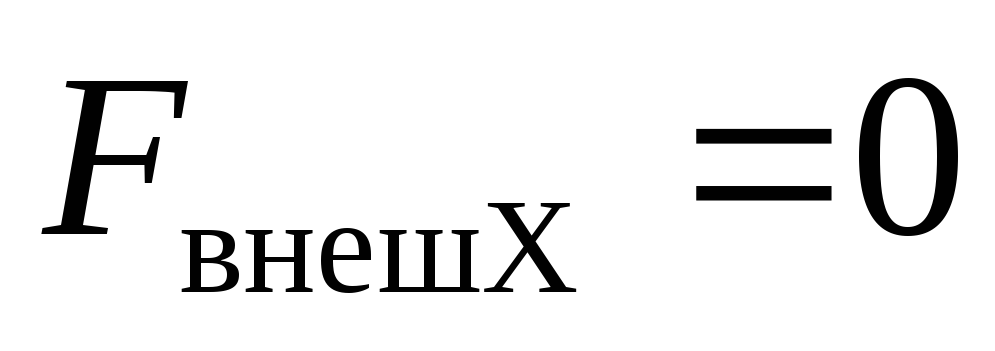 .
Тогда сохраняется только проекция
импульса на соответствующую ось:
Px=const,
что также широко используется в
приложениях.
.
Тогда сохраняется только проекция
импульса на соответствующую ось:
Px=const,
что также широко используется в
приложениях.

