Крутящий момент и момент инерции: подробные объяснения и проблемы
В статье рассматривается связь между крутящим моментом и моментом инерции вращающегося тела и ее решаемые задачи.
Крутящий момент и момент инерции поддерживают вращательное движение тела. Когда на тело наводится крутящий момент, оно начинает ускоряться обратно пропорционально его моменту инерции. Вот почему крутящий момент, действующий на тело, является произведением его момента инерции и углового ускорения.
Законы движения Ньютона заявить, что тело остается неподвижным или движется из одной точки в другую с определенной скоростью; если на него не действует внешняя сила. Это означает, что тело получает ускорение, зависящее от его полной массы и силы приложенной внешней силы.
Используя принцип Ньютона во вращательном движении, когда крутящий момент или момент силы создается на неподвижном или движущемся теле, оно инициирует угловое ускорение. Поэтому каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение когда возникает крутящий момент.
Поэтому каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение когда возникает крутящий момент.
В предыдущих статьях мы поняли, что инерция – это свойство тела, выражающееся в стремлении тела сопротивляться движению. Поэтому инерция обратно пропорциональна ускорению тела.. Следовательно, первый закон движения Ньютона также назвал Закон инерции.
Крутящий момент и момент инерцииКаждая частица внутри такого вращающегося тела имеет свою массу, и все они вращаются вокруг центральной оси вращения тела. Следовательно, величина крутящего момента, необходимая для ускорения частиц внутри тела, зависит от распределения массы всего тела. Величина тела, выражающая распределение массы, называетсямомент инерции».
Момент инерции для различных твердых тел(Кредит: Shutterstock)
При вращательном движении под величиной инерции понимается момент инерции тела, определяемый интегрированием полных масс М частиц и их расстояний R от оси его вращения.
Следовательно, момент инерции тела (I) равен я = МР2.
Крутящий момент и момент инерцииЗаконы движения Ньютона связывают крутящий момент и момент инерции при вращательном движении.
Когда мы включаем вентилятор, мы наводим на него крутящий момент. Теперь ускорение вентилятора будет зависеть от того, насколько велик момент инерции вентилятора и насколько крутящий момент нам нужно вызвать.
The moment of inertia is the rotational mass of the body, whereas torque is the rotational force functioning on it. The torque τ needed to be induced on the body is proportional to both угловое ускорение и момент инерции. Но момент инерции I уменьшает угловое ускорение α of the body.
Утверждение дает связь между крутящим моментом и моментом инерции как,
τ=1α
Крутящий момент и момент инерцииЧитать о крутящем моменте и угловом моменте
Какой крутящий момент необходим для вращения со скоростью 15 рад/с?2 чтобы тело имело момент инерции 5 кгм2?Данный:
я = 5 кгм2
α = 15 рад/с2
Найти: τ =?
Формула:
τ = I α
Решения:
Крутящий момент, необходимый для того, чтобы заставить тело вращаться со скоростью 15 рад/с. 2 рассчитывается с использованием соотношение между крутящим моментом и моментом инерции,
2 рассчитывается с использованием соотношение между крутящим моментом и моментом инерции,
τ= I α
Подставляя все значения,
τ = 5 x 15
τ= 75
Крутящий момент, необходимый для поворота кузова, составляет 75 Нм.
Какой крутящий момент должен возникнуть на расстоянии 2 м от тела массой 4 кг, чтобы оно вращалось со скоростью 5 рад/с?2?Данный:
М = 4 кг
R = 2 м
α = 5 рад/с2
Найти: τ =?
Формула:
τ = I α
Решения:
Крутящий момент, необходимый для тела, рассчитывается как
т = Iα
Но момент инерции диска равен I = MR.2.
τ = MR2α
Подставляя все значения,
τ = 4 x 22 х 5
τ = 4 x 4 x 5
τ = 80
Крутящий момент, необходимый для поворота кузова, составляет 80 Нм.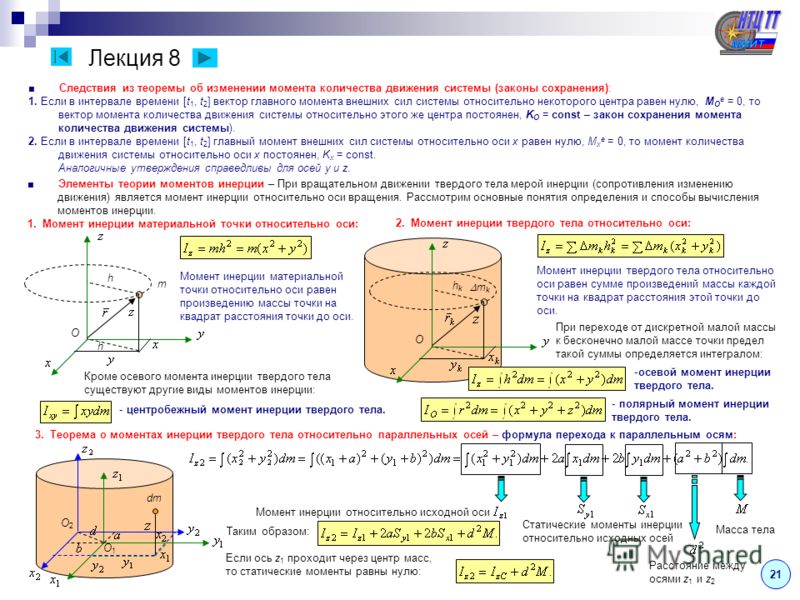
Формула крутящего момента и момента инерции легко определяется путем замены линейного эквивалента в формуле закона движения Ньютона его угловым эквивалентом.
The torque τ is the angular equivalent to the applied force F, and the moment of inertia I is the angular equivalent of the mass m. Hence, Newton’s law of motion (F = ma) for rotational motion becomes,
т = Iα
Как найти крутящий момент по моменту инерцииКрутящий момент от момента инерции является производным от изменения углового момента.
Вращательное движение также подчиняется законам движения Ньютона. Поэтому, когда на тело действует крутящий момент, его угловой момент изменяется из-за ускорения. Поскольку угловой момент является произведением инерции и угловой скорости, мы можем получить необходимый крутящий момент из его момента инерции.
Формула крутящего момента и момента инерции (Кредит: Shutterstock)Игровой автомат угловая импульс тела, когда крутящий момент is induced is given by L = r x P
Где P линейный импульс. т. е. P = mv
т. е. P = mv
L = r x mv
The relation between linear velocity v and angular velocity ω is (r x ω )
L = r x m (r x ω)
L = mr2ω
Но мистер2 срок принадлежит момент инерции (I).
L = I ω
Мы узнали, что крутящий момент, действующий на тело, представляет собой скорость изменения углового момента..
τ = dL/dt
Подставляя формула углового момента,
τ = dIω/dt
τ = Idω/dt
The term dω/dt is the угловое ускорение [latex]\alpha[/latex] of the body. i.e., α= dω/dt
Наконец, крутящий момент получается из момента инерции,
τ = lα
Читать о крутящем моменте и скорости
Диск массой 0.1 кг и радиусом 1 м вращается со скоростью 2 рад/с.2. The moment of inertia of the disc is I = 1/2mr2. Рассчитайте крутящий момент, действующий на диск.Данный:
m = 0. 1 кг
1 кг
г = 1 м
α = 2 рад/с2
Найти: τ=?
Формула:
τ = I α
Решения:
Крутящий момент, создаваемый диском, рассчитывается как
τ= I α
For disc, the moment of inertia is I = 1/2mr2 ……………..(Дано)
τ= 1/2mr2 α
Подставляя все значения,
τ = 1/2 x 0.1 x 12 x2
τ= 0.2/2
τ = 0.2/2
τ = 0.1
Крутящий момент на диске составляет 0.1 Нм.
Тонкий стержень массой 100 кг и длиной 6 м вращается со скоростью 20 рад/с.2. The moment of inertia of the thin rod is I =1/12mr2. Рассчитайте крутящий момент на тонком стержне.Данный:
m = 100 кг
г = 6 м
α= 20 rad/s2
Найти: τ =?
Формула:
τ = I α
Решения:
Крутящий момент, действующий на тонкий стержень, рассчитывается как
τ = I α
For thin rod, the moment of inertia is I = 1/12mr2 ……………. .(Дано)
.(Дано)
τ= 1/12mr2α
Подставляя все значения,
τ = 1/12 x 100 x 62 х 20
τ= 72000/12
τ = 6000
Крутящий момент на диске составляет 6000 Нм.
Момент инерции
Момент инерции. Момент инерции — это величина равная сумме произведений всех масс на квадраты их расстояний от некоторой оси,
I=S miri2.
Моменты инерций простейших тел.
1. Материальная точка I=mr2.
2. Тонкий однородный стержень I=1/12ml2, при оси проходящей через его центр масс.
3. Обруч I=mr2.
4. Диск I=1/2mr2.
5. Шар I=2/5mr2.
Момент инерции для сплошного цилиндра
dI=miri2=ρ*Vi* ri2=ρ*2*π* ri*h*dr*r2
dI=2*π*ρ*h* ri3*dr
I=2*π*ρ*h{0-R}∫ ri3dr
I=2*π*ρ*h*(R4/4)-(m*R2/2)
I=1/2*m*R2
Кинетическая энергия вращающения.
Ek
Ek=(I*w2)/2 – для вращательного движения тела
Ek=(I*w2)/2+(m*v2)/2 – для вращательного и поступательного движения.
Момент силы. Моментом силы F относительно некоторой точки O называется векторная величина M, M=r*F*Sina ,r-радиус-вектор l=r*sina , l-плечо силы. M=F*l;
Плечо силы – это кротчайшее расстояние от точки вращения до линии вдоль которой действует сила
Момент силы относительно оси это проекция момента силы относительно любой точки оси на данную ось.
Момент силы относительно оси не зависит от выбора точки на оси.
Уравнение динамики вращательного движения
dt;dS
S;1->2
dS=r*dφ
dA=F*dScosβ
dA=F*r*dφcos(π/2-α)
dA=F*r*dφ*sinα
dA=d*(I*w2)/2=I/2 * 2*w*dw
da=I*w*dw
M*dφ=I*w*dw
Mdφ/dt=I*w*dw/dt
M*w=I*w*dw/dt
M=I*ε, где ε-угловое ускорение
Условие равновесия тел
1. {1-n}ΣMi=0
{1-n}ΣMi=0
2.{1-n}ΣFi=0
Момент импульса и закон его сохранения
α-момент импульса
α=m*V*r*sinα
α=m*V*l, l=r*sinα
Деформация твёрдого тела — изменение его формы или объёма. Растяните резиновый шнур за концы. Очевидно, участки шнура сместятся друг относительно друга; шнур окажется деформированным — станет длиннее и тоньше. Деформация возникает всегда, когда различные части тела под действием сил перемещаются неодинаково.
Шнур, после прекращения действия на него сил, возвращается в исходное состояние. Деформации, которые полностью исчезают после прекращения действия внешних сил, называются упругими. Кроме резинового шнура, упругие деформации испытывают пружина, стальные шарики при столкновении и т.д.
Теперь сожмите кусочек пластилина. В ваших руках он легко
примет любую форму. Первоначальная форма пластилина не восстановится сама собой.
Пластилин “не помнит” какая форма бы у него сначала. Деформации, которые не
исчезают после прекращения действия внешних сил, называются пластическими.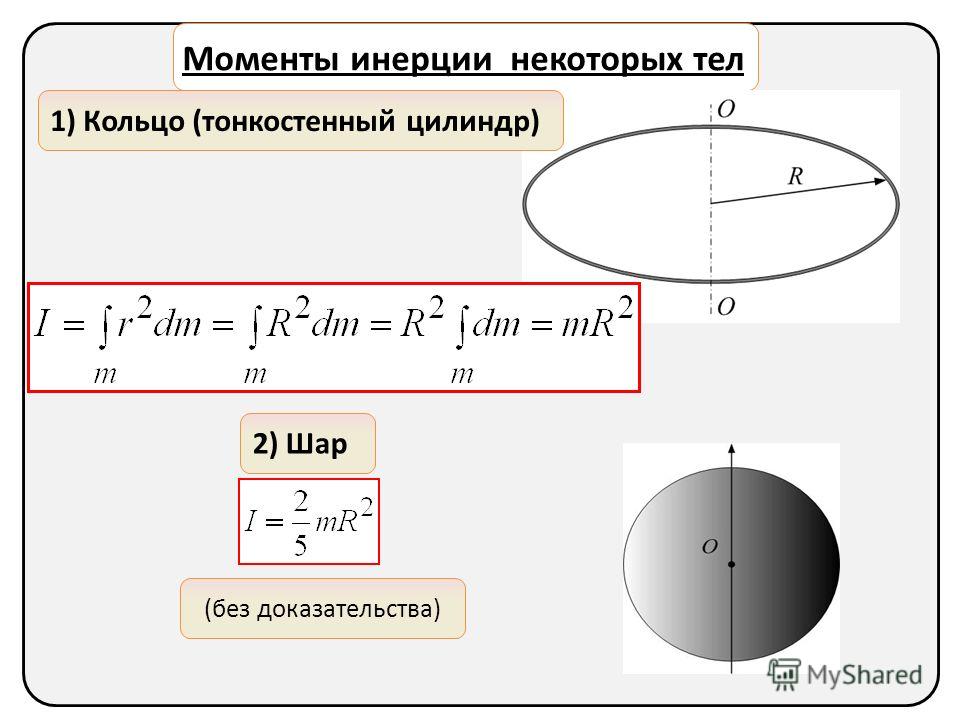
Деформация растяжения (сжатия). Если к одному стержню, закреплённому одним концом, приложить силу F вдоль оси стержня в направлении от этого конца (рис. 2), то стержень подвергнется деформации растяжения. Деформацию растяжения характеризуют абсолютным удлинением.
и относительным удлинением
e = Dl / l0
где l0 — начальная длинна, а l— конечная длинна стержня.
Деформацию растяжения испытывают тросы, канаты, цепи в подъёмных устройствах, стяжки между вагонами и т.д.
При малых растяжениях (l0<<l), деформации большинства тел упругие.
Если на тот же стержень подействовать силой F, направленной к закреплённому
концу (рис. 3), то стержень подвергнется деформации сжатия. В этом случае
относительная деформация отрицательна: e< 0.
При растяжении или сжатии изменяется площадь поперечного сечения тела. Это можно обнаружить, если растянуть резиновую трубку, на которую предварительно надето металлическое кольцо. При достаточно сильном растяжении кольцо падает. При сжатии, наоборот, площадь поперечного сечения тела увеличивается.
Для упругих деформаций справедлив закон Гука
Fy=-RΔl
σ=E|ε|
σп-предел прямой пропорциональности
σу-предел упругости
σт-предел текучести
σпр-предел прочности
ДАВЛЕНИЕ
P=F/S давление твердого тела
P=mg/S=ρ*S*h*g/S=ρ*g*h давление столба житкости
Поток житкости – это движение житкости определяемое совокупностью частиц двигающихся в данном направлении изображающ в виде линий тока.
Турбка тока-часть житскости огрнаничиваемая линиями тока.
ρ=const
m1=m2
ρV1=ρV2
S1l1=S2L2
s1V1t=S2V2t
S1V1=S2V2
S1/S2=V2/V1
Уравнение Бернулли:
A=E1-E2
A=mV12/2+mgh1-mV22/2-mgh2
A=-F1l1+F2l2=-p1S1l1+p2s2l2
mV12/2+mgh1+ p1S1l1= p2s2l2+ mV22/2+mgh2
ρV12/2+ρgh
p1-статическое давление житкости
ρgh-гидростатиеское давление
ρ*V12/2 – динамическое давление
Момент силы, теория и онлайн калькуляторы
Момент силы, теория и онлайн калькуляторыПусть тело вращается около неподвижной оси под действием силы $\overline{F}$. Элементарная работа ($\Delta A$), которую совершает данная сила при повороте тела на малый угол $\Delta \varphi ,$ равна:
Элементарная работа ($\Delta A$), которую совершает данная сила при повороте тела на малый угол $\Delta \varphi ,$ равна:
\[\Delta A=F_r\Delta l\ \left(1\right),\]
где $F_r=F{\sin \alpha \ }$, $\alpha $ — угол между направлением силы и направлением радиус-вектора, проведенного от оси вращения к точке приложения силы; $\Delta l=r\Delta \varphi $. Соответственно выражение (1) преобразуется к виду:
\[\Delta A=F{\sin \alpha \ }r\Delta \varphi \ \left(2\right).\]
Величину:
\[M=Fr{\sin \alpha \ }\ (3)\]
называют моментом силы относительно оси вращения. Самое короткое расстояние от оси вращения до линии действия силы $d=r{sin \alpha \ }$ называют плечом силы, тогда:
\[M=Fd\ \left(4\right).\]
Момент силы — это векторная величина. $\overline{M}\ $направлен по оси вращения тела. Направление момента силы определяют при помощи правила правого винта: если головку винта с правой резьбой вращать по направлению силы, то поступательное перемещение винта указывает на направление вектора момента силы.
Определение момента силы
Определение
Моментом силы ($\overline{M}$) называют векторную физическую величину, которая равна векторному произведению радиус — вектора, который проведен от оси вращения до точки приложения силы $\overline{F}$ на вектор этой силы:
Ньютон, умноженный на метр (ньютон — метр) (Н$\cdot $м) — единицы измерения момента силы в Международной системе единиц (СИ).
Условие равновесия тела, имеющего ось вращения
Пусть на тело, способное вращаться вокруг оси действуют несколько сил, например, ${\overline{F}}_1,\ {\overline{F}}_2,{\overline{F}}_3$. Если тело находится в равновесии, то при повороте на бесконечно малый угол $\Delta \varphi $ его потенциальная энергия не изменится, значит, элементарная работа, равная изменению потенциальной энергии равна нулю, но:
\[\Delta A=F{\sin \alpha \ }r\Delta \varphi =M\Delta \varphi =\Delta A_1+\Delta A_2+\Delta A_3=M_1\Delta \varphi +M_2\Delta \varphi +M_3\Delta \varphi ={(M}_1+M_2+M_3)\Delta \varphi =0\ \left(6\right),\]
так как $\Delta \varphi \ne 0$, то
\[M_1+M_2+M_3=0\left(7\right). 2}{2}\right)=J\omega d\omega \ \left(9\right),\]
2}{2}\right)=J\omega d\omega \ \left(9\right),\]
где $J$ — момент инерции тела относительно неподвижной оси; $\omega $ — угловая скорость тела.
Но элементарную работу при повороте тела на малый угол $d\varphi $ определяют как:
\[dA=Md\varphi \ \left(10\right),\]
следовательно, из (8)-(10) получим:
Принимая во внимание то, что:
\[\frac{d\varphi }{dt}=\omega;\ \frac{d \omega }{dt}=\varepsilon (12)\]
формулу (11) представим в виде:
\[M=J\varepsilon \ \left(13\right),\]
где $\varepsilon $ — угловое ускорение. Уравнение (13) — основной закон динамики вращательного движения твердого тела относительно неподвижной оси. Если ось вращения совпадает с главной осью инерции, которая проходит через центр масс тела, то закон (13) можно записать в виде:
\[\overline{M}=J\overline{\varepsilon }\left(14\right),\]
где $J$ — главный момент инерции тела.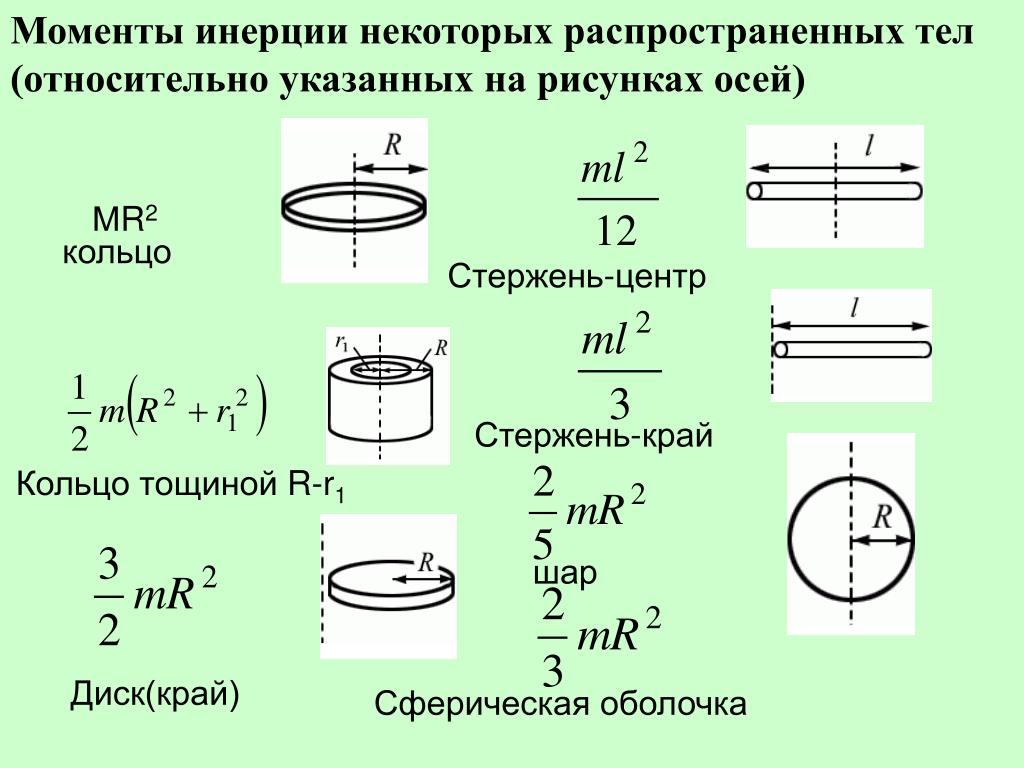 {t_2}_{t_1}{Mdt-}$это площади криволинейных трапеций. В нашем случае получились прямоугольные треугольники. Найдем их площади:
{t_2}_{t_1}{Mdt-}$это площади криволинейных трапеций. В нашем случае получились прямоугольные треугольники. Найдем их площади:
\[S_{{\Delta }_1}=\frac{1}{2}\cdot 2\cdot 5=5.\] \[S_{{\Delta }_2}=\frac{1}{2}\cdot 1\cdot 10=5.\]
Получили, что:
\[S_{{\Delta }_1}=S_{{\Delta }_2}\left(2.3\right).\]
Значит,${\omega }_1={\omega }_2.$
Ответ. ${\omega }_1={\omega }_2$
Читать дальше: сила Архимеда.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Момент инерции: формула. Момент инерции тела
Чтобы изменить скорость перемещения тела в пространстве, необходимо приложить некоторое усилие. Этот факт относится ко всем видам механического движения и связан с наличием инерционных свойств у объектов, имеющих массу. В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.
В данной статье рассматривается вращение тел и дается понятие об их моменте инерции.
Что такое вращение с точки зрения физики?
Ответ на этот вопрос может дать каждый человек, поскольку этот физический процесс ничем не отличается от его понятия в обиходе. Процесс вращения представляет собой перемещение объекта, обладающего конечной массой, по круговой траектории вокруг некоторой воображаемой оси. Можно привести следующие примеры вращения:
- Движение колеса автомобиля или велосипеда.
- Вращение лопастей вертолета или вентилятора.
- Движение нашей планеты вокруг оси и вокруг Солнца.
Какие физические величины характеризуют процесс вращения?
Перемещение по окружности описывается набором величин в физике, основные из которых перечислены ниже:
- r — расстояние до оси материальной точки массой m.
- ω и α — угловая скорость и ускорение, соответственно. Первая величина показывает, на сколько радиан (градусов) поворачивается тело вокруг оси за одну секунду, вторая величина описывает скорость изменения во времени первой.

- L — момент импульса, который подобен аналогичной характеристике при линейном движении.
- I — момент инерции тела. Эта величина рассматривается ниже в статье подробно.
- M — момент силы. Он характеризует степень изменения величины L, если приложена внешняя сила.
Перечисленные величины связаны друг с другом следующими формулами вращательного движения:
- L = I*ω
- M = I*α
Первая формула описывает круговое движение тела в отсутствие действия внешних моментов сил. В приведенном виде она отражает закон сохранения момента импульса L. Второе выражение описывает случай ускорения или замедления вращения тела в результате действия момента силы M. Оба выражения часто используются при решении задач динамики по круговой траектории.
Как видно из этих формул, момент инерции относительно оси (I) в них используется в качестве некоторого коэффициента. Рассмотрим подробнее эту величину.
Откуда появляется величина I?
В этом пункте рассмотрим самый простой пример вращения: круговое перемещение материальной точки массой m, дистанция которой от оси вращения составляет r.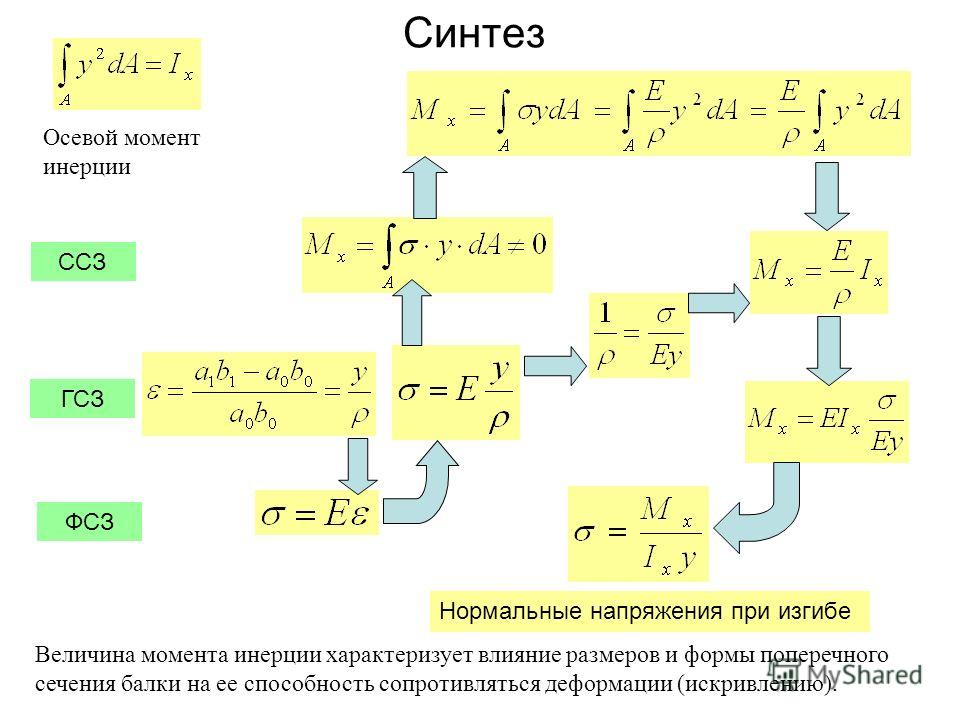 Эта ситуация приведена на рисунке.
Эта ситуация приведена на рисунке.
Согласно определению, момент импульса L записывается, как произведение плеча r на линейный импульс p точки:
L = r*p = r*m*v, поскольку p = m*v
Учитывая, что линейная и угловая скорость связаны друг с другом через расстояние r, это равенство можно переписать так:
v = ω*r => L = m*r2*ω
Произведение массы материальной точки на квадрат расстояния до оси вращения принято называть моментом инерции. Формула выше перепишется в таком случае следующим образом:
I = m*r2 => L = I*ω
То есть мы получили выражение, которое было приведено в предыдущем пункте, и ввели в использование величину I.
Общая формула для величины I тела
Выражение для момента инерции массой m материальной точки является базовым, то есть оно позволяет рассчитать эту величину для любого тела, имеющего произвольную форму и неоднородное распределение массы в нем. Для этого необходимо разбить рассматриваемый объект на маленькие элементы массой mi (целое число i — номер элемента), затем, умножить каждый из них на квадрат расстояния ri2 до оси, вокруг которой рассматривают вращение, и сложить полученные результаты. Описанную методику нахождения величины I можно записать математически так:
Описанную методику нахождения величины I можно записать математически так:
I = ∑i(mi*ri2)
Если тело разбито таким образом, что i->∞, тогда приведенная сумма заменяется интегралом по массе тела m:
I = ∫m(ri2*dm)
Этот интеграл эквивалентен другому интегралу по объему тела V, поскольку dV=ρ*dm:
I = ρ*∫V(ri2*dV)
Все три формулы используются для вычисления момента инерции тела. При этом в случае дискретного распределения масс в системе предпочтительнее пользоваться 1-м выражением. При непрерывном распределении массы применяют 3-е выражение.
Свойства величины I и ее физический смысл
Описанная процедура получения общего выражения для I позволяет сделать некоторые выводы о свойствах этой физической величины:
- она является аддитивной, то есть полный момент инерции системы можно представить, как сумму моментов отдельных ее частей;
- она зависит от распределения массы внутри системы, а также от расстояния до оси вращения, чем больше последнее, тем больше I;
- она не зависит от действующих на систему моментов сил M и от скорости вращения ω.

Физический смысл I заключается в том, насколько сильно система препятствует любому изменению скорости ее вращения, то есть момент инерции характеризует степень «плавности» возникающих ускорений. Например, колесо велосипеда можно легко раскрутить до больших угловых скоростей и также легко его остановить, но чтобы изменить вращение маховика на коленвале автомобиля, понадобится приложить значительное усилие и некоторое время. В первом случае имеет место система с маленьким моментом инерции, во втором — с большим.
Значение I некоторых тел для оси вращения, проходящей через центр масс
Если применить интегрирование по объему для любых тел с произвольным распределением массы, то можно получить для них величину I. В случае однородных объектов, которые имеют идеальную геометрическую форму, эта задача уже решена. Ниже приводятся формулы момента инерции для стержня, диска и шара массой m, в которых составляющее их вещество распределено равномерно:
- Стержень. Ось вращения проходит перпендикулярно ему.
 I = m*L2/12, где L — длина стержня.
I = m*L2/12, где L — длина стержня. - Диск произвольной толщины. Момент инерции с осью вращения, проходящей перпендикулярно его плоскости через центр масс, вычисляется так: I = m*R2/2, где R — радиус диска.
- Шар. В виду высокой симметрии этой фигуры, для любого положения оси, проходящей через ее центр, I = 2/5*m*R2, здесь R — шара радиус.
Далее приведем два примера решения задач на применение общей формулы для расчета I и на использование свойства аддитивности этой величины.
Задача на расчет значения I для системы с дискретным распределением массы
Представим себе стержень длиною 0,5 метра, который сделан из твердого и легкого материала. Этот стержень закреплен на оси таким образом, что она проходит перпендикулярно ему точно посередине. На этот стержень подвешены 3-и груза следующим образом: с одной стороны оси имеются два груза массами 2 кг и 3 кг, находящиеся на расстояниях 10 см и 20 см от его конца, соответственно; с другой стороны подвешен один груз массой 1,5 кг к концу стержня. Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.
Для этой системы необходимо рассчитать момент инерции I и определить, с какой скоростью ω стержень будет вращаться, если к одному из его концов приложить силу 50 Н в течение 10 секунд.
Поскольку массой стержня можно пренебречь, тогда необходимо рассчитать момент I для каждого груза и сложить полученные результаты, чтобы получить полный момент системы. Согласно условию задачи от оси груз массой 2 кг находится на расстоянии 0,15 м (0,25-0,1), груз 3 кг — 0,05 м (0,25-0,20), груз 1,5 кг — 0,25 м. Воспользовавшись формулой для момента I материальной точки, получаем:
I = I1+I2+I3 = m1*r12 + m2*r22 + m3*r32 = 2*(0,15)2+3*(0,05)2+1,5*(0,25)2 = 0,14 625 кг*м2.
Обратим внимание, что при выполнении вычислений все единицы измерения были переведены в систему СИ.
Чтобы определить угловую скорость вращения стержня после действия силы, следует применить формулу с моментом силы, которая была приведена во втором пункте статьи:
M = I*α
Поскольку α = Δω/Δt и M = r*F, где r — длина плеча, получаем:
r*F = I*Δω/Δt => Δω = r*F*Δt/I
Учитывая, что r = 0,25 м, подставляем числа в формулу, получаем:
Δω = r*F*Δt/I = 0,25*50*10/0,14625 = 854,7 рад/с
Полученная величина является достаточно большой. Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
Чтобы получить привычную частоту вращения, следует поделить Δω на 2*pi радиан:
f = Δω/(2*pi) = 854,7/(2*3,1416) = 136 с-1
Таким образом, приложенная сила F к концу стержня с грузами за 10 секунд раскрутит его до частоты 136 оборотов в секунду.
Расчет значения I для стержня, когда ось проходит через его конец
Пусть имеется однородный стержень массой m и длиной L. Необходимо определить момент инерции, если ось вращения расположена на конце стержня перпендикулярно ему.
Воспользуемся общим выражением для I:
I = ρ*∫V(ri2*dV)
Разбивая рассматриваемый объект на элементарные объемы, заметим, что dV может быть записано, как dr*S, где S — площадь сечения стержня, а dr — толщина элемента разбиения. Подставляя это выражение в формулу, имеем:
I = ρ*S*∫L(r2*dr)
Этот интеграл вычислить достаточно просто, получаем:
I = ρ*S* (r3/3)∣0L => I = ρ*S*L3/3
Поскольку объем стержня равен S*L, а масса — ρ*S*L, то получаем конечную формулу:
Любопытно отметить, что момент инерции для того же стержня, когда ось проходит через его центр масс, в 4 раза меньше полученной величины (m*L2/3/(m*L2/12)=4).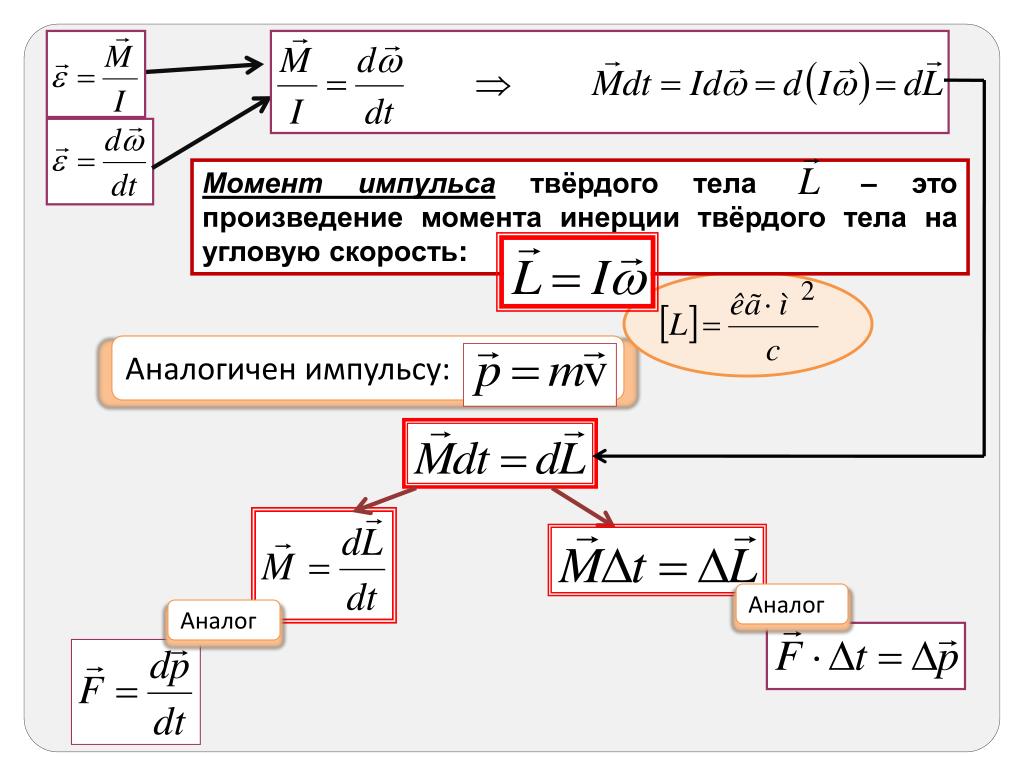
Момент инерции — формулировка, свойства и методы решения
Одним из фундаментальных свойств физических тел является момент инерции. Люди с ним сталкиваются в повседневной жизни при езде на велосипеде или автомобиле, запуске различных механизмов, игре с мячом, катании на карусели и т. д. Изучают характеристику на уроках физики и сопромата. Знание этого параметра важно и в механике, особенно при нахождении силы, которая может привести тело к вращению.
Содержание
- Основные понятия и суть
- Вычисление параметра
- Методика решения
- Моменты простейших объектов
- Теорема Гюйгенса — Штейнера
- Пример задачи
Основные понятия и суть
Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.
Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.
Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r2j. В ней:
- mi — масса в точке;
- rj — расстояние от точки до координаты.
То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.
М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.
Вычисление параметра
Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r2. Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.
Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.
Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.
Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.
Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.
Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.
Методика решения
Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:
- Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
- Формула нахождения момента для материальной точки I = m*r2.

Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri2. Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri2, где i принимает значение от 1 до n.
Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:
- прямая пропорциональность массе;
- соответствие квадрату размера;
- изменение с учетом оси вращения.

Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.
Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.
Моменты простейших объектов
Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:
При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:
 Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r2 / 2.
Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r2 / 2. При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.
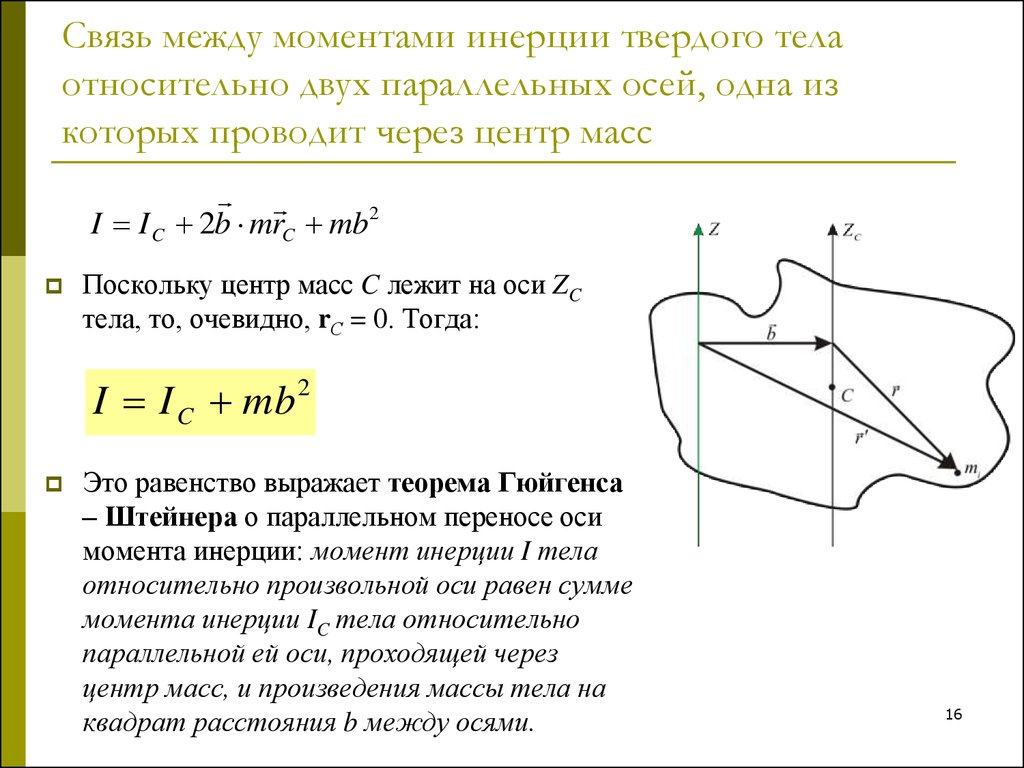
Теорема Гюйгенса — Штейнера
Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:
Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.
Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).
В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r’.
Находится ri’2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri’ совпадает с длиной гипотенузы. Таким образом, ri’2 = (xi — Oц)2 + yi2. Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц)2 + yi2). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i2 — 2*m*xi2 = I — m*xi2.
Так как x центра масс совпадает с d, расстоянием между осями, одну из которых можно направить через центр, то формулу можно переписать как Io = I — m*d2. Выразив из выражения произвольный момент, формула Штейнера примет вид I = Io + m*d2.
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.
Пример задачи
Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.
Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md2. Фактически задача состоит в нахождении Io.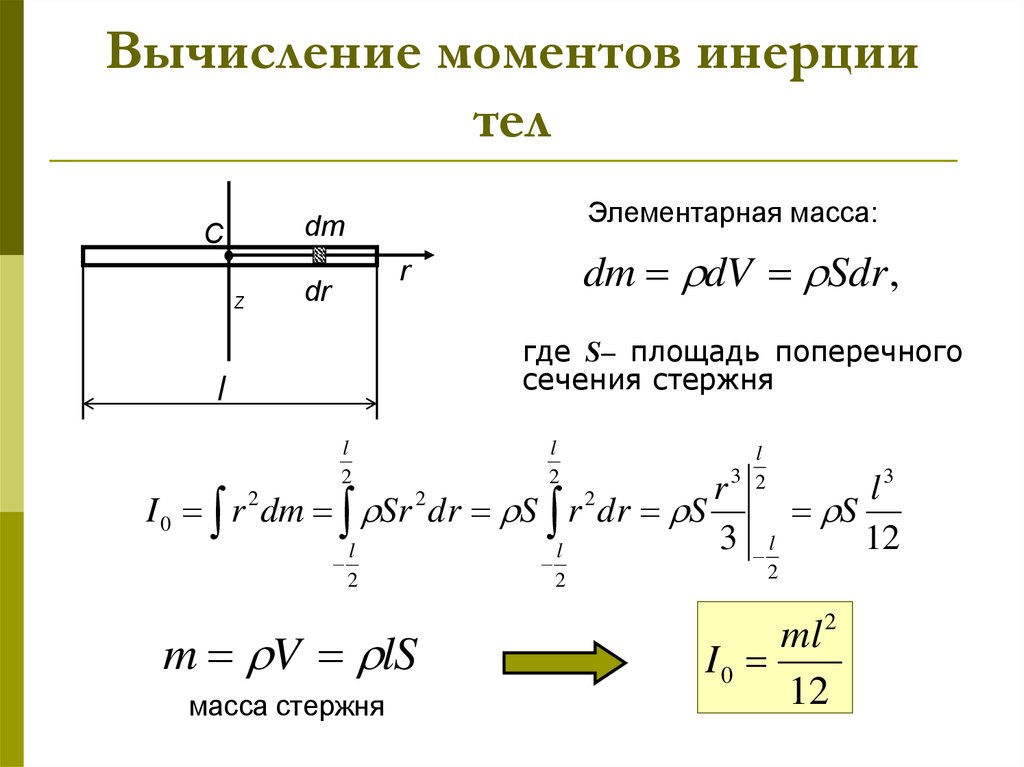 Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.
Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.
Момент вращения относительно диска определяется с помощью выражения I1 = m* d2 / 2. Для решения задачи она будет выглядеть Io = m* d2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.
Предыдущая
ФизикаБроуновское движение в физике
Следующая
ФизикаУсловия плавания тел — формулы, основные принципы и положения закона Архимеда
Момент инерции твердого тела
| на главную | к оглавлению |
Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.
Рассмотрим твердое тело,
которое может вращаться относительно некоторой оси (рис. ). Момент импульса i-й
точки тела относительно этой оси определяется формулой:
). Момент импульса i-й
точки тела относительно этой оси определяется формулой:
. (1.84)
Выражая линейную скорость точки через угловую скорость тела и используя свойства векторного произведения, получим
(1.85)
Спроектируем момент импульса на ось вращения: — эта проекция определяет момент относительно этой оси. Получим
. (1.86)
где zi,- координата i—точки вдоль оси Z, a Ri, — расстояние точки от оси вращения. Суммируя по всем частицам тела, получим момент импульса всего тела относительно оси вращения:
. (1.87)
Величина
(1.88)
является моментом инерции тела относительно оси вращения. Момент импульса тела относительно данной оси вращения принимает, таким образом, вид:
Mz= J·ω. (1.89)
(1.89)
Полученная формула аналогична формуле Pz= mVzдля поступательного движения. Роль массы играет момент инерции, роль линейной скорости — угловая скорость. Подставив выражение (1.89) в уравнение для момента импульса (2.74), получим
J·βz = Nz. (1.90)
где βz. — проекция на ось вращения углового ускорения . Это уравнение эквивалентно по форме второму закону Ньютона.
В общем случае несимметричного тела вектор M не совпадает по направлению с осью вращения тела и поворачивается вокруг этой ocи вместе с телом, описывая конус. Из соображений симметрии ясно что для однородного тела, симметричного относительно оси вращения, момент импульса относительно точки, лежащей на оси вращения, совпадает с направлением оси вращения. В этом случае имеет место соотношение:
. (1.91)
(1.91)
Из выражения (1.90) следует, что при равенстве нулю момент внешних сил произведение Jω остается постоянным Jω = const и изменение момента инерции влечет за собой соответствующее изменение угловой скорости вращения тела. Этим объясняется известное явление, состоящее в том, что человек, стоящий на вертящейся скамье, разводя руки в стороны либо прижимая их к туловищу, изменяет частоту вращения.
Из полученных выше выражений ясно, что момент инерции является такой же характеристикой свойства инерции макроскопического тела в отношении вращательного движения, как инертная масса материальной точки в отношении поступательного движения. Из выражения (1.88) следует, что момент инерции вычисляется путем суммирования по всем частицам тела. В случае непрерывного распределения массы тела по его объему естественно перейти от суммирования к интегрированию, вводя плотность тела. Если тело однородно, то плотность определяется отношением массы к объему тела:
. (1.92)
(1.92)
Для тела с неравномерно распределенной массой плотность тела в некоторой точке определяется производной
. (1.93)
Момент инерции представим в виде:
, (1.94)
где DV — микроскопический объем, занимаемый точечной массой.
Поскольку твердое тело состоит из большого числа частиц, практически непрерывно заполняющих весь занимаемый телом объем, в выражении (1.94) микроскопический объем можно считать бесконечно малым, в то же время полагая, что точечная масса «размазана» по этому объему. Фактически мы производим сейчас переход от модели точечного распределения масс к модели сплошной среды, какой в действительности и является твердое тело благодаря большой его плотности. Произведенный переход позволяет в формуле (2.94) заменить суммирование по отдельным частицам интегрированием по всему объему тела:
. (1.95)
(1.95)
Рис. Вычисление момента инерции однородного диска
Здесь величины ρ и r являются функциями точки, например, ее декартовых координат.
Формула (1.95) позволяет вычислять моменты инерции тел любой формы. Вычислим в качестве примера момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.).
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
, (1.96)
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим:
. (1.97)
Нахождение момента
инерции диска в рассмотренном примере облегчалось тем, что тело было однородным
и симметричным, а момент инерции вычислялся относительно оси симметрии тела. В
общем случае вращения тела произвольной формы вокруг произвольной оси,
вычисление момента инерции может быть произведено с помощью теоремы Штейнера:
момент инерции относительно произвольной оси равен сумме момента инерции J0относительно оси, параллельной данной и проходящей через центр инерции тела,
и произведения массы тела на квадрат расстояния между осями:
В
общем случае вращения тела произвольной формы вокруг произвольной оси,
вычисление момента инерции может быть произведено с помощью теоремы Штейнера:
момент инерции относительно произвольной оси равен сумме момента инерции J0относительно оси, параллельной данной и проходящей через центр инерции тела,
и произведения массы тела на квадрат расстояния между осями:
J=J0+ma2. (1.98)
Например, момент инерции диска относительно оси О’ в соответствии с теоремой Штейнера:
(1.99)
Момент инерции
Момент инерции
| Индекс Понятия момента инерции | ||
| Назад |
| Индекс Понятия момента инерции | ||||
| Назад |
Момент инерции — это название, данное вращательной инерции, вращательному аналогу массы для линейного движения. Он появляется в соотношениях для динамики вращательного движения. Момент инерции должен быть указан относительно выбранной оси вращения. Для точечной массы момент инерции равен произведению массы на квадрат расстояния по перпендикуляру к оси вращения, I = mr 2 . Это отношение точечных масс становится основой для всех других моментов инерции, поскольку любой объект может быть построен из набора точечных масс.
| Индекс Понятия момента инерции | ||||
| Назад |
| Индекс Понятия момента инерции | |||
| Назад |
Момент инерции определяется относительно определенной оси вращения.
| Индекс Понятия момента инерции | ||
| Вернуться |
Поскольку момент инерции обычного объекта включает в себя непрерывное распределение массы на постоянно меняющемся расстоянии от любой оси вращения, расчет моментов инерции обычно включает исчисление, дисциплину математики, которая может обрабатывать такие непрерывные переменные. , то момент инерции, вносимый бесконечно малым элементом массы dm, имеет такой же вид. Такой элемент массы называется дифференциальным элементом массы, а его момент инерции равен Обратите внимание, что дифференциальный элемент момента инерции dI всегда должен определяться относительно конкретной оси вращения. Сумма по всем этим элементам массы называется интегралом по массе. Обычно элемент массы dm выражается через геометрию объекта, чтобы интегрирование можно было проводить по объекту в целом (например, по длинному однородному стержню). Назвав это общей формой, вероятно, уместно указать, что это общая форма только для осей, которые можно назвать «главными осями», термин, который включает все оси симметрии объектов. Понятие момента инерции для общих объектов относительно произвольных осей — гораздо более сложный предмет. Момент инерции в таких случаях принимает форму математической тензорной величины, для полного определения которой требуется девять компонентов.
| Индекс Понятия момента инерции | ||||
| Вернуться |
Момент инерции: определение, формула и уравнения
Момент инерции или момент инерции массы — это скалярная величина , которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем более устойчиво тело к угловому вращению. Тело обычно состоит из нескольких мелких частиц, образующих всю массу. Массовый момент инерции зависит от распределения каждой отдельной массы относительно перпендикулярного расстояния к оси вращения.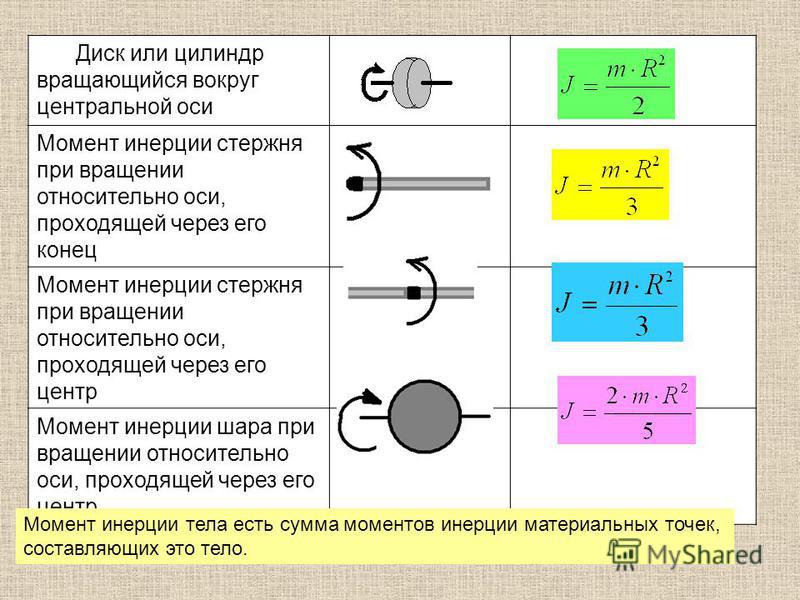 Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центр масс .
Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центр масс .
Уравнение момента инерции
Математически момент инерции может быть выражен через его отдельные массы как сумма произведения каждой отдельной массы и квадрата перпендикулярного расстояния до оси вращения. Вы можете увидеть это в уравнении ниже. I — момент инерции, измеренный в килограммах на квадратный метр (кг·м 2 ), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м).
Мы также можем использовать приведенное ниже уравнение для объекта , масса которого предполагается сосредоточенной в одной точке . На изображении показано расстояние оси вращения r.
Рис. 1 — Диаграмма, показывающая расстояние оси вращения r
Откуда взялся момент инерции?
Закон Ньютона гласит, что линейное ускорение объекта линейно пропорционально суммарной силе, действующей на него, когда масса постоянна. Мы можем сформулировать это с помощью приведенного ниже уравнения, где F t — результирующая сила, m — масса объекта, а t — поступательное ускорение .
Мы можем сформулировать это с помощью приведенного ниже уравнения, где F t — результирующая сила, m — масса объекта, а t — поступательное ускорение .
Аналогично мы используем крутящий момент для вращательного движения , который равен произведению вращательной силы и перпендикулярного расстояния к оси вращения. Однако поступательное ускорение при вращательном движении равно произведению углового ускорения α на радиус r.
Момент инерции равен , обратной массе во втором законе Ньютона для линейного ускорения, но применяется к угловому ускорению. Второй закон Ньютона описывает момент силы, действующий на тело, который прямо пропорционален моменту инерции массы тела и его угловому ускорению. Как видно из приведенного выше вывода, крутящий момент T равен произведению момента инерции I и углового ускорения α.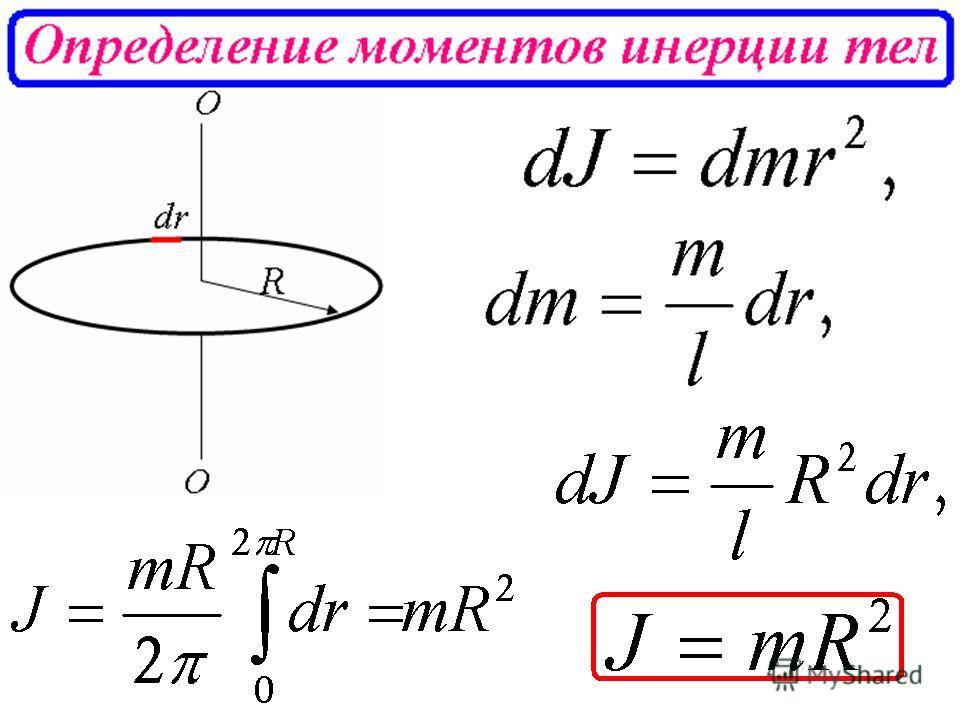
Моменты инерции для различных форм
Момент инерции индивидуален для формы и оси каждого объекта . Из-за различий в геометрических формах момент инерции дан для различных часто используемых форм, которые вы можете увидеть на изображении ниже.
Рис. 2 – Момент инерции для различных форм
Мы можем рассчитать момент инерции для любой формы путем интегрирования (по оси x) произведения уравнения, которое описывает ширину или толщину d, скорость изменения y и A, умноженное на квадрат расстояния до оси.
Чем больше толщина, тем больше момент инерции.
Примеры расчета момента инерции
Тонкий диск диаметром 0,3 м и суммарным моментом инерции 0,45 кг·м 2 вращается вокруг своего центра масс. На внешней части диска находятся три камня массой 0,2 кг. Найдите полный момент инерции системы.
Решение
Радиус диска 0,15м. Мы можем рассчитать момент инерции каждого камня как
Мы можем рассчитать момент инерции каждого камня как
Следовательно, суммарный момент инерции будет равен
Спортсмен сидит на вращающемся стуле, держа в каждой руке тренировочный вес по 10 кг. Когда спортсмен будет чаще вращаться: когда он вытягивает руки далеко от тела или когда он отводит руки близко к телу?
Решение
Когда спортсмен вытягивает руки, момент инерции увеличивается по мере увеличения расстояния между весом и его осью вращения. Когда спортсмен отводит руки назад, расстояние между отягощением и осью вращения уменьшается, а вместе с ним и момент инерции.
Следовательно, спортсмен с большей вероятностью будет вращаться, когда отводит руки назад, так как момент инерции будет меньше, и тело будет иметь меньшее сопротивление вращению.
Очень тонкий диск диаметром 5 см вращается вокруг своего центра масс, а другой более толстый диск диаметром 2 см вращается вокруг своего центра масс.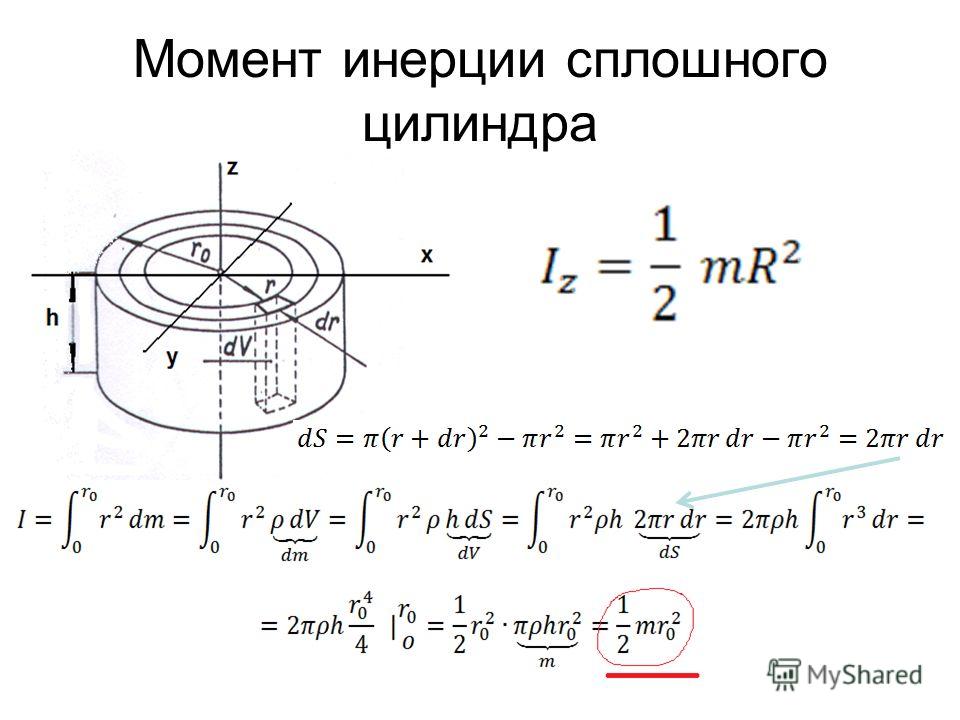 Какой из двух дисков имеет больший момент инерции?
Какой из двух дисков имеет больший момент инерции?
Решение
Диск большего диаметра будет иметь больший момент инерции . Как следует из формулы, момент инерции пропорционален квадрату расстояния до оси вращения, следовательно, чем больше радиус, тем больше момент инерции.
Момент инерции – ключевые выводы
Момент инерции является мерой сопротивления вращающегося объекта вращению. Это зависит от массы и распределения ее массы вокруг оси вращения.
Момент инерции — это величина, обратная массе во втором законе Ньютона, примененном к вращению.
Момент инерции различен и зависит от формы и оси каждого объекта.
Изображения
Инерция вращения. https://web2.ph.utexas.edu/~coker2/index.files/RI.htm
Часто задаваемые вопросы о моменте инерции
Момент инерции можно рассчитать как сумму произведений отдельных масс объект и их соответствующее квадратное расстояние по перпендикуляру к оси вращения.
Момент инерции или момент инерции масс — это скалярная величина, которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем труднее телу вращаться и наоборот.
Момент инерции является величиной, обратной массе во втором законе Ньютона для линейного ускорения, но применяется для углового ускорения.
Последний момент инерции Викторина
Вопрос
Что такое момент инерции?
Показать ответ
Ответ
Момент инерции — это мера сложности вращения объекта вокруг своей оси вращения.
Показать вопрос
Вопрос
Как определяется момент инерции?
Показать ответ
Ответить
Момент инерции — это произведение массы объекта на расстояние от его распределенной массы до оси вращения.
Показать вопрос
Вопрос
Какое уравнение мы используем для расчета момента инерции?
Показать ответ
Ответ
I=m·r 2
Показать вопрос
Вопрос
Что представляет r в уравнении момента инерции?
Показать ответ
Ответить
Расстояние от распределенной массы объекта до его оси вращения.
Показать вопрос
Вопрос
Какова единица момента инерции?
Показать ответ
Ответить
Единицей момента инерции является кг·м 2 .
Показать вопрос
Вопрос
Как момент инерции связан со вторым законом Ньютона?
Показать ответ
Ответить
Момент инерции есть величина, обратная массе во втором законе Ньютона.
Показать вопрос
Вопрос
Какая связь между вторым законом Ньютона и законом вращения Ньютона?
Показать ответ
Ответить
F=m·a и T=I·a. Они имеют одинаковую форму, следовательно, момент инерции есть величина, обратная массе во втором законе Ньютона для линейного ускорения.
Показать вопрос
Вопрос
Означает ли более высокий момент инерции, что тело с большей вероятностью будет вращаться?
Показать ответ
Ответить
Нет, более высокий момент инерции не означает, что тело будет вращаться с большей вероятностью.
Показать вопрос
Вопрос
Означает ли высокий момент инерции, что тело с меньшей вероятностью будет вращаться?
Показать ответ
Ответить
Показать вопрос
Вопрос
Фигурист пытается выполнить аэробику во время катания на коньках. Как он может гарантировать, что он останется стабильным после выполнения своих вращений?
Показать ответ
Ответить
Он может вытягивать руки и ноги как можно дальше от центра масс.
Показать вопрос
Вопрос
Когда кто-то вращается и внезапно вытягивает руки из своего тела, как изменяется момент инерции?
Показать ответ
Ответить
Момент инерции увеличивается по мере увеличения расстояния между распределением массы и осью вращения.
Показать вопрос
Вопрос
Тренировочный груз состоит из двух дисков, соединенных стержнем. Когда будет легче вращать тренировочный вес?
Показать ответ
Ответ
Когда два грузовых диска помещаются в середину стержня.
Показать вопрос
Вопрос
Два человека сидят в маленькой лодке Как они должны сидеть, чтобы сопротивляться вращению лодки?
Показать ответ
Ответить
Они могут сидеть на двух концах лодки.
Показать вопрос
Вопрос
Объект имеет момент инерции 60 кг·м 2 . Как изменится момент инерции, если расстояние по перпендикуляру к оси вращения или его распределенной массе удвоится?
Показать ответ
Ответить
Суммарный момент инерции увеличится в четыре раза.
Показать вопрос
(Момент инерции — TotalConstructionHelp)
Центроиды и момент инерции
Центр тяжести двумерной поверхности (например, поперечного сечения конструктивной формы) — это точка, соответствующая центру тяжести очень тонкой однородной пластины той же площади и формы. Плоская поверхность (или рисунок) может представлять фактическую площадь (например, площадь притока или поперечное сечение балки) или фигуративную диаграмму (например, диаграмму нагрузки или изгибающего момента). Часто бывает полезно определить центроид области в любом случае.
Часто бывает полезно определить центроид области в любом случае.
Симметрия может быть очень полезна для определения положения центра тяжести области. Если площадь (или сечение, или тело) имеет одну линию симметрии, центроид будет лежать где-то вдоль линии симметрии. Это означает, что если бы требовалось уравновесить площадь (или тело, или сечение) в горизонтальном положении, подложив под нее карандаш или ребро, то карандаш лучше всего было бы положить непосредственно под линией симметрии.
Если тело (или область, или сечение) имеет две (или более) линии симметрии, центр тяжести должен лежать где-то вдоль каждой из линий. Таким образом, центроид находится в точке пересечения прямых. Это означает, что если бы требовалось сбалансировать область (или тело, или секцию) в горизонтальном положении, поместив гвоздь под нее, острие гвоздя лучше всего было бы разместить непосредственно под точкой, где пересекаются линии симметрии. Это может показаться очевидным, но концепцию центроида очень важно понимать как в графическом, так и в числовом виде.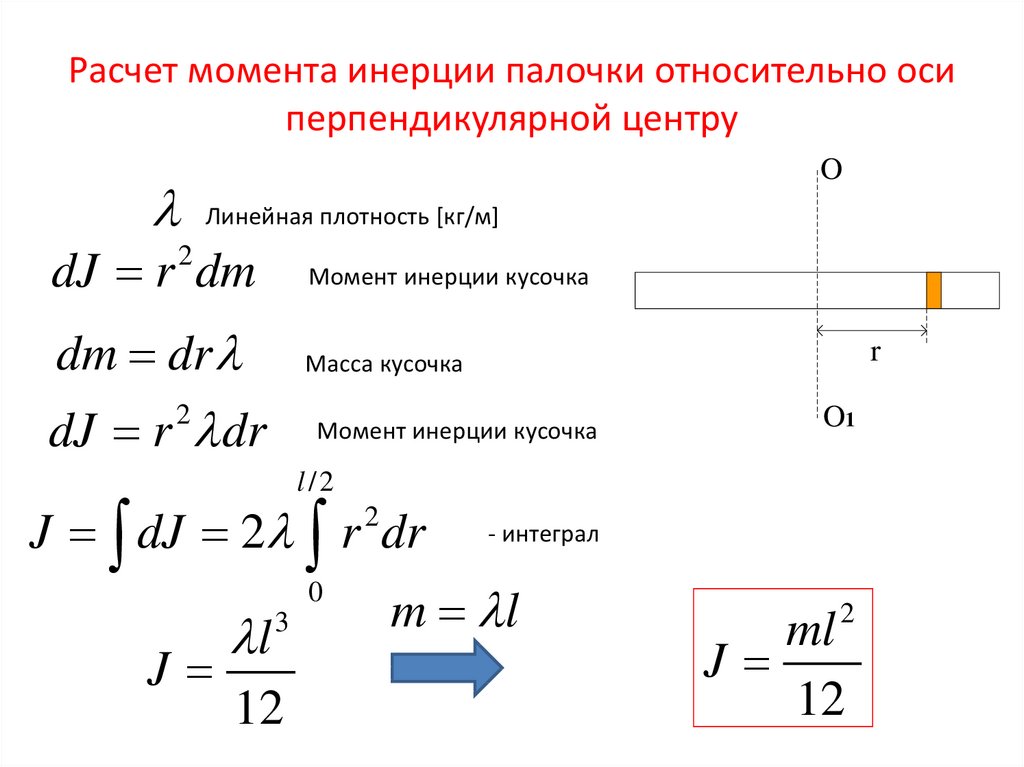 Положение центра тяжести некоторых простых форм легко определяется осмотром. Известно, что центроид круга находится в его центре, а центр тяжести квадрата — на пересечении двух линий, проведенных между серединами параллельных сторон. У круга бесконечное количество линий симметрии, а у квадрата — четыре.
Положение центра тяжести некоторых простых форм легко определяется осмотром. Известно, что центроид круга находится в его центре, а центр тяжести квадрата — на пересечении двух линий, проведенных между серединами параллельных сторон. У круга бесконечное количество линий симметрии, а у квадрата — четыре.
Центроид сечения не всегда находится в пределах площади или материала сечения. Полые трубы, Г-образные и некоторые неправильные секции имеют центр тяжести, расположенный за пределами материала секции. Это не проблема, так как центр тяжести используется только как точка отсчета, от которой измеряются расстояния. Точное местоположение центроида можно определить, как описано выше, с помощью графической статики или численно.
Центр тяжести любой области можно найти, взяв моменты идентифицируемых областей (таких как прямоугольники или треугольники) относительно любой оси. Это делается так же, как можно найти центр тяжести, взяв моменты весов. Момент большой площадки относительно любой оси равен алгебраической сумме моментов составляющих ее площадей. Это выражается следующим уравнением:
Это выражается следующим уравнением:
Сумма MAtotal = MA1 + MA2 + MA3+ …
Момент любой площади определяется как произведение площади на расстояние по перпендикуляру от центра тяжести площади до оси момента. С помощью этого принципа мы можем найти центр тяжести любой простой или составной области.
Центр тяжести:
Дано: плита, показанная на диаграмме, имеет вес 1 #/in 2 (1 фунт на квадратный дюйм) горизонтальной поверхности.
Определить:
центр тяжести пластины, зная, что она симметрична относительно оси X-X.
Решение:
Принцип моментов гласит, что общий вес относительно оси равен сумме моментов весов компонентов относительно той же оси. Таким образом, первое, что нужно сделать, это разделить тарелку на несколько простых частей. Затем определите площадь и центр тяжести (или центр тяжести) для каждой из составных частей. После этого отложите моменты каждой из деталей вокруг удобной оси (в этом случае выберите ось Z-Z, относительно которой отсчитывать эти моменты). Ось Z-Z здесь обозначена как опорная ось.
Ось Z-Z здесь обозначена как опорная ось.
Сумма MAtotal = MA1 + MA2 + MA3
Это простое уравнение можно переписать следующим образом, в котором описывается каждая из составных частей:
(Atotal)(расстояние от базовой оси до центральной оси) = (A1)(расстояние от центральной точки A1 до базовой оси) + (A2)(расстояние от центральной точки A2 до базовой оси) + (A3)(расстояние от центральной оси A3 относительно базовой оси)
, а затем найти у… центральная ось находится на расстоянии 7,3 дюйма от базовой оси.
Фактический центр тяжести находится посередине глубины плиты в точке, рассчитанной выше. По мере уменьшения толщины пластины линия действия центра тяжести будет оставаться, в то время как центр тяжести перемещается пропорционально вдоль этой линии действия, всегда действующей в середине глубины пластины. Если толщина пластины уменьшена до нуля, она не имеет веса, и прежнее положение центра тяжести теперь называется центром тяжести площади.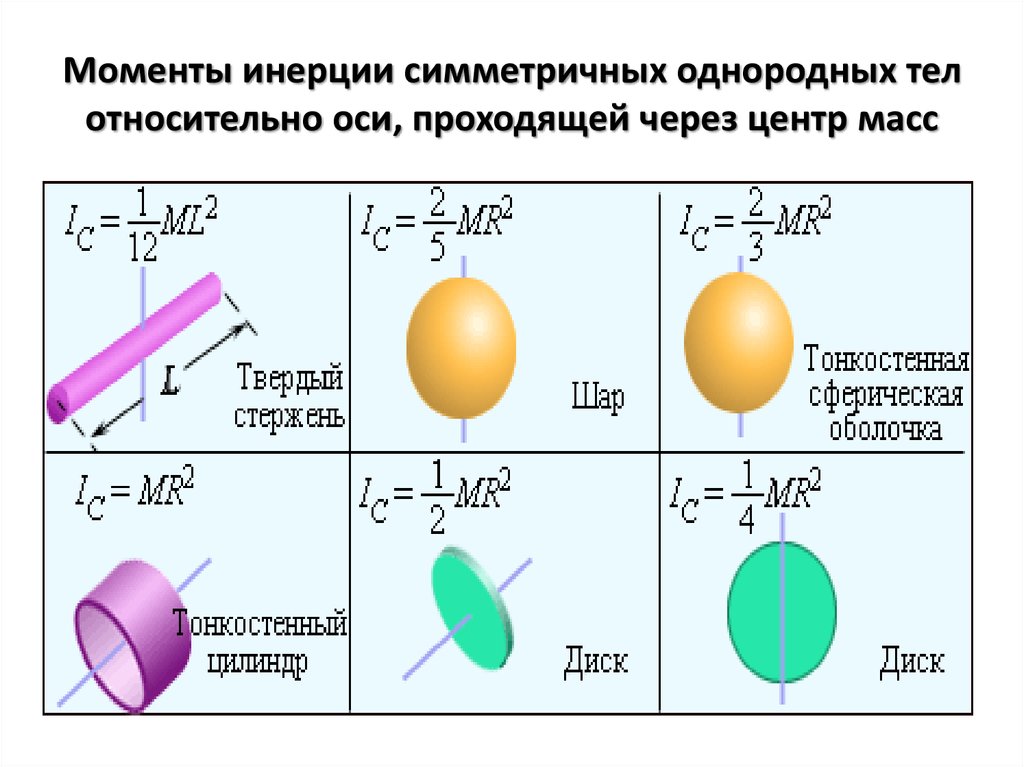
Момент инерции (I) — это термин, используемый для описания способности поперечного сечения сопротивляться изгибу. Он всегда рассматривается относительно базовой оси, такой как X-X или Y-Y. Это математическое свойство сечения, относящееся к площади поверхности и тому, как эта площадь распределяется по базовой оси. Базовой осью обычно является центроидальная ось.
Момент инерции также известен как второй момент площади и математически выражается как:
Ixx = Сумма (A)(y 2 )
В котором:
Ixx = момент инерции вокруг оси x
A = площадь плоскости объекта
y = расстояние между центром тяжести объекта и осью x
Момент инерции является важной величиной, которая используется для определения напряженного состояния в сечении, для расчета устойчивости к продольному изгибу и для определения величины прогиба в балке.
Например, если проектировщику задан определенный набор ограничений для структурной проблемы (т. Е. Нагрузки, пролеты и конечные условия), можно определить «требуемое» значение момента инерции. Тогда любой конструктивный элемент, обладающий хотя бы этим конкретным моментом инерции, сможет быть использован в конструкции. Другой пример мог бы быть, если бы было верно обратное; конкретный элемент дается в дизайне. Затем можно определить несущую способность элемента.
Е. Нагрузки, пролеты и конечные условия), можно определить «требуемое» значение момента инерции. Тогда любой конструктивный элемент, обладающий хотя бы этим конкретным моментом инерции, сможет быть использован в конструкции. Другой пример мог бы быть, если бы было верно обратное; конкретный элемент дается в дизайне. Затем можно определить несущую способность элемента.
Давайте посмотрим на две доски, чтобы интуитивно определить, какая из них будет больше прогибаться и почему. Если две доски с фактическими размерами 2 дюйма на 10 дюймов положить бок о бок — одну со стороны 2 дюймов, а другую со стороны 8 дюймов, то доска, опирающаяся на 2-дюймовый край, будет значительно жестче, чем та, что опирается вдоль. его 10-дюймовый край. Обе доски имеют одинаковую площадь поперечного сечения, но эта площадь по-разному распределяется относительно горизонтальной центральной оси.
Ixx = (1/12) (b)(h 3 ) = (1/12) x (b) x (h x h x h)
В котором значение b всегда принимается за сторону, параллельную базовой оси, а h за высоту сечения. Это очень важно отметить! Если принять неправильное значение для значения b, расчеты будут совершенно неправильными.
Это очень важно отметить! Если принять неправильное значение для значения b, расчеты будут совершенно неправильными.
Момент инерции
Дано: сечение.
Определить: Моменты инерции Ixx и Iyy данного раздела.
Решение:
Момент инерции прямоугольной формы, подобной этой, легко вычислить, используя уравнение I = 1/12 bh4. Однако крайне важно, чтобы b и h были присвоены правильные значения.
Вы можете просто повернуть стержень на 90 градусов и пересчитать, всегда помня исходное положение стержня.
Ixx= 1/12(4″)(10″) 3 = 333,2 дюйма 4
Iyy= 1/12(10″)(4″) 3 = 53,312 в 4
В этом случае наблюдение подтвердит выбор b и h. Логично, что Ixx больше, чем Iyy, потому что большая часть прямоугольной области лежит дальше от оси x-x, чем от оси y-y. Это приводит к тому, что форма имеет большее сопротивление вращению вокруг оси xx и, следовательно, больший момент инерции вокруг этой оси.
Важность распределения площади вокруг ее центральной оси становится понятной при сравнении значений момента инерции ряда типовых конфигураций балки. Все элементы, показанные ниже, имеют размеры 2 x 10 дюймов; в поперечном сечении, равные по длине и одинаково нагруженные.
СБОРНЫЕ СЕКЦИИ Часто выгодно комбинировать несколько меньших элементов, чтобы создать балку или колонну большей прочности. Момент инерции такого сборного сечения находится путем сложения моментов инерции составных частей. Это можно сделать тогда и только тогда, когда моменты инерции каждой составляющей площади взяты относительно общей оси, и тогда и только тогда, когда результирующее сечение действует как единое целое.
Сборные секции
Дано:
следующие сечения
Определить:
Ix каждого раздела с учетом его составных частей.
Решение:
В этом примере Box разбит на 4 отдельных элемента, и показана процедура расчета Ixx.
Ручной расчет с компьютерным расчетом ниже.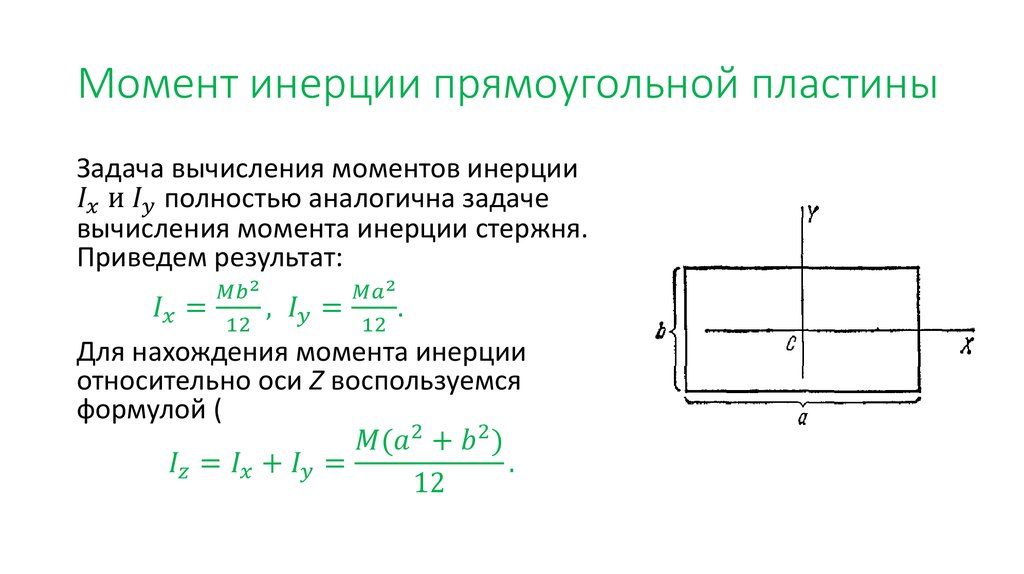
Пример результатов компьютерной программы, доступных в нашем разделе бесплатного программного обеспечения
ФОРМУЛА ПЕРЕДАЧИ
Существует много застроенных участков, в которых составные части не распределены симметрично относительно центральной оси. Самый простой способ определить момент инерции такого сечения — найти момент инерции составных частей относительно их собственной центральной оси, а затем применить формулу переноса. Формула переноса переносит момент инерции сечения или площади с его собственной центральной оси на другую параллельную ось. Из исчисления известно, что:
Ix = Ic + Ad 2
Где:
Ix = момент инерции относительно оси x-x (в 4 )
Ic = момент инерции относительно центральной оси c-c, параллельной x-x (в 4 )
A = площадь сечения (в 2 )
d = перпендикулярное расстояние между параллельными осями x-x и c-c (дюймы)
Формула перевода
Дано:
клееный асимметричный застроенный разрез ниже.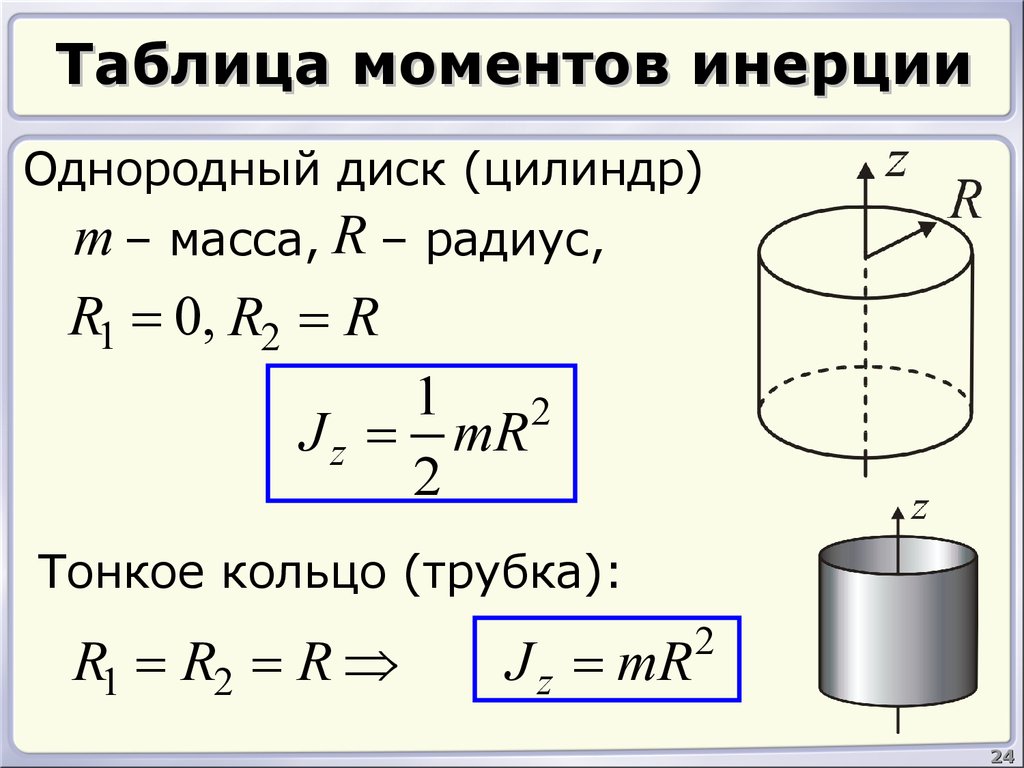
Определить:
момент инерции составной площадки относительно оси x.
Центральная ось и формула переноса
Пример результатов компьютерной программы, доступных в нашем разделе бесплатного программного обеспечения
Момент инерции — Everything2.com
Измерение устойчивости объекта к угловому (вращательному) ускорению. Момент инерции зависит от массы, положения оси вращения и формы объекта. Однако в целом момент инерции зависит от концентрации массы на расстоянии от оси вращения. Например, если у вас есть два диска одинакового радиуса, глубины и массы, но один из них полый (как кольцо), у кольца будет больший момент инерции. Подобно массе в кинематике перемещения, объектам с большим моментом инерции требуется больший крутящий момент, чтобы иметь такое же угловое ускорение. Однако, если два объекта вращаются с одинаковой угловой скоростью, то объект с большим моментом инерции будет иметь большую кенетическую энергию.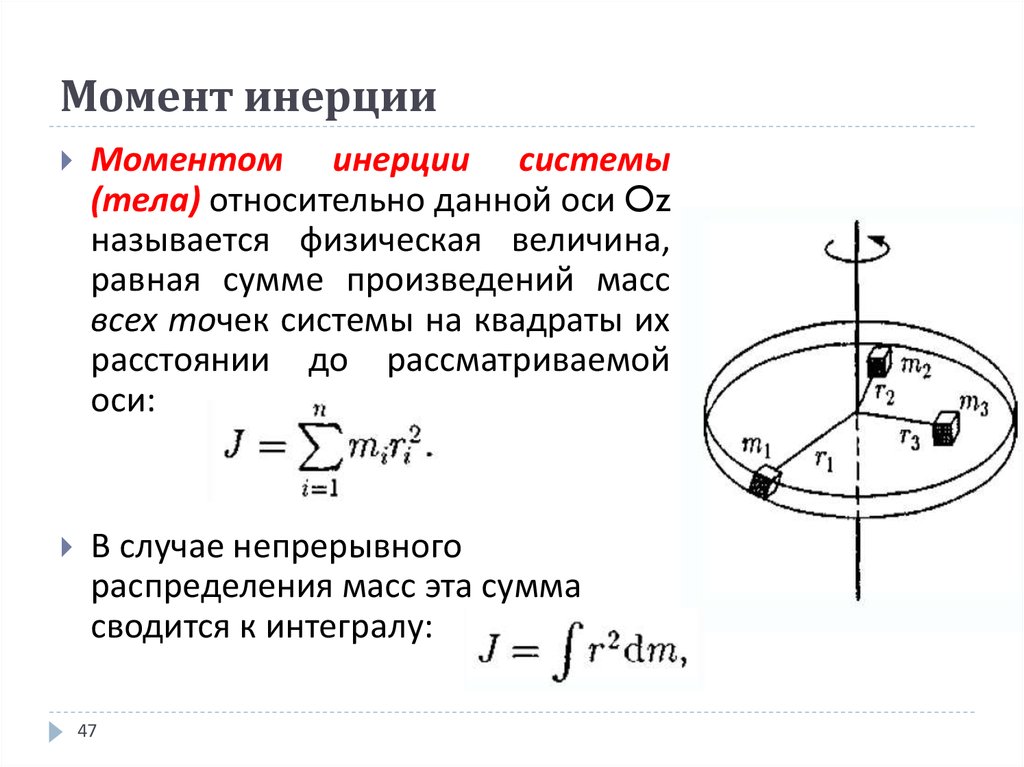
Момент инерции для вращательного движения равен массе для линейное движение, но вращательное движение немного усложняет ситуацию. Масса объекта обеспечивает ему инерцию при движении в пространстве. Вы можете выразить это, сказав, что более массивный объект имеет больший импульс, или что требуется больше силы, чтобы изменить движение более массивного объекта. В линейном движении эти идеи выражаются уравнениями
p = m v и F = m a
Аналогично, момент инерции связывает угловую скорость твердого объекта с его угловым моментом и говорит вам, какой крутящий момент требуется для изменения вращательного движения.
Давайте начнем с разговора об объекте, осесимметричном относительно одной оси 1 . В частности, давайте представим кольцо массы M с радиусом R, вращающееся вокруг своей оси симметрии. В этом случае момент инерции можно записать просто как число 9.0016
I = M R 2
Эта величина называется моментом инерции «относительно оси» симметрии. Затем мы можем записать уравнения для углового момента L, углового ускорения α и крутящего момента τ вдоль этой оси.
Затем мы можем записать уравнения для углового момента L, углового ускорения α и крутящего момента τ вдоль этой оси.
L = I ω и τ = I α
Эти уравнения выглядят точно аналогично уравнениям, которые я написал выше для линейного движения. Второе уравнение аналогично второму закону Ньютона и показывает нам, что чем больше момент инерции, тем труднее ускорить или замедлить вращение. Интуитивно вы, вероятно, догадались бы, что чем массивнее объект, тем больше будет его момент инерции, и это правда. Верно также и то, что чем дальше масса от оси вращения, тем труднее заставить ее вращаться. Это потому, что что-то далекое от оси вращения должно делать очень большой круг во время каждого вращения. Когда угловая скорость вращения немного увеличивается, это означает, что теперь эта масса должна вращаться намного быстрее, чтобы совершить круг за один период; таким образом, небольшое угловое ускорение преобразуется в большое тангенциальное ускорение, которое требует большой силы. Эти зависимости отражены в уравнении для кольца I = M R 2 .
Теперь предположим, что у нас есть какой-то другой объект, который вынужден вращаться вокруг определенной оси. Представим, например, что мы взяли какой-то объект и воткнули в него ось, так что теперь объект должен вращаться только вокруг оси. Если представить, что этот объект состоит из множества точечных масс, то каждая точечная масса массой m q , расположенная на расстоянии r ⊥q от оси вращения, при измерении перпендикулярно оси, вносит момент инерция относительно этой оси м q r ⊥q 2 (где q — просто целое число, обозначающее каждую массу). We can get the total moment of inertia with the formula
I = Σ q m q r ⊥q 2
or
I = ∫ r ⊥ 2 dm = ∫ ρ ( r ) r ⊥ 2 dV
для непрерывной системы, где ρ( r ) — массовая плотность, dV — элемент объема. Используя эти формулы, вот моменты инерции для некоторых однородных по плотности объектов массы M с обычными формами:
- Кольцо радиуса R, вращающееся вокруг своей оси симметрии: I = M R 2
- Цилиндр (или диск) радиуса R, вращающийся вокруг своей оси симметрии: I = 1/2 M R 2
- Кольцо радиусом R, вращающееся вокруг оси, перпендикулярной оси симметрии: I = 1/2 M R 2
- Тонкий стержень длиной L, вращающийся вокруг одного конца вокруг оси, перпендикулярной стержню: I = 1/3 M R 2
- Тонкий стержень длиной L, вращающийся вокруг своего центра вокруг оси, перпендикулярной стержню: I = 1/12 M R 2
- Сфера, вращающаяся вокруг диаметра: I = 2/5 M R 2
Для объектов, которые не вращаются вокруг оси симметрии и не вынуждены вращаться вокруг определенной оси, ситуация становится намного сложнее. В общем, момент инерции — это не просто число, это симметричный тензор ранга 2, поэтому вы можете записать его в виде матрицы 3 на 3. Это имеет много последствий, в том числе то, что вектор углового момента не всегда параллелен вектору угловой скорости, и связь между угловым ускорением и крутящим моментом уже не так проста. Некоторые из повседневных ситуаций, в которых эти эффекты проявляются, относятся к прецессии волчки и колебанию футбольного мяча.0094 2 метание со спиральным проходом. В общем случае, когда угловой момент и угловая скорость не совпадают, момент инерции изменяется со временем (при измерении относительно осей неподвижного наблюдателя, иногда называемых осями, «фиксированными в пространстве»), а соотношение крутящего момента и угловое ускорение становится
В общем, момент инерции — это не просто число, это симметричный тензор ранга 2, поэтому вы можете записать его в виде матрицы 3 на 3. Это имеет много последствий, в том числе то, что вектор углового момента не всегда параллелен вектору угловой скорости, и связь между угловым ускорением и крутящим моментом уже не так проста. Некоторые из повседневных ситуаций, в которых эти эффекты проявляются, относятся к прецессии волчки и колебанию футбольного мяча.0094 2 метание со спиральным проходом. В общем случае, когда угловой момент и угловая скорость не совпадают, момент инерции изменяется со временем (при измерении относительно осей неподвижного наблюдателя, иногда называемых осями, «фиксированными в пространстве»), а соотношение крутящего момента и угловое ускорение становится
τ = d L /dt = I α + dI/dt ω
Один из способов справиться с этим — перейти к «осям тела», что означает решение проблемы. как будто сидишь на вращающемся теле. В этом случае момент инерции не меняется во времени, но теперь вы работаете в неинерциальной системе отсчета, где есть псевдосилы, поэтому у вас все еще нет простого уравнения, связывающего крутящий момент и угловое ускорение. Тем не менее, это может быть очень полезным методом.
В этом случае момент инерции не меняется во времени, но теперь вы работаете в неинерциальной системе отсчета, где есть псевдосилы, поэтому у вас все еще нет простого уравнения, связывающего крутящий момент и угловое ускорение. Тем не менее, это может быть очень полезным методом.
Мы можем получить полную форму тензора момента инерции из определения углового момента для точечной частицы.
L Q = R Q × P Q
Добавить это во всех частицах (все Q значения). q × p q
и
p q = m q ω × r q
so
L = Σ q m q r q × ( ω × r q ) = Σ Q M Q ( ω (R Q ) 2 — R Q ( Ом ⋅ R
). Если мы запишем этот компонент за компонентом, то, немного поработав, мы можем получить
I JK = σ Q M Q (Δ JK R Q 2 — R QJ R QK — R QJ R QK — R QJ R QK ).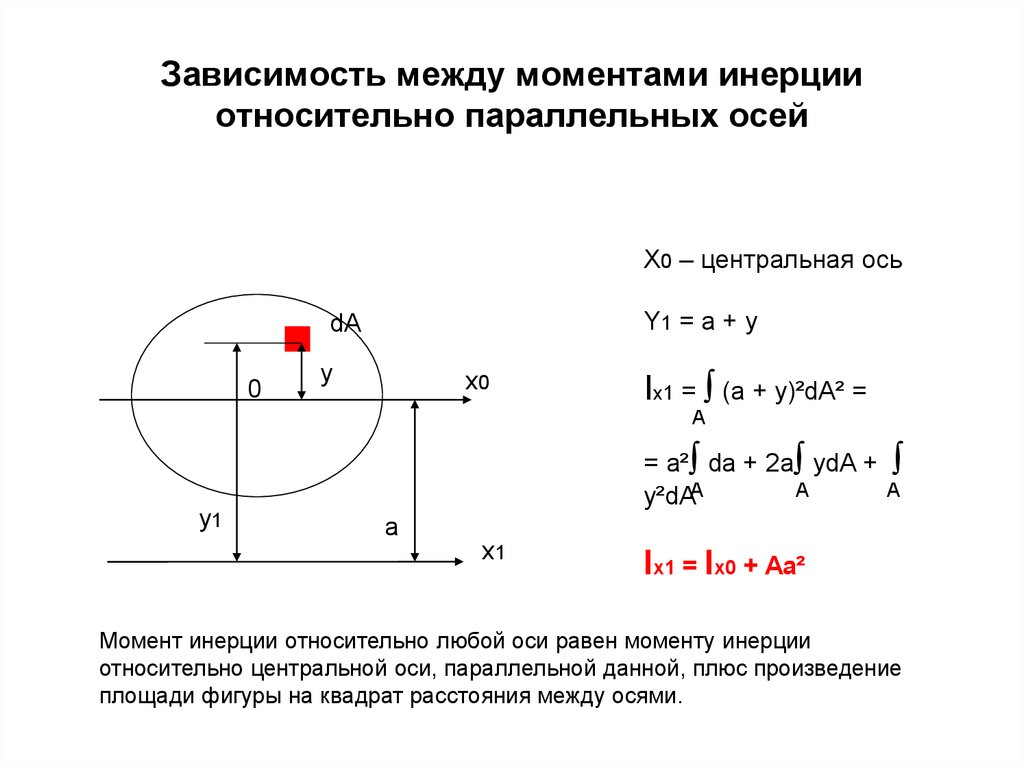 k — это просто числа от 1 до 3 для трех измерений. δ jk — это просто дельта Кронекера, которая равна 1, когда j = k, и 0, когда j ≠ k.
k — это просто числа от 1 до 3 для трех измерений. δ jk — это просто дельта Кронекера, которая равна 1, когда j = k, и 0, когда j ≠ k.
Поскольку I симметричен, его можно диагонализовать с помощью ортогонального преобразования, а это означает, что если мы просто повернем наши координатные оси, мы сможем найти те, где I является диагональным. Три оси этой специальной системы координат называются главными осями тела. Пока тело вращается только вокруг одной из этих осей, вы можете просто использовать значение момента инерции, соответствующее этому элементу на диагонали, известное как главный момент для этой оси. В случаях, когда два или три собственных значения вырождены, может быть более одного набора осей, в которых I является диагональным, как в случае со сферой или диском.
Рассмотрение тензорной природы момента инерции может привести к новым интересным эффектам, таким как прецессия и нутация. Они важны для понимания поведения волчка, гироскопа, вращения Земли и орбит спутников. Это связано с понятием момента, которое также используется в статике. Важным результатом о моменте инерции, который вы часто используете на практике, является теорема о параллельных осях, и углы Эйлера также очень полезны.
Это связано с понятием момента, которое также используется в статике. Важным результатом о моменте инерции, который вы часто используете на практике, является теорема о параллельных осях, и углы Эйлера также очень полезны.
Источники:
- Классическая механика , Goldstein, Poole and Safko, Addison Wesley (2002)
- Newtonian Dynamics , Р. Байерляйн, McGraw Hill (1983)
- Мир физики Эрика Вайсштейна , Эрик В. Вайсштейн, http://scienceworld.wolfram.com/physics/MomentofInertia.html
| Почему банки для напитков имеют вогнутое дно | Как кошка кувыркается в воздухе | Гироскоп | Нутация |
| теорема о параллельных осях | момент | Магазин физики | крутящий момент |
| Как сделать стол | Прецессия | угловая скорость | осевая прецессия |
| инерция вращения | Обратная кинематика | Тензор | У меня были лучшие объятия от порывов ветра и мертвых людей |
| Диетическая кола | телическая грамматика | жесткий корпус | Спасите космический телескоп Хаббла |
| Теорема вириала | гироскопическое движение | стандартная ориентация | угловой момент |
Войдите или зарегистрируйтесь, чтобы написать что-нибудь здесь или связаться с авторами.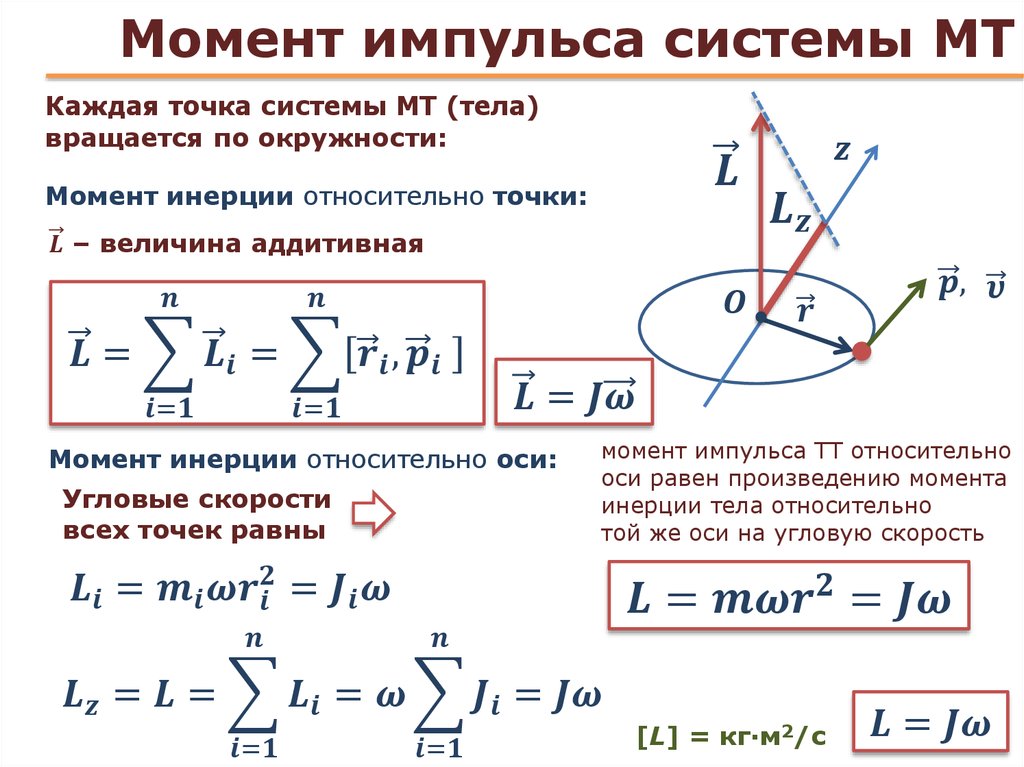
Подробные объяснения и проблемы — Lambda Geeks
В статье рассматривается связь крутящего момента и момента инерции вращающегося тела и ее решаемые задачи.
Крутящий момент и момент инерции поддерживают тело при вращательном движении. Когда на тело наводится крутящий момент, оно начинает ускоряться обратно пропорционально его моменту инерции. Вот почему крутящий момент, передаваемый телу, является произведением его момента инерции и углового ускорения.
Законы движения Ньютона выражают, что тело остается неподвижным или движется из одной точки в другую с определенной скоростью; если на него не действует какая-либо внешняя сила . Это означает, что тело получает ускорение в зависимости от его полной массы и силы приложенной внешней силы.
Используя принцип Ньютона во вращательном движении, когда крутящий момент или момент силы создается на неподвижном или движущемся теле, оно инициирует угловое ускорение. Вот почему каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение, когда индуцируется крутящий момент.
Вот почему каждое твердое тело, совершая вращательное движение вокруг своей оси, несет угловое ускорение, когда индуцируется крутящий момент.
В предыдущих статьях мы поняли, что инерция — это свойство тела, которое представляет тенденцию тела противостоять движению . Вот почему инерция обратно пропорциональна ускорению тела . Следовательно, первый закон движения Ньютона также называется законом инерции 90 270.
Крутящий момент и момент инерцииКаждая частица внутри такого вращающегося тела имеет свою массу, и все они вращаются вокруг центральной оси вращения тела. Следовательно, величина крутящего момента, необходимая для ускорения частиц внутри тела, зависит от распределения массы всего тела. Величина тела, выражающая распределение масс, называется « моментом инерции» .
Момент инерции для различных твердых тел(кредит: Shutterstock)
Величина инерции во вращательном движении рассматривается как момент инерции тела, определяемый путем интегрирования полных масс M частиц и их расстояний R от его ось вращения.
Следовательно, момент инерции тела (I) равен I = MR 2 .
Взаимосвязь крутящего момента и момента инерцииЗаконы движения Ньютона связывают крутящий момент и момент инерции при вращательном движении.
Когда мы включаем вентилятор, мы наводим на него крутящий момент. Теперь ускорение вентилятора будет зависеть от того, какой момент инерции имеет вентилятор и какой крутящий момент нам нужно создать.
Момент инерции – это вращательная масса тела, а крутящий момент – вращательная сила, действующая на него. Крутящий момент τ, который необходимо приложить к телу, пропорционален как угловому ускорению, так и моменту инерции. Но момент инерции I уменьшает угловое ускорение α тела.
Утверждение дает связь между крутящим моментом и моментом инерции как 15 рад/с 2 чтобы тело имело момент инерции 5 кгм 2 ?
Дано :
I = 5 кгм 2
α = 15 рад/с 2
Найти : τ =?
Formula :
τ = I α
Решение :
Трут должен индуцировать, чтобы повернуть его на 15 Rad/S 2 . и момент инерции ,
и момент инерции ,
τ= I α
Подставляя все значения,
τ = 5 x 15
τ= 75
Крутящий момент, необходимый для вращения тела, составляет 75 Нм.
Какой крутящий момент должен возникнуть на расстоянии 2 м от тела массой 4 кг, чтобы оно вращалось со скоростью 5 рад/с 2 ?Указано :
M = 4 кг
R = 2 M
α = 5 RAD/S 2
до : до : до : Формула : τ = I α Решение : Крутящий момент, необходимый для корпуса, рассчитывается как τ = Iα Но момент инерции диска равен I = MR 2 . τ = MR 2 α Заменить все значения, τ = 4 x 2 2 x 5 τ = 4 x 5 τ = 8016 кузов 80 Нм. Формула крутящего момента и момента инерции легко определяется путем замены линейного эквивалента в формуле закона движения Ньютона его угловым эквивалентом. Крутящий момент τ является угловым эквивалентом приложенной силы F, а момент инерции I является угловым эквивалентом массы m. Следовательно, закон движения Ньютона (F = ma) для вращательного движения принимает вид: τ = Iα Вращательное движение также подчиняется законам движения Ньютона. Поэтому, когда на тело действует крутящий момент, его угловой момент изменяется из-за ускорения. Поскольку угловой момент является произведением инерции и угловой скорости, мы можем получить необходимый крутящий момент из его момента инерции. Угловой импульс 1111115
111116
1116?

Где P – линейный импульс 1 . т. е. P = mv
т. е. P = mv
L = r x mv
Соотношение между линейной скоростью v и угловой скоростью ω равно Но мистер 2 срок тела момент инерции (I).
L = I ω
Мы узнали, что крутящий момент, действующий на тело, представляет собой скорость изменения углового момента .
τ = DL/DT
Заменить Аглоумическая формула момента ,
τ = diω/dt
τ = IDω/DT
Термин Dω/DT — Accelerator15. т. е. α= dω/dt
Наконец, крутящий момент получается из момента инерции,
τ = lα
Читать о крутящем моменте и скорости
Диск массой 0,1 кг и радиусом 1 м вращается со скоростью 2 рад/с 2. Момент инерции диска равен I = 1/ 2мр 2 . Рассчитайте крутящий момент, действующий на диск.Указано :
M = 0,1 кг
R = 1 M
α = 2 RAD/S 2
до нахождения: 9096
до Найти: 96966 до Найти:
до:
.
Формула :
τ = I α
Решение :
2 ……………..(Given)
τ= 1/2mr 2 α
Substituting all values,
τ = 1/2 x 0.1 x 1 2 x2
τ = 0,2/2
τ = 0,2/2
τ = 0,1
Крутящий момент на диске составляет 0,1 Нм.
Тонкий стержень массой 100 кг и длиной 6 м вращается со скоростью 20 рад/с 2 . Момент инерции тонкого стержня I =1/12mr 2 . Рассчитайте крутящий момент на тонком стержне.Указано :
M = 100 кг
R = 6 M
α = 20 RAD/S 2
до Найти: 77777777777777777777777777777777777777777777771116
.
Формула :
τ = I α
Решение :
Крутящий момент на тонком стержне рассчитывается как
τ = I α
Для тонкого стержня момент инерции равен I = 1/12mr … . . (дано)
. (дано)
τ = 1/12MR 2 α
Заменить все значения,
τ = 1/12 x 100 x 6 2 x 20
τ = 72000/12
τ = = = 72000/12
τ = = 72000. 6000
Крутящий момент на диске составляет 6000 Нм.
Калькулятор свободного момента инерции (второй момент площади)
Калькулятор поперечного сечения ClearCalcs позволяет пользователю вводить геометрию произвольного поперечного сечения, используя либо простые размеры обычных форм, либо полностью настраиваемые определения контура. Затем он определяет свойства упругости, деформации и/или пластичности этого сечения, включая площадь, координаты центра тяжести, вторые моменты площади/моменты инерции, модули сечения, главные оси, постоянную кручения и многое другое!
Вы можете использовать свойства поперечного сечения из этого инструмента в нашем бесплатном калькуляторе балки.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов, а также позволит использовать эти пользовательские поперечные сечения в этих проектах. ClearCalcs позволяет выполнять проектирование из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
ClearCalcs позволяет выполнять проектирование из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на два основных раздела:
- «Основные свойства», где определяется геометрия поперечного сечения.
- «Сводка», где выбирается тип анализа и отображаются рассчитанные свойства.
Также имеется раздел «Комментарии», в котором пользователь может оставить любые примечания к дизайну. Щелчок по любой из меток ввода/свойства дает описательное справочное объяснение.
1. Введите свойства ключа
Сначала выберите тип поперечного сечения из раскрывающегося меню сразу под диаграммой. Когда вы это сделаете, поля ввода под ним изменятся на те, которые необходимы для данного типа поперечного сечения.
Например, прямоугольник имеет два измерения для его определения: Глубина и Ширина . Оба измерения должны быть больше нуля, но других ограничений нет.
Некоторые другие типы поперечного сечения имеют определенные ограничения. Например, Глубина двутаврового сечения должна быть больше, чем в два раза больше Толщина полки плюс в два раза Внутренний радиус . Подобные ограничения являются просто логическими ограничениями на геометрию; перекрытия или неполные радиусы скругления физически невозможны.
Например, Глубина двутаврового сечения должна быть больше, чем в два раза больше Толщина полки плюс в два раза Внутренний радиус . Подобные ограничения являются просто логическими ограничениями на геометрию; перекрытия или неполные радиусы скругления физически невозможны.
Диаграмма в этом разделе будет отображать поперечное сечение в том виде, в каком оно было введено, а также некоторые ключевые свойства этого поперечного сечения, включая центр тяжести, ориентацию главной оси и, если были выполнены соответствующие типы анализа , пластический центроид и центр сдвига.
Сводка результатов расчета и типы анализа
Доступны четыре различных варианта типа анализа : «Только упругий», «Упругий + деформация», «Упругий + пластик» и «Все». Самый быстрый вариант по умолчанию — «Только эластичный», в то время как другие параметры также добавляют анализ деформации и/или пластичности. Обратите внимание, что расчет упругости всегда выполняется в каждом варианте. Различные результаты, рассчитанные в каждом из этих типов анализа, описаны ниже:
Различные результаты, рассчитанные в каждом из этих типов анализа, описаны ниже:
Анализ упругости
- Угол большой главной оси : Большая главная ось (ось «1») может быть наклонена для несимметричных сечений или может быть под углом 90 градусов, если сечение имеет больше боковых, чем вертикальных жесткость. Это определяет его угол относительно оси X. Обратите внимание, что малая главная ось (ось «2») точно перпендикулярна к ней. Ориентация главной оси также указана на диаграмме поперечного сечения.
- Зона : площадь поперечного сечения секции. Это значение обычно используется при определении осевой прочности колонны.
- Первые моменты площади : Первые моменты площади важны для некоторых расчетов сдвига, таких как сдвиговый поток. Обратите внимание, что первые моменты площади берутся относительно центроида и геометрических осей.
- Секундные моменты площади / Моменты инерции : Секундные моменты площади, также известные в технике как моменты инерции, связаны с прочностью на изгиб и прогибом балки.
 Обратите внимание, что все значения берутся относительно центра тяжести поперечного сечения, хотя значения доступны как для геометрической, так и для главной оси. Полярный момент инерции идентичен для обоих типов осей, так как ось «Z» всегда считается такой же, как ось «3». Произведенный момент инерции по определению равен нулю для главных осей.
Обратите внимание, что все значения берутся относительно центра тяжести поперечного сечения, хотя значения доступны как для геометрической, так и для главной оси. Полярный момент инерции идентичен для обоих типов осей, так как ось «Z» всегда считается такой же, как ось «3». Произведенный момент инерции по определению равен нулю для главных осей. - Модули упругого сечения : Модули упругого сечения равны секундным моментам площади / моментам инерции, деленным на расстояние до самого дальнего волокна в поперечном сечении, перпендикулярном оси изгиба. Приведены значения как для положительного, так и для отрицательного изгиба, где положительный изгиб определяется как самая верхняя или самая левая часть поперечного сечения, находящаяся в сжатом состоянии. Значения также предоставляются как для геометрической, так и для главной оси и всегда относятся к центроиду. Н.Б. Модуль упругого сечения также известен как модуль статического сечения.
- Расстояние от центра тяжести до крайних волокон : Расстояние между центром тяжести поперечного сечения и крайним волокном поперечного сечения, перпендикулярно оси изгиба.
 Секунды моментов площади/моментов инерции, деленные на эти расстояния, будут равны модулям упругого сечения.
Секунды моментов площади/моментов инерции, деленные на эти расстояния, будут равны модулям упругого сечения. - Радиусы вращения : Радиусы вращения представляют собой среднеквадратичное расстояние каждого волокна в поперечном сечении относительно заданной оси. Значения всегда относятся к центроиду и доступны как по геометрической, так и по главной осям. Полярный радиус вращения идентичен для обоих типов осей, так как ось «Z» всегда считается такой же, как ось «3».
- Центроид : Расположение центроида показано на диаграмме поперечного сечения. Наведите указатель мыши на значок зеленого круга, и всплывающая подсказка отобразит точные координаты центроида. Обратите внимание, что исходное положение (0,0) обозначено синим перекрестием.
Анализ коробления
- Постоянная кручения Сен-Венана : Постоянная кручения связана с тем, насколько хорошо поперечное сечение может сопротивляться чистым силам кручения, и обычно используется в формулах потери устойчивости при поперечном кручении.

- Постоянная деформации : При приложении скручивающей или эксцентрической силы поперечное сечение может не только скручиваться, но и деформироваться. Эта константа является мерой того, насколько легко может произойти это искривление, и часто используется в формулах потери устойчивости при поперечном кручении.
- Площади сдвига : Только часть поперечного сечения будет эффективно сопротивляться сдвигающей силе, приложенной вокруг заданной оси (то есть поперечной силе, перпендикулярной данной оси). Показанные значения основаны на интегрировании сдвигового потока, и поэтому они могут не точно соответствовать классическим расчетам, основанным на областях сети.
- Константы моносимметрии : Константы моносимметрии определяют, насколько поперечное сечение близко к симметричному. Константа стремится к нулю, когда поперечное сечение симметрично относительно данной оси.
- Центр сдвига : Расположение центра сдвига показано на диаграмме поперечного сечения.





 I = m*L2/12, где L — длина стержня.
I = m*L2/12, где L — длина стержня.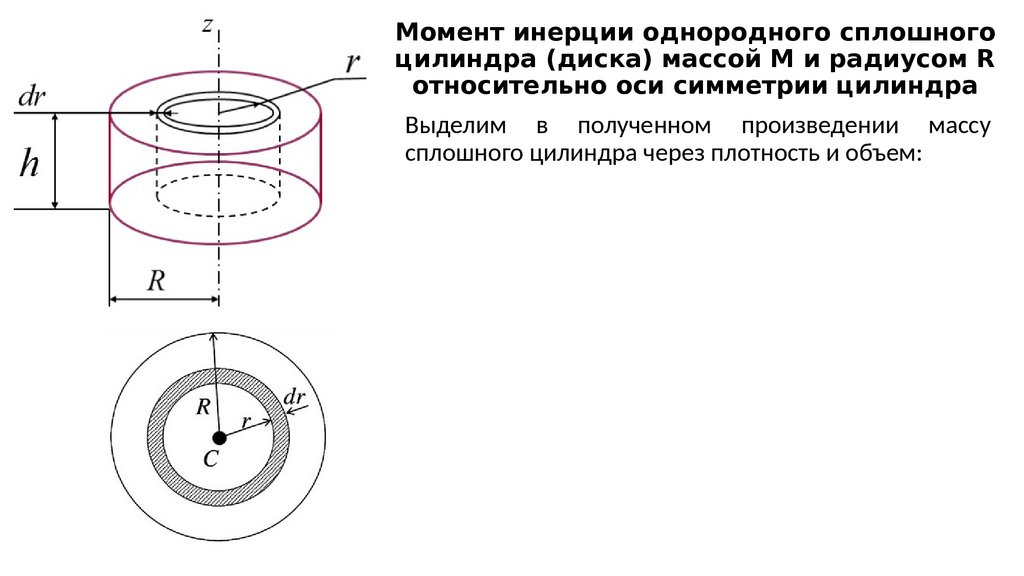


 Это называется прецессией и аналогично орбите массы под действием центральной силы.
Это называется прецессией и аналогично орбите массы под действием центральной силы.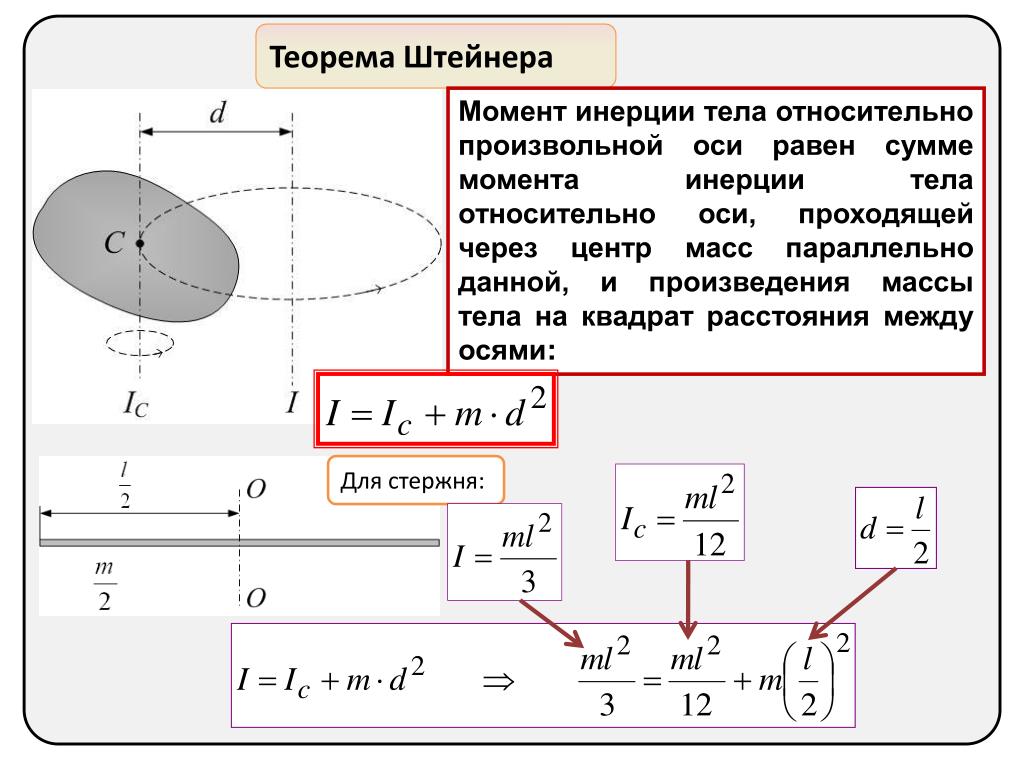 Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл.
Момент инерции точечной массы относительно оси определяется как произведение массы на квадрат расстояния от оси. Момент инерции любого протяженного объекта строится из этого базового определения. Общая форма момента инерции включает интеграл. Поскольку момент инерции точечной массы определяется как
Поскольку момент инерции точечной массы определяется как