6. Момент инерции
Момент инерции — величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:
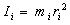 .
.
Момент инерции всего тела относительно оси равен:
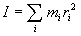
или, для непрерывно распределенной массы:
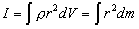 .
.
Момент инерции всего тела сложной конфигурации обычно определяют экспериментально.
Момент инерции некоторых однородных твердых приведены в таблице 1.
|
| Таблица 1 |
Момент инерции некоторых симметричных однородных тел | ||
Твердое тело | Ось вращения | Момент инерции I, кг м2 |
Тонкий стержень длины l | Перпендикулярна стержню, проходит через центр масс | ml2/12 |
Тонкий стержень длины l | Перпендикулярна стержню, проходит через край | ml2/3 |
Сплошной цилиндр радиуса R | Совпадает с осью цилиндра | mR2/2 |
Полый цилиндр радиуса R | Совпадает с осью цилиндра | mR2 |
Шар радиуса R | Проходит через центр шара | 2mR2/5 |
Полый шар радиуса R | Проходит через центр шара | 2mR2/3 |
Тонкий диск радиуса R | Совпадает с диаметром диска | mR2/4 |
Тонкая прямоугольная пластина со сторонами а и b | Проходит через центр пластины перпендикулярно пластине | m (a2+b2)/12 |
Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера. Согласно теореме Штейнера момент инерции тела относительно какой-либо оси IA равен моменту инерции тела равен инерции тела относительно параллельной оси, проходящей через центр масс
IA = IC + ma2.
Понятием о моменте инерции широко пользуются при решении многих задач механики и техники.
7. —————————
8. Гидромеханика. Уравнение Навье — Стокса
Уравнения Навье — Стокса описывают движение вязкой ньютоновской жидкости и являются основой гидродинамики. Численные решения уравнений Навье — Стокса используются во многих практических приложениях и научных работах. Однако в аналитическом виде решения этих уравнений найдены лишь в некоторых частных случаях, поэтому нет полного понимания свойств уравнений Навье — Стокса. В частности, решения уравнений Навье — Стокса часто включают в себя турбулентность, которая остаётся одной из важнейших нерешённых проблем в физике, несмотря на её огромную важность для науки и техники.
[Править]Уравнения Навье — Стокса
Основная статья: Уравнения Навье — Стокса
В математике это система нелинейных дифференциальных уравнений в частных производных для абстрактных векторных полей любой размерности. В физике это система уравнений, которая в рамках механики сплошных сред описывает движение жидкостей или неразреженных газов.
Пусть 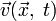
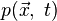 —
давление. Тогда уравнения Навье —
Стокса записываются так:
—
давление. Тогда уравнения Навье —
Стокса записываются так: 
где 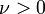 —
это кинематическая вязкость,
—
это кинематическая вязкость,  — плотность,
— плотность,  —
внешняя сила,
—
внешняя сила, 
 — оператор
Лапласа (лапласиан),
который также обозначается, как
— оператор
Лапласа (лапласиан),
который также обозначается, как  .
Отметим, что это векторное уравнение,
то есть оно содержит три скалярных
уравнения. Если обозначить компоненты
векторов скорости и внешней силы, как
.
Отметим, что это векторное уравнение,
то есть оно содержит три скалярных
уравнения. Если обозначить компоненты
векторов скорости и внешней силы, как 
то
для каждого значения 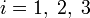 получается
соответствующее скалярное уравнение
Навье — Стокса:
получается
соответствующее скалярное уравнение
Навье — Стокса:

Неизвестными
величинами являются скорость 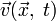 и
давление
и
давление 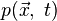 .
Поскольку в трёхмерном случае получается
три уравнения и четыре неизвестных (три
компоненты скорости и давление), то
необходимо ещё одно уравнение.
Дополнительным уравнением является
закон сохранения массы
.
Поскольку в трёхмерном случае получается
три уравнения и четыре неизвестных (три
компоненты скорости и давление), то
необходимо ещё одно уравнение.
Дополнительным уравнением является
закон сохранения массы
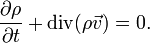
Если среду считать несжимаемой, то это уравнение преобразуется в условие несжимаемости жидкости:
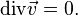
Геометрические характеристики сечений
Одним из наиболее важных понятий во многих дисциплинах, в частности, в сопромате является понятие момента некоторого объекта относительно оси. В различных областях науки вводятся различные моменты в зависимости от исследуемого объекта (например, в теоретической механике вводят момент силы, в теории вероятности вводят моменты случайной величины и т.д.). Все они связаны с понятием плечо, которое представляет собой расстояние от объекта до оси. Если умножить плечо на величину, которая характеризует объект, то получим момент первого порядка. Если взять квадрат плеча, то получим момент второго порядка, если взять плечо в третьей степени, то получим момент третьего порядка и т.д.
Статический момент фигуры
В теории геометрических характеристик сечений бруса исследуемым объектом является площадь этого сечения. Рассмотрим сначала бесконечно малую площадь dA. Расстояние а от центра dA до оси х назовем ее плечом.
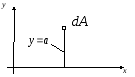
Рис1.1
Статическим моментом dSx относительно оси х бесконечно малой площади dA называется произведение dA на а:
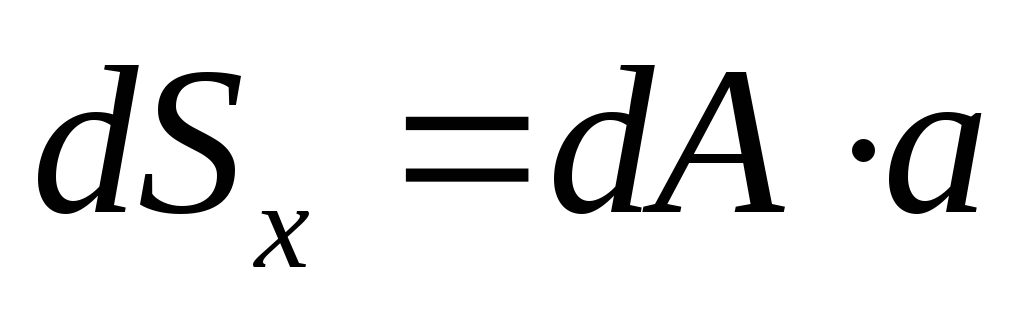
(1.1)
У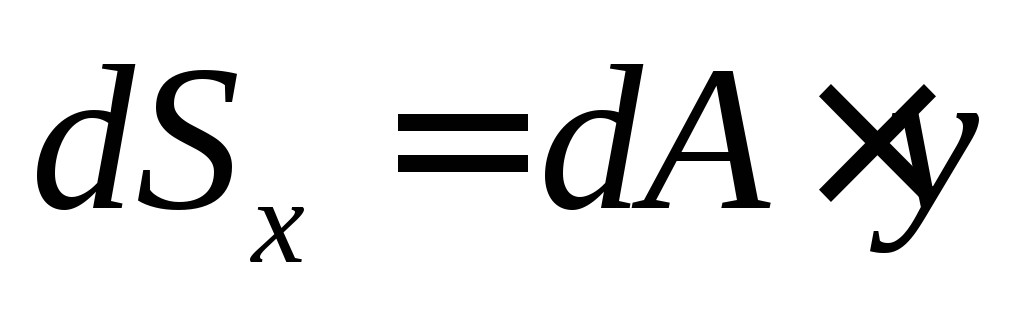 читывая,
чтоа=у запишем:
читывая,
чтоа=у запишем:
Е сли
фигура имеет конечную площадь, то мы её
можем разбить на бесконечно малые
площади и для каждой из них найти
статический момент. Просуммировав их,
найдем статический момент всей фигуры
относительно оси
сли
фигура имеет конечную площадь, то мы её
можем разбить на бесконечно малые
площади и для каждой из них найти
статический момент. Просуммировав их,
найдем статический момент всей фигуры
относительно оси
(1.2)
Аналогично вводится понятие статического момента относительно оси у
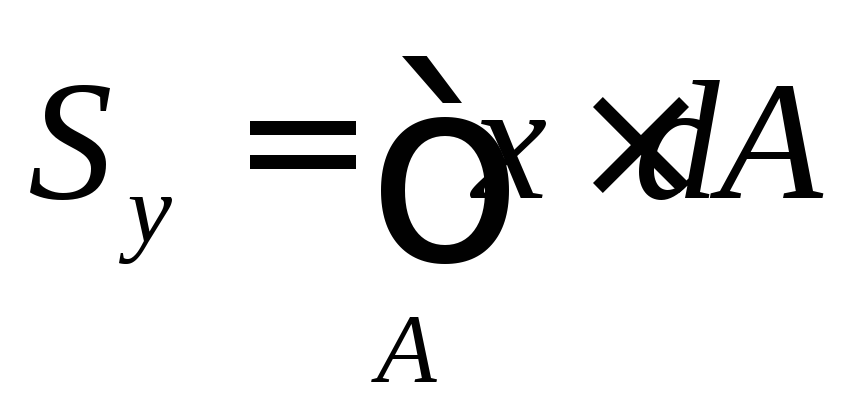 (1.3)
(1.3)
Вычисление статических моментов.
Используем для получения формулы вычисления Sx , Sу аналогию с моментом силы в теоретической механике. Будем считать что наша фигура dA имеет толщину t, тогда объём фигуры :
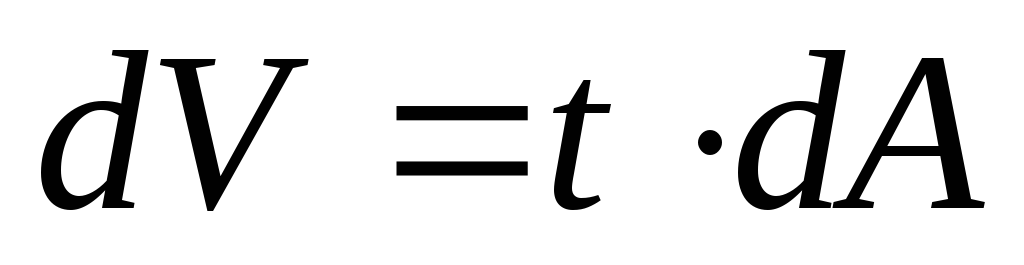
Вес dР фигуры dA равен произведению удельного веса  на объём dV :
на объём dV :
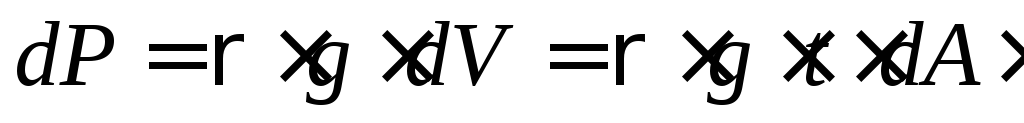
Обозначаем ,
,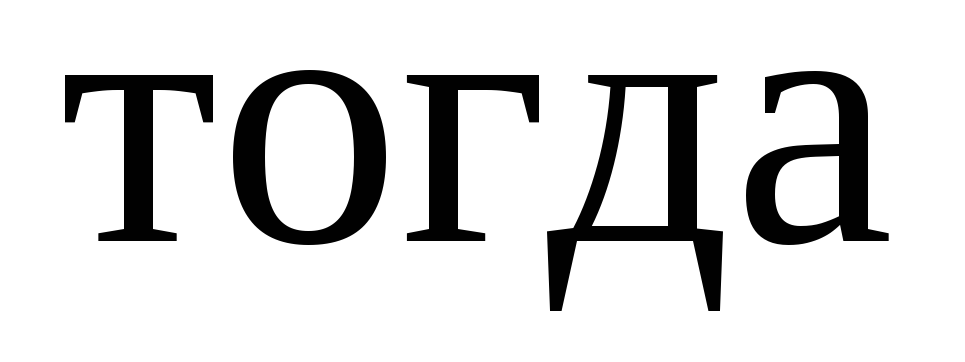
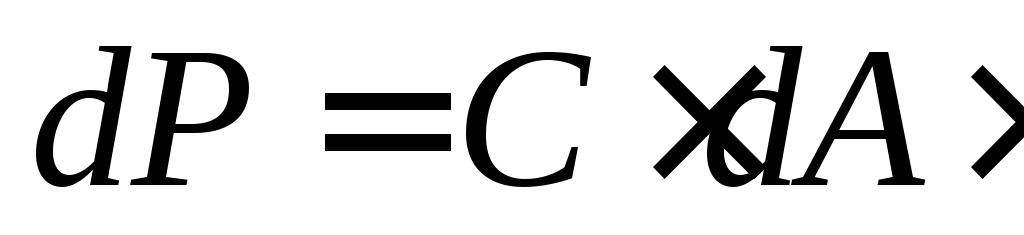
Вес Р всей фигуры вычисляется аналогично:
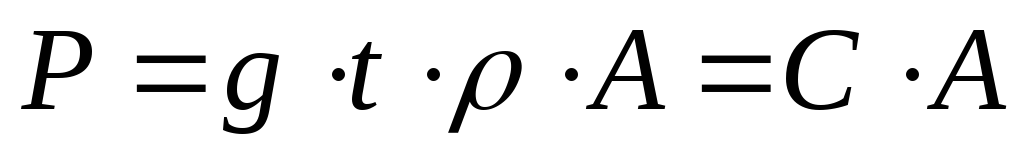 (1.4)
(1.4)

Рис.1.2
Момент силы dР относительно оси х будет:
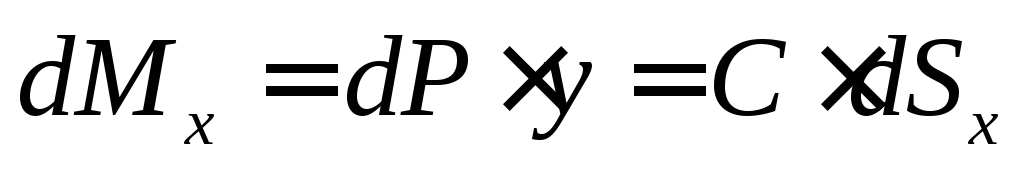 (1.5)
(1.5)
Суммируя эти моменты, получим :
 (1.6)
(1.6)
Из теоретической механики известно, что равнодействующий момент можно вычислить через равнодействующую силу Р следующим образом:
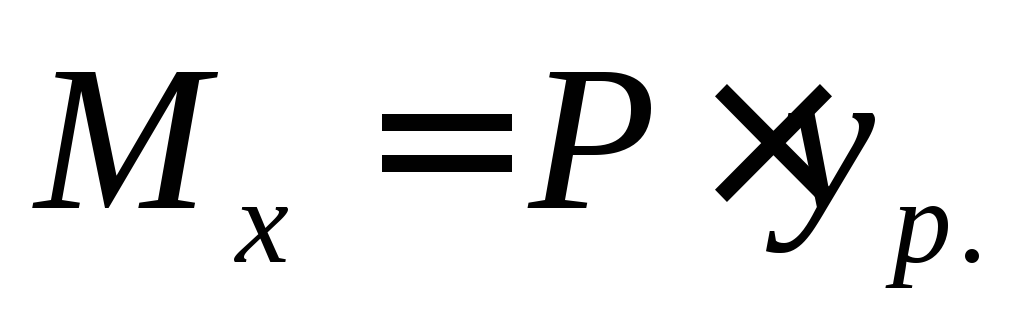
г де
де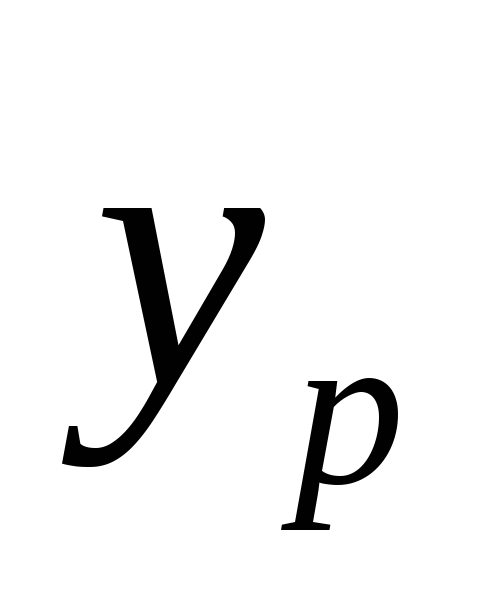 —
координата точки приложения силыР. Но равнодействующая силы тяжести фигуры
приложена в центре тяжести, значит:
—
координата точки приложения силыР. Но равнодействующая силы тяжести фигуры
приложена в центре тяжести, значит:
(1.7)
Подставляя слева (1.4) получим:
Т аким
образом:
аким
образом:
(1.8)
Аналогично вычисляется статический момент относительно оси у:

(1.9)
Отсюда вытекают
формулы для вычисления координат центра
тяжести фигуры: 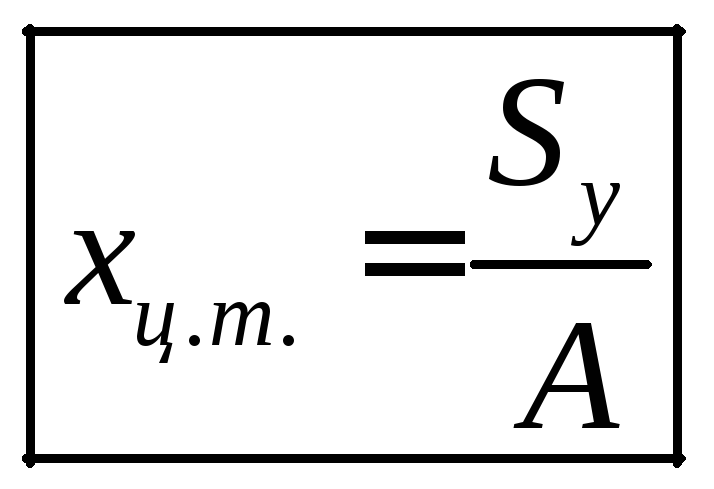
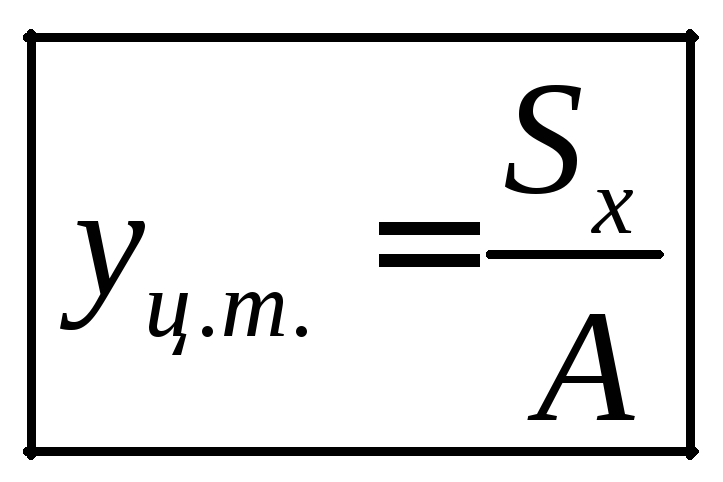 (1.10)
(1.10)
1.2. Моменты второго порядка
Осевой момент инерции
Рассмотрим бесконечно малую площадь dA (см. рис.1.3).
Осевым моментом инерции dJx относительно оси х бесконечно малой площади dA называется произведение dA на квадрат плеча, то есть на у2:


Рис. 1.3
Если фигура имеет конечную площадь А, то как обычно, разбиваем ее на бесконечно малые площади и для каждой из них вычисляем dJx. Просуммировав их, найдем осевой момент инерции всей фигуры:
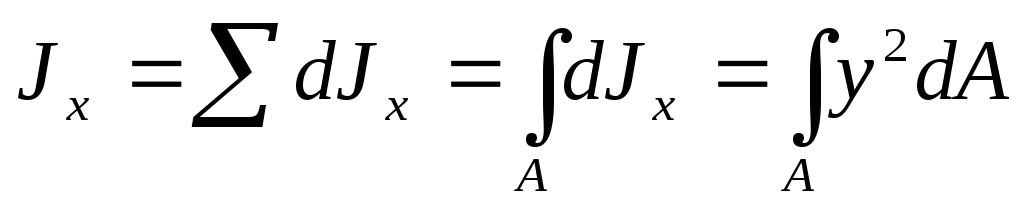 (1.11)
(1.11)
Аналогично вводится осевой момент инерции относительно оси у:
 (1.12)
(1.12)
Из (1.11), (1.12) видно,
что осевые моменты инерции 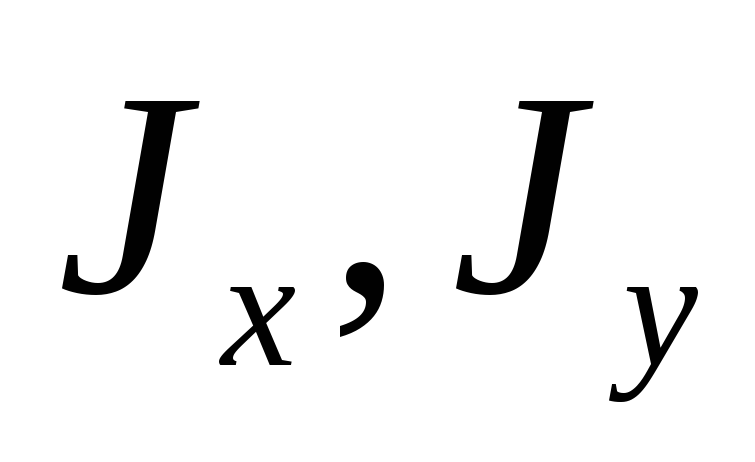 никогда не равны нулю и не бывают меньше
нуля, они всегда положительны.
никогда не равны нулю и не бывают меньше
нуля, они всегда положительны.
Задачи по теме «Момент инерции. Закон сохранения момента
Приложение 1
Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса».
На барабан радиусом R=0,5 м и с горизонтальной осью вращения намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите момент инерции барабана, если известно, что его угловое ускорение равно
 .
Тернием пренебречь.
.
Тернием пренебречь.
Дано: Решение:
m = 10
кг 
R = 0, 5 м

J = ?
Вращение барабана происходит под
действием силы F. Из второго закона Ньютона

ох: ma = mg – F
F = m (g — a)
 =
∆ω/∆t = ∆υ/R∆t = a/R → a = εR
=
∆ω/∆t = ∆υ/R∆t = a/R → a = εR
F = m (g – ε r)
M = Jε – момент силы через момент инерции для вращающегося тела.
M = Fd = FR – момент силы вращающей барабан.
По закону сохранения момента сил
Jε = FR
Jε = m (g – εR) R
J = (m ( g – εR) R)/ ε = 22,5 (кг м²)
Ответ: 22, 5 кг м2
К ободу однородного диска радиусом R=0,2м массой m=1,2 кг приложена постоянная сила 100 Н, при вращении на диск действует момент силы трения, равный 5 нм. Чему равно угловое ускорение диска?
Дано: Решение:
R = 0, 2 м Из оснавного управления динамики вращательного
m = 1, 2 кг движения M=Jε
F = 100 Н Сила действующая на обод F`= F — Fтр. Из M = 5 нм момента силы трения Fтр = M\R = 25 Н
ε = ? Момент силы F`- M=F`R по закону сохранения
момента сил.
Jε = F`R
J = mR² –момент инерции обруча
mR²ε = (F — Fтр.)R

Ответ: ε = 312, 5 с-2.
Шарик, диаметр которого равен 6 см, катится по полу и останавливается через t = 2с, пройдя расстояние S = 70 см. Определите коэффициент трения качения, считая его постоянным.
Дано: Решение:
d = 0, 06 м М=εJ — основное уравнение вращательного движения.
t = 2c J= 0,4mr2 — момент инерции шара.
S=
0,7м. 
μ = ?
M= 0,4 m r2 a/ r= 0,4 a m r
Момент силы трения M = Fтр r
Fтр = μN= μmg
M = μmgr
По закону сохранения момента сил
μmgr=0,4amr
μ = 0,4a/g
S= at2/2  a=2S/t2 =
1,4/4 = 0,35 м/с2
a=2S/t2 =
1,4/4 = 0,35 м/с2
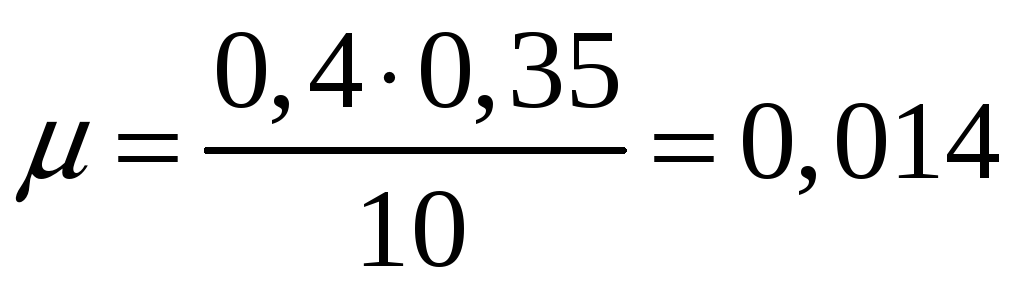
Ответ: 0,014.
Во сколько раз уменьшится угловая скорость вращения человека, если момент инерции изменится от 1 кг м² до 1,25 кг м²?
Дано: Решение:
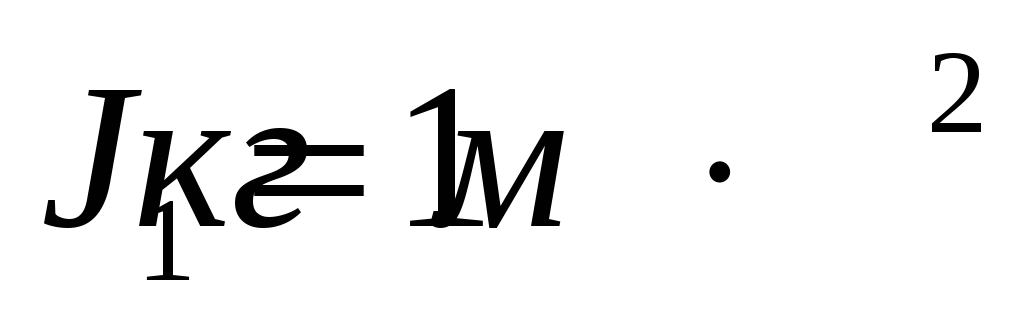 L1 = J1ω1 — момент
импульса в первом состоянии.
L1 = J1ω1 — момент
импульса в первом состоянии.
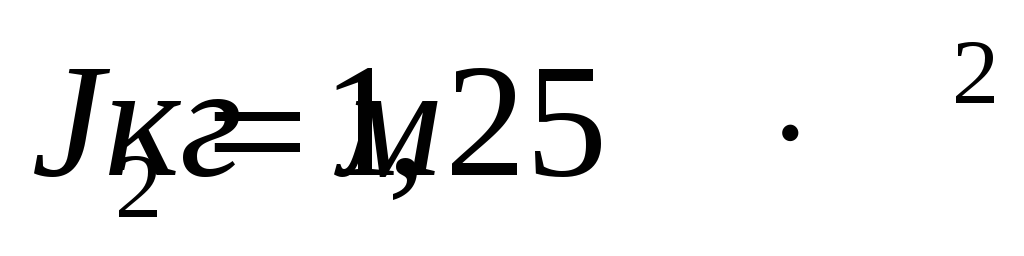 L2 = J2ω2 — момент
импульса во втором состоянии.
L2 = J2ω2 — момент
импульса во втором состоянии.
 L1 = L2 — закон сохранения момента импульса.
L1 = L2 — закон сохранения момента импульса.
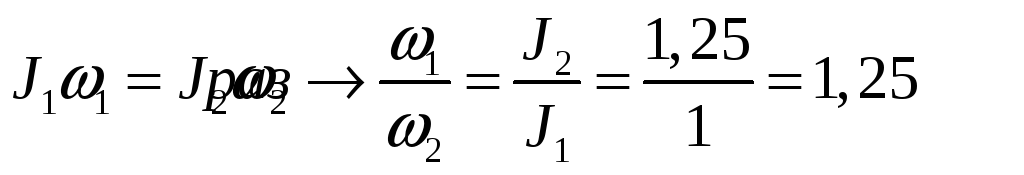
Ответ: 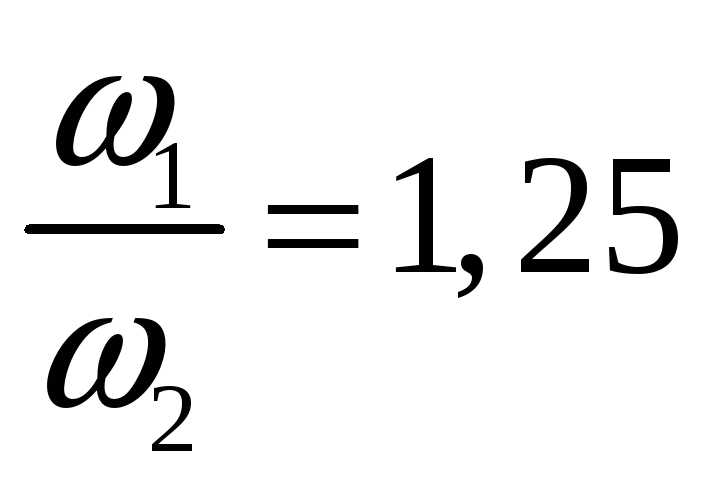
Найти момент импульса Земного шара М3 = 6·1024 кг, R3 = 6,4·10³ км, если точки поверхности Земли вращаются со скоростью 36 км/ ч.
Дано: Решение:
M3 = 6·1024 кг L = Jω J= 0,4 M3R3²- момент инерции шара.
R3 = 6,4·10 6 м ω = υ/ R
υ = 10 м\с L = 0,4 M3 υ R3= 15,36·10³º кг м²/с.
L = ?
Ответ: L = 15, 36·10³º кг м²/с
Комета Галлея движется вокруг солнца по вытянутому эллипсу. Наибольшее удаление от солнца равно 35,2 а. е., а наименьшее удаление — 0,6 а.е.. Найти отношение максимальной скорости кометы к минимальной.
Дано: Решение:
R1 = 35, 2 а. е.  момент
импульса при наибольшем
момент
импульса при наибольшем
R2 = 0, 6 а. е. удалении.
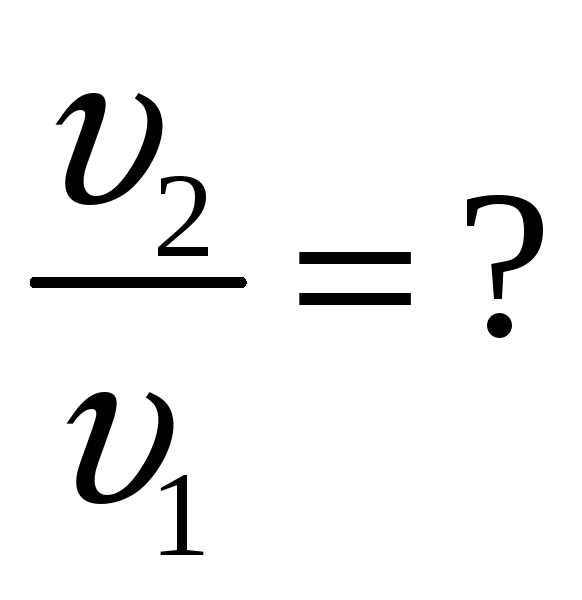
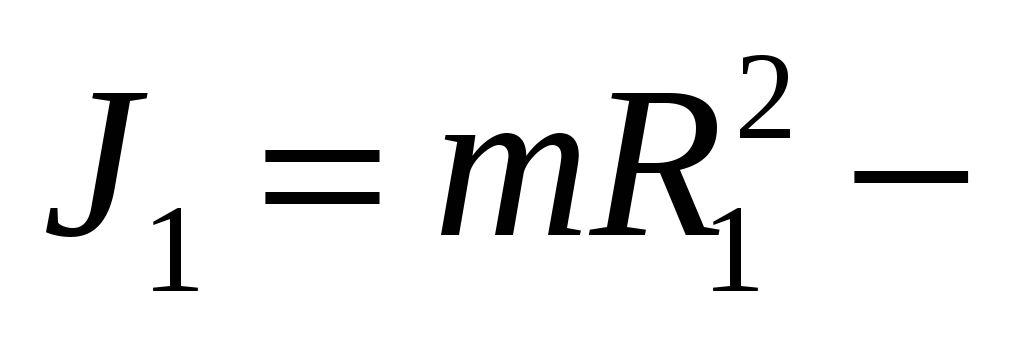 момент
инерции кометы при наибольшем
момент
инерции кометы при наибольшем
удалении.

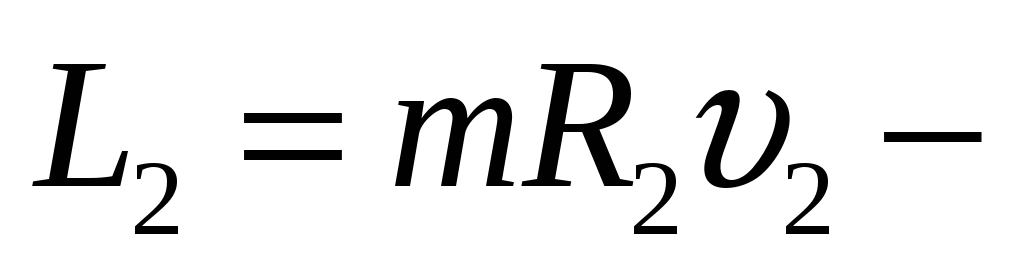 момент
импульса кометы при
момент
импульса кометы при
минимальном удалении.
L1 = L2 – закон сохранения момента импульса.
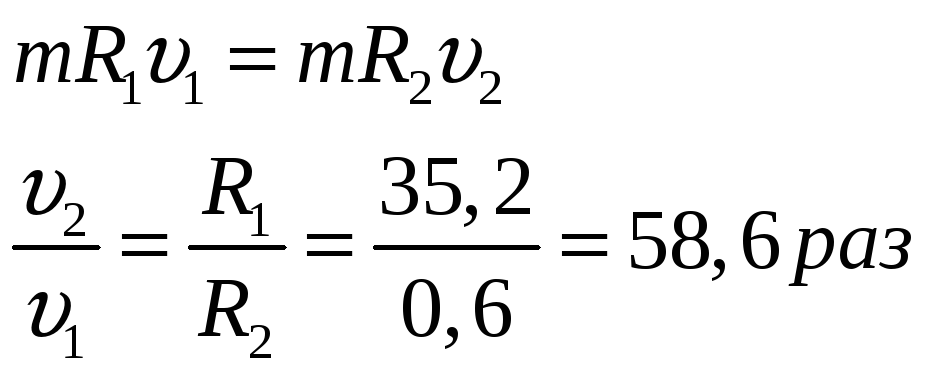
Ответ: 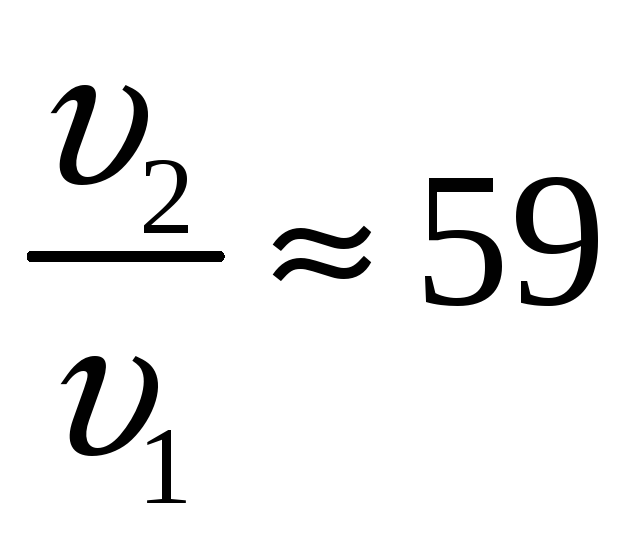
Человек стоит на вращающейся с некоторой угловой скоростью платформе. В вытянутых в сторону руках он держит по гире, массой каждой из них m = 5 кг. Расстояние от гирь до оси вращения R1=0,71м. Во сколько раз изменится частота вращения человека, если он прижмет к себе руки так, что расстояние от оси вращения до гири станет R2= 0,2 м. Момент инерции человека считайте в обоих случаях равным J0 = 1 кг м.²
Дано: Решение:
m = 5 кг Момент импульса в первом случае
R1=0,71м 
R2=
0,2 м 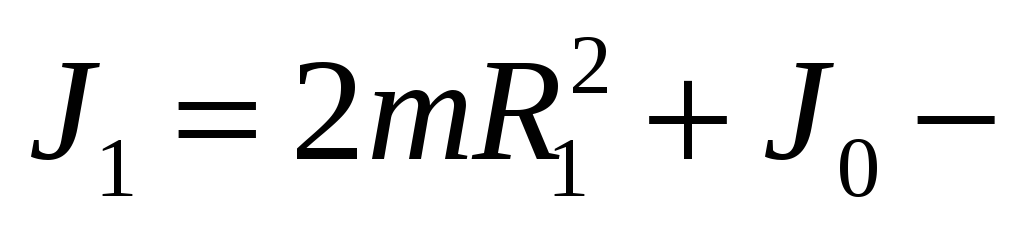 момент
инерции в первом случае.
момент
инерции в первом случае.
J0 = 1 кг м² 

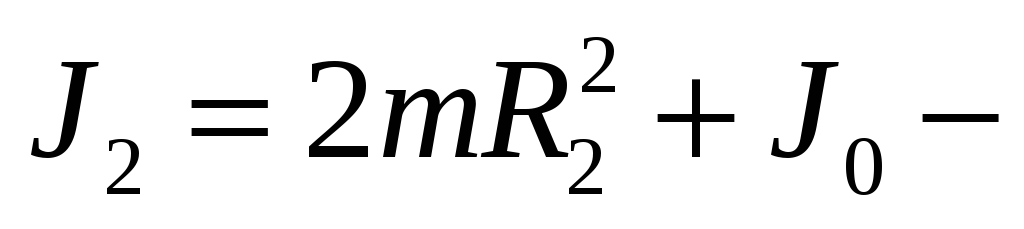 момент
инерции во втором случае.
момент
инерции во втором случае.
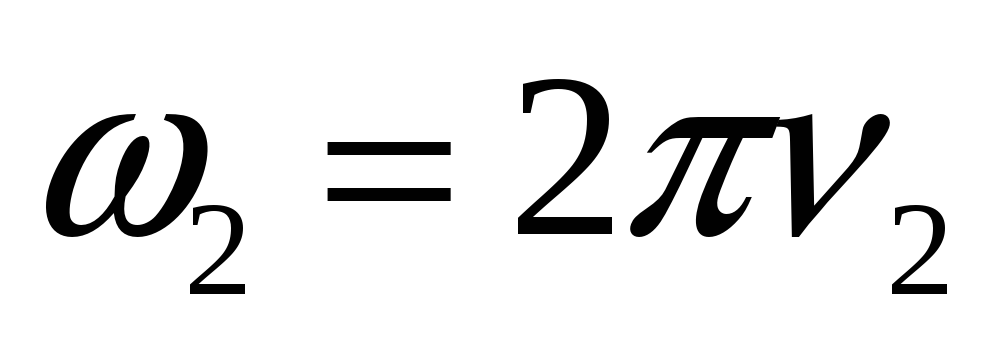
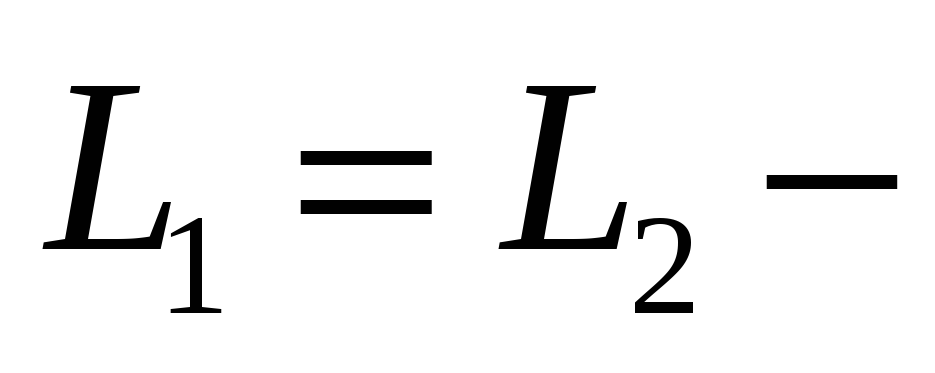 закон
сохранения момента импульса.
закон
сохранения момента импульса.
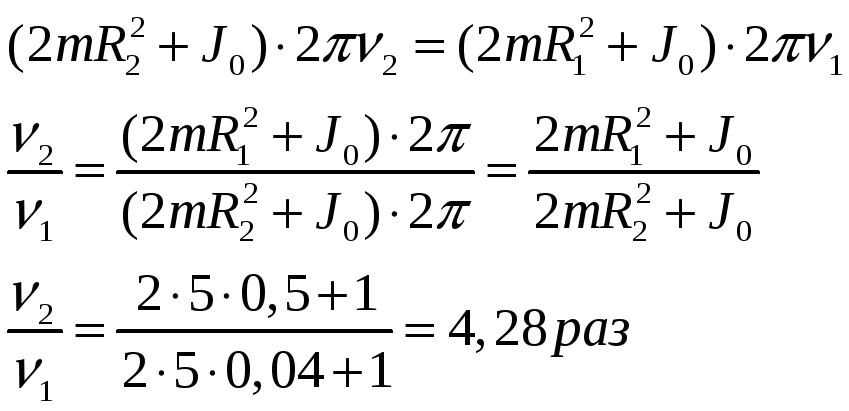
Ответ: 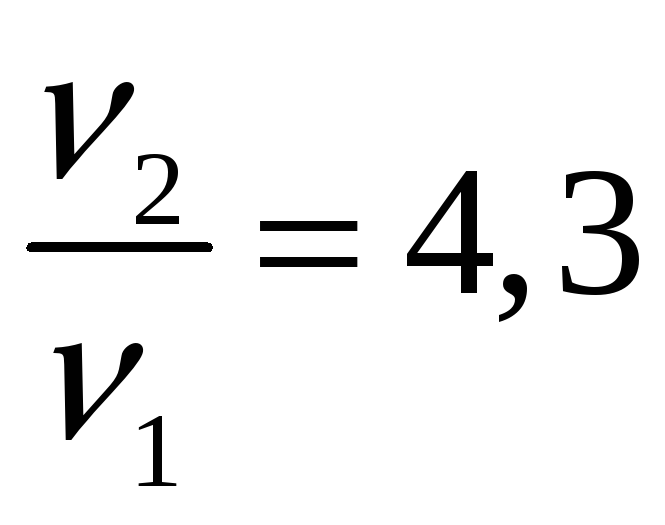
Человек массой m1 = 60 кг находится на неподвижной круглой платформе радиусом R2= 10м и массой m2 = 120 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек станет двигаться по окружности радиусом R1= 5м с линейной скоростью υ1= 2 м/с относительно платформы.
Дано: Решение:
m1 = 60 кг  момент
импульса человека;
момент
импульса человека;
R2=
10м 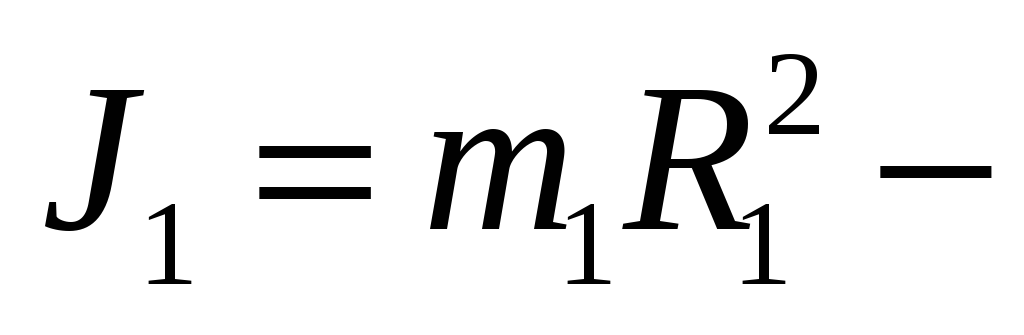 момент
инерции человека.
момент
инерции человека.
m2 = 120 кг 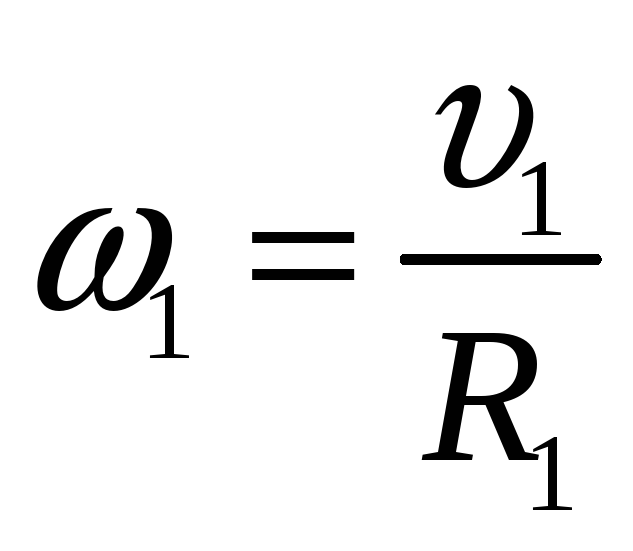
R1=
5м 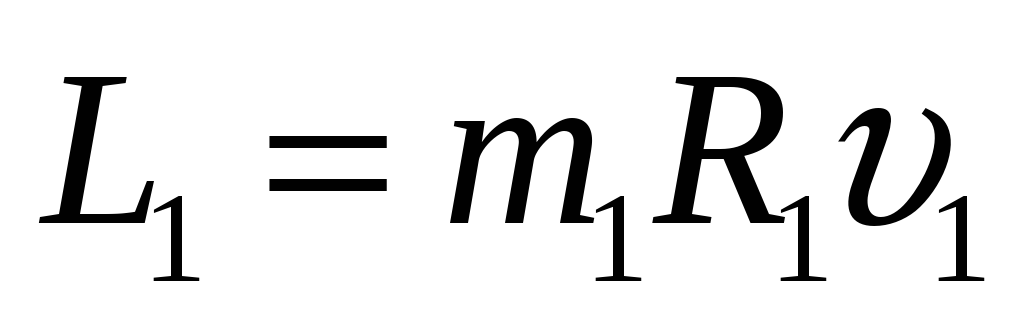
υ1=
2 м/с 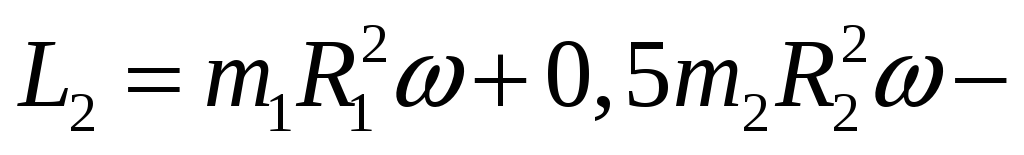 момент
импульса платформы
момент
импульса платформы
ω = ? и человека.
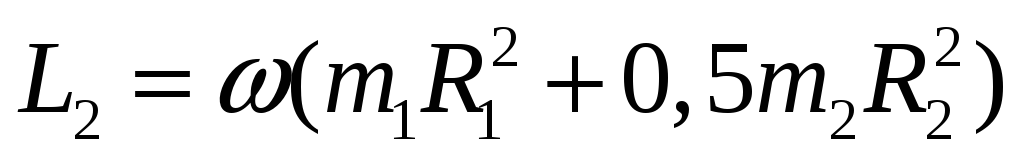
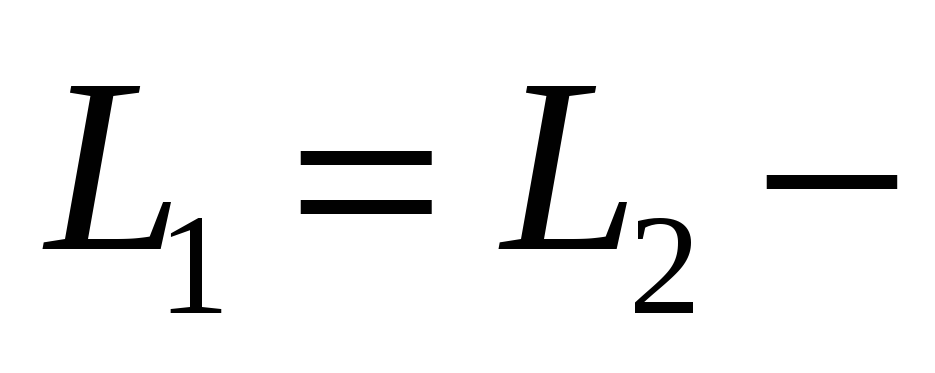 закон
сохранения импульса.
закон
сохранения импульса.
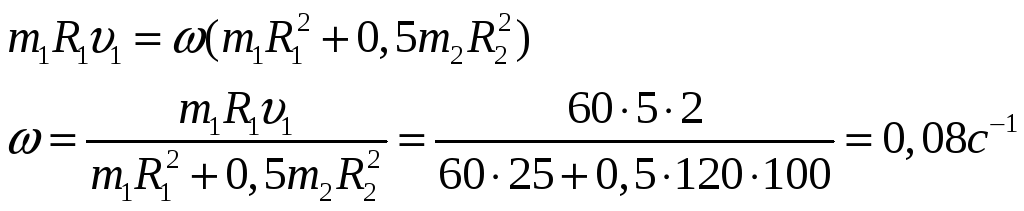
Ответ: 0, 08 с-1
Считая Солнце однородным шаром, оцените минимальный радиус и период вращения вокруг своей оси пульсара, который мог бы образоваться после сжатия Солнца под действием силы тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца Rc= 7·108 м, период вращения вокруг оси Тс = 2,2·106 с. Масса Солнца Мс = 2·10³º кг.
Дано: Решение:
Rc= 7·108 м Момент импульса Солнца
Тс = 2,2·106 с 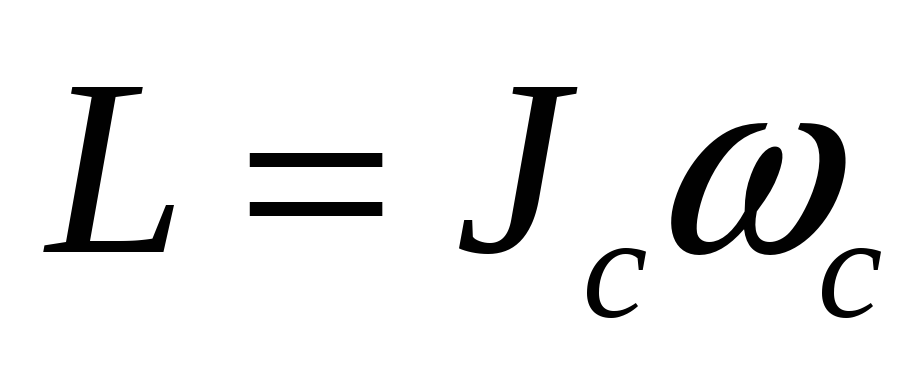
Мс = 2·10³º
кг  момент
инерции Солнца
момент
инерции Солнца
Rп = ? Тп = ? 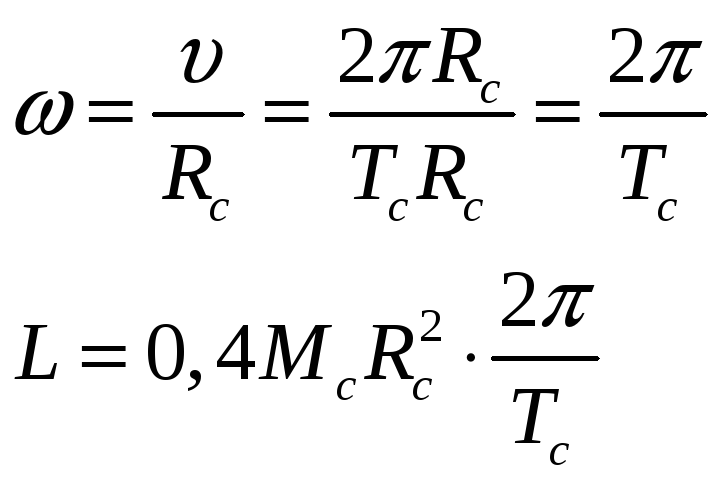
Момент импульса образовавшегося пульсара
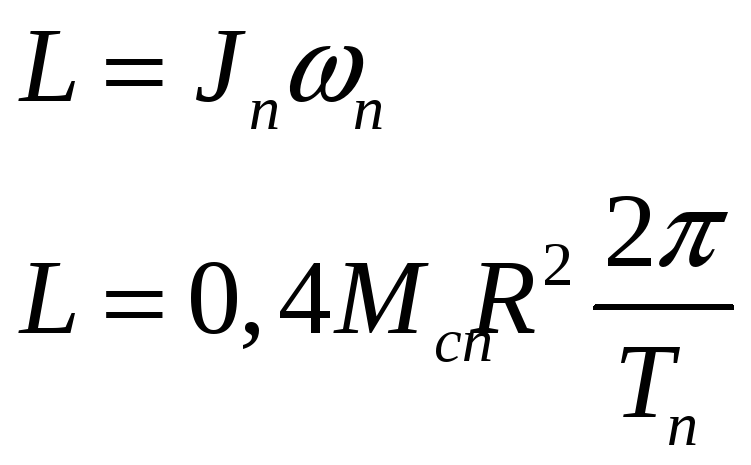
По закону сохранения импульса
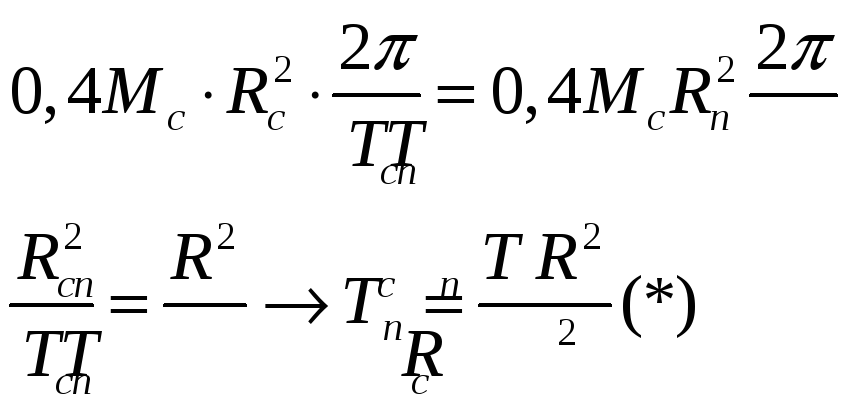
Вращение пульсара происходит под действием силы тяготения.
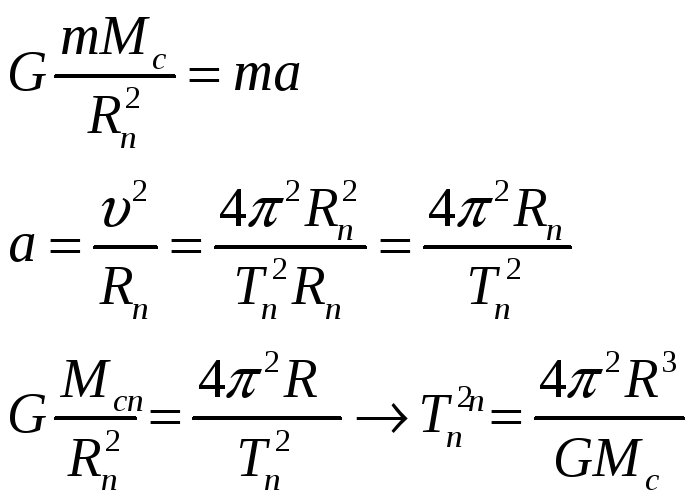
Для удобства расчета (*) возведем в квадрат
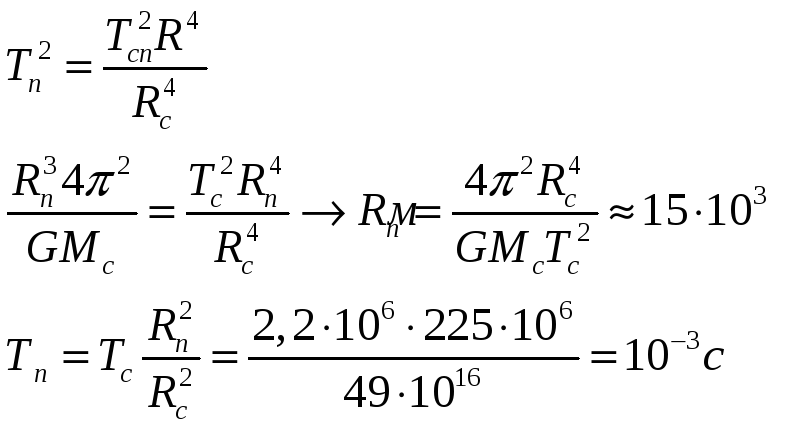
Ответ: Rп =
Tп = 10-3 с
Презентация на тему: Лекция 4 Динамика вращательного
движения
• Момент инерции. Теорема Штейнера
• Главные оси инерции
• Орбитальный и осевой момент импульса
• Момент силы
• Основное уравнение динамики вращательного движения
Момент инерции
•Момент инерции — мера инертности тела при вращательном движении относительно какой- либо оси. В динамике вращательного движения момент инерции играет ту же роль, что и масса тела в динамике поступательного движения.
•Но есть и принципиальная разница. Для разных осей вращения моменты инерции одного и того же тела различны.

Момент инерции МТ,
системы МТ, твердого
тела
• Момент инерции МТ Ii mi ri 2
• Момент инерции системы МТ
I mi ri | 2 | |
• Момент инерции АТТ | i | m |
| i | |
I |
| r 2 dm r 2 dV , |
|
| |
| ( m ) | V |

Вычисление момента инерции тонкого диска (цилиндра) относительно геометрической оси
Разобьем цилиндр на кольцевые слои
радиуса r и толщины dr. Масса
такого слоя dm
dm dV
dI r 2 dV r 2 2 rhdr
R
I dI ( 2 h)r3dr
|
| 0 |
|
|
|
| |
2 h | R 4 |
| 1 | R 2 h R 2 | 1 | mR 2 | |
4 | 2 | 2 | |||||
|
|
|
|
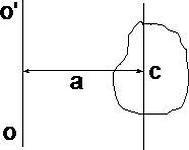
Теорема Штейнера
• Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат
расстояния между2 телами
I Ic ma
Главные оси инерции. Главные моменты инерции
•Главные оси инерции – это три взаимно перпендикулярные оси координат, проходящие через центр масс и совпадающие с осями симметрии.
•Моменты инерции относительно этих осей называются главными моментами инерции тела: Ix, Iy, Iz. Эти моменты инерции в общем случае имеют минимальное,
максимальное и промежуточное значение и непосредственно связаны с устойчивостью вращения.


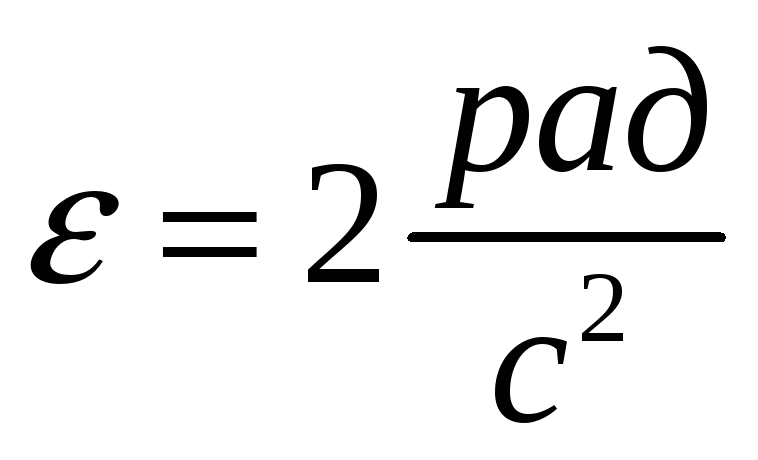 .
Тернием пренебречь.
.
Тернием пренебречь.