Молекула водорода | это… Что такое Молекула водорода?

Моле́кула водоро́да — простейшая молекула, состоящая из двух атомов водорода. В её состав входят два ядра атомов водорода и два электрона. Вследствие взаимодействия между электронами и ядрами образуется ковалентная химическая связь. Кроме основной изотопной модификации H₂, существуют разновидности, в которых один или оба атома протия заменены другими изотопами водорода  — дейтерием или тритием: HD, HT, D₂, DT, T₂. Симметричность или несимметричность молекулы имеет значение при её вращении.

Содержание 1 Модели молекулы водорода 2 Гамильтониан 3 Волновые функции 4 Энергия электронных состояний 5 Зависимость энергии основного состояния от расстояния между ядрами 5.1 Ковалентная связь 5.2 Насыщение ковалентной связи 6 Движение ядер в молекуле водорода 6.1 Вращение 6. 2 Колебания атомов 7 Пара- и ортоводород 8 Характеристики молекулы водорода 9 См. также 10 Примечания 11 Литература

Модели молекулы водорода

Рис.1.Модель водорода по Бору и осевая проекция электронного кольца

Н.Бор ещё в 1913 году дал описание модели молекулы водорода^[1]. Согласно Бору, два внешних электрона, образующих молекулу, вращаются по одной и той же орбите вокруг линии, проходящей через ядра обоих атомов, и удерживают последние на определённом расстоянии друг от друга (рис.1). Боровская модель химической связи давала чёткую картину образования молекулярного водорода — динамическое равновесие системы, содержащей два протона, удерживающихся на определённом расстоянии друг от друга (d), притяжением кольца из двух электронов. При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.

Также как и боровская модель атома, боровская модель молекулы водорода не отражала и не могла отражать волновую природу электрона и статистическую интерпретацию волновой функции. Здесь уместно дополнить боровскую модель молекулы водорода достижениями квантовой механики, аналогично боровской модели атома. В этом случае гипотетическое кольцо электронов в модели молекулы водорода трансформируется в геометрическое место расположения плотности вероятности нахождения связывающих электронов. Электронную пару следует представлять электронным облаком в форме кольца, баранки, тора. При этом предполагается, что электроны в торе удалены друг от друга на максимально возможное расстояние, а электронная плотность в молекуле водорода имеет минимум — «кулоновскую дырку» на линии, соединяющей ядра молекулы водорода. Наиболее вероятный радиус электронного тора (r

e) определяется боровским радиусом a₀ и межъядерным расстоянием (d)

r_e² = a₀² — (d/2)²; r_e = 0,377 Å.

Рис.2.Контурная карта электронной плотности для молекулы водорода^[2]

В теории молекулярных орбиталей, разработанной в 1927—1932 г.г. Ф.Хундом, Р.Малликеном и др., модель молекулы водорода описывали контурными картами электронной плотности (рис.2).

Карта строится как разность между электронной плотностью молекулы и несвязанных атомов. Сплошные линии контурной карты отражают области увеличения электронной плотности (в единицах заряда электрона). Пунктирные — области её уменьшения в молекуле по сравнению с электронной плотностью несвязанных атомов водорода, сближенных на равновесное расстояние.

[2]

Поскольку в теории молекулярных орбиталей учитывается лишь фермиевская корреляция электронов, поэтому электронная плотность в молекуле водорода сконцентрирована на линии, соединяющей ядра молекулы (см. рис.2).

Рис.3.Модель молекулы водорода в теории валентных связей

Квантово-механическую теорию ковалентной связи в молекуле водорода разработали в 1927 году Вальтер Гайтлер и Фриц Лондон. Выполненный ими расчёт волновых функций явился основой теории валентных связей. В этой теории модель молекулы водорода описывали перекрыванием атомных орбиталей атомов водорода (1S типа). Схема перекрывания электронных облаков, образующих сигма-связь молекулы водорода, совпадает с линией соединения атомных центров молекулы (рис.3).

Расчёт молекулы водорода в основном сводится к определению интеграла перекрытия атомных орбиталей.

Гамильтониан

Гамильтониан молекулы водорода H₂ записывается в виде

,

где M — масса протона, m — масса электрона,  — координаты ядер,  — координаты электронов.

В адиабатическом приближении задача нахождения энергетических состояний молекулы водорода разбивается на два этапа. На первом этапе рассматривается только электронная подсистема, а ядра считаются зафиксированными в точках и .

Гамильтониан электронной подсистемы имеет вид

,

Гамильтониан молекулы водорода симметричен относительно переменных и , то есть не изменяется при смене нумерации электронов. Кроме того, он не зависит от спиновых переменных.

Волновые функции

Схематическое изображение симметричной волновой функции молекулы водорода и образования ковалентной связи

Схематическое изображение антисимметричной волновой функции молекулы водорода

Исходя из принципа тождественности частиц и учитывая то, что электроны являются фермионами, волновая функция молекулы водорода должна быть антисимметричной относительно перестановки электронов. Независимость гамильтониана от спиновых переменных позволяет выбрать её в виде произведения двух функций, одна из которых зависит только от координат и называется координатной волновой функцией, а вторая зависит только от спинов и называется спиновой функцией.

Существуют два возможных типа спиновых функций для двух электронов: с параллельными спинами и с антипараллельными спинами.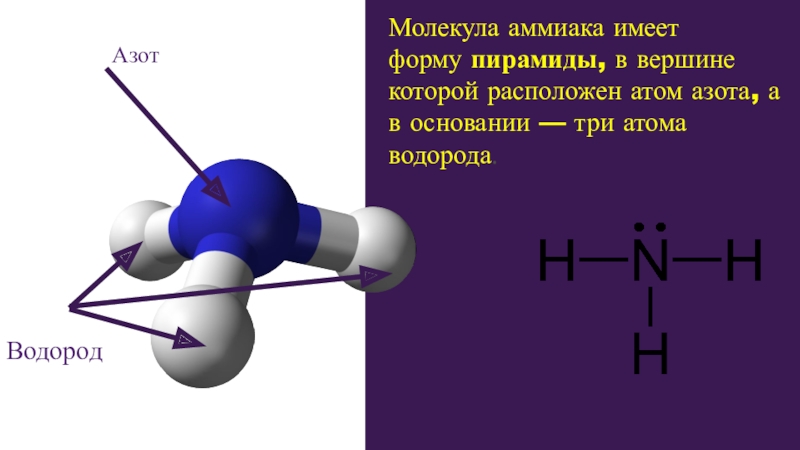

Функции с параллельными спинами симметричны относительно перестановки электронов и образуют триплетные состояния, в которых суммарный спин равен единице. Функции с антипараллельными спинами образуют синглетные состояния с нулевым суммарным спином (см. Мультиплетность, Состояние (квантовая механика)). Они антисимметричны относительно перестановки электронов.

Поскольку волновая функция электрона должна быть антисимметричной относительно перестановки, она может быть произведением либо

• симметричной координатной функции на антисимметричную спиновую функцию, либо
• антисимметричной координатной функции на симметричную спиновую функцию.

Симметричную и антисимметричную координатные функции основного состояния в нулевом приближении теории возмущений можно построить исходя из волновых функций основного состояния атома водорода .

Первый член каждой из приведенных волновых функций отвечает локализации электрона, пронумерованного индексом 1 на атоме с индексом 1 и электрона, пронумерованного индексом 2 на атоме с индексом 2. Второй член отвечает ситуации, когда первый электрон принадлежит второму атому, а второй — первому. При смене нумерации электронов первая (симметричная) функция не меняется, вторая (антисимметричная) — меняет знак.

Энергия электронных состояний

Энергия электронных состояний находится усреднением гамильтониана на волновых функциях

.

Для двух возможных волновых функций основного состояния она приобретает вид

,

где  — расстояние между ядрами,  — значение энергии основного состояния атома водорода,  — интеграл перекрытия, который определяется выражением

,

 — кулоновский интеграл, определяемый как

,

 — обменный интерграл, равный

.

Энергия молекулы водорода состоит из удвоенной энергии атома водорода, энергии кулоновского отталкивания между ядрами и членов, определяющих взаимодействие электронов между собой и с другим ядром.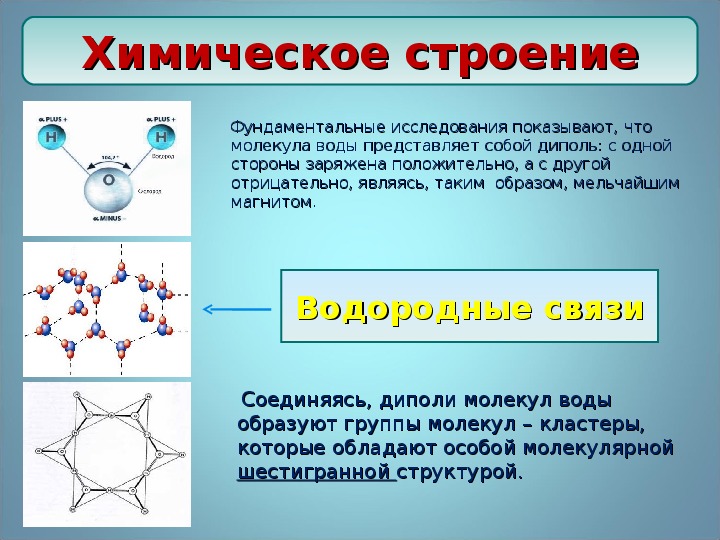 В зависимости от спинового состояния в формуле для следует выбирать знак «+» или знак «-». Знак «+» отвечает синглетному состоянию, знак «-» — триплетному.

Величина  — это средняя энергия кулоновского взаимодействия между двумя электронами и электронов с «чужим ядром». Величина определяет вклад в энергию обменного взаимодействия, которая не имеет аналога в классической механике. Именно этот член определяет существенное различие между синглетными и триплетными состояниями.

Зависимость энергии основного состояния от расстояния между ядрами

Ковалентная связь

Энергия взаимодействия атомов в молекуле водорода для синглетного(сплошная линия) и триплетного (пунктирная линия) состояний

Обменный интеграл для молеклы водорода в определённом диапазоне расстояний между атомами отрицательный. Вследствие этого, для синглетных состояний он обеспечивает дополнительное притягивание между ядрами атомов, а для триплетных — дополнительное отталкивание. Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».

Насыщение ковалентной связи

Для параллельных спинов, то есть для триплетного состояния, дополнительный положительный вклад в энергию приводит к тому, что атому отталкиваются на любом расстоянии. Этим объясняется насыщение ковалентной связи. Молекула водорода может состоять только из двух атомов. Третий атом водорода не может образовать связь с молекулой потому, что его спин непременно будет параллельным одному из спинов электронов в составе молекулы. Параллельность спинов приводит к отталкиванию между ядрами на любом расстоянии.

Необходимо отметить, что на больших расстояниях между атомами они притягиваются в любых состояниях благодаря Ван-дер-Ваальсовому взаимодействию, которое, однако, намного слабее ковалентной связи. Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.

Движение ядер в молекуле водорода

Гамильтониан, описывающий относительное движение двух ядер в молекуле водорода имеет вид

,

где  — приведённая масса двух ядер,  — энергия синглетного электронного состояния, зависящая от расстояния между ядрами (определена в предыдущем разделе),  — оператор углового момента, описывающий вращение молекулы.

Вращение

Оператор углового момента коммутирует с гамильтонианом, поэтому собственные функции гамильтониана можно выбрать общими с собственными функциями оператора углового момента, то есть сферические гармоники:

.

Вклад вращения в энергию молекулы равен

.

Этот вклад мал, потому, что массы ядер намного больше, чем массы электронов. Он зависит от расстояния между ядрами R. При колебаниях ядер это расстояние меняется, поэтому вращательное движение, строго говоря, невозможно отделить от колебательного. Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.

Вращательные уровни вырождены относительно магнитного квантового числа m_l. Кратность вырождения 2l+1.

Колебания атомов

Вблизи минимума функцию можно разложить в ряд Тейлора, ограничившись только квадратичным членом.

,

где

Таким образом, задача об энергетических состояниях колебания ядер сводится к задаче квантового гармонического осциллятора. Следовательно, для низших колебательных и вращательных уровней энергия молекулы водорода равна

,

где  — колебательное квантовое число.

Низшая энергия колебания отвечает нулевым колебаниям.

При больших значениях квантовых чисел n и l колебательное и вращательное движение разделить невозможно.

Таким образом, энергию молекулы при малых квантовых числах можно записать в виде трёх слагаемых — электронного, колебательного и вращательного:

Малым параметром задачи является отношение массы электрона к массе протона.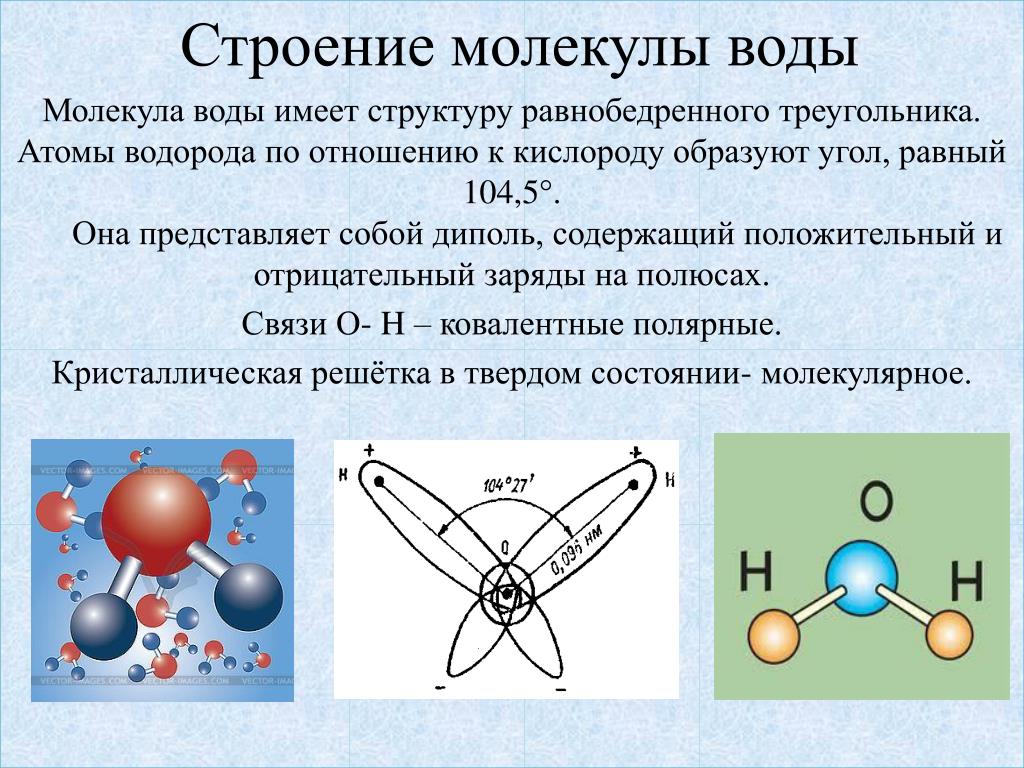 Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому

.

Следовательно, электронный уровень расщепляется на несколько колебательных, каждый из которых, в свою очередь, расщепляется на вращательные. Поскольку энергии вращательных уровней близки, то в оптических спектрах они сливаются в полосы — образуется полосатый спектр, который наблюдается для молекулы HD. Для симметричной молекулы H₂ переходы между орбитальными и колебательными уровнями запрещены правилами отбора, поэтому молекулярный протий не поглощает в инфракрасной области.

Пара- и ортоводород

Схематическое изображене спиновых изомеров водорода

Ядра атомов водорода, входящие в состав молекулы, являются протонами — фермионами со спином 1/2. По правилам сложения спинов ядерный спин молекулы может быть 0 или 1. Молекулы водорода с суммарным ядерным спином 0 называют параводородом, а молекулы с суммарным ядерным спином 1 и тремя возможными проекциями (−1, 0, 1) называют ортоводородом.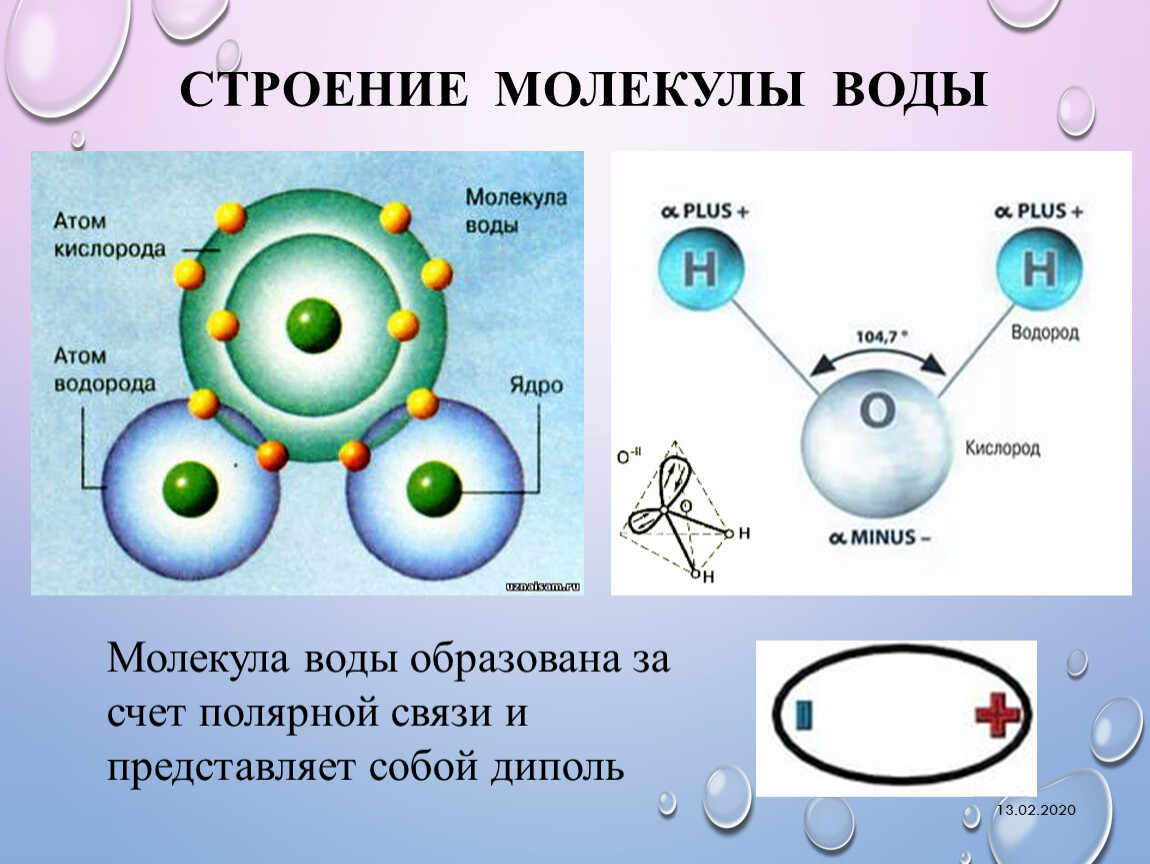 В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.

Характеристики молекулы водорода

Межъядерные расстояния и энергии диссоциации молекул водорода, его изотопов и молекулярного иона водорода^[3]

Молекула	Межъядерное расстояние,Å	Энергия диссоциации, Эв
H2	0,7416	4,477
HD	0,7414	4,512
D2	0,7416	4,555
DT	0,7416	4,570
T2	0,7416	4,588
HT	0,7416	4,524
H2+	1,06	2,648

Константы реакции диссоциации молекулярного водорода (K_p) и степень превращения (α) в зависимости от абсолютной температуры^[4]:

T, к	2000	3000	4000	5000	6000	8000
Кр	2,62 · 10-6	2,47 · 10-2	2,52	4,09 · 10	2,62 · 102	2,70 · 103
α	8,10 · 10-4	7,83 · 10-2	0,621	0,954	0,992	0,999

См.

также

• Молекулярный ион водорода
• Рекомбинация (химия)
• Боровская модель химической связи
• Кулоновская электронная корреляция
• Статистическая интерпретация волновой функции
• Теория молекулярных орбиталей
• Теория валентных связей

Примечания

1. ↑ Бор Н. Избранные научные труды (статьи 1909-1925 г.г). — М.: Наука, 1973. — Т. 1. — С. 133. — 584 с.
2. ↑ ^{1 2} Химический энциклопедический словарь / гл. редактор И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — С. 646. — 792 с.
3. ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1962. — Т. 1. — С. 338. — 1072 с.
4. ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1964. — Т. 3. — С. 24. — 1008 с.

Литература

• Білий М. У. Атомна фізика. — Київ: Вища школа, 1973.  (укр. )
• Федорченко А. М. Теоретична фізика. Квантова механіка, термодинаміка і статистична фізика. Т.2. — Київ: Вища школа, 1993.
• Юхновський І. Р. Основи квантової механіки. — Київ: Либідь, 2002.
• Ландау Л. Д., Лившиц Е. М. Теоретическая физика. т. ІІІ. Квантовая механика. Нерелятивистская теория. — М.: Наука, 1974.

Модель молекулы водорода, химические связи в молекулах разного типа

Home  / Учебник ОБЩАЯ ХИМИЯ / Глава 3. Молекула / Связь в молекуле водорода

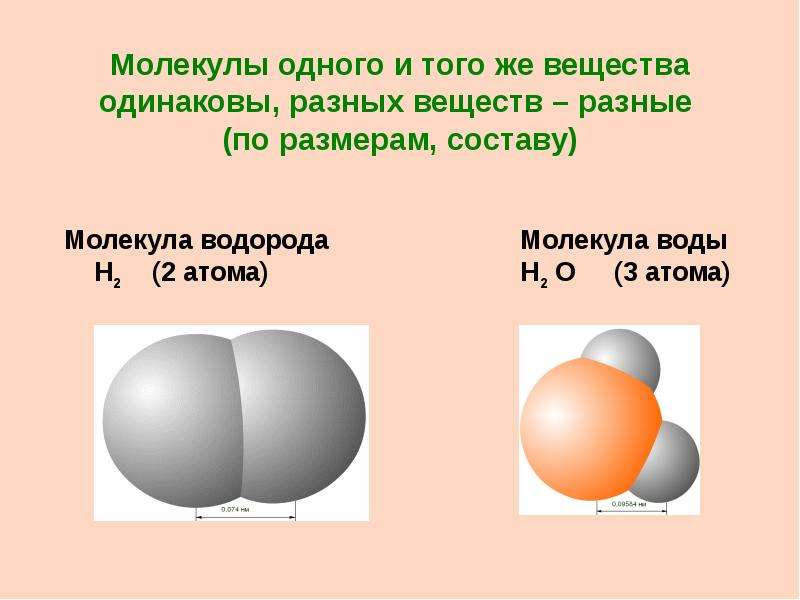
Молекула водорода — это простейшая молекула, которая образуется из двух атомов водорода. Атомы, составляющие молекулу водорода, абсолютно одинаковы, поэтому связывающая пара электронов должна находиться не только на внешних оболочках обоих связываемых атомов, но также на одинаковом расстоянии от ядер. Таким образом, для электронов остается  только одно место — между ядрами, на равном расстоянии от них.

До того, как образовалась связь в молекуле водорода  (т.е. у разделенных атомов), электроны вращались вокруг своих ядер, теперь электроны вращаются посередине между двумя ядрами водорода. По схеме химической связи, в случае с молекулой водорода, связывающая пара электронов вращается в плоскости, перпендикулярной оси, связывающей ядра атомов. Центр вращения электронов находится на одинаковом расстоянии от связываемых ядер. Только так электроны могут одновременно перейти на внешние электронные оболочки обоих связываемых атомов.

Итак, молекулу водорода можно проиллюстрировать следующим образом: 

Рисунок 3.2. Модель химической связи в молекуле водорода

Молекула водорода состоит из 2 ядер атома водорода, расположенных на расстоянии около 0.7Å друг от друга. Два электрона вращаются по круговой орбите в плоскости, перпендикулярной к оси, соединяющей ядра. Эта электронная пара сближает ядра за счет электростатических сил и сил притяжения ядер к двум электронам, вращающимся между ними.   Центр круга, вокруг которого вращаются электроны в молекуле водорода, находится в середине оси, связывающей ядра водорода.

То есть, при образовании связи в молекуле водорода, электроны располагаются на равном расстоянии от связываемых ядер.

Связь, образуемая из разных атомов

Когда атомы одного вида связаны химически (такую же как связь в молекуле водорода  образуют атомы Na-Na, F-F, Cl-Cl и т.д.), связывающие электроны, как и в молекуле водорода, находятся на одинаковом расстоянии от связываемых ими ядер.  Когда химически связаны разные атомы, например, Na-Cl, то центр круга, в котором вращаются связывающие электроны, находится ближе к ядру атома хлора (Cl). То есть, связывающие электроны смещаются к тому атому, который сильнее притягивает электроны, и значит, к атому с более высоким значением энергии сродства.

Связывающие электроны располагаются примерно на одинаковом расстоянии от ядер, связываемых ими, как и несвязывающие электроны. То есть, когда связывающие электроны образуют химические связи, они переходят на внешние оболочки связываемых атомов. Электроны внутренней оболочки часто называют внутренними электронами (см. рис. 3.3).

Рисунок 3.3 Вращение электронов вокруг ядра атома Cl

Точки на кругах — это электроны. Круги меньшего размера — это остов атома. Помимо ядра, остов атома включает в себя все внутренние электронные оболочки, т.е. все электроны внутренних слоев вокруг ядра (эта область окрашена в коричневый цвет). Таким образом, у атома хлора (Cl) этот остов состоит из ядра с 17 протонами и 10 электронами (2 электрона в слое, ближайшем к ядру, и 8 электронов в следующем ближайшем слое). Эти внутренние электроны, подобно ядру атома, не принимают участия в химических трансформациях, поэтому, для удобства, на рисунке они показаны вместе с ядром.

Таким образом, остов хлора (Cl) несет на себе избыточный положительный заряд, равный 17-10 = 7 протонных единиц. Компенсируют этот положительный заряд семь электронов, расположенных на внешней оболочке и показанных на рисунке точками. Они называются валентными электронами, так как только эти электроны в атоме принимают участие в образовании химической связи и химических преобразованиях. 

При формировании молекулы хлора Cl₂, оба атома хлора (Cl) принимают участие в формировании связи и увеличивают количество электронов на своих внешних оболочках на 1; то есть, обе внешние оболочки содержат 8 электронов. При формировании молекулы NaCl, атом натрия (Na) содержит 2 электрона на внешней оболочке (1 предыдущий и 1 приобретенный), в то время как атом хлора (Cl) имеет 8 электронов.

Связь, образовавшаяся между такими атомами, — ковалентная связь. Соответственно, связь в молекуле водорода тоже ковалентная.

Строение молекулы. Химическая связь >>

Ковалентная связь >>

Модель молекулы водорода

Энергия молекулы водорода >>

Энергия иона водорода Н₂⁺ >>

Выводы >>

5.2 Молекула водорода

5.2 Молекула водорода

Квантовая механика для инженеров   © Леон ван Доммелен

Далее: 5. 3 Системы с двумя состояниями

---

Подразделы

---

5.2 Молекула водорода

В этом разделе используются те же приближения, что и для молекулярного водорода. главы 4.6 для изучения нейтрального H молекула водорода. В этой молекуле два электрона вращаются вокруг двух протоны. Выяснится, что в основном состоянии протоны делят два электрона, а не каждый из них назначается по одному. Это типично для ковалентных связей.

Конечно, доля — термин расплывчатый, но дискуссия покажет, что это на самом деле означает с точки зрения шестимерного волновая функция электрона.

5.2.1 Гамильтониан

Как и для молекулярного иона водорода из главы 4.6, для нейтральной молекулы приближение Борна-Оппенгеймера будет сделать так, чтобы протоны находились в заданных фиксированных точках. Итак, проблема упрощается до нахождения волновой функции двух электронов, , где и – позиции двух электронов 1 и 2. С точки зрения скалярных аргументов волна функция может быть записана далее как .

В гамильтониане, следуя ньютоновской аналогии, кинетическая и потенциальные операторы энергии просто добавляют:

(5.3)

В этом выражении лапласианы первых двух, кинетическая энергия, термины относятся к координатам положения двух электроны:

Следующие четыре слагаемых в гамильтониане (5.3) — это потенциалы притяжения между электронами и протонами, с , и будучи расстояниями между электронами 1 и 2 и левый, соответственно правый протон. Последний термин представляет собой отталкивающий потенциал между двумя электронами.

---

Ключевые моменты

Гамильтониан для 6-мерной волновой функции электрона был записан.

---

5.2.1 Контрольные вопросы

1.

Убедитесь, что потенциал отталкивания между электронами бесконечно велик, когда электроны находятся в одном и том же положении.

Примечание. Таким образом, вы можете подумать, что волновая функция должна быть равна нулю в точках шестимерного пространства, где . Некоторые авторы называют это кулоновской дырой ». Но правда в том, что в квантовой механике электроны размыты из-за неопределенности. Это приводит к тому, что электрон 1 «видит электрон 2 со всех сторон 90 076 , и наоборот, и поэтому они не сталкиваются с каким-либо необычно большим потенциалом, когда волновая функция отлична от нуля при . В общем, электронам просто не стоит беспокоиться о том, чтобы оставаться в стороне от одного и того же положения: это уменьшило бы их неопределенность в положении, увеличив их кинетическую энергию, требуемую неопределенностью.

Раствор хмола-а

2.

Обратите внимание, что член полной кинетической энергии просто кратен шестимерному оператору Лапласа. Он обрабатывает все декартовы координаты положения одинаково, независимо от того, в каком направлении или какой электрон это. Будет ли это по-прежнему иметь место, если в дело вовлечены другие частицы?

Раствор хмола-б

5.2.2 Начальное приближение к самому низкому энергетическому состоянию

Следующим шагом является определение приблизительного основного состояния для молекула водорода. Следуя тому же подходу, что и в главе 4.6 сначала предполагается, что протоны относительно далеко друг от друга. Одно очевидное приближенное решение состоит в том, что из двух нейтральных атомов, скажем тот, в котором электрон 1 находится вокруг левый протон в основном состоянии, а электрон 2 находится вокруг правого один.

Чтобы сформулировать волновую функцию для этого, используется сокращенное обозначение снова будет использоваться для волновой функции один электрон, находящийся в основном состоянии вокруг левого протона а для того, который находится в основном состоянии вокруг правая рука один:

где основное состояние атома водорода (4. 40), а и – положения левый и правый протоны.

Волновая функция, описывающая, что электрон 1 находится в земле состояние вокруг левого протона и электрона 2 вокруг правого будет быть аппроксимирован как произведение состояний одного электрона:

Взяв комбинированную волновую функцию как произведение одного электрона состояний действительно эквивалентно предположению, что два электрона являются независимыми. Действительно, для состояния продукта вероятность нахождение электрона 1 в положении и электрона 2 в является:

или словами:

Такие вероятности произведения характерны для статистически независимые величины. В качестве простого примера, шансы получить три при первом броске кости и пять при втором броске или 1 из 36. Выпадение тройки не влияют на шансы получить пятерку во втором броске.

---

Ключевые моменты

Когда протоны далеко друг от друга, приблизительное основное состояние два нейтральных атома.

Одноэлектронные волновые функции для этого случая и .

Полная волновая функция для этого случая , предполагая, что электрон 1 находится вокруг левого протона, а электрон 2 вокруг правого один.

---

5.2.2 Контрольные вопросы

1.

Если электрон 2 не влияет на то, где, вероятно, будет находиться электрон 1, как будет выглядеть серая картина вероятности обнаружения электрона 1?

Раствор hmolb-a

2.

Когда протоны находятся близко друг к другу, электроны влияют друг на друга, и приведенная выше волновая функция больше не действует. Но предположим, что вам дали истинную волновую функцию, и вас снова попросили нарисовать каплю, показывающую вероятность нахождения электрона 1 (скажем, с помощью графического пакета). В чем может быть большая проблема?

Раствор hmolb-b

5. 2.3 Плотность вероятности

Для многочастичных систем, таких как электроны водорода молекула, показывающая величину волновой функции в виде серых тонов нет дольше работает, так как это функция в шестимерном пространстве. Вы не можете визуализировать шестимерное пространство. Однако в любом пространственном положении в обычном пространстве вы можете вместо этого показать «вероятность плотность», которая представляет собой вероятность на единицу объем нахождения любого электрона в окрестности смысл. Эта вероятность находится как

(5.4)

так как первый интеграл дает вероятность нахождения электрона 1 на независимо от того, где находится электрон 2 (т. е. интегрированный по все возможные положения для электрона 2), а второй дает вероятность найти 2 независимо от того, где находится 1. С исчезающе мал, шансы найти и то, и другое частицы в нем при этом равны нулю.

Плотность вероятности для состояния с электроном 1 вокруг левый протон и электрон 2 вокруг правого показаны на рисунке 5.1. Конечно, плотность вероятности для состояния с электронами обмен будет выглядеть точно так же.

Рисунок 5.1: Состояние с двумя нейтральными атомами.

---

Ключевые точки

Плотность вероятности – это вероятность на единицу объема нахождение электрона, какого бы он ни был, вблизи данной точки.

---

5.2.3 Контрольные вопросы

1.

Предположим, что для данной волновой функции вы нашли электрон рядом с левым протоном. Какой электрон, вероятно, это будет? Предположим, вы нашли электрон на полпути между протонами. Какой электрон это может быть?

Раствор hmolc-a

5.2.4 Состояния с общими электронами

В этом разделе будут рассмотрены состояния, в которых протоны разделяют два электроны.

Во-первых, немного сократить обозначения. Итак, государство который описывает, что электрон 1 находится вокруг левого протона, а электрон 2 вокруг правого один будет обозначен , используя соглашение, что первый фактор относится к электрону 1, а второй к электрону 2. В этом соглашении состояние, в котором электрон 1 вокруг правого протона и электрона 2 вокруг левого , сокращение от . это конечно физически то же самое, что и ; в два электрона одинаковы.

все возможные комбинации идея сочетания всех возможное состояние для электрона 1 с каждым возможным состоянием для электрона 2 предполагает, что государства и также должны быть включены. Но эти состояния имеют электроны вокруг одного и того же протона, и это не будут энергетически выгодны из-за взаимного отталкивания электроны. Поэтому они бесполезны для нахождения простого приближенного основное состояние с наименьшей энергией.

Состояния, в которых электроны больше не привязаны к определенному протон можно найти как линейную комбинацию и:

(5.5)

В такой комбинации каждый электрон имеет вероятность быть найденным о любом протоне, но где бы он ни находился, другой электрон будет быть вокруг другого протона.

Собственная функция должна быть нормирована, что, учитывая, что и являются реальными и нормированными производит

(5.6)

при условии, что и являются реальными. В результате только отношение можно выбирать свободно. Плотность вероятности комбинации может оказаться:

(5. 7)

Наиболее важным состоянием комбинации является состояние с:

(5,8)

Это состояние называется «симметричным относительно обмена электрона 1 с электроном 2», или, точнее, по отношению к замена на и наоборот. Такой обмен делает вообще не меняет эту волновую функцию. Если вы переоденетесь в и наоборот, вы все равно получите ту же самую волновую функцию. В терминах волновой функции основного состояния водорода это можно записать полностью как

(5.9)

с, где 0,53 Å — боровский радиус, а , и снова векторы положения электронов и протонов.

Плотность вероятности этой волновой функции выглядит как рисунок 5.2. Увеличивается вероятность того, что электроны находится между протонами, по сравнению с рисунком 5.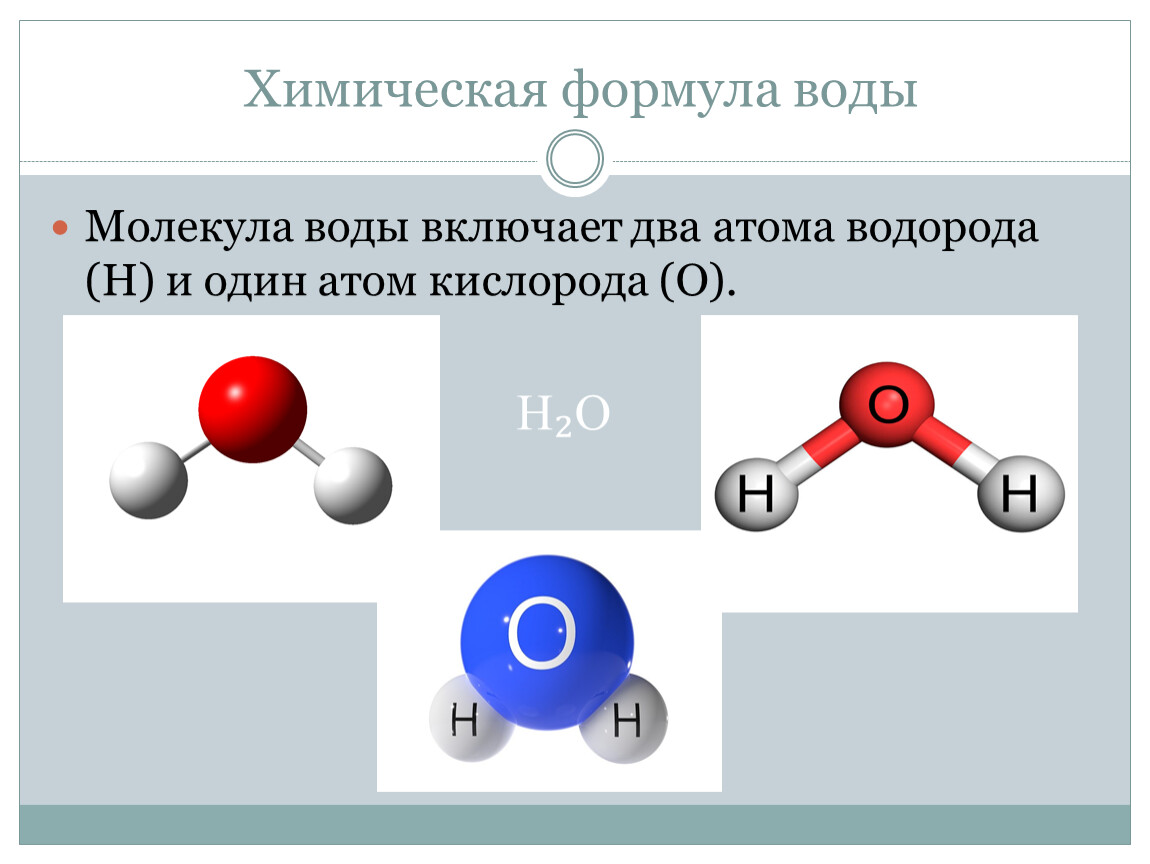 1 в в котором каждый протон имел свой электрон.

Рисунок 5.2: Симметричное распределение электронов.

Состояние с ,

(5.10)

называется антисимметричным по отношению к обмену электрон 1 с электроном 2: обмен местами и изменение знак волновой функции, но оставляет его без изменений. Как видно в рисунок 5.3, антисимметричное состояние уменьшилось вероятность того, что электроны окажутся между протонами.

Рисунок 5.3: Антисимметричное совместное использование электронов.

---

Ключевые моменты

В состоянии электрон номер 1 вокруг левого протона и 2 вокруг правого.

В состоянии электрон номер 1 вокруг правого протона и 2 вокруг левого.

В симметричном состоянии в протоны делят электроны поровну; каждый электрон имеет равный шанс быть найденным вокруг любого протона. В этом состоянии есть повышенная вероятность найти электрон где-то посередине протоны.

В антисимметричном состоянии в протоны также поровну делят электроны; каждый электрон снова имеет равные шансы быть обнаруженными вокруг любого протона. Но в этом состоянии уменьшается вероятность найти электрон где-то в между протонами.

Так, как и для молекулярного иона, при больших расстояниях между протонами странный трюк перетасовки ненаблюдаемых волновых функций делает снова создавать разные физические состояния с почти одинаковыми энергия.

---

5.2.4 Контрольные вопросы

1.

Очевидно, что визуальная разница между различными состояниями незначительна. Может даже показаться нелогичным, что вообще есть какая-то разница: состояния и физически абсолютно одинаковы, с одним электроном вокруг каждого протона. Так почему же их комбинации могут отличаться?

Квантовая разница была бы намного яснее, если бы вы могли видеть полную шестимерную волновую функцию, но визуализация шестимерного пространства просто не работает. Однако если вы ограничитесь взглядом только на -ось через ядра, вы получите нарисованную -плоскость, описывающую вблизи каких комбинаций осевых положений вы, скорее всего, найдете два электрона. Другими словами: каковы были бы шансы найти электрон 1 рядом с некоторым осевым положением и электрон 2 в то же самое время рядом с каким-то другим осевым положением?

Попробуйте угадать эти вероятности в -плоскости в виде серых тонов (темнее, если более вероятно), а затем сравните с ответом.

Раствор hmold-a

2.

Основываясь на предыдущем вопросе, как, по-вашему, будет выглядеть плотность вероятности на оси через ядра, опять же игнорируя существование позиций за осью?

Раствор hmold-b

5.2.5. Вариационное приближение основного состояния.

Цель этого раздела — найти приближение к земле состояние молекулы водорода, используя грубое приближение волновая функция, описанная в предыдущих подразделах.

Как и для молекулярного иона водорода из главы 4.6.6, Идея состоит в том, что, поскольку истинное основное состояние является состоянием с наименьшей энергией среди всех волновых функций наилучшая среди приближенных волновых функции имеет наименьшую энергию. Примерная волна функции здесь имеют вид ; в эти протоны разделяют электроны, но таким образом, что когда один электрон находится вокруг левого протона, другой вокруг правого, и наоборот.

Снова нужна компьютерная программа, чтобы распечатать ожидаемое значение энергии при различных значениях отношения коэффициентов ​ и протон-протонное расстояние. И хуже того, ожидание значение энергии для данного ​ и представляет собой шестимерный интеграл, и некоторые его части не могут быть выполнены аналитически; численное интегрирование должен быть использован. Это делает проблему гораздо более запутанной, {Д.23}.

Вы могли бы просто принять на веру, что энергия связи, состояние с наименьшей энергией оказывается равным 3,2 эВ при протоне до расстояния между протонами 0,87 Å, и что это происходит для симметричного состояние .

---

Ключевые моменты

Для водорода можно найти приблизительное основное состояние молекулы с помощью вариационного метода, очень похожего на молекулярный ион.

---

5.2.6 Сравнение с точным основным состоянием

Решение для основного состояния молекулы водорода, полученное в предыдущий подраздел, как и для молекулярного иона, довольно хороший. Приблизительная энергия связи 3,2 эВ не слишком сильно отличается от экспериментальное значение 4,52 эВ. Точно так же длина связи 0,87 Å не слишком далека от экспериментального значения. 0,74 Å.

Качественно точная волновая функция основного состояния действительна, положительна. и симметричный относительно отражения вокруг плоскости симметрии и вращения вокруг линии, соединяющей протоны, и поэтому приблизительный. Причины этих свойств аналогичны молекулярный ион; {А.8, А.9}.

Одной очень важной новой симметрией для нейтральной молекулы является эффект обмена электронами, замены на и наоборот. Приближенная волновая функция симметрична (неизменна). при таком обмене, как и точная волновая функция. К понять почему, обратите внимание, что операция обмена электронами коммутирует с гамильтонианом (обменивая одинаковыми электронами физически ничего не делает). Таким образом, собственные функции энергии могут быть также считаются собственными функциями «оператора обмена». Кроме того, обменный оператор является эрмитов (перевести его на другую сторону во внутренних произведениях — это эквивалентно простому изменению имени переменных интегрирования), поэтому имеет действительные собственные значения. А точнее, собственные значения могут быть только быть плюс-минус один, так как замена электронов не меняет величина волновой функции. Итак, собственные функции энергии включая основное состояние, должны быть симметричны относительно электронного обмена (собственное значение единица) или антисимметричное (собственное значение минус единица). основное состояние должно быть всюду положительным (точнее, один знак), смена знака за счет перестановки электронов невозможна. Таким образом, для основного состояния существует только симметричная возможность.

Одна проблема, которая не возникает для молекулярного иона, а только для нейтральной молекулы является взаимное отталкивание между двумя электронами. Это отталкивание уменьшается, когда электронные облака начинают сливаться, по сравнению с тем, что было бы, если бы облака были более компактными. (А Аналогичный эффект заключается в том, что сила тяжести Земли уменьшается, когда вы спускаетесь под поверхность. Безусловно, потенциальная энергия остается вниз или вверх для электронных облаков, но не так сильно, как могло бы иначе. Сравните рисунок 13.7.) Так как ядра компактный, он дает преимущество ядерно-электронному притяжению над электрон-электронное отталкивание. Это увеличивает энергию связи значительно; в приближенной модели примерно от 1,8 эВ до 3,2 эВ. Это также позволяет протонам приближаться ближе; {Д.23}.

Был задан вопрос, не должна ли быть «энергия активации», связанная с созданием молекулы водорода. из атомов водорода. Ответ — нет, атомы водорода радикалы, а не стабильные молекулы, которые необходимо разобрать перед рекомбинация. На самом деле атомы водорода притягиваются друг к другу даже при большие расстояния из-за притяжения Ван-дер-Ваальса, глава 10.1, эффект теряется в используемых приближенных волновых функциях. в этом разделе. Но атомы водорода, летящие друг на друга, тоже иметь достаточно энергии, чтобы снова разлететься; часть избыточной энергии должна поглощаться в другом месте с образованием стабильной молекулы. Согласно сети источники, считается, что образование молекул водорода во Вселенной обычно возникают на пылинках.

---

Ключевые моменты

Приблизительное основное состояние довольно хорошее, учитывая его простота.

---

---

Далее: 5.3 Системы с двумя состояниями

Инженерный колледж FAMU-FSU   Обработано с помощью l2h

Водород | Air Liquide Energies

У истоков Вселенной

Водород — самый распространенный элемент во Вселенной. Он присутствует на Земле в больших количествах в сочетании с другими элементами. Следовательно, его необходимо извлечь из этих элементов, чтобы получить газообразный водород, который имеет множество практических применений.

Свойства атома

• Атомная масса:
  1,007825 г.моль -1

• Атомный луч:
  25:00

• Электронная конфигурация:
  1s1

• Кристаллическая структура:
  шестиугольная

Молекула водорода (H ₂ ), которую иногда называют «диводородом», является древнейшей и простейшей молекулой в нашей Вселенной. Он есть у каждой звезды, в том числе и у Солнца, черпающего свою энергию от превращения водорода в гелий в ходе термоядерной реакции. Он состоит из двух атомов водорода, которые являются первыми двумя элементами, образовавшимися более 13 миллиардов лет назад.

• Наименование: Водород
• Обозначение: H
• Номер: 1
• Химическая серия: Неметалл
• Группа: 1
• Период: 1
• Блок: с

Водород содержится в больших количествах на Земле в сочетании с другими элементами, такими как вода и углеводороды, но его почти нет в нашей атмосфере, которая содержит всего 0,00005%. Вот почему для получения водорода в газообразном виде его необходимо производить путем экстракции из содержащих его молекул и хранить.

В течение многих лет водород использовался для различных промышленных применений в самых разных сферах деятельности. Он в основном используется для очистки топлива за счет удаления серы, которая естественным образом содержится в сырой нефти. Когда водород сочетается с топливным элементом, он также является источником устойчивой энергии, область, которая быстро развивается.

ЗНАЕТЕ ЛИ ВЫ?
Водород — самая маленькая и легкая молекула во Вселенной. Это в 50000 раз меньше толщины волоса, а один литр газообразного водорода весит 90 мг при нормальных условиях давления и температуры; это равно трем почтовым маркам.

НАЗВАНИЕ: «Дигидроген» — это научное название того, что обычно называют «водородом».

ХИМИЧЕСКАЯ ФОРМУЛА: h3

СОСТАВ: Два взаимосвязанных атома водорода.

ВОЗРАСТ: Это самая старая молекула во Вселенной. Он появился после Большого взрыва, более 13 миллиардов лет назад.

РАЗМЕР: Это самая маленькая молекула, которая существует во Вселенной.

ВЕС: Это самая легкая молекула во Вселенной.

АДРЕС: Это самая распространенная молекула во Вселенной, она содержится в звездах, таких как Солнце, а также в газообразных планетах, таких как Юпитер.

ХАРАКТЕРИСТИКИ: Молекула водорода бесцветна, не имеет запаха и нетоксична.

РОЛЬ: Это топливо Солнца, позволяющее звезде передавать тепло и свет на Землю. Это также предпочтительное топливо для ракет, и оно уже используется для приведения в движение электромобилей, которые производят собственную энергию на борту. Водород используется в качестве реагента во многих отраслях промышленности, в том числе в нефтепереработке.

У истоков Вселенной

Более 13 миллиардов лет назад, всего через несколько минут после Большого взрыва, появились протоны, составляющие ядра водорода. На этом этапе формирования Вселенной температура была чрезвычайно высокой — близкой к миллиарду градусов.

Затем Вселенная начала фазу расширения и охлаждения. Через несколько миллионов лет стало достаточно холодно, чтобы образовались молекулы водорода. Эти молекулы породили огромные облака, известные как «туманности», которые инициируют формирование звезд.

Туманность также стояла за происхождением Солнца около пяти миллиардов лет назад. Наша звезда в основном состоит из водорода и гелия, образующихся в результате реакции термоядерного синтеза, которая позволяет ей производить энергию. Эти два элемента самые легкие и самые распространенные во Вселенной.

Четыре газообразные планеты-гиганты в нашей Солнечной системе — Юпитер, Сатурн, Уран и Нептун — также в основном состоят из водорода.

Но в атмосфере Земли почти полностью отсутствует водород, потому что гравитационное поле нашей планеты недостаточно сильно, чтобы удерживать эти чрезвычайно легкие молекулы. Однако на Земле мы находим многочисленные источники водорода, где он соединяется с другими элементами, например, в воде и углеводородах.

Узнайте больше в Газовой энциклопедии

Его открытие

Водород был открыт в 1766 году британским физиком Кавендишем. Именно при соединении металлов с сильными кислотами Кавендиш заметил образование газа, который он назвал «горючим воздухом», потому что он был горючим. Этот чрезвычайно легкий газ на самом деле был водородом. Затем он заметил, что при его сжигании образуется водяной пар (пар).

В 1783 году французский химик Лавуазье дал этому легкому газу название «водород», что в переводе с греческого означает «то, что производит воду».

Только в 1838 году немецкий химик Шенбайн открыл эффект топливного элемента, позволяющий производить электричество из водорода и кислорода. Первая модель топливного элемента была построена в лаборатории тремя годами позже английским ученым сэром Уильямом Гроувом.

После этого было проведено много других экспериментов с молекулой водорода. В 1898 году Дьюар успешно сжижал водород, охладив его до -252,87°С. Его процесс сжижения был усовершенствован другим химиком и физиком, французом Жоржем Клодом, который также был одним из основателей Air Liquide.

Раннее использование водорода

Одно из первых применений водорода в области транспорта относится к 18 веку, когда Чарльз и Роберт совершили первый пилотируемый полет на воздушном шаре, названном «водородным аэростатом».