Електродвигуни постійного струму • Приводні системи
Приводні системи > Електродвигуни постійного струму
Наша компанія пропонує колекторні електродвигуни постійного струму (12В, 24В) серії ZYT закритого виконання з самоохолодженням. Електродвигуни даної серії використовуються в якості елементів приводу в різноманітному промисловому обладнанні.
Можлива комплектація черв’ячним редуктором серії NMRV
(див. розділ Черв’ячні мотор-редуктори постійного струму)
Умови експлуатації:
1.Не більш ніж 4000 м над рівнем моря
2.Температура середовища :-25℃~40℃.
3.Відносна вологість ≤95%(при +25℃)
Електродвигуни постійного струму відрізняються екологічністю і надійністю. Їх головною відмінністю від двигунів змінного струму є можливість регулювання вихідних обертів у широкому діапазоні.
Переваги електродвигунів постійного струму:
- Невеликі габаритні розміри
- Легке управління.
- Проста конструкція.

- Можливість плавного регулювання швидкості обертання валу.
Технічні параметри електродвигунів постійного струму серії ZYT:
| Модель | Крутній момент | Швидкість | Потужність | Напруга | Струм |
| (мН.м) | (об/хв) | (Вт) | (В) | ≤ | |
| 55ZYT01 | 63.7 | 3000 | 20 | 24 | 1,50 |
| 55ZYT05 | 55.7 | 6000 | 35 | 24 | 2,50 |
| 55ZYT55 | 79.6 | 6000 | 50 | 24 | 3,45 |
| 70ZYT51 | 223 | 3000 | 70 | 24 | 4,30 |
| 90ZYT105 | 733 | 3000 | 230 | 24 | 13,50 |
| 90ZYT106 | 796 | 1500 | 125 | 24 | 6,50 |
| 110ZYT56 | 1177 | 1500 | 180 | 24 | 8,00 |
| 110ZYT106 | 1560 | 1500 | 250 | 24 | 12,00 |
| 110ZYT155 | 2230 | 3000 | 700 | 24 | 45,00 |
| 110ZYT156 | 2390 | 1500 | 370 | 24 | 22,00 |
| 130ZYT56 | 3185 | 1500 | 550 | 24 | 28,00 |
| 130ZYT105 | 3820 | 1500 | 700 | 24 | 30,00 |
| 130ZYT155 | 4500 | 1500 | 1000 | 24 | 38,00 |
| 130ZYT185 | 6200 | 1500 | 1200 | 24 | 60,00 |
Габаритні та приєднувальні розміри:
Математична модель колекторного двигуна постійного струму зі збудженням від постійних магнітів
JCPEE.
Випуск 5, Номер 1
: c. 33-36
Автори:
- Василь Маляр
- Ігор Гавдьо
1
Національний університет «Львівська політехніка»
2
Національний університет «Львівська політехніка»
На даний час існує тенденція заміни мікродвигунів постійного струму з електромагнітним збудженням на двигуни постійного струму зі збудженням від постійних магнітів (ДПС ПМ). Використання для розрахунків ДПС ПМ польових методів призводить до надмірного ускладнення математичних моделей та значних затрат часу на обробку отриманих результатів. Метою статті є розроблення математичної моделі ДПС ПМ на основі теорії електричних та магнітних кіл. Математична модель ДПС ПМ побудована на основі розгалуженої заступної схеми магнітного кола машини з високим рівнем деталізації магнітопроводу. Описано послідовність розроблення заступної схеми, методику визначення її елементів.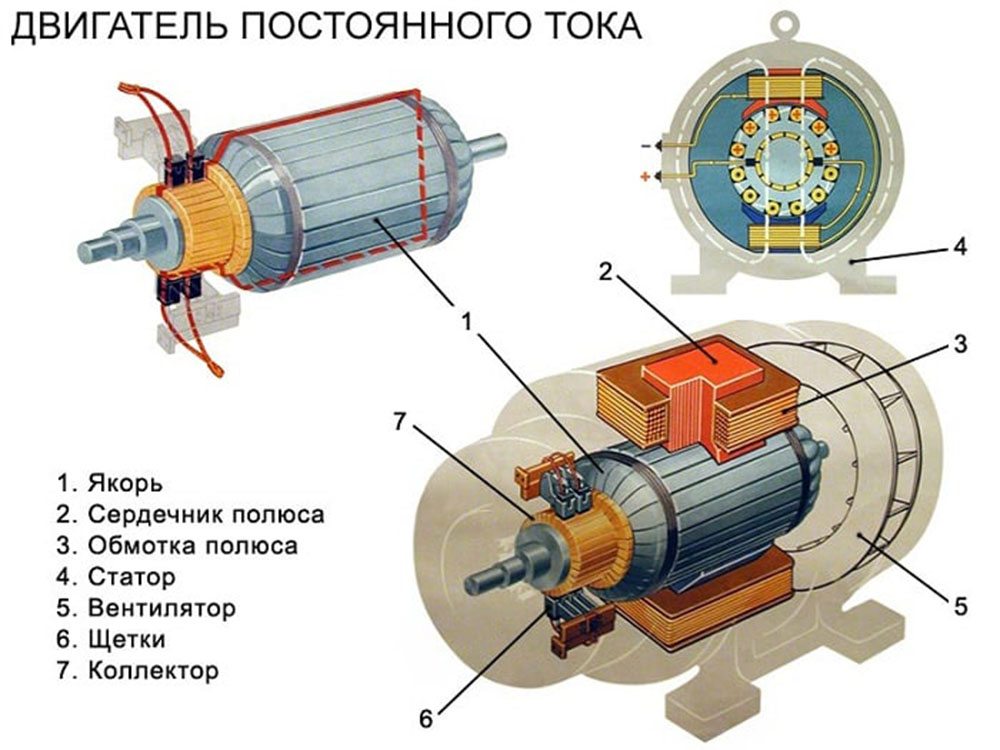
Permanent magnet direct current motor
магнітопровід
схема заміщення
- A. Antonov and V. Kireev, “Construction of an optimal magnetic systems of smooth stator of magnetoelectric motor”, Tekhnichna Elektrodynamika, no. 4, pp. 38-40, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2003.
- A. Afonin, “Magnetic systems of electromechanical convertors of energy with variation of vectors of magnetization of permanent magnets”, Tekhnichna Elektrodynamika, no. 1, pp. 47-55, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2004.
- A. Afonin and M. Vardakh, “Simulation of the magnetic systems of electric motors with flat permanent magnets in the rotor of cylindrical construction”, Tekhnichna Elektrodynamika, no.
 2, pp. 37-44, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2005.
2, pp. 37-44, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2005. - P. Belyi, “Equation for planning of the built-in magnetoelectric motor of disc-type”, Tekhnichna Elektrodynamika, no. 6, pp. 53-56, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2005.
- I. Dudzikowski, “Commutator motor excitated by permanent magnet”, Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Politechniki Wrocławskiej, no. 58, Studia i Materiały, no. 25, 2005. (Polish)
- V. Malyar, L. Hlukhivskyi, A. Malyar, D. Hrechyn, I. Havdo, “Calculation of magnetic circuit of single-phase shaded-pole induction motor”,
 (Russian)
(Russian)
— MATLAB и Simulink
Моделирование и симуляция двигателей помогают выполнять задачи, начиная от анализа производительности на уровне системы и заканчивая детальным проектированием привода электродвигателя. Каждая задача требует отражения различных физических эффектов в модели двигателя и симуляции двигателя. Разработчикам приводов двигателей может потребоваться импорт данных анализа конечных элементов (FEA) для оптимизации параметров конструкции привода при минимальных потерях. Системные инженеры часто полагаются на более абстрактное моделирование двигателя, которое уравновешивает механическую и электрическую мощность, чтобы ускорить моделирование двигателя и проанализировать производительность двигателя на уровне системы.
Simulink ® и Simscape™ поддерживают несколько уровней точности для моделирования и моделирования двигателей:
- Проект системы:
- Без широтно-импульсной модуляции (ШИМ) или силового электронного переключения
- Упрощенная динамика
- Энергетическое моделирование стационарного эквивалента и карты эффективности
- Конструкция управления:
- Идеальное переключение
- Моделирование с сосредоточенными параметрами
- Линейная зависимость момент-ток
- Конструкция моторного привода:
- Неидеальное переключение – основанное на физике моделирование силовых полупроводников
- Насыщение – нелинейная зависимость от тока и/или угла ротора
- Пространственные гармоники, включая пульсации крутящего момента, вызванные зубчатыми зацеплениями и гармониками в потокосцеплении
Для быстрого моделирования двигателя вы можете интегрировать табличную информацию о потерях в модель двигателя
 Вы можете разработать проверенную стратегию управления электроприводом для гибридного электромобиля, используя уровень точности проектирования управления для моделирования синхронного двигателя с постоянными магнитами. Вы можете обеспечить реалистичное поведение симуляции двигателя, оценив значения параметров на основе измеренных данных. Чтобы учесть магнитное насыщение или изменения параметров при различных уровнях нагрузки, вы можете включить данные FEA, которые описывают нелинейную зависимость потока и тока в вашей модели двигателя, используя уровень точности
Вы можете разработать проверенную стратегию управления электроприводом для гибридного электромобиля, используя уровень точности проектирования управления для моделирования синхронного двигателя с постоянными магнитами. Вы можете обеспечить реалистичное поведение симуляции двигателя, оценив значения параметров на основе измеренных данных. Чтобы учесть магнитное насыщение или изменения параметров при различных уровнях нагрузки, вы можете включить данные FEA, которые описывают нелинейную зависимость потока и тока в вашей модели двигателя, используя уровень точности 37:15
Продолжительность видео 37:15.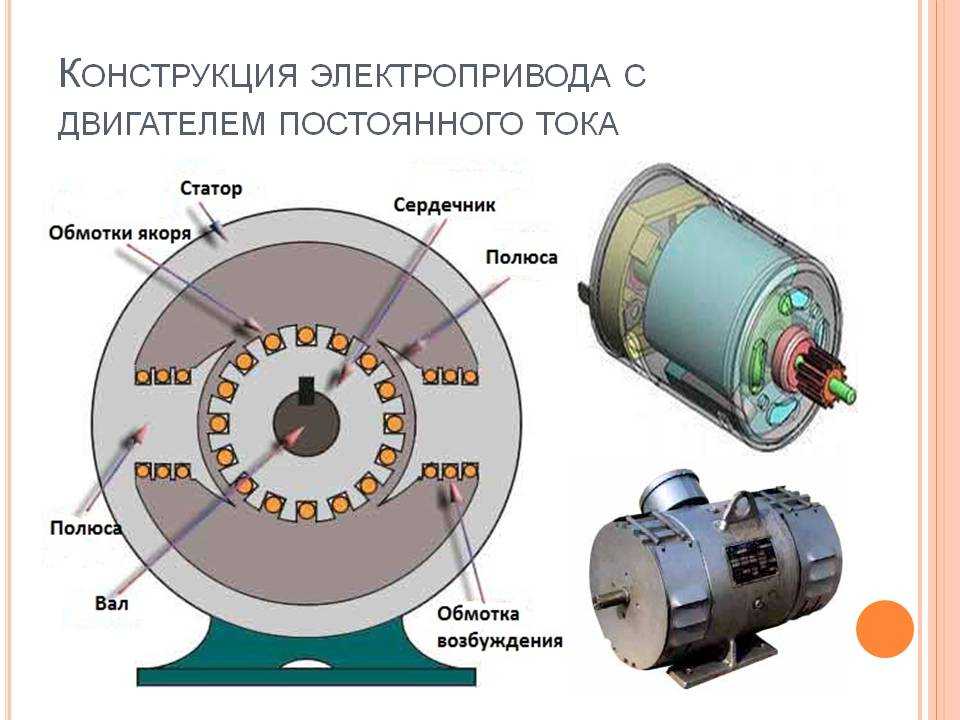
Параметрирование и проверка синхронного двигателя с постоянными магнитами модели
Поле-ориентированное управление PMSM с Simulink и набором блоков управления двигателем.4 видео
Поле-ориентированное управление СДПМ с помощью Simulink и набора блоков управления двигателем (4 видео)
Блок управления двигателем.6 видео
Управление двигателем (6 видео)
Введение в бесщеточный двигатель постоянного тока
Прочитать электронную книгу
Создание высокоточной модели электродвигателя для проектирования и проверки системы управления
Точная модель объекта является основой разработки системы управления с использованием модельно-ориентированного проектирования. С хорошо сконструированной моделью предприятия инженеры могут проверять функциональность своей системы управления, проводить тесты замкнутого контура модели в цикле, настраивать коэффициенты усиления с помощью моделирования, оптимизировать конструкцию и проводить анализ возможных вариантов, что было бы сложно.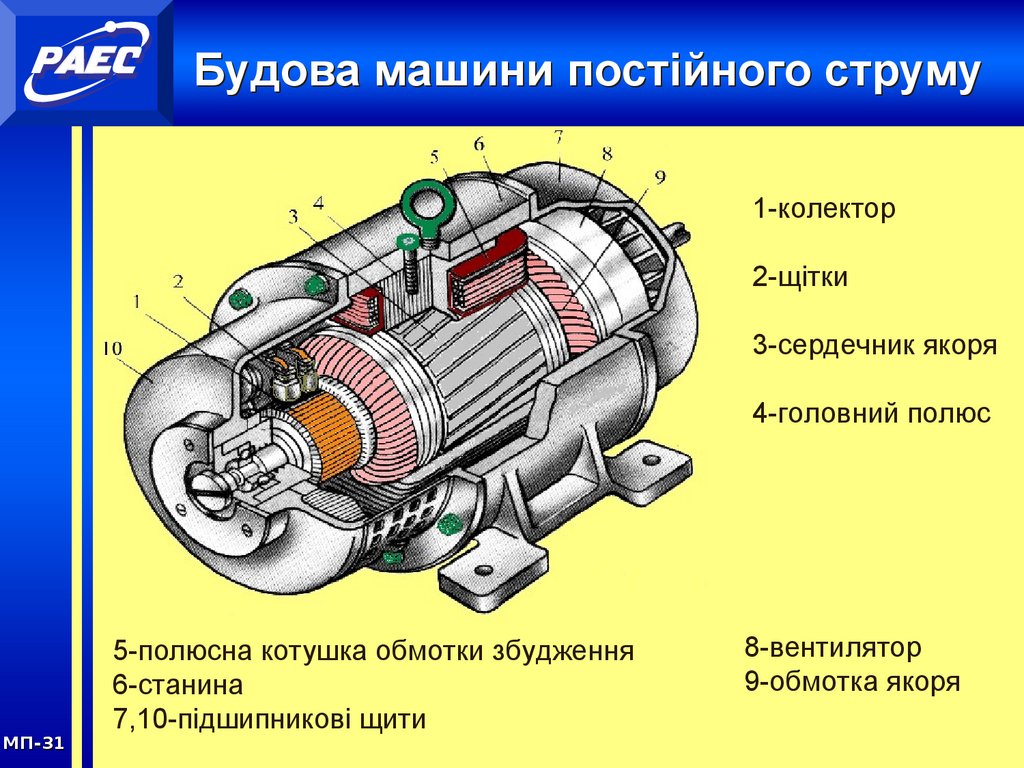
Несмотря на эти преимущества, инженеры иногда неохотно выделяют время и ресурсы, необходимые для создания и проверки модели предприятия. Проблемы включают в себя то, сколько времени потребуется для запуска моделирования, сколько знаний в предметной области и инструментах потребуется для построения и проверки модели, а также какой тип оборудования потребуется для получения данных тестирования оборудования для построения и проверки модели.
В этой статье описывается рабочий процесс для создания модели объекта с синхронной машиной с постоянными магнитами (PMSM) с использованием MATLAB 9.0005® и Simulink ® , а также общедоступное лабораторное оборудование. Рабочий процесс состоит из трех этапов:
- Выполнение тестов
- Определение параметров модели из тестовых данных
- Проверка параметров с помощью моделирования
Мы использовали модель объекта для построения и настройки модели системы управления СДПМ с обратной связью. Мы провели тесты переходной характеристики и выбега с использованием модели контроллера в моделировании и на оборудовании с использованием готовой системы тестирования в реальном времени xPC Target™. Мы обнаружили близкое соответствие результатов моделирования и аппаратных средств с нормированным среднеквадратичным отклонением (NRMSD) ниже 2% для ключевых сигналов, таких как скорость ротора и фазные токи двигателя (рис. 1).
Мы провели тесты переходной характеристики и выбега с использованием модели контроллера в моделировании и на оборудовании с использованием готовой системы тестирования в реальном времени xPC Target™. Мы обнаружили близкое соответствие результатов моделирования и аппаратных средств с нормированным среднеквадратичным отклонением (NRMSD) ниже 2% для ключевых сигналов, таких как скорость ротора и фазные токи двигателя (рис. 1).
Рисунок 1. Сравнение результатов моделирования (синий) с аппаратными результатами (красный) для скорости ротора (слева) и фазного тока (справа).
Модель установки и ее параметры
Модель установки СДПМ, разработанная с помощью SimPowerSystems™, включает в себя двигатель и нагрузку — в данном примере акриловый диск. Модель имеет девять параметров, определяющих ее поведение: один (инерция диска), связанный с нагрузкой, и восемь, связанных с двигателем (рис. 2).
Рисунок 2. Модель Simulink PMSM.
Мы провели пять испытаний, чтобы охарактеризовать эти параметры: испытание бифилярным маятником, испытание обратной ЭДС, испытание трением, испытание выбегом и испытание скачком напряжения постоянного тока (таблица 1). В этой статье мы сосредоточимся на тесте на выбег и тестах на ступенчатом напряжении постоянного тока. Эти тесты демонстрируют все более сложные методы идентификации параметров и иллюстрируют извлечение значений параметров посредством подгонки кривой и оценки параметров соответственно.
В этой статье мы сосредоточимся на тесте на выбег и тестах на ступенчатом напряжении постоянного тока. Эти тесты демонстрируют все более сложные методы идентификации параметров и иллюстрируют извлечение значений параметров посредством подгонки кривой и оценки параметров соответственно.
| Тест | Параметры идентифицированы | Метод идентификации |
|---|---|---|
| Бифилярный маятниковый тест | Инерция диска (\(H_d\)) | Расчет |
| Проверка противоЭДС | Число полюсов (\(P\)) Постоянная потокосцепления (\(A_{pm}\)) Постоянная момента (\(Kt\)) | Расчет |
| Испытание на трение | Коэффициент вязкого демпфирования (\(b\)) Кулоновское трение (\(J_0\)) | Изогнутый фитинг |
| Испытание выбегом | Инерция ротора (\(Н\)) | Изогнутый фитинг |
| Ступенчатое испытание постоянным напряжением | Сопротивление (\(R\)) Индуктивность (\(L\)) | Оценка параметров |
Таблица 1. Параметры модели и тесты, проведенные для их характеристики.
Параметры модели и тесты, проведенные для их характеристики.
Для каждого теста мы описываем настройку теста, а затем объясняем, как мы провели тест, получили данные, извлекли значение параметра и проверили его.
Определение инерции ротора с помощью теста на выбег
Чтобы охарактеризовать инерцию ротора (\(H\)) мы раскручиваем ротор до начальной скорости (\(\omega_{r0}\)) и измеряем скорость вращения (\(\omega\)) при остановке ротора по инерции. Используя этот измеренный результат, можно определить инерцию ротора по кривой, подходящей уравнением для \(\omega_r\) к измеренной скорости вращения в течение периода времени, когда двигатель останавливается выбегом.
Дифференциальное уравнение [1] описывает механическое поведение двигателя. Тест на выбег настроен так, что крутящий момент нагрузки (\(T_{нагрузка}\)) всегда равен \(0\). Как только двигатель достигает начальной установившейся скорости, двигатель выключается, так что электромагнитный вращающий момент (\(T_{em}\)) также равен \(0\).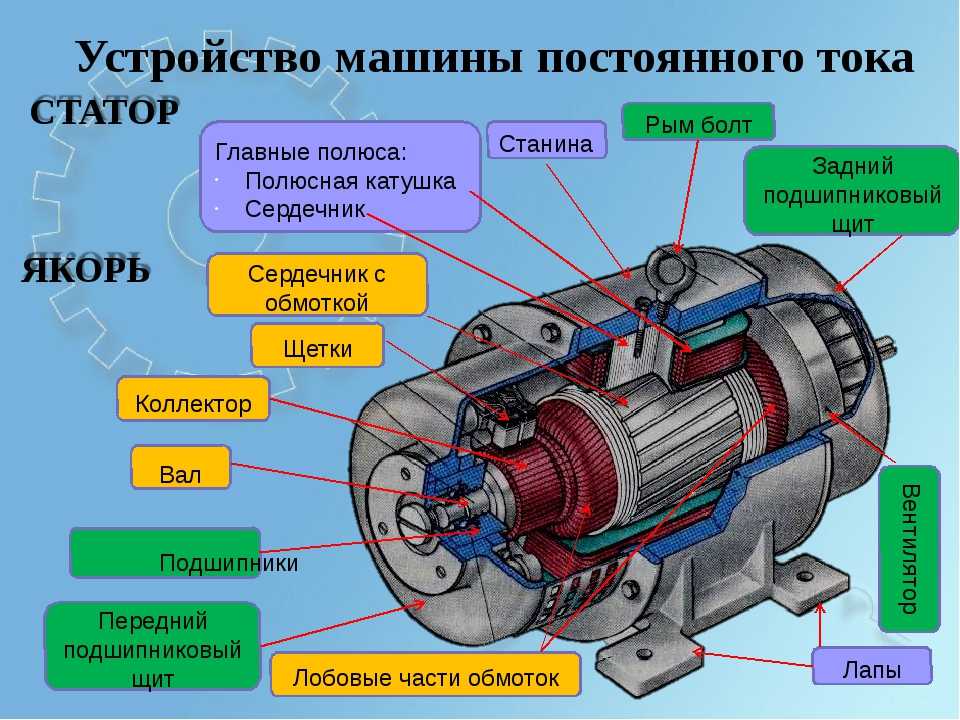 В этих условиях решение задачи [1] дается уравнением для \(\omega_r\) [2], где
В этих условиях решение задачи [1] дается уравнением для \(\omega_r\) [2], где
\(\omega_r\) – скорость вращения вала ротора
(\(\omega_{r0}\)) – начальная скорость вращения вала ротора
\(J_0\) и \(b\ ) — кулоновское трение и коэффициент вязкого демпфирования соответственно, полученные в результате отдельного испытания на трение
\(T_{em}\) — электромагнитный вращающий момент (0 во время этого испытания) момент нагрузки (0 во время этого теста)
\[\begin{equation}\tag{1}\frac{d\omega_r}{dt}=\frac{1}{H}(T_{em}-b\ omega_r-J_0-T_{нагрузка})\end{уравнение}\] 9{-\frac{b}{H}t}-\frac{J_0}{b}\end{equation}\]
Проведение теста и сбор данных
В лаборатории мы создали разомкнутую В тестовой модели Simulink двигатель разгоняется до начальной скорости 150 радиан в секунду, после чего привод двигателя отключается, а ротор останавливается выбегом. На протяжении всего теста модель фиксировала выходной сигнал датчика скорости вращения.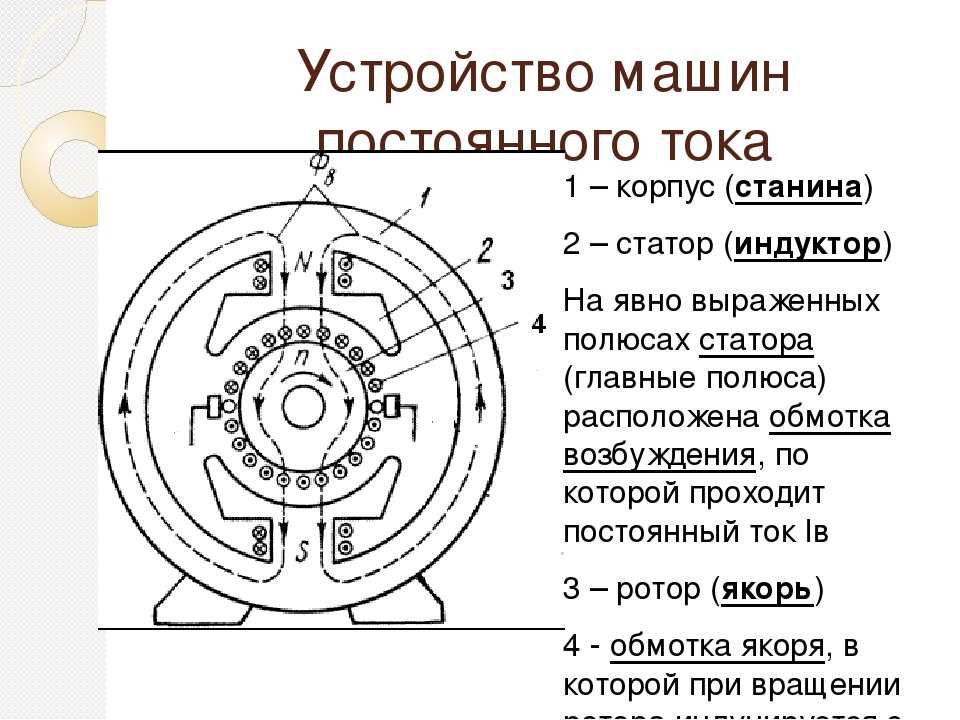 Используя Simulink Coder™ и xPC Target, мы развернули эту модель в готовой системе реального времени xPC Target. Мы выполнили модель с помощью xPC Target и импортировали данные о скорости ротора в MATLAB для анализа.
Используя Simulink Coder™ и xPC Target, мы развернули эту модель в готовой системе реального времени xPC Target. Мы выполнили модель с помощью xPC Target и импортировали данные о скорости ротора в MATLAB для анализа.
Извлечение и проверка значений параметров
После выполнения тестов мы построили измеренные данные скорости в MATLAB и использовали Curve Fitting Toolbox™, чтобы подобрать уравнение [2] для угловой скорости ротора (\(\omega_r\)) к измеренным данным скорости, когда ротор останавливался выбегом. Используя значение \(H\) из аппроксимации кривой, мы оценили уравнение [2] с точки, в которой двигатель начал работать накатом, и нанесли результаты на график с исходными данными испытаний (рис. 3). Как показано на рисунке 3, уравнение [2] со значением \(H\) из аппроксимированной кривой точно предсказывает скорость двигателя во время испытания на выбег. 92 в нашей модели PMSM), мы провели симуляцию теста на выбег в Simulink. Затем мы сравнили и построили смоделированные результаты с результатами измерений (рис. 4). Результаты полностью совпадали с нормализованным среднеквадратичным отклонением (NRMSD) около 2%.
4). Результаты полностью совпадали с нормализованным среднеквадратичным отклонением (NRMSD) около 2%.
Рис. 4. Сравнение измеренной скорости ротора (красный) и смоделированной скорости ротора (синий).
Характеристика сопротивления и индуктивности с помощью ступенчатого теста постоянного напряжения
При ступенчатом тесте постоянного напряжения напряжение постоянного тока прикладывается к соединениям фазы A и фазы B двигателя, и измеряется результирующий ток. Электрически в этих условиях трехфазный СДПМ ведет себя как схема с двумя последовательными резисторами и двумя последовательными катушками индуктивности (рис. 5).
Рис. 5. Эквивалентная электрическая схема для ступенчатого теста постоянным током.
Измеренный ток (\(i\)) используется для определения значений параметров сопротивления и индуктивности. Во время испытания ротор удерживается неподвижным, чтобы не усложнять анализ формами обратной ЭДС, которые имеют тенденцию противодействовать протеканию тока. Чтобы не сжечь двигатель при неподвижном роторе, добавлен токоограничивающий резистор (\(R_{limit}\)) и используется ступенчатый импульс, а не постоянное постоянное напряжение.
Чтобы не сжечь двигатель при неподвижном роторе, добавлен токоограничивающий резистор (\(R_{limit}\)) и используется ступенчатый импульс, а не постоянное постоянное напряжение.
Проведение теста и получение данных
Для проведения теста мы снова использовали xPC Target и готовую систему реального времени xPC Target. В Simulink мы разработали модель, которая генерировала серию 24-вольтовых импульсов длительностью примерно 2,5 миллисекунды. Мы развернули эту модель в нашей системе xPC Target с помощью Simulink Coder и подали импульс напряжения на клеммы фазы A и фазы B модуля PMSM. Мы измерили приложенное напряжение и ток, протекающий через двигатель, с помощью осциллографа, а с помощью Instrument Control Toolbox™ мы считывали измеренные данные в MATLAB, где мы отображали результаты (рис. 6).
Рис. 6. Напряжение (вверху) и ток (внизу) для импульса в ступенчатом тесте постоянного напряжения.
Извлечение и проверка значений параметров
Для извлечения сопротивления фазы из измеренных данных требовалось только применение закона Ома (\(R = V/I\)) с использованием установившихся значений напряжения и тока. Для PMSM мы рассчитали сопротивление как 23,26 вольт / 2,01 ампер = 11,60 Ом. Вычитая 10 Ом (значение токоограничивающего резистора) и разделив результат на 2 для учета двухфазных сопротивлений последовательно, мы рассчитали, что сопротивление фазы двигателя составляет 0,8 Ом.
Для PMSM мы рассчитали сопротивление как 23,26 вольт / 2,01 ампер = 11,60 Ом. Вычитая 10 Ом (значение токоограничивающего резистора) и разделив результат на 2 для учета двухфазных сопротивлений последовательно, мы рассчитали, что сопротивление фазы двигателя составляет 0,8 Ом.
Характеристика индуктивности требовала более сложного подхода. На первый взгляд кажется, что мы могли бы использовать аппроксимацию кривой, как мы это делали при характеристике инерции ротора. Однако из-за внутреннего сопротивления источника постоянного тока измеренное напряжение постоянного тока падает с начального значения 24 В в начале испытания, когда ток в цепи равен 0, до установившегося значения 23,26 В после в цепи течет ток. Поскольку входное напряжение не является чистым ступенчатым сигналом, результаты кривой, аппроксимирующей решение уравнения последовательной цепи RL, будут неточными.
Чтобы преодолеть эту трудность, мы выбрали более надежный подход с использованием оценки параметров и Simulink Design Optimization™. Преимущество этого подхода состоит в том, что он не требует ни чисто ступенчатого ввода, ни подгонки кривой.
Преимущество этого подхода состоит в том, что он не требует ни чисто ступенчатого ввода, ни подгонки кривой.
Мы смоделировали эквивалентную серию RL цепи двигателя с помощью Simulink и Simscape™ (рис. 7). Simulink Design Optimization применил измеренное напряжение в качестве входных данных для модели и, зная значение ограничительного резистора (R_limit) и фазного сопротивления двигателя (R_hat), оценил значение индуктивности (L_hat), чтобы сделать ток прогнозируемым. модели максимально точно соответствуют измеренным текущим данным.
Рисунок 7. Simscape-модель эквивалентной схемы двигателя.
Чтобы проверить значения, которые мы получили для фазового сопротивления (0,8 Ом) и индуктивности (1,15 миллигенри), мы вставили значения в нашу модель СДПМ и стимулировали модель с теми же входными данными, которые мы использовали для стимуляции реального двигателя. Мы сравнили результаты моделирования с результатами наших измерений (рис. 8). Результаты почти совпали, NRMSD около 3%.
Рисунок 8. Сравнение результатов измерений (синий) с результатами моделирования (красный) для напряжения (вверху) и тока (внизу).
Использование модели объекта для проектирования контроллера
После определения и проверки всех ключевых параметров наша модель объекта PMSM была готова к использованию при разработке контроллера двигателя. Мы использовали Simulink Design Optimization для настройки пропорциональных и интегральных коэффициентов внешнего контура контроллера, регулятора скорости. Мы провели моделирование с обратной связью, чтобы проверить функциональность модели контроллера, и использовали Simulink Coder для генерации кода из модели, которую мы развернули на целевой машине xPC Target, работающей в режиме реального времени.
В качестве последнего шага проверки контроллера мы выполнили симуляцию переходной характеристики и выбега в Simulink, а также аппаратные тесты с использованием развернутого кода контроллера в готовой системе реального времени xPC Target. Мы сравнили результаты моделирования и аппаратных испытаний для скорости ротора и фазного тока и снова обнаружили близкое соответствие между моделью и аппаратными средствами, при этом NRMSD ниже 2% в обоих случаях (рис. 9).
Мы сравнили результаты моделирования и аппаратных испытаний для скорости ротора и фазного тока и снова обнаружили близкое соответствие между моделью и аппаратными средствами, при этом NRMSD ниже 2% в обоих случаях (рис. 9).
Рисунок 9. Сравнение результатов моделирования (синий) с аппаратными результатами (красный) для скорости ротора (слева) и фазного тока (справа).
Резюме
При разработке модели объекта PMSM было выделено два теста идентификации параметров. Данные были получены с помощью датчика для испытания на выбег и с помощью Instrument Control Toolbox с помощью осциллографа для испытания на скачкообразное напряжение постоянного тока. Мы извлекли данные с помощью подгонки кривой для испытания на выбег и оценки параметров для испытания на скачкообразное напряжение постоянного тока. Мы проверили значения всех параметров, сравнив результаты моделирования с измеренными данными испытаний, что позволило нам создать модель объекта, которой мы могли доверять при разработке и настройке контроллера.



 2, pp. 37-44, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2005.
2, pp. 37-44, Kyiv, Ukraine: Institute of Electrodynamics of Ukraine, 2005. (Russian)
(Russian)