Атом водорода — Википедия

Атом водорода — физико-химическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра как правило входит протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a₀ = 0,529 Å.

Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решение. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией.

В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощённо рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/

r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.

В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.

Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантово-механическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.

Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следуют полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента

l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.

В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/

r радиальные волновые функции записываются с использованием полиномов Лагерра. Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.

Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми

n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство — особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).

Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода — проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси

Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и m′,{\displaystyle m^{\prime },} полученных для другой выделенной оси Z′,{\displaystyle Z^{\prime },} всегда представляется как подходящая суперпозиция различных состояний с разными m (но тем же самым l), которые были получены для Z.

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид U(r)=−e2r,{\displaystyle U(r)=-{\tfrac {e^{2}}{r}},} где e — заряд электрона (и протона), r — радиус-вектор, то уравнение Шрёдингера запишется следующим образом:

Δψ+2mℏ2(E+e2r)ψ=0.{\displaystyle \Delta \psi +{\frac {2m}{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)\psi =0.}

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, ℏ=h3π{\displaystyle \hbar ={h \over 2\pi }} — постоянная Планка, E — полная энергия

электрона, Δ=∂2∂x2+∂2∂y2+∂2∂z2{\displaystyle \Delta ={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}} — оператор Лапласа. Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно

будет записать лапласиан в сферической системе координат (r,θ,φ).{\displaystyle (r,\theta ,\varphi ).} В ней он выглядит следующим образом:

Δψ=1r2∂∂r(r2∂ψ∂r)+1r2sin2⁡θ∂2ψ∂φ2+1r2sin⁡θ∂∂θ(sin⁡θ∂ψ∂θ).{\displaystyle \Delta \psi ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \varphi ^{2}}}+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right).}

Уравнение Шрёдингера в сферических координатах:

1r2∂∂r(r2∂ψ∂r)+1r2sin2⁡θ∂2ψ∂φ2+1r2sin⁡θ∂∂θ(sin⁡θ∂ψ∂θ)+2mℏ2(E+e2r)ψ=0.{\displaystyle {\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \varphi ^{2}}}+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {2m}{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)\psi =0.}

В этом уравнении ψ{\displaystyle \psi } — функция трёх переменных (r,θ,φ).{\displaystyle (r,\theta ,\varphi ).} Разделим его на три более простых уравнения. Для этого представим функцию ψ(r,θ,φ){\displaystyle \psi (r,\theta ,\varphi )} как произведение трёх функций: ψ(r,θ,φ)=R(r)Θ(θ)Φ(φ).{\displaystyle \psi (r,\theta ,\varphi )=R(r)\Theta (\theta )\Phi (\varphi ).} Эти функции будем обозначать просто R,Θ,Φ.{\displaystyle R,\Theta ,\Phi .} Тогда

∂ψ∂r=∂R∂rΘΦ,  ∂ψ∂θ=∂Θ∂θRΦ,  ∂ψ∂φ=∂Φ∂φΘR.{\displaystyle {\frac {{\partial }{\psi }}{{\partial }r}}={\frac {{\partial }R}{{\partial }r}}{\Theta }{\Phi },~~{\frac {{\partial }{\psi }}{{\partial }{\theta }}}={\frac {{\partial }{\Theta }}{{\partial }{\theta }}}R{\Phi },~~{\frac {{\partial }{\psi }}{{\partial }{\varphi }}}={\frac {{\partial }{\Phi }}{{\partial }{\varphi }}}{\Theta }R.}

После подстановки значений частных производных в уравнение Шрёдингера получим:

1r2∂∂r(r2∂R∂r)ΘΦ+1r2sin2θ∂2Φ∂φ2ΘR+1r2sinθ∂∂θ(sin⁡θ∂Θ∂θ)RΦ+2mℏ2(E+e2r)RΘΦ=0.{\displaystyle {\frac {1}{r^{2}}}{\frac {\partial }{{\partial }r}}\left({r^{2}}{\frac {{\partial }R}{{\partial }r}}\right){\Theta }{\Phi }+{\frac {1}{{r^{2}}{\sin ^{2}}{\theta }}}{{\frac {{{\partial }^{2}}{\Phi }}{{\partial }{{\varphi }^{2}}}}{\Theta }{R}}+{\frac {1}{{r^{2}}{\sin }{\theta }}}{\frac {\partial }{{\partial }{\theta }}}\left(\sin \theta {\frac {{\partial }{\Theta }}{{\partial }{\theta }}}\right){R}{\Phi }+{\frac {2m}{\hbar ^{2}}}{\left(E+{\frac {e^{2}}{r}}\right){R}{\Theta }{\Phi }}=0.}

Умножим уравнение на r2sin2⁡θRΘΦ:{\displaystyle {\tfrac {r^{2}\sin ^{2}\theta }{R\Theta \Phi }}:}

sin2θR∂∂r(r2∂R∂r)+1Φ∂2Φ∂φ2+sin⁡θΘ∂∂θ(sin⁡θ∂Θ∂θ)+2mr2sin2⁡θℏ2(E+e2r)=0.{\displaystyle {\frac {{\sin ^{2}}{\theta }}{R}}{\frac {\partial }{{\partial }r}}\left({r^{2}}{\frac {{\partial }R}{{\partial }r}}\right)+{\frac {1}{\Phi }}{\frac {{{\partial }^{2}}{\Phi }}{{\partial }{{\varphi }^{2}}}}+{\frac {\sin \theta }{\Theta }}{\frac {\partial }{{\partial }{\theta }}}\left(\sin \theta {\frac {{\partial }{\Theta }}{{\partial }{\theta }}}\right)+{\frac {2mr^{2}\sin ^{2}\theta }{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)=0.}

Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.

sin2⁡θR∂∂r(r2∂R∂r)+sin⁡θΘ∂∂θ(sin⁡θ∂Θ∂θ)+2mr2sin2⁡θℏ2(E+e2r)=−1Φ∂2Φ∂φ2.   (1){\displaystyle {\frac {\sin ^{2}\theta }{R}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial R}{\partial r}}\right)+{\frac {\sin \theta }{\Theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \Theta }{\partial \theta }}\right)+{\frac {2mr^{2}\sin ^{2}\theta }{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)=-{\frac {1}{\Phi }}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}.~~~(1)}

Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её ml2.{\displaystyle m_{l}^{2}.} Следовательно,

∂2Φ∂φ2=−ml2Φ.{\displaystyle {\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}=-m_{l}^{2}\Phi .}

Решением этого уравнения являются функции

Φ=A sin⁡(mlφ),  Φ=Acos⁡(mlφ).{\displaystyle \Phi =A~\sin(m_{l}\varphi ),~~\Phi =A\cos(m_{l}\varphi ).}

Угол φ может изменяться от 0 до 2π. Функция Φ{\displaystyle \Phi } должна быть периодической с периодом 2π. Это возможно, только если ml=0,±1,±2,±3,…{\displaystyle m_{l}=0,\pm 1,\pm 2,\pm 3,\dots } Таким образом, из решения уравнения Шрёдингера получаем значение одного из квантовых чисел (конечно, из него можно получить их все). Число ml{\displaystyle m_{l}} называется магнитным квантовым числом.

Далее, интегрируя квадрат модуля функции Φ{\displaystyle \Phi } от 0 до 2π и приравнивая полученное выражение к единице, получим, что A=12π.{\displaystyle A={\tfrac {1}{\sqrt {2\pi }}}.}

Далее рассмотрим левую часть уравнения (1). Она, конечно, равна ml2:{\displaystyle m_{l}^{2}:}

sin2⁡θR∂∂r(r2∂R∂r)+sin⁡θΘ∂∂θ(sin⁡θ∂Θ∂θ)+2mr2sin2⁡θℏ2(E+e2r)=ml2.{\displaystyle {\frac {\sin ^{2}\theta }{R}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial R}{\partial r}}\right)+{\frac {\sin \theta }{\Theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \Theta }{\partial \theta }}\right)+{\frac {2mr^{2}\sin ^{2}\theta }{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)=m_{l}^{2}.}

Разделим уравнение на sin2⁡θ:{\displaystyle \sin ^{2}\theta :}

1R∂∂r(r2∂R∂r)+1Θsin⁡θ∂∂θ(sin⁡θ∂Θ∂θ)+2mr2ℏ2(E+e2r)=ml2sin2⁡θ.{\displaystyle {\frac {1}{R}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial R}{\partial r}}\right)+{\frac {1}{\Theta \sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \Theta }{\partial \theta }}\right)+{\frac {2mr^{2}}{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)={\frac {m_{l}^{2}}{\sin ^{2}\theta }}.}

После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через β,{\displaystyle \beta ,} получаем

ml2sin2⁡θ−1Θsin⁡θ∂∂θ(sin⁡θ∂Θ∂θ)=β.{\displaystyle {\frac {m_{l}^{2}}{\sin ^{2}\theta }}-{\frac {1}{\Theta \sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \Theta }{\partial \theta }}\right)=\beta .}

1R∂∂r(r2∂R∂r)+2mr2ℏ2(E+e2r)=β.{\displaystyle {\frac {1}{R}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial R}{\partial r}}\right)+{\frac {2mr^{2}}{\hbar ^{2}}}\left(E+{\frac {e^{2}}{r}}\right)=\beta .}

Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.

Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален n2.{\displaystyle n^{2}.} Число n называется главным квантовым числом. Оно может иметь значения от 1 до ∞.{\displaystyle \infty .} Его связь с энергией см. ниже.

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).

Магнитное квантовое число ml{\displaystyle m_{l}} определяет проекцию орбитального момента количества движения на выбранную ось в магнитном поле. Эта проекция равна mlℏ.{\displaystyle m_{l}\hbar .}

Математическое описание атома водорода[править | править код]

Энергетический спектр[править | править код]

Энергетические уровни атома водорода, включая подуровни тонкой структуры, записываются в виде

Enj=E0n2(1+α2n2(nj+12−34)){\displaystyle E_{nj}={\frac {E_{0}}{n^{2}}}\left(1+{\frac {\alpha ^{2}}{n^{2}}}\left({\frac {n}{j+{\frac {1}{2}}}}-{\frac {3}{4}}\right)\right)}

где

α{\displaystyle \alpha } — постоянная тонкой структуры,

j{\displaystyle j} — собственное значение оператора полного момента импульса.

Энергию E0{\displaystyle E_{0}} можно найти в простой модели Бора, с массой электрона me{\displaystyle m_{e}} и зарядом электрона e:

E0=−mee48h3ε02{\displaystyle E_{0}=-{\frac {m_{e}e^{4}}{8h^{2}\varepsilon _{0}^{2}}}} (в системе СИ),

где h — постоянная Планка, ε0 −{\displaystyle \varepsilon _{0}~-} электрическая постоянная. Величина E₀ (энергия связи атома водорода в основном состоянии) равна 13,62323824 эВ = 2,182700518⋅10⁻¹⁸ Дж. Эти значения несколько отличаются от действительного значения E₀, поскольку в расчёте не учтена конечная масса ядра и эффекты квантовой электродинамики.

Волновые функции[править | править код]

В сферических координатах волновые функции имеют вид:

ψnlm(r,θ,φ)=(n−l−1)!2n⋅(n+l)!⋅(2na0)32⋅exp⁡(−rna0)⋅(2rna0)lLn−l−12l+1(2rna0)⋅Yl,m(θ,φ),{\displaystyle \psi _{nlm}(r,\theta ,\varphi )={\sqrt {\frac {(n-l-1)!}{2n{\cdot }(n+l)!}}}{\cdot }{\left({\frac {2}{na_{0}}}\right)}^{\frac {3}{2}}{\cdot }\exp {\left({-{\frac {r}{na_{0}}}}\right)}{\cdot }{\left({\frac {2r}{na_{0}}}\right)}^{l}L_{n-l-1}^{2l+1}{\left({\frac {2r}{na_{0}}}\right)}\cdot Y_{l,m}(\theta ,\varphi ),}

где:

a0{\displaystyle a_{0}} — Боровский радиус.

Ln−l−12l+1(2rna0){\displaystyle L_{n-l-1}^{2l+1}{\left({\frac {2r}{na_{0}}}\right)}} — обобщённые полиномы Лагерра степени (n−l−1){\displaystyle {(n-l-1)}} от функции 2rna0{\displaystyle {\frac {2r}{na_{0}}}}

Yl,m(θ,φ){\displaystyle Y_{l,m}(\theta ,\varphi )} — нормированные на единицу сферические функции.

Угловой момент[править | править код]

Собственные значения для оператора углового момента:

L2|n,l,m⟩=ℏ2l(l+1)|n,l,m⟩,{\displaystyle L^{2}|n,l,m\rangle ={\hbar }^{2}l(l+1)|n,l,m\rangle ,}

Lz|n,l,m⟩=ℏm|n,l,m⟩.{\displaystyle L_{z}|n,l,m\rangle =\hbar m|n,l,m\rangle .}

Нахождение энергии электрона из модели Бора[править | править код]

Вычислим уровни энергии атома водорода без учёта тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения e24πε0rn2{\displaystyle {\frac {e^{2}}{4\pi \varepsilon _{0}r_{n}^{2}}}} центростремительной силе mev2r,{\displaystyle {\frac {m_{e}v^{2}}{r}},} получим:

e24πε0rn=mevn2.{\displaystyle {\frac {e^{2}}{4\pi \varepsilon _{0}r_{n}}}=m_{e}v_{n}^{2}.}

Здесь

Модели строения атомов

Первые сведения о сложном строении атома были получены при изучении процессов прохождения электрического тока через жидкости. В тридцатых годах XIX в. опыты выдающегося физика М. Фарадея навели на мысль о том, что электричество существует в виде отдельных единичных зарядов.

Открытие самопроизвольного распада атомов некоторых элементов, названное радиоактивностью, стало прямым доказательством сложности строения атома. В 1902 году английские учёные Эрнест Резерфорд и Фредерик Содди доказали, что при радиоактивном распаде атом урана превращается в два атома – атом тория и атом гелия. Это означало, что атомы не являются неизменными, неразрушимыми частицами.

Модель атома Резерфорда

Исследуя прохождение узкого пучка альфа-частиц через тонкие слои вещества, Резерфорд обнаружил, что большинство альфа-частиц проходит сквозь металлическую фольгу, состоящую из множества тысяч слоёв атомов, не отклоняясь от первоначального направления, не испытывая рассеяния, как будто бы на их пути не было никаких препятствий. Однако некоторые частицы отклонялись на большие углы, испытав действие больших сил.

На основании результатов опытов по наблюдению рассеивания альфа-частиц в веществе Резерфорд предложил планетарную модель строения атома. Согласно этой модели строение атома подобно строению солнечной системы. В центре каждого атома имеется положительно заряженное ядро радиусом ≈ 10^-10м подобно планетам обращаются отрицательно заряженные электроны. Почти вся масса сосредоточена в атомном ядре. Альфа-частицы могут без рассеяния проходить через тысячи слоёв атомов так, как большая часть пространства внутри атомов пуста, а столкновения с лёгкими электронами почти не влияют на движение тяжёлой альфа-частицы. Рассеяние альфа-частиц происходит при столкновениях с атомными ядрами.

Модель атома Резерфорда не смогла объяснить все свойства атомов.

Согласно законам классической физики атом из положительно заряженного ядра и электронов, обращающимся по круговым орбитам, должен излучать электромагнитные волны. Излучение электромагнитных волн должно приводить к уменьшению запаса потенциальной энергии в системе ядро – электрон, к постепенному уменьшению радиуса орбиты электрона и падению электрона на ядро. Однако атомы обычно не излучают электромагнитные волны, электроны не падают на атомные ядра, то есть атомы устойчивы.

Квантовые постулаты Н. Бора

Для объяснения устойчивости атомов Нильс Бор предложил отказаться от привычных классических представлений и законов при объяснении свойств атомов.

Основные свойства атомов получают последовательное качественное объяснение на основе принятия квантовых постулатов Н. Бора.

1. Электрон вращается вокруг ядра только по строго определенным (стационарным) круговым орбитам.

2. Атомная система может находиться лишь в определённых стационарных или квантовых состояниях, каждому из которых соответствует определённая энергия Е. Атом не излучает энергию в стационарных состояниях.

Стационарное состояние атома с минимальным запасом энергии называется основным состоянием, все остальные состояния называются возбуждёнными (квантовыми) состояниями. В основном состоянии атом может находиться бесконечно долго, время жизни атома в возбуждённом состоянии длится 10^-9-10^-7 секунды.

3. Излучение или поглощение энергии происходит только при переходе атома из одного стационарного состояния в другое. Энергия кванта электромагнитного излучения при переходе из стационарного состояния с энергией Е_m в состояние с энергией Е_nравна разности энергий атома в двух квантовых состояниях:

∆Е = Е_m – Е_n = hv,

где v – частота излучения, h = 2ph = 6,62 ∙ 10^-34 Дж ∙с.

Квантовая модель строения атома

В дальнейшем некоторые положения теории Н. Бора были дополнены и переосмыслены. Наиболее значительным изменением стало введение понятие об электронном облаке, которое сменило понятие об электроне только как частице. Позже теорию Бора сменила квантовая теория, которая учитывает волновые свойства электрона и других элементарных частиц, образующих атом.

Основой современной теории строения атома является планетарная модель, дополненная и усовершенствованная. Согласно данной теории, ядро атома состоит из протонов (положительно заряженных частиц) и нейронов (не имеющих заряда частиц). А вокруг ядра по неопределённым траекториям движутся электроны (отрицательно заряженные частицы).

Остались вопросы? Хотите знать больше о моделях строения атома?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Квантовые постулаты Бора. Модель атома водорода по Бору. Трудности теории Бора. Квантовая механика

Квантовые постулаты Бора. Модель атома водорода по Бору. Трудности теории Бора. Квантовая механика

Квантовые постулаты Бора. Модель атома водорода по Бору
Трудности теории Бора. Квантовая механика

«Физика — 11 класс»

Квантовые постулаты Бора. Модель атома водорода по Бору

Выход из крайне затруднительного положения в теории атома был найден в 1913 г. датским физиком Нильсом Бором на пути дальнейшего развития квантовых представлений о процессах в природе.

Эйнштейн оценивал проделанную Бором работу «как высшую музыкальность в области мысли», всегда его поражавшую.
Основываясь на разрозненных опытных фактах, Бор благодаря гениальной интуиции правильно предугадал путь развития теории атома.

Постулаты Бора

Последовательной теории атома Бор, однако, не разработал.
Он в виде постулатов сформулировал основные положения новой теории.
Причем и законы классической физики не отвергались им безоговорочно.
Новые постулаты, скорее, налагали лишь некоторые ограничения на рассматриваемые классической физикой движения.

Успех теории Бора был тем не менее поразительным, и всем ученым стало ясно, что Бор нашел правильный путь развития теории.
Этот путь привел впоследствии к созданию стройной теории движения микрочастиц — квантовой механики.

Первый постулат Бора

Cуществуют особые, станционарные состояния атома, находясь в которых атом не излучает энергию, при этом электроны в атоме движутся с укорением.
Каждому стационарному состоянию соответствует определенная энергия Е_n.

Bторой постулат Бора

Излучение света происходит при переходе атома из стационарного состояния с большей энергией E_k в стационарное состояние с меньшей энергией Е_n. Энергия излученного фотона равна разности энергий стационарных состояний:

hv_kn

= Е_k — Е_n

Отсюда частоту излучения можно выразить так:

Согласно теории Бора энергия электрона в атоме водорода, находящегося на n-м энергетическом уровне, равна:

При поглощении света атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией.

Второй постулат, также как и первый, противоречит электродинамике Максвелла, так как согласно этому постулату частота излучения света свидетельствует не об особенностях движения электрона, а лишь об изменении энергии атома.

Свои постулаты Бор применил для построения теории простейшей атомной системы — атома водорода.
Основная задача состояла в нахождении частот электромагнитных волн, излучаемых водородом.

Эти частоты можно найти на основе второго постулата и правила определения стационарных значений энергии атома.
Это правило (правило квантования) Бору опять-таки пришлось постулировать.

Модель атома водорода по Бору

Используя законы механики Ньютона и правило квантования, на основе которого определяются возможные стационарные состояния атома, Бор смог вычислить радиусы орбит электрона и энергии стационарных состояний атома.
Минимальный радиус орбиты определяет размеры атома.
На рисунке значения энергий стационарных состояний (в электрон- вольтах

¹) отложены на вертикальной оси.

В атомной физике энергию принято выражать в электронвольтах (сокращенно эВ).
1 эВ равен энергии, приобретаемой электроном при прохождении им разности потенциалов 1 В: 1 эВ = 1,6 • 10^-19 Дж.

Теория Бора приводит к количественному согласию с экспериментом для значений этих частот.
Все частоты излучений атома водорода составляют в своей совокупности ряд серий, каждая из которых образуется при переходах атома в одно из энергетических состояний со всех верхних энергетических состояний (состояний с большей энергией).

Переходы в первое возбужденное состояние (на второй энергетический уровень) с верхних уровней образуют

серию Бальмера.
На рисунке эти переходы изображены стрелками.

Е₃ → Е₂, Е₄ → Е₂, Е₃ → Е₂, Е₆ → Е₂.

Данная серия названа по имени швейцарского учителя И. Бальмера, который еще в 1885 г. на основе экспериментальных данных получил простую формулу для определения частот видимой части спектра водорода.

Поглощение света

Поглощение света — процесс, обратный излучению.
Атом, поглощая свет, переходит из низших энергетических состояний в высшие.
При этом он поглощает излучение той же самой частоты, которую излучает, переходя из высших энергетических состояний в низшие.

На основе двух постулатов и правила квантования Бор определил радиус атома водорода и энергии стационарных состояний атома.
Это позволило вычислить частоты излучаемых и поглощаемых атомом электромагнитных волн.

Трудности теории Бора. Квантовая механика

Наибольший успех теория Бора имела в применении к атому водорода, для которого оказалось возможным построить количественную теорию спектра.

Однако разработать количественную теорию для следующего за водородом атома гелия на основе боровских представлений не удалось.
Относительно атома гелия и более сложных атомов теория Бора позволяла делать лишь качественные (хотя и очень важные) заключения.

Это и неудивительно.

Ведь теория Бора является половинчатой, внутренне противоречивой.
С одной стороны, при разработке теории атома водорода использовались привычные законы механики Ньютона и давно известный закон Кулона, а с другой — вводились квантовые постулаты, никак не связанные с механикой Ньютона и электродинамикой Максвелла.

Введение в физику квантовых представлений требовало радикальной переработки как механики, так и электродинамики.
Эта переработка была осуществлена в начале второй четверти XX в., когда были созданы новые физические теории: квантовая механика и квантовая электродинамика.

Постулаты Бора оказались совершенно правильными.
Но они рассматривались уже не как постулаты, а как следствия основных принципов этих теорий.
Правило же квантования Бора, как выяснилось, применимо далеко не всегда.

Представление об определенных орбитах, по которым движется электрон в атоме Бора, оказалось весьма условным.
На самом деле движение электрона в атоме имеет очень мало общего с движением планет по орбитам.
Если бы атом водорода в наинизшем его энергетическом состоянии можно было сфотографировать с большой выдержкой, то мы увидели бы облако с переменной плотностью.

Большую часть времени электрон находится на определенном расстоянии от ядра.
Это расстояние можно принять за грубое подобие радиуса орбиты.
Фотография атома совсем не походила бы на привычный рисунок Солнечной системы, а скорее напоминала бы расплывчатое пятно, полученное при фотографировании бабочки, порхающей около фонаря.

В настоящее время с помощью квантовой механики можно ответить практически на любой вопрос, относящийся к строению и свойствам электронных оболочек атомов.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Атомная физика. Физика, учебник для 11 класса — Класс!ная физика

Строение атома. Опыты Резерфорда — Квантовые постулаты Бора. Модель атома водорода по Бору. Трудности теории Бора. Квантовая механика — Лазеры — Краткие итоги главы

Квантовые постулаты Бора. Модель атома водорода по Бора

Тип урока: Урок конструирования знаний.

Цели:

1. Ввести учащихся в процесс отыскания противоречий между законами классической физики и постулатами Бора.
2. Обеспечить выдвижение учащимися гипотезу, объясняющую стабильность атома.
3. Объяснить линейчатый спектр излучения атома водорода.

Оборудование: Мультимедийное сопровождение.

Ход урока

1. Организационный момент.
2. Проверка домашнего задания, ответы на вопросы:
   • с какой целью был поставлен опыт Резерфорда, какие были сделаны выводы из этих опытов;
   • планетарная модель атома.
3. Изучение нового материала:
   1. неприменимость законов классической физики к явлениям, происходящим внутри атома;
   2. постулаты Бора;
   3. спектр излучения атома водорода;
   4. трудности теории Бора.
4. Подведение итогов урока.

Из опытов Резерфорда непосредственно вытекает планетарная модель атома. В центре расположено положительно заряженное атомное ядро, в котором сосредоточена почти вся масса атома. В целом атом нейтрален. Поэтому число внутриатомных электронов, как и заряд ядра, равно порядковому номеру элемента в периодической системе. Ясно, что покоиться электроны внутри атома не могут, т.к. они упали бы на ядро. Они движутся вокруг ядра, подобно тому, как планеты обращаются вокруг Солнца. Такой характер движения электронов определяется действием кулоновских сил со стороны ядра.

В атоме водорода вокруг ядра обращается всего лишь один электрон. Ядро атома водорода имеет положительный заряд, равный по модулю заряду электрона, и массу примерно в 1836,1 раза большую массы электрона. Это ядро названо протоном и стало рассматриваться как элементарная частица. Размер атома – это радиус орбиты его электрона.

На основе этой модели нельзя объяснить факт существования атом, его устойчивость. Ведь движение электронов по орбитам происходит с ускорением, причем весьма немалым.

Ускоренно движущийся заряд по законам электродинамики Максвелла должен излучать электромагнитные волны с частотой, равной частоте его обращения вокруг ядра. Излучение сопровождается потерей энергии. Теряя энергию, электроны должны приблизиться к ядру. Как показывают строгие расчёты, основанные на механике Ньютона и электродинамике Максвелла электрон за ничтожно малое время (порядка 10^-8с) должны упасть на ядро. Атом должен прекратить свое существование.

В действительности ничего подобного не происходит. Атомы устойчивы и в невозбужденном состоянии могут существовать неограниченно долго, совершенно не излучая электромагнитные волны.

Не согласующийся с опытом вывод о неизбежной гибели атома вследствие потери энергии на излучение – результат применения законов классической физики к явлениям, происходящим внутри атома. Отсюда следует, что к явлениям атомных масштабов законы классической физики неприменимы.

Выход из крайне затруднительного положения в теории в теории атома был найден в 1913 г. датским физиком Нильсом Бором. На пути дальнейшего развития квантовых представлений о процессах в природе.

Последовательной теории атома Бор, однако, не дал. Он в виде постулатов сформулировал основные положения новой теории. Причём и законы классической физики не отвергались им безоговорочно. Новые постулаты, скорее, налагали лишь некоторые ограничения, на допускаемые классической физикой движения.[1]

Первый постулат Бора (постулат стационарных состояний) [2]:

В атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.

В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию [2]:

  (n = 1, 2, 3, … )

где – m_e – масса электрона, – его скорость по n-й орбите радиуса r_n,

Второй постулат Бора(правило частот) [2]:

При переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией:

hv = E_n – E_m

равной разности энергий соответствующих стационарных состояний.

При E_m< E_nпроисходит излучение фотона, при E_m> E_n – его поглощение. Набор возможных дискретных частот h = (E_n – E_m)/h квантовых переходов и определяет линейчатый спектр атома.

Спектр излучения атома водорода

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем-систем, состоящих из ядра с зарядом Ze и одного электрона, а также теоретически вычислить постоянную Ридберга.

Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами.

Выражение для радиуса n-й стационарной орбиты [2]:

, где n = 1, 2, 3, …

Из этого выражения следует, что радиусы орбит растут пропорционально – -квадратам целых чисел.

Для атома водорода(Z=1) радиус первой орбиты электрона при n =1, называемый первым Боровским радиусом (а) равен [2]

= 0,52810^-10 м = 52,8 пм

Учитывая квантованные для радиуса n-й стационарной орбиты, энергия электрона может принимать только следующие дозволенные дискретные значения [2]:

  (n = 1, 2, 3, …)

Согласно теории Бора при движении электрона по ближайшей к ядру дозволенной орбите атом находится в основном состоянии, являющимся наиболее устойчивым. В основном состоянии атом может находиться неограниченно долгое время, поскольку это состояние соответствует наименьшему возможному энергетическому уровню атома. Когда электрон движется по какой-либо другой из дозволенных орбит, состояние атома называется возбужденным. Через небольшое время (порядка 10-8с) атом самопроизвольно переходит из возбужденного состояния в основное, излучая при этом квант энергии. На рисунке 2 изображена схема атома водорода, на которой показаны возможные орбиты электрона [2].

, откуда частота излучения

, где

R=3,29×10¹⁵с^-1 – постоянная Ридберга.

На рисунке 1 изображены энергетические уровни атома водорода, соответствующие различным орбитам электрона. Из рисунка видно, что при переходе электрона с более высоких орбит на первую освобождается энергии гораздо больше, чем при переходе на вторую. Это объясняет, почему серия Лаймана лежит в ультрафиолетовой части спектра, а серия Бальмера – в видимой части.

Энергетические уровни атома водорода

Рис. 1. Энергетические уровни атома водорода.

Рис. 2. Дозволенные орбиты электрона в атоме водорода (стрелками указаны возможные переходы электрона с одной орбиты на другую).

Спектр поглощения атома водорода является линейчатым, но содержит только серию Лаймана. Он также объясняется теорией Бора. Так как свободные атомы водорода обычно находятся в основном состоянии (стационарное состояние с наименьшей энергией при n=1), то при сообщении атомам извне определённой энергии могут наблюдаться лишь переходы атомов из основного состояния в возбуждённое (возникает серия Лаймана).

Теория Бора была крупным шагом в развитии атомной физики и являлась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны применяет законы классической физики, а с другой – основывается на квантовых постулатах). Она рассмотрела спектры атома водорода и водородоподобних систем и вычислила частоты спектральных линий, однако не смогла объяснить их интенсивности и ответить на вопрос: почему совершаются те или иные переходы? Серьёзным недостатком теории Бора была невозможность описания с её помощью спектра атома гелия – одного из простейших атомов, непосредственно следующего за атомом водорода.

Итог урока:

• Разъясните смысл постулатов Бора. Как с их помощью объясняется линейчатый спектр атома водорода?
• Найти наибольшую длину волны в ультрафиолетовом спектре водорода. [4]

Использованная литература:

1. Физика: Учеб. для 11 кл. общеобразоват. учреждений / Г.Я Мякишев, Б.Б.Буховцев. – 9-е изд. – М.: Просвещение, 2002. – 336 с.
2. Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1990. – 478 с.
3. Жданов Л.С. Учеб. по физике для средних специальных учеб. заведений. – М.: Наука, 1975. – 592 с.
4. Рымкевич А.П. Физика. Задачник. 10-11 кл.: Пособие для общеобразоват. учеб. заведений. – 5-е изд., перераб. — М.: Дрофа, 2001. – 192 с.

Математическая модель атома водорода | VAEN.RU

Автор идеи: Зуев Б.К.

Автор статьи: Выволокин В.В.

Введение

Атом водорода является простейшим по своей структуре. Как известно атом водорода имеет ядро, состоящее из одного протона, и одного электрона, расположенного на 1s-орбитали. Поскольку протон и электрон имеют разноименный заряд, то между ними действует сила Кулона. Также известно, что ядра атомов имеют собственный магнитный момент и следовательно собственное магнитное поле. При движение заряженных частиц в магнитном поле на них действует сила Лоренца, которая направлена перпендикулярно вектору скорости частицы и вектору магнитной индукции. Очевидно, что силы Кулона и силы Лоренца недостаточно, для того чтобы электрон оставался на своей орбитали, необходима также сила отталкивания между электроном и протоном. Современные квантовые представления не дают четкого ответа, чем конкретно вызвана квантованность орбиталей и следовательно энергий электрона в атоме. В рамках данной стать мы и рассмотрим причины квантования и получим уравнения описывающие поведения электрона в атоме. Напомню, что по современным представлениям положение электрона в атоме описывается вероятностным уравнение Шредингера. Мы же получим чисто механическое уравнение, которое даст возможность определить положение электрона в любой момент времени, что покажет несостоятельность принципа Гейзенберга.

Баланс сил

На рисунке 1 представлены все силы, которые действуют в атоме.

Рисунок 1 – силы, действующие на электрон в атоме водорода

Запишем второй закон Ньютона для приведенной на рисунке системы сил.

(1)

Запишем систему уравнений проекций этих сил на координатные оси XYZ.

(2)

Здесь угол – это угол между радиус-вектором r(t) и плоскостью XY,

угол – угол между осью X и проекцией радиус-вектора r(t) на плоскость XY.

Распишем каждую силу в системе (2) через известные формулы с учетом их проекций на оси.

Сила Кулона

, (3)

где – электрическая постоянная равная

– модуль заряда электрона или протона

– координаты электрона в выбранной системе координат

Потенциальная сила гравитационных волн

Подробнее об этой силе можно узнать из монографии [1]

(4)

– массы электрона и протона соответственно.

X – Коэффициент пропорциональности численно равный квадрату скорости света.

Сила Лоренца

Как известно сила Лоренца вычисляется следующим образом

(5)

Векторное произведение (5) может быть представлено в компонентах на оси ортогональной систему координат:

(6)

В системе уравнений (6) необходимо определить компоненты вектора магнитной индукции .

Поскольку магнитный момент ядра атома водорода вызван кольцевым током, движущихся в нем по-настоящему элементарных частиц [1], то в соответствии с законом Био-Савара-Лапласа, полученного для кольца с током, запишем компоненты вектора магнитной индукции:

(7)

угол – это угол обхода кольцевого контура

– радиус протона

– сила тока в кольцевом контуре протона

– магнитная постоянная

Центробежная сила

Как известно центробежная сила действует по нормали к траектории движения тела и зависит от массы тела, кривизны траектории и скорости движения.

(8)

– мгновенная кривизна траектории

– скорость электрона относительно начала координат

– вектор нормали к траектории движения электрона

Мгновенная кривизна траектории определяется выражением

(9)

– первая и вторая производные от радиус-вектора по времени.

Скорость электрона – есть корень из суммы квадратов его проекций на оси координат, которые в свою очередь являются первыми производными от проекций радиус-вектора по времени т.е.

(10)

Единичный вектор нормали к траектории движения электрона определяется выражением

(11)

Раскрывая векторные произведения через компоненты вектора на оси координат, записывая радиус вектор через его компоненты, подставляем выражения (9), (10) и (11) в (8), получаем компоненты центробежной силы в проекциях на оси координат:

(12)

Определив проекции всех сил, входящих в систему уравнений (2) её можно переписать, учитывая следующие выражения:

 

Результирующая система имеет вид:

Найти аналитическое решение этой системы не представляется возможным. Решение можно получить численными методами решения систем дифференциальных уравнений второго порядка. Решение приведено в видео-ролике ниже.

Энергетические уровни электрона определяются целым количеством резонансных стоячих волн (шлейф пучностей за электроном), возникающих по траектории движения электрона. Если энергия поглощённого электроном фотона соответствует энергии необходимой для образования целого количества стоячих волн, движение электрона в них повторяется, делая их резонансными, тем самым фотон удерживается электроном определенное время и мы наблюдаем картину поглощения электроном фотона и затем его излучение. Фотоны, энергия которых не приводит к возникновению целого количества пучностей по траектории движения электрона, не захватываются, т.к. резонансной волны не образуется и картины поглощения-излучения не наблюдается.

Список использованных источников

1. Теория рождения и эволюции материи. Зуев Б.К. Самара: Изд-во “СамВен”, 1995.

с вашего сайта.

Модели строения атома

1. Модель Томсона

Первая модель строения атома была предложена Дж. Томсоном в 1904 г., согласно которой атом – положительно заряженная сфера с вкрапленными в нее электронами. Несмотря на свое несовершенство томсоновская модель позволяла объяснить явления испускания, поглощения и рассеяния света атомами, а также установить число электронов в атомах легких элементов.

Рис. 1. Атом, согласно модели Томсона. Электроны удерживаются внутри положительно заряженной сферы упругими силами. Те из них, которые находятся на поверхности, могут легко «выбиваться» , оставляя ионизированный атом.

0. 2.2 Модель Резерфорда

Модель Томсона была опровергнута Э. Резерфордом (1911 г.), который доказал, что положительный заряд и практически вся масса атома сконцентрированы в малой части его объема – ядре, вокруг которого двигаются электроны (рис. 2).

Рис. 2. Эта модель строения атома известна как планетарная, т. к. электроны вращаются вокруг ядра подобно планетам солнечной системы.

Согласно законам классической электродинамики, движение электрона по окружности вокруг ядра будет устойчивым, если сила кулоновского притяжения будет равна центробежной силе. Однако, в соответствии с теорией электромагнитного поля, электроны в этом случае должны двигаться по спирали, непрерывно излучая энергию, и падать на ядро. Однако атом устойчив.

К тому же при непрерывном излучении энергии у атома должен наблюдаться непрерывный, сплошной спектр. На самом деле спектр атома состоит из отдельных линий и серий.

Таким образом, данная модель противоречит законам электродинамики и не объясняет линейчатого характера атомного спектра.

2.3. Модель Бора

В 1913 г. Н. Бор предложил свою теорию строения атома, не отрицая при этом полностью предыдущие представления. В основу своей теории Бор положил два постулата.

Первый постулат говорит о том, что электрон может вращаться вокруг ядра только по определенным стационарным орбитам. Находясь на них, он не излучает и не поглощает энергию (рис.3).

Рис. 3. Модель строения атома Бора. Изменение состояния атома при переходе электрона с одной орбиты на другую.

При движении по любой стационарной орбите запас энергии электрона (Е_1, Е₂ …) остается постоянным. Чем ближе к ядру расположена орбита, тем меньше запас энергии электрона Е₁ ˂Е₂ …˂ Е_n . Энергия электрона на орбитах определяется уравнением:

где m – масса электрона, h – постоянная Планка, n – 1, 2, 3… (n=1 для 1-ой орбиты, n=2 для 2-ой и т.д.).

Второй постулат говорит о том, что при переходе с одной орбиты на другую электрон поглощает или выделяет квант (порцию) энергии.

Если подвергнуть атомы воздействию (нагреванию, облучению и др.), то электрон может поглотить квант энергии и перейти на более удаленную от ядра орбиту (рис. 3). В этом случае говорят о возбужденном состоянии атома. При обратом переходе электрона (на более близкую к ядру орбиту) энергия выделяется в виде кванта лучистой энергии – фотона. В спектре это фиксируется определенной линией. На основании формулы

,

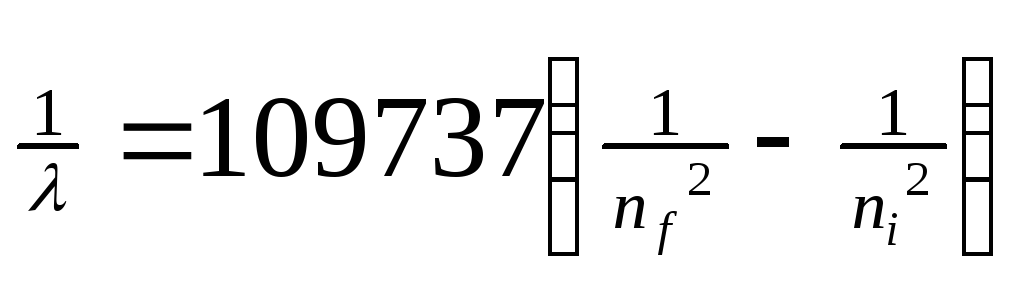где λ – длина волны, n = квантовые числа, характеризующие ближнюю и дальнюю орбиты, Бор рассчитал длины волн для всех серий в спектре атома водорода. Полученные результаты соответствовали экспериментальным данным. Стало ясным происхождение прерывистых линейчатых спектров. Они – результат излучения энергии атомами при переходе электронов из возбужденного состояния в стационарное. Переходы электронов на 1-ю орбиту образуют группу частот серии Лаймана, на 2-ю – серию Бальмера, на 3-ю серию Пашена (рис. 4,табл. 1).

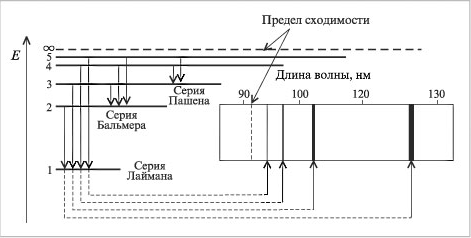
Рис. 4. Соответствие между электронными переходами и спектральными линиями атома водорода.

Таблица 1

Проверка формулы Бора для серий водородного спектра

Название серии	λ, А Экспериментальная	λ, А Вычисленная Бором
Пашена	18751,3 12817,5 10938,0 10049,8	18756 12822 10941 10052
Бальмера	6564,66 4862,71 4102,91 3971,20 3799,00 3712,70	6564,70 4862,80 4341,70 4102,93 3971,23 3799,01 3712,62
Лаймана	1216 1028 972	1215,68 1025,73 972,5

Однако, теория Бора не смогла объяснить расщепление линий в спектрах многоэлектронных атомов. Бор исходил из того, что электрон – это частица, и использовал для описания электрона законы, характерные для частиц. Вместе с тем накапливались факты, свидетельствующие о том, что электрон способен проявлять и волновые свойства. Классическая механика оказалась не в состоянии объяснить движение микрообъектов, обладающих одновременно свойствами материальных частиц и свойствами волны. Эту задачу позволила решить квантовая механика – физическая теория, исследующая общие закономерности движения и взаимодействия микрочастиц, обладающих очень малой массой (табл. 2).

Таблица 2

Свойства элементарных частиц, образующих атом

Частица	Заряд		Масса
	Кл	Условн.ед.	г	А.е.м.
Электрон	— 1,6·10-19	-1	9,10·10-28	0,00055
Протон	1,6·10-19	+1	1,67·10-24	1,00728
Нейтрон	0	0	1,67·10-24	1,00866

Квантово-химические модели атомов и молекул

 

Современные представления о строении атомов и молекул, понимание химических превращений вещества на атомном и молекулярном уровне его организации раскрывает квантовая химия.

С позиции квантовой химии атом – это микросистема, состоящая из ядра и электронов, движущихся в электромагнитном поле ядра. На рис. 1 представлены орбитальные, электронные и электронографические модели атомов первого и второго периодов, построенные с использованием квантовых принципов и правил заполнения электронами энергетических уровней в атомах. Четыре квантовых числа n, l, m_l, m_s полностью характеризуют движение электронов в поле ядра. Главное квантовое число n характеризует энергию электрона, его удалённость от ядра и соответствует номеру энергетического уровня, на котором находится электрон. Орбитальное квантовое число l определяет форму орбитали и энергию подуровней одного и того же энергетического уровня. Понятие «орбиталь» означает наиболее вероятную область движения электрона в атоме. Магнитное квантовое число m_l определяет число орбиталей и их пространственную ориентацию. Главное, орбитальное и магнитное квантовые числа взаимосвязаны. Орбитальное квантовое число l принимает значения на единицу меньше, чем главное квантовое числоn. Если n = 1, то l = 0,  и по форме это сферическая 1s-орбиталь. Если n = 2, то орбитальное квантовое число принимает два значения: l = 0, 1, указывающие на наличие двух подуровней.  Это сферическая 2s— орбиталь (l = 0) и три 2p-орбитали, напоминающие по форме гимнастические гантели, расположенные под углом 90^о по осям декартовой системы координат.

 

Рисунок 1.  Квантово-химические, электронные и электронографические модели атомов первого и второго периодов

 

Число и пространственное расположение 2p-орбиталей определяет магнитное квантовое числоm_l, которое принимает значения в пределах изменения орбитального квантового числа от –l до +l. Если l = 0, то m_l = 0 (одна s—орбиталь). Если l = 1, то m_l принимает три значения –1, 0, +1 (три р-орбитали).

Орбитальные модели атомов показывают пространственное расположение и форму орбиталей, а на электронографических моделях в виде символических квантовых ячеек  дано изображение орбиталей и положение уровней и подуровней на энергетической диаграмме. Следует обратить внимание на размеры атомов. В периодах повторяется одна и та же закономерность – по мере увеличения заряда ядра происходит возрастающая деформация (сжатие) орбиталей под действием электромагнитного притяжения электронов ядром (рис. 1).

Размещение электронов на орбиталях подчиняется одному из важнейших принципов квантовой механики (принцип Паули): на одной орбитали может находиться не больше двух электронов, причем они должны различаться собственным моментом количества движения – спином (англ. spin вращение). Электроны, различающиеся спинами, условно изображают стрелками ­ и ¯. Когда на одной орбитали находятся два электрона, они имеют антипараллельные спины и не мешают друг другу двигаться в поле ядра.

Это свойство напоминает вращение в зацеплении двух шестеренок. Находясь в зацеплении, одна шестеренка вращается по часовой стрелке, другая – против часовой стрелки. Третья шестеренка в зацеплении с двумя другими останавливает вращение. Она лишняя. Так и на одной орбитали может находиться лишь 2 электрона, третий – лишний.

При заполнении электронами энергетических уровней и подуровней в действие вступает квантовый принцип минимума энергии (правило Клечковского). Электроны заполняют орбитали от низшего к высшему энергетическому уровню. Принцип минимума энергии напоминает заполнение этажей многоэтажного дома в период наводнения. Вода поднимается и заполняет все этажи снизу вверх, не пропуская ни одного.

В соответствии с правилом Хунда все р-орбитали заполняются сначала одним электроном и только затем вторым с антипараллельным спином.

Квантовохимические модели атомов позволяют объяснить свойства атомов обмениваться энергией, отдавать и присоединять электроны, изменять геометрическую конфигурацию, образовывать химические связи.

Ковалентная химическая связь образуется при перекрывании валентных электронных облаков. Например, такая связь представлена в орбитальной модели молекулы водорода (рис. 2).

 

Рисунок 2. Модель ковалентной связи в молекуле водорода

 

Использование квантовохимического метода валентных связей основано на представлении, о том, что каждая пара атомов в молекуле удерживается вместе при помощи одной или нескольких электронных пар с антпараллельными спинами. С позиции метода валентных связей молекула – это микросистема, состоящая из двух или большего числа ковалентно связанных атомов.Положительно заряженные ядра атомов удерживаются отрицательным зарядом, сосредоточенным в области перекрывания атомных орбиталей. Притяжение ядер атомов к повышенной электронной плотности между ними уравновешивается силой отталкивания ядер между собой. Образуется устойчивая микросистема, в которой длина ковалентной связи равна расстоянию между ядрами.

В молекуле фтора так же, как и в молекуле водорода, имеется неполярная ковалентная связь. При перекрывании 2р¹-орбиталей электронная пара создает между ядрами атомов повышенную электронную плотность и удерживает молекулу в устойчивом состоянии (рис. 3).

 

F–F

Рисунок 3. Модель ковалентной связи в молекуле фтора

 

Под неполярной ковалентной связью подразумевается такое перекрывание валентных орбиталей, в результате которого совпадают центры тяжести положительных и отрицательных зарядов.

Возможно образование полярной ковалентной связи при перекрывании 1s¹— и 2р¹-орбиталей. На рис. 4 представлена модель фтороводорода с полярной ковалентной связью. Электронная плотность между ковалентно связанными атомами смещается к атому фтора, заряд ядра которого (+9) оказывает большее электромагнитное притяжение по сравнению с ядром атома водорода с зарядом (+1).

 

H–F

Рисунок 4. Модель полярной ковалентной связи в молекуле фтороводорода

 

Ионная связь обусловлена притяжением электрически заряженных частиц – ионов. На рис. 5 представлена модель образования ионной связи во фториде лития. Сильное электромагнитное поле, создаваемое ядром атома фтора, захватывает и удерживает на р-орбитали электрон, принадлежавший атому лития. Атом лития, лишенный электрона, изменяет геометрическую конфигурацию (исчезла 2s-орбиталь), становится положительно заряженным ионом и притягивается к отрицательно заряженному иону фтора, который приобрел лишний электрон на р-орбиталь.

 

Рисунок 5. Модель ионной пары Li⁺F^— фторида лития

 

Силы электростатического притяжения противоположно заряженных ионов и отталкивания электронных оболочек ионов лития и фтора уравновешены и удерживают ионы на расстоянии, соответствующем длине ионной связи. Перекрывание орбиталей в соединениях с ионной связью практически отсутствует.

Особый вид химической связи проявляется в атомах металлов. Кристалл металла (рис. 6) состоит из положительно заряженных ионов, в поле которых свободно движутся валентные электроны («электронное облако»).

 

Рисунок 6. Модель кристалла металлического лития

 

Ионы и «электронное облако» взаимно удерживают друг друга в устойчивом состоянии. Благодаря высокой подвижности электронов металлы обладают электронной проводимостью.

В молекулах атомы, связанные несколькими ковалентными связями, изменяют геометрическую конфигурацию. Рассмотрим проявление этого свойства на примере атома углерода (1s²-орбиталь в моделях атома углерода не изображена, т.к. не участвует в образовании химической связи).

Экспериментально установлено, что в молекуле СН₄ атом углерода образует с атомами водорода четыре одинаковые ковалентные связи, эквивалентные по своим энергетическим и пространственным характеристикам. Трудно представить четыре одинаковые ковалентные связи, если иметь в виду, что в углероде валентные электроны располагаются на двух энергетических 2s и 2p подуровнях:

В основном (невозбужденном) состоянии углерод образует лишь две ковалентные связи. В возбужденном состоянии один электрон с подуровня 2s переходит на более высокий энергетический подуровень 2p. В результате такого перескока электрона увеличивается суммарная энергия 2s— и 2p-орбиталей и валентность атома углерода изменяется до четырех:

И все же этого недостаточно, чтобы объяснить четыре равноценные ковалентные связи в молекуле СН₄, т.к. 2s— и 2p-орбитали имеют разную форму и пространственное расположение. Проблема была решена введением гипотезы огибридизации – смешении валентных электронов в подуровнях одного и того же энергетического уровня. В молекуле метана одна 2s— и три 2р-орбитали атома углерода в результате гибридизации превращаются в четыре равноценные sp³-гибридные орбитали:

В отличие от невозбужденного (основного) состояния атома углерода, в котором три 2р-орбитали атома расположены под углом 90^о (рис. 7,а), в молекуле метана (рис. 7,b) равноценные по форме и размерам sp³ -гибридные атома углерода расположены под углом 109^о28^‘.

 

Рисунок 7. Модель молекулы метана

 

В молекуле этилена С₂Н₄ (рис. 8,а) атомы углерода находятся в sр²-гибридном состоянии. В гибридизации участвует 2s-орбиталь и две 2р-орбитали. В результате гибридизации атомы углерода образуют три равноценные sp²-гибридные орбитали, расположенные под углом 120^о на плоскости; 2p_z-орбиталь не участвует в гибридизации.

 

Рисунок  8. Модель молекулы этилена

 

В молекуле этилена атомы углерода связаны не только s-связью, но и  p-связью. Она образуется в результате перекрывания р_z-орбиталей с образованием двух областей перекрывания над и под осью, соединяющей ядра, по обе стороны от оси s-связи (рис.8).

Модель тройной связи представлена в молекуле ацетилена (рис. 9). При смешении одной 2s— и одной 2р_х—орбитали атома углерода образуются две sp-гибридные орбитали, которые располагаются на линии, соединяющей ядра атомов (угол 180^о). Негибридные 2р_у—и2р_z-орбитали разных атомов углерода перекрываются, образуя две p-связи во взаимно перпендикулярных плоскостях (рис. 9).

 

Рисунок  9. Модель молекулы ацетилена

 

Молекулы, подобно атомам, проявляют свойство разрывать и образовывать химические связи, изменять геометрическую конфигурацию, переходить из электронейтрального в ионное состояние. Указанные свойства представлены в реакции между молекулами аммиака NН₃ и фтороводорода HF (рис. 10). Разрывается ковалентная связь в молекуле фтороводорода, и образуется ковалентная донорно-акцепторная связь между азотом и водородом в молекуле аммиака. Донором выступает неподелённая пара электронов атома азота, акцептором – вакантная орбиталь атома водорода (рис. 10). Геометрическая конфигурация молекулы NН₃ (тригональная пирамида, валентный угол 107^о18′) изменяется на тетраэдрическую конфигурацию иона NН₄⁺ (109^о28′). Завершающим процессом является образование ионной связи в кристаллической структуре фторида аммония. Орбитальные модели молекул позволяют показать все перечисленные выше свойства в одной реакции: разрывать и образовывать химические связи, изменять геометрическую конфигурацию, переходить из электронейтрального в ионное состояние.

 

Рис. 10. Модель образования ионной пары кристаллического NH₄⁺F^—

 

Химическая реакция с использованием символов химических элементов:

NН₃ + HF → NН₄F,

дает обобщенное выражение того, что раскрыто в орбитальных моделях молекул. Химические реакции, представленные орбитальными моделями и символами химических элементов, взаимно дополняют друг друга. В этом их достоинство. Овладение элементарными знаниями квантово-химического выражения структуры и состава атомов и молекул ведет к пониманию ключевых химических понятий: ковалентная полярная и неполярная связь, донорно-акцепторная связь, ионная связь, геометрическая конфигурация атомов и молекул, химическая реакция. И на фундаменте этих знаний можно уверенно использовать символику химических элементов и соединений для краткого описания химических состояний и превращений вещества.

Приведем ещё пример реакции, рассматриваемой с позиций квантовой химии. Вода проявляет свойства слабого электролита. Электролитическую диссоциацию обычно представляют уравнением:

Н₂О ⇄Н⁺ + ОН^—

или

Н₂О + Н₂О ⇄Н₃О⁺ + ОН^—.

Деление молекул воды на положительно и отрицательно заряженные ионы раскрывает квантовохимическая модель реакции электролитической диссоциации (рис. 11).

 

Рисунок 11. Модель электролитической диссоциации воды

 

Молекула воды представляет собой искаженную пирамиду (валентный угол 104^о30′). Две sр³-гибридные орбитали атома кислорода образуют s-связи с атомами водорода. Две другие sр³-гибридные орбитали располагают свободными парами электронов с антипараллельными спинами. Разрыв ковалентной Н−О связи в одной из молекул приводит к образованию на соседней молекуле ковалентной химической связи по донорно-акцепторному механизму. Ион водорода, располагающий вакантной орбиталью, выступает в роли акцептора электронной пары атома кислорода соседней молекулы воды. В этом примере, как и в предыдущем, квантово-химический подход позволяет понять физико-химический смысл процесса электролитической диссоциации воды.

***

Мышление – это процесс, с помощью которого мы опосредствованно можем судить о том, что скрыто от нашего чувственного восприятия. Квантовая химия дает зрительный образ химических процессов и состояний вещества, раскрывает то, что скрыто от нашего чувственного восприятия, побуждает учиться и размышлять.