НОУ ИНТУИТ | Лекция | Цифровая модуляция
Аннотация: В лекции рассматриваются методы модуляции, применяемые при передаче широкополосной информации – фазовая манипуляция, квадратурно-амплитудная модуляция, амплитудно фазовая модуляция с подавлением несущей, сверточные и решетчатые коды, турбо кодирование, цифровой многотональный сигнал
Сведения о системах модуляции
В настоящее время все абонентские терминалы преобразуют сигналы в цифровую форму. Одна из важнейших проблем, как на абонентском участке, так и участке соединительных линий обеспечить максимальную скорость передачи цифровой информации.
Существующая абонентская проводная сеть имеет громадный объем. Замена ее на более скоростную среду передачи, например, на оптоволоконную среду, подобна замене песка на всех пляжах мира и не всегда возможна по экономическим причинам.
Поэтому основная задача, которую успешно решают связисты мира увеличение пропускной способности существующей.
Всегда возникает основной вопрос, телефонная связь уже существует более 150 лет. Эта проводная сеть рассчитана на диапазон человеческого голоса или точнее на пропускание аналоговой частоты в диапазоне от 0,3 до 3,4 кГц.
Как же удалось сегодня многократно увеличить этот диапазон и сделать возможным передачу информации, которая требует ресурс в более чем 100 раз. Это достигнуто различными способами, но в основном благодаря разработке способов модуляции.
Наиболее применяемый в настоящее время класс модуляции фазовый. Мы постепенно рассмотрим этот вид. Начиная от простейших видов такой модуляции, а потом рассмотрим наиболее применяемые методы.
Многоуровневая передача сигналов
Цифровое преобразование сигналов подразумевает двоичное кодирование сигналов. Когда же нужно получить высокую скорость передачи данных в условиях ограниченной полосы прибегают к методам повышения информационной емкости передаваемых символов. Одним из таких методов является многоуровневая система, когда каждый сигнал может принимать несколько уровней амплитуды в зависимости от значения исходного символа. Скорость передачи данных в многоуровневой системе передачи равна.
| ( 4.1) |
где
- – уровней, которые могут быть выбраны для передачи сигналов в данном интервале,
Скорость передачи сигнала, равная обычно называется скоростью передачи символов и измеряется в бодах. На практике понятие «бод» обычно понимают как синоним скорости в битах. Однако, строго говоря, скорость передачи в битах равна скорости передачи в бодах только в случае двоичной передачи (один бит за один интервал сигнала).
На рис.4.1 показан пример восьмиуровневого сигнала. Это позволяет увеличить скорость передачи 3 бита на сигнальный интервал (т.е. 3 бита на бод).
Рис. 4.1. Многоуровневая передача с тремя битами на сигнальный интервал
В современных системах примером применения такой системы может служить организация цифровой абонентской линии в системе ISDN (Integrated Services Digital Network), в которой для достижения скорости 160 кбит/с. используется четырехуровневая передача [ 2 ]
Фазовые методы модуляции
Фазовые методы модуляции XE «Фазовые методы модуляции» являются, в какой — то степени аналогами многоуровневой передачи сигналов, поскольку тоже позволяют увеличить информационную емкость передаваемого символа.
Фазовая манипуляция
Фазовая модуляция связана с манипуляцией фазы. При такой манипуляции для получения бинарного сигнала в каждом тактовом интервале используется одна из фаз, отличающаяся на 180 градусов.
Возможна также многоуровневая ФМ. Фазовая манипуляция XE «Фазовая манипуляция» в настоящее время – наиболее распространенная форма модуляции.
Популярность этого типа модуляции определяется, прежде всего, наличием постоянной огибающей, что обеспечивает то, что она нечувствительна к изменениям уровня сигнала, влиянию затухания и характеристикам аппаратуры усиления и обеспечивает хорошую характеристику. С точки зрения отношения сигнал шум () системы фазовой модуляции обеспечивают оптимальные (теоретически) значения характеристик ошибок.
Общий вид n-уровневой фазовой манипуляции отображается формулой
| ( 4.1) |
где
- -величина, на которую отличаются фазы соседних сигналов;
- — симметричный n –уровневый сигнал «без возвращения к нулю» (NRZ – non return to zero) c уровнями и т.д.
Рис. 4.2. Фазовые манипуляции: а – 2ФМ; б – 4ФМ
На рис.4. 2 показаны примеры типичных 2-ФМ и 4-ФМ – сигналов. На рисунке скорость передачи при 4-ФМ, в два раза меньше, чем 2-ФМ, что обеспечивает одинаковую скорость передачи данных (из-за увеличения информационной емкости). На этом рисунке приведены фазовые диаграммы для косинусоидального сигнала (см. формулу 4.1).
Теория радиоволн: аналоговая модуляция / Habr
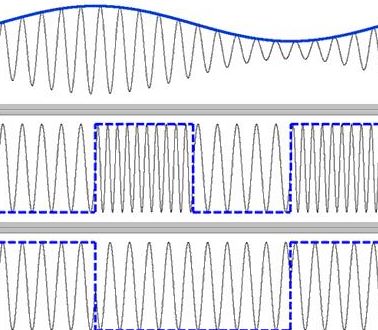
Продолжаем серию общеобразовательных статей, под общим названием «Теория радиоволн».
В предыдущих статьях мы познакомились с радиоволнами и антеннами:
Давайте ближе познакомимся с модуляцией радиосигнала.
В рамках этой статьи, будет рассмотрена аналоговая модуляция следующих видов:
- Амплитудная модуляция
- Амплитудная модуляция c одной боковой полосой
- Частотная модуляция
- Линейно-частотная модуляция
- Фазовая модуляция
- Дифференциально-фазовая модуляция
Амплитудная модуляция
При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.
Спектр АМ
Данный спектр свойственен для модулирующего колебания постоянной частоты.
На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции <=1, амплитуды боковых полос меньше или равны половине амплитуды несущей.
Полезная информация заключена только в верхней или нижней боковых полосах спектра. Основная спектральная составляющая — несущая, не несет полезной информации. Мощность передатчика при амплитудной модуляции в большей части расходуется на «обогрев воздуха», за счет не информативности самого основного элемента спектра.
Амплитудная модуляция с одной боковой полосой
В связи с неэффективностью классической амплитудной модуляции, была придумана амплитудная модуляция с одной боковой полосой.
Суть ее заключается в удалении из спектра несущей и одной из боковых полос, при этом вся необходимая информация передается по оставшейся боковой полосе.
Но в чистом виде в бытовом радиовещании этот вид не прижился, т.к. в приемнике нужно синтезировать несущую с очень высокой точностью. Используется в аппаратуре уплотнения и любительском радио.
При такой модуляции соотношение качество/эффективность наилучшим образом достигается.
Частотная модуляция
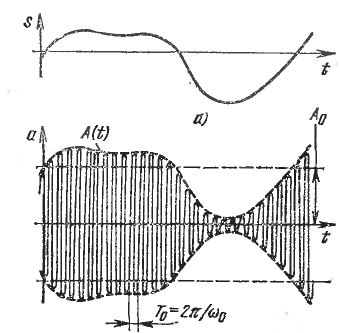
Вид аналоговой модуляции, при которой, частота несущей изменяется по закону модулирующего низкочастотного сигнала. Амплитуда при этом остается постоянной.
а) — несущая частота, б) модулирующий сигнал, в) результат модуляции
Наибольшее отклонение частоты от среднего значения, называется девиацией.
В идеальном варианте, девиация должна быть прямо пропорционально амплитуде модулирующего колебания.
Спектр при частотной модуляции выглядит следующим образом:
Состоит из несущей и симметрично отстающей от нее вправо и влево гармоник боковых полос, на частоту кратную частоте модулирующего колебания.
Данный спектр представляет гармоническое колебание. В случае реальной модуляции, спектр имеет более сложные очертания.
Различают широкополосную и узкополосную ЧМ модуляцию.
В широкополосной — спектр частот, значительно превосходит частоту модулирующего сигнала. Применяется в ЧМ радиовещании.
В радиостанциях применяют в основном узкополосную ЧМ модуляцию, требующую более точной настройки приемника и соответственно более защищенную от помех.
Спектры широкополосной и узкополосной ЧМ представлены ниже
Спектр узкополосной ЧМ напоминает амплитудную модуляцию, но если учесть фазу боковых полос, то окажется, что эти волны имеют постоянную амплитуду и переменную частоту, а не постоянную частоту и переменную амплитуду (AM). При широкополосной ЧМ амплитуда несущей может быть очень малой, что обусловливает высокую эффективность ЧМ; это значит, что большая часть передаваемой энергии содержится в боковых частотах, несущих информацию.
Основные преимущества ЧМ, перед АМ — энергоэффективность и помехоустойчивость.
Как разновидность ЧМ, выделяют Линейно-частотную модуляцию.
Суть ее заключается в том, что частота несущего сигнала изменяется по линейному закону.
Практическая значимость линейно-частотно-модулированных (ЛЧМ) сигналов заключается в возможности существенного сжатия сигнала при приеме с увеличением его амплитуды над уровнем помех.
Фазовая модуляция
В реальности, больше применяют термин фазовая манипуляция, т.к. в основном производят модуляцию дискретных сигналов.
Смысл ФМ таков, что фаза несущей, изменяется скачкообразно, при приходе очередного дискретного сигнала, отличного от предыдущего.
Из спектра можно видеть, почти полное отсутствие несущей, что указывают на высокую энергоэффективность.
Недостаток данной модуляции в том, что ошибка в одном символе, может привести к некорректному приему всех последующих.
Дифференциально-фазовая манипуляция
В случае этой модуляции, фаза меняется не при каждом изменении значения модулирующего импульса, а при изменении разности. В данном примере при приходе каждой «1».
Преимущество этого вида модуляции в том, что в случае возникновения случайной ошибки в одном символе, это не влечет дальнейшую цепочку ошибок.
Стоит отметить, что существуют также фазовые манипуляции такие как квадратурная, где используется изменение фазы в пределах 90 градусов и ФМ более высоких порядков, но их рассмотрение выходит за рамки данной статьи.
PS: хочу еще раз отметить, что цель статей не заменить учебник, а рассказать «на пальцах» об основах радио.
Рассмотрены лишь основные виды модуляций для создания у читателя представления о теме.
3. Общие понятия о многоуровневой модуляции.
3.1 Поле сигналов
Для передачи информационного сигнала по каналу используется синусоидальный сигнал U(t) = Asin(2πfНt + φ), параметрами которого являются амплитуда A, несущая частота fН, и фазовый угол φ. Если зафиксировать m вариантов сочетаний параметров Ar, φr,
r =1,… m, то получим m различных сигналов Ur(t) = Arsin(2πfНt + φr).
Разделим цифровой поток на фрагменты из n последовательно расположенных элементов. Число таких фрагментов, отличающихся друг от друга, равно m=2n. Каждому фрагменту, который называется кортежем, поставим в соответствие один из m различных сигналов Ur(t).
Таким образом, реализуется процесс m уровневой модуляции сигнала несущей частоты сигналом цифрового потока.
Получить m вариантов сочетания параметров Ar, φr, r =1,… m можно множеством способов. Один из вариантов, т.е. один из методов модуляции, является наиболее помехоустойчивым и называется квадратурно-амплитудным методом КAM m [6].
В общем случае, следуя теории многоуровневой модуляции [6], можно рассмотреть плоскость, на которой расположено множество точек, каждая из которых соответствует n-значному двоичному числу, n=ln m/ln2, где m – число уровней модуляции.
Каждой r-ой
точке из множества, 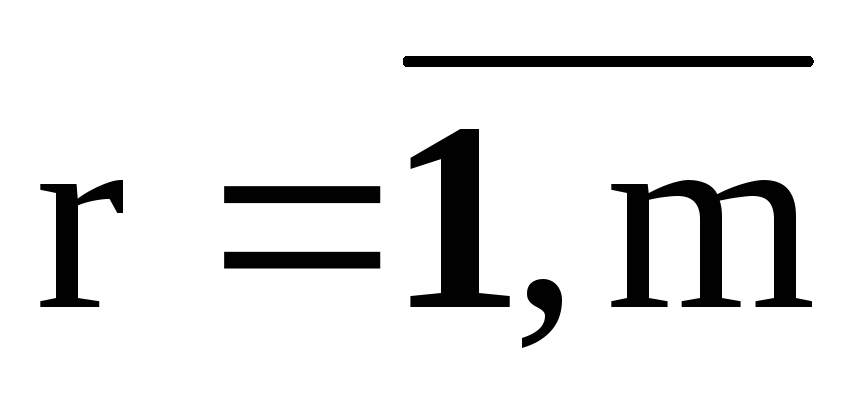 ставится в соответствие сигнал
ставится в соответствие сигнал 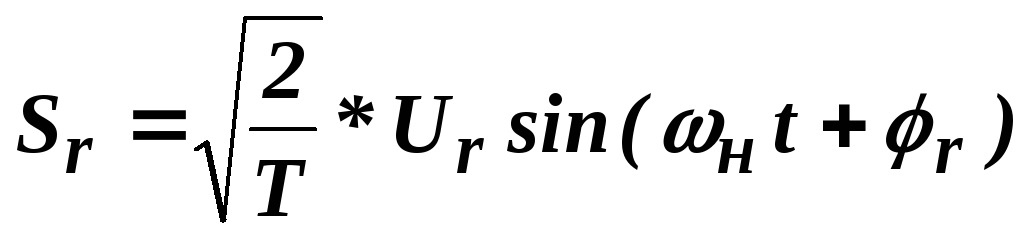 ,
являющиёся гармоническим колебанием
с частотой несущей
,
являющиёся гармоническим колебанием
с частотой несущей ,
амплитудой
,
амплитудой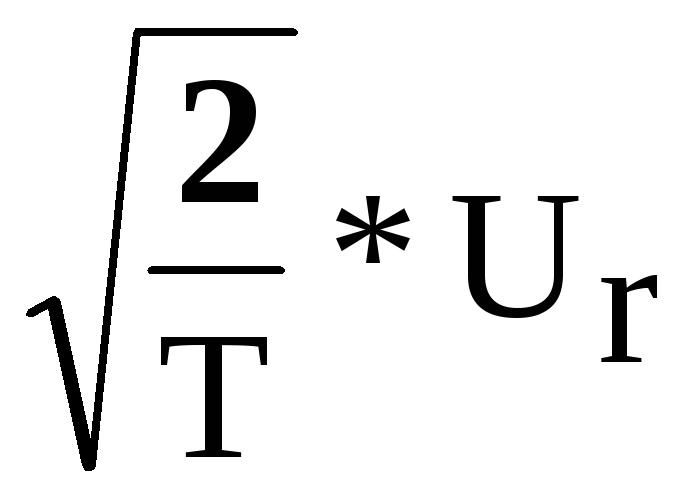 и начальной фазойφr
и начальной фазойφr
Этот сигнал генерируется в передатчике и, пройдя через среду распространения, поступает на вход приемника.
Таким образом, налицо пространство сигналов, которое будем рассматривать как двумерное функциональное гильбертово пространство.
Выделим в этом
пространстве ортонормированный базис 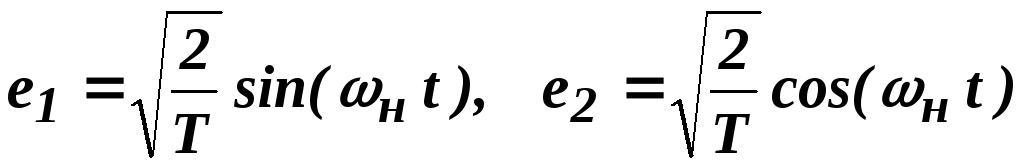 и запишем сигналSr в этом базисе:
и запишем сигналSr в этом базисе:
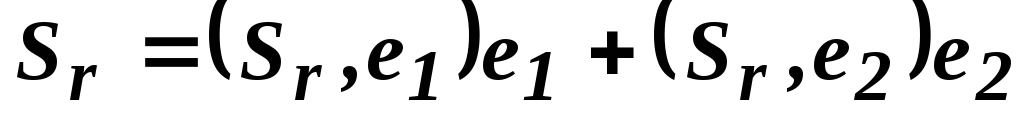 (3.1)
(3.1)
Скалярное произведение в гильбертовом пространстве определяется в виде:
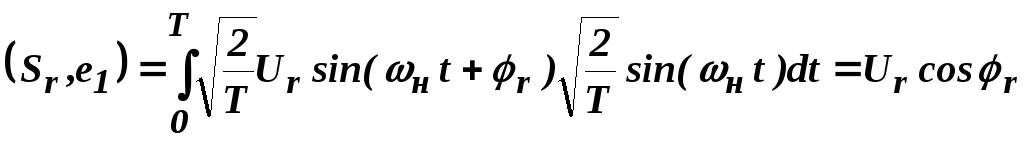 (3.2)
(3.2)
 (3.3)
(3.3)
Подставим (3.2), (3.3) в (3.1):
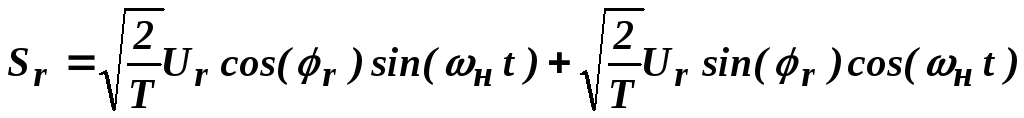 (3.4)
(3.4)
Выражение (3.4) представляет собой запись операций над сигналами, которые производятся в передающих устройствах транспортирования многоуровневого сигнала. Эти устройства построены по принципу квадратурной обработки, т.е. имеют два квадратурных канала в соответствии со структурой устройства, представленной на рисунке 3.5. На вход 1 поступает n-значное двоичное число, на выходе 2 – сигнал Ursin(ωн t + φr).

Рис. 3.5. Структура передающего устройства (1 – Вход, 2 – Выход)
Из
(3.4) следует, что сигнал  можно рассматривать, как вектор в
евклидовом пространстве с осямиI и Q,
координаты которого задаются синфазной
составляющей
можно рассматривать, как вектор в
евклидовом пространстве с осямиI и Q,
координаты которого задаются синфазной
составляющей 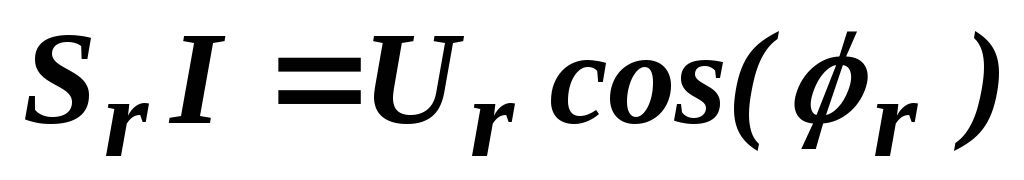 (осьI)
и квадратурной составляющей
(осьI)
и квадратурной составляющей  (осьQ).
(осьQ).
Такое представление сигналов, называемое полем сигналов (constellation), изображено на рис.6.4 для частного случая многоуровневой модуляции – квадратурно-амплитудной модуляции КАМ 64.
3.2 Квадратурно-амплитудная модуляция
Системы m- уровневых сигналов КАМ m обладают свойством эквидистантности. Это свойство определяется как одинаковость расстояний между соседними сигналами, отличающимися по номеру на единицу.

Рис. 3.6 Созвездие сигналов КАМ 64
Следуя определению расстояния D в гильбертовом пространстве, запишем:
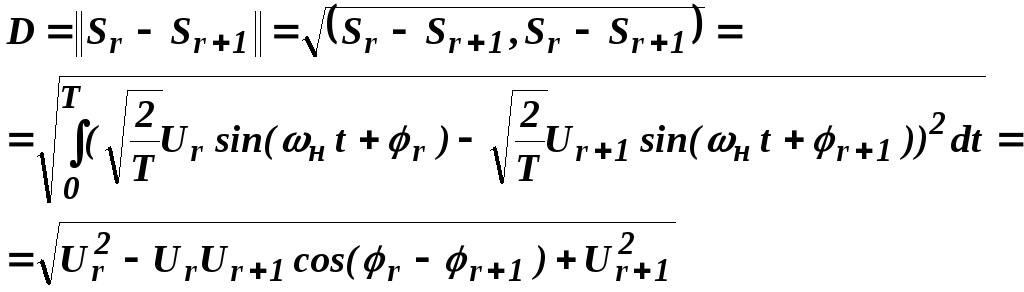
Условие эквидистантности записывается в виде:
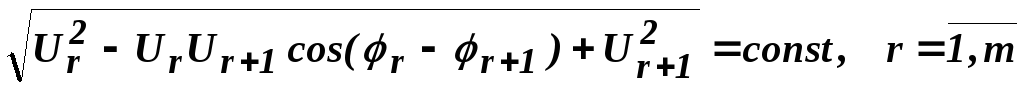
Оно выполняется, если сигналы располагаются в узлах координатной сетки поля сигналов. На рис. 3.6 изображено созвездие сигналов КAM 64, характерное тем, что расстояние между соседними точками (сигналами) одинаково. Это и определяет наибольшую помехоустойчивость сигналов КAM 64 по сравнению с другими шестидесяти четырёх уровневыми сигналами.
В соответствии с рис. 3.5 на вход устройства поступает кортеж, т.е. фрагмент цифрового потока, состоящий из n последовательно расположенных элементов (видеоимпульсов). Кортежу с номером r соответствует точка звёздного поля с амплитудой Ur и фазой φr. В обоих квадратурных каналах производится вычисление амплитуд ортогональных сигналов.
Для этого кортеж, рассматриваемый как n-значный двоичный сигнал, подразделяется на два двоичных сигнала. Каждый из них поступает в свой квадратурный канал и преобразуется в аналоговый сигнал, называемый символом, длительность которого равна длительности кортежа, а амплитуда равна амплитуде гармонического сигнала в квадратурном канале в соответствии с (3.4).
Таким образом, длительность модулирующего сигнала с m-уровневой модуляцией в n раз (n=Ln m/Ln 2) меньше чем длительность видеоимпульса исходного цифрового потока. Соответственно во столько же раз уменьшается ширина спектра передаваемого по каналу сигнала. Применение многоуровневых сигналов позволяет согласовать ширину спектра сигнала источника информации с шириной диапазона частот, занимаемого каналом.
3. Сигналы. Виды сигналов и их параметры. Введение в специальность
Характеристики различных сигналов
Все сигналы могут быть подразделены на периодические и непериодические.
Периодическим называется сигнал, значения которого повторяются через определенные равные промежутки времени, называемые периодом повторения сигнала, или просто периодом. Для непериодического сигнала это условие не выполняется.
Простейшим периодическим сигналом является гармоническое колебание.
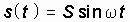 ,
,
где S, w – амплитуда и угловая частота колебания.
Другим примером периодического сигнала является последовательность прямоугольных импульсов (рис. 3.2, а). Как вы думаете, из чего состоит эта последовательность импульсов? Оказывается, из синусоид. Взгляните на рис. 3.2. В качестве исходной синусоиды выберем такую, у которой период колебаний совпадает с периодом T прямоугольных импульсов (рис. 3.2, б)
 , (3.1)
, (3.1)
где 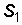 – амплитуда синусоиды, а
– амплитуда синусоиды, а 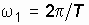 .
.
Колебание (3.2.) заданной частоты  и амплитуды
и амплитуды 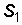 можно представить в виде графика: на оси частот отметить значение
можно представить в виде графика: на оси частот отметить значение  и изобразить вертикальную линию высотой, равной амплитуде сигнала
и изобразить вертикальную линию высотой, равной амплитуде сигнала 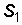 (см. рис. 3.2, б).
(см. рис. 3.2, б).
Следующая синусоида имеет частоту колебаний в 3 раза большую, а амплитуду – в 3 раза меньшую.
Сумма этих двух синусоид 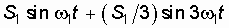 пока еще мало похожа на прямоугольные импульсы (рис. 3.2, в). Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9, 11, и т.д. раз большими, а с амплитудами в 5, 7, 9, 11, и т.д. раз меньшими, то сумма всех этих колебаний:
пока еще мало похожа на прямоугольные импульсы (рис. 3.2, в). Но если мы добавим к ним синусоиды с частотами колебаний в 5, 7, 9, 11, и т.д. раз большими, а с амплитудами в 5, 7, 9, 11, и т.д. раз меньшими, то сумма всех этих колебаний:
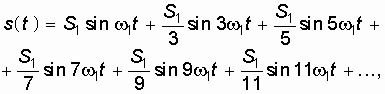
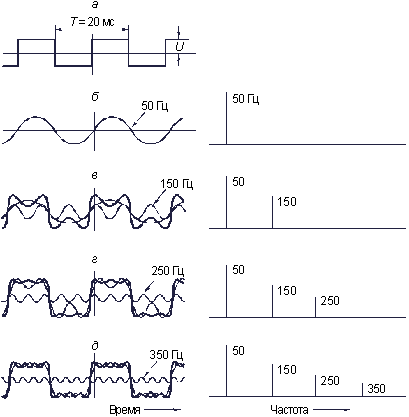
Рис. 3.2. Периодическая последовательность прямоугольных импульсов (а) и формирование ее сигнала (б–д)
где 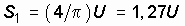 , будет не так уже сильно отличатся от прямоугольных импульсов (рис. 3.2, г и д). Таким образом, степень “прямоугольности” импульсов определяется тем, сколько синусоид со все более высокими частотами колебаний мы будем суммировать.
, будет не так уже сильно отличатся от прямоугольных импульсов (рис. 3.2, г и д). Таким образом, степень “прямоугольности” импульсов определяется тем, сколько синусоид со все более высокими частотами колебаний мы будем суммировать.
Может показаться, что представление прямоугольных импульсов в виде совокупности синусоид есть не более чем математический прием и не имеет никакого отношения к реальности. Однако это не так. Радиоинженерам хорошо знакомы приборы (они называются анализаторами спектров), которые позволяют выделить каждую входящую в сложный сигнал синусоиду.
Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно “разложить” на сумму обыкновенных синусоид, впервые доказал в 20-х годах прошлого века французский математик Ж. Фурье. Такой набор синусоид получил название спектра сигнала. Каждый сигнал (отличающийся от других по форме) имеет свой сугубо индивидуальный спектр, т.е. может быть получен только из синусоид со строго определенными частотами и амплитудами.
Непериодический сигнал легко получить из периодического, увеличивая период вплоть до 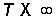 (рис. 3.3, а–г). Спектр амплитуд для сигналов с разными периодами показаны на рис. 3.4, а–в.
(рис. 3.3, а–г). Спектр амплитуд для сигналов с разными периодами показаны на рис. 3.4, а–в.
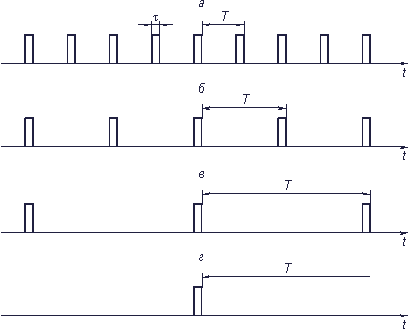
Рис. 3.3. Увеличение периода последовательности прямоугольных импульсов
При увеличении периода сигнала частота первой гармоники 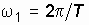 понижается. Спектральные линии становятся гуще. Амплитуды гармоник уменьшаются. Последнее становится понятным, если учесть, что энергия сигнала, оставаясь неизменной, перераспределяется теперь между возросшим числом гармоник. Естественно, доля каждой гармоники в общем сигнале падает.
понижается. Спектральные линии становятся гуще. Амплитуды гармоник уменьшаются. Последнее становится понятным, если учесть, что энергия сигнала, оставаясь неизменной, перераспределяется теперь между возросшим числом гармоник. Естественно, доля каждой гармоники в общем сигнале падает.
Следовательно, при переходе к непериодическому сигналу (например, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колебание, правда, бесконечно малой амплитуды.
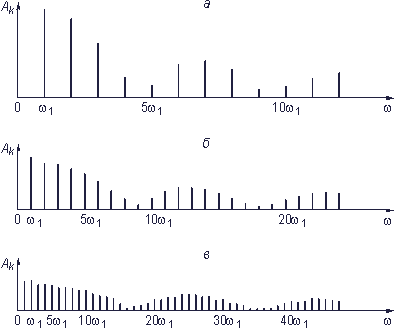
Рис. 3.4. Спектры амплитуд периодических последовательностей импульсов с разными периодами а–в см. в тексте
Поскольку сравнивать между собой бесконечно малые величины неудобно, то вместо амплитуд 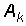 по оси ординат откладывают произведение
по оси ординат откладывают произведение 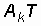 , которое с увеличением периода Т остается постоянным. В новых координатах спектры, показанные на рис. 3.4, а–в, будут выглядеть так, как показано на рис. 3.5, а–г. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз. Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.
, которое с увеличением периода Т остается постоянным. В новых координатах спектры, показанные на рис. 3.4, а–в, будут выглядеть так, как показано на рис. 3.5, а–г. Понятие спектра амплитуд здесь лишено смысла и заменяется понятием спектральной плотности амплитуд, которая указывает, по сути, на удельный вес бесконечно малой амплитуды синусоидального колебания в любой бесконечно узкой полосе частот. Понятие спектра фаз заменяется понятием спектральной плотности фаз. Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.
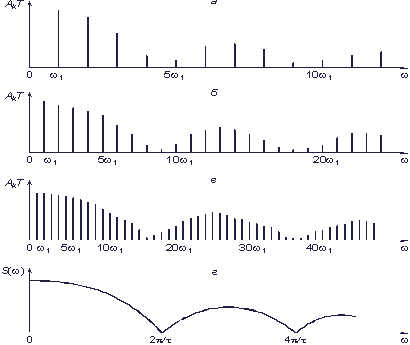
Рис. 3.5. Переход к спектральной плотности (г) одиночного прямоугольного импульса а–в см. в тексте
Уровни сигналов
Для сравнения мощностей сигналов, передаваемых по системе электросвязи, часто пользуются логарифмическими единицами – децибелами. Децибел (русское обознач. ДБ, международное – dB), как показывает приставка “деци”, составляет десятую часть другой, более крупной единицы, названной белом в честь А.Г. Белла – изобретателя телефона. Бел – это десятичный логарифм отношения двух мощностей. Если известны две мощности: Р1 и Р2, то их отношение, выраженное в белах, определяется формулой p=lg(P2/P1).
Для практики бел – слишком крупная величина. Обычно отношение мощностей выражают в децибелах, для чего при расчетах пользуются формулой p=10lg(p2/p1).
Динамический диапазон и пик-фактор сигналов. Мгновенная мощность сигналов связи может принимать различные значения в самых широких пределах. Чтобы охарактеризовать эти пределы, вводят понятия динамического диапазона и пик-фактора сигналов.
Динамический диапазон сигнала, дБ, определяется выражением:
Dc=10lg(Pmax/Pmin),
где Pmax, Pmin – максимальное и минимальное значения мгновенной мощности.
Пик-фактором сигнала называют отношение его максимальной мощности к средней, выраженное в логарифмических единицах:
Q=10lg(Pmax/Pср).
Пример. Пусть имеется периодический прямоугольный сигнал
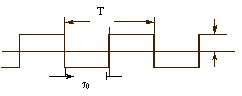
Он может быть разложен на составляющие с частотами f1=1/T, f3=3/T, f5=5/T и т.д. Число составляющих бесконечно, но чем выше частота, тем меньше амплитуда. Следовательно, теоретически полоса частот, которую занимает данный сигнал, стремится к Ґ .
Для передачи такого сигнала требуется канал, имеющий бесконечную полосу пропускания. Во-первых, таких каналов нет, во-вторых, чем шире полоса пропускания канала, тем он дороже. Но т.к. чем выше частота составляющей, тем ниже амплитуда, то составляющими с частотой і fn можно пренебречь.
Возьмём только составляющие f1, f3, f5. Полоса частот, которую занимают эти составляющие, f5 – f1=D fc.
Пусть f1=1000 Гц, f3=3000 Гц, f5=5000 Гц.
Занимаемая этими составляющими, полоса частот:
5000-1000 = 4000 Гц.
Уменьшим длительность единичного элемента в 3 раза, тогда f1=3000 Гц, f3=9000 Гц, f5=15000 Гц и занимаемая полоса 12000 Гц.
Вывод. Чем меньше длительность единичного элемента (t 0), тем шире полоса частот, занимаемая сигналом!
Отсюда следствие: чем больше скорость телеграфирования В, тем шире полоса частот, занимаемая сигналом, и тем шире требуется канал и, следовательно, тем дороже доставка информации.
Сигналы электросвязи и их спектры. Рассмотрим наиболее часто встречающиеся сигналы электросвязи и обсудим их спектры.
Телефонные (речевые) сигналы. Человек набрал в легкие воздух и издал звук. Что же произошло? Воздух, выходя из легких, заставляет вибрировать голосовые связки. От них колебания воздуха передаются через гортань голосовому аппарату, заканчивающемуся ротовой и носовой полостями (рис. 3.6).
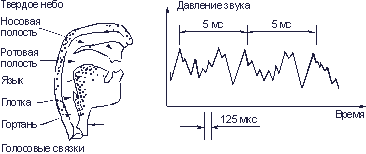
Рис. 3.6. Кривая звукового давления при произнесении звука «а» мужским голосом
Последние выполняют роль резонаторов – они усиливают колебания воздуха, подобно тому, как полый корпус гитары или скрипки, также являясь резонатором, усиливает звуки струн. Колебания воздуха из голосового аппарата человека передаются окружающему воздуху. Возникает звуковая волна. Характер издаваемого звука определяется натяжением голосовых связок, формой ротовой полости, положением языка, губ и т.д.Из описания голосового аппарата человека нетрудно понять, что голосовые связки играют роль своеобразных струн, они создают основной тон и обильное количество обертонов. Частота основного тона речи лежит в пределах от 50…80 Гц (очень низкий голос – бас) до 200…250 Гц (женский и детский голоса). При разговоре частота основного тона меняется в значительных пределах, особенно при переходе от гласных звуков к согласным и наоборот.
В совместном звучании основной тон и обертоны создают соответствующую окраску звука или тембр. Один тембр отличается от другого числом и силой обертонов. При преобладании в человеческом голосе высоких обертонов над низкими мы слышим в нем “звучание металла”. Люди, у которых в голосе преобладают низкие обертоны, говорят мягким, бархатным голосом.
Для получения формы кривой звукового давления, создаваемого речью человека, нужно сложить синусоидальные кривые основного тона и обертонов. Из-за наличия большого числа обертонов форма результирующей кривой будет сложной. На рис. 3.6 показано, какое давление создает звук “а”, произнесенный мужским голосом с частотой основного тона 200 Гц (период основного тона 5 мс). Для передачи звука на расстояние он в телефонном аппарате превращается в сигнал. Для этой цели служит микрофон.
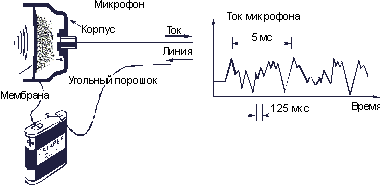
Рис. 3.7. Превращение звука в электрический сигнал с помощью микрофона
Телефон был изобретен А.Г. Беллом, учителем в школе глухонемых в американском городе Бостоне в 1876 г. С тех пор в его конструкцию было внесено много усовершенствований. В частности, в современном телефоне используется чувствительный угольный микрофон (рис. 3.7). В нем мембрана соприкасается с угольным порошком. Пока в микрофон не говорят, сопротивление порошка остается неизменным и через него от батареи в линию (провода) протекает постоянный ток. Стоит произнести в микрофон какое-нибудь слово, порошок под действием колеблющейся мембраны будет то спрессовываться, то разрыхляться. Изменение плотности порошка приводит к изменению его электрического сопротивления, а значит, и к изменению тока, текущего через порошок. В проводах, идущих от микрофона, рождается электрический ток, повторяющий форму звукового давления.
Изучение речи показывает, что речь – это процесс, частотный спектр которого находится в пределах от 50…100 до 8000…10000 Гц. Установлено однако, что качество речи остается вполне удовлетворительным, если ограничить спектр снизу и сверху частотами 300 и 3400 Гц. Эти частоты приняты Международным союзом электросвязи (МСЭ) в качестве границ эффективного спектра речи. При указанной полосе частот сохраняется хорошая разборчивость речи и удовлетворительная натуральность ее звучания.
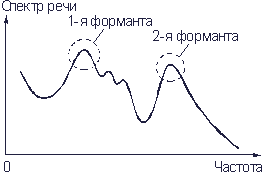
Рис. 3.8. Спектр человеческой речи
На рис. 3.8 показан спектр речи. Как видно из рисунка, некоторые частотные составляющие речи усилены, а другие ослаблены. Усиленные области спектра частот называются формантами. Звуки речи различных людей отличаются числом формант и их расположением в частотном спектре. Отдельные звуки могут иметь до шести формант, из которых только одна или две являются определяющими. Они обязательно находятся в диапазоне частот 300…3400 Гц. Между формантами лежат менее мощные составляющие звуковых частот. Однако именно они придают голосу каждого человека индивидуальность, позволяющую узнавать говорящего.
Сигналы звукового вещания. Источниками звука при передаче программ вещания обычно являются музыкальные инструменты или голос человека. Формирование сигналов звукового вещания и их прием осуществляется так же, как и телефонных сигналов. Используются лишь другие типы микрофонов.
Спектр звукового сигнала занимает полосу частот 20…20000 Гц. Однако в зависимости от требований к качеству воспроизведения ширина спектра сигнала вещания может быть ограничена. Для достаточно высокого качества (каналы вещания первого класса) полоса частот должна составлять 50…10000 Гц, для безукоризненного воспроизведения программ вещания (каналы высшего класса) – 30…15000 Гц.
Факсимильные сигналы. Обратите внимание на то, как вы читаете книгу. Ваши глаза скользят по строке слева направо, затем вы переходите к началу другой строки и т.д. до конца страницы. Словом вы “просматриваете” все элементы строки последовательно. Можно сказать, что при чтении книги происходит построчная развертка текстового изображения.
Именно по такому принципу “просматривается” изображение в современных факсимильных аппаратах, предназначенных для передачи на расстоянии различного рода неподвижных изображений (документов, чертежей, рисунков, фотографий). Для этого с помощью источника света и системы оптических линз формируют световое пятно так, чтобы освещать на передаваемом изображении площадку размером, скажем, 0,2ґ 0,2 мм. Это световое пятно перемещается сначала вдоль одной строки, затем переходит на другую и движется по ней – и так до конца последней строки. Свет, отражаясь от каждой элементарной площадки, попадает на фотоэлемент и вызывает в его цепи ток (рис. 3.9). Значение этого тока зависит от яркости отраженного света, а последняя – от яркости освещенной площадки. Таким образом, при переходе светового пятна на изображении от одной элементарной площадки к другой ток в цепи фотоэлемента меняется пропорционально яркости площадок: мы получаем точную электрическую копию изображения.
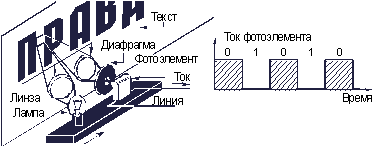
Рис. 3.9. Преобразование изображения в электрический сигнал в факсимильном аппарате
Рассмотрим изображение, состоящее только из двух цветов: черного и белого, например, страницу книги, какой-либо чертеж и т.п. Очевидно, каждый элемент изображения (напомним, что размером он всего 0,2ґ 0,2 мм) будет представлять собой либо черную, либо белую площадку, напоминая чередованием шахматную доску. Черные площадки практически полностью поглощают падающий на них свет. Яркость отраженного ими света при этом настолько ничтожна, что при просмотре черных площадок ток в цепи фотоэлемента не возникает. Наоборот, площадки белого цвета почти полностью отражают падающий на них свет, и при попадании на них светового луча ток в цепи фотоэлемента скачком принимает максимальное значение. Таким образом, перемещая световое пятно, а вслед за ним и фотоэлемент вдоль каждой строки изображения, получаем на выходе фотоэлемента последовательность импульсов (рис. 3.9).
При таком “шахматном” чередовании элементов изображения спектр факсимильного сигнала будет шире, чем для любого другого изображения, поскольку круче фронтов импульсов, чем у прямоугольных, не бывает.
Ширина спектра факсимильного сигнала зависит от скорости развертки изображения и размеров светового пятна.
На стандартном листе бумаги формата А4 в строке помещается примерно 1000 черно-белых элементов изображения при ширине пятна 0,2 мм. Если в факсимильном аппарате скорость развертки составляет 60 строк/мин, т.е. каждая строка считывается за 1 с, то за эту секунду 500 раз будет осуществлен переход с черного на белое, или наоборот. Это означает, что максимальная частота чередования импульсов равна 500 Гц. При ширине светового пятна 0,1 мм в строке будет в 2 раза больше элементов изображения, и максимальная частота чередования импульсов повысится до 1000 Гц. Так как для сохранения хорошей степени “прямоугольности” импульсов нужно передавать кроме основной гармоники еще и несколько высших, то ширина спектра факсимильного сигнала может простираться до 1,5…3,0 кГц.
При увеличении скорости развертки изображения черные и белые площадки будут считываться чаще и, следовательно, спектр факсимильного сигнала будет шире. При передаче изображений с полутонами получается сигнал сложной формы, спектр которого является непрерывным и соединяет все частоты от нуля до максимальной.
Факсимильная связь широко используется для передачи газетных полос (т.е. их изображений) в пункты централизованного печатания. Для передачи газет используют специальные высокоскоростные факсимильные аппараты с шириной светового пятна 0,05 мм. Повышенная скорость развертки позволяет передавать одну газетную полосу за 2–3 минуты. Это приводит к расширению спектра факсимильного сигнала до 180 кГц.
Телевизионные сигналы. Любое подвижное изображение – это, как правило, смена через каждые 40 мс одного неподвижного изображения другим (25 кадров в 1 с). За время между сменой кадров нужно успеть просмотреть все неподвижное изображение, которое содержит полмиллиона элементарных площадок или элементов изображения (625 строк по 833 элемента в строке). Значит, каждый элемент изображения придется рассматривать в течение одной полумиллионной доли от отведенных на весь кадр 40 мс. Это непостижимо короткий отрезок времени – всего две десятимиллиардных доли секунды! Ясно, что ни одно механическое устройство не способно перемещать световое пятно и фотоэлемент по строкам изображения с такой скоростью.
Вы никогда не задумывались над тем, что вы видите на экране телевизора, когда усаживаетесь перед ним в свободный вечер? Изображение? Нет, в действительности на экране никакого изображения нет, абсолютно никакого! Если бы мы сумели открыть глаза на какую-то ничтожную долю секунды (а речь идет о миллионных и даже миллиардных долях), то увидели бы на экране всего одну светящуюся точку. Это она бежит с невероятной скоростью по экрану, оставляя в нашем глазу след (мы видим то, чего уже нет, еще в течение 0,1 с), изменяющийся по яркости.
Что же заставляет светящуюся точку перемещаться с такой головокружительной быстротой? Электронный луч. Это он способен почти мгновенно отклоняться под действием изменяющегося магнитного поля и развертывать “картинки”. Это его можно очень точно сфокусировать с помощью специальных электрических “линз”. Первые опыты с электронным лучом начались в самом начале XX в. Еще в 1907 г. профессор Петербургского технологического института Б.Л. Розинг сконструировал первую электронно-лучевую трубку и получил на ней изображение, правда, невысокого качества. Изобретение в начале 30-х годов этого столетия первых качественных передающих трубок связано с именами советских ученых, пионеров отечественного телевидения С.И. Катаева и П.И. Шмакова.
Как бы не отличались конструкции передающих телевизионных трубок разных лет, все они в чем-то имитируют глаз. Роль хрусталика выполняет объектив, роль зрачка – диафрагма. Имеется в трубке и своя “сетчатка” – пластинка, напоминающая пчелиные соты, в ячейках которых располагаются микроскопические фотоэлементы. Конечно, их намного меньше, чем фоторецепторов в глазу: всего около 0,5 млн. Изображение, которое нужно превратить в серию электрических импульсов, проектируется с помощью объектива на эту искусственную “сетчатку”. Каждый микроскопический фотоэлемент (представляющий собой капельку светочувствительного серебряно-цезиевого сплава) получает свою порцию света и, если его подключить к внешней цепи, создаст ток, пропорциональный освещенности. Что касается электронного луча, то он как раз и подключает поочередно каждый из 500000 фотоэлементов к внешней цепи трубки, причем отводится ему на это всего 40 мс, пока не сменится кадр. Таким образом, на одном элементе изображения луч “задерживается” не более 80 миллиардных долей секунды (т.е. 80 нс). Величина тока во внешней цепи трубки отражает в каждый момент времени яркость соответствующего элемента изображения, спроектированного объективом на “сетчатку” передающей трубки, и является точной электронной копией передаваемого изображения.
Подсчитаем ширину спектра телевизионного сигнала. Пусть и на этот раз чередуются черные и белые площадки (элементы). Всего таких элементов будет 625 строк ґ 833 элемента = 520 625. В секунду меняется 25 кадров, т.е. 25 ґ 520 625 = 133 015 625 элементов. Значит переход с черного на белое, или наоборот, происходит примерно 6500000 раз в 1 с. Максимальная частота повторения импульсов равна 6,5 мГц, что и принято за верхнюю границу ширины спектра телевизионного сигнала. Нижней границей считают 50 Гц (нижняя граница сигнала звукового сопровождения).
Во время смены строк и кадров развертывающий луч приемной трубки должен быть погашен. Кроме того, необходимо синхронизировать лучи приемной и передающей трубок. Таким образом, кроме сигнала изображения необходимо передавать вспомогательные управляющие импульсы (гасящие и синхронизирующие). Электрический сигнал, включающий в себя сигнал изображения и управляющие импульсы, называется полным телевизионным сигналом.
В системах цветного телевидения передаваемое изображение расчленяется с помощью светофильтров на три одноцветных изображения – красное, зеленое и синее. Красные, зеленые и синие лучи попадают каждый на свою телевизионную трубку. В приемном устройстве путем сложения трех одноцветных изображений воспроизводится передаваемое цветное изображение.
Таким образом, спектр телевизионного сигнала простирается от 50 Гц до 6,5 мГц.
Телеграфные сигналы и сигналы передачи данных. Все рассматриваемые до сих пор сообщения и сигналы являются непрерывными. Сообщения и сигналы телеграфии и передачи данных относятся к дискретным.
Устройства преобразования телеграфных сообщений и данных в электрический сигнал представляют каждый знак сообщения (букву, цифру) в виде определенной комбинации импульсов и пауз одинаковой длительности. Импульс соответствует наличию тока на выходе устройства преобразования (например, телеграфного аппарата), пауза – отсутствию тока.
В телеграфии таблица, которая ставит в соответствие буквам, цифрам и другим знакам комбинации импульсов и пауз, называется телеграфным кодом. Если обозначить импульс через 1, а паузу через 0 и воспользоваться международным телеграфным кодом МТК-2, то можно, например, знак А записать в виде 11000, знак В – в виде 10011 и т.д.
Для передачи данных используют более сложные коды, которые позволяют обнаруживать и исправлять ошибки в принятой комбинации импульсов, возникающие от действия помех.
Устройства преобразования сигналов телеграфии и передачи данных в сообщения по принятым комбинациям импульсов и пауз восстанавливают в соответствии с таблицей кода знаки сообщения (буквы, цифры и др.) и выдают их на печатающее устройство либо на экран дисплея.
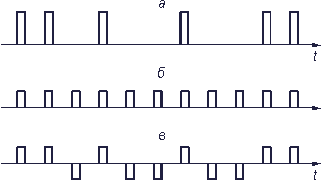
Рис. 3.10. Представление потока импульсов (а) в виде регулярной (б) и случайной (в) составляющих
Заметим, что чем меньше длительность импульсов, отображающих сообщения, тем больше их будет передано в единицу времени. Величина, обратная длительности импульса, называется скоростью телеграфирования: 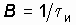 , где
, где 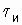 – длительность импульса, с.
– длительность импульса, с.
В честь французского инженера Ж. Бодо единицу скорости телеграфирования назвали бодом. При длительности импульса 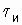 = 1 с скорость В = 1 Бод. В телеграфии используются импульсы длительностью 0,02 с, что соответствует стандартной скорости телеграфирования 50 Бод. Применяются и другие скорости телеграфирования (например, 75 Бод). Скорости передачи данных существенно выше. Существует аппаратура передачи данных со скоростями 200, 600, 1200 Бод и более.
= 1 с скорость В = 1 Бод. В телеграфии используются импульсы длительностью 0,02 с, что соответствует стандартной скорости телеграфирования 50 Бод. Применяются и другие скорости телеграфирования (например, 75 Бод). Скорости передачи данных существенно выше. Существует аппаратура передачи данных со скоростями 200, 600, 1200 Бод и более.
Сигналы телеграфии и передачи данных обычно имеют вид последовательностей прямоугольных импульсов.
Посмотрите внимательно на рис. 3.10. Можно представить (разумеется, чисто условно) поток импульсов в виде суммы двух последовательностей: регулярной и случайной. Спектр регулярной последовательности дискретный и создает нечетные гармоники тактовой частоты (т.е. частоты следования), а случайная последовательность имеет непрерывный заштрихованный спектр. Эти спектры показаны на рис. 3.11.
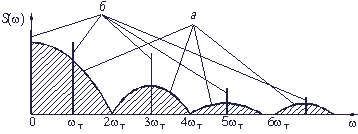
Рис. 3.11. Спектры случайной (а) и регулярной (б) составляющей потока импульсов
При передаче двоичных сигналов (т.е. 0 и 1) нет необходимости восстанавливать в приемнике импульсы без искажений, т.е. сохранять их форму; для восстановления информации достаточно зафиксировать только знак импульса при двуполярном сигнале либо наличие или отсутствие при однополярном сигнале. Расчеты показывают, что импульсы можно уверенно зафиксировать, если для их передачи используется ширина полосы частот, численно равная скорости передачи в бодах. Так, для стандартной скорости телеграфирования 50 Бод ширина спектра телеграфного сигнала составит 50 Гц. При скорости 2400 Бод (среднескоростная система передачи данных) ширина спектра сигнала равна примерно 2400 Гц.
Для удобства спектры основных сигналов электросвязи сведены в табл. 3.1. Даже беглый взгляд на табл. 3.1 позволяет понять, что для передачи разных видов сигналов требуется различная ширина полосы пропускания системы электросвязи.
Таблица 3.1. Ширина спектров сигналов электросвязи
|
Вид сигнала |
Ширина спектра, Гц |
| Телеграфный |
0…100 |
| Передачи данных со скоростью 2 400 Бод |
0…2 400 |
| Телефонный |
300…3 400 |
| Звукового вещания |
50…10 000 |
| Факсимильный – при скорости 120 мин-1 – при передаче газет |
0…1 465 0…180 000 |
| Телевизионный |
50…6 000 000 |
Контрольные вопросы
- На какие простейшие составляющие “раскладывается” периодически повторяющийся прямоугольный импульс?
- Чем отличается спектр периодического сигнала от спектра непериодического сигнала?
- У какого импульса амплитуда спектральных составляющих убывает быстрее: а) более короткого или более длинного? б) с более крутым фронтом или с более пологим? в) повторяющегося чаще или реже?
- Какие частотные диапазоны занимают спектры основных сигналов электросвязи
Список литературы
- Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под ред. В.П.Бакалова. – М.: Радио и связь, 2000. – 592 с.
- Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник для вузов: под ред. В.П. Бакалова – М.: Радио и связь. 1998. – 444 с.
- Бакалов В.П., Журавлева О.Б., Крук Б.И. Анализ линейных электрических цепей: Учебное пособие для дистанционного обучения. – Новосибирск: СибГУТИ. 2001г.
3.6 Многомерные сигналы
3.6.1 Общее описание многомерных сигналов
Рассмотренные ранее амплитудные, фазовые или частотные методы модуляции могут рассматриваться как сигналы одномерные. Под одномерностью сигналов имеется ввиду, что в процессе модуляции происходит изменение одного или нескольких параметров одной единственной несущей частоты.
Так, например, при импульсной амплитудной модуляции изменяется амплитуда несущей частоты бинарным или многоуровневым модулирующим сигналом. При использовании многоуровневого сигнала говорят о многоуровневой (или многопозиционной) модуляции. При QAM модуляции используется принципиально многопозиционный сигнал, одновременно изменяющий и амплитуду, и фазу несущей частоты. При этом понятие спектральной эффективности метода модуляции относится именно к величине отклонения несущей частоты от центральной при воздействии модулирующего сигнала. Спектр несущей частоты при модуляции «расплывается», занимая конечную, строго определенную полосу частот.
При частотной модуляции модулированная псевдослучайным сигналом несущая частота также занимает некоторую, строго определенную полосу частот.
С другой стороны, существуют сигналы с расширенным спектром, имеющие шумоподобный характер. Для таких сигналов обычно говорят не о несущей частоте, сигнала, а о центральной частоте используемой полосы частот. Хотя формально и производится модуляция исходной несущей частоты высокоскоростным baseband сигналом, само понятие о существовании или не существовании в спектре модулированного сигнала несущей частоты не имеет смысла. Точно также обычно не говорят и о законе распределения мощности (спектральной плотности мощности) в сигналах с расширенным спектром. За счет очень высокой скорости модулирующего сигнала спектр модулированного сигнала является «почти» равномерным, «почти» шумовым.
С хорошей степенью точности сигнал с расширенным спектром можно характеризовать как белый шум с постоянной спектральной плотностью мощности в некоторой полосе частот.
Два упомянутых выше класса сигналов можно рассматривать как два полярных случая:
«слегка» расплывшуюся несущую частоту (то, что называется узкополосный сигнал), характеризующуюся определенным распределением спектральной плотности мощности в относительно узкой полосе частот
шумоподобный сигнал в очень широкой полосе частот, характеризующийся, как белый шум, постоянной плотностью мощности в занимаемой полосе частот
Кроме упомянутых выше типов сигналов существуют так называемые многомерные сигналы, которое являются некоторым «средним» между узкополосной и широкополосной модуляцией.
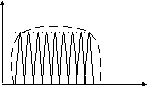
Главное отличительное свойство многомерного сигнала – одновременная передача информации сразу на нескольких поднесущих частотах, количество которых строго ограничено. Общий частотный диапазон, выделенный для передачи информации, делится на независимые каналы (поднесущие частоты). Каждая поднесущая частота генерируется независимым генератором, модулируется и проходит узкополосный фильтр для исключения взаимного перекрытия частотных поддиапазонов. При многомерной модуляции в общем случае к качеству фильтров предъявляются очень высокие требования, т.к. наложение спектров соседних поднесущих частот приводит к появлению межсимвольной интерференции. Для модуляции поднесущей частоты может использоваться любой вид модуляции: амплитудная, фазовая, частотная. Очевидно, что при использовании N поднесущих частот скорость передачи информации в каждом частотном поддиапазоне в N раз меньше, чем в исходном модулирующем сигнале. Соответственно, длительность каждого передаваемого символа на поднесущей частоте велика, а каждая поднесущая частота занимает очень малую часть выделенного частотного диапазона. Типичное распределение спектра в канале при многомерной модуляции общего вида показано на рис.3.33.
 А
А
f
Рис.3.33. Распределение спектра при многомерной модуляции
При этом формально никакого общего сужения спектра не происходит, так как при использовании в N раз более узкого спектра для каждой поднесущей частоты используется N несущих частот. Более того, необходимость жесткого ограничения спектра многих частот в передатчике и реализации гребенчатого фильтра в приемнике для выделения поднесущих частот существенно усложняет построение аппаратуры.
Однако многомерные сигналы обладают рядом других важных преимуществ. И прежде всего, устойчивостью к федингу при многолучевом распространении радиоволн в городских условиях. Среднее время запаздывания копий одного и того же сигнала на входе приемника при многолучевом распространении составляет величину порядка нескольких микросекунд. Следовательно. при высокоскоростной передачи информации с длительностью символов, сравнимой с временем запаздывания в канале, последние будет сильно флуктуировать по величине за счет взаимного наложения. И наоборот, прием более длительных символов повышает достоверность приема, т.к. относительно короткие флуктуации величины принимаемых символов слабо влияют на среднюю энергию принимаемого символа.
Частным видом многомерной модуляции является модуляция типа OFDM (Orthogonal Frequency Division Multiplex), которая позволяет эффективно разделить общий диапазон частот на поддиапазоны, реализовать полностью цифровую модуляцию и демодуляцию поднесущих частот и исключить необходимость использования гребенки узкополосных полосовых фильтров.
Основная идея формирования модулированных сигналов в методе OFDM – это использование ортогональных поднесущих частот. Известно, что в общем случае функции являются ортогональными, если на некотором конечном интервале удовлетворяют условиям:
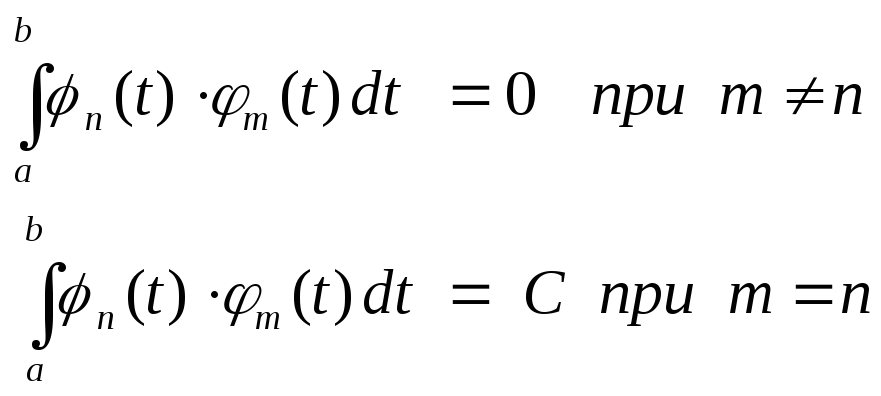 3.92
3.92
Формула 3.92 означает,
что на интервале интегрирования
(ортогональности) две функции могут
анализироваться независимо друг от
друга, между ними нет взаимной
интерференции. Очевидным примером
ортогональных функций на интервале 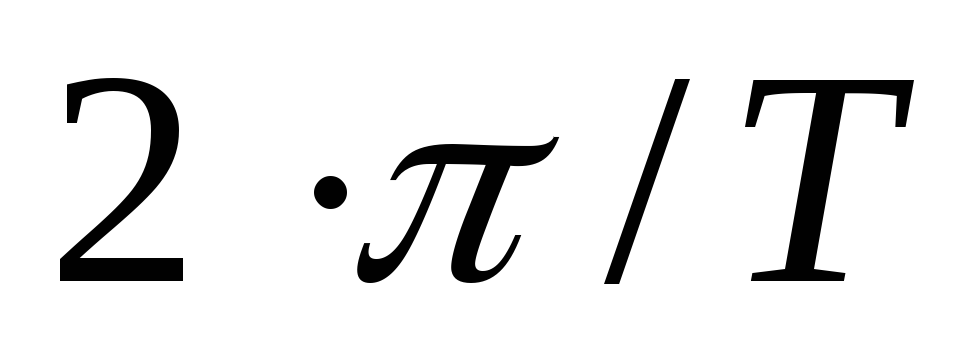 являются следующие функции:
являются следующие функции:
 3.93.а
3.93.а
 3.93.b
3.93.b
Структура OFDM
сигнала основана на использовании
ортогональных функций вида 3.93.b, которые
являются спектральным представлением
импульсно модулированного сигнала. Как
было показано ранее при рассмотрении
импульсной амплитудной модуляции РАМ,
спектральная плотность мощности
одиночного импульса описывает формулой
вида 3.93.b. Из рисунка 3.34.b следует, что
на расстоянии, кратном  ,
спектральная плотность мощности равна
нулю. Следовательно, если расстояние
между импульсно модулированными
поднесущими частотами будет кратно
,
спектральная плотность мощности равна
нулю. Следовательно, если расстояние
между импульсно модулированными
поднесущими частотами будет кратно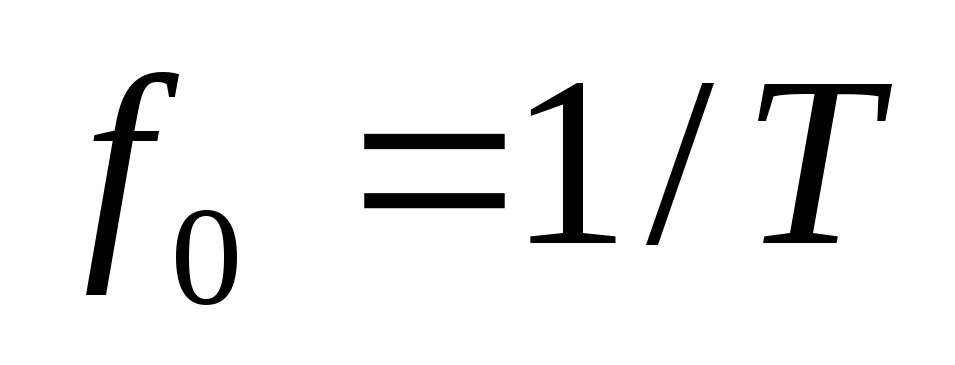 ,
то взаимное влияние передаваемых частот
будет отсутствовать даже при отсутствии
ограничения спектра поднесущих частот.
Ортогональную структуру спектральной
плотности мощности имеют иQAM
сигналы, которые также могут быть
использованы для построения OFDM сигнала.
,
то взаимное влияние передаваемых частот
будет отсутствовать даже при отсутствии
ограничения спектра поднесущих частот.
Ортогональную структуру спектральной
плотности мощности имеют иQAM
сигналы, которые также могут быть
использованы для построения OFDM сигнала.
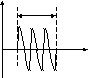


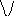

 А
A
А
A
T






t
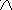
 f
f
2f0 4f0
a b
Рис.3.34. Временная форма (а) и спектральная плотность мощности (b)
радиочастотного импульса
В общем виде многомерные сигналы, как и все другие, определяются через комплексную огибающую:
 3.94
3.94

Комплексная огибающая многомерного сигнала также определяется в baseband диапазоне и отражает амплитудную, фазовую или QAM модуляцию каждой отдельной несущей. Это означает, что многомерная модуляция является линейной модуляцией.
Многомерная ортогональная частотная модуляция (OFDM)
Предполагается,
что исходный информационный сигнал
представляет собой цифровой сигнал,
бинарный или многоуровневый. Длительность
передаваемого символа равна  .
Выделим в передаваемой последовательности
временной интервал
.
Выделим в передаваемой последовательности
временной интервал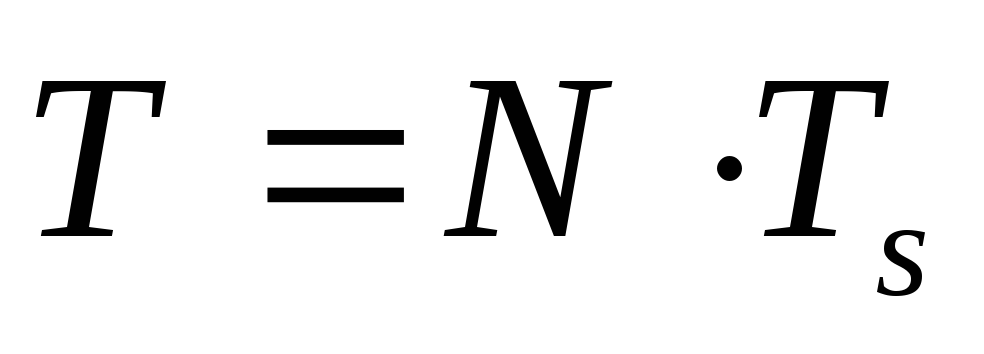 ,
кратный длительности информационного
символа. Комплексная огибающая в 3.94,
записанная как непрерывная функция
времени, характеризуется N коэффициентами
дискретного преобразования Фурье от
исходной информационной последовательности,
существующими в течении этого выделенного
интервала Т:
,
кратный длительности информационного
символа. Комплексная огибающая в 3.94,
записанная как непрерывная функция
времени, характеризуется N коэффициентами
дискретного преобразования Фурье от
исходной информационной последовательности,
существующими в течении этого выделенного
интервала Т:
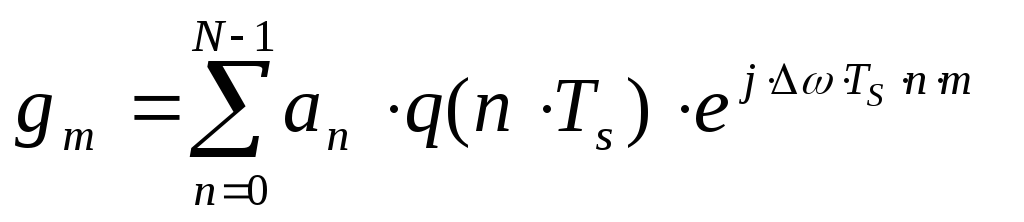 3.95
3.95
При
этом система комплексных функций 3.95
образует ортогональную систему при
условии 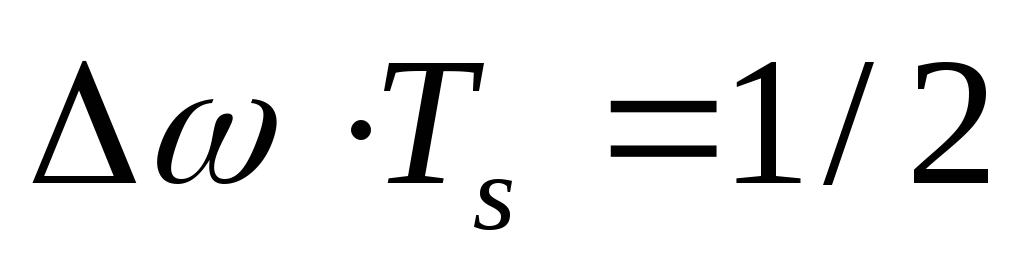 .
Это условие полностью совпадает с
условиями ортогональности двух частот,
полученных для MSK сигнала:
.
Это условие полностью совпадает с
условиями ортогональности двух частот,
полученных для MSK сигнала:
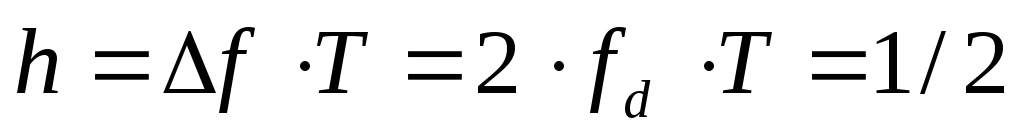 3.96
3.96

Как
следует из 3.96, комплексная огибающая
представляет собой N колебаний с
частотой  каждое, причем амплитуда каждой частоты
зависит от всех
каждое, причем амплитуда каждой частоты
зависит от всех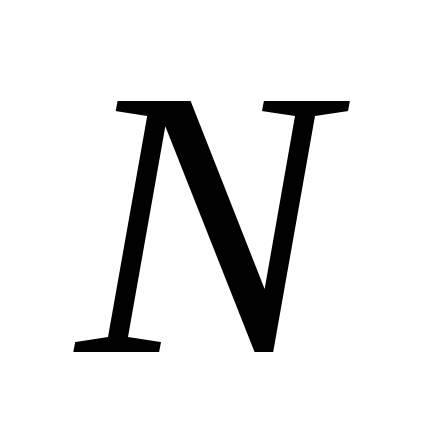 временных отсчетов.
временных отсчетов.
Подставляя 3.95 в 3.94, получим полное выражение для OFDM сигнала во временной области:
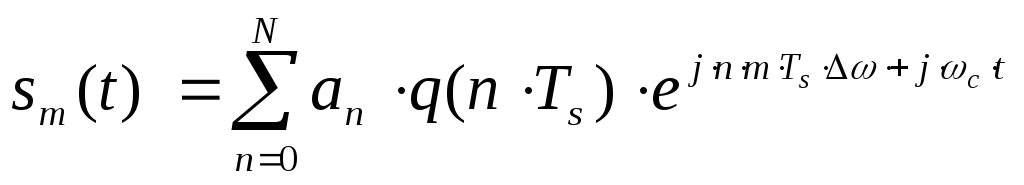 3.97
3.97
Из уравнения 3.97 следует основное преимущества OFDM сигнала: устойчивость к искажениям, т.к. при восстановлении информационной последовательности в приемнике для каждой временной точки используются все гармонические составляющие.
Функциональная схема передатчика и приемника показана на рисунке 3.35
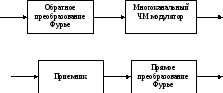
Рис.3.35 Функциональная схема приемника и передатчика OFDM сигналов
Глава 7. Многопозиционные сигналы
7.1. Общие сведения и прием многопозиционных сигналов
Наряду с бинарными сигналами в цифровых системах связи нашли применение многопозиционные сигналы, использование которых позволяет:
1. Повысить скорость передачи информации, по сравнению с двоичными сигналами, при заданной полосе частот. Платой за это является снижение помехоустойчивости приема. Компромисс достигается применением помехоустойчивого кодирования.
2. Обеспечить при одинаковой скорости передачи информации значительный выигрыш в энергетике по сравнению с двоичными сигналами. Платой за это является увеличение занимаемой полосы частот, при той же скорости передачи информации.
3. Реализовывать многоканальные асинхронно-адресные системы связи.
Оптимальный
алгоритм приема детерминированного
многопозиционного сигнала 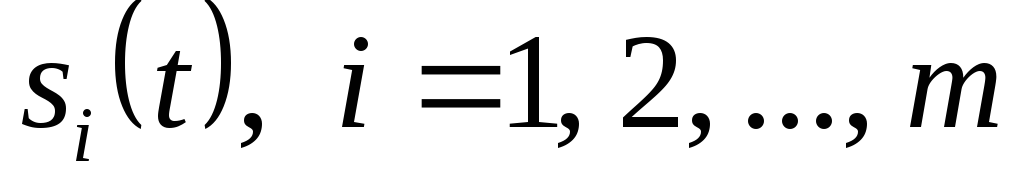 в условиях аддитивного БГШ, полагая,
что
в условиях аддитивного БГШ, полагая,
что 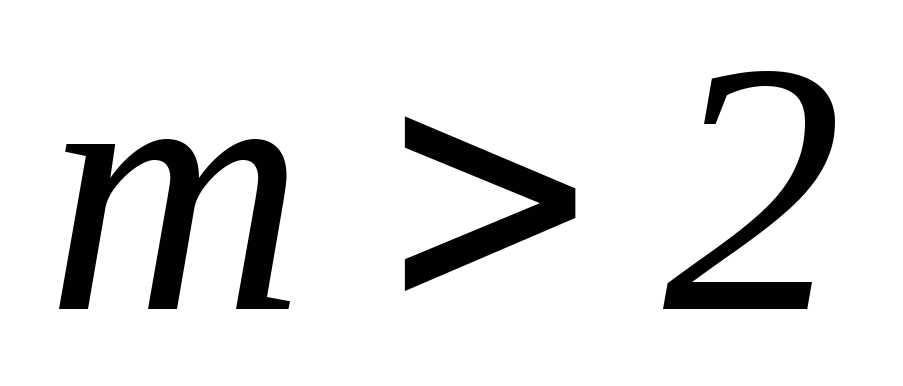 и появление каждого из сигналов
равновероятно, сводится к неравенству:
и появление каждого из сигналов
равновероятно, сводится к неравенству:
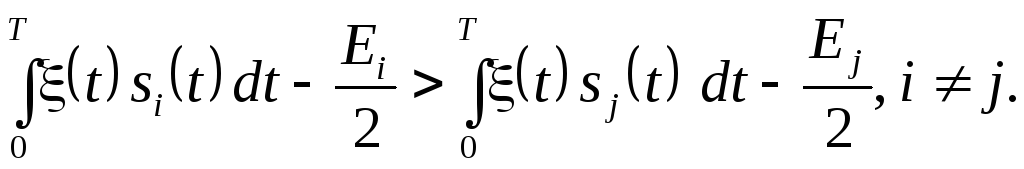 (7.1)
(7.1)
Схема оптимального корреляционного приемника приведена на рис.7.1.

Структурная схема некогерентного демодулятора многопозиционных сигналов на согласованных фильтрах приведена на рис.7.2.

В решающем устройстве
РУ определятся канал с максимальным
откликом, и если им оказывается i-й
канал, то выносится решение о передаче
сигнала 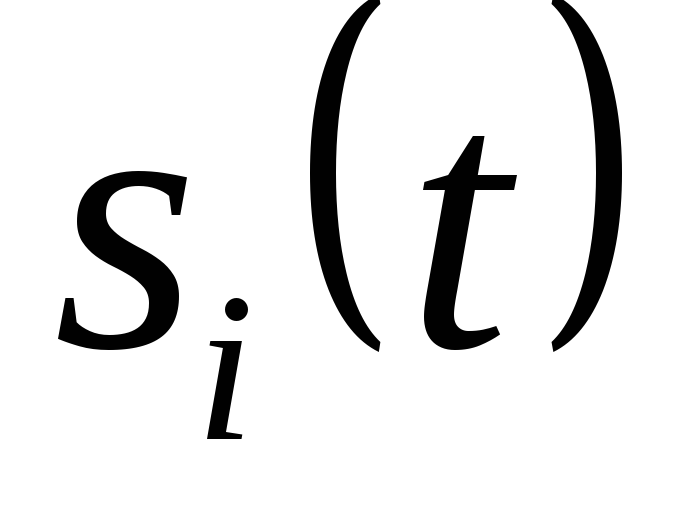 .
.
Помехоустойчивость приема многопозиционных сигналов зависит от минимального расстояния между сигналами
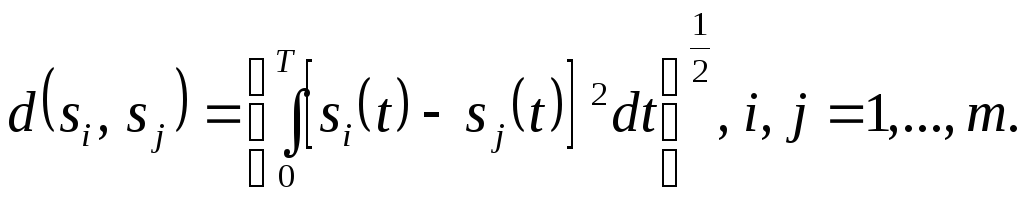 (7.2)
(7.2)
Если сигналы имеют
одинаковые энергии 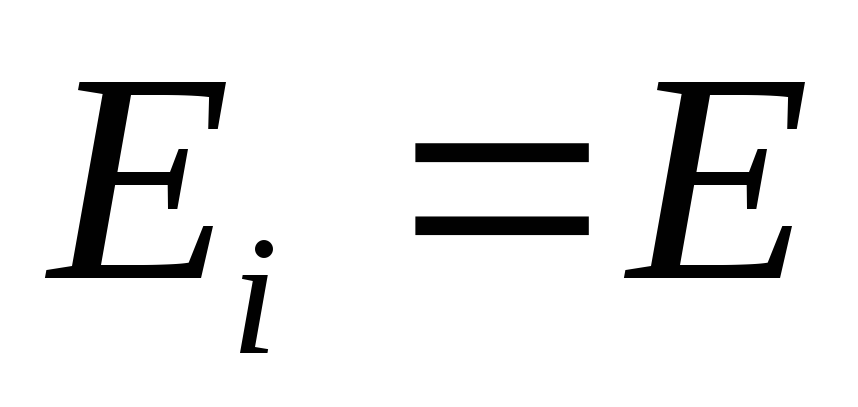 ,
то
,
то
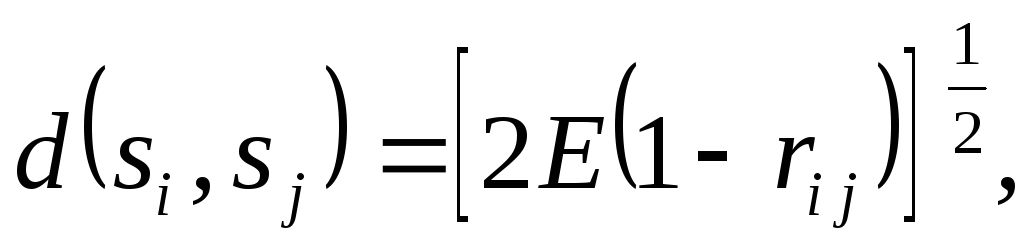
где 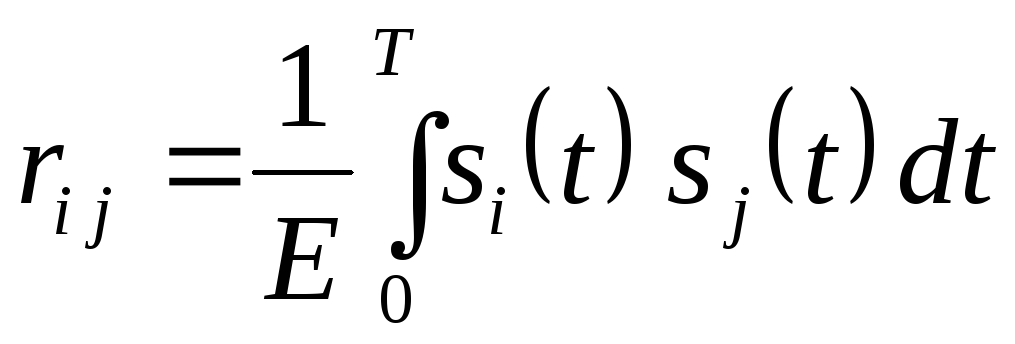 — коэффициент взаимной корреляции
сигналов
— коэффициент взаимной корреляции
сигналов 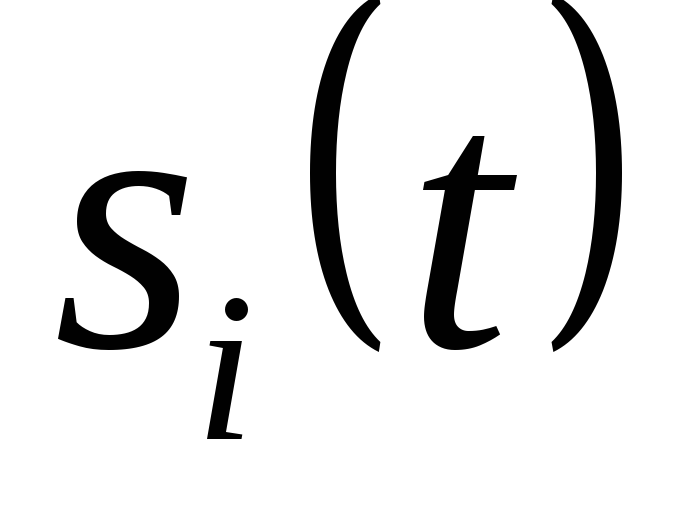 и
и 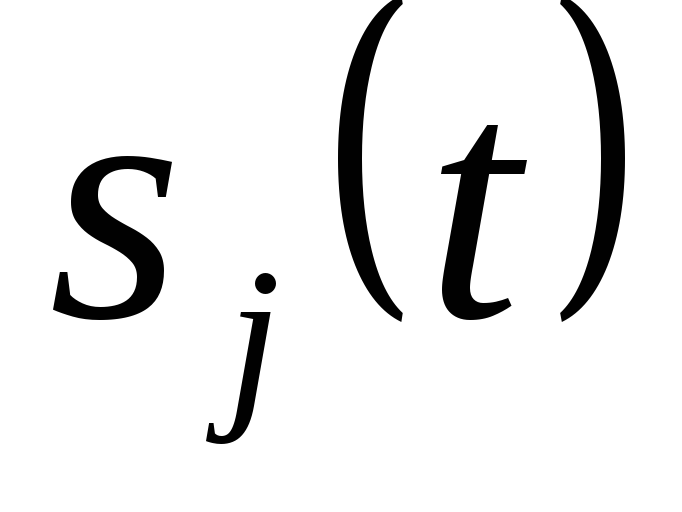 .
Для обеспечения одинаковой вероятности
ошибки для любого
.
Для обеспечения одинаковой вероятности
ошибки для любого  необходимо, чтобы
необходимо, чтобы 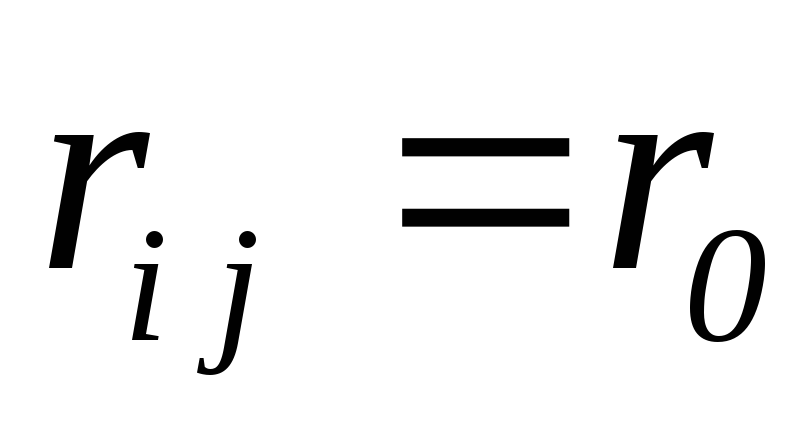 ,
для всех i и j,
кроме
,
для всех i и j,
кроме 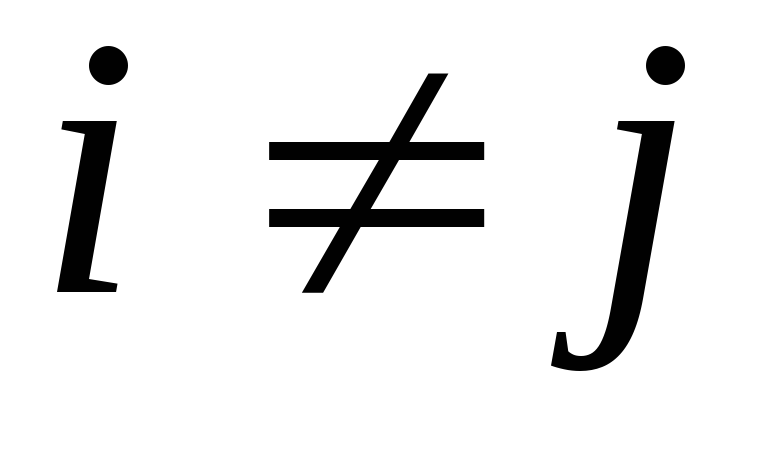 .
Выражение для коэффициента взаимной
корреляции, найдем исходя из следующего
неравенства:
.
Выражение для коэффициента взаимной
корреляции, найдем исходя из следующего
неравенства:
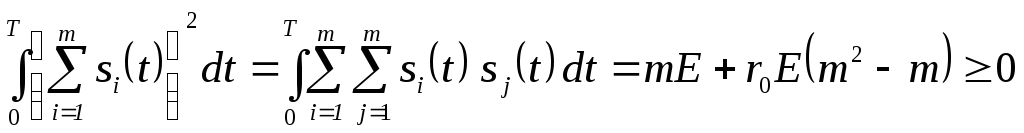 ,
,
решая которое получим, что
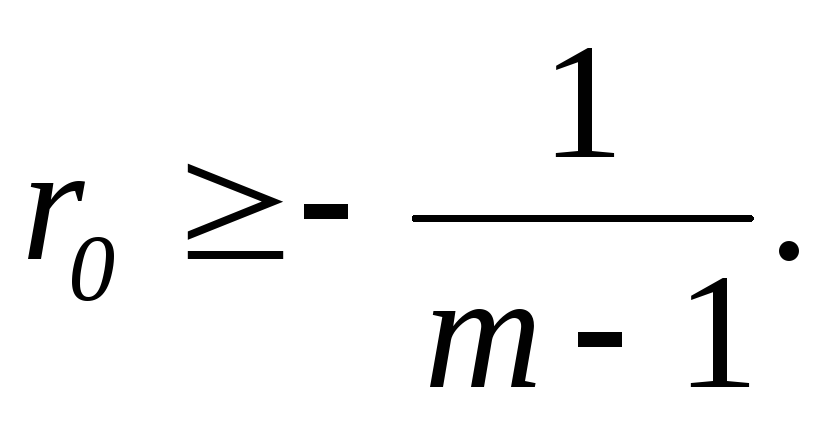 (7.3)
(7.3)
Для оптимальной системы
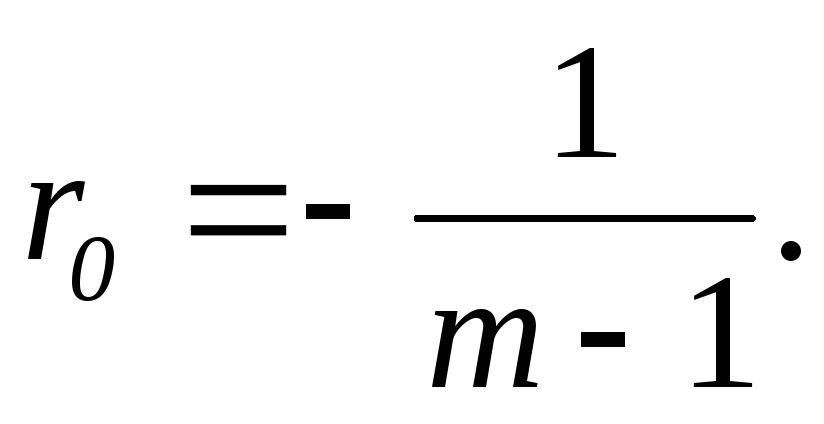 (7.4)
(7.4)
Исходя из коэффициента
взаимной корреляции 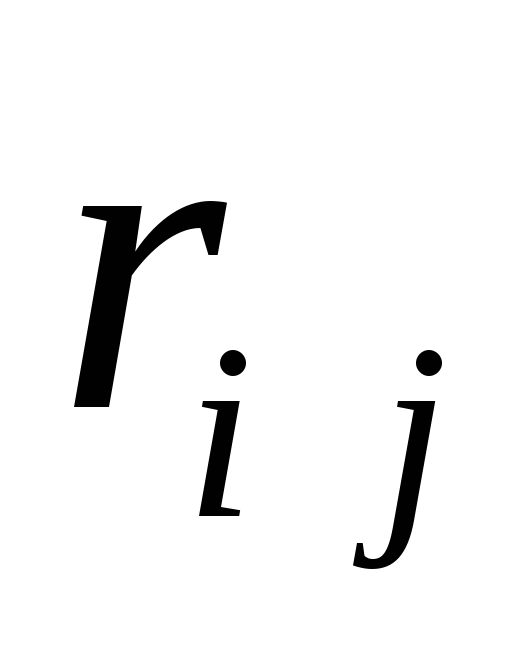 ,
, 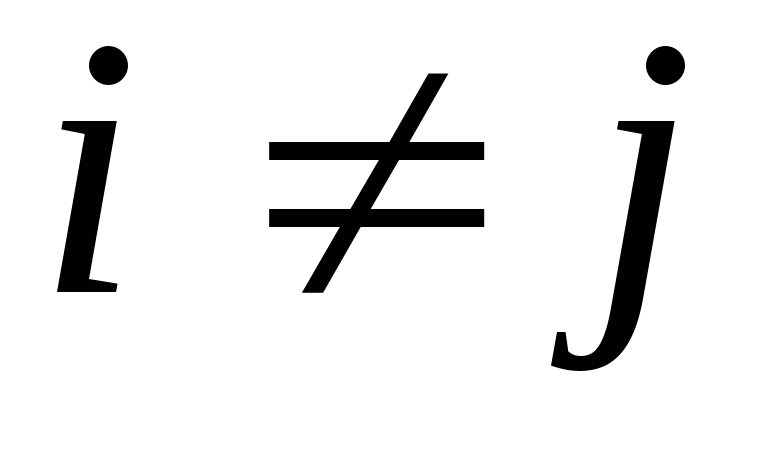 многопозиционные сигналы подразделяются
на симплексные и ортогональные.
многопозиционные сигналы подразделяются
на симплексные и ортогональные.
Симплексные сигналы – это сигналы, для которых
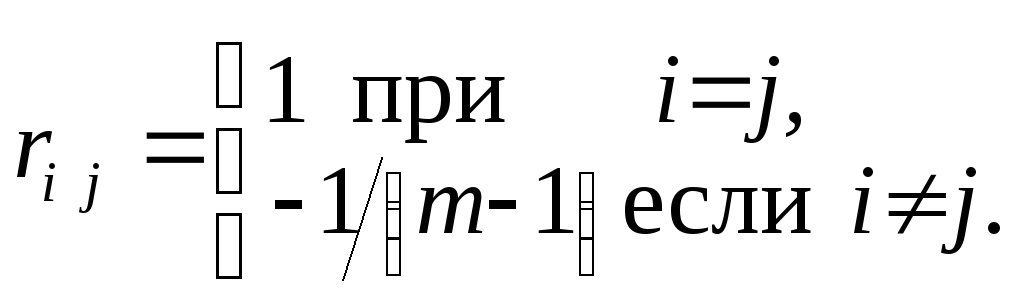 (7.5)
(7.5)
Такие сигналы
являются эквидистантными,
т.е. для всех пар сигналов  и
и 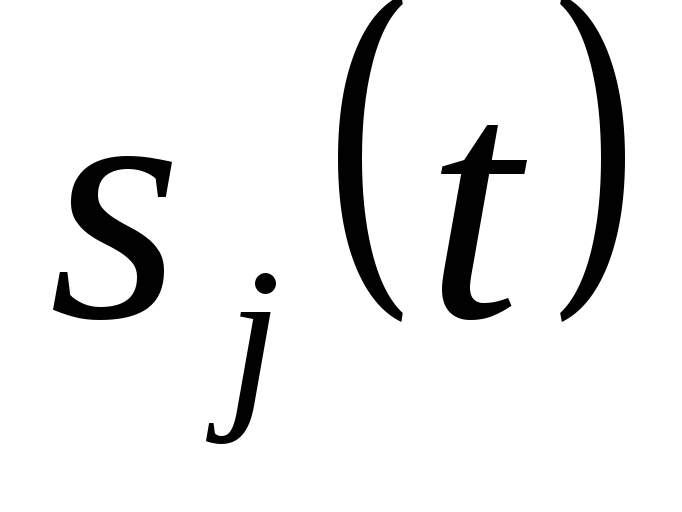 расстояние (7.2)
расстояние (7.2) 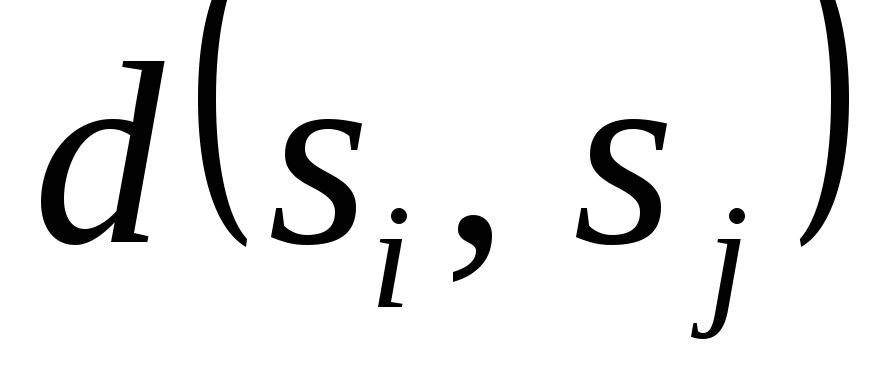 одинаково.
одинаково.
Ортогональные сигналы наиболее часто применяют на практике и для них
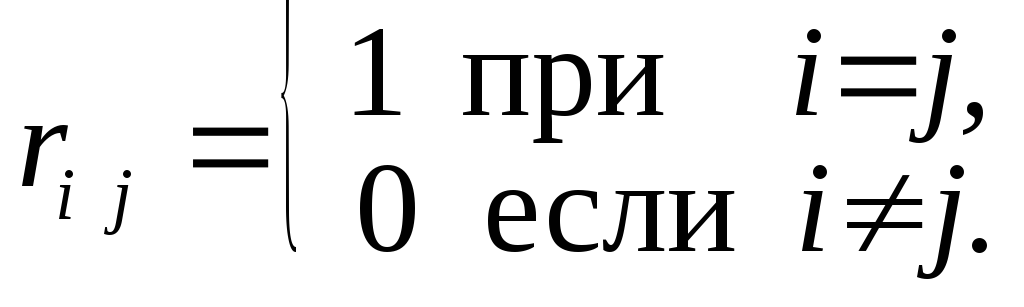 (7.6)
(7.6)
Если все ортогональные сигналы имеют равную энергию, то они также эквидистантны. При больших значениях m помехоустойчивость приема ортогональных сигналов близка к помехоустойчивости симплексных сигналов.
Биортогональные
сигналы формируются по следующему правилу:
каждому из ортогональных сигналов 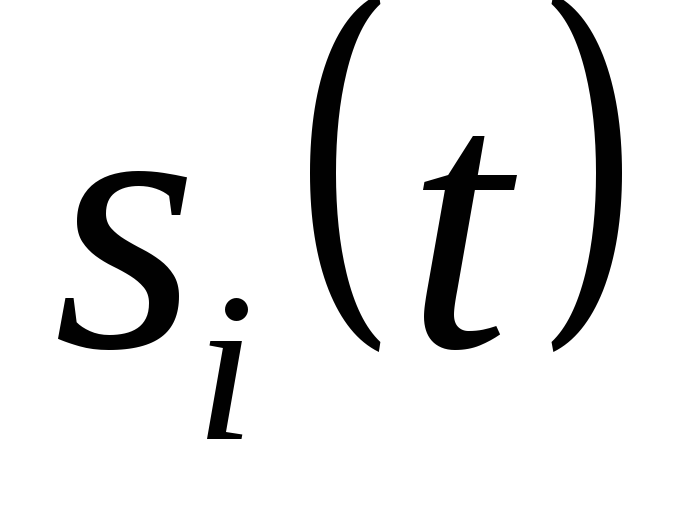 добавляется противоположный
добавляется противоположный 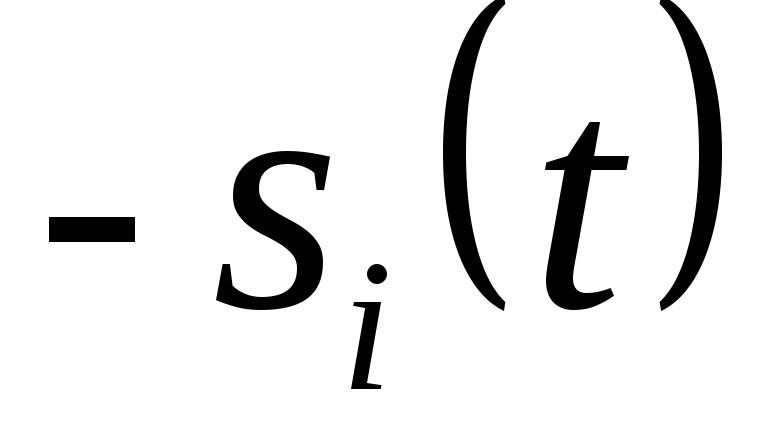 .
При m >> 1 биортогональные сигналы близки
по помехоустойчивости приема к
симплексным.
.
При m >> 1 биортогональные сигналы близки
по помехоустойчивости приема к
симплексным.
7.2. Помехоустойчивость приема многопозиционных сигналов
Помехоустойчивость приема ортогональных сигналов. Вероятность правильного приема i-го сигнала
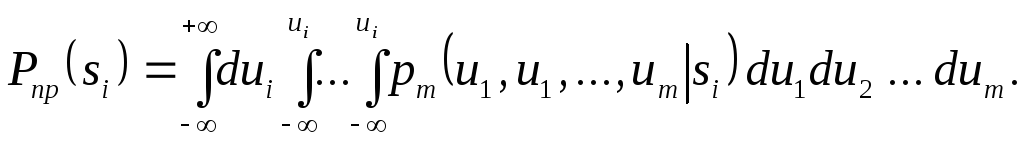 (7.7)
(7.7)
Здесь  — m-мерная
плотность вероятностей случайных
величин u1, u2,
…um при условии,
что передавался сигнал
— m-мерная
плотность вероятностей случайных
величин u1, u2,
…um при условии,
что передавался сигнал 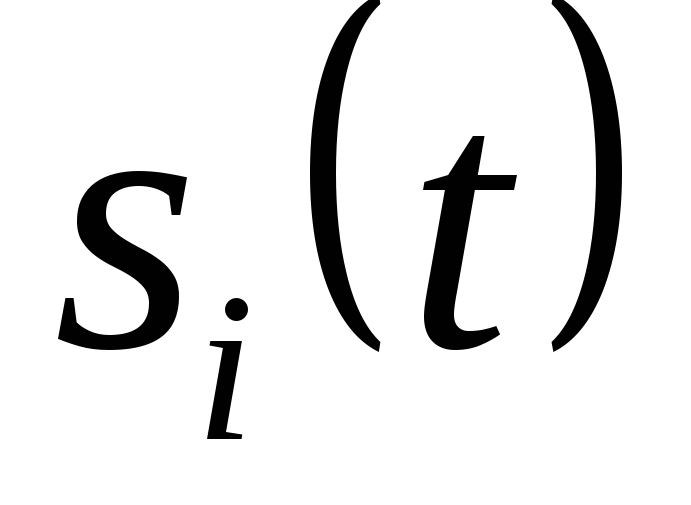 .
Вероятность ошибки при приеме i-го
сигнала
.
Вероятность ошибки при приеме i-го
сигнала
(7.8)
Сигнал на выходе i-го канала
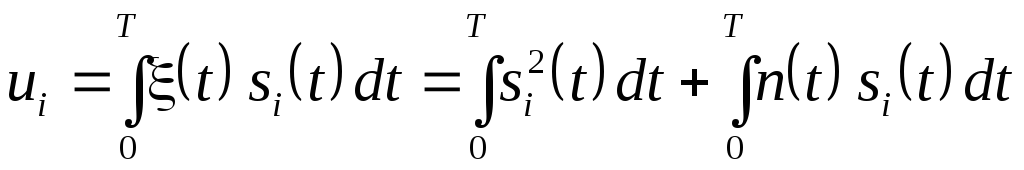
представляет
гауссовскую случайную величину с
математическим ожиданием 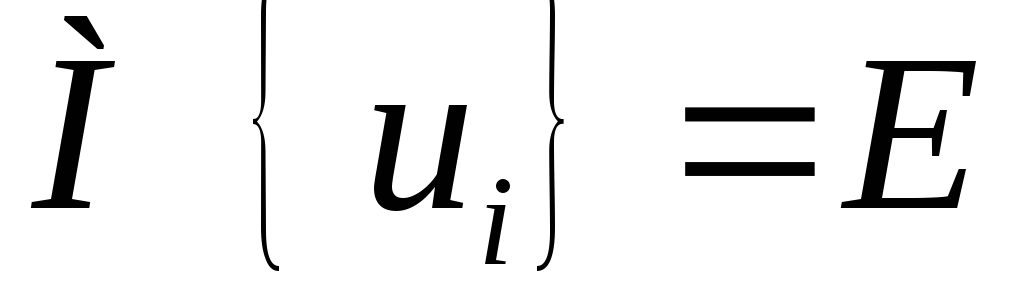 и дисперсией
и дисперсией  Сигналы на выходах остальных каналов
также являются гауссовскими случайными
величинами с той же дисперсией
Сигналы на выходах остальных каналов
также являются гауссовскими случайными
величинами с той же дисперсией 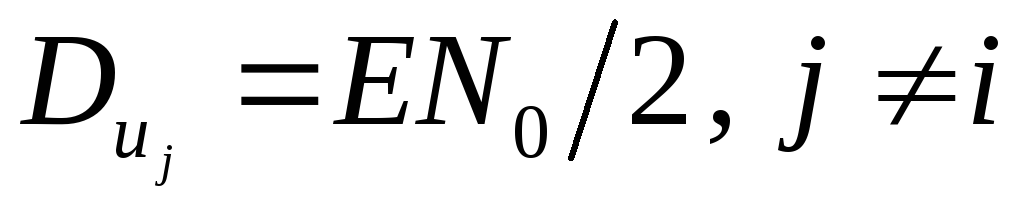 и только математические ожидания равны
нулю. Случайные величины
и только математические ожидания равны
нулю. Случайные величины 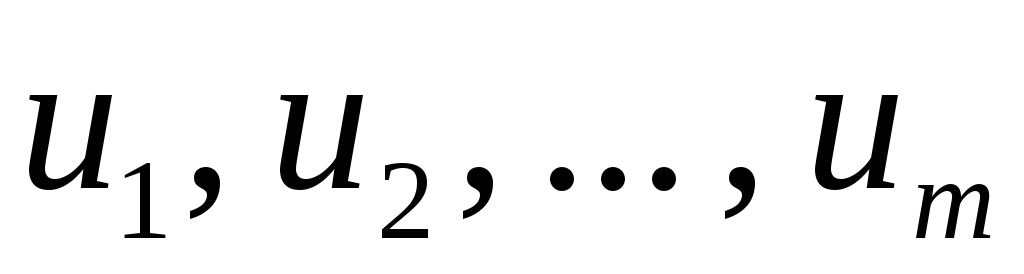 с учетом (7.6) не коррелированны, а поскольку
эти величины также являются гауссовскими,
то и независимыми. Таким образом, m-мерная
плотность вероятности
с учетом (7.6) не коррелированны, а поскольку
эти величины также являются гауссовскими,
то и независимыми. Таким образом, m-мерная
плотность вероятности
 ,
(7.9)
,
(7.9)
где
 ,
(7.10)
,
(7.10)
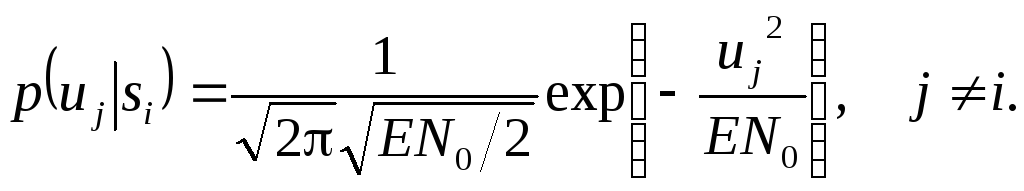 (7.11)
(7.11)
Подставив (7.9) в (7.7) с учетом (7.10) и (7.11) и в соответствии с преобразованиями, приведенными в [ ], получим вероятность правильного приема i-го сигнала
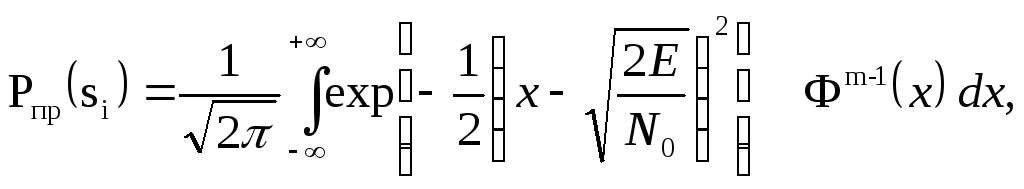 (7.12)
(7.12)
где 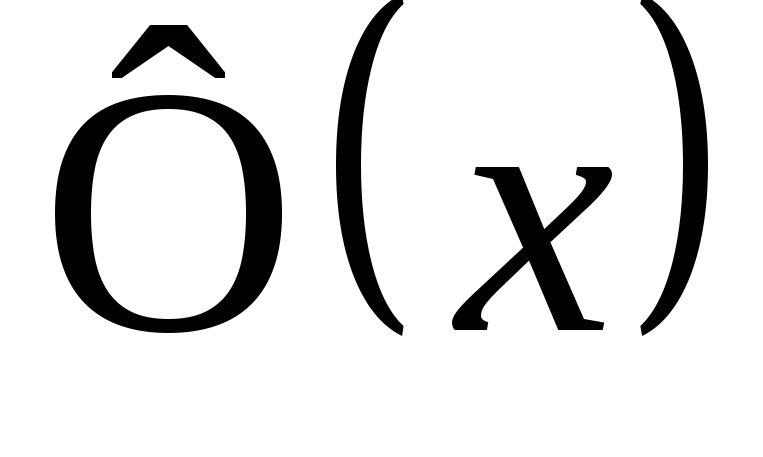 — интеграл вероятности.
— интеграл вероятности.
Полная вероятность
ошибки при различении m равновероятных сигналов, то есть  ,
определяется выражением
,
определяется выражением
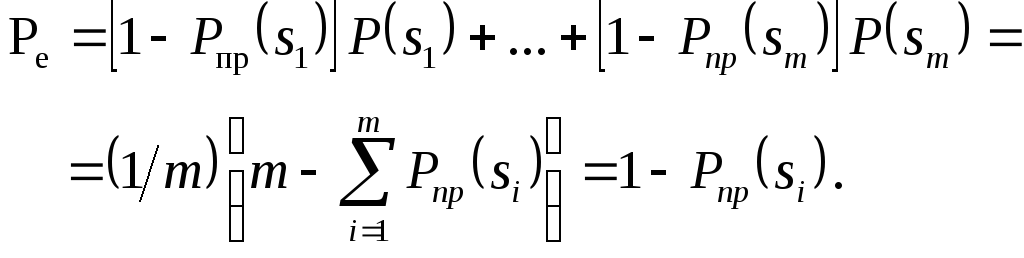 (7.13)
(7.13)
При сравнении
систем необходимо иметь ввиду, что при
фиксированной длительности элемента
сигнала Т,
каждый равновероятный m–ичный
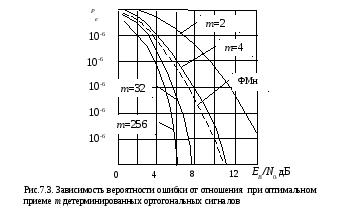
сигнал несет в 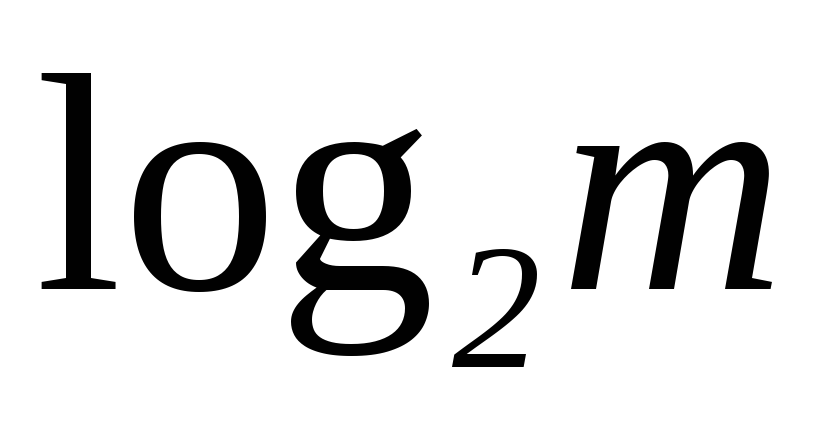 раз больше количества информации, чем
двоичный сигнал. На рис. 7.3 приведены
кривые помехоустойчивости когерентного
приема ортогональных сигналов при m=2,
4, 32 и 256. Для сравнения приведена кривая,
характеризующая помехоустойчивость
когерентного приема детерминированного
бинарного ФМн радиосигнала. Здесь
раз больше количества информации, чем
двоичный сигнал. На рис. 7.3 приведены
кривые помехоустойчивости когерентного
приема ортогональных сигналов при m=2,
4, 32 и 256. Для сравнения приведена кривая,
характеризующая помехоустойчивость
когерентного приема детерминированного
бинарного ФМн радиосигнала. Здесь 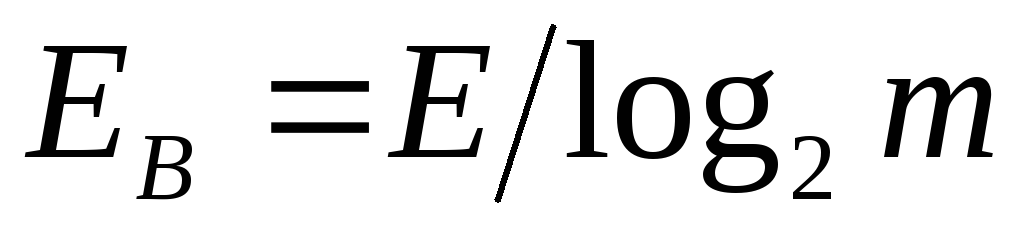 — энергия, затрачиваемая,
на один бит информации.
— энергия, затрачиваемая,
на один бит информации.
Помехоустойчивость
приема симплексных сигналов. Напомним,
что симплексные сигналы образуют
ансамбль из m одинаково коррелированных сигналов с
коэффициентом корреляции 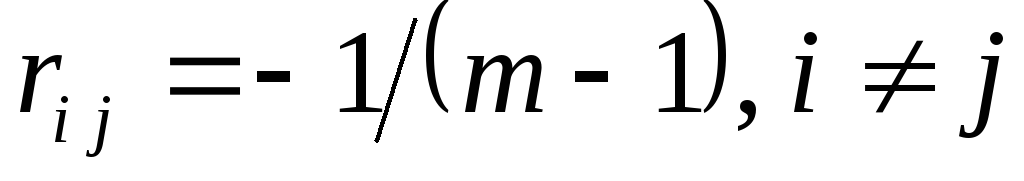 . Минимальное расстояние, если сигналы
имеют одинаковые энергии,
. Минимальное расстояние, если сигналы
имеют одинаковые энергии,
 ,
,
откуда понятно,
что минимальное расстояние ортогональных
сигналов 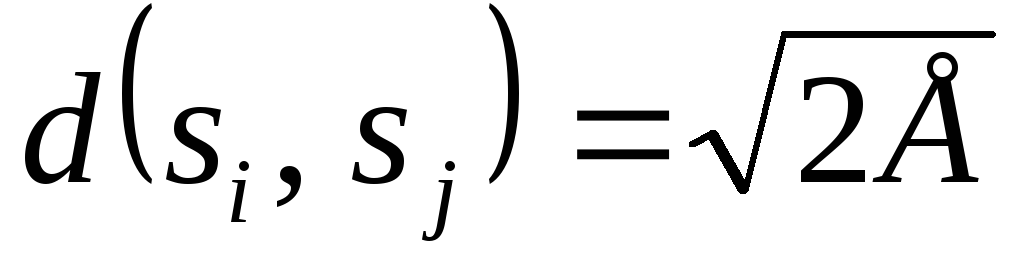 ,
а для симплексных сигналов
,
а для симплексных сигналов 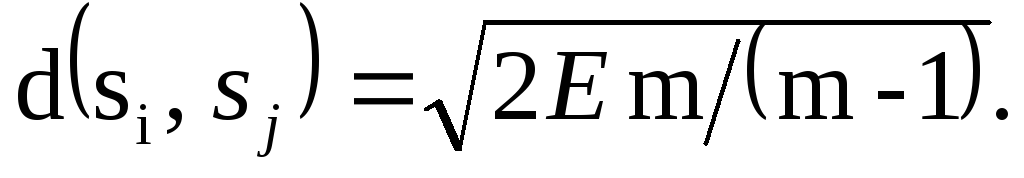 Т. е. для достижения одной и той же
помехоустойчивости приема симплексных
сигналов требуется энергии сигналов в
Т. е. для достижения одной и той же
помехоустойчивости приема симплексных
сигналов требуется энергии сигналов в 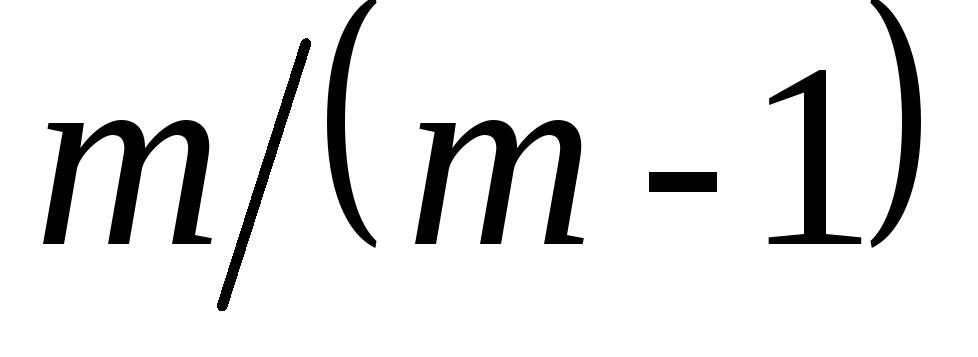 раз меньше, чем для ортогональных
сигналов. Таким образом, вероятность
ошибки для симплексных сигналов
определяется как
раз меньше, чем для ортогональных
сигналов. Таким образом, вероятность
ошибки для симплексных сигналов
определяется как
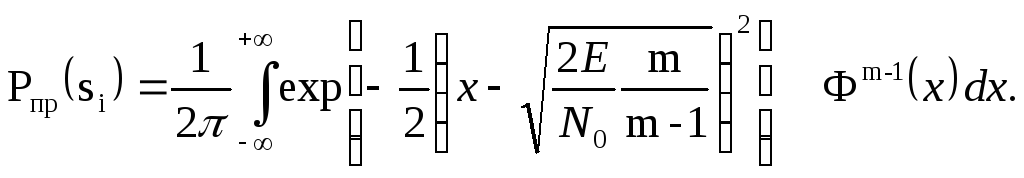 (7.14)
(7.14)
Помехоустойчивость симплексных сигналов выше, чем ортогональных. Однако это различие уменьшается с увеличением m и при m>>1 помехоустойчивость обоих ансамблей оказывается практически одинаковой.
Помехоустойчивость
приема биортогональных сигналов.
Биортогональные сигналы формируются
из  ортогональных сигналов путем их
дополнением сигналами, противоположными
ортогональным. Этим достигается понижение
сложности демодулятора (уменьшение
количества каналов в два раза). Вероятность
правильного приема любого сигнала
ортогональных сигналов путем их
дополнением сигналами, противоположными
ортогональным. Этим достигается понижение
сложности демодулятора (уменьшение
количества каналов в два раза). Вероятность
правильного приема любого сигнала
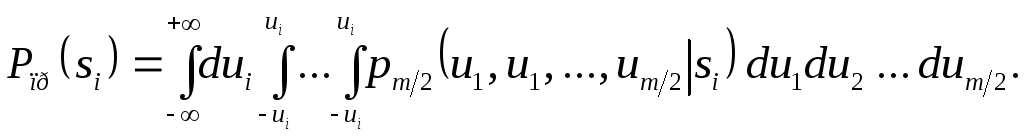
Проведя рассуждения, аналогичные для ортогональных сигналов можно получить выражение для вероятности ошибки биортогональных сигналов:
 (7.15)
(7.15)
Помехоустойчивость приема биортогональных сигналов выше, чем ортогональных, однако при m >>2 эта разница становится пренебрежимо малой.
Сравнение помехоустойчивости приема когерентного и некогерентного приема ортогональных сигналов показывает, что при m=128 различие в помехоустойчивости практически отсутствует. На практике при малой вероятности ошибки приема часто пользуются верхней границей помехоустойчивости
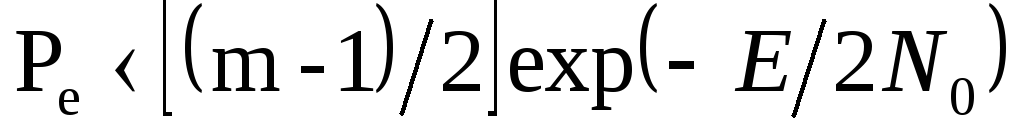 .
(7.16)
.
(7.16)
Модуляция — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 мая 2016; проверки требуют 22 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 мая 2016; проверки требуют 22 правки.Модуля́ция (лат. modulatio — размеренность, ритмичность) — процесс изменения одного или нескольких параметров модулируемого несущего сигнала при помощи модулирующего сигнала.
Передаваемая информация заложена в модулирующем сигнале, а роль переносчика информации выполняет высокочастотное колебание, называемое несущим (модулируемым). Модуляция, таким образом, представляет собой процесс «посадки» информационного колебания на заведомо известную несущую с целью получения нового модулированного сигнала.
В результате модуляции спектр низкочастотного управляющего сигнала переносится в область высоких частот. Это позволяет при организации вещания настроить функционирование всех приёмо-передающих устройств на разных частотах с тем, чтобы они «не мешали» друг другу.
В качестве несущего могут быть использованы колебания различной формы (прямоугольные, треугольные и т. д.), однако чаще всего применяются гармонические колебания. В зависимости от того, какой из параметров несущего колебания изменяется, различают вид модуляции (амплитудная, частотная, фазовая и др.). Модуляция дискретным сигналом называется цифровой модуляцией или манипуляцией.
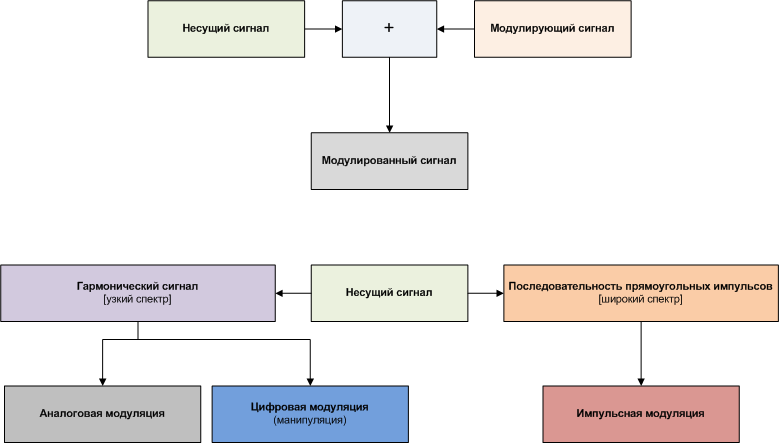
Аналоговая модуляция[править | править код]
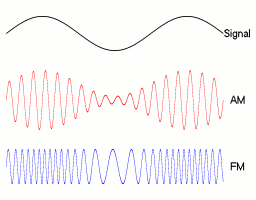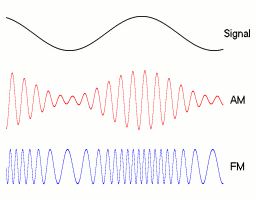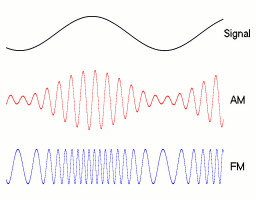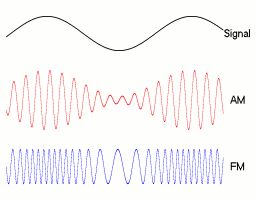
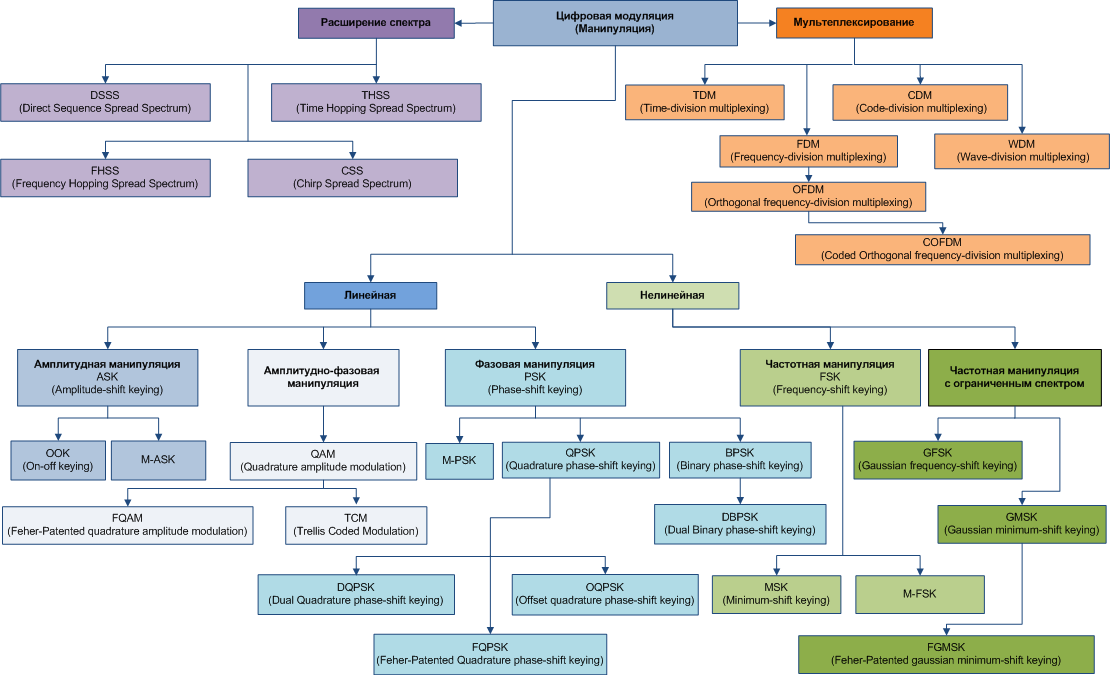
Цифровая модуляция[править | править код]
Импульсная модуляция[править | править код]
 a — несущий сигнал
a — несущий сигналb — полезный сигнал
c — амплитудно-импульсная модуляция
d — частотно-импульсная модуляция
e — широтно-импульсная модуляция
f — фазово-импульсная модуляция
- Энергетическая эффективность (потенциальная помехоустойчивость) характеризует достоверность передаваемых данных при воздействии на сигнал аддитивного белого гауссовского шума, при условии, что последовательность символов восстановлена идеальным демодулятором. Определяется минимальным отношением сигнал/шум (Eb/N0), которое необходимо для передачи данных через канал с вероятностью ошибки, не превышающей заданную. Энергетическая эффективность определяет минимальную мощность передатчика, необходимую для приемлемой работы. Характеристикой метода модуляции является кривая энергетической эффективности — зависимость вероятности ошибки идеального демодулятора от отношения сигнал/шум (Eb/N0).
- Спектральная эффективность CΔF{\displaystyle {C \over \Delta F}} — отношение скорости передачи данных к используемой полосе пропускания радиоканала.
- Устойчивость к воздействиям канала передачи характеризует достоверность передаваемых данных при воздействии на сигнал специфичных искажений: замирания вследствие многолучевого распространения, ограничение полосы, сосредоточенные по частоте или времени помехи, эффект Доплера и др.
- Требования к линейности усилителей. Для усиления сигналов с некоторыми видами модуляции могут быть использованы нелинейные усилители класса C, что позволяет существенно снизить энергопотребление передатчика, при этом уровень внеполосного излучения не превышает допустимые пределы. Данный фактор особенно важен для систем подвижной связи.
- Сложность реализации модемов определяется вычислительным ресурсом, требуемым для реализации алгоритма демодуляции, и требованиями к характеристикам аналоговой части.
- Прокис, Дж. Цифровая связь = Digital Communications / Кловский Д. Д.. — М.: Радио и связь, 2000. — 800 с. — ISBN 5-256-01434-X.
- Левин Б. Р. Теоретические основы статистической радиотехники. Книга 1. — М.: Советское радио, 1974. — 552 с.
- Феер К. Беспроводная цифровая связь. Методы модуляции и расширения спектра = Wireless Digital Communications: Modulation and Spread Spectrum Applications. — М.: Радио и связь, 2000. — 552 с. — ISBN 5-256-01444-7.
- Wilson, S.G. Digital Modulation and Coding. — Prentice Hall, 1996. — 667 p. — ISBN 9780132100717.

