12. Мгновенная и средняя мощности гармонических колебаний.

Мгновенная мощность гармонических колебаний равна: Р_m = i∙u, где u и i — мгновенные значения напряжения и тока. Величины тока и напряжения, входящие в выражение, являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной. График этой величины представлен на рисунке.

Для оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.

Пусть u=U_msinwt и I_msin(wt − φ), тогда средняя мощность будет равна

т.к. интеграл второго слагаемого равен нулю. Величина cosφ

называется коэффициентом мощности.

Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз φ между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в φ = 90° средняя мощность равна нулю.

P = UI cosφ = U(I cosφ ) = UI_а = I(U cosφ ) = IU_а .

Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как

I_а=U/R или U_а=IR , выражение (4) можно записать также в форме P = I²R = U²/R .

Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].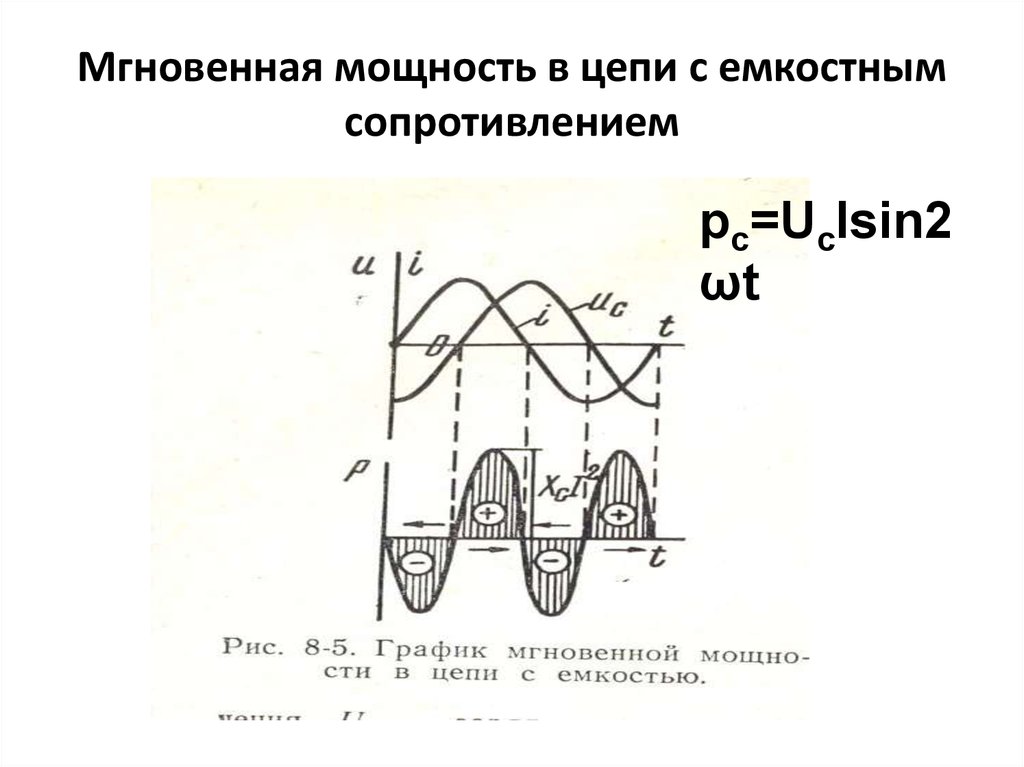

Выделим подинтегральную функцию выражения (3)

Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UIcosφ равной средней или активной мощности.

13. Гармонический ток через резистор, напряжение на резисторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.

Активное электрическое сопротивление – параметр пассивного двухполюсника, равный отношению активной мощности, поглощаемой в этом двухполюснике, к квадрату действующего значения тока через этот двухполюсник (ГОСТ Р52002-2003).

Пусть к активному сопротивлению (рис.2.5) приложено синусоидальное напряжение

u=Um sin(wt+ φ_U ) с начальной фазой φ_U = 0. Тогда по закону Ома

u = iR, iR=U_msinwt,

i =	Um sinwt	, φi = 0
	R

Значит φ = φ_i – φ_U = 0

, .

На участке цепи с активным сопротивлением ток совпадает по фазе с напряжением на этом участке.

Мгновенная мощность:

Рm = i∙U =	U2m sin2wt
	R

Средняя мощность:

Рср =	U2m
	2R

Векторная диаграмма действующих значений тока и напряжения, графики зависимостей мгновенных значений тока и напряжений приведены на рис.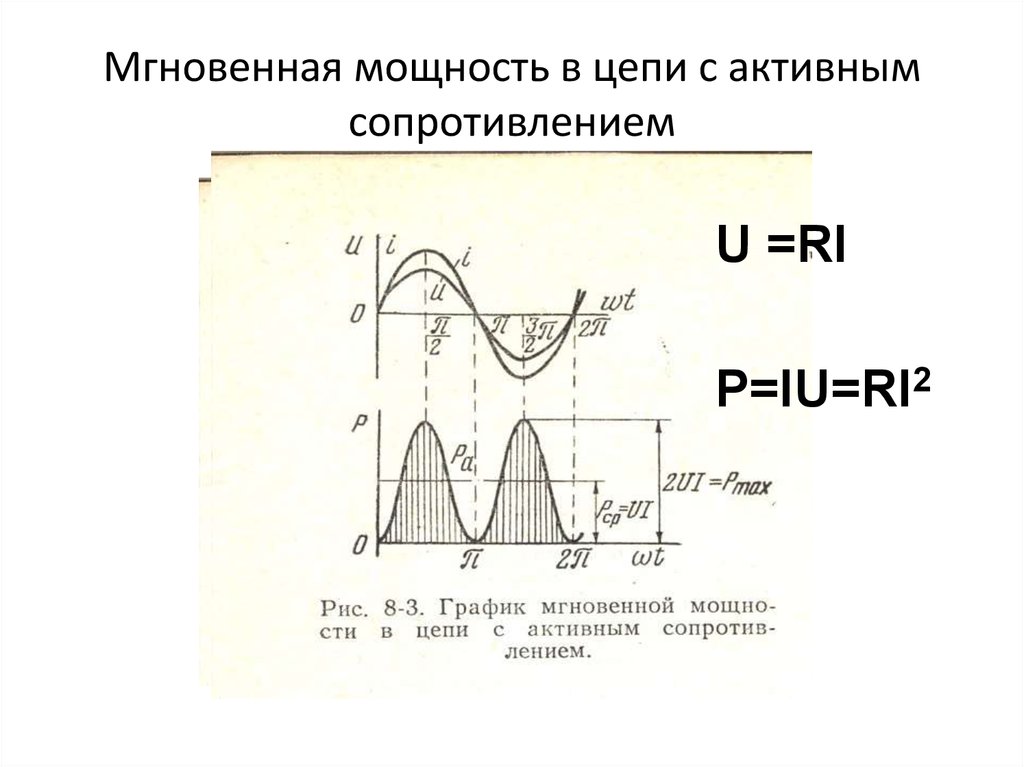 2.6.

Рис. 2.6

Энергетический процесс в цепи с резистором

Мгновенная мощность в цепи с резистором равна произведению мгновенного значения напряжения на мгновенное значение тока.

Перемножим напряжение и ток графически.

Вывод: в цепи с резистором мгновенная мощность всегда положительна. Это значит, что в любой момент времени происходит необратимый процесс преобразования электрической энергии в тепловую. Средняя скорость этого преобразования называется активная мощность (Р). Чтобы ее найти надо сложить все мгновенные мощности за период () и разделить на время равное периоду.

Получаем разность интервалов, где интеграл за период от

, где — напряжение на резисторе.

Измеряется активная мощность в ваттах (Вт).

Пример решения задачи.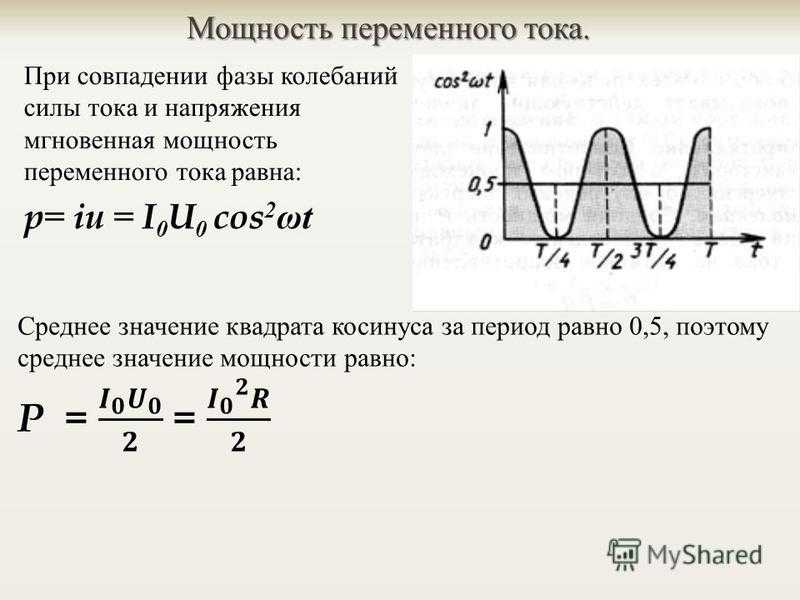

1) Дано:

R=50 Ом

Определить: . Построить векторную диаграмму тока и напряжения.

U_m=I_m·R=10·50=500 В

I= =7,14 АВВт

Тестовые задания:

Задание	Варианты ответов
1.Верно ли, что в цепи с R напряжения и совпадают по фазе?	Да; Нет.
2.Какая единица измерения активной мощности?	а) Вт; б) вар; в) B·A.

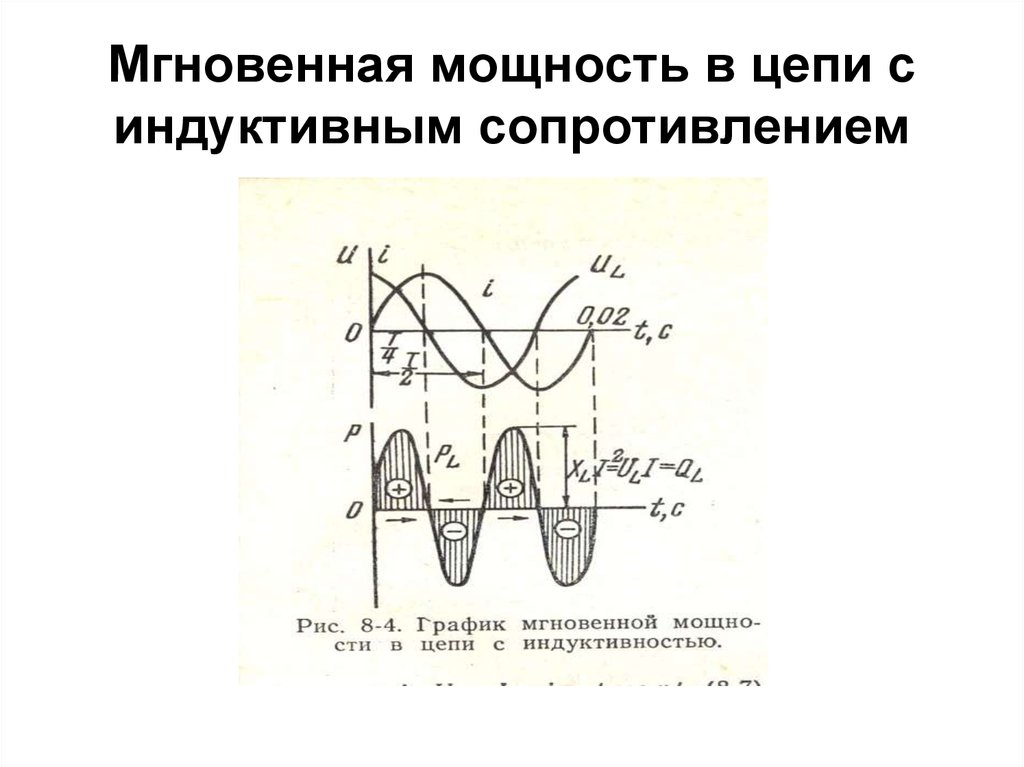
Цепь с идеальной катушкой индуктивности при гармоническом воздействии

Пусть по цепи течет ток

При прохождении тока в катушке возникает ЭДС самоиндукции

-напряжение на входе уравновешивает эту ЭДС.

Подставим в эту формулу значение тока и продифференцируем

Угол сдвига фаз

Вывод: в цепи с идеальной катушкой напряжение опережает ток на угол 90⁰

ЭДС самоиндукции уравновешивает напряжение, значить ЭДС будет отставать от тока на угол равный 90⁰.

— потокосцепление катушки.

Вывод: в цепи с идеальной катушкой ток, потокосцепление и магнитный поток совпадает по фазе.

Построим временную и векторную диаграммы

Закон Ома для цепи с идеальной катушкой. Индуктивное сопротивление

Запишем отдельно выражение

, отсюда , где обозначаем — индуктивное сопротивление

=Ом

Получаем закон Ома для максимальных и действующих значений в цепи с идеальной катушкой

Вывод: в цепи с идеальной катушкой закон Ома справедлив для максимальных и действующих значений, но не справедлив для мгновенных ().

Построим зависимость , где

Вывод: с ростом частоты индуктивное сопротивление растет, значит, катушка хорошо пропускает токи нижних и плохо токи верхних частот. Катушка-фильтр нижних частот.

На постоянном токе

Индуктивное сопротивление равно 0, значит, на постоянном токе вместо идеальной катушки стоит провод.

Энергетический процесс в цепи с идеальной катушкой.

Мгновенная мощность равна произведению мгновенного значения напряжения на мгновенное значение тока.

Перемножим напряжение и ток графически.

Вывод: первую и третью четверти периода напряжение и ток имеют одинаковые знаки, следовательно, источник работает в режиме генератора и отдает свою энергию в магнитное поле катушки, мгновенная мощность положительна. Ворую и четвертую четверти напряжение и ток имеют разные знаки, следовательно, источник работает в режиме потребителя, энергия возвращается обратно к источнику, мгновенная мощность отрицательна.

Вывод: в цепи с идеальной катушкой источник и катушка обмениваются энергией и мерой этого обмена, является реактивная мощность, которая обозначается .

= вар

Пример решения задачи

Дано:

мГн

Найти:

, построить векторные диаграммы напряжения и тока

Ом

А

А

вар

резисторов — Расчет мгновенной и средней мощности

спросил 6 лет, 6 месяцев назад

Изменено 4 года, 4 месяца назад

Просмотрено 3к раз

\$\начало группы\$

извините, что это такой простой вопрос, но мне нужно рассчитать среднюю и мгновенную мощность для следующей цепи: 92(\omega t) \$ за любое целое число циклов равно \$ 1/2 \$, поэтому средняя мощность равна \$ 450\,\rm W \$.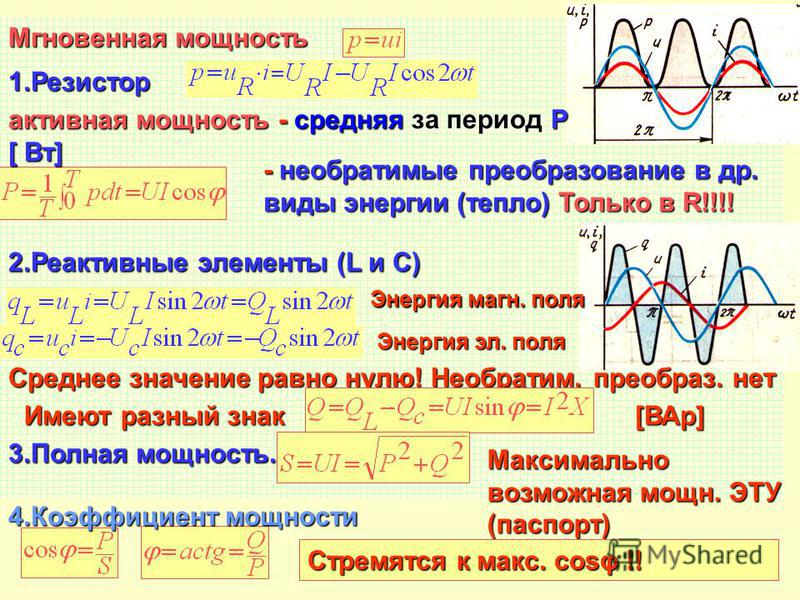

Чтобы обратиться к другой вашей формуле, \$P=VI\cos\phi\$, обратите внимание, что пиковое напряжение равно \$150\,\rm V\$, поэтому среднеквадратичное напряжение равно \$150/\sqrt2\,\rm V\$, а среднеквадратичное значение тока равно \$6/\sqrt 2\,\rm A\$. Поскольку нагрузка резистивная, фазовый угол \$\phi\$ равен нулю, а (средняя) мощность по-прежнему равна \$900/2 = 450\,\rm Вт\$.

\$\конечная группа\$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Переходная мгновенная мощность рассеяния импеданса

Задавать вопрос

спросил 1 год, 11 месяцев назад

Изменено 1 год, 11 месяцев назад

Просмотрено 93 раза

\$\начало группы\$

Предположим, у нас есть резистор номиналом R, подключенный параллельно катушке индуктивности L с последовательным сопротивлением R. Импеданс сети равен $$Z= R\frac{sL+R}{sL+2R}.$$

^{имитация этой схемы – Схема создана с помощью CircuitLab}

Напряжение V0(t) на импедансе можно найти с помощью обратного преобразования Лапласа Z(s)I0(s).

Суммарная мощность, входящая в импеданс, равна $$ P_{total}(t)=V_0(t)I_0(t).