Закон всемирного тяготения, сила тяжести
Закон всемирного тяготения, сила тяжестиОсновные понятия для силы тяжести и закона всемирного тяготения
Исследуя нормальное ускорение, которое возникает при движении Луны вокруг Земли, И. Ньютон пришел к выводу о том, что все тела в природе притягиваются друг к другу с некоторой силой, названной силой тяготения. При этом ускорение, которое вызывается действием данной силы обратно пропорционально квадрату расстояния между рассматриваемыми, воздействующими друг на друга телами.
Допустим, что два точечных тела, имеющих массы $m_1\ и\ m_2$ находятся на расстоянии $r$ друг от друга. Эти тела взаимодействуют с силами:
\[F_1=m_1a_1\ и\ F_2=m_2a_2\left(1\right).\]
В соответствии с третьим законом Ньютона, модули сил равны:
\[F_1=F_2\left(2\right).\]
Из сказанного выше об ускорении и на основании (2) получим:
\[\frac{m_1K_1}{r^2}=\frac{m_2K_2}{r^2}\left(3\right).
2}(4).\]
Строго говоря, формулу (4) можно использовать для вычисления силы тяготения между однородным шарами с массами $m_1{\ и\ m}_2$, считая, что $r$ расстояние между центрами шаров.
Для того чтобы найти силы тяготения, которые действуют на одно тело со стороны другого тела, при этом тела точечными считать нельзя, поступают следующим образом. Оба тела теоретически делят на элементы, которые можно приять за точечные массы. Находят силы тяготения, которые действуют на один выбранный элемент первого тела со стороны всех элементов другого тела, получают силу, которая действует на рассматриваемую точку первого тела. Далее операцию повторяют для каждой точки первого тела. Полученные силы складывают с учетом их направлений. В результате получается сила тяготения, с которой второе тело действует на первое. Такая задача является весьма сложной.
Сила тяжести
Определение
Сила тяжести
2_0}-1}$Читать дальше: закон Паскаля для жидкостей и газов.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Фундаментальные взаимодействия
Фундаментальные взаимодействияФундаментальные взаимодействия.
К настоящему времени известны четыре вида основных
фундаментальных взаимодействий:гравитационное,электромагнитное,сильное,
слабое.Гравитационное взаимодействие характерно для всех материальных объектов
вне зависимости от их природы. Оно заключается во взаимном притяжении тел и
определяется фундаментальным законом всемирного тяготения: между двумя точечными
телами действует сила притяжения, прямо пропорциональная произведению их масс и
обратно пропорциональная квадрату расстояния между ними. Гравитационным
взаимодействием определяется падение тел в поле сил тяготения Земли.
Проблема создания единой фундаментальной теории.В
классификации многочисленных известных к настоящему времени элементарных частиц
гипотеза кварков оказалась довольно плодотворной. Она позволила не только
систематизировать уже известные элементарные частицы, но и предсказать новые, а
также объяснить многие их свойства.
Хостинг от uCoz
Разработка урока по физике «Закон всемирного тяготения» (9класс)
Тема урока: Силы в механике. Силы всемирного тяготения. Закон всемирного тяготения.
Цель: Познакомить учащихся с формулировкой и математической записью закона всемирного тяготения. Научить решать задачи на расчет силы тяготения.
Задачи урока:
Образовательная: изучить закон всемирного тяготения, добиться понимания этого закона, умения применить его для решения задач;
Развивающие — умение делать выводы, совершенствование интеллектуальных способностей и развитие речи учащихся, стимулирование интереса к предмету путём привлечения дополнительного материала. Совершенствовать навыки учащихся и расширять их границы при выполнении качественных, расчетных задач.
Воспитательные: продолжить работу по формированию у учащихся
добросовестного отношения к учебному труду, гуманности, эстетического
восприятия мира; воспитать стремление к познанию.
Тип урока: изучение нового материала
Методы: наглядный, частично-поисковый, беседа
Оборудование: мультимедийный комплекс, презентация, тесты.
Ход урока
1. Психологический настрой. Физминутка.
2. Проверка дом. задания
1.Упр 11. Заслушивание информации о выполнении домашней работы (консультанты). Некоторые задачи, которые вызвали затруднения у учащихся выполнить у доски.
2.Тестирование по законам Ньютона
1. Как формулируется III закон Ньютона?
1.Тело
движется равномерно и прямолинейно (или покоится), если на него не действуют
другие тела (или действие других тел скомпенсировано)
2. Сила упругости,
возникающая при деформации тела, прямо пропорциональна величине абсолютного
удлинения
3. Действие равно
противодействию
4.Тела действуют друг
на друга силами равными по абсолютному значению, направленными вдоль одной
прямой и противоположными по направлению
2.
III закон
Ньютона математически можно записать так:
1.F = ma2.F = μN3.F12 = −F214.Fx = −kx5.затрудняюсь ответить
3. Как формулируется II закон Ньютона?
1.Тело
движется равномерно в инерциальной системе, если воздействие других тел не скомпенсировано
2.Ускорение,
приобретаемое телом, прямо пропорционально равнодействующей всех сил,
действующих на тело, и обратнопропорционально его массе
3.Направление
ускорения тела совпадает с направлением равнодействующей всех сил, действующих
на тело
4.Модуль ускорения
тела прямо пропорционален модулю равнодействующей всех сил и обратно
пропорционален массе тела
5.затрудняюсь ответить
4.Векторная величина, являющаяся мерой взаимодействия тела с другими телами, в результате чего тело приобретает ускорение,- это…
А. — вес тела
Б. Сила реакции опоры
в. Равнодействующая сила
г. Сила упругости
5.
Пружина
динамометра растягивается под действием приложенных двух сил по 3 Н. Каково
показание динамометра?
А. 0Н
Б. 3 Н
В.6 Н
Г. 9 Н.
6. В каких системах отсчета выполняются законы Ньютона?
А.
неинерциальных
Б.инерциальных
В. В любых
Г. подвижных
7. Два
мальчика тянут за концы динамометра в противоположные направления с силой 5 Н.
Каковы показания динамометров?
А. 10 Н и 10 Н.
Б. 5 Н. и 0 Н
В. 5 Н и 5Н
Г. 3 Н и 7 Н
8. Тела действуют друг на друга при их
взаимодействии силами:
А. равными по величине и совпадающими по
направлению
Б. Равными по величине и направленными в
противоположные стороны
В. разными по величине и направленными в одну
сторону
Г. силами разной природы
3. Объяснение новой темы в сочетании с беседой.
Из истории физики…
Датский астроном Тихо Браге (1546-1601), долгие годы наблюдавший за
движением планет, накопил огромное количество интересных данных, но не сумел их
обработать.
Иоганн Кеплер (1571-1630) используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, установил законы движения планет вокруг Солнца, однако и он не смог объяснить динамику этого движения.
Исаак Ньютон открыл этот закон в возрасте 23 лет, но целых 9 лет не публиковал его, так как имевшиеся тогда неверные данные о расстоянии между Землей и Луной не подтверждали его идею. Лишь в 1667 году, после уточнения этого расстояния, закон всемирного тяготения был наконец отдан в печать.
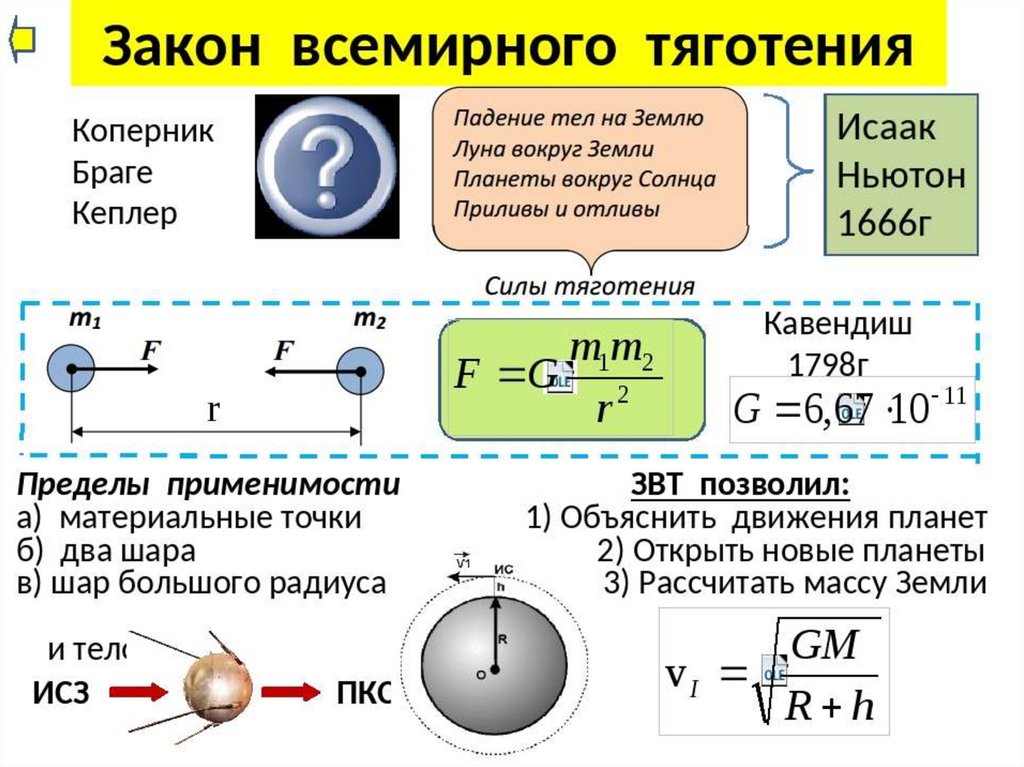
Ньютон предположил, что ряд явлений, казалось бы не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т.д.), вызваны одной причиной.
Окинув единым мысленным взором “земное” и “небесное”, Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной — от яблок до планет!
В 1667 г. Ньютон высказал предположение, что между всеми телами
действуют силы взаимного притяжения, которые он назвал силами всемирного
тяготения.
Исаак Ньютон — английский физик и математик, создатель теоретических основ механики и астрономии. Он открыл закон всемирного тяготения, разработал дифференциальное и интегральное исчисления, изобрел зеркальный телескоп и был автором важнейших экспериментальных работ по оптике. Ньютона по праву считают создателем «классической физики».
Закон всемирного тяготения
В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: “Два любых тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними”
.
где m1 и m2 – массы взаимодействующих тел, r – расстояние между телами, G – коэффициент пропорциональности, одинаковый для всех тел в природе и называемый постоянной всемирного тяготения или гравитационной постоянной.
Запомнить
·
Гравитационное
взаимодействие – это взаимодействие, свойственное всем телам Вселенной и
проявляющееся в их взаимном притяжении друг к другу.
· Гравитационное поле – особый вид материи, осуществляющее гравитационное взаимодействие.
Механизм гравитационного взаимодействия
В настоящее время механизм гравитационного взаимодействия представляется следующим образом: Каждое тело массой М создает вокруг себя поле, которое называют гравитационным. Если в некоторую точку этого поля поместить пробное тело массой т, то гравитационное поле действует на данное тело с силой F, зависящей от свойств поля в этой точке и от величины массы пробного тела.
Эксперимент Генри Кавендиша по определению гравитационной постоянной.
Английский физик Генри Кавендиш определил, насколько велика сила притяжения между двумя объектами. В результате была достаточно точно определена гравитационная постоянная, что позволило Кавендишу впервые определить и массу Земли.
Гравитационная постоянная
G — гравитационная постоянная, она численно равна силе гравитационного
притяжения двух тел, массой по 1 кг.
Каждое, находящихся на расстоянии 1 м одно
от другого.
G — универсальная гравитационная постоянная
G=6,67 * 10 -11 Н м2 /кг 2
Гравитационная постоянная показывает, с какой силой взаимодействуют тела единичной массы на единичном расстоянии друг от друга: .
Сила взаимодействия между двумя точечными телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними: .
— сила тяжести всем телам независимо от их массы сообщает одинаковое ускорение.
Сила взаимного притяжения всегда направлена вдоль прямой, соединяющей тела.
Границы применимости закона
Закон всемирного тяготения имеет определенные границы применимости; он применим для:
1) материальных точек;
2) тел, имеющих форму шара;
3) шара большого радиуса, взаимодействующего с телами, размеры которых
много меньше размеров шара.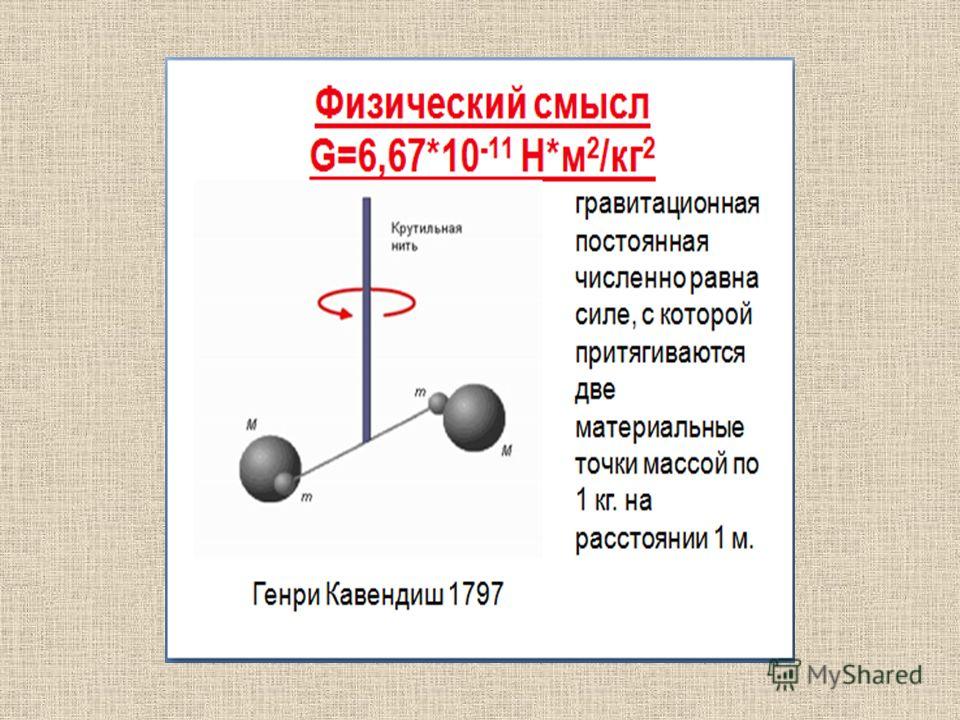
Закон неприменим, например, для взаимодействия бесконечного стержня и шара.
Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет очень большую массу (планета, звезда).
3. Закрепление. Решение задач
1. Почему мы не замечаем гравитационного притяжения между окружающими нас телами?
2. Два корабля массой 50000 т каждый стоят на рейде на расстоянии 1 км друг от друга. Какова сила притяжения между ними?
Д А Н О:
F — ?
Решение:
Ответ: F = 0,17 Н
3. Известно, что период обращения Луны вокруг Земли составляет 27,3 суток, среднее расстояние между центрами Луны и Земли равно 384000 километров. Вычислить ускорение Луны и найти во сколько раз оно отличается от ускорения свободного падения камня вблизи поверхности Земли, то есть на расстоянии равном радиусу Земли (6400 км).
выведение закона
С другой стороны, отношение расстояний от Луны и камня до центра Земли равно:
Нетрудно заметить, что
5.
Прямо прямо пропорцианальная зависимость
Из второго закона Ньютона следует, что между силой и ускорением, которое она вызывает, существует прямо пропорциональная зависимость:
Следовательно, сила тяготения так же, как и ускорение, обратно пропорциональна квадрату расстояния между телом и центром Земли:
Галилео Галилей экспериментально доказал, что все тела падают на Землю с одним и тем же ускорением, называемым ускорением свободного падения (опыт с падением разных тел в трубке с откачанным воздухом)
Почему это ускорение одинаково для всех тел?
Это возможно только в том случае, если сила тяготения пропорциональна массе тела: F ~ m . Действительно, тогда, например, увеличение или уменьшение массы в два раза вызовет соответствующее изменение силы тяготения в два раза, но ускорение по второму закону Ньютона останется прежним
С другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы:
Следовательно, сила тяготения должна быть пропорциональна массе обоих
тел.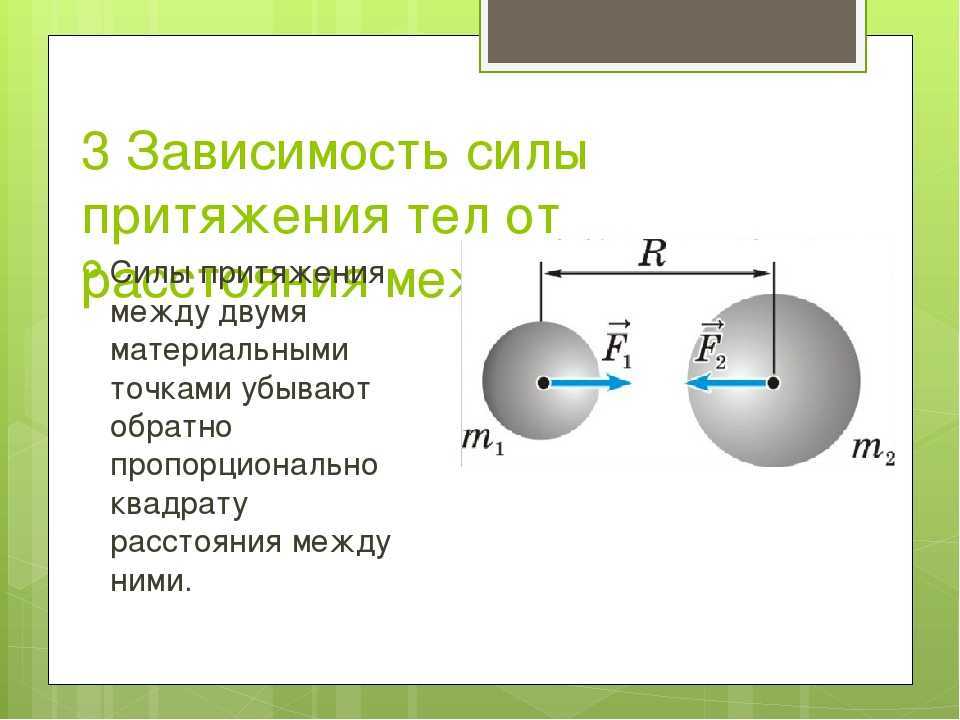
Так Ньютон пришёл к выводу, что сила тяготения между телом и Землёй прямо пропорциональна произведению их масс:
6.Итоги урока
Обобщая всё выше изложенное относительно силы тяготения плане-ты Земля и любого тела, приходим к следующему утверждению : сила тяготения между телом и Землёй прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами, что можно записать в виде
Выполняется ли этот закон только для Земли или является всеобщим?
Чтобы ответить на этот вопрос, Ньютон использовал кинематические законы движения планет Солнечной системы, сформулированные немецким учёным Иоганном Кеплером на основании многолетних астрономических наблюдений датскогоучёного Тихо Браге.
7. Подумай и ответь
1. Почему Луна не падает на Землю?
2. Почему мы замечаем силу притяжения всех тел к Земле, но не замечаем взаимного притяжения между самими этими телами?
3.
Как двигались бы планеты,
если бы сила притяжения Солнца внезапно исчезла?
4. Как двигалась бы Луна, если бы она остановилась на орбите?
5.
Притягивает ли Землю
стоящий на ее поверхности человеке? Летящий самолет? Космонавт, находящийся на
орбитальной станции?
— новый слайд-
Некоторые тела (воздушные шары, дым, самолеты, птицы) поднимаются вверх,
несмотря на тяготение. Как вы думаете, почему? Нет ли здесь нарушения закона
всемирного тяготения?
6. Что нужно сделать, чтобы увеличить силу тяготения между двумя телами?
7. Какая сила вызывает приливы и отливы в морях и океанах Земли?
8. Почему мы не замечаем гравитационного притяжения между окружающими нас телами?
8.Вопрос-ответ
Составьте вопросы и затем дайте ответ к рисункам 1-4.
9. Домашнее задание: §15 Упр
12(3,4)
7. Итоги урока (Выставление оценок и их комментарий).
8. Рефлексия
Работа с сигнальными карточками.
Зеленая карточка. Я удовлетворен уроком. Урок был полезен для меня. Я с пользой и хорошо работал на уроке. Я понимал все, о чем говорилось и что делалось на уроке.
Желтая карточка. Урок был интересен. Я принимал в нем участие. Урок был в определенной степени полезен для меня. Я отвечал с места, выполнил ряд заданий. Мне было на уроке достаточно комфортно.
Красная карточка. Пользы от урока я получил мало. Я не очень понимал, о чем идет речь. Мне это не нужно. К ответу на уроке я был не готов.
Цель урока:
· создавать условия для формирования познавательного интереса, активности учащихся;
· вывести закон всемирного тяготения;
· способствовать развитию конвергентного мышления;
· способствовать эстетическому воспитанию учащихся;
· формирование коммуникационного общения;
Из истории физики.
..
Датский астроном Тихо Браге (1546-1601), долгие годы наблюдавший за движением планет, накопил огромное количество интересных данных, но не сумел их обработать.
Иоганн Кеплер (1571-1630) используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, установил законы движения планет вокруг Солнца, однако и он не смог объяснить динамику этого движения.
Исаак Ньютон открыл этот закон в возрасте 23 лет, но целых 9 лет не публиковал его, так как имевшиеся тогда неверные данные о расстоянии между Землей и Луной не подтверждали его идею. Лишь в 1667 году, после уточнения этого расстояния, закон всемирного тяготения был наконец отдан в печать.
Ньютон предположил, что ряд явлений, казалось бы не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т.д.), вызваны одной причиной.
Окинув единым мысленным взором “земное” и “небесное”, Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной — от яблок до планет!
В 1667 г.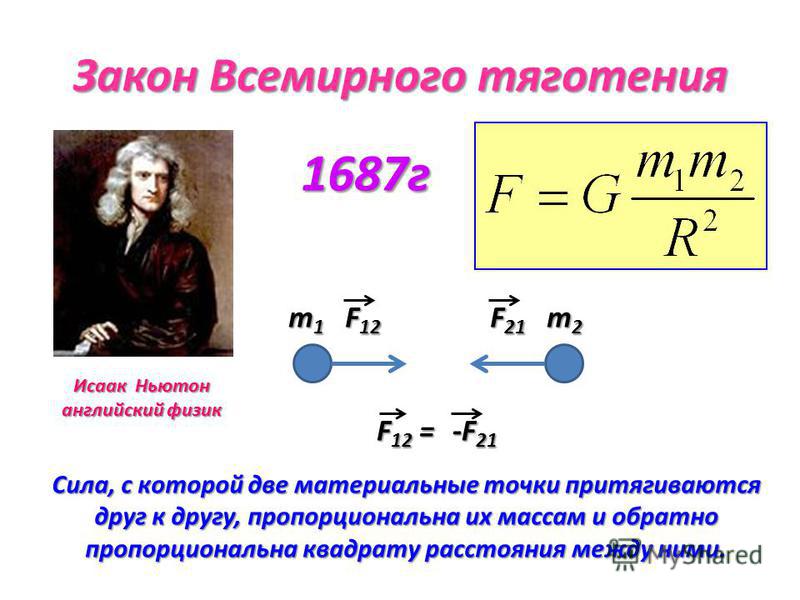
Ньютон высказал предположение, что между всеми телами
действуют силы взаимного притяжения, которые он назвал силами всемирного
тяготения.
Исаак Ньютон — английский физик и математик, создатель теоретических основ механики и астрономии. Он открыл закон всемирного тяготения, разработал дифференциальное и интегральное исчисления, изобрел зеркальный телескоп и был автором важнейших экспериментальных работ по оптике. Ньютона по праву считают создателем «классической физики».
Закон всемирного тяготения
В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: “Два любых тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними”
.
где m1 и m2 –
массы взаимодействующих тел, r – расстояние между телами, G – коэффициент
пропорциональности, одинаковый для всех тел в природе и называемый постоянной
всемирного тяготения или гравитационной постоянной.
Запомнить
· Гравитационное взаимодействие – это взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу.
· Гравитационное поле – особый вид материи, осуществляющее гравитационное взаимодействие.
Механизм гравитационного взаимодействия
В настоящее время механизм гравитационного взаимодействия представляется следующим образом: Каждое тело массой М создает вокруг себя поле, которое называют гравитационным. Если в некоторую точку этого поля поместить пробное тело массой т, то гравитационное поле действует на данное тело с силой F, зависящей от свойств поля в этой точке и от величины массы пробного тела.
Эксперимент Генри Кавендиша по определению гравитационной постоянной.
Английский физик Генри Кавендиш определил, насколько велика сила
притяжения между двумя объектами. В результате была достаточно точно определена
гравитационная постоянная, что позволило Кавендишу впервые определить и массу
Земли.
Гравитационная постоянная
G — гравитационная постоянная, она численно равна силе гравитационного притяжения двух тел, массой по 1 кг. Каждое, находящихся на расстоянии 1 м одно от другого.
G — универсальная гравитационная постоянная
G=6,67 * 10 -11 Н м2 /кг 2
Сила взаимного притяжения всегда направлена вдоль прямой, соединяющей тела.
Границы применимости закона
Закон всемирного тяготения имеет определенные границы применимости; он применим для:
1) материальных точек;
2) тел, имеющих форму шара;
3) шара большого радиуса, взаимодействующего с телами, размеры которых много меньше размеров шара.
Закон неприменим, например, для взаимодействия бесконечного стержня и шара.
Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет очень большую массу (планета, звезда).
Почему мы не замечаем гравитационного притяжения между окружающими нас телами?
Воспользуемся законом всемирного тяготения и сделаем некоторые расчёты:
Два корабля массой 50000 т каждый стоят на рейде на расстоянии 1 км
друг от друга.
Какова сила притяжения между ними?
Д А Н О:
F — ?
Решение:
Ответ: F = 0,17 Н
задача
Известно, что период обращения Луны вокруг Земли составляет 27,3 суток, среднее расстояние между центрами Луны и Земли равно 384000 километров. Вычислить ускорение Луны и найти во сколько раз оно отличается от ускорения свободного падения камня вблизи поверхности Земли, то есть на расстоянии равном радиусу Земли ( 6400 километров ).
выведение закона
С другой стороны, отношение расстояний от Луны и камня до центра Земли равно:
Нетрудно заметить, что
Прямо пропорцианальная зависимость
Из второго закона Ньютона следует, что между силой и ускорением, которое она вызывает, существует прямо пропорциональная зависимость:
Следовательно, сила тяготения так же, как и ускорение, обратно пропорциональна квадрату расстояния между телом и центром Земли:
Галилео Галилей экспериментально доказал, что все тела падают на Землю с одним и тем же ускорением, называемым ускорением свободного падения (опыт с падением разных тел в трубке с откачанным воздухом)
Почему это ускорение одинаково для всех тел?
Это возможно только в том случае, если сила тяготения пропорциональна
массе тела: F ~ m .
Действительно, тогда, например, увеличение или уменьшение
массы в два раза вызовет соответствующее изменение силы тяготения в два раза,
но ускорение по второму закону Ньютона останется прежним
С другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы:
Следовательно, сила тяготения должна быть пропорциональна массе обоих тел.
Так Ньютон пришёл к выводу, что сила тяготения между телом и Землёй прямо пропорциональна произведению их масс:
итоги урока
Обобщая всё выше изложенное относительно силы тяготения плане-ты Земля и любого тела, приходим к следующему утверждению : сила тяготения между телом и Землёй прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами, что можно записать в виде
Выполняется ли этот закон только для Земли или является всеобщим?
Чтобы ответить на этот вопрос, Ньютон использовал кинематические законы
движения планет Солнечной системы, сформулированные немецким учёным Иоганном
Кеплером на основании многолетних астрономических наблюдений датскогоучёного
Тихо Браге.
Подумай и ответь
9. Почему Луна не падает на Землю?
10. Почему мы замечаем силу притяжения всех тел к Земле, но не замечаем взаимного притяжения между самими этими телами?
11. Как двигались бы планеты, если бы сила притяжения Солнца внезапно исчезла?
12. Как двигалась бы Луна, если бы она остановилась на орбите?
13.
Притягивает ли Землю
стоящий на ее поверхности человеке? Летящий самолет? Космонавт, находящийся на
орбитальной станции?
— новый слайд-
Некоторые тела (воздушные шары, дым, самолеты, птицы) поднимаются вверх,
несмотря на тяготение. Как вы думаете, почему? Нет ли здесь нарушения закона
всемирного тяготения?
14. Что нужно сделать, чтобы увеличить силу тяготения между двумя телами?
15. Какая сила вызывает приливы и отливы в морях и океанах Земли?
16. Почему мы не замечаем гравитационного притяжения между окружающими нас телами?
Вопрос-ответ
Составьте вопросы и затем дайте ответ к рисункам 1-4.
5.5: Закон всемирного тяготения Ньютона
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14463
- Безграничный
- Безграничный
Закон всемирного тяготения
Объекты с массой ощущают силу притяжения, пропорциональную их массе и обратно пропорциональную квадрату расстояния.
цели обучения
- Выразить закон всемирного тяготения в математической форме
Хотя яблоко, возможно, и не попало в голову сэру Исааку Ньютону, как предполагает миф, падение одного из них вдохновило Ньютона на одно из величайших открытий в механике: Закон всемирного тяготения .
Размышляя о том, почему яблоко никогда не падает ни вбок, ни вверх, ни в каком-либо другом направлении, кроме перпендикулярного к земле, Ньютон понял, что сама Земля должна быть ответственна за движение яблока вниз.
Теоретизируя, что эта сила должна быть пропорциональна массам двух вовлеченных объектов, и используя предыдущую интуицию об обратной квадратичной зависимости силы между Землей и Луной, Ньютон смог сформулировать общий физический закон по индукции.
Закон всемирного тяготения гласит, что каждая точечная масса притягивает любую другую точечную массу во Вселенной силой, направленной по прямой линии между центрами масс обеих точек, и эта сила пропорциональна массам объектов. и обратно пропорциональна их расстоянию. Эта сила притяжения всегда направлена внутрь, от одной точки к другой. Закон применим ко всем объектам с массой, большой или малой. Два больших объекта можно рассматривать как точечные массы, если расстояние между ними очень велико по сравнению с их размерами или если они сферически симметричны.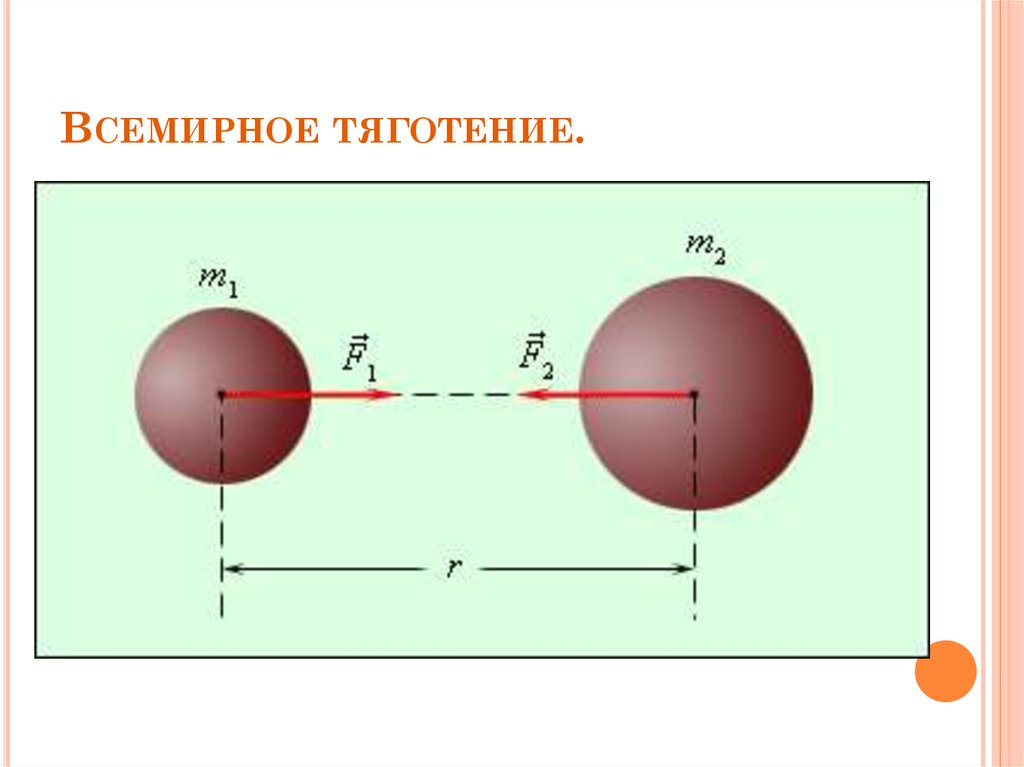
В этих случаях массу каждого объекта можно представить в виде точечной массы, расположенной в его центре масс. 92}\). Из-за величины \(\mathrm{G}\) гравитационная сила очень мала, если только не задействованы большие массы.
Силы, действующие на две массы : Все массы притягиваются друг к другу. Сила пропорциональна массам и обратно пропорциональна квадрату расстояния.
Гравитационное притяжение сферических тел: однородная сфера
Теорема оболочки утверждает, что сферически симметричный объект влияет на другие объекты, как если бы вся его масса была сосредоточена в его центре. 92}}\]
Однако большинство объектов не являются точечными частицами. Чтобы найти гравитационную силу между трехмерными объектами, нужно рассматривать их как точки в пространстве. Для высокосимметричных форм, таких как сферы или сферические оболочки, найти эту точку несложно.
Теорема Оболочки
Исаак Ньютон доказал Теорему Оболочки, которая утверждает, что:
- Сферически симметричный объект гравитационно воздействует на другие объекты, как если бы вся его масса была сосредоточена в его центре,
- Если объект представляет собой сферически симметричную оболочку (т.
е. полый шар), то результирующая гравитационная сила, действующая на тело внутри его, равна нулю.
е. полый шар), то результирующая гравитационная сила, действующая на тело внутри его, равна нулю.Поскольку сила является векторной величиной, сумма векторов всех частей оболочки/сферы дает результирующую силу, и эта результирующая сила эквивалентна одному измерению силы, взятому из середины сферы или центра масс (ЦМ) . Таким образом, при нахождении силы тяжести, действующей на мяч массой 10 кг, расстояние, измеренное от мяча, берется от центра масс мяча до центра масс Земли.
Учитывая, что сферу можно рассматривать как совокупность бесконечно тонких, концентрических, сферических оболочек (подобных слоям луковицы), можно показать, что следствие теоремы об оболочке состоит в том, что сила, приложенная к объекту внутри сплошной сферы зависит только от массы сферы внутри радиуса, на котором находится объект. Это связано с тем, что оболочки с большим радиусом, чем тот, на котором находится объект, вносят , а не силы в объект внутри них (утверждение 2 теоремы).
При рассмотрении гравитационной силы, действующей на объект в точке внутри или вне однородного сферически-симметричного объекта радиуса RR, необходимо рассмотреть две простые и различные ситуации: случай полой сферической оболочки, и твердая сфера с равномерно распределенной массой.
Случай 1: полая сферическая оболочка
Гравитационная сила, действующая сферически-симметричной оболочкой на точечную массу внутри it, представляет собой векторную сумму сил гравитации, действующих на каждую часть оболочки, и эта векторная сумма равна нулю. То есть масса мм внутри сферически-симметричной оболочки массой \(\mathrm{M}\) не будет ощущать результирующей силы (утверждение 2 теоремы оболочки).
Чистая гравитационная сила, которую сферическая оболочка массы \(\mathrm{M}\) оказывает на тело вне ее , представляет собой векторную сумму гравитационных сил, действующих каждой частью оболочки на внешний объект , которые в сумме составляют результирующую силу, действующую так, как будто масса \(\mathrm{M}\) сосредоточена в точке в центре сферы (утверждение 1 теоремы Оболочки).
Диаграмма, используемая в доказательстве теоремы о Шелле : Эта диаграмма описывает геометрию, рассматриваемую при доказательстве теоремы о Шелле. В частности, в этом случае сферическая оболочка массы \(\mathrm{M}\) (левая часть рисунка) действует с силой на массу \(\mathrm{m}\) (правая часть рисунка) вне ее . Площадь поверхности тонкого среза сферы показана цветом. (Примечание: доказательство теоремы здесь не представлено. Заинтересованные читатели могут продолжить изучение, используя источники, перечисленные в нижней части этой статьи.)
Случай 2: сплошная однородная сфера
Вторая ситуация, которую мы рассмотрим, касается сплошной однородной сферы массы \(\mathrm{M}\) и радиуса \(\mathrm{R}\), оказывающей сила, действующая на тело массой \(\mathrm{m}\) с радиусом \(\mathrm{d}\) внутри его (то есть, \(\mathrm{d (\(\mathrm{ρ}\) — плотность массы шара, и мы предполагаем, что она не зависит от радиуса. То есть масса шара распределена равномерно.) Следовательно , объединяя два приведенных выше уравнения, мы получаем: \[\mathrm{F=\dfrac{4}{3}πGmρd}\] , что показывает, что масса mm испытывает силу, линейно пропорциональную ее расстоянию, dd, от центра масс шара. Как и в случае полых сферических оболочек, результирующая гравитационная сила, с которой твердая сфера с равномерно распределенной массой \(\mathrm{M}\) действует на тело вне его, является векторной суммой гравитационных сил, действующих каждой оболочкой сферы на внешний объект. Результирующая чистая гравитационная сила действует так, как будто масса \(\mathrm{M}\) сосредоточена в точке в центре сферы, которая является центром масс или COM (утверждение 1 теоремы Шелла). Когда тела имеют пространственную протяженность, гравитационная сила рассчитывается путем суммирования составляющих их точечных масс. цели обучения Закон всемирного тяготения Ньютона гласит, что каждая точечная масса во Вселенной притягивает любую другую точечную массу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. 92}}\] где \(\mathrm{F}\) — сила между массами, \(\mathrm{G}\) — гравитационная постоянная, \(\mathrm{m_1}\) — первая масса, \(\mathrm{m_2}\) — вторая масса и \(\mathrm{r}\) — расстояние между центрами масс. Если рассматриваемые тела имеют пространственную протяженность (а не являются теоретическими точечными массами), то гравитационная сила между ними рассчитывается путем суммирования вкладов условных точечных масс, составляющих тела. Таким образом можно показать, что объект со сферически-симметричным распределением массы оказывает такое же гравитационное притяжение на внешние тела, как если бы вся масса объекта была сосредоточена в точке в его центре. Для точек внутри сферически-симметричного распределения материи можно использовать теорему Ньютона о Шелле, чтобы найти гравитационную силу. Теорема говорит нам, как различные части распределения масс влияют на гравитационную силу, измеренную в точке, расположенной на расстоянии \(\mathrm{r_0}\) от центра распределения масс: Как следствие, например, внутри оболочки одинаковой толщины и плотности нигде в пределах полой сферы нет результирующего гравитационного ускорения. Кроме того, внутри однородной сферы гравитация линейно увеличивается с расстоянием от центра; увеличение за счет дополнительной массы в 1,5 раза меньше уменьшения за счет большего расстояния от центра. Таким образом, если сферически-симметричное тело имеет однородное ядро и однородную мантию с плотностью, меньшей \(\mathrm{\frac{2}{3}}\) плотности ядра, то гравитация первоначально убывает наружу за границей, и если сфера достаточно велика, дальше наружу гравитация снова увеличивается, и в конечном итоге она превышает гравитацию на границе ядра и мантии. Гравитация Земли может быть максимальной на границе ядра и мантии, как показано на рисунке 1: Гравитационное поле Земли : Диаграмма напряженности гравитационного поля внутри Земли. ЛИЦЕНЗИИ И АВТОРСТВО CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, ПРЕДОСТАВЛЕННЫЙ РАНЕЕ CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, СПЕЦИАЛЬНОЕ АВТОРСТВО Спросил Изменено
1 год, 4 месяца назад 92}$? Я сбит с толку тем, как сила может быть промежуточной, будь то на теле А, или на теле Б, или на обоих. Предположим, что тело A действует с силой $F$ на тело B, поэтому, согласно 3-му закону Ньютона, B также должно действовать на A. Рассмотрим этот случай для гравитационной силы между двумя телами. Если тело A действует с силой $g$ на тело B, то тело B также должно действовать с силой $g$ на A, но B также действует с силой тяжести $X$ на A, следовательно, A также будет действовать с силой $X$ на тело B. Б.
Итак, как действуют две силы?
Я дал представление на этой диаграмме. $\endgroup$ 6 $\begingroup$ Третий закон Ньютона говорит нам, что сила, действующая на А со стороны В, равна (по величине, с противоположным направлением) силе, действующей на В со стороны А. Следовательно, при любом взаимодействии между парой тел достаточно описать действует только на одно из них, так как другое можно вывести из третьего закона Ньютона. При чем здесь X? Другой силы X не существует. На вашей диаграмме « сила реакции G » и X не являются двумя различными силами. Это одно и то же. $\endgroup$ 7 $\begingroup$ Один из способов взглянуть на это так: силы всегда приходят парами. Например, вы начинаете со вселенной, в которой есть только один объект, затем вы добавляете еще один объект, и природа тут же создаст пары сил. Не то чтобы Луна чувствовала, что Земля тянет ее, и в ответ тянула саму Землю. Нельзя взять такую пару сил и обозначить одну как действие, а другую как противодействие, или одну как причину, а другую как следствие. Несмотря на то, что силы не являются фундаментальными, они являются очень полезными математическими объектами, и симметрия, которую они проявляют в третьем законе Ньютона, является лишь одной из многих симметрий, которыми обладает Вселенная. $\endgroup$ 1 $\begingroup$ Значение слова «между» в данном случае такое же, как значение Любовь двух людей Понятно, что любви в воздухе не существует. Один человек любит другого. У воздуха нет мозга, а значит, нет ни эмоций, ни чувств. Слово $\endgroup$ 3 $\begingroup$ Это не индивидуальная сила, которая существует в пространстве между ними, а скорее говоря между в том случае, когда оба тела воздействуют друг на друга силой, которая постепенно притягивает их к точке между ними по мере того, как они притягиваются друг к другу , в конечном счете они просто являются двойниками друг друга, равными и противоположными реакциями. $\endgroup$ 1 $\begingroup$ Сила (нефиктивная) — это описание взаимодействия между двумя объектами. Побочное примечание: Гравитация как взаимодействие между $A$ и $B$ допустима только в самых основных положениях ньютоновской механики. Позже это описывается как другие вещи, но я не хочу смущать вас. $\endgroup$ 2 Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но не отображается Электронная почта Требуется, но не отображается
выше следствие теоремы о оболочках). Имеет значение только масса сферы в пределах желаемого радиуса \(\mathrm{M
В более общем смысле этот результат верен, даже если масса \(\mathrm{M}\) равна , а не равномерно распределена, но ее плотность изменяется радиально (как в случае с планетами). Масса Земли
В пределе, когда точечные массы компонентов становятся «бесконечно малыми», это влечет за собой интегрирование силы (в векторной форме, см. Ниже) по протяженности двух тел.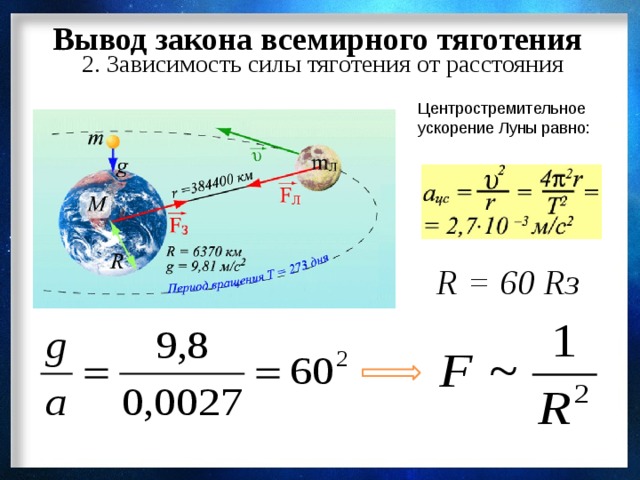
То есть отдельные гравитационные силы, действующие на элементы сферы в точке \(\mathrm{r_0}\) , компенсируют друг друга.
Ключевые моменты
Ключевые термины
Лицензия : CC BY-SA: Attribution-ShareAlike 
Расположен по адресу : en.Wikipedia.org/wiki/Shell_theorem . Лицензия : CC BY-SA: Attribution-ShareAlike 
Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/center%20of%20mass . Лицензия : CC BY-SA: Attribution-ShareAlike 
org/content/m42073/latest/?collection=col11406/1.7 . Лицензия : CC BY: Атрибуция 
Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/point_mass . Лицензия : CC BY-SA: Attribution-ShareAlike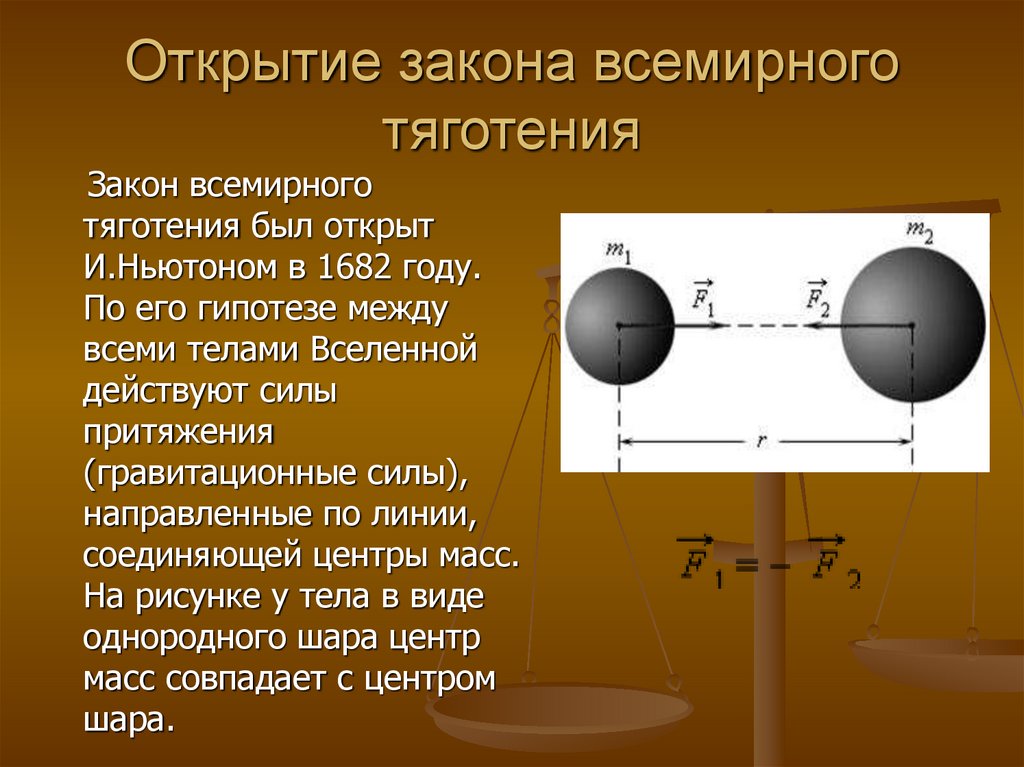 
wikimedia.org/Wikipedia/commons/4/43/Earth-G-force.png . Лицензия : CC BY-SA: Attribution-ShareAlike ньютоновская механика — Что означает, что гравитационная сила находится «между» двумя телами?
2}$, чтобы описать гравитационное взаимодействие между парой масс. 92}$.
B испытывает ту же силу по отношению к A.
Это 2 силы в этом сценарии.
Аналогично, на вашей диаграмме « сила реакции X » и G — одно и то же
Скорее, и являются проявлениями внутренней работы природы, и, насколько нам известно, эти действия лучше всего не описываются с точки зрения силы, а скорее как «если бы все двигалось как 9».0042 это раньше, они будут двигаться как что потом». между в предложении:
между в приведенном выше предложении означает, что человек A любит человека B, а человек B любит человека A. эта сила равна на тело B ), а тело B действует на тело A с силой (эта сила равна на корпусе А).
Так что, конечно, взаимодействие действует на оба объекта с одинаковой величиной (третий закон Ньютона). $A$ действует на $B$ с той же силой, что и $B$ на $A$. Гравитация такая же. Это взаимодействие между $A$ и $B$. Вы можете разделить его на 2 части: форсировать $B$ на $A$ и форсировать $A$ на $B$. Но на самом деле это 1 взаимодействие. Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
13.1 Закон всемирного тяготения Ньютона
Цели обучения
К концу этого раздела вы сможете:
- Перечислить важные вехи в истории гравитации
- Вычислите гравитационную силу между двумя точечными массами
- Оценить гравитационную силу между наборами масс
Сначала мы рассмотрим историю изучения гравитации, уделив особое внимание тем явлениям, которые на протяжении тысячелетий вдохновляли философов и ученых на поиск объяснения. Затем мы исследуем простейшую форму закона всемирного тяготения Ньютона и то, как его применять.
История гравитации
Древние философы задавались вопросом, почему объекты естественным образом имеют тенденцию падать на землю. Аристотель (384–322 гг. до н. э.) считал, что природа камней — искать Землю, а природа огня — искать Небеса. Брахмагупта (598–665 гг. н. э.) постулировал, что Земля представляет собой сферу и что объекты обладают естественным сродством к ней, падая к центру, где бы они ни находились.
Движение Солнца, нашей Луны и планет также изучалось на протяжении тысячелетий. Эти движения были описаны с поразительной точностью Птолемей (90–168 гг. Н. Э.), чей метод эпициклов описывал пути планет как круги внутри кругов. Однако мало свидетельств того, что кто-либо связывал движение астрономических тел с движением объектов, падающих на Землю, — до семнадцатого века.
Николай Коперник (1473–1543) обычно считается первым, кто бросил вызов геоцентрической системе Птолемея (землецентричной) и предложил гелиоцентрическую систему, в которой Солнце находится в центре Солнечной системы. Эта идея была поддержана невероятно точными измерениями движения планет невооруженным глазом с помощью Tycho 9.0058 Браге и их анализ Иоганнесом Кеплером и Галилеем Галилеем. Кеплер показал, что движение каждой планеты является эллипсом (первый из трех его законов, обсуждаемых в Кеплеровских законах движения планет), а Роберт Гук (тот самый Гук, который сформулировал закон Гука для пружин) интуитивно предположил, что эти движения происходят из-за планеты притягиваются к Солнцу.
Однако именно Исаак Ньютон связал ускорение объектов у поверхности Земли с центростремительным ускорением Луны на ее орбите вокруг Земли.
Наконец, в «Теории гравитации Эйнштейна» мы рассматриваем общую теорию относительности, предложенную Альбертом Эйнштейном в 1916 году. Его теория исходит из совершенно иной точки зрения, в которой гравитация является проявлением массового искривления пространства и времени. Последствия его теории породили множество замечательных предсказаний, практически все из которых были подтверждены в течение многих десятилетий после публикации теории (включая измерение гравитационных волн от слияния двух черных дыр в 2015 году). 9{2} [/latex] раз меньше г . Он мог бы объяснить это, постулируя, что между любыми двумя объектами существует сила, величина которой определяется произведением двух масс, деленным на квадрат расстояния между ними. Теперь мы знаем, что этот закон обратных квадратов вездесущ в природе и является функцией геометрии для точечных источников.
{2} [/латексу]. В последующих главах мы видим эту же форму в электромагнитной силе. 9{2}}{\шляпа{r}}_{12} [/latex]
, где [latex] {\overset{\to }{F}}_{12} [/latex] — сила, действующая на объект 1. воздействует объект 2, а [латекс] {\шляпа{r}}_{12} [/латекс] представляет собой единичный вектор, указывающий от объекта 1 к объекту 2.
Как показано на (рис.), [латекс] { \overset{\to }{F}}_{12} [/latex] вектор указывает от объекта 1 к объекту 2 и, следовательно, представляет силу притяжения между объектами. Равная, но противоположная сила [латекс] {\overset{\to}}{F}}_{21} [/латекс] — это сила, действующая на объект 2 со стороны объекта 1.
Рис. 13.2 Гравитационная сила действует вдоль линии, соединяющей центры масс двух объектов.
Эти равные, но противоположные силы отражают третий закон Ньютона, который мы обсуждали ранее. Обратите внимание, что, строго говоря, (Рисунок) относится к точечным массам — вся масса находится в одной точке. Но это в равной степени применимо к любым сферически-симметричным объектам, где r — расстояние между центрами масс этих объектов.
Во многих случаях он достаточно хорошо работает для несимметричных объектов, если расстояние между ними велико по сравнению с их размером, и мы берем r — расстояние между центрами масс каждого тела.
Эксперимент Кавендиша
Через столетие после того, как Ньютон опубликовал свой закон всемирного тяготения, Генри Кавендиш определил константу пропорциональности G , проведя кропотливый эксперимент. Он сконструировал устройство, подобное изображенному на (рис.), в котором на проволоке подвешены небольшие грузы. Находясь в равновесии, два фиксированных больших тела помещаются симметрично рядом с меньшими. Гравитационное притяжение создает кручение (скручивание) несущей проволоки, которое можно измерить. 9{-11}\,\text{N} [/latex] друг на друга. Это вес типичного пыльцевого зерна.
Рис. 13.3 Кавендиш использовал подобный аппарат для измерения гравитационного притяжения между двумя сферами (m), подвешенными на проволоке, и двумя неподвижными сферами (M).
Это обычный эксперимент, проводимый в студенческих лабораториях, но он довольно сложный. Проезжающие мимо лаборатории грузовики могут создавать вибрации, подавляющие гравитационные силы.
Хотя гравитация является самой слабой из четырех фундаментальных сил природы, ее притягательная природа удерживает нас на Земле, заставляет планеты вращаться вокруг Солнца, а Солнце — вокруг нашей галактики и связывает галактики в скопления, начиная от нескольких до миллионов. Гравитация — это сила, формирующая Вселенную.
Стратегия решения задач: Закон всемирного тяготения Ньютона
Чтобы определить движение, вызванное силой гравитации, выполните следующие действия:
- Определите две массы, одну или обе, для которых вы хотите найти силу гравитации.
- Нарисуйте диаграмму свободного тела, изобразив силу, действующую на каждую массу, и указав расстояние между их центрами масс.
- Примените второй закон Ньютона к каждой массе, чтобы определить, как она будет двигаться.
Пример
Столкновение на орбите
Рассмотрим два почти сферических корабля «Союз «, находящихся на орбите вокруг Земли, каждый массой 9000 кг и диаметром 4,0 м. Первоначально они покоятся друг относительно друга на расстоянии 10,0 м от центра к центру. (Как мы увидим в законах движения планет Кеплера, обе планеты вращаются вокруг Земли с одинаковой скоростью и взаимодействуют почти так же, как если бы они были изолированы в глубоком космосе.) Определите гравитационную силу между ними и их начальное ускорение. Оцените, сколько времени им потребуется, чтобы дрейфовать вместе, и насколько быстро они двигаются при столкновении.
Стратегия
Мы используем закон тяготения Ньютона, чтобы определить силу между ними, а затем используем второй закон Ньютона, чтобы найти ускорение каждого из них. Для оценки мы предполагаем, что это ускорение является постоянным, и мы используем уравнения постоянного ускорения из Движения по прямой линии, чтобы найти время и скорость столкновения.
{2}\frac{(9{4}\,\text{s} [/latex] или около 4,6 часов.
Значение
Эти расчеты, включая начальную силу, являются только приблизительными, поскольку транспортные средства, вероятно, не являются сферически симметричными. Но вы можете видеть, что сила невероятно мала. Астронавты должны привязывать себя при выполнении работы даже за пределами массивной Международной космической станции (МКС), как на (Рисунок), потому что гравитационное притяжение не может спасти их даже от малейшего отталкивания от станции.
Рис. 13.4 На этой фотографии изображен Эд Уайт, привязанный к космическому шаттлу во время выхода в открытый космос. (кредит: НАСА)
Проверьте свое понимание
Что происходит с силой и ускорением, когда транспортные средства падают вместе? Какой будет наша оценка скорости при столкновении выше или ниже реальной скорости? И, наконец, что произошло бы, если бы массы не были одинаковыми? Будет ли сила на каждом из них одинаковой или разной? Как у них с ускорением?
Показать решение
Эффект гравитации между двумя объектами с массами порядка этих космических аппаратов действительно мал.
Тем не менее, влияние гравитации с Земли на вас настолько велико, что падение на Землю всего на несколько футов может быть опасным. Мы исследуем силу гравитации у поверхности Земли в следующем разделе.
Пример
Притяжение между галактиками
Найдите ускорение нашей галактики Млечный Путь , обусловленное ближайшей галактикой сопоставимого размера, 9{15}\,\,\text{m}) [/latex].
Рис. 13.5 Галактики гравитационно взаимодействуют на огромных расстояниях. Галактика Андромеды — ближайшая спиральная галактика к Млечному Пути, и в конечном итоге они столкнутся. (кредит: Борис Штромар)
Стратегия
Как и в предыдущем примере, мы используем закон тяготения Ньютона, чтобы определить силу между ними, а затем используем второй закон Ньютона, чтобы найти ускорение Млечного Пути. Мы можем считать галактики точечными массами, так как их размеры примерно в 25 раз меньше их расстояния. Масса Солнца (см. Приложение D) составляет [латекс] 2,0\,×\,{10}^{30}\,\текст{кг} [/латекс], а световой год — это расстояние, которое свет проходит за один год, [латекс] 9{13}\,\text{m} [/latex] ближе.
Это на девять порядков меньше начального расстояния между ними. В действительности такие движения редко бывают простыми. Эти две галактики вместе с примерно 50 другими более мелкими галактиками гравитационно связаны с нашим местным скоплением. Наше локальное скопление гравитационно связано с другими скоплениями в так называемом сверхскоплении. Все это является частью великого космического танца, являющегося результатом гравитации, как показано на (Рисунок).
Рисунок 13.6 Основываясь на результатах этого примера, а также на том, что астрономы наблюдали в других местах Вселенной, наша галактика столкнется с галактикой Андромеды примерно через 4 миллиарда лет. (кредит: НАСА)
Резюме
- Все массы притягиваются друг к другу с гравитационной силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
- Сферически симметричные массы можно рассматривать так, как если бы вся их масса находилась в центре.
- С несимметричными объектами можно обращаться так, как если бы их масса была сосредоточена в их центре масс, при условии, что расстояние до них от других масс велико по сравнению с их размером.
Концептуальные вопросы
Действие на расстоянии, такое как гравитация, когда-то считалось нелогичным и, следовательно, неверным. Что является конечным определителем истины в науке и почему это действие на расстоянии было в конечном счете принято?
Показать решение
В законе всемирного тяготения Ньютон предположил, что сила пропорциональна произведению двух масс ([латекс] ~{м}_{1}{м}_{2} [/латекс]). Хотя все научные предположения должны быть проверены экспериментально, можете ли вы привести аргументы, почему это должно быть так? (Возможно, вы захотите рассмотреть простые примеры, в которых любая другая форма приведет к противоречивым результатам.)
Задачи
Оцените величину гравитационной силы между двумя 5-килограммовыми сферическими стальными шариками, расстояние между центрами которых составляет 15 см.
Показать раствор
Оцените силу притяжения между двумя борцами сумо массами 220 кг и 240 кг, когда они обнимаются и их центры находятся на расстоянии 1,2 м друг от друга.
Астрология уделяет большое внимание положению планет в момент рождения. Единственная известная сила, с которой планета действует на Землю, — гравитационная. (a) Вычислите гравитационную силу, действующую на ребенка весом 4,20 кг со стороны отца весом 100 кг, находящегося на расстоянии 0,200 м при рождении (он оказывает помощь, поэтому он находится близко к ребенку). (b) Рассчитайте силу Юпитера, действующую на ребенка, если он находится на самом близком расстоянии от Земли, несколько [латекс] 6.29{11}\,\text{m} [/latex] далеко. Как сила Юпитера на ребенке соотносится с силой отца на ребенке? Другие объекты в палате и в здании больницы также действуют на подобные гравитационные силы. (Конечно, может действовать неизвестная сила, но сначала ученым нужно убедиться, что эффект есть, а тем более, что его вызывает неизвестная сила.
)
Показать решение
Гора в 10,0 км от человека действует на него с силой тяжести, равной 2,00% его веса. а) Вычислите массу горы. б) Сравните массу горы с массой Земли. в) Что неразумного в этих результатах? (d) Какие посылки являются неразумными или непоследовательными? (Обратите внимание, что точные гравитационные измерения могут легко обнаружить влияние близлежащих гор и изменения в местной геологии.)
Международная космическая станция имеет массу около 370 000 кг. а) Какая сила действует на космонавта массой 150 кг, если он находится на расстоянии 20 м от центра масс станции? б) Насколько точным, по вашему мнению, был бы ваш ответ?
Рисунок 13.33 (фото: ©ESA–David Ducros)
Показать решение
Астероид Тутатис прошел рядом с Землей в 2006 году на расстоянии, в четыре раза превышающем расстояние до нашей Луны. Это был самый близкий подход, который у нас будет до 2060 года.
