ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ — Матющенко. расчет цепей

С этим файлом связано 1 файл(ов). Среди них: ТОЭ.docx. Показать все связанные файлы Подборка по базе: Влияние медиа-спектицизма на сообщения о ковид 19.doc, Сестринская помощь при дискинезиях желчного пузыря и желчевыводя, Пути сообщения вер.1.6.doc, В поисках путей модернизации.pptx, российская Федерация 1 часть.ppt, Отправка СМС сообщения .docx, Древний Восток — сообщения (1).docx, & 3 В поисках путей модернизации конспект.docx, 4 восп. желчевывод. путей.docx, ОБЩАЯ ХАРАКТЕРИСТИКА ПРОВОДЯЩИХ ПУТЕЙ ЦЕНТРАЛЬНОЙ НЕРВНОЙ СИСТЕМ 1   2   3   4   5   6   7 Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n. Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы   . Для напряжения    она направлена отточки  m к точке n. Если мы меняем местами индексы у буквы   , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как   . Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений    и   . Так, для контура m31nm при обходе его по часовой стрелке  . Отсюда  .                                (7.1)  При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа. В указанном контуре напряжение    складывается из трех напряжений:     .                                    (7.2)  Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам   ,    и   . Теперь находим значение каждого слагаемого в последнем уравнении. Величина   , определяющая напряжение между точками mи 3, представляет собой падение напряжения на сопротивлении   , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока   :  . Аналогично  . Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения    и ток    направлены в одну сторону. Третье слагаемое    представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).    Рис. 7.1. Напряжение на зажимах источника Рассмотрим рис. 7.1. При указанной на схеме полярности зажимов источника потенциал точки bвыше потенциала точкиaна величину ЭДС:     .  Поэтому при одинаковых направлениях стрелок    и    (рис. 7.1, а)     .  Если направления стрелок    и    противоположны друг другу (рис. 7.1, б), то  .  С учетом сказанного напряжение на участке 1n(см. рис. 2.1) равно     .  Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1). То же самое напряжение, определяемое по участку m2n, будет равно     .  Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам. 8. ПОСТРОЕНИЕ ГРАФИКОВ 8.1. Общие требования к оформлению графиков. Зависимость мощности от тока Правила построения графиков рассмотрим на примере зависимости мощности Р1,выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:     . Так как   , то     .                                   (8.1) Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1). Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения    и соответственно равны      и   .  По смыслу    – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении   . При токе, равном половине этого значения, мощность    максимальна:     .  Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:      = 72,4 В;      = 130 В;       = 43,6 Ом.  Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения    и   :  ;  .  Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы. В одной единице длины (сантиметре, миллиметре) может содержаться m × 10n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.  Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат. В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения. Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка. Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1). Таблица 8.1 Данные для построения графика  , А 0 0,2 0,4 0,5 0,6 0,66 0,8 0,9 1 1,2 1,32  , Вт 0 9,78 16,1 17,9 18,9 19 18,2 16,5 14 6,34 0 Абсциссы точек, выбираемых для построения графика, желательно располагать по оси равномерно. Но вблизи характерных областей кривой (в нашем случае у вершины параболы) точки можно взять чаще. В таблицу внесены также значения максимальной мощности и тока, которому эта мощность соответствует. При построении графика числа из таблицы на осях не показываются (рис. 8.2).  8.2. Зависимость тока от сопротивления Зависимость тока в первой ветви от сопротивления этой ветви строим по уравнению (6.2), которое при выбранных значениях   ,    и    принимает вид:  . Подставляя сюда различные значения сопротивления   , приходим к результатам, представленным на рис. 8.3.  , Ом  , А 0 1,32 10 1,07 20 0,91 30 0,78 40 0,69 50 0,62 60 0,56 70 0,51 80 0,47     Рис. 8.3. Зависимость тока от сопротивления 8.3. Внешняя характеристика источника энергии Внешняя характеристика источника энергии (генератора) представляет собой зависимость напряжения на его зажимах от протекающего по нему тока. Для цепи, изображенной на рис. 8.4, а,она выражается уравнением   . В соответствии с этим уравнением напряжение на зажимах источника меньше ЭДС на величину падения напряжения на его внутреннем сопротивлении. Общий вид характеристики показан на рис. 8.4, б.     Рис. 8.4. Внешняя характеристика источника энергии   8.4. Потенциальная диаграмма Потенциальная диаграмма представляет собой график распределения потенциала вдоль некоторого контура. По заданию этот контур должен включать два источника ЭДС. Таким может быть, например, контур, состоящий из первой, четвёртой и третьей ветвей (см. рис. 2.1). На рис. 8.5 он показан отдельно. Т очку между источником ЭДС    и сопротивлением    обозначим  какой-нибудь буквой, например, буквой d. Потенциалы точек 2, 3 и 4 известны из метода узловых потенциалов, а для точек m и d делаем следующие расчёты:      или   ;   или   .  Предположим, что нам заданы следующие значения сопротивлений:      = 30 Ом;      = 26 Ом;    = 59 Ом,  а для потенциалов мы получили:      = 0;       = –15 В;      = 70 В;      = 48 В;       = 28 В. Потенциальная диаграмма, соответствующая этим данным, представлена на рис. 8.6. При построении диаграммы контур обходим по часовой стрелке, начиная с точки 4 (вообще, начальную точку и направление обхода контура выбираем произвольно). По оси абсцисс откладываем значения сопротивлений в той последовательности, в которой они нам встречаются, а по оси ординат – потенциалы соответствующих точек. Потенциальная диаграмма даёт полную информацию о рассматриваемом контуре. Кроме сопротивлений она показывает величины и направления ЭДС. С её помощью можно определить также напряжение между двумя любыми точками. На рис. 8.6 показано, как определяется напряжение между точками 3 и 2. Оно равно     .     Рис. 8.6. Потенциальная диаграмма 1   2   3   4   5   6   7

Закон электромагнитной индукции. Вихревое электрическое поле. Школьный курс физики

Главная | Физика 11 класс | Закон электромагнитной индукции

Закон электромагнитной индукции.

Опыты Фарадея показали, что сила индукционного тока I₁ в проводящем контуре пропорциональна скорости изменения числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. Более точно это утверждение можно сформулировать, используя понятие магнитного потока.

Скорость изменения линий магнитной индукции, пронизывающих поверхность площадью S, представляет собой скорость изменения магнитного потока. Если за малый промежуток времени Δt магнитный поток меняется на ΔΦ, то скорость изменения магнитного потока равна Δ

Φ / Δt.

Поэтому утверждение, которое следует из результатов опытов Фарадея, можно сформулировать следующим образом: сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром.

Электрический ток в цепи появляется в том случае, когда на свободные заряды действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют ЭДС. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нём появляются сторонние силы, действие которых характеризуется ЭДС индукции

i.

Сформулируем закон электромагнитной индукции.

ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.

Как в законе электромагнитной индукции учесть направление индукционного тока (или знак ЭДС индукции) в соответствии с правилом Ленца? На рисунке 4. 10 изображён замкнутый контур.

Рис. 4.10

Будем считать положительным направление обхода контура против часовой стрелки. Нормаль к контуру образует правый винт с направлением обхода. Знак ЭДС зависит от направления сторонних сил по отношению к направлению обхода контура. Если эти направления совпадают, _i > 0 и соответственно I_i > 0. В противном случае ЭДС индукции и сила индукционного тока отрицательны.

Пусть вектор индукции внешнего магнитного поля направлен вдоль нормали к контуру и возрастает со временем. Тогда ΔΦ > 0 и ΔΦ / Δt > 0. Согласно правилу Ленца, индукционный ток создаёт магнитный поток

Ф’ < 0. Линии индукции ‘ магнитного поля индукционного тока направлены противоположно . Следовательно, индукционный ток I_i направлен по часовой стрелке (против положительного направления обхода) и ЭДС индукции отрицательна. Поэтому в математической записи закона электромагнитной индукции обычно ставят знак «минус»:

Единицы магнитной индукции и магнитного потока.

В СИ закон электромагнитной индукции используют для установления единицы магнитного потока. Так как ЭДС индукции

i. выражают в вольтах, а время — в секундах, то, согласно закону электромагнитной индукции, вебер можно определить следующим образом: магнитный поток через поверхность, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1c в контуре возникает ЭДС индукции, равная 1 В.

1Bб = 1B∙1с.

Единицу магнитной индукции — тесла (см. § 16 «Индукция магнитного поля») устанавливают на основе соотношения Ф = BScos α. Если вектор однородного магнитного поля перпендикулярен поверхности площадью S, то Φ

_max = BS. Тесла равна магнитной индукции, при которой максимальный магнитный поток через поперечное сечение площадью 1 м² равен 1 Вб.

Вихревое электрическое поле.

Пусть у нас имеются две обмотки (катушки), надетые на сердечник. Включив одну обмотку в сеть, мы получим ток в другой обмотке, если она замкнута (рис. 4.11).

Рис. 4.11

Электроны в проводах второй обмотки придут в движение. Но какие силы заставляют их двигаться? Само магнитное поле, пронизывающее катушку, этого сделать не может, так как магнитное поле действует исключительно на движущиеся заряды, а проводник с находящимися внутри него электронами неподвижен.

Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле непосредственно порождается переменным магнитным полем. Тем самым утверждается новое фундаментальное свойство электромагнитного поля: изменяясь во времени, магнитное поле порождает электрическое поле (к этому выводу пришёл Максвелл). Тогда сущность явления электромагнитной индукции в неподвижном проводнике состоит не столько в появлении индукционного тока, сколько в возникновении электрического поля, которое приводит в движение электрические заряды.

Электрическое поле, возникающее при изменении магнитного поля, не связано непосредственно с зарядами, и его линии напряжённости не могут на них начинаться и кончаться. Они нигде не начинаются и не кончаются, а представляют собой замкнутые линии, подобные линиям индукции магнитного поля. Такое электрическое поле называют вихревым.

Почему это поле называется электрическим, ведь оно имеет иное происхождение и другую конфигурацию, чем электростатическое поле? Ответ прост: вихревое поле действует на заряд q так же, как и электростатическое, а это считается главным свойством поля. Сила, действующая на заряд, по-прежнему равна = q, где — напряжённость вихревого поля.

В отличие от электростатического поля, работа вихревого поля по замкнутому контуру не равна нулю. Ведь при перемещении заряда вдоль замкнутой линии напряжённости электрического поля работа на всех участках контура имеет один и тот же знак, так как сила и перемещение совпадают по направлению.

Вихревое электрическое поле, так же как и магнитное поле, не потенциальное. Работа вихревого электрического поля по перемещению единичного положительного заряда вдоль замкнутого неподвижного про водника численно равна ЭДС индукции в этом проводнике.

ЭДС индукции в движущемся проводнике.

При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует магнитная составляющая силы Лоренца, которая и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет «магнитное происхождение». Вычислим ЭДС индукции в прямоугольном контуре, помещённом в однородное магнитное поле (рис. 4.12).

Рис. 4.12

Пусть сторона контура MN длиной l скользит с постоянной скоростью вдоль сторон NC и MD, оставаясь всё время параллельной стороне CD. Вектор магнитной индукции однородного поля перпендикулярен проводнику MN и составляет угол α с вектором скорости . Магнитная составляющая силы Лоренца, с которой магнитное поле действует на движущуюся заряженную частицу, равна

F_л = qυBsin α.

Согласно правилу левой руки, магнитная составляющая силы Лоренца направлена вдоль проводника MN.

Работа этой силы при перемещении заряда вдоль проводника от M к N

A_л = F_лl cos 0° = qυBsin α.

ЭДС индукции в проводнике MN равна

Эта формула справедлива для любого проводника длиной l, движущегося со скоростью в однородном магнитном поле. В других проводниках контура ЭДС равна нулю, так как проводники неподвижны.

ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Действительно, магнитный поток через контур MNCD равен

Ф = BScos (90° — α) = BSsin α,

где угол 90°, — α — угол между вектором и нормалью к плоскости контура; S — площадь контура MNCD.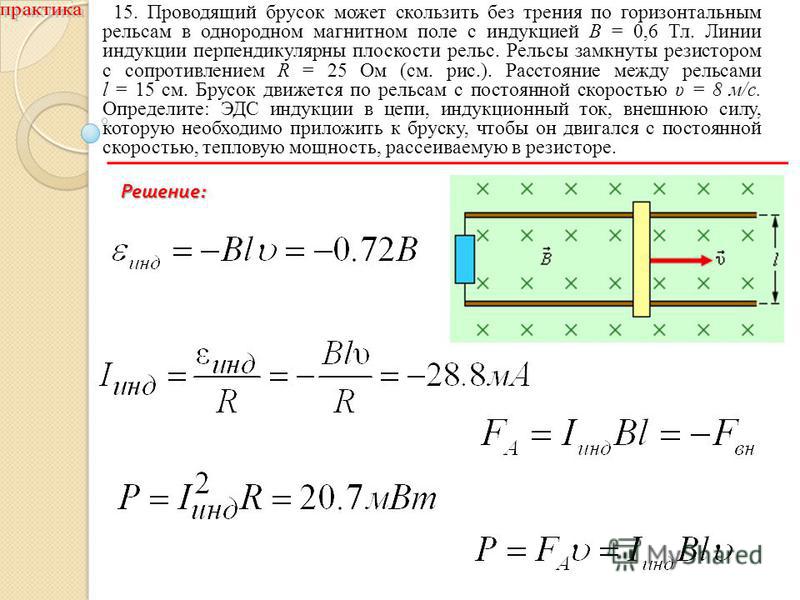 Если считать, что в начальный момент времени (t = 0) проводник MN находился на расстоянии NC от проводника CD (см. рис. 4.12), то при перемещении проводника площадь S изменяется со временем следующим образом:

S = l(NC — υt).

 

За время Δt площадь контура изменяется на ΔS = —lυΔt. Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за время Δt равно ΔФ = —BlυΔtsin α. Следовательно,

(как это и было получено ранее).

Вопросы:

1. Как связаны между собой сила индукционного тока и скорость изменения магнитного потока через поверхность, ограниченную контуром?

2. Запишите и сформулируйте закон электромагнитной индукции.

3. Почему в математической записи закона электромагнитной индукции стоит знак «минус»?

4. Укажите основные свойства вихревого электрического поля.

5. Почему в проводнике, движущемся в магнитном ноле, появляется ЭДС индукции?

Вопросы для обсуждения:

1. Между любыми двумя точками некоторого контура разность потенциалов равна нулю, а ток в контуре существует. Когда это возможно?

2. При каких положениях рамки, вращающейся с постоянной скоростью около прямолинейного проводника с током, возникающая в ней ЭДС будет:

а) максимальной;

б) минимальной?

3. Два одинаковых самолёта летят горизонтально с одинаковыми скоростями (один — вблизи экватора, другой — у полюса). У какого самолёта возникнет большая разность потенциалов на концах крыльев?

Пример решения задачи

Задача 1.

Виток медного провода помещён в изменяющееся во времени однородное магнитное поле перпендикулярно линиям магнитной индукции (рис. 4.13).

Рис. 4.13

Радиус витка равен 10 см, диаметр провода — 2 мм.

Определите скорость изменения магнитной индукции, если сила индукционного тока в витке составляет 5 A.

Удельное сопротивление меди равно l,7∙10 ^-8 Ом • М.

Задача 2.

На двух горизонтальных рельсах, расстояние между которыми равно 1 м, лежит проводник с сопротивлением 1 Ом и массой 0,5 кг. Коэффициент трения проводника о рельсы равен 0,1. Вся система находится в однородном магнитном поле с индукцией 0,1 Тл, вектор которой направлен вертикально. Рельсы подключают к источнику тока с ЭДС, равной 10 В. Пренебрегая внутренним сопротивлением источника тока и сопротивлением рельсов, определите установившуюся скорость движения проводника.

Поскольку F_АО > F_ТР, после замыкания цепи проводник придёт в движение.

При движении проводника магнитный поток через контур ACKD увеличивается (рис. 4.14, б), и в контуре возникает ЭДС индукции _i = Bυl, направленная навстречу ЭДС источника.

  

Рис. 4.14

По закону Ома для полной цепи

По мере увеличения модуля скорости проводника сила тока I уменьшается, а значит, уменьшается и модуль силы Ампера F_А = IBl. В результате устанавливается движение проводника с постоянной скоростью, при котором сила Ампера и сила трения уравновешивают друг друга, т. е. F_Ау = F_ТР.

Поскольку в установившемся режиме

Подставляя числовые данные, найдём:

Ответ: υ_у = 50 м/с.

Упражнения:

1. В витке, выполненном из алюминиевого провода длиной 10 см и площадью поперечного сечения 1,4 мм², скорость изменения магнитного потока равна 10 мВб/с. Найдите силу индукционного тока.

2. Квадратная рамка, сделанная из медной проволоки, со стороной 6,8 мм и площадью поперечного сечения 1 мм², помещена в однородное магнитное поле перпендикулярно линиям магнитной индукции. Индукция магнитного поля равномерно изменяется на 2 Тл за 0,1 с. Определите силу индукционного тока.

3. Какой по модулю заряд пройдёт через поперечное сечение витка, сопротивление которого 0,03 Ом, при уменьшении магнитного потока внутри витка на 12 мВб?

4. Найдите ЭДС индукции в проводнике с длиной активной части 0,25 м, перемещающемся в однородном магнитном поле с индукцией 8 мТл со скоростью 5 м/с под углом 30° к вектору магнитной индукции.

5. Перпендикулярно линиям магнитной индукции перемещается проводник длиной 1,8 м со скоростью 6 м/с. ЭДС индукции в проводнике равна 1,44 В. Найдите модуль индукции магнитного поля.

6. Прямолинейный проводник с длиной активной части 0,7 м пересекает однородное магнитное поле под углом 30° со скоростью 10 м/с.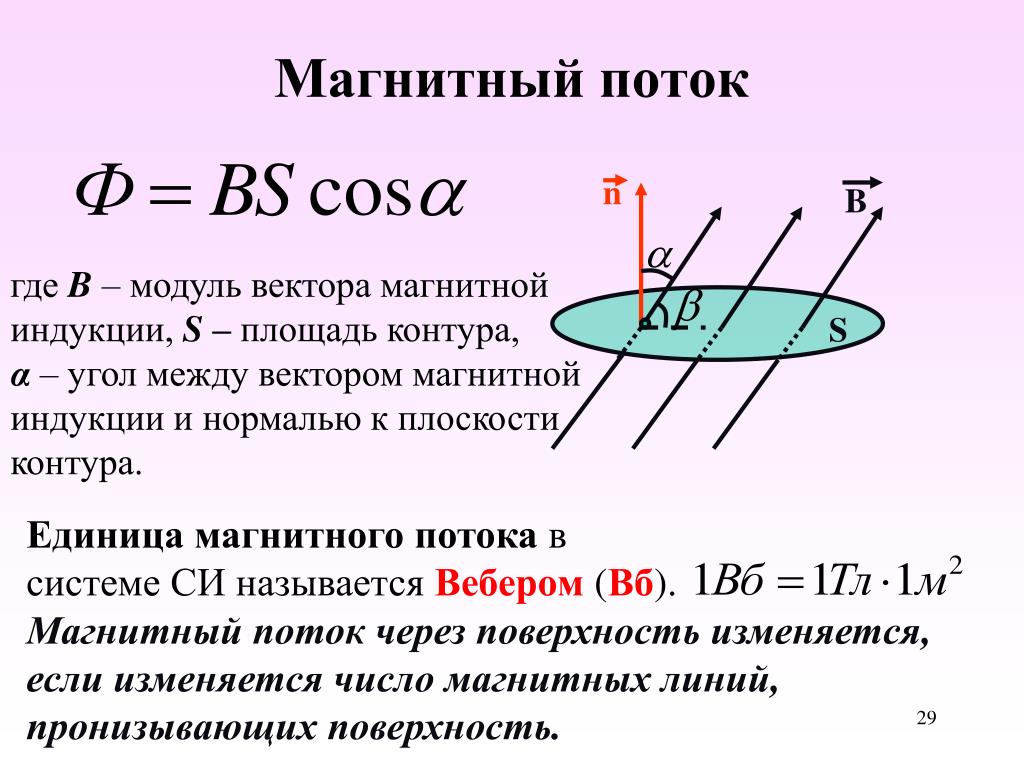 Определите модуль индукции магнитного поля, если ЭДС, индуцируемая в проводнике, равна 4,9 В.

7. C какой скоростью нужно перемещать проводник, длина активной части которого 1 м, под углом 60° к линиям индукции магнитного поля, чтобы в проводнике возникла ЭДС индукции 1 В? Модуль вектора магнитной индукции магнитного поля равен 0,2 Тл.

8. Прямой проводник движется со скоростью 36 км/ч под углом 45° к линиям индукции однородного магнитного поля. Модуль вектора магнитной индукции магнитного поля равен 0,2 Тл. Определите длину проводника, если в нём индуцируется ЭДС, равная 1,4 В.

Предыдущая страницаСледующая страница

Контурные линии – Лаборатория физической геологии

Перейти к содержимому

Элизабет Джонсон

Студенты смогут:

• Определение линии контура и интервала контура.
• Описать правила контурных линий.

Посмотрите это видео, в котором объясняются многие концепции горизонталей. Мы будем использовать многие из этих концепций в этом модуле.

На рис. 6 показан фрагмент современной топографической карты. Коричневые линии контурные линии .

Рис. 6. Фрагмент топографической карты, включая метку контурного интервала.

 

На топографических картах каждая изолиния соединяет точки на одной высоте. Интервал изолинии — это разница высот между соседними изолиниями.

Высота каждой контурной линии иногда отмечается на линии. Чтобы избежать беспорядка, не каждый контур помечен. Отметку немаркированной контурной линии можно определить, зная интервал контура и глядя на соседние контурные линии. Высота точки, расположенной между двумя контурными линиями, может быть оценена путем интерполяции между линиями. Если точка находится на полпути между двумя контурными линиями, она будет примерно на полпути между отметками этих двух контурных линий.

В США на стандартных топографических картах высота отмечена в футов над средним (средним) уровнем моря. Однако на международных картах и ​​картах высот океанского дна (батиметрии) часто отмечают метров .

Есть несколько подсказок, которые помогут вам определить единицы высоты на карте. Во-первых, легенда или информация по краю карты может говорить что-то вроде «интервал контура = 20 футов» или «интервал контура = 20 метров». На картах, в которых для обозначения высоты используются футы, контурные линии могут обозначаться такими единицами, как 400′. ‘ указывает единицы измерения в футах.

1. Каждая точка контурной линии имеет одинаковую отметку . Другими словами, контурные линии соединяют точки с одинаковой высотой.
2. По определению, контурные линии отделяют точки с большей отметкой от точек с меньшей отметкой . Это означает, что всегда можно определить направление «в гору» на одной стороне контура и направление «вниз» на другой стороне.
3. Линии контура никогда не пересекаются. Они могут подойти очень близко друг к другу (например, вдоль утеса), но по определению никогда не могут пересекаться.*  Это потому, что одно место на поверхности Земли не может находиться на двух разных высотах!
4. Линии контура никогда не разделяются . Вместо этого контуров образуют замкнутые контуры . Эти петли повторяют форму земли и могут выходить за край карты.
5. Близко расположенные контуры указывают на крутой склон , в то время как контуры, расположенные далеко друг от друга, указывают на пологий склон или почти плоскую поверхность.

Рис. 7. НЕПРАВИЛЬНАЯ топографическая карта. Рисунок 8. НЕПРАВИЛЬНАЯ топографическая карта.

*Есть одно исключение — нависающий утес!

Ссылки

http://www. iupui.edu/~geogdept/g108/lab_3.htm

https://ceas.uc.edu/content/dam/ceas/documents/CEEMS/instructionalunits/Watershed_LC/1.1.02i.%20Topo%20Basics_Watersheds%20and%20Topography_Lori%20Cooper_070615.pdf

 

Лицензия

Лаборатория физической геологии Элизабет Джонсон находится под лицензией Creative Commons Attribution-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Интерпретация контурных карт | METEO 3: Introductory Meetorology

Топографическая карта Гавайев с обозначением точки «P». Контуры рисуются через каждые 1000 футов.

Авторы и права: Дэвид Бэбб

Метеорологи регулярно используют контурные карты, чтобы увидеть, как погодные переменные (например, температура или давление) изменяются на больших территориях, но они также используют их для оценки значений погодных переменных в отдельных точках. Чтобы начать интерпретацию контурных карт, мы сначала вернемся к нашей топографической карте Гавайев (справа).

Как нам определить высоту точки, отмеченной буквой «P»? Во-первых, мы должны идентифицировать два контура, которые лежат по обе стороны от «P». В некоторых случаях нужные нам контуры четко обозначены; однако в других случаях вам нужно будет использовать интервал контура (в данном случае 1000 футов), чтобы «отсчитывать» вверх или вниз от обозначенного контура. На нашей карте точка «P» лежит между контурами 3000 и 4000 футов, поэтому высота в точке «P» больше (но не равна) 3000 футов, но меньше (но опять же не равна) 4000 футов. Мы знаем, что точка «Р» не равна ни одному из этих значений, потому что она не лежит ни на одной из контурных линий.

Технически, это все, что мы можем сказать наверняка о высоте в точке «P» — она ​​может быть где угодно между 3000 и 4000 футов. Однако часто вместо того, чтобы указывать диапазон высот, мы бы предпочли одно число. В таких случаях мы можем интерполировать (сделать оценку, предполагая линейное изменение высоты) между двумя известными контурами. В этом случае мы можем видеть, что точка «P» находится примерно посередине между двумя контурами и, таким образом, имеет высоту примерно 3500 футов. Использование интерполяции обычно дает нам достаточное приближение, но мы всегда должны понимать, что это всего лишь оценка.

Как насчет замкнутых контуров, внутри которых нет других контуров? Посмотрите еще раз на контурную карту и сосредоточьте свое внимание на самой южной вершине, Мауна-Лоа. Как можно оценить высоту этого пика? Ясно, что у нас нет двух контуров… или есть? Последний нарисованный контур составляет 13 000 футов. Это означает, что пик выше, чем 13 000 футов. Однако мы знаем, что вершина Мауна-Лоа находится на высоте 90 097, а не 90 098 футов над уровнем моря. Почему? Что ж, если бы это было так, то вокруг вершины был бы проведен контур высотой 14 000 футов. Таким образом, для самого внутреннего замкнутого контура диапазон всегда находится между последним нарисованным контуром и следующим ненарисованным контуром. Следует также отметить, что интерполяция в таких случаях невозможна, потому что у нас нет возможности узнать, как далеко находится ненарисованный контур. Вершина Мауна-Лоа составляет 13 452 фута (в пределах нашего предполагаемого диапазона 13 000-14 000 футов), но мы действительно не могли знать этого только по нашей топографической карте (если только высота пика не была отмечена).

Метеорологи обычно определяют две переменные: температуру и атмосферное давление. Изоплеты температуры называются изотермами (контуры постоянной температуры), а изоплеты давления называются изобарами (контуры постоянного давления). Не путайте два! Было бы неправильно смотреть на карту, на которой изображены только контуры постоянной температуры, и называть их, например, изобарами.

Карты с изобарами давления на уровне моря помогают метеорологам распознавать области высокого и низкого давления. Почему это важно? Ну, вообще говоря, области повышенного давления у поверхности часто являются областями «хорошей» погоды (относительно спокойной, хоть и с солнечным светом). В то же время области пониженного давления часто несколько неспокойны (облачны с осадками). Чтобы увидеть карту с изобарами давления на уровне моря, посмотрите на изображение ниже, от 15° по Гринвичу 1 мая 2017 г.

Анализ изобар уровня моря (контуры постоянного давления) на 15° по Гринвичу 1 мая 2017 г. в то время как L отмечают центры низкого давления (самое низкое давление в регионе). Особенность, которая немедленно бросается в глаза синоптикам как область «активной» погоды, — это большая область низкого давления с центром на Среднем Западе (недалеко от границы Айовы и Висконсина).

Первым шагом в интерпретации значений этого изображения является определение интервала контура, который составляет четыре миллибара (миллибары — стандартная единица измерения давления). Зная это, мы можем оценить давление вблизи центра минимума над Средним Западом. Самая внутренняя закрытая изобара составляет 996 мбар (она не помечена, но находится внутри изобары 1000 мбар, и значения уменьшаются к центру минимума), поэтому давление должно быть меньше 996 мбар. Однако изобара 992 мбар не нарисована, поэтому давление должно быть больше 992 миллибара.

Точно так же метеорологи составляют контурные карты температуры, потому что такие карты позволяют им легко определять области с холодным и теплым воздухом. Но карты изотерм часто имеют цветовую маркировку, чтобы упростить интерпретацию (хотя цвета иногда используются и на топографических картах). Я предупреждаю вас, что цветовые схемы и интервалы между контурами могут сильно различаться на изображениях, которые вы можете видеть по телевизору или в Интернете, и определить, какой цвет является каким, иногда может быть реальной проблемой. Но если вы понимаете, как интерпретировать контурные карты, вы можете не отвлекаться и использовать изотермы (в сочетании с цветами, если хотите) для сбора полезной информации.

Например, посмотрите карту изотерм на 15° по Гринвичу 1 мая 2017 года ниже. Интервал контура на изображении составляет 5 градусов по Фаренгейту. Учитывая это, как бы вы назвали подходящий диапазон температур где-нибудь в Индиане? Учитывая, что изотерма 60 градусов по Фаренгейту и изотерма 55 градусов по Фаренгейту почти соответствуют восточной и западной границам штата (соответственно), справедливо сказать, что температура в Индиане была выше 55 градусов по Фаренгейту, но меньше 60 градусов по Фаренгейту. И, если вы посмотрите на цветовой ключ справа от изображения, оттенок желто-зеленого (или это зелено-желтый?) над Индианой соответствует цвету, используемому для температур между 55 и 60 градусами по Фаренгейту (хотя некоторые могут найти трудно сказать).

Анализ изотерм поверхности (контуры постоянной температуры) при 15 градусах по Гринвичу 1 мая 2017 года. , и оценить конкретную температуру, мы могли бы сделать и это. Точка «P» находится примерно посередине между изотермами 55 и 60 градусов по Фаренгейту, поэтому температура в точке «P» находится примерно посередине между 55 и 60 градусами по Фаренгейту. Мы назовем это 57 или 58 градусами по Фаренгейту, зная, что мы просто делаем нашу лучшую оценку, основанную на изотермах.

Я также должен отметить, что иногда вы даже не увидите построенные изотермы, а вместо этого карта температуры будет просто заштрихована. На самом деле каждая граница, на которой меняются цвета, является изотермой (даже если она не нарисована и не помечена), и иногда используются очень маленькие интервалы контура. На таких картах, как этот анализ температуры от 17 градусов по Цельсию 24 мая 2017 года. Использование цветового ключа — единственный выход, и даже тогда (поскольку в данном случае цвета меняются на каждый градус) оценка конкретной температуры в точке может быть трудным, когда оттенки настолько похожи.

Чтобы увидеть еще несколько примеров интерпретации значений из контурной карты, посмотрите короткое видео (3:28) ниже.

Интерпретация контурных карт
Нажмите здесь, чтобы просмотреть стенограмму этого видео.

Извлечение информации из контурных карт — очень ценный навык. Вы увидите контурные карты в телевизионных прогнозах погоды, а также на веб-сайтах и ​​мобильных приложениях о погоде. Так что очень полезно получить от них некоторую информацию, и я собираюсь показать вам несколько примеров того, как интерпретировать контурные карты.

Это карта температуры поверхности на 19 градусов по Гринвичу в четверг, 18 мая 2017 года. Если мы сделаем преобразование времени, это будет 15:00 по восточному летнему времени. Итак, эта карта сделана в полдень на востоке США. На западном побережье был полдень.

На этой карте дневных температур видно, что для середины мая на востоке было действительно тепло. Используя образец изотерм, мы можем оценить фактические температуры в любом месте на карте.

Первым шагом всегда является определение интервала контура, и здесь это 5 градусов по Фаренгейту. Мы видим изотерму 85 градусов, проходящую через Пенсильванию. На всем протяжении этой изотермы температура составляет 85 градусов, а непосредственно к востоку от нее — 9 градусов.изотерма 0 градусов. На протяжении всей этой изотермы температура составляет 90 градусов, поэтому каждая изотерма представляет собой изменение на 5 градусов по сравнению с изотермой, к которой она примыкает.

Зная это, мы можем оценить температуру в любом месте на карте. Если бы мы выбрали место здесь, в центральной части Пенсильвании, мы бы знали, что температура находится между 85 и 90 градусами, потому что оно находится между этими двумя контурами.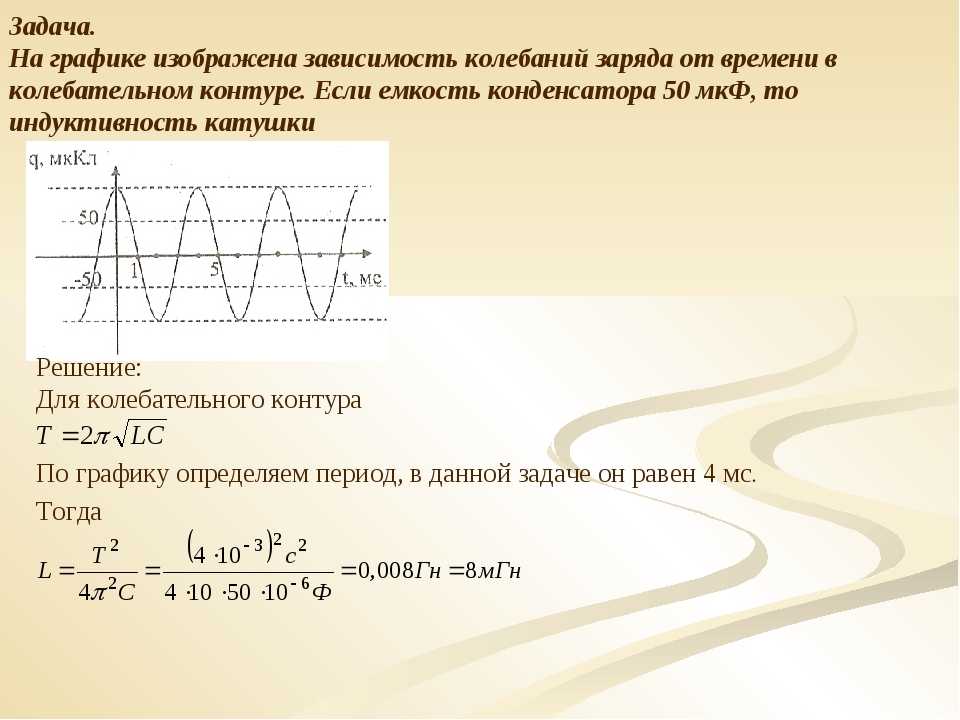

Где-нибудь внутри этой 90-градусной изотермы температура выше 90 градусов, но мы знаем, что она меньше 95 градусов, потому что нет изотермы 95 градусов.

Для другого испытания мы могли бы выбрать место в западной части Северной Каролины. При чем здесь температура? Похоже, что она лежит между двумя изотермами 85 градусов. Но если мы посмотрим на запад, мы увидим эту 80-градусную изотерму, проходящую через Средний Запад. Итак, температура в западной части Северной Каролины больше 80 градусов, но меньше 85 градусов.

Если мы перейдем к карте давления на уровне моря в миллибарах, здесь у нас не будет цветового кодирования, но процесс будет таким же.

Как только мы определили интервал изолинии, все готово, и здесь, похоже, 4 миллибара, поскольку здесь, в Техасе, у нас есть изобара в 1004 миллибара, непосредственно примыкающая к изобаре в 1008 миллибар.

Итак, если мы хотим узнать давление вблизи этого центра низкого давления в Техасе, мы знаем, что оно меньше 1004 мб.