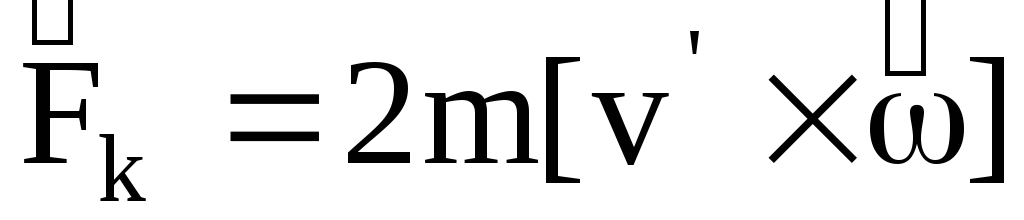Мера инертности тела при поступательном движении: динамические характеристики
Современной физикой установлено, что масса тела увеличивается с возрастанием скорости его движения, т. е. масса и энергия взаимно связаны.
В классической же механике масса движущегося тела принимается равной массе покоящегося тела, т. е. рассматривается как постоянная величина.
Векторному равенству (2.1) соответствует числовое равенство
следующим образом:
 . ( 2.2)
. ( 2.2)
Из этого равенства масса может быть определена по формуле:
 . (2.3)
. (2.3)
Применяя уравнение (2.3) к точке (телу) весом G и учитывая, что ускорение свободного падения равно g, имеем:
 . (2.4)
. (2.4)
т. е. масса материальной точки (тела) численно равна ее весу, деленному на ускорение свободного падения.
 . (2.5)
. (2.5)
Так как ускорение свободного падения в различных местах земной поверхности различно и зависит от географической широты места и от его высоты над уровнем моря, то в отличие от массы тела его вес не является постоянной величиной.
Теоретические основы лабораторной работы. Момент инерции тела является мерой инертности тела при вращательном движении
Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.
Момент инерции сплошного твёрдого тела определяется по формуле
 ,
,
где  — расстояние от элемента объема
— расстояние от элемента объема  с массой dm до оси вращения, r — плотность вещества.
с массой dm до оси вращения, r — плотность вещества.

Рис.1. Общий вид экспериментальной установки
Таким образом, момент инерции тел различной формы можно найти как результат интегрирования по соответствующему объёму тела.
Частные случаи.
1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения
 (1)
(1)
2. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к плоскости основания цилиндра и проходящей через его центр масс (ось цилиндра)

здесь R, m — радиус и масса цилиндра.
Так как момент инерции не зависит от высоты цилиндра, эта же формула справедлива для момента инерции однородного диска относительно оси перпендикулярной к плоскости диска.
3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси, совпадающей с осью цилиндра.
 (3)
(3)
4. Момент инерции шара массой m и радиуса R относительно оси проходящей через его центр масс
 (4)
(4)5. Момент инерции тонкого стержня массой m и длиной l относительно оси проходящей через его середину перпендикулярно стержню.
 (5)
(5)
Эти формулы справедливы для момента инерции относительно оси симметрии.
Момент инерции относительно произвольной оси параллельной оси симметрии можно найти с помощью теоремы Штейнера.
Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр масс тела и произведения массы тела на квадрат расстояния d между осями.

 (6)
(6)
Например, с помощью теоремы Штейнера, зная момент инерции стержня относительно оси перпендикулярной к стержню и проходящей через его центр масс, можно получить формулу для вычисления момента инерции стержня относительно оси проходящей через его конец.

В общем случае расчет момента инерции представляет собой достаточно сложную задачу.
В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний.
Исследуемые тела насаживаются на ось спиральной пружины. В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы)  . Модуль момента пропорционален углу закручивания пружины
. Модуль момента пропорционален углу закручивания пружины
M=Dj (8)
В этой формуле коэффициентом пропорциональности D является модуль кручения пружины.
С другой стороны из определения момента силы следует, что это вектор, модуль которого определяется по формуле
М=Fl (9)
Крутящий момент стремится вернуть пружину в исходное (равновесное) состояние.
Момент инерции для чайников: определение, формулы, примеры решения задач
В результате возникают крутильные колебания.
В соответствии с теорией период крутильных колебаний определяется по формуле
 (10)
(10)
Отсюда момент инерции тела

Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины.
Методика лабораторной работы позволяет измерять моменты инерции стержня без грузов, стержня с грузами, сплошного цилиндра, полого цилиндра, диска и шара.
Порядок выполнения работы
I. Определение модуля кручения пружины.
1. Возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру.
2. Поверните стержень на 90о (p/2 радиан).
| j | F | l | M |
| p/2 | |||
| p | |||
| 3p/2 | |||
| 2p |
3. Прикрепите к стержню (у края грузов) динамометр и измерьте величину силы F, необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню и оси вращения).
4. Проделайте эти измерения для углов j, равных 180о, 270о, 360о.
5. Полученные данные занесите в таблицу 1.
Дата добавления: 2016-11-03; просмотров: 87 | Нарушение авторских прав
Похожая информация:
Поиск Лекций
Динамическая характеристика
Статические характеристики
Под статическими характеристиками чаще всего подразумеваются электромеханическая и механическая характеристика.
Механическая характеристика
Механическая характеристика — это зависимость угловой скорости вращения вала от электромагнитного момента M (или от момента сопротивления Mc). Механические характеристики являются очень удобным и полезным инструментом при анализе статических и динамических режимов электропривода.[1]
Электромеханическая характеристика двигателя
Электромеханическая характеристика — это зависимость угловой скорости вращения вала ω от тока I.
Динамическая характеристика
Динамическая характеристика электропривода — это зависимость между мгновенными значениями двух координат электропривода для одного и того же момента времени переходного режима работы.
3. Ток якоря двигателя изменяется в процессе разгона двигателя и без учёта возникновения эдс самоиндукции в обмотке якоря машины в любой момент времени может быть определён по формуле .
где Ud – напряжение на выходе преобразователя; Ra и Rпуск – соответственно активные сопротивления якорных цепей двигателя и пускового реостата, включённого последовательно с якорем машины; Eа – эдс обмотки якоря, определяемая по формуле
гдеСМ и Се –
Датчики тока предназначены для измерения постоянного или переменного токов.
ЭДС обмотки якоря определяется суммой ЭДС всех секций, образующих одну параллельную ветвь.
4.Пуск — после подачи команды на пуск операции управления сводятся к включению обмоток двигателя на полное напряжение сети, т.е. к прямому пуску двигателя. Асинхронные двигатели с короткозамкнутым ротором и синхронные двигатели большой мощности (больше 100кВт) запускаются при пониженном напряжении.
При пуске ДПТ и АД с фазным ротором автоматически выключаются ступени пускового реостата из цепи протекания тока якоря или ротора соответственно.
Автоматизация процесса торможения работающего двигателя при любом виде электрического торможения предусматривает выполнение двух основных операций управления: 1 – после подачи команды на торможение совершаются переключения в силовых цепях двигателя, приводящие к изменению направления вращающего момента двигателя, т.е. делающие его тормозным; 2 – в конце торможения при скорости близкой к нулю, двигатель, тормозящийся для остановки , отключается от сети и затормаживается механическим тормозом. В другом случае в главных цепях производятся переключения, необходимые для реверса двигателя, т.е. для разгона в противоположном направлении.
Автоматическое управление осуществляется главным образом с помощью релейно-контакторной аппаратуры. Наиболее просто автоматизировать пуск и торможение асинхронных двигателей с короткозамкнутым ротором. Для ограничения пусковых токов мощных электродвигателей необходимо вводить дополнительные сопротивления в цепи ротора асинхронного двигателя или в цепи якоря двигателя постоянного тока, которые, по мере разгона двигателя, должны постепенно исключаться таким образом, чтобы максимальное и минимальное значение тока или момента находилось в заданных пределах I1 иI2рис.18.


Схема автоматического пуска и торможения в функции скорости

Схема автоматического пуска в функции времени

Схема автоматического пуска двигателя в функции тока
6. Современные системы управления электроприводами строятся в виде многоконтурных систем подчиненного регулирования с последовательным включением регуляторов: тока, частоты вращения, положения. При этом задающим сигналом регулятору тока является выходной сигнал регулятора скорости. В свою очередь регулятор скорости получает задание от регулятора положения. Такое построение системы управления позволяет вести раздельное регулирование переменных и раздельную настройку контуров, начиная с внутреннего токового, что упрощает расчет и настройку системы и позволяет получить высокое качество регулирования.
12. Системы импульсно-фазового управления (СИФУ) предназначены для изменения углов а открывания тиристоров в функции входного управляющего сигнала в диапазоне, определяемом типом, условиями работы и параметрами нагрузки. Требования к СИФУ заключаются в обеспечении необходимого диапазона изменения углов а, формировании отпирающих тиристоры импульсов и обеспечении достаточной симметрии углов включения тиристоров в различных фазах. Кроме того, СИФУ должна быть устойчивой к помехам для обеспечения стабильной работы и вместе с тем достаточно быстродействующей для обеспечения заданных динамических режимов.
Одним из наиболее эффективных способов повышения статической и динамической точности систем импульсно-фазового управления (СИФУ) вентильными преобразователями (ВП), а также их помехоустойчивости являются методы интегрирующего развертывающего преобразования.
13. принципы построения системы защиты от неправильного чередования фаз и обрыва фазы СР (Connecting Protection), приведя в качестве примера схему узла защиты привода «КЕМЕК» (рис. 5.1).
Переменное трёхфазное напряжение поступает от сети к точкам A, B и С. Резисторы Ra, RB и RC образуют симметричную измерительную цепь, и при симметричной питающей сети напряжение в их общей точке равно нулю, так как
 A +
A +  B +
B +  C = 0. (5.1)
C = 0. (5.1)
Резистор R1 и конденсатор С1 образуют фазосдвигающую цепь, их величины выбираются таким образом, что напряжение на С1 (UC1) отстаёт от приложенного (UB) на 60° эл. Таким образом, на делитель R2-R3 подаются два противофазных напряжения: UA и UC1 (рис. 5.2).
 Как видно из приведённой векторной диаграммы, напряжение на выходе делителя при соответствующем выборе величин сопротивлений R2 и R3 также равно нулю: R2
Как видно из приведённой векторной диаграммы, напряжение на выходе делителя при соответствующем выборе величин сопротивлений R2 и R3 также равно нулю: R2  С1 + R3
С1 + R3  А= 0.
А= 0.
Диоды D1 и D2 являются однополупериодными выпрямителями и одновременно образуют схему логического элемента ИЛИ. При нарушении условия (5.1), что соответствует несимметричной питающей сети (имитируется в приведённом примере отключение ключа К2) , либо (5.2), вызванного неправильным чередованием фаз питающего напряжения (имитируется переключателем К1), на вход компаратора на элементе DD1 поступает выпрямленное положительное напряжение, DD1 переключается и выдаёт сигнал логической единицы «1» о срабатывании защиты СР. Это отображается свечением индикатора «СР».
14. Упрощенная принципиальная схема широтно-импульсного преобразователя (ШИП) представлена на рис 68. Она содержит четыре ключа ТК1 — ТК4. В диагональ моста, образованного силовыми ключами, включена нагрузка.
Нагрузкой является якорь двигателя постоянного тока. Питание ШИП осуществляется от источника постоянного тока, например, неуправляемого выпрямителя.
Наиболее простым способом управления ШИП по цепи якоря является, так называемый, симметричный способ управления.
При этом способе в состоянии одновременного переключения находятся все четыре силовых ключа моста, а напряжение на выходе ШИП представляет собой знакопеременные импульсы, длительность которых регулируется входным сигналом.
14. 
16. рассмотрим и контур регулирования частоты вращения двигателя.

1 квадрат — передаточная функция пропорционально- интегрального регулятора скорости; J – суммарный момент инерции ЭП;
2 — номинальный моментообразующий ток электродвигателя 2 i и сигнал его задании;
C= M/ I2 конструктивная постоянная АД;
19. Адаптивная система – система, автоматически приспосабливающаяся к возникающим условиям при управлении тем или иным технологическим процессом.
Оптимизирующая система управления — системы управления, которые автоматически ищут оптимальную рабочую точку.
Адаптивные системы управления с эталонной моделью — использовали модель поведения идеальной системы для получения сигналов ошибки, обусловленных отличием действительного поведения системы от требуемого; эти сигналы затем служили для модификации параметров управляющего устройства таким образом, чтобы, насколько это возможно, поддерживать идеальное поведение, несмотря на точно неизвестную и изменяющуюся динамику системы.
Самоосциллирующая адаптивная система — тип адаптивных систем управления, работающих по принципу автоматической компенсации изменчивости параметров с помощью автоколебаний в замкнутом контуре управления.
Системы с переменной структурой — Метод основан на инвариантности траектории системы по отношению к значениям ее параметров в случае, когда управляющее воздействие определяется переключающей функцией и реле. Поведение системы при этом характеризуется движением по переключающей поверхности и называется скользящим режимом.

23. Следящие электроприводы или системы управления положением представляют собой замкнутые электроприводы, управляющие перемещением и обеспечивающие стабилизацию положения объекта регулирования относительно некоторой базовой системы координат. При этом регулируемая величина (положение объекта) с той или иной степенью точности должна соответствовать приложенному к системе управляющему воздействию. Следящие электроприводы могут обеспечивать как линейное, так и угловое перемещение регулируемого объекта. Например, это может быть система наведения солнечной батареи, телескопа и др. или система управления подачей резца в станке с программным управлением.
Во многих случаях следящие электроприводы строятся по принципу подчиненного регулирования на основе двигателей постоянного тока, коллекторных или вентильных. Поэтому основное внимание мы уделим именно таким приводам. Функциональная схема привода представлена на рис. 9.1, где обозначено: РП – регулятор положения; РС – регулятор скорости; РТ – регулятор тока; Д – двигатель; ОР – объект регулирования; ДП, ДС, ДТ – датчики соответственно положения, скорости и тока.
 электропривод содержит три контура регулирования: положения, скорости и тока. Внутренние контуры регулирования (скорости и тока) строятся, как это было показано при рассмотрении систем регулирования скорости. Внешний контур содержит датчик положения объекта относительно базовой системы координат. Это может быть датчик углового положения (сельсин, редуктосин, вращающийся трансформатор и др.) или любой датчик линейного перемещения.
электропривод содержит три контура регулирования: положения, скорости и тока. Внутренние контуры регулирования (скорости и тока) строятся, как это было показано при рассмотрении систем регулирования скорости. Внешний контур содержит датчик положения объекта относительно базовой системы координат. Это может быть датчик углового положения (сельсин, редуктосин, вращающийся трансформатор и др.) или любой датчик линейного перемещения.
Динамические характеристики тела человека.
Сигнал с выхода ДУ сравнивается с управляющим сигналом U0, определяющим положение объекта. По результату сравнения РП – вырабатывается сигнал Uрс регулирования скорости, который, в конечном счете, обеспечивает вращение двигателя и перемещение ОР – на заданный угол или расстояние.
Вопросы:
2.Машина постоянного тока, как звено системы автоматического регулирования, статические и динамические характеристики машины постоянного тока.
3.Датчики тока, ЭДС якоря, частоты вращения, положения, используемые в системах управления электроприводами, их статические и динамические характеристики.
4.Принципы автоматического управления реостатным пуском и торможением электропривода. Узлы пуска, торможения электродвигателей, работающих в функции времени, скорости, тока.
6. Принципы построение многоконтурных систем непрерывного управления электроприводами постоянного тока.
12.Реверсивные тиристорные преобразователи, раздельное и совместное управление выпрямителями.
13.Особенности построения систем защиты электроприводов с непрерывным управлением. Примеры построения элементов систем защиты.
14.Особенности преобразователей с широтно-импульсным регулированием, построение систем управления силовыми ключами.
16.Синтез контура регулирования частоты вращения, обеспечение необходимой точности и устойчивости.
19. Основные понятия адаптивных систем автоматического управления, элементы адаптивных систем управления электроприводами. Типовые узлы адаптивных систем.
23. Системы управления положением, особенности построения систем управления приводов с позиционированием
©2015-2018 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Нарушение авторских прав и Нарушение персональных данных
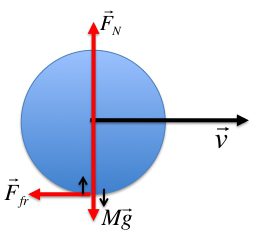
Силы, действующие на звенья механизма
К движущим силам  или моментам движущих сил
или моментам движущих сил  относят такие, которые обеспечивают движение механизма. Векторы движущих сил или совпадают с векторами скоростей тех точек звеньев механизмов, к которым они приложены, или составляют острые углы. Моменты движущих сил направлены в сторону угловой скорости звена (рис.4.1). С энергетической точки зрения работа движущих сил и моментов движущих сил
относят такие, которые обеспечивают движение механизма. Векторы движущих сил или совпадают с векторами скоростей тех точек звеньев механизмов, к которым они приложены, или составляют острые углы. Моменты движущих сил направлены в сторону угловой скорости звена (рис.4.1). С энергетической точки зрения работа движущих сил и моментов движущих сил  положительна.
положительна.
2.Силы сопротивленияи моменты сил сопротивления
Силы сопротивления  или моменты этих сил
или моменты этих сил  делятся на силы
делятся на силы  и моменты
и моменты  полезных или технологических сопротивлений и силы
полезных или технологических сопротивлений и силы  и моменты
и моменты  вредных сопротивлений.
вредных сопротивлений.
2.1.Силами полезных сопротивлений  или моментами этих сил
или моментами этих сил  называют такие, для преодоления которых создана машина. С энергетической точки зрения работа сил полезных сопротивлений
называют такие, для преодоления которых создана машина. С энергетической точки зрения работа сил полезных сопротивлений  отрицательна
отрицательна
2.2.К силам вредных сопротивлений  относят силы трения в кинематических парах, силы аэродинамических сопротивлений и др. На преодоление этих сил затрачивается дополнительная работа сверх той, которая необходима для определения полезного сопротивления. Поэтому работа сил суммарных сопротивлений
относят силы трения в кинематических парах, силы аэродинамических сопротивлений и др. На преодоление этих сил затрачивается дополнительная работа сверх той, которая необходима для определения полезного сопротивления. Поэтому работа сил суммарных сопротивлений  . Векторы сил
. Векторы сил  направлены в противоположную сторону векторов скоростей тех точек звеньев механизма, к которым они приложены, или составляют с ними тупые углы, а моменты сил сопротивления
направлены в противоположную сторону векторов скоростей тех точек звеньев механизма, к которым они приложены, или составляют с ними тупые углы, а моменты сил сопротивления  направлены противоположно вращению звена. (рис.4.1).
направлены противоположно вращению звена. (рис.4.1).
Деление сил на движущие и силы сопротивления имеет некоторую условность.
Тема 6.Динамические характеристики движений человека
Так силы тяжести звеньев при подъёме их центров масс оказывается силами сопротивлений, а при опускании центров – силами движущими; силы трения между шкивом и ремнём в ременной передаче являются движущими.
Примеры сил. У двигателя внутреннего сгорания движущей силой  является давление расширяющегося газа на поршень. Силы вредных сопротивлений: сила трения в подшипниках и цилиндрах, сопротивление воздуха. Силы полезных сопротивлений: сила резания, сила сцепления между колесом и грунтом и т.п.
является давление расширяющегося газа на поршень. Силы вредных сопротивлений: сила трения в подшипниках и цилиндрах, сопротивление воздуха. Силы полезных сопротивлений: сила резания, сила сцепления между колесом и грунтом и т.п.
а) б)








ω
Рис.4.1
3.Силы инерции  и моменты сил инерции
и моменты сил инерции 
Возникают при движении звеньев. В быстроходных механизмах по величине эти силы могут превосходить другие силы. Силы инерции, действующие на каждое звено механизма, приводятся к главному вектору и главному моменту инерционных сил:
 (4.1)
(4.1)
 (4.2)
(4.2)
где m – масса звена;  — ускорение центра массы звена; ε — угловое ускорение звена;
— ускорение центра массы звена; ε — угловое ускорение звена;  – момент инерции масс звена относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена.
– момент инерции масс звена относительно оси, проходящей через центр масс и перпендикулярной плоскости движения звена.
Направление этих сил и моментов обратно направлениям соответствующих ускорений, а их работа за время рабочего цикла равна нулю (рис. 4.2).

Рис.4.2
⇐ Предыдущая12
Дата добавления: 2014-01-06; Просмотров: 533; Нарушение авторских прав?;
Читайте также:
Вращательные движения — Биомеханика движений фигуриста (Мишин А.Н.)
 При рассмотрений обязательных упражнений мы встречались с разновидностями опорных вращательных движений. Мы знаем, что вращательные движения, например повороты, обусловлены главным образом встречным поворотом верхней части тела относительно нижней и не связаны с длительным и быстрым вращением всего тела. Напротив, в произвольном катании наиболее характерными являются движения, связанные с вращением всего тела вокруг продольной оси в 2; 2,5; 3; 3,5 и более оборотов в полете в прыжках, а во вращениях достигают нескольких десятков оборотов. Именно стремительные вращения вокруг вертикальной оси, пожалуй, являются наиболее ярким олицетворением движений произвольного катания.
При рассмотрений обязательных упражнений мы встречались с разновидностями опорных вращательных движений. Мы знаем, что вращательные движения, например повороты, обусловлены главным образом встречным поворотом верхней части тела относительно нижней и не связаны с длительным и быстрым вращением всего тела. Напротив, в произвольном катании наиболее характерными являются движения, связанные с вращением всего тела вокруг продольной оси в 2; 2,5; 3; 3,5 и более оборотов в полете в прыжках, а во вращениях достигают нескольких десятков оборотов. Именно стремительные вращения вокруг вертикальной оси, пожалуй, являются наиболее ярким олицетворением движений произвольного катания.
Основы механики вращений
В связи с особой важностью вращательных движении в общем комплексе упражнений произвольного катания рассмотрим коротко основные понятия и терминологию механики вращательного движения тела вокруг вертикальной оси.
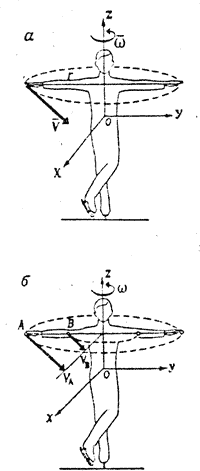
Характеристики вращательных движений. В качестве пример, вращающегося тела рассмотрим тело фигуриста, выполняющего пируэт на одной ноге (рис. 19, а). Будем условно считать, что вращение его тела происходит вокруг неподвижной оси.
Вращательным движением твердого тела относительно неподвижной оси называется такое движение, при котором две его точки остаются неподвижными. Ось, проходящая через эти точки, называется осью вращения. Вращение тела характеризуется угловой скоростью тела. Величина угловой скорости определяется отношением угла поворота тела к времени, за которое произошел этот поворот:
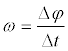
Угловая скорость характеризуется не только величиной, но и направлением в пространстве, т. е. является вектором, направленным по оси вращения в ту сторону, откуда вращение наблюдается против часовой стрелки. Различают среднюю угловую скорость, измеряемую в течение нескольких оборотов, и мгновенную угловую скорость тела в данный момент.
Если угловая скорость всех точек напряженного тела одинакова, то линейная скорость для каждой точки разная. Зависимость между угловой и линейной скоростями точки выражается формулой:
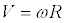
где R — расстояние точки от оси вращения.
Эта простая зависимость имеет во вращениях важное значение, так как при одной и той же угловой скорости тела со линейные скорости точек тела разные; чем дальше они остоят от оси вращения, тем их линейная скорость больше (рис. 19, б).
Рассмотрим ускорения точки вращающегося тела (рис. 20). Скорость точки является величиной векторной, т. е. может изменяться по величине и направлению в пространстве. Ускорение, вызванное изменением величины вектора скорости, называется касательным или тангенциальным; оно направлено по касательной к траектории движения точки, совпадает с направлением вектора скорости при ускоренном движении и противоположно вектору скорости при замедленном движении. Оно равно:
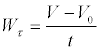 или
или 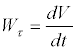
При движении точки по окружности 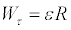 ,где
,где 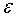 — угловое ускорение тела, имеющее размерность
— угловое ускорение тела, имеющее размерность 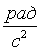
Ускорение, вызванное изменением направления вектора скорости точки, называется нормальным. Оно направлено по нормали в сторону вогнутости траектории и равно 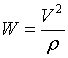 при движении точки по окружности
при движении точки по окружности 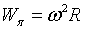 . Ускорение точки имеет размерность м/с2.
. Ускорение точки имеет размерность м/с2.
На рис. 20 приведены векторы касательного и нормального ускорений точки кисти руки фигуриста в пируэте. Таким образом, если вектор скорости изменяется и по величине, и по направлению, то движущаяся точка имеет ускорение, состоящее из касательного и нормального. Геометрическая сумма этих ускорений называется полным ускорением и направлена по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений.
Мерой инертности тела при. поступательном движении является его масса, измеряемая в килограммах. Во вращательном движении особое значение приобретает распределение массы тела относительно оси вращения: удаление массы тела от оси вращения увеличивает инертность тела во вращательном движении вокруг этой оси, а приближение к оси уменьшает.
 |
| Рис. 19. Схема вращения фигуриста |
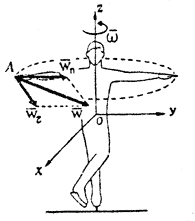 |
| Рис. 20. Ускорения точек вращающегося тела |
Мерой инертности тела во вращательном движении является момент инерции, равный сумме произведений масс частей тела на квадраты их расстояний до оси вращения:
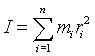
где m — массы частей тела; r — расстояние масс тела до оси вращения.
Следует подчеркнуть, что в выражение для величины момента инерции входят расстояния масс частей тела до оси вращения во второй степени, что объясняет значительное изменение момента инерции тела с постоянной массой при перераспределении масс частей тела относительно оси вращения.
Одной из важных характеристик вращающегося тела является количество запасенного им вращательного движения. Она носит название момента количества движения*
или кинетического момента тела К. Величина кинетического момента вращающегося тела измеряется произведением момента инерции тела относительно оси I и угловой скорости, вращения тела вокруг этой оси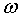 :
:
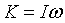
Кинетический момент является характеристикой, свойственной вращательному движению.
Закон сохранения момента количества движения
Для анализа вращательных движений фигуриста очень важно знать закон сохранения кинетического момента. Одним из свойств вращающегося тела является стремление сохранить количество приобретенного вращательного движения, или, другими словами, величину кинетического момента. Для рассматриваемого нами случая закон сохранения кинетического момента может быть упрощенно сформулирован следующим образом:
«Кинетический момент тела относительно оси постоянен, если сумма моментов внешних сил относительно оси равна нулю»:
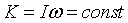
Пренебрегая сопротивлением воздуха и трением конька о лед, можно считать, что при выполнении вращения на тело фигуриста действуют две внешние силы: сила веса и вертикальная составляющая реакции опоры. При хорошем выполнении пируэта эти силы совпадают с осью вращения, поэтому не создают моментов сил относительно оси.
Во вращательном движении при выполнении пируэта зависимость 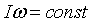 проявляется в постоянной взаимосвязи между величинами момента инерции тела и его угловой скоростью вращения. Другими словами, уменьшение одного множителя вызывает увеличение другого настолько, что их произведение остается неизменным. Именно поэтому приближение звеньев тела к оси вращения в процессе группировки, т. е. уменьшение момента инерции, обусловливает увеличение скорости вращения тела и наоборот.
проявляется в постоянной взаимосвязи между величинами момента инерции тела и его угловой скоростью вращения. Другими словами, уменьшение одного множителя вызывает увеличение другого настолько, что их произведение остается неизменным. Именно поэтому приближение звеньев тела к оси вращения в процессе группировки, т. е. уменьшение момента инерции, обусловливает увеличение скорости вращения тела и наоборот.
Сравнение моментов инерции тела в различных положениях позволяет, в частности, установить, что группировка рук из положения в стороны может увеличить скорость вращения тела почти вдвое, а переход из положения ласточки в положение стоя с руками вдоль тела—более чем в семь раз. Эти данные не учитывают сил сопротивления, испытываемых телом при вращении, поэтому реальное увеличение угловой скорости всегда меньше и зависит от характера контакта конька со льдом. С этой точки зрения выгодны опора на переднюю треть конька без касания льда зубцами и отсутствие так называемого скобления ребром конька о лед. Наименьшее сопротивление оказывается в случае, если конец опорной ноги во время вращения выполняет петли небольшого размера (3—5 см).
Силы инерции при вращениях
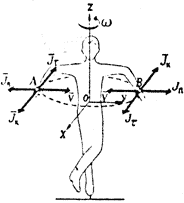
Для определения динамической структуры вращательного движения рассмотрим силы инерции, действующие на звенья тела фигуриста при выполнении пируэта.
При анализе ускорений, действующих на точки вращающегося тела, было определено, что в общем случае таких ускорений два: нормальное и касательное. Отсюда на точки вращающегося тела действуют также две силы инерции: нормальная и касательная.
Возьмем систему координат хОу с началом в центре тяжести тела. Ось Oz направим по оси вращения. При равномерном вращении тела вокруг оси Oz с угловой скоростью w на две симметрично расположенные точки A и B будут действовать только нормальные силы инерции, равные по величине 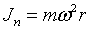 направленные противоположно центростремительному ускорению (рис. 21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения.
направленные противоположно центростремительному ускорению (рис. 21, а). И) формулы видно, что величина этих сил прямо пропорциональна массе точки т, квадрату угловой скорости w и расстоянию r точки от оси вращения.
При изменении угловой скорости 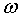 появляются угловое ускорение
появляются угловое ускорение 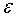 и касательные силы инерции, равные по величине
и касательные силы инерции, равные по величине 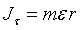 и направленные по касательной к траектории точек А и В в стороны, противоположные касательным ускорениям (рис. 21,б). Касательные силы инерции образуют пару сил, лежащую в плоскости, параллельной плоскости хОу. Эта пара сил препятствует вращению фигуриста вокруг оси Oz.
и направленные по касательной к траектории точек А и В в стороны, противоположные касательным ускорениям (рис. 21,б). Касательные силы инерции образуют пару сил, лежащую в плоскости, параллельной плоскости хОу. Эта пара сил препятствует вращению фигуриста вокруг оси Oz.
Причины изменения скорости вращения
В различных вращательных движениях и пируэтах фигурист меняет угловую скорость вращения своего тела в значительных пределах. В соответствии с законом сохранения кинетического момента изменение скорости вращения сопровождается изменением момента инерции тела— группировкой или раз-группировкой. Причиной изменения скорости являются определенные силы. Какие же силы вызывают изменение скорости вращения фигуриста?
Пренебрегая силами трения, можно сказать, что внешние силы, как мы уже говорили, не создают значительных моментов относительно оси вращения, т. е. не являются причиной изменений скорости вращения. Следовательно, изменение скорости вращения вызывают силы внутренние —группировки и разгруппировки, т. е. силы активного действия, обусловленные мышечной деятельностью человека.
Рассматривая эти силы, легко убедиться, что линии их действия при группировке и разгруппировке направлены к оси вращения или от нее, т. е., грубо говоря, они не поворачивают тело вокруг оси. Какие же силы непосредственно ускоряют или замедляют вращение тела? Это силы инерции Кориолиса, или, говоря точнее, моменты этих сил. Рассмотрим физическую сущность возникновения сил инерции Кориолиса, определим направление их действия и формулу для определения величины этих сил (рис.22).
В пируэте при группировке и разгруппировке имеют место два движения: вращение тела, которое будем называть переносным, и движение рук и свободной ноги вдоль радиуса к оси или от нее, которое будем называть относительным. Когда руки притягиваются к оси вращения (относительное движение), линейные скорости их частей станут меньше, т. е. звенья тела, участвующие в относительном движении, приобретут отрицательное ускорение (кориолисово). Иными словами —ускорение, направленное против вращения. Так-как всякая сила инерции всегда направлена в сторону, противоположную ускорению, то силы инерции Кориолиса будут направлены по ходу вращения. Они приложены к частям тела, выполняющим группировку, направлены в сторону вращения и увеличивают его угловую скорость.
Итак, в процессе вращения тела фигуриста, перемещения рук и свободной ноги к оси вращения или от нее возникают силы инерции Кориолиса, которые ускоряют вращение при группировке и замедляют его при разгруппировке. Кориоли-совы силы инерции зависят от величины угловой скорости вращения тела 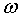 , линейной скорости частей тела при группировке и замедляют его при разгруппировке. Кориолисовы силы инерции зависят от величины угловой скорости вращения тела со, линейной скорости частей тела при группировке и разгруппировке — V, а также от синуса угла между векторами
, линейной скорости частей тела при группировке и замедляют его при разгруппировке. Кориолисовы силы инерции зависят от величины угловой скорости вращения тела со, линейной скорости частей тела при группировке и разгруппировке — V, а также от синуса угла между векторами 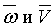 . Величина этих сил определяется по формуле:
. Величина этих сил определяется по формуле:
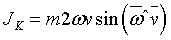
На рис.23 приведена совокупность всех сил инерции, действующих на точки А и В вращающегося тела. Необходимо учитывать, что в действительности на каждую из точек тела действует результирующая сила инерции, равная векторной сумме перечисленных сил инерции: нормальной,касательной и кориоли-совой.
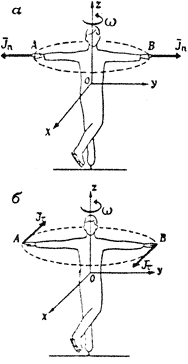 |
| Рис. 21. Силы инерции точек врашающегося тела |
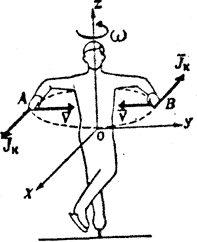 |
| Рис. 22. Силы инерции Кориолиса, действующие на точки вращающегося тела при группировке |
Прецессия оси вращения
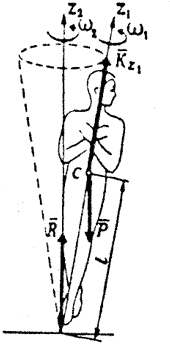
Анализируя вращательное движение, мы говорили, что в процессе вращения о. ц. т. тела находится точно над точкой опоры. В практике фигурного катания встречаются случаи, когда проекция о. ц. г. не совпадает с точкой опоры. В этом случае продольная ось тела z1, проходящая через точку опоры и о. ц. т., начинает вращаться вокруг вертикальной оси z2 с угловой скоростью  (рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения:
(рис. 24). Такое движение оси вращающегося тела называют прецессией, а угловую скорость вращательного движения оси — угловой скоростью прецессии. Угловая скорость прецессии может быть определена из следующего выражения:
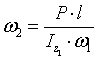
где: l-расстояние от точки опоры до о.ц.т. тела; 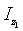 — момент инерции фигуриста относительно оси вращения z1; Р-вес тела фигуриста;
— момент инерции фигуриста относительно оси вращения z1; Р-вес тела фигуриста; 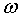 — угловая скорость фигуриста вокруг оси z1;
— угловая скорость фигуриста вокруг оси z1; 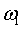 —угловая скорость прецессии оси z1.
—угловая скорость прецессии оси z1.
Прецессионное движение оси вращения нежелательно и с точки зрения качественной оценки пируэта, и, что, пожалуй, главное, с точки зрения управления движением, поскольку ориентация спортсмена, сохранение равновесия резко осложняются.
Из формулы видно, что угловая скорость прецессии  обратно пропорциональна угловой скорости вращения фигуриста: чем больше угловая скорость вращения фигуриста, тем меньше угловая скорость прецессии
обратно пропорциональна угловой скорости вращения фигуриста: чем больше угловая скорость вращения фигуриста, тем меньше угловая скорость прецессии  , и наоборот. Отсюда вытекает важный практический вывод: чем больше скорость вращения тела фигуриста в пируэте, тем устойчивее положение оси вращения.
, и наоборот. Отсюда вытекает важный практический вывод: чем больше скорость вращения тела фигуриста в пируэте, тем устойчивее положение оси вращения.
На устойчивость оси вращения положительно влияет также увеличение момента инерции тела относительно оси вращения  . Однако наиболее важную роль в устойчивости оси вращения играет положение центра тяжести. Момент силы тяжести относительно точки опоры определяет угловую скорость прецессии. Для уменьшения угловой скорости прецессии следует уменьшить величину этого момента, т. е. стремиться к такому положению, при котором о.ц.т. тела находится над точкой опоры.
. Однако наиболее важную роль в устойчивости оси вращения играет положение центра тяжести. Момент силы тяжести относительно точки опоры определяет угловую скорость прецессии. Для уменьшения угловой скорости прецессии следует уменьшить величину этого момента, т. е. стремиться к такому положению, при котором о.ц.т. тела находится над точкой опоры.
Устойчивость вращения к прецессии связана с расстоянием l от о.ц.т. до неподвижной точки вращения. Чем оно меньше, тем при прочих равных условиях меньше угловая скорость прецессии. Не удивительно поэтому, что наиболее устойчивым вращением является волчок —пируэт, в котором расстояние l минимально.
Интересно отметить, что устранение момента силы тяжести приводит к мгновенному устранению прецессии. Дру-гими словами, прецессия не обладает инерцией.
На практике встречаются две основные причины возникновения прецессии в пируэтах. В первом случае несовпадение точки опоры и проекции силы тяжести вызвано несовершенным въездом во вращение, неправильным определением центра вращения. Здесь резкое торможение, раннее начало вращения, неточное маховое движение порождают инерционные силы, отклоняющие о.ц.т. тела от вертикали.
В другом случае смещение о.ц.т. вызвано неправильным перемещением частей тела при смене позы.
Влияние положения тела фигуриста при вращениях на частоту сердечных сокращений*
Влияние положения тела фигуриста на характер кровообращения и частоту сердечных сокращений при вращениях наиболее ярко прослеживается при выполнении таких элементов, как вращение в ласточке, в ласточке со сменой ног, прыжок во вращение ласточка. В это время частота сердечных сокращений оказывается наиболее низка.
Интересна пульсограмма вращения в ласточке. При выполнении данного элемента отмечено заметное уменьшение частоты сердечных сокращений —6—12 уд/мин по сравнению с исходным — фоновым.
Этот интересный факт требует более глубокого исследования. Однако уже на основании проведенных опытов было высказано предположение, что данное явление может быть объяснено антиортостатической реакцией организма. Имеется в виду практически горизонтальное положение верхней части тела и свободной ноги при вращении. Возможно, что урежение пульса действительно является следствием реакции барорецепторов скаротидных синусов на увеличение венозного возврата крови, вызванного центробежными силами инерции.
 |
| Рис. 23. Совокупность сил инерции, действующих на точки вращающегося тела |
 |
| Рис. 24. Прецессия оси вращения тела фигуриста |
Исследования автора, проведенные под руководством профессора А. Б. Гандельсмана, позволяют предположить более сложную природу такого явления. Не отрицая возможности влияния центробежных сил на характер передвижения масс крови, хочется обратить внимание на два обстоятельства. Вращение в ласточке является пируэтом, в котором, пожалуй, в наибольшей степени выражен статический компонент движения. Вот почему энергетика этого упражнения весьма низкая. Кроме того, характер въезда во вращение и выезда из него не связан с необходимостью глубокого приседания и подъема, как в волчке, или группировки, как во вращении винт. Это также свидетельствует о наиболее низкой энергетической стоимости вращения в простой ласточке. Таким образом, можно предположить, что одной из причин урежения сердечного ритма при вращении в простой ласточке является именно низкая энергетика этого упражнения—более низкая, чем энергетика комплекса различных движений, при которых измеряется фоновый пульс.
Необходимо также учитывать эмоциональную сторону упражнения. В этом плане следует отметить, во-первых, сравнительную комфортность положения тела при вращении в ласточке и, во-вторых, наиболее низкую из всех вращений угловую скорость, которая и обусловливает относительно спокойный эмоциональный фон упражнения.
Другие же сходные по биомеханической структуре элементы: вращение в ласточке со сменой ног и прыжок во вращение ласточка —вызывают более выраженную ответную пульсовую реакцию, и феномен уменьшения частоты сердечных сокращений проявляется в меньшей степени. Этот факт связан с тем, что наряду с менее благоприятным эмоциональным фоном при выполнении данных двух элементов фигурист затрачивает дополнительную энергию на отталкивание и смену ног при вращении, что, естественно, увеличивает частоту сердечных сокращений.
Феномен уменьшения частоты сердечных сокращений при простом вращении в положении ласточка может быть использован при составлении произвольных программ.
Рационально включать вращения в ласточке в те места программы, после которых необходим промежуточный отдых, расслабление, снижение эмоционального фона, успокоение.
Анализ техники вращений
Благодаря кривизне лезвия конька в арсенале фигуриста может быть большое количество вращательных движений, возникающих естественно и выполняемых сравнительно легко. Такими движениями являются опорные вращения — пируэты. Они разнообразят произвольную программу, позволяют спортсмену продемонстрировать способность сохранять равновесие в сложной позиции при быстром вращении.
Пируэт представляет собой длительное вращательное движение тела вокруг вертикальной оси без заметного перемещения точки опоры. В зависимости от направления вращения различают пируэты вперед (вращение происходит в сторону опорной ноги) и назад (вращение выполняется в сторону свободной ноги).
С точки зрения позы, в которой выполняется пируэт, можно выделить три основные группы: пируэты стоя, пируэты в приседе (волчки) и пируэты в положении ласточка.
Различают простые пируэты, в которых вращение происходит в относительно неизменной позе, и сложные —со сменой позы (например, с переходом из положения стоя в положение сидя).
Пируэты могут выполняться на одной и обеих ногах. В последнем случае понятие «направление вращения» (вперед или назад) теряет смысл, так как обе ноги являются опорными. Поэтому здесь указывают лишь сторону вращения. В произвольных программах сейчас, как правило, встречаются сложные пируэты, состоящие из комбинаций перечисленных пируэтов.
Пируэт состоит из подхода, въезда, вращения и выезда. На рис. 25 приведены следы, оставленные при выполнении пируэта вперед. Дуги 1, 2, 3 и 4 соответствуют подходу, дуга 5 —въезду, точка 6—вращению, а дуги .7 и 8 —выезду. Подход. Существует несколько вариантов подходов. Наиболее удобным и поэтому целесообразным для начального обучения является сочетание тройки вперед-наружу с перебежкой назад. Используют подходы в виде тройки вперед-внутрь—назад-наружу, а также ходом вперед-наружу, подходе важно сохранять плавность скольжения, хорошу осанку, чтобы вращение было естественным, а приготовление к нему — незаметным.
Въезд. Это наиболее сложная и ответственная часть пируэта. Именно здесь возникает вращение. Как правило, если фигурист сообщил телу устойчивое вращение, то сохранять и поддерживать его не составляет большой сложности. След, оставляемый коньком при въезде, представляет собой кривую с плавно меняющейся кривизной. Выполняют въезд на согнутой ноге и не выпрямляют ее до тех пор, пока не возникнет устойчивое вращение.
Вращение телу можно придать двумя способами: толчком ногой при переходе с последней дуги подхода на въездную дугу, а также круговым маховым движением свободной ноги и руки при въезде. Во вращении стоя и в волчках следует использовать оба способа. При вращениях в ласточке маховое движение не всегда эффективно. Здесь оно приводит к выведению свободной ноги вперед, и для принятия положения ласточки фигурист вынужден в конце въезда резко отводить свободную ногу назад. Это движение часто вызывает потерю равновесия. Более простым и надежным является въезд с отведенной назад свободной ногой и одноименной рукой.
Напротив, при въезде в волчок круговое маховое движение весьма целесообразно и эффективно. Необходимо во время подхода сделать сильный мах руками и свободной ногой назад. Мах, т. е. выведение рук и ноги вперед, следует начинать только тогда, когда дуга достигнет максимальной кривизны.
Въезд во вращение стоя, по существу, не отличается от въезда в волчок. Здесь только опорная нога более выпрямлена. Не следует, однако, выпрямлять ее полностью: это может привести к нарушению равновесия.
Для устойчивости вращения очень важно, как выполнен конечный участок дуги въезда. В пируэтах вперед в конце въезда, когда дуга достигла максимальной кривизны, следует поворот тройкой вперед-наружу, после чего —окружность диаметром 30—40 см, выполняемая ходом назад-внутрь, и только затем начинается вращение.
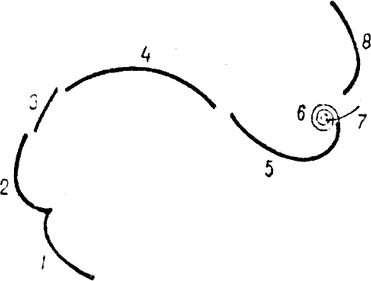 |
| Рис. 25. Следы пируэта вперед |
Вращение. В простых пируэтах группировка отсутствует и положение, принятое в начале вращения, сохраняется почти неизменным. Поэтому здесь, как и при выполнении спиралей, важна точность положения тела, стабильность удержания его. Малейшая погрешность, допускаемая на протяжении пяти, шести и более оборотов, портит впечатление.
В ласточке необходимо вращаться на плоскости конька, не касаясь льда зубцами. Начинающие фигуристы часто теряют равновесие уже в начале вращения, так как чрезмерно перемещают центр тяжести тела вперед. Чтобы избежать этого, необходимо на протяжении всего вращения, особенно в начале его, оттягивать свободную ногу назад. Она должна быть выпрямлена, развернута, голова направлена вперед, а вытянутые руки на одной линии, находящейся в одной плоскости с опорной и свободной ногами.
В волчке вращение происходит на передней трети конька. Для повышения устойчивости в начале вращения допустимо легкое касание льда зубцами. Наиболее распространенная ошибка здесь—падение назад. Чтобы предотвратить ее, развернутая свободная нога и руки должны быть прямыми и вытянутыми вперед. Опорная нога при этом согнута, голова подтянута, плечи опущены.
Вращение стоя также происходит на передней трети конька с легким касанием льда зубцами.
В сложных пируэтах происходит группировка. Ее можно выполнять в двух вариантах: в первом варианте приближение рук и свободной ноги к оси вращения происходит при неизменном основном положении тела (например, стоя или в приседе), во втором поза меняется —части тела приближаются к оси вращения (например, переход из ласточки в волчок или из волчка в положение стоя). При этом скорость вращения тела возрастает.
Рассмотрим пример группировки в пируэте стоя, называемом винтом. Из положения, когда нога вытянута вперед, правую ногу, не опуская, выводят вперед, сгибают в колене и скрещивают с левой, на которой происходит вращение. Затем правую ногу опускают, скользя задней поверхностью голени по левой. Это движение сопровождается группировкой рук одновременно с группировкой ног или несколько позже. В заключительной фазе руки плотно прижимают к телу, а слегка согнутую опорную ногу выпрямляют, что дает дополнительное увеличение скорости вращения. Необходимо следить за симметрией группировки, ибо неодинаковое движение рук вызывает нарушение равновесия. В этом пируэте скорость вращения наибольшая—до 4 и более оборотов в секунду.
Выезд. Выполнению всегда предшествует движение, обратное группировке,— разгруппировка. Делается это для уменьшения скорости вращения, что облегчает выполнение выезда. Здесь важно, чтобы разгруппировка заканчивалась небольшим сгибанием опорной ноги.
Обычно выезд выполняют со сменой ноги: ранее свободная ном становится опорной, и вращение завершается тол-ком, аналогичным толчку в обязательной фигуре № 3, с последующим скольжением назад-наружу. Данный вариант выезда наиболее распространен; его рекомендуют при разучивании пируэтов. В программах мастеров встречаются более сложные выезды (например, вперед-наружу со сменой ноги, назад-внутрь без смены ноги, въезд в остановку, в прыжок). При любом варианте следует стремиться к слитности всех движений, к такому выполнению, при котором выезд является естественным продолжением вращения.
Заклоны. Особой разновидностью пируэтов являются так называемые заклоны. Их выполняют со значительным прогибом назад или в сторону и с откинутой головой. Вращение с необычным положением головы усложняет пространственную ориентировку, вызывает нарушение координации движений, порой сопровождается головокружением. В то же время заклоны —очень ценное упражнение для совершенствования равновесия.
Прежде чем осваивать данную группу пируэтов, фигурист должен научиться уверенно принимать эту позу без коньков. Подход и въезд делают как в обычных вращениях. Положение заклона принимают в тот момент, когда начинается вращение. Далее прогиб рекомендуется увеличить и вместе с тем по возможности (незаметно для наблюдателя) выполнять группировку. Опытные фигуристы иногда поднимают одну руку вверх или опускают вниз, чтобы ее положение совпадало с положением оси вращения: это обеспечивает дополнительную группировку, что вызывает увеличение скорости вращения. С заклонами весьма схожи паузы с захватом свободной ноги одной или двумя руками.
Пируэты назад.Исключительно ценными для дальнейшего овладения прыжками являются пируэты назад. Их выполняют в тех же позах, что и пируэты вперед. Но есть у них некоторые особенности. Так, несмотря на то, что направление общего вращения тела в пируэте назад и вперед может быть одно и то же, ощущения, испытываемые фигуристом, различны. Пируэты назад наиболее точно имитируют движения тела в полете при выполнении прыжков, поэтому важны как подготовительные упражнения. Они красивы; включают их в различные комбинации.
При обучении вращениям назад рекомендуется выполнять подход (рис. 26) в виде крутой дуги вперед-внутрь (дута 1). Въезд представляет собой дугу вперед-внутрь на другой ноге (дуга 2), описывая которую фигурист делает энергичное вращательное движение свободной ноги и рук. Вращение (точка 3) может выполняться в любом положении (в ласточке, волчке, стоя), а также в промежуточных положениях. Выезд (дуга 4) лучше всего разучивать на той же ноге, на которой происходило вращение: это помогает совершенствовать выезд из многооборотных прыжков.
Освоение пируэтов вперед и назад открывает большие возможности для выполнения различных комбинаций: это волчок со сменой ноги, вращение в ласточке со сменой ноги, варианты смены положения тела и ноги.
Для успешного овладения пируэтами важно определить удобную для спортсмена сторону вращения. Большинство фигуристов быстрее овладевают вращениями влево и лучше их переносят. Наиболее простой и верный способ определения «своего» направления вращения —выполнение пируэта назад с выездом без смены ноги. Если этот, пируэт и выезд увереннее и легче получаются на правой ноге, следует лучшие варианты своих вращений планировать влево, и наоборот.
Разучивание пируэтов вперед и назад в различных позах помогает подготовить организм фигуриста к вращательным нагрузкам, которые он постоянно испытывает во время катания.
Специальные упражнения для совершенствования вращений
Одним из важных направлений в тренировке вращений вне льда является работа над гибкостью.
При этом необходимо сочетать традиционные способы развития пассивной гибкости с помощью различных растягиваний, шпагатов, махов и т. п. с развитием активной гибкости. Например, одной из наиболее сложных поз, особенно для мальчиков, является вращение в ласточке. Для ее совершенствования целесообразно применять утяжелитель, прикрепляемый к стопе свободной ноги. Он позволяет добиваться хорошего эффекта при развитии как пассивной гибкости (выполнение махов назад), так и активной (удержание свободной ноги с грузом в требуемой позе).
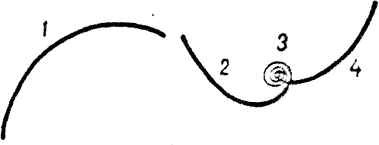 |
| Рис. 26. Следы пируэта назад |
Этот же способ эффективен и в занятиях вне льда. Лучшим способом совершенствования положения тела во вращении ласточка, на наш взгляд, является разучивание так называемой качающейся ласточки—поочередно на обеих нoгax.
Целесообразно использовать тренажер «Грация» для совершенствования точности позы и чувства равновесия. Для совершенствования общей выносливости фигуриста к вращательным нагрузкам весьма эффективны специальные тренажеры в виде вращающихся платформ с электроприводом и плавной регулировкой скорости вращения в пределах от ноля до 5 и более оборотов в секунду.
В тренировках на льду основное внимание следует уделять поиску оптимального варианта въезда во вращение и оптимального контакта конька со льдом во время вращения. Следует анализировать характер следов на льду, обращая главное внимание на отсутствие скоблений, касания льда зубцами.
Хорошим средством совершенствования качества въезда во вращения, повышения стабильности их выполнения являются тренировки с выключением зрения. Надевая специальные непрозрачные очки, фигурист выполняет требуемое вращение. При этом обостряется деятельность двигательного, вестибулярного, тактильного и слухового анализаторов. Опыты показали, что такие упражнения повышают устойчивость навыка, делают выполнение вращений более уверенными, стабильными. Практика показала, что у одних фигуристов принятие требуемой позы происходит с участием зрительного анализатора, выключение зрения у них нарушает точность позы; у других же это происходит практически без участия зрительного анализатора. Сравнение стабильности и качества выполнения вращений показало, что обеспечение позы в основном с помощью двигательного анализатора более совершенно.
Вращательное движение тела. Закон вращательного движения :: SYL.ru
В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».
Основные понятия кинематики вращательного движения
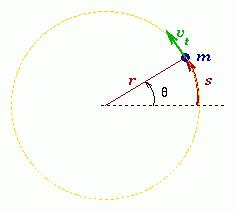
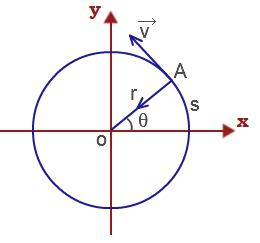
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.
Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.
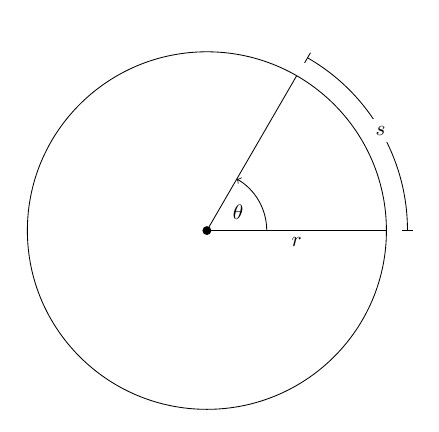
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:
φ = φ(t).
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:
ΔS = Δφr.
Основные элементы кинематики равномерного вращательного движения
Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.
Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:
ω = dφ/dt.
Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле
ω = φ/t.
Согласно предварительной формуле размерность угловой скорости
[ω] = 1 рад/с.
Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то
ω = 2π/T,
поэтому период вращения определим следующим образом:
T = 2π/ω.
Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:
ν = 1/T.
Единицы измерения частоты: [ν]= 1/c = 1 c-1 = 1 Гц.
Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:
ω = 2πν.
Основные элементы кинематики неравномерного вращательного движения
Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.
Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:
ε = dω/dt.
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.
Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.
Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).
Связь величин, характеризующих поступательное и вращательное движение
Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением
ΔS = Δφ r.
Тогда линейная скорость материальной точки, выполняющей вращательное движение
υ = ΔS/Δt = Δφr/Δt = ωr.
Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:
a = υ2/r = ω2r2/r.
Итак, в скалярном виде
a = ω2r.
Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение
a = ε r.
Момент импульса материальной точки
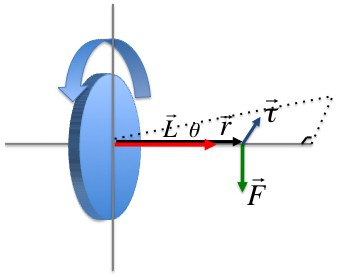
Векторное произведение радиуса-вектора траектории материальной точки массой mi на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.
Момент импульса материальной точки (Li) направлен перпендикулярно плоскости, проведенной через ri и υi, и образует с ними правую тройку векторов (то есть при движении с конца вектора riк υi правый винт покажет направление вектора Li).
В скалярной форме
L = miυirisin(υi,ri).
Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,
sin(υi,ri) = 1.
Так что момент импульса материальной точки для вращательного движения примет вид
L = miυiri.
Момент силы, которая действует на i-ю материальную точку
Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.
В скалярной форме
Mi = riFisin(ri, Fi).
Считая, что risinα = li, Mi = liFi.
Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.
Динамика вращательного движения
Уравнение динамики вращательного движения записывается так:
M = dL/dt.
Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.
Момент импульса и момент инерции
Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой
Li = miυiri.
Если вместо линейной скорости подставить ее выражение через угловую:
υi = ωri,
то выражение для момента импульса примет вид
Li = miri2ω.
Величина Ii = miri2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:
Li = Iiω.
Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:
L = Iω.
Момент силы и момент инерции
Закон вращательного движения гласит:
M = dL/dt.
Известно, что представить момент импульса тела можно через момент инерции:
L = Iω.
Тогда
M = Idω/dt.
Учитывая, что угловое ускорение определяется выражением
ε = dω/dt,
получим формулу для момента силы, представленного через момент инерции:
M = Iε.
Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.
Теорема Штейнера. Закон сложения моментов инерции
Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I0 + ma2,
где I0 — начальный момент инерции тела; m — масса тела; a — расстояние между осями.
Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).
Вращательное движение твёрдого тела
План
Абсолютное твёрдое тело. Вращательное движение. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями вращающегося твёрдого тела.
Момент инерции тела. Кинетическая энергия вращающегося твёрдого тела.
Вычисление моментов инерции. Теорема Штейнера. Свободные оси.
Момент силы. Момент импульса.
Уравнение моментов. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.
Гироскопы. Гироскопический эффект.
1. Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками тела остаётся неизменным.
Всякое движение твёрдого тела можно разложить на два основных вида движения – поступательное и вращательное.
Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Введём
понятие угловой скорости и углового
ускорения. Пусть твёрдое тело вращается
вокруг неподвижной в данной системе
отсчёта оси 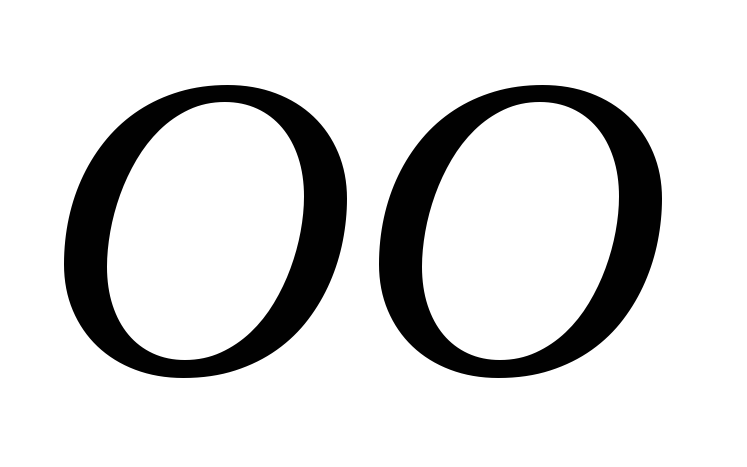
 и за время
и за время совершает бесконечно малый поворот
(рис. 3.1).
совершает бесконечно малый поворот
(рис. 3.1).
Соответствующий
угол поворота будем характеризовать
вектором 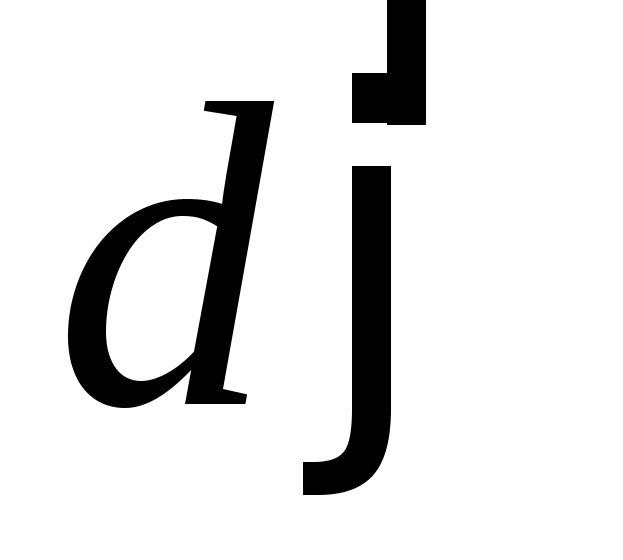 ,
модуль которого равен углу поворота, а
направление совпадает с осью
,
модуль которого равен углу поворота, а
направление совпадает с осью
 ,
причём так, что направление поворота
отвечает правилу правого винта по
отношению к направлению вектора
,
причём так, что направление поворота
отвечает правилу правого винта по
отношению к направлению вектора .
.
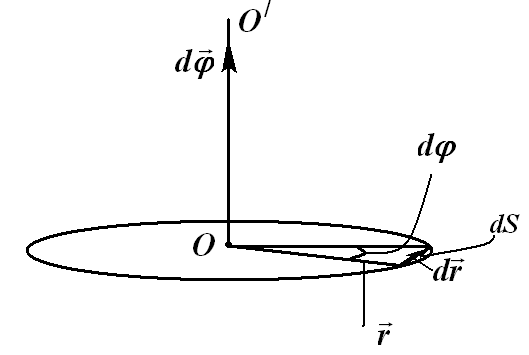
Рис. 3.1
Из
рис. 3.1 следует, что 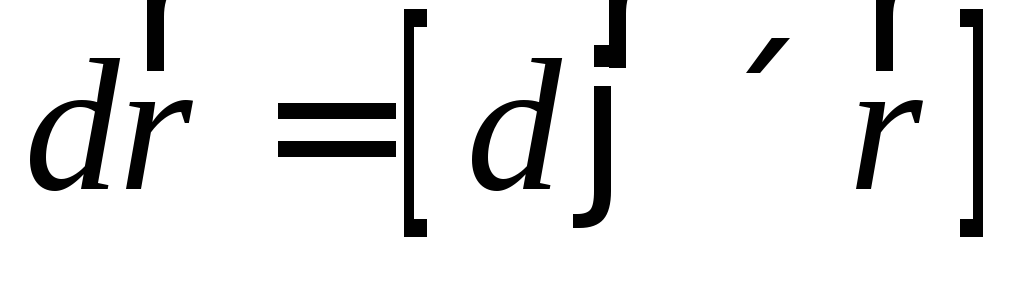 .
Вектор
.
Вектор как бесконечно малую величину можно
считать по модулю равным соответствующей
дуге окружности
как бесконечно малую величину можно
считать по модулю равным соответствующей
дуге окружности ,
его направление соответствует правилу
правого винта по отношению к векторам
,
его направление соответствует правилу
правого винта по отношению к векторам и
и
Разделим
обе части на  :
:
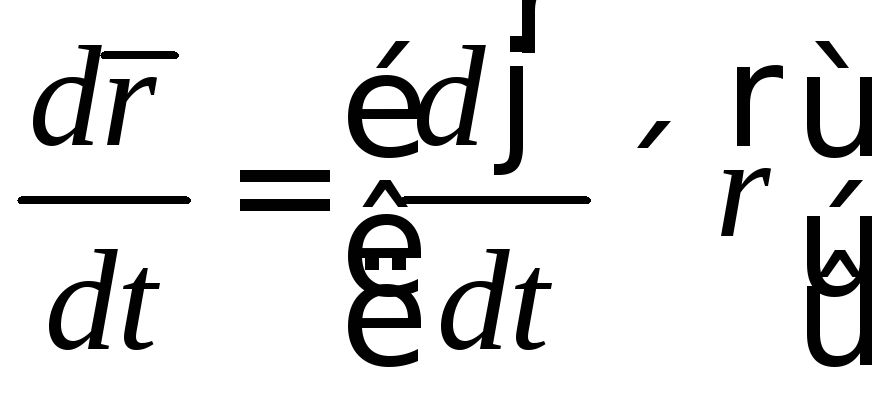 .
(*)
.
(*)
Производная угла поворота по времени называется угловой скоростью.
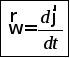
Вектор  совпадает по направлению с вектором
совпадает по направлению с вектором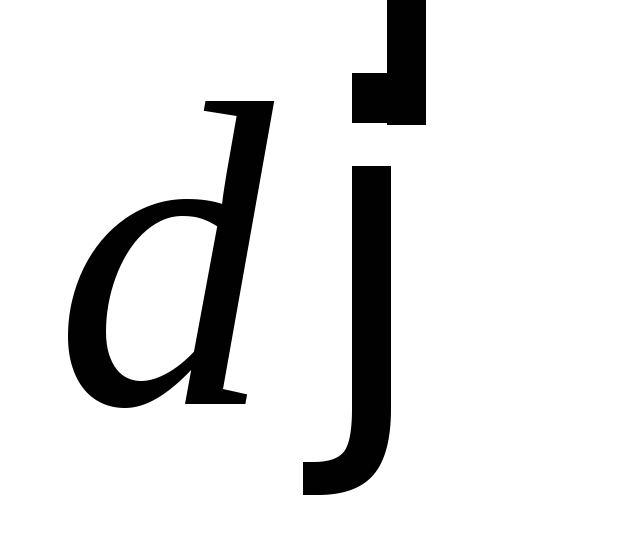 .Изменение
вектора
.Изменение
вектора 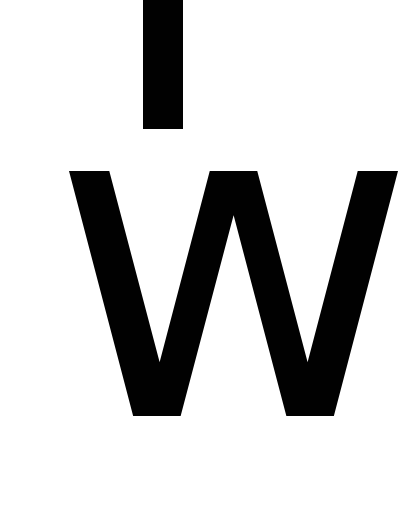 со
временем характеризуют вектором углового
ускорения:
со
временем характеризуют вектором углового
ускорения:
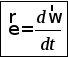
Из
выражения * получаем связь
линейной 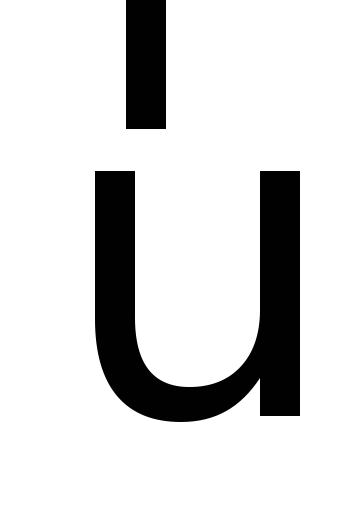 и угловой скоростей:
и угловой скоростей:
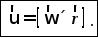 (**)
(**)
То
есть скорость  любой точкиА твёрдого
тела, вращающегося вокруг неподвижной
оси с угловой скоростью
любой точкиА твёрдого
тела, вращающегося вокруг неподвижной
оси с угловой скоростью  ,
равна векторному произведению
,
равна векторному произведению на радиус-вектор
на радиус-вектор точкиА относительно произвольной точки на оси
вращения.
точкиА относительно произвольной точки на оси
вращения.
Если
выбрать в качестве точки отсчёта для
радиус-вектора центр окружности вращения
(точка О), при неизменном радиусе
окружности 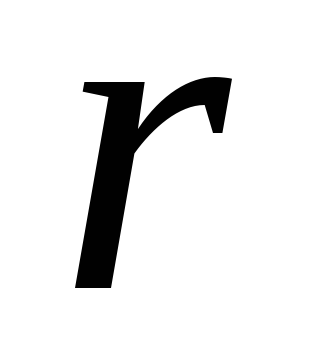 выражение (**) можно записать в скалярном
виде:
выражение (**) можно записать в скалярном
виде:
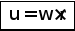
Продифференцируем
это выражение по времени: 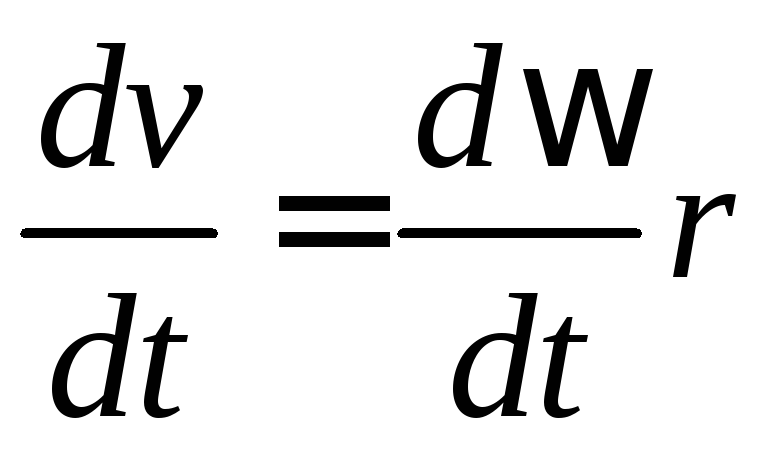 ,
отсюда получаем связь тангенциального
и углового ускорений:
,
отсюда получаем связь тангенциального
и углового ускорений:
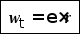
Нормальное ускорение можно представить как
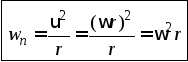
Модуль полного ускорения:

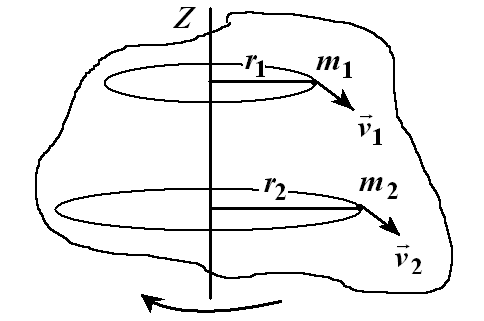
Рис. 3.2
2. Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки (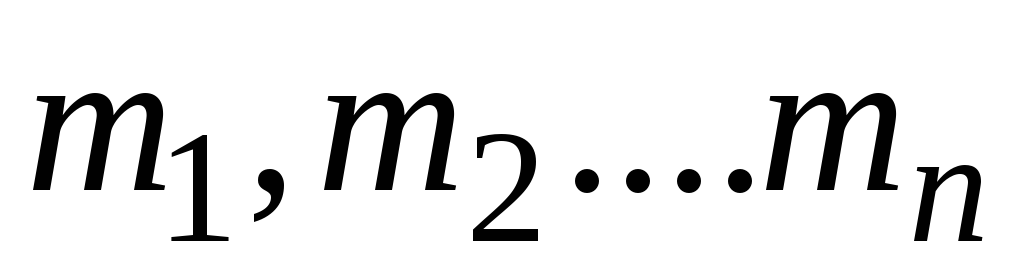 ).
Обозначим массуi-го
элемента
).
Обозначим массуi-го
элемента 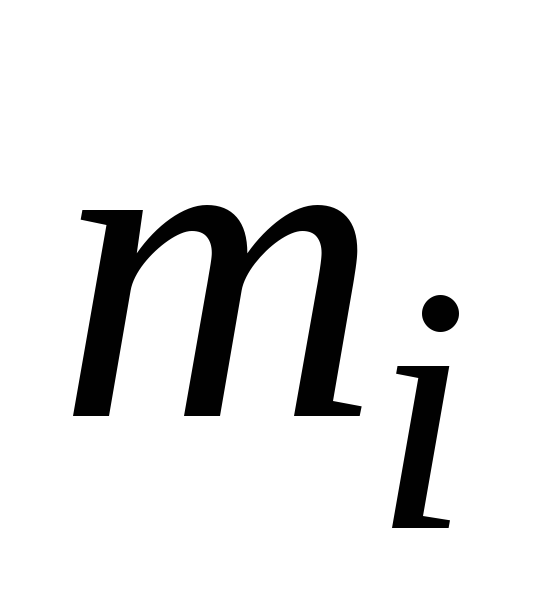 ,
а скорость этого элемента
,
а скорость этого элемента .
.Кинетическая энергия этого элемента
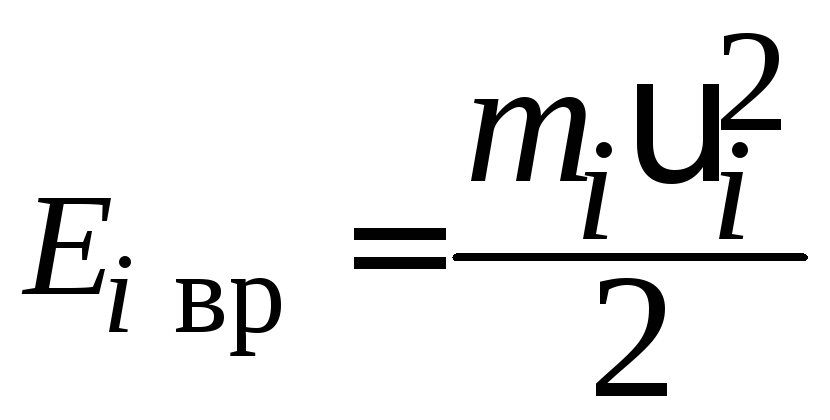 .
.
Просуммировав кинетическую энергию всех элементов, получим кинетическую энергию вращательного движения тела:
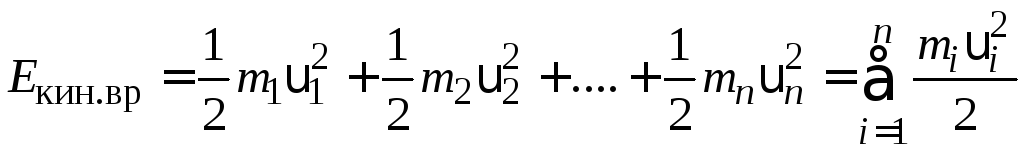 .
.
Линейная
скорость  связана с угловой скоростью вращения
тела
связана с угловой скоростью вращения
тела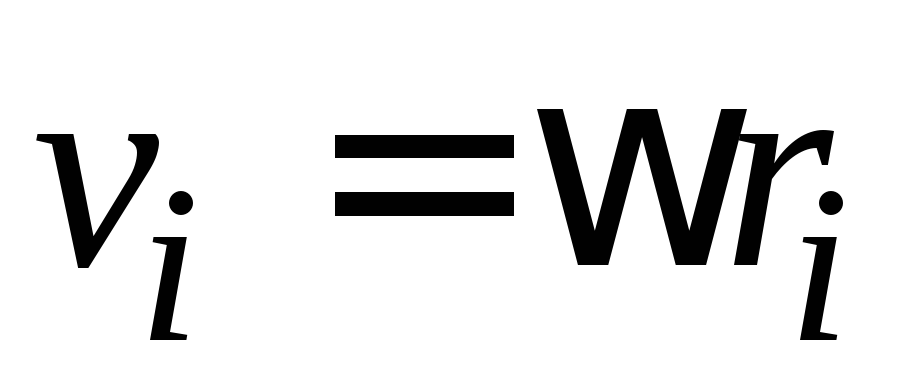 (
( постоянна
для всех точек тела).
постоянна
для всех точек тела).
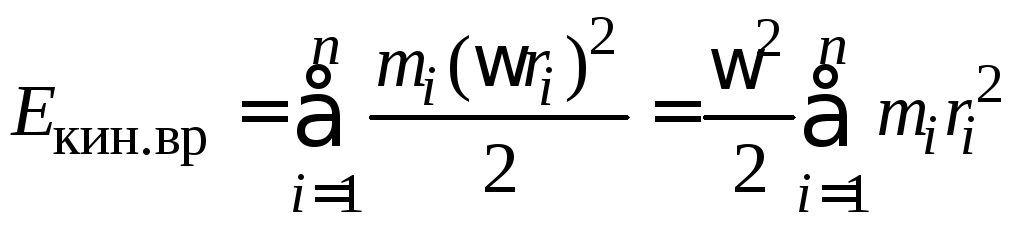 .
.
Определение. Моментом инерции материальной точки относительно оси z называется произведение массы этой точки на квадрат её расстояния от оси вращения:
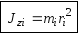
Определение. Моментом инерции твёрдого тела относительно некоторой оси z называется сумма моментов инерций материальных точек относительно данной оси.
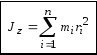
В соответствии с этими определениями:
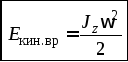
(Сравните
с выражением для кинетической энергии
поступательного движения 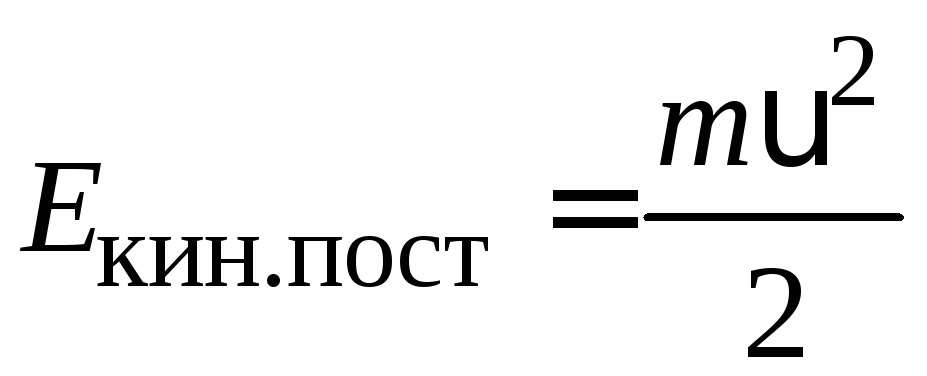 ,
очевидно соответствие
,
очевидно соответствие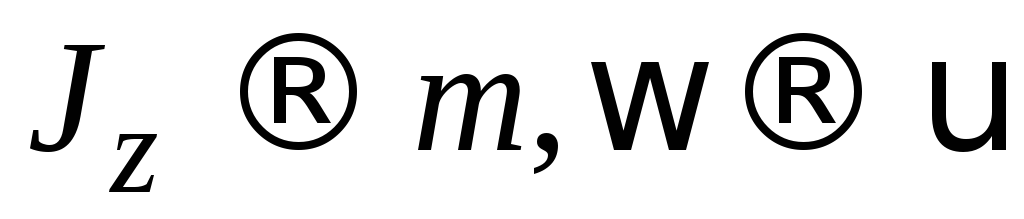 ).
).
Физический смысл момента инерции. Момент инерции во вращательном движении играет такую же роль, как масса при поступательном движении, характеризует меру инертности тела при вращательном движении. Чем больше момент инерции тела, тем труднее при прочих равных условиях привести его во вращательное движение. Момент инерции определяется не только массой, но и тем, как эта масса распределена относительно оси вращения.
Соотношение 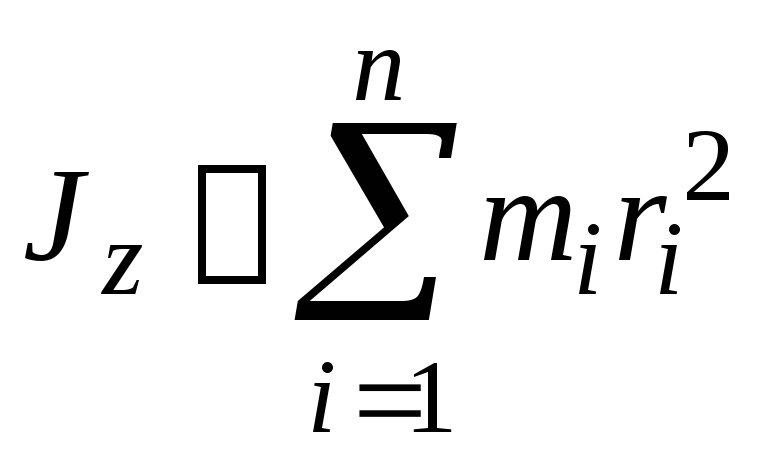 является приближённым, причём тем более
точным, чем меньше элементарные массы
является приближённым, причём тем более
точным, чем меньше элементарные массы .
Задача нахождения моментов инерции
сводится кинтегрированию.
.
Задача нахождения моментов инерции
сводится кинтегрированию.
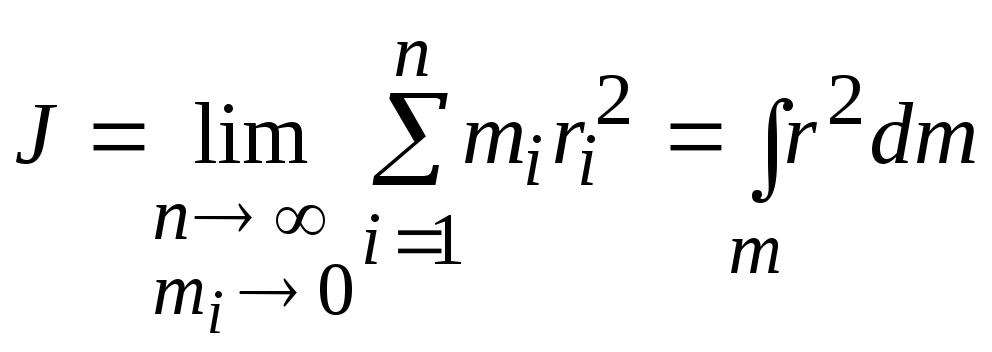
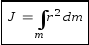
(Интегрирование
ведётся по всей массе тела  ).
).
3
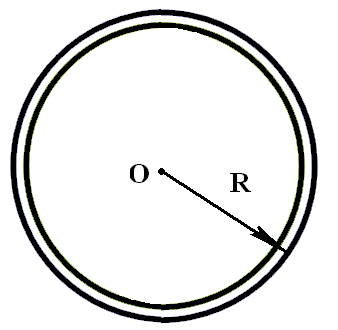
Рис. 3.3
. Вычисление моментов инерции. 1. Кольцо (полый цилиндр) (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии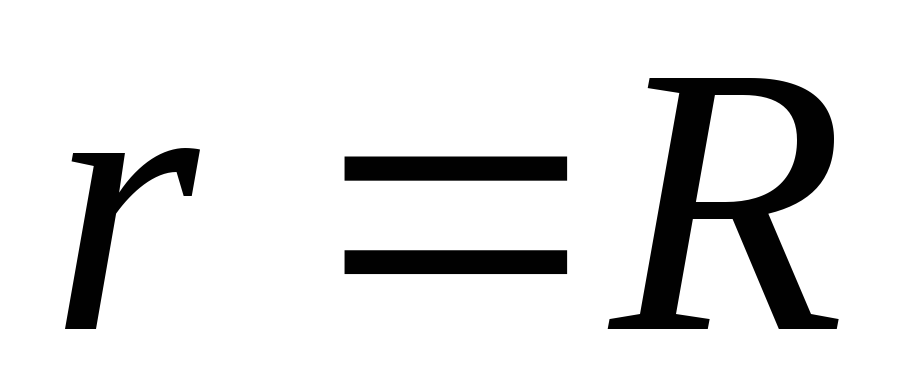 от центра.
от центра.Относительно оси, проходящей через центр кольца:
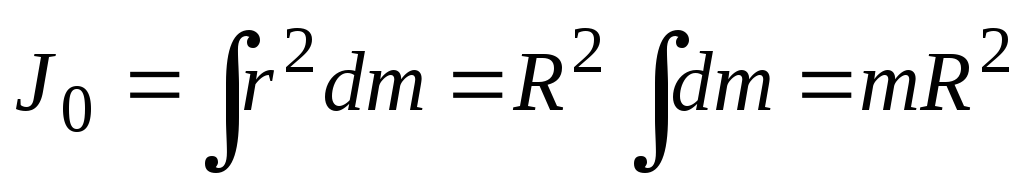 ,
,
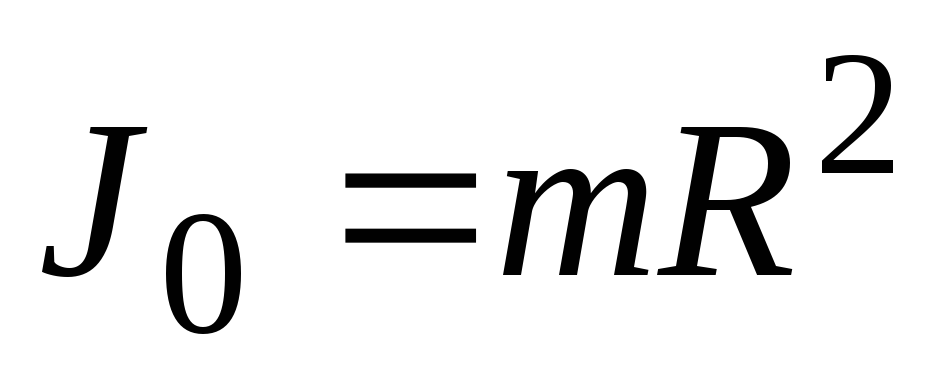 .
.
2. Однородный диск (сплошной цилиндр)
Дано:  радиус
диска,
радиус
диска,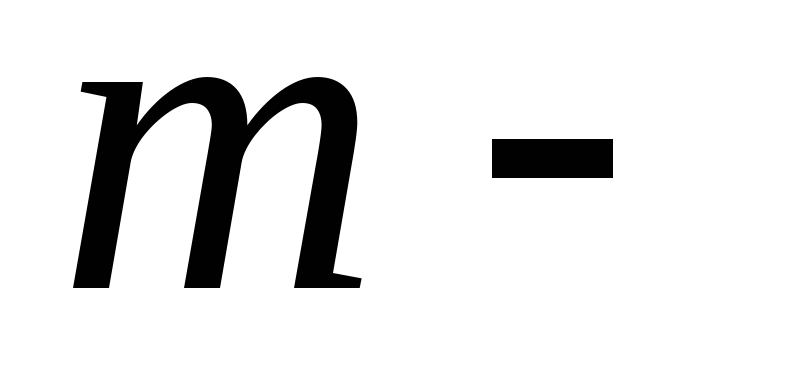 масса
диска.
масса
диска.
Найти: 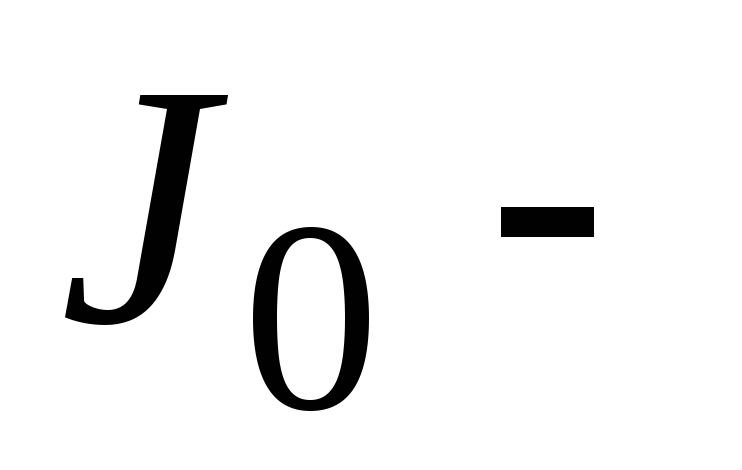 момент
инерции диска относительно оси, проходящей
через центр диска.
момент
инерции диска относительно оси, проходящей
через центр диска.
Разобьём
диск (рис. 3.4) на кольца с радиусом 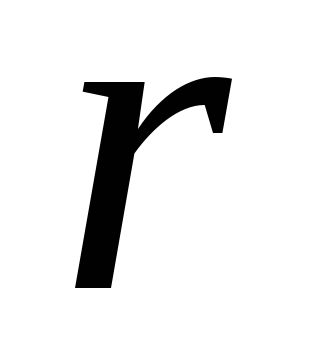 ,
толщиной
,
толщиной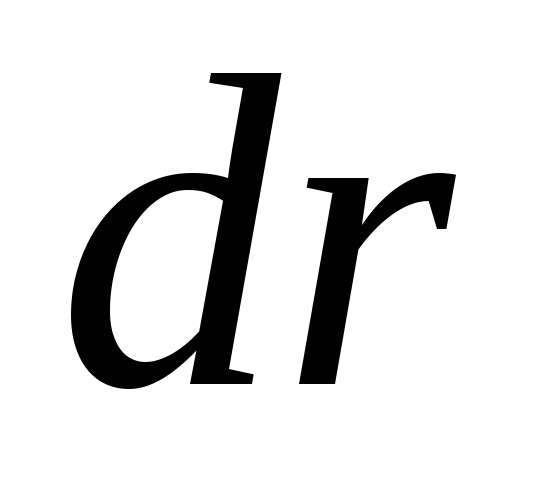 .
По определению момента инерции
.
По определению момента инерции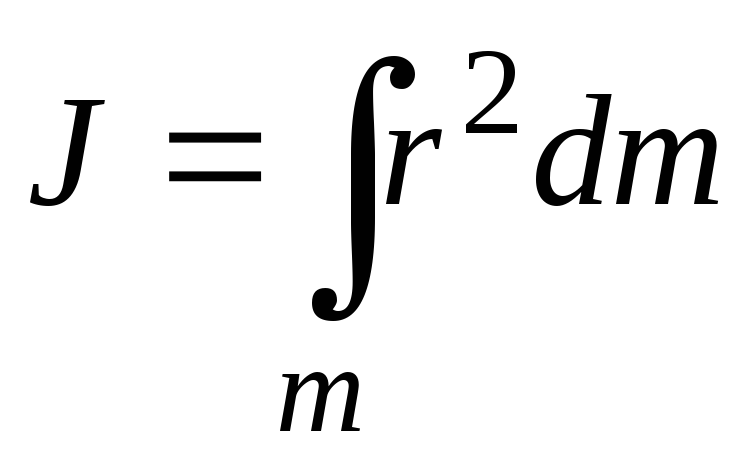 .
Пусть
.
Пусть поверхностная
плотность диска
поверхностная
плотность диска ,
тогда масса кольца
,
тогда масса кольца ,
где
,
где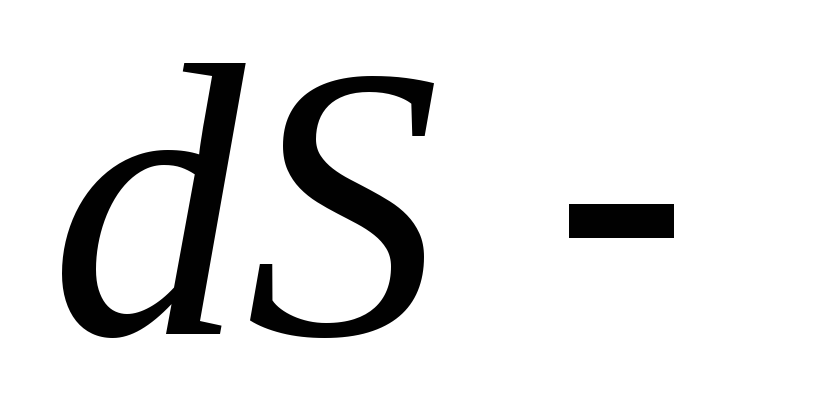 площадь
кольца,
площадь
кольца,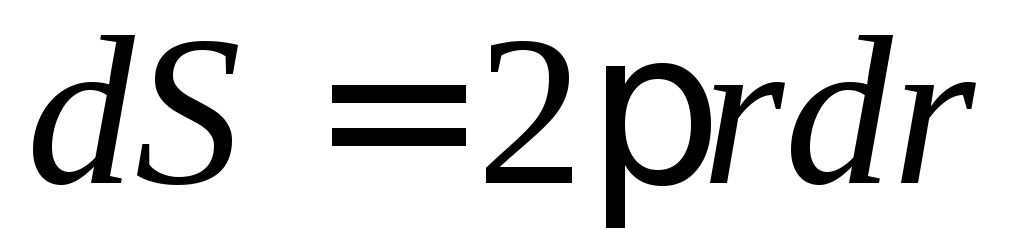 .
Интегрируя по радиусу, находим момент
инерции диска:
.
Интегрируя по радиусу, находим момент
инерции диска:
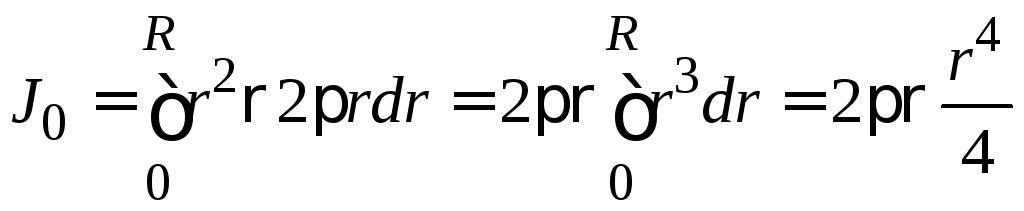

 =
=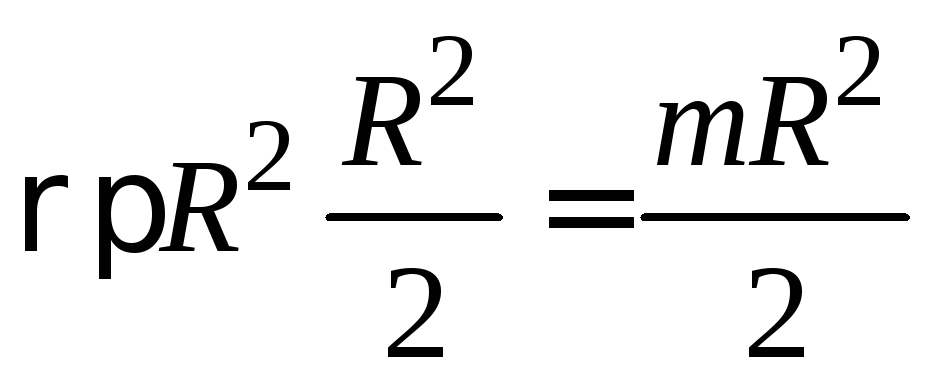 ,
,
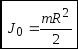
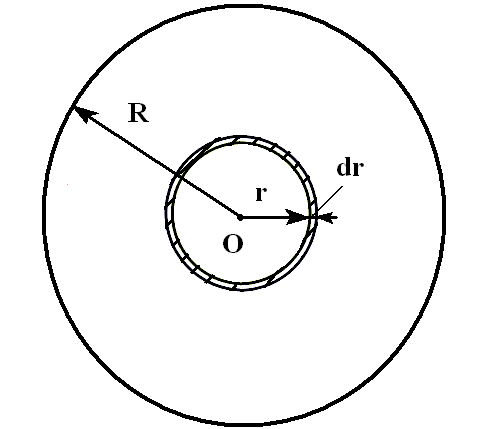
Рис. 3.4
3. Тонкий однородный стержень
Дано: 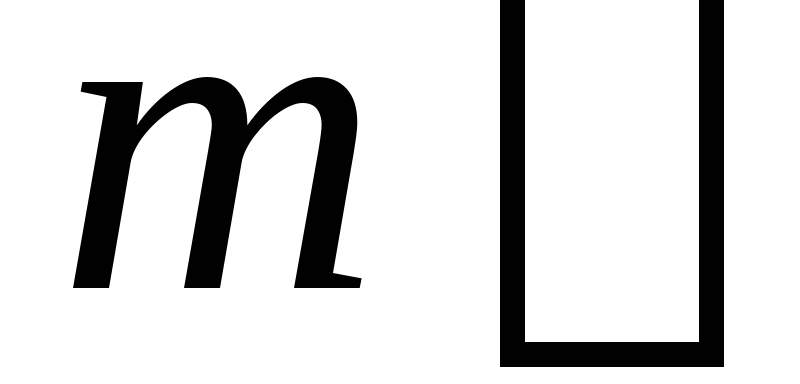 масса
стержня,
масса
стержня,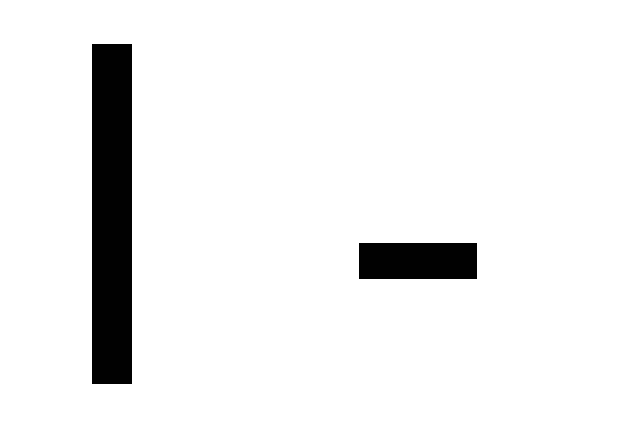 длина
стержня.
длина
стержня.
Найти: 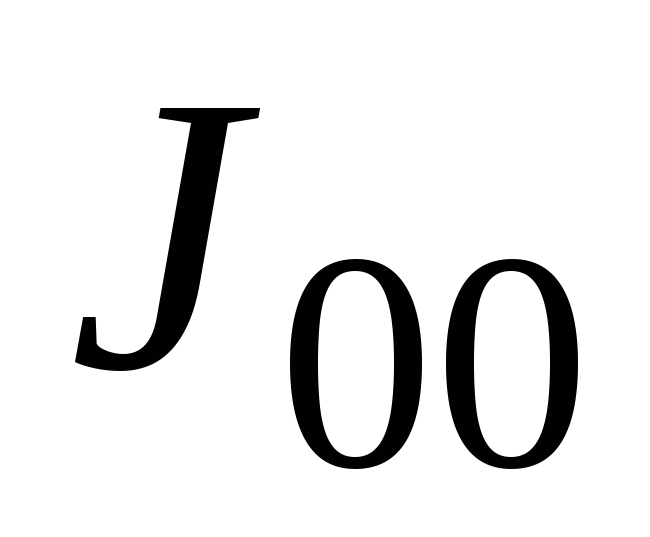 (момент инерции относительно осиОО, проходящей через конец стержня
перпендикулярно ему) (рис. 3.5).
(момент инерции относительно осиОО, проходящей через конец стержня
перпендикулярно ему) (рис. 3.5).
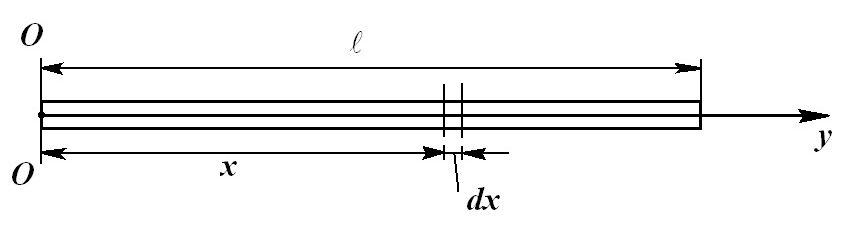
Рис. 3.5
Ввиду
одномерного характера задачи выражение 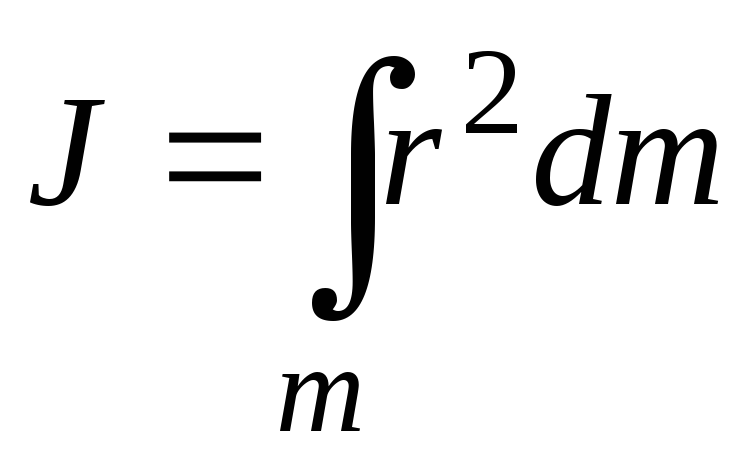 можно заменить на
можно заменить на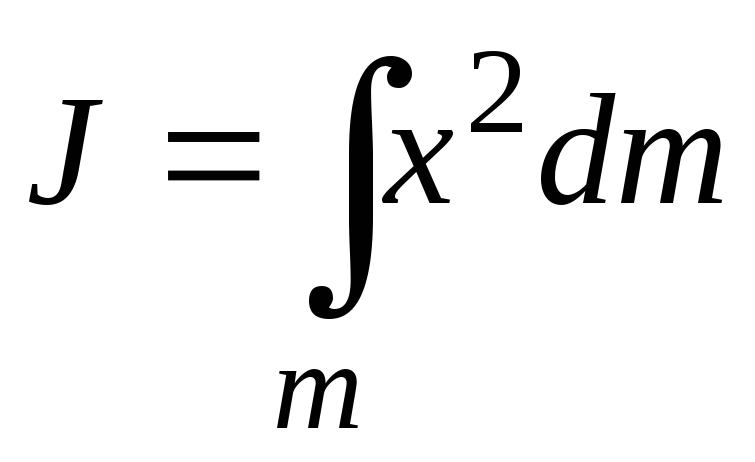 ,
где
,
где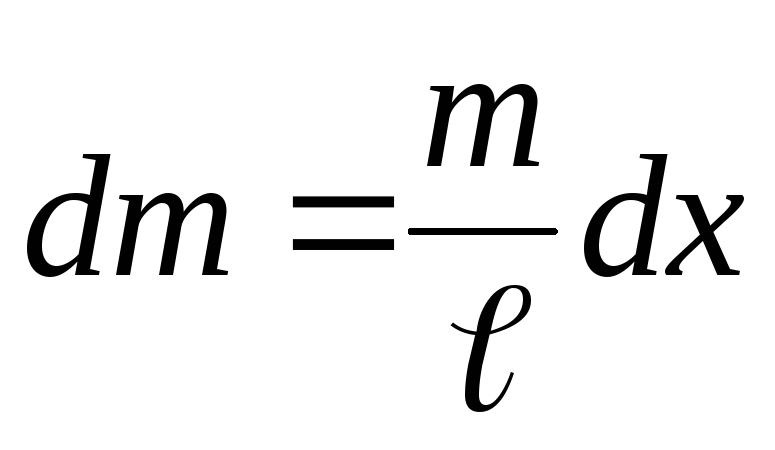 ,
тогда
,
тогда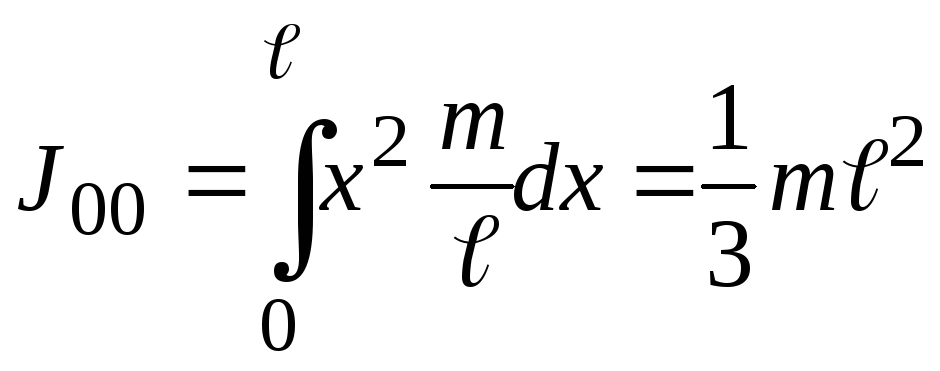 .
.
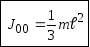
Теорема Штейнера (без вывода)
П
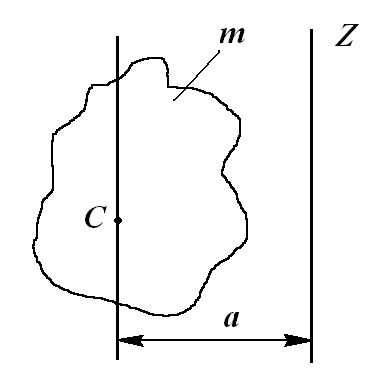
Рис. 3.6
остановка задачи. Известен момент инерции произвольного тела массой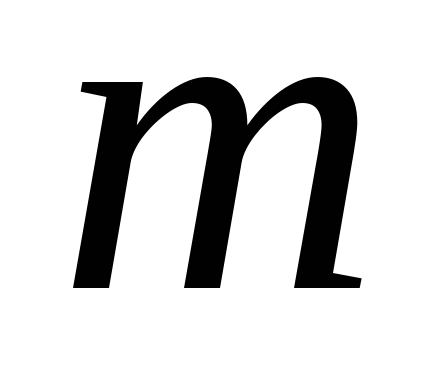 относительно оси, проходящей через его
центр тяжести
относительно оси, проходящей через его
центр тяжести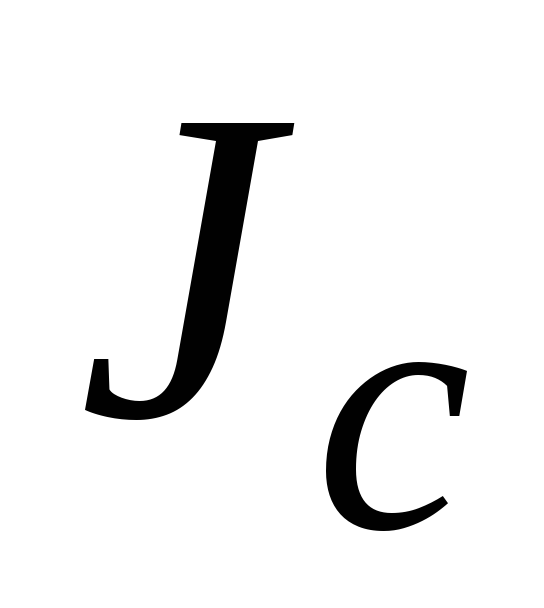 (рис. 3.6).Требуется
найти,
каков момент инерции
(рис. 3.6).Требуется
найти,
каков момент инерции 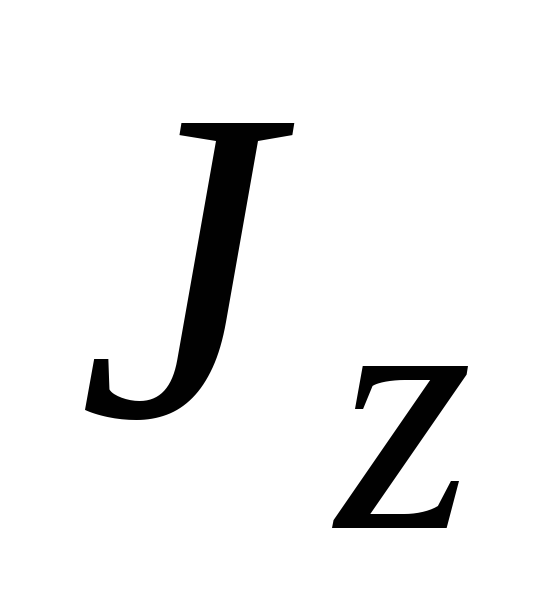 относительно какой-либо оси
относительно какой-либо оси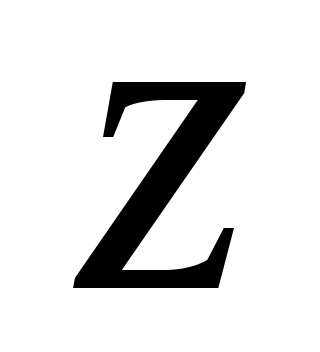 ,
параллельной первой и находящейся на
расстоянии
,
параллельной первой и находящейся на
расстоянии от неё.
от неё.Теорема. Момент инерции тела относительно произвольной оси z равен сумме момента инерции относительно оси, проходящей через центр масс тела С и параллельной данной, и произведения массы тела на квадрат расстояния между осями a:
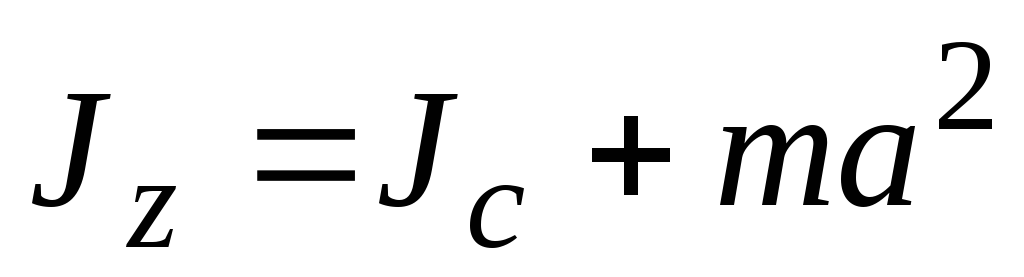 .
.
Пример применения теоремы Штейнера.
Требуется найти момент
инерции тонкого однородного стержня массой 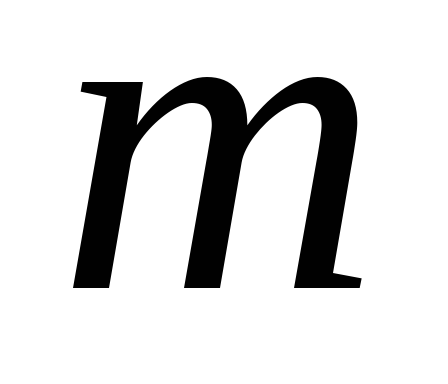 и длиной
и длиной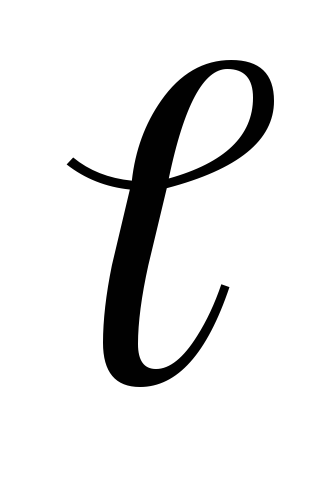 относительно перпендикулярной к нему оси
относительно перпендикулярной к нему оси  ,
проходящейчерез
центр стержня (рис.
3.7).
,
проходящейчерез
центр стержня (рис.
3.7).
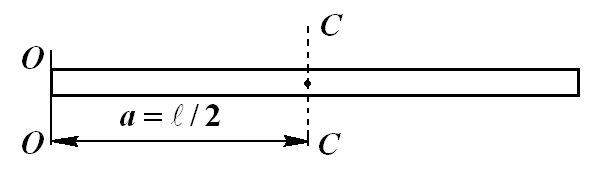
Рис. 3.7
Решение:
Воспользуемся полученным ранее выражением для момента инерции стержня относительно оси, проходящей через его конец:
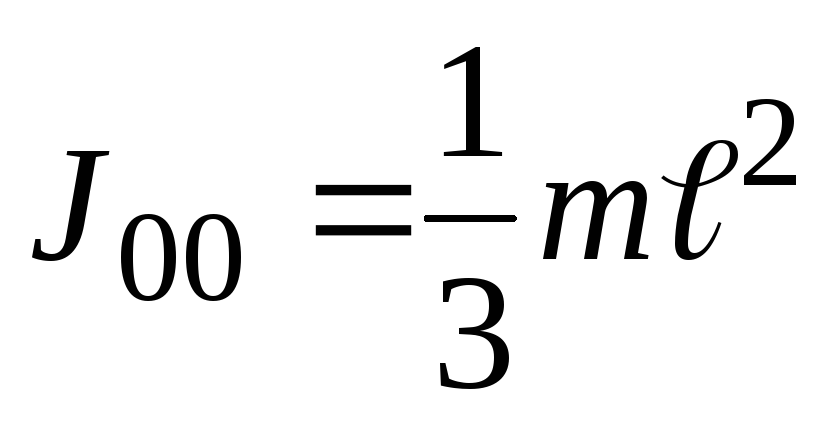 .
Используя теорему Штейнера, получаем:
.
Используя теорему Штейнера, получаем:
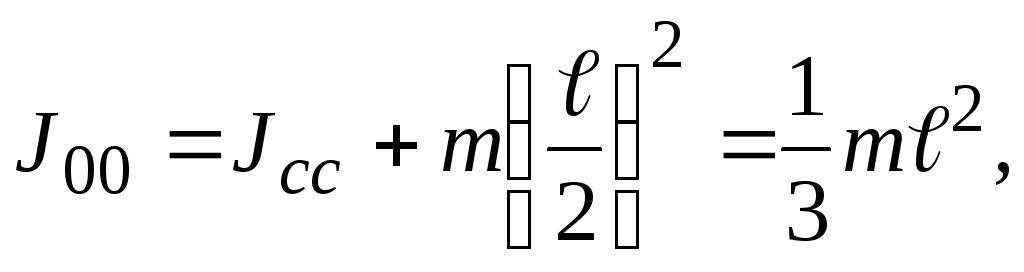 отсюда
отсюда 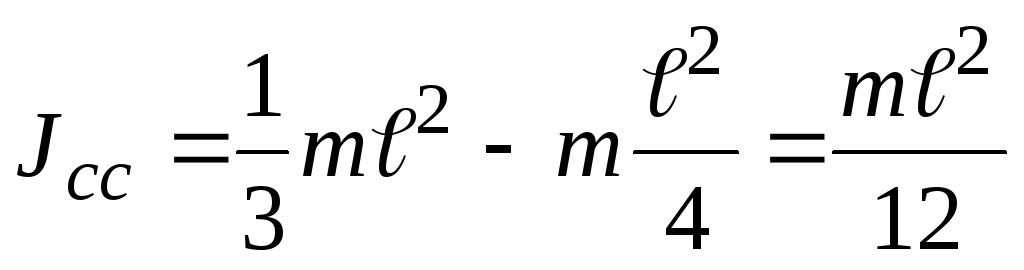 .
.
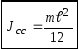
Момент инерции. Свойство аддитивности. Теорема Штейнера. Свободные оси вращения. Понятие о гироскопе его применениях.
Момент инерции тела относительно некоторой оси при вращательном движении представляет собой меру инертности системы.
Величина момента инерции зависит от распределения массы.
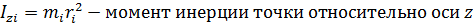
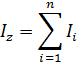
Если тело протяжённое, то суммарный момент инерции рассчитывается путём замены суммы на интеграл.
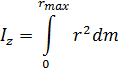
Свойство аддитивности: момент инерции системы МТ относительно некоторой оси равен сумме моментов инерции тел или частей системы (МТ) относительно этой оси.
Теорема Гюйгенса-Штейнера: момент инерции 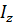 тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси
тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси 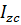 , проходящей через центр масс, и произведения массы тела на квадрат расстояния d между этими осями.
, проходящей через центр масс, и произведения массы тела на квадрат расстояния d между этими осями.
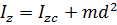
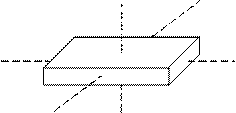 Любое тело произвольной формы имеет три взаимно перпендикулярных оси, проходящих через центр масс, которые называют свободными осями вращения, илиглавными осями инерции.
Любое тело произвольной формы имеет три взаимно перпендикулярных оси, проходящих через центр масс, которые называют свободными осями вращения, илиглавными осями инерции.
Например, для параллелепипеда главными осями инерции являются три оси, которые проходят через центры противоположных граней.
Свойство свободных осей сохранять своё положение в пространстве используется в гироскопах.
Гироскопы представляют собой массивные однородные тела, которые с большой угловой скоростью вращаются вокруг своей оси симметрии, которая является свободной осью. Сила тяжести не может изменить ориентацию оси вращения, так как сила приложена к центру масс, и момент силы относительно центра масс равен нулю. Таким образом, как ни вращать гироскоп, направление его оси вращения
останется неизменным в пространстве. Простейший пример гироскопа — юла. Гироскопы используются в навигации (авиагоризонт, гирокомпас) и в системах ориентации и стабилизации космических аппаратов.
Работа при поступательном и вращательном движении. Мощность.
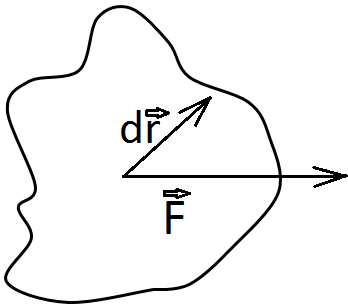
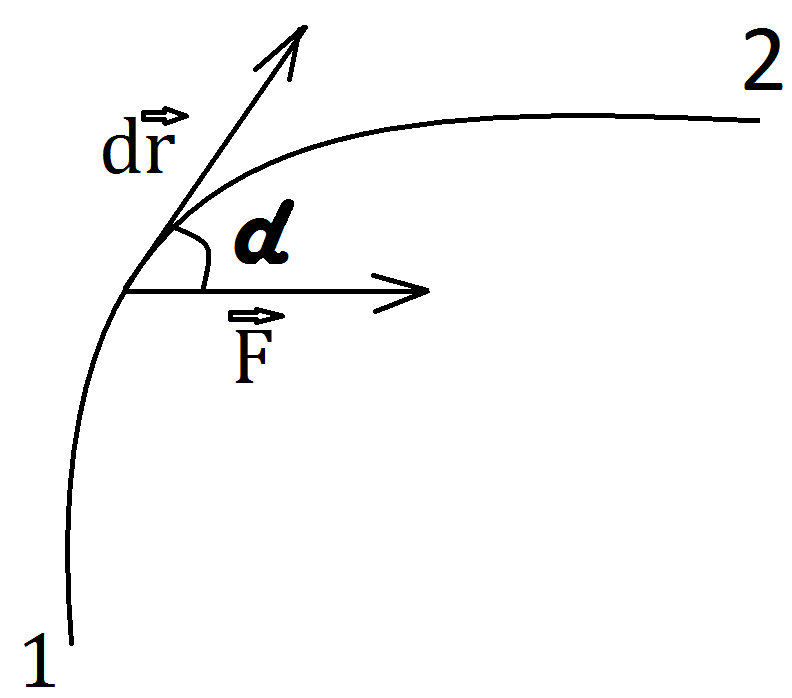 Если сила, действующая на тело, перемещает его на некоторое расстояние, то говорят, что сила совершает работу.
Если сила, действующая на тело, перемещает его на некоторое расстояние, то говорят, что сила совершает работу.
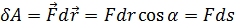
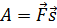
Вывод о том, какова будет величина работы:
1. Если угол между направлениями силы и перемещения лежит в пределах 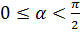 , то сила будет называться движущей, а работа будет положительной
, то сила будет называться движущей, а работа будет положительной 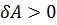 .
.
2. Если 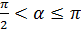 , то сила – тормозящая, а работа отрицательна
, то сила – тормозящая, а работа отрицательна 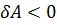 .
.
3. Если 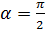 (сила перпендикулярна перемещению) ,то работа не совершается
(сила перпендикулярна перемещению) ,то работа не совершается 
Чтобы найти полную работу (при поступательном движении), необходимо произвести интегрирование:
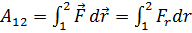
Выражение, которое мы получили для МТ, можно применять и для абсолютно твёрдого тела. В этом случае под величиной перемещения следует понимать перемещение точки приложения сил.
Если на тело действует одновременно несколько сил, то каждая из них совершает работу, а суммарная работа равна сумме работ приложенных сил.
Работа при вращательном движении:
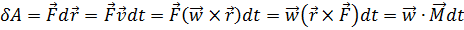
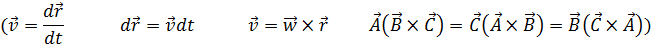
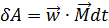
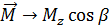
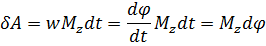
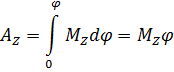
Скорость работы определяется мощностью. Мощность – это работа, совершаемая в единицу времени.
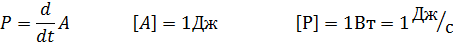
Силы инерции твердого тела в частных случаях его движения
При
поступательном движении. Если твердое тело движется поступательно,
то ускорения его точек одинаковы. Силы
инерции этих точек составляют систему
параллельных сил, направленных в одну
сторону. Такая система сил приводится
к равнодействующей силе  ,
которая равна главному вектору, т. е.
,
которая равна главному вектору, т. е.
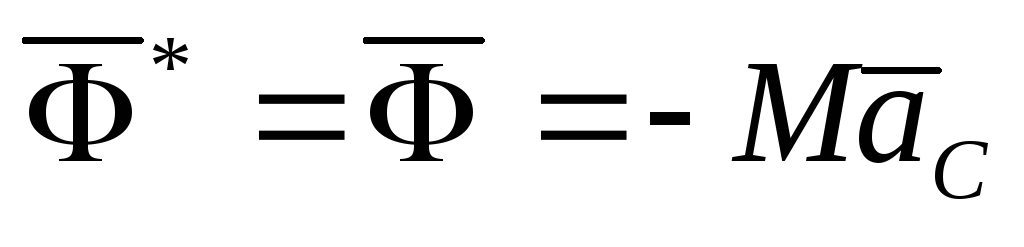 .
.
Линия действия равнодействующей силы инерции в этом случае проходит через центр масс, так как главный момент сил инерции точек тела относительно центра масс
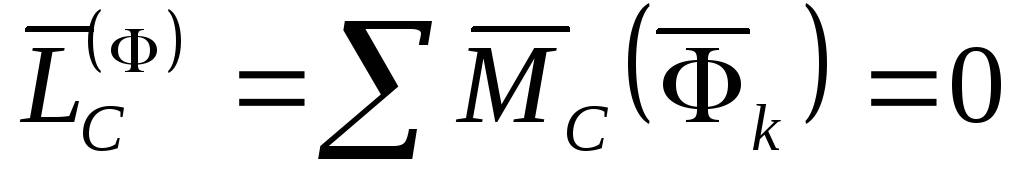 .
.
Действительно, согласно следствию из принципа Даламбера (12) для центра масс, имеем
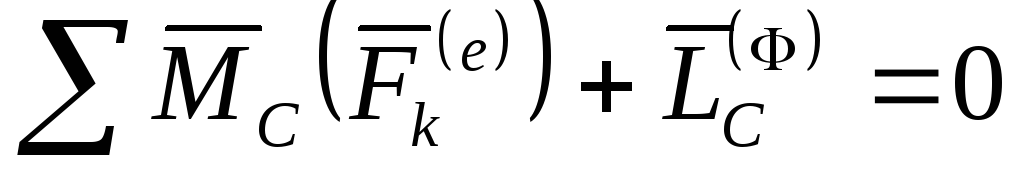 .
.
При
поступательном движении тело не совершает
вращения вокруг центра масс и поэтому 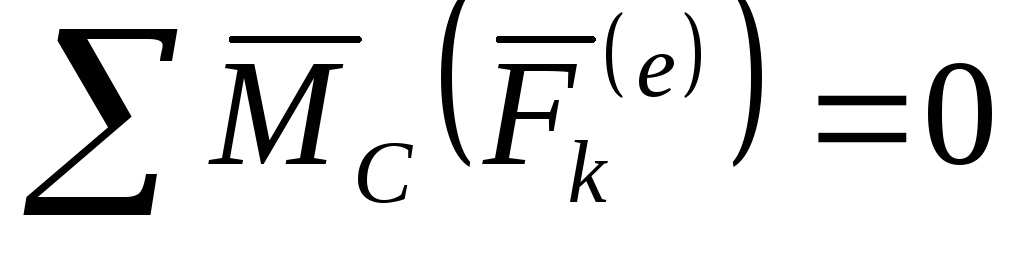 .
Следовательно,
.
Следовательно,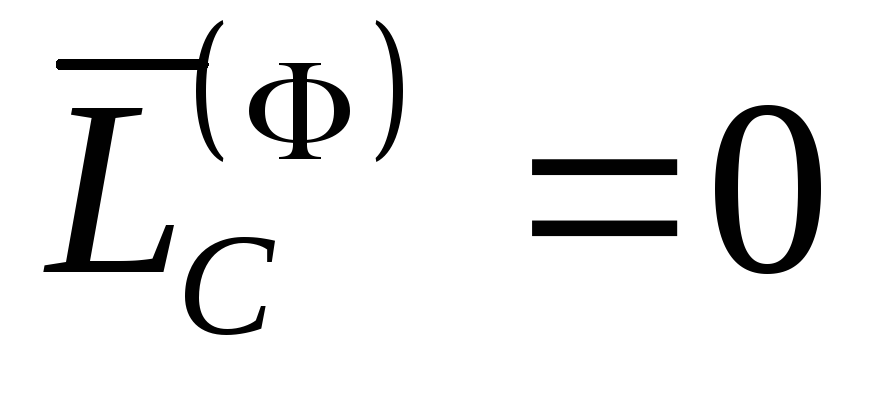
При
вращении вокруг неподвижной оси. Если выбрать за центр приведения сил
инерции точку  на оси вращения
на оси вращения ,
то в этой точке получим главный вектор
и главный момент сил инерции:
,
то в этой точке получим главный вектор
и главный момент сил инерции:
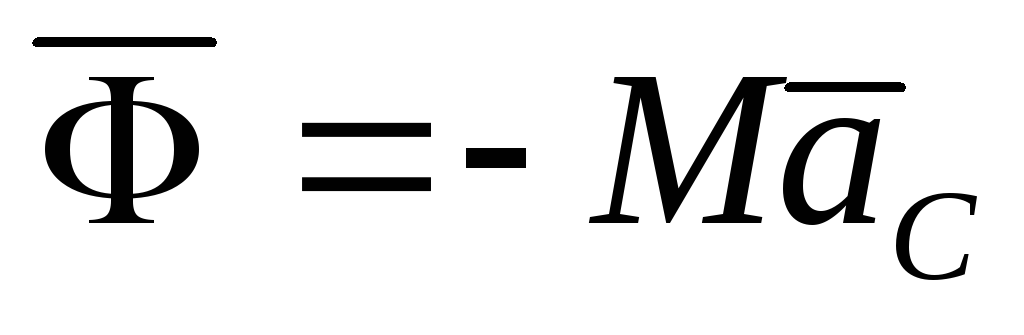 ,
, 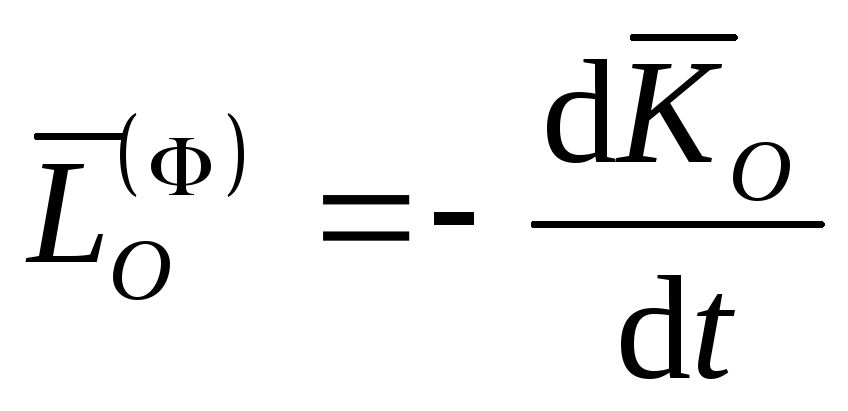 .
.
Если
центр масс находится на оси вращения,
то 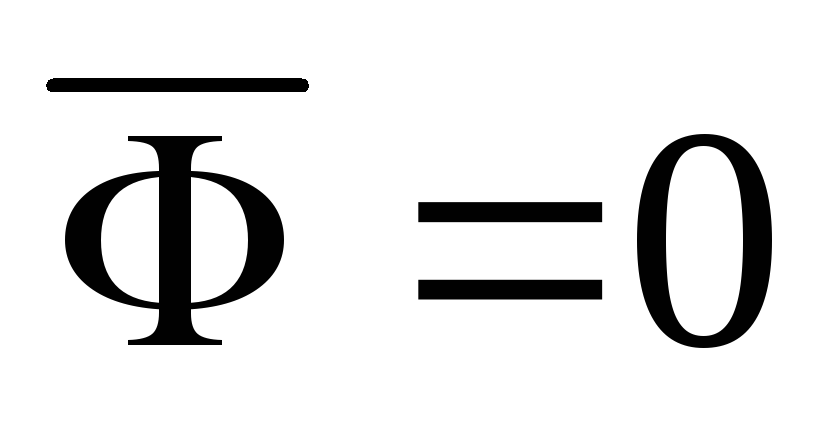 .
Проекции главного момента сил инерции
на неподвижные оси координат в общем
случае можно вычислить по формулам
.
Проекции главного момента сил инерции
на неподвижные оси координат в общем
случае можно вычислить по формулам
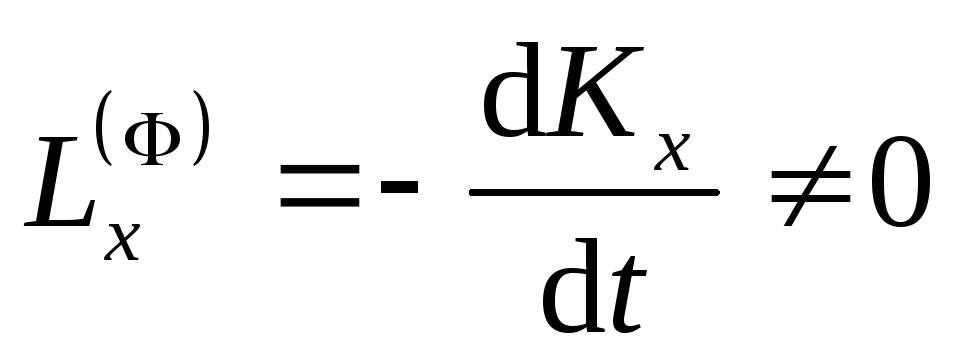 ,
, 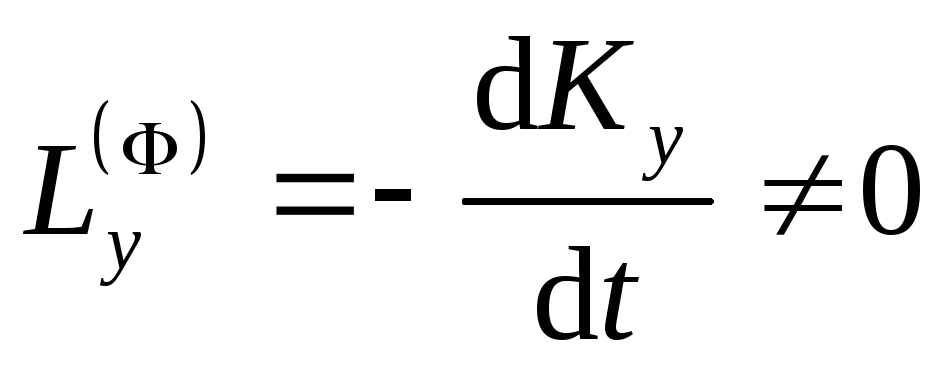 ,
,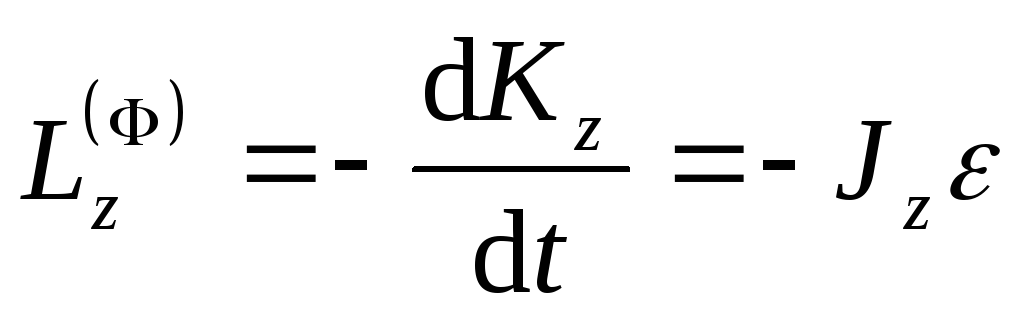 .
.
(Моменты
сил инерции 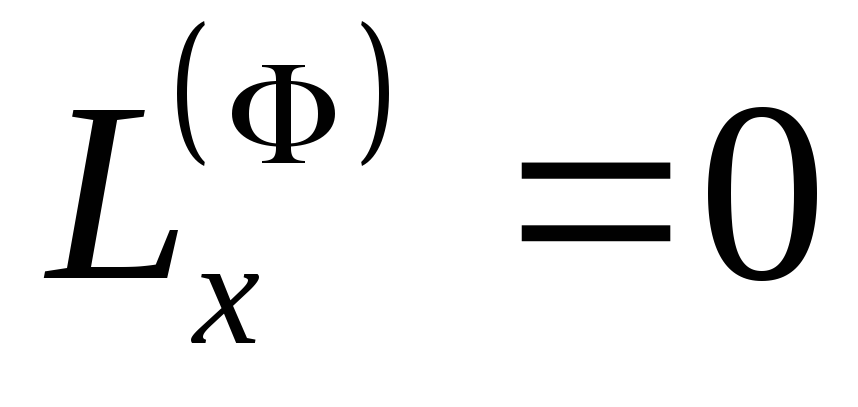 и
и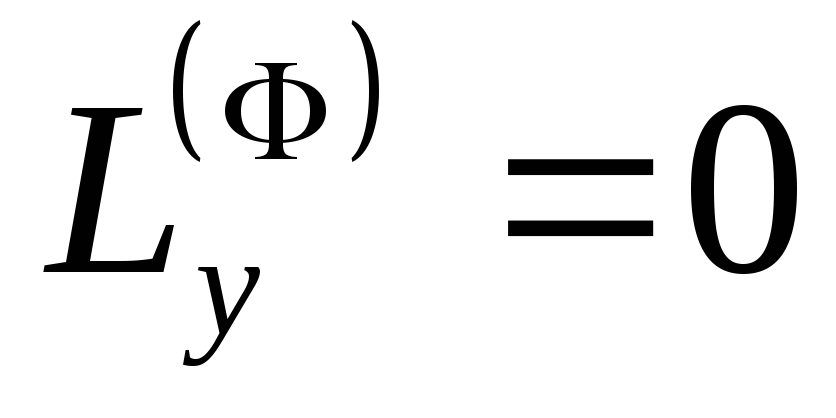 ,
если ось
,
если ось является главной осью инерции для точки
является главной осью инерции для точки .)
.)
При плоском движении. Выбрав за центр приведения сил инерции центр масс, получим в этой точке главный вектор и главный момент сил инерции. Для главного вектора сил инерции имеем
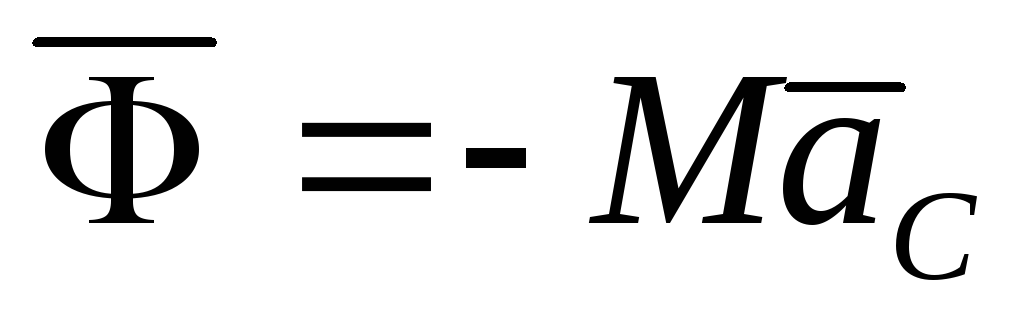 .
.
Для
данного момента сил инерции относительно
центра масс  ,
который является движущейся точкой при
плоском движении тела, получим формулы,
аналогичные формуле (149), выведенной для
неподвижной точки
,
который является движущейся точкой при
плоском движении тела, получим формулы,
аналогичные формуле (149), выведенной для
неподвижной точки .
.
Согласно следствию из принципа Даламбера (147), главный момент сил инерции относительно центра масс удовлетворяет условию
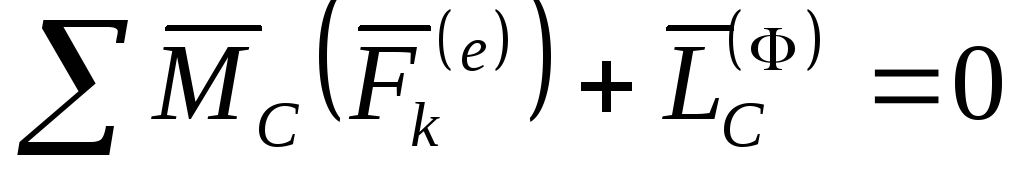 .
.
С другой стороны, из теорем об изменении кинетического момента относительно центра масс для абсолютного и относительного движений имеем
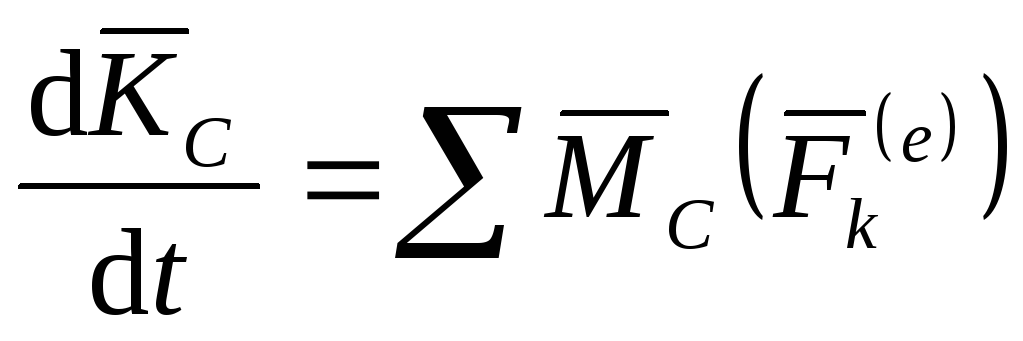 ,
, 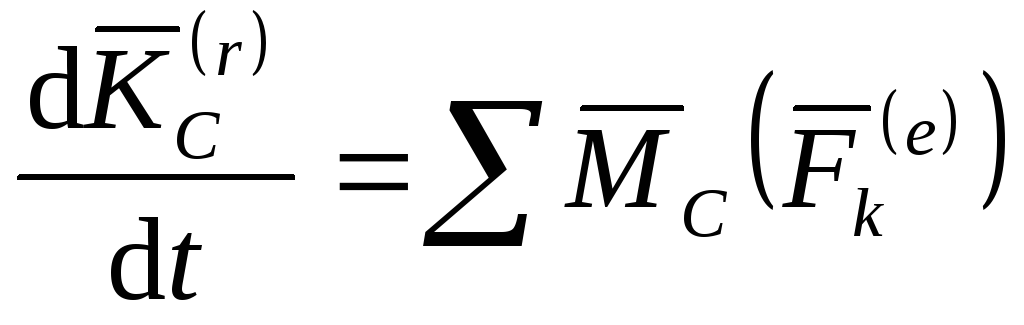 .
.
Из этих соотношений следует
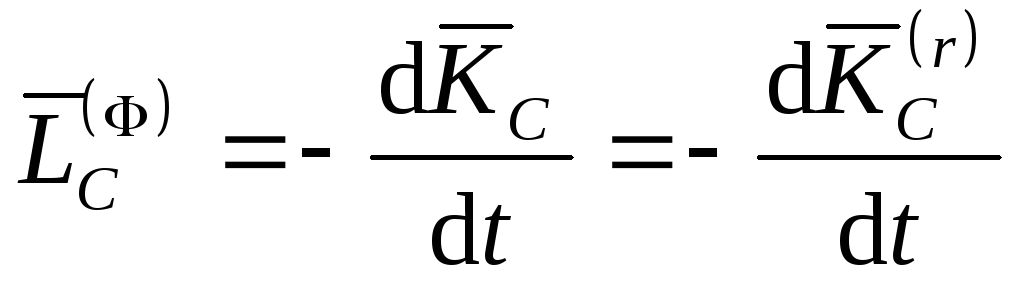 .
.
Проекции главного момента на оси координат с началом в центре масс и движущиеся поступательно вместе с центром масс соответственно
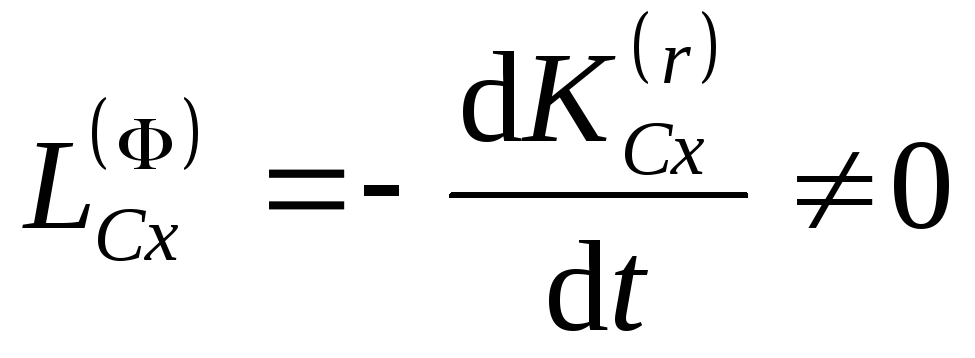 ,
, 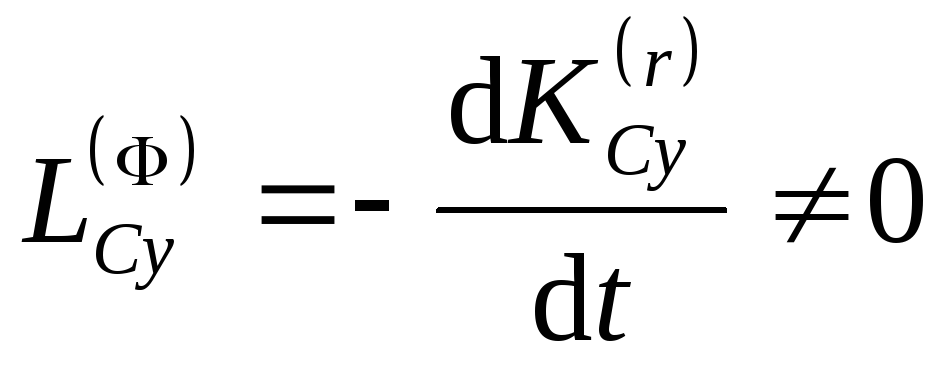 ,
,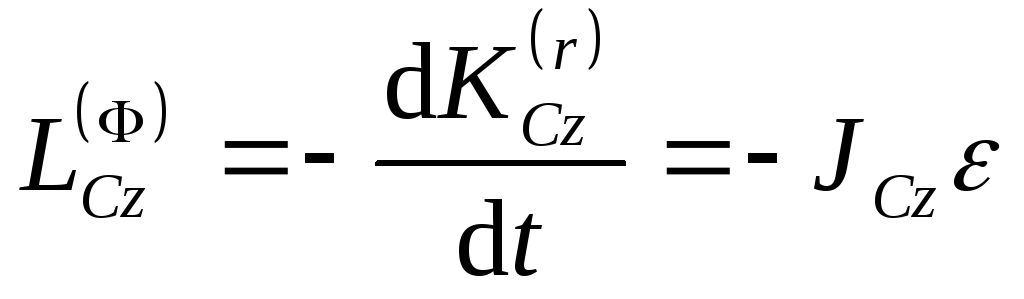 ,
,
где
ось  перпендикулярна плоскости, параллельно
которой совершают движение точки тела.
перпендикулярна плоскости, параллельно
которой совершают движение точки тела.
Моменты
сил инерции 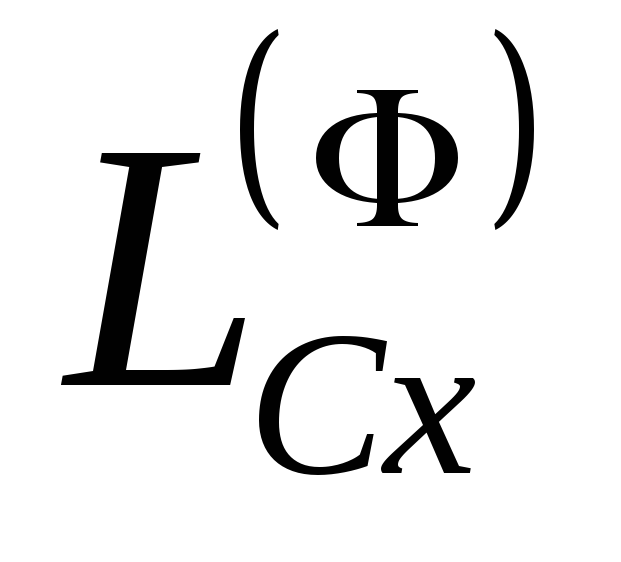 и
и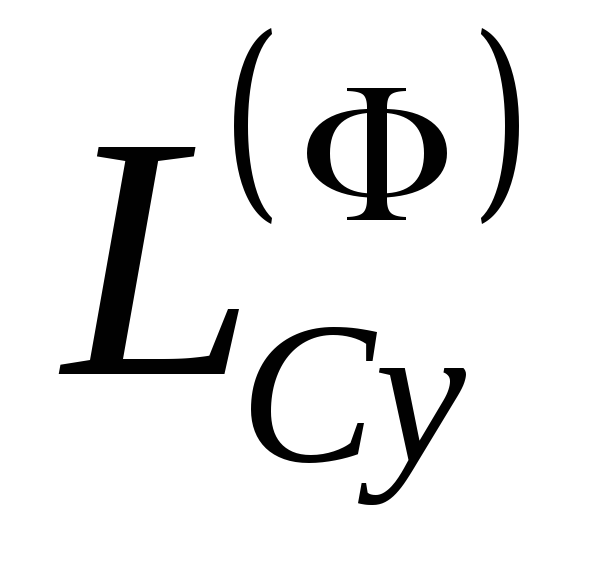 вычисляются так же, как и при вращении
тела вокруг неподвижной оси. Они равны
пулю, если ось
вычисляются так же, как и при вращении
тела вокруг неподвижной оси. Они равны
пулю, если ось является главной осью инерции для точки
является главной осью инерции для точки .
Это, в частности выполняется, если тело
имеет плоскость симметрии, проходящую
через центр масс и параллельную плоскости
движения тела.
.
Это, в частности выполняется, если тело
имеет плоскость симметрии, проходящую
через центр масс и параллельную плоскости
движения тела.
Лекция № 9
3.6. Элементы аналитической механики
3.6.1. Классификация механических связей
В аналитической механике необходимо более подробно рассмотреть связи, налагаемые на точки механической системы. Механической системой, как известно, называют любую совокупность материальных точек. Условия, ограничивающие свободу перемещения точек механической системы, называются связями. Математически связи могут быть выражены уравнениями или неравенствами, в которые входят время, координаты всех или части точек системы и их производные но времени различных порядков. Для одной точки уравнение связи в общем случае можно выразить в форме
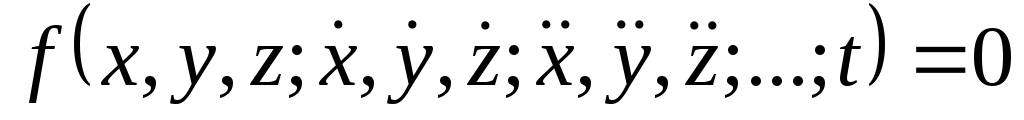 . (217)
. (217)
В дальнейшем ограничимся рассмотрением связей, в уравнения которых могут входить производные по времени от координат не выше первого порядка.
Для
механической системы, состоящей из 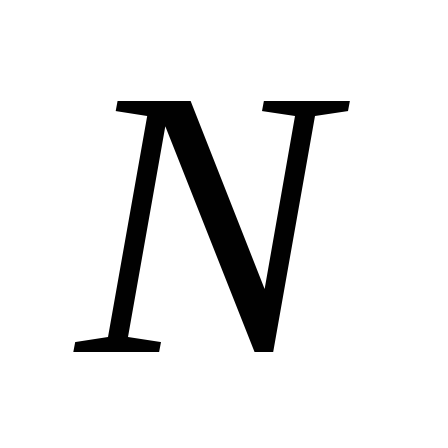 точек,
точек,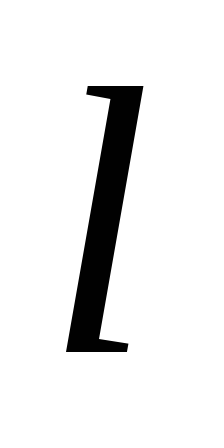 уравнений связей представятся системой
уравнений
уравнений связей представятся системой
уравнений
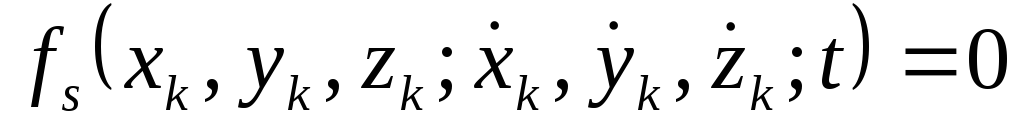 ,
, 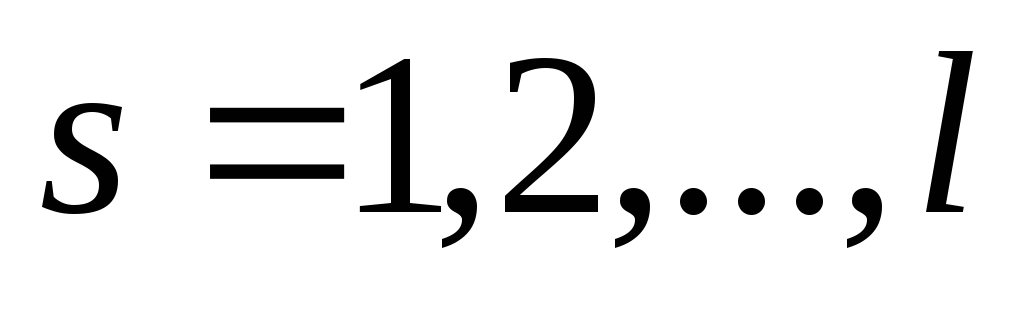 . (218)
. (218)
Считается,
что индекс  принимает все или часть значений от 1
до
принимает все или часть значений от 1
до как для координат, так и для их производных.
как для координат, так и для их производных.
Если в уравнения связей (218) входят только координаты точек и не входят производные от координат, то связи называются геометрическими.
Если в уравнения связей кроме координат входят еще и их производные по времени (проекции скоростей точек на оси координат) или только одни производные, кроме времени, то связи называются кинематическими.
Все геометрические и интегрируемые кинематические связи называются голономными. Неинтегрируемые кинематические связи, которые нельзя свести к геометрическим, являются неголономными.
Связи, в уравнения которых время явно не входит, называются стационарными или склерономными. Если время входит явно в уравнение связи, то связь называется нестационарной и реономной.
Связи называют неосвобождающими или двусторонними, если они выражаются математически уравнениями, и освобождающими или односторонними, если они выражаются неравенствами.
Все связи можно разделить на реальные и идеальные. К идеальным связям относятся все связи без трения. Некоторые связи с трением тоже относятся к идеальным. Понятие идеальных связей дается после введения понятия возможного перемещения системы.
3.3.3. Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета (сила Кориолиса)
При движении тела относительно вращающейся системы отсчета, кроме центробежной силы инерции, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции. Рассмотрим проявление этой силы на одном частном примере.
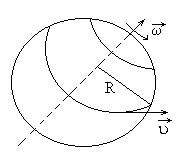
Рис.3.5
Относительно вращающейся системы отсчета тело движется по окружности, лежащей в плоскости, перпендикулярной к оси вращения, причем центр окружности лежит на этой оси. Такой случай реализуется, например, когда тело движется вдоль параллели (экватора) по поверхности вращающегося земного шара (рис.3.5).Относительно неподвижной (инерциальной) системы тело движется равномерно по окружности радиуса R. Так что ускорение тела в этой системе (центростремительное) может быть представлено в виде
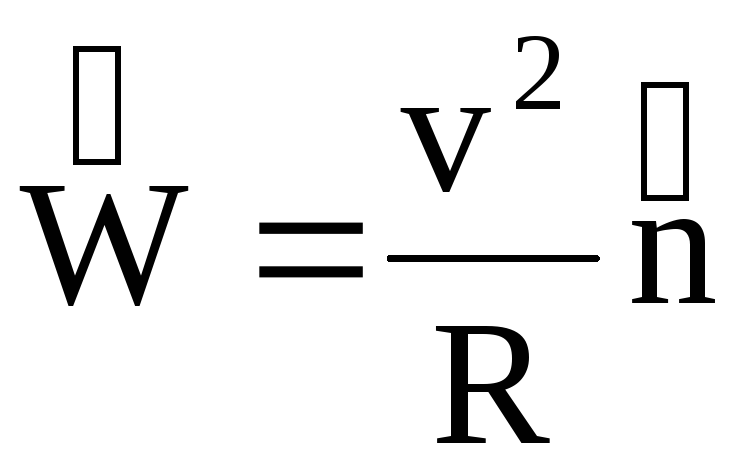 , (3.31)
, (3.31)
где 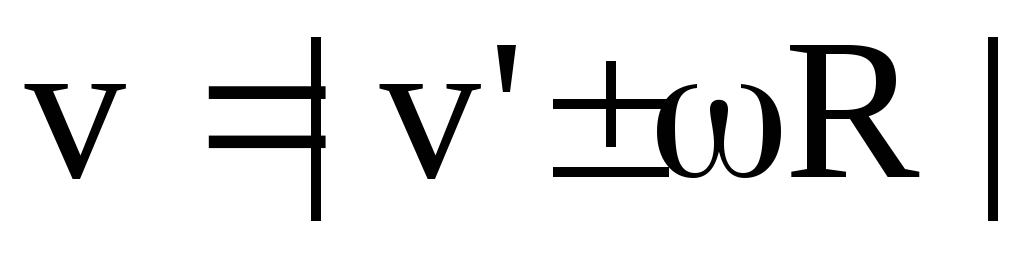 .
.
После выполнения простых преобразований получим
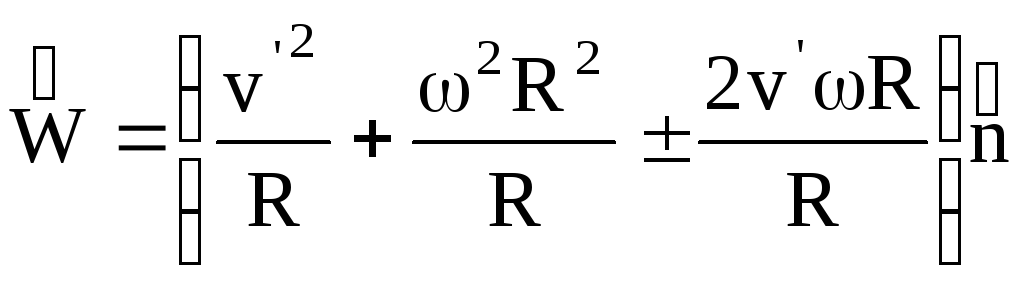 или
или 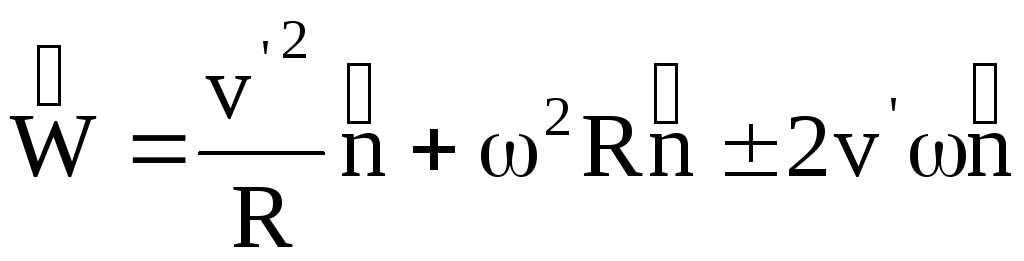 . (3.32)
. (3.32)
По отношению к вращающейся системе тело обладает центростремительным ускорением
 .
(3.33)
.
(3.33)
Откуда
следует, что первое слагаемое в (3.32)
представляет собой ускорение  .
Следовательно,
.
Следовательно,
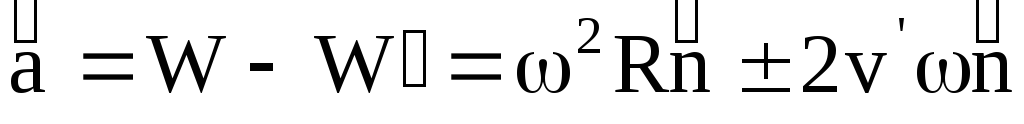 . (3.34)
. (3.34)
В соответствии с этим выражением сила инерции оказывается состоящей из двух компонент:
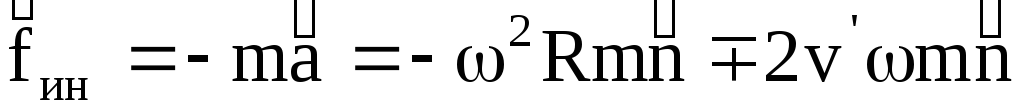 . (3.35)
. (3.35)
Первая
из них есть центробежная сила инерции  ,
вторая – кориолисова сила
,
вторая – кориолисова сила .
Сила
.
Сила имеет направление:
имеет направление:
а) от центра, если скорости v’ и R совпадают по направлению;
б) к центру, если скорости v и R направлены в противоположные стороны.
В общем случае, когда вектор скорости v материальной точки, перемещающейся по вращающейся поверхности, направлен произвольно, математическое выражение силы Кориолиса таково:
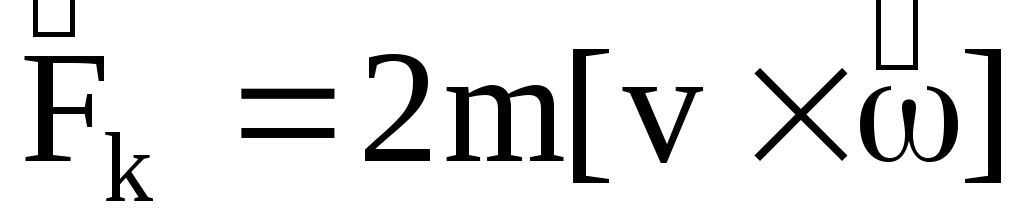 .
(3.36)
.
(3.36)
Вектор Fк перпендикулярен векторам скорости v’ тела и угловой скорости вращения ω системы отсчета в соответствии с правилом правого винта.
В таблице 3.1 наглядно показаны силы инерции, возникающие в зависимости от состояния частицы в неинерциальной системе отсчета и характера движения этой системы относительно инерциальной системы отсчета.
Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Поэтому действием этих сил объясняется ряд наблюдаемых на Земле явлений (подмывание берегов рек; неравномерное изнашивание железнодорожных рельсов; отклонение падающих на поверхность Земли тел; поведение маятника Фуко, явившееся в свое время одним из доказательств вращения Земли). Применительно к рассмотренному выше случаю движения можно привести такой пример: при стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в направлении на запад (т.е. в направлении, противоположном вращению Земли), и поднимать кверху, если выстрел произведен в восточном направлении.
Таким образом, основной закон динамики для неинерциальных систем отсчета можно записать в виде
ma’ = F + Fин + Fц +Fк, (3.37)
где F, Fин, Fц, Fк — ранее рассмотренные силы, действующие в неинерциальных системах отсчета.
Силы инерции, возникающие в неинерциальной системе отсчета в зависимости от состояния частицы
Таблица 3.1
Состояние частицы в неинерциальной
системе | Название и математическое выражение силы инерции | Характер
движения |
Частица находится в покое | Сила инерции | Система прямолинейно
с ускорением |
Центробежная сила инерции | Система | |
Частица
движется со скоростью | Кориолисова сила инерции |
Надо еще раз отметить, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета. Поэтому они не подчиняются третьему закону Ньютона, так как если на какое-либо тело действует сила инерции, то не существует противодействующей силы, приложенной к данному телу. Два основных положения динамики, согласно которым ускорение всегда вызывается силой, а сила всегда обусловлена взаимодействием между телами, в системах отсчета, движущихся с ускорением, одновременно не выполняются.
Для любого из тел, находящегося в неинерциальной системе отсчета, силы инерции являются внешними, следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, момента импульса, энергии.
Силы инерции действуют только в неинерциальных системах отсчета. В инерциальных системах отсчета таких сил нет.
Силы инерции пропорциональны массам частиц (тел, систем) и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают тела, находящиеся под действием сил поля тяготения.
При некоторых условиях силы инерции и силы тяготения невозможно различить. Например, движение тел в равноускоренном лифте происходит точно так же, как и в неподвижном, висящем в однородном поле тяготения. Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.
Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции (принципа эквивалентности Эйнштейна): «Все физические явления в поле тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы». Этот принцип является основой общей теории относительности.
3.4. Элементы динамики материальной точки и твердого тела, совершающих вращательное движение относительно неподвижной оси вращения. Основные понятия и определения: момент силы, момент импульса, момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения
Основной задачей динамики вращательного движения является задача нахождения угловых ускорений, сообщаемых известными силами. Однако одна и та же сила, в зависимости от расстояния между ее направлением и осью вращения, сообщает различные угловые ускорения. Для описания вращательного движения введены специфические параметры: момент силы, момент инерции тела, момент импульса. Благодаря этим параметрам достигается подобие основных уравнений динамики поступательного и вращательного движения.
Момент силы характеризует вращательный эффект силы при действии ее на твердое тело. Различают момент силы относительно центра (точки) и оси вращения.
Моментом силы относительно центра вращения называют векторную физическую величину, модуль которой равен произведению модуля силы на плечо:
M = Fl или M = Fl, (3.38)
где l — плечо силы — кратчайшее расстояние от направления действия силы до центра вращения.
Вектор M направлен вдоль перпендикуляра к плоскости, на которой находится центр вращения и сила. Направление его определяется правилом правого винта. Так как
l = rsinα,
где r численное значение радиус-вектора r, который направлен из центра вращения в точку приложения силы;
α — угол между направлениями F и r,
то
M = Frsinα (3.39)
или в векторной форме
M = [r F].
(3.40)
F].
(3.40)
Момент нескольких сил, имеющих одну точку приложения, равен алгебраической сумме моментов слагаемых сил:
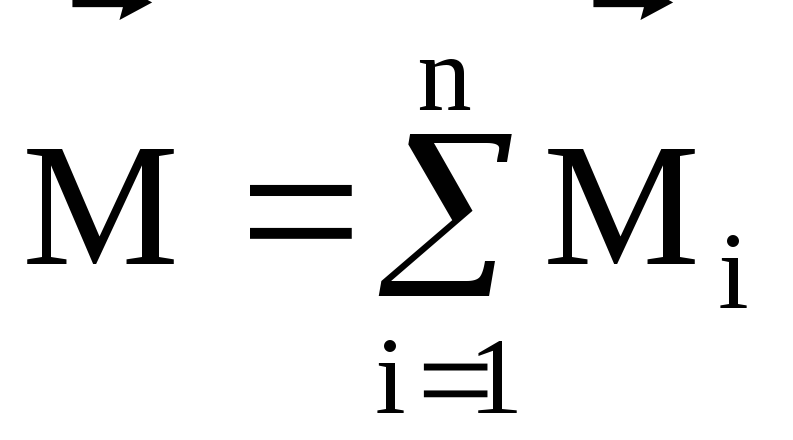 .
(3.41)
.
(3.41)
Этот момент называют главным или результирующим моментом системы сил относительно неподвижной точки вращения (центра; полюса).
Из третьего закона Ньютона следует, что моменты внутренних сил взаимодействия материальных точек системы относительно центра вращения попарно компенсируются. Следовательно, при вычислении главного момента сил необходимо учитывать только внешние силы, действующие на рассматриваемую механическую систему. Иначе результирующий момент внутренних сил системы равен нулю.
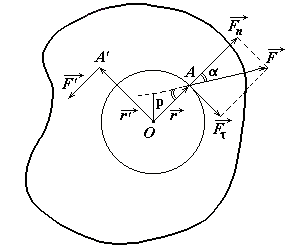
Рис.3.6
Рассмотрим вращение тела вокруг закрепленной оси (рис.3.6). Тело является абсолютно жестким. Пусть к двум точкам этого тела приложены силы ,
,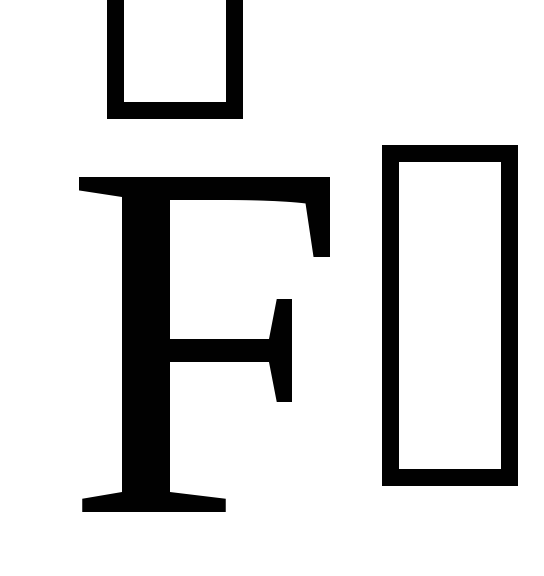 .
. ,
, – радиус-вектора, проведенные из центра
вращения в точку приложения силы.
Предполагается, что вектора сил лежат
в плоскости, перпендикулярной оси
вращения. Во всяком случае, понятно, что
компонента силы, параллельная оси
вращения, при закрепленной оси никакого
вращательного действия произвести не
может.
– радиус-вектора, проведенные из центра
вращения в точку приложения силы.
Предполагается, что вектора сил лежат
в плоскости, перпендикулярной оси
вращения. Во всяком случае, понятно, что
компонента силы, параллельная оси
вращения, при закрепленной оси никакого
вращательного действия произвести не
может. Разложим
силу  на плоскости на две составляющие –
касательную и нормальную к окружности,
по которой движется точка приложения
силы:
на плоскости на две составляющие –
касательную и нормальную к окружности,
по которой движется точка приложения
силы:
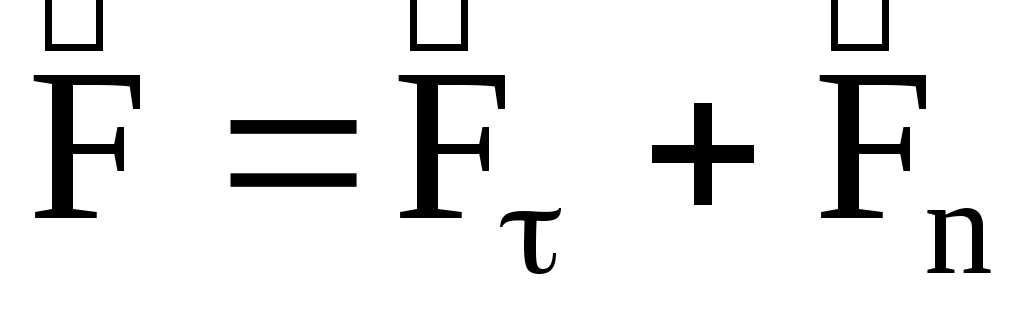 . (3.42)
. (3.42)
Вращательное
действие силы определяется только
касательной составляющей силы и
положением точки приложения силы по
отношению к центру вращения, т.е. радиусом  .
Введем угол
.
Введем угол  ,
образованный между направлениями
векторов
,
образованный между направлениями
векторов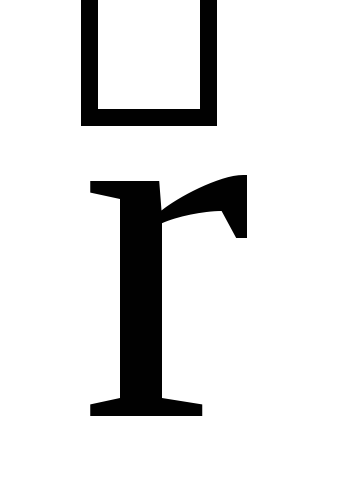 и
и .
Тогда получим
.
Тогда получим
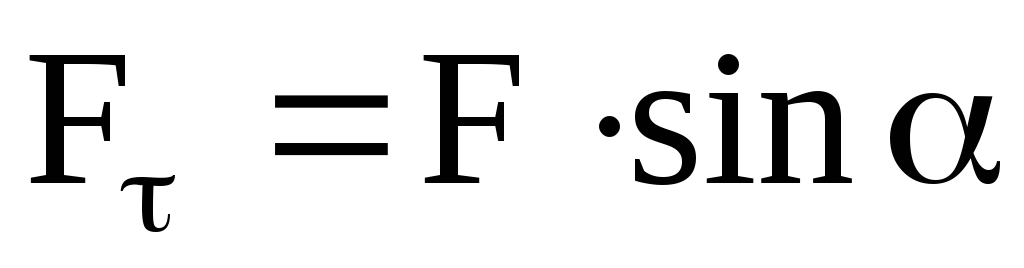 .
(3.43)
.
(3.43)
Вращательное действие любой силы будет пропорционально произведению:
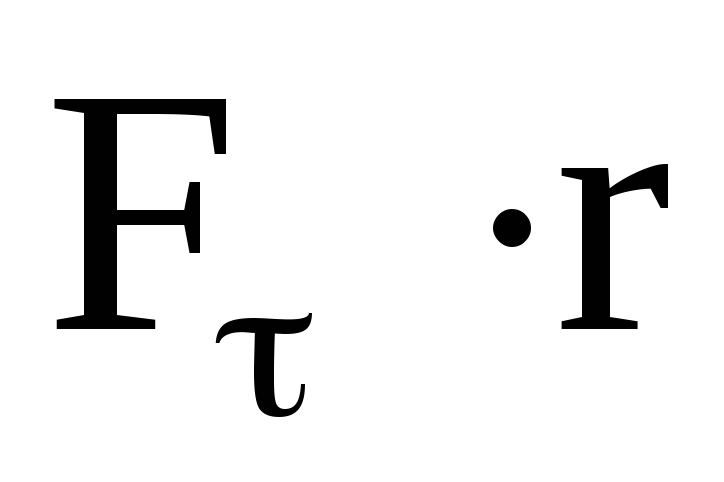 или
или 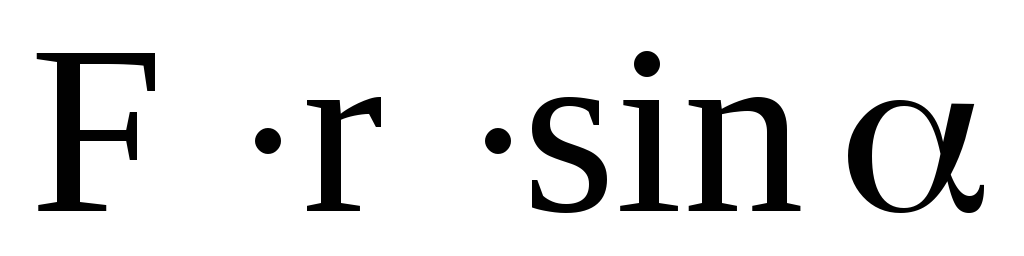 .
(3.44)
.
(3.44)
Выражение 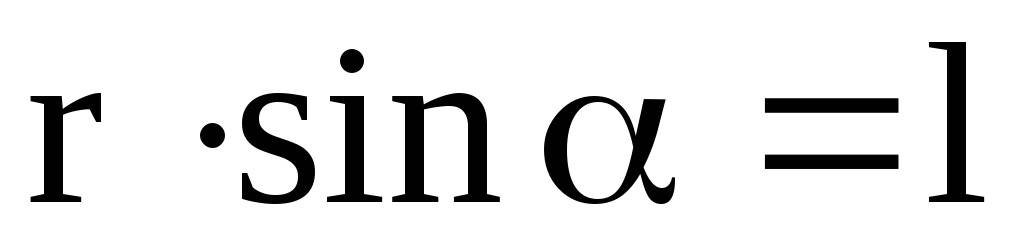 представляет собой плечо силы, т.е.
кратчайшее расстояние от линии действия
силы до оси вращения.
представляет собой плечо силы, т.е.
кратчайшее расстояние от линии действия
силы до оси вращения.
По правилу «рычага» равновесие наступает при равенстве
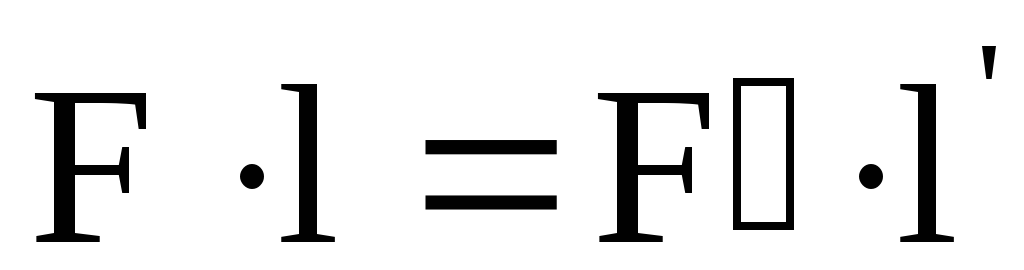 .
(3.45)
.
(3.45)
Произведение 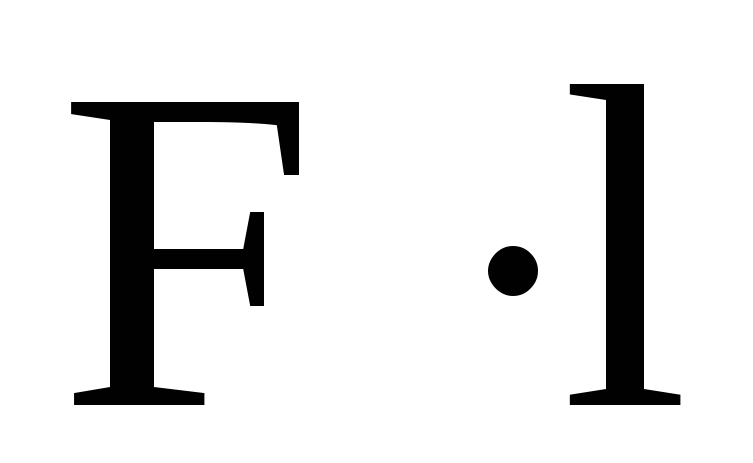 носит название момента силы относительно
оси вращения
носит название момента силы относительно
оси вращения .
Момент силы – это вектор, определяемый
как векторное произведение:
.
Момент силы – это вектор, определяемый
как векторное произведение:
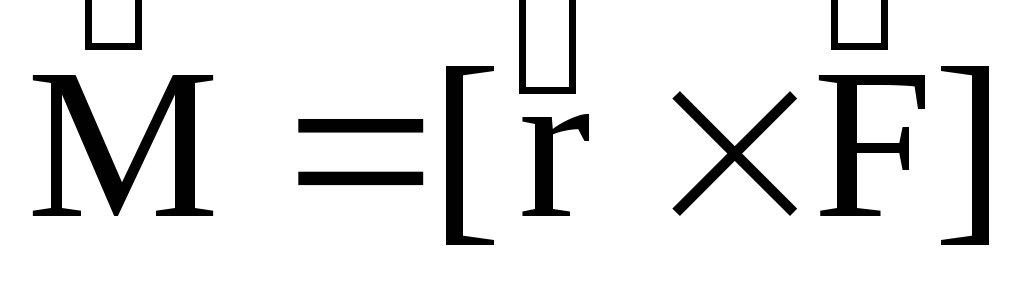 . (3.46)
. (3.46)
Модуль  выражается следующим образом:
выражается следующим образом:
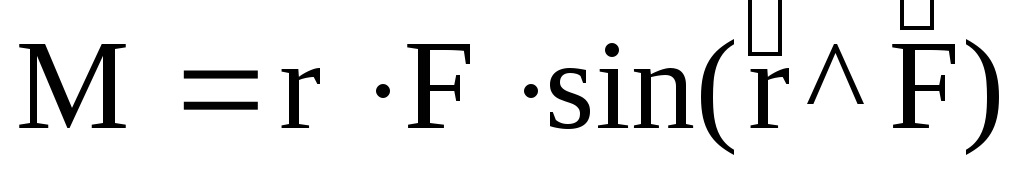 .
(3.47)
.
(3.47)
Этот
вектор всегда перпендикулярен плоскости,
образованной векторами  и
и ,
т.е. направлен по оси вращения «по
правилу правого винта». Поэтому в
случае закрепленной оси вращения вместо
векторного представления момента силы
можно воспользоваться алгебраическим
представлением. Если сила вращает тело
по часовой стрелке, то момент силы будем
считать положительным, если сила вращает
тело против часовой стрелки, то моменту
этой силы будем приписывать знак «минус».
Заметим, что на рис.3.6 направление оси
выбрано «от нас, за чертеж». Для сил
,
т.е. направлен по оси вращения «по
правилу правого винта». Поэтому в
случае закрепленной оси вращения вместо
векторного представления момента силы
можно воспользоваться алгебраическим
представлением. Если сила вращает тело
по часовой стрелке, то момент силы будем
считать положительным, если сила вращает
тело против часовой стрелки, то моменту
этой силы будем приписывать знак «минус».
Заметим, что на рис.3.6 направление оси
выбрано «от нас, за чертеж». Для сил и
и моменты равны
моменты равны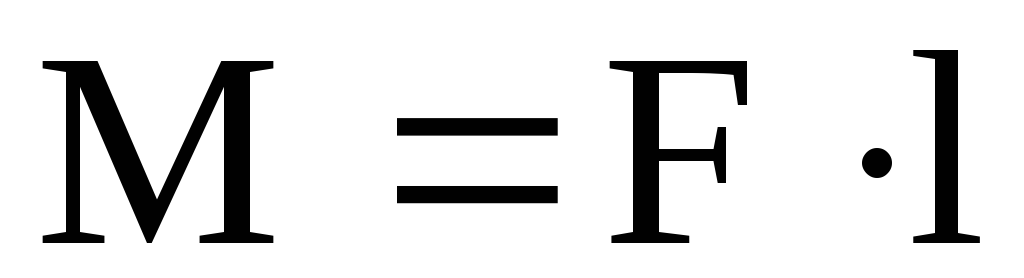 и
и .
Условие равновесия может быть записано
как
.
Условие равновесия может быть записано
как
 .
(3.48)
.
(3.48)
Силы  и
и не вызывают вращение, если их моменты
не вызывают вращение, если их моменты и
и равны по величине и противоположны по
направлению.
равны по величине и противоположны по
направлению.
В
общем случае, когда на тело действует  сил, рассматривают полный момент сил:
сил, рассматривают полный момент сил:
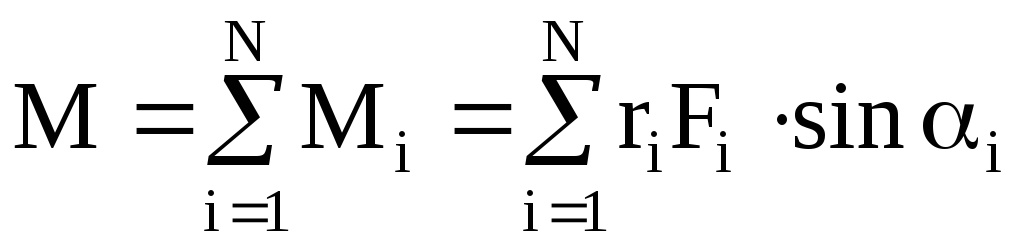 .
(3.49)
.
(3.49)
И условие равновесия тела с закрепленной осью вращения сводится к виду:
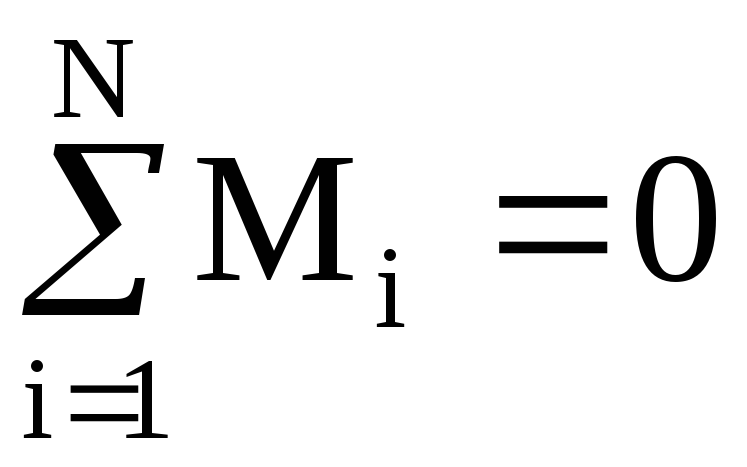 .
(3.50)
.
(3.50)
Оказывается, что один и тот же момент внешней силы, действующей на различные тела (материальные точки), сообщает им различные угловые ускорения.
Для
характеристики инертности тел
(материальных точек) вращательному
движению вводится в рассмотрение
физическая величина, называемая моментом
инерции материальной точки или тела (I
относительно неподвижной оси (центра
вращения). Чем больше  ,
тем меньше угловое ускорение
получит тело под действием данного
момента силы
,
тем меньше угловое ускорение
получит тело под действием данного
момента силы  .
.
Моментом инерции материальной точки относительно какой-либо оси или центра вращения называется физическая величина, равная произведению массы материальной точки на квадрат расстояния от нее до оси или центра вращения:
I = mr2. (3.51)
Момент инерции тела — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Для тела с закрепленной осью вращения момент инерции представляет собой положительную скалярную величину.
Прямой
способ вычисления момента инерции тела
состоит в следующем: мысленно тело
разбивают на совокупность материальных
точек, записывают момент инерции  -й
материальной точки, полный момент
инерции получают суммированием
элементарных моментов:
-й
материальной точки, полный момент
инерции получают суммированием
элементарных моментов:
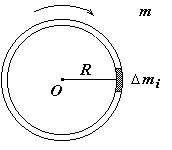 Рис.3.7
Рис.3.7
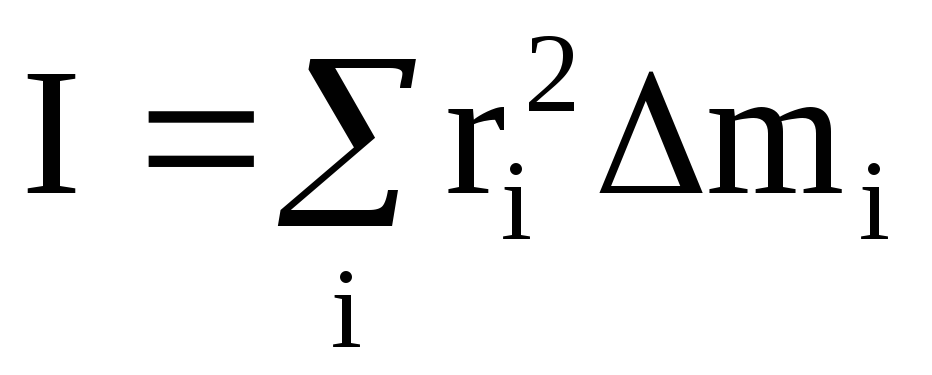 или
или 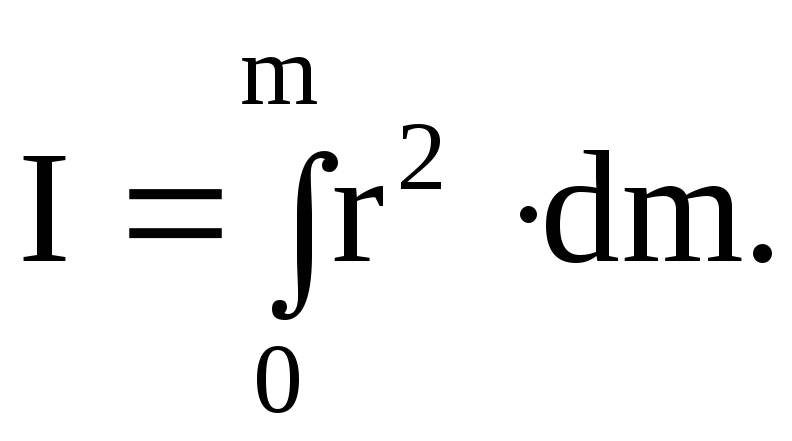 (3.52)
(3.52)Рассмотрим несколько примеров:
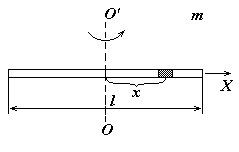
Рис.3.8
1. Момент инерции обруча, вращающегося вокруг собственной оси (рис.3.7). Обруч считаем «тонким» и однородным по плотности. В данном случае все материальные точки (элементарные массы) расположены на одинаковом расстоянии от оси вращения. Поэтому 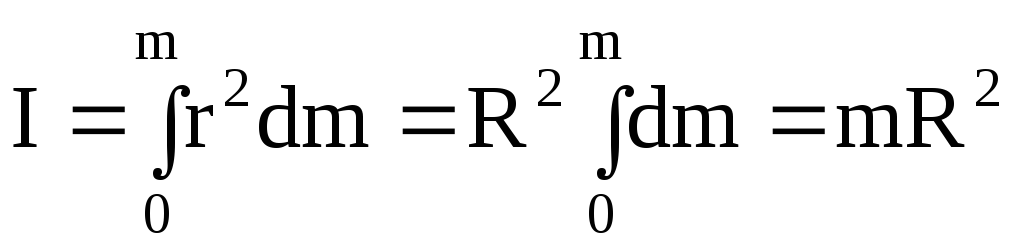 .
(3.53)
.
(3.53)
2.
Момент инерции стержня относительно
оси, проходящей перпендикулярно к нему
через его середину (рис.3.8). Стержень
считаем «тонким», однородным по
сечению и распределению плотности.
Длина стержня – 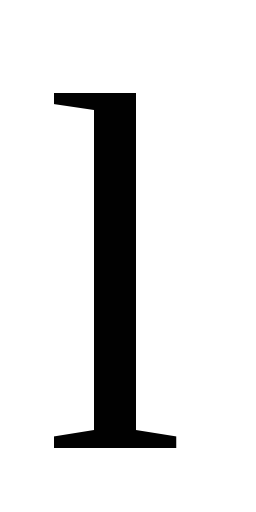 .
Момент инерции материальной точки
представим в виде дифференциала
.
Момент инерции материальной точки
представим в виде дифференциала
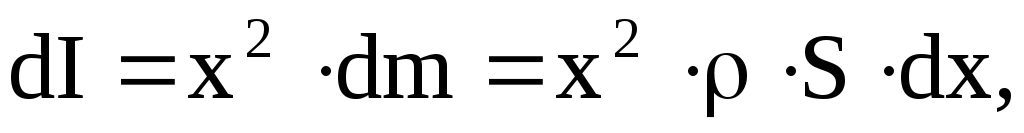 (3.54)
(3.54)
где  – площадь сечения.
– площадь сечения.
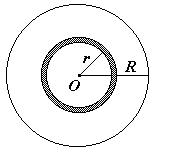
Рис.3.9
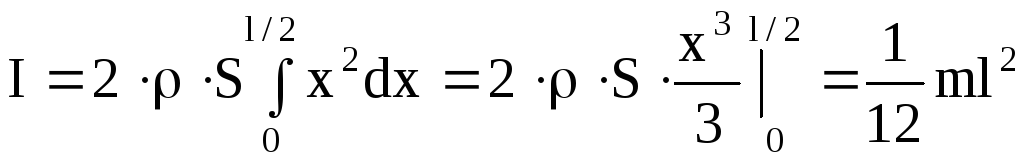 .
(3.55)
.
(3.55) 3.
Момент инерции сплошного цилиндра
относительно собственной оси (рис.3.9).
Цилиндр (диск) считаем однородным по
плотности. Радиус цилиндра –  ,
длина –
,
длина – .
В данном случае целесообразно разбить
цилиндр на совокупность тонкостенных
цилиндров, соосных друг с другом.
Элементарный момент инерции представим
в виде дифференциала
.
В данном случае целесообразно разбить
цилиндр на совокупность тонкостенных
цилиндров, соосных друг с другом.
Элементарный момент инерции представим
в виде дифференциала
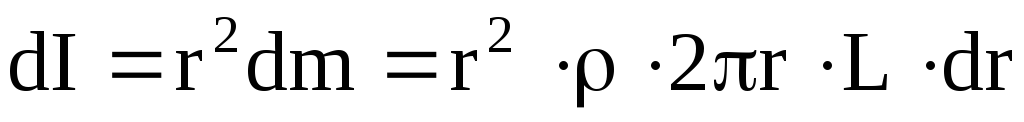 . (3.56)
. (3.56)
Момент инерции цилиндра получим путем интегрирования:
. (3.57)
4. Момент инерции шара относительно оси, проходящей через его центр, можно определить аналогично и вычисляется по формуле
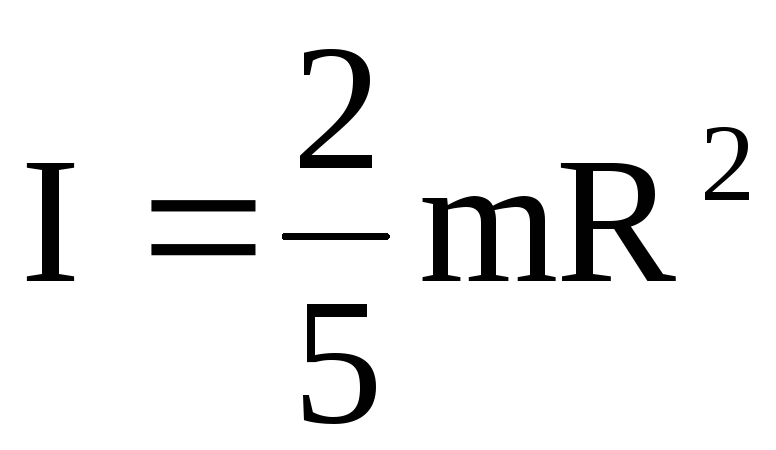 .
(3.58)
.
(3.58)
Рис.3.10
Таким образом, момент инерции тела существенно зависит от его геометрии (формы), а также от положения оси вращения, т.е. зависит от распределения массы тела относительно оси вращения. Если выбрать новую ось вращения, оставив без изменения форму и размеры тела, то изменится и момент инерции тела. Поэтому определенный смысл момент инерции имеет только в том случае, когда задана ось вращения. Значительное упрощение в вычислениях момента инерции тела относительно оси, не проходящей через центр масс этого тела, можно получить, применяя теорему Штейнера, формулировку которой мы примем без доказательства (рис.3.10): «Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, I0 и произведения массы тела m0 на квадрат расстояния между осями», т.е. 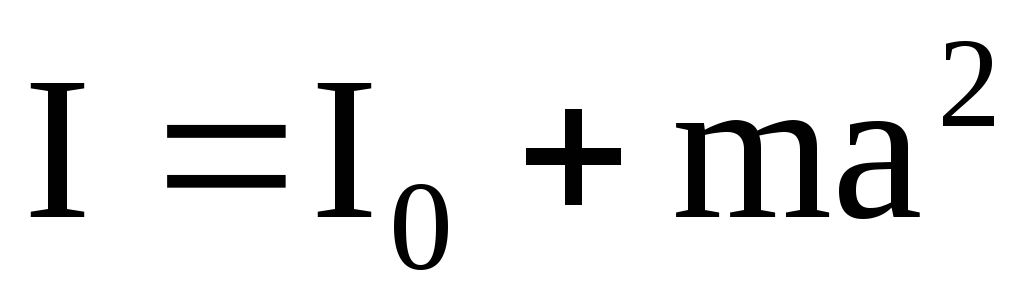 .
(3.59)
.
(3.59)
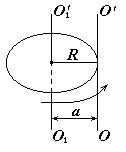
Рис.3.11
Примеры применения теоремы Штейнера:
1. Момент инерции
диска относительно оси  ,
параллельной геометрической оси диска
и проходящей через его край (рис.3.11).
,
параллельной геометрической оси диска
и проходящей через его край (рис.3.11).
Здесь 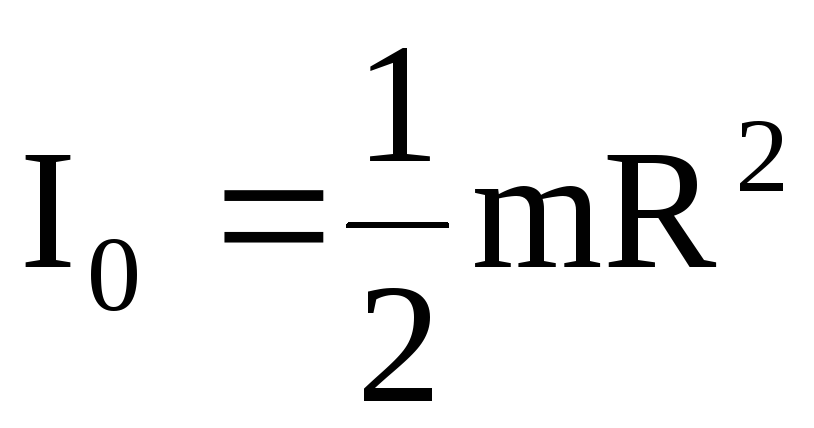 ,
, 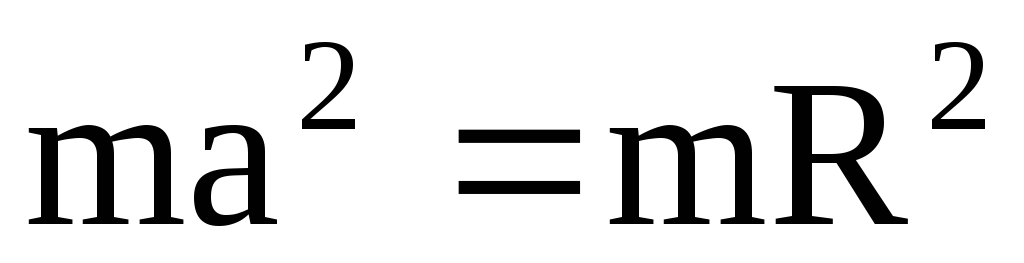 .
Поэтому
.
Поэтому
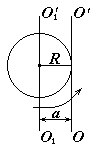
Рис.3.12
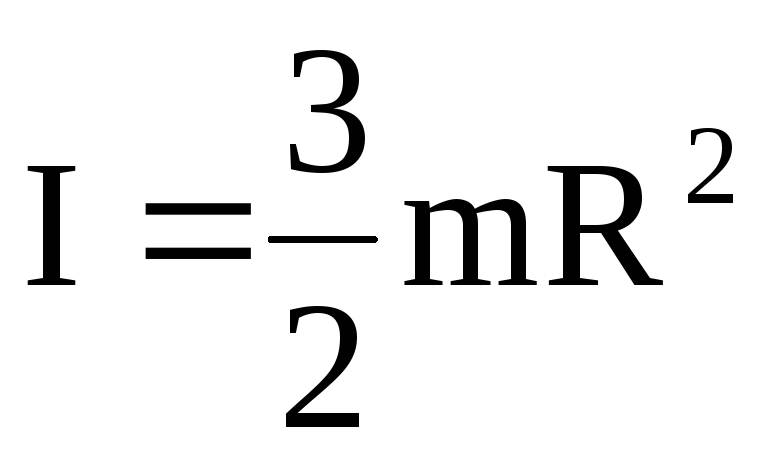 .
(3.60)
.
(3.60)2. Момент инерции шара относительно оси, касательной к его поверхности (рис.3.12).
Здесь 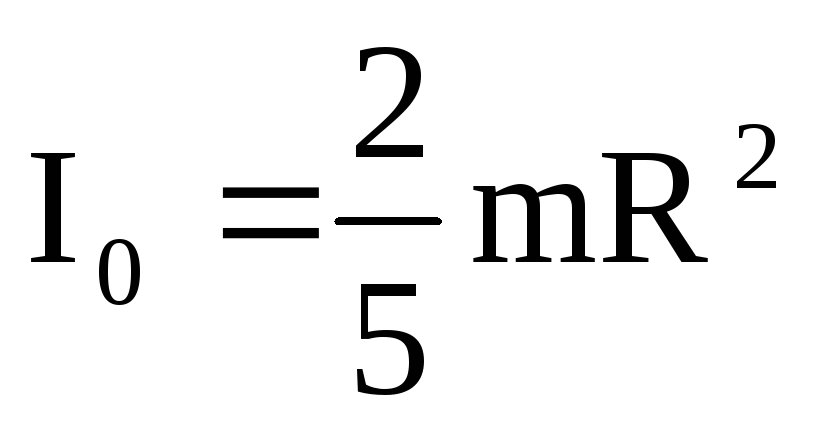 ,
, 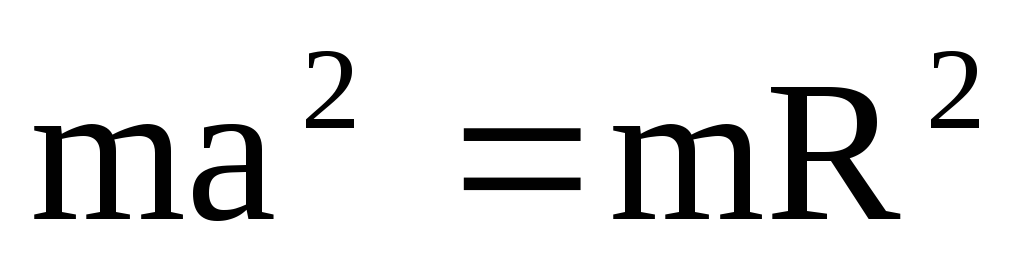 .
Тогда
.
Тогда
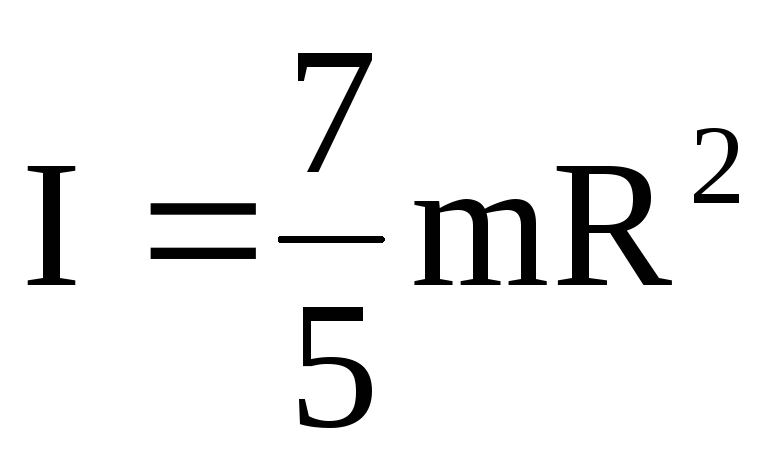 . (3.61)
. (3.61)


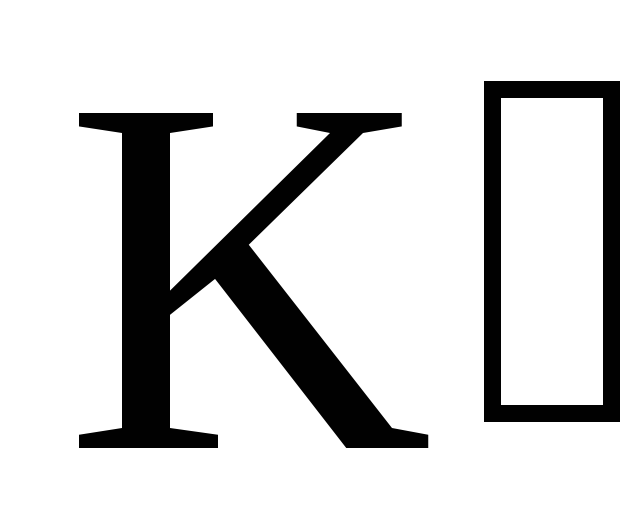
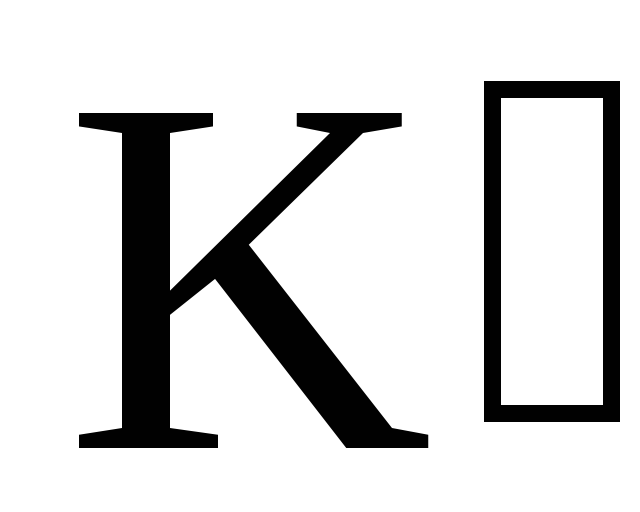 относительно ИСО
относительно ИСО
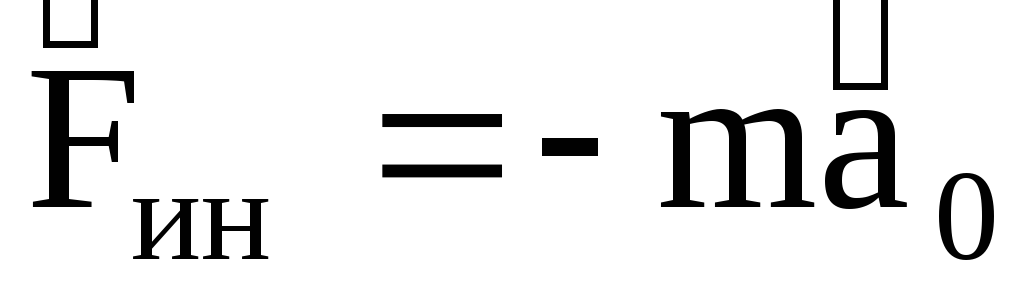
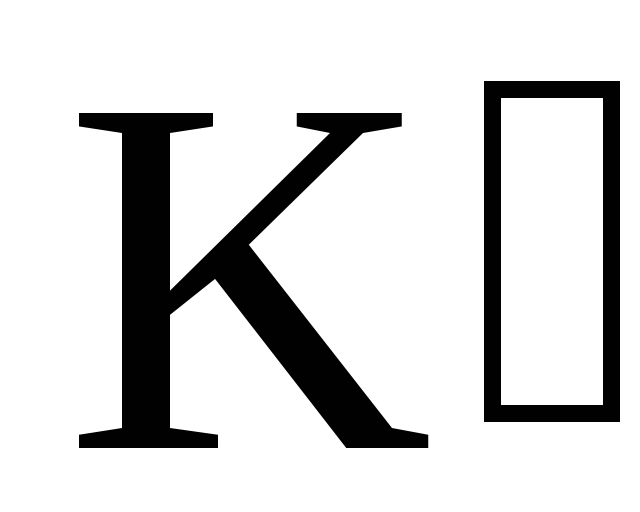 движется
движется
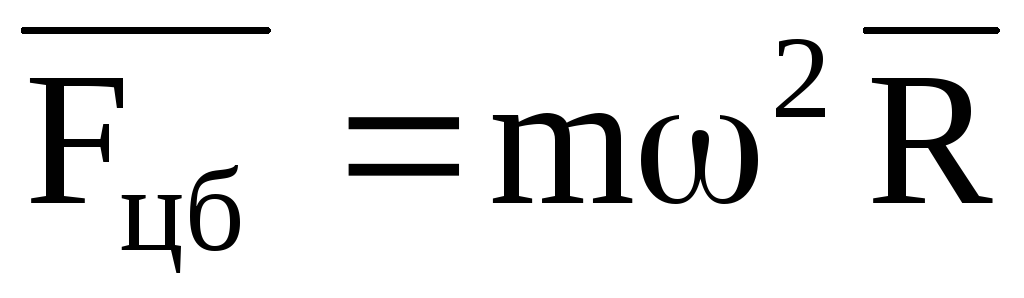
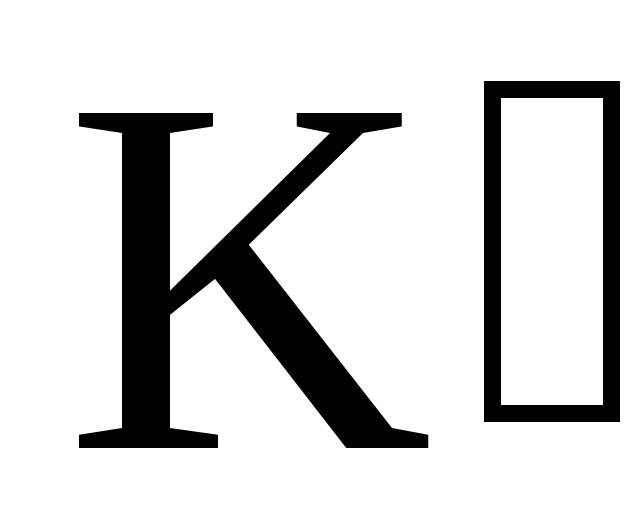 вращается с угловой скоростью
вращается с угловой скоростью