работа 3 Маховик Обербека
Работа 3
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
НА МАХОВИКЕ ОБЕРБЕКА
Цель работы. Измерение характеристик движения маховика и определение моментов инерции грузов на его спицах.
Приборы и принадлежности: маховик Обербека с грузами на спицах; стойка со шкалой; набор грузов с подставкой; секундомер; штангенциркуль.
В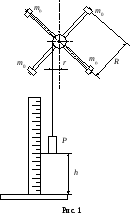 лабораторной работе рассматривается
вращательное движение маховика (рис.
1) относительно неподвижной оси.
лабораторной работе рассматривается
вращательное движение маховика (рис.
1) относительно неподвижной оси.
Вращательным называется такое движение твердого тела, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях. Центры этих окружностей лежат на одной прямой, называемой осью вращения.
Если на тело, закрепленное на неподвижной оси, действует сила, то тело приобретает угловое ускорение, направленное вдоль этой оси. Величина ускорения зависит не только от величины и направления силы, но и от точки ее приложения. Это отражено в понятии момента силы, который, как и сила, является векторной величиной. В случае вращения вокруг неподвижной оси угловое ускорение, направленное вдоль этой оси, определяется результирующей проекцией моментов всех сил на эту ось.
Основной закон динамики вращательного движения твердого тела утверждает, что угловое ускорение тела, вращающегося относительно неподвижной оси, пропорционально результирующей проекции
M I.
Коэффициент пропорциональности I в этом равенстве характеризует инертные свойства тела при вращательном движении и называется моментом инерции.
Для определения понятия момента инерции мысленно разобъём тело на частицы, размеры которых достаточно малы, чтобы их можно было рассматривать как материальные точки массой mi. Момент инерции такой материальной точки
Ii miRi2,
где Ri
Момент инерции тела или системы тел
I 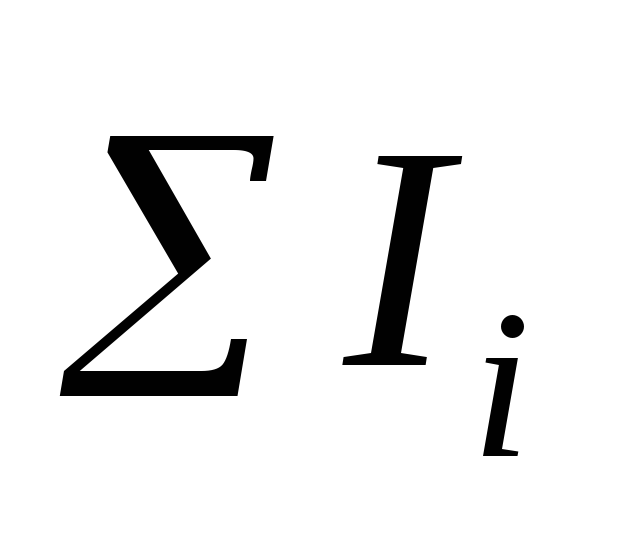
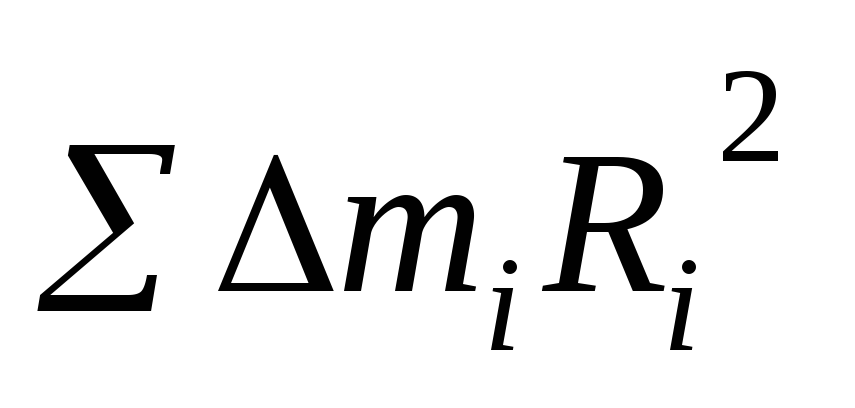 .
.
Понятие момента инерции отражает то, что инертные свойства тел при вращательном движении зависят не только от суммарной массы всех частиц тела, но и от распределения их по отношению к оси вращения. Момент инерции есть величина скалярная и всегда положительная. Из определения понятия момента инерции следует, что если система состоит из нескольких тел, то момент инерции системы равен сумме моментов инерции отдельных тел:
I I1 I2 I3 …
В данной лабораторной работе измеряют момент инерции маховика и грузов массой m0, находящихся на его спицах (см. рис. 1). Спицы крестовины жестко скреплены со шкивом. На шкив наматывается нить, к концу которой прикрепляется груз Р. Рядом с висящим грузом ставится вертикальная шкала для измерения пути h, пройденного грузом. Для приведения крестовины в ускоренное вращательное движение груз Р поднимают на высоту h, затем, груз без толчка отпускают и измеряют время
a  .
(1)
.
(1)
Так как при падении груза Р нить сматывается, то линейное ускорение а груза равно тангенциальному ускорению точек поверхности шкива. Следовательно, можно вычислить угловое ускорение крестовины:
a/r, (2)
где r – радиус шкива.
На основании второго закона Ньютона
ma mg T, (3)
где т – масса груза Р.
Сила натяжения создает момент силы
M Tr m(g a)r. (4)
Измерение момента инерции крестовины и грузов на ней производят, используя основной закон динамики вращательного движения:
M I, (5)
где I – момент инерции вращающегося тела.
Из формулы (5), с учетом формул (4) и (2) следует, что
I 
 .
(6)
.
(6)
Момент инерции крестовины с грузами можно представить в виде
I I0
где I0 и Ir – моменты инерции крестовины без грузов и грузов соответственно.
Следовательно, для определения момента инерции закрепленных на крестовине грузов Ir необходимо определить по формуле (6) момент инерции крестовины с грузами I и ее момент инерции без грузов I0.
Так как линейные размеры грузов на спицах крестовины значительно меньше их расстояния до оси вращения, то их можно считать материальными точками. Поэтому момент инерции грузов можно определить по формуле
Ir 4m0R2, (8)
где m0 – масса одного груза; R – расстояние грузов до оси вращения.
Порядок выполнения работы
I. Измерение моментов инерции I0 крестовины без грузов
Определить массу m грузa P с подставкой (значения масс указаны на грузах).
Измерить штангенциркулем радиус шкива r.
Вычислить линейное ускорение падающего груза по формуле (1).
Измерения, описанные в 3 и 4, проделать три раза с различными значениями высоты h.
Вычислить по формуле (6) момент инерции крестовины I0 для каждого значения а. Найти среднее значение момента инерции I0СР.
Рассчитать погрешность I0 определения I0 как среднюю абсолютную погрешность по формуле
I0 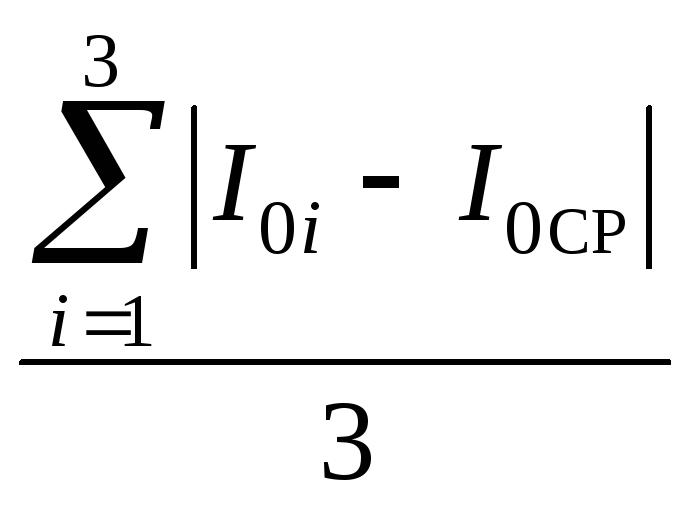 ,
,
Все результаты записать в таблицу, где рядом с обозначениями величин обязательно указать единицы их измерения.
Таблица
Измеряемая величина | Вращение без грузов, R 0 | Вращение с грузами на концах спиц, R …,м | Вращение с грузами на середине спиц, R/2 …м | ||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
h | |||||||||
t | |||||||||
a | |||||||||
I | |||||||||
I СР | |||||||||
I | |||||||||
m … кг; r …. м; m0 … кг;
II. Измерение моментов инерции грузов
Четыре груза с одинаковой массой m0 закрепить на концах спиц на одинаковых расстояниях R от центров грузов до оси вращения. Убедиться, что центр масс системы совпадает с осью вращения, т. е. система сбалансирована.
Записать значения m0 и R в таблицу.
Выполнить измерения, описанные в пунктах 3 – 5 раздела I.
Вычислить момент инерции крестовины с грузами I для каждого значения а. Найти среднее значение IСР.
Рассчитать погрешность определения I как среднюю абсолютную погрешность по формуле
I  ,
,
Вычислить момент инерции грузов по формуле:
IГ I СР I0СР. (9)
Определить погрешность IГ определения момента инерции грузов по формуле:
IГ I I0.
Записать окончательный результат в виде:
I IГ IГ.
Рассчитать величину момента инерции грузов по формуле (8) и сравнить с полученным в пункте 8 экспериментальным значением.
Грузы переместить на середину спиц и закрепить их. Измерить расстояние R от центров грузов до оси вращения. Описанным выше методом (см. пункты 3 – 9 раздела II) определить значения их момента инерции.
Контрольные вопросы
Сформулируйте основной закон динамики вращательного движения.
Напишите формулу пути при равноускоренном поступательном движении опускающегося груза.
Напишите формулу связи углового ускорения маховика с линейным ускорением опускающегося груза.
Проделайте вывод формулы для определения момента инерции грузов на спицах маховика на основании основного закона динамики вращательного движения.
Дайте определение момента инерции тела.
При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением?
Можно ли в данной лабораторной работе изменить момент силы, не меняя массу груза на нити?
Почему в том случае, когда грузы ближе к оси вращения, время движения меньше?
Список литературы
Савельев И.В. Курс общей физики: В 3-х т. Т. 1. М.: – Наука, 1987.
Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000. – С. 294.
Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.
Порядок выполнения работы
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
НА МАХОВИКЕ ОБЕРБЕКА
Цель работы.Измерение характеристик движения маховика и определение моментов инерции грузов на его спицах.
Приборы и принадлежности: маховик Обербека с грузами на спицах; стойка со шкалой; набор грузов с подставкой; секундомер; штангенциркуль.
Введение
В лабораторной работе рассматривается вращательное движение маховика (рис. 1) относительно неподвижной оси.
Вращательным называется такое движение твердого тела, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях. Центры этих окружностей лежат на одной прямой, называемой осью вращения.
Если на тело, закрепленное на неподвижной оси, действует сила, то тело приобретает угловое ускорение, направленное вдоль этой оси. Величина ускорения зависит не только от величины и направления силы, но и от точки ее приложения. Это отражено в понятии момента силы, который, как и сила, является векторной величиной. В случае вращения вокруг неподвижной оси угловое ускорение, направленное вдоль этой оси, определяется результирующей проекцией моментов всех сил на эту ось.
Основной закон динамики вращательного движения твердого тела утверждает, что угловое ускорение e тела, вращающегося относительно неподвижной оси, пропорционально результирующей проекции M моментов всех сил на ось вращения:
M = Ie.
Коэффициент пропорциональности I в этом равенстве характеризует инертные свойства тела при вращательном движении и называется моментом инерции.
Для определения понятия момента инерции мысленно разобъём тело на частицы, размеры которых достаточно малы, чтобы их можно было рассматривать как материальные точки массой Dmi. Момент инерции такой материальной точки
Ii = DmiRi2,
где Ri – расстояние точки до оси вращения.
Момент инерции тела или системы тел
I = = .
Понятие момента инерции отражает то, что инертные свойства тел при вращательном движении зависят не только от суммарной массы всех частиц тела, но и от распределения их по отношению к оси вращения. Момент инерции есть величина скалярная и всегда положительная. Из определения понятия момента инерции следует, что если система состоит из нескольких тел, то момент инерции системы равен сумме моментов инерции отдельных тел:
I = I1 + I2 + I3 + …
В данной лабораторной работе измеряют момент инерции маховика и грузов массой m0, находящихся на его спицах (см. рис. 1). Спицы крестовины жестко скреплены со шкивом. На шкив наматывается нить, к концу которой прикрепляется груз Р. Рядом с висящим грузом ставится вертикальная шкала для измерения пути h, пройденного грузом. Для приведения крестовины в ускоренное вращательное движение груз Р поднимают на высоту h, затем, груз без толчка отпускают и измеряют время t движения его на пути h. Поскольку движение груза является равноускоренным, линейное ускорение груза Р можно вычислить по формуле
a = . (1)
Так как при падении груза Р нить сматывается, то линейное ускорение а груза равно тангенциальному ускорению точек поверхности шкива. Следовательно, можно вычислить угловое ускорение крестовины:
e = a/r, (2)
где r – радиус шкива.
Рассматривая силы, действующие на груз, будем считать, что силы трения малы, и ими можно пренебречь. В этом случае ускорение груза определяется действием силы тяжести mg и силы натяжения нити Т.
На основании второго закона Ньютона
ma = mg — T, (3)
где т –масса груза Р.
Сила натяжения создает момент силы
M = T×r = m(g — a)r. (4)
Измерение момента инерции крестовины и грузов на ней производят, используя основной закон динамики вращательного движения:
M = Ie, (5)
где I – момент инерции вращающегося тела.
Из формулы (5), с учетом формул (4) и (2) следует, что
I = = . (6)
Момент инерции крестовины с грузами можно представить в виде
I = I0 + Ir, (7)
где I0 и Ir – моменты инерции крестовины без грузов и грузов соответственно.
Следовательно, для определения момента инерции закрепленных на крестовине грузов Ir необходимо определить по формуле (6) момент инерции крестовины с грузами I и ее момент инерции без грузов I0.
Так как линейные размеры грузов на спицах крестовины значительно меньше их расстояния до оси вращения, то их можно считать материальными точками. Поэтому момент инерции грузов можно определить по формуле
Ir = 4m0R2, (8)
где m0 – масса одного груза; R – расстояние грузов до оси вращения.
Порядок выполнения работы
I. Измерение моментов инерции I0 крестовины без грузов
1. Определить массу m грузa P с подставкой (значения масс указаны на грузах).
2. Измерить штангенциркулем радиус шкива r.
3. Намотать нить на шкив и подвесить груз Р с подставкой на нить. Отпустив груз Р без толчка, измерить время его движения на пути h.
4. Вычислить линейное ускорение падающего груза по формуле (1).
5. Измерения, описанные в 3 и 4, проделать три раза с различными значениями высоты h.
6. Вычислить по формуле (6) момент инерции крестовины I0 для каждого значения а. Найти среднее значение момента инерции I0СР.
7. Рассчитать погрешность DI0 определения I0 как среднюю абсолютную погрешность по формуле
DI0 = ,
Все результаты записать в таблицу, где рядом с обозначениями величин обязательно указать единицы их измерения.
Таблица
| Измеряемая величина | Вращение без грузов, R = 0 | Вращение с грузами на концах спиц, R =…,м | Вращение с грузами на середине спиц, R/2 =…м | ||||||
| h | |||||||||
| t | |||||||||
| a | |||||||||
| I | |||||||||
| I СР | |||||||||
| DI |
m = … кг; r = …. м; m0 = … кг;
II. Измерение моментов инерции грузов
1. Четыре груза с одинаковой массой m0 закрепить на концах спиц на одинаковых расстояниях R от центров грузов до оси вращения. Убедиться, что центр масс системы совпадает с осью вращения, т. е. система сбалансирована.
2. Записать значения m0 и R в таблицу.
3. Выполнить измерения, описанные в пунктах 3 – 5 раздела I.
4. Вычислить момент инерции крестовины с грузами I для каждого значения а. Найти среднее значение IСР.
5. Рассчитать погрешность DI определения I как среднюю абсолютную погрешность по формуле
DI = ,
6. Вычислить момент инерции грузов по формуле:
IГ = I СР — I0СР. (9)
7. Определить погрешность DIГ определения момента инерции грузов по формуле:
DIГ = DI + DI0.
8. Записать окончательный результат в виде:
I = IГ ± DIГ.
9. Рассчитать величину момента инерции грузов по формуле (8) и сравнить с полученным в пункте 8 экспериментальным значением.
10. Грузы переместить на середину спиц и закрепить их. Измерить расстояние R от центров грузов до оси вращения. Описанным выше методом (см. пункты 3 – 9 раздела II) определить значения их момента инерции.
Контрольные вопросы
1. Сформулируйте основной закон динамики вращательного движения.
2. Напишите формулу пути при равноускоренном поступательном движении опускающегося груза.
3. Напишите формулу связи углового ускорения маховика с линейным ускорением опускающегося груза.
4. Проделайте вывод формулы для определения момента инерции грузов на спицах маховика на основании основного закона динамики вращательного движения.
5. Дайте определение момента инерции тела.
6. При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением?
7. Можно ли в данной лабораторной работе изменить момент силы, не меняя массу груза на нити?
8. Почему в том случае, когда грузы ближе к оси вращения, время движения меньше?
Список литературы
1. Савельев И.В. Курс общей физики: В 3-х т. Т. 1. М.: – Наука, 1987.
2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000. – С. 294.
3. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Машина Обербека — Википедия
Материал из Википедии — свободной энциклопедии
Машина Обербека (маятник Обербека) — лабораторное устройство для изучения законов динамики вращательного движения и проверки теоремы Гюйгенса — Штейнера[1]. Создана А. Обербеком.
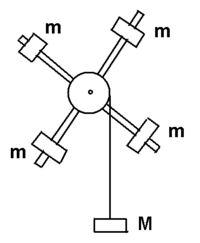
Идеальная машина Обербека имеет следующую конструкцию: на горизонтальную ось насажена свободно вращающаяся втулка с двумя взаимно-перпендикулярными стержнями. К стержням симметрично прикреплены грузы. С втулкой связан шкив с ободом, служащим для намотки нити, на которую подвешивается груз.
Машина Обербека начинает свою работу с опускания под действием силы тяжести подвешенного на нити груза. Сила натяжения нити создает вращающий момент, приводящий в ускоряющееся вращение грузы на стержнях.
После того, когда груз полностью опустится на всю длину нити, нить начнет вновь наматываться на обод шкива под действием вращающихся по инерции грузов на стержнях.
Затем на определённой высоте груз вместе со стержнями прекращает свое движение и затем вновь начинается его движение вниз. Вследствие потери механической энергии под действием сил трения и сопротивления, процесс опускания и подъёма груза повторяется при последовательно уменьшающейся высоте подъёмов груза.
Вследствие закона сохранения энергии при работе машины Обербека потенциальная энергия тела в поле силы тяжести mgh{\displaystyle mgh} преобразуется в кинетическую энергию вращающихся грузов и бесполезные потери энергии на трение A{\displaystyle A}.
- mgh=12Jω2+A.{\displaystyle mgh={\frac {1}{2}}J\omega ^{2}+A.}
Здесь J{\displaystyle J} — момент инерции стержней с грузами относительно оси вращения, ω{\displaystyle \omega } — угловая скорость вращения при полном опускании груза, h{\displaystyle h} — высота полного опускания груза.
- ↑ Сивухин Д. В. Общий курс физики. Механика. — М.: Наука, 1979. — Тираж 50 000 экз. — с. 191.
Методические указания к лабораторной работе, страница 4
При пересечении
грузом верхнего светового луча секундомер начинает отсчёт времени. При
пересечении нижнего светового луча секундомер автоматически выключается. Время
движения груза от одного светового луча до другого высвечивается на индикаторе
секундомера с абсолютной ошибкой 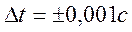 , что намного
меньше точности измерения времени человеком-оператором.
, что намного
меньше точности измерения времени человеком-оператором.
Примечание: при неисправной работе удерживающего электромагнита начало опускания груза 4 можно задавать, удерживая его рукой. При этом одновременно с освобождением груза необходимо нажать кнопку «пуск» на секундомере.
Расстояние 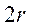 между центрами масс, противоположно
закреплённых грузов, измеряются мерной линейкой. Диаметры шкивов измеряются
штангенциркулем. Массы грузов 4 заданы с абсолютной погрешностью
между центрами масс, противоположно
закреплённых грузов, измеряются мерной линейкой. Диаметры шкивов измеряются
штангенциркулем. Массы грузов 4 заданы с абсолютной погрешностью 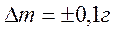 .
.
Перед выполнением опытов на маховике Обербека необходимо добиться симметричного распределения грузов на крестовине. Это делается путём перемещения грузов 2 на противоположных стержнях так, чтобы при ненатянутой нити грузы оставались в состоянии безразличного равновесия.
Для проведения опытов маховик приводят в равноускоренное вращательное движение, опуская груз m1 с заданной высоты и измеряя при этом время его движения t на пути h. Линейное ускорение движения груза можно вычислить по формуле
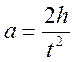 (18).
(18).
Так как при
движении груза нить сматывается со шкива без проскальзывания, то линейное
ускорение груза 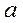 равно касательному
ускорению точек, лежащих на цилиндрической поверхности шкива. Следовательно,
угловое ускорение маховика
равно касательному
ускорению точек, лежащих на цилиндрической поверхности шкива. Следовательно,
угловое ускорение маховика
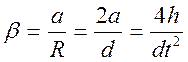 (19)
(19)
(где 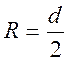 —
радиус шкива).
—
радиус шкива).
С другой
стороны согласно основному закону динамики вращательного движения (6) угловое
ускорение  пропорционально моменту силы
натяжения нити
пропорционально моменту силы
натяжения нити  и обратно пропорционально
моменту инерции I всей системы (блок, крестовина,
грузы) —
и обратно пропорционально
моменту инерции I всей системы (блок, крестовина,
грузы) —  . Момент силы
. Момент силы 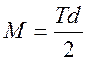
(где Т – сила натяжения нити, d/2 — плечо силы).
Согласно второму закону Ньютона действующая на нить сила
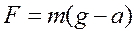 (20),
(20),
(где g –
ускорение свободного падения, 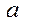 — линейное
ускорение поступательного движения груза).
— линейное
ускорение поступательного движения груза).
Поскольку нить не растяжима сила F, уравновешивается силой T. Следовательно, момент силы
 (21).
(21).
Выразив из
уравнения (6) 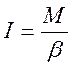 и подставив в эту формулу
и подставив в эту формулу 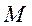 и
и 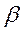 из
(18) и (20) получим:
из
(18) и (20) получим:
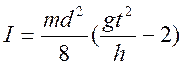 (22).
(22).
Как видно из (22), чтобы косвенно измерить момент инерции, надо прямыми измерениями найти массу груза,
создающего натяжение нити, диаметр блока, по которому движется точка приложения силы, высота с которой опускается груз, и время опускания.
Вычисленное по
формуле (22) значение момента инерции маховика 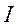 включает
в себя момент инерции крестовины с блоком
включает
в себя момент инерции крестовины с блоком  и
момент инерции четырёх грузов
и
момент инерции четырёх грузов 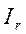 с массой m (2):
с массой m (2):
 (23).
(23).
Искомый момент инерции грузов
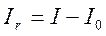 (24),
(24),
где  —
осевой момент инерции вращающихся грузов 2;
—
осевой момент инерции вращающихся грузов 2;
 —
осевой момент инерции маховика без грузов;
—
осевой момент инерции маховика без грузов;
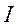 —
осевой момент инерции маховика с грузами.
—
осевой момент инерции маховика с грузами.
Осевой момент
инерции маховика без грузов  измеряется так
же, как и момент инерции
измеряется так
же, как и момент инерции 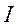 . В формулу
подставляются значения
. В формулу
подставляются значения 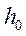 и
и 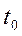 ,
измеренные при вращении крестовины со снятыми с неё грузами.
,
измеренные при вращении крестовины со снятыми с неё грузами.
Считая грузы материальными точками, можно рассчитать теоретическое значение осевого момента инерции по формуле (16):
 (25),
(25),
(где m – масса одного вращающегося груза 2, r – расстояние центра масс груза от оси вращения).
Сопоставление значений моментов инерции четырёх вращающихся грузов, рассчитанных по формулам (23) и (24) позволяет судить о качестве проделанной работы.
Проделав
косвенные измерения момента инерции груза 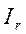 при
разных значениях расстояния
при
разных значениях расстояния 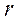 их центров от оси
вращения (поочерёдно размещая грузы 2 на концах стержней, на их середине и
вблизи оси крестовины), можно опытным путём установить характер зависимости
момента инерции от распределения массы относительно оси вращения. По определению
момента инерции, как меры инертности тела при вращательном движении, эта
зависимость является квадратичной (5). Графиком такой зависимости является
парабола
их центров от оси
вращения (поочерёдно размещая грузы 2 на концах стержней, на их середине и
вблизи оси крестовины), можно опытным путём установить характер зависимости
момента инерции от распределения массы относительно оси вращения. По определению
момента инерции, как меры инертности тела при вращательном движении, эта
зависимость является квадратичной (5). Графиком такой зависимости является
парабола 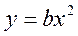 . Откладывая на оси
. Откладывая на оси  значения моментов инерции, рассчитанных
по формулам (23) и (24), а по оси
значения моментов инерции, рассчитанных
по формулам (23) и (24), а по оси 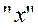 квадрат
расстояния
квадрат
расстояния 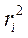 , можно построить экспериментальные и
теоретические параболы. При этом принимать коэффициент
, можно построить экспериментальные и
теоретические параболы. При этом принимать коэффициент  равным
массе 4-х грузов (
равным
массе 4-х грузов (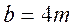 ). Совмещение точек таких
парабол служит подтверждением качества выполнения эксперимента и правомерности
применения модели материальных точек к однородным цилиндрам равной длины.
). Совмещение точек таких
парабол служит подтверждением качества выполнения эксперимента и правомерности
применения модели материальных точек к однородным цилиндрам равной длины.
Порядок выполнения работы.
1. Измерьте
диаметры шкивов  и
и 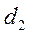 (рис.3).
Измерения проводите не менее 3-х раз для каждого шкива. Полученные данные
занесите в таблицу.
(рис.3).
Измерения проводите не менее 3-х раз для каждого шкива. Полученные данные
занесите в таблицу.
2. Установите верхний кронштейн 3 на выбранной высоте h так, чтобы груз m при движении вниз свободно проходил сквозь рабочие отверстия фотоэлектрических датчиков. Величину h занесите в таблицу.
3. Включите вилку шнура прибора в розетку электрической сети и нажмите клавишу «сеть». При этом крестовина маховика должна удерживаться электромагнитом в состоянии покоя.
4. Закрепите
один конец нити на бортике шкива и намотайте нить в один ряд на шкив меньшего
диаметра  . Перекиньте нить через блок 1, как
указано на рис. 3, и подвесьте на другой конец нити держатель с грузом (масса
держателя учитывается в m). Груз должен находиться над
верхним световым лучом. Величину m занесите в таблицу.
. Перекиньте нить через блок 1, как
указано на рис. 3, и подвесьте на другой конец нити держатель с грузом (масса
держателя учитывается в m). Груз должен находиться над
верхним световым лучом. Величину m занесите в таблицу.
5. Нажмите клавишу «сброс» и убедитесь в том, что секундомер не включен (на табло не появляются цифры).
6. Нажмите клавишу «пуск» и убедитесь, что груз движется вниз, пересекая оба световых луча и не задевая кронштейны. Проверьте зафиксировал ли секундомер время движения груза. Снова нажмите клавишу «сброс», и убедитесь в том, что секундомер не включен.
7. Приведите установку в исходное состояние и проделайте трижды опыт с вращением маховика без грузов, занося значения времени t опускания груза (рис.3, 4) массой m с высоты h в таблицу.
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ — МегаЛекции
НА МАХОВИКЕ ОБЕРБЕКА
Цель работы.Измерение характеристик движения маховика и определение моментов инерции грузов на его спицах.
Приборы и принадлежности: маховик Обербека с грузами на спицах; стойка со шкалой; набор грузов с подставкой; секундомер; штангенциркуль.
Введение
В лабораторной работе рассматривается вращательное движение маховика (рис. 1) относительно неподвижной оси.
Вращательным называется такое движение твердого тела, при котором все точки тела описывают окружности, лежащие в параллельных плоскостях. Центры этих окружностей лежат на одной прямой, называемой осью вращения.
Если на тело, закрепленное на неподвижной оси, действует сила, то тело приобретает угловое ускорение, направленное вдоль этой оси. Величина ускорения зависит не только от величины и направления силы, но и от точки ее приложения. Это отражено в понятии момента силы, который, как и сила, является векторной величиной. В случае вращения вокруг неподвижной оси угловое ускорение, направленное вдоль этой оси, определяется результирующей проекцией моментов всех сил на эту ось.
Основной закон динамики вращательного движения твердого тела утверждает, что угловое ускорение e тела, вращающегося относительно неподвижной оси, пропорционально результирующей проекции M моментов всех сил на ось вращения:
M = Ie.
Коэффициент пропорциональности I в этом равенстве характеризует инертные свойства тела при вращательном движении и называется моментом инерции.
Для определения понятия момента инерции мысленно разобъём тело на частицы, размеры которых достаточно малы, чтобы их можно было рассматривать как материальные точки массой Dmi. Момент инерции такой материальной точки
Ii = DmiRi2,
где Ri – расстояние точки до оси вращения.
Момент инерции тела или системы тел
I = = .
Понятие момента инерции отражает то, что инертные свойства тел при вращательном движении зависят не только от суммарной массы всех частиц тела, но и от распределения их по отношению к оси вращения. Момент инерции есть величина скалярная и всегда положительная. Из определения понятия момента инерции следует, что если система состоит из нескольких тел, то момент инерции системы равен сумме моментов инерции отдельных тел:
I = I1 + I2 + I3 + …
В данной лабораторной работе измеряют момент инерции маховика и грузов массой m0, находящихся на его спицах (см. рис. 1). Спицы крестовины жестко скреплены со шкивом. На шкив наматывается нить, к концу которой прикрепляется груз Р. Рядом с висящим грузом ставится вертикальная шкала для измерения пути h, пройденного грузом. Для приведения крестовины в ускоренное вращательное движение груз Р поднимают на высоту h, затем, груз без толчка отпускают и измеряют время t движения его на пути h. Поскольку движение груза является равноускоренным, линейное ускорение груза Р можно вычислить по формуле
a = . (1)
Так как при падении груза Р нить сматывается, то линейное ускорение а груза равно тангенциальному ускорению точек поверхности шкива. Следовательно, можно вычислить угловое ускорение крестовины:
e = a/r, (2)
где r – радиус шкива.
Рассматривая силы, действующие на груз, будем считать, что силы трения малы, и ими можно пренебречь. В этом случае ускорение груза определяется действием силы тяжести mg и силы натяжения нити Т.
На основании второго закона Ньютона
ma = mg — T, (3)
где т –масса груза Р.
Сила натяжения создает момент силы
M = T×r = m(g — a)r. (4)
Измерение момента инерции крестовины и грузов на ней производят, используя основной закон динамики вращательного движения:
M = Ie, (5)
где I – момент инерции вращающегося тела.
Из формулы (5), с учетом формул (4) и (2) следует, что
I = = . (6)
Момент инерции крестовины с грузами можно представить в виде
I = I0 + Ir, (7)
где I0 и Ir – моменты инерции крестовины без грузов и грузов соответственно.
Следовательно, для определения момента инерции закрепленных на крестовине грузов Ir необходимо определить по формуле (6) момент инерции крестовины с грузами I и ее момент инерции без грузов I0.
Так как линейные размеры грузов на спицах крестовины значительно меньше их расстояния до оси вращения, то их можно считать материальными точками. Поэтому момент инерции грузов можно определить по формуле
Ir = 4m0R2, (8)
где m0 – масса одного груза; R – расстояние грузов до оси вращения.
Порядок выполнения работы
I. Измерение моментов инерции I0 крестовины без грузов
1. Определить массу m грузa P с подставкой (значения масс указаны на грузах).
2. Измерить штангенциркулем радиус шкива r.
3. Намотать нить на шкив и подвесить груз Р с подставкой на нить. Отпустив груз Р без толчка, измерить время его движения на пути h.
4. Вычислить линейное ускорение падающего груза по формуле (1).
5. Измерения, описанные в 3 и 4, проделать три раза с различными значениями высоты h.
6. Вычислить по формуле (6) момент инерции крестовины I0 для каждого значения а. Найти среднее значение момента инерции I0СР.
7. Рассчитать погрешность DI0 определения I0 как среднюю абсолютную погрешность по формуле
DI0 = ,
Все результаты записать в таблицу, где рядом с обозначениями величин обязательно указать единицы их измерения.
Таблица
| Измеряемая величина | Вращение без грузов, R = 0 | Вращение с грузами на концах спиц, R =…,м | Вращение с грузами на середине спиц, R/2 =…м | ||||||
| h | |||||||||
| t | |||||||||
| a | |||||||||
| I | |||||||||
| I СР | |||||||||
| DI |
m = … кг; r = …. м; m0 = … кг;
II. Измерение моментов инерции грузов
1. Четыре груза с одинаковой массой m0 закрепить на концах спиц на одинаковых расстояниях R от центров грузов до оси вращения. Убедиться, что центр масс системы совпадает с осью вращения, т. е. система сбалансирована.
2. Записать значения m0 и R в таблицу.
3. Выполнить измерения, описанные в пунктах 3 – 5 раздела I.
4. Вычислить момент инерции крестовины с грузами I для каждого значения а. Найти среднее значение IСР.
5. Рассчитать погрешность DI определения I как среднюю абсолютную погрешность по формуле
DI = ,
6. Вычислить момент инерции грузов по формуле:
IГ = I СР — I0СР. (9)
7. Определить погрешность DIГ определения момента инерции грузов по формуле:
DIГ = DI + DI0.
8. Записать окончательный результат в виде:
I = IГ ± DIГ.
9. Рассчитать величину момента инерции грузов по формуле (8) и сравнить с полученным в пункте 8 экспериментальным значением.
10. Грузы переместить на середину спиц и закрепить их. Измерить расстояние R от центров грузов до оси вращения. Описанным выше методом (см. пункты 3 – 9 раздела II) определить значения их момента инерции.
Контрольные вопросы
1. Сформулируйте основной закон динамики вращательного движения.
2. Напишите формулу пути при равноускоренном поступательном движении опускающегося груза.
3. Напишите формулу связи углового ускорения маховика с линейным ускорением опускающегося груза.
4. Проделайте вывод формулы для определения момента инерции грузов на спицах маховика на основании основного закона динамики вращательного движения.
5. Дайте определение момента инерции тела.
6. При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением?
7. Можно ли в данной лабораторной работе изменить момент силы, не меняя массу груза на нити?
8. Почему в том случае, когда грузы ближе к оси вращения, время движения меньше?
Список литературы
1. Савельев И.В. Курс общей физики: В 3-х т. Т. 1. М.: – Наука, 1987.
2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000. – С. 294.
3. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.
Работа 60
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Методические указания к лабораторной работе
УДК 531
М — 38
Марченко В.И. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека. Методические указания к лабораторной работе. – М.: МИИТ, 2006,– 20 с.
Изложены физические основы динамики вращательного движения. Описана методика экспериментального измерения осевых моментов инерции твердых тел на маховике Обербека. Соответствует программе дисциплины «Физика» (раздел «Физические основы механики»). Предназначено для студентов 1 курса энергетических, механических и строительных специальностей.
Ó Московский государственный университет путей сообщения
( МИИТ), 2006
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Кафедра «Физика-I»
В. И. Марченко
Утверждено
редакционно-издательским
советом университета
ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ И ИЗМЕРЕНИЕ ОСЕВЫХ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ НА МАХОВИКЕ ОБЕРБЕКА.
Методические указания к лабораторной работе по дисциплине «Физика» №104 для студентов 1 курса энергетических, механических и строительных специальностей.
Москва – 2006
Работа №104. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека.
Цель работы. Усвоить основной закон динамики вращательного движения. Косвенно измерить момент инерции цилиндрических тел. Установить зависимость осевых моментов инерции вращающихся на маховике грузов от расстояния до оси вращения.
Приборы и принадлежности.Маховик Обербека, автоматический счётчик времени, четыре цилиндрических тела с одинаковой массой, масштабная линейка.
Введение.
Вращательным
движением тела назывется такое движение, при котором все точки тела движутся по
окружностям, плоскости которых параллельны друг другу, а центры лежат на одной
прямой, называемой осью вращения. Для любого элемента массы тела Dmi,
расположенного на расстоянии riот оси вращения, существует полная аналогия между
законами динамики поступательного и вращательного движений. Умножая левую и
правую части основного закона динамики поступательного движения точки ai = 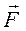 /Dmi на радиус-вектор точки
/Dmi на радиус-вектор точки 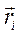 и, считая что в
этой точке сосредоточена часть массы тела
и, считая что в
этой точке сосредоточена часть массы тела 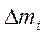 ,
получим:
,
получим: 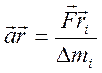 , где ai – линейное ускорение поступательного движения точки,
, где ai – линейное ускорение поступательного движения точки, 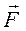 –
сила, приложенная в точке. Заменив в левой части полученнного равенства aiна
угловое ускорение
–
сила, приложенная в точке. Заменив в левой части полученнного равенства aiна
угловое ускорение 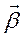 (связанные соотношением
(связанные соотношением 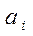 = bri):
= bri): 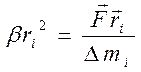 ,
придем к формуле связи между угловым ускорением (одинаковым для любой точки
тела) и приложенной силой Fi.
,
придем к формуле связи между угловым ускорением (одинаковым для любой точки
тела) и приложенной силой Fi.
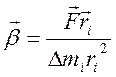 (*)
(*)
В этой формуле
векторное произведение 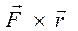 называется моментом силы
называется моментом силы 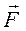 , действующей на i-ый
элемент массы тела, положение которого задано радиусом вектором
, действующей на i-ый
элемент массы тела, положение которого задано радиусом вектором 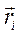 . В общем виде, когда сила F приложена к телу в точке на
растоянии r от оси вращения:
. В общем виде, когда сила F приложена к телу в точке на
растоянии r от оси вращения:
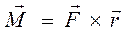 (1)
(1)
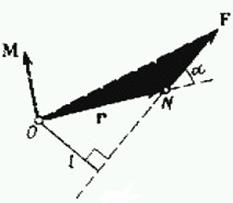
Как видно из равенства (1), момент силы – это векторное произведение действующей на тело силы на радиус-вектор точки ее приложения.
Векторы 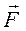 и
и 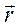 лежат
в плоскости окружности, по которой движется точка и в соответствии с правилом
умножения векторов, лежащих в одной плоскости, вектор-произведение
лежат
в плоскости окружности, по которой движется точка и в соответствии с правилом
умножения векторов, лежащих в одной плоскости, вектор-произведение 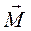 лежит в перпендикулярной плоскости.
Он направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости
лежит в перпендикулярной плоскости.
Он направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости 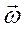 . Модуль вектора момента силы
вычисляется по формуле:
. Модуль вектора момента силы
вычисляется по формуле:
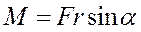 (2)
(2)
(где 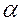 — угол между направлением вектора
— угол между направлением вектора 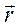 и направлением действия силы
и направлением действия силы 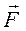 ) (Рис. 1).
) (Рис. 1).
Перпендикуляр 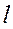 , опущенный из центра вращения О, на
направление действия силы
, опущенный из центра вращения О, на
направление действия силы 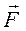 , называется
плечом силы. Как видно из рис. 1:
, называется
плечом силы. Как видно из рис. 1:
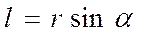 (3)
(3)
Заменяя в (2) 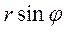 на
на 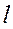 , получим:
, получим:
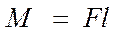 (4).
(4).
Рис.1 |
Согласно (4) модуль момента силы равняется произведению силы на плечо. Размерность момента силы:
[M] = кг . м2/с2.
Произведение 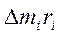 2 в знаменателе правой
части формулы (*) называется моментом инерции i-го
элемента массы тела
2 в знаменателе правой
части формулы (*) называется моментом инерции i-го
элемента массы тела
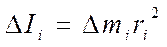 (5)
(5)
Момент инерции  характеризует инертные свойства
точки тела, в которой сосредоточена малая часть его массы Dmi,
а момент инерции всего тела равен сумме моментов инерции всех точек:
характеризует инертные свойства
точки тела, в которой сосредоточена малая часть его массы Dmi,
а момент инерции всего тела равен сумме моментов инерции всех точек:
 (5’)
(5’)
Равномерность [I]= кг . м2.
После
подстановки в равенство (*) значений момента силы, действующей на i-ый элемент массы 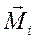 (1) и момента
инерции этого элемента (5) получим:
(1) и момента
инерции этого элемента (5) получим:
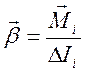
Такое же
соотношение сохранится и для всего тела, поскольку угловое ускорение всех его
точек одинаково, а отношение 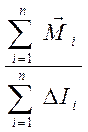 равно отношению
момента силы приложенной к телу М к моменту инерции тела относительно
оси его вращения I.
равно отношению
момента силы приложенной к телу М к моменту инерции тела относительно
оси его вращения I.
Таким образом, мы получили зависимость между
угловым ускорением 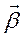 , моментом силы,
приложенной к телу М и моментом инерции тела относительно оси вращения I.
, моментом силы,
приложенной к телу М и моментом инерции тела относительно оси вращения I.
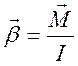 (6)
(6)
Это соотношение является основным законом динамики вращательного движения твёрдого тела, вокруг неподвижной оси, который формулируется так: угловое ускорение тела пропорционально моменту приложенной к телу силы и обратно пропорционально моменту инерции тела относительно заданной оси вращения.
Он аналогичен второму закону Ньютона при поступательном движении тела с постоянной массой m.
Момент инерции тела относительно оси (осевой момент инерции) в равенстве (6) является аналогом массы, но он зависит не только от величины массы тела, но и от распределения массы относительно этой оси. Как масса является мерой инертности тела при поступательном движении, так и момент инерции есть мера инертности тела при вращательном движении. Каждое тело, независимо от того, вращается оно или покоится, обладает определённым моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или покоится.
При непрерывном распределении массы тела по его объему вычисление момента инерции сводится к интегрированию бесконечно малых элементов массы dm = r dV, умноженных на квадрат расстояния от оси вращения.
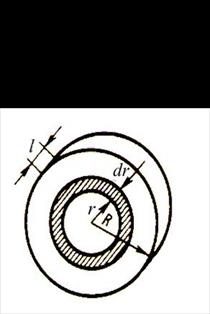
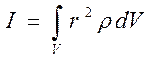 (7)
(7)
(где 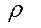 —
плотность вещества в элементе объёма тела dV,
находящегося на расстоянии r от оси вращения).
—
плотность вещества в элементе объёма тела dV,
находящегося на расстоянии r от оси вращения).
ческого слоя радиусом r и толщиной dr.
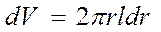 ,
,
(где l – длина цилиндра).
Подстановка dV в (7) и интегрирование по переменной r, в пределах от 0 до R даёт:
 .
.
Нетрудно увидеть,
что 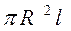 — это объём цилиндра V, а
— это объём цилиндра V, а  =m
– его масса. Таким образом, момент инерции цилиндра относительно оси,
проходящей через центры его оснований вычисляется по формуле
=m
– его масса. Таким образом, момент инерции цилиндра относительно оси,
проходящей через центры его оснований вычисляется по формуле
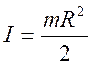 (8).
(8).
По формуле (8)
вычисляют осевые моменты инерции дисков, блоков, маховых колёс, вращающихся
вокруг неподвижной оси, проходящей через центры инерции этих тел,
перпендикулярно плоскостям окружностей, по которым движутся точки тела. Центром
инерции тела называется точка тела, положение которой относительно начала
координат задаётся радиус-вектором , 
(где 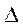 mi– масса i-го элемента тела, а
mi– масса i-го элемента тела, а 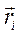 — радиус-вектор элемента).
— радиус-вектор элемента).
Таким же образом можно показать, что момент инерции тонкостенного кольца, обруча или трубы с радиусом R и массой m вычисляются по одинаковой формуле:
 (9).
(9).
Изучение законов вращательного движения твердого тела на маятнике Обербека
Принадлежности: маятник Обербека, грузы, штангенциркуль, миллиметровая линейка, секундомер.
Краткая теория. Под твердым телом в механике понимается такое тело, взаимное расположение частей которого остается неизменным во время движения. При движении такое тело выступает как единое целое. Произвольное плоское движение твердого тела можно представить в виде суммы двух движений: поступательного и вращательного. При поступательном движении за один и тот же промежуток времени все точки тела получают равные по величине и направлению перемещения, вследствие чего скорости и ускорения этих точек в каждый момент времени оказываются одинаковыми. При вращательном движении все точки твердого тела движутся по окружностям, центры которых находятся на одной и той же прямой, называемой осью вращения. Для описания вращательного движения необходимо задать положение оси вращения и угловую скорость тела в каждый момент времени.
Круговое движение материальной точки. Пусть материальная точка массой 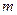 вращается вокруг неподвижной оси
вращается вокруг неподвижной оси  , проходящей через точку
, проходящей через точку 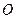 (рис. 1). Для описания вращательного движения введем понятия моментов. Их три: момент инерции, момент импульса и момент силы.
(рис. 1). Для описания вращательного движения введем понятия моментов. Их три: момент инерции, момент импульса и момент силы.
Момент инерции равен произведению массы материальной точки на квадрат расстояния между точкой и остью вращения 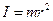 .
.
Под действием приложенной силы точка движется с некоторой линейной скоростью 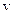 и обладает при этом импульсом
и обладает при этом импульсом 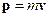 . Направление вектора импульса
. Направление вектора импульса 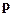 совпадает с направлением вектора скорости.
совпадает с направлением вектора скорости.
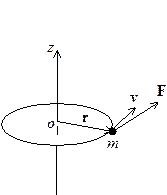 Рис. 1
Рис. 1
|  Рис. 2
Рис. 2
|
Момент импульса равен векторному произведению радиус-вектора 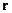 на вектор
на вектор 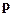 :
:
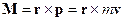 . .
|
Момент силы определяется как векторное произведение:
 . .
|
Величина радиус-вектора 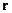 равна расстоянию
равна расстоянию 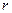 от оси вращения до материальной точки (до точки приложения силы).
от оси вращения до материальной точки (до точки приложения силы).
Из определения моментов видно, что  – скалярная величина, а
– скалярная величина, а 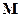 и
и 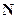 – векторы (псевдовекторы), направление которых определяется по правилу векторного произведения.
– векторы (псевдовекторы), направление которых определяется по правилу векторного произведения.
Вращение твердого тела вокруг неподвижной оси. Абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Моментом инерции тела относительно оси вращения называется величина  , равная сумме произведений элементов масс
, равная сумме произведений элементов масс  на квадрат их расстояния до оси:
на квадрат их расстояния до оси:
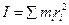 . .
|
Момент импульса твердого тела относительно точки 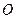 , находящейся на оси вращения, определяется как сумма моментов импульса
, находящейся на оси вращения, определяется как сумма моментов импульса  отдельно взятых частиц:
отдельно взятых частиц:
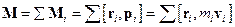 . .
|
Момент силы, действующей на твердое тело, есть сумма моментов сил, действующих на отдельные частицы:
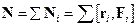 . .
|
Здесь 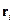 – радиус-вектор
– радиус-вектор 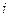 -ой частицы.
-ой частицы.
Для всякой системы частиц справедливо уравнение:
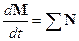 . .
| (1) |
Уравнение (1) носит название основного закона динамики вращательного движения твердого тела. Оно выражает второй закон Ньютона для вращательного движения и аналогично уравнению для поступательного движения тела. Роль силы при вращательном движении играет момент силы, роль массы – момент инерции тела, роль импульса – момент импульса.
Учитывая, что момент импульса относительно произвольной оси вращения в проекции на ось равен
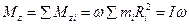 , ,
| (2) |
основной закон можно записать в виде:
 | (3) |
где 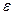 – проекция углового ускорения на ось
– проекция углового ускорения на ось  ,
, 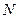 – геометрическая сумма моментов сил, приложенных к телу, также в проекции на ось вращения.
– геометрическая сумма моментов сил, приложенных к телу, также в проекции на ось вращения.
Описание прибора. Маятник Обербека представляет собой маховик крестообразной формы (рис. 2). На четырех взаимно перпендикулярных стержнях укреплены грузы одинаковой массы 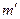 , которые могут перемещаться вдоль стержней и закрепляться в нужном положении. На общей оси с маховиком находится шкив радиуса
, которые могут перемещаться вдоль стержней и закрепляться в нужном положении. На общей оси с маховиком находится шкив радиуса 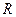 . На шкив наматывается нить с прикрепляемым к концу грузом массы
. На шкив наматывается нить с прикрепляемым к концу грузом массы 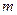 . Последний, опускаясь, приводит маховик в равноускоренное вращательное движение. Таким образом, к точке на поверхности шкива приложена касательная сила, направленная вниз и равная по величине силе натяжения нити; эта сила и создает вращающий момент (момент силы).
. Последний, опускаясь, приводит маховик в равноускоренное вращательное движение. Таким образом, к точке на поверхности шкива приложена касательная сила, направленная вниз и равная по величине силе натяжения нити; эта сила и создает вращающий момент (момент силы).
учитывая (3) и пренебрегая силами трения, можно записать уравнение вращательного движения маятника
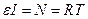 , ,
| (4) |
уравнение поступательного движения груза на нити
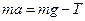 | (5) |
и уравнение, связывающее линейное и угловое ускорения,
 . .
| (6) |
Здесь 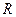 – радиус шкива,
– радиус шкива, 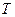 – сила натяжения нити,
– сила натяжения нити, 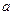 – ускорение движения груза на нити,
– ускорение движения груза на нити, 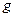 – ускорение силы тяжести,
– ускорение силы тяжести, 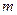 – масса груза.
– масса груза.
Из совместного решения уравнений (4–6) следует, что ускорение имеет постоянную величину:
 . .
| (7) |
С другой стороны, груз 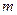 движется равноускоренно, начиная со скорости, равной нулю, и за время
движется равноускоренно, начиная со скорости, равной нулю, и за время 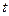 проходит расстояние
проходит расстояние 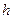 , поэтому ускорение
, поэтому ускорение
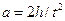 . .
|
1-й случай проверки: постоянный момент инерции, различные моменты сил.
Из уравнения (3) имеем:
 . .
| (8) |
Уравнения (4–8) дают:
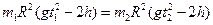 , ,
|
и окончательно имеем:
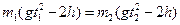 . .
| (9) |
В уравнение (9) входят величины, которые можно определить экспериментально.
2-й случай проверки: различные моменты инерции; постоянными величинами являются масса падающего разновеса и радиус шкива.
По теореме о параллельном переносе осей моментов инерции (теорема Штейнера) имеем:
 | (10) |
где 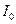 – момент инерции тела
– момент инерции тела 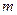 относительно оси, проходящей через центр масс тела,
относительно оси, проходящей через центр масс тела,  – момент инерции того же тела относительно оси, удаленной на расстояние
– момент инерции того же тела относительно оси, удаленной на расстояние 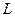 от прежней и расположенной параллельно ей.
от прежней и расположенной параллельно ей.
Пусть 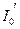 – суммарный момент инерции четырех грузов (масса каждого из них равна
– суммарный момент инерции четырех грузов (масса каждого из них равна 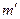 ) в случае расположения их центров масс на оси вращения. Если центры масс находятся на расстоянии
) в случае расположения их центров масс на оси вращения. Если центры масс находятся на расстоянии 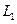 от оси вращения, то момент инерции
от оси вращения, то момент инерции  системы из четырех тел равен
системы из четырех тел равен
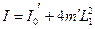 . .
|
Если 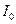 – момент инерции маятника без грузов, то полный момент инерции маятника с грузами, расположенными на расстоянии
– момент инерции маятника без грузов, то полный момент инерции маятника с грузами, расположенными на расстоянии 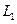 от оси вращения, будет равен:
от оси вращения, будет равен:
 . .
|
При расположении грузов на расстоянии 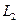 соответственно имеем:
соответственно имеем:
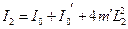 . .
|
Разность моментов инерции, если 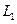 не равно
не равно 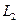 , будет равна:
, будет равна:
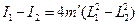 . .
| (11) |
Решение уравнений (4) и (11) дает:
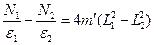 . .
| (12) |
Решая совместно уравнения (4–7) и (12), получим окончательное равенство для проверки второго случая:
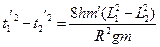 . .
| (13) |
Уравнения (9) и (13) используются для проверки законов вращательного движения твердого тела в двух различных случаях: во-первых, когда изменяется момент силы при постоянном моменте инерции, во-вторых, когда изменяется момент инерции при неизменной массе тела, подвешенного на нити. Оба уравнения получены без учета трения в оси маятника и трения о воздух.
Порядок выполнения работы
1-й случай проверки (постоянный момент инерции)
1. Измерить высоту, на которую опустится укрепленный на нити груз массы 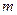 .
.
2. Установить и закрепить грузы 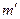 на одинаковом расстоянии от оси вращения, например, минимальном. Масса грузов
на одинаковом расстоянии от оси вращения, например, минимальном. Масса грузов 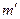 указана на маятнике.
указана на маятнике.
3. Затем одновременно отпустить маятник и пустить секундомер, записать время падения груза массой 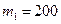 г. Измерения провести 5–7 раз, определить среднее значение времени
г. Измерения провести 5–7 раз, определить среднее значение времени  .
.
4. Точно так же определить время  падения груза массой
падения груза массой 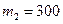 г (т.е. при другом значении момента силы).
г (т.е. при другом значении момента силы).
5. По результатам измерений проверить уравнение (9), и, следовательно, уравнение (3).
6. Результат записать в виде равенства. Объяснить причину заметного различия, если оно имеется.
2-й случай проверки (постоянная масса разновеса)
1. Сохраняя грузы 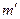 в прежнем положении, измерить расстояние
в прежнем положении, измерить расстояние 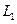 от оси вращения до центров грузов.
от оси вращения до центров грузов.
2. При помощи штангенциркуля измерить радиус шкива, на который наматывается нить.
3. Выбрать груз 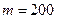 г (или 300 г), время падения которого для расстояния
г (или 300 г), время падения которого для расстояния 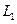 определено. Это будет время
определено. Это будет время 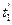 .
.
4. Перемещая грузы на расстояние 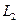 (измерить его) от оси вращения, изменить момент инерции маятника.
(измерить его) от оси вращения, изменить момент инерции маятника.
5. Измерить время опускания выбранного груза (не менее 5–7 раз) и определить среднее значение времени 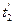 .
.
6. Проверить соотношение (13) и записать ответ.
Контрольные вопросы
1. Что называется моментом инерции материальной точки и моментом инерции твердого тела относительно некоторой оси?
2. Определение момента силы. При каких условиях сила не создает вращающего момента?
3. Что такое импульс и момент импульса?
4. Как определить направление векторов момента силы и момента импульса?
5. Различаются ли кинетическая энергия вращающегося вокруг неподвижной оси тела и кинетическая энергия тела, которое катится (в качестве примера можно использовать колесо)?
6. Доказать теорему Штейнера. В чем суть теоремы?
7. Записать основной закон динамики для поступательного и вращательного движений твердого тела.
8. Маятник Обербека раскручивается падающим грузом 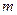 . При каком положении грузов
. При каком положении грузов 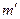 (см. рис.2) катушка будет раскручиваться с наибольшим ускорением?
(см. рис.2) катушка будет раскручиваться с наибольшим ускорением?
9. С какими способами проверки основного закона динамики вращательного движения знакомит данная работа?
10. Вывести уравнения для обоих случаев проверки законов вращательного движения твердого тела.
Список рекомендуемой литературы
1. Савельев И.В. Курс общей физики. М., 1977. т. 1. гл. 5.
2. Ландау Л.Д., Ахиезер А.И., Лифшиц Е.М. Курс общей физики. Механика и молекулярная физика. М., 1965. Гл. 3.
3. Рымкевич П.А. Курс физики. М., 1975. гл. 3.
Лабораторная работа № 3
Рекомендуемые страницы: