Два вида физических величин: скалярные величины и векторные величины | LAMPA
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
- скалярная величина;
- векторная величина.
Скалярная величина — это просто число. Ну, например, масса тела MMM — это скалярная величина. Пусть, например, M=3M = 3M=3 кг. Время ttt — скалярная величина. Например, время может быть такое: t=7t = 7t=7 сек.
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
вектор — это направленный отрезок.
Стрелка — по-простому. У стрелки (вектора) есть длина (длина стрелки) и направление. Вектор — это нечто, что обладает длиной и направлением.
Примеры векторных величин: сила F⃗\vec {F}F⃗, скорость V⃗\vec{V}V⃗.
Длина вектора обозначается специальным символом — символом модуля | | — это две параллельные палочки. Например, ∣F⃗∣|\vec{F}|∣F⃗∣ — модуль силы; ∣V⃗∣|\vec{V}|∣V⃗∣ — модуль скорости. Модуль вектора — это уже число. Например, может быть так, что модуль силы ∣F⃗∣=8|\vec{F}|=8∣F⃗∣=8 H, модуль скорости ∣V⃗∣=8|\vec{V}|=8∣V⃗∣=8 м/с.
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т. д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Может возникнуть вопрос: а как отличить векторную величину от скалярной? Или так: как я узнаю, что передо мной вектор, а не скаляр?
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Физические величины, обозначение, векторные и скалярные
Тестирование онлайн
Тест по теме: «Физические величины»
Что такое физическая величина?
Нас окружает много различных материальных предметов. Материальных, потому что их возможно потрогать, понюхать, увидеть, услышать и еще много чего можно сделать. То, какие эти предметы, что с ними происходит, или будет происходить, если что-нибудь сделать: кинуть, разогнуть, засунуть в печь. То, почему с ними происходит что-либо и как именно происходит? Все это изучает физика. Поиграйте в игру: загадайте предмет в комнате, опишите его несколькими словами, друг должен угадать что это. Указываю характеристики задуманного предмета. Прилагательные: белый, большой, тяжелый, холодный. Догадались? Это холодильник. Названные характеристики — это не научные измерения вашего холодильника. Измерять у холодильника можно разное. Если длину, то он большой.![]() Если цвет, то он белый. Если температуру, то холодный. А если его массу, то выйдет, что он тяжелый. Представляем, что один холодильник можно исследовать с разных сторон. Масса, длина, температура — это и есть физическая величина.
Если цвет, то он белый. Если температуру, то холодный. А если его массу, то выйдет, что он тяжелый. Представляем, что один холодильник можно исследовать с разных сторон. Масса, длина, температура — это и есть физическая величина.
Но это лишь та небольшая характеристика холодильника, которая приходит на ум мгновенно. Перед покупкой нового холодильника можно ознакомиться еще с рядом физических величин, которые позволяют судить о том, какой он, лучше или хуже, и почему он стоит дороже. Представь масштабы того, на сколько все окружающее нас разнообразно. И на сколько разнообразны характеристики.
Обозначение физической величины
Все физические величины принято обозначать буквами, чаще греческого алфавита. НО! Одна и та же физическая величина может иметь несколько буквенных обозначений (в разной литературе).
И, наоборот, одной и той же буквой могут обозначаться разные физические величины.
Несмотря на то, что с такой буквой вы могли не сталкиваться, смысл физической величины, участие ее в формулах остается прежним.
Векторные и скалярные величины
В физике существует два вида физических величин: векторные и скалярные. Основное их отличие в том, что векторные физические величины имеют направление. Что значит физическая величина имеет направление? Например, число картофелин в мешке, мы будем называть обыкновенными числами, или скалярами. Еще одним примером такой величины может служить температура. Другие очень важные в физике величины имеют направление, это, например, скорость; мы должны задать не только быстроту перемещения тела, но и путь, по которому оно движется. Импульс и сила тоже имеют направление, как и смещение: когда кто-нибудь делает шаг, можно сказать не только, как далеко он шагнул, но и куда он шагает, то есть определить направление его движения. Векторные величины лучше запомнить.
Почему над буквами рисуют стрелку?
Рисуют стрелку только над буквами векторных физических величин. Согласно тому, как в математике обозначают вектор! Действия сложения и вычитания над этими физическими величинами выполняются согласно математическим правилам действий с векторами.
В чем сила измеряется?
Во всех учебниках и умных книжках, силу принято выражать в Ньютонах, но кроме как в моделях которыми оперируют физики ньютоны ни где не применяются. Это крайне неудобно.
Ньютон newton (Н) — производная единица измерения силы в Международной системе единиц (СИ).
Исходя из второго закона Ньютона, единица ньютон определяется как сила, изменяющая за одну секунду скорость тела массой один килограмм на 1 метр в секунду в направлении действия силы.
Таким образом, 1 Н = 1 кг·м/с².
Килограмм-сила (кгс или кГ) — гравитационная метрическая единица силы, равная силе, которая действует на тело массой один килограмм в гравитационном поле земли. Поэтому по определению килограмм-сила равна 9,80665 Н. Килограмм-сила удобна тем, что её величина равна весу тела массой в 1 кг.
1 Н ≈ 0,10197162 кгс ≈ 0,1 кгс
1 Н = 1 кг x 1м/с2.
Закон тяготения
Каждый объект Вселенной притягивается к любому другому объекту с силой, пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.![]() 2 \right ) }$. Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т.е. гравитационное взаимодействие приводит всегда к притяжению тел.
2 \right ) }$. Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т.е. гравитационное взаимодействие приводит всегда к притяжению тел.
В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал и сила зависят только от положения тела в данный момент времени.
Тяжелее — Легче
Вес тела ${\large P}$ выражается произведением его массы ${\large m}$ на ускорение силы тяжести ${\large g}$.![]() 2 }$
2 }$
В результате произведение ${\large m \cdot g }$, а следовательно и вес уменьшаются в 6 раз.
Но нельзя обозначить оба эти явления одним и тем же выражением «сделать легче». На луне тела становятся не легче, а лишь менее стремительно падают они «менее падучи»))).
Векторные и скалярные величины
Векторная величина (например сила, приложенная к телу), помимо значения (модуля), характеризуется также направлением. Скалярная же величина (например, длина) характеризуется только значением. Все классические законы механики сформулированы для векторных величин.
|
|

На рис. 1 изображены различные варианты расположения вектора ${ \large \overrightarrow{F}}$ и его проекции ${ \large F_x}$ и ${ \large F_y}$ на оси ${ \large X}$ и ${ \large Y}$ соответственно:
- A. величины ${ \large F_x}$ и ${ \large F_y}$ являются ненулевыми и положительными
- B.
- C. ${\large F_y}$ — положительная ненулевая величина, ${\large F_x}$ равна нулю, т.к. вектор ${\large \overrightarrow{F}}$ направлен перпендикулярно оси ${\large X}$
Момент силы
Моментом силы называют векторное произведение радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы.![]()
Важно понимать, что ось мы можем выбирать произвольным образом — если тело не вращается, то сумма моментов сил относительно любой оси равна нулю. Второе важное замечание — если сила приложена к точке, через которую проходит ось, то момент этой силы относительно этой оси равен нулю (поскольку плечо силы будет равно нулю).
Проиллюстрируем вышесказанное примером, на рис.2. Предположим, что система, изображенная на рис.![]() {gr}}}$
{gr}}}$
Теперь рассмотрим условие равенства моментов сил, действующих на опору, относительно оси, проходящей через точку А (и, как мы договаривались ранее, перпендикулярную плоскости рисунка):
${\large N \cdot l_1 — N_2 \cdot \left ( l_1 +l_2 \right ) = 0}$
Обратите внимание, что в уравнение не вошёл момент силы ${\large \overrightarrow{N_1}}$, поскольку плечо этой силы относительно рассматриваемой оси равно ${\large 0}$. Если же мы по каким-либо причинам хотим выбрать ось, проходящую через точку С, то условие равенства моментов сил будет выглядеть так:
${\large N_1 \cdot l_1 — N_2 \cdot l_2 = 0}$
Можно показать, что с математической точки зрения два последних уравнения эквивалентны.
Центр тяжести
Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.
Центр масс
Точка центра масс замечательна тем , что если на частицы образующие тело (неважно будет ли оно твердым или жидким, скоплением звезд или чем то другим) действует великое множество сил (имеются ввиду только внешние силы, поскольку все внутренние силы компенсируют друг друга), то результирующая сила приводит к такому ускорению этой точки, как будто в ней вся масса тела ${\large m}$.
Положение центра масс определяется уравнением:
${\large R_{c.m.} = \frac{\sum m_i\, r_i}{\sum m_i}}$
Это векторное уравнение, т.е. фактически три уравнения — по одному для каждого из трех направлений. Но рассмотрим только ${\large x}$ направление. Что означает следующее равенство?
${\large X_{c.m.} = \frac{\sum m_i\, x_i}{\sum m_i}}$
Предположим тело разделено на маленькие кусочки с одинаковой массой ${\large m}$, причем полная масса тела равна будет равна числу таких кусочков ${\large N}$, умноженному на массу одного кусочка, например 1 грамм. Тогда это уравнение означает, что нужно взять координаты ${\large x}$ всех кусочков, сложить их и результат разделить на число кусочков. Иными словами, если массы кусочков равны то ${\large X_{c.m.}}$ будет просто средним арифметическим ${\large x}$ координат всех кусочков.
Тогда это уравнение означает, что нужно взять координаты ${\large x}$ всех кусочков, сложить их и результат разделить на число кусочков. Иными словами, если массы кусочков равны то ${\large X_{c.m.}}$ будет просто средним арифметическим ${\large x}$ координат всех кусочков.
|
центр масс сложного тела лежит на линии, соединяющей центры масс двух составляющих его частей |
Масса и плотность
Масса — фундаментальная физическая величина. Масса характеризует сразу несколько свойств тела и сама по себе обладает рядом важных свойств.
- Масса служит мерой содержащегося в теле вещества.
- Масса является мерой инертности тела. Инертностью называется свойство тела сохранять свою скорость неизменной (в инерциальной системе отсчёта), когда внешние воздействия отсутствуют или компенсируют друг друга.
 При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса.
При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса. - Массы тел являются причиной их гравитационного притяжения друг к другу (см. раздел «Сила тяготения»).
- Масса тела равна сумме масс его частей. Это так называемая аддитивность массы. Аддитивность позволяет использовать для измерения массы эталон — 1 кг.
- Масса изолированной системы тел не меняется со временем (закон сохранения массы).
- Масса тела не зависит от скорости его движения. Масса не меняется при переходе от одной системы отсчёта к другой.
- Плотностью однородного тела называется отношение массы тела к его объёму:
${\large p = \dfrac {m}{V} }$
Плотность не зависит от геометрических свойств тела (формы, объёма) и является характеристикой вещества тела.![]() Плотности различных веществ представлены в справочных таблицах. Желательно помнить плотность воды: 1000 кг/м3.
Плотности различных веществ представлены в справочных таблицах. Желательно помнить плотность воды: 1000 кг/м3.
Второй и третий законы Ньютона
Взаимодействие тел можно описывать с помощью понятия силы. Сила — это векторная величина, являющаяся мерой воздействия одного тела на другое.
Будучи вектором, сила характеризуется модулем (абсолютной величиной) и направлением в пространстве. Кроме того, важна точка приложения силы: одна и та же по модулю и направлению сила, приложенная в разных точках тела, может оказывать различное воздействие. Так, если взяться за обод велосипедного колеса и потянуть по касательной к ободу, то колесо начнёт вращаться. Если же тянуть вдоль радиуса, никакого вращения не будет.
Второй закон Ньютона
Произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу:
${\large m \cdot \overrightarrow{a} = \overrightarrow{F} }$
Второй закон Ньютона связывает векторы ускорения и силы. Это означает, что справедливы следующие утверждения.
Это означает, что справедливы следующие утверждения.
- ${\large m \cdot a = F}$, где ${\large a}$ — модуль ускорения, ${\large F}$ — модуль равнодействующей силы.
- Вектор ускорения имеет одинаковое направление с вектором равнодействующей силы, так как масса тела положительна.
Третий закон Ньютона
Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.
Принцип суперпозиции
Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции.
Принцип суперпозиции сил. Пусть на тело действуют силы ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ Если заменить их одной силой ${\large \overrightarrow{F} = \overrightarrow{F_1} + \overrightarrow{F_2} \ldots + \overrightarrow{F_n}}$, то результат воздействия не изменится.
Сила ${\large \overrightarrow{F}}$ называется равнодействующей сил ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ или результирующей силой.
📝векторные и скалярные велечины
Часто многим ученикам или даже студентам сложно понять отличия векторной и скалярной величины. Поэтому я хотел бы объяснить максимально понятным языком суть каждого из этих понятий и на примерах показать главные их отличия. Так как они оба часто используются в математических задачах, для правильного и быстрого решения которых нужно знать это.
Начнём с определений:
Векторной величиной, или вектором (в широком смысле), называется всякая величина, обладающая направлением.
Скалярной величиной, или скаляром, называется величина, не обладающая направлением.
То есть у вас уже должна появиться основная картина, если есть направление у величины, то это вектор, а если нет, то это скаляр. Далее рассмотрим всё на конкретных примерах.
Далее рассмотрим всё на конкретных примерах.
Пример 1. Когда какая-то сила действует на материальную точку, то она будет вектором, так как она обладает направлением. Так же и скорость материальной точки — тоже вектор.
Пример 2. А от уже температура тела будет скаляром, так как с ней не связано никакое направление. Поэтому масса тела и его плотность — тоже будут скалярами.
Если не учитывать направление векторной величины, то ее, как и скалярную, можно измерить, выбрав соответствующую единицу измерения. Но в этом случае полученное число, характеризует скалярную величину полностью, а векторную только частично. Её можно полностью охарактеризовать направленным отрезком, предварительно задав линейный масштаб. И это хорошо показано в следующем примере.
Пример 3. Направленный отрезок АВ при введенном масштабе MN, изображающем единицу силы (1 Н) (более подробно смотрите на рисунке), характеризует силу в 3,5 Н, направление которой совпадает с направлением отрезка АВ (указанным стрелкой).
Думаю, после таких явных данных у вас уже не должно появиться проблем, при различии этих понятий.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Урок 11. импульс. закон сохранения импульса — Физика — 10 класс
Физика, 10 класс
Урок 11.Импульс. Закон сохранения импульса
Перечень вопросов, рассматриваемых на уроке:
1) импульс тела, импульс силы, замкнутая система;
2) абсолютно упругий, абсолютно неупругий удар;
3) закон сохранения импульса;
4) границы применимости закона;
5) проявление закона сохранения импульса в технике и природе.
Глоссарий по теме
Импульс тела (материальной точки) — векторная величина, равная произведению массы тела на скорость тела.
Импульс силы — произведение силы на время её действия.
Импульс тела равен сумме импульсов отдельных его элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы.
Внутренние силы — это силы, с которыми взаимодействуют тела системы между собой.
Внешние силы — это силы, создаваемые телами, которые не принадлежат к данной системе.
Замкнутая система — это система, в которой внешние силы не действуют или сумма внешних сил равна нулю.
Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Абсолютно упругий удар — столкновение тел, при котором тела не соединяются и их внутренние энергии остаются неизменными.
Закон сохранения импульса: векторная сумма импульсов тел, образующих замкнутую систему, не меняется при любых взаимодействиях между телами системы.
Основная и дополнительная литература по теме урока:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 123 – 130.
Рымкевич А. П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1979/10/zakon_sohraneniya_impulsa_reak.htm
Основное содержание урока
Импульс тела (материальной точки) представляет собой векторную величину, равную произведению массы тела на скорость тела:
Направление импульса всегда совпадает с направлением скорости, так как m > 0, то
Любое движущееся тела имеет импульс.
Единица измерения импульса:
.
Произведение силы на время её действия называется импульсом силы.
Второй закон Ньютона в импульсной форме.
Изменение импульса тела (материальной точки) равно импульсу действующей на него силы:
Импульс тела равен сумме импульсов отдельных его элементов:
Импульс системы тела равен векторной сумме импульсов каждого из тел системы:
Импульс обладает интересным свойством сохраняться, которое есть только у нескольких физических величинах.![]()
Силы, с которыми взаимодействуют тела системы друг с другом, называются внутренними, а силы, создаваемые телами, которые не принадлежат этой системе, являются внешними силами.
Система, в которой внешние силы не действуют или сумма внешних сил равна нулю, называется замкнутой.
Полный импульс тел сохраняется, в замкнутой системе тела могут только обмениваться импульсами.
Столкновение тел представляет собой взаимодействие тел при их относительном перемещении. Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Закон сохранения импульса при неупругом ударе:
Абсолютно упругий удар — столкновение тел, при котором тела не соединяются в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса при упругом ударе:
Закон сохранения импульса.
Если внешние силы на систему не действуют или их сумма равна нулю, то импульс системы остается неизменным:
Закон сохранения импульса является одним из основных законов физики.![]()
Границы применимости закона сохранения импульса: замкнутая система.
Закон сохранения импульса с честью выдержал испытание временем и до сих пор он продолжает свое триумфальное шествие.
Он дал неоценимый инструмент для исследования ученым, как один из фундаментальных законов физики, ставя запрет одним процессам и открывая дорогу другим.
Действие этого закона проявляется в науке, в технике, в природе и в повседневной жизни. Всюду этот закон работает отлично — реактивное движение, атомные и ядерные превращения, взрыв и т.д.
Во многих повседневных ситуациях помогает разобраться понятие импульса.
Рене Декарт попытался использовать термин «импульс» вместо силы. Это связано с тем, что силу трудно измерить, а массу и скорость измерить несложно. Поэтому вместо импульса часто говорят количество движения (Именно Ньютон первым назвал произведение массы тела на скорость количеством движения).
Декарт понимал большое значение понятия количества движения — или импульса тела — как произведения массы тела на скорость.![]() Но он совершил ошибку, не рассматривая количество движения как векторную величину. Ошибка эта была исправлена в начале XVIII века.
Но он совершил ошибку, не рассматривая количество движения как векторную величину. Ошибка эта была исправлена в начале XVIII века.
Используя закон сохранения импульса можно «найти» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.
Разбор тренировочных заданий
1. Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг∙м/с. Чему равна масса тела?
Дано: ∆t =𝟤 c; g ≈ 𝟣0 м∕с2; ∆р =𝟣0 кг∙м ∕с.
Найти: m.
Решение:
т.к. тело свободно падает.
Запишем второй закон Ньютона в импульсной форме:
∆р = F∆t,
F = mg – т.к. при свободном падении действует только сила тяжести,
тогда ∆р = mg∆t, откуда:
Делаем расчёт:
Ответ: m = 0,5 кг.
2. Тело массой 400 г изменяет свои координаты по закону:
Тело будет иметь импульс 8 Н·с после начала движения за промежуток времени равный __________?
Дано:
m = 400 г = 0,4 кг; p = 8 Н∙с
Найти: t.
Решение:
Записываем формулу импульса:
p = mv,
скорость равна 1-й производной от х по времени:
v = x'(t)= 4 + 4t
Из 1-й формулы скорость равна: v = p/m
4 + 4t = 8 / 0,4,
4t = 20 − 4 = 16,
t = 16 / 4,
t = 4 с.
Ответ: t = 4 с.
8. Векторные бозоныВекторные бозоны в распадах с участием мюонов и электронов Достигнутые энергии
соударений протонов на БАК обеспечивает рождение большого количества векторных
бозонов
W± и Z. Регистрация векторных
бозонов указывает на присутствие в событии жесткого рассеяния и позволяет
исследовать физику электрослабых взаимодействий. Напомним, что масса W бозона составляет mW = 80.385±0.015 ГэВ,
масса
Z бозона равна mZ = 91.1876±0.0021 ГэВ (PDG2012, http://pdg.lbl.gov), их значения связаны
соотношением
mW = mZ∙cosθW, θW – угол слабого
смешивания.
Мюонный спектрометр
установки позволяет регистрировать пары мюонов с противоположными электрическими
зарядами. Спектр инвариантных масс таких пар, полученный в самом начале
эксперимента, показан на рис.8.1. На нем хорошо видны резонансные состояния
мезонов ρ/ω, φ, J/ψ, ψ’, и сигнал Z бозона на конце спектра.
Рисунок интересен тем, что все эти состояния наблюдаются в одном эксперименте,
тогда как ранее для открытия части из них строились новые ускорители. Полное сечение рождения Z бозонов, умноженное на
парциальную ширину распада в электроны и мюоны, σZ/γ* ∙ Вr(Z/γ*→ℓℓ), ℓ = е,μ, составило
0.82±0.06(стат.)±0.05(сист.)нб для массы Z бозона в интервале
66-116 ГэВ. Полное сечение рождения W→ℓν, ℓ = е,μ, измерено равным Распределения векторных бозонов, рожденных на адронных коллайдерах, являются
важной проверкой Стандартной модели, где они определяются структурными функциями
сталкивающихся адронов (PDF) и величиной констант
связи бозонов с партонами. Кроме того, для этого процесса существенны поправки
высших порядков теории возмущений КХД (NLO+NNLO). Инклюзивное
дифференциальное сечение
Z бозонов по быстроте dσz/d׀yz׀ приведено на рис.6 слева. Большая масса Z бозона и жесткость
процесса рождения обеспечивает большую величину поперечной массы Z бозона и,
соответственно, относительно небольшие значения быстроты. На рис.8.6а показаны объединенные данные по зарядовой асимметрии лептонов от
распада W из трех экспериментов. Соотношение сечений рождения W+ и W— , умноженных на относительную парциальную ширину распадов (бренчинг), в объеме установки ATLAS показано на рис.8.7 слева в сравнении с предсказаниями разных PDF. Темная область соответствует 68% области достоверности. Аналогичное сравнение для распадов заряженных и нейтральных бозонов приведено на рис.8.7 справа. Рис.8.7. Сечения рождения W+ и W— бозонов, умноженных на относительную парциальную ширину распадов (Br), в объеме установки ATLAS – слева. Сравнение тех же величин для распадов заряженных и нейтральных бозонов приведено справа. Показаны предсказания разных PDF. Темная область соответствует 68% области достоверности. Инвариантность распадов
векторных бозонов по отношению к электронам и мюонам показана путем сравнения
отношений сечений, умноженных на бренчинг, для W и Z в сравнении с
предсказаниями Стандартной модели на рис. Рождение векторных бозонов сопровождается рождением струй. Характеристики такого
совместного рождения тщательно исследуются и сопоставляются с расчетами [5,6]. В
качестве примера на рис.8.9 слева приведены сечения рождения Z бозонов в событиях с
числом струй
Njet больше или равным
заданному числу, т.е. ≥ Njet. Струи определялись алгоритмом анти-кТ с радиусом R = 0.4.
В распределении учитывались струи с рТ> 30 ГэВ. Сравнение данных с
предсказаниями различных генераторов NLO QCD показано в нижней части
рисунка и на самом рисунке. В работах [5,6] детально анализируются зависимости
от поперечного импульса струй, углового расстояния между ними. На рис.8.9 справа
показаны распределения разности азимутальных углов Δφ между двумя лидирующими
струями в событиях с рождением Z бозона, когда в событии
имеется по крайней мере две струи с рТ> 30 ГэВ/с и |y| < 4. Поляризация W бозоновВ распадах W бозонов с участием мюонов и электронов в рр взаимодействиях при 7 ТэВ на интегральной светимости 35 пб-1 была измерена поляризация W бозонов [9]. Измерения поляризации особенно чувствительны к механизму рождения частицы. На адронных коллайдерах при малых поперечных импульсах рождение W бозонов описывается преимущественно электрослабыми механизмами в лидирующем порядке ud → W+ и du → W— . В протонных соударениях на БАК кварки несут большую долю импульса начального
протона, чем антикварки. Это приводит к тому, что распределения Wбозонов в продольном направлении сдвинуты в
сторону движения кварка. В безмассовом приближении кварки имеют левые
спиральности (left-handed), антикварки – правые (right-handed). В итоге в областях
фрагментации протона (больших значениях быстроты ׀yW ׀) W-бозоны должны иметь
преимущественно левые спиральности. ug → W+d, ud → W+g и gd → W+ u. Поскольку во всех трех
реакциях участвует глюон g со спином 1, то простой анализ, использованный в
предыдущем случае для небольших рТW , неприменим. Требуется
точный расчет спиральности конечного состояния. В лидирующем (LO) и следующим за
лидирующем (NLO) порядке теории
возмущения КХД такие расчеты выполнены в работах [10] для
р и рр
взаимодействий. Из-за более сложных механизмов рождения W бозонов с большими
поперечными импульсами появляется вклад состояний с продольной поляризацией.
Вклад такого состояния модно обозначить как ƒ0. Измерение этой величины
в эксперименте представляет особый интерес, поскольку этот эффект напрямую
связан с массивной природой калибровочных бозонов.
Тау (τ) лептоны играют важную роль при поиске новой физики на БАК. Для её
обнаружения необходимо понимать роль фоновых по отношению к новым процессам
распадов векторных бозонов
Z → ττ и W → τν. Сами по себе эти
распады важны для сравнения с распадами Z и W в электроны и мюоны для
проверки лептонной инвариантности. Методика измерений тау лептонов
включает несколько этапов, и важно быть уверенными в достоверности результатов. где ℓ – лептон. Таблица 1. Эффективные области наблюдения распада Z→ττ для различных мод регистрации τ-лептона: с образованием мюона τμ, электрона τе или адронов τh. Таблица 2. Измеренные сечения распадов Z→ττ для различных мод распада τ-лептона для эффективного объема установки (fiducial cross section) в верхней части таблицы и полных сечений в нижней части. Сравнение измеренных сечений для распадов Zв ее, μμ и ττ представлено на рис. 8.12. Сравнение сечений для распадов W на еν, μν и τν приведено на рис.8.13. Литература к разделу 8
|
12. СКАЛЯРЫ и ВЕКТОРЫ — Физика это просто!!! 2016
В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».
Упрощенно можно сказать, что скаляр — это просто число.
Векторная величина — это когда есть число, которое имеет еще и направление в пространстве. Вектор в трехмерном пространстве можно представить в виде тройки чисел, каждое из которых есть компонента вектора относительно соответствующей координаты в трехмерной системе координат.
Запутанно?
Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.
Для тех, кто любит попроще — первый том Фейнмановских лекций по физике.
Для нас важно понять два момента:
1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.
Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.
2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.
Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.
И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.
Представили?
Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (Ах, Аy, Аz). Будет ли эта тройка чисел вектором?
Будет! Мы же сами задали эти три числа, как координаты вектора.
Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.
А теперь вывод. То, что важно для физики!
Если у нас есть три какие-то величины (возможно, мы даже не знаем, связаны ли они между собой), которые изменяются с изменением системы координат, по такому же закону, по которому изменяются компоненты вектора из предыдущего абзаца ((Ах, Аy, Аz) —> (Аx’, Аy’, Аz’)), то мы можем смело утверждать, что эти три величины представляют собой компоненты какого-то вектора.
Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!
Рассмотрим подробнее физические величины в нашем трехмерном пространстве. Зададим прямоугольную систему координат X, Y, Z. Помним, что у нас есть еще время t.
Теперь посмотрим, что есть что.
Путь вектор или скаляр? Скаляр. Почему?
Перемещение — вектор. У перемещения есть начало и конец, есть величина перемещения и направление перемещения. Таким образом, у него три компоненты — три величины, по одной на каждую из координат.
Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!
Физическая величина |
Размерность |
|
Скорость | м/с | Вектор |
Ускорение | м/с2 | Вектор |
Сила | Н = кг*м/с2 | Вектор |
Вес | Н = кг*м/с2 | Вектор |
Давление | Па = кг/(м*с2) | Скаляр |
Плотность | кг/м3 | Скаляр |
Импульс массы | кг*м/с | Вектор |
Импульс силы | Н*с | Вектор |
Работа | Дж = кг*м2/с2 | Скаляр |
Энергия | Дж = кг*м2/с2 | Скаляр |
Момент силы | Дж= кг*м2/с2 | Вектор |
Температура | К | Скаляр |
Относительное удлинение | % | Скаляр |
Механическое напряжение | Н/м2 | Скаляр |
Количество теплоты | Дж = кг*м2/с2 | Скаляр |
Удельная теплоемкость | Дж/ | Скаляр |
Удельная теплота плавления | Дж/кг = м2/с2 | Скаляр |
Удельная теплота парообразования | Дж/кг = м2/с2 | Скаляр |
Электрический заряд | Кл = с*А | Скаляр |
Напряженность электрического поля | В/м = кг*м/(с3*А) | Вектор |
Работа по перемещению заряда в эл. поле | Дж = кг*м2/с2 | Скаляр |
Потенциал электрического поля | В == кг*м2/(с3*А) | Скаляр |
Напряжение | В == кг*м2/(с3*А) | Скаляр |
Электрическая емкость | Ф == с4*А2/ (кг*м2) | Скаляр |
Сопротивление проводника | Ом == кг*м2/(с3*А2) | Скаляр |
Работа эл. тока | Дж = кг*м2/с2 | Скаляр |
Мощность эл. тока | Вт = кг*м2/с3 | Скаляр |
Электродвижущая сила | В == кг*м2/(с3*А) | Скаляр |
Магнитная индукция | Тл == кг/(с2*А) | Вектор |
Магнитный поток | Вб == кг*м2/(с2*А) | Вектор |
Индуктивность | Гн == кг*м2/(с2*А2) | Скаляр |
Энергия магнитного поля | Дж = кг*м2/с2 | Скаляр |
Фокусное расстояние | м | Скаляр |
Оптическая сила линзы | Дптр = 1/м | Скаляр |
Длина волны | м | Скаляр |
Частота | Гц = 1/с | Скаляр |
Скаляров и векторов
Чтобы лучше понять науку о движении необходимо использовать некоторые математические идеи из векторный анализ . Большинство людей знакомятся с переносчиками в средней школе или колледже, но для учащихся начальной и средней школы, а также для детей с математическими проблемами:
НЕ ПАНИКА! .В векторном анализе есть много сложных частей, и мы не собираемся туда идти.Мы собираемся ограничиться самыми основами. Векторы позволяют нам смотреть на сложные, многомерные проблемы. как более простая группа одномерных задач. Мы будем интересоваться в основном определениями Слова немного странные, но идеи очень мощный, как вы увидите. Если вы хотите узнать больше о векторах, вы можете скачать этот отчет о векторный анализ.
Математика и естественные науки были изобретены людьми для описания и понять мир вокруг нас.Мы живем в (по крайней мере) четырехмерном мире, управляемом течение времени и трех пространственных измерений; вверх и вниз, влево и вправо, вперед и назад. Мы наблюдаем, что есть некоторые количества и процессы в наш мир, который зависит от направления , в котором они происходят, и есть некоторые количества, которые не зависят по направлению. Например, объем объекта, трехмерное пространство, которое занимает объект, не зависит от направления.Если у нас есть железный блок объемом 5 кубических футов, и мы перемещаем его вверх и вниз и затем налево и направо, у нас все еще остается железный блок объемом 5 кубических футов. С другой стороны, место расположения, объекта действительно зависит от направления. Если мы переместим блок 5 кубических футов на 5 миль к север, результирующее местоположение сильно отличается от если мы переместим его на 5 миль к востоку. Математики и ученые называют количество которое зависит от направления , вектор, величина .Количество которое не зависит от направления, называется скалярной величиной .
Векторные величины имеют две характеристики: величину и направление. Скалярные величины имеют только величину. Когда сравнение две векторные величины одного типа, необходимо сравнить обе величина и направление. Для скаляров вам нужно только сравнивать величина. При выполнении любой математической операции над векторной величиной (например, сложение, вычитание, умножение..) ты должен рассмотреть возможность как по величине, так и по направлению. Это делает работу с вектором величины немного сложнее скаляров.
На слайде мы перечисляем некоторые из обсуждаемых физических величин. в Руководство по воздухоплаванию для новичков и сгруппируйте их в векторные или скалярные величины. В частности интерес, силы которые работают на летающих самолетах, масса, тяга, и аэродинамические силы, все векторные величины.Результирующий движение самолета с точки зрения водоизмещения, скорости и ускорение — это тоже векторные величины. Эти количества можно определить, применяя Законы Ньютона для векторов. Скалярные величины включают большую часть термодинамическое состояние переменные, связанные с двигательной установкой, такие как плотность, давление и температура порохов. В энергия Работа, а также энтропия с двигателями также связаны скалярные величины.
У векторов есть величина и направление, у скаляров — только величина. Тот факт, что величина встречается как для скаляров, так и для векторов, может привести к некоторой путанице. Есть несколько величин, например скорость , которые имеют очень специальные определения для ученых. По определению, скорость — это скалярная величина вектора скорости . Автомобиль при движении по дороге скорость составляет 50 миль в час. Его скорость 50 миль / ч в северо-восточном направлении.Это может быть очень сбивает с толку, когда термины используются как синонимы! Другой пример масса и масса . Вес — это сила, которая является вектором и имеет величину и направление. Масса — скаляр. Масса и масса связаны друг с другом, но это не одно и то же.
В то время как законы Ньютона описывают результирующее движение твердого тела существуют специальные уравнения, описывающие движение жидкостей, газы и жидкости.Для любой физической системы масса, импульс, и энергия системы должны быть сохранены. Масса и энергия — скалярные величины, а импульс — вектор количество. Это приводит к связанной системе уравнений, называется Уравнения Навье-Стокса, которые описывают, как жидкости ведут себя под воздействием внешних сил. Эти уравнения являются жидким эквивалентом законов движения Ньютона. и их очень сложно решить и понять.Упрощенная версия уравнений, названная Уравнения Эйлера может быть решена для некоторых проблем с жидкостями.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Физика элементарных частиц — Значение массы вектора
Я подозреваю, что вы сбиты с толку и на самом деле слышите о массивных скалярных частицах и массивных векторных частицах, а не о терминах «скалярная масса» или «векторная масса», хотя контекст, в котором вы слышали эти термины, может прояснить ситуацию и пролить свет на другое значение в конкретном контексте. {2}
долл. СШАКто-то мог бы назвать компонент энергии «скалярной массой», а компонент импульса «векторной массой», поскольку энергия — это скалярная величина (она определяется одним числом), а импульс — это векторная величина (она имеет как величину, так и направление). .Еще раз, однако, я лично никогда не слышал, чтобы это использовалось.
Другой контекст, в котором термин «векторная масса» используется в некоторых статьях, — это масса векторного бозона.
ОБНОВЛЕНО НА ОСНОВЕ РАЗЪЯСНЕНИЯ ВОПРОСА:
И победителем является ни один из вышеперечисленных. Исходя из контекста, указанного в уточненном вопросе, векторная масса относится к чему-то, описанному в этой публикации Physics Stack. Об этом говорится в соответствующей части:
Меня интересует вычисление (однопетлевой) бета-функции для «векторная масса» в SUSY-модели.Под векторной массой я подразумеваю что-то вроде μQμQ в сверхпотенциальном члене
μQQ ¯QμQQ ¯Q,
где Q, Q¯Q, Q¯ — суперполя в фундаментальной и сопряженной представления калибровочной группы соответственно. Это очевидно полностью аналогичен суперсимметричному массовому члену Хиггса
μHuHdμHuHd.
Как и член μμ Хиггса в MSSM, в этой модели член μQμQ будет находиться в сочетании с другими массовыми терминами в соответствующей массе матрицы.Например, ур. 8.1.2 в книге Мартина о суперсимметрии A Primer (http://arxiv.org/abs/hep-ph/9709356) показывает коэффициенты квадратичные члены скалярных полей H0u, H0dHu0, Hd0 представляют собой комбинации значений μ, m2Hu, m2Hd, b, g, g′μ, mHu2, mHd2, b, g, g ′. А еще есть Матрицы масс Хиггсино (или массовые матрицы нейтралино и чарджино и т. Д. точно, частью которого являются Хиггсино), в котором он также появляется.
В моей модели тот факт, что член μQμQ находится в сочетании с другие массовые члены следует из наличия других членов в суперпотенциал, такой как термин Юкавы
yuQU¯HuyuQU¯Hu,
, а также из мягких условий взлома SUSY.
Проще говоря, это обобщение массы, возникающей из Хиггса Юкавы, хотя я понятия не имею, почему это можно назвать «векторной массой». Возможно, кто-то другой из stack exchange сможет прояснить этот лингвистический скачок.
КОНЕЦ ОБНОВЛЕНИЯ
Скалярные бозоны
Скалярная частица — это бозон с полным угловым моментом (обычно называемым «спином»), равным 0, который не является псевдоскалярным (т.е. имеет четную, а не нечетную четность). (Спин частицы — это в основном симметрия, которая относится к тому, какое вращение частица должна испытать, чтобы действовать так же, как она действовала до вращения.) Скалярная частица в принципе может быть массивной или безмассовой, но на практике все известные скалярные бозоны массивны. Если бы ньютоновская гравитация переносилась бозоном и распространялась со скоростью света, а не мгновенно, ее переносил бы безмассовый фундаментальный скалярный бозон (но, конечно, ньютоновская гравитация на самом деле является лишь грубым приближением общей теории относительности, и поэтому таких бозонов нет).
Единственным известным фундаментальным скалярным бозоном является бозон Хиггса с массой около 125 ГэВ $ / c ^ {2} $.{2} $, который играет важную роль в переносе остаточной сильной силы, связывающей протоны и нейтроны в атомных ядрах. Остаточные сильные силовые поля, которые связывают протоны и нейтроны, действительно вносят вклад в массу атомов атомных ядер, которые они связывают (которые, вероятно, можно было бы назвать «псевдоскалярной массой» или можно было бы сократить до «скалярной массы»).
Векторные бозоны
Векторная частица — это бозон со спином 1 (в зависимости от его четности это может быть либо истинный векторный бозон, либо аксиальный векторный бозон).{2} $). Первые три включают различные комбинации верхних и нижних валентных кварков и антикварков. У фи-мезона есть странный кварк и кварк-антистран в качестве валентных кварков.
Тензорные бозоны
Для полноты, если бозон имеет спин-2, он называется тензорным бозоном. Существует один широко предполагаемый фундаментальный безмассовый тензорный бозон — гравитон. Существует множество массивных тензорных мезонов, которые представляют собой составные бозоны, связанные сильным взаимодействием, большинство из которых обычно рассматриваются как возбужденные состояния низших спиновых бозонов.
В целом
Все эти частицы подчиняются статистике Бозе-Эйнштейна, поэтому их называют бозонами. Действительно, все частицы с целым спином являются бозонами.
Масса массивных фундаментальных бозонов и масса фундаментальных фермионов (по крайней мере, кварков и заряженных лептонов, мы не совсем уверены, откуда берется масса нейтрино) возникает в результате взаимодействия рассматриваемой фундаментальной частицы. в поле Хиггса.
Масса составных мезонов возникает частично из-за комбинации массы кварков в этих мезонах, которая возникает из поля Хиггса, и частично из-за массы-энергии глюонных полей, связывающих эти кварки, которые можно было бы назвать «векторная масса». В мезонах, состоящих из легких кварков (верхних, нижних и странных), большая часть массы приходится на глюонное поле. В мезонах, состоящих из тяжелых кварков (очаровательных и нижних), большая часть массы приходится на валентные кварки в мезоне.
вектор | Определение, физика и факты
Вектор , в физике величина, которая имеет как величину, так и направление. Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами.Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник.Если A, B и C — векторы, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C. Величины, такие как смещение и скорость, обладают этим свойством (закон коммутативности). , но есть величины (например, конечные вращения в пространстве), которые не являются векторами и поэтому не являются векторами.
векторный параллелограмм для сложения и вычитанияОдин из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм.Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов. Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopdia Britannica, Inc.Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. .Нет операции, соответствующей делению на вектор. См. векторный анализ для описания всех этих правил.
Правило правой руки для векторного векторного произведенияОбычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения задается формулой v w sin θ , где θ — это угол между исходными векторами v и w .
Encyclopædia Britannica, Inc. Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасХотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Сила и масса | Безграничная физика
Сила
Сила — это любое влияние, которое заставляет объект изменяться в отношении его движения, направления или геометрической конструкции.
Цели обучения
Разработайте взаимосвязь между массой и ускорением при определении силы
Основные выводы
Ключевые моменты
- Сила указывается как векторная величина, что означает, что она имеет элементы как величины, так и направления.Масса и ускорение соответственно.
- С точки зрения непрофессионала, сила — это толчок или тяга, которые можно определить с помощью различных стандартов.
- Динамика — это исследование силы, которая заставляет объекты и системы двигаться или деформироваться.
- Внешние силы — это любые внешние силы, действующие на тело, а внутренние силы — это любые силы, действующие внутри тела.
Ключевые термины
- сила : Сила — это любое влияние, которое заставляет объект претерпевать определенные изменения, касающиеся его движения, направления или геометрической конструкции.
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
Обзор сил
В физике сила — это любое влияние, которое заставляет объект претерпевать определенные изменения, касающиеся его движения, направления или геометрической конструкции. Он измеряется в системе СИ — Ньютон.Сила — это сила, которая может заставить объект с массой изменять свою скорость, то есть ускоряться, или которая может вызвать деформацию гибкого объекта. Сила также может быть описана интуитивно понятными понятиями, такими как толчок или тяга. Сила имеет как величину, так и направление, что делает ее векторной величиной.
Что такое сила? : Описывает, что такое силы и что они делают.
Качества силы
Исходная форма второго закона Ньютона гласит, что результирующая сила, действующая на объект, равна скорости, с которой изменяется его импульс.Этот закон также означает, что ускорение объекта прямо пропорционально чистой силе, действующей на объект, происходит в направлении чистой силы и обратно пропорционально массе объекта.
Как мы уже упоминали, сила — это векторная величина. Вектор — это одномерный массив с элементами как величины, так и направления. В векторе силы масса [latex] \ text {m} [/ latex] является составляющей величины, а ускорение [latex] \ text {a} [/ latex] — составляющей направления.Уравнение для силы записано:
[латекс] \ text {F} = \ text {m} \ cdot \ text {a} [/ latex]
Понятия, связанные с силой, включают тягу, которая увеличивает скорость объекта; сопротивление, уменьшающее скорость объекта; и крутящий момент, который вызывает изменения скорости вращения объекта. Силы, которые не действуют равномерно на все части тела, также вызывают механические напряжения — технический термин, обозначающий воздействия, вызывающие деформацию материи. В то время как механическое напряжение может оставаться внутри твердого объекта, постепенно деформируя его, механическое напряжение в жидкости определяет изменения ее давления и объема.
Динамика
Динамика — это изучение сил, которые заставляют объекты и системы двигаться. Чтобы понять это, нам нужно рабочее определение силы. Наше интуитивное определение силы, то есть толчка или тяги, — хорошее место для начала. Мы знаем, что толчок или притяжение имеют как величину, так и направление (следовательно, это векторная величина) и могут значительно различаться в каждом отношении.
показывает несколько примеров «тяни-толкай» природы силы. Верхний левый пример — это система шкивов.Сила, которую кто-то должен был бы потянуть за кабель, должна была бы равняться и превышать силу, создаваемую массой объекта и действием силы тяжести на этот объект, чтобы система двигалась вверх. Правый верхний пример показывает, что любой объект, лежащий на поверхности, по-прежнему будет оказывать на эту поверхность силу. Нижний пример — это два магнита, притягивающиеся друг к другу под действием магнитной силы.
Примеры силы : Некоторые ситуации, в которых действуют силы.
Масса
Масса — это физическое свойство материи, которое зависит от размера и формы материи и выражается в килограммах в системе СИ.
Цели обучения
Обоснуйте значение понимания массы в физике
Основные выводы
Ключевые моменты
- Масса определяется как количественная мера сопротивления объекта ускорению.
- Согласно второму закону движения Ньютона, если на тело фиксированной массы m действует единственная сила F, его ускорение a определяется как F / m.
- Масса занимает центральное место во многих понятиях физики, включая вес, импульс, ускорение и кинетическую энергию.
- Согласно второму закону движения Ньютона, если на тело фиксированной массы m действует единственная сила F, его ускорение a определяется как F / m.
Ключевые термины
- масса : количество вещества, которое содержится в теле, независимо от его массы или объема. Это одно из четырех основных свойств материи. В системе СИ измеряется в килограммах.
Что такое масса?
Все элементы обладают физическими свойствами, значения которых могут помочь описать физическое состояние элемента. Изменения этих свойств могут описывать элементные преобразования. Физические свойства не меняют химическую природу вещества. Физическое свойство, которое мы покрываем в этом атоме, называется массой.
Масса определяется как количественная мера сопротивления объекта ускорению. Термины «масса» и «вес» часто меняют местами, но это неверно.Вес — это другое свойство материи, которое, хотя и связано с массой, является не массой, а, скорее, величиной гравитационной силы, действующей на данное тело материи. Масса — это внутреннее свойство, которое никогда не меняется.
Единицы массы
Чтобы что-то измерить, необходимо установить стандартное значение, которое будет использоваться по отношению к объекту измерения. Это отношение называется единицей. Международная система единиц (СИ) измеряет массу в килограммах или кг. Существуют и другие единицы массы, в том числе следующие (в системе СИ принимаются только первые две):
- т — Тонна; 1т = 1000кг
- u — атомная единица массы; 1у ~ = 1.66 × 10 -27 кг
- sl — пуля
- фунт-фунт
Концепции, использующие массу
- Масса, см.
- Ньютон Второй закон — масса играет центральную роль в определении поведения тел. 2} \ vert [/ latex]
Квазиупругая аксиально-векторная масса из экспериментов по рассеянию нейтрино на ядрах
A. Liesenfeld et al., Phys. Lett. B 468 , 20 (1999) [arXiv: nucl-ex / 9
Артикул ОБЪЯВЛЕНИЯ Google Scholar
В. Бернар, Л. Элуадрири, У.-Г. Meißner, J. Phys. G 28 , R1 (2002) [arXiv: hep-ph / 0107088]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
А. Бодек, С. Аввакумов, Р. Брэдфорд, Х. Бадд, arXiv: 0709.3538 [hep-ex]
K2K Collaboration, R. Gran et al., Phys. Ред. D 74 , 052002 (2006) [arXiv: hep-ex / 0603034]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
MiniBooNE Collaboration, A.A. Агилар-Аревало и др., Phys. Rev. Lett. 100 , 032301 (2008) [arXiv: 0706.0926 [hep-ex]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
MiniBooNE Collaboration, T.Катори, AIP Conf. Proc. 967 , 123 (2007) [arXiv: 0709.4498 [hep-ex]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
P.E. Бостед, Phys. Ред. C 51 , 409 (1995)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Х. Бадд, А. Бодек, Дж. Аррингтон, arXiv: hep-ex / 0308005
Р. Брэдфорд, А. Бодек, Х. Бадд, Дж. Аррингтон, Nucl.Phys. Proc. Дополнение 159 , 127 (2006) [arXiv: hep-ex / 0602017]
Статья ОБЪЯВЛЕНИЯ Google Scholar
R.A. Смит, Э.Дж. Мониш, Nucl. Phys. B 43 , 605 (1972)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
R.A. Смит, Э.Дж. Мониш, Nucl. Phys. B 101 , 547 (1975) [Исправление]
Статья Google Scholar
Т. Новей, Proc. R. Soc. Лондон A 301 , 113 (1967)
ADS Статья Google Scholar
R.L. Kustom et al., Phys. Rev. Lett. 22 , 1014 (1969)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
W.A. Mann et al., In: Proceedings of 16th International Conference on High Energy Physics, National Accelerator Laboratory, Chicago-Batavia, Illinois, 6–13 сентября 1972 г., изд.Джексон, А. Робертс (Национальная ускорительная лаборатория, Батавия, Иллинойс, 1973), статья № 784
W.A. Mann et al., Phys. Rev. Lett. 31 , 844 (1973)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
ANL-Purdue Collaboration, S.J. Barish et al., Препринты COO-1428-428, ANL-HEP-CP-75-38 (неопубликовано)
R.A. Зингер, в: Материалы Международной конференции по физике нейтрино и астрофизике, «Нейтрино’77», Баксанская долина, СССР, 18–24 июня 1977 г., изд.М.А.Маркова и др. (Изд-во «Наука», Москва, СССР, 1978), Т. 2, стр. 95
S.J. Barish et al., Phys. Ред. D 16 , 3103 (1977)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
К.Л. Миллер и др., Phys. Ред. D 26 , 537 (1982)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
E.G. Cazzoli et al., в: Материалы Международной конференции по нейтрино, Аахен, Западная Германия, 8–12 июня 1976 г., изд. Х. Файсснер, Х. Рейтлер, П. Зервас (Vieweg, 1977), стр. 405
E.G. Cazzoli et al., Препринт BNL-21677, NG-349, Brookhaven National Laboratory, 1976 (не опубликовано)
A.M. Кнопс и др., В: Труды тематической конференции по физике нейтрино на ускорителях, Оксфорд, Англия, 4–7 июля 1978 г., изд. Авторы: A.G. Michette, P.B. Рентон (Лаборатория Резерфорда, 1978), стр.62
A.M. Cnops et al., Препринт BNL-24848, OG431, Brookhaven National Laboratory, 1978 (не опубликовано)
G. Fanourakis et al., Phys. Ред. D 21 , 562 (1980)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
N.J. Baker et al., Phys. Ред. D 23 , 2499 (1981)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
T. Kitagaki et al., Phys. Ред. D 34 , 2554 (1986)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Т. Китагаки и др., В: Материалы 12-й Международной конференции по нейтринной физике и астрофизике, «Нейтрино’86», Сендай, Япония, 3–8 июня 1986 г., изд. Т. Китагаки, Х. Юта (World Scientific, 1987), стр. 525
K. Abe et al., Phys. Rev. Lett. 56 , 1107 (1986)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
L.A. Ahrens et al., Phys. Ред. D 35 , 785 (1987)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
L.A. Ahrens et al., Phys. Lett. B 202 , 284 (1988)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
T. Kitagaki et al., Phys. Ред. D 42 , 1331 (1990)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
М. Сакуда, в: Материалы 4-го Международного семинара по колебаниям нейтрино и их происхождению («ПОЛДЕНЬ 2003»), Канадзава, Япония, 10–14 февраля 2003 г., изд. Ю. Сузуки и др. (World Scientific, River Edge, 2004), стр. 253
К. Фуруно и др., Доклад на 2-м международном семинаре по нейтрино-ядерным взаимодействиям в области нескольких ГэВ, NuInt’02, Калифорнийский университет, Ирвин, 12–15 декабря 2002 г., RCNS-03-01, Препринт КЭК 2003-48, сентябрь 2003 г. (не опубликовано)
Асратян А.Е. и др., В: Материалы 12-й Международной конференции по нейтрино «Нейтрино’82», Балатонфюред, Венгрия, 14–19 июня 1982 г., изд. А. Френкель, Л. Дженик (Центральный научно-исследовательский институт физики, Будапешт, 1982 г.), Дополнение Том. 2, стр. 139
T. Kitagaki et al., Phys. Ред. D 28 , 436 (1983)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Асратян А.Е. и др., Яд. Физ. 39 , 619 (1984) [Сов. J. Nucl. Phys. 39 , 392 (1984)]
Google Scholar
Асратян А.Е. и др., Phys. Lett. B 137 , 122 (1984)
Статья ОБЪЯВЛЕНИЯ Google Scholar
В.В. Аммосов и др., Письма. Ж. Эксп. Теор. Физ. 43, , 554 (1986) [Письма в ЖЭТФ. 43 , 716 (1986)]
Google Scholar
Сотрудничество ИФВЭ-ИТЭП-МЭИ, В.В. Аммосов и др., Z. Phys. C 36 , 377 (1987)
Статья ОБЪЯВЛЕНИЯ Google Scholar
Н. Сувонджанди, докторская диссертация, Университет Цинциннати, Цинциннати, 2004 г., FERMILAB-THESIS-2004-67, Национальная ускорительная лаборатория Ферми, Иллинойс, 2004 г. (не опубликовано), UMI 31-20857
Х. Бурмейстер и др., В: Труды неофициальной конференции по экспериментальной нейтринной физике, ЦЕРН, Женева, 20–22 января 1965 г., изд.К. Франзинетти, Желтый отчет ЦЕРН № 65-32, Европейская организация ядерных исследований, Женева, 1965 г., стр. 25
К. Франзинетти, Лекция на Чикагской встрече Американского физического общества, Чикаго, 28 октября 1965 г., желтый отчет ЦЕРН № 66-13, Европейская организация ядерных исследований, Женева, март 1966 г. ( неопубликовано)
ECM Янг, докторская диссертация, желтый отчет ЦЕРН № 67-12, Европейская организация ядерных исследований, Женева, 1967 (неопубликовано)
A. Orkin-Lecourtois, C.A. Пикетти, Нуово Цим. A 50 , 927 (1967)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
M. Holder et al., Nuovo Cim. A 57 , 338 (1968)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Будагов И. и др., Lett. Nuovo Cimento 2 , 689 (1969)
Артикул Google Scholar
T. Eichten et al., Phys. Lett. B 40 , 593 (1972)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
T. Eichten et al., Phys. Lett. B 46 , 274 (1973)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Ф.Дж. Скиулли, в: Труды 4-й Международной конференции по нейтринной физике и астрофизике «Нейтрино’74», Даумигтаун, Пенсильвания, 26–28 апреля 1974 г., изд.К. Балтай, AIP Conf. Proc. 22 , 166 (1974)
Коллаборация Аахен-Брюссель-ЦЕРН-Париж-Милан-Орсе-Лондон, М. Хагенауэр, в: Труды 17-й Международной конференции по физике высоких энергий, Лондон, 1 июля –10, 1974, изд. Дж. Р. Смит (Резерфордская лаборатория высоких энергий, Дидкот, Беркшир, Англия, 1975), стр. IV-95
Aachen-Bruxelles-CERN-Ecole Polytechnique-Orsay-London Collaboration, M. Rollier, in: Proceedings of the International Colloquium on High Energy Neutrino Physics, Paris, France, 18–20 марта 1975 г. , (Editions du CNRS, École Polytechnique, 1975), стр.349
Gargamelle Neutrino Collaboration, H. Deden et al., Nucl. Phys. B 85 , 269 (1975)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
S. Bonetti et al., Nuovo Cim. A 38 , 260 (1977)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
O. Erriquez et al., Phys. Lett. B 70 , 383 (1977)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Gargamelle Antineutrino Collaboration, Бари-Милан-Страсбург-Туринский университетский колледж, Лондон, М. Роллиер, в: Труды тематической конференции по физике нейтрино на ускорителях, Оксфорд, Англия, 4–7 июля 1978 г., изд. Авторы: A.G. Michette, P.B. Рентон (Лаборатория Резерфорда, 1978), стр. 68
Aachen-Bruxelles-CERN-Ecole Polytechnique-Orsay-Padova Collaboration, M. Dewit, in: Proceedings of the Topical Conference on Neutrino Physics at Accelerators, Oxford, England, 4-7 июля 1978, ed. .Авторы: A.G. Michette, P.B. Рентон (Лаборатория Резерфорда, 1978), стр. 75
O. Erriquez et al., Nucl. Phys. B 140 , 123 (1978)
Статья ОБЪЯВЛЕНИЯ Google Scholar
Gargamelle Neutrino Propane Collaboration, M. Pohl et al., Lett. Nuovo Cimento 26 , 332 (1979)
Артикул Google Scholar
N. Armenise et al., Nucl. Phys. B 152 , 365 (1979)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Амстердам-Берген-Болонья-Падуя-Пиза-Сакле-Турин Сотрудничество, Д. Алласия и др., Nucl. Phys. B 343 , 285 (1990)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
NOMAD Collaboration, Р. Петти, в: Материалы 32-й Международной конференции по физике высоких энергий (ICHEP’04), Пекин, Китай, 16–22 августа 2004 г., изд.Х. Чен, Д. Ду, В. Ли, К. Лу (Hackensack, World Scientific, 2005), Vol. 1 , п. 468 [arXiv: hep-ex / 0411032]
В.В. Любушкин, Б.А. Попов, Яд. Физ. 69 , 1917 (2006) [Phys. Атом. Nucl. 69 , 1876 (2006)]
Google Scholar
А. Мартинес де ла Осса Ромеро, arXiv: hep-ex / 0703026
В.В. Любушкин, кандидатская диссертация, ОИЯИ, Дубна, 2008 (не опубликовано)
В.В. Макеев и др., Письма. Ж. Эксп. Теор. Физ. 34 , 418 (1981) [Письма в ЖЭТФ. 34 , 397 (1981)]
Google Scholar
IHEP-ITEP Collaboration, S.V. Беликов и др., Препринт ИФВЭ 81-146 ОНФ СЕРП-Э-45, Серпухов, 1981 (не опубликовано)
С.В. Беликов и др., Препринт ИФВЭ 82-107 ОНФ СЕРП-Э-45, Серпухов, 1982 (не опубликовано)
С.В. Беликов и др., Яд. Физ. 35 , 59 (1982) [Сов. J. Nucl. Phys. 35 , 35 (1982)]
Google Scholar
S.V. Беликов и др., Письма. Ж. Эксп. Теор. Физ. 38, , 547 (1983) [Письма в ЖЭТФ. 38 , 661 (1983)]
Google Scholar
S.V. Беликов и др., Яд. Физ. 41 , 919 (1985) [Сов. J. Nucl. Phys. 41 , 589 (1985)]
Google Scholar
С.В. Беликов и др., Z. Phys. A 320 , 625 (1985)
Артикул Google Scholar
SKAT Collaboration, HJ Grabosch et al., Препринты PHE 86-11, Berlin-Zeuthen, 1986 и IFVE 86-221 ONF SERP-E-107, Серпухов, 1986 (неопубликовано)
HJ Grabosch et al., Yad. Физ. 47 , 1630 (1988) [Сов. J. Nucl. Phys. 47 , 1032 (1988)]
Google Scholar
SKAT Collaboration, J. Brunner et al., Z. Phys. C 45 , 551 (1990)
Статья ОБЪЯВЛЕНИЯ Google Scholar
A. Bodek, S. Avvakumov, R. Bradford, H. Budd, Eur. Phys. J. C 53 , 349 (2008) [arXiv: 0708.1946 [hep-ex]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
А. Бодек, С. Аввакумов, Р. Брэдфорд, Х. Бадд, arXiv: 0708.1827 [hep-ex]
E.L. Lomon, arXiv: nucl-th / 0609020
A. Strumia, F. Vissani, Phys. Lett. B 564 , 42 (2003) [arXiv: astro-ph / 0302055]
Статья ОБЪЯВЛЕНИЯ Google Scholar
К.С. Кузьмин, В. Любушкин, В.А. Наумов, Nucl. Phys. B Proc. Дополнение 139 , 154 (2005) [arXiv: hep-ph / 0408107]
Статья ОБЪЯВЛЕНИЯ Google Scholar
К.С. Кузьмин, В. Любушкин, В.А. Наумов, Acta Phys. Pol. B 37 , 2337 (2006) [arXiv: hep-ph / 0606184]
ADS Google Scholar
C.H. Ллевеллин Смит, Phys. Отчет 3 , 261 (1972)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
D.H. Wilkinson, Eur. Phys. J. A 7 , 307 (2000)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
D.H. Wilkinson, Nucl. Instrum. Методы A 456 , 655 (2000)
Google Scholar
D.H. Wilkinson, Nucl. Instrum. Методы A 469 , 286 (2001)
Статья ОБЪЯВЛЕНИЯ Google Scholar
S. Gardner, C. Zhang, Phys. Rev. Lett. 86 , 5666 (2001) [arXiv: hep-ph / 0012098]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
J.J. Келли, Phys. Ред. C 70 , 068202 (2004)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
М.Ф. Gari, W. Krüempelmann, Phys. Lett. B 274 , 159 (1992)
Статья ОБЪЯВЛЕНИЯ Google Scholar
М.Ф. Gari, W. Krüempelmann, Phys. Lett. В 282 , 483 (Е) (1992)
Google Scholar
E.L. Ломон, Phys. Ред. C 64 , 035204 (2001) [arXiv: nucl-th / 0104039]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
E.L. Ломон, Phys. Ред. C 66 , 045501 (2002) [arXiv: nucl-th / 0203081]
Статья ОБЪЯВЛЕНИЯ Google Scholar
J. Arrington, Phys. Ред. C 68 , 034325 (2003) [arXiv: nucl-ex / 0305009]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
J. Arrington, Eur. Phys. J. A 17 , 311 (2003) [arXiv: hep-ph / 0209243]
Статья ОБЪЯВЛЕНИЯ Google Scholar
JLab E93-038 Collaboration, J.M. Finn, Fizika B 13 , 545 (2004)
Google Scholar
Jefferson Lab E95-001 Collaboration, B. Anderson et al., Phys. Ред. C 75 , 034003 (2007) [arXiv: nucl-ex / 0605006]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
D. Day, Eur. Phys. J. A 31 , 560 (2007)
Статья ОБЪЯВЛЕНИЯ Google Scholar
C.F. Perdrisat, V. Punjabi, M. Vanderhaeghen, Prog. Часть. Nucl. Phys. 59 , 694 (2007) [arXiv: hep-ph / 0612014]
Статья ОБЪЯВЛЕНИЯ Google Scholar
K. Hagiwara, K. Mawatari, H. Yokoya, Phys. Lett. B 591 , 113 (2004) [arXiv: hep-ph / 0403076]
Статья ОБЪЯВЛЕНИЯ Google Scholar
К.С. Кузьмин, В. Любушкин, В.А. Наумов, Мод. Phys. Lett. A 19 , 2919 (2004) [arXiv: hep-ph / 0403110]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Группа данных по частицам, W.M. Yao et al., J. Phys. G 33 , 1 (2006)
Статья ОБЪЯВЛЕНИЯ Google Scholar
D. Pocanic et al., Phys. Rev. Lett. 93 , 181803 (2004) [arXiv: hep-ex / 0312030]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
S. Nakamura et al., Nucl. Phys. A 707 , 561 (2002) [arXiv: nucl-th / 0201062]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
D.H. Perkins, in: Proceedings of 16th International Conference on High Energy Physics, National Accelerator Laboratory, Chicago-Batavia, Illinois, 6–13 сентября 1972 г., изд. Дж. Д. Джексон, А. Робертс (Национальная ускорительная лаборатория, Батавия, Иллинойс, 1973), Vol. IV , стр.189
М. Деррик, в: Труды 17-й Международной конференции по физике высоких энергий, Лондон, 1–10 июля 1974 г., изд. Дж. Р. Смит (Резерфордская лаборатория высоких энергий, Дидкот, Беркшир, Англия, 1975), стр. II-166
Д. Х. Перкинс, в: Материалы Международного симпозиума 1975 г. по взаимодействию лептонов и фотонов при высоких энергиях, Стэнфордский университет, 21–27 августа 1975 г., изд. автор T.W. Кирк (Стэнфордский центр линейных ускорителей, Стэнфорд, 1975), стр.571
D. Cline, W.F. Фрай, Энн. Преподобный Nucl. Часть. Sci. 27 , 209 (1977)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Х. Ваксмут, «Физика ускорительных нейтрино», Лекции, проведенные в Herbstschule für Hochenergiephysik, Мария Лаах, Эйфель, Германия, 14–24 сентября 1976 г., препринт CERN / EP / PHYS 77-40, 17 августа , 1977 (не опубликовано)
ПФ Ермолов, А. Мухин, Усп.Физ. Наук. 124 , 385 (1978) [Сов. Phys. Успехи 21 , 185 (1978)]
Google Scholar
P. Musset, J.-P. Vialle, Phys. Республика 39 , 1 (1978)
Статья ОБЪЯВЛЕНИЯ Google Scholar
С.И. Алехин и др., Отчет CERN-HERA 87-01, Европейская организация ядерных исследований, Женева, 1987
М. Сакуда, Nucl. Phys. B Proc. Дополнение 112 , 109 (2002)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
В.В. Аммосов и др., Физ. Элем. Част. Атом. Ядра 23 , 648 (1992) [Сов. J. Part. Nucl. 23 , 283 (1992)]
Google Scholar
C. Baltay, Nucl. Phys. B Proc. Дополнение 36 , 363 (1994)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Г.П. Зеллер, доклад на 2-м международном семинаре по нейтрино-ядерным взаимодействиям в области нескольких ГэВ, NuInt’02, Калифорнийский университет, Ирвин, 12–15 декабря 2002 г. [arXiv: hep-ex / 0312061]
Б. Флеминг, AIP Conf. Proc. 815 , 1 (2006)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
М. Сорель, AIP Conf. Proc. 967 , 17 (2007) [arXiv: 0710.3966 [hep-ex]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
Р. Гран, AIP Conf. Proc. 967 , 141 (2007) [arXiv: 0711.3024 [hep-ex]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
Ф. Джеймс, «MINUIT, Справочное руководство, версия 94.1», Длинная запись библиотеки программ ЦЕРН D506 (Европейская организация ядерных исследований, Женева, 1994)
Ф. Джеймс, М. Роос , Вычисл. Phys. Commun. 10 , 343 (1975)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Будагов И. и др., Phys. Lett. B 29 , 524 (1969)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Амстердам-Берген-Болонья-Падуя-Пиза-Сакле-Турин Сотрудничество, Д. Алласия и др., Nucl. Phys. B 239 , 301 (1984)
Статья ОБЪЯВЛЕНИЯ Google Scholar
S.K. Сингх, Nucl. Phys. B 36 , 419 (1972)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
N.J. Baker et al., Phys. Ред. D 28 , 2900 (1983)
Артикул ОБЪЯВЛЕНИЯ Google Scholar
А.В. Буткевич, С.П.Михеев. Ред. C 72 , 025501 (2005) [arXiv: hep-ph / 0505008]
Статья ОБЪЯВЛЕНИЯ Google Scholar
А.В. Буткевич, С.А.Кулагин. Ред. C 76 , 045502 (2007) [arXiv: 0705.1051 [nucl-th]]
Статья ОБЪЯВЛЕНИЯ Google Scholar
К.С. Кузьмин, В. Любушкин, В.А. Наумов, Яд. Физ. 69 , 1898 (2006) [Phys. Атом. Nucl. 69 , 1857 (2006)] [arXiv: hep-ph / 0511308]
Google Scholar
K2K Collaboration, M.H. Ан и др., Phys. Rev. Lett. 93 , 051801 (2004) [arXiv: hep-ex / 0402017]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
K2K Collaboration, М.H. Ahn et al., Phys. Ред. D 74 , 072003 (2006) [arXiv: hep-ex / 0606032]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Super-Kamiokande Collaboration, Y. Ashie et al., Phys. Ред. D 71 , 112005 (2005) [arXiv: hep-ex / 0501064]
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Вектор-тензорно-скалярная геометрия, начальная функция масс, образование черных дыр и планет
Распределение звездных масс при рождении звезд называется начальной функцией масс или IMF.Почему МВФ поддерживает образование звезд с малой массой? Предлагаемое объяснение включает в себя две вещи: 1) кое-что, что я разработал на основе предыдущих уроков математики и назвал векторно-тензорно-скалярной геометрией, и 2) ключ в отчете о том, что большинство планетных систем, кажется, перевешивают протопланетные диски (PPD), в которых они сформировались, предполагая, что формирование планет — это нечто большее, чем наращивание массы в результате столкновений между частицами пыли и камнями в диске, и заставляет астрономов пересмотреть теории образования планет.125 ГэВ / c2, объединенное со спином 0, означает, что центральная скалярная точка бозона Хиггса связана с вектором гравитона, а поле Хиггса (бозон является возбуждением этого поля), следовательно, объединено с предположительно несвязанным гравитационным полем ( вместе с постоянным взаимодействием последнего с электромагнитным полем). Возведение скорости света в квадрат приводит к очень большому числу, поскольку эта скорость составляет 300 000 километров в секунду, но эта скорость относится к возмущению в пространстве-времени (ударная волна), которое возбуждает фотоны.Как сказал Пол Кэмп, доктор философии в теоретической физике пишет (Camp 2016)
«Фотон — это квант возбуждения электромагнитного поля. Это поле заполняет все пространство, как и его квантовые моды».
Сами фотоны относительно фиксированы в положении и имеют нулевую скорость. Принимая во внимание, что 125 гига электронвольт, разделенные на квадрат скорости света, дают практически несуществующий результат, если скорость ударной волны возведена в квадрат, любую математическую операцию, включающую ноль, можно рассматривать как операцию, которая не выполняется и делит 125 на 0 — скорость фотонов — квадрат не изменяет массу бозона Хиггса по сравнению с экспериментально подтвержденными 125 гига электронвольт.) из 1 ÷ 2 взаимодействия вектор-тензор-скалярная геометрия. Это приводит к образованию тел, относительно низкая масса которых едва позволяет осуществить синтез водорода с гелием до образования звезд большой массы. Следовательно, звезд с малой массой больше, чем их собратьев с большой массой. К тому же маломассивные звезды превосходят по численности коричневые карлики, несостоявшиеся звезды, которые недостаточно массивны, чтобы выдержать термоядерный синтез. В свою очередь, количество коричневых карликов меньше, чем планет. По оценкам исследователей, минимальное количество коричневых карликов в Млечном Пути составляет от 25 миллиардов до 100 миллиардов (максимальная оценка звезд в Млечном Пути составляет 400 миллиардов), но они отмечают, что даже эта верхняя цифра для коричневых карликов может быть равной. заниженная оценка, учитывая вероятность того, что существует еще много несостоявшихся звезд, слишком слабых, чтобы их вообще можно было увидеть.Работа планетолога Лидии Халлис и ее коллег предполагает, что вода на Земле произошла из солнечной туманности, вероятно, путем адсорбции на пылинках. (Халлис и др., 2015)
Похоже, что черная дыра — это фокус гравитационных волн, лишенный «семенного» материала и не способный создавать физические астрономические тела. Если волны фокусируются на области пространства, где нет материи, происходит противоположное взаимодействие, и спин гравитона 2 делится на спин фотона 1, чтобы получить 2 ÷ 1.Произведенная масса имеет спин, присущий телу гравитационных волн (волны состоят из гравитонов), и может быть альтернативным сверхновым методом для создания черных дыр, поскольку общая теория относительности утверждает, что гравитация — это толчок, вызванный кривизной пространства-времени. . Повышенная гравитация, связанная со Стрельцом A *, сверхмассивной черной дырой в центре нашей галактики, может позволить концентрической конструкции, влияющей на звезды, которые будут вращаться вокруг Стрельца A * в пределах примерно 30 000 световых лет, чтобы они были «сверхмассивными» и производили более массивные звезды. предпочтение маломассивным.(Бате 2009)
Эта высокая тяжесть может быть результатом увеличения силы сканирования как гравитационных, так и электромагнитных векторов в геометрии выше (из-за огромной гравитации, связанной со Sgr *, а также из-за видимого света, тепла, рентгеновских лучей и т. Д., Связанных с вращением аккреционного диска по орбите. сверхмассивная черная дыра). Квантовые спины фотона и гипотетического гравитона могут производить квантовый спин частиц материи через их 1/2 взаимодействия. Благодаря своей энергии и импульсу фотон и гравитон могут производить то, что мы называем массой частиц материи.11 гравитонов могут привести к слабому взаимодействию этой материи.
Список литературы
(Bate 2009), «Зависимость звездообразования от начальных условий и структуры молекулярного облака» — Ежемесячные уведомления Королевского астрономического общества, том 397, выпуск 1, страницы 232–248, https://doi.org/10.1111/ j.1365-2966.2009.14970.x
(Camp 2016), ответ на вопрос «Насколько велик фотон?» — https://www.quora.com/How-big-is-a-photon
(Халлис и др., 2015 г.), «Доказательства наличия первичной воды в глубокой мантии Земли» — Science 13, ноябрь 2015 г., Vol.350, выпуск 6262, стр. 795-797, DOI: 10.1126 / science.aac4834
(Манара и др., 2018), «Почему протопланетные диски кажутся недостаточно массивными, чтобы сформировать известную популяцию экзопланет?» https://doi.org/10.1051/0004-6361/201834076
(Музич и др., 2017), «Низкомассовое содержание массивного молодого звездного скопления RCW 38» — https://arxiv.org/abs/1707.00277, Ежемесячные уведомления Королевского астрономического общества, том 471, выпуск 3 , Страницы 3699–3712, https://doi.org/10.1093/mnras/stx1906
Вектор Разработка и производство
Услуги
AAV
Запросить услугу
векторов AAV, доступных через ядро, несут элементы ITR AAV2, серотипированные с капсидами AAV1, 2, 4, 5, 8, 9 или rh20.AAV очищают центрифугированием в градиенте плотности с последующей хроматографией FPLC. Благодаря наличию ряда флуоресцентных белков, секретируемых и цитозольных люцифераз, бицистронных конструкций и тканеспецифичных промоторов, наши AAV полезны для заражения культур клеток, а также тканей живых организмов.
ТОВАР | PHS | ЦЕНА ПО НЕПОСРЕДСТВЕННОЙ ИНФОРМАЦИИ | ТИТР |
AAV | 1 500 долл. США | 2160 долл. США | 10 11-10 13 гк / мл |
Посмотреть список наших векторов AAV
Чтобы просмотреть руководство по выбору правильного прототипа AAV для вашего проекта, щелкните здесь
Чтобы просмотреть сравнение наших продуктов и цен с нашими конкурентами в этом регионе, нажмите здесь
Лентивирус
Запросить новую услугу
Лентивирусные векторы, доступные через Core, представляют собой LTR cary HIV-1, псевдотипированные белком оболочки VSV-G.
ТОВАР | ЦЕНА НА ТЕЛЕФОН | ЦЕНА ПО НЕПОСРЕДСТВЕННОЙ СВЯЗИ | ТИТР |
Маломасштабный лентивирус | 500 долларов США | $ 720 | 10 6-10 8 МЕ / мл |
Концентрированный лентивирус | 1000 долларов США | $ 1,440 | 10 9-10 10 МЕ / мл |
Чтобы просмотреть список наших лентивирусных переносчиков, щелкните здесь
Чтобы просмотреть сравнение наших продуктов и цен с нашими конкурентами в этом регионе, нажмите здесь
Препарат плазмиды
Запросить услугу
Для достижения наивысшего возможного титра вируса MGH Vector Core требует от клиентов стерильной плазмидной ДНК, свободной от эндотоксинов.Хотя доступны коммерческие наборы для подготовки ДНК, многие лаборатории считают более удобным и экономичным, чтобы мы сделали это за них. Ниже приведена таблица, в которой указана стоимость нашего плазмидного препарата.
СТАРТОВЫЙ МАТЕРИАЛ | ЦЕНА НА ТЕЛЕФОН | ЦЕНА ПО НЕПОСРЕДСТВЕННОЙ ИНФОРМАЦИИ |
Планшет с LB-агаром | 175 долларов США | $ 252 |
Глицерин на складе | 175 долларов США | $ 252 |
Мини-приготовленная ДНК | 250 долларов США | $ 360 |
ДНК с макси-препарированием | 250 долларов США | $ 360 |
Обмен плазмидами
Запросить услугу
Скоро в продаже!
Ретровирус
Запросить услугу
ТОВАР | ЦЕНА НА ТЕЛЕФОН | ЦЕНА ПО НЕПОСРЕДСТВЕННОЙ ИНФОРМАЦИИ | ТИТР |
Концентрированный ретровирус | $ 1,200 | $ 1 728 | 10 6-10 8 МЕ / мл |
Аликвоты вируса
Запросить услугу
ВИРУС | ЦЕНА НА ТЕЛЕФОН | ЦЕНА ПО НЕПОСРЕДСТВЕННОЙ ИНФОРМАЦИИ |
Аликвота AAV | 250 долларов США | $ 360 |
Аликвота лентивируса | 150 долларов США | $ 216 |
Аликвота концентрированного лентивируса | $ 200 | $ 288 |


 При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса.
При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса. Как заряженные W±, так и нейтральный Z бозон впервые
наблюдались в ЦЕРН при столкновениях протонов и антипротонов на SPS в 1985г. и электронов и
позитронов на
LEP в 1989г.,
соответственно. Прецизионное измерение масс и парциальных ширин векторных
бозонов важно для уточнения констант Стандартной модели.
Как заряженные W±, так и нейтральный Z бозон впервые
наблюдались в ЦЕРН при столкновениях протонов и антипротонов на SPS в 1985г. и электронов и
позитронов на
LEP в 1989г.,
соответственно. Прецизионное измерение масс и парциальных ширин векторных
бозонов важно для уточнения констант Стандартной модели. Их рождение в сопровождении струй позволяет исследовать процессы более
высокого порядка квантовой хромодинамики. Для электрослабых взаимодействий важны
исследования лептонной универсальности, поляризации τ-лептона в распадах W → τντ , угла электрослабого смешивания,
парного рождения бозонов.
Их рождение в сопровождении струй позволяет исследовать процессы более
высокого порядка квантовой хромодинамики. Для электрослабых взаимодействий важны
исследования лептонной универсальности, поляризации τ-лептона в распадах W → τντ , угла электрослабого смешивания,
парного рождения бозонов.
 8.4. Изображение события – кандидата распада
W→ μν в установке
ATLAS в рр взаимодействиях при
энергии 7 ТэВ, поперечный импульс мюона рТ(μ+) = 29 ГэВ,
η(μ+) = 0.66, недостающая энергия ЕТнед = 24 ГэВ,
инвариантная поперечная масса масса μν составляет МТ = 53 ГэВ. Пунктирной линией обозначено направление недостающей поперечной
энергии.
8.4. Изображение события – кандидата распада
W→ μν в установке
ATLAS в рр взаимодействиях при
энергии 7 ТэВ, поперечный импульс мюона рТ(μ+) = 29 ГэВ,
η(μ+) = 0.66, недостающая энергия ЕТнед = 24 ГэВ,
инвариантная поперечная масса масса μν составляет МТ = 53 ГэВ. Пунктирной линией обозначено направление недостающей поперечной
энергии. 5. Они хорошо согласуются как с теоретическими
предсказаниями, так и данными эксперимента CMS.
5. Они хорошо согласуются как с теоретическими
предсказаниями, так и данными эксперимента CMS.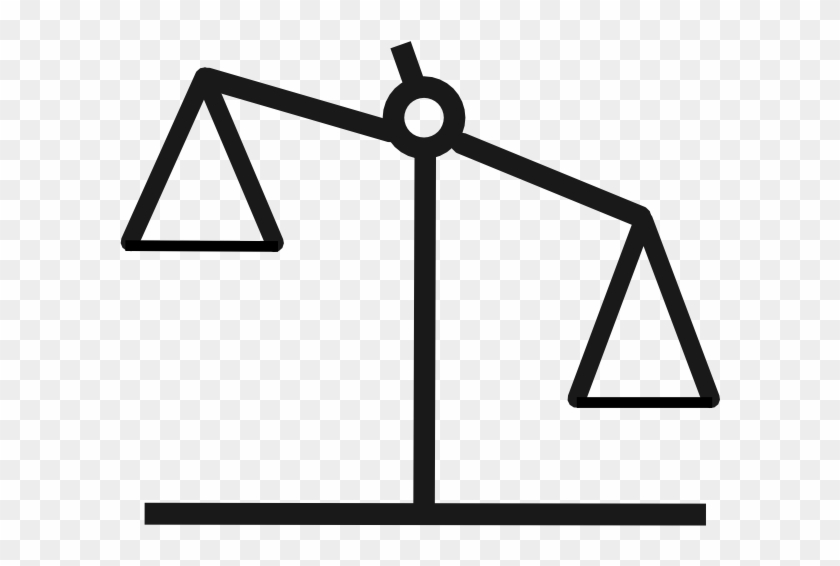 Видно, что спектр Z бозона практически
сосредоточен в пределах эффективной области установки ATLAS ׀yz׀≤3.5.
Светлыми точками показаны предсказания NNLO с использованием разных
структурных функций протона. Расчетные точки смещены в стороны для упрощения
представления. Темные области соответствуют экспериментальным неопределенностям.
Видно, что отклонения предсказаний для разных PDF достигают 10%. Спектры
заряженных
W бозонов, очевидно,
подобны спектрам
Z бозонов. Однако, спектры
W+ и W— различаются вследствие
положительного заряда протонов. Влияние валентных кварков протона проявляется
заметнее при увеличении быстроты. На рис.6 справа показано распределение
зарядовой асимметрии спектров лептонов от распада W→ℓν. Параметр
асимметрии Аl = (dσ(W+)/dηl — dσ(W—)/dηl)/ (dσ(W+)/dηl + dσ(W—)/dηl) приведен на рис.6
справа в зависимости от псевдобыстроты заряженного лептона от распада W бозона ηl.
Видно, что спектр Z бозона практически
сосредоточен в пределах эффективной области установки ATLAS ׀yz׀≤3.5.
Светлыми точками показаны предсказания NNLO с использованием разных
структурных функций протона. Расчетные точки смещены в стороны для упрощения
представления. Темные области соответствуют экспериментальным неопределенностям.
Видно, что отклонения предсказаний для разных PDF достигают 10%. Спектры
заряженных
W бозонов, очевидно,
подобны спектрам
Z бозонов. Однако, спектры
W+ и W— различаются вследствие
положительного заряда протонов. Влияние валентных кварков протона проявляется
заметнее при увеличении быстроты. На рис.6 справа показано распределение
зарядовой асимметрии спектров лептонов от распада W→ℓν. Параметр
асимметрии Аl = (dσ(W+)/dηl — dσ(W—)/dηl)/ (dσ(W+)/dηl + dσ(W—)/dηl) приведен на рис.6
справа в зависимости от псевдобыстроты заряженного лептона от распада W бозона ηl. 8.8.
8.8. 4. Видно, это распределение очень
широкое, хотя и имеет максимум при ׀Δφ׀ ~ π. Отдельно выполнены измерения рождения векторных бозонов со
струями
b-кварков [7,8].
4. Видно, это распределение очень
широкое, хотя и имеет максимум при ׀Δφ׀ ~ π. Отдельно выполнены измерения рождения векторных бозонов со
струями
b-кварков [7,8].

 Результаты, приведенные на рис.8.11,
показывают итоговые значения для ƒ0 и разности ƒL —
ƒR для двух
интервалов поперечных импульсов Wбозона: с 35 < рTW< 50 ГэВ/с слева и с рTW> 50 ГэВ/с справа в сравнении с расчетными значениями для
генераторов
MC@NLO и POWHEG. Затемненная область
вокруг экспериментального значения соответствует одному стандартному отклонению.
Видно, что расчетные значения согласуются с результатами эксперимента.
Результаты, приведенные на рис.8.11,
показывают итоговые значения для ƒ0 и разности ƒL —
ƒR для двух
интервалов поперечных импульсов Wбозона: с 35 < рTW< 50 ГэВ/с слева и с рTW> 50 ГэВ/с справа в сравнении с расчетными значениями для
генераторов
MC@NLO и POWHEG. Затемненная область
вокруг экспериментального значения соответствует одному стандартному отклонению.
Видно, что расчетные значения согласуются с результатами эксперимента.
 В случае двух лептонных мод, когда оба τ распадались на мюон или
электрон, требовалось наличие двух изолированных лептонов с порогами ниже, чем
при регистрации распадов Z → μμ/ее. Во
всех четырех модах наблюдения предусматривалось наличие недостающей энергии
вследствие присутствия нейтрино в распадах τ. Для ее измерения использовались
данные всех детекторов установки.
В случае двух лептонных мод, когда оба τ распадались на мюон или
электрон, требовалось наличие двух изолированных лептонов с порогами ниже, чем
при регистрации распадов Z → μμ/ее. Во
всех четырех модах наблюдения предусматривалось наличие недостающей энергии
вследствие присутствия нейтрино в распадах τ. Для ее измерения использовались
данные всех детекторов установки.