Электродвигатели Электромомент — EM-07-ER
Базовый электродвигатель с воздушным охлаждением для средних БВС со взлётной массой до 250кг
- синхронный электродвигатель с независимым возбуждением
- номинальный КПД > 98%
- вес – 3,6 кг
- встроенные энкодер и датчик температуры
- конструкция с внешним ротором (вращающийся корпус)
- пыле-влагозащита
- малая инерционность ротора
- принудительное воздушное охлаждение
- отсутствие магнитного «залипания» ротора
- эффективный режим генератора
- запатентованная композитная конструкция статора (CCSC) и ротора (MFF)
Прикладные примеры:
EM-07-ER 3000
EM-07L-ER 3000
СравнитьАртикул: EM-07-ER Категория: Серия EM
- Описание
- Детали
Описание
ОСНОВНЫЕ МОДИФИКАЦИИ
Электродвигателей серии EM-07 имеют следующие модификации:
EM-07-ER — стандартное исполнение с комбинированным воздушным охлаждением, встроенным энкодером, датчиком температуры и базовыми характеристиками. Приоритеты — низкая цена и максимальное импортозамещение при обеспечении высоких удельных характеристик.
Приоритеты — низкая цена и максимальное импортозамещение при обеспечении высоких удельных характеристик.
EM-07L-ER — версия с улучшенными или максимальными удельными характеристиками относительно стандартных модулей EM-07-ER. Приоритет — высокие или предельные удельные характеристики в своём классе (удельный крутящий момент или удельная мощность). Ограниченное импортозамещение для РФ, так как для получения лучших удельных характеристик применяются импортные материалы и комплектующие. Как правило, выпускаются ограниченными партиями из-за относительно более высокой стоимости изделий данной модификации.
Базовая комплектация:
В базовую комплектацию EM-07-ER входит:
- электродвигатель EM-07-ER;
- встроенный энкодер с кабелем длиной 2м;
- встроенный датчик температуры;
- инструкция по подключению и эксплуатации;
- транспортировочная упаковка.
Дополнительная комплектация:
- вставка-адаптер для воздушного винта по ТЗ заказчика;
- дополнительный датчик температуры.

Арт.: EM-07-ER
Базовый электродвигатель с воздушным охлаждением для средних БВС со взлётной массой до 250кг
- синхронный электродвигатель с независимым возбуждением
- номинальный КПД > 98%
- вес – 3,6 кг
- встроенные энкодер и датчик температуры
- конструкция с внешним ротором (вращающийся корпус)
- пыле-влагозащита
- малая инерционность ротора
- принудительное воздушное охлаждение
- отсутствие магнитного «залипания» ротора
- эффективный режим генератора
- запатентованная композитная конструкция статора (CCSC) и ротора (MFF)
Прикладные примеры:
EM-07-ER 3000
EM-07L-ER 3000
Сравнить
- Описание
- Характеристики
- Документы
ОСНОВНЫЕ МОДИФИКАЦИИ
Электродвигателей серии EM-07 имеют следующие модификации:
EM-07-ER — стандартное исполнение с комбинированным воздушным охлаждением, встроенным энкодером, датчиком температуры и базовыми характеристиками. Приоритеты — низкая цена и максимальное импортозамещение при обеспечении высоких удельных характеристик.
Приоритеты — низкая цена и максимальное импортозамещение при обеспечении высоких удельных характеристик.
EM-07L-ER — версия с улучшенными или максимальными удельными характеристиками относительно стандартных модулей EM-07-ER. Приоритет — высокие или предельные удельные характеристики в своём классе (удельный крутящий момент или удельная мощность). Ограниченное импортозамещение для РФ, так как для получения лучших удельных характеристик применяются импортные материалы и комплектующие. Как правило, выпускаются ограниченными партиями из-за относительно более высокой стоимости изделий данной модификации.
Базовая комплектация:
В базовую комплектацию EM-07-ER входит:
- электродвигатель EM-07-ER;
- встроенный энкодер с кабелем длиной 2м;
- встроенный датчик температуры;
- инструкция по подключению и эксплуатации;
- транспортировочная упаковка.
Дополнительная комплектация:
- вставка-адаптер для воздушного винта по ТЗ заказчика;
- дополнительный датчик температуры.

| Номинальная мощность, кВт: | 90 |
| Номинальный крутящий момент (реж. S1), Н*м: | 15, 20 |
| Число фаз: | 2, 3 |
| Диапазон оборотов, об/мин: | 0-60 |
| Рабочий диапазон температур, градусы Цельсия: | -50…+45 |
| Класс изоляции: | F, H |
| Класс защиты: | IP65 |
| КПД на номин. оборотах, %: | 98,5 |
| Момент инерции ротора, кг*кв.м: | 0,01 |
| Максимальный крутящий момент, Н*м: | 30 |
| Номинальные обороты, об/мин: | 50 |
| Максимальный фазный ток, А: | 15 |
| Напряжение питания, В: | 400 |
| Напряжение питания ПЧ, В: | 98 |
| Номинальный фазный ток, А: | 102 |
| Номинальный фазный ток (для Uф = 220В), А: | 12,4 |
| Размеры секции, мм: | Ø220*45 |
Удельный момент на номин. | 3,1 |
| Вес, кг: | 12,5 |
| Номинальный крутящий момент, Н·м | 15-20 * |
| Максимальный крутящий момент, Н·м | 30 |
| Удельный крутящий момент, Н·м/кг | 3-8 * |
| Базовый вес модуля, кг | 3,6 |
| Базовые размеры модуля, мм | Ø220×45 |
| Базовый диапазон температур, oС | -50…+45 |
| Модульное масштабирование | «нет» |
| Номинальный КПД, % | >98 |
| Момент инерции ротора, кг·м2 | 0,01 |
| Тип охлаждения | воздушное принудительное |
| Количество фаз, шт. | 3/2 * |
| Соединение обмоток статора | «звездой» |
| Класс защиты | IP65 |
| Клемма заземления | «нет» |
| Класс изоляции | F/H * |
Встроенные датчики температуры, шт. | 1-2 * |
| Соединение вала | 6 отв. M8 |
(*) – первое значение данной характеристики соответствует стандартному исполнению, остальные – специальному исполнению «L» или индивидуальному ТЗ заказчика.
| Габаритный чертёж EM-07L-ER |
7.3: Электромоторы постоянного тока
Приводы — это механизмы, которые используются для воздействия на окружающую среду, обычно для перемещения механизмов или систем и управления ими. Приводы заставляют двигаться все элементы соревновательного робота, которые могут двигаться. Наиболее распространенным типом привода является электромотор, в частности, в роботах VEX используются электромоторы постоянного тока.
Электромоторы преобразуют электрическую энергию в механическую энергию путем использования электромагнитных полей и вращающихся проволочных катушек. При вводе напряжения в электромотор, последний выводит установленное количество механической мощности. Механическая мощность рассматривается как выход электромотора (обычно это ось, разъем или передача), вращающегося с определенной скоростью и при определенном крутящем моментe.
При вводе напряжения в электромотор, последний выводит установленное количество механической мощности. Механическая мощность рассматривается как выход электромотора (обычно это ось, разъем или передача), вращающегося с определенной скоростью и при определенном крутящем моментe.
Нагружение электромотора
Электромоторы выводят крутящий момент только в ответ на нагружение. При отсутствии нагружения на выходе, электромотор будет вращаться очень быстро при нулевом крутящем моменте. Этого никогда не происходит в реальной жизни, так как в системе электромотора всегда присутствует трение, выполняющее роль нагрузки и заставляющее электромотор выводить крутящий момент для его преодоления. Чем больше нагрузка на электромотор, тем больше он «сопротивляется» с помощью противодействующего крутящего момента. Тем не менее, так как электромотор выводит заданное количество мощности, чем больше крутящий момент, выводимый электромотором, тем меньше его вращательная скорость.
Потребление электроэнергии
Электромотор потребляет определенное количество электрического тока (выражаемого в Амперах), которое зависит от количества приложенной к нему нагрузки. При повышении нагрузки на электромотор, потребление электроэнергии электромотором увеличивается пропорционально повышению производимого им крутящего момента.
Как показано на графике выше, ток прямо пропорционален нагружающему моменту (крутящий момент нагрузки). Чем больше нагружающий момент, тем больше потребление электроэнергии, при этом ток частота вращения обратно пропорциональны друг другу. Чем быстрее вращается электромотор, тем меньше электроэнергии он потребляет.
Ключевые характеристики электромотора
Электромоторы отличаются друг от друга и обладают различными свойствами, в зависимости от типа, конфигурации и способа производства. Существуют четыре основные характеристики, которыми обладают все электромоторы постоянного тока, используемые в соревновательной робототехнике.
Существуют четыре основные характеристики, которыми обладают все электромоторы постоянного тока, используемые в соревновательной робототехнике.
Заданный крутящий момент (Н-м) — количество нагрузки, при приложении которого к электромотору последний перестанет двигаться.
Свободная скорость (об/мин) — максимальная частота вращения электромотора, работающего без нагрузки.
Ток заторможенного электромотора (Ампер) — количество электрического тока, потребляемого остановленным электромотором.
Свободный ток (Ампер) — количество электрического тока, потребляемого электромотором, работающим без нагрузки.
На этих взаимосвязях основывается концепция мощности. При заданном нагружении, электромотор может вращаться только с определенной скоростью.
Линейная и пропорциональная природа представленных выше взаимосвязей позволяет легко составлять графики «крутящий момент — скорость» и «крутящий момент — ток» для любого электромотора путем экспериментального определения двух точек на каждом графике.
Изменение мощности за счет напряжения
Выходная мощность электромотора постоянного тока зависит от входного напряжения. Это означает, что чем больше входное напряжение, тем больше мощности производится и тем быстрее может работать электромотор.
Если электромотор имеет заданное нагружение, что будет происходить при повышении напряжения (в результате увеличения мощности)? Электромотор будет вращаться быстрее! Для выполнения того же объема работы доступно большее количество мощности.
Это означает, что характеристики электромотора, приведенные выше, изменяются в зависимости от входного напряжения электромотора, поэтому их значения необходимо устанавливать при заданном напряжении (при испытаниях с напряжением 12 В). Эти четыре характеристики изменяются пропорционально входному напряжению. Например, если свободная скорость электромотора составляет 50 об/мин при напряжении 6 В, при удваивании напряжения до 12 В свободная скорость также удваивается и принимает значение 100 об/мин.
Значения этих характеристик при определенном напряжении могут быть рассчитаны в том случае, если известны их значения при другом напряжении, путем умножения известного значения на коэффициент значений напряжения. Этот подход не применим к определению свободного тока электромотора, так как его значение остается постоянным при любом напряжении.
Новое значение = Определенное значение х (Новое значение/Определенное значение)
Из примера выше видно, что свободная скорость электромотора составляет 50 об/мин при напряжении 6 В. Проектировщик планирует использовать электромотор при напряжении 8 В. Какова будет свободная скорость электромотора при этом напряжении?
Свободная скорость @ 8 В = Свободная скорость @ 6 В x (8 В / 6 В) = 50 об/мин x (8/6) = 66,66 об/мин
Как можно использовать изменение напряжения в управлении роботом? Электромоторы робота представляют собой не просто устройства, работающие по системе «вкл/откл». Проектировщик робота может изменять напряжение электромотора, работающего при нагрузке, для получения различных значений мощности и скорости. Для этого используются моторные контроллеры, регулирующие напряжение, поступающее к электромоторам.
Для этого используются моторные контроллеры, регулирующие напряжение, поступающее к электромоторам.
Предельные значения и расчеты для электромотора
Означает ли это, что проектировщик может продолжать увеличивать напряжение электромотора до тех пор, пока последний не сможет выводить количество мощности, достаточное для выполнения задачи? Не совсем так. Электромоторы имеют ограничения. С одной стороны, приобретенная мощность будет слишком большой для электрических обмоток (как правило, обмотка начнет гореть, выделяя белый дым). К счастью, электромоторы VEX лишены подобных проблем, так как снабжены встроенными тепловыми реле, блокирующими поступление электрического тока в электромотор в случае его перегрева. Такое решение является очень удачным, так как электромотор не может перегореть, но при этом возникает новое условие для проектировщиков, выраженное в необходимости предотвращения срабатывания предохранителей электромотора. Как это сделать? Путем проектирования системы таким образом, чтобы исключить превышение установленного потребления тока электромотором за счет ограничения количества нагрузки на него.
Расчет нагрузки на руку
В примере, представленном выше, известный электромотор управляет движением руки робота при известном напряжении. В данном сценарии, какую максимальную массу может стабильно удерживать робот?
Чтобы решить эту задачу, проектировщик должен понимать, что максимальная масса, которую робот может удерживать стабильно, возникает при предельном перегрузочном моменте электромотора. Если электромотор находится в остановленном состоянии, он прикладывает к руке робота длиной 0,25 метра крутящий момент, равный 1 Н. Крутящий момент = Сила * Расстояние
Сила = Крутящий момент/Расстояние = 1 ньютон-метр/0,25 метра = 4 ньютона
Рука может удерживать до 4 ньютонов при остановленном электромоторе. При любом превышении, рука опрокинется.
Расчет крутящей нагрузки из предельного тока:
Это просто, но ситуация усложняется, когда необходимо учесть предельный ток. Например, в электромоторе из примера, представленного выше, установлен выключатель предельного тока, который сработает при потреблении свыше 2 ампер. Какова максимальная масса, которую робот может удерживать без срабатывания выключателя?
Какова максимальная масса, которую робот может удерживать без срабатывания выключателя?
Теперь, электромотор не работает при предельном перегрузочном моменте — в режиме останова электромотор будет потреблять ток заторможенного электромотора, равный 3 амперам, что вызовет срабатывание предохранителя. Проектировщик должен выяснить, какую крутящую нагрузку должен испытывать электромотор, чтобы его потребление тока не достигало 2 ампер. Как это реализовать?
Глядя на график выше и помня о том, что взаимосвязи линейны, крутящая нагрузка при любом заданном потреблении тока может быть рассчитана с помощью уравнения.
Уравнение для линии: y = mx + b, где y — это значение по оси y, x — это значение по оси x, m — это уклон линии, и b — это место пересечения линии с осью y (точка пересечения с осью y).
Уклон линии может быть выражен как: m = (изменение по Y / изменение по X) = (ток заторможенного электромотора — свободный ток) / предельный перегрузочный момент
Точка пересечения с осью Y обозначает свободный ток.
Значение Y — это ток в заданной точке линии, и значение X — это крутящая нагрузка в этой точке.
Уравнение может быть представлено следующим образом:
Ток = ((ток заторможенного электромотора — свободны ток) / предельный перегрузочный момент) х крутящая нагрузка + свободный ток
Для крутящей нагрузки это же уравнение выглядит следующим образом:
Крутящая нагрузка = (ток — свободный ток) х предельный перегрузочный момент / (ток заторможенного электромотора — свободный ток)
С помощью параметров из примера выше может быть установлена крутящая нагрузка, при которой значение потребления тока будет равно 2 амперам.
Крутящая нагрузка = (2 ампера — 1 ампер) х 1 Н-м / (3 ампера — 1 ампер)
Крутящая нагрузка = (1,9 ампер) х 10 Н-м / (2,9 ампер)
Крутящая нагрузка = 0,655 Н-м
На основании данного расчета проектировщик может сделать вывод, что если значение крутящего момента электромотора превышает 0,655 Н-м, его потребление электричества превысит 2 ампера, при этом предохранитель сработает. Остается рассчитать количество силы, которой должна обладать рука.
Остается рассчитать количество силы, которой должна обладать рука.
Сила = Крутящий момент/Расстояние = 0,655 Н-м / 0,25 м = 2,62 Н
Если рука робота подбирает объект, масса которого превышает 2,62 Н, это спровоцирует срабатывание предохранителя.
Расчет скорости электромотора из крутящей нагрузки
В примере, представленном выше, какова скорость электромотора при предельном токе? На основании расчетов, выполненных на предыдущем этапе, проектировщик должен определить скорость электромотора при нагрузке 0,655 Н-м.
Глядя на график, изображенный выше, скорость электромотора при любой крутящей нагрузке может быть рассчитана с помощью уравнения, аналогичного уравнению для расчета потребления тока (предыдущий пример).
В этом случае, уклон линии выражается как m = (изменение по Y) / (изменение по X) = (свободная скорость) / (предельный перегрузочный момент).
Примечание: уклон имеет отрицательное значение.
Точка пересечения с осью Y обозначает свободную скорость.
Значение Y — это скорость в заданной точке линии, и значение X — это крутящая нагрузка в этой точке.
Уравнение выглядит следующим образом:
Скорость = (свободная скорость / предельный перегрузочный момент) х крутящая нагрузка + свободная скорость
С помощью параметров из примера выше может быть установлена скорость электромотора при крутящей нагрузке, равной 6,55 фунто-дюймов:
Скорость = -(100 об/мин / 1 Н-м) x 0,655 Н-м + 100 об/мин
Скорость = -(100 об/мин/Н-м) x 0,655 Н-м + 100 об/мин
Скорость = 65,5 об/мин + 100 об/мин = 34,5 об/мин
При потреблении 2 ампер тока и подъеме объекта массой 2,62 Н, электромотор будет вращаться со скоростью 34,5 об/мин при крутящей нагрузке 0,655 Н-м.
Несколько электромоторов
Если для выполнения задачи требуется больше мощности, чем может обеспечить один электромотор, у проектировщика есть три варианта действий:
- 1. Изменить проектные требования таким образом, чтобы для выполнения задачи было достаточно меньшей мощности.

2. Перейти на использование более мощного электромотора.
3. Увеличить количество электромоторов.
Что произойдет при использовании в проекте нескольких электромоторов? Очень просто — крутящая нагрузка будет распределена между ними. При крутящем моменте 2 Н-м, каждый электромотор будет иметь крутящую нагрузку 1 Н-м и реагировать соответственно.
Это можно представить так, что электромоторы принимают на себя характеристики супер-мотора, при этом характеристики отдельных электромоторов суммируются. Суммируются значения предельного перегрузочного момента, тока заторможенного электромотора, свободного тока, при этом свободная скорость остается неизменной.
В таблице выше представлены спецификации 2-проводного электромотора VEX 393, а также спецификации при комбинировании двух электромоторов для выполнения одной задачи.
В примере выше, сколько электромоторов VEX 393 необходимо для стабильного удерживания объекта?
Крутящая нагрузка на электромоторы рассчитывается следующим образом:
Крутящая нагрузка = сила х расстояние = 22 Н х 0,25 м = 5,5 Н-м
Данную крутящую нагрузку можно сравнить с предельным перегрузочным моментом электромотора VEX 393 и определить требуемое количество.
5,5 Н-м / 1,67 Н-м = 3,29 электромоторов
Таким образом, для удержания руки в поднятом положении (пример выше) необходимо 4 электромотора.
4.2: Магнитный момент и крутящий момент
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 21529
- Том Вайдеман
- Калифорнийский университет, Дэвис
Крутящий момент на проволочной петле
Используем наш результат для силы, действующей на отрезок проволоки, для анализа случая воздействия магнитного поля на замкнутую проволочную петлю. Для этого анализа мы выберем простую геометрию — прямоугольную проволочную петлю с двумя сторонами, параллельными однородному магнитному полю.
Рисунок 4.2.1 – Замкнутая прямоугольная проволочная петля в однородном магнитном поле0034 Силы, воздействующие на горизонтальные сегменты, нейтрализуются, что приводит к нулевой результирующей силе на петле, но, конечно, имеет место результирующий крутящий момент. Выбрав ось, представляющую собой горизонтальную линию, проходящую через центры двух вертикальных сегментов, мы можем вычислить чистый крутящий момент в петле. При выборе положительного направления крутящего момента влево силы сверху и снизу создают крутящие моменты в этом положительном направлении, поэтому: \[\tau_{net} = F_{top}\left(\dfrac{z}{2}\right) + F_{bottom}\left(\dfrac{z}{2}\right) = 2\ left(IyB\right)\left(\dfrac{z}{2}\right) = I\left(yz\right)B\] Здесь мы вводим сокращение для будущих расчетов крутящего момента. Величина \(yz\) есть площадь петли \(A\). В будущих приложениях ток может подаваться в петлю по одному проводу, который несколько раз обмотан по периметру. Затем сила, действующая на каждую сторону петли (и, следовательно, крутящий момент), будет умножена на количество витков в проводе \(N\). \[\overrightarrow \mu \equiv NI\overrightarrow A\] Вектор \(\overrightarrow A\) имеет величину, равную площади петли и имеет направление, перпендикулярное плоскости петли, в направлении, определяемом следующим образом: согните пальцы правой руки в направлении, прослеживающем направление тока вокруг петли, и большой палец эта рука указывает направление вектора. Например, петля на рис. 4.2.1 будет иметь магнитный момент, направленный за пределы страницы. Теперь вектор крутящего момента можно рассчитать по моменту магнитного диполя так же, как вычисляли крутящий момент, действующий на электрический диполь: \[\overrightarrow\tau_{electric} = \overrightarrow p \times \overrightarrow E \ ;\;\;\Стрелка влево\;\;\; \overrightarrow\tau_{магнитный} = \overrightarrow \mu \times \overrightarrow B\] Мы можем видеть, что это работает для случая, показанного на рис. 4.2.1: угол между магнитным дипольным моментом (который указывает вне стр.), а магнитное поле равно \(9o\), поэтому синус угла между этими векторами, который появляется в перекрестном произведении, равен 1, что дает ответ, который мы нашли выше. Когда петля вращается вокруг горизонтальной оси, угол между магнитным дипольным моментом и полем изменяется, уменьшая плечо моментов сил в \(\sin\theta\) раз — ровно столько, сколько указано в кресте. -продукт. Когда петля вращается до точки, где ее плоскость перпендикулярна полю, магнитный момент и поле параллельны, что делает крутящий момент нулевым, как мы обнаружили выше. Пример \(\PageIndex{1}\) Ток \(2,00\;A\) течет по круглому проводнику радиусом \(12,0\;см\) и лежит в \( х\)-\(у\) плоскость. Если смотреть с оси +\(z\), ток течет по часовой стрелке. Эта петля находится в присутствии однородного магнитного поля: \[\overrightarrow B = B_o\left(\widehat i-3\widehat j + 2\widehat k\right)\;,\;\ ;\;\;где:\;\;B_o=1,50T\номер\] Найти крутящий момент (вектор), действующий на проводник. 92\вправо)\широкая шляпа к\правая]\раз\влево[\влево(1,50Т\вправо)\влево(\широкая я-3\широкая шляпа j + 2\широкая шляпа к\правая)\правая] = -\влево( 0.136\;N\cdot m\right)\left(3\widehat i + \widehat j\right)\nonnumber\] Хотя мы вывели формулу для магнитного дипольного момента с помощью прямоугольника, оказывается, что пока петля лежит в плоскости, формула работает независимо от ее формы. В качестве наглядного примера мы решим крутящий момент на круговой петле. Это более сложный пример, чем прямоугольник, по причинам, которые станут ясны позже, но он демонстрирует важные инструменты для интегрирования бесконечно малых вкладов и работы с векторными произведениями. Рисунок 4.2.2a – Крутящий момент на замкнутом круговом витке проволоки в однородном магнитном поле убедитесь, что он правый, т.е. выберите оси так, чтобы \(\widehat i \times \widehat j = \widehat k\) ), выберите бесконечно малый участок петли и опишите его в терминах координат , помечая любые переменные, которые нам нужно будет знать по пути. Рисунок 4.2.2b – Крутящий момент на замкнутом кольце из проволоки в однородном магнитном поле ) плоскости, а магнитное поле указывает в направлении \(+x\). Был выбран бесконечно малый кусок провода под углом \(\phi\) вверх от оси \(+x\). Далее нам нужно математически выразить вектор \(\overrightarrow {dl}\). Его величина равна длине бесконечно малого сегмента дуги, которая равна \(R\;d\phi\). Направление придумать сложнее, но увеличив картинку и немного поработав с геометрией, мы можем определить ее компоненты: Рисунок 4. \[\overrightarrow {dl} = R\;d \phi\left(-\sin\phi\;\widehat i + \cos\phi\;\widehat j\right)\] Теперь у нас есть все, что нам нужно. Какой бы сложной ни была геометрия с силой, а затем с крутящим моментом, нам не нужно ее отслеживать — все, что нам нужно сделать, это правильно рассчитать вектор. Например, сила на текущем элементе равна: \[d\overrightarrow F = I \overrightarrow {dl} \times \overrightarrow B = I\left[R\;d\phi\left(-\sin\phi\;\widehat i + \cos\phi\ ;\widehat j\right)\right]\times\left[B \;\widehat i\right]\] Вспоминая векторные произведения единичных векторов из Physics 9A, мы подставляем \(\widehat i\times\ widehat i = 0\) и \(\widehat j\times\widehat i = -\widehat k\), и сила, действующая на этот элемент, принимает вид: \[d\overrightarrow F = IRB\cos\phi\;d \phi \left(-\widehat k\right)\] Чтобы получить крутящий момент, мы выбираем начало координат в качестве точки отсчета и напрямую вычисляем бесконечно малый вклад в крутящий момент. Действительно, величина крутящего момента получается \(\mu\;B\), где \(\mu=IA\). И используя правило правой руки, чтобы получить направление магнитного момента (вне страницы), за которым следует направление крутящего момента из правила правой руки, примененного к \(\overrightarrow\mu\times\overrightarrow B\ ), подтверждает, что направление тоже работает. Эта проблема казалась очень сложной, потому что направление \(\overrightarrow {dl}\) меняется повсюду на окружности, но как только этот вектор записывается в терминах \(\phi\) и единичных векторов, математика делает остальные! Мы обнаружили, что с электрическими диполями можно делать больше, чем просто вычислять крутящие моменты, и то же самое верно и для магнитных диполей. Приятно то, что нам не нужно прорабатывать все заново — те же результаты просто переводятся путем замены \(\overrightarrow p\) на \(\overrightarrow \mu\) и \(\overrightarrow E\) с \(\overrightarrow B\). \[U_{electric} = -\overrightarrow p \cdot \overrightarrow E \;\;\;\Leftrightarrow\;\;\; U_{магнитный} = -\overrightarrow \mu \cdot \overrightarrow B\] Как мы видели с электрическим диполем, мы можем объяснить нестабильность положения против выравнивания с точки зрения наличия максимальной потенциальной энергии. Пример \(\PageIndex{2}\) Устройство, показанное на схеме, состоит из прямоугольной петли, по которой протекает постоянный ток, расположенной в однородном магнитном поле и прикрепленной к оси, вращающей колесо. Вокруг колеса намотана (безмассовая) струна (струна проходит через переднюю часть колеса, как показано на диаграмме), на которой висит масса. Масса поднимается и опускается так, что она покоится, когда плоскость петли вертикальна, и снова покоится, когда плоскость петли горизонтальна (т. и далее). 92} \;,\;\;\; m=0,45\;кг\;,\;\;\; В=1,2\;Т\;,\;\;\; \text{длина сторон петли} = 0,54м\;,\;\;\; \text{радиус колеса} = 0,25 м\номер\] а. б. Система сохраняет энергию, а масса не движется ни вверху, ни внизу своего пути, поэтому кинетическая энергия не меняется. Следовательно, все изменения энергии имеют форму потенциальной энергии. На вершине своего пути масса приобретает гравитационную потенциальную энергию, и она должна исходить от магнитной потенциальной энергии диполя в поле. Колесо поворачивается на угол \(\frac{\pi}{2}\), поэтому мы можем вычислить, сколько нити намотано на колесо (что равно изменению высоты массы). Полезно провести прямое сравнение этих двух диполей в соответствующих полях с помощью диаграммы. Рис. 4.2.4. Сравнение электрических и магнитных диполей Осталась еще одна особенность диполей, на которую нам нужно обратить внимание — как они реагируют на неоднородные поля. Рассмотрим электрический диполь в электрическом поле, усиливающемся в определенном направлении. Когда мы обсуждали крутящий момент, мы использовали однородное поле и обнаружили, что их результирующая сила не действует на диполь. Но когда поле неоднородно, тогда половина диполя может находиться в области, где поле сильнее, чем область, где находится другая половина диполя, что приводит к большей силе на одну часть диполя, чем на другую, и результирующая сила, действующая на диполь в целом. Рисунок 4.2.5 – Суммарная сила, действующая на электрический диполь от неоднородного поля t имеют два отдельных заряда. Рисунок 4.2.6 – Суммарная сила, действующая на магнитный диполь от неоднородного поля вправо (линии поля сближаются). Ток циркулирует по часовой стрелке, если смотреть слева, так что он входит в страницу в нижнем сегменте прямоугольника и выходит из страницы в верхнем сегменте. Сила на верхнем и нижнем сегментах должна быть перпендикулярна полю, поэтому существуют горизонтальные составляющие этой силы, которые складываются, и вертикальные части, которые сокращаются, при этом результирующая сила направлена вправо, как и в аналогичном случае для электрический диполь. Фактически мы можем выразить количество результирующей силы, создаваемой неоднородным полем, через скорость, с которой поле изменяется в направлении действия силы, используя тот факт, что сила представляет собой отрицательный градиент потенциальной энергии. Выровняв дипольный момент с полем (положением, в которое вращающий момент будет стремиться его повернуть), мы получим: \[\begin{array}{l} \text{electric:} && F_x = -\dfrac {\ парциальное} {\ парциальное х} U_E = — \ dfrac {\ парциальное} {\ парциальное х} \ влево (- \ overrightarrow p \ cdot \ overrightarrow E \ вправо) = — \ dfrac {\ парциальное} {\ парциальное х } \left(-p_xE_x\right) = +p_x\dfrac{\partial E_x}{\partial x} \\ \text{магнитный:} && F_x = -\dfrac{\partial}{\partial x} U_B = — \dfrac{\partial}{\partial x} \left(-\overrightarrow \mu \cdot \overrightarrow B\right) = -\dfrac{\partial}{\partial x} \left(-\mu_xB_x\right) = +\mu_x\dfrac{\partial B_x}{\partial x} \end{массив}\] Создавая крутящий момент в проводящем контуре, по которому течет ток, мы можем заставить его работать. Рисунок 4.2.7 – Двигатель постоянного тока Стационарным источником постоянного магнитного поля является стержневой магнит (это мы обсудим в следующем разделе). Эта страница под названием 4.2: Magnetic Moment and Torque распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts. спросил Изменено
7 лет, 9 месяцев назад Просмотрено
839 раз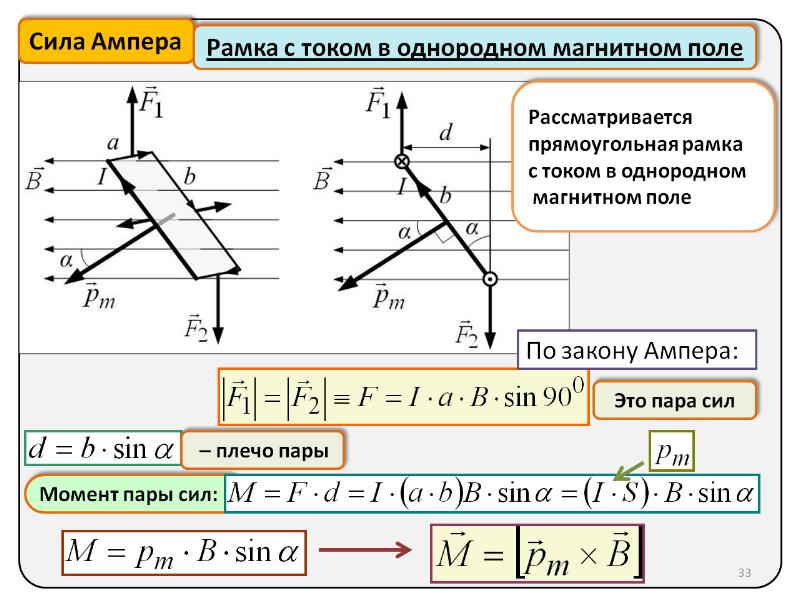
Момент магнитного диполя
 Произведение \(N\), \(I\) и \(A\) записывается как одна величина \(\mu\), что дает величину крутящего момента для этого случая в простой форме \(\ тау = \mu B\). 9o\), то силы на эти сегменты будут направлены прямо друг от друга. Эти силы действуют прямо через ось, поэтому создаваемый ими крутящий момент равен нулю. Мы знаем, что крутящий момент и магнитное поле являются векторами, и создаваемый крутящий момент связан с ориентацией петли в поле. Мы можем учесть ориентацию петли, определив магнитный дипольный момент :
Произведение \(N\), \(I\) и \(A\) записывается как одна величина \(\mu\), что дает величину крутящего момента для этого случая в простой форме \(\ тау = \mu B\). 9o\), то силы на эти сегменты будут направлены прямо друг от друга. Эти силы действуют прямо через ось, поэтому создаваемый ими крутящий момент равен нулю. Мы знаем, что крутящий момент и магнитное поле являются векторами, и создаваемый крутящий момент связан с ориентацией петли в поле. Мы можем учесть ориентацию петли, определив магнитный дипольный момент :


 2.3 – Запись вектора текущего элемента вместе в один вектор:
2.3 – Запись вектора текущего элемента вместе в один вектор: Подключение вектора положения и выполнение векторной математики дает: 92\right)B\;\widehat j\]
Подключение вектора положения и выполнение векторной математики дает: 92\right)B\;\widehat j\] Сравнение магнитного и электрического
 Итак, мы имеем потенциальную энергию диполя в поле:
Итак, мы имеем потенциальную энергию диполя в поле: Магнитное поле поворачивает петлю так, что верхний сегмент входит в страницу. Сгибание пальцев в этом направлении дает направление крутящего момента влево. Направление крутящего момента определяется перекрестным произведением магнитного момента и поля. Поле вверху, поэтому, чтобы перекрестное произведение было слева, пальцы должны сгибаться от страницы вверх. Следовательно, магнитный момент направлен наружу страницы. Сгибание пальцев против часовой стрелки дает это направление, то есть направление тока.
Магнитное поле поворачивает петлю так, что верхний сегмент входит в страницу. Сгибание пальцев в этом направлении дает направление крутящего момента влево. Направление крутящего момента определяется перекрестным произведением магнитного момента и поля. Поле вверху, поэтому, чтобы перекрестное произведение было слева, пальцы должны сгибаться от страницы вверх. Следовательно, магнитный момент направлен наружу страницы. Сгибание пальцев против часовой стрелки дает это направление, то есть направление тока.  Затем это используется для нахождения изменения гравитационного PE: 92} = 4.9\;А\номер\]
Затем это используется для нахождения изменения гравитационного PE: 92} = 4.9\;А\номер\] 
Двигатель постоянного тока
 То есть имеем задатки электродвигателя. Есть одна проблема, которую нужно преодолеть. Когда катушка поворачивается, направление магнитного момента меняется вместе с ней. Если магнитное поле неизменно, то вращение магнитного момента заставит крутящий момент изменить направление, что означает, что крутящий момент заставляет петлю ускоряться в противоположном направлении. Это заставляет катушку колебаться вперед и назад, а не вращаться в одном направлении. Один из способов исправить это — обеспечить ЭДС, которая периодически меняет направление, так что ток переворачивается, когда магнитный момент вот-вот создаст неправильный крутящий момент. На рисунке ниже представлена простая конструкция, которая устраняет эту проблему с неизменной ЭДС.
То есть имеем задатки электродвигателя. Есть одна проблема, которую нужно преодолеть. Когда катушка поворачивается, направление магнитного момента меняется вместе с ней. Если магнитное поле неизменно, то вращение магнитного момента заставит крутящий момент изменить направление, что означает, что крутящий момент заставляет петлю ускоряться в противоположном направлении. Это заставляет катушку колебаться вперед и назад, а не вращаться в одном направлении. Один из способов исправить это — обеспечить ЭДС, которая периодически меняет направление, так что ток переворачивается, когда магнитный момент вот-вот создаст неправильный крутящий момент. На рисунке ниже представлена простая конструкция, которая устраняет эту проблему с неизменной ЭДС. Катушка вращается, но двигатель включает в себя часть, называемую коммутатором , который изменяет направление тока в нужный момент. Он состоит из кольца с разрывом, которое вращается внутри двух трущихся соединений. Когда катушка повернется \(9о\), ток течет на от колеса в фиолетовом сегменте, а не к нему, но ток все еще идет к колесу в сегменте, ближайшем к северному магниту, поэтому направление крутящего момента остается прежним. . Иными словами, коммутатор удерживает магнитный момент катушки в направлении, компонент которого всегда направлен вниз — когда он вот-вот начнет указывать вверх, направление тока меняется.
Катушка вращается, но двигатель включает в себя часть, называемую коммутатором , который изменяет направление тока в нужный момент. Он состоит из кольца с разрывом, которое вращается внутри двух трущихся соединений. Когда катушка повернется \(9о\), ток течет на от колеса в фиолетовом сегменте, а не к нему, но ток все еще идет к колесу в сегменте, ближайшем к северному магниту, поэтому направление крутящего момента остается прежним. . Иными словами, коммутатор удерживает магнитный момент катушки в направлении, компонент которого всегда направлен вниз — когда он вот-вот начнет указывать вверх, направление тока меняется. угловой момент — Результирующий центр вращения из-за множественных моментов
Допустим, на тело (неправильной формы) действуют кратные моменты (M1, M2, M3) в точках P1, P2, P3 соответственно. Тело свободно вращается вокруг любой точки.
Тело свободно вращается вокруг любой точки.
Теперь, вокруг какого равнодействующего центра (точки, которая вообще не вращается, по крайней мере в мировой системе координат) вращается тело в этом состоянии?
Трудности:
- Это чистые мгновения, и их нельзя выразить в виде сил, что я обычно и вижу в книгах
- Результирующий момент легко вычислить с помощью векторов, но он не дает положения результирующего момента
- Всегда ли свободное тело вращается вокруг своего центра? (В этом случае я совершенно неправильно подхожу к этому)
- Работает ли это так же, как нахождение центра масс для нескольких точечных масс? Это мое лучшее предположение, но я не уверен.
- угловой момент
- вращательная динамика
- вращение
- момент
Никаких сложностей.
Если результирующая сила, приложенная к телу, равна нулю, то центр масс не собирается двигаться ускоряться.