Отсутствие в природе магнитных зарядов
Математическая запись отсутствия магнитных зарядов
На ранних стадиях изучения магнитных явлений предполагалось, что источниками магнитных полей являются магнитные заряды, которые взаимодействуют по закону Кулона. Однако такое предположение не согласуется с одним из основных уравнений магнитостатики:
Или в интегральном виде:
Электрические токи — источники магнитных полей
Сам Кулон еще отмечал на принципиальное различие между электрическими и магнитными явлениями. Оно, прежде всего в том, что ни как не можем разделить в теле серверный и южный полюса магнита, чтобы получить тело только с одним магнитным полюсом. И мы не можем получить тела с избытком того или иного магнетизма (северного или южного). Из этой ситуации Кулон сделал вывод о том, что два вида магнитных зарядов неразрывны. Дальнейшее изучение магнитных явлений показало, что гипотеза существования магнитных зарядов неверна в корне. Магнитных зарядов не существует. Каждый атом вещества надо рассматривать как круговой ток. Магнитное поле намагниченного тела складывается из магнитных полей кругового тока.
Доказательство того, что магнитный поток вектора магнитной индукции через замкнутую поверхность равен нулю
Формулы (1) и (2) показывают, что магнитных зарядов не существует. Докажем, что магнитный поток $\oint{\overrightarrow{B}d\overrightarrow{S}}$ через любую замкнутую поверхность S равен нулю (2).
Предположим, что магнитное поле создают точечные заряды (q), которые равномерно движутся. Тогда индукцию магнитного поля ($\overrightarrow{B_q}$) таких зарядов модно представить как:
где $\overrightarrow{v}$ — скорость движения заряженной частицы, $\overrightarrow{r}$ — радиус — вектор, который проводится из заряда, в рассматриваемую току поля, $\left [\overrightarrow{v}\overrightarrow{r}\right]\ $- векторное произведение соотвествующих векторов. Так как для магнитных полей движущихся зарядов выполняется принцип суперпозиции. Поток векторной суммы нескольких векторов через любую поверхность равен алгебраической сумме потоков отдельных векторов через ту же поверхность. Значит, мы при доказательстве можем ограничиться рассмотрением одной движущейся частицей. Пусть заряд движется с постоянной скоростью перпендикулярно плоскости рис.1.
Магнитные силовые линии при этом — коаксиальные окружности. Их плоскости параллельны плоскости рис.1, а центры расположены на прямой, по которой движется заряд. Рассмотрим бесконечно тонкую кольцевую трубку, которую образуют магнитные силовые линии (АВСД). Из-за осевой симметрии магнитный поток через поперечное сечение этой трубки постоянный на всей ее длине. Трубка пересекает замкнутую поверхность S четное число раз. Магнитные потоки через площадки $dS_1и\ dS_2$, которые вырезаны трубкой на поверхности S, одинаковы по модулю, противоположны по знаку. В результате сумма таких потоков равна нулю. Все пространство можно разбить на подобные тонкие кольцевые магнитные трубки.
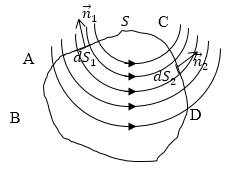
Рис. 1
Так, суммарный магнитный поток через замкнутую поверхность S равен нулю. Мы доказали, что:
Уравнение (2) и эквивалентное ему уравнение (1) в дифференциальном виде:
справедливы для любых магнитных полей.
Определение
Силовые поля, дивергенции которых везде равны нулю, называются соленоидальными полями.
Источником магнитного поля являются не магнитные заряды, а электрические токи.
Пример 1
Задание: Найдите модуль вектора магнитной индукции поля, которое создано двумя длинными прямолинейными проводниками с токами $I_1\ и\ $ $I_2$, которые текут в одном направлении. Расстояние между проводами равно d. Точка, в которой надо найти поле, находится на расстоянии r=d от каждого из проводников.
Решение:
На рис.2 проводники с токами перпендикулярны плоскости рисунка, причем текут от нас.
Силовые линии магнитного поля представляют собой окружности с центрами на проводнике с током.
Векторы магнитной индукции являются касательными к этим окружностям в точке, где мы ищем поле.
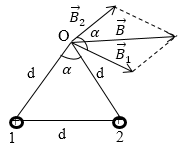
Рис. 2
Таких вектора у нас два (${\overrightarrow{B}}_1и\ {\overrightarrow{B}}_2$). Результирующий вектор будет найден как:
\[{\overrightarrow{В}=\overrightarrow{B}}_1+\ {\overrightarrow{B}}_2\left(1.1\right).\]По теореме косинусов модуль вектора $\overrightarrow{В}$ равен:
\[B=\sqrt{{B_1}^2+{B_2}^2+2B_1B_2cos\alpha }\left(1.2\right).\]Так как треугольник на рис.2 равносторонний, то $\alpha =\frac{\pi }{3}.$ Модуль вектора магнитной индукции поля, которое создает бесконечно длинный проводник с током (для проводника 1) в вакууме в точке О равно:
\[B_1=\frac{{\mu }_0I_1}{2\pi d}\left(1.3\right),\]для проводника (2):
\[B_2=\frac{{\mu }_0I_2}{2\pi d}\left(1.4\right).\]Подставим (1.3) и (1.4) в (1.2) найдем искомое поле, учтем, что $cos\alpha =cos\frac{\pi }{3}=\frac{1}{2}$:
\[B=\frac{{\mu }_0}{2\pi d}\sqrt{{I_1}^2+{I_2}^2+I_1I_2.}\]Ответ: $B=\frac{{\mu }_0}{2\pi d}\sqrt{{I_1}^2+{I_2}^2+I_1I_2.}$
Пример 2
Задание: Найдите магнитную индукцию поля, которое создает электрон, двигаясь по круговой орбите, если ее радиус в атоме водорода равен r.
Решение:
Для решения задачи воспользуемся формулой для определения вектора магнитной индукции, если поле создает движущийся заряд, а именно:
\[\overrightarrow{B_q}=\frac{{\mu }_0}{4\pi }q\frac{\left[\overrightarrow{v}\overrightarrow{r}\right]}{r^3}\left(2.1\right),\]где $\widehat{\overrightarrow{v}\overrightarrow{r}}=\frac{\pi }{2}$ так как из условия электрон движется по окружности, вектор скорости направлен по касательной к окружности, радиус вектор $\overrightarrow{r}$ — проведен в точку касания. Заряд электрона величина известная и он равен $q=1,6\cdot {10}^{-19}Кл$. Тогда вектор магнитной индукции запишем как:
\[B=\frac{{\mu }_0}{4\pi }\frac{qv}{r^2}\left(2.2\right).\]В соответствии со вторым законом Ньютона на электрон действует кулоновская сила притяжения к ядру атома водорода и она равна:
\[ma=k\frac{q^2}{r^2}\to m\frac{v^2}{r}=k\frac{q^2}{r^2}\ \left(2.3\right),\]где $k=\frac{1}{4\pi {\varepsilon }_0}$, m — масса электрона.
Выразим из (2.3) скорость движения электрона по своей орбите, получим:
\[v=\sqrt{\frac{q^2}{4\pi {\varepsilon }_0rm}}\left(2.4\right).\]Подставим (2.4) в (2.2), получим:
\[B=\frac{{\mu }_0}{8\pi }\frac{q^2}{r^2\sqrt{\pi {\varepsilon }_0rm}}\ .\]Ответ: $B=\frac{{\mu }_0}{8\pi }\frac{q^2}{r^2\sqrt{\pi {\varepsilon }_0rm}}\ .$ Магнитные поля создаются движущимися зарядами.
Магнитные монополи
Магнитные монополи
Магнитный монополь — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд определяет напряжённость магнитного поля совершенно так же, как электрический заряд определяет напряжённость электрического поля.
Магнитный монополь можно представлять как отдельно взятый полюс длинного и тонкого постоянного магнита. Однако у обычного магнита всегда два полюса, то есть он является диполем. Если разрезать магнит на две части, то у каждой его части по-прежнему будет два полюса. Все известные элементарные частицы, обладающие электромагнитным полем, являются магнитными диполями.
У любого магнита есть два полюса — северный (отрицательный) и южный (положительный). Однако если разрезать магнит пополам, вы не получите отдельно южный и отдельно северный полюс — вы получите два магнита половинного размера, и у каждого снова окажется два полюса, ориентированные так же, как и у исходного магнита. И, сколько бы вы ни повторяли процесс такого деления магнитов, вы просто будете получать всё больше и больше двухполюсных магнитиков или, выражаясь научным языком, магнитных диполей. Как бы вы ни изощрялись, однополярного магнита — положительного или отрицательного магнитного заряда, или монополя, — вы не получите. Иными словами, в природе магнитных монополей не существует.
Этот факт сразу же подчеркивает удивительную асимметрию между магнетизмом и электричеством. Согласно закону Био—Савара, магнитные поля возбуждаются при движении электрических зарядов, а первый из законов электромагнитной индукции Фарадея показывает, что движение магнитов возбуждает электрические токи. Однако носители электрических зарядов выделить можно — например, электроны несут отрицательный единичный заряд, а протоны — положительный. С магнитами же, судя по всему, дело обстоит иначе.
С созданием физики как науки, основанной на опыте, утвердилось мнение, что электрические и магнитные свойства тел существенно различаются. Это мнение было чётко выражено Уильямом Гильбертом в 1600 году. Установленное Шарлем Кулоном тождество законов притяжения и отталкивания для электрических зарядов и магнитных зарядов — полюсов магнитов, вновь подняло вопрос о сходстве электрических и магнитных сил, однако к концу XVIII века было выяснено, что в лабораторных условиях невозможно создать тело с ненулевым полным магнитным зарядом. Понятие о «магнитно заряженной субстанции» было надолго изгнано из физики после работы Ампера в 1820, в которой было доказано, что контур с электрическим током создаёт такое же магнитное поле, как магнитный диполь.
Вначале 30-х годов 20-го века Поль Дирак предложил теорию, в которой естесственным образом был введен магнитный монополь (монополь Дирака) из условия квантования электрического заряда. С этого времени начались, пока безуспешные, попытки экспериментального обнаружения монополя Дирака.
В последнее время группа специалистов по твердому телу объявила о том, что они косвенным образом наблюдали магнитные монополи в спиновых стеклах. Дело в том, что при низких температурах при достаточно сильном внешнем поле магнитные диполи спиновых стекол поляризуются (позитивный магнитный заряд находится на одной плоскости, а негативный – на второй, причем они соединены тонкими «дираковскими нитями»), создавая таким образом т.н. твердотельный «магнитный конденсатор». Если пропускать через плоскости такого конденсатора пучек нейтронов (они имеют не нулевой магнитный момент), то последние определенным образом отклоняются. Таким образом, по полученной картине рассеяния нейтронов в спиновых стеклах делается предположение о наличии магнитных монополей. В действительности в спиновых стеклах мы имеем квазичастицы, которые имеют свойства магнитного диполя. На концах диполя находятся также магнитные квазизаряды (позитивные и негативные), соединенные тонкой дираковской нитью. Эксперименты на нейтронах подтверждают только «тонкость» дираковских нитей диполя в сравнении с размерами нейтронов.
Ученые уже давно ведут теоретические дискуссии о том, существуют ли магнитные монополи, и пытаются обнаружить их экспериментально, однако до сих пор тщетно. Во многом эти усилия обусловлены критерием красоты теории. Для физиков-теоретиков Вселенная без магнитного монополя подобна прекрасной картине с зияющей дырой в холсте. В ранней Вселенной должно было сформироваться великое множество магнитных монополей, однако при последующем стремительном расширении они оказались размазанными очень тонким слоем по холсту мироздания. Возможно, во всей видимой части Вселенной существуют считанные единицы магнитных монополей, хотя, рискну предположить, что их все-таки несколько больше, и рано или поздно они объявятся.
Если монополи будут открыты, придется пересмотреть формулировки некоторых законов, описывающих явления магнетизма, в частности теорему Гаусса для магнитного поля. Представьте себе изолированный в пространстве магнитный монополь, окруженный замкнутой поверхностью произвольной конфигурации. В каждой точке поверхности будет наблюдаться магнитное поле, производимое монополем. Согласно закону Гаусса, суммарный магнитный поток, проходящий через такую замкнутую поверхность, должен равняться нулю, а в случае присутствия внутри нее магнитного монополя он будет, очевидно, отличен от нуля. То есть закон Гаусса не допускает существования магнитных монополей.
Закон Гаусса, собственно, и исходит из того, что магнитные поля производятся диполями, их силовые линии замыкаются и, как следствие, проходят сквозь окружающую поверхность дважды — в ту и другую сторону. Поэтому суммарное поле и обнуляется. В случае же монополя, каковым, в частности, является электрический заряд, силовые линии не замыкаются сами на себя, и закон Гаусса не выполняется.
То есть если допустить существование магнитного монополя, суммарный поток магнитного поля через поверхность не будет равен нулю, а будет пропорционален магнитному заряду, и будут выполняться два закона Гаусса для электрического поля.
Явления, наблюдаемые очень редко и проявляющиеся неожиданно, наиболее трудны как для исследований, так и для понимания их природы. Наблюдают их, как правило, случайные и неподготовленные люди, свидетельства которых довольно противоречивы и поверхностны. С другой стороны, даже подготовленный специалист при встрече с ними нередко оказывается бессилен – у него не оказывается под рукой аппаратуры, не хватает времени для подготовки к измерениям и т.д. В силу ограниченности возможностей остаётся только сопоставлять разрозненные данные, анализировать, строить недоказуемые в настоящий момент гипотезы, всё же надеясь, что и эти методы способны приблизить к ожидаемому результату.
Уже довольно давно две научные загадки не дают покоя исследователям – природа шаровой молнии и монополь Дирака. Первая из них наблюдается слишком редко, второй до сих пор не обнаружен и существует лишь теоретически. Может быть, стоит попытаться два этих явления объединить?
Приведём предполагаемые свойства монополя Дирака. При движении в среде (например, в атмосфере или в жидкости), содержащей частицы, обладающие магнитными моментами, монополь должен обрастать ими подобно тому, как обрастает полюс полосового магнита, если вы проведете им над рассыпанными булавками (для более полной аналогии надо брать очень длинный магнит, т. е. почти отдельный магнитный заряд, и магнитные стрелки—диполи). Монополь, обросший магнитными диполями, из-за резкого увеличения массы должен стать менее подвижным и будет медленно дрейфовать в среде (это довольно похоже на «плывущую» в воздухе ШМ). Постоянные магниты и обыкновенное мягкое железо должны быть настоящими ловушками для монополей (замечена способность ШМ «прилипать» к железным предметам).
Движущийся монополь должен ионизовать атомы среды, через которую он движется (ионизирует атомы и ШМ), причем ионизующая способность должна быть тем больше, чем больше значение магнитного заряда монополя. Сходство свойств этих явлений ещё ничего не доказывает, но всё же несколько обнадёживает. Попробуем взглянуть на вопрос иначе – а почему предсказанный Дираком магнитный монополь обязательно должен быть постоянным? В обычном магните противоположные полюса существуют одновременно (в общей точке времени), но разделены в пространстве определённым расстоянием. Почему не может быть наоборот — противоположные полюса разделены во времени определённым периодом (северный полюс сменяется южным и наоборот) и совмещены в одной пространственной точке? Такое состояния будет представлять собой переменный магнитный монополь – и оно, если вдуматься, ещё более сочетается с труднообъяснимыми свойствами ШМ.
Спустя почти 85 лет после того, как физик-теоретик Поль Дирак предсказал возможность существования магнитных монополей, современные ученые-физики синтезировали, идентифицировали и зарегистрировали на фотоснимках искусственные магнитные монополи.
Это инновационное достижение, о котором была публикация в журнале Nature, прокладывает путь к обнаружению магнитных монополей природного происхождения. И если это произойдет в недалеком будущем, то по важности данное открытие можно будет сопоставить только с открытием электрона.
Группа ученых, получивших искусственные магнитные монополи, применила инновационный подход к исследованиям теории Дирака и использовала этот подход для создания и идентификации искусственных монополей в пределах магнитного поля, индуцированного конденсатом Бозе-Эйнштейна, газом из чрезвычайно холодных атомов, температура которых лишь на несколько миллиардных долей градусов была выше температуры абсолютного нуля.
В своих исследованиях группа опиралась на теоретическую работу, изданную Микко Мёттёненом (Mikko Mottonen) и Вилл Питилэ (Ville Pietila), научным сотрудником и его студентом из университета Аальто (Финляндия). Эти ученые предположили, что особая последовательность изменений внешних магнитных полей может привести к возникновению искусственного магнитного монополя.
В результате экспериментов ученые были вознаграждены чередой фотоснимков, служивших подтверждением присутствия монополей на концах воронок крошечных квантовых «водоворотов» из сверххолодного атомарного газа. Полученный результат является экспериментальным доказательством того, что предполагаемые магнитные структуры Дирака могут действительно существовать в природе.
Произведенное учеными открытие может привести к пониманию принципов и разработке принципиально новых материалов, таких, как высокотемпературные сверхпроводники, которые смогут передавать электричество без потерь при нормальной температуре окружающей среды. Кроме этого, открытие искусственных монополей и дальнейшие исследования их природы могут послужить толчком исследований, направленных на обнаружение естественных магнитных монополей, которые проводятся на Большом Адронном Коллайдере в ЦЕРНе.
Следите за новостями!
Источники:
http://www.seti-ceti.ru/synthetic-magnetic-monopoles
http://tainy.net/19156-peremennyj-magnitnyj-monopol-dvizhitel-nlo.html
http://elementy.ru/trefil/21161/Magnitnye_monopoli
Магнитный монополь — лекции на ПостНауке
Магнитные монополи могут существовать в теориях великого объединения. Тогда встает вопрос, почему мы не видим их или косвенных улик их присутствия во Вселенной. Возможно, они присутствуют во всех вариантах великого объединения. Тогда это, безусловно, проблема: либо великого объединения нет, либо нам нужно объяснять, куда делись магнитные монополи.
Есть другая возможность, где монополи могут себя проявлять. Существует проблема конфайнмента, которая ставит вопрос, почему мы видим, когда рассеиваем частицы на протонах, что рассеяние происходит при очень высоких энергиях, как будто бы частицы рассеиваются на очень точечных трех центрах внутри нуклона. Причем рассеяние устроено так, как у Резерфорда. Он рассеивал альфа-частицы на атомах, а рассеяние происходило на ядре как на точечном объекте. Мы наблюдаем аналогичную ситуацию только на трех центрах. Соответственно, должны присутствовать кварки, однако свободных кварков мы не видим. Приблизительно понятно, почему так происходит, но хочется аналитического объяснения этого эффекта.
Один из механизмов конфайнмента кварков использует возможность наличия магнитных монополей. Откуда он берется? Известно, что существует теория сверхпроводимости, казалось бы, совершенно не имеющая отношения к тому, о чем я до сих пор говорил. В этой теории, теории Бардина — Купера — Шиффера, происходит конденсация куперовских пар. Электрические заряженные частицы в сверхпроводниках при очень низких температурах ведут себя таким образом, что магнитные поля в сверхпроводниках собираются в трубки Абрикосова. В сверхпроводниках первого рода эти трубки собираются не в кристалл, а по границе сверхпроводника. Важно, что конденсат электрических зарядов ведет себя так, что он не пускает в ту область, где он находится, магнитное поле. Но может его пропускать только в виде таких тонких трубок.
Представьте, что у вас есть два магнитных заряда, и вспомните силовые линии электромагнитного поля, которые рисуют во всех книжках. Оказывается, что если вы этот магнит поместите в сверхпроводник, то линии соберутся в одну трубку. Это вихрь Абрикосова, или струна Абрикосова — Нильсена — Олесена. А теперь представьте себе, что мы сделаем преобразование дуальности, о котором я уже упомянул, то есть поменяем электрические и магнитные заряды и поля местами. И после будем рассматривать электрические заряды, а конденсироваться у нас будут магнитные заряды. Тогда электрическое поле соберется, и мы не сможем отделить электрические заряды друг от друга, потому что между ними будет перетянута трубка. Если у нас есть динамические заряды в системе, то трубка разорвется в момент, когда в ней энергия будет больше, чем 2mc в квадрате, и тогда появится два новых заряда.
В обычном сверхпроводнике у нас есть конфайнмент магнитных зарядов. Если бы мы их поместили в обычный сверхпроводник, то мы не смогли бы положительный от отрицательного заряды отделить потому, что они связаны трубкой, а при удалении трубка рвется и рождает новые две частицы. В дуальном сверхпроводнике у нас, где сконденсированы магнитные заряды, был бы конфайнмент электрических зарядов. Мы не смогли бы отдельно держать противоположный электрический заряд.
МАГНИТНЫЙ ЗАРЯД — это… Что такое МАГНИТНЫЙ ЗАРЯД?
- МАГНИТНЫЙ ЗАРЯД
- МАГНИТНЫЙ ЗАРЯД
-
вспомогательное понятие, вводимое при расчётах статич. магн. полей (по аналогии с понятием электрич. заряда, создающего электростатич. поле). М. з., в отличие от электрич. зарядов, реально не существует, т. к., согласно классич. теории магнетизма, магн. поле не имеет особых источников, помимо электрич. токов. Гипотеза англ. физика П. Дирака (1931) о существовании в природе М. з.— т. н. магнитных монополей — экспериментально пока не подтверждена, но попытки обнаружить М. з. продолжаются. Для тел, обладающих намагниченностью, можно ввести понятия объёмной rm и поверхностной sm плотности М. з. Первая связана с неоднородным распределением намагниченности по объёму тела, вторая — со скачком норм. составляющей намагниченности на поверхности магнетика. Принято считать, что М. з. располагаются двойными слоями на поверхностях, где происходит скачок норм. составляющей намагниченности, причём элементарные М. з. противоположных знаков связаны в магн. диполи.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МАГНИТНЫЙ ЗАРЯД
-
— вспомогательное понятие, вводимое при расчётах статич. магн. полей (по аналогии с понятием электрич. заряда, создающего электро-статич. поле). Согласно классич. теории магнетизма, магн. поле не имеет иных источников, кроме электрич. токов. Однако П. А. М. Дирак (P. A. M. Dirac) в 1931 выдвинул гипотезу о существовании в природе обособленных М. з.- магнитных монополей, существование последних также предсказывается в теории великого объединения. Гипотеза экспериментально пока не подтверждена, но поиски магн. монополей продолжаются. Для тел, обладающих намагниченностью М, можно ввести понятия объёмной
 и поверхностной
и поверхностной  плотностей М. з.; первая связана с неоднородным распределением М по объёму тела и определяется как
плотностей М. з.; первая связана с неоднородным распределением М по объёму тела и определяется как  , вторая — со скачком
, вторая — со скачком  (норм. составляющей намагниченности) на поверхности тела:
(норм. составляющей намагниченности) на поверхности тела:
 , где
, где  — разность норм. составляющих вектора М по обе стороны граничной поверхности магнетика. Плотности М. з.
— разность норм. составляющих вектора М по обе стороны граничной поверхности магнетика. Плотности М. з.  и (или)
и (или)  определяют магнитостатическую энергию магнетика. C. В. Вонсовский.
определяют магнитостатическую энергию магнетика. C. В. Вонсовский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
- МАГНИТНЫЙ ГИСТЕРЕЗИС
- МАГНИТНЫЙ МОМЕНТ
Смотреть что такое «МАГНИТНЫЙ ЗАРЯД» в других словарях:
МАГНИТНЫЙ ЗАРЯД — вспомогательное понятие, вводимое при расчетах статических магнитных полей (по аналогии с электрическим зарядом, создающим электростатическое поле). Реальный источник статического магнитного поля стационарный электрический ток или постоянный… … Большой Энциклопедический словарь
магнитный заряд — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN magnetic charge … Справочник технического переводчика
магнитный заряд — вспомогательное понятие, вводимое при расчётах статических магнитных полей (по аналогии с электрическим зарядом, создающим электростатическое поле). Реальный источник статического магнитного поля стационарный электрический ток или постоянный… … Энциклопедический словарь
магнитный заряд — magnetinis krūvis statusas T sritis Standartizacija ir metrologija apibrėžtis Pagalbinė sąvoka, vartojama apibūdinant statinį magnetinį lauką. atitikmenys: angl. magnetic charge vok. magnetische Ladung, f rus. магнитный заряд, m pranc. charge… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
магнитный заряд — magnetinis krūvis statusas T sritis fizika atitikmenys: angl. magnetic charge vok. magnetische Ladung, f rus. магнитный заряд, m pranc. charge magnétique, f … Fizikos terminų žodynas
Магнитный заряд — вспомогательное понятие, вводимое при расчётах статических магнитных полей (по аналогии с электрическим зарядом, создающим электростатическое поле). М. з., в отличие от электрических зарядов, реально не существуют, так как магнитное поле… … Большая советская энциклопедия
МАГНИТНЫЙ ЗАРЯД — вспомогат. понятие, вводимое при расчётах статич. магн. полей (по аналогии с электрич. зарядом, создающим электро статич. поле). Реальный источник статич. магн. поля стационарный электрич. ток или пост. магнит … Естествознание. Энциклопедический словарь
магнитный заряд полюса — magnetinio poliaus stipris statusas T sritis fizika atitikmenys: angl. magnetic pole strength vok. magnetische Polstärke, f rus. магнитная масса полюса, f; магнитный заряд полюса, m pranc. intensité du pôle magnétique, f; masse magnétique du pôle … Fizikos terminų žodynas
Заряд — Заряд: Заряд в физике Электрический заряд количественная характеристика, показывающая степень возможного участия тела в электромагнитных взаимодействиях. Магнитный заряд Цветной заряд квантовое число в квантовой хромодинамике, приписываемое… … Википедия
МАГНИТНЫЙ МОМЕНТ — основная величина, характеризующая магн. свойства в ва. Источником магнетизма (М. м.), согласно классич. теории эл. магн. явлений, явл. макро и микро(атомные) электрич. токи. Элем. источником магнетизма считают замкнутый ток. Из опыта и классич.… … Физическая энциклопедия
Способности магнитного монополя • Игорь Иванов • Научно-популярные задачи на «Элементах» • Физика
На заряженную частицу, двигающуюся в магнитном поле B, действует сила Лоренца: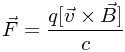
Напряженность магнитного поля от монополя выражается формулой: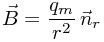
Здесь 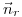 обозначает единичный вектор, направленный от монополя к заряду. Обе эти формулы записаны в естественной системе единиц СГС, которая удобна для описания электромагнитных явлений. Если вторую формулу подставить в первую, то получится сила, действующая на пролетающую частицу.
обозначает единичный вектор, направленный от монополя к заряду. Обе эти формулы записаны в естественной системе единиц СГС, которая удобна для описания электромагнитных явлений. Если вторую формулу подставить в первую, то получится сила, действующая на пролетающую частицу.
В этой задаче нас интересуют не сами эти формулы, а то, куда направлена сила. Пусть частица пролетает так, как показано на рис. 3. Мы знаем по условию, что траектория отклонится не сильно, но не знаем, в какую именно сторону. Ответ на этот вопрос как раз и дают написанные выше формулы. Они говорят, что направление силы определяется векторным произведением скорости и единичного радиус-вектора. Если частица движется, как на рисунке 3, то оба этих вектора лежат в плоскости рисунка (и не параллельны друг другу), а значит, их векторное произведение направлено перпендикулярно плоскости рисунка. Для верхней траектории это направление от рисунка на нас, для нижней траектории — от нас вглубь рисунка. Этот вывод справедлив для любых точек траектории. Поэтому когда эти частицы пролетят мимо монополя, их траектории отклонятся в ту же сторону, т.е. они выйдут из плоскости рисунка, одна чуть выше, другая чуть ниже (рис. 4).
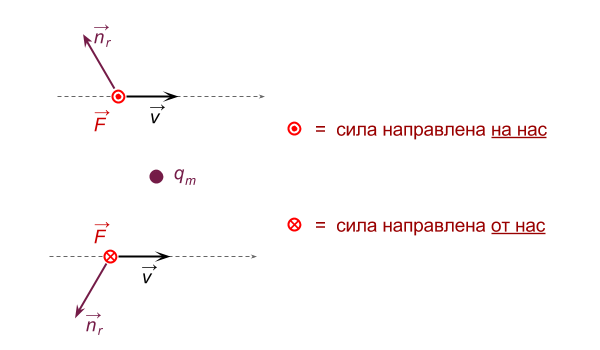
Аналогично действуем для любой другой частицы: надо лишь представить себе новую плоскость (она задается векторами скорости и 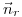 ) и отклонить траекторию из этой плоскости. Траектория каждой частицы будет отклоняться в одну сторону, например вправо, по часовой стрелке, если смотреть с направления, откуда частицы прилетели (это направление определяется знаком зарядов). И поэтому совокупный эффект для всего облака в результате будет выглядеть, как на рис. 2.
) и отклонить траекторию из этой плоскости. Траектория каждой частицы будет отклоняться в одну сторону, например вправо, по часовой стрелке, если смотреть с направления, откуда частицы прилетели (это направление определяется знаком зарядов). И поэтому совокупный эффект для всего облака в результате будет выглядеть, как на рис. 2.
Подчеркнем, что облако после пролета мимо монополя, конечно, начнет не только вращаться, но и расширяться, поскольку траектории отдельных частиц больше не параллельны друг другу. Но такое расширение, вызванное силовым возмущением, будет и для электрических, и для гравитационных сил. Особенность же взаимодействия в паре «монополь + заряд» именно в новом эффекте, во вращении. Пока расширение облака не слишком заметно, можно сказать, что пролет сквозь монополь просто передал облаку некий механический вращательный момент. А возникает он именно потому, что в паре «заряд + монополь» силы действуют «вбок», в не «вдоль».
Магнитные монополи • Джеймс Трефил, энциклопедия «Двести законов мироздания»
В природе до сих пор не найдено изолированных магнитных зарядов. Поток магнитного поля, проходящий через замкнутую поверхность, равен нулю.
У любого магнита есть два полюса — северный (отрицательный) и южный (положительный). Однако если разрезать магнит пополам, вы не получите отдельно южный и отдельно северный полюс — вы получите два магнита половинного размера, и у каждого снова окажется два полюса, ориентированные так же, как и у исходного магнита. И, сколько бы вы ни повторяли процесс такого деления магнитов, вы просто будете получать всё больше и больше двухполюсных магнитиков или, выражаясь научным языком, магнитных диполей. Как бы вы ни изощрялись, однополярного магнита — положительного или отрицательного магнитного заряда, или монополя, — вы не получите. Иными словами, в природе магнитных монополей не существует.
Этот факт сразу же подчеркивает удивительную асимметрию между магнетизмом и электричеством. Согласно закону Био—Савара, магнитные поля возбуждаются при движении электрических зарядов, а первый из законов электромагнитной индукции Фарадея показывает, что движение магнитов возбуждает электрические токи. Однако носители электрических зарядов выделить можно — например, электроны несут отрицательный единичный заряд, а протоны — положительный. С магнитами же, судя по всему, дело обстоит иначе.
Ученые уже давно ведут теоретические дискуссии о том, существуют ли магнитные монополи, и пытаются обнаружить их экспериментально, однако до сих пор тщетно. Во многом эти усилия обусловлены критерием красоты теории. Для физиков-теоретиков Вселенная без магнитного монополя подобна прекрасной картине с зияющей дырой в холсте. В ранней Вселенной должно было сформироваться великое множество магнитных монополей, однако при последующем стремительном расширении они оказались размазанными очень тонким слоем по холсту мироздания. Возможно, во всей видимой части Вселенной существуют считанные единицы магнитных монополей, хотя, рискну предположить, что их все-таки несколько больше, и рано или поздно они объявятся.
Если монополи будут открыты, придется пересмотреть формулировки некоторых законов, описывающих явления магнетизма, в частности теорему Гаусса для магнитного поля. Представьте себе изолированный в пространстве магнитный монополь, окруженный замкнутой поверхностью произвольной конфигурации. В каждой точке поверхности будет наблюдаться магнитное поле, производимое монополем. Согласно закону Гаусса, суммарный магнитный поток, проходящий через такую замкнутую поверхность, должен равняться нулю, а в случае присутствия внутри нее магнитного монополя он будет, очевидно, отличен от нуля. То есть закон Гаусса не допускает существования магнитных монополей.
Закон Гаусса, собственно, и исходит из того, что магнитные поля производятся диполями, их силовые линии замыкаются и, как следствие, проходят сквозь окружающую поверхность дважды — в ту и другую сторону. Поэтому суммарное поле и обнуляется. В случае же монополя, каковым, в частности, является электрический заряд, силовые линии не замыкаются сами на себя, и закон Гаусса не выполняется.
То есть если допустить существование магнитного монополя, суммарный поток магнитного поля через поверхность не будет равен нулю, а будет пропорционален магнитному заряду, и будут выполняться два закона Гаусса для электрического поля.
См. также:
Монополь Дирака. Элементарный магнитный заряд.
© «Знания-сила».
Несимметрия уравнений электродинамики. — Магнитный заряд. — Свойства монополя. — Поиски монополей на ускорителях. — Рождение монополей космическим излучением. — Поиски монополей в метеоритах и на Луне. — Использование магнитного поля Земли. — Существует ли монополь?
Из курса общей физики известно, что между электричеством и магнетизмом существует теснейшая связь. Электричество и магнетизм входят в физику почти симметричным образом. Движение зарядов, т.е. электрический ток, создает магнитное поле. Изменение магнитного потока создает электродвижущую силу, которая в замкнутом проводнике порождает электрический ток.
Такая симметрия в представлениях о природе электричества и магнетизма существовала не всегда. Очень долго электричество и магнетизм изучались раздельно. Но с тех пор как Эрстед в 1820 г. открыл магнитные свойства электрического тока, физиков не оставляла мысль о необходимости существования обратного явления: магнитное поле должно порождать электрический ток. Наконец, в 1831 г. Фарадей открыл электромагнитную индукцию. С этого момента физики уже не забывали о всеобщей взаимосвязанности электричества и магнетизма: они никогда не говорят об электрических и магнитных явлениях в отдельности, а всегда имеют в виду электромагнитные явления в целом.
Учение об электромагнитных явлениях — электродинамика (для макрообъектов) и квантовая электродинамика (для всех объектов, включая микрочастицы), пожалуй, является самой точной наукой из числа наук о взаимодействиях между частицами и полями. На её счету имеются не только объяснение всех макроскопических и микроскопических электромагнитных явлений от излучения радиоволн гигантскими антеннами до излучения γ-квантов атомными ядрами, но и предсказание существования радикально нового состояния материи в форме антивещества, а также количественных оценок очень тонких эффектов типа взаимодействия электрона с его собственным электромагнитным полем. И всё же современная электродинамика не полностью удовлетворяет физиков, и опять по причине несимметрии между электричеством и магнетизмом. Оказывается, основные уравнения электродинамики (уравнения Максвелла) почти, но не вполне симметричны относительно электрических и магнитных явлений.
В эти уравнения входят напряженность электрического поля Е, напряженность магнитного поля Н, плотность электрического тока j и плотность электрического заряда р. Для вакуума, например, уравнения Максвелла записываются следующим образом:
Даже человеку, не знакомому с высшей математикой, видно, что Е и Н входят в уравнения симметричным образом (над ними производятся одинаковые математические операции). Однако симметрия уравнений в целом получается неполной из-за того, что в одну их группу входят плотность электрического заряда р и плотность тока j, а в другую не входят аналогичные им плотность магнитного заряда и плотность магнитного тока.
Вы, конечно, понимаете, почему так получилось? Потому что многолетний опыт физиков показывает, что магнитные заряды никогда не наблюдались, т.е. получить отдельно северный или южный магнитный полюс никому не удавалось. Так что уравнения Максвелла правильно отражают ситуацию, существующую в природе, и, казалось бы, ни в каком усовершенствовании не нуждаются. Однако отмеченная выше несимметрия уравнений всё же вызывает некоторую неудовлетворенность. Эту неудовлетворенность можно сформулировать так: в связи с симметрией электрических и магнитных явлений было бы естественнее, если бы уравнения Максвелла, оставаясь правильными, выглядели вполне симметрично, т.е. содержали бы плотность магнитного заряда и плотность магнитного тока. Другими словами, хочется думать, что в природе существуют магнитные заряды (и, следовательно, магнитные токи), которые, однако, обладают такими свойствами, что их пока никто не мог обнаружить ни в одном из множества сделанных опытов.
Теоретически такую возможность впервые обосновал в 1931 г. Поль Дирак, который показал, что наряду с общепринятой несимметричной (но проверенной многими экспериментами) квантовой электродинамикой может быть построена непротиворечивая с ней симметричная квантовая электродинамика, учитывающая существование магнитных зарядов. Гипотетический магнитный заряд, введенный Дираком, принято называть монополем Дирака.
С тех пор прошло около 80 лет, а проблема существования монополя Дирака всё ещё не решена: не доказано ни его наличие, ни его отсутствие. Поэтому проблема монополя остается актуальной до сих пор, и для её разрешения ставятся всё новые и новые эксперименты.
Какие же это эксперименты и почему они не дают результатов? Для ответа на эти вопросы предположим, что монополь существует, и познакомимся с его предполагаемыми свойствами сначала качественно, а затем и количественно.
Мы уже говорили, что гипотетический монополь Дирака — это отдельный магнитный заряд, подобный отдельному электрическому заряду (либо положительному, либо отрицательному). Поэтому монополь Дирака должен вести себя по отношению к магнитному полю так же, как электрический заряд ведёт себя по отношению к электрическому полю. В частности, вокруг монополя должно возникать магнитное поле, подобное электростатическому полю, возникающему вокруг электрического, заряда, т.е. силовые линии магнитного поля должны начинаться или кончаться на магнитных зарядах; напряженность магнитного поля, созданного точечным магнитным зарядом µ, должна изменяться по закону Н = (µ/г3) r [подобно тому как напряженность электрического поля, создаваемого электрическим зарядом е, изменяется по закону Е = (е/r3) r].
Сила F, действующая на магнитный заряд µ в магнитном поле Н, должна быть равна: F = µH.
Взаимодействие двух магнитных зарядов µ1 и µ2 будет определяться законом, аналогичным закону Кулона:
Vµ = µ1µ2/ r ;
В однородном магнитном поле монополь должен ускоряться подобно электрическому заряду в электрическом поле (магнитные диполи, например магнитные стрелки, в однородном магнитном поле не ускоряются, а только ориентируются).
При движении в среде (например, в атмосфере или в жидкости), содержащей частицы, которые обладают магнитными моментами, монополь должен обрастать ими подобно тому, как обрастает полюс полосового магнита, если вы проведете им над рассыпанными булавками (для более полной аналогии надо брать очень длинный магнит, т.е. почти отдельный магнитный заряд, и магнитные стрелки — диполи). Монополь, обросший магнитными диполями, из-за резкого увеличения массы должен стать менее подвижным и медленно дрейфовать в среде.
При попадании монополя в среду с примесью парамагнитных веществ монополь будет притягиваться ими и образовывать связанные системы с энергией связи около 1 эВ. Постоянные магниты и обыкновенное мягкое железо должны быть настоящими ловушками для монополей; они должны захватывать монополи столь прочно, что для вырывания их оттуда нужны магнитные поля очень высокой индукции. Это свойство парамагнетиков и ферромагнетиков можно использовать для накопления монополей, если последние стабильны , т.е. не распадаются со временем.
Стабильность монополя является прямым Следствием (во всяком случае, для монополя с наименьшей массой) естественного предположения о существовании для магнитного заряда закона сохранения, аналогичного закону сохранения электрического заряда.
Взаимосвязь магнитного монополя с электрическим полем тоже вполне аналогична связи электрического заряда с магнитным полем. Подобно тому как при движении электрического заряда возникает магнитное поле Н, при движении магнитного монополя должно возникать электрическое поле Е. А это означает, что движущийся монополь должен ионизовать атомы среды, через которую он движется, причем ионизирующая способность должна быть тем больше, чем больше значение магнитного заряда монополя.
Наконец, по аналогии с образованием γ-квантом электрон-позитронной пары за счёт энергии электромагнитного поля можно представить существование процесса рождения быстрым γ-квантом и монополь-антимонопольной пары (ведь монополь благодаря магнитному заряду участвует в электромагнитном взаимодействии).
Чтобы сделать все эти рассуждения из качественных количественными, т.е. ответить на вопросы: с какой силой притягивается монополь, как велика производимая им ионизация, при какой энергии γ-квант может родить пару монополь — антимонополь и другие, нужны количественные характеристики свойств монополя. Такие характеристики также были даны Дираком.
Дирак показал, что если монополь существует, то его магнитный заряд µ должен быть связан с элементарным электрическим зарядом е соотношением:
2µe/c = nh , (1)
где n — произвольное целое число; h — постоянная Планка.
µ = nhc/2e = (1/2) (hc/e2) ne,
и так как e2/hc = 1/137 (величина e2/hc, называемая постоянной тонкой структуры, играет важную роль в квантовой электродинамике), имеем:
µ =68,5ne.
Таким образом, по Дираку минимальное значение магнитного заряда в 68,5 раза больше элементарного электрического заряда e, т.е. заряда электрона. Он может быть также равен 2 • 68,5е = 137е; 3 • 68,5е = 205,5е и т.д..
Частица со столь большим магнитным зарядом при движении со скоростью V ~ с должна ионизовать атомы окружающей среды в (68,5)2 ~ 4700 раз сильнее, чем релятивистский электрон. Благодаря этому обстоятельству след монополя должен быть совершенно отчетливо виден в трековом детекторе, например в фотопластинке (в которой виден под микроскопом даже след релятивистского электрона). Этот след будет отличаться от следов тяжёлых ядер с зарядом Z ~ 70 (которые производят такую же ионизацию) равномерной толщиной по всей длине (следы тяжёлых ядер утончаются к концу из-за обрастания ядер электронами).
Вследствие большого магнитного заряда монополь должен очень легко приобретать энергию в магнитном поле. Например, пройдя путь 1 см в сравнительно слабом поле индукцией 0,1 Тл, монополь приобретает энергию около 2 • 107 эВ. Для сравнения заметим, что электрон может приобрести такую же энергию, пройдя 1 см в электрическом поле Е = 20000000 В/см.
Массу монополя можно оценить, если сделать какое-то разумное предположение о его размерах. Считая, например, что масса монополя имеет электромагнитную природу, и предполагая, что его радиус равен классическому радиусу электрона.
rе = е2/mес2 = 2,8 • 10-13 см,
mµ = µ2/rес2 = (µ/е)2 е2/rес2 = (µ/е)2 mе ~ 4700•0.5 = 2350 МэВ/с2
или, mµ ~ 2,5mp
Если же радиус монополя положить равным радиусу протона (около 0,8 • 10-13 см), то для массы монополя получается значительно большее значение:
mµ ~ 8,2 ГэВ/с2 = 8,7mp
Рассмотрим далее возможные способы поисков монополя.


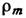 и поверхностной
и поверхностной 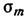 плотностей М. з.; первая связана с неоднородным распределением М по объёму тела и определяется как
плотностей М. з.; первая связана с неоднородным распределением М по объёму тела и определяется как 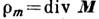 , вторая — со скачком
, вторая — со скачком 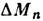 (норм. составляющей намагниченности) на поверхности тела:
(норм. составляющей намагниченности) на поверхности тела: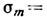
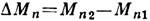 , где
, где 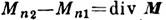 — разность норм. составляющих вектора М по обе стороны граничной поверхности магнетика. Плотности М. з.
— разность норм. составляющих вектора М по обе стороны граничной поверхности магнетика. Плотности М. з. 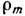 и (или)
и (или) 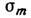 определяют магнитостатическую энергию магнетика. C. В. Вонсовский.
определяют магнитостатическую энергию магнетика. C. В. Вонсовский.