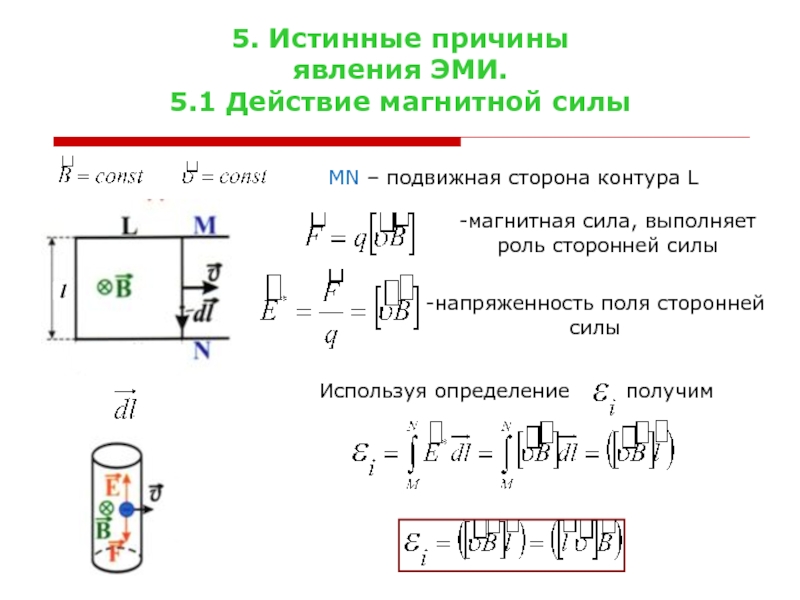
Магнитное поле — что это, определение и ответ

Электрические и магнитные явления связаны, так как имеют общую природу ― электромагнитное поле. Движение электрических зарядов всегда создает магнитное поле, а магнитное поле, в свою очередь, всегда вызывает перемещение электрических зарядов.

Так как ток ― это направленное перемещение электрических зарядов, то протекание тока в проводнике всегда создает магнитное поле вокруг проводника.

Линии магнитного поля, которое создается проводниками с электрическим током.

Для изображения магнитных полей используют магнитные силовые линии ― линии, на которых модуль вектора магнитной индукции одинаков и равен В, а сам вектор магнитной индукции \(\overrightarrow{B}\) направлен по касательной к линии. Линии магнитной индукции всегда замкнуты.

Для обозначения направлений движения тока и направлений магнитных силовых линий, помимо стрелок «вправо» → и «влево» ←, используются знаки «от нас» ― ⊗ или ⊕ (как торец оперения стрелы, летящей от нас), и «к нам» • или ⊙ (как острие летящей на нас стрелы).

Чтобы определить направление вектора магнитной индукции \(\overrightarrow{B}\), которое создает ток, протекающий в прямом проводнике, используется правило правого винта: если представить, что вкручиваешь винт по направлению тока ― то направление вращения винта покажет направление вектора магнитной индукции.

Магнитное поле, которое создает ток в прямом проводнике, представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. При этом, некоторая область магнитного поля всегда направлена на нас, а другая ― от нас.

Чтобы определить направление вектора магнитной индукции \(\overrightarrow{B}\), которое создает ток, в круговом проводнике или витках катушки, используется правило правого винта: если ток вращается по часовой стрелке, то магнитное поле будет направленно «от нас». Если ток течет против часовой стрелки, то ток будет направлен «на нас».

Сила Ампера ― сила, действующая на проводник с током со стороны магнитного поля.

Сила ампера равна

F_A = IBLsinα, где

F_A ― сила Ампера [Н];

I ― сила тока в проводнике [A];

B ― магнитная индукция [Тл];

L ― длина проводника [м];

sinα ― синус угла между проводником и вектором магнитной индукции.

Сила Ампера максимальна, если между проводником и вектором магнитной индукции угол равен α = 90°, так как sinα = sin90° = 1 и F_A = IBLsin90° = IBL.

Если проводник расположен параллельно вектору магнитной индукции, т. е. α = 0° ― сила Ампера отсутствует, так как sinα = sin0° = 0 и F_A = IBLsin0° = 0.

Направление силы Ампера определяется по правилу левой руки: если ладонь расположить так, чтобы линии магнитного поля входили в ладонь, а четыре пальца указывали направление тока ― то противопоставленный большой палец укажет направление силы Ампера.

Взаимодействие проводников с током

Ток, протекающий в проводнике, создает магнитное поле. Если рядом расположен еще один проводник, в котором протекает ток ― то второй проводник оказывается в магнитном поле, которое создает первый. На проводник в магнитном поле действует сила Ампера, в результате чего проводники с током или притягиваются, или отталкиваются друг от друга.

Пусть в проводниках 1 и 2 токи текут в одном направлении. Тогда первый проводник создает магнитное поле, направленное против часовой стрелки. В области, близлежащей к проводнику 2 это поле направлено перпендикулярно проводнику и от него. Согласно правилу левой руки, сила Ампера, которая действует со стороны магнитного поля, создаваемого проводником 1 на проводник с током 2, F_1-2 направлено в сторону проводника 1.

Проводник 2 действует на проводник 1 аналогично, и сила ампера, с которой магнитное поле проводника 2 действует на проводник 1 F_2-1 направлена в сторону проводника 2.

Таким образом, силы Ампера, с которым действуют проводники друг на друга ― F_1-2 и F_2-1 направлены навстречу друг другу и проводники притягиваются.

Пусть теперь ток в проводнике 2 течет в том же направлении, а ток в проводнике 1 ― в противоположном. Магнитное поле, которое создает проводник 1, будет направлено по часовой стрелке, а в ближайшей к проводнику 2 области ― на нас. Согласно правилу левой руки, такое магнитное поле создает силу Ампера, направленную от проводника 1.

Магнитное поле, которое создает проводник 2, будет направлено как в первом случае, но из-за того, что ток в проводнике 1 течет в противоположную сторону, сила Ампера F_2-1 будет направлена от проводника 2.

Силы Ампера, с которым действуют проводники друг на друга ― F_1-2 и F_2-1 направлены в разные стороны и проводники отталкиваются.

Магнитное поле постоянного магнита. Магниты обладают собственным магнитным полем. Силовые линии магнита выходят из северного магнитного полюса (N) и входят в южный магнитный полюс (S).

Магнитные поля двух магнитов взаимодействуют друг с другом, переориентируя магниты так, чтобы магнитные линии выходили из северного магнитного полюса и входили в ближайший южный магнитный полюс. При этом одинаковые полюса двух магнитов, отталкиваются, а разные ― притягиваются.

Магнитные силы — Технарь

«Первые опыты по вопросу, рассматриваемому в настоящем труде, связаны с лекциями об электричестве, гальванизме и магнетизме, читанными мною прошедшей зимой».

В ту зиму 1819—1820 гг. электричеством называли силы, действующие между неподвижными зарядами (закон Кулона). К гальванизму же относились те явления, которые наблюдались при движении зарядов, т. е. при наличии тока, а к магнетизму — явления, связанные с такими загадочными предметами, как магниты и стрелки компасов, находящиеся в магнитном поле Земли. Все три вида явлений считались самостоятельными; хотя многие чувствовали, что между ними должна существовать некая связь, обнаружить ее никому не удавалось. В ту зиму Эрстед занимался тем, что пропускал гальванический ток по проводу, расположенному параллельно небольшой магнитной стрелке, в результате чего он обнаружил (фиг. 299), что:

«В данном случае стрелка изменит свое положение, и полюс, находящийся под той частью соединительной проволоки, которая ближе к отрицательному концу гальванического аппарата

1), отклонится к западу».

Мы видели, что силы, действующие между заряженными частицами, являются чисто ньютоновскими. Кулоновская сила не только подчиняется третьему закону, но и совпадает по форме с гравитационной.

1) Устройство, создающее разность потенциалов с помощью химических реакций, например, батарея.

Если бы на кулоновской силе наука кончалась, то в процессе изучения гравитационных сил можно было бы ограничиться небольшой ссылкой на то, что в некоторых случаях сходные силы действуют и между так называемыми

заряженными частицами. Величины этих сил различаются: помимо притяжения возможно отталкивание частиц, но в остальном эти силы неразличимы. Однако наука не кончается на силах Кулона. При дальнейшем изучении электрических сил обнаруживается столько разнообразных и тонких эффектов, что мы вынуждены не только расширять пределы применимости ньютоновской системы, но в конце концов выйти за ее рамки.

Открытие Эрстеда возвестило о начале активных исследований в этой области; в течение последующих десяти лет Ампер и Фарадей разработали теорию магнитных взаимодействий токов.

Эрстеду удалось не только установить эффект воздействия движущегося заряда, или тока, на магнитную стрелку, но и обнаружить удивительное свойство этого эффекта: магнитная стрелка устанавливалась перпендикулярно направлению движения тока (фиг. 300). Более того, оказалось, что в плоскости, перпендикулярной проводу, направления стрелки образуют замкнутые окружности. Это можно проиллюстрировать с помощью простенького опыта, которым любят забавляться дети в дождливые дни. Если насыпать на бумагу мелкие металлические стружки (каждая из которых ведет себя, как маленькая магнитная стрелка), они наглядно передадут конфигурацию поля для различных систем токов.

Наиболее удивительная особенность этого открытия, которая отчасти объясняет, почему оно не было сделано ранее, связана с тем, что неподвижный заряд не оказывает никакого воздействия на магнитную стрелку. Чтобы вызвать эффект, который обнаружил Эрстед, необходимо, чтобы заряд пришел в движение. Таким образом, мы впервые встречаемся с силой, которая оказывается зависящей от движения тел, порождающих ее.

Менее чем через год (2 октября 1820 г.) Ампер опубликовал в журнале «Annals of Chemistry and Physics» работу, в которой он установил, что два токонесущих провода взаимодействуют друг с другом. Он обнаружил, что два провода, по которым текут токи в одном направлении, притягиваются, а два провода, по которым токи текут в противоположные стороны, отталкиваются.

Казалось, что эти новые силы существенно отличались от электрических, так как они не зависели от величины не скомпенсированного заряда в проводах. Если имеется очень длинный токонесущий провод и параллельно ему расположен второй провод, как показано на фиг. 301, то первый провод будет притягивать второй, если ток в последнем течет в том же направлении, что и в первом, и будет отталкивать, если направление тока противоположное. Величина силы зависит от расстояния между проводами, от токов в проводах и от длины второго провода; в системе СГС выражение для силы имеет вид:

Здесь I₁ — ток в первом проводе, I₂ — ток во втором проводе, l — длина второго провода и r — расстояние между проводами. Буква с, стоящая в знаменателе (20.9), обозначает постоянную:

Она имеет размерность скорости, и сейчас мы знаем, что ее величина совпадает со скоростью света²⁾.

Чтобы дать представление о величине силы, которая действует между проводами, положим, что длина второго провода 1 см, отстоит ом от первого на расстоянии тоже 1 см, а токи в проводах равны 10 А.

2) Ответ на вопрос: «Почему собственно в знаменателе стоит значение скорости света?» (это не единственное выражение, куда входит скорость света; мы увидим позже, что она появляется во многих уравнениях, описывающих электрические и магнитные явления) будет указан при изучении электромагнитной теория света. Когда впервые было получено это соотношение, в него не входила скорость света. Просто в результате измерений токов в двух проводах и расстояния между ними было найдено, что величина силы удовлетворяет соотношению:

Значение постоянной зависит от используемой системы единиц. В системе СГС (которая, кстати, не использовалась при выводе этого соотношения) ее значение равно примерно:

Значительно позже (как мы увидим) ее отождествили с величиной 2/(скорость света)².

(Для перевода амперов в единицы СГС обратимся к табл. 10: 10 А— с единиц СГС, т. е. с статампер.) Подставляя эти величины в (20.9), получаем:

Сила 2 дин не очень велика (порядка двух, тысячных грамма), однако измерить ее легко. Для сравнения укажем, например, что если в проводе диаметром 0,1 см нескомпенсирован всего лишь один электрон на каждые 10⁶ атомов, то возникает сила 10⁸ дин (порядка 0,1 т) на каждый сантиметр провода.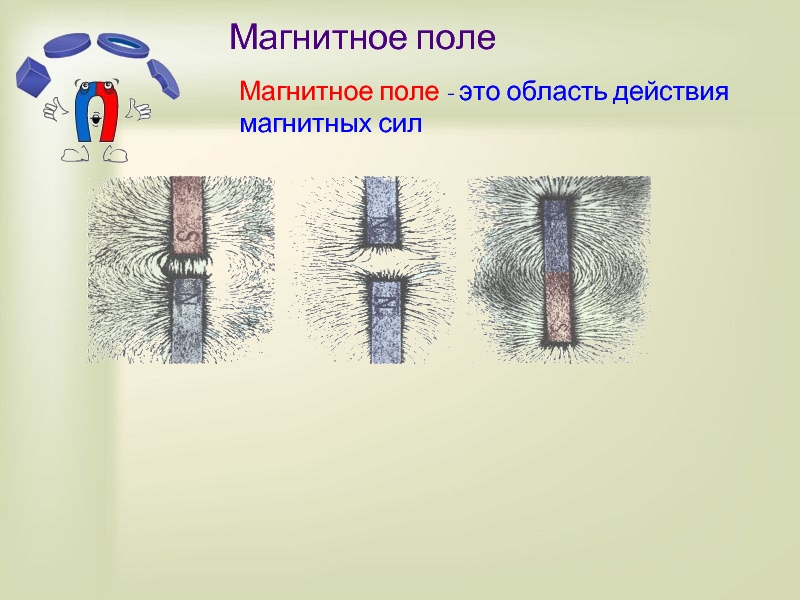

Мы могли бы ожидать, что ток окажет силовое воздействие на движущийся заряд. Именно так и происходит. Сила, действующая на провод, фактически приложена к движущимся зарядам, создающим ток. Она проявляется как сила, приложенная к проводу. С помощью электронной пушки можно наглядно продемонстрировать силу, с которой провод с током действует на пучок заряженных частиц (электронов) (фиг. 302). Невооруженным глазом видно, что пучок электронов отклоняется под действием силы, вызванной током, текущим по проводу.

Качественные свойства этой силы оказываются сложными и весьма необычными. Рассмотрим провод, по которому течет ток (фиг, 303). Если электрон движется в направлении тока (а), сила отклоняет его от провода; если же он движется против тока (б), сила приближает его в проводе. Если направление движения электрона произвольно относительно провода, действующая сила все равно изменяет это направление; однако в любом случае действующая сила будет перпендикулярна скорости электрона (фиг. 304), а ее величина будет прямо пропорциональна этой скорости и обратно пропорциональна расстоянию между проводом и электроном.

Таким образом, мы обнаружили силу, которая зависит не только от положения электрона, но и от его скорости и направления движения. Свойства этой силы гораздо сложнее, чем свойства сил, рассмотренных ранее. Для дальнейшего ее изучения удобно ввести понятие магнитного поля.

Магнитная сила | Определение, формула, примеры и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полета на Луну до управления космосом — мы изучаем широкий спектр тем, которые питают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Викторины

• Физика и естественное право

4.

1: Магнитная сила — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

21525

• Том Вайдеман
• Калифорнийский университет в Дэвисе

Силы, действующие на движущиеся заряженные частицы

Если пропустить ток по двум параллельным проводам, произойдет нечто неожиданное — провода воздействуют друг на друга! Сначала можно было бы попытаться объяснить это, утверждая, что пропускание тока по проводам создает в них электрический заряд и что электрические заряды действуют друг на друга электрическими силами. Но это неправильно. Ток — это просто устойчивый поток заряда — в проводе нет накопленного заряда. На каждый электрон, входящий в провод, выходит соответствующий электрон.

Итак, сила должна иметь какое-то отношение к движению зарядов. После дальнейших экспериментов мы находим, что если мы поместим стационарный чистый заряд рядом с проводником с током, между ними не будет силы. Таким образом, очевидно, должно быть движение для обоих наборов зарядов , чтобы проявить эту силу.

Хотя эта сила связана с электрическим зарядом, она явно не является электрической по своей природе. То есть она совершенно отлична от кулоновской силы. Поэтому мы даем ему другое имя… Мы называем его магнитная сила . Подобно электрической силе, мы будем объяснять ее с точки зрения векторного поля. И, как и в случае с электрической силой, здесь потребуется двухступенчатая теория, которая сначала объяснит, как заряд действует как источник поля, а затем как другой заряд реагирует на присутствие поля. Мы пока отложим первый шаг и сосредоточимся на втором, что означает, что мы просто начнем с магнитного поля (не беспокоясь о том, как оно туда попало) и обсудим, как поле воздействует на магнит. подвижный заряд.

Мы подойдем к этой теме так, как если бы мы проводили эксперименты по извлечению необходимой информации. Вот список наших наблюдений из этих экспериментов:

• Сила магнитного поля, действующая на заряд, пропорциональна магнитному полю, в котором движется заряд . электрическая сила и поле, но, что более важно, это действительно результат нашего определения магнитного поля.

\[\left|\overrightarrow F_B\right| \propto \left|\overrightarrow B\right|\]

[ Примечание: традиционной переменной для магнитного поля является \(B\).]

• Сила магнитного поля, действующая на заряд, пропорциональна величина заряда – Опять же, неудивительно.

\[\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow B\right|\]

• Сила магнитного поля, действующая на заряд, пропорциональна скорости, с которой заряд движется через поле – Это было упомянуто выше, и это первое отклонение от электрического случая.

\[\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow v\right|\left|\overrightarrow B\right|\]

• Сила магнитного поля на заряде изменяется в зависимости от относительных направлений магнитного поля и скорости заряда вектор – Теперь этот новый! В частности, мы находим, что сила равна нулю, если заряд движется параллельно полю, и является самой сильной, когда поле и скорость перпендикулярны друг другу. Дальнейшие эксперименты показывают, что сила силы пропорциональна синусу угла между векторами поля и скорости.

\[\left|\overrightarrow F_B\right| \propto q\left|\overrightarrow v\right|\left|\overrightarrow B\right|\sin\theta\]

• Направление магнитной силы перпендикулярно как направлению скорости, так и направлению магнитного поля 90 177. Это сильно отличается от электрического случая, для которого направление силы и поля всегда совпадают или противоположны.

Возможно, читатель собрал все кусочки головоломки, чтобы получить окончательное выражение магнитной силы, действующей на движущийся точечный заряд:

\[\overrightarrow F_B = q\overrightarrow v \times \overrightarrow B\]

На рисунке ниже показано соотношение векторов скорости, поля и силы. Следует отметить, что символы \(\odot\) и \(\otimes\) с этого момента начнут играть общие роли на диаграммах, и они представляют направления «со страницы» и «на страницу» соответственно. . Также важно отметить, что, как и в случае с электрической силой, отрицательно заряженная частица испытывает магнитную силу в направлении, противоположном положительно заряженной частице, при тех же условиях.

Рисунок 4.1.1 – Направление магнитной силы по скорости и направлению поля

[ Для обзора надлежащего использования векторных («перекрестных») продуктов, включая правило правой руки для определения направления в пространстве, см. Раздел 1.2 в Physics 9A LibreText. ]

Нет причин, по которым электрические и магнитные поля не могут сосуществовать в одном и том же пространстве. Когда они это делают, сила, действующая на точечный заряд, представляет собой векторную сумму двух сил. Комбинация (часто называемая сила Лоренца ) равна:

\[\overrightarrow F = q\left(\overrightarrow E + \overrightarrow v \times \overrightarrow B\right)\]

Прежде чем двигаться дальше, следует сказать несколько слов о единицах измерения. . Чтобы уравнение, приведенное выше, имело правильные единицы измерения, единица измерения магнитного поля должна быть равна силе, деленной на заряд-время-скорость. Учитывая, сколько у нас различных имен для различных единиц, мы, конечно, можем выразить это многими способами, но мы снова дадим этой величине собственное имя:

\[\left[B\right] = \dfrac{\left[F\right]}{\left[q\right]\left[v\right]}=\dfrac{N}{C\cdot \ frac{m}{s}}= \dfrac{N}{A\cdot m}\equiv T\;\;\left(«Tesla»\right)\]

Получается, что магнитное поле величиной из \(1T\) довольно сильно. Это не выходит за рамки обычного опыта (неодимовые стержневые магниты достигают этой силы), но более часто встречающиеся магнитные поля (такие как поле Земли или стрелка компаса) значительно меньше, и чаще можно увидеть, что эти силы поля описаны в единицах Gauss (\(G\)), что составляет одну десятитысячную часть Тесла.

Движение заряда в магнитном поле

Заряд в магнитном поле, на который не действуют никакие другие силы, кроме магнитной силы, следует движению с очень интересным свойством. Магнитная сила действует только перпендикулярно направлению движения, а это означает, что заряд никогда не сможет ускориться . Такая сила может изменить только направление движения. Это должно быть ясно из базовой векторной математики, но, возможно, это легче понять с точки зрения энергии. Если сила всегда перпендикулярна направлению движения частицы, то эта сила никогда не может совершить никакой работы, а это значит, что она никогда не может вызвать изменение кинетической энергии частицы.

Рассмотрим простой случай, когда заряженная частица движется в плоскости, перпендикулярной однородному магнитному полю. На этот заряд будет воздействовать сила, величина которой никогда не меняется (поскольку заряд остается неизменным, поле однородно, направление скорости всегда перпендикулярно полю, и, как мы сказали выше, оно не может увеличиваться. Это сила постоянной величины также всегда перпендикулярна движению частицы. Эти два условия для силы (постоянная величина и всегда под прямым углом к ​​движению) звучат очень знакомо — это условия кругового движения! частица будет двигаться по замкнутому кругу. Мы можем использовать 2-й закон Ньютона и то, что мы знаем о центростремительном ускорении, чтобы связать магнитную силу с кинематическими деталями движения этой частицы.2R \;\;\;\Стрелка вправо\;\;\; \omega = \dfrac{q}{m}B\]

Угловая скорость частицы зависит только от ее заряда, массы и напряженности магнитного поля.

Хорошо, а что если частица не движется в этой плоскости? Предположим, что у него есть составляющая скорости в эту плоскость или из нее. Что ж, эта составляющая будет параллельна магнитному полю и, следовательно, не будет способствовать силе, действующей на частицу. Составляющие скорости в плоскости, перпендикулярной полю, по-прежнему действуют так же. В результате движение частицы параллельно полю совершенно не изменяется, в то время как она движется по окружности в плоскости, перпендикулярной полю. То есть частица следует за винтовая дорожка .

Силы, действующие на проводники с током

У нас есть векторное уравнение, описывающее силу, действующую на точечный заряд, движущийся в поле, и теперь мы хотели бы распространить этот результат на токи, протекающие по проводникам в магнитном поле. Чтобы сделать это, мы используем обычный трюк с цепным правилом, чтобы связать ток через короткий отрезок провода с движущимся зарядом:

\[I = \dfrac{dq}{dt} = \dfrac{dq}{dl}\ dfrac{dl}{dt}\;\;\;\Стрелка вправо\;\;\; I\;dl = dq\dfrac{dl}{dt} = dq\;v\]

Если принять во внимание направление тока, протекающего через \(dl\) и скорость, мы имеем векторную версию вклада небольшого отрезка тока, и мы можем подставить ее в уравнение силы:

\[I \;\overrightarrow {dl} = dq \;\overrightarrow v \;\;\;\Rightarrow\;\;\; d\overrightarrow F = dq \;\overrightarrow v \times \overrightarrow B = I \;\overrightarrow {dl} \times \overrightarrow B\]

Рисунок 4.1.1 нужно лишь немного изменить, чтобы изобразить эту ситуацию – провод может быть изогнутым, но крошечный его сегмент ведет себя как точечный заряд.

Рисунок 4.1.3 – Сила, действующая на крошечный отрезок провода с током . Это может представлять проблему, если провод не прямой, так как \(\overrightarrow {dl}\) меняет направление, или, конечно, если магнитное поле изменяется от одной точки провода к другой.