Магнитные бури: как влияют на здоровье и чем от них защититься

Магнитные бури случаются в среднем 5-6 раз в год и могут длиться несколько дней. Серьезной опасности они не несут, но могут осложнить жизнь тем, у кого есть проблемы со здоровьем. Рассказываем, что такое магнитная буря и как ее пережить.

Что такое магнитная буря

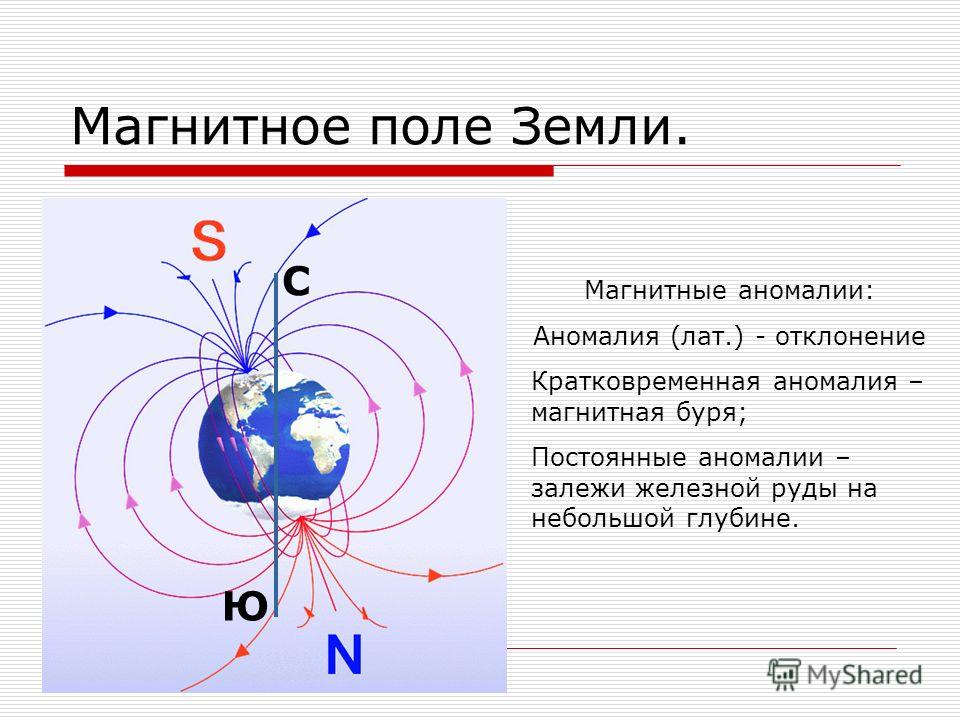
Вокруг Земли есть невидимая оболочка — магнитосфера, которая защищает нашу планету от солнечной радиации. Из космоса на нее воздействует поток солнечного ветра — так называют ионизированные частицы, которые постоянно разлетаются от Солнца со скоростью 400 км/сек. Обычно сила давления солнечного ветра и давление магнитной оболочки Земли равны.

На эту тему

Но когда на Солнце случаются вспышки, скорость солнечного ветра увеличивается, баланс давления меняется, магнитосфера как бы сжимается над Землей и в ней начинают меняться величины токов. Эту «болтанку» давления ученые и называют магнитной бурей. Вспышки некоторых молодых звезд так сильны, что могли бы разрушить атмосферу своих планет. Активность Солнца ниже, но все сравно может повлиять на земных обитателей, вызвать помехи в радиосвязи и сбои в работе приборов. 

Есть ли опасность для людей? 

Однозначного мнения ученых о том, как влияет это природное явление на людей и животных, — нет. Исследования показывают, что в период магнитных бурь повышается число смертей от инфаркта миокарда и инсульта. Но это повышение незначительно (около 20%), к тому же это только данные статистики. Оценить влияние конкретного геомагнитного события на здоровье человека трудно.

«Чтобы провести исследование влияния магнитной бури на здоровье и состояние человека, необходимо иметь четкие критерии, которые можно измерить, — рассказывает ведущий научный сотрудник Института космических исследований РАН Алексей Струминский. — Головная боль или тахикардия — это не критерий, такие симптомы могут быть вызваны массой других причин, той же сменой погоды, например, сменой атмосферного давления. А магнитная буря на атмосферное давление не влияет».

Гипертоникам в дни магнитных бурь нужно пить побольше воды и снизить употребление соли, потому что соль задерживает жидкость в организме и ведет к повышению давления. А гипотоникам можно принять тонизирующую настойку элеутерококка или лимонника

Елена Тихомирова

врач-терапевт

Однако у многих врачей — другое мнение. О том, что рекордные по силе вспышки на Солнце, которые наблюдаются последние дни, могут повлиять на самочувствие метеозависимых людей, ТАСС рассказал член-корреспондент РАН Игорь Бобровницкий.

«Вспышки на Солнце, как и другие гео- и гео-гелиомагнитные факторы не на всех людей действуют негативно. Влияют они на так называемых метеочувствительных людей, у которых ослаблены какие-то системы организма, на здоровых людей подобные факторы не действуют», — рассказал академик.

Бобровницкий уточнил, что механизмы воздействия электромагнитных возмущений на человека изучены слабо. Однако даже у пациентов, не знающих о факте солнечной вспышки, наблюдается ухудшение в самочувствии.

Предполагается несколько эффектов воздействия возмущений магнитного поля, возникающих из-за вспышек на Солнце: это повышение артериального давления, снижение работоспособности, головные боли, повышение тревожности и обострения хронических заболеваний, в том числе и аллергии

Игорь Бобровницкий

член-корреспондент РАН

Есть мнение, что колебания магнитного фона Земли человек инстинктивно воспринимает как угрозу жизни. А увеличение гормонов стресса — кортизола и адреналина — ведет к спазму сосудов и повышению давления.

Советы врачей 

Несмотря на то что ученые пока недостаточно изучили, как колебания магнитного поля воздействуют на организм, врачи советуют людям, которые плохо переносят скачки давления, в дни магнитных бурь подстраховаться и соблюдать нехитрые правила. 

«В такие дни мы наблюдаем, что у гипертоников давление подскакивает, а у гипотоников, наоборот, падает, — объясняет терапевт Елена Тихомирова. — Для того чтобы нивелировать эти неприятности, гипертоникам нужно пить побольше воды и снизить употребление соли в этот период, потому что соль задерживает жидкость в организме и ведет к повышению давления. А гипотоникам можно принять тонизирующую настойку элеутерококка или лимонника». 

Метеочувствительным людям во время магнитных бурь также важно хорошо высыпаться, избегать повышенных нагрузок, занятий спортом и утомительных походов по магазинам.

Карина Салтыкова, Мария Сотскова

Прогноз геомагнитной обстановки на неделю

11.11.2022 — 17.11.2022

---

       ОБЗОР СОСТОЯНИЯ КОСМИЧЕСКОЙ ПОГОДЫ ЗА 08 НОЯБРЯ 2022 Г.
       И ПРОГНОЗ НА ПЕРИОД С 11 ПО 17 НОЯБРЯ 2022 Г.
       ИНТЕГРАЛЬНАЯ СОЛНЕЧНАЯ АКТИВНОСТЬ - УМЕРЕННАЯ.
       НА ВИДИМОМ ДИСКЕ СОЛНЦА НАБЛЮДАЛОСЬ: ШЕСТЬ ГРУПП ПЯТЕН 3135 (N27W80),
3137 (N27W22), 3140 (N26E14), 3141 (N14E25), 3142 (N26W04), 3143 (S13E41)
И ТРИ ФЛОККУЛА ГРУПП 3136 (S08W62), 3138 (S39W83), 3139 (N28E18).
ПЛОЩАДЬ ГРУППЫ ПЯТЕН 3135 УМЕНЬШИЛАСЬ ДО 50 МДП, МАГНИТНАЯ КОНФИГУРАЦИЯ
ALPHA. ПЛОЩАДЬ ГРУППЫ ПЯТЕН 3137 НЕ ИЗМЕНИЛАСЬ (10 МДП), МАГНИТНАЯ
КОНФИГУРАЦИЯ ALPHA. ПЛОЩАДЬ ГРУППЫ ПЯТЕН 3140 УМЕНЬШИЛАСЬ ДО 80 МДП,
МАГНИТНАЯ КОНФИГУРАЦИЯ ALPHA.  ПЛОЩАДЬ ГРУППЫ ПЯТЕН 3141 УМЕНЬШИЛАСЬ ДО
540 МДП, МАГНИТНАЯ КОНФИГУРАЦИЯ BETA-GAMMA. ПЛОЩАДЬ ГРУППЫ ПЯТЕН 3142
УВЕЛИЧИЛАСЬ ДО 50 МДП, МАГНИТНАЯ КОНФИГУРАЦИЯ BETA. ПЛОЩАДЬ ГРУППЫ ПЯТЕН
3143 УМЕНЬШИЛАСЬ (МЕНЕЕ 10 МДП), МАГНИТНАЯ КОНФИГУРАЦИЯ BETA.
       ВСПЫШЕЧНАЯ СОЛНЕЧНАЯ АКТИВНОСТЬ - НИЗКАЯ.
       В РЕНТГЕНОВСКОМ ДИАПАЗОНЕ ЗАРЕГИСТРИРОВАНО: ДВЕ ВСПЫШКИ КЛАССА С,
ОДНА ВСПЫШКА КЛАССА B И ПЯТЬ ВСПЛЕСКОВ КЛАССА В, СРЕДИ НИХ:
ВСПЫШКА С1.2 В ГРУППЕ ПЯТЕН 3141, ВРЕМЯ МАКСИМУМА 20.02 МСК, КООРДИНАТЫ
N16E33, ПРОДОЛЖИТЕЛЬНОСТЬ 46 МИНУТ.
       В ОПТИЧЕСКОМ ДИАПАЗОНЕ ЗАРЕГИСТРИРОВАНА ОДНА СУБВСПЫШКА.
       ГЕОМАГНИТНОЕ ПОЛЕ.
       ПО ДАННЫМ СРЕДНЕШИРОТНЫХ СТАНЦИЙ - СПОКОЙНОЕ С ОТДЕЛЬНЫМИ ПЕРИОДАМИ
НЕУСТОЙЧИВОСТИ.
       ПО ДАННЫМ ВЫСОКОШИРОТНЫХ СТАНЦИЙ - ОТ НЕУСТОЙЧИВОГО ДО СЛАБО
ВОЗМУЩЕННОГО. ПО ДАННЫМ СТАНЦИИ МУРМАНСК В 13.// МСК ЗАРЕГИСТРИРОВАНА
МАГНИТНАЯ БУРЯ С ПОСТЕПЕННЫМ НАЧАЛОМ.
       ПОТОКИ ПРОТОНОВ НЕ ПРЕВЫШАЛИ УРОВЕНЬ ФОНОВЫХ ЗНАЧЕНИЙ.
       РАДИАЦИОННАЯ ОБСТАНОВКА В ОКП И НА ТРАССАХ ПИЛОТИРУЕМЫХ КОСМИЧЕСКИХ
АППАРАТОВ ОЦЕНИВАЛАСЬ КАК НЕВОЗМУЩЕННАЯ.
   
       ИНТЕГРАЛЬНАЯ СОЛНЕЧНАЯ АКТИВНОСТЬ УМЕРЕННАЯ.
ВСПЫШЕЧНАЯ СОЛНЕЧНАЯ АКТИВНОСТЬ ОЖИДАЕТСЯ, В ОСНОВНОМ, НИЗКАЯ, ЕСТЬ
ВЕРОЯТНОСТЬ ВСПЫШЕК КЛАССА М И НЕБОЛЬШАЯ ВЕРОЯТНОСТЬ ВСПЫШЕК КЛАССА Х.
      РЕКУРРЕНТНЫЕ ВОЗМУЩЕНИЯ ГЕОМАГНИТНОГО ПОЛЯ ОЖИДАЮТСЯ 11-12, 16-17
НОЯБРЯ.
      РАДИАЦИОННАЯ ОБСТАНОВКА ОЖИДАЕТСЯ НЕВОЗМУЩЕННАЯ.

Индексы состояния геомагнитного поля

Дата	Ap Mos-индекс	Характеристика
11.11.2022	12	Спокойное
12.11.2022	14	Спокойное
13.11.2022	12	Спокойное
14.11.2022	8	Спокойное
15.11.2022	8	Спокойное
16.11.2022	12	Спокойное
17. 11.2022	12	Спокойное

---

Возмущенность магнитного поля в течение суток количественно характеризуется в Гелиогеофизической службе региональным индексом возмущенности A_p Моs. A_p Mos формируется как среднее из восьми трехчасовых значений a_{p Моs}-индекса, получаемого как среднее из a_k-индексов на каждой из среднеширотных магнитных обсерваторий Евразийского региона (Москва, Подкаменная Тунгуска, Магадан, Паратунка, Санкт-Петербург, Новосибирск, Шамбон, Вингст, Какиока). Для каждой из обсерваторий вначале формируются трехчасовые квазилогарифмические К-индексы, которые отображают в условных единицах изменение магнитного поля от невозмущенного состояния (K=0) до наибольшего наблюдавшегося для данной станции возмущения (K=9). Для сохранения подобия изменений a

k-индекса ходу магнитных возмущений в средних широтах, шкала преобразований K-индекса в a_k такова, что на 50° дипольной широты a_k — индекс приближенно равен половине амплитуды возмущенности наиболее возмущенного компонента магнитного поля, измеренной в нанотеслах:

 

K	0	1	2	3	4	5	6	7	8	9
ak	0	4	7	15	27	48	80	140	240	400

 

Степень возмущенности геомагнитного поля может быть оценена по A_p Mos-индексу по следующей таблице:

Значения Ap Mos	0 — 7	8 — 14	15 — 19	20 — 29	30 — 49	>= 50
Состояние магнитного поля	очень спокойное	спокойное	неустойчивое	слабо возмущенное	умеренно возмущенное	сильно возмущенное

Зависимость системы Кондо от температуры и магнитного поля в режиме слабой связи

• Список журналов
• Открытый доступ НПГ
• PMC3730050

Связь с природой

Нац.

коммун. 1 июля 2013 г .; 4: 2110.

Published online 2013 Jul 1. doi: 10.1038/ncomms3110

, ^{1, 2, 7} , ^{1, 7} , ¹ , ³ , ^{3, 4} , ¹ , ¹ , ^{A, 1, 5} и ^{1, 6}

Авторская информация Примечания к сообщению и получение лицензии

Подоплаченная статья

40054. эффект возникает из-за взаимодействия между локализованным спином и электронами окружающего хозяина. Исследования отдельных магнитных примесей с помощью сканирующей туннельной спектроскопии возродили интерес к физике Кондо; однако количественное сравнение с теоретическими предсказаниями оставалось сложной задачей. Здесь мы показываем, что аномалия нулевого смещения, обнаруженная на органическом радикале, слабо связанном с поверхностью Au (111), может быть описана с удивительной точностью теорией возмущений, первоначально разработанной Кондо 60 лет назад. Наши результаты показывают, что физика Кондо может быть полностью понята только при изучении зависимости резонанса как от температуры, так и от магнитного поля. Идентификация системы Кондо со спином 1/2 имеет значение не только как эталон для предсказаний физики Кондо, но и для материалов с коррелированными электронами в целом.

Эффект Кондо, первоначально обнаруженный в разбавленных магнитных сплавах1, повсеместно проявляется в, казалось бы, несвязанных контекстах, таких как аномалии нулевого смещения, наблюдаемые в квантовых точках и нанопроволоках2,3, или динамическое поведение, близкое к переходу Мотта4,5. Простота лежащего в основе модельного гамильтониана — одного спина, связанного обменным взаимодействием с ванной электронов проводимости — контрастирует со сложной физикой, которую прояснило только развитие совершенно нового теоретического понимания6,7,8.

Эффект Кондо обычно рассматривают для антиферромагнитного (АФМ) взаимодействия между локализованным спином и блуждающей спиновой ванной с обменной спин-спиновой связью J <0. Это взаимодействие приводит в режиме сильной связи, т.е. при температурах ниже характерной температуры Кондо, Тл _К , к экранированию магнитного момента примеси и приводит к стабильному немагнитному синглетному основному состоянию9 (см. ) .

Открыть в отдельном окне

Различные режимы эффекта Кондо.

Взаимодействие Кондо −

J S·σ связывает блуждающие электроны хозяина со спином σ с магнитной примесью со спином S. Для обменного взаимодействия J <0 антиферромагнитная (АФМ) связь приводит к запутанному многочастичному состоянию, где антипараллельное расположение спинов электронов проводимости эффективно экранирует примесный спин. Основное состояние при температурах T ниже характерной температуры Кондо T _K представляет собой синглет с полным спином S =0 (красная область), хорошо защищенный от высших энергетических состояний. Напротив, при J >0 ферромагнитная (ФМ) связь стремится создать экранирующее облако спинов, ориентированных параллельно примесному спину, который становится асимптотически свободным при низких температурах. Для FM-связи или при температурах T >> T _K система находится в режиме слабой связи, который можно трактовать пертурбативно.

Гораздо меньше внимания уделялось режиму слабой связи, который актуален для ферромагнитного (ФМ) взаимодействия ( J > 0 ) или при повышенных температурах ( T >> T _K ). При ФМ-взаимодействии спин примеси всегда слабо связан и становится асимптотически свободным в пределе низких температур6,10. Для АФМ-взаимодействий и высоких температур тепловые флуктуации разрушают синглетное состояние. Для обоих случаев, ФМ-взаимодействия и АФМ-взаимодействия в режиме слабой связи, физика может быть описана теорией возмущений6. В прошлых исследованиях одиночных адсорбатов Кондо с помощью сканирующей туннельной спектроскопии детальная количественная характеристика физики Кондо была затруднена из-за орбитального вырождения11, спиновых квантовых чисел>1/2 (ссылка 12) и довольно высоких температур Кондо13,14.

Здесь мы исследуем чисто органическую молекулу, имеющую радикальную нитронилнитроксильную боковую группу15, адсорбированную на поверхности Au (111). Было показано, что молекулы с одной и той же боковой радикальной группой образуют кристаллы ферромагнитных молекул ниже температуры Кюри 0,6 К (ссылка 16). Вместо локализации на конкретном атоме неспаренный электрон пространственно делокализован по части O–N–C–N–O боковой группы (), стабилизируя его против химической реакции и переноса заряда, что привело бы к системе с нулевым спином. . Неспаренный электрон не имеет дальнейшего орбитального вырождения. Это позволяет нам изучать физику чистого спина 1/2, взаимодействующего с электронами проводимости, что было предметом интенсивных теоретических исследований.

Открыть в отдельном окне

Топография молекулы органического радикала на Au (111).

( a ) Химическая структура исследуемой молекулы органического радикала (C ₂₈ H ₂₅ O ₂ N ₄ ) с нитронил-нитроксильной боковой группой, занятой нитронил-нитроксильной орбитой. Молекула нарисована с такой же ориентацией, как и на топографии c . ( b ) Обзорная топография ( T =6,7 К, смещение В =50 мВ, ток уставки I =30 пА) отдельных молекул на Au(111). Нижняя правая молекула украшена тремя соседними молекулами дихлорметана. Масштабная линейка соответствует 5 нм. ( c ) Топография одной молекулы органического радикала с высоким разрешением ( V = 100 мВ, I = 33   пА). Горизонтали расположены с интервалом высоты 50 pm. Масштабная линейка соответствует 1 нм.

Топографическая визуализация органических радикалов

Снимки, полученные с помощью сканирующей туннельной микроскопии постоянного тока (СТМ) при низких температурах, показывают, что молекулы, адсорбированные на поверхности, имеют тенденцию к зародышеобразованию в местах перегиба реконструированной поверхности Au (111) (). Подробные топографии показывают удлиненную молекулярную основу и радикальную боковую группу, которая изображена как выступ высотой ~ 0,3 нм и шириной 1,0 нм ().

Температурная зависимость пика нулевого смещения

Обнаружен сильный резонанс на уровне Ферми при измерении дифференциальной проводимости (d I/ d V , подробнее см. раздел «Методы») на боковой группе молекулы при температурах от T =1,5 K до 15,7 K (), который не обнаруживается ни на остове молекулы, ни на чистая поверхность. Наблюдение этого резонанса не зависит от ориентации молекулы по отношению к подложке Au (111) или от присутствия рядом с молекулой соосажденных молекул дихлорметана, тогда как его кажущаяся ширина и амплитуда незначительно различаются между разными молекулами. Резонанс показывает четкую логарифмическую зависимость от напряжения почти на два порядка () и значительно расширяется при повышении температуры — намного больше, чем ожидалось для одночастичного резонанса. Кажущаяся ширина резонанса не сходится к естественной ширине в низкотемпературном пределе в доступном нам диапазоне температур, как можно было бы ожидать для кондо-системы со спином 1/2 с АФМ-взаимодействием в пределе сильной связи при Т << Т _К . Спектры скорее имеют плоскую вершину, ширина которой зависит от тепловой энергии k _B T ( k _B — постоянная Больцмана).

Открыть в отдельном окне

Температурная зависимость аномалии нулевого смещения.

( a ) Типичные спектры дифференциальной проводимости, снятые на боковой радикальной группе молекулы при температурах между T =1,5 K и T =15,7 K (черный), смоделированные спектры с использованием теории возмущений (красный) и подгонки функции Фрота (синие пунктирные линии). Все спектры нормализованы и смещены для наглядности. ( b ) Два примерных спектра (черные точки) и проводимость, полученная из модели Андерсона-Аппельбаума (красная линия), нанесенные с логарифмической абсциссой. Синие линии отмечают диапазон с плоской вершиной (пересечение между проводимостью при нулевом смещении и экстраполяцией логарифмического увеличения проводимости, показанное пунктирными линиями), ширина которого зависит от температуры. ( c ) График эффективной температуры T _eff , полученный путем подгонки спектров примерно 35 молекул с использованием модели Андерсона-Аппельбаума, в зависимости от экспериментальной температуры T . Сплошная линия: T _эфф = T . Столбики погрешностей включают отклонения от спектров, полученных для разных молекул. ( d ) Полуширина на полувысоте (HWHM), извлеченная из подгонки функций Фрота в a как функция температуры, синие пунктирные линии указывают на ожидаемую температурную зависимость ширины резонанса Кондо в сильном режим связи в теории ферми-жидкости с α =2 π (ссылка 31), красная линия соответствует свободному α =15,2.

Сравним наши данные с кондактансом, рассчитанным по гамильтониану рассеяния Кондо с переворотом спина1 в пертурбативном подходе, учитывающем процессы до третьего порядка по обменному взаимодействию J . В этой модели Андерсона-Аппельбаума [17,18,19] туннелирование между двумя электродами через магнитную примесь приводит при нулевом магнитном поле к температурно-уширенному логарифмическому резонансу проводимости как функции смещения, ε = эВ ( e — элементарный заряд), вида

, где звездочкой обозначена свертка, f (ε ,T ) — распределение Ферми–Дирака, f′ (ε ,T ) его производная по ε , ρ ₀ плотности состояний зоны проводимости при энергии Ферми, ω ₀ энергии обрезания и c постоянной фон. В то время как пертурбативный подход может иметь некоторые ограничения, более поздние подходы, которые рассматривают неравновесные эффекты слабой связи Кондо более точно20, потребуют обобщения на конечные температуры, чтобы быть применимыми здесь. Было показано, что пертурбативный подход дает правильное описание, если магнитная примесь связана преимущественно с одним из двух электродов и система близка к равновесию21.

Мы выполняем подбор по методу наименьших квадратов, принимая температуру в качестве единственного соответствующего параметра (подробности см. в дополнительном примечании 1). Обозначим температуру, полученную из подгонок T _eff . показывают отличное согласие между моделью и нашими данными. Извлеченные эффективные температуры T _eff хорошо согласуются с температурой T эксперимента с отклонениями в сторону меньших значений для T _eff при температурах Т ≤6 К (). Для сравнения в также показаны подгонки функции Фрота22 к данным с извлеченными полуширинами, нанесенными на график в .

Зависимость спектров от магнитного поля

При приложении магнитного поля B перпендикулярно поверхности Au (111) резонанс распадается на два пика с наложенными симметричными ступеньками, как только зеемановская энергия превышает тепловую энергию (), то есть г ₀ μ _B B > k _B T ( μ _B — магнетон Бора, g ₀ — фактор Ланде свободного электрона). Ступени в дифференциальной проводимости обусловлены неупругими возбуждениями с переворотом спина23 и могут быть описаны с прекрасным согласием с использованием того же пертурбативного подхода (подробнее см. Дополнительное примечание 1)24. Теория возмущений точно учитывает не только ступени, но и пики на вершинах этих ступеней. Энергии положений пиков и возбуждений с переворотом спина, извлеченные из подгонок, линейно масштабируются с приложенным магнитным полем и дают фактор Ланде, равный 9.0061 г =1,98±0,04, что несколько отличается от ожидаемого значения для свободного электрона г ₀ =2. Эта разность дает оценку обменного взаимодействия Jρ ₀ : из-за связи локализованного спина с электронами проводимости и их поляризации магнитным полем эффективный фактор Ланде будет модифицирован по сравнению со значением для свободного спин25. Для оценки Jρ ₀ ошибка определения положения пика и ступеньки и, следовательно, г является критическим (см. Дополнительный рисунок S2). Как видно из , полосы погрешностей становятся меньше при большем магнитном поле. Это связано с тем, что только при больших магнитных полях спектры становятся плоскими при нулевом напряжении смещения, что повышает точность подгонки. Поэтому для оценки Jρ ₀ из зеемановского расщепления мы оцениваем g только для самых высоких магнитных полей ( B ≥10 Тл). Получаем г =1,93±0,02 и Jρ ₀ =-0,04±0,01. Мы получаем вторую независимую оценку Jρ ₀ , сравнивая амплитуды различных порядков рассеяния в модели: ступеней из-за спин-флип-возбуждений пропорциональна ( Jρ ₀ ) ² . Находим Jρ ₀ = −0,04±0,02, что согласуется со значением, полученным из зеемановского расщепления (). Наши подгонки указывают на слабое АФМ-обменное взаимодействие между локализованным спином на молекуле и поверхностью Au. FM-связь между спином и электронами проводимости, как показано на рисунке, привела бы к аналогичной физике. Спектроскопическим признаком обменного FM-взаимодействия является провал в спектральной функции в примесном узле, в то время как в зоне проводимости матрицы формируется пик при энергии Ферми [26], что противоположно случаю АФМ-взаимодействия. Этот результат также может быть получен из теории возмущений, которая для ФМ-связи остается справедливой при всех температурах, так как знак g ( ε ) меняется на J >0 (см. уравнение 1). В наших измерениях мы всегда обнаруживаем пик в радикальной боковой группе. Из этого вывода и оценки Jρ ₀ мы можем исключить ЧМ связь в нашей системе. В отличие от случая адатомов, где предполагается, что резонанс Кондо исследуется довольно косвенно через зону проводимости поверхности27, здесь резонанс исследуется напрямую путем туннелирования от острия во многие телесные состояния в соответствии с уравнением Андерсона–Аппельбаума. теория. Обсуждение случая слабой связи острия с резонансом адсорбата см. в дополнительном примечании 39.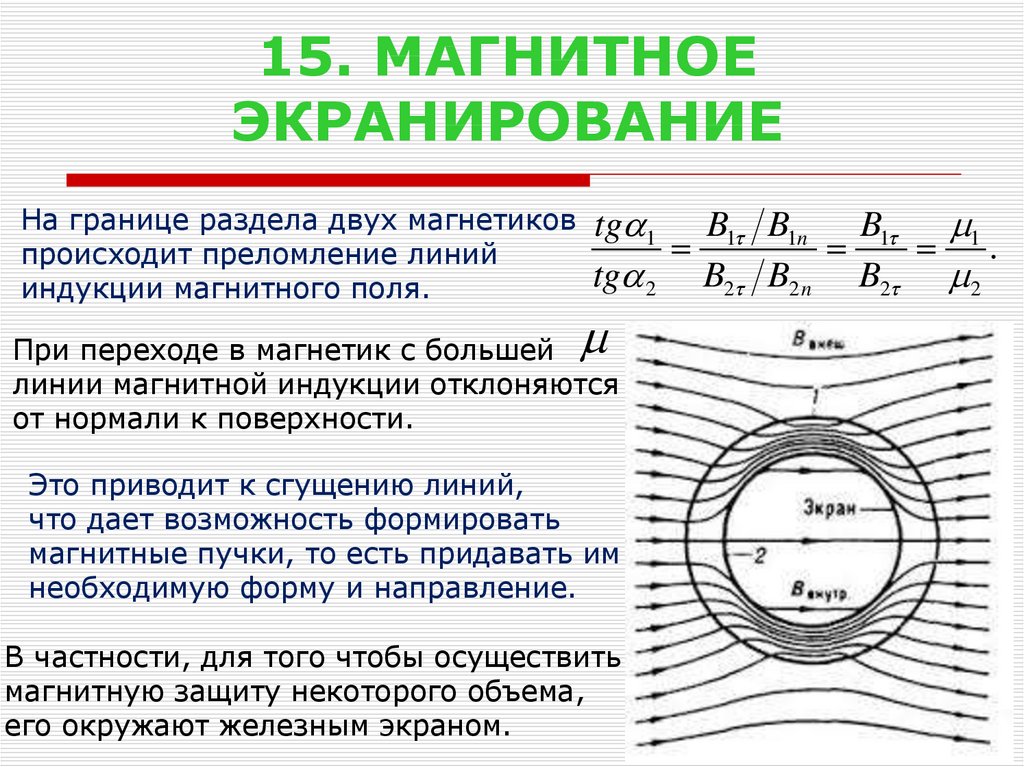 0011

Открыть в отдельном окне

Расщепление резонанса в магнитном поле.

( a ) Измерения дифференциальной проводимости, проведенные при последовательном увеличении магнитных полей на радикальной боковой группе молекулы ( T =1,8 K). Все спектры нормализованы и смещены для ясности. Красные кривые соответствуют моделированию кондактанса с использованием теории возмущений до третьего порядка по обменному взаимодействию J . Синяя кривая на B =14 Тл показывает примерный вклад второго порядка по Дж в дифференциальную проводимость. ( b ) извлек зеемановское расщепление как функцию магнитного поля. Линейная подгонка (красная линия) дает г =1,98±0,04. ( c ) магнитная связь Jρ ₀ , полученная из отношения вкладов второго и третьего порядка в подгонку (синие точки), со средней связью Jρ ₀ = −0,04±0,02 и из Зеемановское расщепление (и, следовательно, г фактор) (красные точки). Для последнего анализа в каждом магнитном поле зеемановское расщепление Δ _Z ( B ) определяется из подгонок (см. Также дополнительное примечание 1), а коэффициент г получается из г ( B ). =Δ _Z ( B )/( μ _B B ). Планки погрешностей в b и c включают изменение спектров, полученных для разных молекул.

В прошлом аномалии нулевого смещения, наблюдаемые с помощью сканирующей туннельной спектроскопии на отдельных атомах и молекулах, обычно интерпретировались как резонанс Кондо в пределе сильной связи. Анализируя наши данные с этим предположением, подгоняя спектры функцией Фрота22, которая, как было показано, хорошо описывает резонанс Кондо (при T < T _K )22,28, дает на первый взгляд разумное описание наших данных (см. Дополнительное примечание 2). В низкотемпературном пределе получаем полуширину Г _К ≈1,3 мВ, что соответствовало бы Полевая зависимость отличается от поведения, ожидаемого для модели Кондо АФМ для спина 1/2 в пределе сильной связи 29,30 и T _K ≈16 К.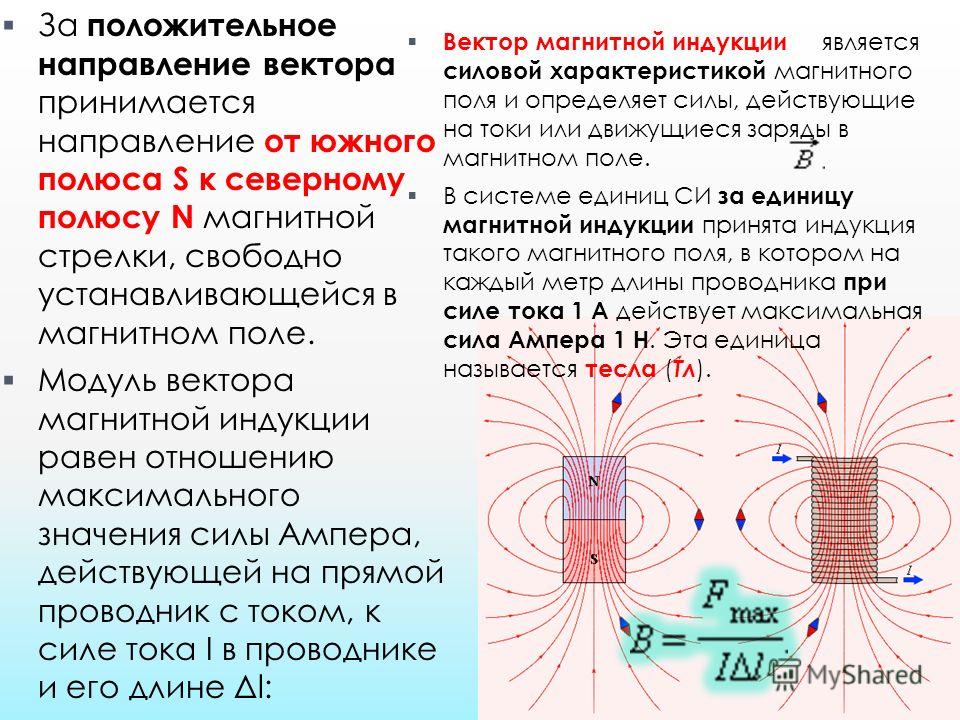 Для T << T _K , резонанс Kondo не будет расколоться на магнитные поля до B _C ≈0,5 K _B 666 ≈0,5 K _B 9666 ≈0,5 K _B 6669 K _B 6669 K _B 6669 K _B 669 K _B 669 K _B 669 K _B 669 /( гмк _B ) (ссылка 29). Таким образом, мы должны наблюдать расщепление только при B > B _C ≈6 T, в отличие от нашего наблюдения четкого расщепления при полях до 2 Тл. Это дает для нашей системы верхний предел T _K ≤5,4  K. Кроме того, должна быть лишь довольно слабая температурная зависимость ширины резонанса для T < T _K (см. наших измерений, вопреки нашим наблюдениям (см. ).

Разногласие возникает из-за того, что полуширина логарифмической особенности не является четко определенной величиной и, таким образом, определение T _K через полуширину ошибочно. Только принимая во внимание зависимость как от температуры, так и от магнитного поля, мы можем сделать вывод, что истинная температура Кондо должна быть существенно ниже.

Мы заключаем, что наблюдаемый нами резонанс обусловлен одиночным неспаренным спином со слабой АФМ-связью с зоной проводимости. Спустя почти 60 лет после того, как Кондо идентифицировал правильный гамильтониан для одиночной магнитной примеси в металлическом носителе и показал нарушение теории возмущений в масштабе характеристической энергии1, наши результаты демонстрируют его справедливость для одиночной примеси со спином 1/2 в режиме слабой связи: для которого характерна почти универсальная зависимость от температуры и магнитного поля. Оба существенно отличаются от поведения, предсказанного для АФМ-модели Кондо со спином 1/2 в пределе сильной связи. Несмотря на то, что аномалии с нулевым смещением наблюдались ранее на чисто органических молекулах, адсорбированных на металлических поверхностях32,33, количественный уровень согласия между данными и теорией является беспрецедентным для измерений одиночных примесей с помощью низкотемпературной СТМ.

Идентификация истинной системы со спином 1/2 позволяет провести количественную проверку теоретических предсказаний, которые можно проверить в измерениях, выполненных при еще более низких температурах. Помимо возможности изучения физики Кондо со спином 1/2 на одной примеси, возможны эксперименты на системах связанных примесей. Здесь отметим, что большинство теоретических исследований решеток Кондо построено на кондо-примесях со спином 1/2. Адаптация остова при синтезе молекул способствует самоорганизующемуся росту упорядоченных одно- или двумерных решеток этих молекул. Это потенциально позволяет проводить экспериментальные исследования модельных гамильтонианов для материалов с коррелированными электронами.

Измерения СТМ

Эксперименты проводились на двух различных самодельных СТМ, работающих в сверхвысоком вакууме, один с базовой температурой 6,7 К и магнитными полями до 5 Тл, второй с базовой температурой 1,5 К и поля до 14   Т. Обе установки позволяют подготовить образец на месте и перенести его в СТМ.

Дифференциальная спектроскопия проводимости

Спектры проводимости получали, помещая наконечник над боковой группой молекулы, поворачивая z — обратная связь выключена, а качание напряжения смещения В . Для непосредственного обнаружения сигнала d I /d V методом синхронизации к V добавляется малое синусоидальное модуляционное напряжение V _m с частотой в диапазоне 800–1100 Гц. Типичные заданные значения туннелирования перед деактивацией контура обратной связи были В = -20 мВ и I = 0,1–1 нА. Спектры обычно снимались в диапазоне от −20 мВ до +20 мВ симметрично вокруг нулевого смещения. V _m было выбрано достаточно малым, чтобы уширение сигнала из-за напряжения модуляции всегда было меньше, чем тепловое уширение; точнее, в результате были использованы типичные значения В _м (среднеквадратичное значение) = 0,1–0,3 мВ при низких температурах, а при более высоких температурах (T>5 K) использовалось 0,5–1 мВ. До и после того, как были измерены спектры на радикале, эталонные спектры были сняты на чистой поверхности Au, чтобы обеспечить безликую проводимость наконечника. Измеренные спектры были нормализованы, и линейная базовая линия была вычтена для учета эффектов дрейфа, которые также были видны в эталонных спектрах.

Подготовка образца

Поверхность Au (111) подготовлена ​​циклами распыления Ar ⁺ и отжига до ~800 К. Молекулы осаждаются из кристаллического порошка, содержащего равные количества молекул радикала и дихлорметана, путем сублимации с использованием кварцевого тигля. при температуре ≈200 °C в течение нескольких минут с образцом при T = от 150 до 180  K. Матричная лазерная десорбция/ионизация подтвердила, что молекулы остаются нетронутыми во время сублимации. Молекулы слабо связаны с поверхностью; осаждение при комнатной температуре приводит к зародышеобразованию на краях ступенек.

Синтез

Молекула (2′-нитронилнитроксил-5′-метил-[1, 1′;4′,1″]терфенил-4,4″-дикарбонитрил (C ₂₈ H ₂₅ O ₂ N ₄ )) был синтезирован с использованием реакции кросс-сочетания по типу Сузуки со спин-меченым дииодсодержащим предшественником и 4-цианофенилбороновой кислотой в присутствии Pd(PPh ₃ ) ₄ в качестве катализатора и Na ₂ CO ₃ в качестве основания.

П.В., М.Т. и К.К. придумали и курировали проект; Ю.З., С.К. и Т.Х. провел эксперименты с помощью США; К.С. и М.М. синтезированы и очищены молекулы; М.Т., П.В., С.К. и Ю.З. сделал анализ данных; все авторы внесли свой вклад в рукопись и обсудили ее.

Как цитировать эту статью: Zhang, Y.-h. и др. Зависимость системы Кондо от температуры и магнитного поля в режиме слабой связи. Нац. коммун. 4:2110 doi: 10.1038/ncomms3110 (2013).

Дополнительная информация:

Дополнительные рисунки S1-S4, дополнительные примечания 1-3 и дополнительные ссылки

Щелкните здесь для просмотра. ^{(403K, pdf)}

Мы выражаем благодарность П.П. Баруселли, Р. Реквист, М. Фабрицио и Э. Тосатти. Кроме того, мы подтверждаем обсуждения с Д. Ле и Т. Рахманом, а также с Т. Кости, К. Хули, Н. Лоренте, Дж. Мерино, Э. Села, П. Саймон и Р. Зитко. Мы благодарим С. Раушенбаха за проведение MALDI-анализа тестовых отложений. Ю.З. признает поддержку со стороны Китайского стипендиального совета. С.К., Т.Х., М.Т. и П.В. признать поддержку со стороны SFB 767 и США по программе Emmy-Noether. Поддержка Baden-Württemberg-Stiftung признана. CS и MM признают финансовую поддержку Фонда Александра фон Гумбольдта.

• Кондо Дж. Минимум сопротивления в разбавленных магнитных сплавах. прог. Теор. физ. 32, 37–49 (1964). [Google Scholar]
• Гольдхабер-Гордон Д. и др. Эффект Кондо в одноэлектронном транзисторе. Природа 391, 156–159 (1998). [Google Scholar]
• Нюгард Дж., Кобден Д. Х. и Линделоф П. Э. Физика Кондо в углеродных нанотрубках. Природа 408, 342–346 (2000). [PubMed] [Google Scholar]
• Джордж А., Котляр Г., Краут В. и Розенберг М. Дж. Динамическая теория среднего поля сильнокоррелированных фермионных систем и предел бесконечных измерений. Преподобный Мод. физ. 68, 13–125 (1996). [Google Scholar]
• Нозьер. П. Решетки Кондо и переход металл-изолятор Мотта. Дж. Физ. соц. Япония 74, 4–7 (2005). [Google Scholar]
• Андерсон. П. В. Вывод бедняком законов подобия для задачи Кондо. Дж. Физ. С 3, 2436–2441 (1970). [Google Scholar]
• Уилсон. КГ. Ренормализационная группа: критические явления и проблема Кондо. Преподобный Мод. физ. 47, 773–840 (1975). [Google Scholar]
• Андрей Н. Диагонализация гамильтониана Кондо. физ. Преподобный Летт. 45, 379–382 (1980). [Google Scholar]
• Хьюсон А. С. Проблема Кондо для тяжелых фермионов Издательство Кембриджского университета: Кембридж, (1997). [Google Scholar]
• Джентиле П., де Лео Л., Фабрицио М. и Тосатти Э. Отсутствие кондо-экранирования на наноконтактах почти магнитных металлов. Еврофиз. лат. 87, 27014 (2009). [Google Scholar]
• Минамитани Э. и др. Новый эффект Кондо в молекуле, основанный на симметрии. физ. Преподобный Летт. 109, 086602 (2012). [PubMed] [Академия Google]
• Отте А. Ф. и др. Роль магнитной анизотропии в эффекте Кондо. Нац. физ. 4, 847–850 (2008). [Google Scholar]
• Мадхаван В., Чен В., Джамниала Т., Кромми М. Ф. и Уингрин. Н. С. Туннелирование в одиночный магнитный атом: спектроскопические свидетельства резонанса Кондо. Наука 280, 567–569 (1998). [PubMed] [Google Scholar]
• Валь П. и др. Температура Кондо магнитных примесей на поверхности. физ. Преподобный Летт. 93, 176603 (2004). [PubMed] [Академия Google]
• Осецки Дж. Х. и Ульман Э. Ф. Исследования свободных радикалов. I. α-нитронилнитроксилы, новый класс стабильных радикалов. Варенье. хим. соц. 90, 1078–1079 (1968). [Google Scholar]
• Тамура М. и др. Объемный ферромагнетизм в кристалле β-фазы п-нитрофенилнитронилнитроксильного радикала. хим. физ. лат. 186, 401–404 (1991). [Google Scholar]
• Аппельбаум. Дж. А. Обменная модель s-d аномалий туннелирования с нулевым смещением. физ. Преподобный Летт. 17, 91–95 (1966). [Академия Google]
• Андерсон П. В. Локализованные магнитные состояния и аномалии поверхности Ферми при туннелировании. физ. Преподобный Летт. 17, 95–97 (1966). [Google Scholar]
• Аппельбаум Дж. А. Обменная модель аномалий туннелирования с нулевым смещением. физ. преп. 154, 633–643 (1967). [Google Scholar]
• Рош А., Пааске Дж., Кроха Дж. и Вельфе. П. Неравновесный перенос через точку Кондо в магнитном поле: теория возмущений и скейлинг бедняка. физ. Преподобный Летт. 90, 076804 (2003). [PubMed] [Академия Google]
• Пааске Й., Рош А. и Вельфе П. Неравновесный перенос через точку Кондо в магнитном поле: теория возмущений. физ. Преподобный Б 69, 155330 (2004). [Google Scholar]
• Фрота Х. О. Форма резонанса Кондо. физ. Преподобный Б 45, 1096–1099 (1992). [PubMed] [Google Scholar]
• Генрих А. Дж., Гупта Дж. А., Лутц С. П. и Эйглер. Д. М. Одноатомная спин-флип-спектроскопия. Наука 306, 466–469 (2004). [PubMed] [Google Scholar]
• Wyatt A.F.G. & Wallis R.H. Обменное рассеяние в туннельных переходах Al/оксид Al/Ag, легированных Ti. II. Магнитное поле. Дж. Физ. C. Физика твердого тела. 7, 1293–1302 (1973). [Google Scholar]
• Вольф Э. Л. и Лоси. Д. Л. g — сдвиги в теории обмена s — d туннельных аномалий с нулевым смещением. физ. лат. А 29, 334–335 (1969). [Google Scholar]
• Коллер В., Хьюсон А.С. и Мейер Д. Сингулярная динамика недоэкранированных моделей магнитных примесей. физ. Преподобный Б 72, 045117 (2005). [Google Scholar]
• Уйсаги О., Кроха Дж., Шуньох Л. и Завадовски А. Теория резонанса Фано в СТМ туннельной плотности состояний, обусловленной одиночной кондо-примесью. физ. Преподобный Летт. 85, 2557–2560 (2000). [PubMed] [Академия Google]
• Прюзер Х. и др. Дальняя кондо-сигнатура одиночной магнитной примеси. Нац. физ. 7, 203–206 (2011). [Google Scholar]
• Кости. Т. А. Эффект Кондо в магнитном поле и магнитосопротивление сплавов Кондо. физ. Преподобный Летт. 85, 1504–1507 (2000). [PubMed] [Google Scholar]
• Мур Дж. Э. и Вэнь С. Г. Аномальное магнитное расщепление резонанса Кондо. физ. Преподобный Летт. 85, 1722–1725 (2000). [PubMed] [Google Scholar]
• Нагаока К., Джамниала Т., Гробис М. и Кромми. М. Ф. Температурная зависимость одиночной примеси Кондо. физ. Преподобный Летт. 88, 077205 (2002). [PubMed] [Академия Google]
• Фернандес-Торренте И., Франке К. Дж. и Паскуаль Дж. И. Колебательный эффект Кондо в чисто органических сборках с переносом заряда. физ. Преподобный Летт. 101, 217203 (2008). [PubMed] [Google Scholar]
• Темиров Р., Ласси А., Андерс Ф. Б. и Таутц Ф. С. Эффект Кондо за счет контролируемого расщепления одиночного молекулярного контакта. Нанотехнологии 19, 065401 (2008). [PubMed] [Академия Google]

13.6 Ядерный магнитный резонанс

13.6 Ядерный магнитный резонанс

Квантовая механика для инженеров   © Леон ван Доммелен

Далее: 14. Ядра [Незавершенный черновик]

---

Подразделы

---

13.6 Ядерный магнитный резонанс

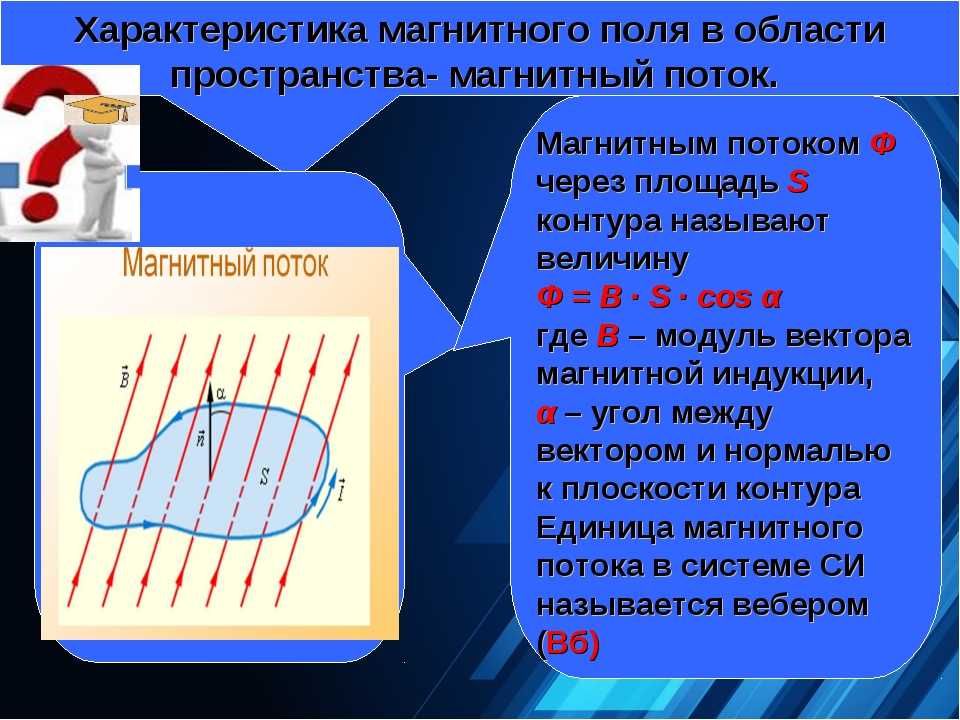
Ядерный магнитный резонанс, или ЯМР, является ценным инструментом для изучения ядер, для исследования структуры молекул, в частности органических те, и для медицинской диагностики, как МРТ. Этот раздел даст основное квантовое описание идеи. Будет использоваться линейная алгебра.

13.6.1 Описание метода

Впервые независимо продемонстрированный Блохом и Перселлом в 1946 г., ЯМР исследует ядра с чистым спином, в частности, ядра водорода или другие ядра со спином. Различные общие ядра, такие как углерод и кислород не имеют чистого спина; это может быть благословением, поскольку они не может испортить сигналы от ядер водорода, или ограничение, в зависимости от того, как вы хотите на это смотреть. Во всяком случае, при необходимости можно использовать изотопы, такие как углерод 13, которые имеют чистый спин.

На самом деле это не спин, а связанный с ним магнитный дипольный момент. ядра, которое имеет значение, поскольку это позволяет ядрам быть управляется магнитными полями. Сначала образец помещают в чрезвычайно сильное постоянное магнитное поле. Типичные поля в терминах Теслы. (Тесла примерно в 20000 раз сильнее силы магнитное поле земли.) В поле ядро ​​имеет два возможные энергетические состояния; основное состояние, в котором спиновая компонента в направление магнитного поля совпадает с ним, и повышенное энергетическое состояние, в котором спин противоположен {N.33}. (Несмотря на большую напряженность поля, разница энергий между двумя состояниями чрезвычайно мала по сравнению тепловой кинетической энергии при комнатной температуре. Количество ядра в основном состоянии могут только превышать ядра в приподнятом энергетическое состояние, скажем, на один из 100 000, но это все равно большое абсолютное количество ядер в образце. )

Теперь потревожьте ядра вторым, намного меньшим и радио частота, магнитное поле. Если радиочастота в самый раз, избыточные ядра в основном состоянии могут быть подняты из самой низкой энергии состояние, поглощающее энергию, которую можно наблюдать. резонанс частота при которой это происходит то дает информация о ядрах. Чтобы наблюдать резонанс частота очень точно, возмущающее радиочастотное поле должно быть очень слабым по сравнению с первичным постоянным магнитным полем.

В непрерывном ЯМР возмущающая частота варьируется, а поглощение исследовано, чтобы найти резонанс. (В качестве альтернативы, напряженность первичного магнитного поля можно варьировать, что дает к тому же, используя соответствующую формулу.)

В ЯМР с преобразованием Фурье возмущение применяется в виде короткого импульса. достаточно долго, чтобы полностью поднять лишние ядра из земли государство. Затем наблюдается распад обратно к исходному состоянию. Затем опытный оператор может многое узнать о окружение ядер. Например, ядро ​​в молекуле будет быть немного экранированным от основного магнитного поля остальной частью молекулы, и это приводит к наблюдаемому частотному сдвигу. Количество сдвига дает представление о молекулярной структуре в ядро, поэтому информация о молекуле. Кроме того, соседние ядра могут вызвать расщепление резонансных частот на несколько через их магнитные поля. Например, один соседний возмущающий ядро приведет к тому, что резонансная частота разделится на две, одна для спин вверх соседнего ядра и один для спина вниз. это еще одна подсказка о молекулярной структуре. Время распада вернуться в исходное состояние — это еще один важный ключ к местные условия, в которых находятся ядра, особенно на МРТ. подробности находятся за пределами знаний этого автора; цель здесь только для того, чтобы взглянуть на основы квантовой механики, лежащие в основе ЯМР.

13.6.2 Гамильтониан

Будем считать, что магнитные поля имеют вид

(13. 44)

где – первичное магнитное поле с силой Тесла, очень слабая возмущающая напряженность поля, а частота возмущение.

Компонента магнитного поля в -​плоскости, , вращается вокруг оси -​с угловой скоростью . Такое вращающееся магнитное поле может быть получено с помощью пара правильно сфазированных катушек, расположенных по осям и . (В ЯМР с преобразованием Фурье, один импульс возмущения фактически содержит диапазон различных частот и преобразование Фурье используются, чтобы разобрать их.) Поскольку аппарат и длина волны радиочастотного поля очень велико в масштабе ядра, пространственные вариации магнитного поля можно не учитывать.

Теперь предположим, что вы поместили спиновое ядро ​​в центр этой магнитное поле. Как обсуждалось в разделе 13.4, частица со вращением будет действовать как маленькая стрелка компаса, а его энергия будет самый низкий, если он выровнен с направлением окружающего магнитного поле. В частности, энергия определяется выражением

где называется силой магнитного диполя ядра. Эта сила диполя пропорциональна угловому моменту его вращения. :

где константа пропорциональности называется гиромагнитное отношение. Численное значение гиромагнитного отношения можно найти как

В случае ядра водорода протона масса и заряд можно найти в разделе обозначений, а протон экспериментально найденный -коэффициент равен 5,59.

Суть в том, что вы можете написать гамильтониан взаимодействия ядра с магнитным полем с точки зрения численного значение гиромагнитного отношения, спин и магнитное поле:

(13.45)

Теперь, обращаясь к волновой функции ядра, ее можно записать как сочетание состояний спин-вверх и спин-вниз,

где имеет вращение в -направлении, вдоль первичное магнитное поле, и имеет . Обычно и описывала бы пространственные вариации, но пространственные вариации не имеют отношения к анализу, и можно рассматривать как простые числа.

Вы можете использовать краткие обозначения линейной алгебры, комбинируя а в двухкомпонентном вектор-столбце (точнее, спиноре)

В этих терминах спиновые операторы становятся матрицами, так называемыми Спиновые матрицы Паули раздела 12.10,

(13.46)

Подстановка этих выражений для спина и (13.44) для магнитное поле в (13.45) дает после очистки окончательный гамильтониан:

(13.47)

Постоянные и имеют размерность частота; называется «ларморовой частотой». Что касается важно помнить, что он намного меньше, чем Лармор частота, потому что магнитное поле возмущения мало по сравнению с первичным.

13.6.3 Невозмущенная система

Прежде чем рассматривать возмущенный случай, полезно сначала взглянуть на ненавязчивое решение. Если есть только основное магнитное поле воздействие на ядро ​​без радиочастотного возмущения , гамильтониан, полученный в предыдущем пункте упрощается до

Собственные энергетические состояния — это состояние со спином вверх, с энергией , и состояние со спином вниз с энергией .

Разница в энергии в релятивистских терминах в точности равна фотон с ларморовской частотой. В то время как трактовка электромагнитного поля в этом обсуждении будет классической, а не релятивистской, кажется очевидным, что ларморовская частота должна играть более чем поверхностную роль.

Нестационарное уравнение Шредингера говорит вам, что волновая функция эволюционирует вовремя вроде , так что если ,

Решение для коэффициентов и спина вверх и вниз состояния:

если и — значения этих коэффициентов в нулевой момент времени.

С тех пор и во все времена вероятности измерения вращения вверх или вниз не меняются с время. Этого следовало ожидать, так как вращение вверх и вращение вниз представляют собой энергию состояний стационарной системы. Чтобы получить более интересную физику, вы действительно нужно нестационарное возмущение.

Но сначала, чтобы лучше понять квантовые процессы с точки зрения идеи неквантовой физики, будет полезно написать нестационарная квантовая эволюция в терминах средних значений компонент углового момента. ожидаемое значение -​компоненты углового момента равно

Чтобы более четко указать, что значение должно быть между ​2 и ​2, вы можете записать величину коэффициентов в с точки зрения угла , «прецессия угол»,

С точки зрения так определенного , вы просто имеете, используя формулы триггера половинного угла,

Ожидаемые значения угловых моментов в и направления могут быть найдены как внутренние продукты а также , глава 4.4.3. Подставляя представление в терминах спиноров и спина Паули матрицы и очистку по формуле Эйлера (2. 5), Вы получаете

где – некоторый постоянный фазовый угол, который далее не имеет значения.

Первое, что видно из этих результатов, это то, что длина ожидаемого вектора углового момента равен ​2. Далее, компонент с осью -​, направление первичного магнитного поля поле,. всегда . Это подразумевает что вектор ожидаемого углового момента находится под постоянным углом с основным магнитным полем.

Рисунок 13.18: Лармор прецессия вектора ожидаемого спина (или магнитного момента) вокруг магнитного поля.

Компонент в -​плоскости , и этот компонент вращается вокруг -​ось, как показано на рисунке 13.18, вызывая конец точка ожидаемого вектора углового момента, чтобы заметать круговой путь вокруг магнитного поля. Это вращение вокруг оси — называется «ларморовской прецессией». Поскольку магнитный дипольный момент равен пропорциональный спину, он следует той же конической траектории.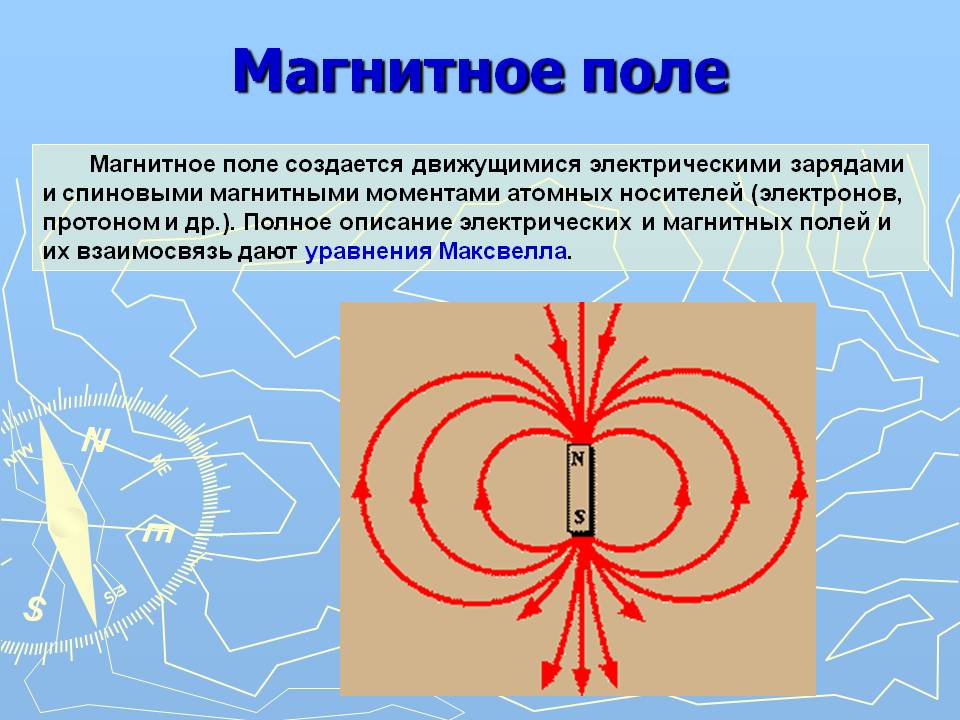

Следует проявлять осторожность, чтобы не придавать слишком большого значения этому классическая картина прецессирующего магнита. Ожидание угловое вектор импульса не является физически измеримой величиной. Один вопиющий несоответствие ожидаемого вектора углового момента относительно истинный угловой момент состоит в том, что квадрат величины ожидания вектор углового момента равен ​4, что в три раза меньше вектора истинный квадрат величины углового момента.

13.6.4 Влияние возмущения

В присутствии возмущающего магнитного поля нестационарная Уравнение Шредингера становится

(13.48)

где – ларморовская частота, – частота возмущения и является мерой силы возмущение и мало по сравнению с .

Вышеупомянутые уравнения могут быть решены точно с использованием стандартной линейной алгебраические процедуры, хотя алгебра довольно удушающая {Д. 75}. Анализ вносит дополнительное количество который будет называться «резонансным фактором»

(13.49)

Обратите внимание, что имеет максимальное значение, единица, при резонанс, т.е. когда частота возмущения равна ларморовской частоте.

Анализ находит коэффициенты спин-вверх и спин-вниз заявляет быть:

					(13.50)
					(13.51)

где и – начальные коэффициенты закрутки и состояния со спином вниз.

Это решение выглядит довольно неприступным, но оно не так уж плохо в приложение. Основной интерес представляют ядра, которые начинаются в основное состояние вращения, поэтому вы можете установить 1 и 0. Кроме того, основной интерес представляет вероятность того, что ядра можно обнаружить на повышенном энергетическом уровне, т.

(13.52)

Это довольно простой результат. Когда вы начинаете, ядра вы смотрите at находятся в основном состоянии, поэтому равно нулю, но со временем rf поле возмущения увеличивает вероятность нахождения ядер в повышенное энергетическое состояние в конечном итоге достигает максимума, когда синус становится единицей.

Рисунок 13.19: Вероятность обнаружения ядер при повышенных энергии в зависимости от времени для данной частоты возмущения.

Продолжение возмущения после этого времени — плохая новость; уменьшается вероятность повышенных состояний снова. Как показано на рисунке 13.19 показывает, что в течение длительного времени между ядрами происходит триггер находясь с уверенностью в основном состоянии и имея вероятность находиться в приподнятом состоянии. Частота, при которой вероятность колеблется, называется «частотой колебаний Раби». Источники автора разнятся о точном определении этой частоты, а та, что кажется быть наиболее логичным является.

Рисунок 13.20: Максимальная вероятность нахождения ядер при повышенных энергия.

В любом случае, поддерживая возмущение в нужное время, вы можете поднять вероятность повышенной энергии до максимума . График зависимости от возмущающей частоты называется «резонансная кривая», показанная на рис. 13.20. Чтобы возмущение имело максимальный эффект, его частота должна равняться ларморовской частоте ядер. Кроме того, для эту частоту можно очень точно наблюдать, шип на рисунке 13.20 должен быть узким, а так как его ширина пропорциональна , это означает, что возмущающее магнитное поле должно быть очень слабое по сравнению с первичным магнитным полем.

Рисунок 13.21: Возмущающее магнитное поле, вращающееся точно Ларморовская частота приводит к приходу ожидаемого вектора вращения. каскадом вниз из основного состояния.

Есть два качественных способа понять необходимость частота возмущения равна ларморовской частоте. Один геометрическим и классическим: как отмечалось в предыдущем подразделе, ожидаемый магнитный момент прецессирует вокруг первичного магнитного поле с ларморовской частотой. Для того чтобы для малого поля возмущения приложить долгосрочный нисходящий крутящий момент на этом прецессирующем магнитном момент, как на рис. 13.21, он должен вращаться вдоль с этим. Если он вращается с любой другой частотой, крутящий момент быстро изменить направление по сравнению с магнитным моментом, и вектор снова пойдет вверх. Другой способ взглянуть на это с релятивистской квантовой точки зрения: если магнитное поле равна ларморовской частоте, его фотоны имеют в точности энергия, необходимая для перевода ядра из основного состояния в возбужденное состояние.

На ларморовской частоте наивно казалось бы, что оптимальное время поддерживать возмущение до тех пор, пока вектор спина ожидания не станет вертикально вниз; то ядро ​​находится в возбужденном энергетическом состоянии с уверенность. Если вы затем дадите природе время исследовать ее состояние, каждый ядро окажется в возбужденном состоянии и испустит фотон. (Если не испорчено каким-то столкновением или чем-то еще, жизнь идеальна, не так ли?) Однако, судя по реальным описаниям Приборы ЯМР лучше остановить возмущение раньше, когда вектор вращения ожидания стал горизонтальным, а не полностью направленным вниз.