Потенциальное и вихревое поле

Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.

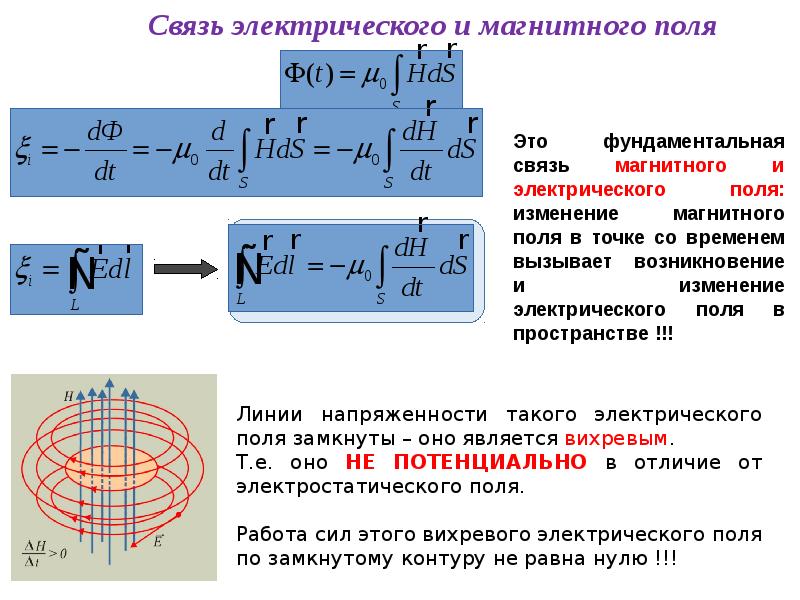
Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок Рисунок 12 ).

12. −Потенциальное и вихревое поля

Для потенциального поля имеем

,

то есть циркуляция вектора по любому замкнутому контуруравна нулю.

Если поле является вихревым, то поток вектора через любую замкнутую поверхность равен нулю:

.

В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.

3. Градиент, оператор Гамильтона

Далее мы рассмотрим некоторые дифференциальные операции с векторыми и скалярными полями, а именно градиент, дивергенцию (расхождение) и ротор (вихрь).

Эти операции потребуются нам при рассмотрении уравнений Максвелла.

Каждое поле порождает собой еще три поля, которые мы и будем рассматривать: векторные поля градиента и ротора и скалярное поле дивергенции.

Градиентом скалярного поля называется вектор, имеющий направление быстрейшего увеличенияи по величине равный производной по этому направлению.

В векторном анализе часто удобно использовать условный вектор, т.н. оператор Гамильтона. В декартовых координатах он имеет вид

.

Тогда можно записать

.

Градиент совпадает по направлению с нормалью к поверхности уровня и направлен в ту сторону, кудавозрастает (рисунок Рисунок 13 ).

13. −Градиент

Градиент будет применяться при анализе потенциальных векторных полей. Другое применение вектора градиента – численная оптимизация функций.

4. Дивергенция, физический смысл дивергенции

Для анализа явлений, происходящих в электромагнитном поле, важно знать, где находятся источники того или иного вектора. За меру источника можно выбрать поток вектора через замкнутую поверхность, но внутри данной замкнутой поверхности могут быть источники разных знаков, взаимно уничтожающие свое действие. Чтобы выявить распределение источников в пространстве, можно устремить эту замкнутую поверхность к нулю, но тогда поток вектора через эту бесконечно малую поверхность будет бесконечно малым. Это затруднение ликвидируется тем, что поток вектора через замкнутую поверхность делят на объем, окруженный этой поверхностью. Устремляя объем к нулю, получим предел этого отношения, который и называется дивергенцией.

Дивергенция дает возможность точно указать, в каких точках пространства расположились источники вектора.

Возьмем какую-либо точку поля , окружим ее малым объемоми вычислим поток векторачерез поверхность, ограничивающую объем. Разделим этот поток на, чтобы отнести его к единице объема и перейдем к пределу, устремляя к нулю все размеры, что мы будем обозначать символом. При этом объембудет стягиваться к точке.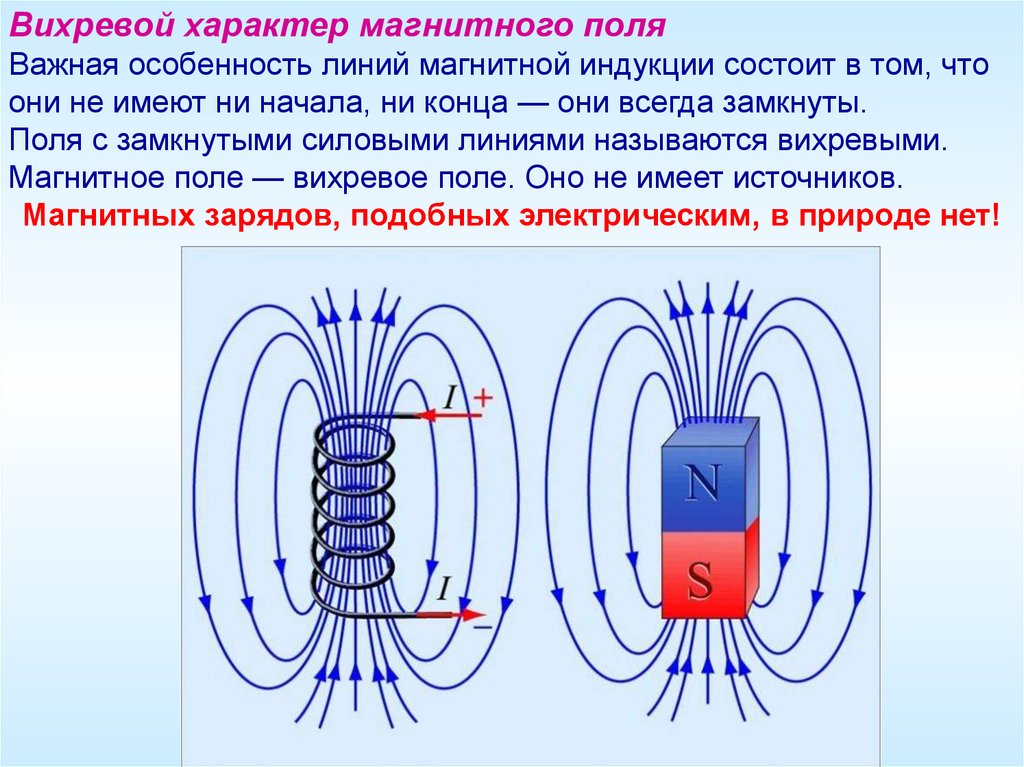

В результате получится некоторое число, зависящее от поведениявблизи точки, и характеризующее степень истечения из точки. Это число называется расхождением, или дивергенцией векторав точке. Дивергенция обозначается символом. Таким образом,

В векторном анализе доказывается, что

или, с применением оператора Гамильтона,

,

т.е., скалярное произведение оператора набла на вектор .

Рассмотрим значения дивергенции для разных случаев поля (рисунок Рисунок 14 ).

14. −Дивергенция

При положительной в точке дивергенции внутри областипоток векторачерез ограничивающую поверхность больше нуля, то есть линии вектора расходятся из этой области. Таким образом, внутринаходятся источники вектора. При отрицательной дивергенции, наоборот, линии вектора сходятся в областьи тогда внутри нее находятся стоки векторного поля.

Если же во всех точках некоторой области поля дивергенция оказывается равной нулю, что силовые линии поля либо пронизывают ее, либо являются замкнутыми.

Основы теории электричества

Основы теории электричества

Тамм И. Е. Основы теории электричества: Учеб. пособие для вузов. — 11-е изд., испр. и доп. — М.: ФИЗМАТЛИТ, 2003. — 616 с. Дано систематическое изложение основных положений теории электричества. Главное внимание уделено физическому содержанию теории. Подготовлено 11-е издание, как и предыдущее, без переработки, с тем чтобы дать возможность современному читателю ознакомиться именно с оригинальной, фундаментальной в мировой литературе работой академика И.Е. Тамма. Добавлена таблица физических констант, изменено несколько примечаний, обновлены ссылки на литературу и, наконец, исправлены замеченные опечатки. Для студентов физических специальностей вузов, а также научных и инженерно-технических работников. Оглавление ПРЕДИСЛОВИЕ К ОДИННАДЦАТОМУ ИЗДАНИЮ ВВЕДЕНИЕ ГЛАВА I. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ НЕПОДВИЖНЫХ ЗАРЯДОВ В ОТСУТСТВИЕ ДИЭЛЕКТРИКОВ § 1. Закон Кулона § 2. Электрическое поле § 3. Теорема Гаусса § 4. Электрическое поле заряженных поверхностей § 5. Проводники в электрическом поле § 6. Истоки электрического поля. Поверхностная дивергенция § 7. Работа электрических сил. Независимость ее от формы пути. Непрерывность тангенциальных слагающих вектора Е § 8. Потенциал электростатического поля § 9. Емкость. Конденсаторы § 10. Градиент электростатического потенциала. Линии сил § 11. Уравнения Пуассона и Лапласа § 12. Потенциал объемных и поверхностных зарядов § 13. Типичные задачи электростатики § 14. Двойной электрический слой § 15. Энергия взаимодействия электрических зарядов § 16. Энергия электрического поля § 17. Пондеромоторные силы § 18. Определение пондеромоторных сил из выражения энергии § 19. 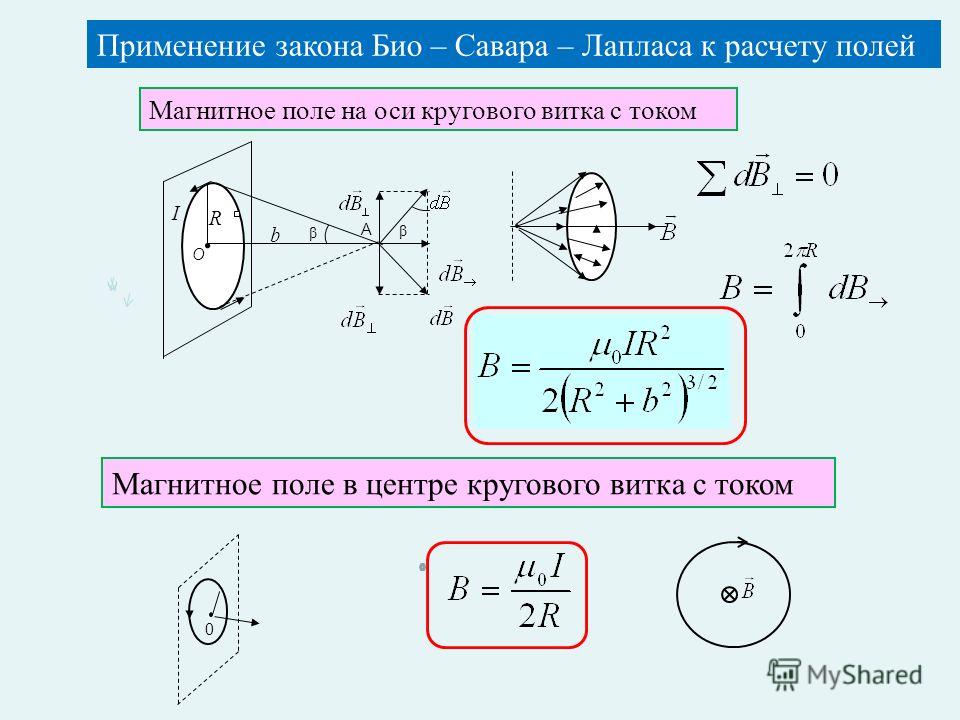Неустойчивость электрических систем. Связи ГЛАВА II. ДИЭЛЕКТРИКИ § 20. Диэлектрики. Электрический момент и потенциал нейтральной молекулы. Поляризация диэлектрика § 21. Свободные и связанные заряды. Потенциал электрического поля при наличии диэлектриков. Зависимость поляризации от поля § 22. Вектор электрической индукции. Дифференциальные уравнения поля в произвольной среде. Линии индукции § 23. Электрическое поле в однородном диэлектрике § 24. Непосредственный подсчет поля при наличии диэлектрика (в простейших случаях) § 25. Микро- и макроскопические значения физических величин § 26. Вывод уравнений поля в диэлектриках путем усреднения микроскопического поля § 27. Два класса диэлектриков. Квазиупругие диполи § 28. Отличие действующего на диполь поля от среднего § 29. Поляризация диэлектриков, молекулы которых обладают постоянным электрическим моментом. Зависимость диэлектрической проницаемости от температуры § 30. Энергия электрического поля в диэлектриках § 31. Преобразования энергии, связанные с поляризацией диэлектриков. Свободная энергия электрического поля § 32. Пондеромоторные силы в диэлектриках § 33. Сведение объемных сил к натяжениям § 34. Тензор натяжений электрического поля ГЛАВА III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 35. Электрический ток в металлах. Законы Ома и Джоуля. Напряжение § 36. Плотность тока. Дифференциальная форма уравнений Ома и Джоуля § 37. Условия стационарности токов. Уравнение непрерывности. Нити тока § 38. Сторонние электродвижущие силы. Квазилинейные токи. Второй закон Кирхгофа § 39. Превращения энергии в цепи тока. Контактные ЭДС § 40. Основные представления электронной теории металлов. Опыты Толмена § 41. Электронная теория электропроводности. Трудности классической теории. Теория Зоммерфельда ГЛАВА IV. ПОНДЕРОМОТОРНОЕ ВЗАИМОДЕЙСТВИЕ ПОСТОЯННЫХ ТОКОВ И ИХ МАГНИТНОЕ ПОЛЕ (В ОТСУТСТВИЕ НАМАГНИЧИВАЮЩИХСЯ СРЕД) § 42. Магнитное поле токов § 43. Взаимодействие элементов тока. 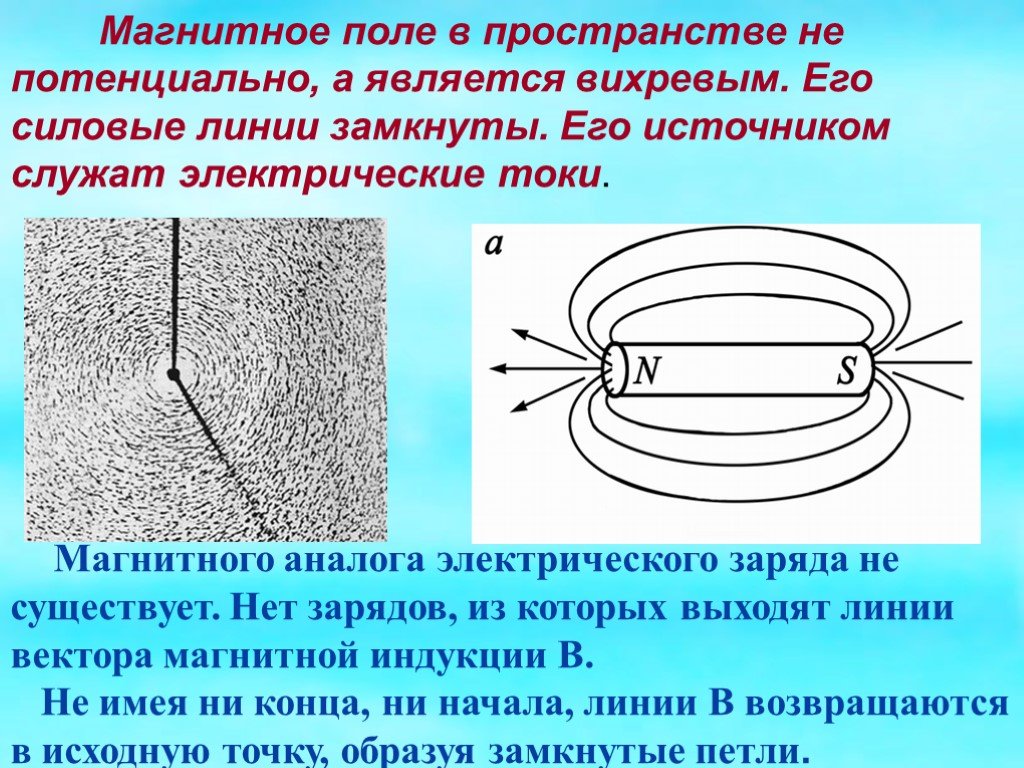Электродинамическая постоянная § 44. Переход от линейных токов к токам конечного сечения § 45. Лоренцева сила § 46. Вектор-потенциал магнитного поля § 47. Дифференциальные уравнения магнитного поля. Циркуляция напряженности магнитного поля § 48. Поля потенциальные и поля соленоидальные. Сопоставление дифференциальных уравнений электрического и магнитного полей § 49. Пограничные условия в магнитном поле токов. Поверхностные токи. Поверхностный ротор. Поле бесконечного соленоида § 50. Пондеромоторные силы, испытываемые в магнитном поле замкнутым током. Потенциальная функция тока во внешнем магнитном поле § 51. Пондеромоторное взаимодействие токов. Коэффициент взаимной индукции § 52. Коэффициент самоиндукции. Полная потенциальная функция системы токов § 53. Магнитные силовые линии § 54. Топология вихревого (магнитного) поля. Условные перегородки § 55. Магнитные листки. Эквивалентность их токам § 56. Магнитный момент тока. Элементарные токи и магнитные диполи § 57. 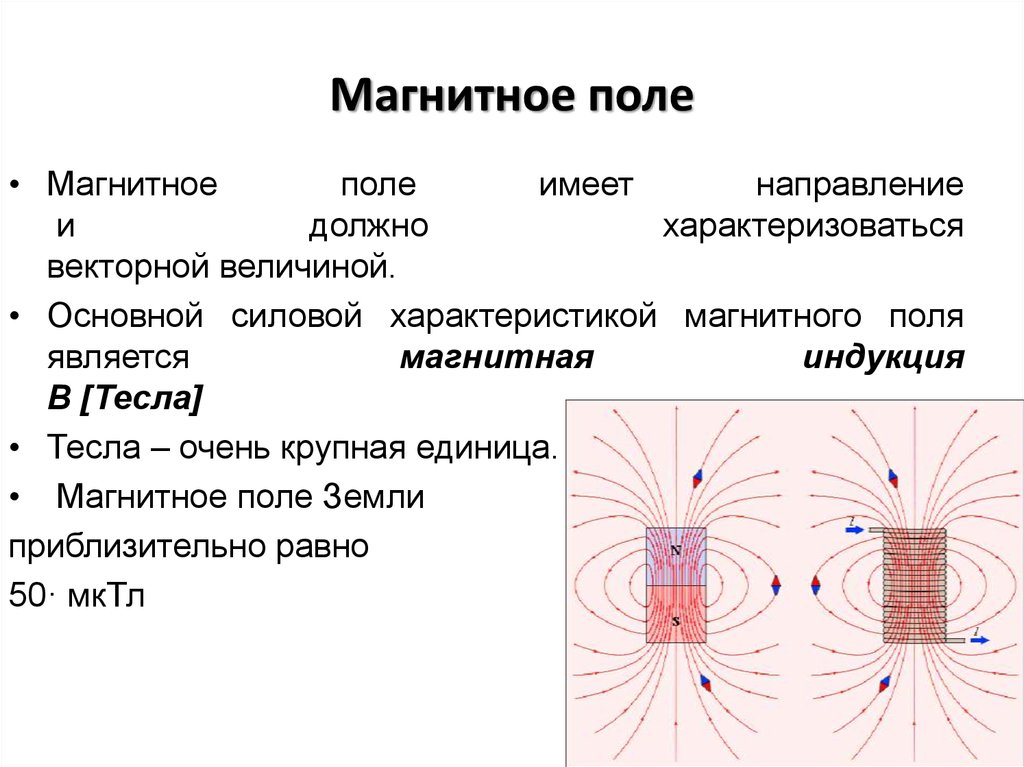Непосредственное определение поля элементарных токов и сил, ими испытываемых § 58. Эволюция представлений о природе магнетизма. Спин электронов § 59. Абсолютная (гауссова) и другие системы единиц. Электродинамическая постоянная ГЛАВА V. МАГНЕТИКИ (НАМАГНИЧИВАЮЩИЕСЯ СРЕДЫ) § 60. Намагничение магнетиков. Молекулярные токи и токи проводимости § 61. Векторный потенциал магнитного поля при наличии магнетиков. Средняя плотность объемных и поверхностных молекулярных токов § 62. Дифференциальные уравнения макроскопического магнитного поля в магнетиках. Напряженность магнитного поля в магнетиках и вектор магнитной индукции § 63. Зависимость намагничения от напряженности магнитного поля. Пара-, диа- и ферромагнетики § 64. Полная система уравнений поля постоянных токов. Однородная магнитная среда § 65. Механические силы, испытываемые токами в магнитном поле. Взаимодействие токов § 66. Пондеромоторные силы, испытываемые магнетиками в магнитном поле § 67. 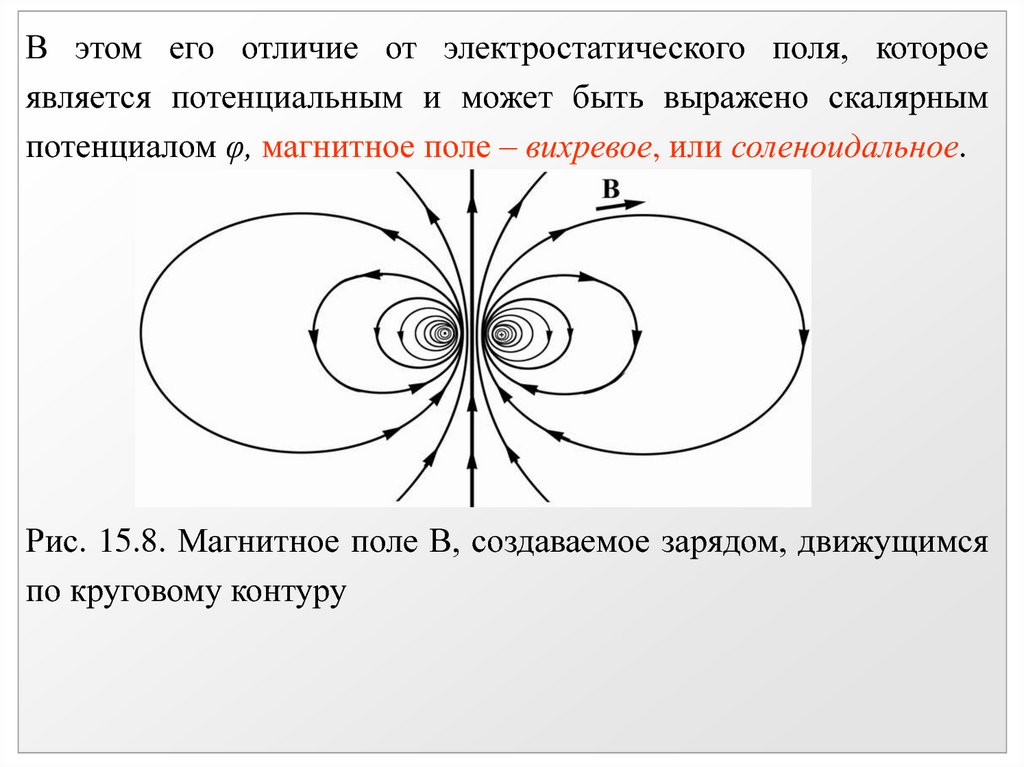Дополнение к выводу макроскопических уравнений магнитного поля в магнетиках § 68. Механизм намагничения магнетиков. Теорема Лармора § 69. Диамагнетизм § 70. Парамагнетизм § 71. Уточнения и дополнения к теории намагничения. Роль спина. Гиромагнитные явления § 72. Ферромагнетизм. Молекулярное поле Вейсса § 73. Уравнения поля в идеализированных ферромагнетиках (обычный вариант). Постоянные магниты § 74. Другой вариант уравнений магнитного поля в идеализированных ферромагнетиках. Эквивалентность электрических токов и постоянных магнитов § 75. Пондеромоторные силы, испытываемые постоянными магнитами во внешнем магнитном поле ГЛАВА VI. КВАЗИСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 76. Индукция токов в движущихся проводниках § 77. Закон электромагнитной индукции. Закон Ома для переменных токов § 78. Квазистационарные токи. Дифференциальные уравнения переменных токов § 79. Преобразование энергии в поле переменных токов. Энергия магнитного взаимодействия токов. 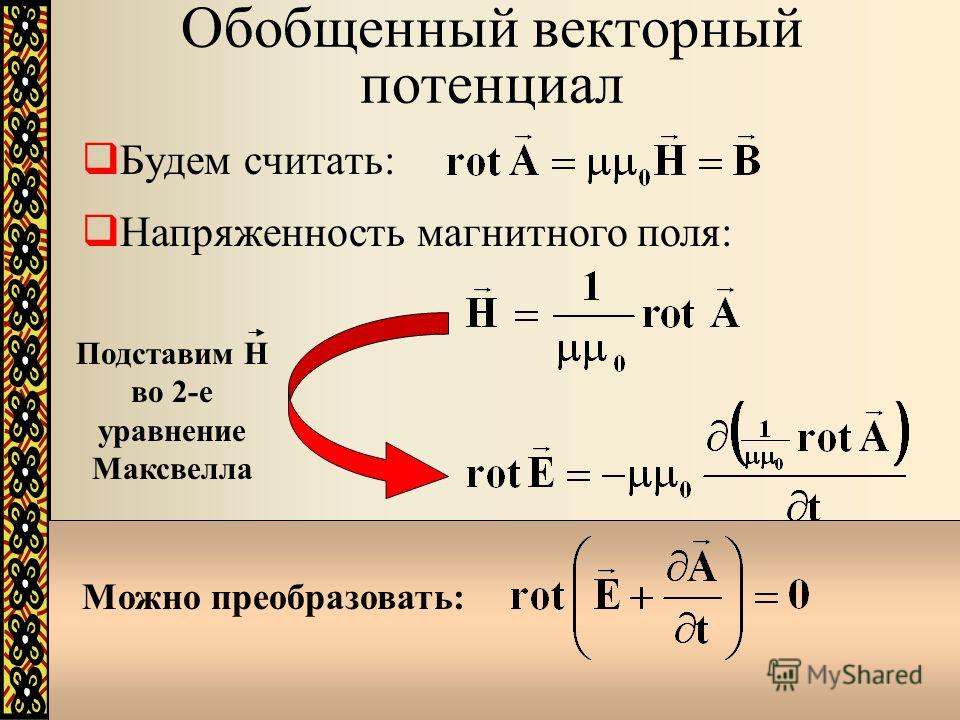Правило Ленца § 80. Простейшие применения теории переменных токов. Трансформатор § 81. Энергия магнитного поля. Энергетическое значение коэффициентов индукции § 82. Преобразование энергии при намагничении пара- и диамагнетиков. Свободная энергия магнитного поля § 83. Определение пондеромоторных сил магнитного поля из выражения энергии § 84. Тензор натяжения магнитного поля § 85. Вихри электрического поля § 86. Зависимость электрического напряжения от пути интегрирования. Напряжение переменного тока § 87. Уравнение непрерывности § 88. Токи смещения § 89. Конденсатор в цепи квазистационарного тока. Электрические колебания § 90. Скин-эффект ГЛАВА VII. ПЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В НЕПОДВИЖНОЙ СРЕДЕ И ЕГО РАСПРОСТРАНЕНИЕ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 91. Система максвелловых уравнений макроскопического электромагнитного поля § 92. Теорема Пойнтинга. Поток энергии § 93. Однозначность решений уравнений Максвелла § 94. Дифференциальные уравнения для потенциалов электромагнитного поля § 95. Решение волнового уравнения и уравнения Даламбера § 96. Запаздывающие и опережающие потенциалы. Калибровочная инвариантность § 97. Скорость распространения электромагнитных возмущений. Условия квазистационарности § 98. Осциллятор. Запаздывающие потенциалы поля осциллятора § 99. Поле осциллятора. Его излучение § 100. Электромагнитная природа света. Плоские волны в диэлектрике § 101. Отражение и преломление плоских волн в диэлектриках § 102. Распространение волн в проводящей среде. Отражение света от металлической поверхности § 103. Световое давление. Количество движения электромагнитного поля § 104. Электромагнитный момент количества движения. Частный случай статического поля § 105. Тензор натяжений и пондеромоторные силы электромагнитного поля § 106. Пример неквазистационарных токов: волны вдоль кабеля § 107. Приближенная теория быстропеременных токов. «Уравнение телеграфистов» § 108. Свободная энергия ферромагнетиков. Гистерезис § 109. Общая характеристика теорий близко- и дальнодействия ГЛАВА VIII. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ В МЕДЛЕННО ДВИЖУЩИХСЯ СРЕДАХ § 110. Дифференциальные уравнения поля в движущихся средах § 111. Конвекционный ток. Поляризация и намагничение движущихся сред § 112. Закон Ома и электромагнитная индукция в движущихся проводниках. Униполярная индукция § 113. Диэлектрик, движущийся в электромагнитном поле § 114. Распространение света в движущихся диэлектриках. Коэффициент увлечения Френеля. Отражение от движущегося зеркала § 115. Преобразования системы отсчета. Относительный характер различия между электрическими и магнитными полями ПРИЛОЖЕНИЯ I. ВЕКТОРНЫЙ АНАЛИЗ § 1. Векторная алгебра § 2. Векторные и скалярные поля. Градиент § 3. Поток вектора через поверхность § 4. Теорема Гаусса. Дивергенция § 5. Циркуляция вектора. Ротор вектора. Теорема Стокса § 6. Производная вектора по направлению § 7. Оператор набла. Вторые производные. Производные от произведений § 8. 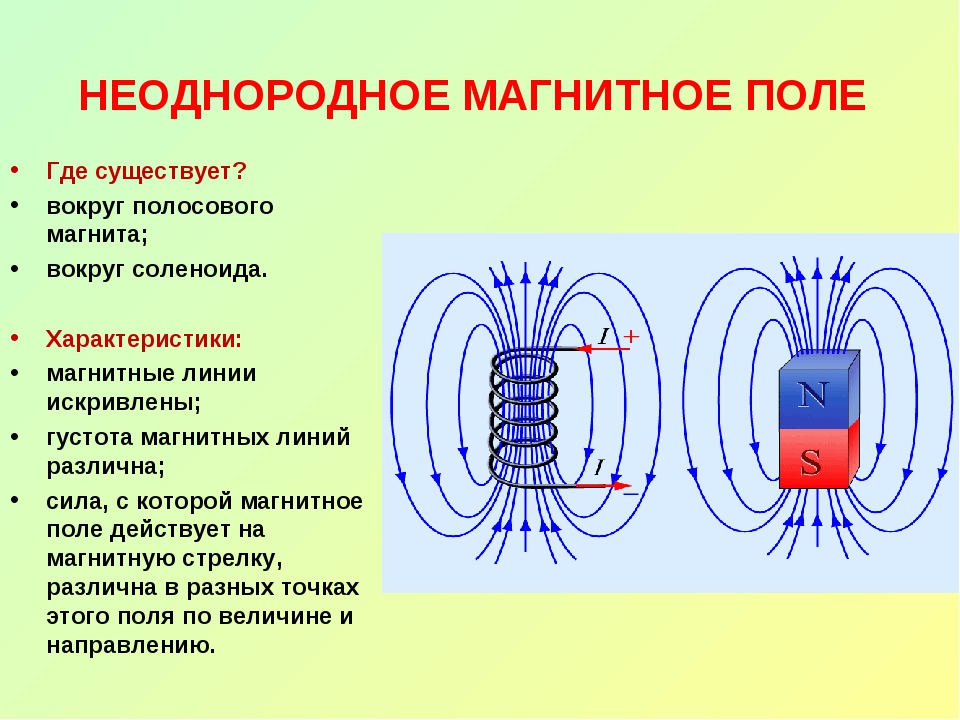Интегральные соотношения. Теорема Грина II. ОСНОВНЫЕ ФОРМУЛЫ В СИ И В ГАУССОВОЙ СИСТЕМЕ ДОПОЛНЕНИЯ

Магнитный векторный потенциал | Brilliant Math & Science Wiki

июль Томас внес

Содержание

• Расчет магнитного векторного потенциала
• Магнитное поле
• Электрическое поле

Магнитный векторный потенциал, вносимый длиной ds⃗d\vec{s}ds с протекающим через него током III, равен 9\begin{выровнено} \vec{B} = \frac{1}{r\sin\theta} \left( \ гидроразрыва {\ парциальное} {\ парциальное \ тета} \ влево (А_ \ varphi \ грех \ тета \ вправо) — \ гидроразрыва {\ парциальное А_ \ тета} {\ парциальное \ varphi} \справа) &\шляпа{\mathbf r} \\ {}+ \frac{1}{r} \left( \frac{1}{\sin\theta} \frac{\partial A_r}{\partial \varphi} — \frac{\partial}{\partial r} \left( r A_\varphi \right) \справа) &\шляпа{\boldsymbol \theta} \\ {}+ \frac{1}{r} \left( \frac{\partial}{\partial r} \left( r A _{\theta} \right) — \ гидроразрыва {\ парциальное A_r} {\ парциальное \ тета} \справа) &\шляпа{\boldsymbol \varphi} \end{aligned}B=rsinθ1​(∂θ∂​(Aφ​sinθ)−∂φ∂Aθ​)+r1​(sinθ1​∂φ∂Ar​​-∂r∂​(rAφ​))+ r1​(∂r∂​(rAθ​)−∂θ∂Ar​​)​r^θ^φ^​​ 9​=r1​(2r−cos(θ))=2−rcos(θ)​​

Частная производная магнитного векторного потенциала частично вносит вклад в индуцированное электрическое поле в соответствии с законом Фарадея.

E⃗=−∂A⃗∂t\vec{E} = — \frac{\partial \vec{A} }{ \partial t} E=−∂t∂A​

Вспомним закон Фарадея:

∇×E⃗=−∂B⃗∂t\nabla \times \vec{E} = — \frac{\partial \vec{B} }{\partial t}∇×E=−∂t∂B​

∇×E⃗=−∂(∇×A⃗)∂t\nabla \times \vec{E} = — \frac{\partial \big( \nabla \times \vec{A} \big) }{\partial t }∇×E=−∂t∂(∇×A)​

∇×E⃗=−∇×∂A⃗∂t\nabla \times \vec{E} = — \nabla \times \frac{ \partial \vec{A} }{\partial t}∇×E=−∇× ∂t∂A​

→E⃗=−∂A⃗∂t\стрелка вправо \vec{E} = — \frac{ \partial \vec{A} }{\partial t}→E=−∂t∂A​

Процитировать как: Магнитный векторный потенциал. Brilliant.org . Извлекаются из https://brilliant.org/wiki/ Magnetic-vector-potential/

9.2: Магнитный векторный потенциал

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5467

• Джереми Татум
• Университет Виктории

Хотя мы не можем выразить магнитное поле как градиент скалярной потенциальной функции, мы определим вектор величина \(\textbf{A}\), чей curl равен магнитному полю:

\[\textbf{B} = \textbf{curl A} = \nabla \times \textbf{A}. \label{9.2.1}\]

Точно так же, как \(\textbf{E} = −\nabla V\) не определяет \(V\) однозначно (потому что мы можем добавить к нему произвольную константу), так и уравнение \ref{9.2.1} не определяет \(\textbf{A}\) однозначно. В самом деле, если \(ψ\) — некоторая скалярная величина, мы всегда можем добавить \(\nabla ψ\) к \(\textbf{A}\), не затрагивая \(\textbf{B}\), потому что \(\ набла \times \набла ψ = \textbf{curl grad }ψ = 0\). 92\) можно записать \(-\набла (1/r)\). (Если это не очевидно, перейдите к выражению для \(\nabla ψ\) в сферических координатах и ​​поставьте \(ψ = 1/r\).) Закон Био-Савара принимает вид

\[\textbf{дБ}=-\frac{\mu I}{4\pi}\nabla (1/r)\times \textbf{ds}=\frac{\mu I}{4\pi}\ textbf{ds}\times\nabla (1/r).\label{9.2.3}\]

Поскольку \(\textbf{ds}\) не зависит от \(r\), набла может быть перемещена влево от перекрестного произведения, чтобы получить

\[\textbf{dB}=\nabla \times\frac{\mu I}{4\pi r}\textbf{ds}.\label{9.2.4}\]

Выражение \(\frac{\mu I}{4\pi r}\textbf{ds}\) является вкладом \(\textbf{dA}\) в магнитный векторный потенциал от элемента цепи \ (\textbf{дс}\).