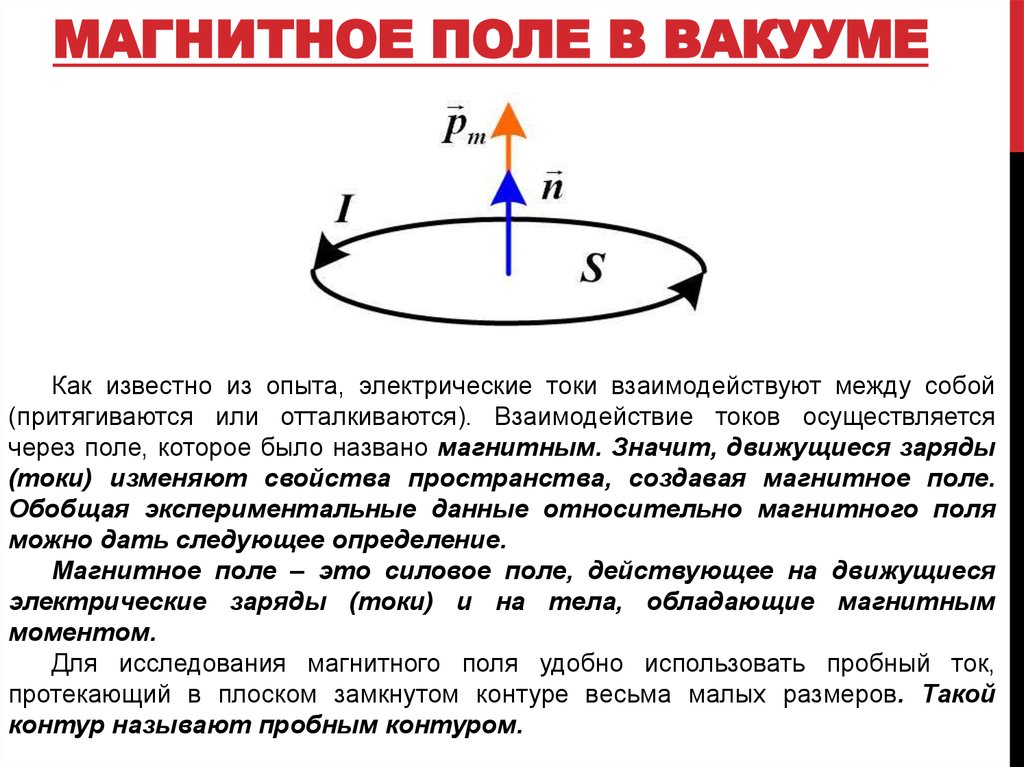
Магнитные поля: опасность или польза
В современной медицине прослеживается такая закономерность: чем выше уровень знаний о каком-либо способе лечения, тем шире он применяется. Именно поэтому терапия магнитными полями занимает сейчас одно из ведущих мест среди физиотерапевтических методов.
В настоящее время опубликовано уже несколько тысяч работ по магнитотерапии, среди которых есть статьи, монографии, международные исследования.
Однако человеку без специальной подготовки бывает непросто в них разобраться, понять в каких случаях магнитное поле может принести пользу, а в каких – вред.
Давайте попробуем сделать это вместе.
Безопасны ли магнитные поля в целом?
Таким вопросом люди стали задаваться по мере развития промышленности и возникновения большого количества антропогенных источников магнитного поля.
С 1960-х гг. стали появляться исследования, посвященные этому вопросу1. А к 1992 году группа ученых из СССР, США, Франции и других стран подготовила по заданию Всемирной организации здравоохранения обзор 557 таких публикаций2.
На основе изложенных в них фактов удалось определить, как человеческий организм реагирует на магнитные поля. Выяснилось, что опасность представляют только постоянные поля интенсивностью более 5 Тл, а также переменные с плотностью магнитных потоков 50-5000 мТл (при частоте 50-60 Гц) или 1–10 Тл (при частоте 3 Гц) и более3.
Подвергнуться такому воздействию в быту, случайно практически невозможно. С подобными полями могут столкнуться, в основном, работники радиоцентров и некоторых промышленных предприятий. Магнитные поля с другими характеристиками вполне безобидны – в конце концов, это привычный раздражитель, ведь люди постоянно находятся в магнитном поле Земли.
Могут ли магнитные поля быть полезными для здоровья?
Как показывает всё тот же обзор, могут. Магнитные поля со специально подобранными параметрами при небольшом времени использования подстегивают адаптационные возможности организма4.
Сейчас уже удалось выяснить, что с терапевтической целью лучше всего использовать импульсные магнитные поля, поскольку чувствительность к ним биологических тканей самая высокая.
Основными эффектами использования такого магнитного поля будут:
- Противовоспалительный
- Обезболивающий
- Улучшающий микроциркуляцию крови
- Противоотечный
- Регенеративный
Именно поэтому низкочастотные импульсные поля часто применяют для лечения суставных заболеваний.
Какого эффекта можно ожидать от магнитотерапии остеоартрита?
Судите сами: в 2020 году под руководством НИИ Ревматологии им. В.А. Насоновой было проведено многоцентровое слепое рандомизированное плацебоконтролируемое исследование КОСМО (Клиническая Оценка Современной Магнитотерапии при Остеоартрите).
В ходе него сравнивался результат использования магнитотерапии и плацебо при остеоартрите коленного сустава. Экспериментальная группа получала магнитотерапию от действующего устройства, а контрольной группе накладывали модифицированный аппарат, внешне не отличающийся от обычного, но не индуцирующий магнитное поле. В эксперименте принял участие 231 пациент, испытывающий умеренную или выраженную боль и нуждающийся в регулярном приеме нестероидных противовоспалительных препаратов. Эксперимент длился 2 недели.
В эксперименте принял участие 231 пациент, испытывающий умеренную или выраженную боль и нуждающийся в регулярном приеме нестероидных противовоспалительных препаратов. Эксперимент длился 2 недели.
На фоне проводимой терапии отмечалось статистически значимое уменьшение боли и скованности, улучшение функции коленного сустава в группе, получавшей подлинную магнитотерапию. Также у пациентов снизилась потребность в приеме НПВП: в экспериментальной группе препарат был отменен или снижена его доза у 33,1% больных, в группе плацебо – только у 16,8%. По всем показателям в первой группе положительная динамика была статистически более значимой, чем во второй. Субъективно результаты лечения как «хорошие» и «отличные» оценили 58,5% пациентов в группе, получавшей магнитотерапию, и 39,8% в группе плацебо6
Примечательно и то, что переносимость терапии оказалась хорошей. Не было ни одного случая, чтобы из-за серьезных нежелательных реакций на фоне подлинной магнитотерапии пришлось прервать лечение, а вот двое пациентов, получавших плацебо-воздействие, вынуждены были прервать участие в эксперименте из-за усиления суставной боли7.
Поэтому исследователи пришли к выводу, что магнитотерапия при кратковременном применении обеспечивает значимое улучшение состояния больных остеоартритом коленного сустава, хорошо переносится и не вызывает серьезных осложнений8
Похоже, использование магнитного поля в лечебных целях может быть весьма перспективным.
1 См., например, О биологическом действии электромагнитных полей радиочастот. – М., 1964.; Вопросы профпатологии. – М., 1964.
2,3,4 Сердюк В.В. Магнитотерапия: Прошлое, настоящее, будущее. Справочное пособие. – К.: «Азимут-Украина», 2004. – 536 с. С.20.
5 Золотухина Е.И., Улащик В.С. ОСНОВЫ ИМПУЛЬСНОЙ МАГНИТОТЕРАПИИ. Справочное пособие. — Витебская областная типография. 2008.
6,7,8 Каратеев А.Е., Погожева Е.Ю., Сухарева М.Л. и др. Оценка эффективности и безопасности магнитотерапии при остеоартрите. Результаты многоцентрового слепого плацебоконтролируемого исследования КОСМО (Клиническая Оценка Современной Магнитотерапии при Остеоартрите).
Могут ли люди чувствовать магнитное поле? Да! – отвечает электроэнцефалография
Физиология
«Снимок» магнитного поля на поверхности Земли (разным цветом отмечена разная интенсивность). Июнь 2014 г.
: 22.03.2019
Мы привыкли выделять пять органов чувств: зрение, слух, обоняние, осязание и вкус. Но это вопрос классификации: ведь есть еще, к примеру, чувство равновесия, не говоря уже о чувстве боли. Что же касается способности ощущать магнитные поля – магниторецепции, то она доказана для многих животных, таких как перелетные птицы, морские черепахи, моллюски и др. У всех у них при экспериментальном изменении магнитного поля менялось поведение, но подобные эксперименты на людях не дали результатов. Недавние исследования говорят о том, что ответ на вопрос «могут ли люди чувствовать магнитное поле?» может быть положительным
Считается, что магнитное поле Земли формируется благодаря тепловой конвекции в жидком внешнем ядре планеты, состоящем из расплавленного железа, в результате чего там образуется система течений электропроводящей жидкости, что аналогично движению проводника с током. Глазами человека магнитное поле нельзя увидеть, но некоторые организмы научились его воспринимать и использовать его силовые линии для пространственной ориентации.
Глазами человека магнитное поле нельзя увидеть, но некоторые организмы научились его воспринимать и использовать его силовые линии для пространственной ориентации.
Существует несколько гипотез физической основы «магнитного чувства». Согласно одной из них, магниторецепция обеспечивается за счет органелл с кристаллами минерала магнетита (Fe3O3), имеющихся в живых клетках. Вращение таких частиц под действием поля предположительно способствует открытию клеточных ионных каналов и генерации нервного импульса. Магнетит был обнаружен в клетках ряда организмов: бактерий, моллюсков, рептилий, рыб и птиц.
Еще одна гипотеза делает акцент на особых белках в сетчатке глаза – криптохромах, известных как регуляторы циркадных (внутренних биологических) ритмов. Под действием света синего спектра между структурными элементами этих белков происходит перераспределение зарядов с образованием устойчивой радикальной пары с неспаренными электронами. Такая конфигурация белка оказывается чувствительной к магнитному полю, так что клетка каким-то образом «узнает» о его значении в той или иной точке. Криптохромы были обнаружены у многих животных, включая мушек-дрозофил.
Криптохромы были обнаружены у многих животных, включая мушек-дрозофил.
У перелетных птиц, похоже, работают оба механизма магниторецепции. Первый является своего рода «компасом», благодаря которому птицы, вероятно, способны буквально видеть магнитное поле и определять, в каком направлении расположен ближайший магнитный полюс. С помощью же клеток с магнетитом, расположенных в области клюва, они оценивают более тонкие изменения магнитного поля, на основе которых можно составить подробную «карту». В результате птицы прокладывают свои полетные маршруты на основе точных географических координат.
Эксперименты на дрозофилах дали косвенные доказательства того, что и человек может в принципе «чувствовать» магнитные поля. Когда этих мушек с помощью методов генной инженерии заставили вместо собственного криптохрома производить белок, характерный для позвоночных животных, они стали воспринимать магнитное поле немногим хуже, чем раньше.
Но здесь есть одно «но»: люди магнитное поле в прямом смысле не видят. Подобная информация поступает в мозг животных через тройничный нерв, через который человек получает чувствительные сигналы, лежащие вне области сознательного восприятия (например, «служебные» сигналы от глазодвигательных мышц). Поэтому работа системы «магнитного чувства», которую мы могли унаследовать от животных, должна восприниматься нами практически неосознанно.
Подобная информация поступает в мозг животных через тройничный нерв, через который человек получает чувствительные сигналы, лежащие вне области сознательного восприятия (например, «служебные» сигналы от глазодвигательных мышц). Поэтому работа системы «магнитного чувства», которую мы могли унаследовать от животных, должна восприниматься нами практически неосознанно.
Учитывая эти данные и негативный опыт предыдущих исследований на людях, группа ученых из США и Японии провели эксперимент, в котором проверили реакцию человеческого мозга на изменения магнитного поля с помощью метода электроэнцефалографии. В эксперименте приняли участие 34 жителя Северного полушария. Испытуемых помещали в клетке Фарадея – устройстве для экранирования аппаратуры от внешних электромагнитных полей, внутри которой создавали искусственное магнитное поле, ориентацию которого меняли.
По словам участников эксперимента, они не чувствовали каких-либо изменений в своем состоянии. Но электроэнцефалограмма показала, что изменения магнитного поля сопровождались падением амплитуды альфа ритма мозга (с частотой колебаний 8–13 Гц). Такой ритм типичен для бодрствующего мозга в состоянии относительного покоя, а падение его амплитуды говорит о восприятии каких-то внешних сигналов. Этот эффект проявлялся у всех испытуемых по-разному, но отличался высокой воспроизводимостью при повторных измерениях, что может указывать на генетически обусловленную чувствительность индивидуумов.
Такой ритм типичен для бодрствующего мозга в состоянии относительного покоя, а падение его амплитуды говорит о восприятии каких-то внешних сигналов. Этот эффект проявлялся у всех испытуемых по-разному, но отличался высокой воспроизводимостью при повторных измерениях, что может указывать на генетически обусловленную чувствительность индивидуумов.
При этом интенсивность реакции мозга зависела от направления вращения поля. Как предположили ученые, мозг может настраиваться на восприятие геомагнитных сигналов определенного уровня, характерных для конкретного региона. К примеру, подобная «настройка» есть у морских черепах, обитающих в Саргассовом море: если они случайно уплывают далеко от «дома», то какие-то изменения характеристик геомагнитного поля приводят к тому, что они резко меняют направление движения, стремясь возвратиться обратно. Возможно, реакции участников эксперимента были бы иными, если бы они проживали не в Северном, а в Южном полушарии.
Интересно, что в данном случае метод электроэнцефалографии был применен для изучения магниторецепции не впервые: результаты аналогичной работы были опубликованы еще в 2002 г. , и они оказались отрицательными. Более удачливые экспериментаторы объясняют казус своих коллег недостаточной мощностью аналитических методов того времени. Что и доказали, безуспешно проанализировав нынешние данные с помощью «старых» методик.
, и они оказались отрицательными. Более удачливые экспериментаторы объясняют казус своих коллег недостаточной мощностью аналитических методов того времени. Что и доказали, безуспешно проанализировав нынешние данные с помощью «старых» методик.
Можно надеяться, что сегодняшний успех не является очередным «артефактом» вычислительных технологий, только уже со знаком «плюс». В любом случае его нужно подтвердить в дополнительных экспериментах, например, по исследованию влияния на мозг поля разной напряженности и т.п.
Остается неизвестным и сам механизм магниторецепции у человека. Предположение о «визуальном», криптохром-зависимом механизме ученые отвергают из-за обнаруженной способности мозга различать полярность магнитных полюсов. И хотя в эволюционно древних регионах мозга человека – стволе и мозжечке – были найдены частицы магнетита, у нас нет каких-либо специальных сенсорных структур, содержащих этот минерал, поэтому находка таких частиц может отражать лишь степень загрязнения окружающей среды.
Так что вопросов о магниторецепции у человека по-прежнему больше, чем ответов. И даже если наше слабое «чувство поля» есть – велик ли от него прок в современном мире, где есть карты, компасы и GPS? К тому же и пробиться сквозь изобилие окружающих нас антропогенных электромагнитных волн ему будет трудно – даже птицы сбиваются с пути во время магнитных бурь. Кстати, про магнитные бури: опять болит голова – не проверить ли геомагнитный прогноз? Чем черт не шутит…
Фото: https://uk.wikipedia.org, https://vimeo.com, https://www.flickr.com, https://www.nps.gov
Подготовила Мария Перепечаева
: 22.03.2019
Магнитные поля
Тел.: +79607089657 +7(4822)58-06-60; Почта: [email protected]
система онлайн-бронирования
- Магнитные поля
Кроме местной магнитотерапии в ООО «Санаторий «Бобачевская роща» проводятся также сеансы общей низкочастотной магнитотерапии с помощью специальной установки с регулировкой частоты, модуляции и индукции вращающегося магнитного поля УМТвп-«МАДИН» (Магнототурботрон).
Что такое «Магнитотурботрон»
Это магнитотерапевтическая низкочастотная установка с регулировкой частоты, модуляции и индукции вращающегося магнитного поля. Установка предназначена для лечения и профилактики различных заболеваний вращающимся магнитным полем , а также для исследовательских целей.
Установка обеспечивает создание вращающегося относительно продольной оси лечебной камеры магнитного поля с возможностью регулировки следующих параметров:
- модуляции (различное нарастание и спад) амплитуды от минимума до максимума;
- максимальной величины индукции;
- направления вращения поля;
- числа циклов модуляции;
- остановки режима модуляции в любой момент времени.
Установка по электробезопасности соответствует по типу защиты изделиям класса 1, по степени защиты изделиям типа В по ГОСТ 50267.0-92.
Установка в зависимости от потенциального риска применения относится к классу 2А по ГОСТ Р 51609-2000.
Физические основы и механизм действия
Наверное, многие, кто знаком с основами электротехники, обращали внимание на то, что сердечники трансформаторов набраны из отдельных железных пластин, разделенных слоями диэлектрика. Это делается для того, чтобы не допустить больших потерь энергии на вихревые токи («токи Фуко»), которые индуцируются переменным магнитным полем в массивных проводниках. Но то, что является нежелательным в электротехнике, может быть желанным явлением в медицине.
Существует много способов ускорения кровотока в сосудах малого калибра: массаж, тепловые и физиопроцедуры, сауна и т.д. Но тело человека достаточно «инертно»: прогрев от поверхности в глубь идет медленно ввиду низкой теплопроводности и высокой теплоемкости тела, а механически промассировать глубоко расположенные ткани — задача не из легких. Общая магнитотерапия (магнитотурботрон) выгодно отличается от них возможностью воздействия сразу на всю глубину, причем по всему организму, а не локально. К тому же, это воздействие легко программируется: существуют разные режимы и варианты модуляции переменного магнитного поля, которые мы можем выбирать в зависимости от ведущей патологии.

Показания для лечения на установке ЭОЛ «Магнитотурботрон»
I. Неопухолевые заболевания:
1. Нарушения функций опорно-двигательного аппарата (остеохондроз позвоночника, ревматоидный артрит, деформирующий остеоартроз, артриты, ушибы, эпикондилит).
2. Психосоматические расстройства (синдром хронической усталости, вегетативно-сосудистая дистония, депрессивные и астенические состояния, неврозы).
4. Артериальная гипертония, местные нарушения системы кровообращения застойного и отечного характера, сопровождающиеся изменениями гемодинамики магистральных сосудов и микроциркуляции (облитерирующий эндартериит и атеросклероз сосудов конечностей, хроническая венозная недостаточность, в том числе с трофическими нарушениями, васкулиты с наличием трофических язв, мигрирующий тромбофлебит, геморрой, первичный и приобретенный лимфостаз).
5. Заболевания органов пищеварения (не осложненные формы язвенной болезни желудка и двенадцатиперстной кишки, гастриты, холециститы, панкреатиты, энтероколиты, состояния через 3-4 недели после операций на желудке и кишечнике).
6. Заболевания органов дыхания (затяжная пневмония, бронхиальная астма, туберкулез легких, острые и хронические бронхиты, синуситы, фарингиты и тонзиллиты, ОРВИ).
7. Заболевания желез внутренней секреции (сахарный диабет и его осложнения, увеличения щитовидной железы, гипоталамический синдром).
8. Заболевания мочеполовой системы (мочекаменная болезнь, пиелонефрит, простатит, аденома предстательной железы, острые и хронические аднекситы, сальпингоофориты, миома матки до 12 недель).
9. Системные заболевания соединительной ткани.
10. Кожные заболевания (экзема, нейродермит, псориаз, в т.ч. псориатический артрит).
11. Наркомания (наркотический абстинентный синдром), алкоголизм.
12. Иммунодефицитные состояния.
II. Онкологические заболевания следующих форм и стадий:
— неоперабельные послеоперационные рецидивы и метастазы злокачественных новообразований;
— местно распространенный рак молочной железы в фазе предоперационного лечения;
— злокачественные опухоли молочной железы и других органов в послеоперационном периоде;
— лимфоррея после обширных операций на молочной железе;
— для предотвращения или снижения побочных эффектов (эритем, отеков, эпителиитов) при лучевой терапии и химиотерапии;
— лимфомы, лимфогранулематоз;
— болевые синдромы при неоперабельных новообразованиях;
— мастопатии при отсутствии показаний к хирургическому лечению.
Противопоказания для лечения:
1. Беременность
2. Декомпенсированная недостаточность кровообращения IIБ — Ш ст.
3. Системные заболевания крови (лейкозы)
4. Наличие инородных магнитных тел (например, кардиостимуляторов)
5. Острые инфекционные заболевания
6. Геморрагические васкулиты и другие патологические процессы, сопровождающиеся повышенной кровоточивостью.
7. Психические заболевания.
8. Индивидуальная непереносимость магнитотерапии.
9. Ранний постинфарктный период.
10. Тяжелое нестабильное течение ИБС.
11. Некомпенсированная глаукома.
12. Гипертиреоз.
Продолжительность процедуры обычно составляет от 10 до 15 минут, курс 10 сеансов.
Индуктотермия
Суть метода заключается в том, что кабелю, располагаемому у тела больного, пропускают ток высокой частоты, образующий переменное магнитное поле, индуцирующее в тканях вихревые токи. В результате прохождения этих токов в тканях выделяется тепловая энергия, являющаяся при индуктотермии основным лечебным фактором.
Следует отметить, что, действие этого тепла значительно сильнее, чем тепла, подводимого извне. Разогрев происходит в глубине тканей (главным образом в мышцах), а поскольку большая часть терморецепторов расположена в поверхностных тканях, при индуктотермии оказывается возможным обеспечить прогрев без перенапряжения естественных механизмов терморегуляции.
При неинтенсивных кратковременных воздействиях индуктотермии повышаются возбудимость нервной системы, скорость проведения возбуждения по нервам и интенсивность окислительно-восстановительных процессов.
Воздействия средней интенсивности сопровождаются ощущением умеренного тепла. При этом ускоряется кровоток и скорость обменных процессов. В частности, повышается синтез глюкокортикоидных гормонов, усиливаются гликогенообразовательная и желчевыделительная функции печени. Кроме того, активируется фагоцитоз, рассасываются воспалительные очаги. Тонус поперечнополосатой и гладкой мускулатуры (в том числе сосудистых стенок) снижается, отмечается уменьшение повышенного артериального давления. Заметно общеседативное и болеутоляющее действие, связанное со снижением возбудимости центральной и периферической нервной систем.
Заметно общеседативное и болеутоляющее действие, связанное со снижением возбудимости центральной и периферической нервной систем.
Все перечисленные реакции являются основой для применения индуктотермии при различных хронических воспалительно-дистрофических процессах.
Местная низкочастотная магнитотерапия
В ОАО «Санаторий «Бобачевская роща» для проведения низкочастотной магнитотерапии используются аппараты «ПОЛЮС-101» и «ПОЛЮС-1».
Местная низкочастотная магнитотерапия применяется с лечебной целью на тот или иной участок тела в виде переменных низкочастотных либо постоянных магнитных полей. Магнитное поле может быть прерывистым или непрерывным.
Магнитного поля в диапазоне использующихся сейчас частот и индуктивности относится к слабым физическим факторам. Количество энергии, поглощаемой организмом при местной низкочастотной магнитотерапии невелико, количество тепла от процедуры выделяется значительно меньше, чем от протекания обычных обменных процессов. Поэтому провести параллель между количеством поглощенной энергии и величиной эффекта невозможно. Эффективность метода (как и сам механизм действия магнитотерапии) еще нуждается в дальнейшем изучении и объяснении.
Поэтому провести параллель между количеством поглощенной энергии и величиной эффекта невозможно. Эффективность метода (как и сам механизм действия магнитотерапии) еще нуждается в дальнейшем изучении и объяснении.
Магнитотерапия нашла широкое применение при лечении начальных проявлений цереброваскулярной недостаточности и последствий инсультов, а также расстройствах вегетативной нервной системы, например, патологии симпатических узлов. Метод также с успехом применяется при язвенной болезни (в стадии затухающего обострения), в процессе восстановительного лечения опорно-двигательного аппарата после перенесенных травм и ортопедических вмешательств, при лечении диффузной патологии, связанной с патологией обмена веществ, нарушением сосудистой и нервной трофики и во многих других случаях.
Показания и противопоказания
Тверь Санаторий «Бобачевская Роща»
Постоянное магнитное поле и его физиотерапевтическое воздействие на организм
Главная / Статьи / Лечебное и профилактическое воздействие постоянного магнитного поля на организм человека
Что такое физиотерапия?
Не всегда даже медики – профессионалы четко понимают, что такое физиотерапия. Физис – природа, т.е. использование природных факторов в лечебных, профилактических и реабилитационных целях.
Физис – природа, т.е. использование природных факторов в лечебных, профилактических и реабилитационных целях.
А что такое природные или физические факторы? Вы хорошо их знаете. Они делятся на так называемые естественные – это солнце, воздух, вода, лечебные грязи и вторую часть – это преформированные (т.е. видоизмененные) – по сути это те же природные факторы, но они видоизменены при помощи аппаратов. Это — электрическая энергия, магнитные поля, все это есть в природе, та же световая энергия, но при помощи аппарата они подводятся к человеку, это составляет второй раздел физиотерапии – аппаратная физиотерапия, которая и используется в кабинетах физиотерапии каждой поликлиники. 115 лет назад профессором Штанге была создана Санкт-Петербургская кафедра физиотерапии. Сразу хочу обратить внимание, что наряду с тем, что физиотерапия это была медицинская специальность, всегда существовала домашняя физиотерапия. Хотя, по большому счету, домашняя физиотерапия присутствовала у человечества всегда: во-первых, это лёд, который прикладывали к ушибам и травмам, это и грелки для прогревания. Естественно, с развитием цивилизации, под влиянием технического прогресса появилась аппаратная физиотерапия и для домашнего применения. Человек дома всегда использовал методы физиотерапии и знал, что это поможет. Кстати, очень важный вопрос: «А это поможет?» Вроде дозы такие небольшие. Вы должны четко понимать: «Да, это поможет.»
Естественно, с развитием цивилизации, под влиянием технического прогресса появилась аппаратная физиотерапия и для домашнего применения. Человек дома всегда использовал методы физиотерапии и знал, что это поможет. Кстати, очень важный вопрос: «А это поможет?» Вроде дозы такие небольшие. Вы должны четко понимать: «Да, это поможет.»
Это связано с жизнью в целом. Дело в том, что Вы хорошо знаете, что человек живет в различных условиях от Сахары до Арктики. Наш организм всегда подвергается воздействию всевозможных факторов: то дождь льет, то жара, то холод и пр. Это очень серьёзная нагрузка на защитные силы организма. Несмотря на это, мы живы и наш организм нормально работает в пределах каких-то величин. У нас постоянная температура тела, постоянное давление (у здоровых, конечно), нормально работает желудок. Т.е. организм работает в системе, какого-то постоянства. Это состояние было названо гомеостазом. Гомеостаз — это постоянство каких-то величин, которые позволяют организму существовать независимо от того, что происходит в окружающей среде, а иногда и внутри организма.
Как же организм приспосабливается, в результате чего? Дело в том, что приспособиться можно по-разному. Эволюция, т.е. развитие, привела к тому, что наш организм приспосабливается по-разному. Во-первых, можно просто не реагировать на изменения. Но все живые организмы, ткани выбрали другое направление — это реагирование и настройка на изменяющиеся условия. Наверное, самая интересная реакция живого организма на внешние какие-то раздражители была открыта доктором Селье в 1932 году. Он обратил внимание, что первая реакция организма практически на любые раздражители — это реакция стресса.
Кто из нас не знает, что все болезни от стрессов? И действительно, стресс крайне важная реакция организма. Но она возникает на мощные раздражители, воздействующие на нас. При этом стресс бывает также и хроническим, если раздражители не только сильные, но и продолжительные. Наша жизнь, её темп, мы должны всё успеть. Как Вы понимаете, это как раз и способствует такому состоянию. Мы сидим за компьютерами, пользуемся мобильными телефонами и смотрим телевизор. И всё это время на нас действуют электромагнитные поля. Особенно интенсивные поля на нас действуют в метрополитене, там доза электромагнитных излучений превышает норму на 500 пдн. Организм, естественно, реагирует на такое воздействие и реакция — это стресс. Стресс протекает фазно, и при этом происходят различные изменения в организме, причем некоторые приводят к разрушениям тканей. При начальной фазе могут возникать даже язвы в желудочно-кишечном тракте, что в дальнейшем может привести к тяжелым заболеваниям. Нашими отечественными специалистами в 69-м году были выделены другие системы реакции организма. Такими системами является реакция на малые раздражители. Это так называемая реакция тренировки. И на раздражители средней степени – это реакции активации. Я бы хотела обратить внимание на реакцию тренировки, т.е. ответ организма на раздражения малой силы по своей величине.
И всё это время на нас действуют электромагнитные поля. Особенно интенсивные поля на нас действуют в метрополитене, там доза электромагнитных излучений превышает норму на 500 пдн. Организм, естественно, реагирует на такое воздействие и реакция — это стресс. Стресс протекает фазно, и при этом происходят различные изменения в организме, причем некоторые приводят к разрушениям тканей. При начальной фазе могут возникать даже язвы в желудочно-кишечном тракте, что в дальнейшем может привести к тяжелым заболеваниям. Нашими отечественными специалистами в 69-м году были выделены другие системы реакции организма. Такими системами является реакция на малые раздражители. Это так называемая реакция тренировки. И на раздражители средней степени – это реакции активации. Я бы хотела обратить внимание на реакцию тренировки, т.е. ответ организма на раздражения малой силы по своей величине.
А стоит ли использовать раздражения малой величины? А зачем они нам нужны? Так вот, нашими исследователями, физиологами было доказано, что даже на малые раздражители организм реагирует. Причем он тоже реагирует, как и на стресс – есть три стадии. Первое, что организм всегда спрашивает: «А что это такое?», т.е. стадия ориентировки, он должен сориентироваться в этот момент. Как и при стрессе у нас немного увеличивается щитовидная железа, изменяется соотношение в крови форменных элементов, но все эти изменения не выходят за пределы нормы. При настоящем стрессе все показатели далеко выходят за рамки нормы, а здесь они всего лишь достигают верхних границ нормы. Меняется соотношение в гормональной системе, но эти изменения незначительны. Если слабый фактор действует на протяжении нескольких дней, то организм, разобравшись, что ничего страшного не происходит, просто перестаёт реагировать. Если же этот слабый фактор каждый день действует, но чуть выше, т.е. сегодня в одной дозе воздействует, а завтра чуть в большей дозе. Что происходит? Возникает реакция тренированности для организма. Эту стадию назвали стадией тренировки, организм на этой стадии начинает функционировать на чуть более высоком физиологическом уровне.
Причем он тоже реагирует, как и на стресс – есть три стадии. Первое, что организм всегда спрашивает: «А что это такое?», т.е. стадия ориентировки, он должен сориентироваться в этот момент. Как и при стрессе у нас немного увеличивается щитовидная железа, изменяется соотношение в крови форменных элементов, но все эти изменения не выходят за пределы нормы. При настоящем стрессе все показатели далеко выходят за рамки нормы, а здесь они всего лишь достигают верхних границ нормы. Меняется соотношение в гормональной системе, но эти изменения незначительны. Если слабый фактор действует на протяжении нескольких дней, то организм, разобравшись, что ничего страшного не происходит, просто перестаёт реагировать. Если же этот слабый фактор каждый день действует, но чуть выше, т.е. сегодня в одной дозе воздействует, а завтра чуть в большей дозе. Что происходит? Возникает реакция тренированности для организма. Эту стадию назвали стадией тренировки, организм на этой стадии начинает функционировать на чуть более высоком физиологическом уровне.
Что же меняется? Повышается устойчивость защитных сил организма к неблагоприятным условиям, а их у нас более чем достаточно. Вот на этом принципе и основано наше так называемое профилактическое направление физиотерапии, т.е. закаливание организма. И неважно чем закаливаться, можно холодной водой, можно заниматься на тренажерах. Однако при всей видимой простоте кто из нас выполняет эти нехитрые процедуры? Мы предлагаем Вам проводить тренировки с помощью магнитного поля аппликатора магнитостимулирующего НЕВОТОН.
Магнитное поле.
Почему именно магнитное поле? Дело в том, что именно магнитное поле наиболее близко нам по своей природе и его воздействие максимально физиологично. Что же такое магнитное поле, и как оно возникает? Многие из Вас, так или иначе, связаны с техникой и знают, что там, где есть электрические заряды, там есть электрический ток и, соответственно, электромагнитное поле. Но это искусственно созданное магнитное поле. С другой стороны, наша Земля также обладает магнитным полем и имеет соответственно Северный и Южный полюса. Мы с Вами живём в своеобразной электромагнитной колыбели, и если вдруг человеческий организм или любую живую клетку лишить этой колыбели, она перестает функционировать и погибает достаточно быстро. Магнитное поле Земли чутко реагирует на все изменения, происходящие в космосе. Так называемые вспышки на Солнце становятся причиной электромагнитных бурь на Земле. Эти бури становятся настоящим врагом для не очень здоровых людей. На сегодняшний день известно, что в дни магнитных бурь резко ухудшается самочувствие, особенно у тех, кто страдает заболеваниями сердечно-сосудистой системы. В частности, было установлено, что накануне магнитных бурь происходит смена погоды, резко увеличивается количество гипертонических кризов, инфарктов миокарда, кровоизлияний, легочных кровотечений, нарушается реакция вегетативной нервной системы, т.е. той нервной системы, которая осуществляет регуляцию работы всех внутренних органов. Вегетативная система обеспечивает всю нашу жизнедеятельность. Таким образом, перед нами встает необходимость постоянно поддерживать и усиливать устойчивость организма к неблагоприятным факторам внешней среды.
Мы с Вами живём в своеобразной электромагнитной колыбели, и если вдруг человеческий организм или любую живую клетку лишить этой колыбели, она перестает функционировать и погибает достаточно быстро. Магнитное поле Земли чутко реагирует на все изменения, происходящие в космосе. Так называемые вспышки на Солнце становятся причиной электромагнитных бурь на Земле. Эти бури становятся настоящим врагом для не очень здоровых людей. На сегодняшний день известно, что в дни магнитных бурь резко ухудшается самочувствие, особенно у тех, кто страдает заболеваниями сердечно-сосудистой системы. В частности, было установлено, что накануне магнитных бурь происходит смена погоды, резко увеличивается количество гипертонических кризов, инфарктов миокарда, кровоизлияний, легочных кровотечений, нарушается реакция вегетативной нервной системы, т.е. той нервной системы, которая осуществляет регуляцию работы всех внутренних органов. Вегетативная система обеспечивает всю нашу жизнедеятельность. Таким образом, перед нами встает необходимость постоянно поддерживать и усиливать устойчивость организма к неблагоприятным факторам внешней среды.
Воздействие магнитного поля на организм.
Я недаром Вам рассказывала про реакции тренировки. Повышать устойчивость организма можно большим количеством способов. Однако на сегодняшний день современная жизнь не позволяет нам уделять много времени на здоровье, а молодым и красивым хочется быть всегда. В этом отношении магнитное поле, создаваемое приборами, позволяет восстановить нарушенные функции организма. Почему? Потому что было установлено, что магнитное поле, влияя на организм, вызывает в нём те же самые физические и химические процессы. Когда магнитное поле проникает в ткани человека, оно вызывает упорядочивание движения электрически заряженных частиц в жидких средах. Меняются свойства крови, она становится более текучей, перераспределяются форменные элементы: эритроциты и лейкоциты, тромбоциты. Меняется так называемая реология крови, и это, по существу, профилактика ИБС и прочих сердечно-сосудистых заболеваний, бронхитов, тромбозов и т.д. Одновременно с изменениями крови в клетках тканей происходят удивительные процессы: меняется соотношение ядерного вещества, ферментов, активнее начинают работать митохондрии (так называемые энергетические станции клетки), меняется проницаемость клеточной оболочки, и соответственно, газообмен, и обмен веществ клетки.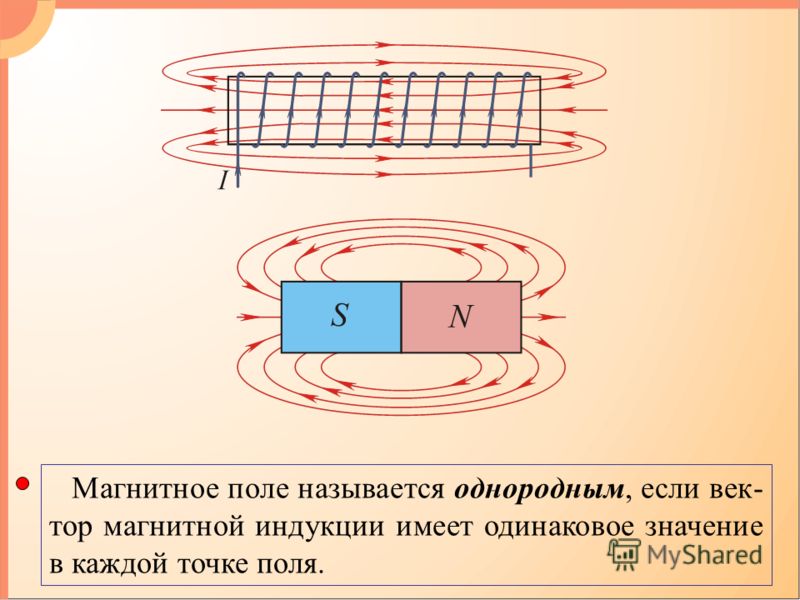 Особенно подвержены воздействию магнитного поля центральная и периферическая нервная система.
Особенно подвержены воздействию магнитного поля центральная и периферическая нервная система.
Что это даёт? В нервном волокне улучшается проведение нервного импульса, человек легче реагирует на всевозможные изменения окружающей среды. Улучшение работы головного мозга, прежде всего, выражается в своевременном проявлении важной реакции торможения. Реагируя на всевозможные воздействия, человек приходит в состояние возбуждения. И длительное пребывание в этом состоянии приводит к серьёзному истощению организма. Становится очевидно, что реакция торможения жизненно необходима для нормального функционирования организма. И именно эту реакцию восстанавливает и усиливает магнитное поле, т.е. поддерживает жизненные силы организма и защищает от истощения.
Хотелось бы также обратить внимание на то, что магнитное поле благотворно влияет на саму сосудистую стенку, повышает ее тонус. В зоне действия поля в активный кровоток включаются резервные сосуды и капилляры, просвет сосудов расширяется, и кровоснабжение тканей значительно увеличивается.
Этим свойством нередко пользуются косметологи, они говорят: «Хотите быть красивой?» Что надо для этого сделать? Чтобы личико всегда имело здоровый розовый цвет, необходимо улучшить кровоток в тканях лица. Таким образом, обеспечивается доставка питательных веществ, кислорода и в итоге усиливаются обменные процессы, накапливается белок в тканях, т.е. строительный материал для молодых клеток. По этому же принципу осуществляется лечение магнитным полем трофических язв, дряблости кожи и пр. Кстати, существуют методики электромагнитного стимулирования по формированию красивых, рельефных мышц. В то же время наблюдается противовоспалительный эффект магнитного поля. Однако в первую очередь магнитное поле влияет на форменные элементы крови. Ведь именно они и создают так называемый иммунитет. Причиной нарушений в иммунной системе организма являются нехватка форменных элементов крови, их плохое функционирование. Форменные элементы крови вырабатываются стволовыми клетками, которые располагаются в костях. В силу разных причин у каждого человека возникают проблемы с иммунитетом, а воздействие магнитным полем на области стволовых клеток позволяют увеличить количество вырабатываемых лимфоцитов и, следовательно, повысить иммунологический ответ организма. Расположение прибора в медальонной зоне, в месте традиционной китайской точки, которая ответственна за кроветворение, повышает иммунологическую реактивность. В чем же феномен этой зоны? Дело в том, что в медальонной зоне находится грудина. Это губчатая кость, где формируется большое количество стволовых клеток. Поэтому, воздействуя на эту зону, мы непосредственно стимулируем кроветворение и, соответственно, иммунитет.
В силу разных причин у каждого человека возникают проблемы с иммунитетом, а воздействие магнитным полем на области стволовых клеток позволяют увеличить количество вырабатываемых лимфоцитов и, следовательно, повысить иммунологический ответ организма. Расположение прибора в медальонной зоне, в месте традиционной китайской точки, которая ответственна за кроветворение, повышает иммунологическую реактивность. В чем же феномен этой зоны? Дело в том, что в медальонной зоне находится грудина. Это губчатая кость, где формируется большое количество стволовых клеток. Поэтому, воздействуя на эту зону, мы непосредственно стимулируем кроветворение и, соответственно, иммунитет.
Хочу обратить Ваше внимание, что при любом физиотерапевтическом воздействии крайне важна дозировка, т.к. результаты могут быть не только положительные, но и разрушительные для организма.
Для постоянного магнитного поля показательной величиной является напряженность порядка 1 мТл. 1 мТл – это та величина, которая уже вызывает значимые лечебные изменения на уровне тканей нашего организма, т.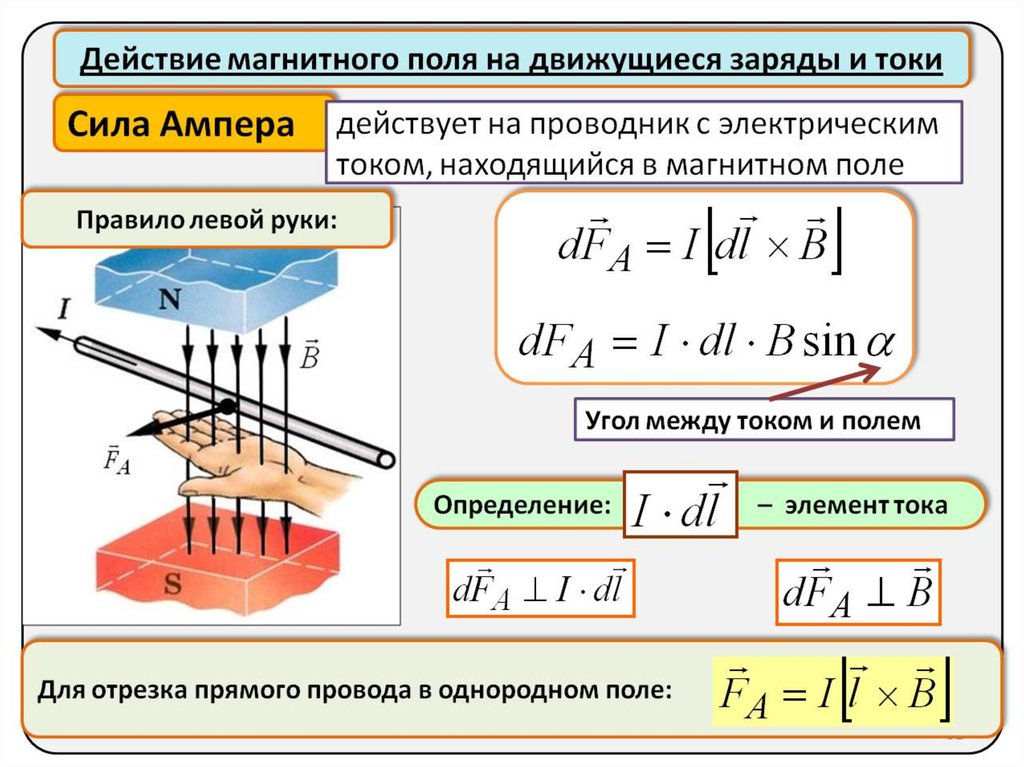 е. улучшения со стороны кроветворения, проведения нервных импульсов и пр. В изделиях фирмы НЕВОТОН напряженность магнитного поля составляет 12 мТл. Эта величина появилась не случайно. Т.к. напряженность магнитного поля падает пропорционально квадрату расстояния от прибора, то для локального воздействия она оптимальна. Официально Минздравом РФ разрешено применение гражданами в домашних условиях без контроля врача магнитных полей до 30 мТл. Однако, чем больше напряженность, тем более внимательно нужно следить за дозировкой. 12 мТл – это та величина, которая позволяет применение аппликатора без опасности передозировки: она не окажет повреждающего воздействия на человека, поле проникает в глубину в пределах нескольких сантиметров. Естественно, что при применении такого мягкого воздействия максимальный лечебный эффект проявится при воздействии на самые чувствительные точки, т.е. точки акупунктуры. Хотелось бы подчеркнуть мысль о том, что при воздействии слабым фактором организм к нему привыкает и перестает на него реагировать.
е. улучшения со стороны кроветворения, проведения нервных импульсов и пр. В изделиях фирмы НЕВОТОН напряженность магнитного поля составляет 12 мТл. Эта величина появилась не случайно. Т.к. напряженность магнитного поля падает пропорционально квадрату расстояния от прибора, то для локального воздействия она оптимальна. Официально Минздравом РФ разрешено применение гражданами в домашних условиях без контроля врача магнитных полей до 30 мТл. Однако, чем больше напряженность, тем более внимательно нужно следить за дозировкой. 12 мТл – это та величина, которая позволяет применение аппликатора без опасности передозировки: она не окажет повреждающего воздействия на человека, поле проникает в глубину в пределах нескольких сантиметров. Естественно, что при применении такого мягкого воздействия максимальный лечебный эффект проявится при воздействии на самые чувствительные точки, т.е. точки акупунктуры. Хотелось бы подчеркнуть мысль о том, что при воздействии слабым фактором организм к нему привыкает и перестает на него реагировать. Чтобы этого не происходило, чтобы организм постоянно реагировал на воздействие надо постоянно повышать дозу. Что такое доза? Это сила воздействия и время. Т.к. силу воздействия изменить мы не можем, увеличение дозировки производится за счет увеличения времени проведения процедуры. В нашем случае применение НЕВОТОНА мы рекомендуем начинать с 1,5 – 2 часов, через два-три дня увеличить дозу до 3-4 часов и т.д. Однако, когда проблема стоит остро, к примеру сильные боли, то аппликатор закрепляется на длительный срок 5-12 часов и боль проходит. Как долго необходимо пользоваться прибором? Реакция тренировки может формироваться в течение 15-20 процедур, максимум 25, поэтому постоянно носить аппарат нет необходимости. Через 20-30 дней обычно проводят повторный курс. При решении более сложных проблем курс лечения подобран для каждого заболевания индивидуально и указан в подробной инструкции. Поскольку применение НЕВОТОНА выполняет как профилактические, так и лечебные функции, то пользоваться прибором можно практически всю жизнь.
Чтобы этого не происходило, чтобы организм постоянно реагировал на воздействие надо постоянно повышать дозу. Что такое доза? Это сила воздействия и время. Т.к. силу воздействия изменить мы не можем, увеличение дозировки производится за счет увеличения времени проведения процедуры. В нашем случае применение НЕВОТОНА мы рекомендуем начинать с 1,5 – 2 часов, через два-три дня увеличить дозу до 3-4 часов и т.д. Однако, когда проблема стоит остро, к примеру сильные боли, то аппликатор закрепляется на длительный срок 5-12 часов и боль проходит. Как долго необходимо пользоваться прибором? Реакция тренировки может формироваться в течение 15-20 процедур, максимум 25, поэтому постоянно носить аппарат нет необходимости. Через 20-30 дней обычно проводят повторный курс. При решении более сложных проблем курс лечения подобран для каждого заболевания индивидуально и указан в подробной инструкции. Поскольку применение НЕВОТОНА выполняет как профилактические, так и лечебные функции, то пользоваться прибором можно практически всю жизнь.
«Наш курский чернозем может быть связан с магнитным полем»
Университетские спутники «ЮЗГУ-55», доставленные на МКС, позволят ученым создать точную карту магнитного поля Земли и, возможно, – разгадать секрет Курской магнитной аномалии, плотность поля которой может быть связана с особой плодородностью земли в регионе. Об этом «Газете.Ru» рассказал главный разработчик спутников. Аппараты будут отправлены в открытый космос в конце лета.
К МКС пристыковался грузовой корабль «Прогресс МС-19», запущенный 15 февраля. Он доставил 1600 кг аппаратуры и средств технического обслуживания бортовых систем станции, одежду и рационы питания для членов экипажа, а также полезную нагрузку для российских научных исследований. Среди оборудования для исследований находятся шесть кубсатов серии «ЮЗГУ-55», созданных НИИ космического приборостроения и радиоэлектронных систем Юго-западного государственного университета в городе Курск.
Кубсаты – это особый формат сверхмалых космических спутников. Их вес не должен превышать нескольких килограмм, а размер варьируется от 10х10х10 до 10х10х30 см, в зависимости от числа стандартных блоков в спутнике. Главным преимуществом кубсатов являются простота и низкая цена изготовления и вывода на орбиту, и потому их производство могут себе позволить учебные заведения и даже радиолюбители.
Их вес не должен превышать нескольких килограмм, а размер варьируется от 10х10х10 до 10х10х30 см, в зависимости от числа стандартных блоков в спутнике. Главным преимуществом кубсатов являются простота и низкая цена изготовления и вывода на орбиту, и потому их производство могут себе позволить учебные заведения и даже радиолюбители.
«Газета.Ru» поговорила с Егором Шиленковым, главным разработчиком аппаратов «ЮЗГУ-55», кандидатом технических наук, директором НИИ космического приборостроения и радиоэлектронных систем ЮЗГУ. Он рассказал о конструкции и назначении этих спутников.
close
100%
«На всех шести аппаратах установлены прецизионные сенсоры, так называемые цифровые компасы, или магнитометры, работающие в различных осях, – сообщил инженер. – С их помощью планируется измерение плотности магнитного поля на высоте полета МКС, это примерно 400 км. Как известно, в этом диапазоне высот магнитное поле довольно плотное».
Шиленков отметил, что эти кубсаты представляют из себя не просто набор спутников, а интеллектуальную группировку. Это означает, что аппараты автоматически обмениваются данными между собой без вмешательства наземных операторов.
Это означает, что аппараты автоматически обмениваются данными между собой без вмешательства наземных операторов.
В итоге группировка выступает как разнесенный датчик, который за счет одновременных измерений в разных точках орбиты позволяет получить особо точные данные о магнитном поле Земли.
В задачу «ЮЗГУ-55» входит лишь проведение измерений. Главный разработчик также рассказал, для чего нужны данные о магнитном поле:
«Поскольку наших спутников много, и их измерения будут особо точными, с их помощью мы будем строить подробные карты магнитного поля Земли. Эти карты позволят ученым оценивать риски для разных отраслей человеческой жизни, в том числе для космических полетов и земледелия: как известно, Курская область – это аграрный регион. Кроме того, эти данные будут интересны Министерству транспорта, в частности, для мониторинга воздушной обстановки. Грубо говоря, специалистам необходимо исследовать комплексное воздействие магнитосферы на человеческую деятельность, в этом заинтересована и Российская академия наук. »
»
Объясняя пользу изучения магнитного поля для земледелия, создатель кубсатов привел в примеры Курскую магнитную аномалию и черноземы Курской области. Известно, что плотность магнитного поля над аномалией в четыре раза больше, чем над Северным полюсом, а магнитное поле защищает растения от космической радиации.
«Наш курский чернозем может быть связан с магнитным полем, – существует такая гипотеза»,
– говорит Шиленков. В качестве антипода инженер приводит в пример Бразильскую магнитную аномалию, где магнитное поле ослаблено, и в результате местность является опасной для сельского хозяйства. Кубсаты «ЮЗГУ-55» позволят построить точную трехмерную карту магнитного поля Земли, что в дальнейшем даст возможность проверить гипотезу о связи магнитной аномалии и чернозема.
Звезда натянулась на соседку: найдены странные объекты, бросающие вызов науке
Астрономы обнаружили особый тип небольших, но сверхгорячих звезд, внешне покрытых углеродом и кислородом…
15 февраля 11:33
Итоговая группировка «ЮЗГУ-55» будет состоять из восьми аппаратов, дополнительные два кубсата доставит на МКС другой корабль снабжения в июне. После этого в августе или сентябре космонавт Олег Артемьев запустит их в открытый космос, где они просуществуют около полутора лет. Чтобы аппараты не мешали МКС после окончания срока службы, они оборудованы специальным тормозом, который ускорит сведение кубсатов с орбиты.
После этого в августе или сентябре космонавт Олег Артемьев запустит их в открытый космос, где они просуществуют около полутора лет. Чтобы аппараты не мешали МКС после окончания срока службы, они оборудованы специальным тормозом, который ускорит сведение кубсатов с орбиты.
Проект «Радиоскаф» длится уже более 15 лет. В первую очередь, он служит образованию и популяризации исследований космоса. «Роскосмос» задумал этот проект для привлечения молодежи и школьников к науке. Именно поэтому к созданию кубсатов «ЮЗГУ-55» активно привлекались студенты и аспиранты университета, а также школьники, которые записали послание для радиолюбителей.
Как рассказал Шиленков, это послание будет непрерывно транслироваться с орбиты на выделенных частотах и его сможет услышать любой желающий.
МИЛИТЕРА —[ Военная альтернатива ]
Получение в лабораторной обстановке сверхсильных магнитных полей невольно порождает мысль об использовании их в обороне страны. Забегая на много лет вперед, когда, быть может, будут созданы магниты огромной, фантастической силы, можно высказать некоторые предположения о способах применения их в условиях обороны.
Для того, чтобы уяснить, на чем основаны наши предположения, вспомним механику действия магнитного поля. Возьмем подковообразный магнит и железную палочку. Начнем двигать палочкой так, чтобы она при своем движении пересекала магнитные силовые линии, которые расположены в пространстве между полюсами. Нетрудно убедиться, что магнит противодействует движению железной палочки. Тормозящее действие магнитного поля будет тем больше, чем сильнее магнит и чем быстрее движение палочки.
Вместо железной палочки возьмем ртутный термометр и начнем его так же быстро двигать в магнитном поле. Если магнит сильный и термометр движется достаточно быстро, то магнит и на этот раз будет тормозить движение металлического предмета (ртутный шарик в термометре). Кроме того, во время движения термометр несколько нагреется.
Можно сделать вывод, что магнитное поле стремится тормозить движение металлических предметов, особенно железных и стальных. При этом металлические тела во время движения в магнитном поле нагреваются.
Эти действия магнитного поля на металлические предметы тем сильнее, чем больше сила магнита. Техника получения постоянных магнитов большой силы в данное время сделала большие успехи, но принципиально с помощью электромагнитов можно получить гораздо более мощные магнитные поля, чем при помощи постоянных магнитов.
Как же эти свойства магнитного поля можно использовать, например, в обороне укрепленного района?
Представим себе мощные электромагниты, расположенные под землей на подступах к укрепленному району.
Сверхсильный электромагнит располагается под землей на подступах к укрепленному району. Он создает над поверхностью земли магнитное поле огромной силы. Танки, врываясь на полном ходу в зону действия магнита, испытывают резкое торможение, равносильное удару по ним, и выходят из строя. Такой же магнитный удар испытывают и снаряды, залетающие в магнитное поле. Они рвутся раньше срока и не долетают до цели.
Питание электромагнита осуществляется импульсным генератором, который соединен подземным кабелем с электросиловой сетью. Чувствительный механизм, расположенный также под землей, при прохождении над ним автомашин, танков и т. п. автоматически включает импульсный генератор. Генератор посылает ток в обмотки электромагнита, вследствие чего на пути следования танков устанавливается мощное магнитное поле.
Чувствительный механизм, расположенный также под землей, при прохождении над ним автомашин, танков и т. п. автоматически включает импульсный генератор. Генератор посылает ток в обмотки электромагнита, вследствие чего на пути следования танков устанавливается мощное магнитное поле.
Любой движущийся экипаж — автомобиль, танк, бронеавтомобиль, — обладающий большой железной массой, проходя в сфере действия электромагнита, испытывает его тормозящее действие. Оно может проявиться различно. Например, танк на малой скорости может быть сразу остановлен магнитным полем. Если же танк идет полным ходом и вследствие этого имеет большую кинетическую энергию, то он может по инерции проскочить сферу действия электромагнита, испытав при этом большое замедление скорости. Но большое замедление скорости равносильно удару по танку, и тем большей силы, чем больше замедление. Экипаж танка будет с силой отброшен к передней стенке, а двигатели, вращаясь по инерции, порвут сцепление. Танк выйдет из строя.
Что произойдет со снарядами и пулями, которые будут пролетать в зоне действия магнитного поля?
Снаряд, влетая в магнитное поле, также испытает его тормозящее действие, которое будет равносильно удару по снаряду. Но различные типы снарядов будут по-разному реагировать на такой магнитный «удар». Снаряды, которые рвутся через определенные дистанции или имеют взрыватели замедленного действия, испытав тормозящее действие магнитного поля, упадут, не достигнув цели, а снаряды, которые взрываются от удара, пролетая магнитное поле, будут взрываться преждевременно.
Невозможна будет и пристрелка снарядами, которые на своем пути пересекают сферу действия мощного электромагнита, так как снаряды будут разрываться в одном и том же месте, недалеко от электромагнита.
Если магнитное поле тормозит движение снаряда, то в еще большей мере оно будет тормозить полет пули. И это понятно: кинетическая энергия летящей пули значительно меньше, чем энергия снаряда в полете. Поэтому при вполне определенной силе магнитного поля возможны полная остановка пули и ее падение на землю тут же, около электромагнита.
Таким образом, сверхмощное магнитное поле образует как бы невидимую стену, о которую разбиваются танки противника и которая ограждает обороняющиеся части от артиллерийского и пулеметного огня.
Расположив в соответствующих местах электромагниты, можно с их помощью обеспечить надежную защиту наиболее важных объектов обороны.
Танк смерти: Советская оборонная фантастика 1928-1940 / Сост. М. Фоменко. — Б. м.: Salamandra P.V.V., 2015. — 223 c., илл. — (Polaris: Путешествия, приключения, фантастика. Вып. XC).
Сильнейшие магнитные поля во Вселенной: насколько сильными они могут стать?
1. Введение
Крупномасштабная динамика Вселенной определяется общим космическим расширением и гравитационным полем массивных объектов. Считается, что в первом магнитные поля не играют существенной роли [1, 2]. Считается, что магнитные поля не присутствовали или, по крайней мере, не имели заметной силы при Большом взрыве и в последующий инфляционный период. Если они и присутствовали, то в виде ложных магнитных монополей. Они становятся важными в меньших масштабах. В масштабах компактных намагниченных объектов они начинают становиться непренебрежимо малыми, а для ряда процессов [3] даже становятся доминирующей силой.
Они становятся важными в меньших масштабах. В масштабах компактных намагниченных объектов они начинают становиться непренебрежимо малыми, а для ряда процессов [3] даже становятся доминирующей силой.
Магнитные поля связаны с протеканием электрического тока и поэтому, в отличие от электрических полей, источниками которых являются элементарные заряды и разности зарядов, генерируются процессами, вызывающими электрические токи. Токи предполагают неамбиполярный перенос зарядов. Таким образом, вопрос о том, насколько сильными могут быть магнитные поля, сводится к вопросу о том, насколько сильными могут стать любые токи. В классической электродинамике из закона Ампера для стационарных магнитных полей следует, что
∇×B=µ0J, J=e(NiVi−NeVe)≈−eN(Ve−Vi)(1)
, если ограничиться только переносом заряда и принять немагнитные среды (для простоты однозарядные) ионов и электронов плотности и объемные скорости N i,e , V i,e соответственно. В противном случае можно было бы добавить член намагниченности M , который зависит от свойств материи. Определение M требует квантово-механической обработки в рамках физики твердого тела.
В противном случае можно было бы добавить член намагниченности M , который зависит от свойств материи. Определение M требует квантово-механической обработки в рамках физики твердого тела.
Предполагая без ограничений квазинейтральность N e ≈ N i = N , вклад вносят только разности скоростей. Поскольку электроны значительно более подвижны, чем ионы, ток можно разумно аппроксимировать электронным током Дж ≈ — eN В e , условие строго выполняется в ионной системе отсчета. Поскольку скорости ограничены скоростью света c , магнитное поле классически ограничено величиной
∇×B<μ0eNc, или B<μ0eNcL≈6×10−8NccLkm(2)
, что позволяет предположить, что магнитное поле растет с плотностью 10 0 11 л л 900 и Здесь N куб.см выражено в электронах на см -3 , а L км — масштаб длины нити тока в единицах км. В коре нейтронной звезды, например, мы имеем L км ~ 1. Если бы примерно все электроны в коре участвовали в протекании тока, мы имели бы N куб.см × ~ 10 30 . Следовательно, напряженность магнитного поля может достигать B ~ 10 28 Гаусс, огромное число по сравнению с максимальным значением B ~ 10 15 − 10 16 Гаусс, наблюдаемым в магнетарах.
В коре нейтронной звезды, например, мы имеем L км ~ 1. Если бы примерно все электроны в коре участвовали в протекании тока, мы имели бы N куб.см × ~ 10 30 . Следовательно, напряженность магнитного поля может достигать B ~ 10 28 Гаусс, огромное число по сравнению с максимальным значением B ~ 10 15 − 10 16 Гаусс, наблюдаемым в магнетарах.
Эту приблизительную оценку необходимо прокомментировать во избежание недоразумений. Считается, что магнитные поля генерируются преимущественно действием динамо-машины. Такие действия предположительно не действуют в белых карликах, нейтронных звездах, магнетарах или любых других компактных объектах. Поля производятся в их дифференциально вращающихся прародителях. Возьмем в качестве примера Солнце с динамо-действием в зоне конвекции толщиной L ☉ ~ 2 × 10 5 км и средней плотности N ☉ куб. см ~ 8 × 10 23 90. Использование общей ширины зоны конвекции сильно завышает текущую ширину нити. Абсолютный верхний предел составит л ☉ км ≲ 2 × 10 4 . Ясно, что скорости также намного меньше, чем c . Таким образом, использование c дает крайний абсолютный верхний предел магнитного поля B < 10 21 T. Сравнительно сильные поля в нейтронных звездах возникают впоследствии при быстром коллапсе намагниченной тяжелой звезды-прародителя, не успевшей за время коллапса рассеять магнитную энергию, которая сжимается в крошечные объем нейтронной звезды. Коэффициент сжатия порядка ~ 10 12 , что дает предельные поля B ≲ 10 35 Гаусса. Классическая электродинамическая оценка явно не дает верхнего предела напряженности магнитного поля, который соответствовал бы данным наблюдений.
см ~ 8 × 10 23 90. Использование общей ширины зоны конвекции сильно завышает текущую ширину нити. Абсолютный верхний предел составит л ☉ км ≲ 2 × 10 4 . Ясно, что скорости также намного меньше, чем c . Таким образом, использование c дает крайний абсолютный верхний предел магнитного поля B < 10 21 T. Сравнительно сильные поля в нейтронных звездах возникают впоследствии при быстром коллапсе намагниченной тяжелой звезды-прародителя, не успевшей за время коллапса рассеять магнитную энергию, которая сжимается в крошечные объем нейтронной звезды. Коэффициент сжатия порядка ~ 10 12 , что дает предельные поля B ≲ 10 35 Гаусса. Классическая электродинамическая оценка явно не дает верхнего предела напряженности магнитного поля, который соответствовал бы данным наблюдений.
Другие не менее серьезные расхождения получаются, если положить энергию магнитного поля нейтронной звезды равной полной доступной энергии вращения как в прародителе, так и в нейтронной звезде, предполагая равное распределение вращательной и магнитной энергии — явно мало обоснованное предположение в обоих случаях. Магнитная энергия не может стать больше, чем первоначально доступная динамическая энергия ее причины, частью которой она является. По-видимому, принципиально сомнительно, чтобы магнитные поля когда-либо создавались каким-либо классическим механизмом, значительно более сильным, чем наблюдаемые в нейтронных звездах (за исключением короткой фазы динамо-усиления после коллапса продолжительностью ~ 10 с, в лучшем случае дающей еще один множитель ~ 10–10). 100 [8]) и, за счет дальнейшей концентрации магнитной энергии в меньших объемах, группирования магнитных силовых трубок, как считается, происходит в магнетарах. Если вообще генерировались гораздо более сильные поля, то это должно было происходить во времена и в объектах, где магнитные поля могли создаваться процессами, отличными от классического динамо. Таким образом, нужно войти в квантовую электродинамику, соответственно квантовую теорию поля, чтобы сделать вывод о принципиальные физические ограничения на генерацию любых магнитных полей.
Магнитная энергия не может стать больше, чем первоначально доступная динамическая энергия ее причины, частью которой она является. По-видимому, принципиально сомнительно, чтобы магнитные поля когда-либо создавались каким-либо классическим механизмом, значительно более сильным, чем наблюдаемые в нейтронных звездах (за исключением короткой фазы динамо-усиления после коллапса продолжительностью ~ 10 с, в лучшем случае дающей еще один множитель ~ 10–10). 100 [8]) и, за счет дальнейшей концентрации магнитной энергии в меньших объемах, группирования магнитных силовых трубок, как считается, происходит в магнетарах. Если вообще генерировались гораздо более сильные поля, то это должно было происходить во времена и в объектах, где магнитные поля могли создаваться процессами, отличными от классического динамо. Таким образом, нужно войти в квантовую электродинамику, соответственно квантовую теорию поля, чтобы сделать вывод о принципиальные физические ограничения на генерацию любых магнитных полей.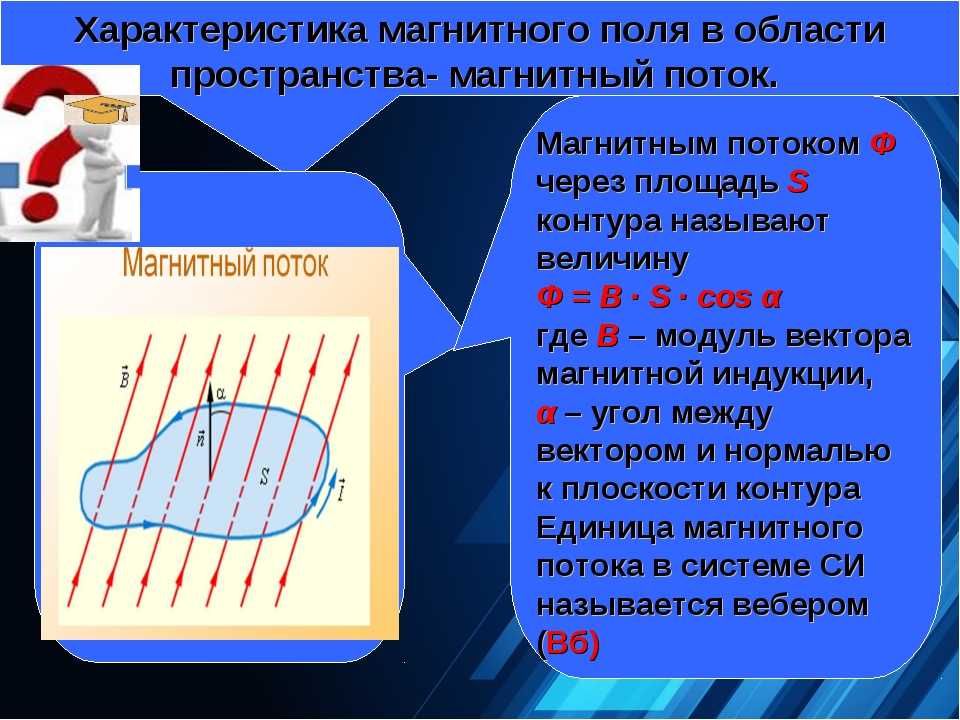 Следующее исследование мотивировано не столько наблюдениями, сколько этим фундаментальным теоретическим вопросом.
Следующее исследование мотивировано не столько наблюдениями, сколько этим фундаментальным теоретическим вопросом.
2. Элементы потока
Квантовая механика позволяет получить первое ограничение на магнитное поле из решения уравнения Шредингера, первоначально найденного Ландау [4] в 1930 году, для электрона, вращающегося по орбите в однородном магнитном поле. Физическая интерпретация этого решения была дана значительно позже в теории Ааронова-Бома [5]. Из требования, чтобы магнитный поток Ф поля B , удерживаемый на орбите вращения электрона, должен быть однозначным, Ааронов и Бом сделали вывод, что Φ = ν Φ 0 квантуется с элементом потока Φ 0 = 2πħ/e, e — элементарный заряд, а ν = 1, 2, …. Поскольку ν = Φ/Φ 0 — число элементарных потоков, переносимых полем, а B = Φ/π l 2 , полагая ν = 1, мы определяем наименьшую магнитную длину
ℓB=(Φ0πB )12=(2ℏeB)12(3)
Эту длину, представляющую собой гирорадиус электрона на низшем энергетическом уровне Ландау, можно интерпретировать как радиус линии магнитного поля в магнитном поле Б . Силовые линии становятся уже, чем сильнее магнитное поле. С другой стороны, переписывая уравнение (3), получаем выражение для магнитного поля
Силовые линии становятся уже, чем сильнее магнитное поле. С другой стороны, переписывая уравнение (3), получаем выражение для магнитного поля
Bc=2ℏeℓc2(4)
, из которого для данной кратчайшей «критической» длины l B ≡ l c максимальное магнитное поле B c , соответствующее l c , в принципе можно оценить. Ставим, например, л с = 2πħ/ MC , равная длине электрона Compton λ 0 = 2πħ/ MC , один получает критический пульсар (нейтронная звезда). 3 × 10 9 T = 3 × 10 13 Гаусс. Представляет значительный интерес тот факт, что примерно такая напряженность поля была действительно получена из наблюдения основной (ν = 1) электронной циклотронной рентгеновской линии, обнаруженной пульсаром HerX1 [7], примерно через два десятилетия после Ааронова и Бома, и через полвека. столетие после теории Ландау.
3. Обобщение
Использование длины волны Комптона связывает предельную напряженность поля в нейтронных звездах с квантовой электродинамикой. Это ставит вопрос о более точном теоретическом определении квантовой электродинамической предельной напряженности поля с учетом релятивистских эффектов. Это также поднимает вопрос, может ли ссылка на другие фундаментальные масштабы длины дать другие принципиальные ограничения на магнитные поля, если только такие поля могут быть созданы каким-либо образом, т. Е. Если электрические токи достаточной силы могут протекать при других условиях, как, например, в квантовой хромодинамике. .
Очень формально, за исключением учета релятивистских эффектов, уравнение (4) дает модельное уравнение для предельного поля в зависимости от любого заданного фундаментального масштаба длины l c . При этом упрощающем предположении критическое магнитное поле B c масштабируется просто обратно пропорционально квадрату соответствующей фундаментальной длины.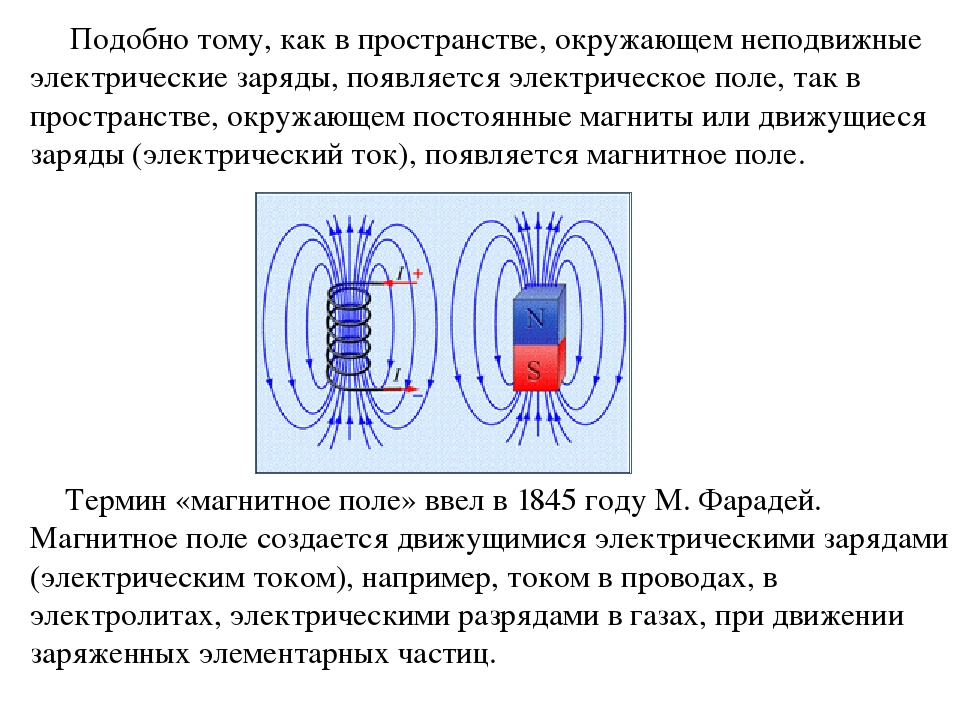 Формально это графически показано на рис. 1 в предположении справедливости скейлинга Ааронова-Бома при более высоких энергиях.
Формально это графически показано на рис. 1 в предположении справедливости скейлинга Ааронова-Бома при более высоких энергиях.
Рис. 1. Логарифмическое масштабирование максимально возможной напряженности магнитного поля, B c , нормированное к (фиктивному) планковскому магнитному полю, B Pl , как функция масштабов фундаментальной длины на основе уравнения (3) . Масштабы длины l по оси абсцисс нормированы на планковскую длину l Pl . Красный пунктирный крест указывает точку пересечения комптоновской длины с линией критического магнитного поля Ааронова-Бома в так называемом квантовом предельном поле B q ≈ 10 9 Тл, критическое поле замагниченных нейтронных звезд (пульсаров) согласуется с наблюдением сильнейших циклотронных линий. Горизонтальные линии показывают связь между другими шкалами длины и критическими магнитными полями при допущении справедливости шкалы Ааронова-Бома. Космические магнитные поля соответствуют масштабам ~ 1 мм. Сильнейшие обнаруженные магнитарные поля соответствуют релятивистской поправке первого порядка на самом низком уровне Ландау с энергией E LLL (показан в виде графика справа с α = α/2π приведенной постоянной тонкой структуры). Включение поправок более высокого порядка позволило бы учитывать поля до B qed ~ 10 28 Тл глубоко в (заштрихованной) релятивистской области, которые не наблюдались. Интересно, что этот предел примерно совпадает с измеренным [6] абсолютным верхним пределом на радиус электрона (вертикальная синяя пунктирная линия). В масштабах ТВО поля теоретически могут достигать значений ~ 10 45 T, по простой шкале Ааронова-Бома. Черная пунктирная кривая указывает на возможное отклонение скейлинга Ааронова-Бома вблизи квантового электродинамического предела.
Космические магнитные поля соответствуют масштабам ~ 1 мм. Сильнейшие обнаруженные магнитарные поля соответствуют релятивистской поправке первого порядка на самом низком уровне Ландау с энергией E LLL (показан в виде графика справа с α = α/2π приведенной постоянной тонкой структуры). Включение поправок более высокого порядка позволило бы учитывать поля до B qed ~ 10 28 Тл глубоко в (заштрихованной) релятивистской области, которые не наблюдались. Интересно, что этот предел примерно совпадает с измеренным [6] абсолютным верхним пределом на радиус электрона (вертикальная синяя пунктирная линия). В масштабах ТВО поля теоретически могут достигать значений ~ 10 45 T, по простой шкале Ааронова-Бома. Черная пунктирная кривая указывает на возможное отклонение скейлинга Ааронова-Бома вблизи квантового электродинамического предела.
Комптоновский предел магнитных полей был известен из прямых энергетических соображений [ср. например, 8 для обзора], которые предсказывают распад вакуума до образования пар в магнитных полях сильнее, чем B нс . По этой причине обнаружение магнитных полей, превышающих квантовый предел до трех порядков в магнетарах, было первоначальным сюрпризом. Однако более точные релятивистские электродинамические расчеты, включая графики Фейнмана более высокого порядка, легко показали, что предел Комптона вполне может быть превышен. В первом приближении по аномальному магнитному моменту электронов [9] низший уровень Ландау смещается согласно
например, 8 для обзора], которые предсказывают распад вакуума до образования пар в магнитных полях сильнее, чем B нс . По этой причине обнаружение магнитных полей, превышающих квантовый предел до трех порядков в магнетарах, было первоначальным сюрпризом. Однако более точные релятивистские электродинамические расчеты, включая графики Фейнмана более высокого порядка, легко показали, что предел Комптона вполне может быть превышен. В первом приближении по аномальному магнитному моменту электронов [9] низший уровень Ландау смещается согласно
ELLL≈mc2(1−α¯B/Bq)12(5)
с α = α/2π приведенной постоянной тонкой структуры. Эта формула действительна для B < B q . Это предполагает уменьшение нижнего уровня энергии Ландау для увеличения полей, очевидно, с сильными нефизическими последствиями для астрофизических объектов [10]. Таким образом, необходимо учитывать диаграммы Фейнмана, включающие самопритяжение электронов высших порядков, особенно при больших полях.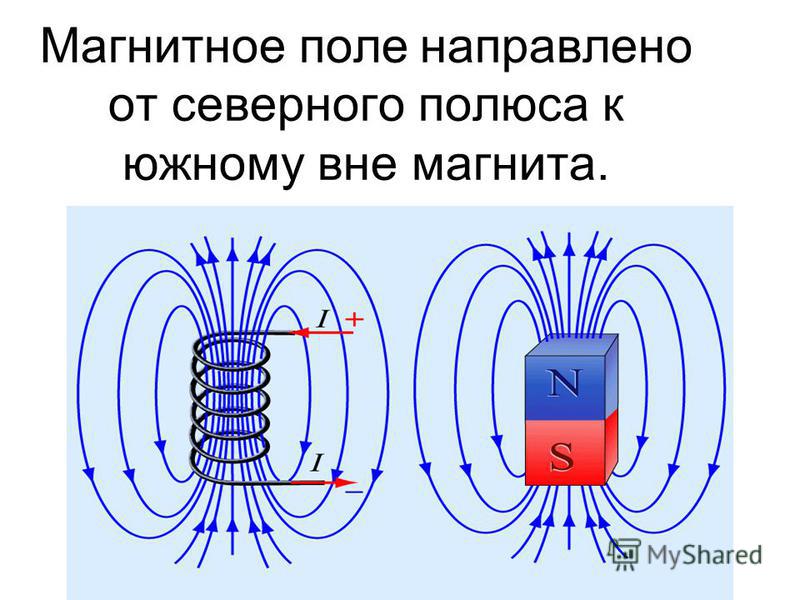 В полях B ≫ B q существенно превышающих B q , электроны становятся релятивистски массивными, а нижний уровень Ландау после прохождения минимума возрастает [11, 12] как
В полях B ≫ B q существенно превышающих B q , электроны становятся релятивистски массивными, а нижний уровень Ландау после прохождения минимума возрастает [11, 12] как
ELLL≈mc + α¯[log2BBq−2,077]2+3,9α¯}, B≫Bq(6)
Отсюда следует, что энергия нижнего уровня Ландау удваивается только при магнитных полях порядка B ~ 10 28 T (~ 10 32 Гаусса), намного выше магнитных полей поверхности любой нейтронной звезды или магнетара. Таким образом, релятивистские поправки на собственную энергию, вызывающие затухание магнитного поля, будут действовать только при этих энергиях, которые могут быть окончательным пределом напряженности магнитного поля.
Примечательно, что этот предел примерно совпадает с лучшими последними экспериментальными определениями верхнего предела радиуса электрона [6]. Ниже этой шкалы должны проявляться дополнительные эффекты, в основном препятствующие дальнейшему увеличению напряженности магнитного поля или даже существованию магнитных полей. Таким образом, кажется, что до этого масштаба масштаб Ааронова-Бома, на котором основан рисунок 1, не является полностью необоснованным. Это наиболее интересно еще и с той точки зрения, что шкалы как электрослабого, так и сильного взаимодействия находятся в разрешенной области просто потому, что электроны сохраняют свою природу во всех этих шкалах. Исключается только пустынный диапазон энергий соответственно масштабов. Он включает в себя, в частности, диапазон великого объединения ТВО, а также квантовую гравитацию, области, которые играли роль только в очень ранней Вселенной. Любые рудиментарные магнитные поля того времени были разбавлены инфляцией и космологическим расширением только до низких значений [1, 2], расположенных внизу рисунка 1.
Таким образом, кажется, что до этого масштаба масштаб Ааронова-Бома, на котором основан рисунок 1, не является полностью необоснованным. Это наиболее интересно еще и с той точки зрения, что шкалы как электрослабого, так и сильного взаимодействия находятся в разрешенной области просто потому, что электроны сохраняют свою природу во всех этих шкалах. Исключается только пустынный диапазон энергий соответственно масштабов. Он включает в себя, в частности, диапазон великого объединения ТВО, а также квантовую гравитацию, области, которые играли роль только в очень ранней Вселенной. Любые рудиментарные магнитные поля того времени были разбавлены инфляцией и космологическим расширением только до низких значений [1, 2], расположенных внизу рисунка 1.
4. Обсуждение и выводы
Если бы во Вселенной не существовало и не сохранилось магнитных монополей, то магнитные поля в любое время должны были создаваться путем генерации электрических токов. Поля, созданные в ранней Вселенной, впоследствии были разбавлены до сегодняшних низких крупномасштабных значений, как обсуждалось в других работах [1, 2]. Они могли быть сильными изначально, и в этом случае их сильные стороны также могут быть ограничены. Однако все разумные силы, оцененные по динамо и другим моделям в классической и хромодинамической теориях [1], скорее всего, не достигают ни одного из указанных квантово-электродинамических пределов. По-видимому, нет необходимости призывать к дополнительным хромодинамическим ограничениям. Это утверждение может быть основано на роли электронов в генерации тока, которая лежит в основе любого крупномасштабного производства магнитного поля. Электроны и их спины также ответственны за магнетизм в твердом веществе. До сих пор считается, что электроны не имеют структуры. Во всяком случае, на масштабах «внутри» электрона, т. е. ниже фиктивного радиуса электрона r e , токи должны либо утратить всякий смысл, либо вообще не существовать и, следовательно, понятие магнитного поля, вероятно, уже не будет иметь особого смысла. Таким образом, можно полагать, что верхний квантово-электродинамический предел устанавливает абсолютную границу любой реалистичной напряженности магнитного поля.
Они могли быть сильными изначально, и в этом случае их сильные стороны также могут быть ограничены. Однако все разумные силы, оцененные по динамо и другим моделям в классической и хромодинамической теориях [1], скорее всего, не достигают ни одного из указанных квантово-электродинамических пределов. По-видимому, нет необходимости призывать к дополнительным хромодинамическим ограничениям. Это утверждение может быть основано на роли электронов в генерации тока, которая лежит в основе любого крупномасштабного производства магнитного поля. Электроны и их спины также ответственны за магнетизм в твердом веществе. До сих пор считается, что электроны не имеют структуры. Во всяком случае, на масштабах «внутри» электрона, т. е. ниже фиктивного радиуса электрона r e , токи должны либо утратить всякий смысл, либо вообще не существовать и, следовательно, понятие магнитного поля, вероятно, уже не будет иметь особого смысла. Таким образом, можно полагать, что верхний квантово-электродинамический предел устанавливает абсолютную границу любой реалистичной напряженности магнитного поля.
Применение масштабирования Ааронова-Бома на Рисунке 1 к магнитным полям во Вселенной, по-видимому, дает разумное представление об ожидаемых абсолютных ограничениях напряженности магнитного поля на квантово-электродинамических шкалах. Ясно, что вакуум меняет свой характер на малых масштабах и высоких энергиях, поскольку фотоны становятся тяжелыми, переключаясь на электрослабые бозоны, а в материю вступают в игру кварки. Электроны остаются неизменными, по крайней мере, до r e ~ 10 −22 м, текущий верхний предел радиуса электрона [6]. Это предлагает записать уравнение критического магнитного поля (4) как
Bc(ℓc)=Bmax/[1+(ℓc/ℓ0−1)2], Bmax=2ℏ/eℓ02(7)
, где l c ≥ l 0 и l 0 ≳ r e – соответствующая минимальная длина, выше которой магнитные поля имеют смысл. На рис. 1 это поведение обозначено пунктирной черной кривой, отклоняющейся от диагонали. Однако устойчивость вакуума не столь очевидна, как в квантово-электродинамическом диапазоне при наличии сверхсильных магнитных полей в электрослабом и хромодинамическом диапазонах. Проблема остается в том, что магнитные поля должны генерироваться либо в этих малых масштабах, либо в гораздо больших электродинамических масштабах, от которых они коллапсируют до этих малых масштабов.
Однако устойчивость вакуума не столь очевидна, как в квантово-электродинамическом диапазоне при наличии сверхсильных магнитных полей в электрослабом и хромодинамическом диапазонах. Проблема остается в том, что магнитные поля должны генерироваться либо в этих малых масштабах, либо в гораздо больших электродинамических масштабах, от которых они коллапсируют до этих малых масштабов.
Что касается генерации магнитных полей до коллапса с помощью общепринятых эффектов динамо или батареи, напряженность магнитного поля строго ограничена доступной динамической энергией, которая намного ниже любого квантово-электродинамического предела. Можно утверждать, что до тех пор, пока шкала радиуса электрона не достигается во время коллапса, квантовое электродинамическое масштабирование обеспечивает разумное абсолютное ограничение на любую возможную напряженность магнитного поля. Нейтронные звезды и магнетары имеют масштабы, значительно превышающие электронные масштабы. Более тяжелые объекты при уменьшении их масштаба могли бы обладать значительно более сильными полями, но допустимый диапазон сужается из-за того, что такие объекты при коллапсе легко становятся черными дырами, которые, согласно знаменитой теореме об отсутствии волос, не содержат никаких магнитных полей. Неизвестно, что произойдет с полем при пересечении горизонта, поскольку никакая информация о поле не останется для внешнего наблюдателя. Теорема об отсутствии волос предполагает, что поле просто засасывается в дыру и исчезает вместе с коллапсирующей массой. Обычное рассуждение, предполагающее сохранение вмороженного состояния, затем предполагает, что поле внутри горизонта должно еще больше возрасти в предположительно продолжающемся гравитационном коллапсе.
Неизвестно, что произойдет с полем при пересечении горизонта, поскольку никакая информация о поле не останется для внешнего наблюдателя. Теорема об отсутствии волос предполагает, что поле просто засасывается в дыру и исчезает вместе с коллапсирующей массой. Обычное рассуждение, предполагающее сохранение вмороженного состояния, затем предполагает, что поле внутри горизонта должно еще больше возрасти в предположительно продолжающемся гравитационном коллапсе.
Доступные сильные поля, приближающиеся к квантовым электродинамическим пределам, обнаружены в нейтронных звездах и магнетарах. До сих пор никаких странных магнитных полей звезд не обнаружено. Было даже показано [13], что такие поля, возможно, присутствующие в сверхпроводящих странных звездах, будут вращательно затухать за времена, меньшие ~20 млн лет. В магнетарах присутствие полей сильнее, чем B ns = B q , в настоящее время хорошо изучено [обзор многих аспектов см., 8] как следствие коровых эффектов, вызывающих локальную концентрацию магнитных полей. и протяженные магнитные петли, имеющие некоторое сходство с известными солнечными пятнами [см. также сборник статей в 3]. Воздействие на вещество в сверхсильных полях впервые было исследовано Рудерманом [14] и рассмотрено в [15, 16] и других.
и протяженные магнитные петли, имеющие некоторое сходство с известными солнечными пятнами [см. также сборник статей в 3]. Воздействие на вещество в сверхсильных полях впервые было исследовано Рудерманом [14] и рассмотрено в [15, 16] и других.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Ссылки
1. Widrow LM, Ryu D, Schleicher DRG, Subramanian K, Tsagas CG, Treumann RA. Первые магнитные поля. Космическая наука, версия . (2012) 116 : 37–70. doi: 10.1007/s11214-011-9833-5
CrossRef Полный текст | Академия Google
2. Ryu D, Schleicher DRG, Treumann RA, Tsagas CG, Widrow LM. Магнитные поля в крупномасштабной структуре Вселенной. Космическая наука, версия . (2012) 166 : 1–35. doi: 10.1007/s11214-011-9839-z
CrossRef Полный текст | Google Scholar
3. Балог А., Бескин В.С., Фаланга М., Лютиков М., Мерегетти С., Пиран Т. Сильнейшие магнитные поля во Вселенной, ISSI Space Science Series . Нью-Йорк, штат Нью-Йорк: Springer (в печати).
Балог А., Бескин В.С., Фаланга М., Лютиков М., Мерегетти С., Пиран Т. Сильнейшие магнитные поля во Вселенной, ISSI Space Science Series . Нью-Йорк, штат Нью-Йорк: Springer (в печати).
4. Ландау Л. Диамагнетизм металла. Z. Physik (1930) 64 : 629–37. doi: 10.1007/BF01397213
Google Scholar
5. Ааронов Ю., Бом Д. Значение электромагнитных потенциалов в квантовой теории. Физика, версия . (1959) 115 : 485–91. doi: 10.1103/PhysRev.115.485
CrossRef Полный текст | Google Scholar
6. Габриэль Г., Ханнеке Д., Киношита Т., Нио М., Одом Б. Новое определение постоянной тонкой структуры электрона г Значение и QED. Phys Rev Lett . (2006) 97 :030802. doi: 10.1103/PhysRevLett.97.030802
Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar
7. Трюмпер Дж., Питч В., Реппин С., Сакко Б. Доказательства сильного циклотронного излучения в жестком рентгеновском спектре Her X-1 (Восьмой Техасский симпозиум по релятивистской астрофизике).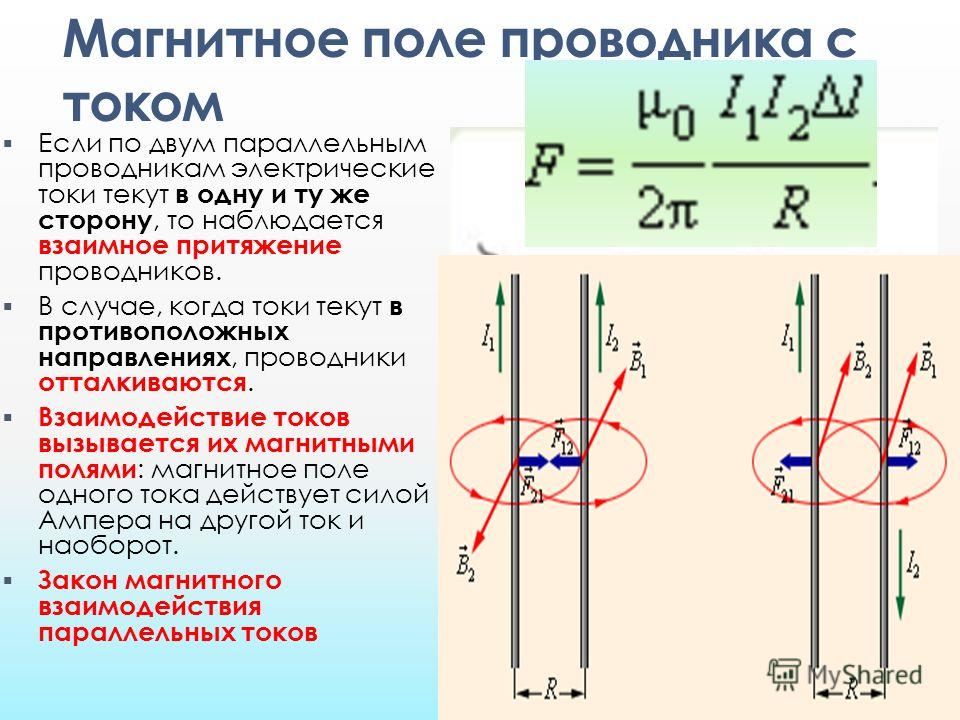 Ann NY Acad Sci . (1977) 302 : 538–44. doi: 10.1111/j.1749-6632.1977.tb37072.x
Ann NY Acad Sci . (1977) 302 : 538–44. doi: 10.1111/j.1749-6632.1977.tb37072.x
Полнотекстовая перекрестная ссылка | Google Scholar
8. Дункан Р.С. Физика в сверхсильных магнитных полях. В: Гамма-всплески, 5-й Хантсвиллский симпозиум , Vol. 526, Хантсвилл, Алабама (2000). п. 830–41.
Опубликован Аннотация | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar
9. Швингер Дж. Квантово-электродинамика и магнитный момент электрона. Физика, версия . (1948) 73 : 416–7. doi: 10.1103/PhysRev.73.416
CrossRef Полный текст | Академия Google
10. Чиу Х.Л., Кануто В. Проблемы интенсивных магнитных полей при гравитационном коллапсе. Астрофиз J . (1968) 153 : 157–61. doi: 10.1086/180243
CrossRef Полный текст | Google Scholar
11. Янковичи Б. Радиационная поправка к энергии основного состояния электрона в сильном магнитном поле. Физика, версия . (1969) 187 : 2275–6. doi: 10.1103/PhysRev.187.2275
Физика, версия . (1969) 187 : 2275–6. doi: 10.1103/PhysRev.187.2275
CrossRef Полный текст | Google Scholar
12. Гепрегс Р., Рифферт Х., Герольд Х., Рудер Х., Вуннер Г. Собственная энергия электрона в однородном магнитном поле. Phys Rev D (1994) 49 :5582–9. doi: 10.1103/PhysRevD.49.5582
Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar
13. Чау Х.Ф. Об эволюции вращения и магнитного поля сверхпроводящих странных звезд. Астрофиз J . (1997) 479 : 886–901. doi: 10.1086/303898
CrossRef Полный текст | Google Scholar
14. Рудерман М. Вещество в сверхсильных магнитных полях. В: Hansen CJ, редактор. Физика плотной материи, Материалы симпозиума IAU , Том. 53. Дордрехт; Бостон (1974). п. 117–31.
Google Scholar
15. Lai D, Salpeter EE, Shapiro SL. Молекулы и цепочки водорода в сверхсильном магнитном поле. Phys Rev A (1992) 45 : 4832–47. doi: 10.1103/PhysRevA.45.4832
Phys Rev A (1992) 45 : 4832–47. doi: 10.1103/PhysRevA.45.4832
Pubmed Abstract | Опубликован полный текст | Полный текст перекрестной ссылки | Google Scholar
16. Лай Д. Вещество в сильных магнитных полях. Rev Mod Phys . (2001) 73 : 629–62. doi: 10.1103/RevModPhys.73.629
Полнотекстовая перекрестная ссылка | Google Scholar
Магнитные поля
Магнетизм тесно связан с электричеством. По сути, магнетизм — это сила, вызванная движущимися зарядами. В случае постоянных магнитов движущиеся заряды представляют собой орбиты электронов, вращающихся вокруг ядер. Проще говоря, сильные постоянные магниты имеют много атомов с электронами, вращающимися в одном направлении. Немагнитные частицы имеют более случайное расположение электронов, вращающихся вокруг ядра. Для электромагнитов сам ток обеспечивает движущиеся заряды. Во всех случаях магнитные поля можно использовать для описания сил, вызванных магнитами.
Вопрос: Какой тип поля существует вблизи движущегося электрического заряда?
- электрическое поле, только
- магнитное поле, только
- как электрическое поле, так и магнитное поле
- ни электрическое поле, ни магнитное поле
Ответ: (3) Электрическое поле существует из-за электрического заряда, а магнитное поле из-за движения заряда.
Магниты поляризованы, то есть каждый магнит имеет два противоположных конца. Тот конец магнита, который указывает на географический северный полюс Земли, называется северным полюсом магнита, а противоположный конец по понятным причинам называется южным полюсом магнита. У каждого магнита есть северный и южный полюса. Нет ни одиночных изолированных магнитных полюсов, ни монополей. Если вы разделите магнит пополам, каждая половина исходного магнита будет иметь как северный, так и южный полюса, что даст вам два магнита.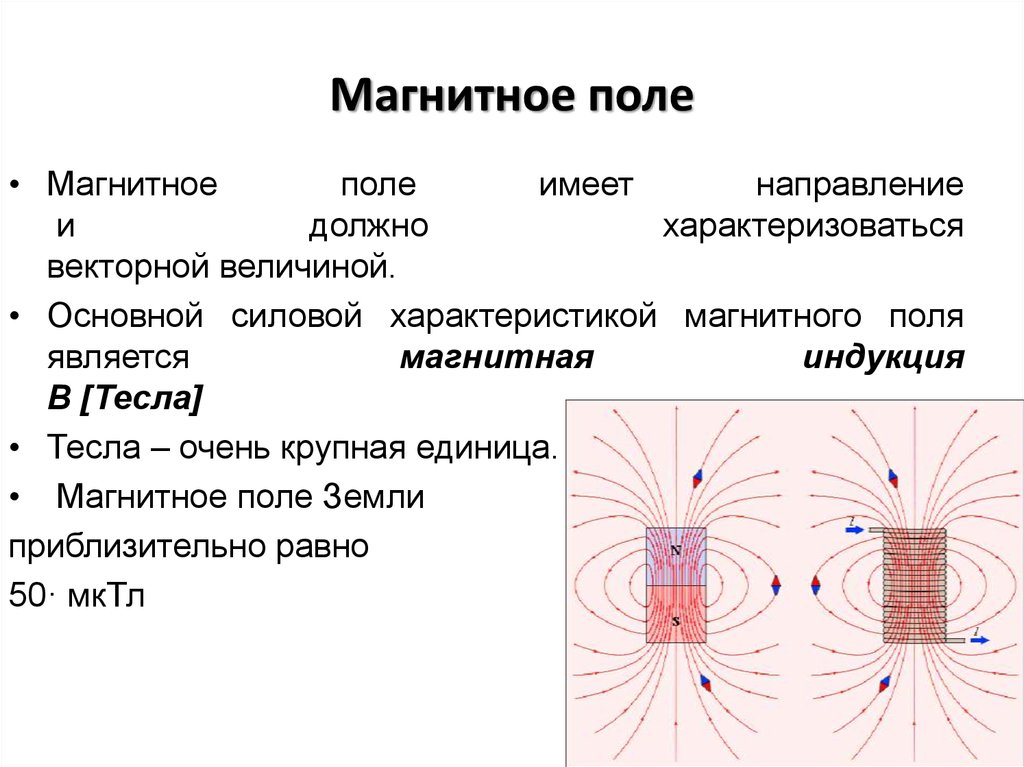 Физики продолжают поиски как физически, так и теоретически, но на сегодняшний день никто никогда не наблюдал северный полюс без южного полюса или южный полюс без северного полюса.
Физики продолжают поиски как физически, так и теоретически, но на сегодняшний день никто никогда не наблюдал северный полюс без южного полюса или южный полюс без северного полюса.
Вы использовали линии электрического поля, чтобы визуализировать, что произойдет с положительным зарядом, помещенным в электрическое поле. Чтобы визуализировать магнитное поле, вы можете нарисовать линии магнитного поля (также известные как линии магнитного потока), которые показывают направление, в котором северный полюс магнита должен указывать, если его поместить в поле. Линии магнитного поля рисуются в виде замкнутых петель, начинающихся с северного полюса магнита и продолжающихся до южного полюса магнита. Внутри самого магнита силовые линии проходят от южного полюса к северному. Магнитное поле является самым сильным в областях с наибольшей плотностью силовых линий магнитного поля или в областях с наибольшей плотностью магнитного потока. Сила магнитного поля (B) измеряется в единицах, известных как тесла (T).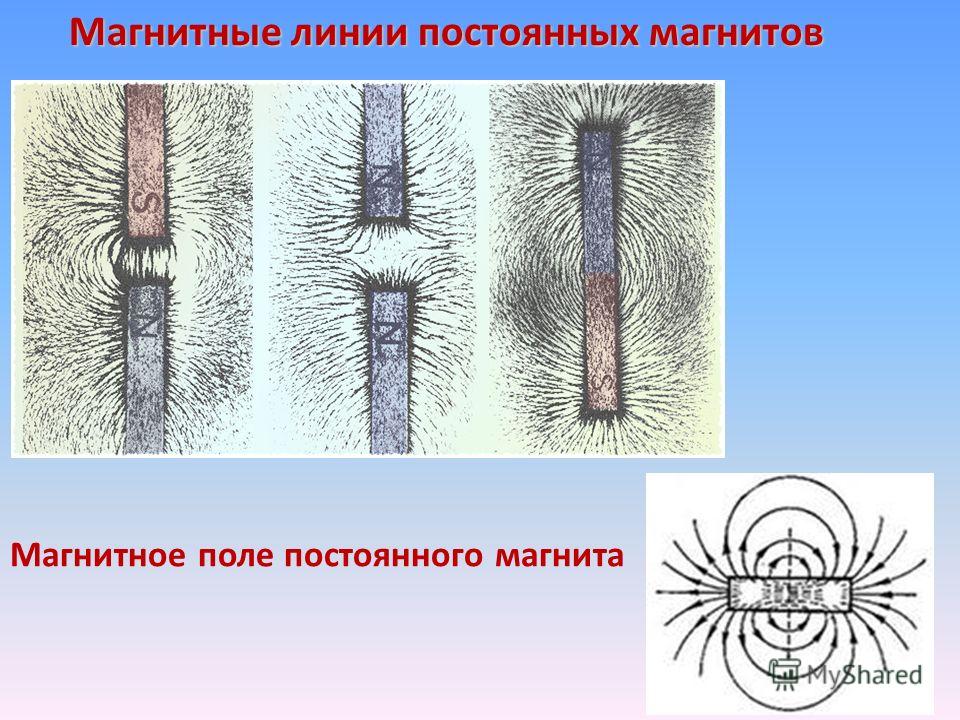
Подобно электрическим зарядам, полюса отталкивают друг друга, а противоположные полюса притягивают друг друга. Материалы можно разделить на магниты, притягивающие магниты (материалы, которые сами по себе не являются магнитами, но могут притягиваться магнитами) и непритягиваемые.
Вопрос: На приведенном ниже рисунке показаны силовые линии магнитного поля между двумя северными магнитными полюсами. В какой точке напряженность магнитного поля наибольшая?
Ответ: (B) имеет наибольшую напряженность магнитного поля, потому что он расположен в месте наибольшей плотности силовых линий магнитного поля.
Вопрос: На приведенной ниже схеме представлены стержневой магнит массой 0,5 кг и стержневой магнит массой 0,7 кг с расстоянием между их центрами 0,2 метра.
Какое утверждение лучше всего описывает силы между стержневыми магнитами?
- Гравитационная и магнитная силы отталкивают друг друга.
- Гравитационная сила отталкивает, а магнитная притягивает.
- Сила гравитации притягивает, а сила магнита отталкивает.
- Гравитационная и магнитная силы притягиваются.
Ответ: (3) Гравитация всегда притягивает, а северные полюса отталкиваются.
Вопрос: Учащемуся дают два куска железа и просят определить, являются ли один или оба куска магнитами. Сначала учащийся прикасается концом одной части к одному концу другой. Две железяки притягиваются. Затем учащийся переворачивает одну из частей и снова соединяет концы вместе. Две части снова притягиваются. Что студент определенно знает о первоначальных магнитных свойствах двух кусков железа?
Ответ: По крайней мере, один из кусков железа является магнитом, но мы не можем с уверенностью утверждать, что оба являются магнитами.
Вопрос: Начертите как минимум четыре силовые линии, чтобы показать величину и направление магнитного поля в области, окружающей стержневой магнит.
Ответ:
Вопрос: Когда два кольцевых магнита помещаются на карандаш, магнит А остается подвешенным над магнитом В, как показано справа. Какое утверждение описывает гравитационную и магнитную силы, действующие на магнит А из-за магнита В?
- Сила гравитации притягивает, а сила магнита отталкивает.
- Гравитационная сила отталкивает, а магнитная притягивает.
- Сила гравитации и сила магнитного поля являются притягивающими.
- И гравитационная сила, и магнитная сила отталкивают.
Ответ: (1) Гравитация может только притягивать, а поскольку магнит А подвешен над магнитом В, магнитная сила должна быть отталкивающей.
Электрические токи — Магнитные поля
Взаимодействия между электрическими токами и магнитными полями создают силы.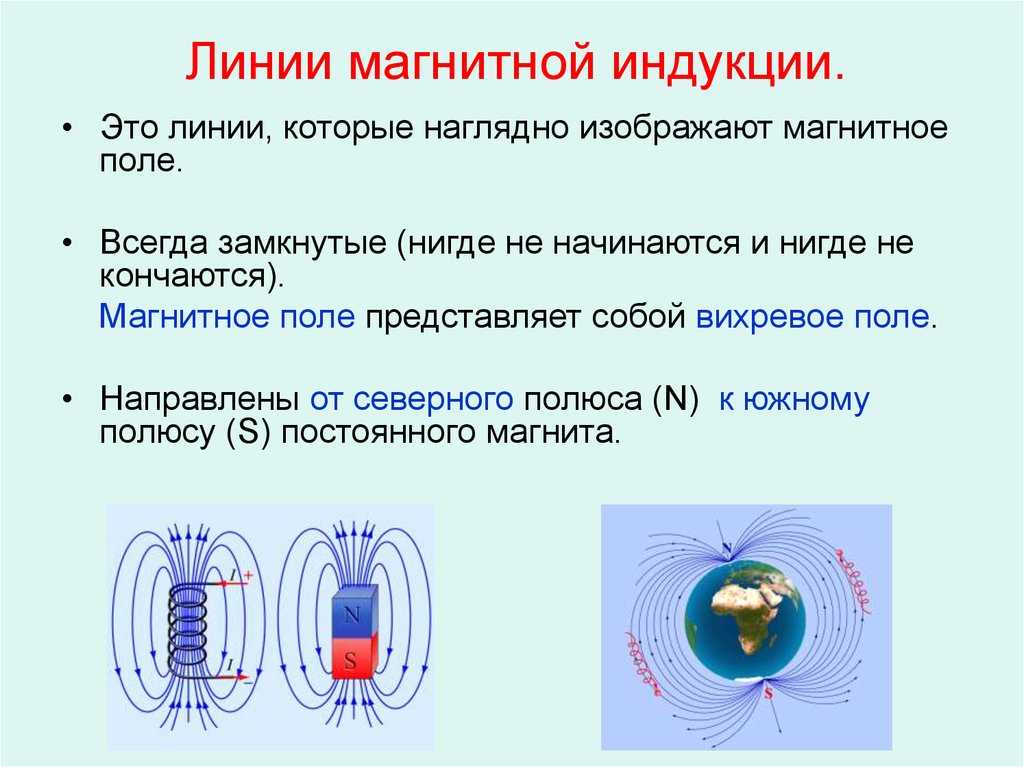 Магнитная сила на токе в магнитное поле = ток x смещение поперек магнитного поля . Эту силу можно предсказать, используя правило правой руки. Когда два тока направлены через магнитные поля в одном направлении, они притягиваются. Когда они направлены в противоположные стороны, они будут отталкиваться.
Магнитная сила на токе в магнитное поле = ток x смещение поперек магнитного поля . Эту силу можно предсказать, используя правило правой руки. Когда два тока направлены через магнитные поля в одном направлении, они притягиваются. Когда они направлены в противоположные стороны, они будут отталкиваться.
электрический ток магнитное поле
Хорошо, давайте поговорим о взаимодействии между токами и магнитными полями. Теперь есть два основных типа взаимодействия. У нас есть только ток, который находится в магнитном поле, он почувствует на себе силу, и это первое, о чем мы собираемся поговорить, а затем есть еще одно взаимодействие, связанное с магнитным полем, которое будет генерировать сам ток, и это отдельный мы поговорим об этом через минуту.
Итак, во-первых, если у меня есть ток в магнитном поле, ток состоит из множества движущихся зарядов, и каждый раз, когда у меня есть движущиеся заряды в магнитном поле, у меня есть сила, так что давайте посмотрим, можем ли мы связать эту силу, используя закон силы Лоренца, с током. Что ж, у нас будет пересечение скорости заряда с магнитным полем. Что мы собираемся сделать, так это представить скорость как смещение над изменением во времени, а затем мы собираемся подложить это изменение во времени под заряд. Что хорошо в этом, так это то, что заряд с течением времени представляет собой ток, а это говорит нам о том, что магнитная сила, действующая на ток в магнитном поле, равна просто произведению тока на смещение, пересекающее магнитное поле. Хорошо, давайте посмотрим на это в действии. Хорошо, магнитное поле направлено на доску, у нас есть ток, и я хочу знать, в каком направлении сила, хорошо, это дельта или смещение, которое представляет собой вектор, который просто идет вверх от того места, где он входит, туда, где он выходит из поля там так, что сила слева.
Что ж, у нас будет пересечение скорости заряда с магнитным полем. Что мы собираемся сделать, так это представить скорость как смещение над изменением во времени, а затем мы собираемся подложить это изменение во времени под заряд. Что хорошо в этом, так это то, что заряд с течением времени представляет собой ток, а это говорит нам о том, что магнитная сила, действующая на ток в магнитном поле, равна просто произведению тока на смещение, пересекающее магнитное поле. Хорошо, давайте посмотрим на это в действии. Хорошо, магнитное поле направлено на доску, у нас есть ток, и я хочу знать, в каком направлении сила, хорошо, это дельта или смещение, которое представляет собой вектор, который просто идет вверх от того места, где он входит, туда, где он выходит из поля там так, что сила слева.
Хорошо, а теперь предположим, что у меня такая же ситуация, когда провода изогнуты? Что ж, дельта r, пока магнитное поле постоянно, дельта r — это вектор от места, где ток входит в поле, до места, где он выходит, так что это будет дельта r, так что теперь все, что мне нужно сделать, это положить большой палец в направлении дельты. r, мои пальцы в направлении магнитного поля и моя ладонь указывает в направлении силы. Обратите внимание, что это своего рода комбинация между тем, что было бы, если бы у меня было просто прямо вверх, и тем, что было бы, если бы у меня было просто горизонтально, хорошо, это комбинация, это векторная сумма этих двух вещей.
r, мои пальцы в направлении магнитного поля и моя ладонь указывает в направлении силы. Обратите внимание, что это своего рода комбинация между тем, что было бы, если бы у меня было просто прямо вверх, и тем, что было бы, если бы у меня было просто горизонтально, хорошо, это комбинация, это векторная сумма этих двух вещей.
Хорошо, давайте решим пример задачи, поэтому я хочу узнать силу, приложенную к 50-сантиметровому проводу, несущему ток 5 ампер вверх в магнитном поле 3 Тесла вне доски. Хорошо, сначала давайте проложим направление, 3 Тесла вне доски, верно? У меня ток идет вверх и большой палец тоже пойдет, пальцы сила направлена вправо все в порядке. Что это за сила? Хорошо, f равно ILB, I — ток, L — длина вектора смещения, теперь мы можем использовать это только в том случае, если смещение с током и магнитное поле перпендикулярны, иначе нам понадобилась бы часть того, что было перпендикулярно, но большинство этих задач уже перпендикулярны, поэтому мы будем делать ток. Что это было? 5 ампер длина 50 сантиметров, но, конечно, мы должны работать в единицах СИ, поэтому мы напишем пункт 5, хорошо? И тогда у нас есть магнитное поле 3 Тесла 5 раз точка 5 два с половиной, два с половиной раза 3 о боже, три четверти это 75 центов, так что это будет 7 с половиной ньютонов, и вот вы идете это так просто, единственное, о чем иногда вам, возможно, придется беспокоиться, это то, что, возможно, ток не перпендикулярен магнитному полю, и тогда вам просто нужно взять компонент, который перпендикулярен, это не должно быть легко найти не должно быть трудно .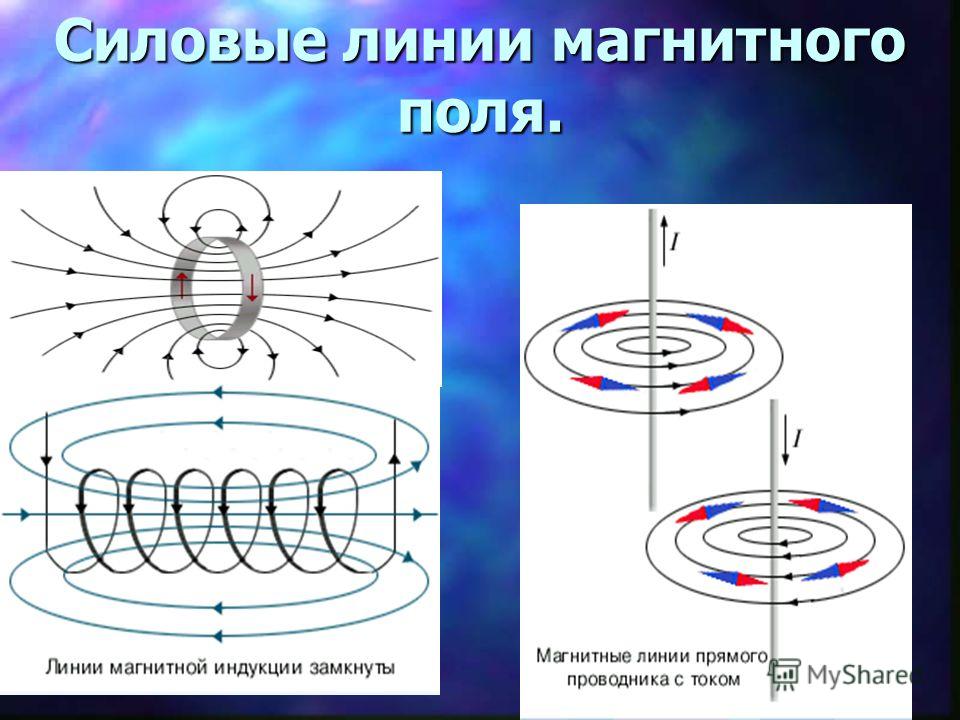
Хорошо, давайте посмотрим на второй случай. Теперь это несколько отличается, поэтому сила между проводами. Хорошо, если у меня есть два провода, по которым течет ток в одном направлении, они будут воздействовать друг на друга, почему? Ну, потому что этот верхний провод создает магнитное поле только потому, что он несет ток, так что магнитное поле я получаю, используя правило правой руки, хватая этот верхний провод большим пальцем в направлении тока, а затем смотрю вниз под провод, магнитное поле направлен в плату, так что это означает, что этот ток, поскольку он находится в непосредственной близости от этого другого провода, находится в магнитном поле, которое направлено в плату, хорошо, бум, бум, посмотри на это! На этот нижний провод действует сила, действующая вверх, а это означает, что если два тока имеют одинаковое направление, магнитная сила между ними будет притягательной. Теперь мы можем понять это непосредственно из диаграммы магнитного поля, так что вот два тока, они оба выходят из платы, что означает, что они в одном направлении, верно? Поэтому я хочу знать, как выглядит магнитное поле для обоих этих парней. Итак, начнем. Я схвачу провод большим пальцем, указывающим в направлении тока, а мои пальцы будут магнитным полем, так что это магнитное поле будет вращаться вот так.
Итак, начнем. Я схвачу провод большим пальцем, указывающим в направлении тока, а мои пальцы будут магнитным полем, так что это магнитное поле будет вращаться вот так.
А здесь? То же самое, хорошо, есть следующая строка, следующая строка, и теперь, когда мы становимся больше, замечаем, что в середине это магнитное поле ослабевает, а то поднимается, так что это позволит им отменить, так что мы получаем эти странные очки, выглядящие как фигура. хорошо, а затем мы продолжим и посмотрим, как вы можете видеть притяжение на этой диаграмме, потому что магнитное поле может гаснуть в середине, и это означает, что оно не так сильно в середине, хорошо? И это будет хорошо притягивать два провода вместе. Давайте посмотрим, что произойдет, когда мы изменим направление этого донного течения, так что теперь оно пойдет в другую сторону. Магнитное поле остается прежним, потому что я не изменил верхний ток, но теперь посмотрите, что происходит, когда я выполняю правило правой руки, я получаю отталкивающую силу, поэтому, когда два тока идут в противоположном направлении, я получаю отталкивание, так что это немного странно, потому что с зарядами противоположности притягиваются, но с токами противоположности отталкиваются, так что давайте посмотрим, как это происходит, у нас здесь есть отталкивание, и давайте посмотрим, что покажет нам линия магнитного поля, так что мы вышли из, хорошо давайте нарисуем эти. Теперь здесь я должен вставить большой палец, так что это означает, что я буду получать круги, но они будут идти в другую сторону, ну, в середине обратите внимание, что они больше не могут отменить, так что это означает, что, пока я продолжаю рисовать их они собираются распространить на другую сторону, но я больше не могу делать эту фигуру из очков, потому что теперь все эти силовые линии направлены одинаково, так что это отталкивание, так что, когда токи направлены в противоположных направлениях, они отталкиваются То же направление, в котором они притягиваются, на самом деле было тем, что привело к определению ампера.
Теперь здесь я должен вставить большой палец, так что это означает, что я буду получать круги, но они будут идти в другую сторону, ну, в середине обратите внимание, что они больше не могут отменить, так что это означает, что, пока я продолжаю рисовать их они собираются распространить на другую сторону, но я больше не могу делать эту фигуру из очков, потому что теперь все эти силовые линии направлены одинаково, так что это отталкивание, так что, когда токи направлены в противоположных направлениях, они отталкиваются То же направление, в котором они притягиваются, на самом деле было тем, что привело к определению ампера.
Ампер — это сила тока, которая течет по двум идентичным очень длинным проводам, параллельно расположенным на расстоянии одного метра друг от друга, и ощущает силу, равную 2 умножить на 10 до минус 7 ньютонов, и это на самом деле определение ампера, немного странное, но это взаимодействие токов с магнитными полями.
электромагнетизм — Может ли магнитное поле существовать без электрического поля?
Спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 21k раз
$\begingroup$
Я знаю, что электрическое поле может существовать без магнитного поля, как в случае, когда у вас есть стационарный точечный заряд.
Но магнитные поля создаются движущимися зарядами , так разве вам не всегда нужно электрическое поле, чтобы иметь магнитное поле? Даже в случае с постоянными магнитами, насколько я знаю, это выровненные движущиеся электроны в атомах материала, которые вызывают магнитные свойства, так что не означает ли это, что всегда есть электрическое поле, чтобы иметь магнитное поле?
- электромагнетизм
- магнитные поля
- системы отсчета
- электрические поля
$\endgroup$
3
$\begingroup$
«Магнитное поле» — это концепция классической электродинамики. Уравнения Максвелла были разработаны в середине 19 века, когда фундаментальная атомная физика все еще находилась в зачаточном состоянии.
В современном историческом контексте постоянный магнит является прекрасным примером магнитного поля без электрического поля.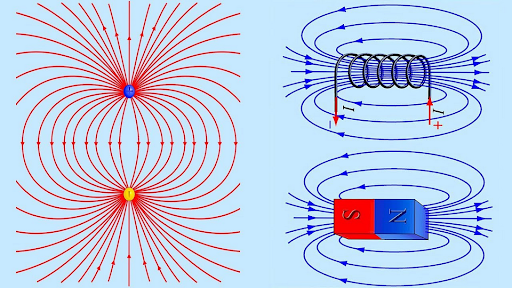 В рамках теории классической электродинамики нет объяснения тому, почему существует магнитное поле, а только то, что оно действительно существует и как оно связано с электрическим полем. Постоянные магниты обладают магнитным полем как неотъемлемым фундаментальным свойством, подобным тому, по которому камни имеют массу. Они просто делают.
В рамках теории классической электродинамики нет объяснения тому, почему существует магнитное поле, а только то, что оно действительно существует и как оно связано с электрическим полем. Постоянные магниты обладают магнитным полем как неотъемлемым фундаментальным свойством, подобным тому, по которому камни имеют массу. Они просто делают.
За последние полтора столетия были разработаны другие теории. Например, магнитное поле может быть объяснено специальной теорией относительности как сокращение длины, очевидно создающее дисбаланс заряда, поэтому можно сказать, что магнитное поле не существует как фундаментальное свойство, а скорее является проявлением электрического поля в движущейся системе отсчета. а квантовая физика объясняет постоянные магниты движущимися зарядами на субатомных масштабах.
Таким образом, в контексте современной физики фундаментальное магнитное поле вообще не нужно, поскольку его можно объяснить в терминах электрического поля и движения.
Открытие магнитного монополя изменило бы это положение, но, хотя оно принесло бы элегантную симметрию существующим видам частиц, экспериментально пока не было обнаружено никаких доказательств наличия магнитного монополя.
$\endgroup$
2
$\begingroup$
Я полагаю, что это вариант ответа квантовой спагеттификации, но очевидным примером является токовая петля, используемая в электромагнитах с тех пор, как люди впервые открыли электричество.
Нет чистого электрического поля, потому что существует одинаковое количество положительных и отрицательных зарядов, поэтому их поля уравновешиваются. Однако существует магнитный диполь из-за движения электронов.
$\endgroup$
1
$\begingroup$
Нет, у вас может быть магнитное поле без электрического поля. Рассмотрим стержень с равным количеством положительных и отрицательных зарядов (таким, что они расположены на одинаковом расстоянии друг от друга). Пусть плюс движется влево со скоростью $v$, а минус вправо со скоростью $v$. Это приведет к магнитному полю, но не к электрическому полю.
Пусть плюс движется влево со скоростью $v$, а минус вправо со скоростью $v$. Это приведет к магнитному полю, но не к электрическому полю.
$\endgroup$
10
$\begingroup$
В каком-то смысле это простой вопрос, как отмечали другие. Довольно просто построить примеры случаев с нулевым электрическим полем и ненулевым магнитным полем.
С другой стороны, это не тривиальный вопрос. Например, если в одном кадре вы видите только магнитное поле, то в другом кадре вы увидите магнитное и электрическое поля, которые смещаются при изменении скорости. Тогда есть пример эффекта Аронова-Бома. В этом случае у вас есть область, где и электрическое, и магнитное поля равны нулю, но электрон все еще чувствует электромагнитную силу.
Принципиальным является четырехвекторный потенциал $A_\mu$. Электрические и магнитные поля представляют собой частные сочетания частных производных этого поля. Именно $A_\mu$ появляется в уравнениях, описывающих электромагнетизм, таких как уравнение Максвелла или уравнение Дирака. В некоторых важных частных случаях мы можем игнорировать $A_\mu$ и работать с полями $E_i$ и $B_i$. Но основное понимание всегда будет основываться на $A_\mu$.
Именно $A_\mu$ появляется в уравнениях, описывающих электромагнетизм, таких как уравнение Максвелла или уравнение Дирака. В некоторых важных частных случаях мы можем игнорировать $A_\mu$ и работать с полями $E_i$ и $B_i$. Но основное понимание всегда будет основываться на $A_\mu$.
$\endgroup$
1
$\begingroup$
На уровне фундаментальных элементарных частиц ответ таков: пока не обнаружены магнитные монополи, диполю магнитного поля нужна заряженная частица.
Электрон имеет магнитный момент:
В атомной физике магнитный момент электрона или, точнее, магнитный дипольный момент электрона — это магнитный момент электрона, обусловленный присущими ему свойствами спина и электрического заряда. 92 > 0$, то можно перейти в систему отсчета, где электрическое поле равно нулю, а магнитное поле отлично от нуля.
$\endgroup$
Магнитное поле [Encyclopedia Magnetica]
Содержание
Магнитное поле
Различные подходы к магнитным полям, B и H
Магнитное поле в теоретической физике
Магнитное поле B
Намагничивание M
Поляризация J
Вспомогательное поле H
Восприимчивость и проницаемость
Магнитное поле в технике
Напряженность магнитного поля H
Плотность магнитного потока B
Проницаемость и восприимчивость
Количество и единицы
Энергия магнитного поля
Трудности с определением магнитного поля
Электромагнитное и магнитостатическое поле
Среда магнитного и электромагнитного поля
Линии магнитного поля
Магнитный диполь и момент
Магнитные столбы
Тип магнетизма
Уравнения Максвелла
Генерация магнитного поля
Электрический ток
По собственным магнитным моментам
С помощью излучения фотонов
Магнитное поле и релятивистские эффекты
См.
также
Внешние видеоматериалы
Каталожные номера
Стэн Зурек, Магнитное поле, Encyclopedia Magnetica, E-Magnetica.pl Магнитное поле — область пространства, в которой наблюдаются магнитные силы. Магнитные силы — это механические силы, действующие в результате магнитных взаимодействий.
. оба B и vМагнитное поле всегда создается вокруг электрического тока или, в более общем смысле, движущимися электрическими зарядами или переменным электрическим полем E , а также собственными магнитными дипольными моментами субатомных частиц. Существование магнитного поля отвечает за магнетизм и электромагнетизм.
В вакууме сила F (сила Лоренца), действующая на электрический заряд q движется со скоростью v за счет электрического поля E и магнитного поля B (плотность магнитного потока): $\vec{F} = q·\vec{E} + q·\vec{v} × \vec{B}$
Поле, которое удовлетворяет действию вектора B в уравнении силы Лоренца, считается определением магнитного поля .

В физике поле — это величина или значение, присвоенное каждой точке пространства или объема. Следовательно, магнитное поле можно математически описать, приписав каждой точке пространства, заполненной этим полем, физическую величину. В зависимости от требуемой математической обработки описание может быть скалярным полем векторного поля, также являющимся функцией положения или времени.
Для полной количественной оценки воздействия магнитного поля на данный материал или среду целесообразно использовать две величины, такие как плотность магнитного потока B и напряженность магнитного поля H .
→ → →
Полезная страница? Поддержите нас!
→ → →PayPal ← ← ←
Помогите нам с всего за $0,10 в месяц? Давай…
← ← ←Iron filings attracted in magnetic field of a horseshoe magnet
Iron filings follow magnetic field lines around a single wire with current (perpendicular to the page ) от Popular Science Montly, Vol.
56, 1899–1900, общественное достояние
Стрелки компаса следуют направлению магнитного поля ( B или H ) вокруг провода с током I6 9040 правило)
Различные подходы к магнитным полям, B и H
И B , и H строго определены с точки зрения единиц измерения, а также их физического и технического значения. Однако существует два основных подхода к анализу, полезности и важности магнитных полей B и H : теоретическая физика и инженерия .
Если используется одна и та же система единиц, т.е. SI, то оба подхода полностью эквивалентны с точки зрения числовых значений и единиц. Только названия или проблематичны, а не единицы измерения или математические расчеты.

Эти два подхода дополняют друг друга, предоставляя доступ к типу уравнения, который более полезен для данного расчета. Одно не «лучше» другого просто потому, что одна группа людей считает его более «фундаментальным». «Качество» любой формы определения зависит от ее полезности для конкретной цели, такой как расчет эффектов с релятивистскими явлениями или разработка эффективного трансформатора или электромагнита.
Однако теоретическая физика уделяет больше внимания B , тогда как в технике и H , и B считаются одинаково важными. Соглашения об именах могут существенно различаться. Кроме того, ранее использовавшаяся система единиц СГС (до сих пор используемая некоторыми странами и отраслями науки) имеет еще один набор наименований и коэффициентов. Все это создает часто запутанную смесь, и во многих книгах по электромагнетизму приводится полный список коэффициентов преобразования между различными системами.
См. также: Путаница между B и H.
Особое внимание следует уделить некоторым уравнениям, потому что они могут быть записаны в заданной форме, которая требует выполнения определенных неявных условий — эти условия часто не указываются.
Например, закон Био-Савара, записанный в физической форме $B = f (μ_0 · I)$, справедлив только в вакууме, тогда как инженерная форма $H = f (I)$ является более общей и справедливой для любая однородная изотропная среда.
Магнитное поле в теоретической физике
В теоретическом подходе больше внимания уделяется выводу уравнений из первых принципов и полезности данных выражений для вывода других уравнений. Микроскопическое (атомный и субатомный уровень) понимание является фундаментальным, но между и внутри атомов любой материи существует вакуум. Ферромагнитным материалам уделяется ограниченное внимание или вообще не уделяется , с объяснениями, соответствующими инженерному подходу.
Единицы используются с соблюдением всех обычных физических и математических правил.
Однако отношения между единицами измерения и именами переменных, по-видимому, трактуются менее строго: тесла и А/м используются почти взаимозаменяемо для B , H и M с использованием магнитной постоянной $μ_0$ как средство преобразования.
Магнитное поле В
С точки зрения теоретической физики, единственной формой магнитного поля, необходимой для любого анализа, является магнитное поле B , которое считается «бесспорно фундаментальным». Определение B — это поле, которое вызывает силу, описываемую уравнением (1).
В зависимости от типа обозначений в различной литературе могут использоваться либо обозначения с жирным шрифтом, обозначающие векторы (уравнение (1a)) либо со стрелками над переменными (уравнение (1b)) — оба в точности эквивалентны.
(1a) $$ \mathbf{F} = q·\mathbf{E} + q·\mathbf{v} × \mathbf{B} $$
(Н)(1b) $$ \vec{F} = q·\vec{E} + q·\vec{v} × \vec{B} $$ где: $q$ — электрический заряд (Кл), $E$ — электрическое поле (В/м), $v$ — скорость (м/с) заряда, $B$ — магнитное поле (Тл) Сила из-за электрического поля действует в направлении этого поля (скалярное произведение «·» в уравнениях (1ab)).
Сила из-за магнитного поля действует перпендикулярно как направлению движения заряда, так и направлению магнитного поля (перекрестное произведение «×» в уравнениях (1ab)).
, в) общая сила F = F e + F м в обоих полях; зеленая сплошная стрелка показывает скорость и направление движения, зеленая пунктирная стрелка — развитие траектории
Другие названия для B , такие как «плотность магнитного потока» и «магнитная индукция», даже считаются «абсурдным выбором». Количество H рассматривается как «вспомогательное» и не имеющее названия. Некоторые теоретики даже считают единицы СИ «произвольными и немного глупыми». Другие системы единиц могут использоваться для теоретических расчетов, таких как Лоренц-Хевисайд или естественные единицы, которые могут быть определены с проницаемостью вакуума или скоростью света как единица (безразмерная), что может упростить некоторые расчеты.

Магнитное поле B создается электрическим током и собственными магнитными дипольными моментами субатомных частиц.
Магнитная сила, определяемая силой Лоренца, пропорциональна B , и такая сила принимается за определение плотности потока B . Полная форма уравнения Максвелла всегда показывает B , а не H . Это связано с тем, что дивергенция B всегда равна нулю, тогда как для 9 она может быть отличной от нуля.0639 Н .
На микроскопическом уровне между атомами и внутри них существует вакуум, и для всех расчетов можно использовать B .
Если используются единицы СИ, то B имеет размерность тесла.
Намагничивание M
Магнитные свойства вещества являются следствием макроскопического усреднения микроскопических эффектов, особенно за счет векторного суммирования магнитных дипольных моментов субатомных частиц (и атомов), которые могут ориентироваться на магнитное поле, приложенное к материалу.
Материал реагирует намагничиванием M при воздействии некоторого магнитного поля B . Если достигается полное выравнивание всех свободных магнитных моментов, то говорят, что материал магнитонасыщен, и значение M больше не может увеличиваться.
Намагниченность М сумма магнитных дипольных моментов на единицу объема Намагничивание M is определил как сумму магнитных моментов на единицу объема в данном материале согласно уравнению (2).
(2) $$ \vec{M} \equiv \frac{\text{магнитный момент}}{\text{единица объема}} \equiv \frac{ \sum_i \vec{m_i} } {V} $$ (А·м 2 / м 3 )
≡ (А/м)где: $\vec{m}$ — магнитный дипольный момент (А·м 2 ), $i$ — счетный индекс (безразмерный), $V$ — единица объема (м 3 ) Во многих исследовательских работах по физике намагниченность выражается как массовая намагниченность, при этом отклик измеряется единицей массы, а не единицей объема, с популярной единицей emu/g.

Коэффициент преобразования в единицы СИ: 1 эме/г = 1 А⋅м 2 /кг, а плотность материала можно использовать для преобразования его в объемную намагниченность.
Поляризация J
Намагничивание М (А/м) иногда также называют «магнитной поляризацией».
В исследовательских работах, написанных физиком-теоретиком, если намагниченность M используется для выражения измеряемой величины в единицах тесла (а не в А/м), то это значение просто умножается на $μ_0$ (проницаемость вакуума) или выражается непосредственно в теслах (с неявным предположением, что оно умножается на $μ_0$).
Даже в некоторых превосходных книгах по теоретическому электромагнетизму (например, ссылки ) поляризация J не упоминается (и, следовательно, не определяется).
Однако магнитная поляризация J может быть определена и рассчитана как: $J = μ_0 · M$, с единицей тесла.

Вспомогательное поле H
С макроскопической точки зрения существуют дополнительные эффекты, потому что атомы взаимодействуют друг с другом магнитным образом, и признано, что «вспомогательное» поле H может быть определено, и хотя оно «нелогично», оно может быть «полезным», потому что его можно непосредственно связанные со свободными токами, так что прямая зависимость между током и H можно указать.
Следовательно, вспомогательное поле H определяется как , как в уравнении (3).
(3) $$ \vec{H} \equiv \frac{ \vec{B} }{µ_0} — \vec{M} $$ (А/м) где: $B$ — магнитное поле (Тл), $μ_0$ — проницаемость вакуума (Гн/м), $M$ — намагниченность (А/м) Даже если используются единицы СИ, иногда H выражается в теслах.
Восприимчивость и проницаемость
Магнитная восприимчивость χ может быть определена более чем одним способом.
Для материалов, которые линейно реагируют на приложенное магнитное поле, при допущении, что M пропорционально B или H , объемная восприимчивость может быть определена как: $ \vec{M} = χ_{(B)} · \frac{ \vec{B} }{µ_0} $$
(А/м) (4b) $$ \vec{M} = χ_{(H)} · \vec{H} $$ (A/m) Для диамагнетиков восприимчивость отрицательна, для парамагнетиков положительна. Для вакуума он равен нулю.
Эти два определения (4a, 4b) отличаются тем, что:
(5) $$ χ_{(H)} = \frac{χ_{(B)}}{1 — χ_{(B)}} $$ (безразмерное) Для немагнитных материалов $χ << 1$ и разница незначительна, и $χ = χ_{(H)} \ приблизительно χ_{(B)}$.
Однако при больших значениях $χ$, встречающихся в ферромагнетиках, определения (4а,б) менее полезны, так как (5) расходится и вместо восприимчивости используется магнитная проницаемость.
Магнитная проницаемость мк определяется по отношению к восприимчивости:
(6а) $$ µ \экв µ_0 · (1 + χ) $$ (Н/м) (6b) $$ μ = μ_0 · μ_r $$ (H/m) где: $μ_r$ — относительная проницаемость (безразмерная) и может использоваться как коэффициент пропорциональности между B и H :
(7) $$ \vec{B} = µ · \vec{H} = µ_0 · µ_r · \vec{H} $$ (T) Однако у этого уравнения есть ограничения, так как в ферромагнетиках $µ_r$ является нелинейной функцией B или H .
Магнитное поле в технике
В инженерном подходе меньше внимания уделяется фундаментальным физическим понятиям, а больше — свойствам непосредственно измеряемых величин, полезных для практических приложений и проектирования устройств.
Магнитные величины связаны с макроскопическими электрическими величинами, которые можно непосредственно измерить или контролировать в электромагнитных устройствах, таких как электрическое напряжение и ток.
Это приводит к другой концепции взаимосвязи возбуждения и реакции и к соглашению об именах, как это определено в международной системе единиц СИ.
Напряженность магнитного поля H
См. также основную статью: Напряженность магнитного поля. Напряженность магнитного поля H измеряется в амперах на метр, А/м (или масштабируется с помощью множителей СИ: кА/м, МА/м и т. д.)
Закон Био-Савара: $P$ — точка, в которой рассчитывается напряженность магнитного поля $\vec H$, $R$ — перпендикулярное расстояние от проводника, $I$ — ток, $\vec J$ — плотность тока, $d \vec l$ — бесконечно малая длина проводника, дающего вклад в магнитное поле, $r$ — расстояние, $\vec r$ — вектор пути, $\hat r$ — орт вдоль направления $r $, $\theta$ — угол между $d \vec l$ и $r$
Источником H являются электрические токи.
Пропорциональность определяется длиной рассматриваемого пути (длиной магнитного пути) и суммарной величиной тока I , содержащейся в одном проводнике, или числом N проводников. Вычисление H может быть основано либо на законе Био-Савара, либо на схемном законе Ампера, причем оба подхода дают одинаковые результаты для одной и той же конфигурации. 92}$$
(А/м) $I$ — сила тока (А), $d \vec l$ — бесконечно малая длина (м) проводника, дающего вклад в магнитное поле, $\hat r$ — орт вдоль направления $r$ (безразмерный), $ r$ — радиальное расстояние (м) В альтернативном подходе интеграл по замкнутому контуру тангенциальной составляющей H дает значение замкнутого холостого тока. Из окружного закона Ампера:
(9) $$ \int_C \vec{H} · d \vec{l} = I $$ (A) где: C — замкнутый путь, по которому вычисляется интеграл Electric current I generates around itself magnetic field strength H
Как показано выше, оба уравнения можно сформулировать так, чтобы магнитная проницаемость не появлялась — магнитные свойства материи (или проницаемость вакуума) не важны для генерации H (строго применим только в однородной и изотропной среде, независимо от того, является ли она немагнитной, магнитной, нелинейной и т.
д.)
Уравнение (9) можно переформулировать так, чтобы электрический ток I создавал вокруг себя четко определенную напряженность магнитного поля H , амплитуда которого не зависит от типа намагниченного материала. Для однородной среды (без дополнительных источников магнитного поля, таких как магнитные полюса из-за размагничивающего фактора) существует прямая зависимость между I и H (например, мгновенное изменение I приводит к мгновенному изменению H , если предположить, что изменения пренебрежимо медленны со скоростью света):
(10) $$ H = \frac{N · I}{l} $$ (А/м) где: $N$ — число жил в проводе или витков в катушке (безразмерное), $I$ — ток (А), $l$ — длина магнитного пути (м) Например, ток 1 А в прямом проводе дает H , циркулирующий по проводу (по правилу правой руки), такой, что на радиусе r = 0,1 м (от центра провода), относящийся к окружности с длиной пути $l = 2· π·r$ = 0,628 м, что примерно равно H = 1,59 А/м (см.
также: Расчет магнитного поля прямого круглого проводника).
Простая магнитопровод: сердечник и воздушный зазор
Если среда не изотропна или имеется несколько разных материалов, то на распределение поля влияет размагничивающее поле, вызванное магнитными полюсами. Эти полюса становятся новыми источниками магнитного поля, которые изменяют распределение исходного приложенного поля.
Произведение Н·л также известно как магнитодвижущая сила (МДС), которую можно рассматривать как приложенное возбуждение, а составляющая Г·л представляет падение МДС в магнитной цепи (по аналогии к падению напряжения в электрической цепи). Если магнитная цепь содержит магнитопровод с высокой магнитной проницаемостью и воздушный зазор (оба имеют одинаковую площадь поперечного сечения), то уравнение (10) можно применить как:
(11а) $$ H_{жила}·l_{жила} + H_{зазор}·l_{зазор} = N · I $$ (А) или
( ампер-витков ), но $H_{core}·l_{core} \ll H_{gap}·l_{gap}$, так что: (11b) $$ H_{разрыв}·l_{разрыв} \приблизительно N · I $$ (А) или
( ампер-витков )и он широко используется для проектирования электродвигателей, электромагнитов, магнитных датчиков, трансформаторов обратного хода и т.
д.
В единицах СГС H измеряется в эрстедах (Э) с коэффициентом преобразования: 1 Э = 1000 / (4⋅π) А/м ≈ 79,58 А/м.
Плотность магнитного потока B
См. также основную статью: Плотность магнитного потока. В ферромагнетиках зависимость B-H нелинейна, зависит от истории и обычно анизотропна
1 1 10881Плотность магнитного потока B представляет собой реакцию среды на намагничивание H . Амплитуда B зависит как от приложенного возбуждения, так и от свойств материала (и магнитной предыстории материала в случае предварительного намагничивания ферромагнетиков).
Как упоминалось выше, H можно количественно определить по току намагничивания (но также используются прямые методы измерения, такие как H-катушка).
B измеряется с помощью закона индукции Фарадея (одно из уравнений Максвелла), который можно записать как:
(12a) \frac{dB}{dt} $$ (В) (12b) $$V(t) = N · A · \frac{dB}{dt} $$ (V) (12c)
(для синуса)$$V_{rms} = π · \sqrt{2} · f ·B_p · N · A $$ (В) где: ЭДС(т) — электродвижущая сила (В), В(т) — измеренное напряжение (В), Н — число витков сенсорной катушки, А — активное перекрестное площадь сечения (м 2 ), В действующее значение — действующее значение напряжения (В), B p — пик синусоидальной индукции (Тл) Иллюстрация зависимости в ферромагнетике между напряженностью магнитного поля H , плотность магнитного потока B , намагниченность M и магнитная поляризация J
Таким образом, значение B (или непрерывный сигнал) может быть получено вычислением интеграла измеренного напряжения (с помощью аналоговой схемы с интегрирующим операционным усилителем или с помощью цифровых расчетов дискретизированного сигнала).
Разница знаков в обоих уравнениях возникает из-за того, что (12а) описывает электродвижущую силу (ЭДС), индуцируемую внутри данной чувствительной катушки (В-катушки), но эта информация никак не доступна — только внешнее напряжение (12б) может измеряться. Эта разница часто неявно предполагается, но иногда даже неправильно понимается, показывая знак минус даже для измеренных напряжений.
Поскольку уравнение (12a,b) определяет зависимость посредством производной, невозможно измерить постоянную составляющую так же просто, как переменную составляющую. Требуется некоторая изменчивость, которая может быть достигнута путем перемещения катушки (баллистические измерения, магнитометр с вибрационной катушкой) или перемещения образца (магнитометр с вибрационным образцом).
Для преобразования энергии очень полезно использовать возбуждение переменным током. Если применяется полный цикл возбуждения и обе формы волны H и B , затем можно построить петлю B-H (петля гистерезиса), как показано на рисунке.
Площадь петли пропорциональна всей энергии, потерянной при намагничивании материала, и это основной инструмент, с помощью которого измеряются полные магнитные потери в материале. Все составляющие магнитных потерь включаются автоматически (гистерезис, вихревые токи, избыточные потери), поэтому так важно практически точно измерить обе: напряженность магнитного поля H и плотность магнитного потока B . Уравнение (12с) является основой для проектирования всех силовых трансформаторов, работающих с синусоидальным напряжением.
Существует несколько международных стандартов, определяющих такие процедуры измерения потерь для важных в промышленном отношении магнитомягких материалов, таких как электротехническая сталь.
Проницаемость и восприимчивость
См. также основную статью: Магнитная проницаемость. Проницаемость магнитных материалов (например, ферромагнетиков $μ_{ferro}$) намного выше, чем у немагнитных материалов (например, вакуум $μ_0 = μ_{vac}$, диамагнетики $μ_{dia}$ и парамагнетики $µ_{para}$)
Магнитная проницаемость μ – это величина, выражающая коэффициент пропорциональности между H и B .
Магнитомягкие материалы играют ключевую роль в эффективном преобразовании энергии, поэтому им уделяется много внимания, а значение проницаемости используется как показатель качества. Для любого такого материала можно написать, что:
(13a) $$B = μ · H$$
(T)(13b) $$B = µ_r · µ_0 · H$$ где: $µ = µ_r · µ_0$ (Гн/м), и, следовательно, относительная магнитная проницаемость $µ_r = µ / µ_0$ (безразмерная) Для вакуума зависимость B-H полностью линейна, и $μ_0$ = 4·π·10 -7 (Гн/м), что является универсальной физической константой, и $μ_r = 1$. На практике для большинства немагнитных материалов $µ_r$ настолько близко к единице, что этой разницей можно пренебречь.
Проницаемость среды, отличной от вакуума, может быть определена как произведение безразмерного числа на $μ_0$.
Следовательно, $µ = µ_r · µ_0$. Так, например, относительная проницаемость $μ_r$ = 100 означает, что данный материал имеет проницаемость в 100 раз выше, чем значение $μ_0$ (измеряется в Гн/м). Это означает, что для того же нанесенного H материал будет реагировать с B , что в 100 раз больше, чем для вакуума (или немагнитного материала).
Отношение B / H в данной точке кривой намагничивания может быть использовано для расчета значения проницаемости
Для однородных и изотропных материалов проницаемость может быть выражена как скаляр, хотя H и B являются векторами. Для анизотропных материалов проницаемость различна в разных направлениях и для более точного представления необходимо использовать векторный или тензорный подход. Однако на практике часто используется скалярный подход из-за его простоты (и достаточно точных результатов для большинства практических целей, таких как проектирование магнитных цепей).
Когда возбуждение H изменяется во времени, появляются дополнительные эффекты, например вихревые токи, которые влияют на кажущуюся проницаемость. На эффективную проницаемость также влияет анизотропия формы. В магнитных материалах, таких как ферромагнетики, соотношение между B и H может быть нелинейным, зависящим от истории и сильно анизотропным.
Существует множество различных типов проницаемости, которые могут быть получены из измеренных характеристик B-H, необходимых для конкретного практического применения: относительная, амплитудная, реверсивная, импульсная и т. д. Расчет всегда выполняется как отношение $μ = f (ΔB/ΔH )$, где дельта Δ определяет точку отсчета (например, начало графика, положение предыдущего импульса и т. д.)
Магнитомягкие материалы насыщаются, если применяется достаточно сильное возбуждение. Это приводит к уменьшению отношения B/H и, следовательно, проницаемости.
При приближении к полному насыщению относительная проницаемость будет приближаться к единице (т.е. такой же, как для вакуума).
Для магнитотвердых материалов значение магнитной проницаемости малопригодно, и оно не обсуждается с такой же глубиной или даже опускается в некоторых книгах.
Восприимчивость редко используется в инженерных приложениях.
Количество и единицы
Электрические заряды (в форме электронов и протонов) являются основными компонентами, ответственными за все макроскопические электрические явления. Однако в практической электротехнике гораздо полезнее оперировать такими величинами, как напряжение $V$ (связанное с концентрацией и распределением электрических зарядов) и электрический ток $I$ (отражающий движение электрических зарядов).
Комбинация этих двух значений полностью определяет влияние электричества, например, рассеиваемую мощность P , так как $P = V·I$. Дополнительные параметры, такие как сопротивление R , определяют пропорциональность электрического отклика или зависимость V-I (закон Ома) $I = V / R$ для данного материала.
Проводимость G (обратная величине сопротивления, $G = 1 / R$) может быть использована для выражения уравнения в другой, но эквивалентной форме: $I = G·V$.
По аналогии, в технике для количественной оценки эффектов магнетизма в материи, например накопленной или потерянной энергии, требуются как плотность магнитного потока $B$, так и напряженность магнитного поля $H$ (или их эквиваленты). Эти две величины определяются отдельно в Международной системе единиц (СИ), где $H$ соответствует единице измерения ампер на метр (А/м), а $B$ — тесла (Тл).
Плотность энергии в данном магнитном материале можно рассчитать как $E_{density}=B·H$. Проницаемость µ определяет пропорциональность магнитного отклика: $B = µ·H$. Эти соотношения широко используются в инженерном подходе.
Магнитное поле – это понятие энергии, содержащейся в данном объеме пространства. Эта энергия может быть физически и математически описана различными средствами или величинами.
Есть шесть наиболее часто используемых магнитных величин, которые взаимосвязаны, как показано в таблице ниже.
Общее поле Поле, связанное с намагниченным веществом Свойство материала $B$ (Тл)
плотность магнитного потока
( магнитная индукция, магнитное поле )$H$ (А/м)
напряженность магнитного поля
( магнитное поле, напряженность магнитного поля )$J$ (T)
магнитная поляризация
( собственная магнитная индукция, собственная индукция, индукция железа )$M$ (А/м)
намагниченность
( магнитная поляризация )$µ_r$ (безразмерная)
относительная проницаемость$χбезразмерная
восприимчивостьв материи: $$B = µ_r · µ_0 · H$$ $$H = \frac{B}{µ_0} — M$$ $$J = µ_0 · M$$ $$M = χ · \frac{B}{µ_0}$$ $$µ_r = χ + 1$$ $$χ = \frac{µ_0·M}{B}$$ $$B = µ_0 · H + µ_0 · M$$ $$B = µ_0 · H + J$$ $$J = B — µ_0 · H$$ $$M = \frac {B}{µ_0} — H$$ $$µ_r = \frac{B}{µ_0 · H}$$ $$χ = µ_r — 1$$ в вакууме: $$B = µ_0 · H$$ $$H = \frac{B}{µ_0}$$ $$J = 0$$ $$M = 0$$ $$μ_r = 1$$ $$χ = 0$$ $μ_0$ = 4·π·10 -7 (Гн/м) — проницаемость вакуума, $μ = μ_r · μ_0$ (Гн/м) — проницаемость данного материала Энергия магнитного поля
Магнитное поле содержит энергию, объемную плотность которой можно рассчитать по следующему уравнению (для среды с постоянной магнитной проницаемостью).

(14а) 9T \left( \frac{dB}{dt} · H \right) dt $$(Вт/кг) где: $T$ — период (с) возбуждения переменного тока, $f$ — частота (Гц), $D$ — плотность материала (кг/м 3 ),
ед.: H (A /м), В (Т)Возможность временного накопления энергии может быть использована с немагнитным материалом, напр. в воздушном зазоре дросселя или обратноходового трансформатора. В такой магнитопроводе, если $B_{материал} \приблизительно B_{зазор}$ (что обычно имеет место при малом воздушном зазоре), то значение $H$ будет отличаться в множитель относительной магнитной проницаемости материал, поэтому воздушный зазор может хранить значительно больше энергии, чем магнитопровод.
Optimum operating point P for a permanent magnet is where the product B and H reaches maximum BH max
В постоянных магнитах теоретическая максимальная величина плотности энергии, которая может быть получена для данного материала, пропорциональна квадрату значения остаточной намагниченности $B_r = J_r$.
На практике достижимо только около 60% этого значения. 92}{4 · μ_0}$$
(Дж/м 3 )Оптимальная рабочая точка P для постоянного магнита находится там, где произведение B и H достигает максимума BH max .
Трудности с определением магнитного поля
Трудно дать простое определение магнитного или электромагнитного поля.
Прогресс науки и техники базируется на некоторых величинах, которые пока не могут быть точно определены. Например, основной электрический заряд q или время t упоминаются без определения того, что они собой представляют. Ученые могут описать, но все еще не могут объяснить, что такое время или электрический заряд. Предполагается, что они существуют, имеют некоторый физический смысл и измеримы в данной системе единиц.
Магнитное поле может быть создано электрическим током, который сам по себе определяется как поток электрического заряда во времени.
Эмпирически известно, что магнитное поле действует с механической силой на движущиеся заряженные частицы особым образом, описываемым уравнениями Максвелла. Следовательно, действие таких специфических механических сил в конечном итоге определяет наличие или отсутствие магнитного поля.
Или, другими словами, обнаружение магнитного поля можно свести к анализу таких механических сил, действующих на движущиеся электрически заряженные частицы. Это причина того, что в этой статье используется вводное определение, которое относится только к магнитным силам (механическим силам, вызванным магнитным полем). Такое определение кажется несколько замкнутым, но, как указано выше, из-за необъяснимой природы лежащей в его основе физики его нельзя сделать более точным.
По этим причинам многие книги и публикации по магнетизму либо вообще не дают определения, либо используют определение, подобное приведенному выше в этой статье. Типичные примеры приведены в таблице ниже.
Публикация Определение Магнитное поле Определение . Ричард М. Бозорт
ФерромагнетизмМагнит притягивает кусок железа, даже если они не соприкасаются, и это действие на расстоянии считается вызванным магнитным полем. поле или силовое поле. Напряженность силового поля, напряженность магнитного поля или намагничивающая сила H могут быть определены с точки зрения магнитных полюсов: в одном сантиметре от единичного полюса напряженность поля равна одной эрстеде. Фарадей показал, что некоторые свойства магнетизма можно уподобить потоку, и представил бесконечные линии индукции , которые представляют направление и, благодаря их концентрации, поток в любой точке. […] Общее количество линий, пересекающих данную область под прямым углом, является потоком в этой области. Поток на единицу ар – это плотность потока, или магнитная индукция и обозначается символом B. Дэвид С. Джайлс
Введение в магнетизм и магнитные материалыОдной из самых фундаментальных идей в магнетизме является концепция магнитного поля. Когда поле генерируется в объеме пространства, это означает, что происходит изменение энергии этого объема и, кроме того, существует градиент энергии, так что создается сила, которую можно обнаружить по ускорению электрического заряда, движущегося в нем. поле, силой, действующей на проводник с током, крутящим моментом на магнитном диполе, таком как стержневой магнит, или даже переориентацией спинов электронов внутри определенных типов атомов.
Существует несколько способов определения напряженности магнитного поля H. В соответствии с развитыми здесь идеями мы хотим подчеркнуть связь между магнитным полем H и генерирующим электрическим током. Поэтому мы определим единицу напряженности магнитного поля, ампер на метр, в терминах генерирующего тока. Самое простое определение состоит в следующем. Ампер на метр — это напряженность поля, создаваемого бесконечно длинным соленоидом, содержащим n витков на метр катушки и пропускающий ток 1 /n ампер. Когда магнитное поле H создается в среде током, в соответствии с законом Ампера, реакция среды представляет собой ее магнитную индукцию B, также иногда называемую плотностью потока. 
Магнитное поле , Британская энциклопедия Магнитное поле, область вблизи магнитного поля, электрического тока или изменяющегося электрического поля, в которой наблюдаются магнитные силы. Магнитное поле H можно рассматривать как магнитное поле, создаваемое протеканием тока в проводах […] […] магнитное поле B [можно рассматривать] как полное магнитное поле включая также вклад магнитных свойств материалов в поле. Э. М. Перселл, Д. Дж. Морин, Электричество и магнетизм Это взаимодействие токов и других движущихся зарядов можно описать, введя магнитное поле. […] Мы предлагаем продолжать называть $\mathbf{B}$ магнитным полем. Если мы теперь определим векторную функцию $\mathbf{H}(x, y, z)$ в каждой точке пространства соотношением $$ \mathbf{H} \equiv \frac{\mathbf{ B}}{µ_0} — \mathbf{M} $$ […] Что касается $\mathbf{H}$, хотя для него придуманы и другие названия, мы будем называть его полем $\mathbf{H} $, или даже магнитное поле $\mathbf{H}$. 
[…] на любую движущуюся заряженную частицу, оказавшуюся в этом поле, действует сила […], определяемая выражением $$ \mathbf{F} = q·\mathbf{E} + q·\mathbf{v} × \mathbf{B} $$ […] Мы возьмем уравнение в качестве определения $\mathbf{B}$. Название электромагнитное поле используется для обозначения поля, непрерывно изменяющегося во времени. Говорят, что переменное электрическое поле (движущиеся электрические заряды) создает переменное магнитное поле, а переменное магнитное поле, в свою очередь, создает переменное электрическое поле. В результате возникает электромагнитное поле, в котором электрическая и магнитная составляющие неразрывно связаны между собой.
Однако, если, например, магнитное поле создается постоянным магнитом, результирующее поле не меняется со временем, поэтому составляющая электрического поля не создается. Такое поле тогда упоминается как магнитостатическое поле (постоянное во времени), чтобы явно отличить его от «электромагнитного поля» (которое изменяется во времени и сосуществует с переменной составляющей электрического поля).
Различие аналогично анализу электрических цепей с электростатическими эффектами. Если нет изменений в распределении заряда (т. е. нет протекания тока), то анализ называют электростатическим, чтобы отличить его от других случаев.
Магнитное поле вокруг движущегося электрона; распределение магнитного поля можно рассчитать по закону Био-Савара, предполагая, что скорость намного меньше скорости света
В своем узком значении название « магнитное поле » относится только к магнитостатическому полю или магнитной составляющей электромагнитного поля.
Однако в более широком смысле «магнитное поле» также используется для обозначения электромагнитного поля. Это потому, что электромагнитное поле содержит компонент магнитного поля , в котором магнитные силы «наблюдаемы» в соответствии с определением магнитного поля (см. также приведенную выше таблицу с кавычками различных определений).
Более узкое или более широкое значение обычно ясно из контекста, если не определено явно.
Движущийся электрический заряд присоединил к себе магнитное поле, распределение которого подчиняется закону Био-Савара. Такое магнитное поле называется полем скорости и не излучается, если заряд движется с постоянной скоростью. Электростатическое поле простирается до бесконечности как от статического, так и от движущегося заряда.
Однако, когда заряд ускоряется (или замедляется), на протяжении всего времени ускорения и электрическое, и магнитное поля, окружающие заряд, искажаются. Пульсация включает в себя обе составляющие поля и излучается в сторону от заряда, неся с собой некоторую энергию.
Схема, иллюстрирующая создание электромагнитного поля электрическим зарядом: статический заряд (серый маленький кружок в центре) создает электростатическое поле (синяя область), которое статически распространяется в космос.
Внезапное ускорение заряда (темно-синий маленький кружок) создает электромагнитный импульс (красное кольцо), который излучается в космос со скоростью света, а далекое пространство все еще содержит электростатическое поле того времени, когда заряд был неподвижен ( как показано серыми линиями). Заряд движется с постоянной скоростью v создает электрическое и магнитное поле, связанное с зарядом (зеленая область). Линии поля (черные линии) показывают направление и напряженность электрического поля.
Если заряд движется синусоидально, то и излучение принимает синусоидальный характер, что обеспечивает основу для беспроводной передачи информации (эквивалентной некоторому количеству энергии) через объем пространства.
Прием электромагнитных волн представляет собой тот же процесс, но в обратном порядке: электрические и магнитные компоненты поля могут перемещать заряды в антенне и, таким образом, создавать напряжение и ток, которые затем могут обрабатываться соответствующей электронной схемой для восстановления информации.
(беспроводная связь) или энергии (беспроводная зарядка). Резонансные LC-цепи используются для повышения эффективности передачи-приема.
При анализе электромагнитных полей вводятся понятия ближнего поля и дальнего поля. Все магнитостатические эффекты можно рассматривать как возникающие в ближней области поля.
Электромагнитная волна с длиной волны λ , распространяющаяся в направлении x , содержащая компоненту электрического поля E в фазе с магнитным полем 0 B ; все три направления ( E , B и x ортогональны друг другу
Среда магнитного и электромагнитного поля
Статическое магнитное поле проникает в вещество, за исключением сверхпроводников, которые могут вытеснять поле изнутри ( B =0, H >0, M <0), поддерживая поверхностные токи.
Математические уравнения могут использоваться для описания электромагнитного поля либо как волны (электромагнитные волны), либо как частицы (например, фотоны), и оба представления оказались правильными с конкретной экспериментальной точки зрения.
Если электромагнитное поле является волной, то неизвестно, в какой среде должна существовать такая волна, так как она одинаково хорошо распространяется и через вакуум, не содержащий никакой материи.
В квантовых теориях поля, таких как квантовая хромодинамика (КХД), отсутствие элементарных частиц не обязательно должно означать отсутствие какой-либо среды. Например, можно анализировать воздействие электромагнитного поля на вакуум в различных энергетических режимах. В результате такого анализа вакуум больше не является «свободным пространством», и теоретически частицы могут непрерывно создаваться и уничтожаться. Таким образом, это свойство может быть причиной распространения электромагнитной энергии в кажущейся «пустой» среде.
В квантовой теории поля электростатические силы между двумя зарядами можно рассматривать как возникающие из-за обмена виртуальными фотонами, которые представляют собой «флуктуации» пустого пространства.
Линии магнитного поля
См. также основную статью: Линии магнитного поля.
Силовые линии магнитного поля являются теоретическим понятием, и в действительности «линий» не существует. Однако эта концепция очень полезна для визуализации распределения магнитного потока или электрического поля. Линии представляют направление, которое касается направления данной векторной величины, такой как плотность магнитного потока в данном месте.
Если частицы железа поместить вблизи магнита, то они образуют вытянутые структуры, которые следуют линиям, проходящим между магнитными полюсами. Точно так же стрелка магнитного компаса, помещенная рядом с магнитом или электромагнитом, будет следовать контурам, созданным магнитными частицами.
Моделирование МКЭ, иллюстрирующее воображаемые линии магнитного поля вокруг стержневого магнита
Железо.

«линии магнитного поля» простираются в трехмерное пространство вокруг магнита от JanDerChemiker, CC-BY-3.0
По этой причине их также можно назвать «магнитными силовыми линиями», и их можно использовать для визуализации магнитного поля вокруг данного источника при нанесении на заданное поперечное сечение (двумерную плоскость). Плотность линий (например, количество линий на единицу площади) представляет амплитуду (чем ближе линии друг к другу, тем больше амплитуда). Линии никогда не могут пересекаться, и каждая линия представляет собой замкнутую кривую (т. е. не имеет ни начала, ни конца). Линии являются теоретической концепцией и поэтому могут простираться на бесконечную длину.
С чисто теоретической точки зрения силовые линии магнитного поля могут простираться до бесконечности, что означает, что один движущийся электрон может создавать магнитное поле, распространяющееся на всю вселенную, а если имеет место электромагнитное излучение, электромагнитное поле действительно может распространяться на огромные расстояния по всей вселенной.
.
Однако напряженность магнитного поля уменьшается по мере удаления от источника. Поэтому на практике поля становятся исчезающе малыми на достаточно больших расстояниях от данного источника.
Аналогичная концепция используется для силовых линий электрического поля, но они начинаются с положительных зарядов и заканчиваются с отрицательными (линии электрического поля имеют источники, силовые линии магнитного поля — нет).
Магнитный диполь и момент
Магнитный дипольный момент $\vec m$ петли тока $\vec I$ с площадью петли $A$ и единичным вектором $\vec a$ (нормально к $А$)
Круговая петля с током — одна из простейших цепей, создающих магнитное поле. На большом расстоянии от такой петли поле подобно полю, создаваемому магнитный диполь из двух гипотетических магнитных монополей с противоположными зарядами, разнесенными на заданное расстояние (по аналогии с диполем, созданным двумя электрическими зарядами).
Магнитный момент будет действовать на магнитный диполь, помещенный во внешнее магнитное поле. Действующий момент будет пропорционален векторному произведению двух векторов: магнитного момента и плотности потока.
Магнитные моменты важны при анализе магнитных явлений, потому что орбита электрона в атоме в некотором смысле аналогична петле тока, следовательно, с ней связан магнитный момент. Эта аналогия лежит в основе объяснения диамагнетизма, при котором на орбитальные «петлевые токи» электронов воздействует внешнее магнитное поле.
Магнитные столбы
Простейший магнитный диполь создается петлей тока. Силовые линии, входящие в петлю с одной стороны, образуют южный магнитный полюс, а те, которые выходят из петли с другой стороны, создают противоположный северный магнитный полюс, так что линии указывают с севера на южный магнитный полюс.
Магнитные полюса создаются для любого контура электрического тока
Стержневой магнит с маркировкой магнитных полюсов N и S
Правило правой руки определяет направление и смысл векторов, и общепринятое соглашение состоит в том, что если смотреть на токовую петлю с током, текущим против часовой стрелки, то это северный полюс.
В то же время, если смотреть с другого конца, будет казаться, что ток течет по часовой стрелке, и будет южный полюс.
Соглашение также таково, что конец стрелки компаса, указывающий на север, считается самим северным полюсом. Поскольку противоположные полюса притягиваются, то на географическом северном полюсе Земли находится магнитный южный полюс. Это просто следствие принятого соглашения об именах.
Магнитные полюса могут быть созданы в разных местах благодаря наличию магнитного материала. Из-за магнитной индукции материал будет намагничиваться и сам станет источником магнитного поля, простым примером является стержневой магнит.
Расположение магнитных полюсов зависит от геометрии магнитной цепи, ее магнитной истории, распределения источников магнитодвижущей силы и размагничивающего фактора цепи.
Магнитные монополи были теоретически предложены Полем Дираком в 1931 году как возможное объяснение квантования электрического заряда. До сих пор все эксперименты по прямому обнаружению существования магнитных монополей не увенчались успехом.

Тип магнетизма
По определению, магнитные эффекты вызываются магнитным полем, и все такие явления называются магнетизмом. Название «электромагнетизм» используется взаимозаменяемо с «магнетизмом», поскольку изменения электрического поля всегда создают магнитное поле.
Однако слово «магнетизм» также имеет несколько различных значений. Вся материя, состоящая из атомов, проявляет некоторый тип магнитного поведения, из которых существует несколько основных типов, зависящих от типа используемых химических элементов, атомной и кристаллической структуры, температуры и т. д. Все они возникают из-за взаимодействия собственных магнитных диполей в атомах, благодаря магнитному полю:
диамагнетизм
парамагнетизм
ферромагнетизм
ферримагнетизм
антиферромагнетизм
суперпарамагнетизм
и другие, менее технические значения: суперферромагнетизм, супердиамагнетизм, гелимагнетизм, метамагнетизм, микромагнетизм, спиновое стекло, спиновый лед
Уравнения Максвелла
См. также основную статью: Уравнения Максвелла.
Уравнения Максвелла в дифференциальной форме Закон Гаусса для электростатики $$ \text{div } \mathbf{E} = \frac {\rho_{charge}}{\epsilon_0}$$ Закон Гаусса для магнетизма $$ \text{div } \mathbf{B} = 0$$ Закон электромагнитной индукции Фарадея $$ \text{curl } \mathbf{E} = — \frac {\partial \mathbf{B}}{\partial t}$$ Круговой закон Ампера $$ \text{curl } \mathbf{B} = \mu_0 · \mathbf{J} + \mu_0 · \epsilon_0 · \frac {\partial \mathbf{E}}{\partial т}$$ Уравнения Максвелла математически полностью описывают взаимосвязь между электрическим и магнитным полями. Ранняя версия этих уравнений была впервые сопоставлена шотландским физиком Джеймсом Клерком Максвеллом. Впоследствии они были унифицированы и выражены в векторной записи Оливером Хевисайдом, так что сегодня используются четыре фундаментальных уравнения, физический смысл которых можно резюмировать следующим образом:
Закон Гаусса для электростатики связывает распределение электрического заряда с электрическим полем,
Закон Гаусса для магнетизма утверждает, что магнитных монополей не существует,
Закон электромагнитной индукции Фарадея утверждает, что электрические поля создаются переменными магнитными полями,
Контурный закон Ампера гласит, что магнитные поля создаются электрическими токами или изменяющимися электрическими полями.
Уравнения могут быть математически записаны разными способами (например, в дифференциальной или интегральной форме) или в разных единицах (например, СГС или МКС). Их также можно сформулировать на основе более фундаментальной теории квантовой электродинамики.
В вакууме уравнения упрощаются, потому что нет ни зарядов, ни токов, ни свойств материала.
Генерация магнитного поля
Существует три основных источника магнитного поля, все они неразрывно связаны с электрическими зарядами и их свойствами:
электрический ток (макроскопический)
магнитные моменты субатомных частиц (собственные магнитные дипольные моменты, такие как спиновой момент электрона)
испускание фотонов (электромагнитное излучение) из-за девозбуждения электронов в атомах.
Сила магнитного поля, действующая на магнитные полюса (соответственно отклоняется положение висящего магнита), слева направо: одинаковые полюса отталкиваются, противоположные полюса притягиваются, гвоздь (мягкий ферромагнитный материал) притягивается намагничивается и притягивается к любому полюсу магнита, сила на немагнитных материалах, таких как пластик и медь (без электрического тока), как правило, незначительна, электромагнитная катушка с током может отталкивать или притягивать магнит (в зависимости от полярности тока) , а сила на немагнитную нержавеющую сталь (например, типа 316) пренебрежимо мала
По электрическому току
Компасы обнаруживают магнитное поле внутри и вокруг катушки с электрическим током
Макроскопически генерация магнитного поля связана с неуравновешенным движением электрических зарядов.
Например, в проводнике положительные заряды остаются связанными преимущественно с неподвижными атомами, а электроны могут свободно двигаться.
При подаче напряжения электроны дрейфуют и генерируют магнитное поле, распространяющееся на большие расстояния вокруг такого тока. Каждый отдельный электрон и каждый отдельный движущийся электрический заряд (положительный или отрицательный) создает вокруг себя магнитное поле.
В практических приложениях общее количество тока может быть увеличено за счет использования нескольких витков в обмотке. Например, ток на уровне миллиампер можно сделать эквивалентным нескольким амперам, используя достаточное количество витков (это значение 9).0639 N в уравнении (10)).
Все электрические токи генерируют магнитное поле, и даже очень слабые электрические сигналы посылаются в нервную систему, а нейроны генерируют обнаруживаемые магнитные поля. Такую активность можно обнаружить с помощью устройств SQUID, чтобы можно было провести магнитоэнцефалографию.

Ток в проводе можно измерить с помощью трансформатора тока путем обнаружения магнитного поля вокруг провода
Меньший ток можно использовать для создания сильного магнитного поля, используя несколько витков провода (как в катушке этого реле)
Электромагнит — источник магнитного поля
Изменение электрического поля приводит к генерации изменяющегося магнитного поля, и наоборот. Таким образом создается электромагнитное поле, включающее в себя как электрическую, так и магнитную составляющие. Высокочастотные синусоидальные токи (с некоторой модуляцией) могут использоваться для излучения электромагнитных волн от и к антеннам.
Молния – это внезапный разряд электрического тока, генерирующий импульс магнитного поля от Nico36, Public Domain
намагниченный кусок железа, притягивающий и удерживающий
В природе примером генерации магнитного поля является молния, представляющая собой внезапный разряд электрического тока, создающий вокруг себя импульс магнитного поля, а также электромагнитные волны широкого спектра, включая видимый свет.
Такой магнитный импульс способен намагничивать природные минералы, такие как магнетит.
Эти естественные эффекты были первыми проявлениями магнетизма, которые позволили людям открыть, приручить и использовать магнитные и электромагнитные эффекты.
By intrinsic magnetic moments
Simplified illustration of electron’s orbital magnetic moment $\vec m_o$ and spin magnetic moment $\vec m_s$
На атомном и субатомном уровне такие частицы, как электрон, протон или нейтрон, обладают магнитным моментом.
Магнитные моменты можно концептуально представить как движение электрона (орбитальное или вращательное), которое было бы эквивалентно электрическому току. Однако эти эффекты не следуют классической физике — вместо этого они являются квантовыми явлениями.
Следовательно, они также являются источниками магнитного поля и соответственно взаимодействуют друг с другом.
При соответствующих условиях взаимодействия достаточно сильны, чтобы спины электронов выровнялись параллельно друг другу, что привело к ферромагнетизму, ответственному за большинство «магнитных» эффектов в обычном понимании.
Ферромагнитные материалы (так называемые магнитомягкие материалы) обладают относительно высокой магнитной проницаемостью, поэтому они реагируют большим значением B для того же возбуждения, что и H (по сравнению с неферромагнитными материалами). По этой причине они используются для концентрации и проведения магнитного поля, чтобы можно было создать подходящую магнитную цепь, такую как в электромагните, трансформаторе или электродвигателе.
Постоянные магниты используются в двигателях, генераторах, приводах, громкоговорителях, держателях, игрушках и т. д.
Если требуются очень сильные магнитные поля, то полезность ферромагнетиков уменьшается.
Поля, превышающие 3 Тл, могут быть созданы с помощью электромагнитов Биттера, сверхпроводящих магнитов, импульсных методов или методов сжатия магнитного потока. Они способны создавать магнитные поля без помощи магнитного сердечника, но за счет других параметров, таких как очень высокие уровни электрической мощности, криогенное охлаждение, очень короткая длительность импульса и т. д.
Постоянный магнит представляет собой ферромагнитный материал, который изготовлен таким образом, чтобы максимизировать накопление энергии. Обычно это достигается за счет соответствующего химического состава и состава кристаллов, которые препятствуют движению доменных стенок, чтобы максимизировать коэрцитивную силу. В процессе намагничивания внутренние спины перестраиваются так, что их векторная сумма приводит к значительной магнитной поляризации.
Антенна в мобильном телефоне может быть просто плоской медной полосой (0,2 × 10 × 30 мм)
После удаления внешнего поля постоянные магниты сохраняют намагниченность и, таким образом, становятся новым источником магнитного поля без необходимости в источнике питания.
Для некоторых приложений нет необходимости в магнитных сердечниках или их использование нецелесообразно. Большинство телекоммуникаций, основанных на электромагнитных волнах (например, мобильный телефон), могут использовать неферромагнитные антенны для передачи и приема электромагнитных сигналов.
Затем электромагнитное поле передается через непроводящие среды (воздух, вакуум, строительные материалы, стекло). Проводящие материалы вызывают поглощение или отражение волн. Имеют место и другие волновые явления, такие как преломление и дифракция.
Антенны приводятся в действие электрическими токами высокой частоты (обычно от кГц до диапазона кГц, в зависимости от применения).
По фотонному излучению
Электрон переходит в более высокое энергетическое состояние, поглощая квант энергии, и высвобождается фотон, когда электрон переходит на более низкий энергетический уровень.
Фотон — это квант электромагнитной энергии, и, как и все электромагнитные волны, он содержит компоненты магнитного и электрического поля.
Электроны в атомах занимают квантованные энергетические уровни, и если все электроны занимают нижние позиции, говорят, что атом находится в основном состоянии.
Энергия может быть поглощена атомом электронами, перескакивающими на более высокий энергетический уровень. А если есть незанятый нижний энергетический уровень, то есть некоторая вероятность, что такой возбужденный электрон прыгнет вниз, испустив при этом фотон. Энергия такого фотона напрямую связана с разницей энергий между двумя состояниями электрона. Таким образом можно генерировать фотоны очень высокой энергии, с энергией жесткого рентгеновского излучения и выше.
Используя упрощенную аналогию, прыжок электрона — это движение, требующее ускорения, поэтому в некотором смысле это сродни генерации электромагнитной волны за счет электрического тока, как описано выше.
Однако эта аналогия также неверна, потому что аналогия классической физики не может полностью представить квантовое по своей сути явление испускания фотона.
Высокоэнергетические процессы, такие как молния, создают плазму с сильно возбужденными электронами, которые излучают свет, когда перескакивают на более низкие энергетические уровни. По той же причине пламя и огонь производят фотоны, причем цвет света зависит от вовлеченных химических компонентов.
Однако даже обычное тепло способно возбуждать электроны, а вся материя выше абсолютного нуля излучает электромагнитное излучение. На этом основана работа тепловизионных камер, обнаруживающих инфракрасное излучение. Если вещество достаточно горячее, оно светится в видимом человеческому глазу спектре.
Магнитное поле и релятивистские эффекты
Магнитное поле или его эффекты зависят от системы отсчета: на верхнем изображении показан провод (серый) с положительными зарядами в неподвижном состоянии и отрицательными зарядами в движении — магнитная сила F м толкает один движущийся заряд к проводу; на нижнем изображении система отсчета перемещается с движущимся зарядом (поэтому этот заряд остается неподвижным) — магнитная сила исчезает, и отрицательный заряд прижимается к проводу из-за электростатической силы F e потому что в проводе изменяется концентрация зарядов (из-за лоренцева сокращения)
Существование магнитного поля зависит от системы отсчета.
Магнитная сила зависит от скорости движущегося заряда. Поэтому, если инерциальная система отсчета (без ускорения) выбрана такой, что она движется вместе с зарядом, то заряд становится неподвижным и на него в этот момент не действует магнитная сила.
Из-за лоренцева сокращения из-за релятивистских эффектов кажущаяся плотность электрических зарядов изменяется, так что возникает электростатический дисбаланс и вместо магнитной силы может появиться электростатическая сила.
Движение электронов внутри атома не может быть описано классической физикой, но требует квантовой механики, которая также должна учитывать релятивистские эффекты.
Решения уравнений Максвелла, включающие замедление времени, требуют вывода очень сложных математических уравнений.
Хотя само существование магнитного поля связано с релятивистскими эффектами, для большинства практических целей и конструкций (особенно на более низких частотах) анализ можно свести к упрощенным случаям, безопасно игнорируя принципы относительности.
Это похоже на законы движения Ньютона, для которых при обычных скоростях релятивистскими эффектами можно пренебречь.
См. также
Электромагнетизм
Напряженность магнитного поля
Плотность потока
Путаница между B и H
Линии магнитного поля
Магнитные материалы
Внешние видеоматериалы
Ссылки
1) Магнитное поле, Британская энциклопедия, {дата обращения 27 ноября 2013 г.}
2) 2) 2) , 2) , 2) , 2) , 2) , 2) , 2) , 2) , 2) Дэвид С. Джайлс, Введение в магнетизм и магнитные материалы, 2-е издание, CRC Press, 1998, ISBN 9780412798603
3) , 3) Никола А. Спалдин, Магнитные материалы, основы и приложения, второе издание, Cambridge University Press, 2011, ISBN 9780521886697
4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) , 4) Э.
М. Перселл, Д.Дж. Морин, Электричество и магнетизм, 3-е издание, Cambridge University Press, 2013, ISBN 9781107014022
5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) , 5) Дэвид Дж. Гриффитс, Введение в электродинамику, 4-е изд., Пирсон, Бостон, 2013, ISBN 0321856562
6) Алан Джеффри, Advanced Engineering Mathematics, Academic Press, стр. 2, 2008 . 626
7) Производные единицы, выраженные в базовых единицах, брошюра СИ, {по состоянию на 6 января 2014 г.}
8) Единицы со специальными названиями и символами; единицы, которые включают специальные названия и символы, брошюра SI, {по состоянию на 6 января 2014 г.}
9) , 9) , 9) Дэвид Тонг, Электромагнетизм, Кембриджский университет, часть IB и часть II. Редди, К.
М. и другие. Прогресс в синтезе тонких пленок уникального магнитомягкого высокоэнтропийного сплава CoCuFeNiZn. Научный доклад 11, 8836 (2021)
11) Rajasekhar Madugundo, Ozlem Koylu-Alkan, and George C. Hadjipanayis, «Постоянные магниты на основе Mn-Al-C, полученные различными методами», AIP Advances 6, 056009 (2016)
6 ) T.M. Pekarek, P.S. Edwards, T.L. Olejniczak, C. Lampropoulos, I. Miotkowski, and A.K. Ramdas, «Магнитные свойства слоистого III-VI разбавленного магнитного полупроводника Ga1-xFexTe», AIP Advances 6, 056222 (2016)
13) , 13) , 13) IEEE Magnetics, MAGNETIC UNITS, {дата обращения: 01.05.2021}
14) Zhang, Y., Zuo, T., Cheng, Y. et al. Высокоэнтропийные сплавы с высокой намагниченностью насыщения, удельным электрическим сопротивлением и ковкостью. Sci Rep 3, 1455 (2013)
15) Y. Wu, X. L. Dong, H. X. Yang, X. J. Wang, X.
J. Huang, J. Q. Li, F. Zhou, X. J. Zhou, and Z. X. Zhao, «Магнитный переход в α-NaCuPO4 с цепями Cu-O», AIP Advances 2, 032172 (2012)
16) Джи Чен, Мансур Бин Абдул Джалил и Сенг Гхи Тан, «Спиновый крутящий момент на поверхности графена при наличии спин-орбитального расщепления», AIP Advances 3, 062127 (2013)
0 17) , 17) Bureau International des Poids et Mesures, Международная система единиц (СИ), 9-е издание, 2019 г., {дата обращения: 10.04.2021}
18) , 18) , 18) Славомир Туманьски, Справочник по магнитным измерениям, CRC Press / Taylor & Francis, Boca Raton, FL, 2011, ISBN 9780367864958
19) , 19) , 19) , 19) , 19) , 19) С. Зурек, Характеристика магнитомягких материалов при намагничивании вращением, CRC Press, 2019, ISBN 97803678
20) , 20) , 20) , 20) Марцин Леонович, Ежи Й.
Выслоцкий, Современные магниты, технологии, механизмы коэрцитивной силы, приложения (на польском языке: Współczesne magnesy, Technologie, Mechanizmy koercji, Zastosowania), Wydawnictwa Naukowo-Techniczne, Варшава, 2005, ISBN 3 0926
21) Мэри Энн Уайт, Физические свойства материалов, второе издание, CRC Press, 2011, ISBN 9781439866511, с. 359
22) Производные единицы, выраженные в базовых единицах, брошюра СИ, {по состоянию на 6 января 2014 г.} единицы, которые включают специальные названия и символы, брошюра SI, {по состоянию на 6 января 2014 г.}
24) , 24) , 24) Б.Д. Каллити, К.Д. Грэм, Введение в магнитные материалы, 2-е издание, Wiley, IEEE Press, 2009, ISBN 9780471477419
25) Райнер Хильзингер, Вернер Родевальд, Магнитные материалы, основы, продукты, свойства, приложения, VAC Vacuumschmelze201, Publicis , ISBN 9783895783524
26) Бхаг Сингх Гуру, Хусейн Р.
Хизироглу, Основы теории электромагнитного поля, Cambridge University Press, 2004, ISBN 9781139451925, с. 1
27) Ричард М. Бозорт, Ферромагнетизм, IEEE Press, 2003, ISBN 0780310322, с. 1-3
28) Магнитное поле, Британская энциклопедия онлайн, {дата обращения: 07.03.2020}
29) На момент написания этой статьи не было отдельной записи под названием «напряженность магнитного поля» {проверено 7 марта 2020 г.}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г.}.
30) На момент написания этой статьи не было отдельной записи под названием «плотность магнитного потока» {дата обращения: 07.03.2020}. Краткое определение было включено в статью «Магнитное поле» Британской энциклопедии онлайн, {по состоянию на 07 марта 2020 г.}.
31) Мехта Нирадж, Прикладная физика для инженеров, PHI Learning Pvt.
Ltd., ISBN 9788120342422, с. 541
32) Джулиус Адамс Стрэттон, Электромагнитная теория, John Wiley & Sons, 2007, ISBN 9780470131534, с. 225
33) C. Максфилд и др., Электротехника: все знать, Newnes, 2011, ISBN 9780080949666, с. 1004
34) Натан Ида, Инженерная электромагнетика, Springer Science & Business Media, 2004, ISBN 9780387201566, с. 1149
35) Элизабет Вербос, Вакуумные свойства КХД в электромагнитном поле, Мэрилендский университет, Колледж-Парк. Физика, ISBN 978110
52, с. 1-32
36) Махмуд Нафуси, Виртуальные частицы, включая виртуальные фотоны, https://medium.com / виртуальные частицы, {дата обращения: 15 мая 2021 г.}
37) Джон Битесон , Визуализация магнитных полей, Решатели численных уравнений в действии, Academic Press, 2001, ISBN 9780120847310, с. 7-9
38) , 38) Джо Розен, Энциклопедия физики, Infobase Publishing, 2009, ISBN 9781438110134, с.
198-200
39) Trower, W., Магнитное обнаружение магнитных монополей, IEEE Transactions on Magnetics, vol. 19 (5), 1983, с. 2061
40) М. В. Рэй, Э. Руококоски, С. Кандель, М. Мёттонен, Д. С. Холл, Наблюдение монополей Дирака в синтетическом магнитном поле, Nature, 505, январь 2014 г., с. 657
41) Уравнения Максвелла, Британская энциклопедия, {по состоянию на 18 декабря 2013 г.}
42) , 42) , 42) Махеш С. Джайн, Учебник инженерной физики, часть 2, PHI Learning Pvt. ООО, с. 4.42-4.70, ISBN 9788120340602
43) Дипак Л. Сенгупта, Валдис В. Лиепа, Прикладная электромагнетика и электромагнитная совместимость, John Wiley & Sons, 2005, ISBN 978024517462 28
44) Хьюберт Прейсль, Магнитоэнцефалография, Gulf Professional Publishing, 2005, ISBN 9780123668691, с. хи
45) Бхаг Сингх Гуру, Хусейн Р.
Хизироглу, Основы теории электромагнитного поля, Cambridge University Press, 2004, ISBN 9781139451925, с. 8
46) JFW Bowles, R.A. Howie, DJ Vaughan, J. Zussman, Породообразующие минералы, Лондонское геологическое общество, 2011, ISBN 97818623, с. 403
47) , 47) J.M.D. Коуи, Магнетизм и магнитные материалы, Cambridge University Press, 2010, ISBN 9780521816144
48) Тапан Чаттерджи, Рассеяние нейтронов на магнитных материалах, Gulf Professional Publishing, 2005, ISBN 9780080457055, с. 3
49) Алмадена Щелканова, Стюарт А. Вольф, Ив Идзерда, Магнитные взаимодействия и спиновой перенос, Springer, 2003, ISBN 9780306473524, с. 316
50) , 50) Сошин Чикадзуми, Физика ферромагнетизма, 2-е издание, Oxford University Press, 2009 г., ISBN 9780199564811
51) Уоррен Л. Штуцман, Гэри А. Тиле, Теория и конструкция антенн, John Wiley & Sons, 2012, ISBN 9780470576649, стр.
88
52) , 52) Чарльз Х. Холброу, Джеймс Н. Ллойд, Джозеф К. Амато, Энрике Гальвес, М. Элизабет Паркс, Современная вводная физика, 2-е изд., Спрингер, Нью-Йорк, ISBN 97803877
53) , 53) Ринальдо М., Нири и Вудман. (2020, 5 ноября). Электрические и магнитные поля и специальная теория относительности, Libretexts.org, {дата обращения: 10 мая 2021 г.}
Магнитное поле, Теория магнетизма, Counter
5 фактов о том, что увеличивает силу магнитного поля? – Lambda Geeks
Сила проводника с током в магнитном поле увеличивается за счет увеличения тока, возникающего в проводнике за счет увеличения энергии магнитного поля. Магнитное поле и напряженность магнитного поля обозначаются буквами B и H.
Магнитное поле может полностью воздействовать на электрический заряд, если его бегущий заряд генерирует магнитное поле. Эта сила увеличивается с одним, а с другим увеличивается заряд и напряженность магнитного поля.
Что увеличивает магнитную силу магнита?Кроме того, сила больше, когда заряды имеют большие скорости. Формула силы, выраженная как F= qvB sinƟ, где Ɵ — угол меньше 180 градусов.
Подводя один магнит к другому, насыпь является примером, насыпные магниты будут функционировать как один большой магнит и использовать более высокие магнитные достижения. При соединении дополнительных магнитов прочность увеличивается, поскольку длина насыпи совпадает с диаметром.
По мере наложения дополнительного заряда в дополнительном или большем движении, стойкость магнитного поля увеличивается. Мы можем усилить магнит, связав катушку куском железа, например железным гвоздем, подведя дополнительные витки к катушке и увеличив ток, протекающий через катушку.
Магнит, притягивающий монеты Изображение предоставлено: pixabayРассмотрим стержневой магнит. Поднесите железный гвоздь к магниту; по мере того, как мы приближаем магнит к гвоздю, в какой-то момент гвоздь движется к магниту и прилипает к магниту, это из-за магнитной силы притяжения магнита и гвоздя увеличивается.
Магнитное поле усиливается путем связывания катушки с железом Изображение предоставлено pixabay Что увеличивает магнитную силу Земли?Гвоздь прикладывает эту силу; следовательно, это магнитная сила.
Заземляющая втулка нагревается и расплывается. Следовательно, конвективный ток в земной ступице увеличивает магнитную силу Земли. Магнитная сила Земли также увеличивается за счет электрического тока в водном внешнем центре или жидком внешнем ядре. Общая магнитная сила Земли составляет от 25 000 до 65 000 нТл.
Центр Земли состоит из расплавленной жидкости, состоящей из таких металлов, как железо и никель. Из-за механизма сбора эти металлы имеют множество свободных электронов, начиная с этих сплавленных металлов. Это означает, что сплавленные жидкости вместе со свободными электронами начинаются с центра земли.
Движущиеся электроны называют током, который создает магнитное поле вокруг объекта; следовательно, благодаря этому жесту свободные электроны могут увеличить магнитную силу Земли.
Магнитная сила земли Изображение предоставлено: pixabay Что увеличивает силу магнитного поля между двумя пластинами?Земляной хаб имеет температуру более 1043 К.
Ток, протекающий в пластинах, и плотность потока в воздушном зазоре ответственны за увеличение силы магнитного поля между двумя пластинами. Если расстояние между двумя пластинами увеличить вдвое, магнитные силы между ними упадут до четверти начального значения.
Если две пластины заряжаются, происходит изменение электрического поля. Это модифицированное электрическое поле порождает точно такое же магнитное поле, приобретаемое током по проводу. Линии магнитного поля загибаются по окружности по траектории между пластинами.
Сила магнитного поля между двумя пластинами увеличивается, потому что ток течет в обратном направлении в двух пластинах и создает магнитное поле B путем размещения или наложения. Поле, в результате, на одной из пластин всего 21В.
Что увеличивает силу магнитного поля провода?Сила, действующая на пластину, составляет 21B×i×длина×ширина=2µ0B2 на единицу площади.
Величина силы, действующей на проводник с током, увеличивается при увеличении емкости магнитной связи. Безмерность магнитной силы также зависит от размеров провода в магнитном поле. Чем выше провод в магнитном поле, тем больше сила на проводе.
Плавкий провод, несущий электрический ток, объединил с собой магнитное поле. Безмерность магнитного поля, создаваемого в точке доступа, увеличивается по мере увеличения тока и длины провода. Магнитное поле, создаваемое допустимым током в проводнике, уменьшается по мере удаления его от него.
Небольшие магнитные поля, приобретаемые током во всех витках катушки, суммируются друг с другом, создавая мощное всестороннее магнитное поле. Мощность магнитного поля над соленоидом можно увеличить, увеличив несколько витков катушки, увеличив ток.
Сила магнитного поля в проводе увеличивается Изображение предоставлено: pixabay Что увеличивает силу магнитного поля объекта?Два объекта, имеющих заряд с одинаковой ориентацией движения, содержат между собой вынужденную магнитную силу, увеличивающую силу магнитного поля объекта. Следовательно, магнитная сила является развитием электромагнитной силы и вызывается движением зарядов.
Магнитные поля — это места, где Объект отображает магнитное воздействие. Поля изменяют соседние объекты через вещи, называемые силовыми линиями магнитного поля. Магнитный объект может захватить или оттолкнуть другой магнитный объект. Магнитные силы не имеют отношения к гравитации.
Невидимое положение вокруг магнитного объекта относительно него или отталкивание магнитного объекта от него называется магнитным полем. Емкость магнита можно увеличить, увеличив количество проволочных петель на железной ступице и увеличив ток или напряжение.
Что увеличивает силу магнитного поля на движущийся заряд?Магнитное поле может воздействовать на электрический заряд, только если он находится в движении, только так, как движущийся заряд создает магнитное поле. Эта сила увеличивается как с увеличением заряда, так и с силой магнитного поля. Кроме того, магнитное поле — это сила, которая выше, когда заряды имеют большие скорости.
Магнитная сила не может быть приложена. Следовательно, он каждый раз находится под прямым углом к скорости. Силы нет, если скорость объекта совпадает с направлением вектора магнитного поля. Сила увеличивается с зарядом, скоростью и емкостью магнитного поля.
Магнитное поле, создаваемое движущимися зарядами, представляет собой электрическое поле, являющееся следствием специальной теории относительности. Правило правой руки определяет направление магнитного поля. Сила определяется зарядами, умноженными на произведение скорости и магнитного поля.
Наиболее часто задаваемые вопросы Что такое магнитное поле?Магнитное поле определяется как «часть пространства, примыкающая к магнитному телу или телу с током, в котором возникает магнитная форма. В результате тело или ток могут быть идентифицированы».
Ряд магнитных частиц или движение электрического заряда, ограниченное силой магнетизма, приводит в действие. Магнитное поле — это векторная область в окружении магнита, электрического тока или запрещающего электрического поля, в которой заметны магнитные силы.
Магнитные поля, подобные земным, заставляют магнитные стрелки компаса и еще один вечный магнит выстраиваться в соответствии с ориентацией поля. Магнитные поля заставляют электрически заряженные молекулы двигаться по округлой или спиральной траектории.
Как лечат магниты?Магниты не лечат. Магнитно-резонансная томография применяет очень мощные магнитные поля и еще более мощные, чем может генерировать обычный магнит; магнитно-резонансная томография не оказывает прямого влияния на состояние больного и может иметь косвенный эффект в качестве инструмента атрибуции.

Железо в нашей крови находится на слишком низком уровне конвергенции, чтобы быть поврежденным слабыми магнитными полями обычных магнитов. Более того, молекулы железа в нашей крови сдерживаются молекулами гематина. Атом железа в молекуле гематина удерживается химической связью, опосредованной состоянием электронов, что приводит к снижению ферромагнитных характеристик атома железа.
Дефицит исцеляющих персонажей для магнитов был представлен много раз через командную демонстрацию.
Магнитно-резонансная томография Изображение предоставлено: pixabay Какое самое сильное магнитное поле когда-либо наблюдалось?Самые сильные магнитные поля, которые воспринимаются с точки зрения защиты, находятся в магнетарах, а магнетары — это нейтронные звезды со странно большими или высокими магнитными полями, примерно в 100 000 раз превышающими магнитное поле обычного пульсара.
Чрезвычайно сильное магнитное поле скрыто под и снаружи звезды, но внезапно вырывается наружу, создавая чрезвычайно сильную кратковременную вспышку твердого рентгеновского излучения, а также значительно улучшая обычное рентгеновское
переменное состояние.
Почему все металлы магнитятся?В остальное время магнетары сравнительно малоподвижны и в последнее время вращаются со сравнительно небольшими дипольными полями.
Магнетизм в металле создается неравномерным рассеянием электронов в молекуле определенных компонентов. Неравномерная циркуляция и движение, возникающие в результате этого неравномерного рассеяния электронов, передают заряд внутрь молекул туда и обратно, создавая магнитные диполи.
Магнитные материалы постоянно собираются из металла, но не каждый металл является магнитным. Железо магнитное, поэтому каждый металл и железо в нем будут пленены магнитом. Сталь состоит из железа, так что этот стальной зажим для драгоценных камней тоже будет притягиваться к магниту. Большинство разнородных металлов, таких как алюминий, золото и медь, не обладают магнитными свойствами.
Все металлы не являются магнитными, потому что при применении они должны быть магнитными материалами, и они должны иметь поглощательную способность больше, чем у свободной площади, которая, как считается, имеет поглощательную способность на единицу большую, чем единица, означает, что изменчивость предпочтительно может происходить вместе с материалом, чем пройти через область рядом с ним.


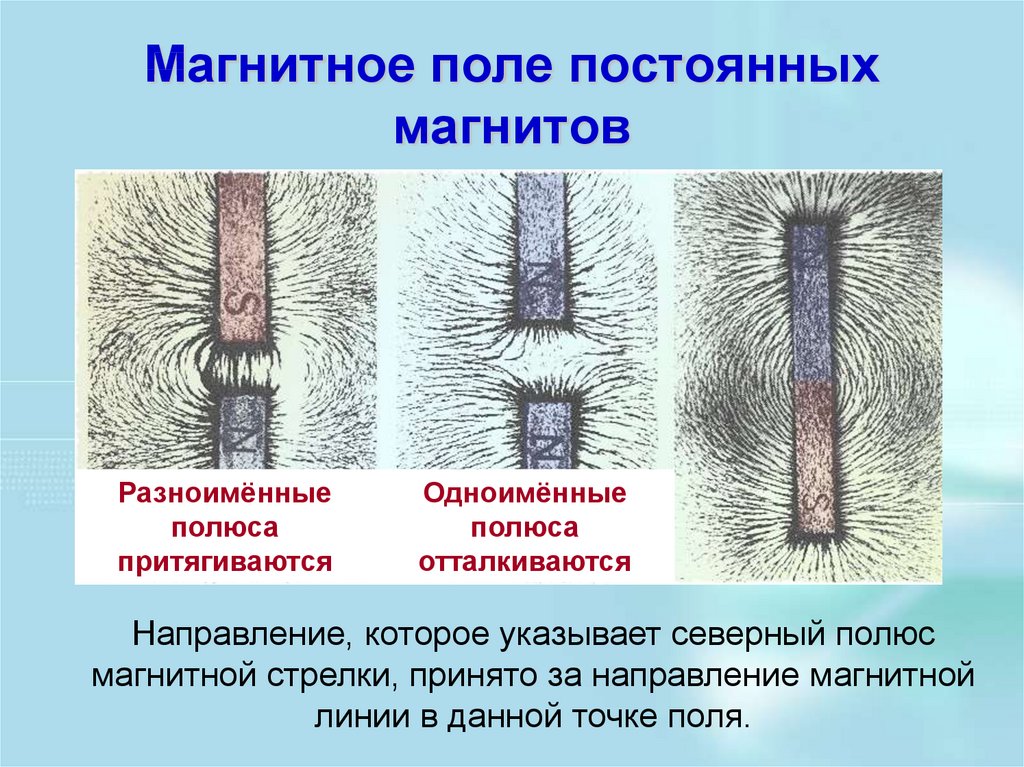
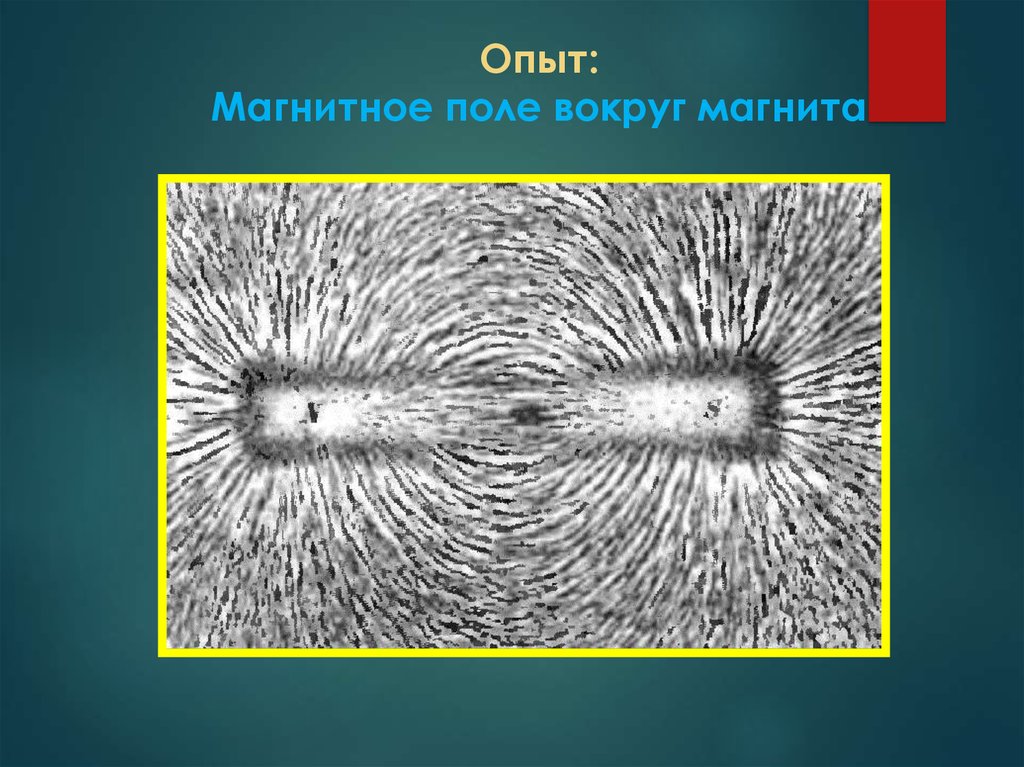
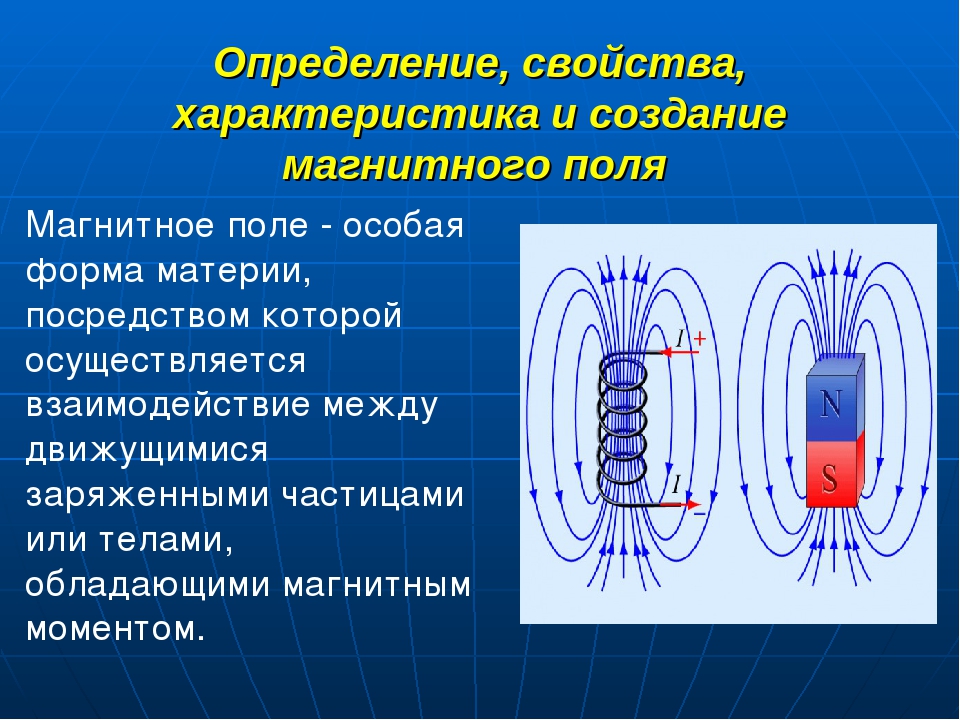 также
также
 56, 1899–1900, общественное достояние
56, 1899–1900, общественное достояние 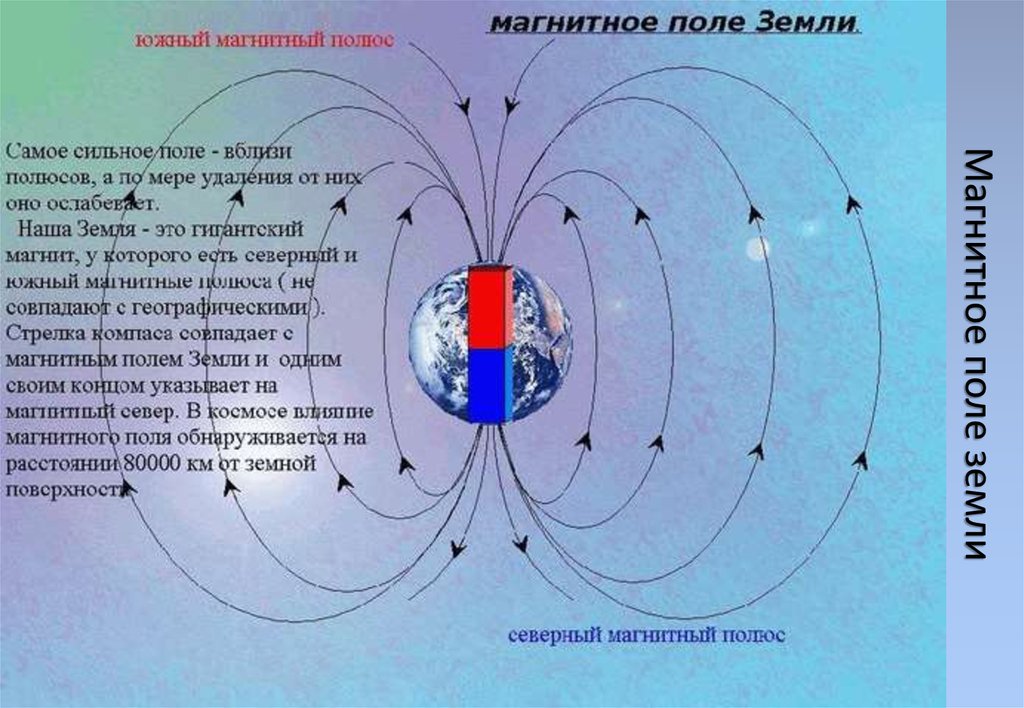
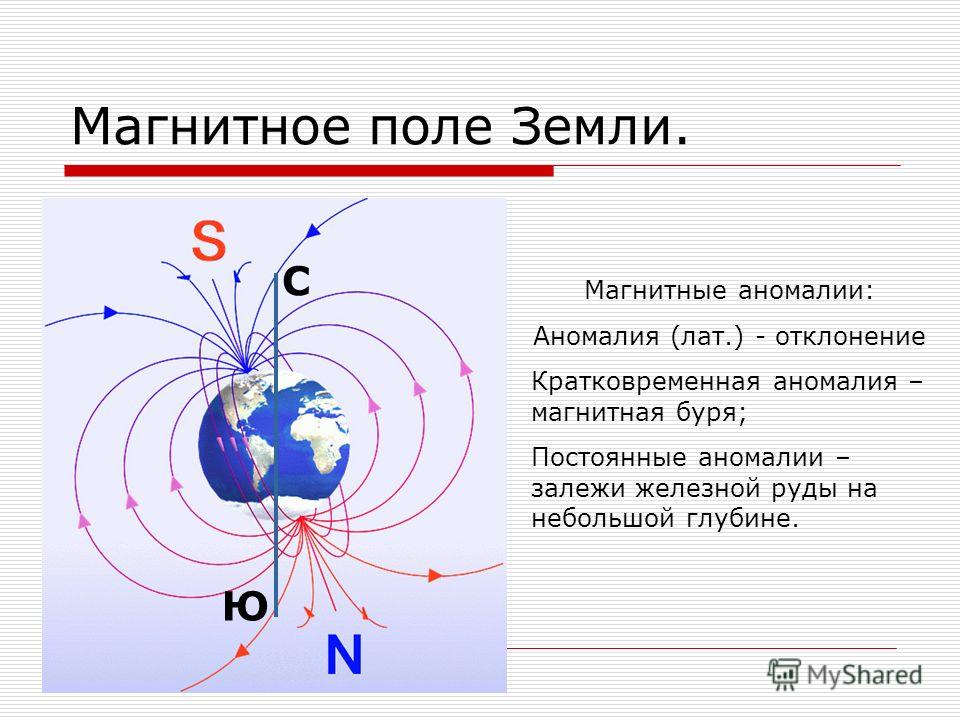 также: Путаница между B и H.
также: Путаница между B и H. 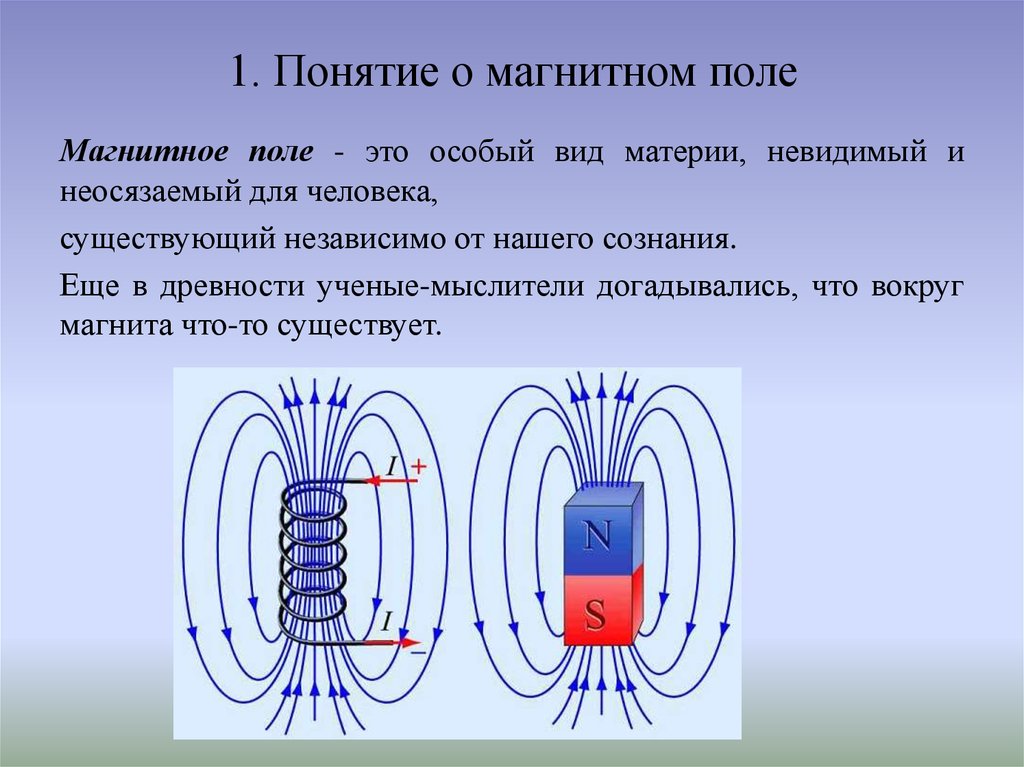 Однако отношения между единицами измерения и именами переменных, по-видимому, трактуются менее строго: тесла и А/м используются почти взаимозаменяемо для B , H и M с использованием магнитной постоянной $μ_0$ как средство преобразования.
Однако отношения между единицами измерения и именами переменных, по-видимому, трактуются менее строго: тесла и А/м используются почти взаимозаменяемо для B , H и M с использованием магнитной постоянной $μ_0$ как средство преобразования. Сила из-за магнитного поля действует перпендикулярно как направлению движения заряда, так и направлению магнитного поля (перекрестное произведение «×» в уравнениях (1ab)).
Сила из-за магнитного поля действует перпендикулярно как направлению движения заряда, так и направлению магнитного поля (перекрестное произведение «×» в уравнениях (1ab)).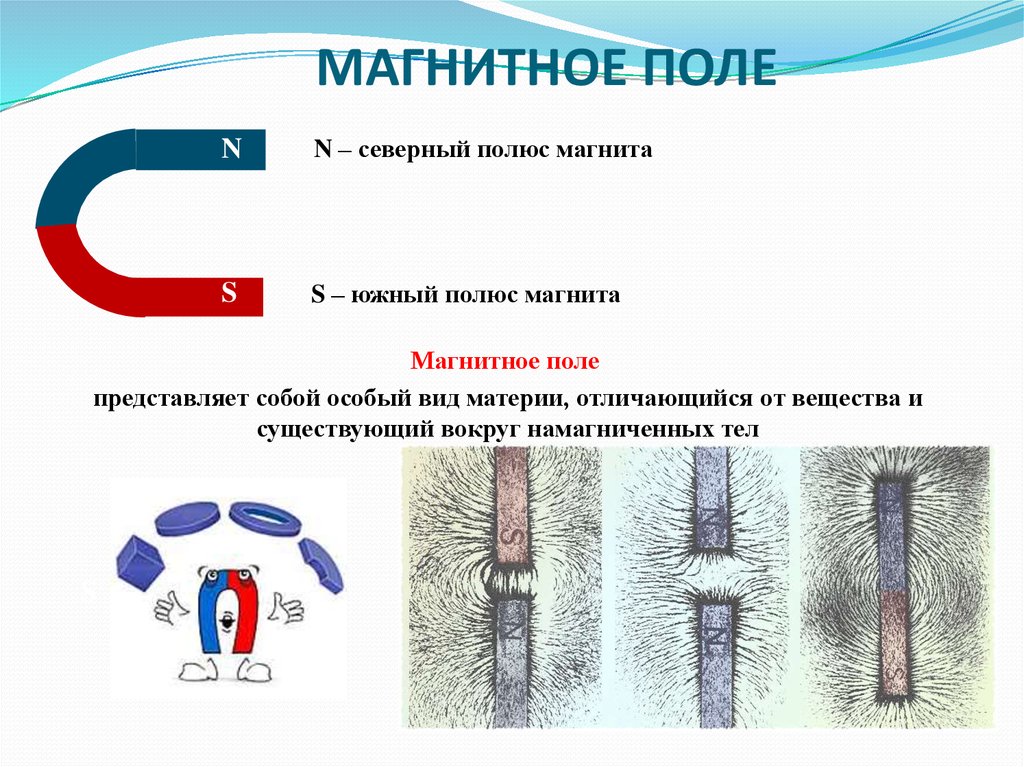
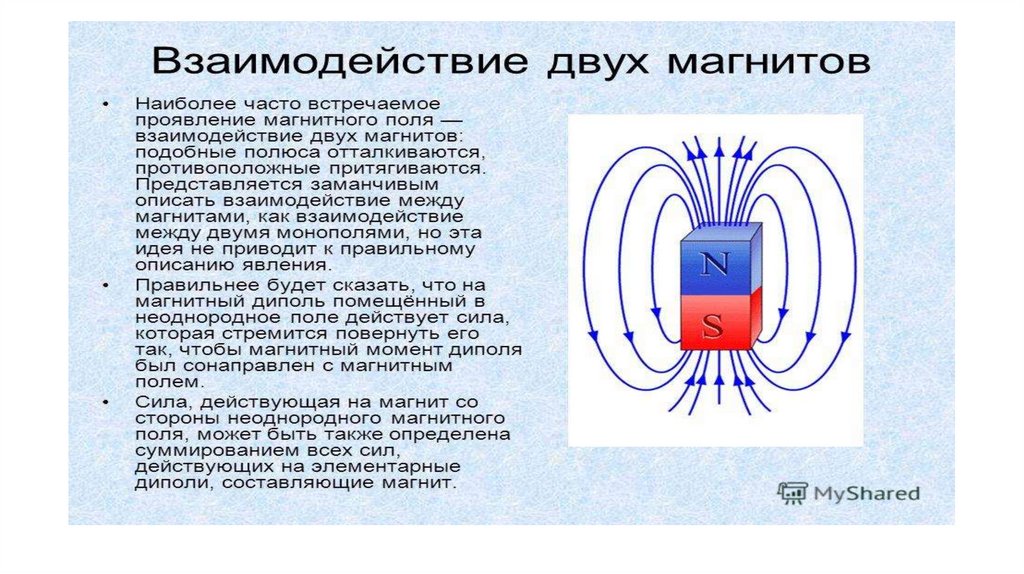 Материал реагирует намагничиванием M при воздействии некоторого магнитного поля B . Если достигается полное выравнивание всех свободных магнитных моментов, то говорят, что материал магнитонасыщен, и значение M больше не может увеличиваться.
Материал реагирует намагничиванием M при воздействии некоторого магнитного поля B . Если достигается полное выравнивание всех свободных магнитных моментов, то говорят, что материал магнитонасыщен, и значение M больше не может увеличиваться. 

 Для материалов, которые линейно реагируют на приложенное магнитное поле, при допущении, что M пропорционально B или H , объемная восприимчивость может быть определена как: $ \vec{M} = χ_{(B)} · \frac{ \vec{B} }{µ_0} $$
Для материалов, которые линейно реагируют на приложенное магнитное поле, при допущении, что M пропорционально B или H , объемная восприимчивость может быть определена как: $ \vec{M} = χ_{(B)} · \frac{ \vec{B} }{µ_0} $$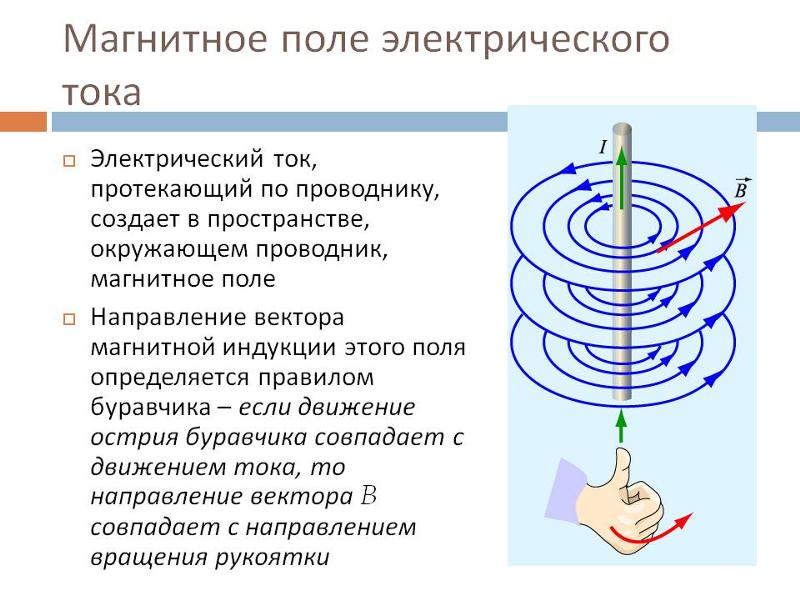
 Магнитные величины связаны с макроскопическими электрическими величинами, которые можно непосредственно измерить или контролировать в электромагнитных устройствах, таких как электрическое напряжение и ток.
Магнитные величины связаны с макроскопическими электрическими величинами, которые можно непосредственно измерить или контролировать в электромагнитных устройствах, таких как электрическое напряжение и ток.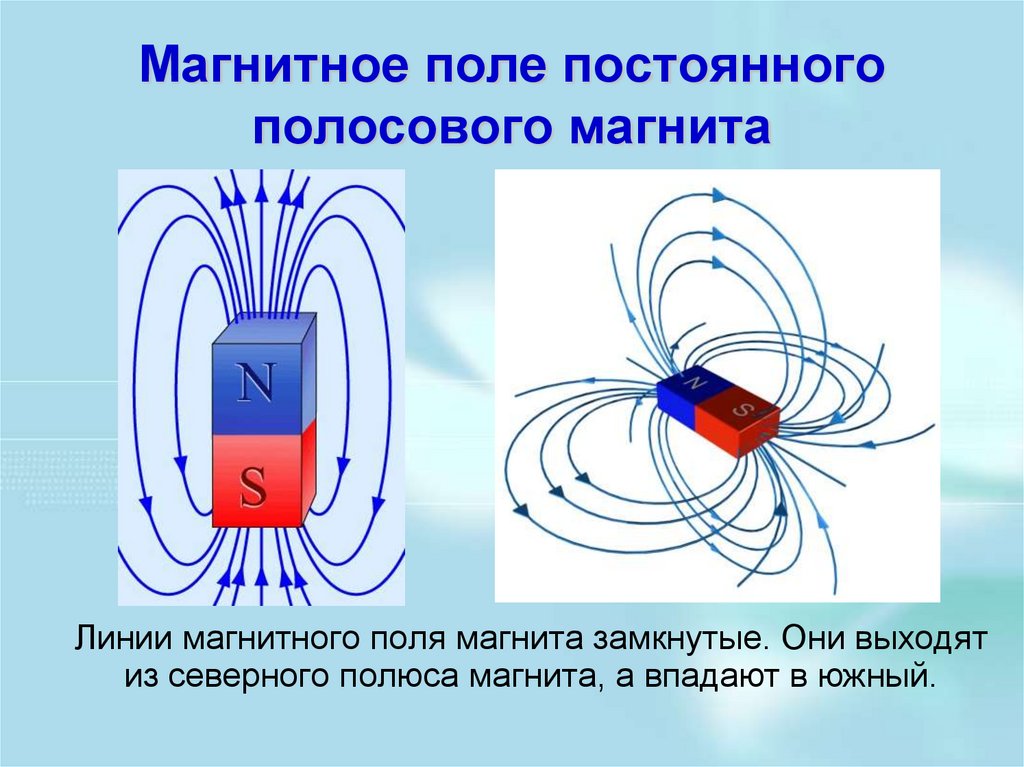 Пропорциональность определяется длиной рассматриваемого пути (длиной магнитного пути) и суммарной величиной тока I , содержащейся в одном проводнике, или числом N проводников. Вычисление H может быть основано либо на законе Био-Савара, либо на схемном законе Ампера, причем оба подхода дают одинаковые результаты для одной и той же конфигурации. 92}$$
Пропорциональность определяется длиной рассматриваемого пути (длиной магнитного пути) и суммарной величиной тока I , содержащейся в одном проводнике, или числом N проводников. Вычисление H может быть основано либо на законе Био-Савара, либо на схемном законе Ампера, причем оба подхода дают одинаковые результаты для одной и той же конфигурации. 92}$$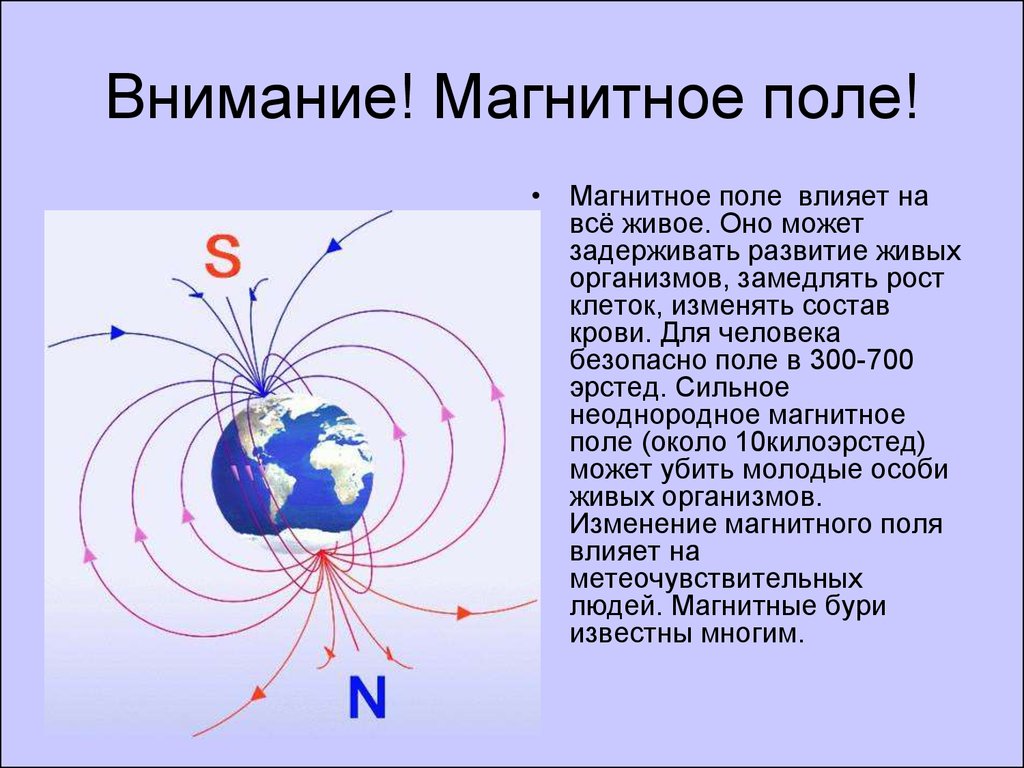 д.)
д.) 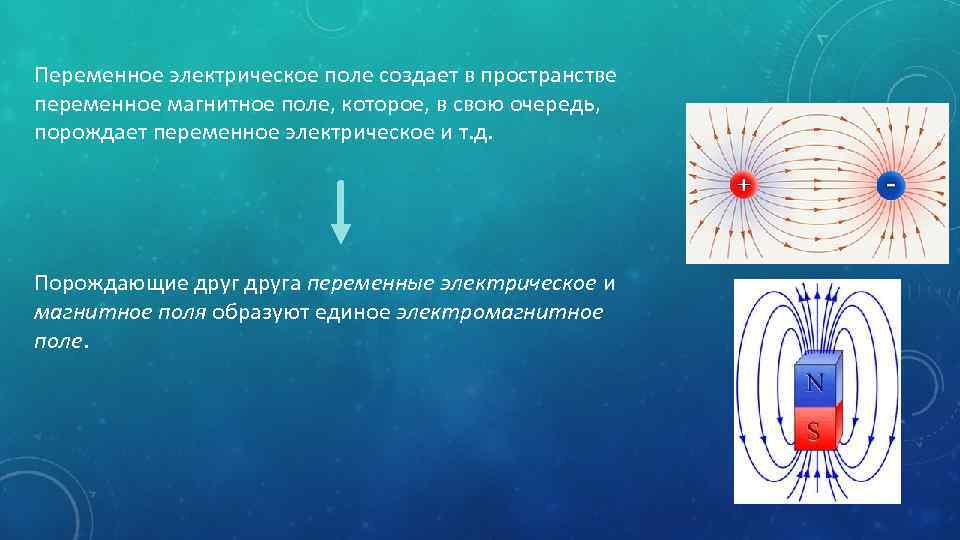 также: Расчет магнитного поля прямого круглого проводника).
также: Расчет магнитного поля прямого круглого проводника). д.
д. B измеряется с помощью закона индукции Фарадея (одно из уравнений Максвелла), который можно записать как:
B измеряется с помощью закона индукции Фарадея (одно из уравнений Максвелла), который можно записать как: 

 Магнитомягкие материалы играют ключевую роль в эффективном преобразовании энергии, поэтому им уделяется много внимания, а значение проницаемости используется как показатель качества. Для любого такого материала можно написать, что:
Магнитомягкие материалы играют ключевую роль в эффективном преобразовании энергии, поэтому им уделяется много внимания, а значение проницаемости используется как показатель качества. Для любого такого материала можно написать, что: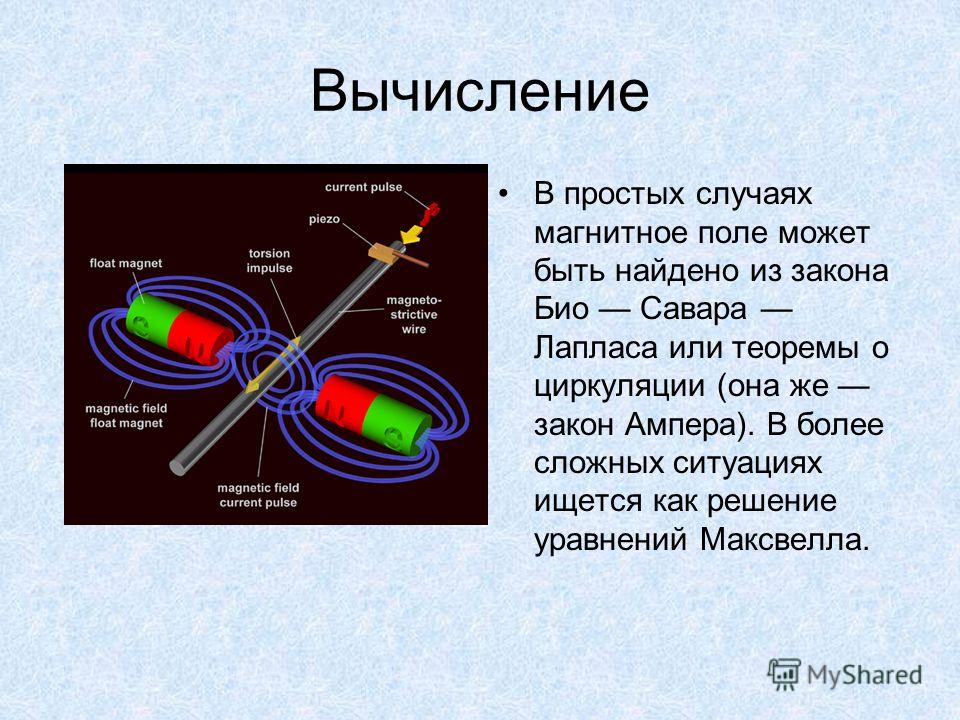 Следовательно, $µ = µ_r · µ_0$. Так, например, относительная проницаемость $μ_r$ = 100 означает, что данный материал имеет проницаемость в 100 раз выше, чем значение $μ_0$ (измеряется в Гн/м). Это означает, что для того же нанесенного H материал будет реагировать с B , что в 100 раз больше, чем для вакуума (или немагнитного материала).
Следовательно, $µ = µ_r · µ_0$. Так, например, относительная проницаемость $μ_r$ = 100 означает, что данный материал имеет проницаемость в 100 раз выше, чем значение $μ_0$ (измеряется в Гн/м). Это означает, что для того же нанесенного H материал будет реагировать с B , что в 100 раз больше, чем для вакуума (или немагнитного материала).