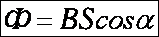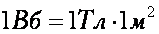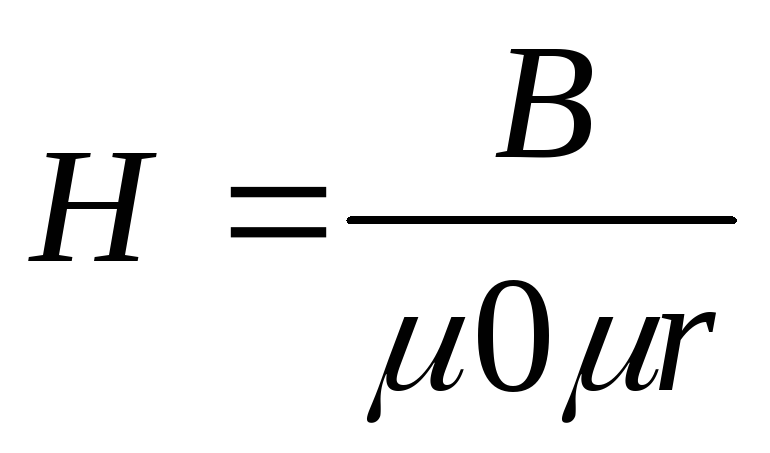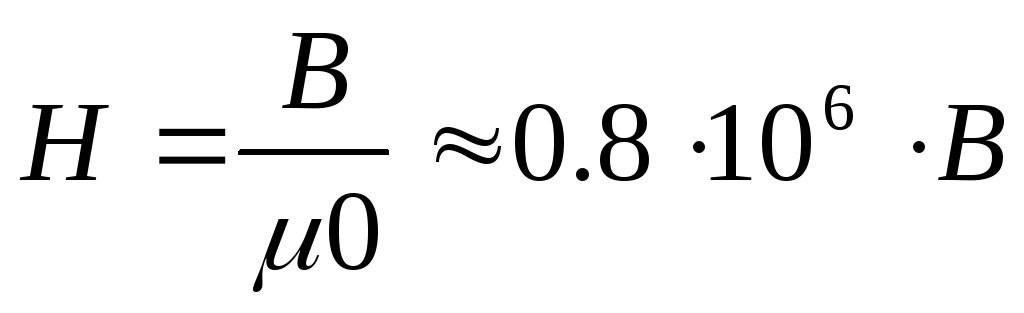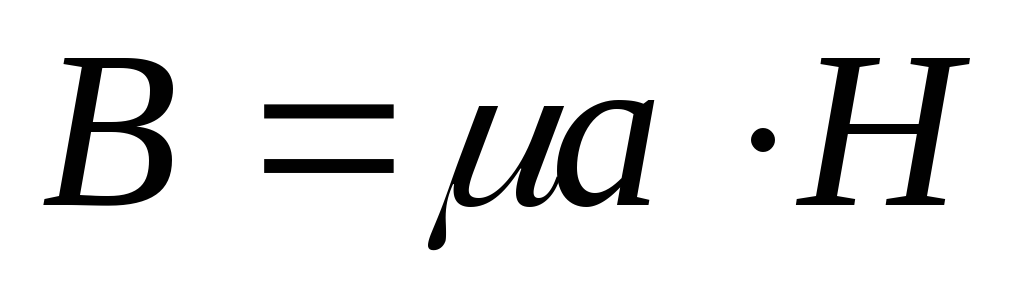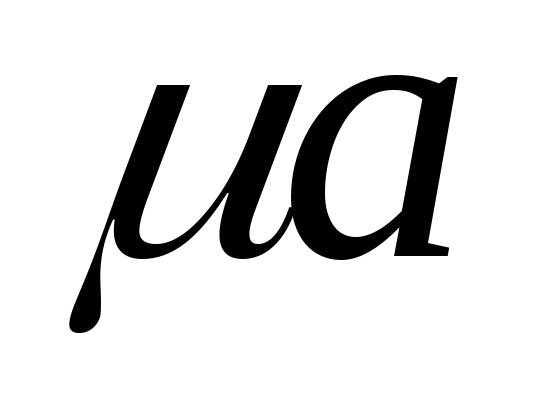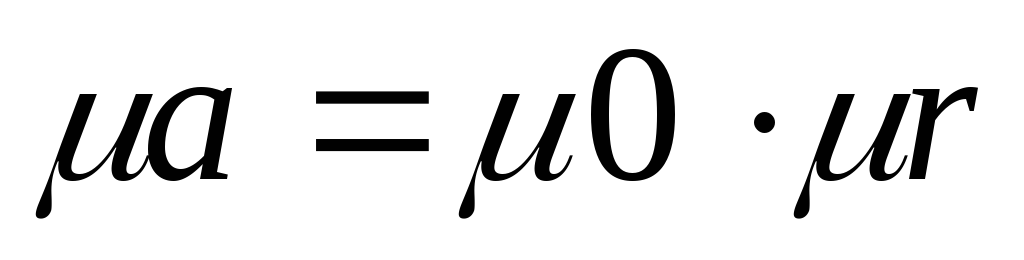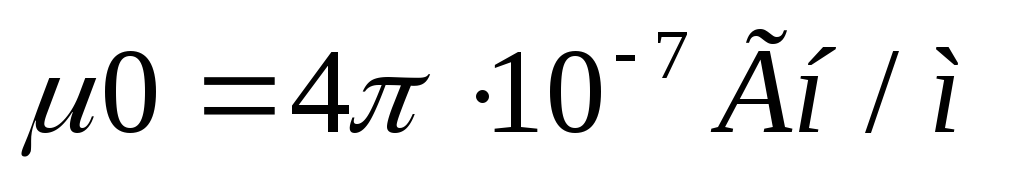Магнитная индукция — Википедия
Материал из Википедии — свободной энциклопедии
Магни́тная инду́кция B→{\displaystyle {\vec {B}}} — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой F→{\displaystyle {\vec {F}}} магнитное поле действует на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}.
Более конкретно, B→{\displaystyle {\vec {B}}} — это такой вектор, что сила Лоренца F→{\displaystyle {\vec {F}}}, действующая со стороны магнитного поля[1] на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}, равна
- F→=q[v→×B→]{\displaystyle {\vec {F}}=q\left[{\vec {v}}\times {\vec {B}}\right]}
- F=qvBsinα{\displaystyle F=qvB\sin \alpha }
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора F→{\displaystyle {\vec {F}}} перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС единицей магнитной индукции является гаусс (Гс), в СИ — тесла (Тл)
- 1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
- (Здесь формулы приведем в СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике[править | править код]
В магнитостатическом пределе[4] наиболее важными являются:
- Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:
- B→(r→)=μ04π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- B→(r→)=μ04π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- Теорема Ампера о циркуляции магнитного поля[5]:
- ∮∂SB→⋅dl→=μ0IS≡μ0∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}
- rotB→≡∇→×B→=μ0j→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}
В общем случае[править | править код]
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:
- divE→=ρε0, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}
- divB→=0, rotB→=μ0j→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}
- а именно:
- divB→=0,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}
- rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}
- rotB→=μ0j→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}
- F→=qE→+q[v→×B→],{\displaystyle {\vec {F}}=q{\vec {E}}+q\left[{\vec {v}}\times {\vec {B}}\right],}
- Следствия из неё, такие как
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- dF→=[Idl→×B→],{\displaystyle d{\vec {F}}=\left[I{\vec {dl}}\times {\vec {B}}\right],}
- dF→=[j→dV×B→],{\displaystyle d{\vec {F}}=\left[{\vec {j}}dV\times {\vec {B}}\right],}
- M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}
- выражение для потенциальной энергии магнитного диполя в магнитном поле:
- U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для плотности энергии магнитного поля
- w=B22μ0{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}
- Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
- ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- F→=qE→+q[v→×B→].{\displaystyle {\vec {F}}=q{\vec {E}}+q[{\vec {v}}\times {\vec {B}}].}
- ↑ Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
- ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
- ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в статье далее).
Магнитная индукция, магнитный поток: определение, формулы, смысл
 Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.


Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

Магнитная индукция
2
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — существует вокруг электрического заряда, материально. Основное свойство электрического поля: действие с силой на эл.заряд, внесенный в него. Электростатическое поле— поле неподвижного эл.заряда, не меняется со временем. Напряженность электрического поля. — количественная характеристика эл. поля. — это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда. — не зависит от величины внесенного заряда, а характеризует электрическое поле!
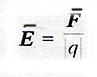
Направление вектора напряженности совпадает с направлением вектора силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
Напряженность поля точечного заряда:
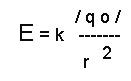 где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
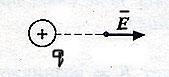
3
ПРИНЦИП СУПЕРПОЗИЦИИ ( НАЛОЖЕНИЯ ) ПОЛЕЙ
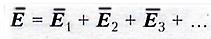
Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3… и т.д. создают электрические поля с напряженностью Е1, Е2, Е3 … и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.
Силовые линии эл. поля — непрерывные линии, касательными к которым являются векторы напряженности эл.поля в этих точках. Однородное эл.поле — напряженность поля одинакова во всех точках этого поля. Свойства силовых линий: не замкнуты (идут от + заряда к _ ), непрерывны, не пересекаются, их густота говорит о напряженности поля (чем гуще линии, тем больше напряженность).
Графически надо уметь показать эл.поля: точечного заряда, двух точечных зарядов, обкладок конденсатора ( в учебнике есть).
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ заряженного шара.
Есть заряженный проводящий шар радиусом R.
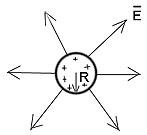
— заряд равномерно рапределен лишь по поверхности шара! Напряженность эл. поля снаружи:
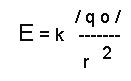
Напряженность внутри шара: Е = 0
12
ЭЛЕКТРОЕМКОСТЬ — характеризует способность двух проводников накапливать электрический заряд. — не зависит от q и U. — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
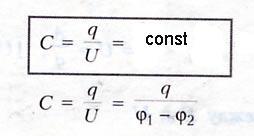 Единицы
измерения в СИ: ( Ф — фарад )
Единицы
измерения в СИ: ( Ф — фарад )
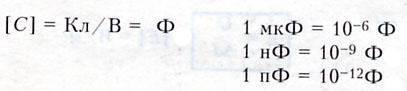
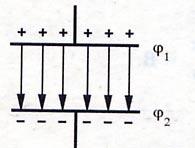
КОНДЕНСАТОРЫ
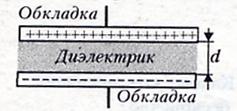
— электротехническое устройство, накапливающее заряд ( два проводника, разделенных слоем диэлектрика ).
 где
d много меньше размеров проводника. Обозначение
на электрических схемах:
где
d много меньше размеров проводника. Обозначение
на электрических схемах:
 Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные).
Электроемкость плоского конденсатора
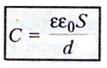 где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
Включение конденсаторов в электрическую цепь
параллельное
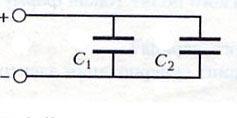
последовательное
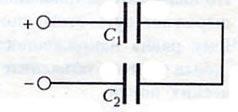
Тогда общая электроемкость (С):
при параллельном включении
.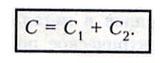 при
последовательном включении
при
последовательном включении
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
Конденсатор — это система заряженных тел и обладает энергией. Энергия любого конденсатора:
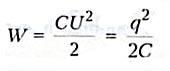 где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
Энергия
конденсатора приблизительно равна
квадрату напряженности эл. поля внутри
конденсатора.
Плотность энергии эл.
поля конденсатора: 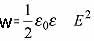
14
Электри́ческий
ток —
направленное (упорядоченное)
движение заряженных частиц[1][2][3].
Такими частицами могут являться:
в металлах —электроны,
в электролитах — ионы (катионы и анионы),
в газах — ионы и электроны,
в вакууме при
определенных условиях — электроны,
вполупроводниках —
электроны и дырки (электронно-дырочная
проводимость). Иногда электрическим
током называют также ток
смещения,
возникающий в результате изменения во
времени электрического поля
Сила
тока — физическая
величина 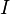 ,
равная отношению количества
заряда
,
равная отношению количества
заряда 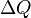 ,
прошедшего через некоторую поверхность
за время
,
прошедшего через некоторую поверхность
за время 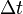
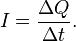
В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семиосновных единиц СИ. 1 А = 1 Кл/с.
По закону
Ома сила
тока 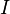 для
участка цепи прямо пропорциональна
приложенному напряжению
для
участка цепи прямо пропорциональна
приложенному напряжению 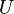
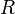 проводника этого
участка цепи:
проводника этого
участка цепи: 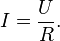
Носителями
заряда, движение которых, приводит к
возникновению тока, являются заряженные
частицы, в роли которых обычно
выступаютэлектроны, ионы или дырки.
Сила тока зависит от заряда 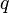 этих
частиц, их концентрации
этих
частиц, их концентрации 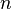 ,
средней скорости упорядоченного движения
частиц
,
средней скорости упорядоченного движения
частиц 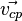
 и
формы поверхности, через которую течёт
ток.
и
формы поверхности, через которую течёт
ток. Если 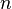 и
и 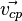 постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
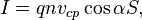
где 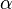
В
более общем случае, когда сформулированные
выше ограничения не выполняются,
аналогичное выражение можно записать
только для силы тока 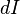 ,
протекающего через малый элемент
поверхности площадью
,
протекающего через малый элемент
поверхности площадью 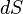 :
:
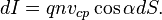
Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности
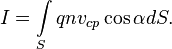
В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид
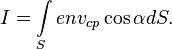
где e — элементарный электрический заряд.
Вектор 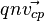 называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости
называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости 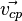 ,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).
В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).
Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичной площади[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:
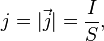
где I — сила тока через поперечное сечение проводника площадью S (также см.рисунок).
Иногда речь может идти о скалярной[2] плотности тока, в таких случаях под ней подразумевается именно та величина j, которая приведена в формуле.
В общем случае:
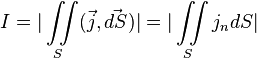 ,
,
где 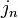 —
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью
—
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью 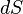 ;
вектор
;
вектор 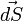 —
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
—
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность.
В
простейшем предположении, что все
носители тока (заряженные частицы)
двигаются с одинаковым вектором
скорости 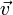 и
имеют одинаковые заряды
и
имеют одинаковые заряды 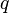 (такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их
(такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их 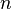 ,
,
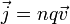
или
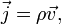
где 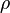 —
плотность заряда этих носителей.
—
плотность заряда этих носителей.
Направление
вектора 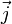 соответствует
направлению вектора скорости
соответствует
направлению вектора скорости 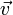 ,
с которой движутся заряды,
создающие ток, если q положительно.
,
с которой движутся заряды,
создающие ток, если q положительно.
В
реальности даже носители одного типа
движутся вообще говоря и как правило с
различными скоростями. Тогда под 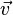 следует
понимать среднюю скорость.
следует
понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
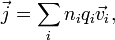
то
есть вектор плотности тока есть сумма
плотностей тока по всем типам подвижных
носителей; где 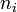 — концентрация
частиц каждого
типа,
— концентрация
частиц каждого
типа, 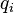 —
заряд частицы данного типа,
—
заряд частицы данного типа, 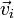 —
вектор средней скорости частиц этого
типа.
—
вектор средней скорости частиц этого
типа.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
15
Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В
своей оригинальной форме он был записан
его автором в виде : 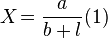 ,
,
Здесь X —
показания гальванометра,
т.е в современных обозначениях сила
тока I, a —
величина, характеризующая свойства
источника тока, постоянная в широких
пределах и не зависящая от величины
тока, то есть в современной терминологии
электродвижущая сила (ЭДС)  , l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
, l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
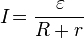 ,
(2)
,
(2)
где:
 — ЭДС источника
напряжения,
— ЭДС источника
напряжения, — сила
тока в
цепи,
— сила
тока в
цепи, — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
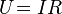 (3)
(3)
(где 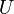 есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
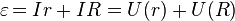 (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
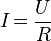 (5)
(5)
применима другая формулировка:
| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
|
Выражение (5) можно переписать в виде:
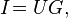 (6)
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.
ЗАКОН ДЖОУЛЯ -ЛЕНЦА
При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
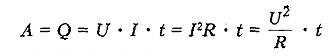
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.
В системе СИ:
[Q] = 1 Дж
19
МАГНИТНОЕ ПОЛЕ
— это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
СВОЙСТВА ( стационарного) МАГНИТНОГО ПОЛЯ
Постоянное (или стационарное) магнитное поле — это магнитное поле, неизменяющееся во времени .
1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.
2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.
3. Магнитное поле вихревое, т.е. не имеет источника.
— это силовая характеристика магнитного поля.
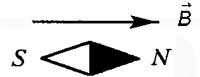
Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.
Единица измерения магнитной индукции в системе СИ:
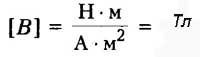
Направление линий магнитной индукции
— определяется по правилу буравчика или по правилу правой руки.
Правило буравчика ( в основном для прямого проводника с током):
Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
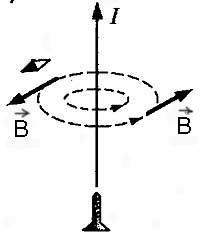
Правило правой руки ( в основном для определения направления магнитных линий внутри соленоида):
Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.
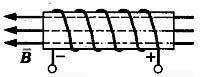
Существуют другие возможные варианты применения правил буравчика и правой руки.
Сила ампера
— это сила, с которой магнитное поле действует на проводник с током.
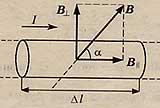

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индуции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки:
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.
Примеры:
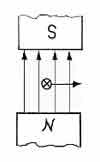 или
или 
Действие магнитного поля на рамку с током
Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).
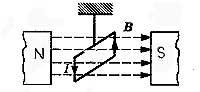
Неоднородное магнитное поле ориентирует + притягивает или отталкивает рамку с током. Так, в магнитном поле прямого проводника с током (оно неоднородно) рамка с током ориентируется вдоль радиуса магнитной линии и притягивается или отталкивается от прямого проводника с током в зависимости от направления токов.
22
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.
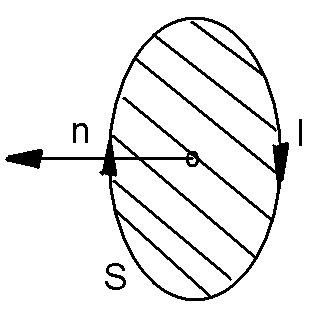
Рисунок — 1 круговой виток с током
Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.
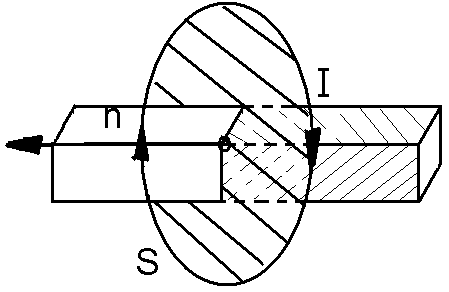
Рисунок— 2 Воображаемый полосовой магнит на оси витка
На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.
Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.
Величину магнитного момента кругового витка с током можно определить по формуле.
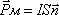
Магнитное действие электрического тока | |
1820 г. X. Эрстед — датский физик, открыл магнитное действие тока. (Опыт: действие электрического тока на магнитную стрелку). 1820 г. А. Ампер — французский ученый, открыл механическое взаимодействие токов и установил закон этого взаимодействия. | |
Магнитное взаимодействие, как и электрическое, удобно рассматриватьвводя понятие магнитного поля:
| |
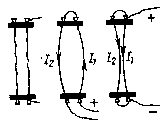
Для двух параллельных бесконечно длинных проводников было установлено: противоположно направленные токи отталкиваются, однонаправленные токи притягиваются, причем | |
Отсюда устанавливается единица силы тока ампер в СИ: сила тока равна 1 А, если между отрезками двух бесконечных проводников по 1 м каждый, находящимися в вакууме на расстоянии 1 м друг от друга, действует сила магнитного взаимодействия 2.10 7Н. | |
В СИ удобно ввести магнитную проницаемость вакуума | |
Вектор магнитной индукции.Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. | |
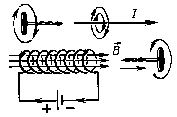
Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта с правой нарезкой) совпадает с направлением тока, то направление вращения ручки буравчика покажет направление линий магнитной индукции. Вектор магнитной индукции направлен по касательной к линиям. | |
На практике удобно пользоваться следующим правилом: если большой палец правой руки направить по току, то направление обхвата тока остальными пальцами совпадет с направлением линий магнитной индукции. |
|
Модуль вектора магнитной индукции Магнитная индукция В зависит от I и r, где r — расстояние от проводника с током до исследуемой точки. Если расстояние от проводника много меньше его длины (т. е. рассматривать модель бесконечно длинного проводника), то где k — коэффициент пропорциональности. Подставляя эту формулу в уравнение для силы взаимодействия двух проводников с током, получим F=B .I.ℓ. Отсюда Таким образом, модуль вектора магнитной индукции | |
Единица измерения в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла. | |
Магнитный поток | |
Магнитный поток (поток линий магнитной индукции) через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром. | |
| |
Единица магнитного потока в СИ — вебер (Вб). В честь немецкого физика В. Вебера. | |
Опыт показывает, что линии магнитной индукции всегда замкнуты, и полный магнитный поток через замкнутую поверхность равен нулю. Этот факт является следствием отсутствия магнитных зарядов в природе. |
|
Магнитная индукция и магнитные поток
Напряженность магнитного поля не является основной величиной, характеризующей магнитное поле, хотя определение напряжённости действительно для расчёта катушек без магнитопровода.
Для катушки с магнитопроводом основной величиной характеризующей магнитное поле, является магнитная индукция В. Это векторная величина, т.е. она (как и напряженность) задаётся численным значением и направлением в пространстве. Магнитная индукция определяется по силе, действующей на движущуюся заряженную частицу. При изображении картины магнитного поля при помощи магнитных линий, их рисуют гуще в той части поля, где больше индукция.
Единицей измерения магнитной индукции является тесла (Тл). Ранее применялась другая единица измерения магнитной индукции – гаусс (Гс).
Эти единицы связаны соотношением: 1Тл = 10000Гс.
Произведение магнитной индукции В на площадь S, перпендикулярную вектору магнитной индукции (магнитным линиям), называется магнитным потоком Ф. Таким образом магнитный поток:
Ф = B*S
Единицей измерения магнитного потока является вебер (Вб). При одной и той же напряжённости магнитного поля Н, в разных материалах получаются различные магнитные индукции В. Отношение В/Н называется абсолютной магнитной проницаемостью материала μа, т.е.
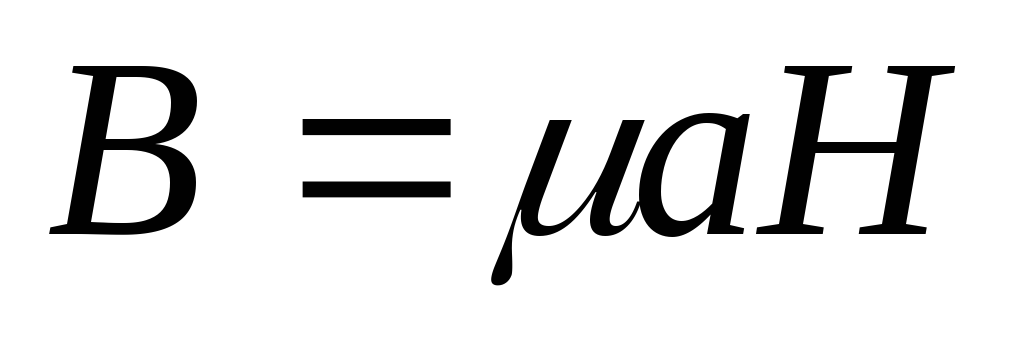
Абсолютная магнитная проницаемость материала μа равна произведению магнитной постоянной (магнитной проницаемости вакуума) μ0 и относительной магнитной проницаемости μr:
раоорропор
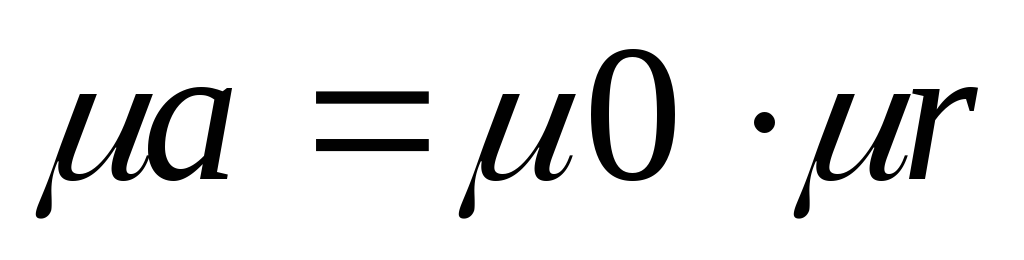
М агнитная
постоянная
агнитная
постоянная
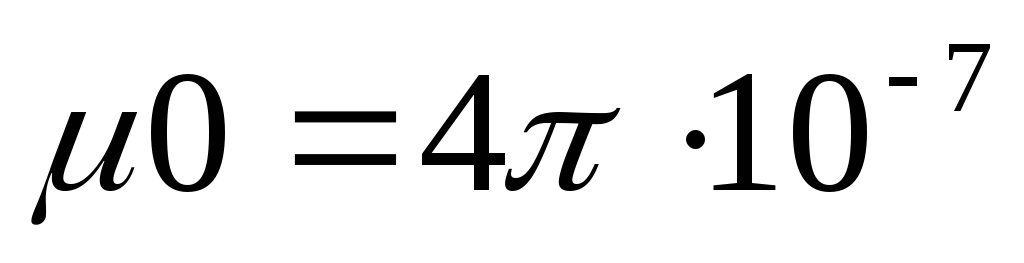 Гн/м
(генри на метр, генри единица измерения
индуктивности).
Гн/м
(генри на метр, генри единица измерения
индуктивности).
Величина μrпоказывает, во сколько раз μа материала больше, чем магнитная постоянная μ0.
В материале, магнитная проницаемость которого равна μr,
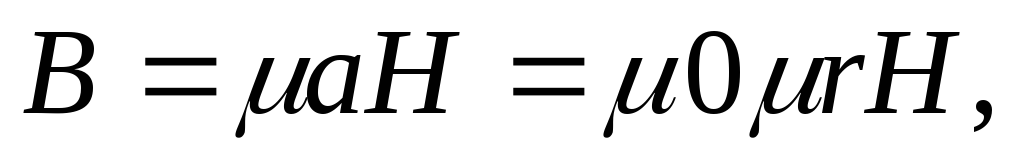
а в вакууме (практически и в воздухе)
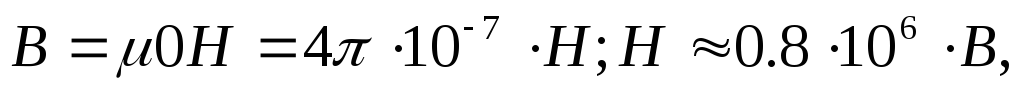
где В выражается в теслах, а Н в А/м.
При измерении магнитной индукции в гауссах, а напряжённости магнитного поля в А/см, для магнитной индукции в воздухе получим:
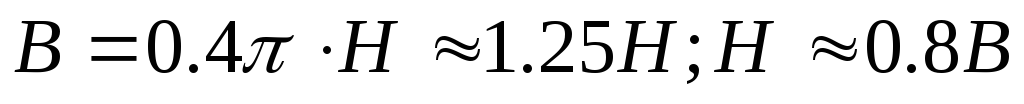
У ферромагнитных материалов относительная магнитная проницаемость μr во много раз больше 1, она изменяется с изменением индукции В. Зависимость между В и Н для ферромагнитных материалов чаще изображается графиком в виде кривых намагничивания.
В практических задачах (магнитные цепи электрических машин и аппаратов) для расчёта силы тяги, ЭДС, силы притяжения и т.д. требуется определить магнитный поток Ф или индукцию В. Значение этих величин определяют по кривым намагничивания, если известна напряженность магнитного поля Н, которая, в свою очередь, задаётся магнитным напряжением или МДС.
Величина | Обозначение | Единица величины | Обозначение единицы | Расчётная формула |
Напряженность магнитного поля а. в магнитном материале | Н | Ампер на метр | А/м |
Н=Iw/l |
б. в вакууме (воздухе) |
| |||
Магнитная сила | F | Ампер | F=wI | |
Магнитная индукция | В | Тесла (Вебер на 1 м2) | Тл (Вб/м2) |
|
Магнитный поток | Ф | Вебер | Вб | Ф = ВS |
Абсолютная магнитная проницаемость |
| Генри на метр | Гн/м |
|
Задача 1.
Н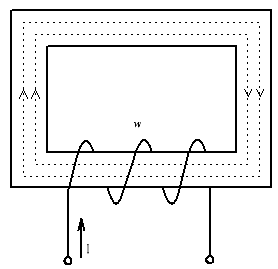 апряжённость
магнитного поля катушки
апряжённость
магнитного поля катушки
H = 500 А/м. Какова будет магнитная индукция, если в катушку вставить магнитопровод из трансформаторной стали (на рис.), относительная магнитная проницаемость которой μr= 2400.
Решение
B = μа*Н = μо*μr*Н = 4*π*10-7*2400*500 = 1.5 Тл
Задача 2.
Для трансформаторной стали, содержащей 4% Si, магнитная индукция В при напряжённости магнитного поля катушки 500 А/м равна 1.19 Тл (см. кривые намагничивания на рис.). Определить абсолютную магнитную проницаемость трансформаторной стали в рабочей точке μа и относительную магнитную проницаемость μr. Напомним, что величина μr показывает во сколько раз μа материала больше, чем магнитная проницаемость
μо = 4*π*10-7.
Решение
Абсолютная магнитная проницаемость
μа = В/Н = 1.19/500
μа = μr*μо = 4*π*10-7*μr.
Отсюда
μr = μа/μо = В/Н =1.19/(500*4*π*10-7) = 1893.9
Задача 3.
По заданным экспериментальным зависимостям В и Н для различных материалов определить коэффициенты полиномов второго порядка, наилучшим способом (по минимуму суммы квадратов ошибок) обеспечивающих аналитическое их описание (математическую модель).
Листовая сталь
Н (А/м)
100
150
200
250
300
350
400
450
500
550
В (Тл)
0.60
0.75
0.86
0.96
1.05
1.12
1.19
1.23
1.30
1.36
Трансформаторная сталь (4% Si)
Н (А/м)
100
200
300
400
500
600
В (Тл)
0.48
0.78
0.96
1.08
1.19
1.27
Литая сталь
Н (А/м)
100
200
300
400
500
600
В (Тл)
0.35
0.60
0.85
1.00
1.10
1.16
Решение
Для оценки коэффициентов полинома
В = a*Н2 + b*Н + С
Запишем вектор
Н = [100 150 200 250 300 350 400 450 500 550]’. size A = 10,1
Затем составим матрицу А:
А = [Н^2 Н ones(V(1),1)]
И образуем вектор В:
B = [0.6 0.75 0.86 0.96 1.05 1.12 1.19 1.23 1.3 1.36]’.
Выполним оценку коэффициентов
а х = А\В
С помощью файла sah575.m. В нём выполнены оценки коэффициентов квадратного полинома для листовой стали
а1 = [-0.0206 0.2952 0.3429],
для трансформаторной стали
а2 = [-0.0246 0.3239 0.2000]
и для листовой стали
а3 = [-0.0277 0.2566 0.0150].
Необходимо выполнить расчёты для каждого вида материала в режиме прямых вычислений.
/здесь приводится файл sah 375.m/
Задача 4.
Каков будет магнитный поток Ф в магнитопроводе (см. задачу 1.), если сечение магнитопровода S = 4 см²?
Решение
Магнитный поток, измеряемый в веберах (Вб), равен
Ф = В*S = 1.5*4*10-4 = 0.0006 Вб
(Тл = Вб/м²)
Задача 5.
Число витков катушки w=500. В магнитопроводе из трансформаторной стали длиной l=25 см необходимо обеспечить магнитную индукцию В=1.19 Тл. Какая м.д.с. и ток необходим для этого?
Решение
По кривой намагничивания трансформаторной стали (см. рис.) находим, что для создания В = 1.19 Тл требуется создать напряжённость магнитного поля Н = 500 А/м. При длине магнитопровода (с катушкой) l = 25 см = 0.25 м необходимая м.д.с. вычисляется по формуле
I*w = H*l = 500 А/м * 0.25 м = 125 А,
Отсюда I = I*w/w = 125/500 = 0.25 А
Задача 6.
Каковы напряжённость, индукция и магнитный поток внутри цилиндрической катушки (рис.) которая имеет длину 20 см, диаметр 3см, число витков 1600 и ток 3 А?
Решение
Напряжённость магнитного поля
Н = I*w/l = 3*1600/0.2 = 24000 А/м
Поскольку катушка без сердечника, то магнитную индукцию следует вычислять по формуле:
В = μо*Н = 4*π*10-7*2.4*104 = 3.02*10-2 Тл
Сечение катушки
S = π*d2/4 = 3.14*0.032/4 = 7.06*10-4 м².
Следовательно, магнитный поток
Ф = В*S = 3.02*10-2*7.06*10-4 = 21.3*10-6 Вб

Дополнение
Задача 1
Какое количество электричества пройдёт через лампу за 3 часа при токе 0,18А?
Решение:
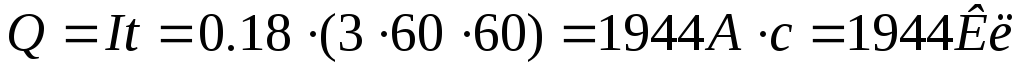
Задача 2
Свинцовый аккумулятор ёмкостью 14А*ч заряжается током I зар = 1.4А. Как долго он должен заряжаться и через сколько времени он разрядится через лампы током Iраз = 0.3А?
Решение:
Зарядка: t = Q/Iзар = 14А*ч/1.4А = 10ч,
т.е. аккумулятор должен заряжаться 10ч
Разрядка: t = Q/Iраз = 14А*ч/0.3А = 47ч,
т.е. лампы горели 47ч. Через лампы прошёл ток 14А*ч, пока аккумулятор не разрядился.
Задача 3
Заряженный аккумулятор имеет ёмкость 28А*ч. 1) Какое количество электричества в кулонах содержит аккумулятор? 2) Какой ток необходим для зарядки аккумулятора за 10ч. Каким током разрядится он за 140ч.?
Решение.
1А*ч = 360 А*с = 3600Кл
28А*ч = 28*3600Кл = 100800 Кл.
Iзар = Q/t = 28А*ч/10ч = 2.8А, т.е. аккумулятор зарядится за 10часов током 2.8А
Iраз = Q/t = 28А*ч/140ч = 0.2А.
Задача 4
Сколько ампер-часов содержтся в 96480 кулонах (заряд Фарадея)?
1А*ч = 3600А*с = 3600Кл;
96480/3600 = 26.8 А*ч, т.е. 96489 Кл. эквивалентен 26,8 А*ч
Задачи для самостоятельного решения:
Какой электрический заряд нужен от гальванического элемента, если он разряжается током 0,05А в течении 12ч.? (0,6 А*ч)
Через электродвигатель при токе I проходит количество электричества Q = 7500А*с за время t = 5мин/ Чему равен ток? (30мА)
Какой ток протекал по проводнику, если через его поперечное сечение за 30мин прошел заряд 54А*с? (30мА)
Через аппарат проходит ток I = 20мА в течение 9мин. Определить количество электричества, которое прошло через аппарат?
Аккумулятор ёмкостью 10А*ч заряжается током 4А. Как долго должен заряжаться? (10ч)
Задача 1.
Через медный проводник с площадью поперечного сечения S = 4 мм²
протекает ток I=10А. Какова плотность тока?
Решение:
Плотность тока
J = I/S = 10A/4мм² = 2.5 A/мм²
По площади 1 мм² поперечного сечения протекает ток I = 2.5A;
По всему поперечному сечению S проходит общий ток I = 10А.
По таблице проверить, допустима ли плотность тока 2.5 А/мм²?
Задача 2.
По шине разделительного устройства площадью прямоугольного поперечного сечения (20х80)мм проходит ток I = 1000A. Какова плотность тока в шине?
Решение
Площадь поперечного сечения шины S = 20х80 = 1600 мм². Плотность тока
J = I/S = 1000A/1600 мм² = 0.625A/мм²
Задача 3.
У катушки провод имеет круглое сечение диаметром 0,8мм и допускает плотность тока 2,5А/мм². Какой допустимый ток может проходить по проводу (нагрев не должен превышать допустимый)?
Решение:
Площадь поперечного сечения провода:
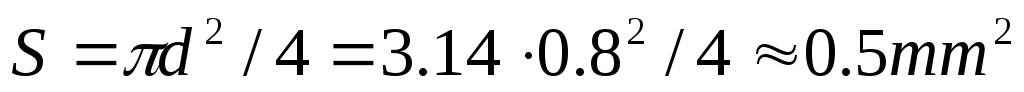
Д опустимый
ток:
опустимый
ток:
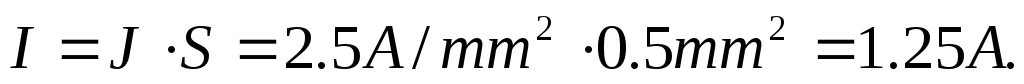
Задача 4.
Допустимая плотность тока для обмотки трансформатора J = 2.5 А/мм²
Через обмотку проходит ток I = 4A. Каким должно быть поперечное сечение круглого проводника, чтобы обмотка не перегревалась?
Решение:
Площадь поперечного сечения
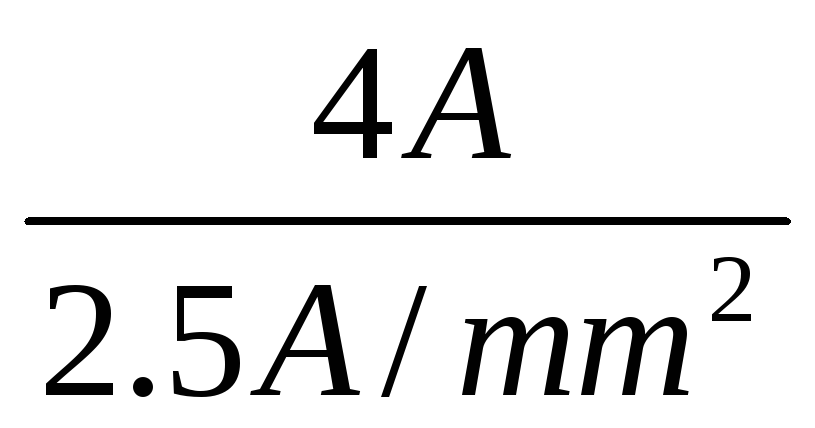
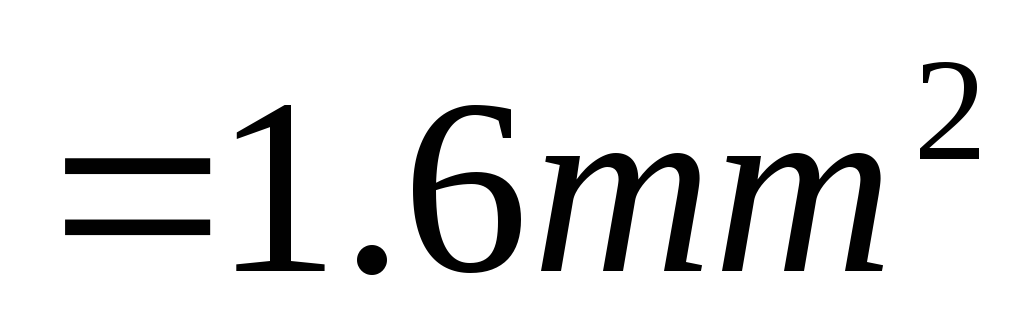
S=I/J=
Этому сечению соответствует диаметр провода 1.42мм.
Задача 5.
По изолированному медному проводу сечением 4 мм² проходит максимально допустимый ток 38А (см таблицу). Какая допустимая плотность тока? Чему равны допустимые плотности токов для медных проводов с площадями поперечного сечения 1, 10, 16 мм²?
Решение.
Допустимая плотность тока
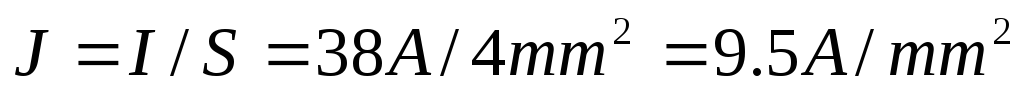
Для сечения 1 мм² допустимая плотность тока (см табл)
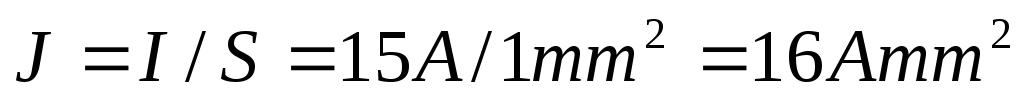
Для сечения 10 мм² допустимая плотность тока
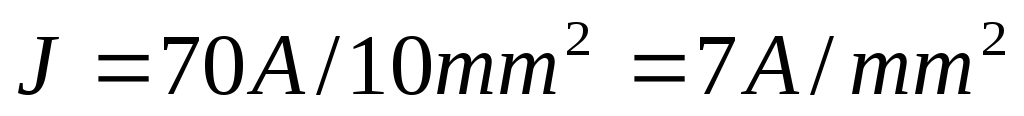
Для сечения 16 мм² допустимая плотность тока
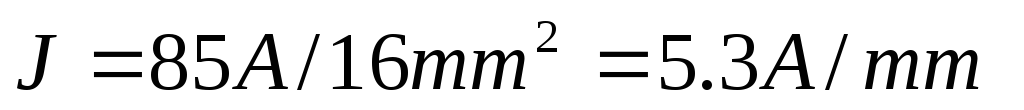
Допустимая плотность тока с увеличением сечения кабеля тоже действительна для проводов с изоляцией класса В.
Задачи для самостоятельного решения.
Через обмотку трансформатора должен протекать ток I = 4A. Каким должно быть сечение обмоточного провода при допустимой плотности тока J = 2.5 А/мм² (S = 1.6 мм²)
По проводу диаметром 0,3 мм проходит ток 100А. Какова плотность тока (J = 1.415 А/мм²)
По обмотке электромагнита из медного изолированного провода диаметром d = 2.26мм (без учёта изоляции) проходит ток 10А. Какова плотность тока? (J= 2.5 А/мм²)
Магнитная индукция — Знаешь как
 Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током. Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.
Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током. Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.
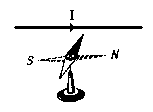
Направление, которое указывается северным концом магнитной стрелки, установившейся под действием сил магнитного поля, принимается за направление магнитного поля.
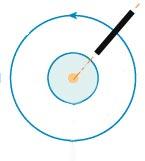
Рис. 3-1. Правило буравчика.
Магнитное поле изображается магнитными линиями (линиями магнитной индукции), Они проводятся так, чтобы направление касательной в каждой точке линии совпадало с направлением поля.
Направление магнитного поля связано с направлением тока. Эта связь устанавливается правилом буравчика: если поступательное движение буравчика совпадает с направлением тот (рис 3-1), то направление вращения рукоятки буравчика укажет направление магнитных линий. Иногда лучше пользоваться другой формулировкой этого правила: если направление вращения рукоятки буравчика совпадает с направлением тока в контуре (рис. 3-2), то поступательное движение его укажет направление магнитных линий, пронизывающих поверхность, ограниченную контуром.
Поместим в магнитное поле перпендикулярно его направлению участок прямолинейного провода длиной l, по которому проходит ток I (рис. 3-3).

Из опыта можно убедиться, что на участок провода будет действовать сила F, по величине пропорциональная току, длине участка проводника и интенсивности магнитного поля, которая характеризуется величиной магнитной индукции В.
Таким образом, сила
F=IBl
Рис. 3-2. Правило буравчика для кольцевого тока.
Из написанного следует, что
B = F : (Il)
т. е. магнитная индукция измеряется отношением механической силы, действующей на участок провода, по которому проходит ток, к произведению тока и длины участка провода, причем провод должен быть расположен перпендикулярно направлению поля.
В международной системе единиц (СИ) сила измеряется в ньютонах, ток — в амперах, длина — в метрах, поэтому единица измерения магнитной индукции
[B] = [F : (Il)] = н : (a • м) = дж/м : (a • м) = (в • k) : (a • м2) = (в • а • сек) : (a • м2) = (в • сек) : м2
Единица вольт-секунда называется в е б е р (вб), а вебер, деленный на квадратный метр, — тесла (тл),
таким образом:
[B] = вб : м2 = тл
Кроме единицы тесла, иногда применяется гаусс (гс) — единица магнитной индукции, не принадлежащая к системе
СИ, при этом
1 гс — 10-4 тл, или 1 тл = 104 гс.

Рис. 3-3. Провод с током в магнитном поле.
Магнитная индукция — векторная величина. Направление вектора магнитной индукции совпадает с направлением поля в данной точке.
Магнитное поле, во всех точках которого векторы магнитной индукции одинаковы по величине и параллельны друг другу, называется однородным.
Магнитные линии можно использовать не только для указания направления поля, но и для характеристики его интенсивности. Для этого условно через единичную площадку, перпендикулярную к направлению поля, проводят число линий, равное или пропорциональное величине магнитной индукции в данном месте поля.
Произведение магнитной индукции В на площадь S, перпендикулярную к вектору магнитной индукции, называется магнитным потоком, т. е.
Ф= BS.
Так как магнитная индукция измеряется в теслах (тл), а площадь — в квадратных метрах, и учитывая, что 1 тл = 1вб : 1м2 получим, что магнитный поток измеряется в веберах:
[Ф] = тл • м2 = (вб : м2) • м2 = вб.
Более мелкой единицей магнитного потока, не относящейся к системе СИ, является максвелл
1 мкс = 10-8вб = 1 гс•см2.
Так как магнитная индукция характеризуется числом магнитных линий, проходящих через единицу площади поверхности, перпендикулярной направлению поля, то магнитный поток будет характеризоваться числом линий, проходящих через площадь S.
Статья на тему Магнитная индукция
Магнитная индукция — это… Что такое Магнитная индукция?
Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .
Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля[1] на заряд , движущийся со скоростью , равна
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)
- 1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Основные уравнения
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
- (Здесь формулы приведем в системе единиц СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике
В магнитостатическом пределе[4] наиболее важными являются:
В общем случае
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :
- Формула силы Лоренца
- Следствия из нее, такие как
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):
- выражение для потенциальной энергии магнитного диполя в магнитном поле:
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- Следствия из нее, такие как
- Выражение для плотности энергии магнитного поля
- Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Примечания
- ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
- ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
- ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).



 — ЭДС источника
напряжения,
— ЭДС источника
напряжения,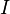 — сила
тока в
цепи,
— сила
тока в
цепи,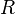 — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.

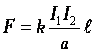 , где k — коэффициент пропорциональности.
, где k — коэффициент пропорциональности.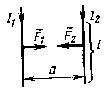
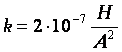
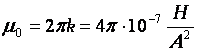 .
.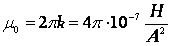
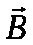
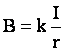 ,
,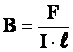 .
. есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.
есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.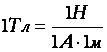
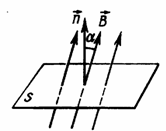
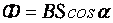 , где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур.
, где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур.