4 закона логики, которые помогут определить ложные суждения
Содержание статьи
В жизни мы часто слышим фразы «это не поддается логике» или «это нелогично». В целом мы понимаем, что речь идет про неверное суждение, ошибочные выводы. Но в чем конкретно нарушена логика — сказать трудно. Существуют 4 закона логики, с помощью которых можно легко отделить ложь от правды. Логика — это древняя наука, появившаяся в 4 веке до н.э., ее основателями были Аристотель, Сократ, Платон и многие другие известные философы, которые усердно изучали законы и формы правильного логического мышления. Давайте разберем на простых примерах значения основных четырех законов логики и как их применить в жизни.
Закон тождества
Любая мысль должна соответствовать самой себе, то есть иметь конкретное значение и быть точной и понятной. Самый известный пример: «ученики прослушали урок». Термин «прослушали» в этом предложение может иметь два определения: то ли ученики ничего не слушали на уроке, то ли, наоборот, внимательно изучали новую тему.
Главное, на что необходимо обращать внимание, так это на неоднозначные слова, которые могут иметь несколько значений. Сложнее всего распознать нарушение тождества в сложных утверждениях:
- Что вы выберите: счастье или конфету? — Счастье.
- Как вы считаете, что лучше счастья? —Ничто!
- Но конфета лучше, чем ничто.
- Поэтому конфета получается лучше счастья.
В примере понятие «ничто» в первом варианте означало «отказ от выбора варианта», во втором, как отсутствие чего-либо.
Закон противоречия
Две отрицающих друг друга мысли не могут быть одинаково верными. Например, когда говорят «черный пес» и «белый пес», имея в виду одного и того же пса в одном промежутке времени, то правильным может быть только одно утверждение. В жизни важно выявлять противоречия, отделять игру слов от лжи.
Закон исключенного третьего
Два противоречащих утверждения не должны быть одинаково ложными. Тут важно отличать противоречащие от противоположных утверждений.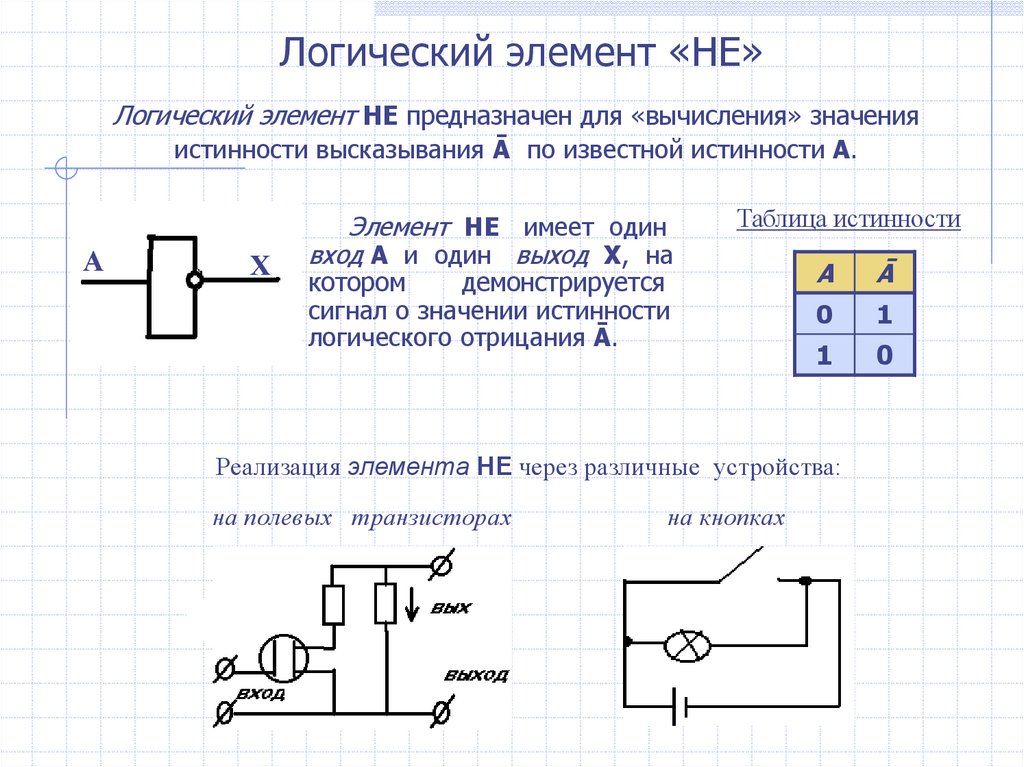
Первые суждения не имеют третьего варианта, например, большая квартира и небольшая квартира. Противоположные суждения допускают, что возможен и другой вариант, например, «маленькая квартира» и «большая квартира», другой вариант — «средняя квартира». На простых примерах принцип понятен, а вот в жизни противоречащие суждения обычно разделены длинным предисловием, который сбивает с мысли.
Закон достаточного основания
Истинная мысль должна быть основана на аргументах, чтобы быть истинной. Важно, что само утверждение должно следовать из этих фактов. Например, «я готовился к экзамену, поэтому я не заслужил двойку». Один факт не подтверждает утверждение, студент мог просто прочесть лекции и не заучивать нужный материал. Данный закон помогает не делать преждевременных выводов и не верить, например, разной желтой прессе.
Проверьте себя прямо сейчас, как хорошо вы разбираетесь в логике, пройдите бесплатный онлайн-тест на логику.
Физика двоичной логики / Хабр
Вопрос «Как работает компьютер?» чрезвычайно многогранен и ответ на него зависит от выбранного уровня абстракции.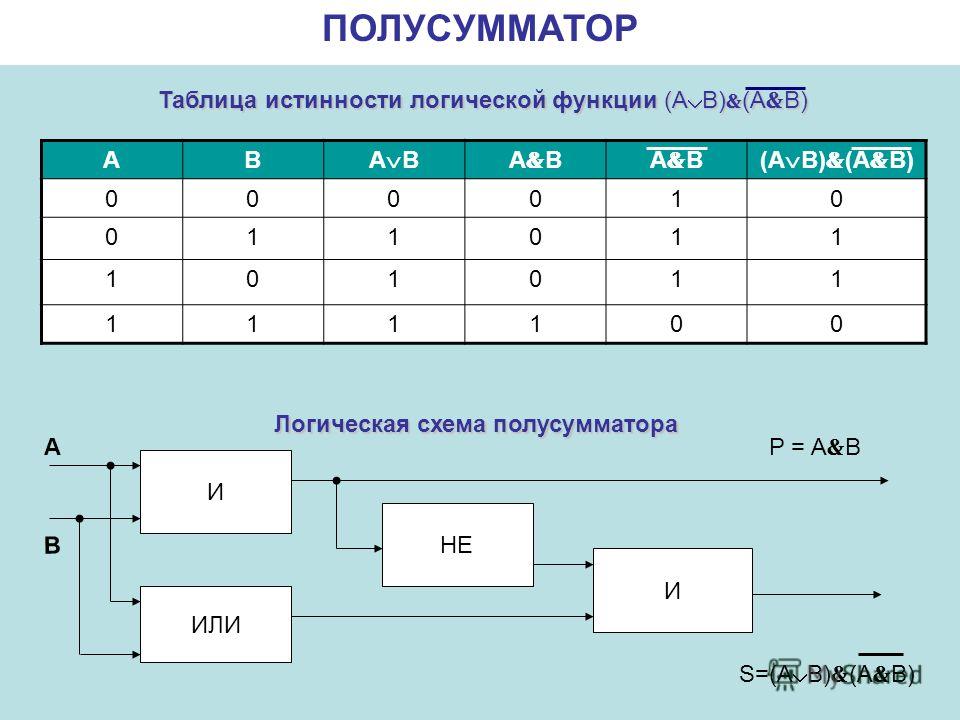
О системах счисления
Система счисления — это метод записи чисел. В повседневной жизни мы используем арабскую систему счисления, а именно десятичную позиционную. По мнению историков, арабские цифры появились в Индии ориентировочно до 5 века нашей эры. В Европу они пришли в начале второго тысячелетия из арабских стран, собственно, поэтому и принято называть привычные нам цифры арабскими. В России арабская система счисления появилась в 14-15 веке, а к 18 веку и вовсе вытеснила отечественную разработку под названием
Причины использования арабской системы довольно тривиальны. Человеку попросту проще оперировать с ней, чем с другими непозиционными системами.
Так сложилось, что в компьютеростроении десятичная система показывает себя не с лучшей стороны.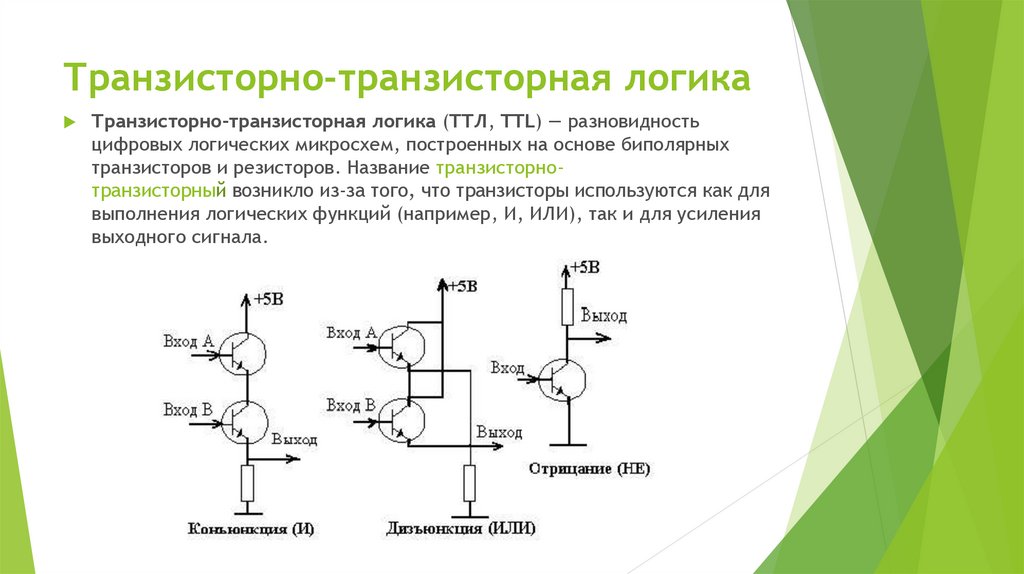
На её основе сложно проектировать вычислительные устройства, как с точки зрения технологической сложности самого вычисления, так и с точки зрения работоспособности устройства под действием факторов окружающей среды, например, помех.
Двоичная система счисления минимизирует эти сложности, хотя есть примеры ЭВМ и на других системах, например, ЭВМ «Сетунь» на троичной логике.
Цифровая абстракция
Как правило, физические величины изменяются непрерывно. В противовес им, цифровое представление информации дискретно и строго определенно. В компьютере, построенном на двоичной логике, для абстракции нулей и единиц используется напряжение: высокое значение величины — это логическая единица, а низкое — логический ноль.
Для реализации логических схем отлично подходит алгебра логики, поскольку оперирует величинами с двумя значениями — правда или ложь, единица или ноль. Собственно, как и двоичный компьютер. Однако стоит понимать, что алгебра логики — это абстракция логических выражений и связанных с ними операций, а не двоичной системы счислений.
Логические выражения
Алгебра логики — это раздел математики над логическими выражениями. Под логическими выражениями подразумеваются суждения, высказывания, предложения и т.п., истинность которых можно определить однозначно — правда или ложь. Разумеется, не любое высказывание является логическим. Например, выражение «в декабре 31 день» является логическим, потому что однозначно истинно, а выражение «новая матрица — сомнительное кинопроизведение» не является логическим, поскольку отражает субъективную позицию и содержит неопределенную характеристику «сомнительное», хотя спорить с данным тезисом довольно сложно, если и вообще возможно. Вопросительные высказывания также не являются логическими выражениями, так как судить об их истинности не имеет смысла. Также стоит отметить, что зачастую сложно определить, является ли выражение логическим.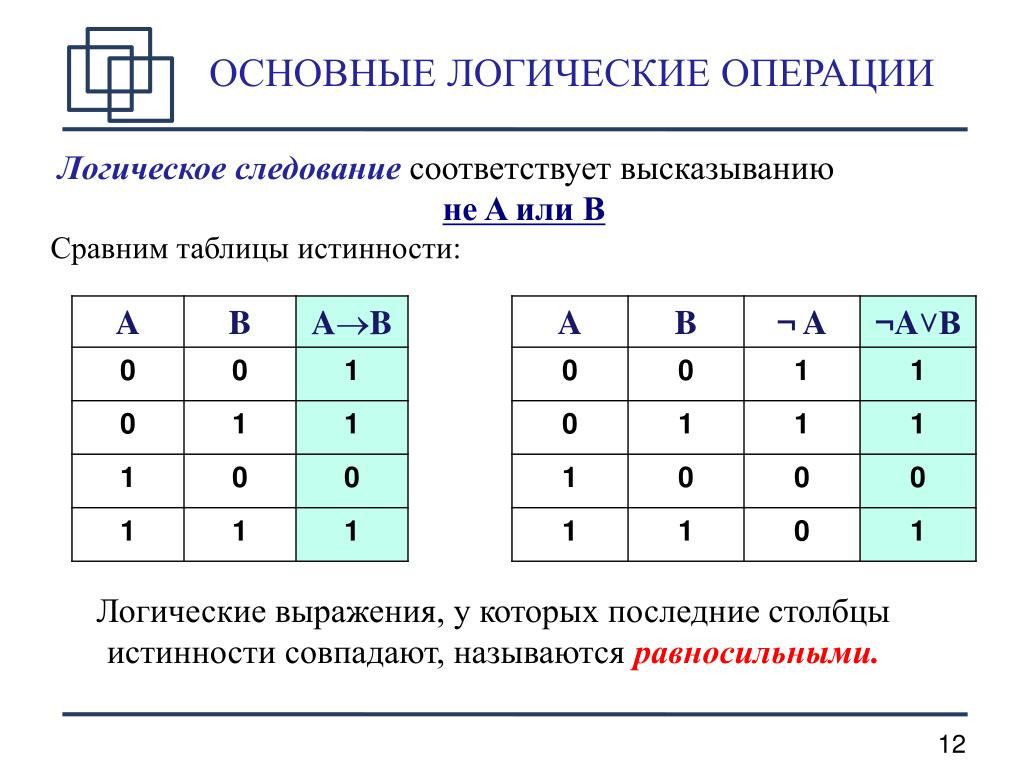
Логические связки
Разобравшись непосредственно с логическими выражениями, определим операции над ними. Под операциями над логическими выражениями принято подразумевать логические связки. Типичными примерами логических связок являются «и», «или», «если …, то» и т.п., позволяющие составлять из логических выражений новые. Например, «Столица России — Москва и столица США — Вашингтон». Это высказывание является истинным, поскольку его составные также являются истинными. Подробнее логические связки и правила их работы мы разберем далее.
Математический язык
В рамках данной части будут введены основные логические операции и их обозначения, аксиомы алгебры логики и её законы.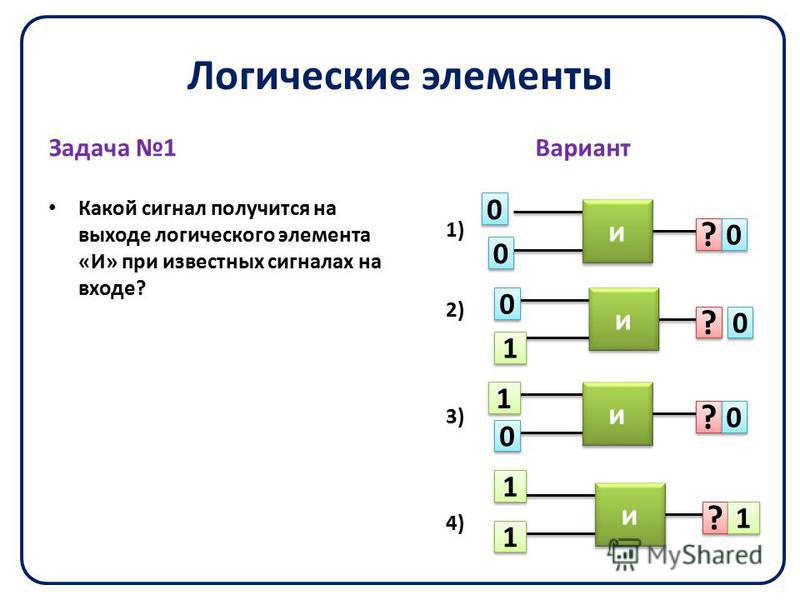
Логические операции
| Название операции | Обозначение | Речевой оборот |
| Инверсия (отрицание, логическое НЕ) | ¬A; A̅; | Не A; Неверно, что A; |
| Дизъюнкция (логическое ИЛИ) | A V B; A + B; | А или В или оба вместе; |
| Конъюнкция (логическое И) | A Λ B; A & B; A · B; | A и B вместе; |
| Импликация (следование) | A → B; | если A, то B; |
| Эквивалентность (тождество) | A↔B; A≡B; | A эквивалентно/равносильно B; |
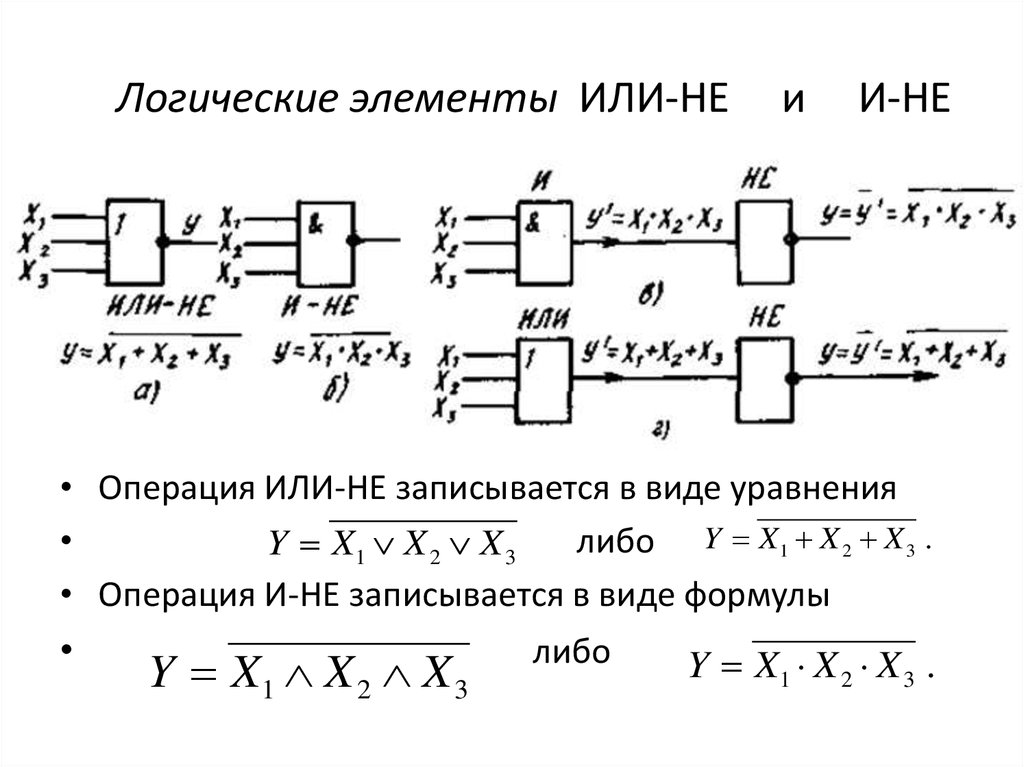
| Стрелка Пирса (ИЛИ-НЕ) | A↓B; | Ни A, ни B; |
| Штрих Шеффера (И-НЕ) | Неверно, что A и B; | |
| Сложение по модулю 2 (строгая дизъюнкция, XOR) | A⊕ B; | Либо A, либо B; |
Символами A и B обозначены условные логические высказывания.
На логические операции распространяется определенный порядок выполнения:
- Инверсия;
- Конъюнкция и штрих Шеффера;
- Дизъюнкция и стрелка Пирса;
- Импликация и сложение по модулю 2;
- Эквивалентность;
Аксиомы
Свойства и законы
Булевы функции
Булева функция — это брат-близнец функций из алгебры. Только вместо чисел в качестве переменных в ней логические высказывания.
Предположим, у нас есть такая простецкая функция:
«Если A истинно, то B тоже истинно«, где А и В — это некие логические высказывания.
На математическом языке эта функция имеет такой вид:
В случае с булевой функцией применяются таблицы истинности.Таблица истинности — это таблица, описывающая логическую функцию. В ней значения аргументов сопоставляются со значениями функциями. Для нашей функции таблица истинности будет следующей:
| A | B | F(A.B) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
На булевы функции распространяются законы и правила алгебры логики. Применим их для упрощения булевой функции f(A, B, C):
С таким видом этой функции работать проще. В том числе проще и составить таблицу истинности:
| A | B | C | F(A, B,C) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Базис
В алгебре логики функцию, реализующую одну и ту же таблицу истинности, можно реализовать с помощью разных операций.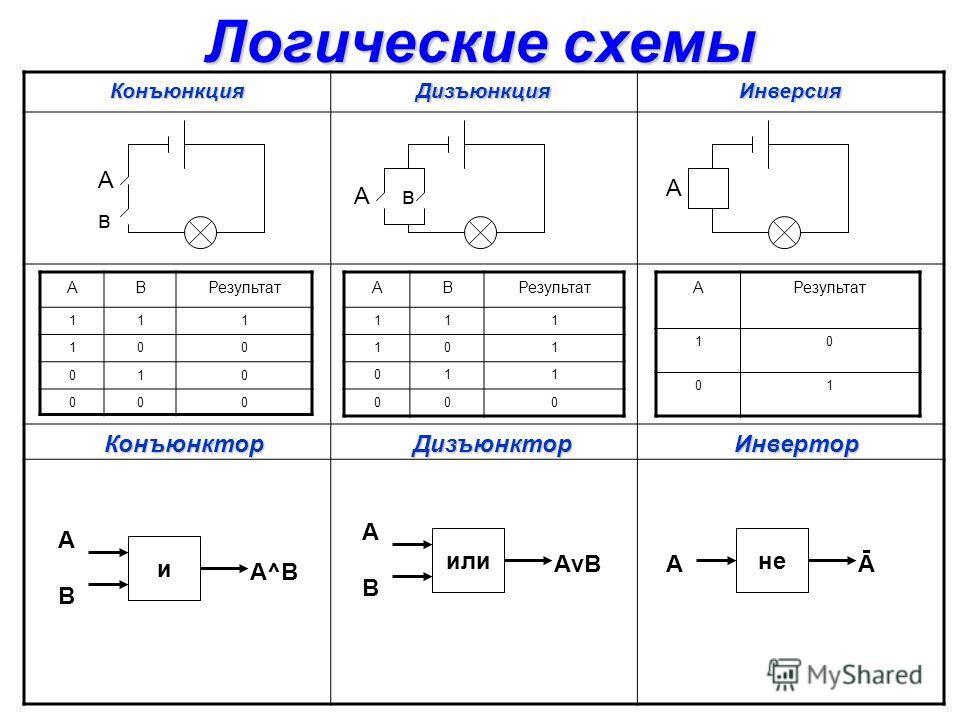
Базис — это набор операций, позволяющий построить любые, сколь угодно сложные функции. Например, наиболее распространенным является базис {И, ИЛИ, НЕ}. Базисы особенно полезны при построении логических схем.
Логические схемы
Логические схемы необходимы для реализации функций алгебры логики в цифровом устройстве. Для составления логических схем используются логические вентили (элементарные логические схемы), реализующие логические операции. Упомянутые базисы позволяют сократить перечень логических вентилей, хотя и стремление к полной минимизации этого перечня путем использования наименьших базисов не совсем практично. Мы рассмотрим логические вентили упомянутого базиса {И, ИЛИ, НЕ}
Логические вентиль И
У логического вентиля И два входа (А, В) и один выход (Z). Вентиль можно описать логической функцией Z=F(A,B)=A & B и таблицей истинности:
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический вентиль ИЛИ
У логического вентиля ИЛИ, как и у вентиля И, два входа и один выход.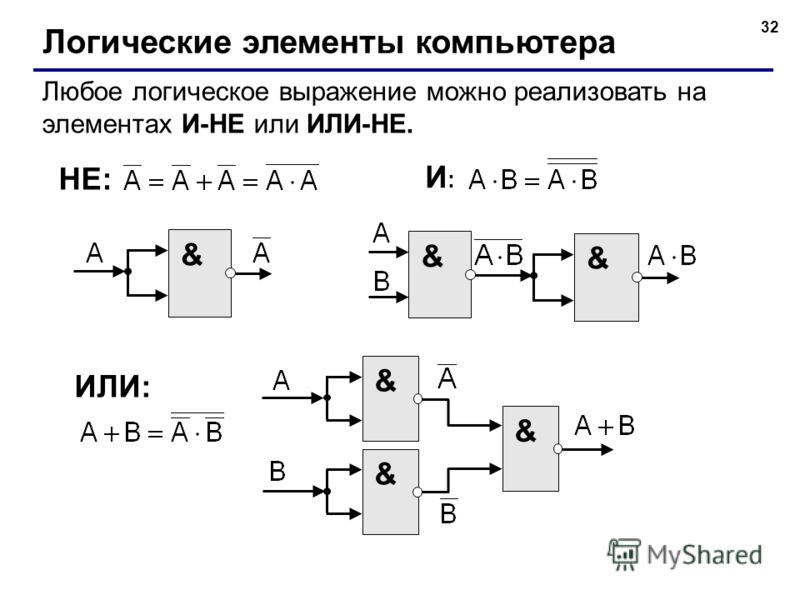
Его описывает функция Z=F(A,B)=A v B и таблица истинности:
| A | B | Z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логический вентиль НЕ
Логический вентиль НЕ имеет только один вход и один выход. На выход поступает инвертированное значение А. Функция вентиля НЕ: Q=F(A)=¬A
Обозначения по ГОСТ и другим стандартам
Сумматор
В качестве примера логической схемы, реализующей математическую операцию, рассмотрим многоразрядный двоичный сумматор. Складывать мы будем два двоичных числа. Для построения многоразрядного двоичного сумматора нам понадобится одноразрядный сумматор. Начнем с него.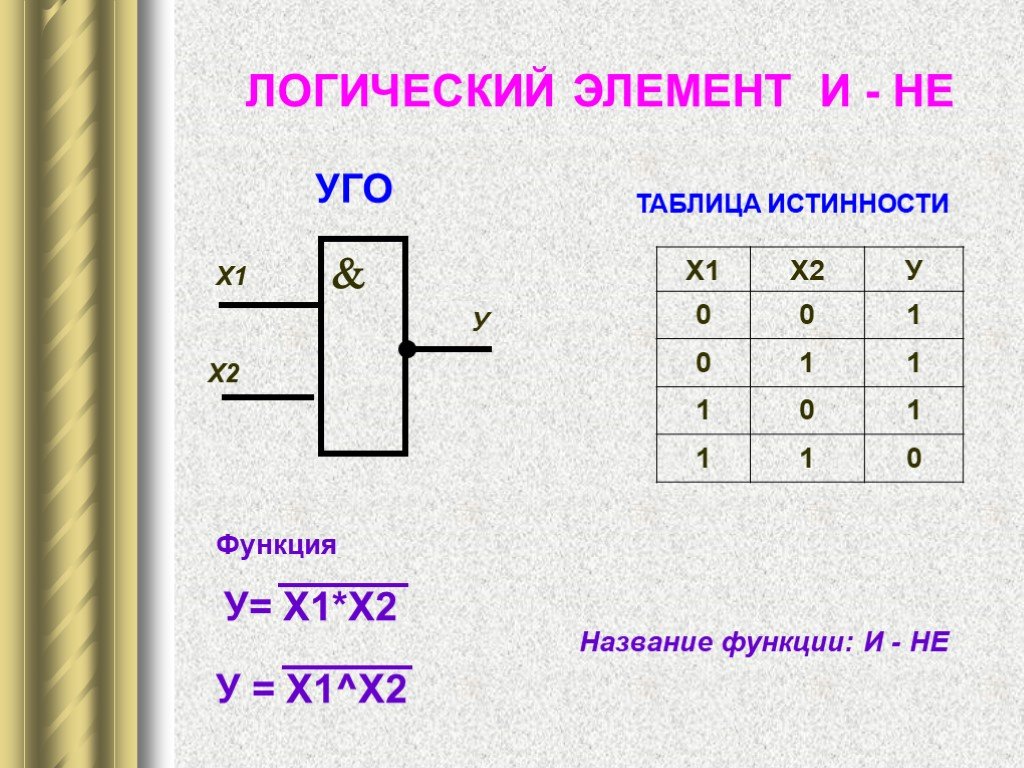
Разберемся с чем мы будем оперировать: две двоичных цифры. При сложении чисел нам, так или иначе, придется работать с переносом. Например, при сложении двух единиц в двоичной системе счисления мы получим 10:
В случае с одноразрядным сумматором на выход будут поступать две величины: перенос (в данном случае 1) и текущий разряд (0). Пока что мы проигнорируем перенос и составим таблицу истинности для разряда:
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Имея таблицу истинности, мы можем составить для неё булеву функцию:
Запомним эту функцию.
Добавим в наш сумматор перенос: как с предыдущего разряда (еще один вход), как и для следующего (ещё один выход).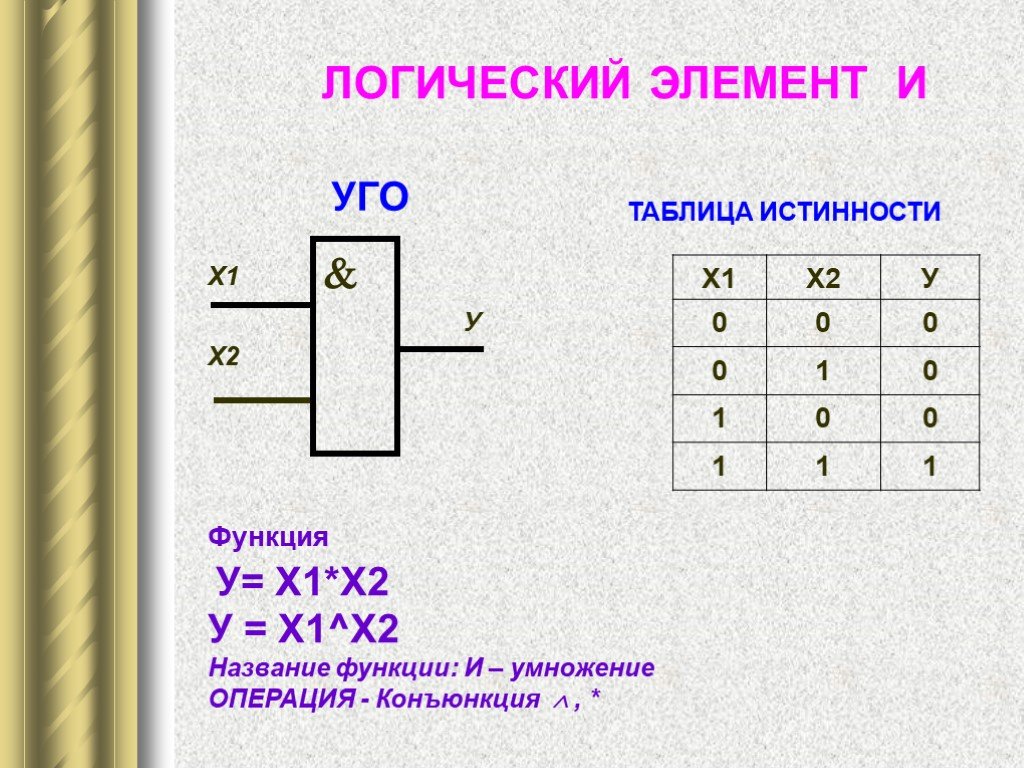
Таблица истинности для сумматора с переносом:
| A | B | P вход | S | P выход |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Теперь необходимо составить две булевы функции: для переноса и новую для разряда.
Чисто математически перенос для разряда — это ещё одно слагаемое в сумме. У нас уже есть функция для суммы, воспользуемся ей:
Нам необязательно раскрывать и упрощать эту функцию. Для построения логической схемы такой формы будет достаточно. Определимся с функцией для переноса.
Перенос равен единице в том случае, если из трех входных величин как минимум две равны единицы. Исходя из этого, можно составить вот такую функцию:
На основе двух имеющихся булевых функций для разряда и переноса мы можем составить логическую схему нашего одноразрядного сумматора. Не будем сразу бросаться в бой и начнем со схем поменьше.
Обозначение будет использовано в следующих схемах. Теперь составим схему для функции переноса:
Имея две логические схемы мы можем составить из них одноразрядный двоичный сумматор:
Если несколько одноразрядных сумматоров соединить последовательно, то получится многоразрядный сумматор:
Физика логического уровня
Итак, мы рассмотрели базовые концепции логического уровня: вентили и булеву алгебру.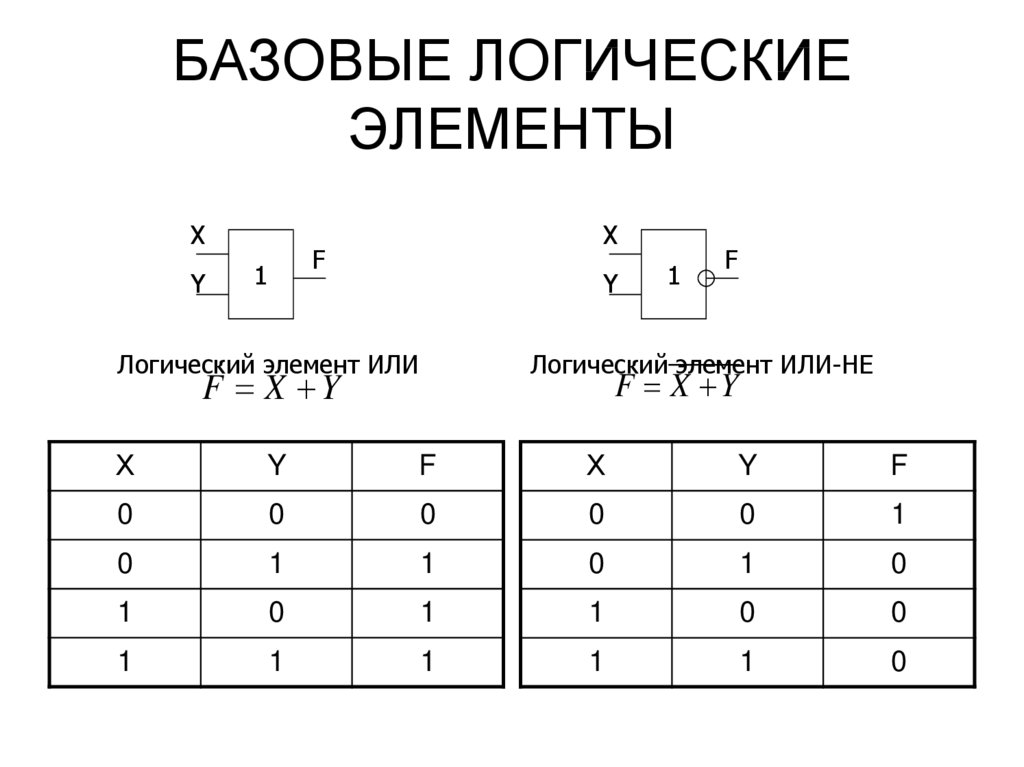
Из простейших логических элементов, как из кирпичиков Лего, строятся более сложные устройства (сумматор, шифратор, мультиплексоры, триггеры и другие), из них — еще более нетривиальные схемы и так далее, пока не получится цифровая схема с необходимой логикой. Теперь опустимся на уровень ниже и выясним, какие физические процессы заставляют все это добро работать на практике.
Физические принципы
Физически логические элементы могут быть самыми разнообразными: механическими, электромеханическими, электронными, оптическими и т.д. Некоторые умудряются конструировать схемы на основе жидкости или газов, как в этом видео:
Конечно, сегодня практичность таких «компьютеров» весьма сомнительна. Но когда-то транзисторов и полупроводниковой промышленности не существовало, и инженеры-первопроходцы выкручивались как могли. Например, в Z1 Конрада Цузе, одной из первых программируемых вычислительных машин, логические элементы были реализованы в виде набора металлических пластин, снабженных хитрыми вырезами.
Логический вентиль AND в Z1, реализованный с помощью металлических пластин. Более подробное описание устройства Z1 тут.
Конечно же, такие механизмы часто заедали и искажали результат, делая Z1 почти бесполезной на практике. В Z2-Z4 Цузе заменил пластины на электромагнитные реле и даже просил у правительства Третьего Рейха денег на полностью электронные компоненты, но ему отказали.
Первые полностью электронные компьютеры были ламповыми (в прямом и переносном смысле слова), так как логические элементы в них реализовывались с помощью электровакуумных ламп. Радиолампа — это электронный прибор, выполненный в виде запаянной стеклянной колбы с электродами, из которой откачан воздух. Работа радиолампы основывается на явлении термоэлектронной эмиссии: в диоде (простейшей радиолампе) отрицательно заряженные электроны покидают разогретый электрод (катод) и под действием разности потенциалов притягиваются к другому электроду (аноду).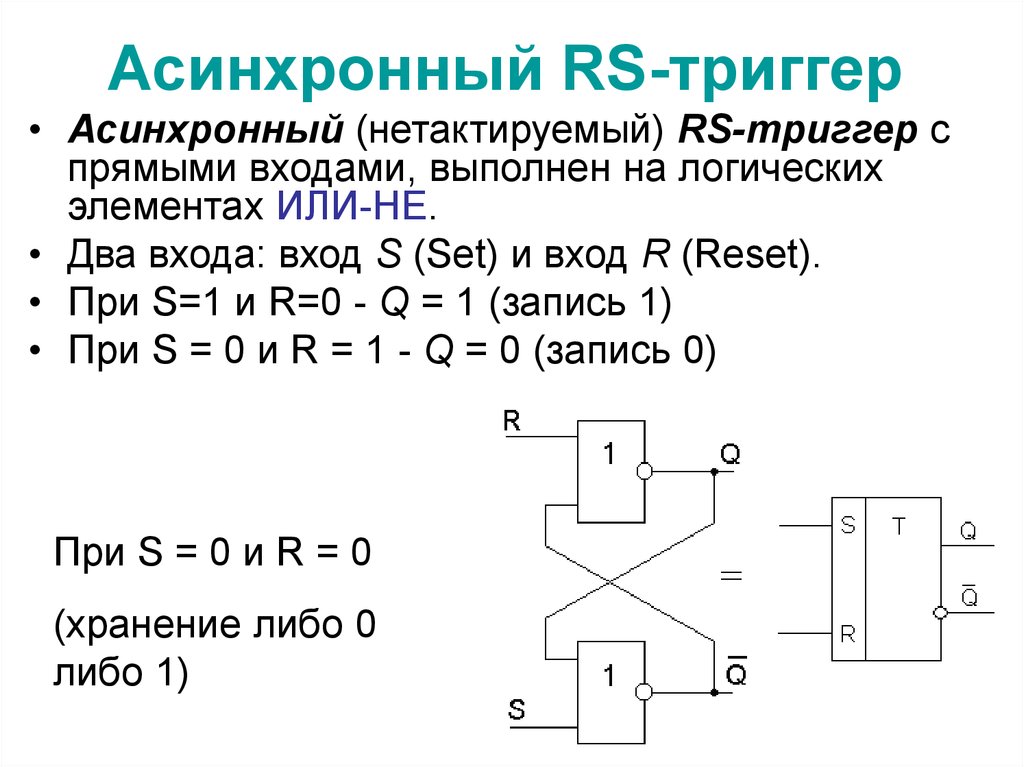
В обратном направлении заряд не передается, так как холодный анод не производит эмиссии, а заряженных ионов в колбе нет (потому что в ней вакуум). При изменении полярности включения диода в цепь, электроны с разогретого электрода будут тут же притягиваться к нему обратно под действием положительного потенциала.
Радиолампа (двойной триод)
Если добавить между двумя электродами третий электрод (сетку), то получится триод. Изначально триоды предназначались для усиления сигналов, так как ток через триод повторяет изменение потенциала на сетке и может быть намного сильнее. Однако нам интересней другое свойство: при подаче отрицательного потенциала на сетку, она начнет отталкивать электроны, не позволяя им достичь анода. С помощью такого эффекта управления можно реализовывать простейшие логические схемы. Например, возьмем два триода и соединим анод каждого с сеткой другого. Получиться устройство под названием триггер, которое может находиться в одном из двух устойчивых состояний (ток идет либо через первый триод, либо через второй), что позволяет хранить один бит информации.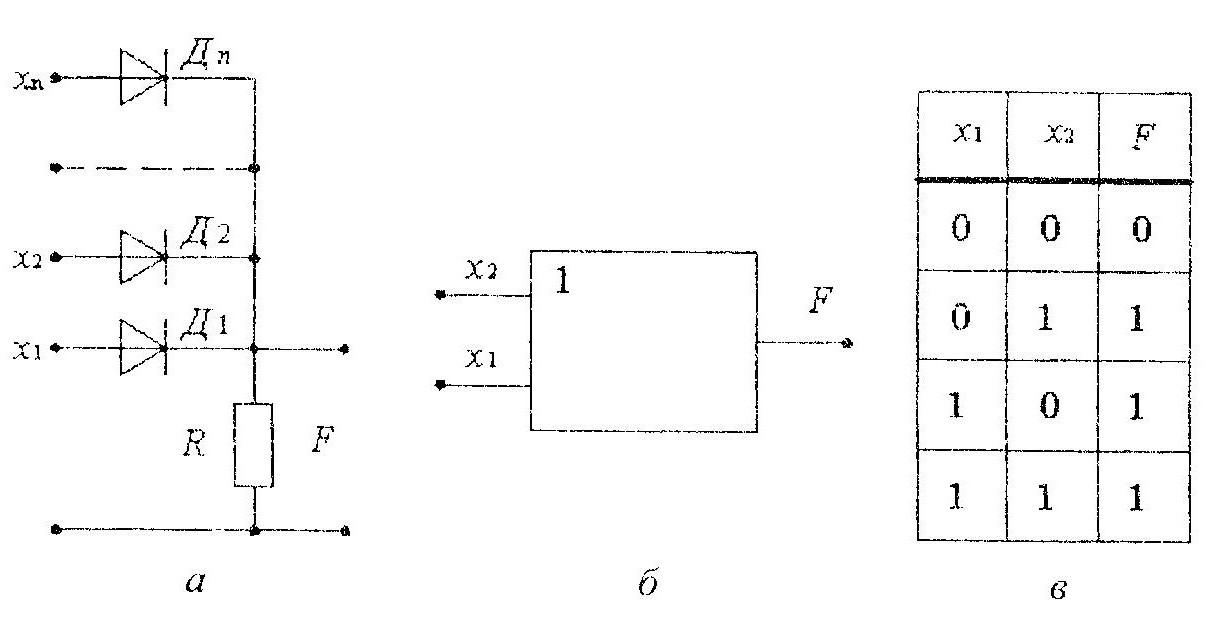
Другие схемы соединения триодов позволяют строить логические вентили.
Схема триггера на двух ламповых триодах. Через один из триодов идет ток (триод открыт), благодаря этому на сетке второго возникает потенциал, не позволяющий току идти через второй триод (триод закрыт). Если кратковременно подать отрицательный потенциал на сетку открытого триод, то ток прекратится, поэтому второй триод откроется и закроет первый, тем самым перейдя во второе устойчивое состояние.
Хоть устройства на лампах работают быстрее механических и электромеханических, радиолампа остается крайне ненадежным прибором. Колба может потерять герметичность, спираль нагрева со временем перегорает, а сама лампа потребляет много энергии и имеет внушительные габариты. Если учитывать что первые ЭВМ состояли из тысяч ламп, обслуживание лампового монстра превращалось в головную боль для инженеров.
В 1947 Уильям Шокли, Джон Бардин и Уолтер Браттейн создали усилитель нового типа, состоявший из германиевой пластины и полоски золотой фольги.
Спустя несколько лет им присудили Нобелевскую премию по физике. Этим изобретением был транзистор — устройство, полностью изменившее индустрию вычислительной техники.
Копия первого в мире работающего транзистора.
Транзистор
С концептуальной точки зрения транзистор очень похож на радиолампу-триод. Это переключатель с двумя положениями «включить» и «выключить», управляемый с помощью подачи напряжения или тока. Однако в сравнении с вакуумными лампами транзисторы имеют ряд преимуществ: они миниатюрны, потребляют значительно меньше электроэнергии и крайне редко выходят из строя (относительно тех же ламп). Благодаря изобретению транзистора компоненты логических элементов перешли из разряда «расходных материалов» в разряд «постоянных узлов конструкции».
Существуют два основных типа транзисторов — биполярные транзисторы и МОП-транзисторы (металл-оксид-полупроводник-транзистор или полевой транзистор).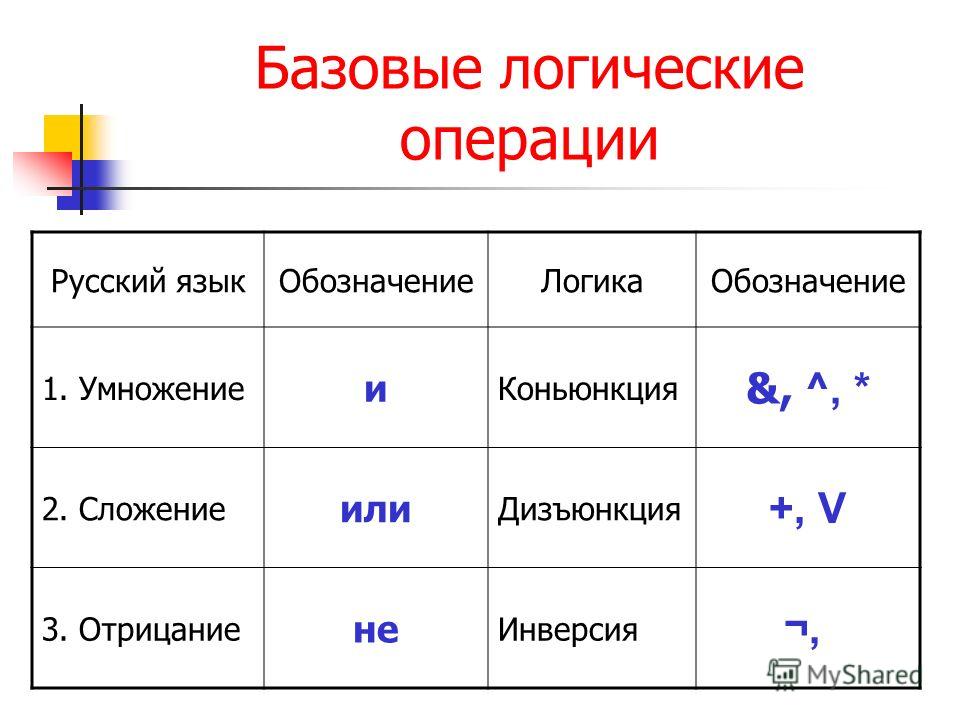
Различаются они тем, что первый управляется током, а второй — электрическим полем (отсюда и название «полевой»). В сфере производства цифровых интегральных схем полевые транзисторы практически полностью вытеснили биполярные.
Сегодня, после нескольких десятилетий развития полупроводниковых технологий, инженеры способны «упаковать» около одного миллиарда МОП-транзисторов на квадратном сантиметре кристалла кремния (с себестоимостью транзистора менее десяти микроцентов).
Полупроводники
Выше мы говорили о «полупроводниковых технологиях». Что такое полупроводник? Некоторые могут подумать, что полупроводники проводят электрический ток в два раза хуже обычных проводников (таких, как медь, золото или серебро). Это не так! МОП-транзисторы изготавливаются из кремния, элемента 14-й группы (4-й по устаревшей классификации, далее будем придерживаться именно ей). Благодаря 4 электронам, атом кремния может образовывать связи с 4 соседними атомами, формируя кристаллическую решетку.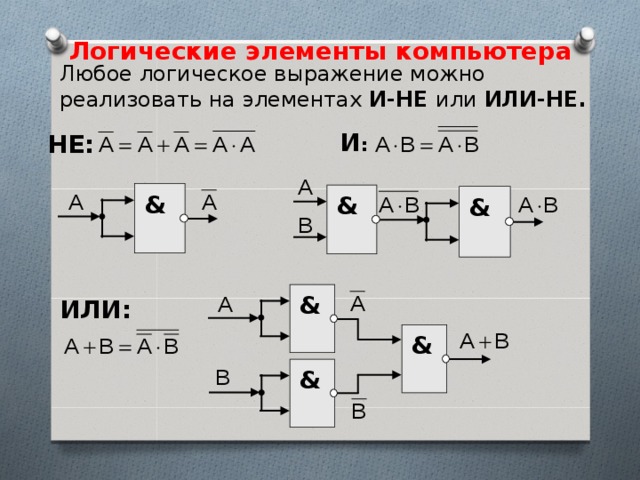
Кремний — так себе проводник (точнее плохой, так как все электроны заняты в ковалентных связях), однако при добавлении в него небольшого количества другого вещества (легировании) его проводимость может улучшиться. Если добавить атом 5 группы (примесь n-типа), то в нем останется один свободный электрон, который легко «гуляет» внутри кристаллической решетки. А если добавить элемент 3 атомной группы (примесь p-типа), то в атоме примеси будет отсутствовать один электрон (дырка). Дырка может перемещаться в кристаллической решетки подобно электрону, причем она будет вести себя как положительно заряженная частица. Отсюда и название «полупроводник» — с помощью концентрации примесей можно управлять проводимостью кремния.
Кристаллическая решетка атомов кремния. В качестве примеси n-типа (центр) использован мышьяк (атом, потерявший электрон, становится положительным ионом), в качестве примеси p-типа (справа) использован бор (при перемещении дырки атом бора получает дополнительный электрон и становится отрицательным ионом).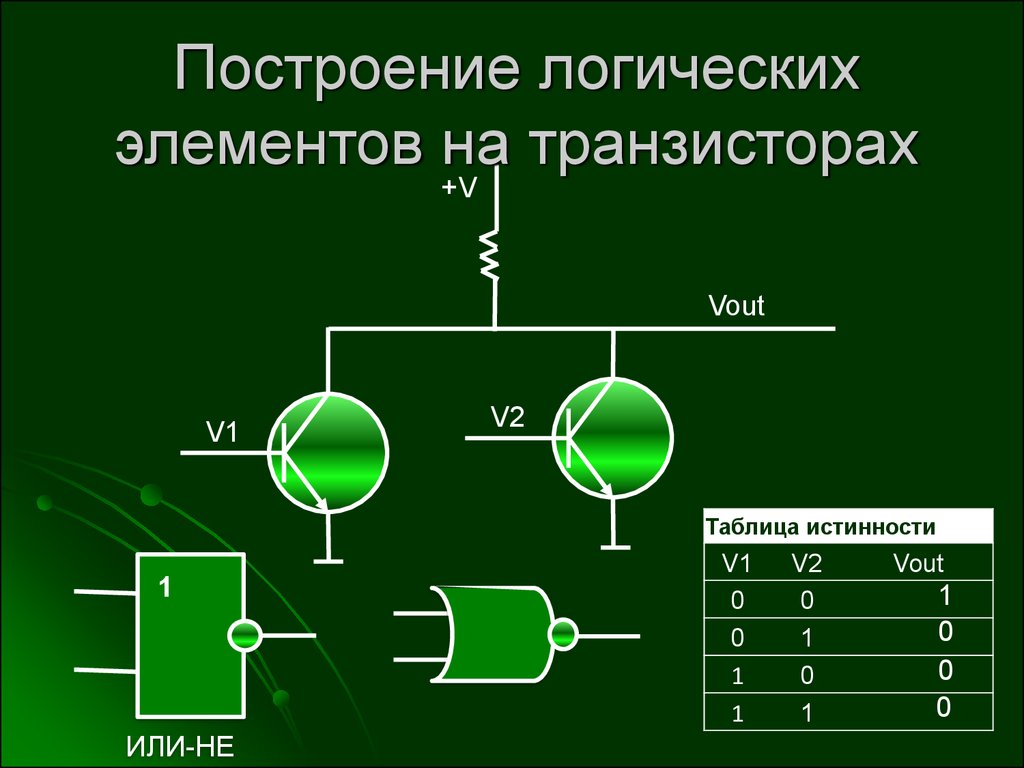
n-МОП и p-МОП транзисторы
Полевой МОП-транзистор можно представить в виде «сэндвича» из нескольких слоев. Верхний слой называется затвором. Он наложен на слой изолятора — диоксида кремния (SiO2, иногда его называют просто оксидом). Этот слой в свою очередь располагается над кремниевой пластиной, называемой подложкой. Сегодня в качестве металла затвора используется поликристаллический кремний, поскольку он не плавится в ходе высокотемпературной обработки кристалла. Слои металл-оксид-полупроводника образуют конденсатор, в котором тонкий слой оксида (диэлектрик) изолирует металлическую пластину от полупроводниковой.
Существуют два вида полевых МОП-транзисторов: n-МОП и p-МОП. В транзисторах n-типа, называемых n-МОП, области, где расположены полупроводниковые примеси n-типа – в свою очередь называемые истоком и стоком – находятся рядом с затвором, причем вся эта структура размещается на подложке p-типа. В транзисторах же p-МОП и исток, и сток – это области p-типа, размещенные на подложке n-типа.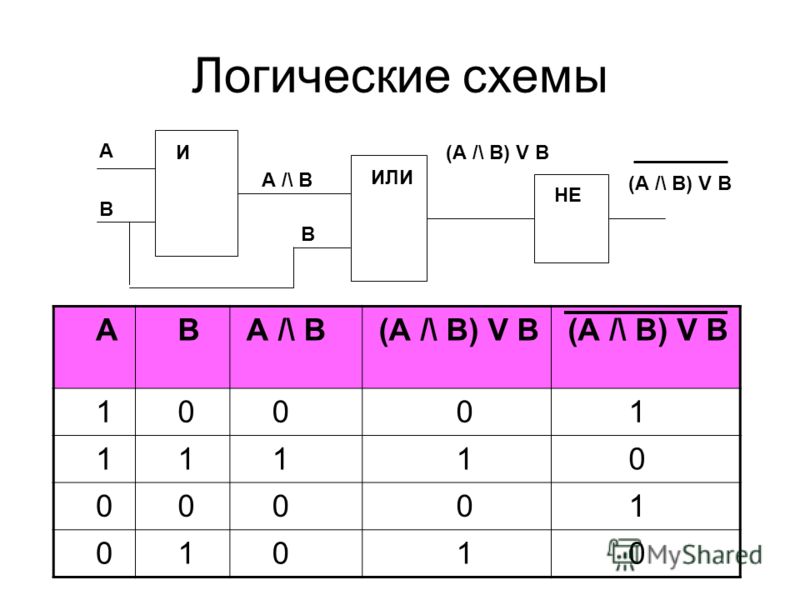
Полевой МОП-транзистор ведет себя как переключатель, управляемый приложенным к нему напряжением. В таком транзисторе напряжение перехода создает электрическое поле, включающее или отключающее линию связи между источником и стоком.
Диод — соединение p-полупроводника (катода) и n-полупроводника (анода). Когда напряжение на аноде превышает напряжение на катоде, ток идет (от анода к катоду). В обратном случае ток не течет. На рисунке представлена схема работы n-МОП транзистора. Когда напряжение на затворе равно 0 В, канал движения тока между истоком и стоком закрыт (транзистор выключен). Когда напряжение на затворе равно напряжению питания (Vdd), это создает электрическое поле между затвором и подложкой, в результате в зону между истоком и стоком под слоем окисла формируется избыток электронов. При достаточно высоком напряжении на нижней границе затвора накапливается настолько много электронов, что область с полупроводником p-типа превращается в область с полупроводником n-типа.
Такая область называется каналом. В этот момент в транзисторе образуется область проводимости от источника n-типа, через каналы n-типа к стоку n-типа, и через этот канал электроны могут беспрепятственно перемещаться от истока к стоку. Транзистор включен. p-МОП-транзисторы работают ровно наоборот.
К сожалению, полевые МОП-транзисторы плохо работают в роли переключателя. n-МОП-транзисторы хорошо передают логический 0 и плохо логическую единицу. p-МОП — наоборот. Поэтому для создания хороших логических вентилей, хотелось бы иметь оба транзистора на одном кристалле. Однако для n-МОП- и p-МОП-транзисторов требуются разные типы подложек. Для размещения двух типов транзисторов на одном кристалле применяется комплементарный МОП (КМОП). В настоящее время КМОП-процесс используется для изготовления подавляющего большинства транзисторов и микросхем.
Логические вентили на КМОП-транзисторах
Для подробного описания построения всевозможных логических вентилей здесь просто не хватит места.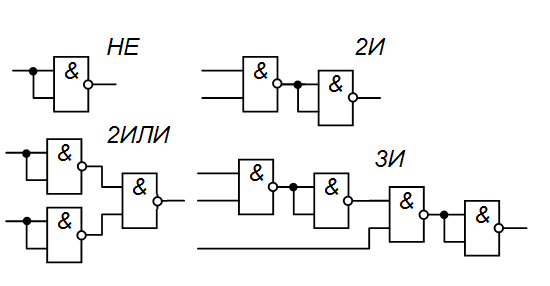
Поэтому в качестве примера возьмем простейшие логические элементы и рассмотрим их реализацию на КМОП-транзисторах. Вентиль НЕ:
n-МОП-транзистор N1 включен между землей GND и выходным контактом Y. В свою очередь, p-МОП транзистор P1 включен между напряжением питания VDD и выходным контактом Y. Напряжение на входном контакте А управляет переходами обоих транзисторов.
Если напряжение на А соответствует логическому нулю, то транзистор N1 выключен, а транзистор P1 включен. При этом, напряжение на контакте Y равно напряжению питания, а не земли, что соответствует логической единице. В этом случае говорят, что Y «подтянут» к единице. Включенный транзистор P1 хорошо передает логическую единицу (равную напряжению питания), то есть напряжение на контакте Y очень близко к VDD. Если же напряжение на контакте А равно логической единице, то транзистор N1 включен, а транзистор P1 выключен, и напряжение на контакте Y равно напряжению земли, что соответствует логическому нулю.
В этом случае говорят, что Y «подтянут» к нулю. Включенный транзистор N1 хорошо передает логический ноль, то есть напряжение на контакте Y очень близко к GND. Получается, что если A=1, то Y=0, а если A=0, то Y=1. Это соответствует таблице истинности для логического вентиля НЕ.
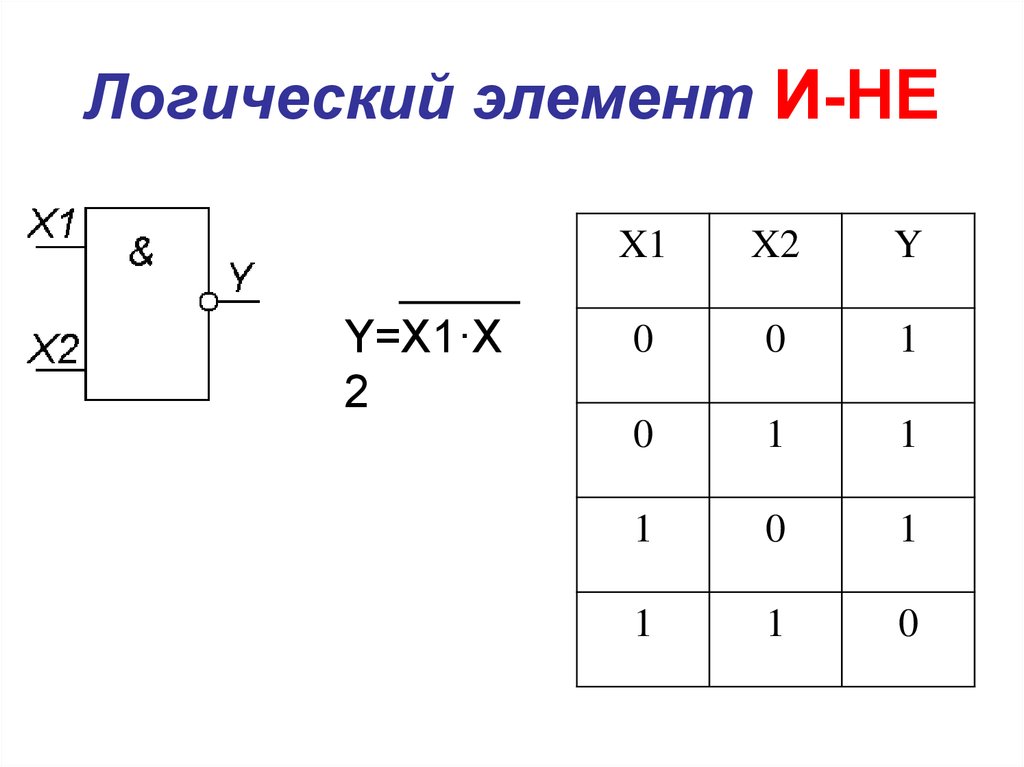
Схемы вентилей И-НЕ и ИЛИ-НЕ с двумя входами:
Вентиль И-НЕ
n-МОП-транзисторы N1 и N2 соединены последовательно. Причем, чтобы замкнуть выходной контакт на землю GND – то есть понизить логический уровень, оба этих транзистора должны быть включены. В то время как p-МОП-транзисторы P1 и P2 соединены
параллельно, и только один из них должен быть включен, чтобы соединить выходной контакт с напряжением питания – то есть повысить логический уровень.
Вентиль ИЛИ-НЕ
В этом случае все ровно наоборот. n-МОП транзисторы соединены параллельно, а p-МОП последовательно.
Заключение
В этой статье мы затронули только самые основы логического цифрового уровня и физики его работы.
Возможно эта обширная и сложная область вас заинтересовала. В таком случае можем порекомендовать следующую литературу:
Computer Systems: A Programmer’s Perspective
The Elements of Computing Systems (Nand2Tetris)
Digital Design and Computer Architecture
[L01] Что такое логика?
Термин «логика» произошел от греческого слова logos , что иногда переводится как «предложение», «дискурс», «причина», «правило» и «отношение». Конечно, этих переводов недостаточно, чтобы помочь нам. понять более специализированное значение слова «логика», как оно используется сегодня.
Так что же такое логика? Короче говоря, мы могли бы определить логику как изучение принципов правильного мышления . Это грубое определение, потому что вопрос о том, как правильно определить логику, на самом деле довольно спорный. Однако для целей этого тура мы подумали, что было бы полезно дать вам хотя бы приблизительное представление о предмете, который вы будете изучать.
Именно это мы и попытаемся сделать на этой странице.
§1. Логика — это не психология рассуждений
Одна вещь, которую вы должны отметить в отношении этого определения, заключается в том, что логика связана с принципами правильного рассуждения. Изучение правильных принципов рассуждения — это не то же самое, что изучение психологии рассуждения. Логика — это прежняя дисциплина, и она говорит нам, как мы должны рассуждать, если хотим рассуждать правильно. Действительно ли люди следуют этим правилам правильного рассуждения — это эмпирический вопрос, который не касается логики.
Психология рассуждения, с другой стороны, является эмпирической наукой. Он рассказывает нам о реальных привычках людей рассуждать, в том числе об их ошибках. Психолога, изучающего рассуждения, может интересовать, как способность людей рассуждать меняется с возрастом. Но такие эмпирические факты не интересуют логика.
§2. Принципы логики
Так что же это за принципы рассуждения, которые являются частью логики? Таких принципов много, но главное (не единственное), что мы изучаем в логике, это принципы, регулирующие обоснованность аргументов — следуют ли определенные выводы из некоторых заданных предположений.
Например, рассмотрим следующие три аргумента:
Если Том философ, то Том беден.
Том — философ.
Значит, Том беден.
Если К>10, то К>2.
К>10.
Следовательно, К>2.
Если Таррагона находится в Европе, то Таррагона не в Китае.
Таррагона находится в Европе.
Значит, Таррагона не в Китае.
Эти три аргумента здесь, очевидно, хорошие аргументы в том смысле, что их выводы следуют из предположений. Если предположения аргумента верны, вывод аргумента также должен быть истинным. Логик скажет нам, что все они являются случаями особой формы аргументации, известной как « modus ponens »:
Если P, то Q. P. Следовательно, Q.
Позже мы еще вернемся к вопросу о законности. Следует отметить, что логика занимается не только обоснованностью аргументов. Логика также изучает непротиворечивость, логические истины и такие свойства логических систем, как полнота и обоснованность. Но мы увидим, что эти другие понятия также очень тесно связаны с понятием значимости.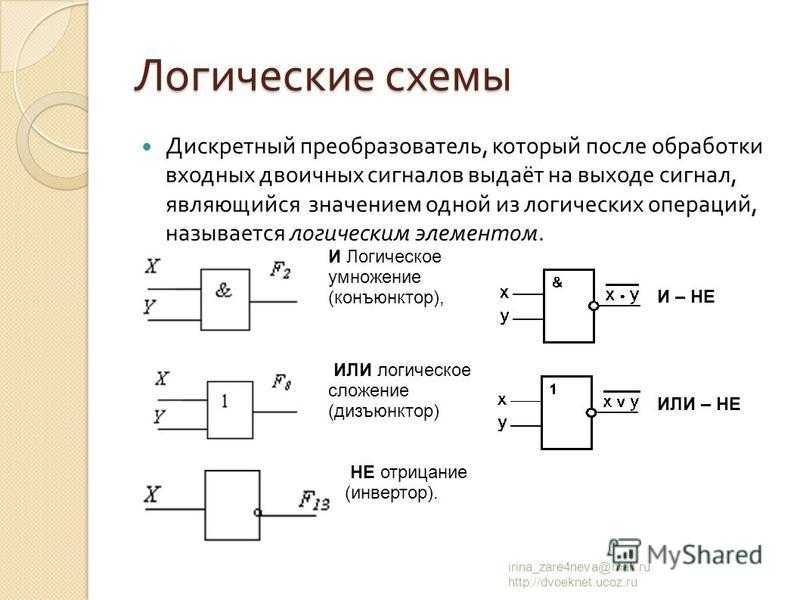
§3. Тематический нейтралитет
Modus ponens можно использовать для иллюстрации двух особенностей правила рассуждения в логике. Первая особенность его тематическая нейтральность. Как показывают четыре примера, modus ponens можно использовать в рассуждениях на разные темы. Это верно для всех принципы рассуждения в логике. Законы биологии могут быть правдой только живых существ, и законы экономики применимы только к коллекциям агентов, которые занимаются финансовыми операциями. Но принципы логики являются универсальными принципами, которые являются более общими чем биология и экономика. Отчасти это подразумевается в следующие определения логики двумя очень известными логиками:
[Логика] … название дисциплины, которая анализирует смысл понятий, общих для всех наук, и устанавливает общие законы, управляющие понятиями. Альфред Тарский (1901–1983). Из его Введение в логику и методологию дедуктивных наук , Дувр, стр. XI.
Открывать истины — задача всех наук; логике приходится различать законы истины.… Я ставлю перед логикой задачу открытия законов истины, а не утверждения или мысли. Готтлоб Фреге (1848-1919 гг.)25). Из его статьи 1956 года «Мысль: логическое исследование» в Mind Vol. 65.
… Я ставлю перед логикой задачу открытия законов
истины, а не утверждения или мысли.
Готтлоб Фреге (1848-1919 гг.)25). Из его статьи 1956 года «Мысль: логическое исследование» в Mind Vol. 65.§4. Необходимость в логике
Второй особенностью принципов логики является
что они не являются случайными в том смысле, что они не зависят от
любые частные случайные особенности мира. Физика и прочее
эмпирические науки исследуют то, каков мир на самом деле.
Физики могли бы сказать нам, что ни один сигнал не может распространяться быстрее, чем
со скоростью света, но если бы законы физики были другими, то
возможно, это было бы неправдой. Точно так же биологи могут
изучить, как дельфины общаются друг с другом, но если ход
эволюция была иной, то, возможно, дельфины не
существовал. Таким образом, теории в эмпирических науках зависят от
ощущение, что они могли быть иными. Принципы логики,
с другой стороны, выводятся только с помощью рассуждений, и их достоверность
не зависит от каких-либо случайных особенностей мира.
Например, логика говорит нам, что любое утверждение вида «Если P , затем P ». Это принцип второго рода, который изучает логика. Этот принцип говорит нам, что такое утверждение, как «если идет дождь, то идет дождь», должно быть истинным. можно легко увидеть что это действительно так, независимо от того, идет ли дождь на самом деле. Более того, даже если законы физики или погодные условия изменится, это утверждение останется верным. Таким образом, мы говорим, что научный истин (кроме математики) условное тогда как логические истины необходимые . Это снова показывает, насколько логика отличается от эмпирических наук, таких как физика, химия или биология.
§5. Формальная и неформальная логика
Иногда проводится различие между неформальной логикой и формальной логикой .
Термин «неформальная логика» часто используется для обозначения того же, что и
критическое мышление. Иногда его используют для обозначения изучения
рассуждения и заблуждения в контексте повседневной жизни.
«Формальная логика»
в основном занимается формальными системами логики. Это специально
построены системы для проведения доказательств, где языки и
правила рассуждения точно и тщательно определены. Логика предложений (также известная как «логика высказываний») и Логика предикатов являются примерами формальных систем логики.
Есть много причин для изучения формальной логики. Один из них формальный
логика помогает нам идентифицировать модели хороших рассуждений и модели плохих
рассуждения, чтобы мы знали, чему следовать, а чего следует избегать. Вот почему
изучение базовой формальной логики может помочь улучшить критическое мышление. Формальный
системы логики также используются лингвистами для изучения естественных языков.
Ученые-компьютерщики также используют формальные системы логики в исследованиях.
относящийся к искусственному интеллекту. Наконец, многие философы также
любят использовать формальную логику при работе со сложными философскими
проблемы, чтобы сделать их рассуждения более явными и точными.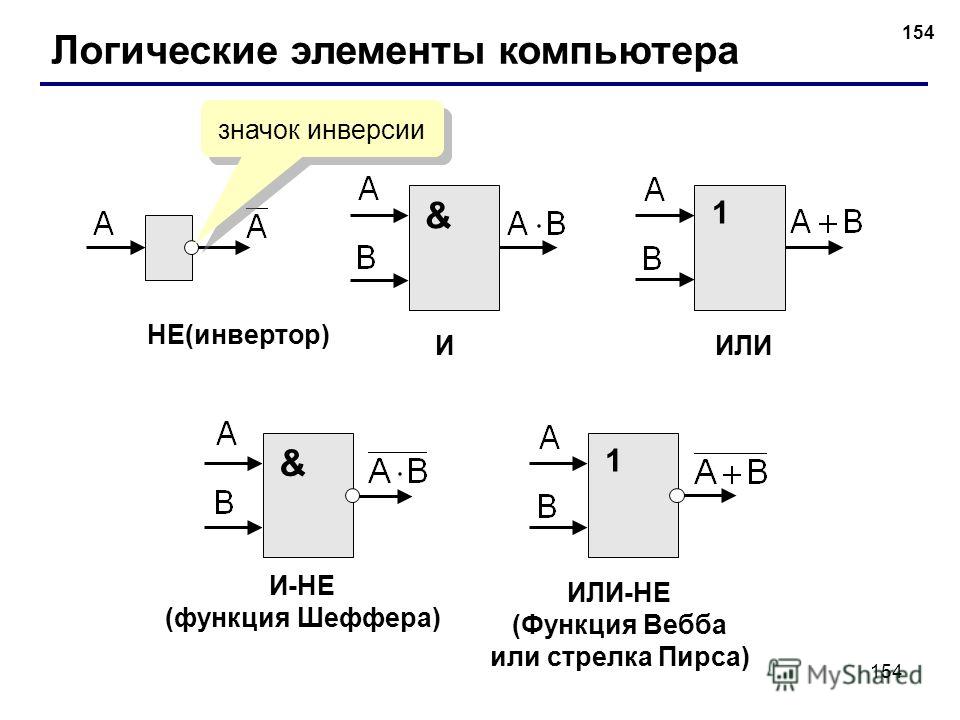
§6. Дополнительная литература
- Записи по логике в Стэнфордской энциклопедии философии. Это трудные статьи по философии логики.
- Предположим, мы обнаруживаем, что люди лучше рассуждают, когда не находятся в состоянии стресса. Следует ли это считать принципом логики?
- Чем наука отличается от логики?
- Чем математика отличается от логики?
следующий учебник
Функция логического НЕ — Electronics-Lab.com
Функция логического НЕ
Состояние выхода функции логического НЕ НЕ совпадает с состоянием входа. Логическая функция НЕ выполняет функцию инверсии на своем входе и выводит дополнение к входу. Выход логической функции НЕ является ложным, когда его вход истинен, и истинен, когда его вход ложен. Это простейшая логическая функция, имеющая один вход и один выход.
Логическое выражение логической функции НЕ представлено надчеркиванием или чертой (¯) над входом. Эта полоса или надчеркивание обозначает инверсию или дополнение состояния или ввода.
Логическую функцию НЕ выполняют логические элементы НЕ, которые иногда называют инверторами (поскольку они выполняют функцию инверсии). Символ логического вентиля НЕ вместе с выражением показан на следующем рисунке.
На выходе символа логического НЕ имеется пузырек (o), который обозначает инверсию сигнала и поэтому называется «пузырьком инверсии». Аналогом инвертора является буфер, который не инвертирует сигнал, а выполняет только его усиление.
Представление функции НЕ с использованием переключателя
Логическую функцию НЕ можно проиллюстрировать с помощью следующей схемы. На рисунке показана лампа вместе с двумя выключателями. Положения переключателей обратны или дополняют друг друга. Переключатель без штриха или надчеркивания представляет собой логический вход (X), а переключатель с чертой или надчеркиванием — инвертированное состояние входа (X). Логические состояния «0» и «1» представляют собой переключатель с положениями «Открыто» и «Закрыто» соответственно.
Когда вход имеет значение ИСТИНА или переключатель (X) находится в замкнутом состоянии, его дополнительный переключатель будет разомкнут, а лампа останется выключенной, пока вход (X) включен. состояние.
Рисунок 3: Функция логического НЕ с использованием переключателей с включенной лампойОднако, когда вход ЛОЖЬ или переключатель (X) находится в разомкнутом состоянии, его дополнительный переключатель будет замкнут, и лампа загорится, пока вход (X) находится в состоянии ВЫКЛ.
Из приведенных выше сценариев видно, что состояние лампы представляет собой инверсию относительно входа (X).
Таблица истинности логического НЕ
Таблица истинности логического вентиля НЕ показана ниже.
Законы булевой алгебры
В булевой алгебре закон дополнения включает в себя логическую функцию НЕ и показан на следующем рисунке, где он выполняет функцию инверсии.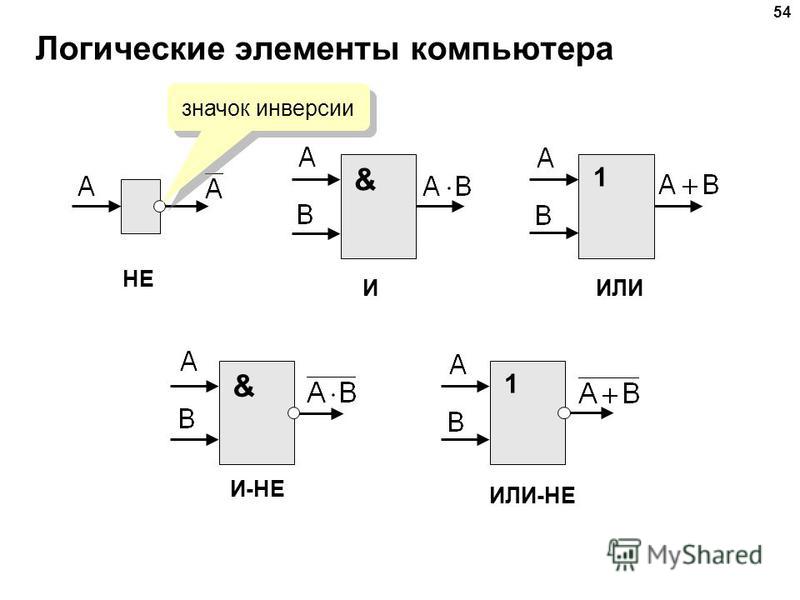
Построение других логических элементов
Логические элементы И-НЕ и ИЛИ-НЕ могут быть построены путем размещения логического элемента «НЕ» на выходе логических элементов «И» и «ИЛИ» соответственно. Элементы NAND и NOR называются универсальными логическими элементами, поскольку они могут использоваться для создания любой другой логики. Точно так же каскадирование двух логических вентилей НЕ возвращает исходный входной сигнал, и такое расположение создает цифровой буфер.
Рисунок 5: Эквиваленты И-НЕ и ИЛИ-НЕ с использованием логических элементов НЕПостроение функции логического НЕ
Функция логического НЕ широко используется в цифровых схемах и доступна в специализированных корпусах ИС, имеющих несколько логических элементов НЕ. Однако логическая функция НЕ также может быть построена с использованием вентилей НЕ-И или ИЛИ-НЕ, поскольку они являются универсальными вентилями. Построение логики НЕ с использованием вентилей НЕ-И или ИЛИ-НЕ экономит место и стоимость использования отдельного пакета ИС логических вентилей НЕ-И.
На следующем рисунке показаны эквиваленты функции НЕ
Имеющиеся в продаже логические вентили НЕ
пакет, содержащий несколько вентилей НЕ. И.К. пакеты поставляются как в семействе транзисторно-транзисторной логики (TTL), так и в семействе комплементарных металлооксидных полупроводников (CMOS). Несколько имеющихся в продаже логических вентилей НЕ приведены ниже:
- TTL 74LS04 Не вентили НЕ
- CMOS 4049 Hex НЕ Gates
- КМОП 4069Шестигранник НЕ Ворота
Заключение
- Логическая функция НЕ инвертирует или дополняет входной сигнал. Он выводит ЛОЖЬ, когда ввод ИСТИНА, и ИСТИНА, когда ввод ЛОЖЬ.
- Логический элемент НЕ также называется «инвертором» из-за его функции инвертора.
- Логический вентиль НЕ используется в конструкции универсальных логических вентилей, таких как вентили НЕ-И и ИЛИ-НЕ.
- Функция логического НЕ может быть реализована в цифровых схемах с использованием логических элементов НЕ-И или ИЛИ-НЕ, что устраняет необходимость в использовании специального пакета микросхем логического элемента НЕ.
