Логика и компьютеры.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§8. Логика и компьютеры.Что такое высказывание?
Ключевые слова:• логика • формальная логика • логическое высказывание • алгебра логики • логические переменные • логическая операция • операция «НЕ» • операция «И» • операция «ИЛИ» • логическая функция
В быту мы часто используем слова «логика», «логично». Логика (наука о рассуждении) — это наука о том, как правильно рассуждать, делать выводы, доказывать утверждения.
В естественном языке рассуждения связаны с самыми разными предметами и понятиями, и поэтому изучать их достаточно сложно. Древнегреческий философ Аристотель начал изучать общие правила построения правильных выводов из известной информации, которая считается истинной. Такая логика называется формальной, она изучает истинность и ложность логических высказываний, отвлекаясь от их содержания.
Логическое высказывание — это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно.
Используя это определение, проверим, можно ли считать логическими высказываниями следующие предложения:
1) Сейчас идёт дождь.
2) Вчера жирафы улетели на север.
3) Беги сюда!
4) Который час?
5) В городе N живёт более 2 миллионов человек.
6) У квадрата 10 сторон, и все разные.
7) История — интересный предмет.
Здесь высказываниями являются только предложения 1, 2 и 6, остальные не подходят под определение. Предложения 3 и 4 не повествовательные (призыв к действию и вопрос). Предложение 5 станет высказыванием только в том случае, если N заменить на название конкретного города. Утверждение 7 кто-то считает истинным, а кто-то — ложным (нет однозначности), его можно более строго сформулировать в виде «По мнению N, история — интересный предмет». Для того чтобы оно стало высказыванием, нужно заменить N на имя человека.
Используя определение, проверьте, являются ли логическими высказываниями предложения:
1) Лошади едят сено.
2) Карету мне, карету!
3) Где расположен Канин Нос?
4) Восемью три — двенадцать.
5) Программировать очень просто.
Логика и компьютеры тесно связаны.
В классической формальной логике высказывание может быть истинно или ложно, третий вариант исключается 1). Если обозначить истинное значение единицей, а ложное — нулём, то получится, что формальная логика изучает правила выполнения операций с нулями и единицами, т. е. с двоичными кодами. Оказалось, что всю обработку двоичных данных можно свести к выполнению логических операций.
1) Существуют неклассические логические системы, например трёхзначная логика, где кроме «истинно» и «ложно» есть ещё состояние «не определено» (или «возможно»).
Важный шаг в этом направлении сделал английский математик Джордж Буль. Буль впервые ввёл в науку двоичные переменные, принимающие только два значения — «истина» и «ложь», — и три основные логические операции:
Буль впервые ввёл в науку двоичные переменные, принимающие только два значения — «истина» и «ложь», — и три основные логические операции:
Алгебра логики — это математический аппарат, с помощью которого записывают, упрощают и преобразуют логические высказывания, вычисляют их значения.
Алгебра логики определяет правила выполнения операций с логическими значениями «ложь» и «истина». Если обозначить эти значения как 0 и 1, то получается, что с помощью алгебры логики можно описать алгоритмы работы с двоичными данными. Например, так можно построить запоминающие элементы и выполнять арифметические действия.
Используя дополнительные источники, выясните, как называлась основная научная работа Дж.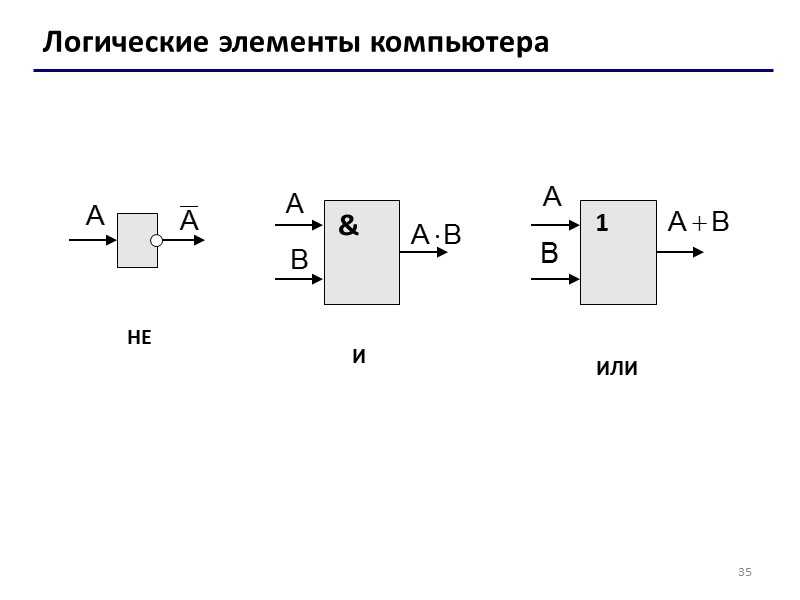 Буля и в каком году она была написана. Сколько лет было тогда учёному?
Буля и в каком году она была написана. Сколько лет было тогда учёному?
Простые и сложные высказывания
Высказывания бывают простые и сложные (составные). Простые высказывания нельзя разделить на более мелкие высказывания, например: «Сейчас идёт дождь» или «Форточка открыта». Сложные (составные) высказывания строятся из простых с помощью логических связок — логических операций НЕ, И, ИЛИ.
В алгебре логики высказывания обычно обозначаются латинскими буквами. Таким образом, мы уходим от конкретного содержания высказываний, нас интересует только их истинность или ложность. Например, можно обозначить буквой А высказывание «Сейчас идёт дождь», а буквой В — высказывание «Форточка открыта».
Так как высказывания могут быть истинными или ложными, введённые символы А и В можно рассматривать как логические переменные, которые могут принимать два возможных значения: «ложь» (0) и «истина» (1). Из них строятся сложные высказывания:
не А = Неверно, что сейчас идёт дождь.
А и В = Сейчас идёт дождь и открыта форточка.
А или В = Сейчас идёт дождь или открыта форточка.
Если и другие логические операции, но НЕ, И и ИЛИ используются чаще всего. Оказывается, с их помощью можно выразить любую логическую операцию, поэтому эти три операции можно считать основными, базовыми, и говорят, что они составляют базис.
Различные устройства компьютера строятся на основе элементов, выполняющих логические операции НЕ, И, ИЛИ.
При введённых выше обозначениях А и В запишите на русском языке высказывания:
а) не В; б) (не А) и В; в) А или (не В).
При тех же обозначениях запишите в символьном виде высказывания:
а) «Неверно, что сейчас идёт дождь и открыта форточка».
б) «Неверно, что сейчас идёт дождь или закрыта форточка».
Операция НЕ
Операция НЕ часто называется отрицанием или инверсией.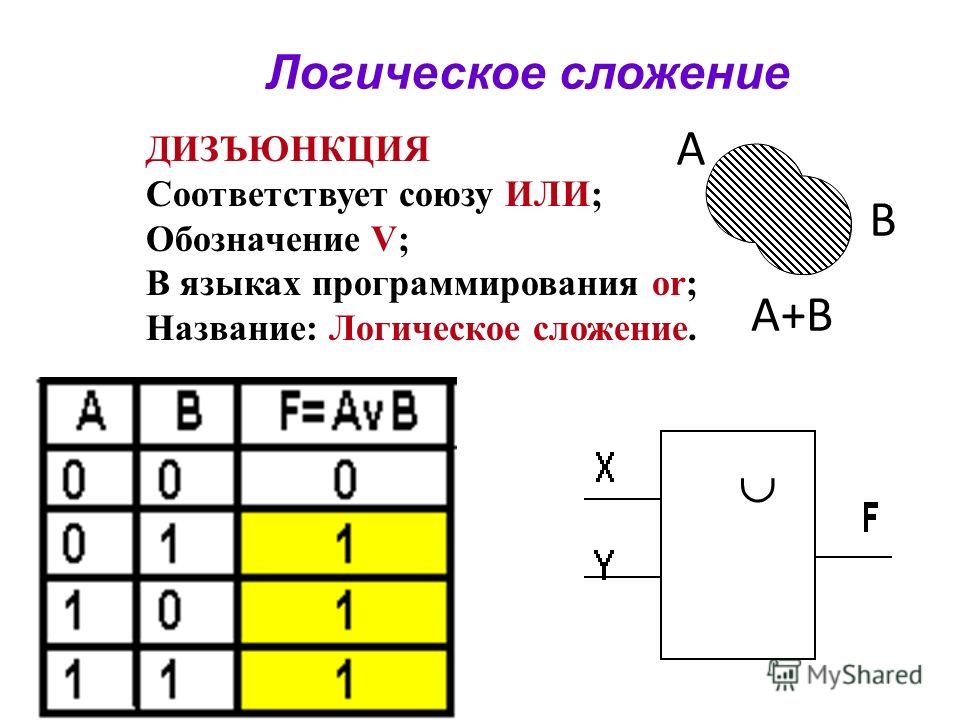 В алгебре логики всего два возможных значения (0 и 1), поэтому логическое отрицание — это переход от одного значения к другому: от 1 к 0 или наоборот. Если высказывание А истинно, то НЕ А ложно, и наоборот.
В алгебре логики всего два возможных значения (0 и 1), поэтому логическое отрицание — это переход от одного значения к другому: от 1 к 0 или наоборот. Если высказывание А истинно, то НЕ А ложно, и наоборот.
Используя дополнительные источники, переведите на русский язык слово inverse, от которого произошло слово «инверсия».
Операцию НЕ обозначают чертой сверху, например: А.
В школьном алгоритмическом языке 1) эта операция обозначается словом не, а в языке программирования Паскаль — английским словом not.
1) Вспомним, что мы договорились называть его просто «алгоритмический язык».
Используя дополнительные источники, найдите другие обозначения операции НЕ.
Операцию НЕ можно задать в виде таблицы (рис. 2.1).
Рис. 2.1
Эта таблица состоит из двух частей:
слева перечисляются все возможные значения исходной величины (их всего два — 0 и 1), а в последнем столбце записывают результат выполнения логической операции для каждого из этих вариантов. Такая таблица называется таблицей истинности логической операции. Таблица истинности задаёт логическую функцию.
Такая таблица называется таблицей истинности логической операции. Таблица истинности задаёт логическую функцию.
Логическая функция — это правило преобразования входных логических значений в логическое значение-результат.
Используя таблицу истинности на рис. 2.1, определите, как можно упростить выражение не (не А). Рассмотрите оба варианта: когда А = 0 и когда А = 1. Сделайте вывод.
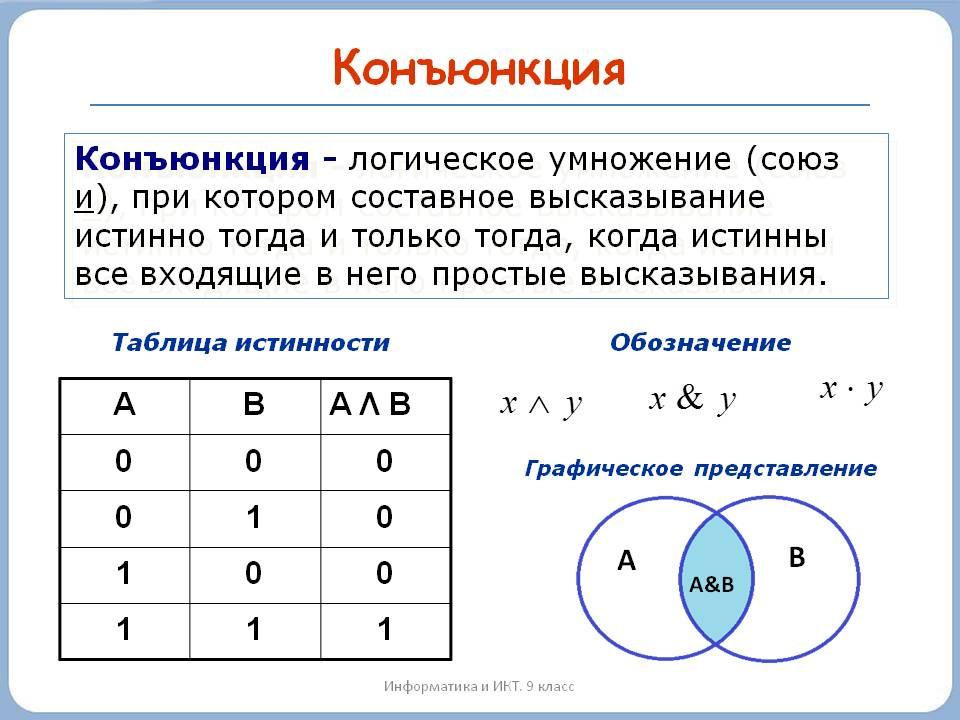
Операция И
Из двух простых высказываний А и В (например, А = Сейчас идёт дождь, В = Форточка открыта) можно составить сложное высказывание А и B. Высказывание А и B истинно в том и только в том случае, когда оба высказывания, А и B, истинны одновременно.
Для понимания операции И можно представить себе простую схему, в которой для включения лампочки используются два выключателя, соединённых последовательно (рис. 2.2).
Рис. 2.2
Чтобы лампочка загорелась, нужно обязательно включить оба выключателя. Вместе с тем, чтобы выключить лампочку, достаточно выключить любой из них.
Операция И (в отличие от НЕ) выполняется с двумя логическими значениями. В алгоритмическом языке системы КуМир операция И обозначается словом и, а в Паскале — словом and.
Используя дополнительные источники, найдите другие обозначения операции И.
В таблице истинности операции И будет уже не один столбец с исходными данными, а два, мы обозначим исходные данные как А и B. Число строк также выросло, с 2 до 4, поскольку с помощью 2 бит можно записать 4 разных комбинации значений двух переменных: 00, 01, 10 и 11. Как следует из определения операции И, в последнем столбце будет всего одна единица, для варианта А = B = 1 (оба высказывания, А и Б, истинны одновременно) — рис. 2.3.
Рис. 2.3
Из значений А и В в каждой строке этой таблицы составьте двоичное число и запишите его в десятичной системе счисления. Почему строки в таблице расположены именно так?
Легко проверить, что этот результат можно получить «обычным» умножением А на В, поэтому операцию И называют логическим умножением. Она часто обозначается знаком умножения (точкой): А • В.
Она часто обозначается знаком умножения (точкой): А • В.
С точки зрения обычной математики, эта операция выбирает наименьшее из исходных значений. Математики используют ещё одно название операции И — конъюнкция.
Используя дополнительные источники, выясните, от какого слова произошло слово «конъюнкция» и что оно обозначает.
С помощью таблицы истинности можно упрощать логические выражения. Например, рассмотрим выражение А и 1. По таблице истинности на рис. 2.3 получаем:
при А = 0: А и 1 = 0 и 1 = 0
при А = 1: А и 1 = 1 и 1 = 1.
Можно заметить, что в любом случае результат совпадает с А, поэтому А и 1 = А.
Используя таблицу истинности операции И, упростите выражения: а) А и 0; б) А и А; в) А и (не А).
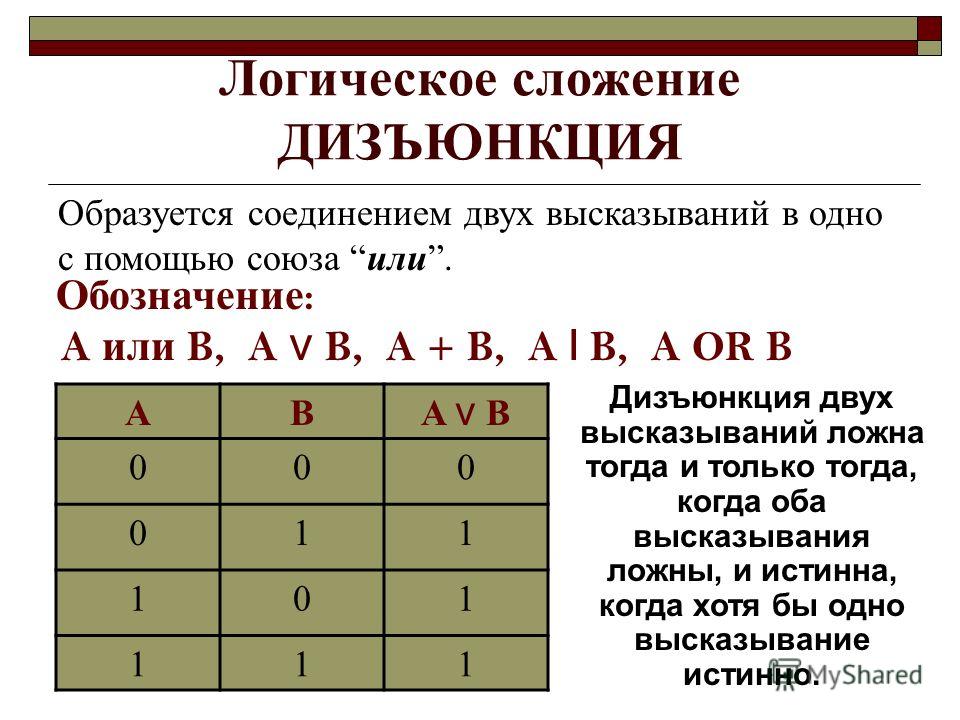
Операция ИЛИ
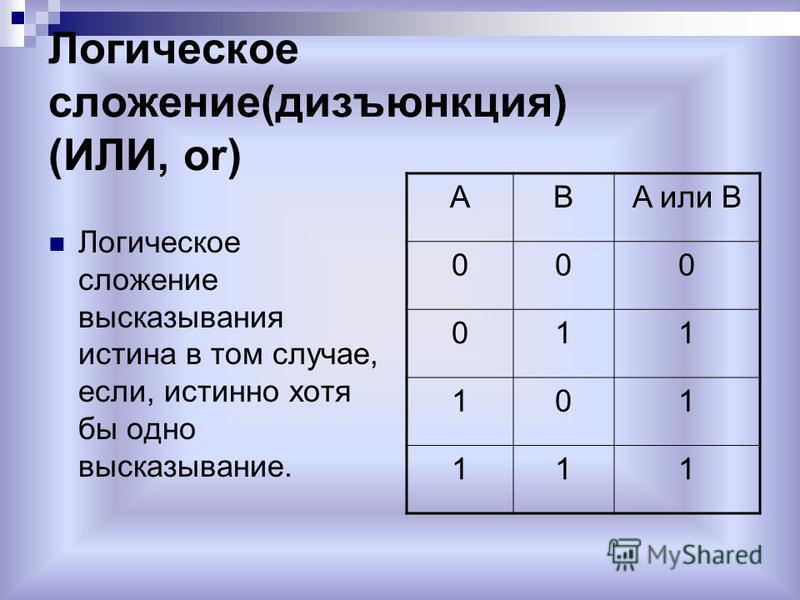
Высказывание А или В (например, «Сейчас идет дождь или форточка открыта») истинно тогда, когда истинно хотя бы одно из входящих в него высказываний или оба одновременно.
В алгоритмическом языке операция ИЛИ обозначается словом или, а в языке Паскаль — английским словом or.
Используя дополнительные источники, найдите другие обозначения операции ИЛИ.
Для понимания операции ИЛИ можно представить себе схему с двумя выключателями, соединёнными параллельно (рис. 2.4).
Рис. 2.4
Чтобы лампочка загорелась, достаточно включить хотя бы один из выключателей. Чтобы выключить лампочку, необходимо обязательно выключить оба. В таблице истинности будет только один ноль — для варианта А = В = 0 (рис. 2.5).
Рис. 2.5
Операцию ИЛИ называют логическим сложением, потому что она похожа на обычное математическое сложение. Поэтому она часто обозначается знаком сложения: А+В. Единственное отличие — в последней строке таблицы истинности: в математике 1+1 равно 2, а в алгебре логики — единице.
Можно считать, что в результате применения операции ИЛИ из исходных значений выбирается наибольшее. Другое название этой операции — дизъюнкция.
Используя дополнительные источники, выясните, от какого слова произошло слово «дизъюнкция» и что оно обозначает.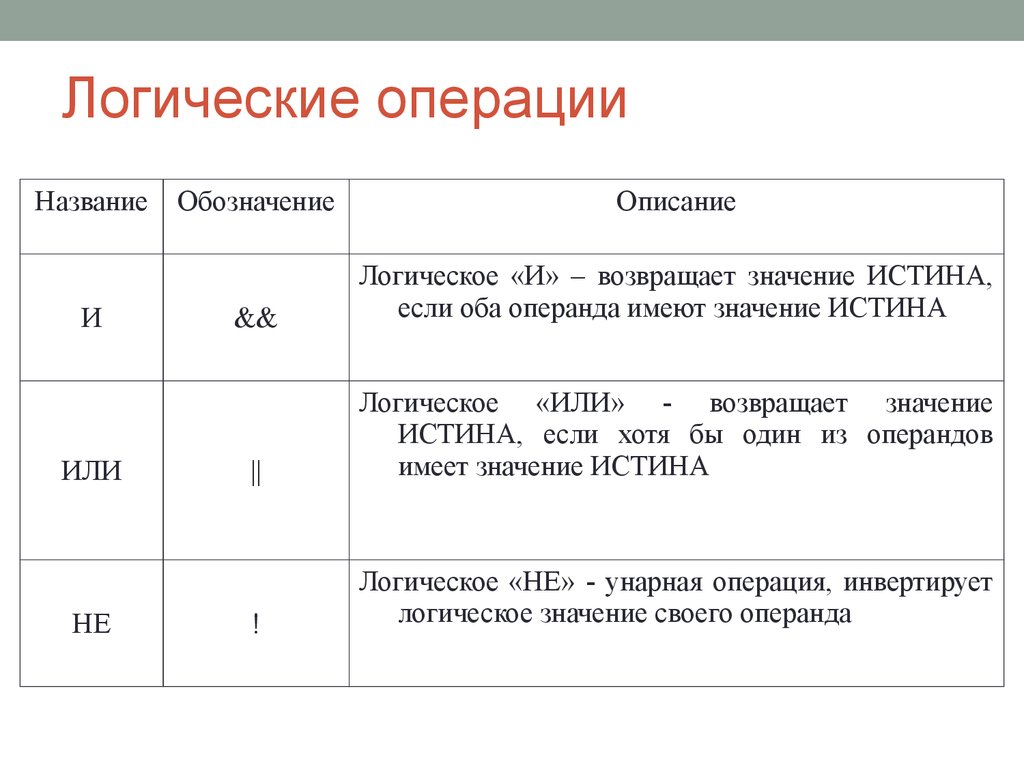
Запишите в тетради ответы на следующие вопросы.
— Сколько строк в таблице истинности функции с двумя переменными?
— Сколько существует возможных вариантов распределения нулей и единиц в последнем столбце?
— Сколько можно придумать различных логических функций с двумя переменными?
Используя таблицу истинности операции И, упростите выражения:
а) А или 0; б) А или 1; в) А или А; г) А или (не А).
Выводы
• Логическое высказывание — это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно.
• Алгебра логики — это математический аппарат, с помощью которого записывают, упрощают и преобразуют логические высказывания, вычисляют их значения.
• Логическая функция — это правило преобразования входных логических значений в логическое значение-результат.
• Если высказывание А истинно, то не А ложно, и наоборот.
• Высказывание А и В истинно тогда и только тогда, когда оба высказывания, А и В, истинны одновременно.
• Высказывание А или В истинно тогда, когда истинно хотя бы одно из высказываний, А или Б, или оба они истинны одновременно.
• С помощью операций НЕ, И, ИЛИ можно выразить любую логическую операцию, поэтому говорят, что эти три операции составляют базис.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Объясните значения слов «логика», «формальная логика», «алгебра логики».
2. Можно ли считать высказываниями эти предложения?
1) Не плачь, девчонка!
2) Почему я водовоз?
3) Купите слоника!
4) Клубника очень вкусная.
5) Сумма X и Y равна 36.
3. Как вы думаете, зачем в курсе информатики изучается логика?
4. Почему в таблице истинности для операции НЕ две строки, а для других изученных операций — четыре?
5. Сколько строк в таблице истинности выражения с тремя переменными? С четырьмя? С пятью?
6. В каком порядке обычно записываются значения переменных в таблице истинности? Зачем это нужно?
В каком порядке обычно записываются значения переменных в таблице истинности? Зачем это нужно?
7. В чём различие арифметического и логического сложения?
8. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Информатика и логика»
б) «Логическая операция исключающее ИЛИ»
в) «Логическая операция импликация»
г) «Логическая операция эквиваленция»
Оглавление
§7. Язык HTML.
§8. Логика и компьютеры.
§9. Логические элементы.
7 — Логика и компьютер
1. Отметьте все фразы, которые являются высказываниями. | |
| Прошлогодний снег. | |
| Сегодня пасмурно. | |
| В N-ской воинской части обед. | |
| В Санкт-Петербурге 4 миллиона жителей. | |
| Почему я водовоз? | |
2. Какой ученый разработал основы алгебры логики? | |
| Аристотель | |
Дж. Буль Буль | |
| Б. Паскаль | |
| К. Шеннон | |
| И. Ньютон | |
3. Как называется правило преобразования входных логических значений в логическое значение-результат? | |
| логическая функция | |
| логическое выражение | |
| логическое правило | |
| логическая задача | |
| логическое высказывание | |
4. Какую логическую операцию иллюстрирует этот рисунок? | |
| И | |
| ИЛИ | |
| НЕ | |
5. Какую логическую операцию иллюстрирует этот рисунок? | |
| И | |
| ИЛИ | |
| НЕ | |
6. Какой логической операции соответствует эта таблица истинности? | |
| И | |
| ИЛИ | |
| НЕ | |
7. | |
| И | |
| ИЛИ | |
| НЕ | |
8. Какая операция называется «конъюнкцией»? | |
| НЕ | |
| И | |
| ИЛИ | |
9. Какая операция называется «дизъюнкцией»? | |
| НЕ | |
| И | |
| ИЛИ | |
10. Какие из этих логических выражений ложны независимо от логического значения A? | |
| A или A | |
| A и 0 | |
| A или A | |
| (не A) и 0 | |
| (не A) или 1 | |
11. Какие из этих логических выражений истинны независимо от логического значения A? | |
| A или 1 | |
| A и 1 | |
| (не A) или 1 | |
| (не A) или A | |
| 1 или (0 и A) | |
12. |
| Ответ: |
13. Какие операции обратимы, то есть, применив ту же самую операцию дважды можно восстановить исходное значение? | |
| НЕ | |
| И | |
| ИЛИ | |
14. Какая фраза является отрицанием утверждения «На улице идет снег и ветрено»? | |
| На улице нет ни снега, ни ветра. | |
| На улице или нет снега, или безветрие. | |
| На улице нет снега и ветрено. | |
| На улице идет снег и нет ветра. | |
| На улице идет снег или дует ветер. | |
Лица, принимающие решения: И, ИЛИ и НЕ
Жизнь полна решений. То, что верно для нас, верно и для ПЛК.
В качестве примера того, как мы используем логику в повседневной жизни, рассмотрим следующие утверждения:
- Если Томми ИЛИ Боб хочет играть в баскетбол, я тоже буду играть.
- Сейчас 6 часов И Я НЕ голоден, поэтому я буду продолжать играть.
- Если мама выйдет И прикажет мне войти ИЛИ стемнеет, тогда я перестану играть.
Это довольно простые решения, особенно если вы десятилетний мальчик. Вы заметите, что все они включают три типа сравнений: И, ИЛИ и НЕ. Теперь мы могли бы усложнить, но все, что мы будем делать, это использовать эти простые строительные блоки.
В мире автоматизации эти типы условий ИСТИНА или ЛОЖЬ сводятся к тому, что устройство ВКЛЮЧЕНО или ВЫКЛЮЧЕНО, ЗАКРЫТО или ОТКРЫТО, ПРИСУТСТВУЕТ или ОТСУТСТВУЕТ, 24 ВОЛЬТА или 0 ВОЛЬТ.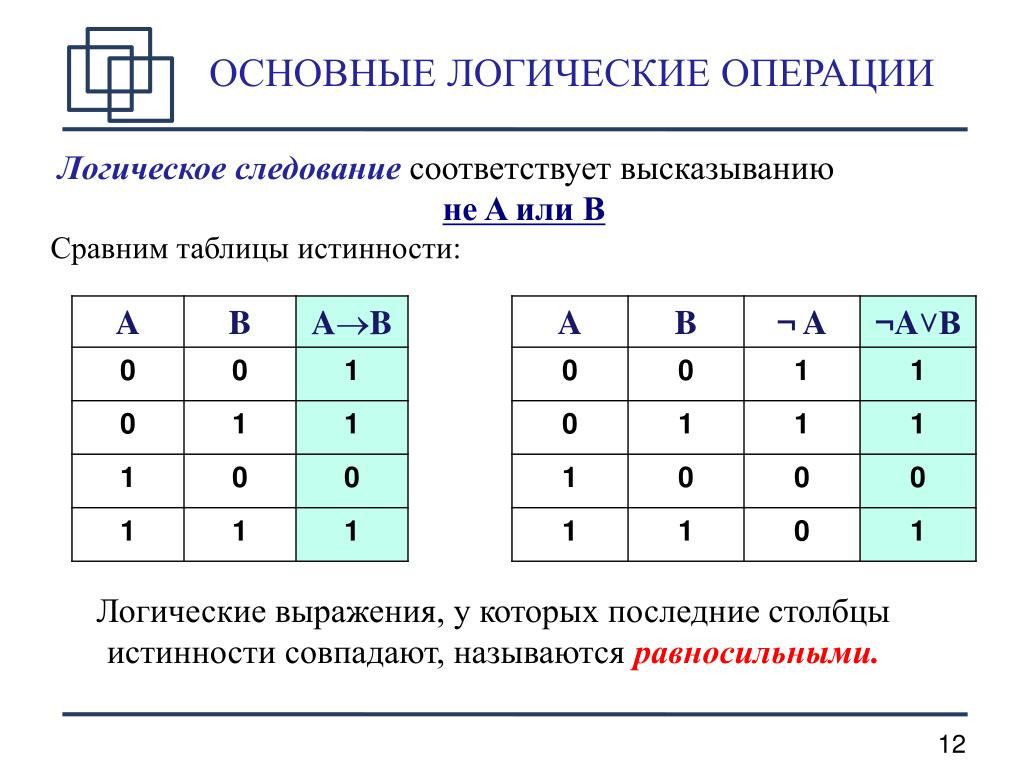 В ПЛК все сводится к уже знакомой нам двоичной системе, состоящей из 1 или 0. Обычно наличие бита ВКЛ представляет собой условие ИСТИНА, а ВЫКЛ — ЛОЖЬ. Однако это произвольно, поскольку может иметь смысл использовать так называемую отказоустойчивую логику и иметь бит ON в качестве условия FALSE.
В ПЛК все сводится к уже знакомой нам двоичной системе, состоящей из 1 или 0. Обычно наличие бита ВКЛ представляет собой условие ИСТИНА, а ВЫКЛ — ЛОЖЬ. Однако это произвольно, поскольку может иметь смысл использовать так называемую отказоустойчивую логику и иметь бит ON в качестве условия FALSE.
Давайте снова обратимся к некоторым простым операторам, но на этот раз с примерами автоматизации.
- При нажатии кнопки И дверь закрывается, затем включается двигатель.
- Если процесс выполнен ИЛИ , сигнал кнопки аварийного останова НЕ включен, затем выключите двигатель. (Это пример безотказной работы, поскольку кнопка аварийной остановки могла быть нажата или провод был отсоединен. В любом случае мы хотим проверить это из соображений безопасности. Использование сигнала для включения, когда провод давно отвалился назад может вызвать неловкий момент, когда нам действительно нужно остановить машину в экстренной ситуации.

- Если бак полон ИЛИ кнопка нажата И аварийных сигналов нет, запустите процесс.
Было бы неплохо программировать таким образом, но компьютеры любят быть немного более структурированными. Ряд графических объектов использовался в течение многих лет для представления этих логических элементов, и их можно легко преобразовать в эквивалент обычной лестничной логики. Эти функции также называются воротами, поскольку они действуют как привратники для другой логики.
Функция НЕ
Простейшей из всех логических функций является вентиль НЕ.
Его единственная функция в жизни — инвертировать или перевернуть логическое состояние. Таким образом, ввод 1 будет выглядеть как 0 и наоборот. Ниже показана таблица истинности (она не лжет), показывающая все возможные входные данные и результирующий логический вывод.
| Вход А | Выход |
| 0 | 1 |
| 1 | 0 |
Эквивалент лестничной логики для функции НЕ выглядит как обычный контакт, но с косой чертой.
Функция И
Элемент И связан со следующим символом, который может иметь любое количество входов, но только один выход.
Таблица истинности ниже показывает, что выход включается только тогда, когда все входы верны (1). Простой способ запомнить это — И работает как умножение.
| Вход А | Вход Б | Вывод |
| 0 | 0 | 0 |
| 0 | 0 | |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Эквивалент лестничной логики для функции И выглядит как два обычных контакта рядом.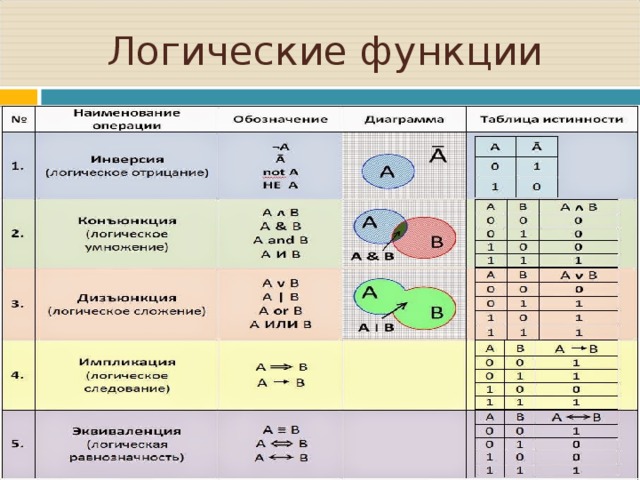
Функция ИЛИ
И последнее, но не менее важное: элемент ИЛИ связан со следующим символом, который также может иметь любое количество входов, но только один выход.
Таблица истинности ниже показывает, что выход включается (1), когда любой из входов истинен (1). Простой способ запомнить это — ИЛИ работает как сложение.
| Вход А | Вход Б | Выход |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Эквивалент лестничной логики для функции ИЛИ выглядит как два обычных контакта друг над другом.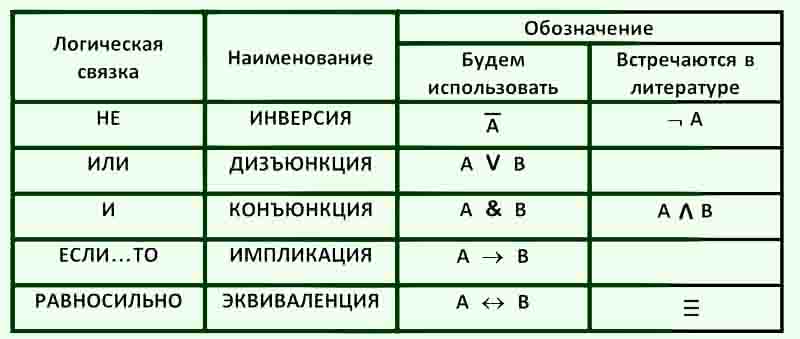
Комбинация И или ИЛИ с НЕ
Логический элемент НЕ может показаться не очень полезным, если вы не слишком много программировали, но на самом деле вы обнаружите, что используете его часто. Его очень часто используют в сочетании с И и ИЛИ. Поэтому инженерные боги решили сделать для этих комбинаций какие-то символы.
Объединение вентилей НЕ и И образует вентиль И-НЕ. Таблица истинности ниже показывает, что это просто инвертированный выход логического элемента И.
| Вход А | Вход Б | Вывод |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Небольшой кружок (или, если хотите, пузырь) в конце вентиля И используется для обозначения функции И-НЕ.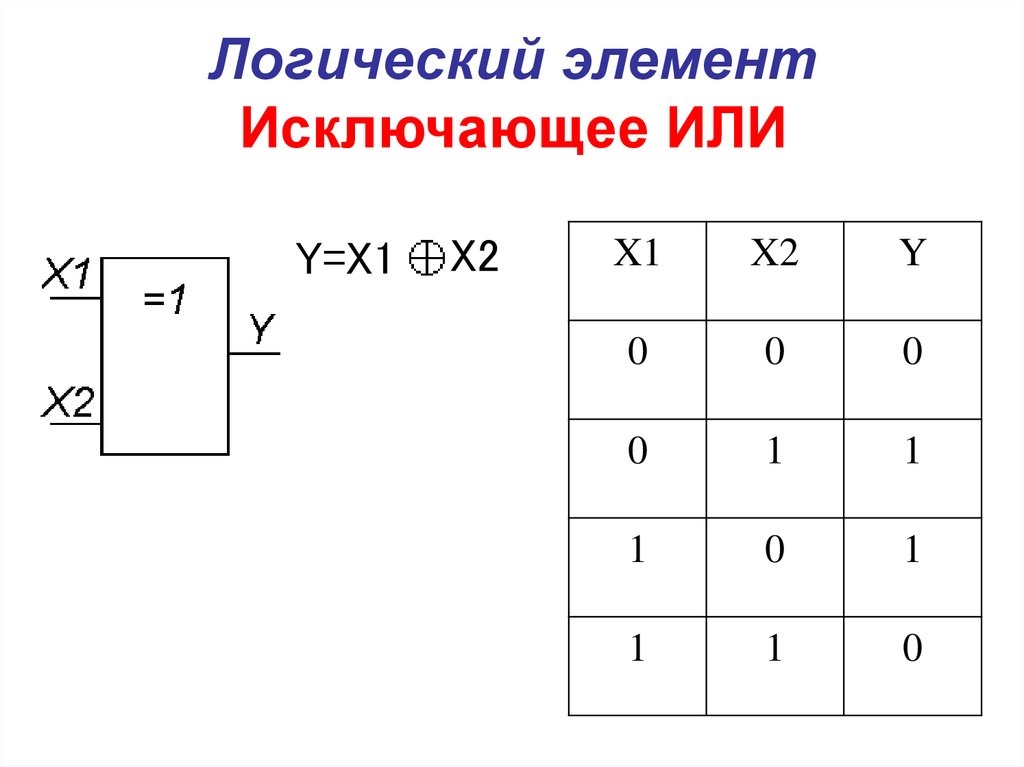 Его символ и соответствующая лестничная логика показаны ниже. Теперь обратите особое внимание на лестничную логику, потому что контакты параллельны, а не последовательно, как в функции И.
Его символ и соответствующая лестничная логика показаны ниже. Теперь обратите особое внимание на лестничную логику, потому что контакты параллельны, а не последовательно, как в функции И.
Соединение ворот НЕ и ИЛИ образует… вы поняли… ворота ИЛИ-НЕ. Таблица истинности ниже показывает, что это просто инвертированный выход вентиля ИЛИ.
| Вход А | Вход Б | Вывод |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Снова маленький кружок помещается в конце вентиля ИЛИ, чтобы обозначить функцию НЕ-ИЛИ.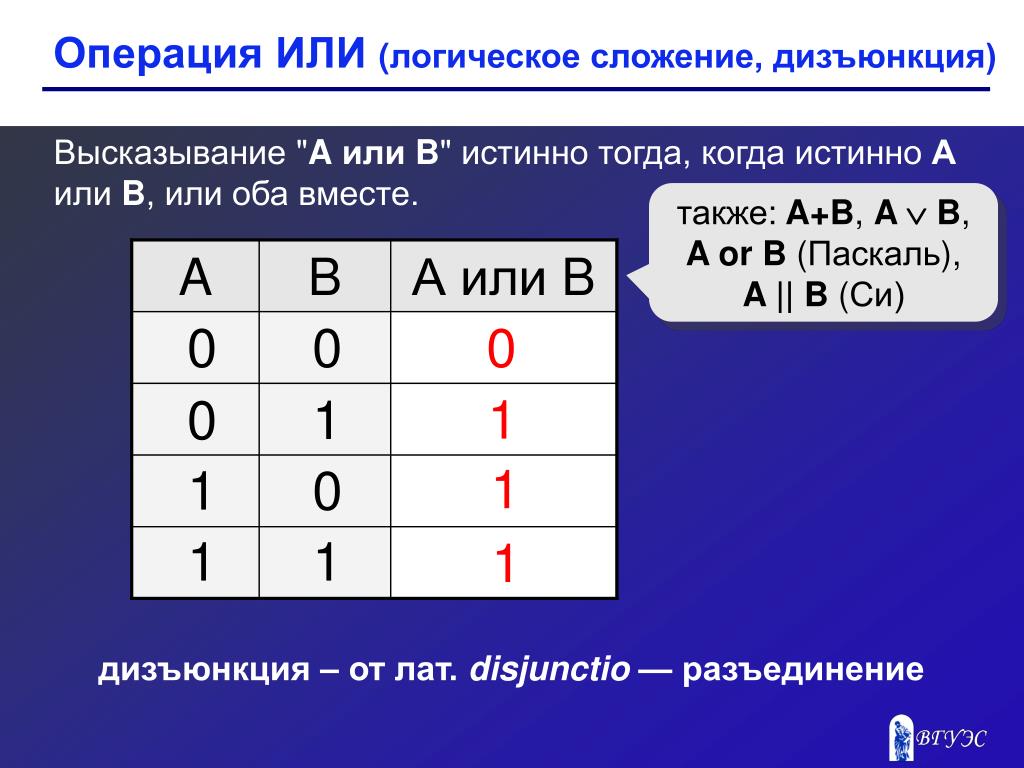 Его символ и соответствующая лестничная логика показаны ниже. Лестничная логика сильно отличается от обычного вентиля ИЛИ.
Его символ и соответствующая лестничная логика показаны ниже. Лестничная логика сильно отличается от обычного вентиля ИЛИ.
Но подождите! Пока не заказывайте… ворота XOR.
До сих пор с нашими логическими элементами мы рассмотрели почти все возможные комбинации, кроме одной, показанной в таблице истинности ниже.
| Вход А | Вход Б | Вывод |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Логика для создания этого вывода называется вентилем исключающее ИЛИ, также известным как вентиль исключающее ИЛИ.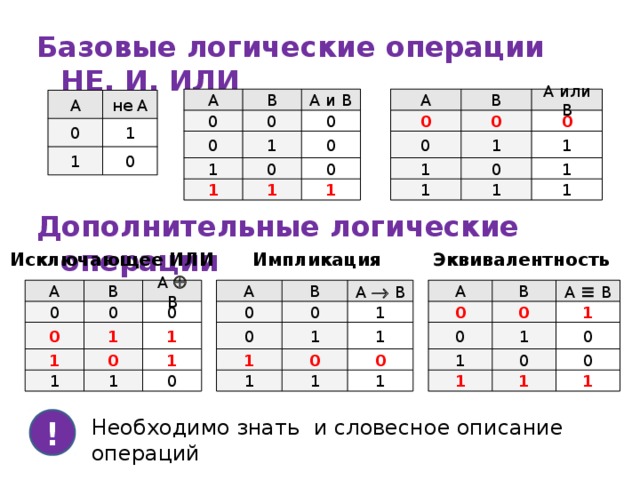 Это особая форма ворот ИЛИ. Так что если один из входов включен, то выход истинен, иначе вам не повезло. Символ вентиля XOR показан добавлением изогнутой линии к символу вентиля OR.
Это особая форма ворот ИЛИ. Так что если один из входов включен, то выход истинен, иначе вам не повезло. Символ вентиля XOR показан добавлением изогнутой линии к символу вентиля OR.
Лестничная логика для реализации вентиля XOR немного сложнее, чем другие.
Насколько полезна логика XOR? Вы, вероятно, используете ворота XOR каждый день, не задумываясь об этом, если у вас есть комната со светом, который работает от двух выключателей. Если оба переключателя находятся в одинаковом положении, свет будет выключен. Поэтому просто щелкнув одним выключателем, вы включите свет. В программе ПЛК это может быть чрезвычайно полезно для программирования чередующихся действий или кодов Грея.
Хорошо, есть еще один логический элемент, но я обещаю, что он последний. Имеет смысл, что есть вентиль XNOR, который представляет собой комбинацию логики NOT и XOR. Он просто инвертирует вывод функции XOR.
| Вход А | Вход Б | Вывод |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Символ вентиля XNOR показан ниже вместе с его эквивалентом в релейной логике.
Надежда на будущее
Хотя эти термины и символы могут показаться немного эзотерическими для новичков в ПЛК, они важны в долгосрочной перспективе. Хорошее понимание этих основных моментов сделает программирование ПЛК проще, проще и сэкономит память. Следующий урок прояснит это, когда мы рассмотрим Булева алгебра.
‹ Черное и белое серого кода
Формальная логика | Определение, примеры, символы и факты
Alfred North Whitehead
Смотреть все СМИ
- Ключевые люди:
- Станислав Лесневский Джордж Буль Джон Венн Август Де Морган Джузеппе Пеано
- Похожие темы:
- теория множеств исчисление предикатов модальная логика исчисление высказываний аксиоматический метод
Просмотреть весь связанный контент →
формальная логика , абстрактное исследование предложений, утверждений или утвердительно используемых предложений и дедуктивных аргументов. Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Дисциплина абстрагирует от содержания этих элементов структуры или логические формы, которые они воплощают. Логик обычно использует символическую нотацию для ясного и недвусмысленного выражения таких структур и для облегчения применения манипуляций и проверок достоверности. Хотя в последующем обсуждении свободно используются технические обозначения современной символической логики, ее символы вводятся постепенно и с сопутствующими пояснениями, чтобы серьезный и внимательный читатель мог следить за развитием идей.
Формальная логика является априорным, а не эмпирическим исследованием. В этом отношении она контрастирует с естественными науками и со всеми другими дисциплинами, данные которых зависят от наблюдений. Его ближайшая аналогия — чистая математика; действительно, многие логики и чистые математики считали бы свои соответствующие предметы неразличимыми или просто двумя этапами одной и той же единой дисциплины. Поэтому формальную логику не следует смешивать с эмпирическим изучением процессов рассуждения, которое принадлежит психологии.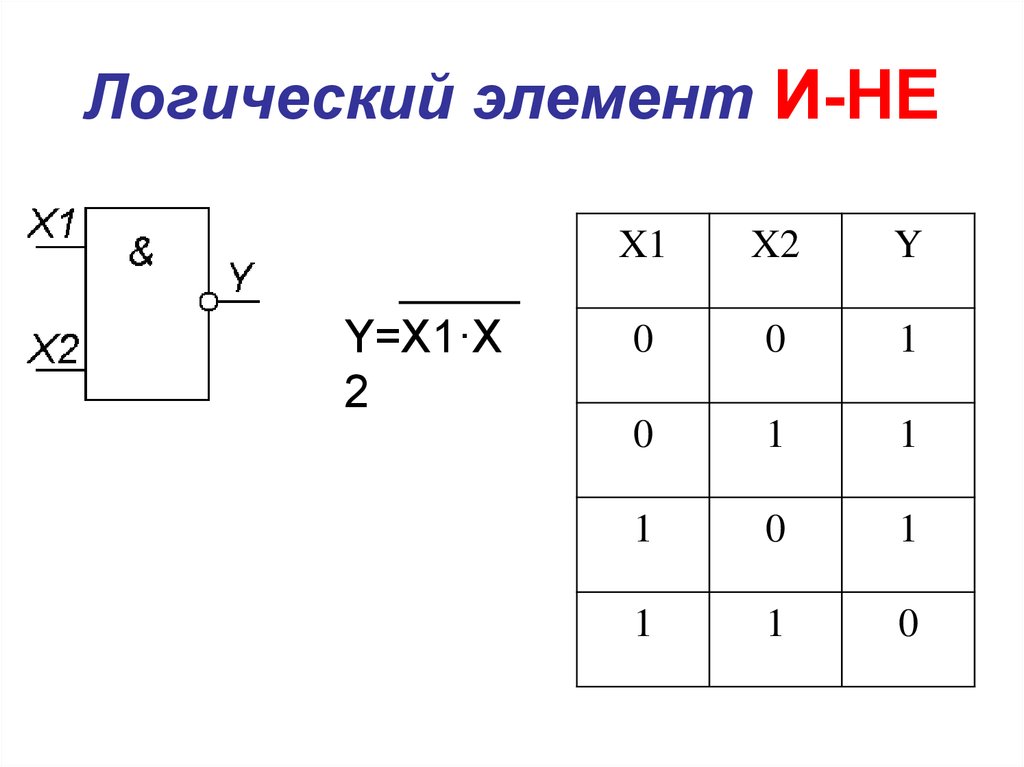 Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Его также следует отличать от искусства правильного рассуждения, которое представляет собой практический навык применения логических принципов к конкретным случаям; и, что еще более резко, его следует отличать от искусства убеждения, в котором неверные доводы иногда оказываются более действенными, чем веские.
Вероятно, наиболее естественным подходом к формальной логике является представление о достоверности аргумента, известного как дедуктивное. Дедуктивный аргумент можно грубо охарактеризовать как аргумент, в котором утверждается, что какое-то суждение (заключение) следует со строгой необходимостью из какого-то другого предложения или предложений (посылок), т. е. что было бы непоследовательно или внутренне противоречиво утверждать предпосылки, но отрицают заключение.
Чтобы дедуктивному аргументу удалось установить истинность своего вывода, должны быть выполнены два совершенно разных условия: во-первых, вывод должен действительно следовать из посылок, т. е. дедукция вывода из посылок должна быть логически правильной — и, во-вторых, сами посылки должны быть истинными. Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Аргумент, отвечающий обоим этим условиям, называется обоснованным. Из этих двух условий логика как такового интересует только первое; второе, определение истинности или ложности посылок, является задачей какой-либо специальной дисциплины или обычного наблюдения, соответствующего предмету рассуждения. Когда вывод аргумента правильно выводится из его посылок, говорят, что вывод от посылок к заключению (дедуктивно) действителен, независимо от того, истинны эти посылки или ложны. Другие способы выражения факта дедуктивной достоверности вывода заключаются в том, чтобы сказать, что истинность посылок дает (или будет давать) абсолютную гарантию истинности вывода или что он будет включать в себя логическую непоследовательность (в отличие от простой фактическая ошибка) предположить, что посылки верны, а заключение ложно.
Дедуктивные выводы, с которыми имеет дело формальная логика, как следует из названия, для которых достоверность зависит не от каких-либо особенностей их предмета, а от их формы или структуры. Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Таким образом, два вывода (1) Каждая собака является млекопитающим. Некоторые четвероногие — собаки. ∴ Некоторые четвероногие млекопитающие. и (2) Каждый анархист верит в свободную любовь. Некоторые члены правительственной партии являются анархистами. ∴ Некоторые члены правительственной партии верят в свободную любовь. различаются по предмету и, следовательно, требуют разных процедур для проверки истинности или ложности их предпосылок. Но их достоверность обеспечивается тем, что у них есть общего, а именно тем, что аргумент в каждом из них имеет вид (3) Every X это Y . Некоторые Z — это X . ∴ Некоторые Z — это Y .
Строка (3) выше может быть названа формой вывода, а (1) и (2) тогда являются экземплярами этой формы вывода. Буквы — X , Y и Z — в (3) отмечают места, в которые могут быть вставлены выражения определенного типа. Символы, используемые для этой цели, известны как переменные; их использование аналогично использованию x в алгебре, которое отмечает место, в которое можно вставить цифру. Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. теми, которые имеют смысл в контексте) и при этом единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее.
Экземпляр формы вывода создается заменой всех переменных в ней соответствующими выражениями (т. е. теми, которые имеют смысл в контексте) и при этом единообразно (т. е. заменой одного и того же выражения везде, где повторяется одна и та же переменная). Признак (3), гарантирующий, что каждый его экземпляр будет верным, состоит в его построении таким образом, что любой унифицированный способ замены его переменных, чтобы сделать посылки истинными, автоматически делает вывод также верным, или, другими словами, что ни один его пример не может иметь истинных предпосылок, кроме ложного заключения. В силу этого признака форма (3) называется корректной формой вывода. Напротив, (4) Каждые X это Y . Некоторые Z — это Y . ∴ Некоторые Z — это X . не является действительной формой вывода, поскольку, хотя могут быть получены примеры, в которых все посылки и заключение верны, могут также быть получены примеры, в которых посылки истинны, но заключение ложно, например, (5) Всякий собака это млекопитающее. Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Некоторые крылатые существа являются млекопитающими. ∴ Некоторые крылатые существа — собаки.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Формальная логика как наука связана с формами вывода, а не с их конкретными примерами. Одна из его задач состоит в том, чтобы различать верные и неверные формы вывода, а также исследовать и систематизировать отношения, которые существуют между верными формами.
С идеей верной формы вывода тесно связана идея верной формы предложения. Форма пропозиции — это выражение, экземпляры которого (полученные, как и прежде, соответствующими и единообразными заменами переменных) являются не выводами из нескольких пропозиций к заключению, а, скорее, пропозициями, взятыми по отдельности, и действительная форма пропозиции — это та, для которой все экземпляры являются истинными предложениями. Простой пример: (6) Ничто не равно X и не- X . Формальная логика имеет дело как с формами высказывания, так и с формами вывода.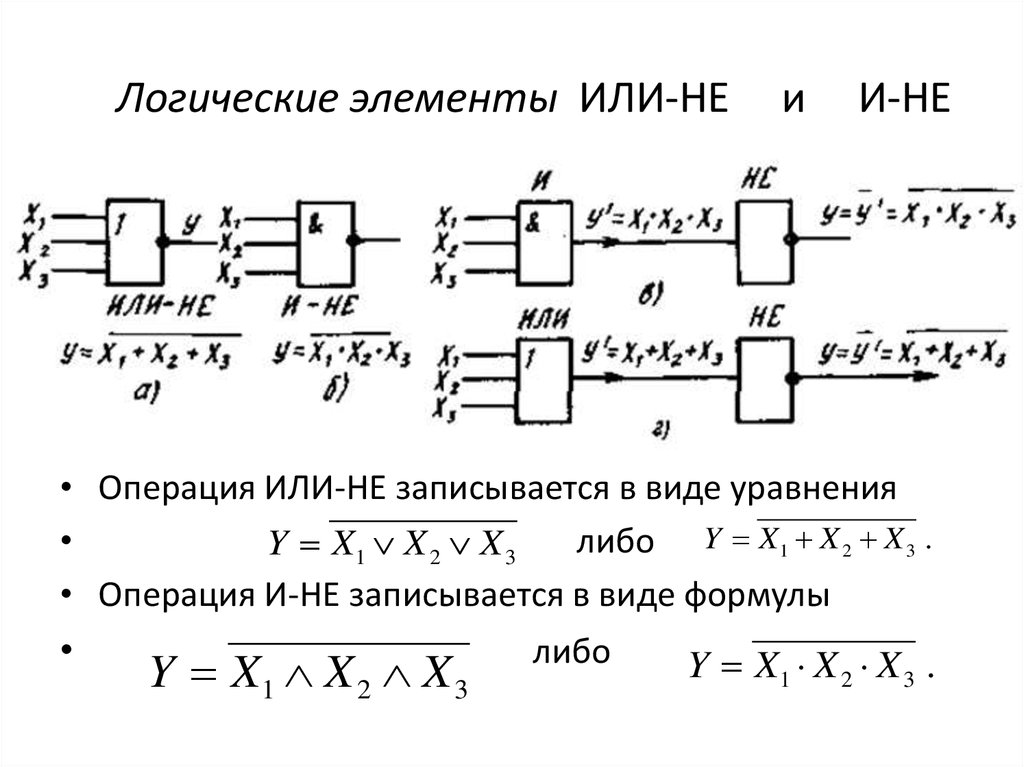 На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
На самом деле изучение форм высказывания можно включить в изучение форм вывода следующим образом: пусть посылки любой данной формы вывода (взятые вместе) обозначаются буквой альфа (α), а ее вывод — буквой бета (β). . Тогда условие, сформулированное выше для правильности формы вывода «α, следовательно, β», сводится к утверждению, что ни один экземпляр формы суждения «α и не-β» не является истинным, т. е. что каждый экземпляр формы суждения (7) Не то и другое: α и не-β истинны, или эта строка (7), полностью изложенная, конечно, является допустимой формой предложения. Однако изучение форм пропозиций не может быть аналогичным образом приспособлено к изучению форм вывода, и поэтому из соображений полноты формальную логику обычно рассматривают как изучение форм пропозиций. Поскольку работа логика с формами высказываний во многом аналогична работе математика с числовыми формулами, системы, которые он строит, часто называют исчислениями.
Большая часть работы логика протекает на более абстрактном уровне, чем тот, о котором говорилось выше. Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны.
Даже такая формула, как (3) выше, хотя и не относящаяся к какому-либо конкретному предмету, содержит такие выражения, как «каждый» и «есть», которые считаются имеющими определенное значение, а переменные предназначены для обозначения мест. для выражений одного конкретного вида (грубо говоря, нарицательных существительных или имен классов). Однако возможно — и для некоторых целей это необходимо — изучать формулы, не придавая им даже этой степени осмысленности. В самом деле, построение системы логики включает в себя два различных процесса: один состоит в создании символического аппарата — набора символов, правил их объединения в формулы и правил манипулирования этими формулами; второй состоит в придании этим символам и формулам определенных значений. Если выполняется только первое, система называется неинтерпретируемой или чисто формальной; если последнее также выполняется, говорят, что система интерпретируется. Это различие важно, потому что логические системы обладают определенными свойствами совершенно независимо от каких-либо интерпретаций, которые им могут быть даны.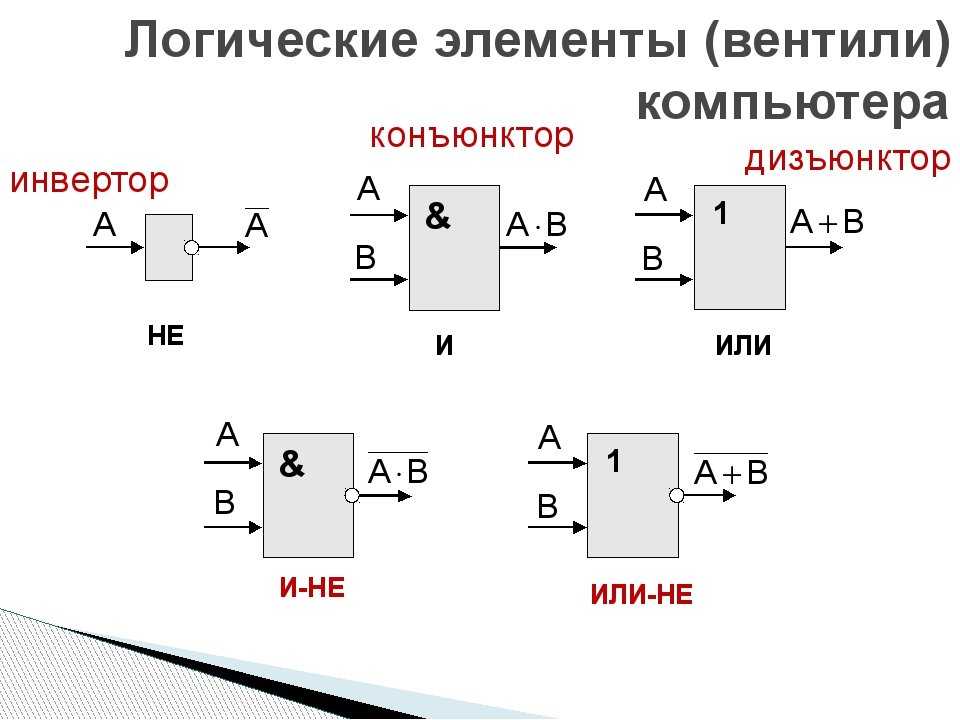 В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.
В качестве примера можно взять аксиоматическую систему логики, т. е. такую систему, в которой за исходные положения берутся некоторые недоказанные формулы, называемые аксиомами, и на их основании доказываются дальнейшие формулы (теоремы). Как будет позже ( см. ниже Аксиоматизация ПК), вопрос о том, является ли последовательность формул в аксиоматической системе доказательством или нет, зависит исключительно от того, какие формулы принимаются за аксиомы и каковы правила вывода теорем из аксиом, а вовсе не о том, что означают теоремы или аксиомы. Более того, данная неинтерпретируемая система вообще может быть одинаково хорошо интерпретирована множеством различных способов; следовательно, при изучении неинтерпретируемой системы изучают структуру, общую для множества интерпретируемых систем. Обычно логик, конструирующий чисто формальную систему, имеет в виду конкретную интерпретацию, и его мотивом для ее построения является вера в то, что, когда ей будет дана эта интерпретация, формулы системы смогут выражать истинные принципы в некоторой области.


 Какой логической операции соответствует эта таблица истинности?
Какой логической операции соответствует эта таблица истинности?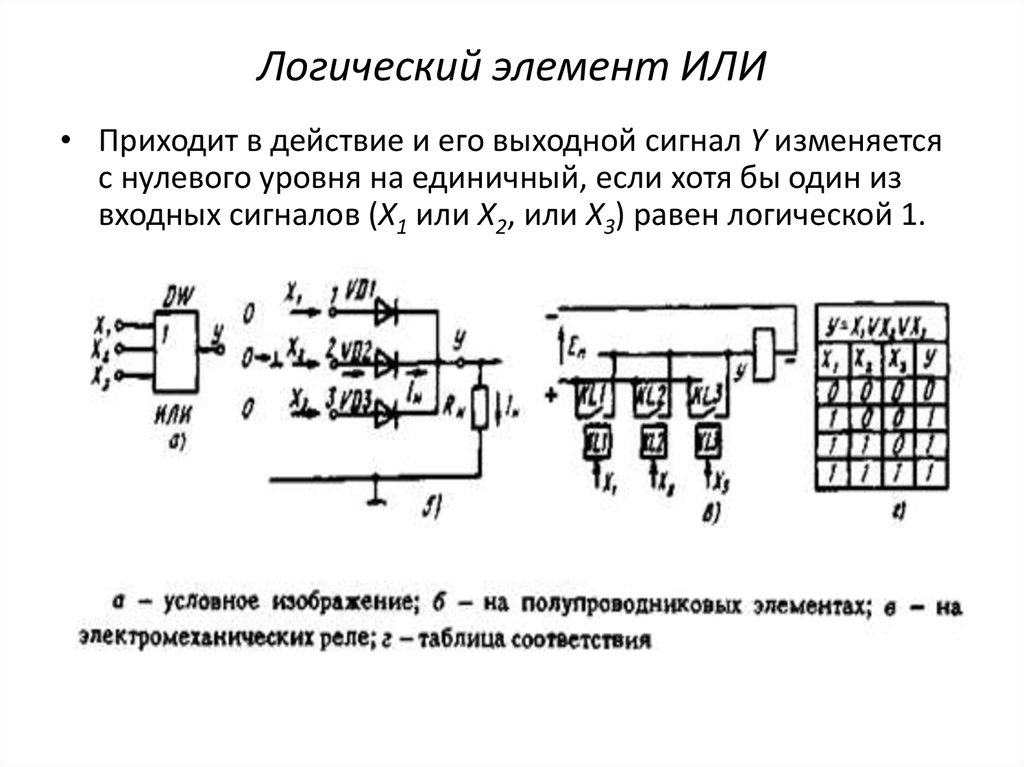 Сколько существует различных логических операций с двумя логическими значениями?
Сколько существует различных логических операций с двумя логическими значениями?