Цифровые логические схемы и системы

Цифровое управление — сравнительно новая область в электронике. Оно ведет свое происхождение от теории связи. Цифровое управление охваты­вает компьютерную технику, электронные АТС, промышленные системы управления, системы обработки данных и множество других подобных систем. Цифровые приборы работают в дискретном режиме, обычно ON (включено) или OFF (выключено). Главной и неотъемлемой особенно­стью цифрового прибора является переход из одного состояния в другое без «остановки» в каком-либо промежуточном положении.

 

Логические схемы

Логические элементы, или схемы, — это цифровые приборы, которые имеют на выходе одно из двух состояний: нулевой выход (обозначает­ся 0) и фиксированный выход (обозначается 1). Логическая схема может иметь несколько входов и только один выход.

Логическая схема И (рис. 11.1)

Схема И выдает на выходе логическую 1, когда на все ее входы подан сигнал, соответствующий логической 1. На рис. 11.1 показана схема И с двумя входами. Ее выход равен 1 только в том случае, если и на вход А, и на вход В подана 1. В табл. 11.1 функция И представлена в виде так называемой

таблицы истинности.

На рис. 11.2 показаны типичные формы входных и выходных сигналов.

 

Входы		Выход
А	В
0	0	0
0	1	0
1	0	0
1	1	1

Таблица 11.1. Таблица истинности схемы И

 

 

 

 

 

 

 

 

 

 

Таблица 11.2. Таблица истинности схемы И-НЕ

Входы		Выход
А	В
0	0	1
0	1	1
1	0	1
1	1	0

                        

 

 

Рис. 11.1. Схема И.           

 

Рис. 11.2. Входные и выходные им­пульсные сигналы в схеме И с двумя входами 

  

                              

                 

Рис. 11.3. Схема           Рис. 11.4. Входные и выходныеимпульсные     Рис. 11.5. Схема ИЛИ.

         И-НЕ.                       сигналы в схеме И-НЕ с  двумя входами.

Обратите внимание, что на выходе логическая 1 появляется только тогда, когда на обоих входах присутствует 1.

Логическая схема И-НЕ (рис. 11.3 и табл. 11.2)

Логическая схема И-НЕ имеет на выходе логический 0, когда на все ее входы поданы сигналы, соответствующие логической 1. И наоборот, если хотя бы на одномиз входов схемы И-НЕ присутствует 0, на ее выходе появляется 1 (см. рис. 11.4). Таким образом, схема И-НЕ является логической противоположностью схемы И.

 

Таблица 11.3. Таблица истинности схемы ИЛИ          

 

Входы		Выход
А	В
0	0	1
0	1	0
1	0	0
1	1	0

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблица 11.4. Таблица истинности схемы ИЛИ-НЕ

 

Входы		Выход
А	В
0	0	0
0	1	1
1	0	1
1	1	1

 

                              

 

                                                                 

 

Рис. 11.6. Схема ИЛИ-НЕ.

 

 

 

Рис. 11.7. Входные и выходные им­пульсные сигналы в схеме ИЛИ-НЕ с двумя входами.

Логическая схема ИЛИ (рис, 11.5 и табл. 11.3)

Логическая схема ИЛИ дает на выходе 1, если хотя бы на одном из ее входов присутствует 1. Логический 0 появляется на ее выходе только в том случае, если на всех ее входах действуют логические 0.

Логическая схема ИЛИ-НЕ (рис. 11.6 и табл. 11.4)

 

Схема ИЛИ-НЕ дает на выходе 0, если хотя бы на одном ее входе при­сутствует 1. Логическая 1 появляется на ее выходе только тогда, ко­гда на всех ее входах присутствует логический 0. Таким образом, схема ИЛИ-НЕ является логической противоположностью схемы ИЛИ. На рис. 11.7 показаны типичные формы сигналов, действующих в схеме ИЛИ-НЕ.

Логическая схема НЕ (рис. 11.8 и табл. 11.5)

Логическая схема НЕ является инвертором. Когда на ее входе присут­ствует 1, на выходе появляется 0, и наоборот. Если соединить между собой входы логических схем И-НЕ или ИЛИ-НЕ (рис. 11.8(б) и (в)), то

	Таблица 11.5. Таблица  истинности схемы НЕ   Вход Выход 0 1 1 0		Таблица 11.6. Таблица истинности схемы ИсключающееИЛИ   Входы Выход А В   0 0 0 0 1 1 1 0 1 1 1 0		Таблица 11.7. Табли­ца истинности схемы Исключающее ИЛИ-НЕ   Входы Выход А в   0 0 1 0 1 0 1 0 0 1 1 1

 

Динамическая логика (цифровая электроника) — Карта знаний

• Динамическая логика (или тактированная логика) — методология разработки комбинационных схем, при которой проектируемая схема работает по тактам. Реализуется, в частности, по технологии КМОП. Применяется при проектировании интегральных схем.

Источник: Википедия

Связанные понятия

Асинхро́нная ло́гика — разновидность взаимодействия логических элементов цифровых устройств. Отличается от синхронной тем, что её элементы действуют асинхронно, не подчиняясь глобальному генератору тактовых импульсов. Проектирование на основе стандартных ячеек (англ. standard cell) — метод проектирования интегральных схем с преобладанием цифровых элементов. В данном методе наиболее низкий уровень проектирования СБИС скрыт от проектировщика абстрактными логическими элементами (например, узел NAND). Методология проектирования на базе ячеек позволяет одним разработчикам сфокусироваться на высокоуровневом аспекте цифрового дизайна, когда другие разработчики работают над физическими реализациями ячеек. Вместе с достижениями… Сверхпроводящая логика — класс логических схем, построенных на основе сверхпроводников и джозефсоновских контактов, и использующих эффект квантования магнитного потока. Отсутствие электрического сопротивления позволяет создавать логические схемы с высоким быстродействием, а последние разработки обладают и высокой энергоэффективностью. Сверхпроводящая логика является вариантом для создания процессоров, с высокой частотой переключения отдельных логических элементов — до сотен ГГц. Электронная схема — это сочетание отдельных электронных компонентов, таких как резисторы, конденсаторы, индуктивности, диоды, транзисторы и интегральные микросхемы, соединённых между собой. Различные комбинации компонентов позволяют выполнять множество как простых, так и сложных операций, таких как усиление сигналов, обработка и передача информации и т. д. Гибридный компьютер, гибридная вычислительная машина, аналого-цифровая система — вид гибридной вычислительной системы (ГВС), сочетающий в себе свойства аналоговых и цифровых вычислительных устройств. Электро́ника (от греч. Ηλεκτρόνιο «электрон») — область науки и техники, занимающаяся созданием и практическим использованием различных устройств и приборов, работа которых основана на изменении концентрации и перемещении заряженных частиц (электронов) в вакууме, газе или твердых кристаллических телах, и других физических явлениях (НБИК). Задача характеризации элементов микросхем заключается в получении зависимостей функциональных параметров библиотечного элемента или блока от длительности фронтов сигналов на входе и от величины нагрузочных емкостей для заданных наборов этих величин. В коммерческих системах характеризации (SiliconSmart , Virtuoso Liberate Characterization Solution , Virtuoso Variety Statistical Characterization Solution , Virtuoso Liberate MX Memory Characterization Solution , Kronos Characterizer Plus ) такие зависимости… Произвольная (нерегулярная) логика (англ. Random logic) — метод реализации схем комбинационной логики путём синтеза схемы из логических элементов по высокоуровневому описанию. Название метода происходит из того факта, что расположение элементов и их соединений на первый взгляд кажется произвольным. В частности, в отличие от, например, схем памяти, произвольная логика практически не образует различимой структуры в расположении элементов на кристалле. В СБИС произвольная логика часто реализуется с… Триггер (триггерная система) — класс электронных устройств, обладающих способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время. Нейроуправление (англ. Neurocontrol) — частный случай интеллектуального управления, использующий искусственные нейронные сети для решения задач управления динамическими объектами. Нейроуправление находится на стыке таких дисциплин, как искусственный интеллект, нейрофизиология, теория автоматического управления, робототехника. Нейронные сети обладают рядом уникальных свойств, которые делают их мощным инструментом для создания систем управления: способностью к обучению на примерах и обобщению данных… Разработка синхронных цифровых интегральных схем на уровне передач данных между регистрами (англ. register transfer level, RTL — уровень регистровых передач) — способ разработки синхронных (англ.) цифровых интегральных схем, при применении которого работа схемы описывается в виде последовательностей логических операций, применяемых к цифровым сигналам (данным) при их передаче от одного регистра к другому (не описывается, из каких электронных компонентов или из каких логических вентилей состоит схема…

Подробнее: Уровень регистровых передач

Аппара́тный генера́тор случа́йных чи́сел (генератор истинно случайных чисел) — устройство, которое генерирует последовательность случайных чисел на основе измеряемых, хаотически изменяющихся параметров протекающего физического процесса. Работа таких устройств часто основана на использовании надёжных источников энтропии, таких, как тепловой шум, дробовой шум, фотоэлектрический эффект, квантовые явления и т. д. Эти процессы в теории абсолютно непредсказуемы, на практике же получаемые из них случайные… Программи́руемая по́льзователем ве́нтильная ма́трица (ППВМ, англ. field-programmable gate array, FPGA) — полупроводниковое устройство, которое может быть сконфигурировано производителем или разработчиком после изготовления; отсюда название: «программируемая пользователем». ППВМ программируются путём изменения логики работы принципиальной схемы, например, с помощью исходного кода на языке проектирования (типа VHDL), на котором можно описать эту логику работы микросхемы. ППВМ является одной из архитектурных… Цифровой сигнальный процессор (англ. digital signal processor, DSP, цифровой процессор обработки сигналов (ЦПОС)) — специализированный микропроцессор, предназначенный для обработки оцифрованных сигналов (обычно, в режиме реального времени). Нагрузочная способность — параметр выхода микросхемы, характеризуемый быстродействием и выходным током драйвера, определяющим количество подключаемых входов микросхем или прямой токовой нагрузки для подключения реле, светодиода или какого-либо другого элемента. Диодно-транзисторная логика (ДТЛ), англ. Diode–transistor logic (DTL) — технология построения цифровых схем на основе биполярных транзисторов, диодов и резисторов. Своё название технология получила благодаря реализации логических функций (например, 2И) с помощью диодных цепей, а усиления и инверсии сигнала — с помощью транзистора (для сравнения см. резисторно-транзисторная логика и транзисторно-транзисторная логика). В информатике параллели́зм — это свойство систем, при котором несколько вычислений выполняются одновременно, и при этом, возможно, взаимодействуют друг с другом. Вычисления могут выполняться на нескольких ядрах одного чипа с вытесняющим разделением времени потоков на одном процессоре, либо выполняться на физически отдельных процессорах. Для выполнения параллельных вычислений разработаны ряд математических моделей, в том числе сети Петри, исчисление процессов, модели параллельных случайных доступов… Вычисления с памятью — способ построения вычислительных платформ, в которых используются принцип хранения результатов функций в массивах памяти, одномерных или двухмерных, в виде таблиц поиска, а вычисление функций заменяется извлечением значения из таблиц. Такие вычислительные платформы могут следовать как чисто пространственной модели вычислений, как в ПЛИС, так и временно́й модели вычислений (процедурной), когда функция вычисляется за множество тактов. Второй подход нацелен на уменьшение избыточности… Счётчик числа импульсов — устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики могут строиться на двухступенчатых D-триггерах, T-триггерах и JK-триггерах. Бы́страя одноква́нтовая ло́гика (БОК-логика, англ. Rapid Single Flux Quantum, RSFQ) — это технология создания электроники, основанная на квантовых эффектах (эффекте Джозефсона) в сверхпроводящих устройствах, один из вариантов сверхпроводящей логики. Джозефсоновские контакты играют в электронике на основе БОК-логики ту же роль, что и транзисторы в полупроводниковой. Секвенциальная логика — это логика памяти цифровых устройств. Название «секвенциальная» восходит к англ. sequential. Соответствующая логика может именоваться также как последовательностная, хотя последний термин по преимуществу употребляется в связи с логическими автоматами. Статический временной анализ (СВА, англ. Static timing analysis) — это метод расчета временных параметров СБИС, не требующий полноценного электрического моделирования работы схемы. То́ковый конве́йер (англ. current conveyor, СС) — абстрактная модель универсального трёхвыводного электронного устройства обработки аналоговых сигналов в базисах токов и напряжений, идеализированный аналог транзистора. Два входа токового конвейера (аналоги затвора и истока полевого транзистора либо эмиттера и базы биполярного транзистора) оперируют токами и напряжениями и передают (англ. convey, отсюда конвейер) ток на выход конвейера (аналог стока либо коллектора), обладающий бесконечно большим… Цифровые технологии (англ. Digital technology) основаны на представлении сигналов дискретными полосами аналоговых уровней, а не в виде непрерывного спектра. Все уровни в пределах полосы представляют собой одинаковое состояние сигнала. Программи́руемый логи́ческий контро́ллер (сокр. ПЛК; англ. programmable logic controller, сокр. PLC; более точный перевод на русский — контроллер с программируемой логикой), программируемый контроллер — специальная разновидность электронной вычислительной машины. Чаще всего ПЛК используют для автоматизации технологических процессов. В качестве основного режима работы ПЛК выступает его длительное автономное использование, зачастую в неблагоприятных условиях окружающей среды, без серьёзного обслуживания… Яче́йка Ги́лберта (англ. Gilbert cell) в электронике — схема четырёхквадрантного аналогового умножителя, предложенная Барри Гилбертом в 1968 году. Она представляет собой ядро умножителя на трёх дифференциальных каскадах, дополненное диодными преобразователями входных напряжений — в токи (V1, V2 на схемах). Ячейка Гилберта, в модифицированной бета-зависимой форме, выполняет функцию смесителя или балансного модулятора в большинстве современных радиоприёмников и сотовых телефонов. Це́лостность сигна́лов (англ. Signal Integrity) — наличие достаточных для безошибочной передачи качественных характеристик электрического сигнала. Импульсная нейронная сеть (ИмНС, англ. Pulsed neural networks, PNN) или Спайковая нейронная сеть (СНН, англ. Spiking neural network, SNN) — третье поколение искусственных нейронных сетей (ИНС), которое отличается от бинарных (первое поколение) и частотных/скоростных (второе поколение) ИНС тем, что в нем нейроны обмениваются короткими (у биологических нейронов — около 1-2 мс) импульсами одинаковой амплитуды (у биологических нейронов — около 100 мВ). Является самой реалистичной, с точки зрения физиологии… Высокоимпедансное состояние, высокоомное состояние, Z-состояние или состояние «Выключено» — состояние вывода цифровой микросхемы, при котором сопротивление между её внутренней схемой, подключённой к данному выводу, и внешней схемой очень велико. Физически реализуется закрытым транзистором, работающим в ключевом режиме. Цифровая антенная решётка (ЦАР) (антенная решётка с цифровой обработкой сигнала) — антенная решётка с поэлементной обработкой сигналов, в которой сигналы от излучающих элементов подвергаются аналого-цифровому преобразованию с последующей обработкой по определённым алгоритмам. Долгая краткосрочная память (англ. Long short-term memory; LSTM) — разновидность архитектуры рекуррентных нейронных сетей, предложенная в 1997 году Сеппом Хохрайтером и Юргеном Шмидхубером. Как и большинство рекуррентных нейронных сетей, LSTM-сеть является универсальной в том смысле, что при достаточном числе элементов сети она может выполнить любое вычисление, на которое способен обычный компьютер, для чего необходима соответствующая матрица весов, которая может рассматриваться как программа. В… Адаптивный фильтр — система с линейным фильтром, имеющим передаточную функцию, контролируемую переменными параметрами и средствами для установки этих параметров согласно оптимизационному алгоритму. Ввиду сложности оптимизационных алгоритмов почти все адаптивные фильтры являются цифровыми фильтрами. Адаптивные фильтры требуются для некоторых приложений, поскольку некоторые параметры желательной операции обработки (например, местоположение отражающих поверхностей в реверберирующем пространстве) заранее… Асинхронность (Асинхронизм) (от греч. α — отрицание, συν — вместе, χρονος — время) — не совпадение с чем-либо во времени; неодномоментность, неодновременность, несинхронность — характеризует процессы, не совпадающие во времени. Термин используемый в специальной литературе, предназначенный для особого применения, в общем смысле, это состояние не являющееся синхронизированным. Та или иная форма используется в зависимости от контекста или исторически сложившихся традиций использования в конкретных областях… Интегра́льная (микро)схе́ма (ИС, ИМС, IC (англ.)), микросхе́ма, м/сх, чип (англ. chip «тонкая пластинка»: первоначально термин относился к пластинке кристалла микросхемы) — микроэлектронное устройство — электронная схема произвольной сложности (кристалл), изготовленная на полупроводниковой подложке (пластине или плёнке) и помещённая в неразборный корпус или без такового, в случае вхождения в состав микросборки.

Подробнее: Интегральная схема

Моде́ль биологи́ческого нейро́на — математическое описание свойств нейронов, целью которого является точное моделирование процессов, протекающих в таких нервных клетках. В отличие от подобного точного моделирования, при создании сетей из искусственных нейронов обычно преследуются цели повышения эффективности вычислений. Оптические или фотонные вычисления — гипотетические вычислительные устройства, вычисления в которых производятся с помощью фотонов, сгенерированных лазерами или диодами.

Подробнее: Оптический компьютер

Распознавание по голосу — одна из форм биометрической аутентификации, позволяющая идентифицировать личность человека по совокупности уникальных характеристик голоса. Относится к динамическим методам биометрии. Однако, поскольку голос человека может меняться в зависимости от возраста, эмоционального состояния, здоровья, гормонального фона и целого ряда других факторов, не является абсолютно точным. По мере развития звукозаписывающей и воспроизводящей техники, технология распознавания применяется с… В криптографии атака по энергопотреблению является одной из форм атак по сторонним каналам, при которой криптоаналитик изучает потребляемую мощность устройства, выполняющего криптографические задачи (как например смарт-карта, устойчивый к взлому «черный ящик», интегральная схема и тому подобное). С помощью такой атаки возможно извлечь криптографические ключи или другую секретную информацию из устройства, не оказывая на него непосредственного воздействия. Специальные регулируемые асинхронные двигатели создаются в результате адаптации общепромышленных асинхронных двигателей к их условиям эксплуатации в управляемых электроприводах, имеющие в итоге более высокие энергетические и массогабаритностоимостные показатели по сравнению с неадаптированными. Яче́йка Блэ́кмера (англ. Blackmer cell) — схема электронного управляемого напряжением усилителя (УНУ, амплитудный модулятор) с экспоненциальной характеристикой управления, предложенная и доведённая до серийного выпуска Дэвидом Блэкмером в 1970—1973 годы. Четырёхтранзисторное ядро схемы образовано двумя встречно включёнными токовыми зеркалами на комплементарных биполярных транзисторах. Входной транзистор каждого из зеркал логарифмирует входной ток, а выходной транзистор антилогарифмирует сумму логарифма… Переме́нная в императивном программировании — поименованная, либо адресуемая иным способом область памяти, адрес которой можно использовать для осуществления доступа к данным. Данные, находящиеся в переменной (то есть по данному адресу памяти), называются значением этой переменной. Логический синтез в электронике — процесс получения списка соединений логических вентилей из абстрактной модели поведения логической схемы (например, на уровне регистровых передач). Наиболее распространенный пример этого процесса — синтез спецификаций, написанных на языках описания аппаратуры. Синтез выполняют программы-синтезаторы, способные оптимизировать проект согласно различным особенностям устройства, таким как временные ограничения, площадь и используемые компоненты. Такие программы обычно… Параллелизм на уровне команд (англ. Instruction-level parallelism — ILP) является мерой того, какое множество операций в компьютерной программе может выполняться одновременно. Потенциальное совмещение выполнения команд называется «параллелизмом на уровне команд». Клэйтро́ника — абстрактная концепция будущего, состоящая в объединении наномасштабных роботов и информатики с целью создания индивидуальных компьютеров атомных размеров, называемых клэйтронными атомами или к-атомами. Они могут вступать в контакт друг с другом и создавать материальные 3-D объекты, с которыми может взаимодействовать пользователь. Эта идея входит в более общую идею создания программируемой материи. Многочисленные исследования и эксперименты с клэйтроникой проводятся группой учёных в… Вычислительная гидродинамика (также CFD от англ. computational fluid dynamics) — подраздел механики сплошных сред, включающий совокупность физических, математических и численных методов, предназначенных для вычисления характеристик потоковых процессов. Декомпозиция — разделение целого на части. Также декомпозиция — это научный метод, использующий структуру задачи и позволяющий заменить решение одной большой задачи решением серии меньших задач, пусть и взаимосвязанных, но более простых. Плезиохронная цифровая иерархия (ПЦИ, также PDH от англ. Plesiochronous Digital Hierarchy) — цифровой метод передачи данных и голоса, основанный на временном разделении канала и технологии представления сигнала с помощью импульсно-кодовой модуляции (ИКМ).

Интегрально-инжекционная логика — Википедия

Материал из Википедии — свободной энциклопедии

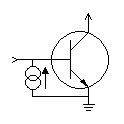Упрощенная символическое обозначение И2Л инвертора

Интегра́льно-инжекцио́нная ло́гика (распространённые аббревиатуры ИИЛ, И²Л, И2Л, И3Л, I2L, IIL, I²L) — схемотехника и технология изготовления логических элементов на биполярных транзисторах.

Интегрально-инжекционная логика предложена в конце 1971 г. — начале 1972 г. почти одновременно сотрудниками фирмы IBM Х. Бергером и З. Видманом (Бёблинген, ФРГ) и сотрудниками фирмы Philips В. К. Хартом и А. Слобом (Эйндховен, Голландия).

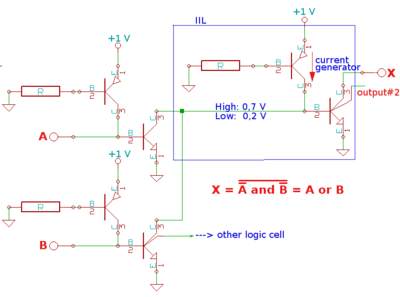Принципиальная схема логического элемента «ИЛИ». P-n-p транзисторы в базах служат для инжекции зарядов в базы основных транзисторов.

ИИЛ является развитием технологии НСТЛ (логика с непосредственными связями между транзисторами, которая в иностранной литературе называется MTL — Merged Transistor Logic или DCTL — Direct-Coupled Transistor Logic). В свою очередь, НСТЛ можно рассматривать как предельный вариант РТЛ, в НСТЛ отсутствуют резисторы между выходом (коллектором) n-p-n транзистора логического элемента-источника и входом (базой) элемента-приёмника.

Вообще говоря, ИИЛ не является разновидностью транзисторно-транзисторной логики. В основе функционирования ИИЛ лежит использование «особых» транзисторов с объединённой базой. Эти транзисторы не способны проводить ток из-за низкой концентрации носителей зарядов в базе. Поэтому рядом с основным транзистором, входящим в логический элемент находится «инжектор» — электрод, инжектирующий носители заряда в базу. При инжекции транзистор включается и может выполнять заданную логическую функцию.

При проектировании микросхем ИИЛ основную роль отводят именно инжекторам. Эмиттеры, как правило, соединены — ими является подложка микросхемы. На поверхности кристалла выходят базовые области транзисторов со сформированными на них коллекторными областями. Благодаря такой технологии ИИЛ-транзистор по размеру (если не считать инжектора) занимает на кристалле меньшую площадь чем МОП-транзистор. Так как один инжектор может использоваться для инжекции в несколько транзисторов, в результате получается выигрыш в степени интеграции.

Преимущества таких ИМС:

• Высокая степень интеграции (например, «проводное ИЛИ» осуществляется простым соединением коллекторов транзисторов, то есть логическая функция ИЛИ-НЕ реализуется вообще без дополнительных ключей), высокая степень интеграции, иногда выше, чем микросхем с МОП-логикой.
• Иногда меньшая стоимость, чем у устройств, построенных по принципам других логик. Высокий выход годных при производстве.
• Малое потребление энергии на одно элементарное переключение вентиля ~10⁻¹² Дж и как следствие — сниженное энергопотребление.
• Низкое напряжение питания: 1—3 В.
• Хотя логические уровни ИИЛ очень близки (логический ноль ~0,2 В, логическая единица ~0,7 В) схемы ИИЛ имеют высокую помехоустойчивость, поскольку логические уровни передаются током, а не напряжением.

К недостаткам относят:

• Относительно низкое быстродействие, максимальная рабочая частота ~50 МГц.

В СССР выпускались микропроцессорные наборы серий К582 и К584 на основе технологии ИИЛ. Также выпускались серии микросхем статических запоминающих устройств К558 и К541 небольшой ёмкости, которые благодаря встроенным преобразователям логических уровней были совместимы по уровням входных и выходных сигналов с ТТЛ.

• Хвощ С. Т., Смолов В. Б., Белоус А.И. Инжекционные микропроцессоры в управлении промышленным оборудованием. — Л.: Машиностроение, Ленинградское отделение, 1985. — 182 с.

Логические элементы — это… Что такое Логические элементы?

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.

Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

Всего возможно логических функций и соответствующих им логических элементов, где  — основание системы счисления,  — число входов (аргументов),  — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.

Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).

Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).

Содержание 1 Двоичные логические операции с цифровыми сигналами (битовые операции) 1.1 Отрицание, НЕ 1.2 Повторение, ДА 1.3 Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B) 1.4 Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B) 1.5 Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера) 1.6 Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса) 1.7 Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ 1.8 Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности. 1.9 Импликация от A к B (прямая импликация, инверсия декремента, A<=B) 1.10 Импликация от B к A (обратная импликация, инверсия инкремента, A>=B) 1.11 Декремент. Запрет импликации по B. Инверсия импликации от A к B 1.12 Инкремент. Запрет импликации по A. Инверсия импликации от B к A 2 Физические реализации логических элементов 3 Классификация электронных транзисторных физических реализаций логических элементов 4 Применение логических элементов 5 Комбинационные логические устройства 6 Последовательностные цифровые устройства 7 См. также 8 Ссылки 9 Литература

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

Отрицание, НЕ

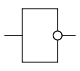Инвертор, НЕ

0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

Повторение, ДА

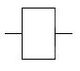
0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)

2И

		٨
0	0	0
1	0	0
0	1	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)

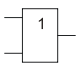2ИЛИ

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
• «0» тогда и только тогда, когда на всех входах действуют «0»

Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)

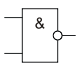2И-НЕ

Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
• «0» тогда и только тогда, когда на всех входах действуют «1»

Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)

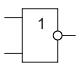2ИЛИ-НЕ

		↓
0	0	1
0	1	0
1	0	0
1	1	0

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «0»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «1»

Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ

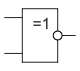ИСКЛ-ИЛИ-НЕ

		↔
0	0	1
0	1	0
1	0	0
1	1	1

Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует четное количество,
• «0» тогда и только тогда, когда на входе действует нечетное количество

Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

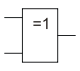ИСКЛ-ИЛИ

В англоязычной литературе 2XOR.

Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует нечётное количество ,
• «0» тогда и только тогда, когда на входе действует чётное количество

Импликация от A к B (прямая импликация, инверсия декремента, A<=B)

		→
0	0	1
0	1	1
1	0	0
1	1	1

Мнемоническое правило для инверсии декремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» меньше «А»,
• «1» тогда и только тогда, когда на «B» больше либо равно «А»

Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)

		→
0	0	1
0	1	0
1	0	1
1	1	1

Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» больше «А»,
• «1» тогда и только тогда, когда на «B» меньше либо равно «А»

Декремент. Запрет импликации по B. Инверсия импликации от A к B

Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «A» больше «B»,
• «0» тогда и только тогда, когда на «A» меньше либо равно «B»

Инкремент. Запрет импликации по A. Инверсия импликации от B к A

Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «B» больше «A»,
• «0» тогда и только тогда, когда на «B» меньше либо равно «A»

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

• И, НЕ (2 элемента)
• ИЛИ, НЕ (2 элемента)
• И-НЕ (1 элемент)
• ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.

Физические реализации логических элементов

Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.

Классификация электронных транзисторных физических реализаций логических элементов

Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

• РТЛ (резисторно-транзисторная логика)
• ДТЛ (диодно-транзисторная логика)
• ТТЛ (транзисторно-транзисторная логика)

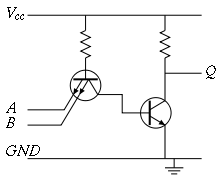Упрощённая схема двухвходового элемента И-НЕ ТТЛ .

Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.

В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.

Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.

Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).

Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.

Инвертор

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Применение логических элементов

Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Комбинационные логические устройства

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:

Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностные цифровые устройства

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.

См. также

Ссылки

Литература

Логические элементы — Википедия. Что такое Логические элементы

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.

Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

Всего возможно  x(xn)∗m{\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где  x{\displaystyle \ x} — основание системы счисления,  n{\displaystyle \ n} — число входов (аргументов),  m{\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.

Всего возможны 2(22)∗1=24=16{\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2(23)∗1=28=256{\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).

Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Из 2(21)=22=4{\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

Отрицание, НЕ

Инвертор, НЕ (IEC) 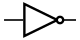Инвертор, НЕ (ANSI)

A{\displaystyle A}	¬A{\displaystyle A}
0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

Повторение

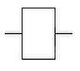
A{\displaystyle A}	A{\displaystyle A}
0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из 2(22)=24=16{\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция И

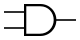
A{\displaystyle A}	B{\displaystyle B}	A∧B{\displaystyle A\land B}
0	0	0
0	1	0
1	0	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».

Дизъюнкция (логическое сложение). Операция ИЛИ

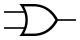
A{\displaystyle A}	B{\displaystyle B}	A∨B{\displaystyle A\lor B}
0	0	0
0	1	1
1	0	1
1	1	1

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
• «0» тогда и только тогда, когда на всех входах действуют «0»

Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)

A{\displaystyle A}	B{\displaystyle B}	A|B{\displaystyle A|B}
0	0	1
0	1	1
1	0	1
1	1	0

Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
• «0» тогда и только тогда, когда на всех входах действуют «1»

Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)

В англоязычной литературе NOR.

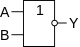
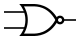
A{\displaystyle A}	B{\displaystyle B}	A{\displaystyle A}↓B{\displaystyle B}
0	0	1
0	1	0
1	0	0
1	1	0

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «0»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «1»

Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ

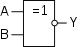ИСКЛ-ИЛИ-НЕ (IEC) 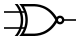ИСКЛ-ИЛИ-НЕ (ANSI)

A{\displaystyle A}	B{\displaystyle B}	A{\displaystyle A}↔B{\displaystyle B}
0	0	1
0	1	0
1	0	0
1	1	1

Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует чётное количество,
• «0» тогда и только тогда, когда на входе действует нечётное количество

Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».

Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

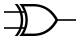
В англоязычной литературе XOR.

A{\displaystyle A}	B{\displaystyle B}	A⊕B{\displaystyle A\oplus B}
0	0	0
0	1	1
1	0	1
1	1	0

Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует нечётное количество ,
• «0» тогда и только тогда, когда на входе действует чётное количество

Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».

Импликация от A к B (прямая импликация, инверсия декремента, A<=B)

A{\displaystyle A}	B{\displaystyle B}	A{\displaystyle A}→B{\displaystyle B}
0	0	1
0	1	1
1	0	0
1	1	1

Мнемоническое правило для инверсии декремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» меньше «А»,
• «1» тогда и только тогда, когда на «B» больше либо равно «А»

Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)

A{\displaystyle A}	B{\displaystyle B}	B{\displaystyle B}→A{\displaystyle A}
0	0	1
0	1	0
1	0	1
1	1	1

Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» больше «А»,
• «1» тогда и только тогда, когда на «B» меньше либо равно «А»

Декремент. Запрет импликации по B. Инверсия импликации от A к B

A{\displaystyle A}	B{\displaystyle B}	f(A,B){\displaystyle f(A,B)}
0	0	0
0	1	0
1	0	1
1	1	0

Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «A» больше «B»,
• «0» тогда и только тогда, когда на «A» меньше либо равно «B»

Инкремент. Запрет импликации по A. Инверсия импликации от B к A

A{\displaystyle A}	B{\displaystyle B}	f(A,B){\displaystyle f(A,B)}
0	0	0
0	1	1
1	0	0
1	1	0

Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «B» больше «A»,
• «0» тогда и только тогда, когда на «B» меньше либо равно «A»

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

• И, НЕ (2 элемента)
• ИЛИ, НЕ (2 элемента)
• И-НЕ (1 элемент)
• ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.

Физические реализации

Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:

• механические,
• гидравлические,
• пневматические,
• электромагнитные,
• электромеханические,
• электронные,
• оптические.

Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.

Классификация электронных транзисторных физических реализаций логических элементов

Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

• РТЛ (резисторно-транзисторная логика)
• ДТЛ (диодно-транзисторная логика)
• ТТЛ (транзисторно-транзисторная логика)

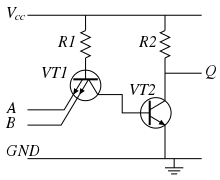Упрощённая схема двухвходового элемента И-НЕ ТТЛ .

Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.

В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.

Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.

Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).

Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.

Инвертор

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Применение логических элементов

Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Комбинационные логические устройства

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:

Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностные цифровые устройства

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.

См. также

Примечания

Литература

Ссылки

Логические элементы — это… Что такое Логические элементы?

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.

С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.

Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

Всего возможно логических функций и соответствующих им логических элементов, где  — основание системы счисления,  — число входов (аргументов),  — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.

Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).

Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).

Содержание 1 Двоичные логические операции с цифровыми сигналами (битовые операции) 1.1 Отрицание, НЕ 1.2 Повторение, ДА 1.3 Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B) 1.4 Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B) 1.5 Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера) 1.6 Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса) 1.7 Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ 1.8 Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности. 1.9 Импликация от A к B (прямая импликация, инверсия декремента, A<=B) 1.10 Импликация от B к A (обратная импликация, инверсия инкремента, A>=B) 1.11 Декремент. Запрет импликации по B. Инверсия импликации от A к B 1.12 Инкремент. Запрет импликации по A. Инверсия импликации от B к A 2 Физические реализации логических элементов 3 Классификация электронных транзисторных физических реализаций логических элементов 4 Применение логических элементов 5 Комбинационные логические устройства 6 Последовательностные цифровые устройства 7 См. также 8 Ссылки 9 Литература

Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.

Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.

Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.

Отрицание, НЕ

Инвертор, НЕ

0	1
1	0

Мнемоническое правило для отрицания звучит так: На выходе будет:

Повторение, ДА

0	0
1	1

Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.

Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.

Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)

2И

		٨
0	0	0
1	0	0
0	1	0
1	1	1

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «0»

Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)

2ИЛИ

Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
• «0» тогда и только тогда, когда на всех входах действуют «0»

Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)

2И-НЕ

Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
• «0» тогда и только тогда, когда на всех входах действуют «1»

Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)

2ИЛИ-НЕ

		↓
0	0	1
0	1	0
1	0	0
1	1	0

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «0»,
• «0» тогда и только тогда, когда хотя бы на одном входе действует «1»

Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ

ИСКЛ-ИЛИ-НЕ

		↔
0	0	1
0	1	0
1	0	0
1	1	1

Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует четное количество,
• «0» тогда и только тогда, когда на входе действует нечетное количество

Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

ИСКЛ-ИЛИ

В англоязычной литературе 2XOR.

Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на входе действует нечётное количество ,
• «0» тогда и только тогда, когда на входе действует чётное количество

Импликация от A к B (прямая импликация, инверсия декремента, A<=B)

		→
0	0	1
0	1	1
1	0	0
1	1	1

Мнемоническое правило для инверсии декремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» меньше «А»,
• «1» тогда и только тогда, когда на «B» больше либо равно «А»

Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)

		→
0	0	1
0	1	0
1	0	1
1	1	1

Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:

• «0» тогда и только тогда, когда на «B» больше «А»,
• «1» тогда и только тогда, когда на «B» меньше либо равно «А»

Декремент. Запрет импликации по B. Инверсия импликации от A к B

Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «A» больше «B»,
• «0» тогда и только тогда, когда на «A» меньше либо равно «B»

Инкремент. Запрет импликации по A. Инверсия импликации от B к A

Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:

• «1» тогда и только тогда, когда на «B» больше «A»,
• «0» тогда и только тогда, когда на «B» меньше либо равно «A»

Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.

Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:

• И, НЕ (2 элемента)
• ИЛИ, НЕ (2 элемента)
• И-НЕ (1 элемент)
• ИЛИ-НЕ (1 элемент).

Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.

Физические реализации логических элементов

Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.

Классификация электронных транзисторных физических реализаций логических элементов

Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

• РТЛ (резисторно-транзисторная логика)
• ДТЛ (диодно-транзисторная логика)
• ТТЛ (транзисторно-транзисторная логика)

Упрощённая схема двухвходового элемента И-НЕ ТТЛ .

Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.

В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.

Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.

Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).

Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.

Инвертор

Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).

Применение логических элементов

Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.

Комбинационные логические устройства

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:

Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностные цифровые устройства

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.

См. также

Ссылки

Литература