Логические операции и таблицы истинности

Похожие презентации:

Основы логики. Таблица истинности. Равносильные логические выражения

Логические операции

Базовые логические операции и функции. Таблицы истинности. Контактные схемы

Основы программирования на языке Python. Логическая операция

Алгебра логики и таблицы истинности. (лекция 4)

Логические операции

Логические операции

Логические операции компьютеров

Элементарные логические операции

Элементы математической логики

1. Логические операции и таблицы истинности

Учитель информатики
Поборцева Елена Валентиновна

2. КОНЪЮНКЦИЯ

F = A & B.
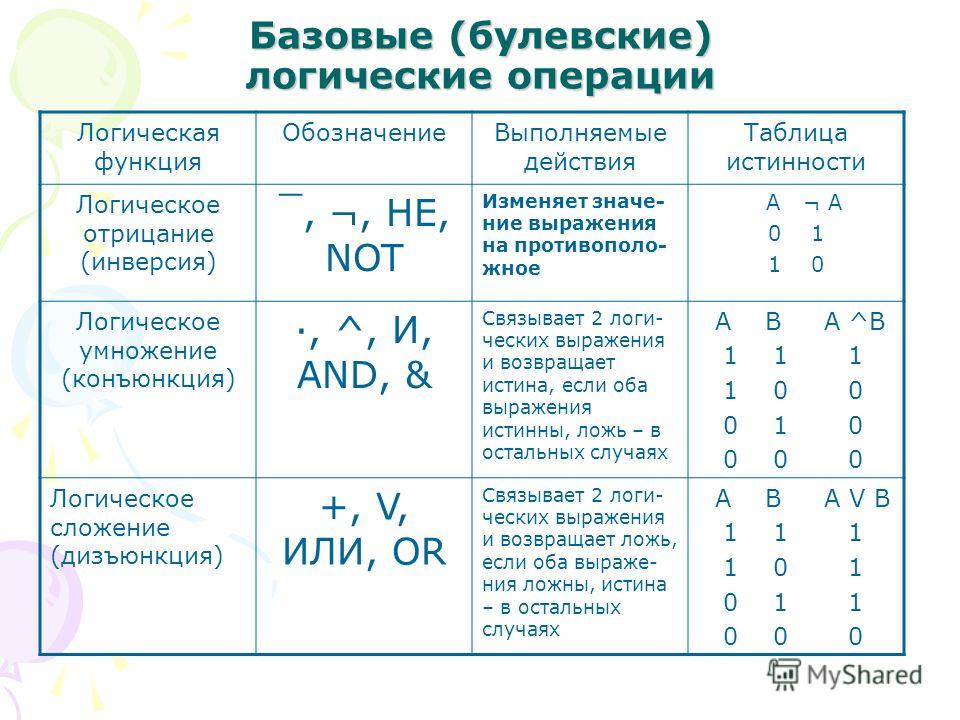
Логическое умножение
КОНЪЮНКЦИЯ — это
новое сложное выражение
будет истинным только
тогда, когда истинны оба
исходных простых
выражения.
Конъюнкция определяет
соединение двух
логических выражений с
помощью союза И.
A
B
F
1
1
1
1
0
0
0
1
0
0
0
0

3.

Примеры:
10
10
10
10
делится на
не делится
делится на
не делится
2 и 5 больше 3
на 2 и 5 больше 3
2 и 5 не больше 3
на 2 и 5 не больше 3
► F=A&B
Задание: Определить, чему будет равно значение F
для каждого выражения.

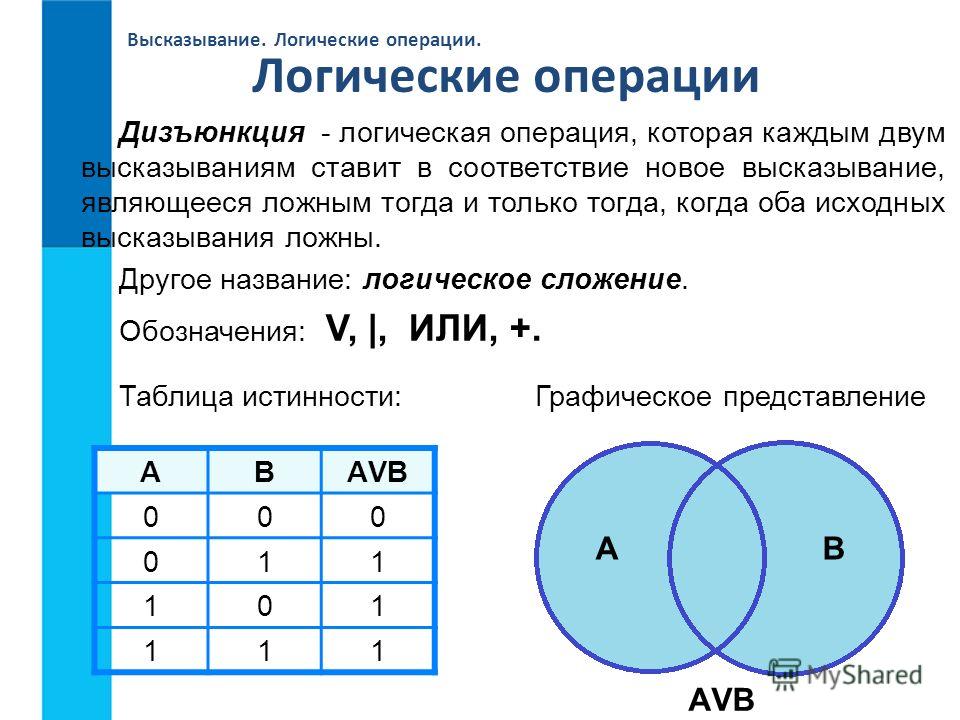
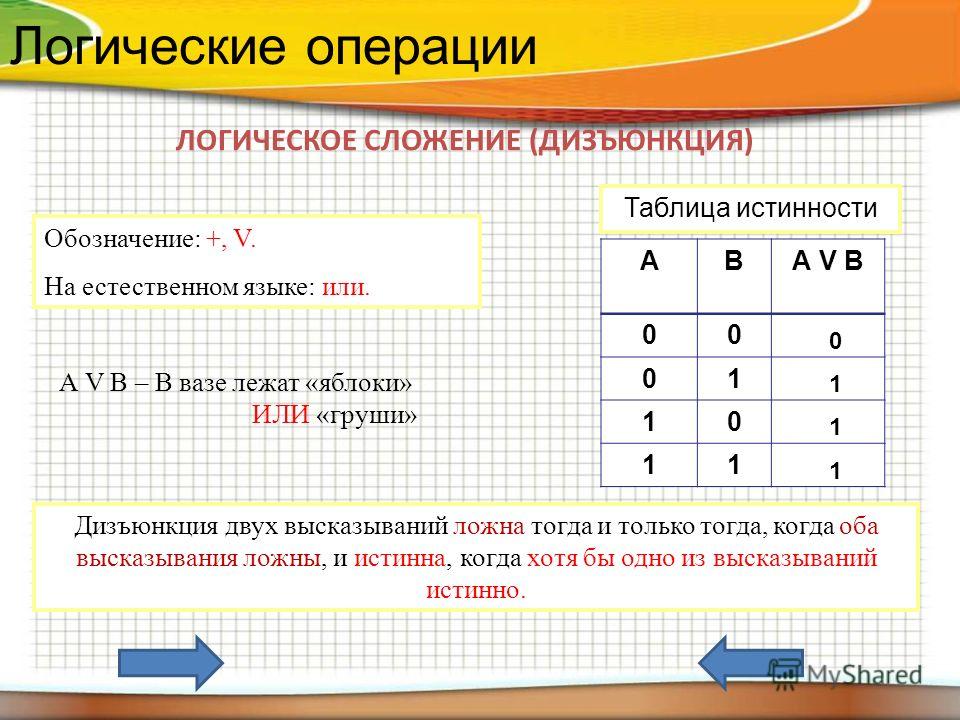
4. ДИЗЪЮНКЦИЯ

F=A+B
Логическое сложение –
ДИЗЪЮНКЦИЯ — это
новое сложное выражение
будет истинным тогда и
только тогда,
когда истинно хотя бы
одно из исходных (простых)
выражений.
► Дизъюнкция определяет
соединение двух
логических выражений с
помощью союза ИЛИ
A
B
F
1
1
1
1
0
1
0
1
1
0
0
0

5. Примеры:

► 10
делится на
► 10 не делится
► 10 делится на
► 10 не делится
2 или 5 больше 3
на 2 или 5 больше 3
2 или 5 не больше 3
на 2 или 5 не больше 3
F=AVB
Задание: Определить, чему будет равно значение F для
каждого выражения.

6. ИНВЕРСИЯ

Логическое отрицание :
ИНВЕРСИЯ — если исходное
выражение истинно, то
результат отрицания будет
ложным, и наоборот, если
исходное выражение ложно,
то результат отрицания будет
истинным/
Данная операция означает,
что к исходному логическому
выражению добавляется
частица НЕ или слова
НЕВЕРНО, ЧТО
A
_
F=A
1
0
0
1
► Пример:
► Луна
— спутник Земли (А).
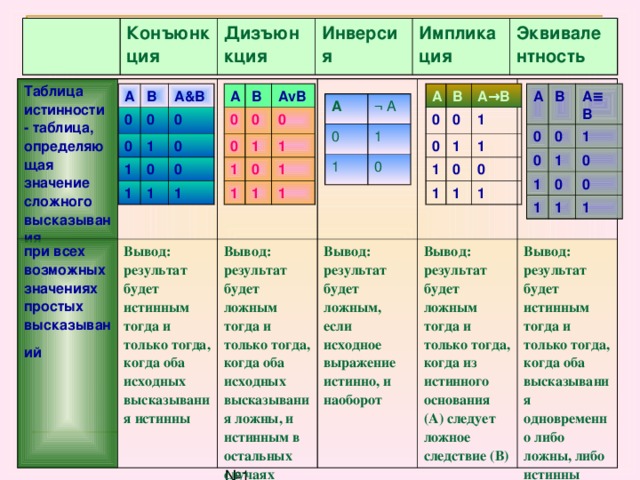
► Луна — не спутник Земли (не A)
_
F= A

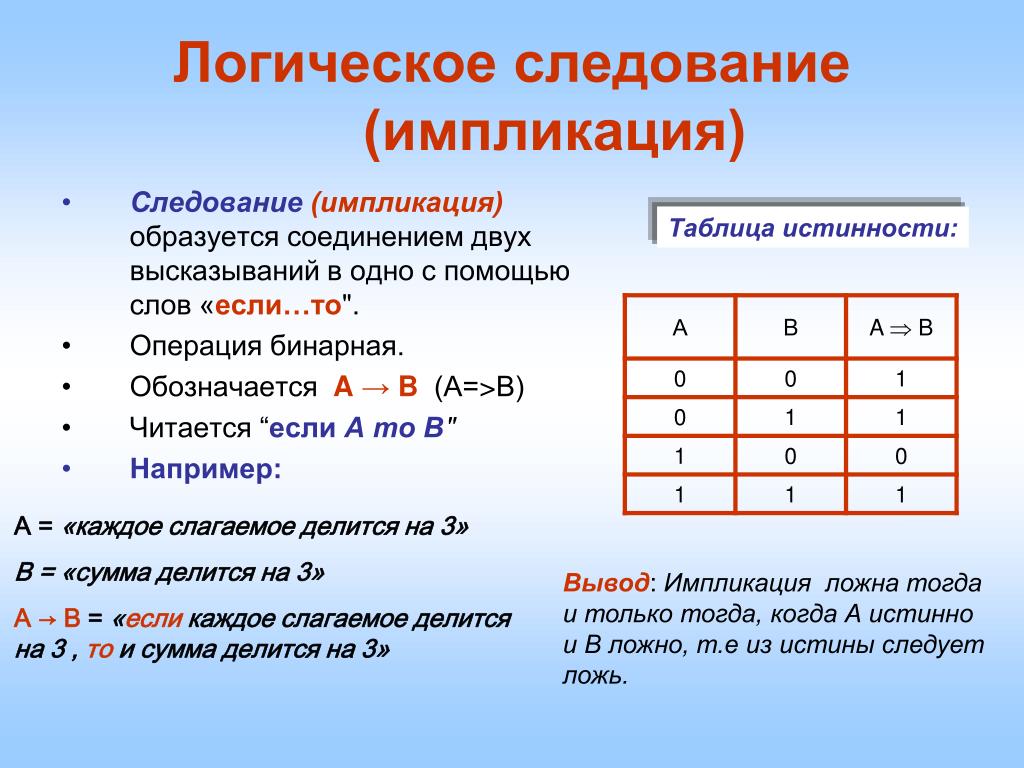
8. Логическое следование (импликация)

Логическое следование (Импликация) образуется
соединением двух высказываний в одно с помощью союза
«если… то…».
Импликация записывается как посылка следствие; (остриё
всегда указывает на следствие).
F = A B, составное высказывание, образованное с помощью
операции: логическое следование (импликация)
Суждение, выражаемое импликацией, выражается также
следующими способами:
1. Посылка является условием, достаточным для выполнения следствия;
2. Следствие является условием, необходимым для истинности посылки.

9. «Житейский» смысл импликации.

«Житейский» смысл
импликации.
Для более лёгкого понимания смысла импликации и
запоминания ее таблицы истинности может
пригодиться житейская модель:
А — начальник. Он может приказать «работай» (1) или
сказать «делай что хочешь» (0).
В — подчиненный. Он может работать (1) или
бездельничать (0).
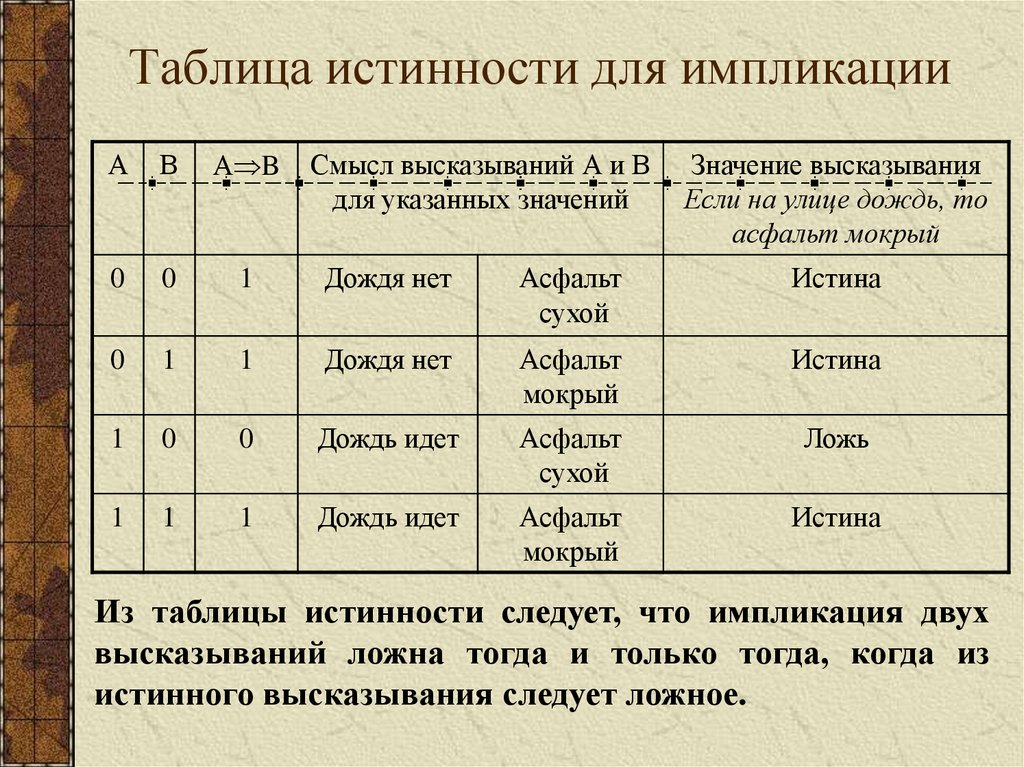
В таком случае импликация — не что иное, как
послушание подчиненного начальнику.
По таблице истинности легко проверить, что
послушания нет только тогда, когда начальник
приказывает работать, а подчиненный бездельничает.

10. ИМПЛИКАЦИЯ

Логическое
следование: ИМПЛИКАЦИЯ связывает два простых логических
выражения, из которых первое
является условием (А), а второе
(В)– следствием из этого условия.
Результатом ИМПЛИКАЦИИ
является ЛОЖЬ только тогда,
когда условие А истинно, а
следствие В ложно.
Обозначается A B
символом «следовательно» и
выражается словами ЕСЛИ … ,
ТО …
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1

11. Примеры:

Если данный четырёхугольник квадрат, то около него
можно описать окружность
Если данный четырёхугольник не квадрат, то около
него можно описать окружность
Если данный четырёхугольник квадрат, то около него
нельзя описать окружность
Если данный четырёхугольник не квадрат, то около
него нельзя описать окружность
A B
Задание: Определить, чему будет равно значение F для каждого
выражения.

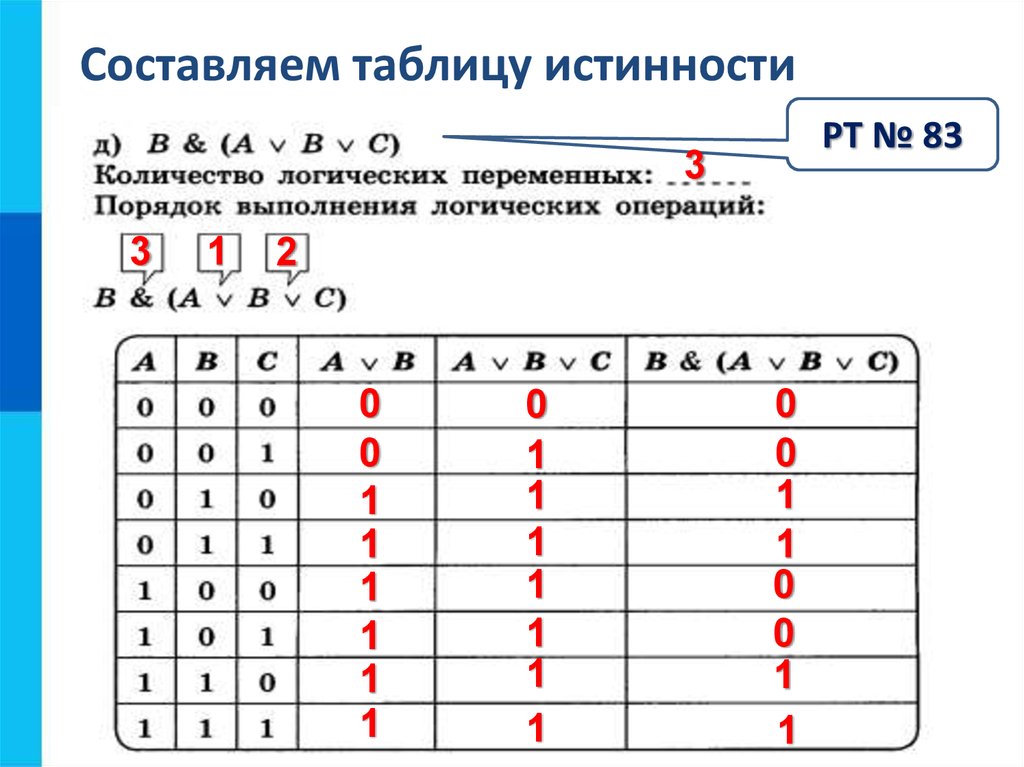
12. Порядок выполнения логических операций

► 1.
инверсия
► 2. конъюнкция
► 3. дизъюнкция
► 4. импликация
Для изменения указанного порядка
выполнения операций используются
скобки.

13. Пример задания 1:

Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
►Какое
1) ¬X ¬Y ¬Z
X
Y
Z
F
1
0
0
1
0
0
0
1
1
1
1
0
выражение соответствует F?
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z

14. Решение :

нужно для каждой строчки подставить заданные
значения X, Y и Z во все функции, заданные в
ответах, и сравнить результаты с соответствующими
значениями F для этих данных
если для какой-нибудь комбинации X, Y и Z результат
не совпадает с соответствующим значением F,
оставшиеся строчки можно не рассматривать,
поскольку для правильного ответа все три результата
должны совпасть со значениями функции F

первое выражение, равно 1 только при X=Y=Z=0 , поэтому это
неверный ответ (первая строка таблицы не подходит)
второе выражение, равно 1 только при X=Y=Z=1, поэтому это
неверный ответ (первая и вторая строки таблицы не подходят)
третье выражение, равно нулю при X=Y=Z=0, поэтому это
неверный ответ (вторая строка таблицы не подходит)
наконец, четвертое выражение, равно нулю только тогда, когда
X=Y=Z=1, а в остальных случаях равно 1, что совпадает с
приведенной частью таблицы истинности
X
Y
Z
F
таким образом, правильный ответ – 4
1) ¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
1
0
0
1
0
0
0
1
1
1
1
0
4) ¬X ¬Y ¬Z

16.

Пример задания 2:
Символом F обозначено
одно из указанных ниже
логических выражений от
трех аргументов: X, Y, Z.
Дан фрагмент таблицы
истинности выражения F:
X
Y
Z
F
1
0
0
1
0
0
0
0
1
1
1
0
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z
2) X Y Z
3) X ¬Y ¬Z
4) X ¬Y ¬Z

17. Решение :

В столбце F есть единственная единица
для комбинации X=1, Y=Z=0,
простейшая функция, истинная (только)
для этого случая, имеет вид , она есть
среди приведенных ответов (ответ 3)
таким образом, правильный ответ – 3.

18. Пример задания 3:

Дан фрагмент таблицы
истинности выражения F
(см. таблицу справа).
Какое выражение
соответствует F?
1) (X ¬Y)→ Z
2) (X Y)→ ¬Z
X
Y
Z
F
0
0
0
0
0
1
1
1
1
0
0
1
3) X (¬Y → Z)
4) X Y ¬Z

19. Ответ к заданию 3:

► Найди
правильный ответ:
► 1, 2, 3, 4

English     Русский Правила

Персональный сайт — 55.

Логические операции над высказываниями. Основные равносильности алгебры логики. Пример в MS Exсel.

Сводная таблица истинности логических функций

 

 

 

Построение таблиц истиности с помощью электронных таблиц

 

Цель работы: познакомиться с логическими функциями MSExcel , научиться строить таблицы истинности сложных высказываний

 

Краткие теоретические сведения:

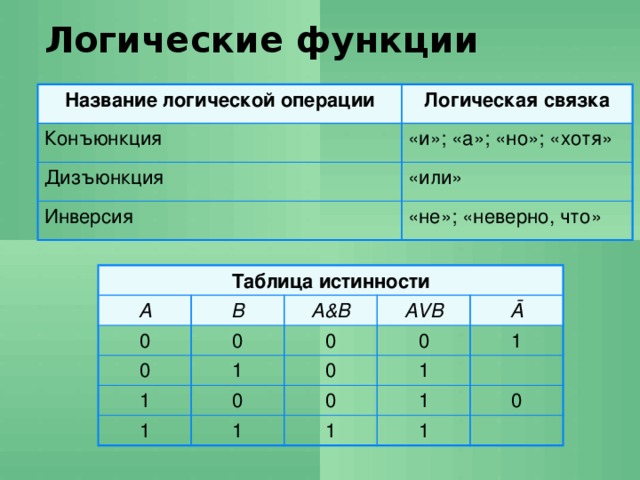
Аргументами логических функций являются логические значения ИСТИНА и ЛОЖЬ.

Логическая функция «И» имеет в качестве аргументов логические значения, которые могут быть истинными или ложными, и задается формулой =И(лог_знач1; лог_знач2; …). Принимает значение ИСТИНА тогда и только тогда, когда все аргументы имеют значение ИСТИНА.

 Логическая функция «ИЛИ» имеет в качестве аргументов логические значения и задается формулой =ИЛИ(лог_знач1; лог_знач2; …). Принимает значение ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА.

Логическая функция «НЕ» имеет один аргумент и задается формулой =НЕ(лог_знач).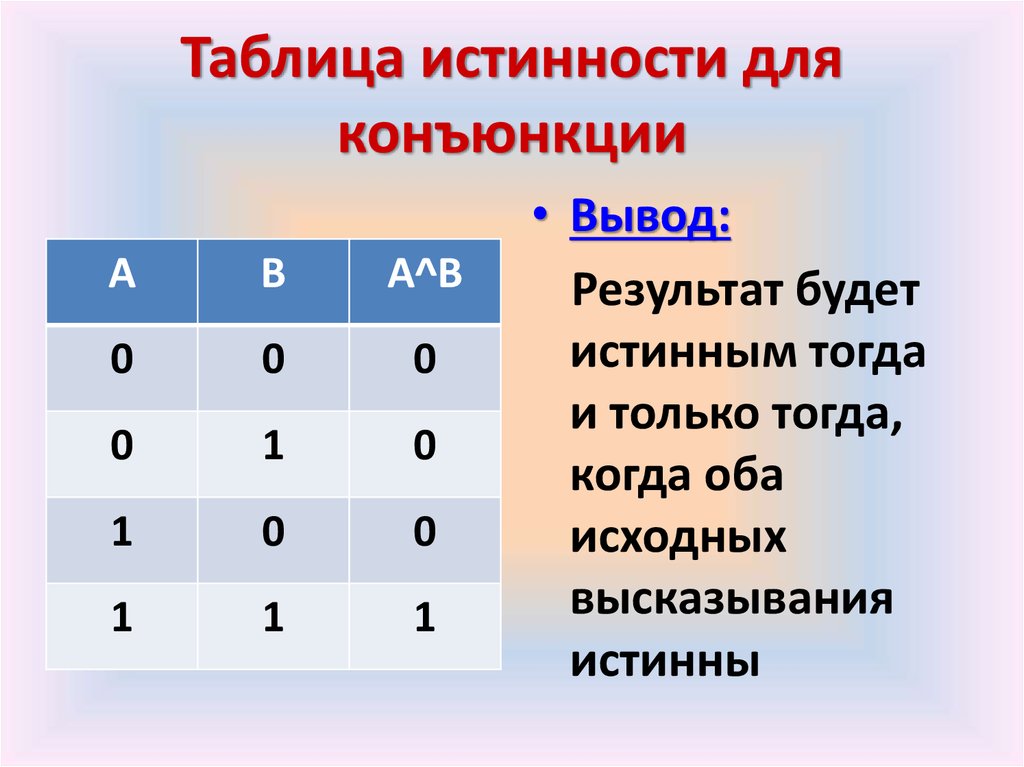 Принимает значение ИСТИНА, если аргумент имеет значение ЛОЖЬ, и наоборот.

Порядок выполнения работы:

Для того, чтобы разобраться, как выполнять работу сделаем задание: «Построим таблицу истинности операции логического умножения А&В»

Алгоритм выполнения:

1. В ячейках А1, В1, С1 ввести заголовки «шапки» таблицы.

2. В паре ячеек (А2, В2), (А3, В3), (А4, В4), (А5, В5) ввести пары значений аргументов логической операции (ЛОЖЬ, ЛОЖЬ), (ИСТИНА, ЛОЖЬ), (ЛОЖЬ, ИСТИНА), (ИСТИНА, ИСТИНА).

3. Выделить ячейку С2, в которую нужно вставить первое значение функции.

4. Ввести команду [Вставка–Функция…].

5. На диалоговой панели  Мастер функций в списке Категория: выбрать вариант Логические, а в списке Функция: выбрать вариант И.

Щелкнуть на кнопке OK.

6. На появившейся панели Аргументы функции ввести значения для лог_знач1 и лог_знач2.

Для ввода имени ячейки, где хранится  лог_знач1, щелкнуть по кнопке со стрелочкой в поле Логическое значение 1 и в электронной таблице выделить ячейку А2.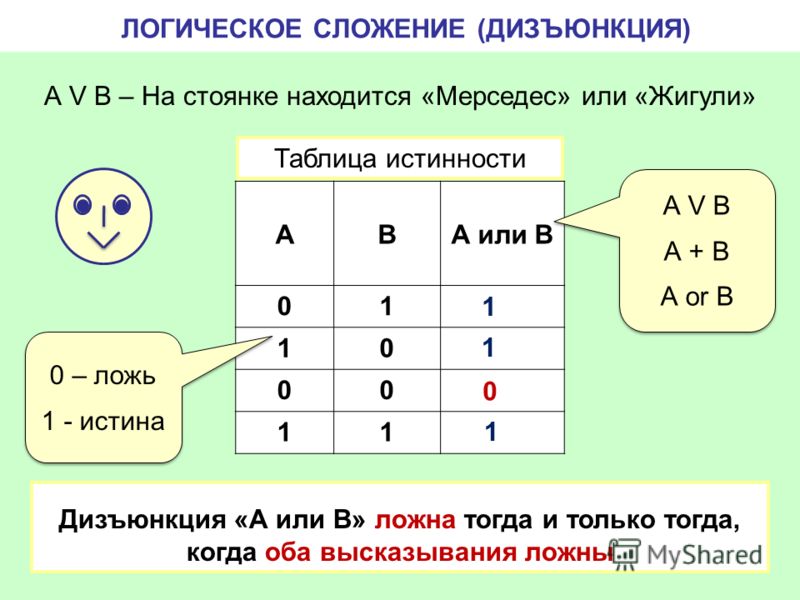

Для ввода имени ячейки, где хранится  лог_знач2, щелкнуть по кнопке со стрелочкой в поле Логическое значение 2 и в электронной таблице выделить ячейку В2.

 7. Выделить ячейку С2, в которой теперь хранится формула =И(А2;В2) и протягиванием вниз скопировать формулу в ячейки С3, С4 и С5.

8. Значением этой функции в трех случаях является ЛОЖЬ и только в последнем − ИСТИНА.

Мы получили таблицу истинности операции логического умножения (конъюнкции).

Аналогично строятся таблицы истинности для других логических операций.

 

Пример задания. «Построить таблицу истинности логического выражения от двух переменных»

 

	А	В	С
1	А	В	А&В
2	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ
3	ИСТИНА	ЛОЖЬ	ЛОЖЬ
4	ЛОЖЬ	ИСТИНА	ЛОЖЬ
5	ИСТИНА	ИСТИНА	ИСТИНА

 

Математические/Сравнение/Логические операторы, Приоритет, Таблица истинности

Охватывает символы операций, используемые в выражения сравнения. Включает порядок старшинства и таблицу истинности.

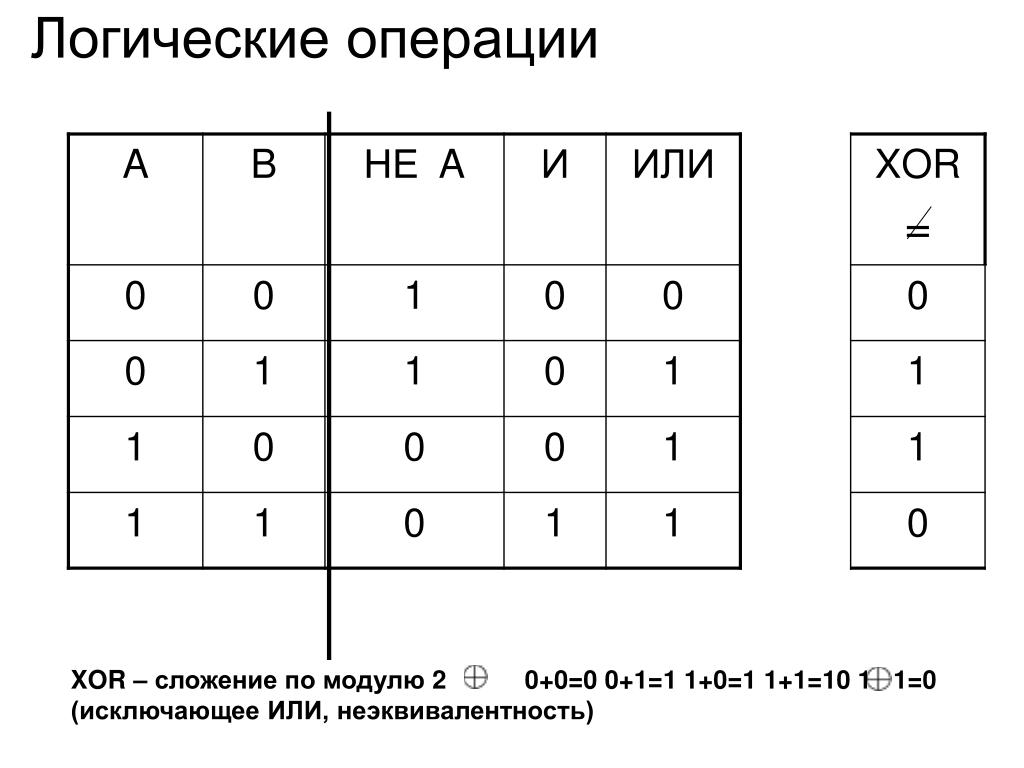
Следующая таблица истинности содержит все правила, необходимые для оценки логические выражения.

А	Б	А И В	А ИЛИ В	НЕ
Т	Т	Т	Т	Ф
Ф	Т	Ф	Т	Т
Т	Ф	Ф	Т	Ф
Ф	Ф	Ф	Ф	Т

Столбцы И и ИЛИ таблицы истинности можно резюмировать следующим образом:

• «А . И.В» истинно, только если истинны и А, и В.
• «A .AND.B» ложно, если либо A, либо B ложно.
• «A .OR. B» истинно, если верно либо A, либо B.
• «A .OR. B» ложно, только если ложны и A, и B.

Символы логических операторов

Логические или логические операторы используются в логических (булевых) выражениях. (Пример: (А .И. Б .ИЛИ. В) ).

Символ	Значение
НЕТ	Логическое НЕ
А ТАКЖЕ	Логическое И
ИЛИ ЖЕ	Логическое ИЛИ

Как и в математических выражениях, существует определенный порядок приоритет для вычисления логических выражений, которые имеют более двух операторы.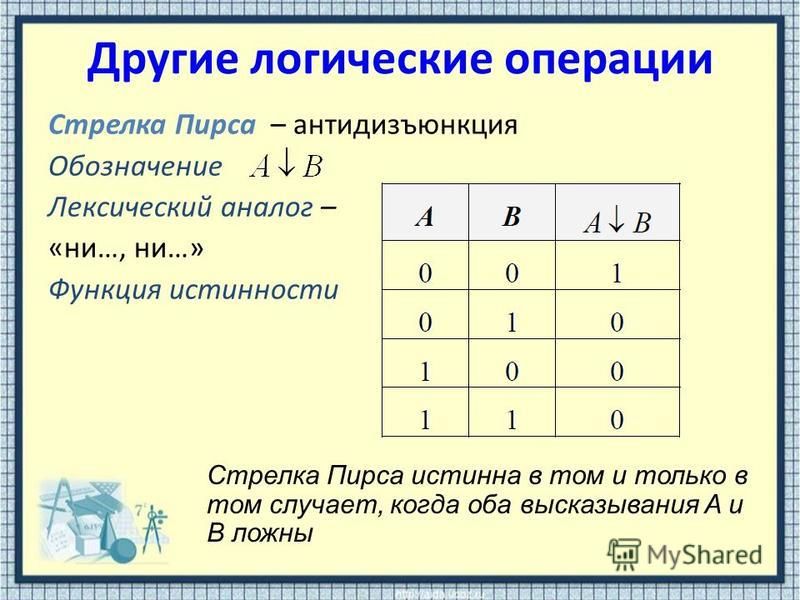 Выражения внутри круглых скобок оцениваются первыми, а логические операторы оцениваются в следующем порядке:

1. .НЕ.
2. .И.
3. .ИЛИ.

Пример: скобки в следующем примере означают два утверждения логически разные:

• А .И. Б .ИЛИ. С
• А .И. (Б.ИЛИ.С)

Символы математических операторов

Символы математических операторов указывают, какие операции необходимо выполнить при вычислении арифметического выражения, такого как X/Y*(A+B*A).

Символы

Символ	9	Возведение в степень
*	Умножение
/	Разделение
+	Добавление
—	вычитание

Порядок старшинства

При вычислении математического или логического выражения выражения, содержащие в круглых скобках всегда оцениваются первыми. Приказ приоритет для остальных математических операторов слева направо в следующий порядок:

1. E возведение в степень
2. M умножение и D ivision
3. Дополнение A и удаление S

Следующая фраза полезна для запоминания порядка старшинства для математических операторов. Только не забудьте понять, что умножение не предшествует делению (они равны и выполняются слева направо правильно, если нет круглых скобок) и сложение не приходит перед вычитанием (они равны и выполняются слева направо, если нет стоят скобки).

P аренда E извините M y D ухо A unt S союзник.

Символы операций со строками

Символы операций со строками показывают, как две или более строк символов объединяются, операция, известная как конкатенация.

Символ	Операция
+	Объединить две строки символов
—	Объединить две строки символов (конечные пробелы 1-й строки добавляются к концу результирующей строки)

Пример (_ обозначает пробелы)

• «Здравствуйте____»+»Здесь. «=»Здравствуйте____Здесь.»
• «Здравствуйте____»-«Туда.»=»ЗдравствуйтеТам.____»

Символы операторов сравнения

Операторы сравнения используются для сравнения математических, символы или выражения даты. Они приводят к логическим значениям True или False, как используется с булевой логикой.

Символ	Значение
	Меньше, чем
>	Лучше чем
знак равно	Равно
<> или #	Не равно
	Меньше или равно
>=	Больше или равно
$	Сравнение подстрок Пример, если A и B представляют собой строки из символов, A$B возвращает логическое значение True, если A либо идентично B , либо содержится внутри B.

Таблица операторов — служба поддержки Microsoft

Access для Microsoft 365 Access 2021 Access 2019Access 2016 Access 2013 Access 2010 Access 2007 Больше…Меньше

Оператор — это знак или символ, указывающий тип вычисления, выполняемого в выражении. Существуют математические, сравнительные, логические и ссылочные операторы. Access поддерживает различные операторы, включая арифметические операторы, такие как + ,

— , умножение ( * ) и деление (/), а также операторы сравнения для сравнения значений, текстовые операторы для объединения текста, и логические операторы для определения истинных или ложных значений. В этой статье приведены подробные сведения об использовании этих операторов.

Примечание. Начиная с Access 2010, в построителе выражений есть IntelliSense, поэтому вы можете видеть, какие аргументы требуются вашему выражению.

В этой статье

• Арифметические операторы

• Операторы сравнения

• Логические операторы

• Операторы конкатенации

• Специальные операторы

Арифметические операторы

Вы используете арифметические операторы для вычисления значения из двух или более чисел или для изменения знака числа с положительного на отрицательное или наоборот. Оператор Назначение Пример + Сложите два числа. [Промежуточный итог]+[Налог с продаж] — Найти разницу между двумя числами или указать отрицательное значение числа. [Цена]-[Скидка] * Умножить два числа. [Количество]*[Цена] / Разделите первое число на второе число. [Всего]/[Количество предметов] \ Округлите оба числа до целых чисел, разделите первое число на второе число, а затем усеките результат до целого числа. [Зарегистрировано]\[Комнаты] Мод Разделите первое число на второе и верните только остаток. [Зарегистрировано] Мод [Комнаты] 9Показатель

Верх страницы

Операторы сравнения

Вы используете операторы сравнения для сравнения значений и возврата результата True, False или Null.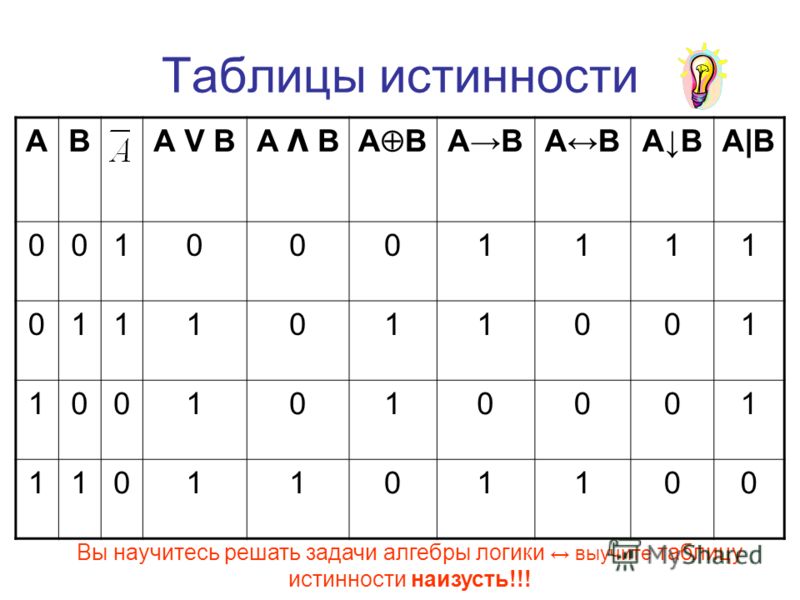

Оператор	Назначение	Пример
<	Возвращает True, если первое значение меньше второго.	Значение1 < Значение2
<=	Возвращает True, если первое значение меньше или равно второму значению.	Значение1 <= Значение2
>	Возвращает True, если первое значение больше второго.	Значение1 > Значение2
>=	Возвращает True, если первое значение больше или равно второму значению.	Значение1 >= Значение2
=	Возвращает True, если первое значение равно второму значению.	Значение1 = Значение2
<>	Возвращает True, если первое значение не равно второму значению.	Значение1 <> Значение2

Примечание.  Во всех случаях, если первое или второе значение равно NULL, результат также будет NULL. Поскольку null представляет собой неизвестное значение, результат любого сравнения с нулевым значением также неизвестен.

Верх страницы

Логические операторы

Вы используете логические операторы для объединения двух логических значений и возврата истинного, ложного или нулевого результата. Логические операторы также называются булевыми операторами. Оператор Назначение Пример и Возвращает True, если Expr1 и Expr2 верны. Выражение1 и Выражение2 или Возвращает True, если Expr1 или Expr2 имеет значение true. Выражение1 или Выражение2 Экв. Возвращает True, если оба Expr1 и Expr2 верны или когда оба Expr1 и Expr2 ложны. Expr1 Eqv Expr2 Не Возвращает True, если Expr не равно true. Не выражение Хор Возвращает True, если Expr1 имеет значение true или Expr2 имеет значение true, но не оба одновременно. Expr1 Xor Expr2

Верх страницы

Операторы конкатенации

Вы используете операторы конкатенации для объединения двух текстовых значений в одно. Оператор Назначение Пример и Объединяет две строки в одну строку. строка1 и строка2 + Объединяет две строки в одну строку и распространяет нулевые значения (если одно значение равно Null, все выражение оценивается как Null). строка1 + строка2

Верх страницы

Специальные операторы

Вы используете специальные операторы для возврата результата True или False, как описано в следующей таблице. Оператор Назначение Пример равно нулю или не равно нулю Определяет, является ли значение Null или Not Null. Поле 1 не равно нулю Нравится «узор» Соответствует строковым значениям с помощью операторов подстановки ? и *. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника