Логическая операция — Википедия
Материал из Википедии — свободной энциклопедии
В логике логи́ческими опера́циями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.
Логические операции с понятиями — такие мыслительные действия, результатом которых является изменение содержания или объёма понятий, а также образование новых понятий.
К операциям, которые связаны преимущественно с изменением содержания понятий, относятся:
К операциям, которые связаны преимущественно с объёмами понятий, относятся:
Данные операции могут быть записаны математически с помощью теории множеств.
Переход же к математической логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.
Логическая операция (логический оператор, логическая связка, пропозициональная связка
В качестве основных обычно называют конъюнкцию (∧{\displaystyle \land } или &), дизъюнкцию (∨{\displaystyle \lor }), импликацию (→{\displaystyle \to }), отрицание (¬{\displaystyle \neg }). В смысле классической логики логические связки могут быть определены через алгебру логики. В асинхронной секвенциальной логике определена логико-динамическая связка в виде операции венъюнкции (∠{\displaystyle \angle }).
Логическая операция — в программировании операция над выражениями логического (булевского) типа, соответствующая некоторой операции над высказываниями в алгебре логики. Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.
В некоторых языках программирования (например, в языке Си) вместо логического типа или одновременно с ним используются числовые типы. В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.
Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций. Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений.
Среди логических операций наиболее известны конъюнкция (&&), дизъюнкция (||), отрицание (!). Их нередко путают с битовыми операциями, хотя это разные вещи. Например, следующий код на языке Си:
if (action_required && some_condition())
{
/* какие-то действия */
}
не выполнит вызов подпрограммы some_condition(), если значение логической переменной action_required ложно. При такой операции второй аргумент операции «&&» вообще не будет вычислен.
В языках программирования[править | править код]
В следующей таблице для некоторых языков программирования приведены встроенные операторы и функции, реализующие логические операции.
| Формальная | |
|---|---|
| Математическая (теоретическая, символическая) |
|
| См. также | |
Логические операции и таблицы истинности
Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера. Это три логические операции: И, ИЛИ, НЕ, которые называют «тремя китами машинной логики».
В компьютере логические функции реализуют логические элементы. Логический элемент (вентиль) – это часть электронной логической схемы, которая реализует элементарную логическую функцию, т.е. это электронная схема, которая формирует выходной сигнал в соответствии с простой булевой операцией преобразования сигналов, поданных на его входы.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие, а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Самой простой логической операцией является операция НЕ, по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают NOT ( ).
Если А – истинно, то Ā – ложно и наоборот
Таблица истинности:Результат отрицания всегда противоположен значению аргумента. Логическая операция НЕ является унарной, т.е. действие выполняются над одним операндом. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.
Например, A – идет дождь; Ā – не идет дождь (не(А) или not(A))
Логическое И еще часто называют конъюнкцией, или логическим умножением, Операция И (обозначается «И», «and», «&», А•В) имеет результат «истина» только в том случае, если оба ее операнда истинны.
Таблица истинности:
A | B | F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Если F = A&B, то F истинно тогда и только тогда,
когда истинны и А и В
Например, A – пасмурно; B – идет дождь.
Можно записать: A&B (читается пасмурно и идет дождь)
Операция ИЛИ – дизъюнкция, или логическое сложение.
(обозначается «ИЛИ», «or», А+В) «менее привередлива» к исходным данным. Она дает «истину», если значение «истина» имеет хотя бы один из операндов. Разумеется, в случае, когда справедливы оба аргумента одновременно, результат по-прежнему истинный.
A | B | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Если F = A+B, то F ложно тогда и только тогда, когда ложны и А и В.
Например, A – пасмурно; B – идет дождь.
Можно записать: A+B (читается пасмурно или идет дождь)
Операции И, ИЛИ, НЕобразуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение. В вычислительной технике также часто используется операции импликация и эквивалентность.
Логическое следование: импликация– связывает два простых логических выражения, из которых первое является условием (А), а второе (В) – следствием из этого условия. Результатом импликации является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом «следовательно» и выражается словами ЕСЛИ … , ТО …
Таблица истинности:
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 1 |
0 | 0 | 1 |
Таблица истинности:
A | B | F |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
2.2. Высказывания. Логические операции и их основные свойства
Определение 1. Суждением называется форма мышления, в которой что-либо утверждается или отрицается о существовании предмета, связях между предметом и его свойствами или об отношениях между предметами.
Определение 2. Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.
Будем обозначать высказывания латинскими буквами:
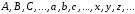
Логическое значение высказывания «истина» обозначается цифрой «1», «ложь» – «0».
Предложения: «Который час?», «ответьте на вопрос», «добро пожаловать!» – не являются высказываниями.
Предложение «Была метель» также не является высказыванием, поскольку нет достаточной информации, чтобы установить истинно оно или ложно (где и когда?).
Определение 3. Формализацией высказываний называют операцию замены высказывания естественного языка формулой математического языка, включающего высказывательные переменные и символы тех логических операций, которые соответствуют структуре самого высказывания.
Определение 4. Если суждение об истинности высказывания можно вынести из самого высказывания, то такое высказывание называют простым. В противном случае мы имеем сложное (составное) высказывание.
Значение истинности составного высказывания определяется значениями истинности его компонент.
Из простых высказываний можно образовать новые составные высказывания с помощью союзов «и», «или», «либо», «если…, то», «тогда и только тогда, когда», «неверно, что». Эти союзы называются логическими связками. Построение из данных высказываний нового составного высказывания называется логической операцией над высказываниями.
Основные логические операции: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность (табл. 1).
Таблица 1
Логические операции
Название | Прочтение | Обозначение |
Отрицание | Не; неверно, что |
|
Конъюнкция | И; а |
|
Дизъюнкция | Или |
|
Импликация | Если … то |
|
Эквивалентность | Тогда и только тогда, когда |
|
Логическое значение сложного высказывания можно описать с помощью таблицы, называемой таблицей истинности (верхняя строка содержит обозначения высказываний, последующие строки – логическое значение высказываний).
Пусть
даны два произвольных высказывания 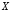 и
и .
.
Определение
5. Отрицанием высказывания 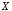 называется высказывание
называется высказывание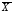 («не
(«не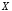 »,
«неверно, что
»,
«неверно, что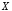 »),
которое истинно, когда
»),
которое истинно, когда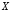 ложно, и ложно, когда
ложно, и ложно, когда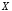 истинно.
истинно.
Таблица истинности для отрицания:
|
|
0 | 1 |
1 | 0 |
Определение
6. Конъюнкцией (логическим умножением) двух высказываний 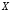 ,
,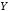 называется высказывание
называется высказывание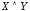 («
(«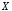 и
и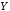 »),
которое истинно только в том случае,
когда
»),
которое истинно только в том случае,
когда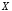 и
и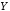 оба истинны.
оба истинны.
Таблица истинности для конъюнкций:
Определение
7. Дизъюнкцией (логическим сложением) двух высказываний 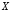 ,
,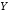 называется высказывание
называется высказывание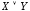 («
(«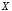 или
или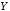 »),
которое истинно, когда хотя бы одно из
них истинно.
»),
которое истинно, когда хотя бы одно из
них истинно.
Таблица истинности для дизъюнкций:
Определение
8. Импликацией двух высказываний 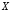 ,
, называется
высказывание
называется
высказывание 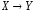 («если
(«если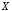 ,
то
,
то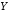 »,
«
»,
«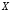 влечёт
влечёт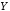 »,
«из
»,
«из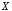 следует
следует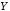 »,
«
»,
«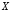 имплицирует
имплицирует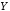 »),
которое ложно тогда и только тогда,
когда
»),
которое ложно тогда и только тогда,
когда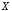 истинно, а
истинно, а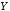 ложно.
ложно.
Таблица истинности для импликаций:
Определение
9. Эквивалентностью высказываний  ,
,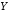 называется высказывание
называется высказывание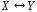 («
(«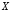 эквивалентно
эквивалентно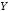 »,
«
»,
«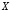 тогда и только тогда, когда
тогда и только тогда, когда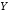 »,
«для того, чтобы
»,
«для того, чтобы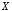 ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы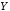 »),
которое истинно тогда и только тогда,
когда
»),
которое истинно тогда и только тогда,
когда и
и  оба истинны или ложны.
оба истинны или ложны.
Таблица истинности для эквивалентности:
Для образования составных высказываний наряду с единичным использованием каждой основной связки можно пользоваться основными связками многократно, получая более сложные составные высказывания, – аналогично тому, как с помощью основных арифметических операций образуются сложные алгебраические выражения.
Например,
составными будут высказывания:  ;
;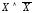 ;
;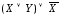 .
.
Замечание
1. Скобки указывают порядок выполнения
действий. Если скобок нет, то операции
надо выполнять в следующем порядке:
конъюнкция, дизъюнкция, импликация,
эквивалентность. Если отрицание относится
ко всему высказыванию, например, 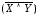 ,
то оно выполняется последним. Если
отрицание относится только к одному
высказыванию, например,
,
то оно выполняется последним. Если
отрицание относится только к одному
высказыванию, например, ,
тогда оно выполняется первым.
,
тогда оно выполняется первым.
Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.
Определение
10. Формулой
алгебры логики высказываний называется всякое простое высказывание,
обозначаемое буквой, а также всякое
составное высказывание, которое
получается комбинированием простых
высказываний с помощью конечного числа
указанных выше основных операций
( ;
; ;
;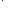 ;
;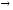 ;
; ).
Для любых формул можно построитьтаблицу
истинности.
).
Для любых формул можно построитьтаблицу
истинности.
Определение
11. Таблицей
истинности формулы называется сводная таблица всех значений
входящих в нее высказываний и
соответствующих значений самой формулы.
Если формула содержит  элементарных высказываний, то таблица
содержит
элементарных высказываний, то таблица
содержит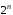 строк.
строк.
Пример
1. Составьте таблицу истинности  .
.
Решение
Составим таблицу истинности, последовательно выполняя логические операции, входящие в формулу:
|
|
|
|
|
|
|
0 | 0 | 0 | 1 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 1 | 1 |
Пример
2. Пусть 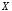 ,
,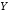 и
и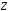 обозначают соответственно высказывания:
«Тимофей любит шахматы», «Тимофей любит
футбол», «Тимофей любит баскетбол».
Требуется записать высказывание:
«Тимофей любит шахматы и неверно, что
он любит футбол или баскетбол» в
символической форме и указать
соответствующую таблицу истинности.
обозначают соответственно высказывания:
«Тимофей любит шахматы», «Тимофей любит
футбол», «Тимофей любит баскетбол».
Требуется записать высказывание:
«Тимофей любит шахматы и неверно, что
он любит футбол или баскетбол» в
символической форме и указать
соответствующую таблицу истинности.
Решение
Высказывание
«Тимофей любит футбол или баскетбол»
в символической форме записывается
как 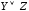 .
Высказывание «Неверно, что Тимофей
любит футбол или баскетбол» символически
записывается как
.
Высказывание «Неверно, что Тимофей
любит футбол или баскетбол» символически
записывается как ,
поскольку отрицание применяется ко
всему высказыванию.
,
поскольку отрицание применяется ко
всему высказыванию.
Итак,
исходное высказывание символически
изображается 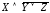 .
.
Таблица истинности этого высказывания:
|
|
|
|
|
|
1 1 1 1 0 0 0 0 | 1 1 0 0 1 1 0 0 | 1 0 1 0 1 0 1 0 | 1 1 1 0 1 1 1 0 | 0 0 0 1 0 0 0 1 | 0 0 0 1 0 0 0 0 |
Пример 3. Запишите высказывание «Если число 72 делится на 6, а число 6 делится на 2, то число 72 делится на 2» в символической форме.
Решение
Выделим
простые высказывания «число 72 делится
на 6», «число 6 делится на 2», «число 72
делится на 2» и заменим их логическими
переменными 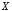 ,
,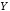 и
и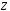 соответственно.
соответственно.
Тогда
исходное высказывание символически
изображается 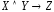 .
.
Особый интерес представляют сложные высказывания, имеющие различное строение, но принимающие одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний. Такие высказывания называются логически эквивалентными (равносильными). Эквивалентность двух высказываний легко установить посредством сравнения их таблиц истинности.
Определение
12. Две
формулы алгебры логики 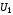 и
и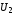 называютсяравносильными,
если они принимают одинаковые логические
значения
(0 или 1) при одинаковых наборах
значений входящих в них высказываний
(пишут
называютсяравносильными,
если они принимают одинаковые логические
значения
(0 или 1) при одинаковых наборах
значений входящих в них высказываний
(пишут 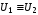 ).
).
Например, 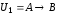 ,
,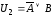 – равносильные формулы:
– равносильные формулы:
 ,
так как
,
так как 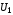 и
и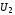 либо
одновременно ложны, либо одновременно
истинны при любом наборе значений
высказываний, входящих в эти формулы,
что и показано в таблице истинности:
либо
одновременно ложны, либо одновременно
истинны при любом наборе значений
высказываний, входящих в эти формулы,
что и показано в таблице истинности:
|
|
|
|
|
0 0 1 1 | 0 1 0 1 | 1 1 0 1 | 1 1 0 0 | 1 1 0 1 |
Определение 13. Формула называется тавтологией или тождественно истинной, если она принимает значение «истина» при всех значениях входящих в неё переменных.
Формулы 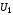 и
и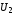 равносильны тогда и только тогда, когда
их эквивалентность
равносильны тогда и только тогда, когда
их эквивалентность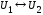 тождественно истинна. Запись
тождественно истинна. Запись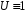 означает, что формула
означает, что формула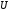 является тождественно истинной.
является тождественно истинной.
Теорема. 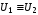 тогда и только тогда, когда
тогда и только тогда, когда .
.
Каждое
высказывание вида  – тавтология.
– тавтология.
Определение
14. Логическая
формула 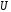 называетсятождественно
ложной,
или противоречием (записывается
называетсятождественно
ложной,
или противоречием (записывается 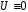 ),
если для всех наборов значений входящих
в нее переменных (высказываний) она
принимает значение 0 («ложь»), т. е. если
высказывание ложно в каждом случае.
),
если для всех наборов значений входящих
в нее переменных (высказываний) она
принимает значение 0 («ложь»), т. е. если
высказывание ложно в каждом случае.
Таблица истинности для противоречия содержит только значения 0 в итоговом столбце.
Заметим,
что отрицание любой тавтологии есть
противоречие: 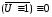 .
.
Определение 15. Формулы, не являющиеся ни тавтологией, ни противоречием, называются выполнимыми (разрешимыми). Таблица истинности таких формул содержит как 1, так и 0.
Равносильность формул можно доказывать либо с помощью таблиц истинности, либо методом равносильных (эквивалентных) преобразований, используя основные равносильности алгебры логики высказываний. Основные равносильности называют законами логики, они также применяются для упрощения формул, для приведения формул к заданному виду.
Основные равносильности алгебры высказываний:
 –ассоциативность
операций
–ассоциативность
операций  и
и ;
;  –коммутативность
операций
–коммутативность
операций  и
и ;
; –закон
идемпотентности;
–закон
идемпотентности; –законы
дистрибутивности;
–законы
дистрибутивности; –законы
поглощения;
–законы
поглощения; –законы
склеивания;
–законы
склеивания; –законы
Порецкого;
–законы
Порецкого; –законы
де
Моргана;
–законы
де
Моргана; ;
;;
 ;
;
 –закон
двойного отрицания;
–закон
двойного отрицания; –закон
исключения третьего;
–закон
исключения третьего; –закон
противоречия;
–закон
противоречия; –закон
контрапозиции.
–закон
контрапозиции.
Пример 4. Докажите равносильность с помощью формул алгебры высказываний:
а) 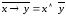 ;
;
б) .
Решение:
a)
используя формулу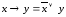 ,
запишем:
,
запишем: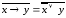 ,
тогда по закону де Моргана
,
тогда по закону де Моргана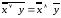 и по закону двойного отрицания
и по закону двойного отрицания 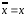 получим
получим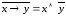 ,
что и требовалось доказать;
,
что и требовалось доказать;
б) преобразуем левую и правую части к одному и тому же виду. Согласно законам де Моргана и двойного отрицания получим следующие выражения.
Левая
часть: 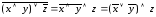 .
.
Правая
часть: 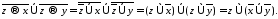
После равносильных преобразований получили одинаковые формулы. Равносильность доказана.
Вопросы и задачи для самостоятельного решения
1. Определите, какие из следующих предложений являются высказываниями:
а) «ученики школы»;
б) «7 + 5 = 12»;
в) «сегодня плохая погода»;
г)
«если 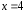 ,
то
,
то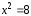 »;
»;
д) «у каждого человека есть домашнее животное»;
е)
«для всех действительных чисел 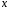 и
и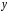 верно равенство
верно равенство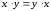 »;
»;
ж)
«треугольник 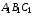 равен треугольнику
равен треугольнику »;
»;
и) «берегись автомобиля!».
2. Составьте таблицы истинности для логических формул:
а) 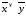 ;
г)
;
г)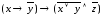 ;
;
б) 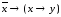 ;
д)
;
д)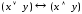 .
.
в) 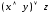 .
.
3. Запишите следующие высказывания в символической форме и укажите соответствующую таблицу истинности:
а) «неверно, что ни Евгений, ни Николай не умеют играть на гитаре»;
б) «если числовая последовательность монотонна и ограничена, то она имеет предел»;
в) «неверно, что если белый кубик больше зеленого, а зеленый – больше синего, то синий кубик больше белого».
4. Проверьте с помощью таблицы истинности, будут ли эквивалентны следующие логические формулы:
а) 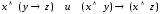 ;
;
б) 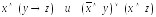 ;
;
в) 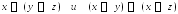 .
.
5. Используя
основные законы логических операций,
докажите равносильность формул 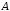 и
и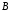 ,
когда:
,
когда:
Дополнительные
логические операции. Кроме
указанных ранее логических операций
(отрицание, конъюнкция, дизъюнкция,
импликация, эквивалентность), существуют
и другие. Например, операция, через
которую могут быть выражены все ранее
указанные логические операции – штрих
Шеффера.
Эта операция обозначается символом 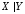 .
.
Таблица истинности штриха Шеффера:
Очевидно,
что 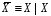 ,
, .
Из этих двух равносильностей следует,
что всякая формула алгебры логики может
быть заменена равносильной формулой,
содержащей только штрих Шеффера. Операцию
«штрих Шеффера» обычно определяют
следующим образом.
.
Из этих двух равносильностей следует,
что всякая формула алгебры логики может
быть заменена равносильной формулой,
содержащей только штрих Шеффера. Операцию
«штрих Шеффера» обычно определяют
следующим образом.
Штрих
Шеффера 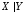 ,
или антиконъюнкция,
по определению
,
или антиконъюнкция,
по определению 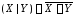 (читается «
(читается «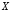 несовместимо с
несовместимо с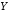 »).
»).
В дополнение к ранее указанным пяти основным операциям перечислим новые логические операции (табл. 2).
Таблица 2
Свойства логических операций — урок. Информатика, 8 класс.
Рассмотрим основные свойства логических операций, называемых также законами алгебры логики.
Переместительный (коммутативный) закон:
- для логического умножения: A&B=B&A;
- для логического сложения: A∨B=B∨A.
Сочетательный (ассоциативный) закон:
- для логического умножения: A&B&C=A&B&C;
- для логического сложения: A∨B∨C=A∨B∨C.
Обрати внимание!
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон:
- для логического умножения: A&B∨C=A&B∨A&C;
- для логического сложения: A∨B&C=A∨B&A∨C.
Закон двойного отрицания:
A¯¯=A.
Обрати внимание!
Двойное отрицание исключает отрицание.
Закон исключённого третьего:
- для логического умножения: A&A¯=0;
- для логического сложения: A∨A¯=1.
Обрати внимание!
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Закон повторения:
- для логического умножения: A&A=A;
- для логического сложения: A∨A=A.
Законы операций с \(0\) и \(1\):
- для логического умножения: A&0=0; A&1=A;
- для логического сложения: A∨0=A; A∨1=1.
Законы общей инверсии:
- для логического умножения: A&B¯=A¯∨B¯;
- для логического сложения: A∨B¯=A¯&B¯.
Законы алгебры логики могут быть доказаны с помощью таблиц истинности. Докажем распределительный закон для логического сложения:
A∨B&C=A∨B&A∨C.
\(A\) | \(B\) | \(C\) | B&C | A∨B&C | A∨B | A∨C | A∨B&A∨C |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Источники:
Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний, 30 с.


 (
(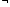 )
) (
(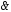 )
)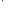
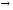
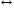 (~)
(~)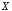
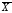
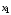
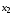
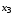
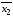
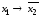

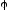
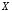
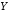
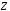
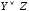

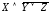
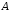

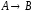
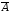
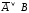
 –ассоциативность
операций
–ассоциативность
операций 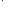 и
и ;
; 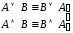 –коммутативность
операций
–коммутативность
операций 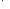 и
и ;
;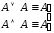 –закон
идемпотентности;
–закон
идемпотентности;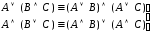 –законы
дистрибутивности;
–законы
дистрибутивности;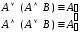 –законы
поглощения;
–законы
поглощения;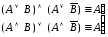 –законы
склеивания;
–законы
склеивания;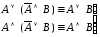 –законы
Порецкого;
–законы
Порецкого;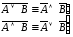 –законы
де
Моргана;
–законы
де
Моргана; ;
; ;
;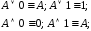
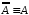 –закон
двойного отрицания;
–закон
двойного отрицания;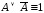 –закон
исключения третьего;
–закон
исключения третьего;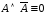 –закон
противоречия;
–закон
противоречия; –закон
контрапозиции.
–закон
контрапозиции.