3 Логические операторы — Всё для чайников

Подробности

Категория: Простое и понятное программирование в «CODESYS».

Документальные учебные фильмы. Серия «Программирование на CODESYS».

 

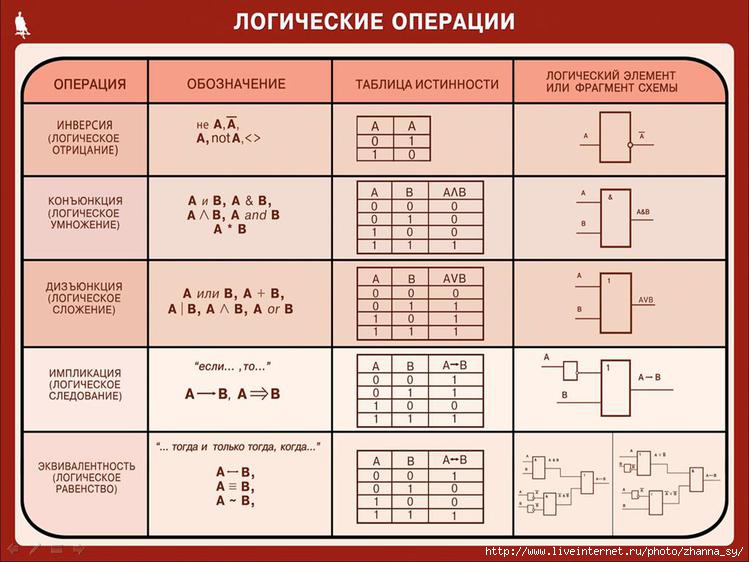
Речь пойдет о логических операциях, то есть об операциях «И», «ИЛИ», «НЕ».

Они составляют основу любых дискретных алгоритмов. На использовании этих логических операций построена работа многих шкафов автоматики и релейных схем. Такие решения до сих пор массово используются на значительном числе производств. Это один из советов читателям, куда нужно применить информацию, полученную на этих страницах. Представьте, огромный шкаф релейной автоматики Вы можете заменить одним или несколькими маленькими ПЛК. При этом перестанете постоянно следить за состоянием вечно ломающихся реле.

 

 Напомним, с чего мы начинаем всякий раз работу с CoDeSys. Когда Вы загрузили систему программирования, Вы создаете новый проект через меню «Файл».

Там необходимо выбирать пункт «Создать». В появившемся окне «Настройки целевой платформы» мы выбираем тот тип ПЛК, с которым будем работать. В данном случае я выбираю ПЛК150-И-М, это не так важно, нам подойдет любой из них. Мы продолжаем работать с языком функциональных блоков CFC. Именно этот язык выбираем при создании главной программы PLC_ PRG .

После этого переходим на вкладку ресурсы, выбираем пункт «Конфигурация ПЛК». Ранее я уже упоминал, что работа ПЛК происходит циклически. В программе мы описываем действия для одного цикла, одного повторения. А дальше, после загрузки проекта в ПЛК, котроллер постоянно повторяет подготовленный нами алгоритм. Именно в этом разница между программированием приложений для персонального компьютера, и работой с задачами АСУ ТП. Итак, нам необходимо задать контроллеру время цикла его работы (время цикла ПЛК). То есть определить, с какой частотой необходимо повторять обработку программы. Для этого в окне «Конфигурации ПЛК» выделяем верхний пункт «PLC 150 I».

У Вас, в зависимости от вашей модели ПЛК, могут быть другие обозначения. Затем переходим на вкладку «Параметры модуля», расположенную в правой верхней части экрана.

По умолчанию, время цикла ПЛК1хх составляет 1 мс. То есть каждую миллисекунду ПЛК заново запускает обработку нашего алгоритма. И должен успеть ее завершить. Для тех простых программ, которыми мы занимаемся в рамках обучения, такая скорость обработки вполне допустима. С другой стороны, в более серьезных задачах полезно задать некоторый запас производительности ПЛК. То есть указать время цикла, скажем, 10 мс. Для 80% задач, решаемых ПЛК1хх, этого будет достаточно. Возьмите себе за правило сразу же после создания проекта задавать время цикла 10 мс. Для этого в первой строчке, в поле «Значение» вместо 1 мс поставьте 10 мс. Это время цикла, за которое контроллер будет обрабатывать нашу программу.

Для того чтобы разобраться с работой дискретной логики, нам понадобится несколько входов и выходов ПЛК.

Для этого Вы раскрываете элементы конфигурации ПЛК и задаете шесть дискретных входов. Пусть это будут переменные x1, х2, хЗ и т.д.

Напомню, для того, чтобы определить имя переменной для того или иного входа или выхода, Вы два раза щелкаете ЛКМ на надписи «АТ» в нужной строчке. Затем вводите имя переменной (английскими буквами и цифрами без пробелов), нажимаете «Enter» на вашей клавиатуре. Таким образом, у нас получилось 6 дискретных входов. По аналогии задаем четыре дискретных выхода. Пусть это будут переменные у1, у2, уЗ

и у4.

•    Вы определились с target-файлом,

•    создали главную программу и выбрали язык программирования,

•    задали время работы цикла ПЛК,

•    определились с необходимыми входами и выходами,

•    сохранили проект на вашем компьютере.

Вернемся к нашей главной программе. Напомню, она находится на вкладке «POU». Переходим нее и два раза щелкаем ЛКМ на программу «PLC PRG»

Для того чтобы задать в вашем алгоритме ту или иную логическую операцию, поступаем следующим образом. В верхней части экрана, на панели быстрого доступа есть кнопка «Элемент» ().

. Нажимаем на нее, переносим курсор на рабочую область и нажимаем левой кнопкой мыши еще раз, устанавливая элемент в нужном месте рабочей области. По умолчанию блок, который мы добавили, будет выполнять операцию логического «И». Она задается ключевым словом «AND».

Аналогичный блок можно вызвать через контекстное меню, нажав в рабочей области ПКМ и выбрав пункт «Элемент».

На вход операции «AND» подаются переменные типа «BOOL». Как раз такими переменными являются наши дискретные входы. В нашей программе мы вызываем значение переменной,

используя кнопку «Вход»  . Можно это сделать через кнопку «F2» на вашей клавиатуре. В появившемся окне выбираем список глобальных переменных, и в нем находим нужные нам переменные

х1 и х2 (рис.3.7).

Затем проводим линии связи.

На выходе операции логического «И» (блок AND) будет появляться сигнал TRUE или FALSE («ИСТИНА» или «ЛОЖЬ»), То есть значение типа BOOL. Это значение мы можем присвоить  переменной того же типа, например, выходу y1. Для этого добавляем выход () на рабочую область.

Вместо знаков вопроса прописываем имя переменной y1. Затем проводим линию связи между выходом операции AND и переменной

y1.

 Во время первых опытов работы с CoDeSys у Вас могут возникать некоторые сложности с изменением положения тех или иных элементов программы в рабочей области. Давайте разберем подробнее этот момент. Если Вам необходимо передвинуть один или несколько элементов программы в другое место, Вы выделяете нужную часть алгоритма, удерживая ЛКМ .

Постарайтесь сделать так, чтобы все элементы целиком попали в выделенную область. В результате, после отпускания ЛКМ один или несколько элементов окажутся выделенными пунктиром .

Давайте посмотрим, какие еще логические операции можно добавить в наш проект. Если Вам необходимо поработать с операцией «ИЛИ» вместо «И», то сделать это можно следующим образом.

Вы добавляете новый элемент, выделяете заголовок ЛКМ и печатаете новое название «OR», затем нажимаете «Enter» .

Получили блок «ИЛИ». Принцип работы с ним абсолютно тот же самый. Мы вызываем в алгоритме значения дискретных входов ПЛК, на этот раз хЗ и х4. Затем подводим линии связи к нашему блоку OR. Результат работы этого блока мы будем передавать на второй дискретный выход контроллера, т.е. в переменную у2. На рисунке изображено то,

что должно было у Вас получиться.

Теперь поработаем с операцией «логическое НЕ» — блок NOT. Она, по сути, является той же самой инверсией . Сейчас мы разберем просто другой способ, как ее можно задать. Нажимаете кнопку «Элемент» или через ПКМ вызываете контекстное меню и выбираете пункт «Элемент». Таким образом создается новый блок и вместо надписи AND в нем задаете ключевое слово NOT. На выход операции NOT подключаете переменную уЗ.

Важный момент! С выхода одного и того же блока или из одной и той же переменной линию связи Вы можете вести на один или несколько возможных приемников этого самого сигнала. Поясню: из операции OR мы можем протянуть вторую линию связи на вход операции NOT. Для этого нажимаем ЛКМ на выход блока OR, т.е. на самый конец выходящей из него линии связи .

 

Удерживая ЛКМ, перетаскиваем вторую линию связи на вход блока NOT

, затем отпускаем ЛКМ. Полученный результат изображен на рисунке.

Таким же образом можно добавить и третью, и четвертую, и еще большее количество связей. Тут главное — не переусердствовать, во всем необходима мера.

Тем же способом вы можете значение одной и той же переменной передавать на несколько блоков.

 

 

 

Для того чтобы удалить ненужную линию связи, Вы выделяете один из ее концов . Затем нажимаете на клавиатуре кнопку Del (Delete).

 Вернемся к нашему алгоритму. Теперь, когда на выходе операции OR будет значение FALSE, у нас с Вами на выходе уЗ будет появляться сигнал TRUE, в то время как в переменной у2 он будет пропадать. И наоборот, когда на выходе OR появляется сигнал TRUE, он записывается в у2. В блоке NOT этот сигнал будет преобразовываться в FALSE и поступать в переменную

уЗ. А в результате релейные выходы нашего ПЛК все время будут в разных состояниях.

Последний логический оператор в рамках этой главы — это «Исключающее ИЛИ». Он довольно часто используемый, например, для реализации проходных выключателей. «Исключающее ИЛИ» задается с помощью ключевого слова XOR.

На вход этой операции будем подавать значения переменных типа BOOL, например, переменные х5 и хб. Для того чтобы использовать повторно какие-то готовые части уже написанного алгоритма, мы можем воспользоваться стандартными операциями «Копировать» и «Вставить».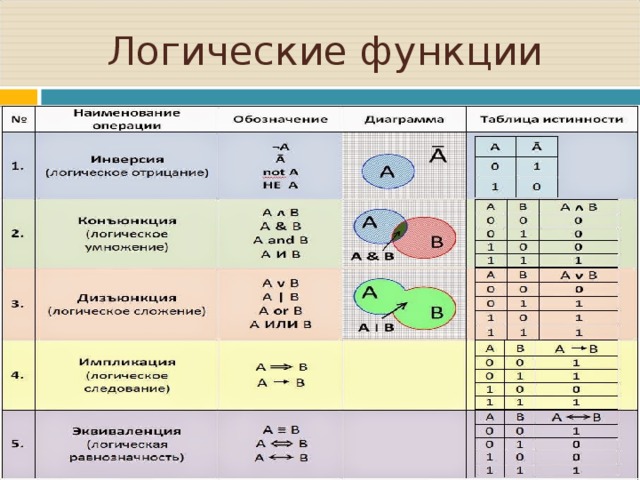 При добавлении блока XOR используем их. Для начала, выделим цепь с оператором OR.

Затем сверху, на панели быстрого доступа нажимаем кнопку «Копировать» . Можно также использовать хорошо знакомое многим сочетание клавиш Ctrl+C.

Затем мы вставляем сделанную копию, для этого нажимаем кнопку «Вставить» . 

На экране появляется копия выбранной части алгоритма. Нажав и удерживая ЛКМ на выделенных частях появившейся копии, мы перетаскиваем ее на новое место в рабочей области.

Теперь нам необходимо поменять в заголовке элемента оператор OR на оператор XOR. В качестве входных данных мы будем использовать переменные х5 и хб. Для замены имени переменной Вы просто нажимаете на соответствующий блок входа ЛКМ. Затем с клавиатуры вводите новое имя. Результат работы блока XOR будем передавать в переменную у4.

Суть операции XOR в следующем: когда значение переменных х5 и хб будут неодинаковыми, например, один — FALSE, а другой — TRUE, в переменной у4 будет сигнал TRUE.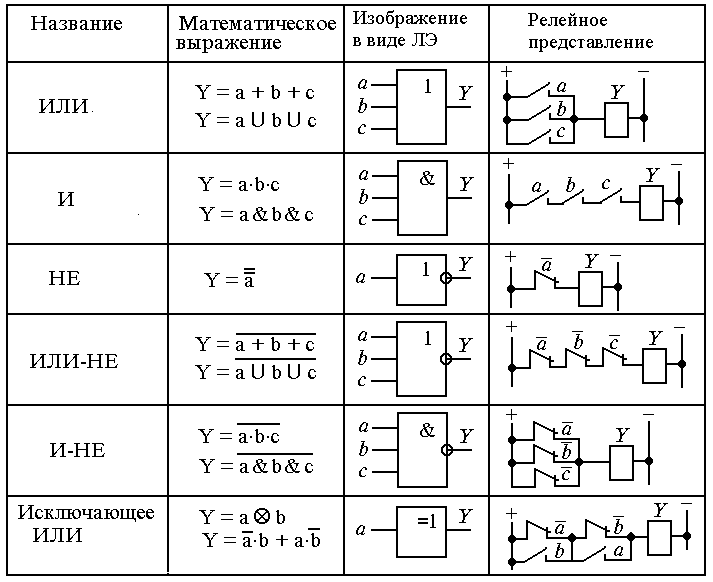 То есть выход у4 будет включен. Когда же х5 равно хб (либо обе переменные в состоянии «ЛОЖЬ», либо обе в состоянии «ИСТИНА»), тогда на выходе «ИСКЛЮЧАЮЩЕГО ИЛИ» будет значение «ЛОЖЬ».

Сейчас мы с Вами все это проверим, запустив программу непосредственно на ПЛК. Прежде чем это делать, еще несколько вещей, которые полезно себе записать и запомнить.

 

Перед загрузкой проекта на исполнение:

•    Расставляем порядок обработки: нажимаем ПКМ на свободную область, выбираем «Порядок», а затем «В соответствии с потоком данных». Нумерация элементов, то есть порядок их обработки, станет более правильной.

•    Сохраняем проект (Ctrl+s).

•    Запускаем проект на проверку, т.е. компилируем. Для этого в меню «Проект» выбираем пункт «Компилировать все», либо нажимаем клавишу F11. Внизу, в окне сообщений, мы должны увидеть, что ошибок у нас «О». То есть можно этот простой алгоритм запускать на исполнение. Если ошибки все-таки есть, вам необходимо их исправить и снова запустить компиляцию.

Мы заходим в меню «Онлайн», выбираем пункт «Подключение». Связываемся с нашим ПЛК, загружаем новую программу. Видим, что у нас внизу загорается надпись «ОНЛАЙН», это означает, что есть связь с контроллером. На самом ПЛК в этот момент должен загореться на светодиод «СВЯЗЬ». Проверьте себя. Для того чтобы эта программа начала работать, нам необходимо снять ее с паузы. Для этого, напоминаю, в меню «Онлайн» выбираем пункт «Старт», либо нажимаем клавишу F5. Внизу появится активная надпись «ЗАПУЩЕНО» .

Сразу же начинает действовать блок NOT. На вход у него приходит значение «ЛОЖЬ», на выходе мы видим сигнал «ИСТИНА», который передается на соответствующий дискретный выход уЗ.

 

Ну и теперь ваша задача заключается в том, чтобы просто проверить то, что Вы запрограммировали. То есть Вы подаете сигнал на переменную x1, на переменную х2, и у Вас появляется «ИСТИНА» в переменной у1.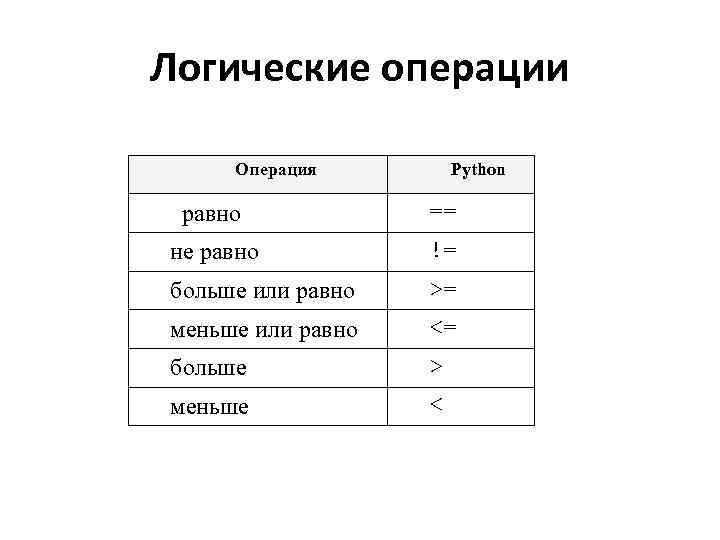

То есть срабатывает первый выход. Если один из входных сигналов отключить, то в у1 будет «ЛОЖЬ» (FALSE).

В заключение этой части хочу показать одну полезную «фишку». Достаточно часто бывают ситуации, когда для операции AND или для операции OR Вам будет необходимо больше, чем два входных значения. Задать дополнительные входы можно следующим образом: Вы выделяете ЛКМ блок, в котором Вам необходимо добавить вход. Затем нажимаете на нем ПКМ, выбираете пункт «Вход блока». Появляется еще один вход.

Такого же эффекта можно добиться, выделив блок и нажав сочетание клавиш Ctrl+A. Если какой-то вход Вам не нужен, то выделяете его ЛКМ и нажимаете Delete на вашей клавиатуре .

 

 

 

Статья создана на основе книги Кирилла Гайнутдинова «Простое и понятное программирование в CODESYS».

Логические операции and, or и not в Python.

Синтаксис:

x or y
x and y
not x

Операторы and и or закорачивают вычисление своих операндов: правый операнд вычисляется лишь в том случае, если его значение необходимо для получения истинного значения в операциях and или or.

• or — оценивает второй аргумент, только если первый равен False. Если какой либо операнд в цепочке or является истиной, немедленно возвращается результат — первое истинное значение.
• and — оценивает второй аргумент, только если первый равен True. Если в цепочке and все операнды являются истиной, результатом будет последнее значение. А если какой-либо из операндов является False, результатом будет первое ложное значение.
• not имеет более низкий приоритет, чем операторы сравнения, так not a == b интерпретируется как not (a == b), а выражение a == not b вовсе является синтаксической ошибкой. Единственный логический оператор с одним аргументом. Он принимает один аргумент x и возвращает противоположный результат: False для истинного значения и True для ложного значения.

Операторы and и or не приводят свои результаты принудительно к значениям True или False, а возвращают один из своих операндов. Такой подход позволяет использовать эти операторы в более общих, а не только булевых операциях. Если другие операторы, прежде чем выполнить операцию, вычисляют все свои операнды, то в случае операторов and и or с их семантикой закорачивания необходимость вычисления правого операнда определяется результатом вычисления левого.

Из булевых операторов, not имеет самый высокий приоритет, а or самый низкий, так что A and not B or C эквивалентно (A and (not B)) or C. Как всегда, скобки могут быть использованы для выражения желаемого приоритета в операциях.

Логические операции, упорядоченные по приоритету выполнения:

1. not x — если x ложно, то возвращается True, иначе False.
2. x and y — если x ложно, то возвращается x, иначе у.
3. x or y — если x ложно, то возвращается у, иначе x

Также смотрите встроенные функции all() и any()

Пример c and:

a = 'a'
b = 'b'
c = 'c'
>>> a and b
# 'b'
>>> '' and b
# ''
>>> a and b and c
# 'c'

Пояснения к примеру выше с оператором and:

1. Оператор and вычисляет значения в булевом контексте слева направо. Значения 0, '', [], (), {} и None являются ложью, все остальное является истиной. Если у and оба операнда являются истиной, результатом будет последнее значение.
2. Если какой-либо из операндов является ложью, результатом будет первое такое значение. В данном случает это '' — пустая строка, первое значение которое является ложью.
3. Все значения являются истиной, так что в результате мы получаем последнее c.

Пример c or:

a = 'a'
b = 'b'
>>> a or b
# 'a'
>>> '' or b
# 'b'
>>> '' or [] or {}
# {}
>>> def func():
...        return 1
>>> a or func()
# 'a'

Пояснения к примеру выше с оператором or:

1. Оператор or вычисляет значения в булевом контексте слева направо. Если операнд является истиной, or немедленно возвращает результат. В данном случае a, первое истинное значение.
2. or вычисляет выражение '', которое является ложью, затем b, которое является истиной, и возвращает его значение.
3. Если все значения являются ложью, or возвращает последнее.
4. Обратите внимание, что or вычисляет операнды до тех пор, пока не найдет истинное значение, остальное игнорируется. Это имеет значение, когда вычисление операнда дает сторонние эффекты. В данном случае функция func() не вызывается, так как для получения результата выражения с оператором or достаточно того, что первый операнд a является истиной.

Другие примеры с and и or:

>>> a = 'one'
>>> b = 'two'
>>> 1 and a or b
# 'one'
>>> 0 and a or b
# 'two'
>>> a = ''
>>> b = 'two'
# 'a' - пустая строка, которую Python считает ложью,
# следовательно 1 and '' дает '', а '' or 'two' дает 'two'.
>>> 1 and a or b
# 'two'

Логика | Британика

Готтлоб Фреге

Смотреть все СМИ

Ключевые люди:

Аристотель Джон Стюарт Милль Бертран Рассел Людвиг Витгенштейн Альфред Норт Уайтхед

Похожие темы:

история логики формальная логика прикладная логика металогический философия логики

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

логика , изучение правильных рассуждений, особенно в том, что касается выводов.

В этой статье рассматриваются основные элементы и проблемы современной логики, а также дается обзор ее различных областей. Для лечения исторического развития логики см. логика, история. Для подробного обсуждения конкретных областей см. см. статьи прикладной логики, формальной логики, модальной логики и логики, философии.

Вывод — это управляемый правилом шаг от одного или нескольких предложений, называемых посылками, к новому предложению, обычно называемому заключением. Правило вывода называется сохраняющим истину, если вывод, вытекающий из применения правила, истинен всякий раз, когда истинны посылки. Выводы, основанные на правилах сохранения истины, называются дедуктивными, а изучение таких выводов известно как дедуктивная логика. Правило вывода считается действительным или дедуктивно действительным, если оно обязательно сохраняет истину. То есть в любом мыслимом случае, когда посылки верны, вывод, сделанный правилом вывода, также будет истинным.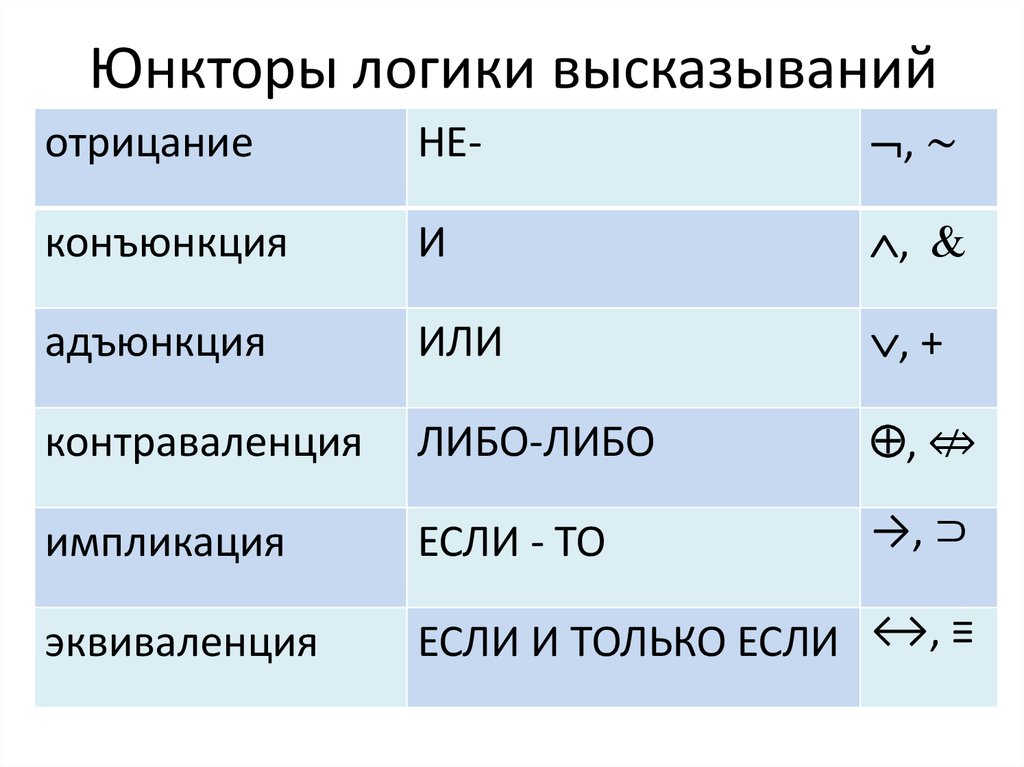 Выводы, основанные на действительных правилах вывода, также называются действительными.

Логика в узком смысле эквивалентна дедуктивной логике. По определению такое рассуждение не может дать никакой информации (в виде вывода), которая уже не содержится в посылках. В более широком смысле, близком к обыденному, логика также включает в себя изучение выводов, которые могут привести к выводам, содержащим действительно новую информацию. Такие выводы называются ампликативными или индуктивными, а их формальное изучение известно как индуктивная логика. Они иллюстрируются выводами, сделанными умными детективами, такими как вымышленный Шерлок Холмс.

Различие между дедуктивным и ампликативным выводами можно проиллюстрировать следующими примерами. Из посылки «кто-то всем завидует» можно сделать правильный вывод, что «все кому-то завидуют». Невозможно вообразить случай, когда посылка этого вывода верна, а заключение ложно. Однако, когда судебно-медицинский эксперт на основании определенных свойств набора человеческих костей делает вывод о приблизительном возрасте, росте и различных других характеристиках умершего человека, используемое рассуждение является ампликативным, потому что, по крайней мере, можно предположить, что сделанные им выводы являются ложными.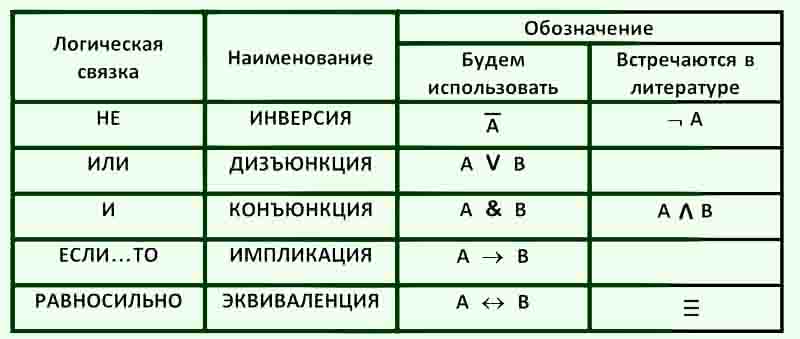 ошибся.

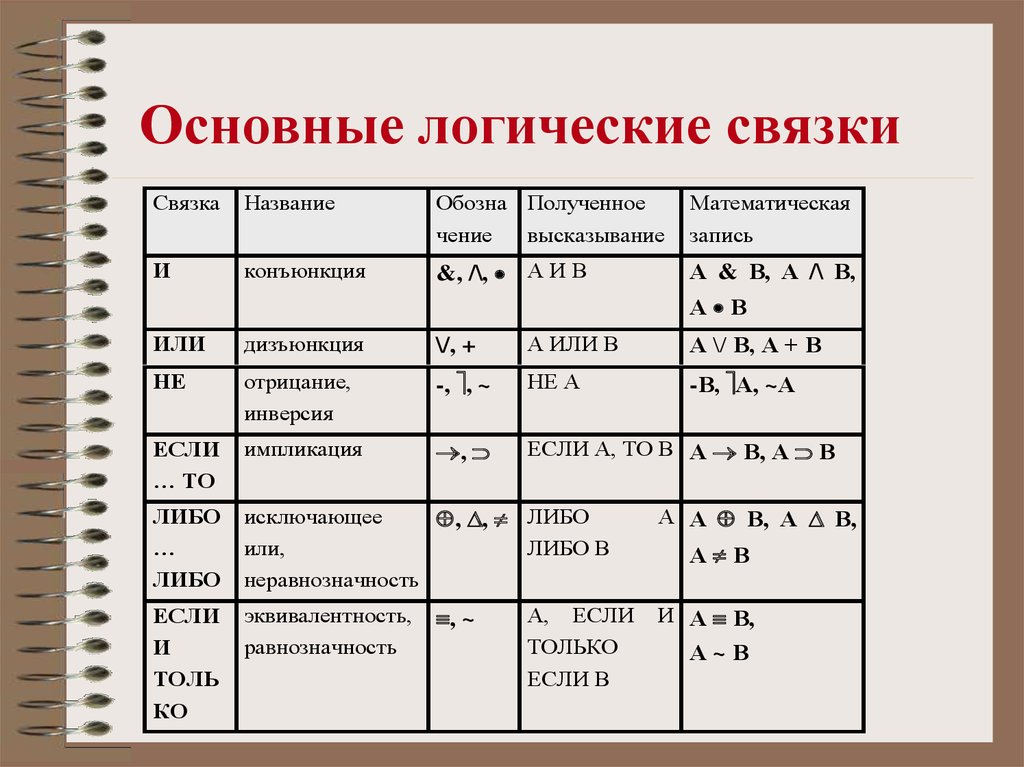
В еще более узком смысле логика ограничивается изучением умозаключений, зависящих только от определенных логических понятий, выражаемых тем, что называется «логическими константами» (логику в этом смысле иногда называют элементарной логикой). Наиболее важными логическими константами являются кванторы, пропозициональные связки и тождество. Квантификаторы являются формальными аналогами английских фраз, таких как «есть…» или «там существует…», а также «для каждого…» и «для всех…». Они используются в формальных выражениях, таких как (∃ x ) (читается как «есть индивидуум, назовите его x , такой, что для x верно, что…») и (∀ y ) (читается как «для каждого индивидуума назовите его y , это верно для y что …»). Основные пропозициональные связки в английском языке аппроксимируются «не» (~), «и» (&), «или» (∨) и «если…, то…» (⊃). Идентичность, представленная знаком ≡, обычно переводится в английском языке как «… есть…» или «… идентично…». Два вышеприведенных примера предложений могут быть выражены как (1) и (2) соответственно:

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

(1) (∃ x )(∀ y ) ( x завидует y )

(2) (∀ y )(∃ x ) ( x завидует y )

Способ, которым различные логические константы в предложении связаны друг с другом, известен как логическая форма предложения. Логическую форму также можно рассматривать как результат замены всех нелогических понятий в предложении логическими константами или общими логическими символами, известными как переменные. Например, заменив относительное выражение «a завидует b» на «E(a,b)» в (1) и (2) выше, можно получить (3) и (4) соответственно:

(3) (∃ x )(∀ y ) E( x , y )

(4)(∀ y )(∃ x ) E( x , y )

Формулы в (3) и (4) выше являются явными представлениями логических форм соответствующих английских предложений. Изучение отношений между такими неинтерпретируемыми формулами называется формальной логикой.

Следует отметить, что логические константы имеют то же значение в логических формулах, таких как (3) и (4), как и в предложениях, которые также содержат нелогические понятия, такие как (1) и (2). Логическая формула, переменные которой заменены нелогическими понятиями (значениями или референтами), называется «интерпретируемой» пропозицией или просто «интерпретацией». Один из способов выразить справедливость вывода из (3) в (4) состоит в том, чтобы сказать, что соответствующий вывод из предложения, подобного (1), в предложение, подобное (2), будет верным для всех возможных интерпретаций (3) и (4).

Правильные логические выводы становятся возможными благодаря тому факту, что логические константы в сочетании с нелогическими понятиями позволяют предложению представлять реальность. Действительно, эту репрезентативную функцию можно считать их наиболее фундаментальной чертой. Утверждение G, например, может быть правильно выведено из другого утверждения F, когда все сценарии, представленные F — сценарии, в которых F истинно, — также являются сценариями, представленными G — сценариями, в которых G истинно. В этом смысле (2) можно правильно вывести из (1), потому что все сценарии, в которых верно, что кто-то всем завидует, также являются сценариями, в которых верно, что всем завидует по крайней мере один человек.

Утверждение считается логически истинным, если оно истинно во всех возможных сценариях или «возможных мирах». Предложение противоречиво, если оно ложно во всех возможных мирах. Таким образом, еще один способ выразить правильность вывода от F к G состоит в том, чтобы сказать, что условное суждение «Если F, то G» (F ⊃ G) логически истинно.

Однако не все философы принимают эти объяснения логической достоверности. Для некоторых из них логические истины — это просто самые общие истины о реальном мире. Для других это истины об определенной незаметной части реального мира, содержащей абстрактные сущности, подобные логическим формам.

В дополнение к дедуктивной логике существуют другие разделы логики, которые изучают выводы, основанные на таких понятиях, как знание того, что (эпистемическая логика), убеждение, что (доксатическая логика), время (логика времени) и моральное обязательство (деонтическая логика). другие. Эти области иногда известны вместе как философская логика или прикладная логика. Некоторые математики и философы считают теорию множеств, изучающую отношения принадлежности между множествами, еще одной ветвью логики.

обозначение — «такой, что» логический символ

Задавать вопрос

спросил 9 лет, 8 месяцев назад

Изменено 3 года, 3 месяца назад

Просмотрено 36 тысяч раз

$\begingroup$

Итак, в определении того, что такое квадратный корень,

$\sqrt{x}$ — все числа $y$ такие, что $y×y=x$.

Существуют ли какие-либо логические математические символы, чтобы приведенное выше определение можно было записать с использованием только логических операторов и без использования естественного языка?

Где я могу получить вводные или справочные материалы по всем таким логическим символам?

обновление : Через некоторое время после того, как я задал вопрос, я заметил, что определение квадратного корня, которое я даю, неверно.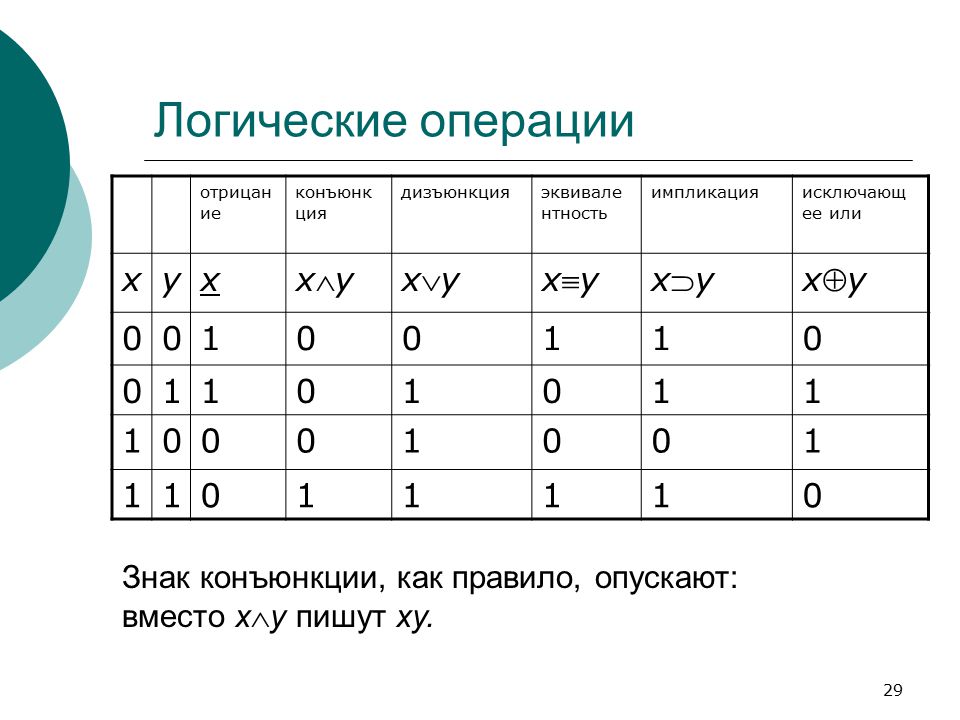 Квадратный корень из $x$ определяется как неотрицательное число $y$, удовлетворяющее условию $y*y=x$. Но вопрос был об обозначениях, а не о квадратных корнях, поэтому я оставляю его как есть из-за некоторых ответов, использующих предоставленное (ошибочное) определение. 92=х\} $$

Я также вижу, как люди используют (и сам использовал) «s.t.» как сокращение для таких, что в формулах.

$\endgroup$

3

$\begingroup$

Обычно не требуется никакого другого символа, кроме двоеточия или $\mid$ для «такой, что».

В англоязычной версии вашего утверждения $\sqrt x$ описывается как множество. Вы можете написать это как:

$$y\in \sqrt{x} \iff y\in\mathbb R \land y\cdot y = x$$

Обратите внимание, я добавил $y\in\mathbb R$, потому что вам нужно знать домен, в котором вы работаете. Вы могли бы изменить это, конечно.