ЕСЛИ (функция ЕСЛИ) — Служба поддержки Майкрософт

Формулы и функции

Формулы и функции

Формулы и функции

Функция ЕСЛИ

• Общие сведения о формулах в Excel
  Статья
• ПРОСМОТРX
  Статья
• ВПР
  Статья
• Функция СУММ
  Статья
• Функция СЧЁТЕСЛИ
  Статья
• Функция ЕСЛИ
  Статья
• ЕСЛИМН
  Статья
• СУММЕСЛИ
  Статья
• СУММЕСЛИМН
  Статья
• ПОИСКПОЗ
  Статья

Далее: Использование функций

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще. ..Меньше

Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.

Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.

Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).

Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.

ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])

Например:

Имя аргумента	Описание
лог_выражение    (обязательно)	Условие, которое нужно проверить.
значение_если_истина    (обязательно)	Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА.
значение_если_ложь    (необязательно)	Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ.

Простые примеры функции ЕСЛИ

• =ЕСЛИ(C2=»Да»;1;2)

В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)

В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.

В примере выше функция ЕСЛИ в ячейке D2 означает:

ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)

На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).

В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)

Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»).

Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.

Распространенные неполадки

Проблема	Возможная причина
0 (ноль) в ячейке	Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ.
#ИМЯ? в ячейке	Как правило, это указывает на ошибку в формуле.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Операторы вычислений и их приоритеты в Excel

Использование вложенных функций в формуле

Использование функции ЕСЛИ для проверки ячейки на наличие символов

Видео: расширенное применение функции ЕСЛИ

Функция ЕСЛИМН (Microsoft 365, Excel 2016 и более поздние версии)

Усложненные функции ЕСЛИ: как работать с вложенными формулами и избежать ошибок

Обучающие видео: усложненные функции ЕСЛИ

Подсчет значений на основе одного условия с помощью функции СЧЁТЕСЛИ

Подсчет значений на основе нескольких условий с помощью функции СЧЁТЕСЛИМН

Суммирование значений на основе одного условия с помощью функции СУММЕСЛИ

Суммирование значений на основе нескольких условий с помощью функции СУММЕСЛИМН

Функция И

Функция ИЛИ

Функция ВПР

Полные сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Поиск ошибок в формулах

Логические функции

Функции Excel (по алфавиту)

Функции Excel (по категориям)

Дизъюнктивные и конъюнктивные совершенные нормальные формы

Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул.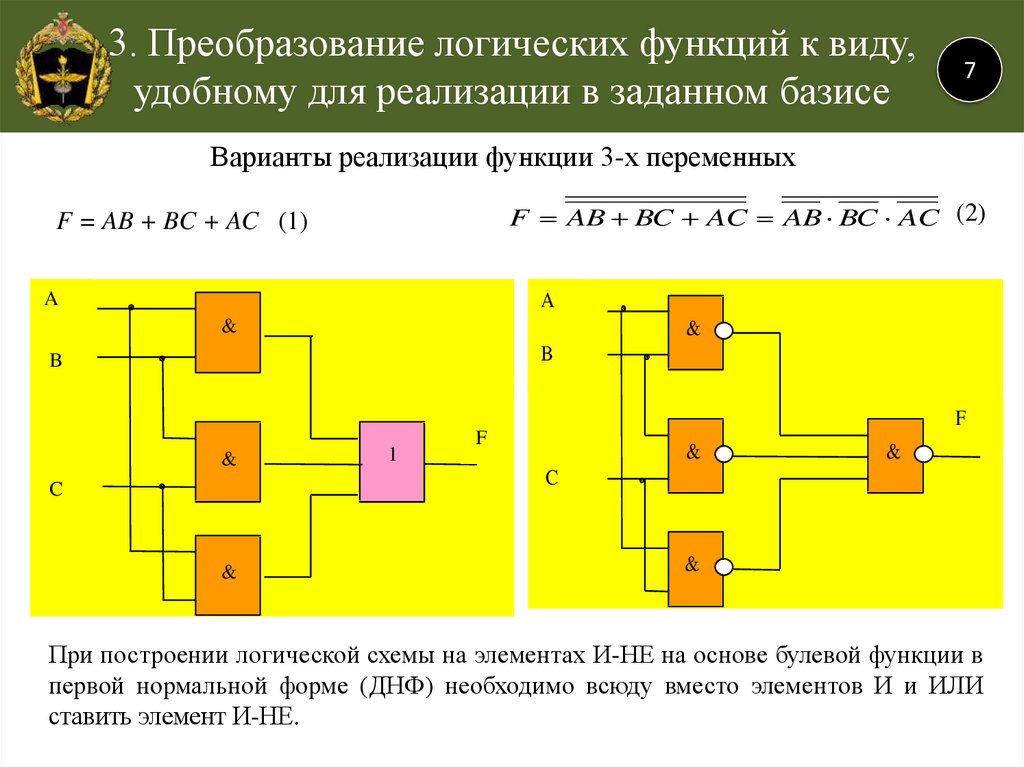 В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).

Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.

Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).

Совершенная дизъюнктивная нормальная форма (СДНФ)

Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.

Примеры: y,   ¬ y,   х₁ ∧ ¬ х₂ ∧ х₃ ∧ х₄

Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.

ДНФ записывается в следующей форме: F₁ ∨ F₂ ∨ … ∨ F_n, где F_i — элементарная конъюнкция

Примеры: ¬ х₁ ∧ х₂ ∨ х₁ ∧ ¬ х₂ ∨ х₁ ∧ ¬ х₂ ∧ х₃,   ¬ y₁ ∨ y₁ ∧ y₂ ∨ ¬ y₂

Определение.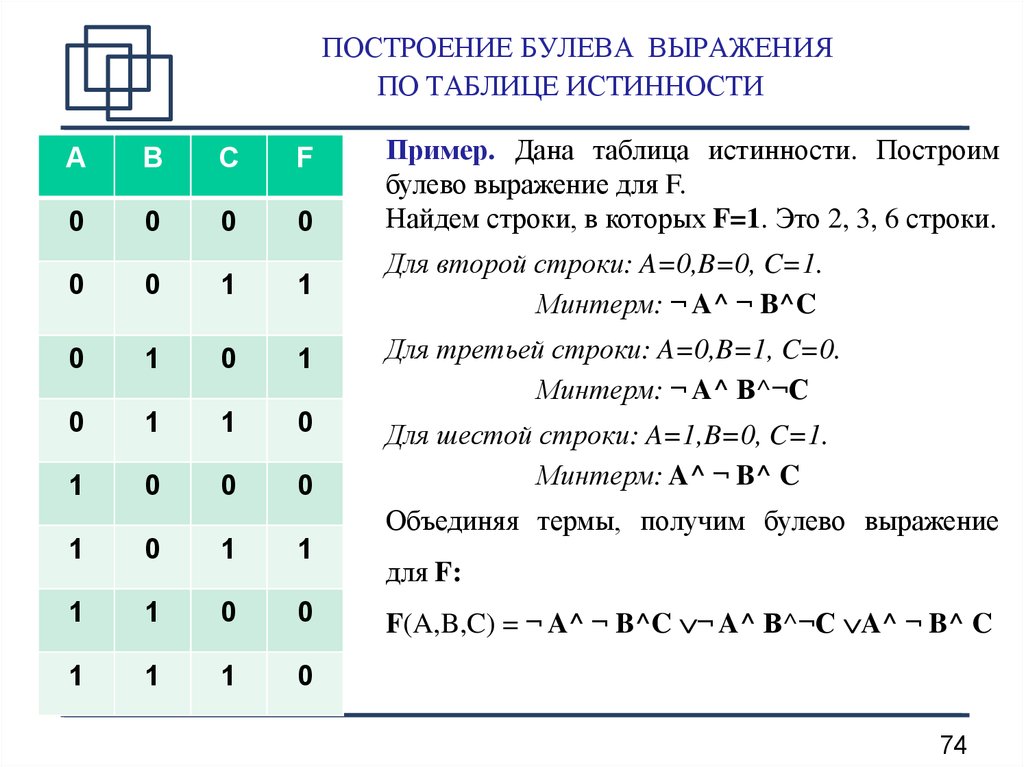 Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой конъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.

Пример: (¬ х₁ ∧ х₂ ∧ х₃) ∨ (х₁ ∧ ¬ х₂ ∧ х₃) ∨ (х₁ ∧ х₂ ∧ ¬ х₃)

Совершенная конъюнктивная нормальная форма (СКНФ)

Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.

Примеры: ¬ х₃,    х₁ ∨ х₂,    х₁ ∨ х₂ ∨ ¬ х₃

Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.

КНФ записывается в следующей форме: F₁ ∧ F₂ ∧ … ∧ F_n, где F_i — элементарная дизъюнкция

Примеры: (х₁ ∨ ¬ х₂) ∧ х₃,    (х₁ ∨ х₂) ∧ ( ¬ х₁ ∨ х₂ ∨ х₃) ∧ ( х₁ ∨ ¬ х₂ ∨ ¬ х₃)

Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой дизъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.

Пример: (х₁ ∨ х₂ ∨ х₃) ∧ ( ¬ х₁ ∨ ¬ х₂ ∨ х₃)

Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ.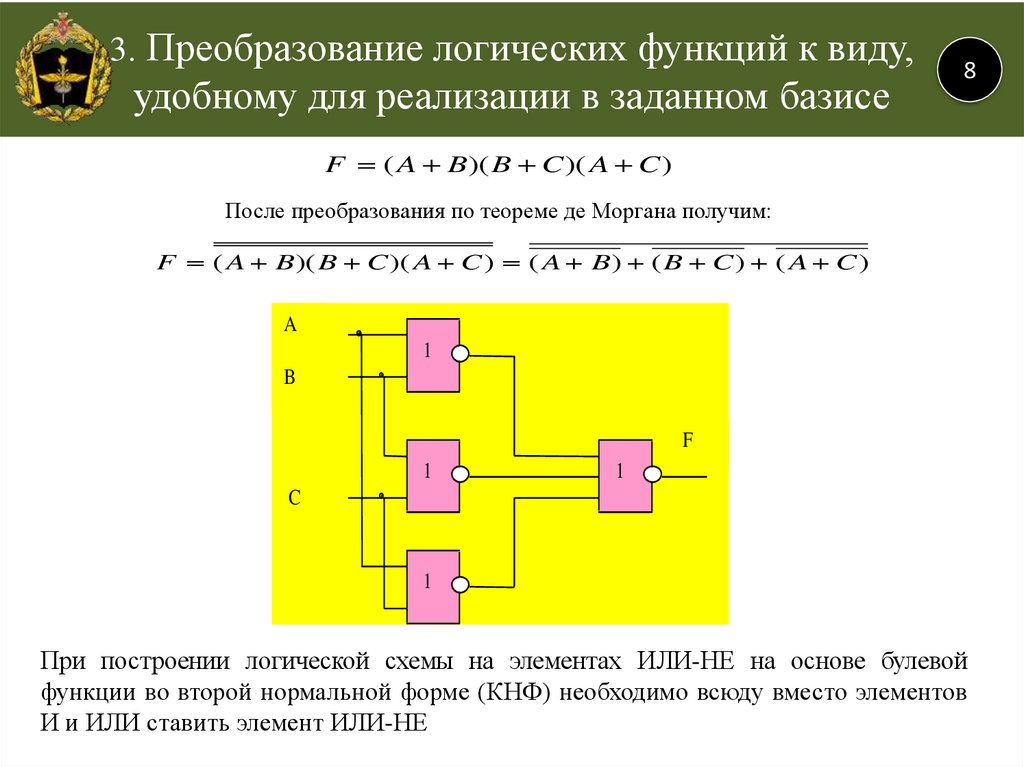

Алгоритм построения СДНФ по таблице истинности

1. Выбрать все строки таблицы, в которых значение функции равно единице.
2. Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.

Алгоритм построения СКНФ по таблице истинности

1. Выбрать все строки таблицы, в которых значение функции равно нулю.
2. Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные дизъюнкции связываем операциями конъюнкции.

Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае — СКНФ.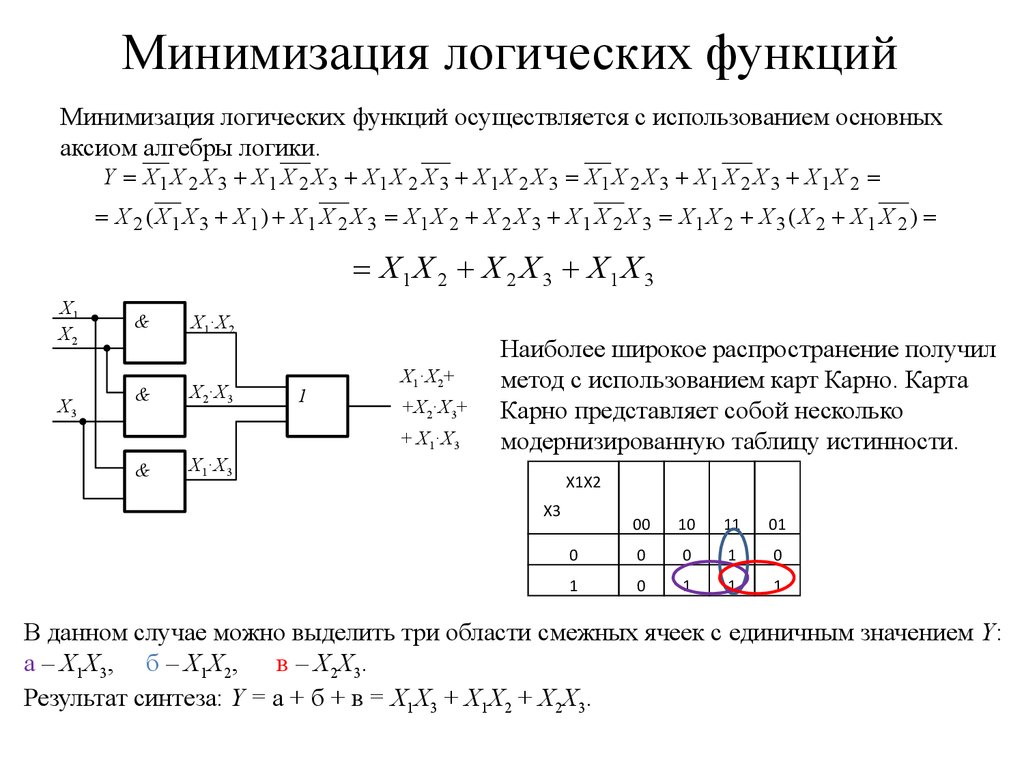

Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.

x	y	z	F (x, y, z)
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)

Проверим полученную формулу. Для этого построим таблицу истинности функции.

x	y	z	¬ x	¬ x ∨ y ∨ z	¬ z	¬ x ∨ y ∨ ¬ z	F (x, y, z)
0	0	0	1	1	1	1	1
0	0	1	1	1	0	1	1
0	1	0	1	1	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	0	1	1	0
1	0	1	0	1	0	0	0
1	1	0	0	1	1	1	1
1	1	1	0	1	0	1	1

Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.

Булева алгебра — Курс цифровой электроники

Булева алгебра, логическая алгебра, позволяет применять к логике правила, используемые в алгебре чисел. Он формализует правила логики. Булева алгебра используется для упрощения логических выражений. которые представляют собой комбинационные логические схемы. Он сводит исходное выражение к эквивалентному выражению с меньшим количеством членов, что означает, что для реализации требуется меньше логических вентилей. комбинационная логическая схема.

Калькулятор логических выражений

Используйте калькулятор, чтобы найти сокращенное логическое выражение или проверить свои (промежуточные) ответы.

Логическое выражение

Ваш ответ

Примечания:
• Используйте ~ * + для обозначения НЕ И ИЛИ соответственно. Не пропускайте оператор * для операции И.
  • (~AB)+(B~C)+(AB) вернет ошибку
  • (~A*B)+(B*~C)+(A*B) в порядке
• Логические операции следуют порядку приоритета НЕ И ИЛИ. Выражения в квадратных скобках () всегда вычисляются первыми, переопределяя порядок приоритета.
• Пожалуйста, вводите только переменные, константы типа 0,1 не допускаются.
• Переменные E, I, N, O, Q, S не допускаются

Упрощение логического выражения

В следующем примере показано, как использовать алгебраические методы для упрощения логического выражения

~(A * B) * (~A + B) * (~B + B)
~(A * B) * (~A + B) * 1	6 — Закон дополнения
~(A * B) * (~A + B)	5 — Закон тождества
(~A + ~B) * (~A + B)	8 — Закон Де Моргана
~A + ~B * B	4 — Распределительный закон
0	3	6 — Закон дополнения
~A	5 — Закон тождества

Каждая строка (или шаг) дает новое выражение и правило или правила, используемые для его получения из предыдущего. Прийти к конечному результату можно несколькими способами. Вы можете использовать наш калькулятор, чтобы проверить промежуточные шаги вашего ответа. Эквивалент означает, что ваш ответ и исходное логическое выражение имеют одну и ту же таблицу истинности.

Законы булевой алгебры

Законы булевой алгебры Используются для упрощения логических выражений.

Основные логические законы

1. Закон идемпотента
   • А * А = А
   • А + А = А
2. Ассоциативное право
   • (А * В) * С = А * (В * С)
   • (А + В) + С = А + (В + С)
3. Коммунативное право
   • А * В = В * А
   • А + В = В + А
4. Распределительное право
   • А * (В + С) = А * В + А * С
   • А + (В * С) = (А + В) * (А + С)
5. Закон о личности
   • А * 0 = 0     А * 1 = А
   • А + 1 = 1     А + 0 = А
6. Закон о дополнении
   • А * ~А = 0
   • А + ~А = 1
7. Закон об инволюции
   • ~(~А) = А
8. Закон Де Моргана
   • ~(А * В) = ~А + ~В
   • ~(А + В) = ~А * ~В

   Законы о резервировании

9. Поглощение
   • А + (А * В) = А
   • А * (А + В) = А
10. • (А * В) + (А * ~ В) = А
    • (А + В) * (А + ~В) = А
11. • А + (~А * В) = А + В
    • А * (~А + В) = А * В

Каждый закон описывается двумя частями, двойственными друг другу. Принцип двойственности

• Замена операций + (ИЛИ) и * (И) выражения.
• Замена элементов 0 и 1 выражения.
• Без изменения формы переменных.

Применение булевой алгебры

Разработка комбинационной логической схемы включает следующие этапы

1. Из спецификации проекта получить таблицу истинности
2. Из таблицы истинности выведите логическое выражение суммы произведений.
3. Используйте Булеву алгебру для упрощения логического выражения. Чем проще логическое выражение, тем меньше логических элементов будет использоваться.
4. Используйте логические вентили для реализации упрощенного логического выражения.

Поскольку доходы от рекламы падают, несмотря на увеличение числа учащихся, нам нужна ваша помощь, чтобы поддерживать и улучшать этот сайт, что требует времени, денег и тяжелой работы. Благодаря щедрости наших учеников, которые пожертвовали ранее, вы можете пользоваться этим сайтом бесплатно.

Если вы воспользовались этим сайтом и можете, пожалуйста, отправьте через Paypal . Это позволит нам продолжаться в будущем. Это займет всего минуту. Спасибо!

2 доллара США 5 долларов США 10 долларов США

Если вы хотите повеселиться с акустической гитарой, наша веб-гитара гарантирует вам быстрый старт.

Играть

Комбинационные логические схемы

• Комбинационная логическая схема Анализ
• Стандартные формы логических выражений
• Упрощение логических выражений
  • Булева алгебра
  • Карта Карно
• Проектирование комбинационной логики

Применение комбинационной логики

• Арифметические схемы
• Компараторы
• Кодировщики и дешифраторы
• Мультиплексоры и демультиплексоры
• Средства проверки четности

Булева алгебра

Логические функции, в которых значения переменных истинны (1) или ложны (0).

Рекламные ссылки

В булевой алгебре значения переменных истинны (1) или ложны (0) .

БУФ

y = a                        (1)

a	y
0	0
1	1

AND

y = a & b                        (2)

a	b	y
0	0	0
0	1	0
1	0	0
1	1	1

OR

y = a | b                        (3)

a	b	y
0	0	0
0	1	1
1	0	1
1	1	1

XOR

y = a ⊻ b                    (4)

a	b	y
0	0	0
0	1	1
1	0	1
1	1	0

NOT

y = a                     (5)

a	y
0	1
1	0

NAND

y = a & b                    (6)

a	b	y
0	0	1
0	1	1
1	0	1
1	1	0

NOR

y = a  | b                     (7)

a	b	y
0	0	1
0	1	0
1	0	0
1	1	0

XNOR

y = a  ⊻ b                     (8)

a	b	y
0	0	1
0	1	0
1	0	0
1	1	1

Рекламные ссылки

Связанные темы

Связанные документы

Engineering ToolBox -3 SketchUp Extension — Online моделирование!

Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширение SketchUp, которое можно использовать с потрясающими, интересными и бесплатными приложениями SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!

Перевести

О Engineering ToolBox!

Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.

Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.

Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.