История логики Логические задачи Высказывания Логические функции … Таблицы истинности Запись выражений на языке алгебры логики Законы логики Решение задач
|
Логическая функция — это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции. Это определение почти не отличается от определения числовой функции. Как можно составить логическую функцию? Очень просто. Приведем пример: Пусть дано высказывание А. Оно может быть либо истинно, либо ложно. Мы только что установили соответствие между высказыванием А и высказыванием Функция, определённая таким образом, называется отрицанием и записывается так:
Определим логические функции: 1) Инверсия (отрицание) — это логическое не. Говорят, что имея суждение А, можно образовать новое суждение,
которое читается как « Для обозначения отрицания суждения употребляется символ ¬ или – над переменной. Запись ¬А читается как «не А».
2) Коньюкция — это логическое умножение. Обозначение: А & В ( АВ, А /\ В ) .
3) Дизьюкция — это логическое сложение. Обозначение: А V В , ( А + В ). Читается так: “ А или В ”.
4) Эквиваленция — это функция тождества. Она обозначается символами = , ~ , или <=>. Выбираем
обозначение А = В. («тогда и только тогда»).
5) Импликация — это логическое следование. Импликация двух высказываний А и В соответствует союзу
«ЕСЛИ…ТО». Читается как «из А следует В» Обозначение:
Импликация устроена немного сложнее других функций. |
что такое, способы представления, значение / Справочник :: Бингоскул
Логическая функция: что такое, способы представления, значениедобавить в закладки удалить из закладок
Содержание:
Логическая функция — это такая функция, которая может принимать только одно из 2-х значений: 0 («ложь», «false») или 1 («истина», «true»). Логическую функцию можно обозначить как F (A), где А — это логический аргумент, чье количество в функции никак не ограничено.
Любая современная компьютерная система состоит из множества логических схем, где присутствуют логические функции и логические переменные.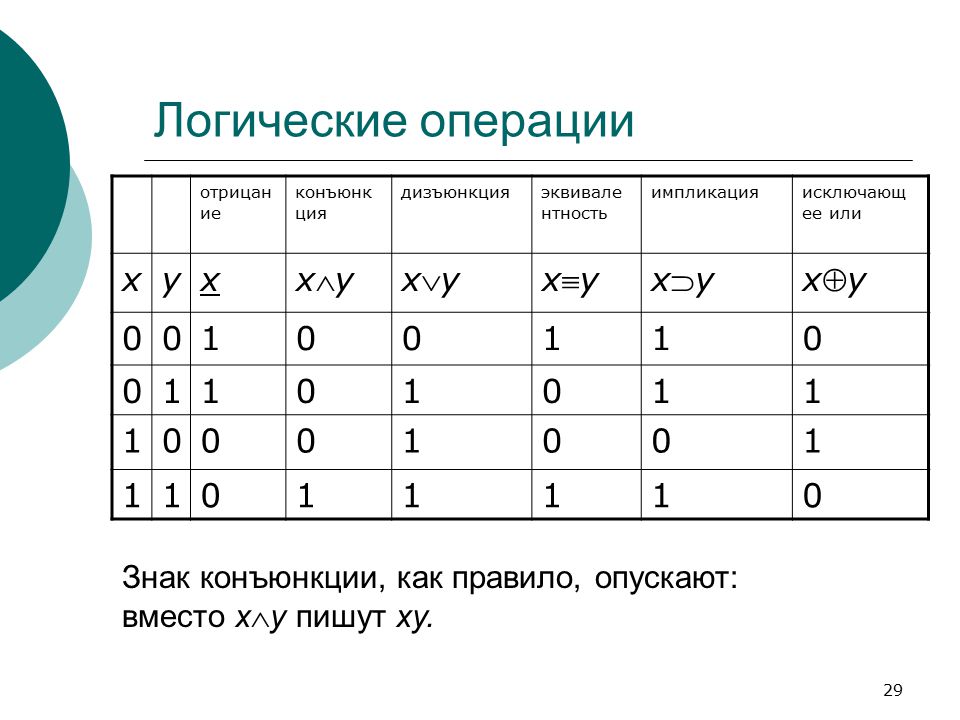 Для того чтобы описать эти взаимоотношения, есть таблицы истинности, в которых расписаны значения логической функции для разных наборов аргументов функции.
Для того чтобы описать эти взаимоотношения, есть таблицы истинности, в которых расписаны значения логической функции для разных наборов аргументов функции.
Логическая функция, что это
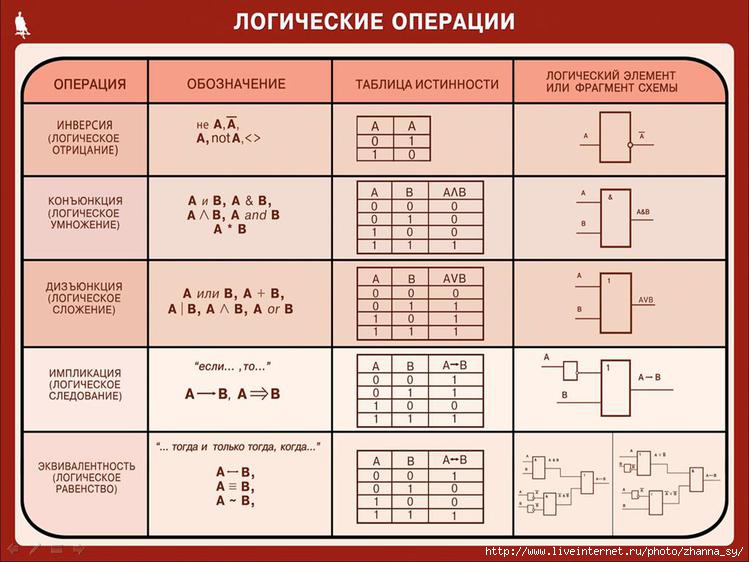
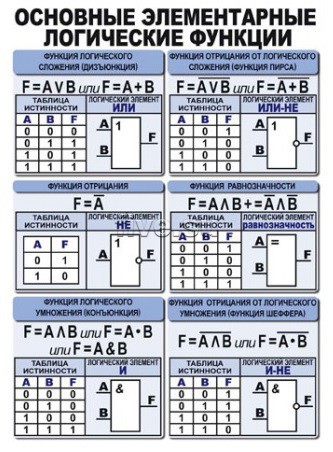
Над аргументами логической функции можно выполнить различные операции. В зависимости от операций можно выделить основные логические функции:
- отрицание;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквиваленция.
Логическая функция: отрицание
Под отрицанием понимается логическая функция с аргументом «не А» (обозначается в виде «¬ А»), которая в конечном счете является истинной, если аргумент будет «false» и ложной, если аргумент будет «true»:
- если А будет 1, то ¬ А будет 0;
- если А будет 0, то ¬ А будет 1.
Логическая функция: конъюнкция
Логическая функция «конъюнкция» всегда представлена несколькими аргументами. Она будет являться «true» только в том случае, если все аргументы внутри нее будут тоже «true». Например, у нас есть два аргумента «А и В». Если рассматривать их точки зрения истинности конъюнкции, тогда мы получаем следующее:
Она будет являться «true» только в том случае, если все аргументы внутри нее будут тоже «true». Например, у нас есть два аргумента «А и В». Если рассматривать их точки зрения истинности конъюнкции, тогда мы получаем следующее:
- если А будет 1 и В будет 1, тогда А˄В будет тоже 1;
- если А будет 1, а В будет 0, тогда А˄В будет 0;
- если А будет 0, а В будет 1, тогда А˄В будет 0;
- если А будет 0 и В будет 0, тогда А˄В будет тоже 0.
Логическая функция: дизъюнкция
Эта логическая функция, как и предыдущая, должна быть представлена несколькими аргументами. Ее значение буде «false» только в том случае, когда значения всех аргументов будет «false», во всех остальных случаях она будет «true».
Например нам даны два аргумента «А и В», тогда их таблица дизъюнкции будет выглядеть следующим образом:
- если А будет 1 и В будет 1, тогда и А˅В будет 1;
- если А будет 1, а В будет 0, тогда А˅В все равно будет 1;
- если А будет 0, а В будет 1, А˅В также будет 1;
- если А будет 0 и В будет 0, только тогда А˅В будет 0.

Логическая функция: импликация
Логическая функция «импликация» — это такое выражение, которое показывает зависимость одного аргумента от другого. Его еще можно «прочитать» как «если А, то В». Обозначается как «А→В» и оно будет считаться «false» только тогда, когда А будет «true», а «В» будет «false».
Например:
- если А будет 1 и В будет 1, тогда А→В будет тоже 1;
- если А будет 1, а В будет 0, только тогда А→В будет тоже 0;
- если А будет 0, а В будет 1, то А→В будет 1;
- если А будет 0 и В будет 0, тогда А→В также будет 0.
Логическая функция: эквиваленция
Логическая функция «эквиваленция» простыми словами может читаться как «для А нужно и достаточно В». Его значение будет «true», только тогда, когда А и В вместе, либо «false», либо «true». Такая функция обозначается как «А↔В».
Вот как выглядит таблица истинности эквиваленции:
- если А будет 1 и В будет 1, тогда А↔В тоже будет 1;
- если А будет 1, а В будет 0, тогда А↔В будет 0;
- если А будет 0, а В будет 1, тогда А↔В будет 0;
- если А будет 0 и В будет 0, тогда А↔В будет 1.

Заключение
Логическая функция — это основа вычислений любого компьютера. Компьютеру постоянно приходится обрабатывать какую-то информацию, причем ему нужно приводить ее к логической последовательности нулей и единиц. Любые операции в компьютере с нулями и единицами происходят по условиям математической логики. А это означает, что для более глубокого понимания вычислительной мощности компьютерного устройства знать, что такое логическая функция очень важно.
Поделитесь в социальных сетях:
9 сентября 2021, 17:46
Информатика
Could not load xLike class!
определение логики+функции по The Free Dictionary
Логика+функция — определение логика+функция по The Free DictionaryЛогика+функция — определение логики+функции в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова по отдельности:
логика функция
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?
- ▲
- логическая секция
- логический секвенсор
- Логическое моделирование
- Логические очки
- Анализатор логического состояния
- Логическая студия
- логические колебания
- логический переключатель
- Логический синтез
- Логический синтез
- Логический синтез
- Логический синтез
- Логический синтез
- Логическая система
- Логическая система
- Функциональный тест логической системы
- Логические системы
- Логические системы
- Разработка логических технологий
- Теоретик логики
- Теория логики
- Логическая магистральная радиостанция
- Логический транковый радиомодуль
- логический блок
- Группа пользователей логики
- логическая переменная
- Логика разобьет вам сердце
- логическое слово
- Логические Работы
- Логический ноль
- логика+функция
- Логика, алгебра и степени истинности
- Логика, предметные области и языки программирования
- Логика, Закон
- логика, многозначная
- логика, многозначная
- Логика, методология и философия науки
- Логический, Модальный
- Логический, Модальный
- Логика, рациональность и взаимодействие
- логико-арифметический блок
- Логический синтез и преобразование программ
- Логическое переключение
- логическое прерывание
- Логически развитая модель принятия решений
- логический принтер
- Логическая система
- Логическая система
- Логические системы
- Логические системы
- Логика/альтернативный пуск
- Логика/альтернативный пуск
- Логика/альтернативный пуск
- Логический/логический канал
- Логика
- Логика
- Логика Бизнес Консалтинг
- Логика Центр компьютеров и управления
- Логика Нова
- LogicaCMG
- логический
- ▼
Сайт: Следовать:
Делиться:
Открыть / Закрыть
[PDF] Логические функции и уравнения
- title={Логические функции и уравнения},
автор={Кристиан Постхофф и Бернд Штайнбах},
booktitle={Кембриджский журнал международного права},
год = {2005}
}
I.
 Теоретические основы.- 1. Основные алгебраические структуры.- 2. Логические функции.- 4. Булево дифференциальное исчисление.- 5. Решение логических уравнений.- II. Приложения.- 6. Логика и арифметика.- 7. Комбинационные схемы.- 8. Конечные автоматы.- III. Инструменты.- 9. Xboole.
Теоретические основы.- 1. Основные алгебраические структуры.- 2. Логические функции.- 4. Булево дифференциальное исчисление.- 5. Решение логических уравнений.- II. Приложения.- 6. Логика и арифметика.- 7. Комбинационные схемы.- 8. Конечные автоматы.- III. Инструменты.- 9. Xboole.View on Springer
link.springer.comТрехуровневая иерархия моделей решеток булевых функций
- B. Steinbach, C. Posthoff
Информатика
EUROCAST
- 2017
Использование решеток булевых функций для синтеза схем сочетает в себе преимущества большей свободы для оптимизации с ограниченными вычислениями по меточным функциям для расширения возможностей подходов к синтезу.
Полная эквациональная аксиоматизация частичной дифференцировки
- G. Плоткин
Математика
MFPS
- 2020
Деривативные операции для классов C N $A \ MathCAL {C.NAN $ $0179
- Б.
 Штейнбах, К. Постхофф
Штейнбах, К. Постхофф Информатика, математика
Усовершенствованные булевы методы
- 2019
Известная теория дифференциального каннового исчисления производной расширяется таким образом, что каждая из десяти дифференциальных канюльных операций исчисления производных к классам булевых функций без необходимости вычислять производную операцию для каждой булевой функции класса отдельно.
КОНЦЕПТУАЛЬНАЯ МОДЕЛЬ ДЛЯ (ПОЛУ-)АВТОМАТИЗИРОВАННОГО ПОЛУЧЕНИЯ КРИТЕРИЙ ОЦЕНКИ ПРИ МОДЕЛИРОВАНИИ ТРЕБОВАНИЙ
Новый подход к связыванию моделей требований и критериев оценки для решения проблемы забытых требований, которые могут привести к неправильным решениям при их использовании в качестве основы для принятия решений.
Прогнозирование эффективности биомиметических адаптивных оболочек зданий: интеграция многофункциональности с помощью новой среды моделирования
- А.
 Куру, Филип Олдфилд, С. Бонсер, Ф. Фиорито
Куру, Филип Олдфилд, С. Бонсер, Ф. Фиорито Инженерное дело
Солнечная энергия
3
30024
Булево дифференциальное исчисление
Булево дифференциальное исчисление представляет собой мощную теорию, основанную на определениях дифференциалов булевых переменных и нескольких дифференциальных операций и производных логических функций, и открывает широкую область применения булевого дифференциального исчисления.
Проверка и тестирование реальных схем
В этой статье представлен метод проверки с сохранением структуры, который проиллюстрирован на реальной цифровой схеме путем проверки схемы и, соответственно, проверки ее на наличие известных самоинжектируемых неисправностей.
с показателем 1-10 из 83 ссылок
сортировка Byrelevancemost, повлиявшие на работу,
Boolean Functions и вычислительные модели
- P.
 Clote, E. Kranakis
Clote, E. Kranakis Computing Science, Mathematics
Texts in Thuctritic Ncience. Серия EATCS
- 2002
1. Булевы функции и схемы.- 2. Нижние границы схемы.- 3. Верхние границы схемы.- 4. Случайность и выполнимость.- 5. Системы доказательств высказываний.- 6. Модели машин и алгебры функций.-…
Задачи и упражнения по дискретной математике
- Гаврилов Г., Сапоженко А.А.
Информатика, Математика
- 1996
обобщены в одной главе.
Булевы рассуждения — логика булевых уравнений
- Ф. Браун
Математика
- 1990
Математический анализ логики: эссе на пути к исчислению дедуктивного мышления разработка классных педагогических практик.
Решетчатые функции и уравнения
- Профессор Сергей Рудяну
Математика, информатика
Дискретная математика и теоретическая информатика
- 2001
В этой главе обсуждаются основы логики, логическое дифференциальное исчисление, булевы преобразования и приложения булевых функций и приложений.

Логические функции и уравнения: примеры и упражнения. и Уравнения могут быть решены с помощью этого программного пакета, и можно решить множество соответствующих задач и изучить решения, основанные на этом программном обеспечении.
Булевы дифференциальные уравнения
Булево дифференциальное исчисление (БДК) — очень мощная теория, которая значительно расширяет структуру булевой алгебры и может широко использоваться для анализа, синтеза и тестирования цифровых схем.
Логическое исчисление разностей
Различия булевых функций сравниваются с теорией переключения, чтобы выяснить, можно ли переключать логические функции между положительными и отрицательными значениями.
Новый метод декомпозиции для проектирования многоуровневых схем
Представляет новую методологию декомпозиции булевых функций, основанную исключительно на использовании свойств функций. Основным пунктом в этой связи является «групповая способность»…
подходов к сдвигу ограничений сложности булевых задач
- B.




 Читается так “ А и В “.
Читается так “ А и В “.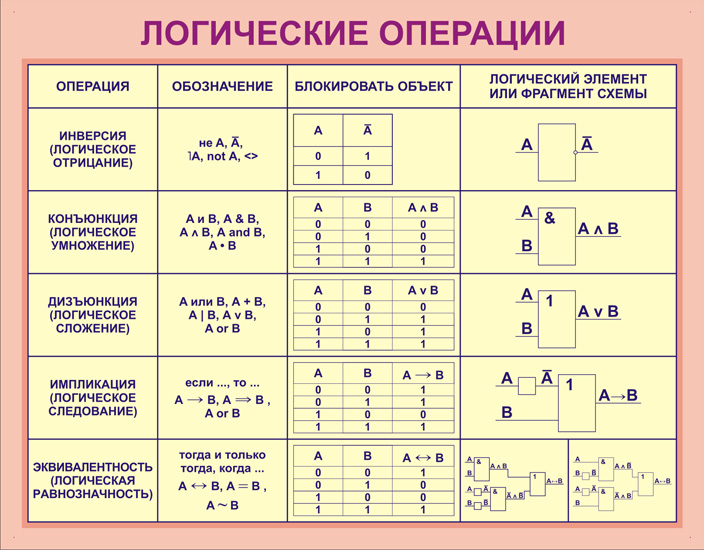

 В импликации существенное значение имеет порядок аргументов. Первый называется посылкой, а второй следствием. Можно сказать, что первое высказывание является как бы причиной второго, а второе как бы вытекает из первого.
В импликации существенное значение имеет порядок аргументов. Первый называется посылкой, а второй следствием. Можно сказать, что первое высказывание является как бы причиной второго, а второе как бы вытекает из первого.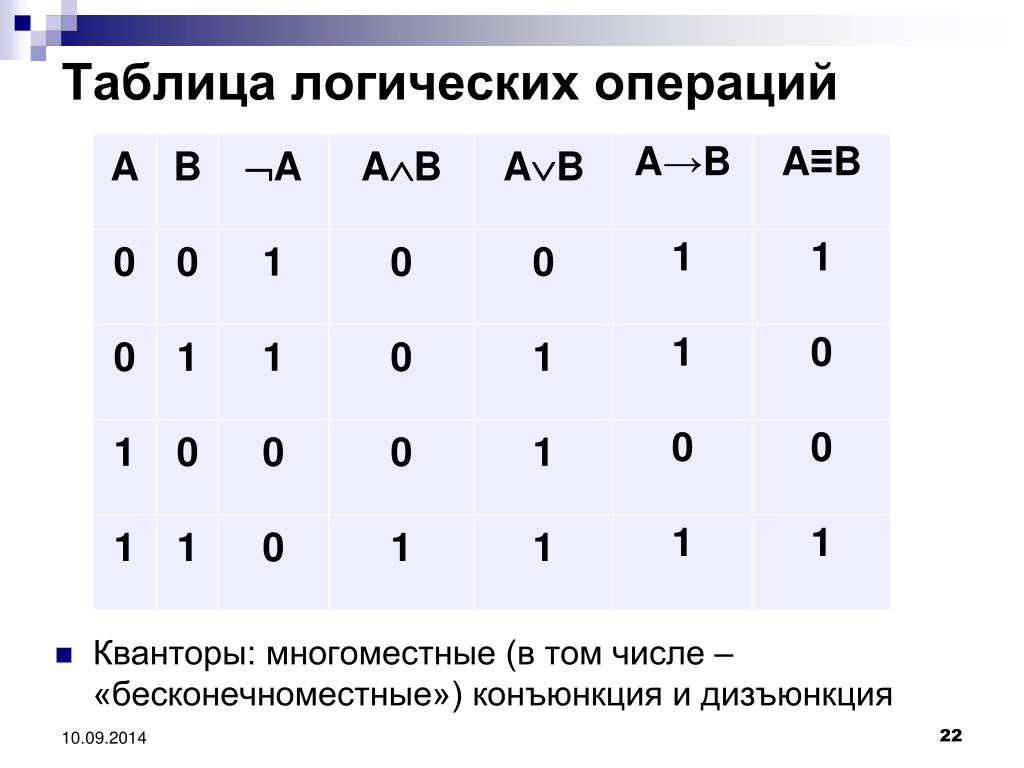

 Теоретические основы.- 1. Основные алгебраические структуры.- 2. Логические функции.- 4. Булево дифференциальное исчисление.- 5. Решение логических уравнений.- II. Приложения.- 6. Логика и арифметика.- 7. Комбинационные схемы.- 8. Конечные автоматы.- III. Инструменты.- 9. Xboole.
Теоретические основы.- 1. Основные алгебраические структуры.- 2. Логические функции.- 4. Булево дифференциальное исчисление.- 5. Решение логических уравнений.- II. Приложения.- 6. Логика и арифметика.- 7. Комбинационные схемы.- 8. Конечные автоматы.- III. Инструменты.- 9. Xboole. Штейнбах, К. Постхофф
Штейнбах, К. Постхофф Куру, Филип Олдфилд, С. Бонсер, Ф. Фиорито
Куру, Филип Олдфилд, С. Бонсер, Ф. Фиорито Clote, E. Kranakis
Clote, E. Kranakis
