НОУ ИНТУИТ | Лекция | Логические основы ЭВМ

Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.

Ключевые слова: логический, выражение, истина, ложь, алгебра, представление, переменная, значение, функция, инверсия, дизъюнкция, конъюнкция, таблица, очередь

Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.

Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.

Основные логические функции и элементы

Логический элемент — графическое представление элементарной логической функции.

Логическое умножение (конъюнкция) — функция И

Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:

• на входе схемы разомкнутое состояние соответствующего ключа, например, ;
• intuit.ru/2010/edi»>на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток
  не протекает.

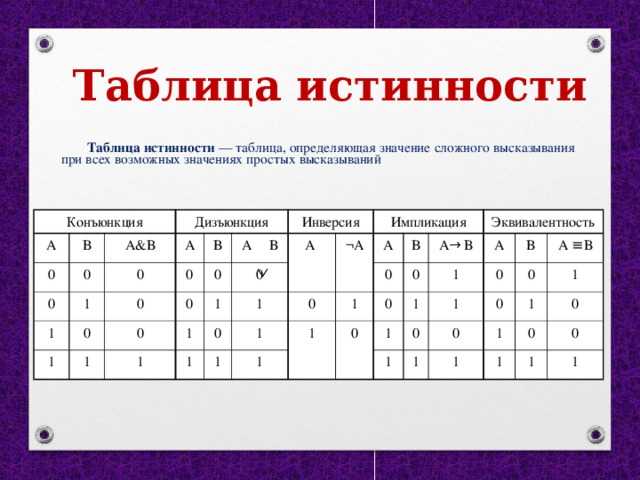
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И

Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и , и , и . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис.

1.1,в.

Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.

Уровень логического 0 является решающим для логического умножения .

В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:

• либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
• либо ;
• либо — с использованием знака конъюнкции;
• либо , но при этом из контекста должно быть ясно, что между переменными , и производится логическое умножение.

Логическое сложение (дизъюнкция) — функция ИЛИ

Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ

. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.

Рис. 1.2. Логический элемент ИЛИ на два входа

Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.

Для логического сложения решающим является уровень логической 1

.

В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:

• либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
• либо — с использованием знака дизъюнкции.

Логическое отрицание (инверсия) — функция НЕ

Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной

логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.

Рис. 1.3. Логический элемент НЕ

Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.

В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.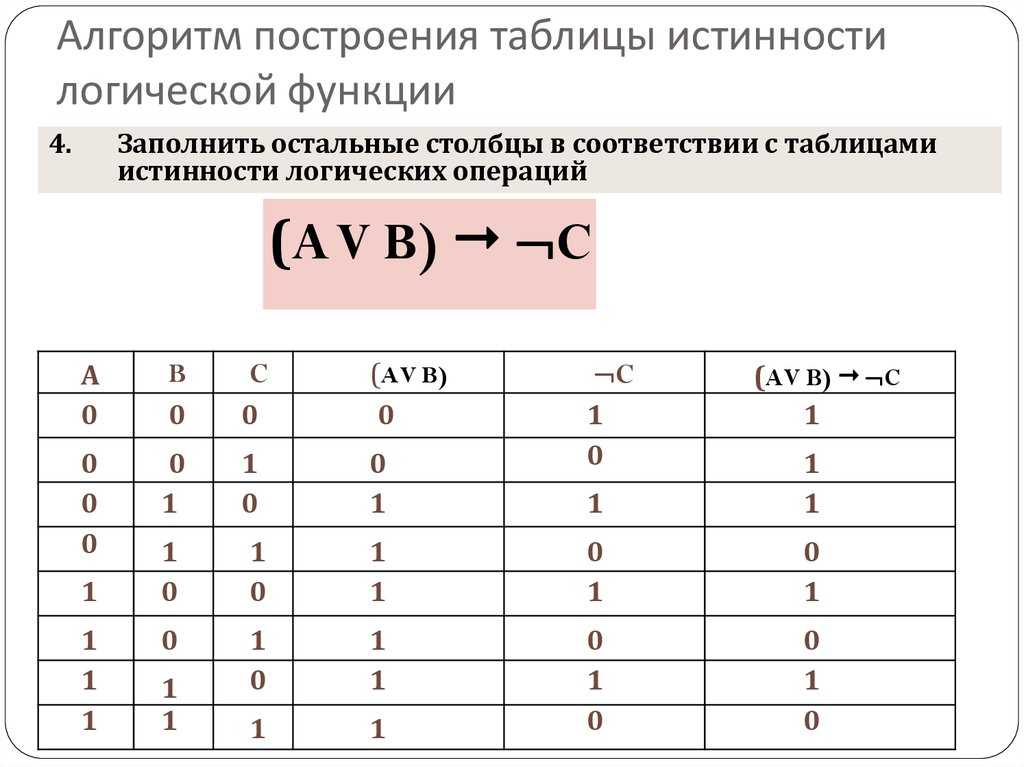

Логическая функция и элемент И-НЕ

Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.

Рис. 1.4. Логический элемент И-НЕ на три входа

Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1

.

В логических выражениях применяются обозначения:

• либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
• intuit.ru/2010/edi»>либо ;
• либо ;
• либо .

Логическая функция и элемент ИЛИ-НЕ

В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а.

Таблица истинности приведена на рис. 1.5,б.

Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:

• либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
• либо .

Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа

Логические функции в excel с примерами их использования

Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.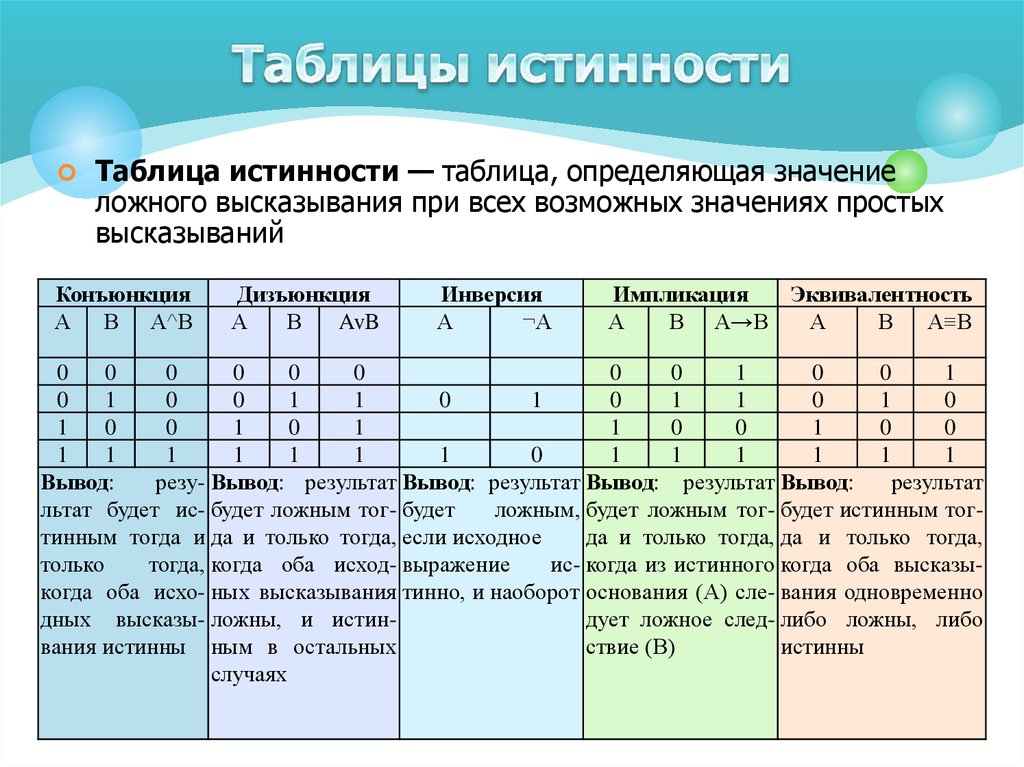

Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.

Использование логических функций в Excel

Название функции	Значение	Синтаксис	Примечание
ИСТИНА	Не имеет аргументов, возвращает логическое значение «ИСТИНА».	=ИСТИНА ()	Редко используется в качестве самостоятельной функции.
ЛОЖЬ	Не имеет аргументов, возвращает логическое выражение «ЛОЖЬ».	=ЛОЖЬ ()	——-//——-
И	Если все заданные аргументы возвращают истинный результат, то функция выдает логическое выражение «ИСТИНА». В случае хотя бы одного ложного логического значения вся функция выдает результат «ЛОЖЬ».	=И (Лог_знач. 1; Лог_знач. 2;…)	Принимает до 255 аргументов в виде условий или ссылок. Обязательным является первый.
ИЛИ	Показывает результат «ИСТИНА», если хотя бы один из аргументов является истинным.	=ИЛИ (Лог_знач.1; Лог_знач. 2;…)	——-//——-
НЕ	Меняет логическое значение «ИСТИНА» на противоположное – «ЛОЖЬ». И наоборот.	#ИМЯ?	Обычно сочетается с другими операторами.
ЕСЛИ	Проверяет истинность логического выражения и возвращает соответствующий результат.	#ИМЯ?	«Логическое_выражение» при вычислении должно иметь результат «ИСТИНА» или «ЛОЖЬ».
ЕСЛИОШИБКА	Если значение первого аргумента истинно, то возвращает сам аргумент. В противном случае – значение второго аргумента.	#ИМЯ?	Оба аргумента обязательны.



Логические функции в Excel и примеры решения задач

Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.

Сформируем таблицу с исходными параметрами:

Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ.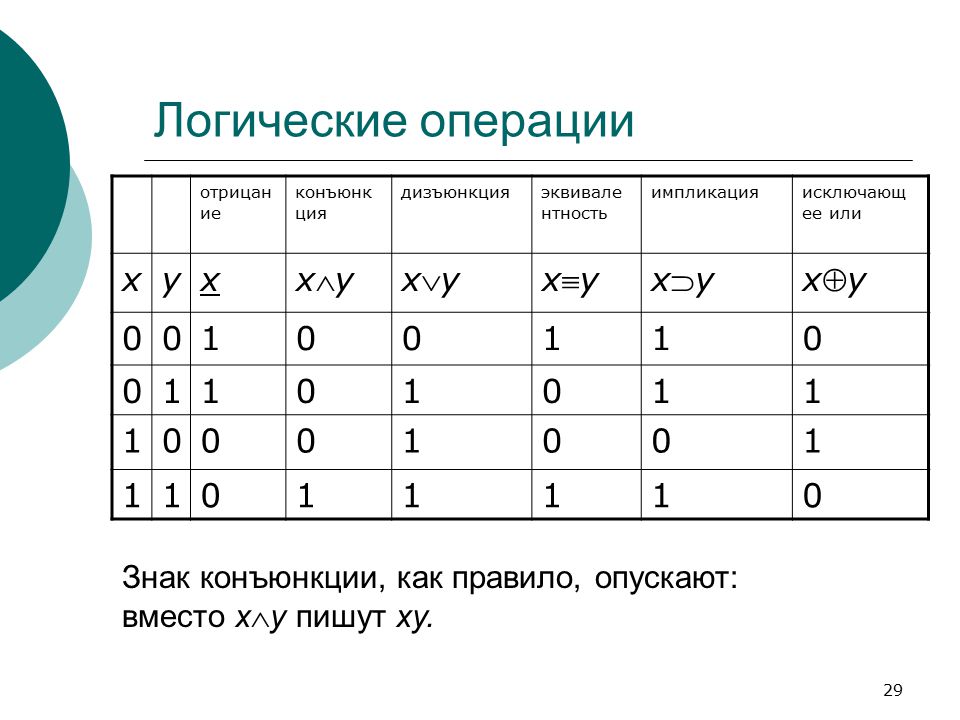 Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).

Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».

Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.

Формула приобретает следующий вид: .

В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.

Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.

Для решения используем логические функции ЕСЛИ и ИЛИ: . Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.

При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.

В качестве аргументов можно использовать другие функции. К примеру, математические.

Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.

Составим таблицу с исходными данными:

Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».

Введем формулу вида: . Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.

Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.

Статистические и логические функции в Excel

Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.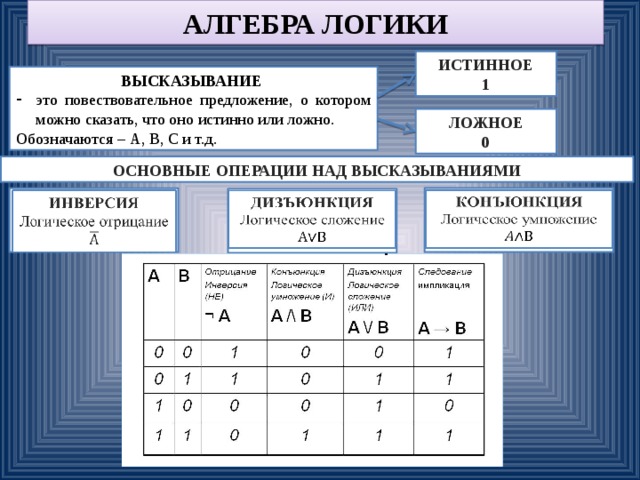

Работаем с таблицей из предыдущего раздела:

Для решения задачи используем формулу вида: . В логическом выражении «D2

Задача 2. Найти средние продажи в магазинах сети.

Составим таблицу с исходными данными:

Необходимо найти среднее арифметическое для ячеек, значение которых отвечает заданному условию. То есть совместить логическое и статистическое решение.

Чуть ниже таблицы с условием составим табличку для отображения результатов:

Решим задачу с помощью одной функции: . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.

Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.

Задача 3. Найти средние продажи в магазине №1 г.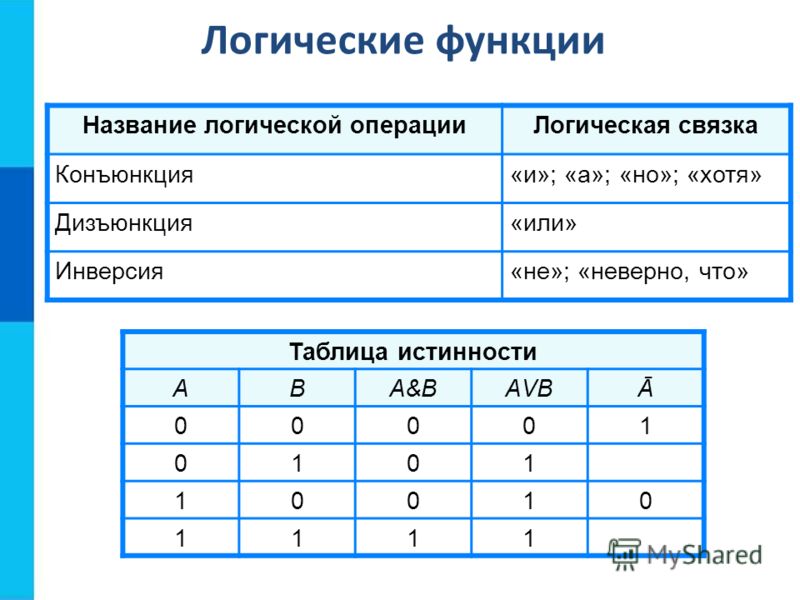 Москва.

Видоизменим таблицу из предыдущего примера:

Нужно выполнить два условия – воспользуемся функцией вида: .

Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.

Скачать примеры логических функций

Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.

Функция учитывает только те значения, которые соответствуют всем заданным условиям.

логических функций | Примечания GATE

Булева функция относится к функции, имеющей n элементов или переменных, поэтому она имеет 2n возможных комбинаций заданных переменных. Такие функции предполагают только 0 или 1 на выходе. Примером булевой функции является f(p,q,r) = p X q + r. Мы реализуем эти функции с помощью логических вентилей.

В этой статье мы рассмотрим логические функции в соответствии с программой GATE для CSE (компьютерная инженерия). Читайте дальше, чтобы узнать больше.

Содержание

• Что такое логические функции?
• Формирование таблицы истинности
• методов упрощения булевой функции
  • Карно-карта или К-карта
    • Сумма произведений (СОП) Форма
    • Произведение сумм (POS) Форма
  • Реализация вентилей NAND
• Практические задачи по булевой алгебре
• Видео о логических вентилях и минимизации булевых функций
• Часто задаваемые вопросы

Что такое логические функции?

В булевой алгебре мы имеем дело с различными логическими операциями и бинарными переменными. Здесь мы используем алгебраическое выражение, известное как логическое выражение, для описания логической функции. Логическое выражение содержит символы логических операций, двоичные переменные и константы 1 и 0. Рассмотрим теперь пример, приведенный ниже:

.

F (W, X, Y, Z) = W + XȲ + WZY Уравнение № 1

Левая часть этого уравнения здесь представляет выход B. Таким образом, мы можем сформулировать уравнение №. 1

B = W + XȲ + WZY

Формирование таблицы истинности

Мы используем таблицу истинности для представления таблицы, в которой есть все комбинации входных данных вместе с соответствующими им результатами. Также возможно преобразование уравнения переключения в таблицу истинности. Например, давайте рассмотрим уравнение переключения, данное следующим образом:

F (W, X, Y) = W + XY

Выход здесь будет высоким (1), когда W = 1 или XY = 1, или когда оба они равны 1. Для этого уравнения мы получаем таблицу истинности по Таблице (a). Общее количество строк, присутствующих в таблице истинности, будет равно 2n, где n относится к общему количеству входных переменных (для данного уравнения n=3). Следовательно, всего 23 = 8 возможных комбинаций входных данных.

Методы упрощения булевой функции

Вот методы, которые мы использовали для упрощения булевой функции:

• Метод вентиля И-НЕ
• К-карта или Карно-карта

Карно-карта или К-карта

Теоремы Де-Моргана и булевы теоремы полезны при манипулировании данным логическим выражением. Можно использовать вентили для реализации логического выражения. Общее количество логических элементов, которое нам требуется для реализации любого логического выражения, должно быть уменьшено до минимально возможного значения с помощью метода K-карты. Мы можем выполнить этот метод двумя разными способами, и мы обсудили эти методы ниже. Читайте дальше, чтобы узнать больше.

Сумма произведений (СОП) Форма

Если у нас есть три выражения, то известно, что эти выражения находятся в форме SOP, когда они представляют собой сумму трех членов WX, WY, XY, где все отдельные члены являются произведением двух переменных ( например, W. X или W.Y и т. д.). Поэтому они известны как сумма продуктов или SOP. Помните, что произведения и сумма в форме СОП НЕ являются фактическими умножениями или сложениями. На самом деле это функции И и ИЛИ. В форме SOP 1 представляет собой отсутствие полосы, а 0 — полосу. Форма SOP в основном представлена ​​.

Вот пример СОП для вашего понимания:

Произведение сумм (ПОС) Форма

Если у нас есть три выражения, то известно, что эти выражения находятся в своей POS-форме, когда они представлены в форме произведения трех членов (A+B), (X+Y) или (W+Y), где каждый член находится в форме суммы двух переменных. Поэтому эти выражения называются формой «Продукты сумм» или формой POS. В форме POS 1 представляет полосу, а 0 — отсутствие полосы. Форма POS в основном представлена ​​.

Вот пример POS для вашего понимания:

Реализация вентилей NAND

Мы можем использовать вентили И-НЕ для упрощения заданных логических функций. Мы показали это на примере ниже. Проверьте это.

Практические задачи по булевой алгебре

1. Мы используем _________ для реализации любой булевой функции.

а) Арифметическая логика

б) Логические обозначения

в) Выражения

г) Логические элементы

Ответ – (d) Логические элементы

2. Мы выполняем инверсию одного бита ввода в вывод, используя вентиль _________.

а) НЕ-И

б) И

в) НО

г) НЕ

Ответ – (г) НЕ

3. Какой из них относится к булевой переменной?

а) Строка

б) Буквальный

в) Идентификатор

г) Ключевое слово

Ответ – (б) Буквальный

4. Минимизация функции F(X,Y,Z) = X*Y*(Y+Z) равна _________:

а) Y+Z

б) ХЗ

в) XY

г) Д`

Ответ – (с) XY

Видео о логических вентилях и минимизации булевых функций

Часто задаваемые вопросы

Что такое логическая функция? Объясните примерами.

Логическая функция относится к функции, имеющей n элементов или переменных, поэтому она имеет 2n возможных комбинаций заданных переменных. Такие функции предполагают только 0 или 1 на выходе. Примером булевой функции является f(p,q,r) = p X q + r. Мы реализуем эти функции с помощью логических вентилей.

Какие бывают булевы функции?

Различные логические функции имеют три или более входных данных. Наиболее распространенными из них являются OR, AND, XOR, NOR, XNOR и NAND. Логический элемент И с N-входами будет давать ИСТИННЫЙ выходной сигнал только тогда, когда все N входных сигналов будут ИСТИННЫМИ.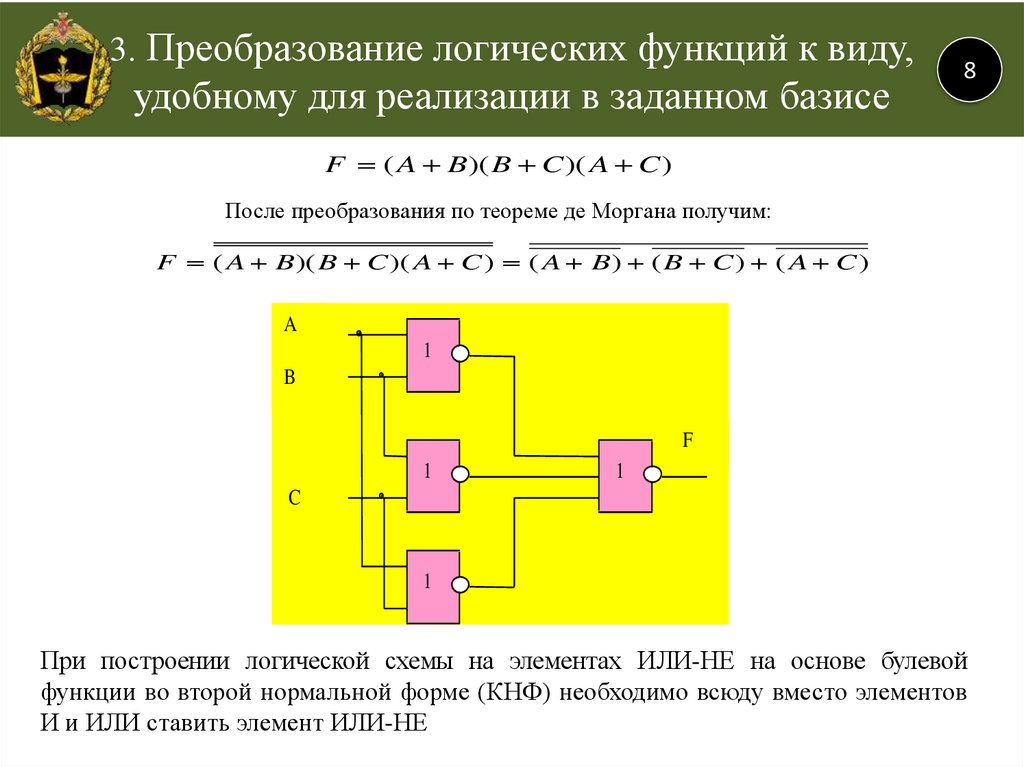 С другой стороны, вентиль ИЛИ с N-входами будет выдавать ИСТИНА на выходе только тогда, когда хотя бы один из входов окажется ИСТИНА.

Как определить булеву функцию?

Булеву функцию F=ab’ c+p можно определить в терминах четырех двоичных переменных a, b, c и p. Такая функция будет равна 1, когда a=1, b=0 или c=1. Кроме того, помимо алгебраического выражения, мы также можем описать булевую функцию в терминах таблицы истинности.

Продолжайте учиться и следите за обновлениями, чтобы получать последние обновления об экзамене GATE, а также критерии приемлемости, учебную программу GATE для CSE (компьютерная инженерия), заметки GATE CSE, вопросник GATE CSE и многое другое.

Булева логика и функции

Любые вопросы о чтении рекомендуется задавать на доске обсуждений курса!

Наш первый шаг в создании компьютера — изучение схем! Чтобы иметь возможность рассуждать и строить схемы, нам нужно сначала немного узнать о булевой логике.

Что такое булева логика?

Булева логика — это определение, основанное на двух логических значениях : правда и ложь. На самом деле вы использовали эти логические значения в Java раньше! Оказывается, наличие формального способа рассуждения об этих значениях очень полезно при создании оборудования, и определение этого рассуждения — наш первый шаг к созданию компьютера.

Почему два значения? Важная абстракция

Оказывается, сигналы на физических проводах нашего компьютерного оборудования могут постоянно иметь любое количество вольт от 0 до 5. Для наших целей мы собираемся выбрать абстракцию, которая имеет только 2 значения: «высокий» сигнал (около 5 вольт) или «низкий» сигнал (около 0 вольт). Вам может быть интересно, зачем ограничиваться только двумя значениями, высоким и низким? На самом деле большинство аппаратных средств рассчитано на абстракцию всего двух значений напряжения. Это значительно уменьшает количество ошибок в аппаратном обеспечении и в конечном итоге упрощает рассмотрение (поскольку позволяет нам использовать логическую логику).

Как мы отмечали выше, логическая логика также традиционно имеет только два значения: true и false. Затем мы можем сопоставить нашу двухзначную систему напряжения с этими двумя значениями: «высокие» сигналы соответствуют истине, а «низкие» сигналы соответствуют ложным. Кроме того, часто двоичные цифры 1 и 0 используются для обозначения значений в этой системе, где 1 означает высокий сигнал/истинное значение, а 0 — низкий уровень сигнала/ложное значение. Много разных способов обозначить одно и то же!

Это первая из многих мощных абстракций, с которыми мы столкнемся при сборке компьютера — наша дискретная система с двумя значениями позволяет нам не беспокоиться о фактических показаниях напряжения при интерпретации значения провода.

Булева алгебра

Булева алгебра — это набор операций для объединения логических значений. Так же, как в алгебре, которую вы изучали в школе, есть операции для объединения десятичных значений (например, 3 + 5 = 8), булева алгебра определяет набор операций для объединения логических значений. Булева операция определяется так называемой таблицей истинности . Таблица истинности перечисляет все возможные комбинации входных данных для этой логической операции, а затем указывает, каким должен быть результат для каждой входной комбинации. Три общие логические операции:

x And y — выводит true (1), только если оба x и y верны. Таблица истинности:

х	и	из
0	0	0
0	1	0
1	0	0
1	1	1

x Or y — выводит true (1), только если хотя бы одно из x или y истинно. Таблица истинности:

х	и	из
0	0	0
0	1	1
1	0	1
1	1	1

Not x — выводит true (1), если x — false (0), и false, если x — true. Таблица истинности (обратите внимание, что теперь у нас есть только 2 строки, потому что для одного входа есть только 2 возможных значения):

х	из
0	1
1	0

Обратите внимание, что вы можете определить логическую операцию как с помощью письменного описания, так и с помощью таблицы истинности.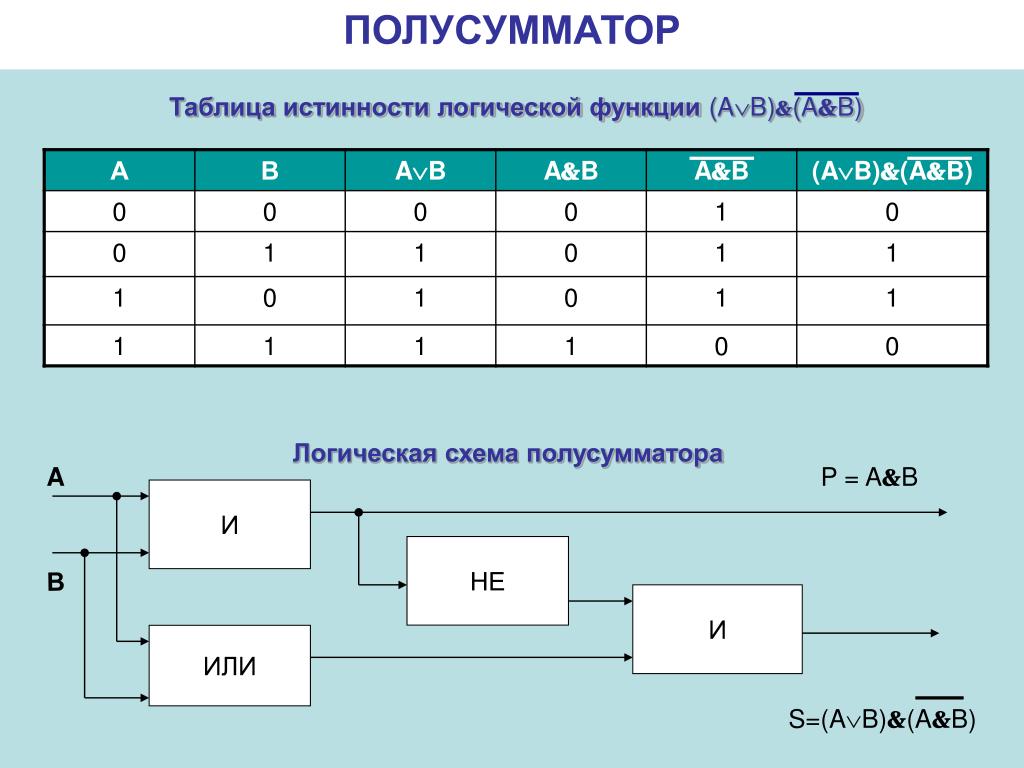 Последний — гораздо более явный способ определения функции — он точно говорит вам, что делает эта функция для каждой возможной комбинации выходных данных.

Логические выражения представляют собой комбинации логических операторов, результатом которых является значение. Мы можем оценить логическое выражение, применяя таблицу истинности снова и снова, пока не останемся с одним значением.

Пример: Не(0 или (1 И 1)) = Не (0 или 1) = Не (1) = 0

Логические функции

Мы также можем определить наши собственные булевы функции! Все, что нам нужно сделать, это дать имена входам для нашей функции, а затем указать, какие выходы будут для этих входов. Это может быть указано либо как таблица истинности, либо как логическое выражение наших входных данных!

Например, мы могли бы указать функцию как: f(x, y, z) = (x And y) Or (Not(x) And z)

Теперь кто-то может вычислить результат для комбинации входных данных, подставив входные значения в наше логическое выражение. Мы также можем использовать это логическое выражение для построения таблицы истинности для нашей логической функции. Все, что нам нужно сделать, это оценить наше логическое выражение для каждой строки нашей таблицы истинности.

Например, вторая строка в приведенной ниже таблице истинности оценивается следующим образом:

.
f(0, 0, 1) = (0 И 0) Или ((Не 0) И 1)
           = 0 Или ((Не 0) И 1)
           = 0 или (1 и 1)
           = 0 или 1
           = 1 

Посмотрите, сможете ли вы заполнить оставшиеся строки нашей таблицы истинности (полная таблица истинности приведена в разделе «Решения для упражнений» в нижней части этого чтения).
f(x, y, z) = (x And y) Или (Not(x) And z)

х	и	по	из
0	0	0
0	0	1	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Булева логика, аппаратные средства и принципиальные схемы

Почему мы изучаем булевы функции? Оказывается, компьютерные схемы могут быть представлены булевыми функциями! Значения (например, 0 и 1) передаются по проводам, операторы (например, и ) сопоставляются с физическими логическими элементами, а комбинации проводов и физических логических элементов создают наши аппаратные устройства. Когда мы говорим x And y , мы описываем физическую схему с проводом, соответствующим входу x , проводом, соответствующим входу y , и вентилем And , соединяющим два входных провода и отправляющим выходной сигнал. на другом проводе. Это основа нашей работы в течение первых нескольких недель этого класса.

Принципиальные схемы — это еще один способ представления логической логики, который часто используется при разработке аппаратного обеспечения. Они используют обычные символы для представления логических вентилей (дополнительные сведения об этих символах см. в главе 1 учебника).

Пример: а или б

Мы также можем комбинировать операции, соединяя логические вентили вместе.

Пример: Не((а Или б) И в)

Упрощение логических функций

Упрощение логических функций на самом деле является главным приоритетом при разработке аппаратного обеспечения. Для реализации более простых логических функций требуется меньше проводов и логических элементов, что в конечном итоге приводит к более дешевому и быстрому оборудованию. Один из способов упростить логические функции — применить логических идентификаторов в логическую функцию. Эти тождества определяют эквивалентные логические выражения, которые позволяют нам манипулировать нашими логическими функциями и потенциально создавать более простые выражения. Неполный список:

• Коммутативность
  • (х И у) = (у И х)
  • (х или у) = (у или х)
• Ассоциативность
  • (х И (у И z)) = ((х И у) И z)
  • (х или (у или г)) = ((х или у) или г)
• Распределительная собственность
  • (х И (у Или z)) = (х И у) Или (х И z)
  • (х или (у и z)) = (х или у) и (х или z)
• Закон Де Моргана
  • Не(х и у) = не(х) или не(у)
  • Не(х или у) = не(х) и не(у)
• Двойное отрицание
  • Не(Не(х)) = х

Допустим, у нас есть функция f(x, y) = Not(Not(x) And Not(y)) . Мы можем применить тождества, чтобы потенциально упростить эту функцию:

 Not(Not(x) And Not(y)) **используйте закон де Моргана**
= Not(Not(x)) Or Not(Not(y)) **используйте двойное отрицание**
= х или у 

Другой способ упростить наше выражение — составить для него таблицу истинности и посмотреть, соответствует ли оно каким-либо уже известным нам функциям.
f(x, y) = Not(Not(x) And Not(y))

х	и	из
0	0	0
0	1	1
1	0	1
1	1	1

Это выглядит точно так же, как таблица истинности для x Or y ! Мы не будем просить вас делать слишком много упрощений в этом курсе, но это важная часть проектирования оборудования, поэтому мы подумали, что стоит упомянуть об этом.

Синтез булевых функций

Мы говорили о создании таблицы истинности из существующего логического выражения, теперь давайте поговорим о создании логического выражения из существующей таблицы истинности! Это важная часть аппаратного проектирования — часто мы знаем, какие выходные данные нам нужны для каждого набора входных данных (т. е. мы знаем таблицу истинности), а затем нам нужно создать логическое выражение, чтобы мы могли определить логические элементы для нашего функционировать и, в конечном счете, создавать аппаратное обеспечение, соответствующее этому. Предположим, у нас есть следующая таблица истинности для нашей функции:

х	и	по	из
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

Наш план будет таким: во-первых, для каждой строки, где вывод «истинен», определите функцию, которая «истинна» для этой строки, и только что один ряд.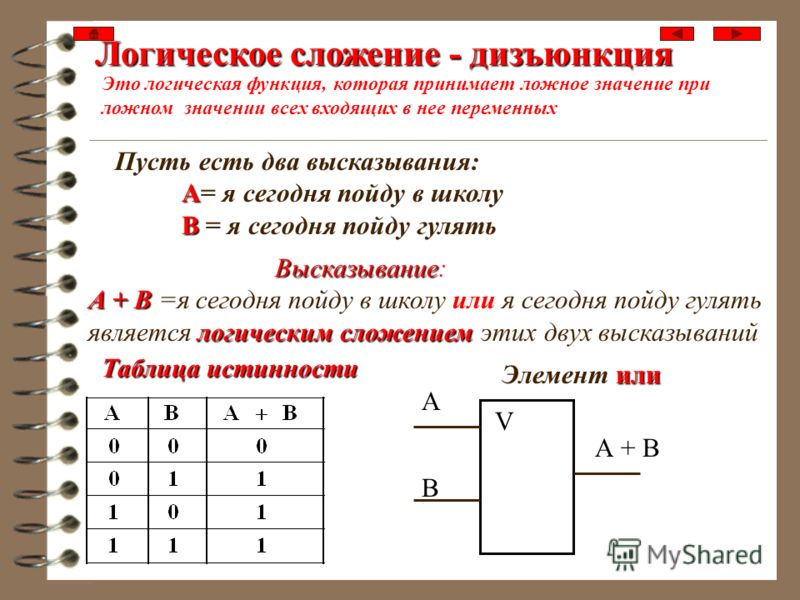 Затем, поскольку у нас есть выражения для каждой из истинных строк, мы можем объединить их вместе, чтобы получить выражение для всей таблицы истинности.

Оказывается, мы можем описать любой ряд в терминах И и Не вентилей. Для каждого ввода, если в строке появляется 1, мы будем использовать только ввод, а если появляется 0, мы отрицаем ввод. Затем мы можем объединить наши входы с вентилями и . Например: row1(x, y, z) = Not(x) And Not(y) And Not(z)

Мы видим, что row1 верно только для первой строки нашей таблицы истинности!

х	и	по	из	ряд1
0	0	0	1	1
0	0	1	0	0
0	1	0	1	0
0	1	1	0	0
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	0	0

Проделаем то же самое для остальных «истинных» строк:
row3 = Not(x) And y And Not(z)
row5 = x And Not(y) And Not(z)

х	и	по	из	ряд1	строка3	ряд5
0	0	0	1	1	0	0
0	0	1	0	0	0	0
0	1	0	1	0	1	0
0	1	1	0	0	0	0
1	0	0	1	0	0	1
1	0	1	0	0	0	0
1	1	0	0	0	0	0
1	1	1	0	0	0	0

Теперь нам просто нужно объединить наши различные выражения строк, чтобы получить наше окончательное выражение (мы назовем нашу функцию f ).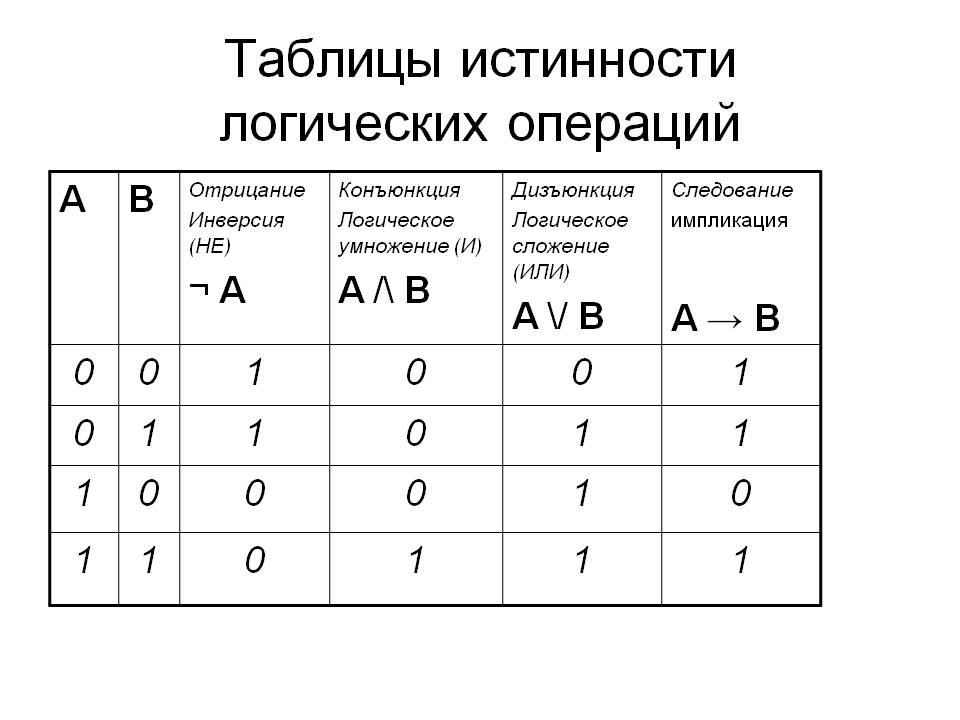 Обратите внимание, что для получения f , мы хотим, чтобы 1 появлялась в строке, если в одной из других строк есть хотя бы одна 1. Какую операцию вам напоминает «по крайней мере»? Ага, операция или ! Мы объединяем наши выражения строк, используя или , чтобы получить наше окончательное выражение для f .
f(x, y, z) = строка1 или строка2 или строка3 f(x, y, z) = (Не(x) И Не(y) И Не(z)) Или (Не(x) И y И Не(z)) Или (x И Не(y) И Не (г))

Это абсолютно правильное логическое выражение! Мы можем упростить это выражение, если хотим (оно довольно длинное…), но я думаю, важно отметить, что приведенное выше выражение правильно описывает таблицу истинности, с которой мы начали; это просто может быть немного более многословно, чем нам хотелось бы. Отсюда мы можем упростить, используя логические тождества (опуская шаги, потому что это не является предметом этого раздела), что приводит к окончательному выражению:
f(x, y, z) = Not(z) And (Not(x) Or Not(y))

Очень удобно, что этот процесс работает для каждой возможной таблицы истинности/логического выражения! Подводя итог процессу, чтобы получить логическое выражение для данной таблицы истинности, мы:

1. Создайте выражение для каждой «истинной» строки в таблице истинности, используя И и Не .