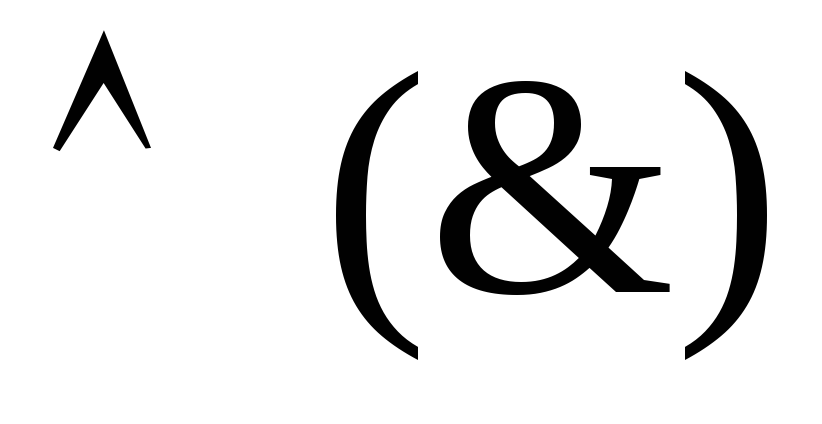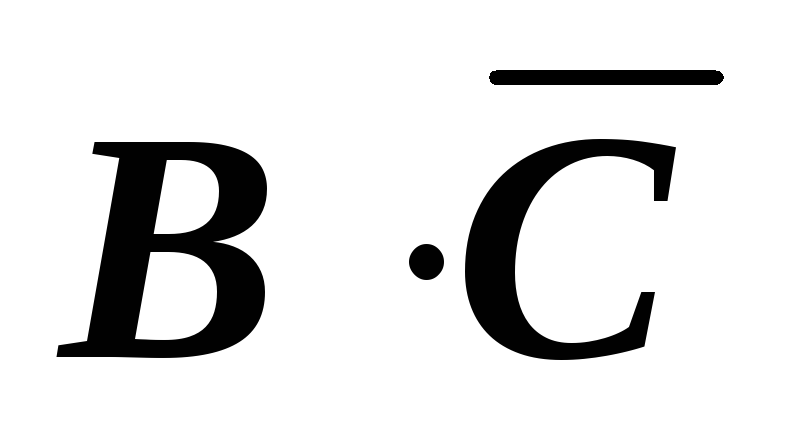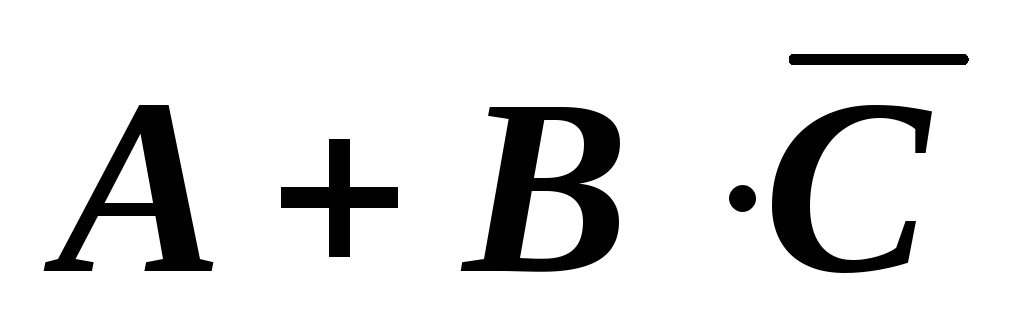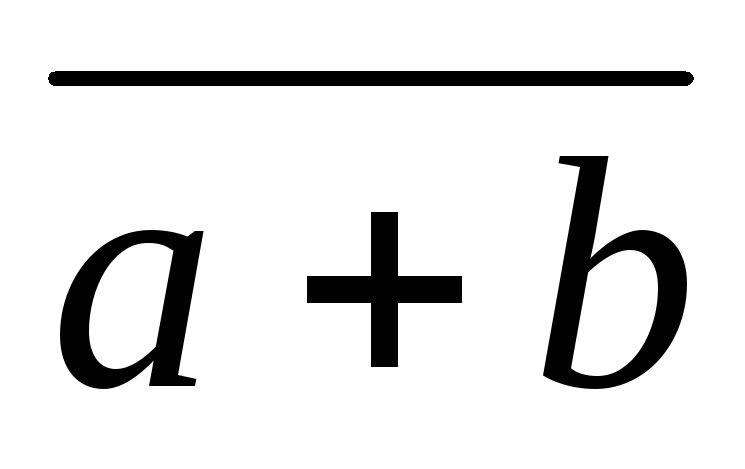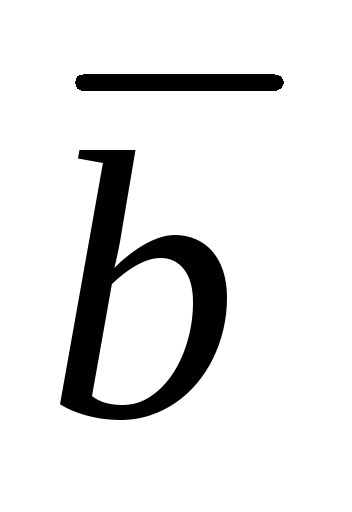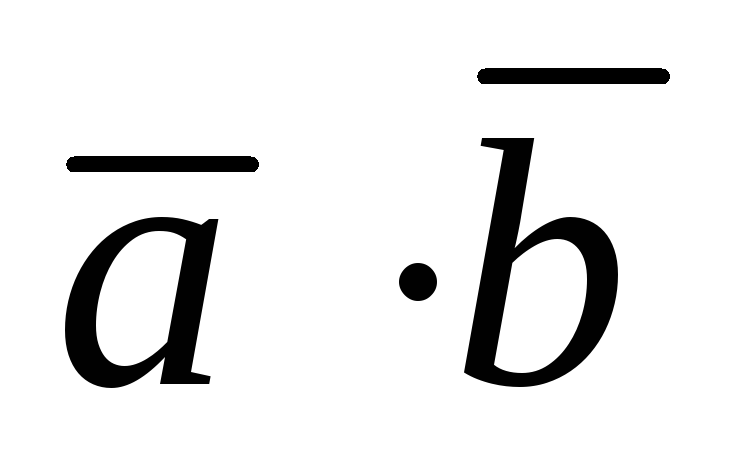Основные логические функции
Лабораторная работа №3
Решение логических задач школьного курса повышенной сложности
Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Алгебра логики возникла в середине 19 века в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С. Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.) и дальнейшим развитием математической логики (последняя четверть 19 в. — 1-я половина 20 в.), предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием
В отличие от обычной алгебры, изучающей математические функции, алгебра логики изучает логические функции. Известно, что функция — это закон соответствия между переменными. Следовательно,
Логическим выражением называется выражение, о котором можно сказать истинно оно или ложно.
Примеры:
«5>8» — логическое выражение, т.к. о нем можно сказать, что оно ложно.
«Эту девочку зовут Юля» — логическое выражение.
«Подайте книгу» — это не логическое выражение, т.к. о нем нельзя сказать, истинно оно или ложно
Логическая функция может также принимать два значения.
Таким образом, логические переменные и функции определены на множестве двух значений — {0,1}.
ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое — единицей. На такие компоненты воздействуют двоичные сигналы. Под воздействием сигналов компоненты изменяют свои состояния, т. е. состояние компонентов или значения их выходных сигналов зависят от значений воздействующих сигналов. Очевидно, что функционирование компонентов ЭВМ следует описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.
Логические функции характеризуются (задаются) так называемыми таблицами истинности, или соответствия. Таблица истинности— это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.
Функция отрицания
Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот. Запись этой функции:
F=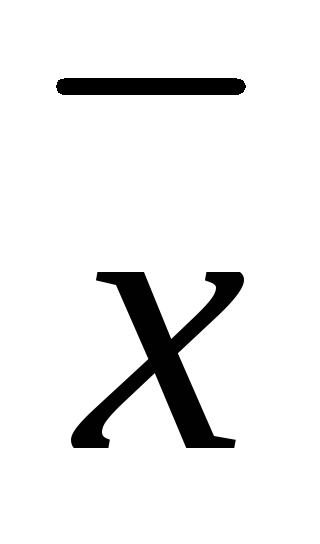
Конъюнкция может быть обозначена следующими символами:
¬,¯, не, not.
Черта над переменной xявляется признаком отрицания (инверсии). Таблица истинности этой функции представлена на рис. 1а. Функция логического отрицания описывает функционирование логического элемента НЕ (рис. 1б).
Условно-графическое обозначение элемента НЕ приведено на рис. 1в. Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (x=0,F=1) и, наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x=1,F=0). Графически отрицание можно представить с помощью кругов Эйлера (рис. 2).
а) б) в)
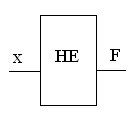
Рис. 1. Элемент НЕ
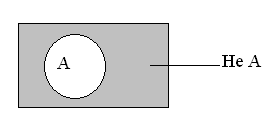
Рис. 2. Графическое представление отрицания на множестве
Функция логического умножения (конъюнкция)
Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Эта функция называется также конъюнкцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты записи конъюнкции:
F=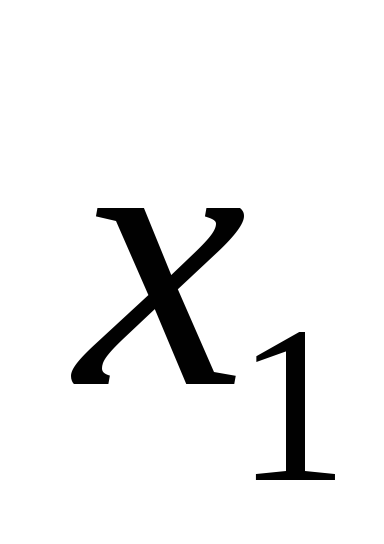
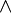
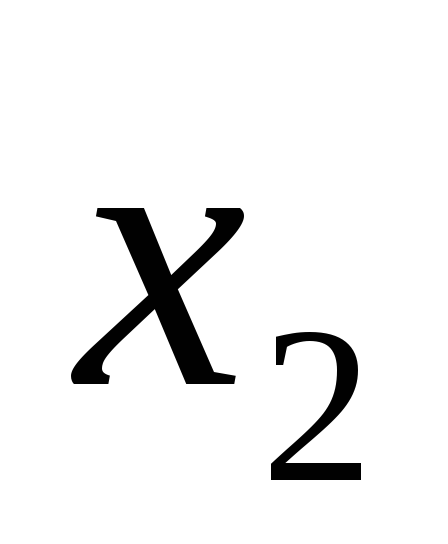 ;F=
;F=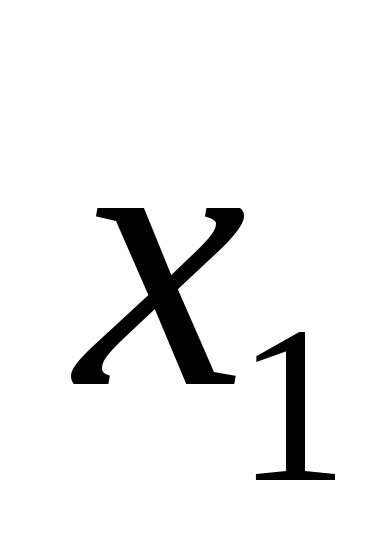 •
•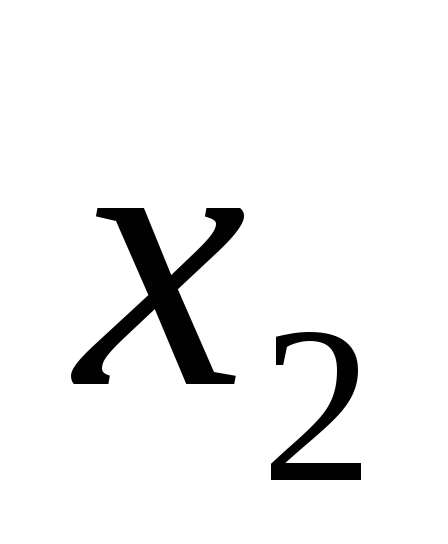 ;F=
;F=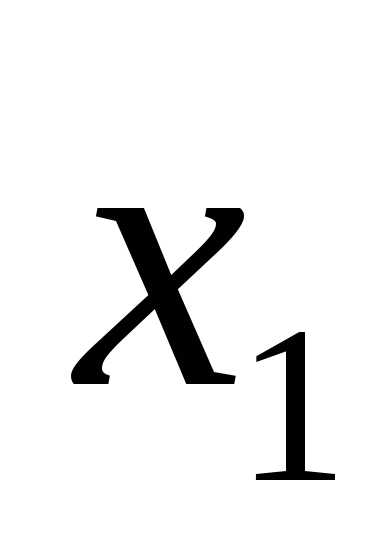
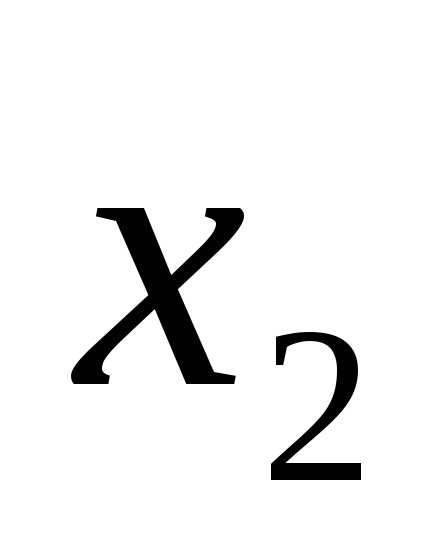
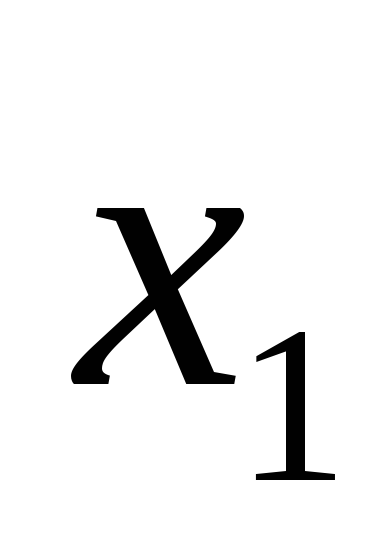 &
&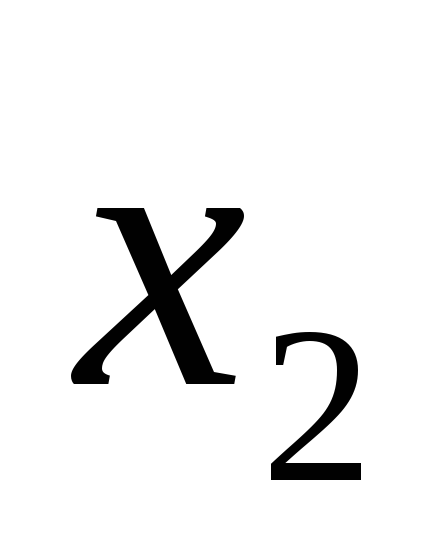 .
.Конъюнкция может быть обозначена следующими символами:
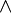 ,
&, •, ∩, and, и.
,
&, •, ∩, and, и.
Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а. Из рассмотрения таблицы следует, что эта функция принимает единичное значение на наборе 4. Логическое умножение описывает работу элемента И (рис. 3б). Графически конъюнкцию можно представить с помощью кругов Эйлера (рис. 4).
а) б) в)
|
| F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
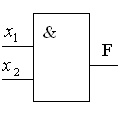
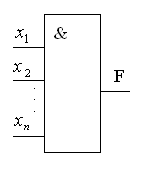
Рис. 3. Элемент И
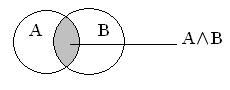
Рис. 4. Графическое представление конъюнкции на множествах
Конъюнкция на числовых множествах
(операция пересечения): {a,b,c} 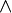 {b,c,d,e}={b,c}.
{b,c,d,e}={b,c}.
Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе 1, и на входе 2.
В общем случае элемент И может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.:
F=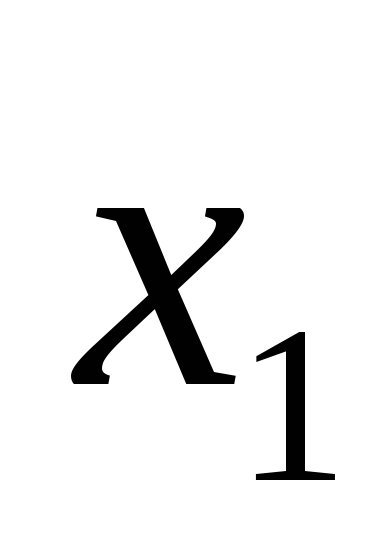 •
•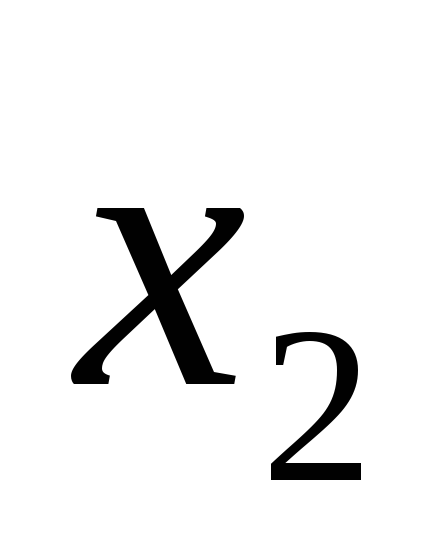 •
•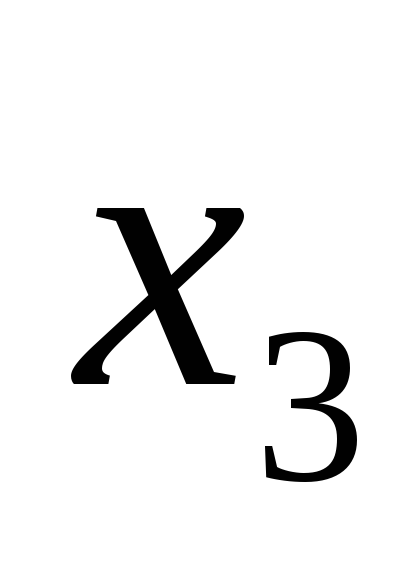
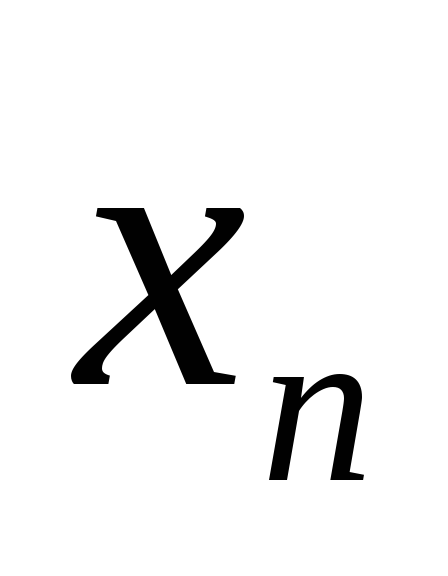 .
.Функция логического сложения (дизъюнкция)
Логическое сложение – это логическая
функция, по крайней мере, от двух
переменных, которая принимает нулевое
значение при нулевых значениях всех
переменных. Эта функция называется
также дизъюнкцией. Таблица истинности
элементарной дизъюнкции представлена
на рис. 3а. Элементарная дизъюнкция
принимает единичное значение на наборах
1, 2, 3 и нулевое значение – только на
наборе 0. Функция записывается в одном
из двух видов: F=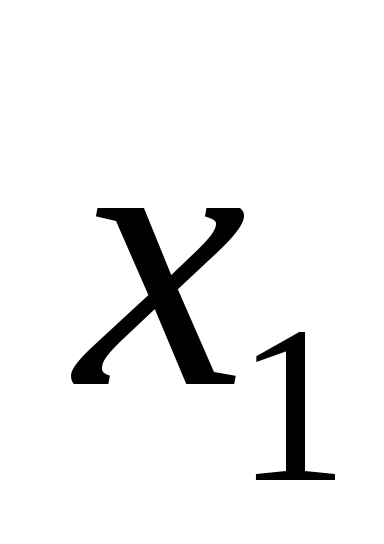
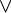
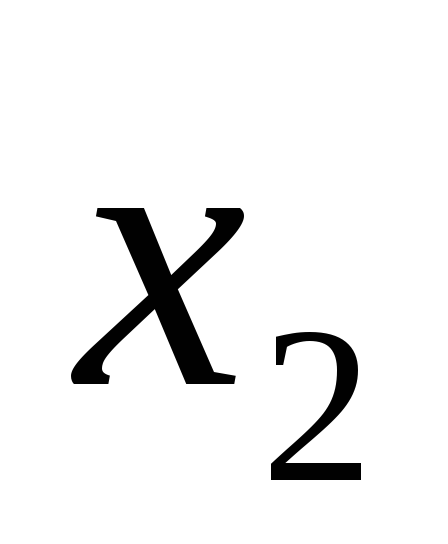 илиF=
илиF=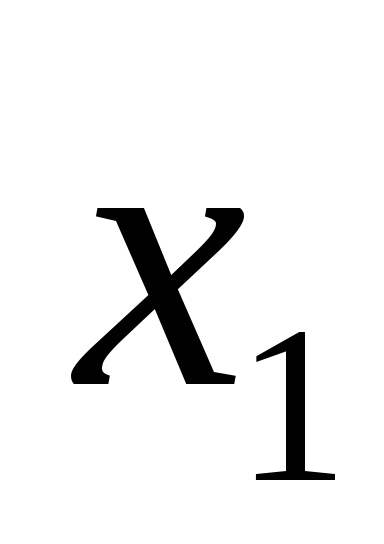 +
+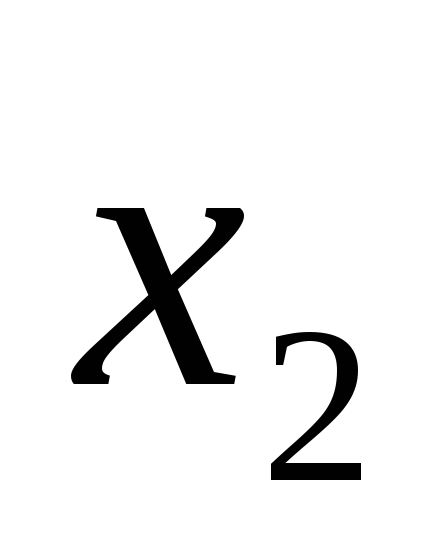 .
. Знак «плюс» не является алгебраическим,
т.к. при 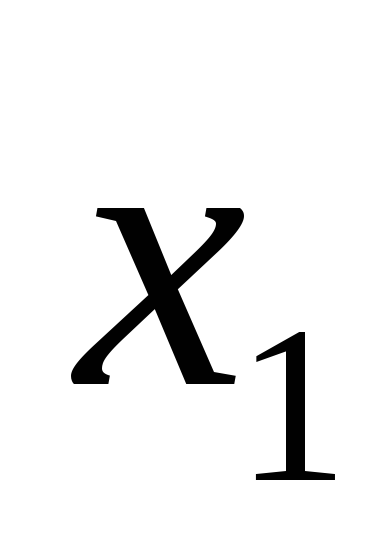 =1,
=1, 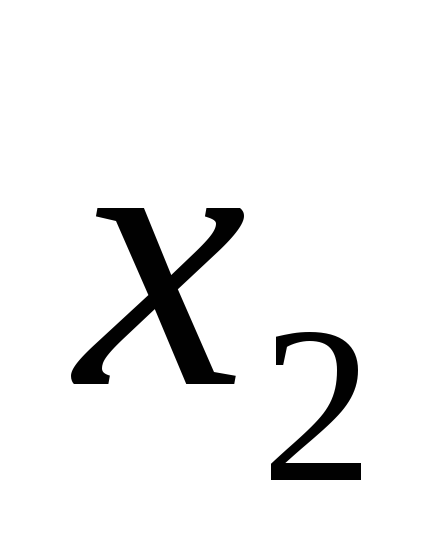 =1
дизъюнкцияF=
=1
дизъюнкцияF=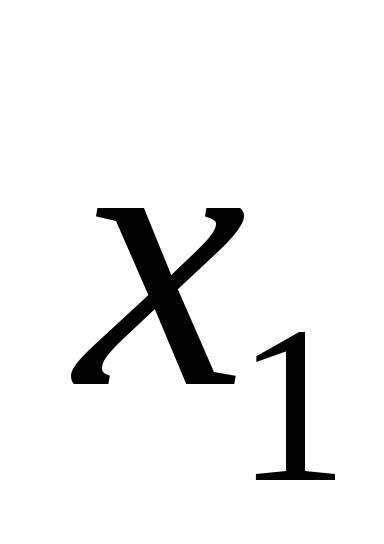 +
+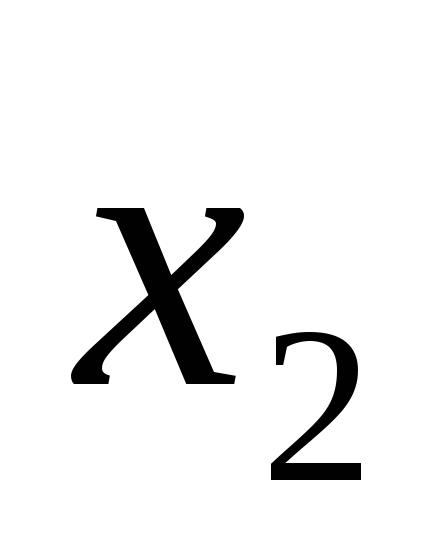 =1
=1
Дизъюнкция может быть обозначена следующими символами:
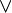 ,
+,
,
+, ,
or, или.
,
or, или.
Дизъюнкция описывает функционирование элемента ИЛИ (рис. 5б). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или на входе 2, или на двух входах единичные сигналы. И только в том случае, когда на оба входа поступают нулевые сигналы, на выходе элементов появляется нулевой сигнал.
В общем случае элемент ИЛИ может иметь n входов (рис. 5в). При этом он реализует дизъюнкцию от n переменных.
а) б) в)
|
| F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
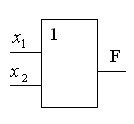
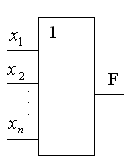
Рис. 5. Элемент ИЛИ
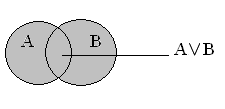
Рис. 6. Графическое представление дизъюнкции на множествах
Дизъюнкция на числовых множествах
(операция объединения):
{a,b,c}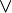 {b,c,d,e}={a,b,c,d,e}.
{b,c,d,e}={a,b,c,d,e}.
Равнозначность (эквиваленция)
Равнозначность – это логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных. Одинаковые по значению переменные называются равнозначными, поэтому функция носит название «равнозначность».
Запись функции:
F=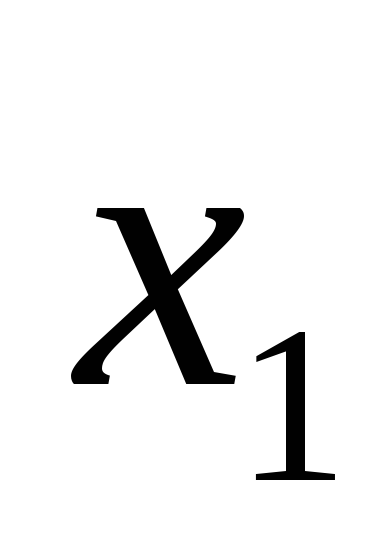
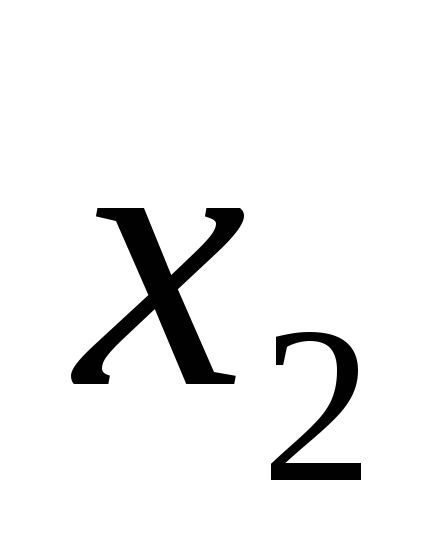 +
+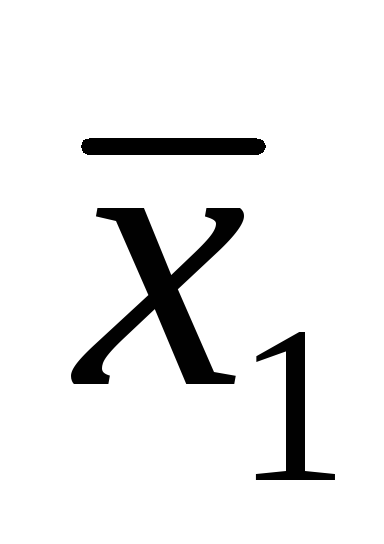
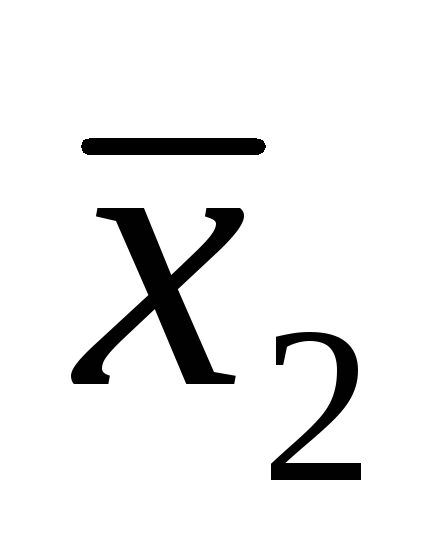 .
.
Таблица истинности функции равнозначности представлена на рис. 7а. Эта функция реализуется элементом равнозначности (сравнения), который показан на рис. 7б.
Эквиваленция может быть обозначена следующими символами:
~, 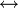 ,
,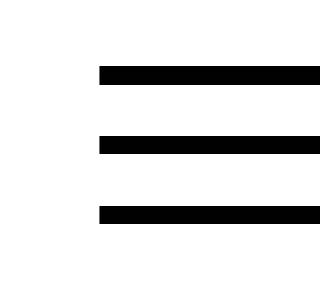 ,
, .
.
Элемент используется для сравнения двоичных сигналов.
|
| F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
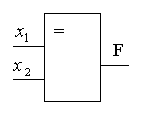
а) б)
Рис. 7. Элемент равнозначности
Логическое следование (импликация)
Обозначение логического следования:
F=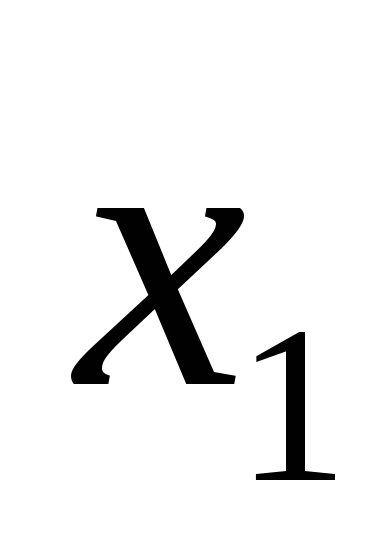 →
→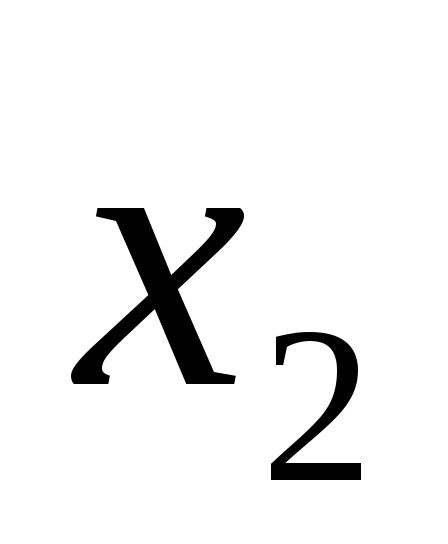 .
.
Высказывание F=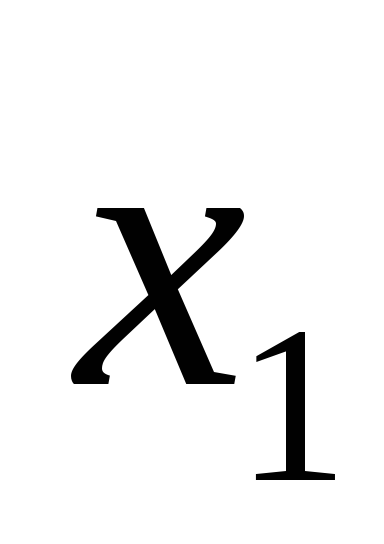 →
→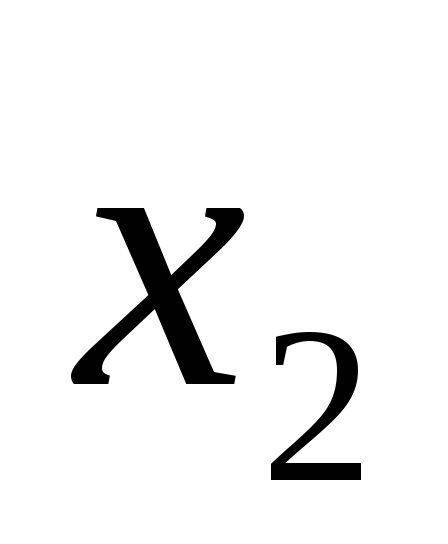 будем
считать истинным во всех случаях, кроме
случая, когда
будем
считать истинным во всех случаях, кроме
случая, когда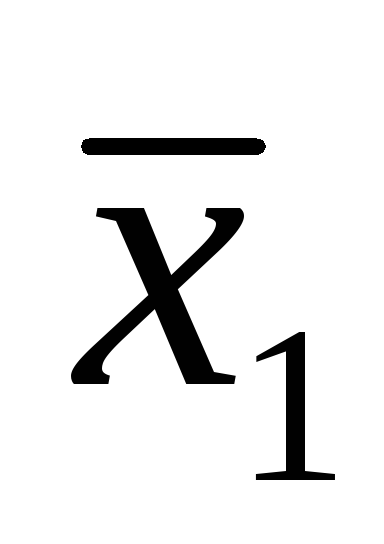 истинно, а
истинно, а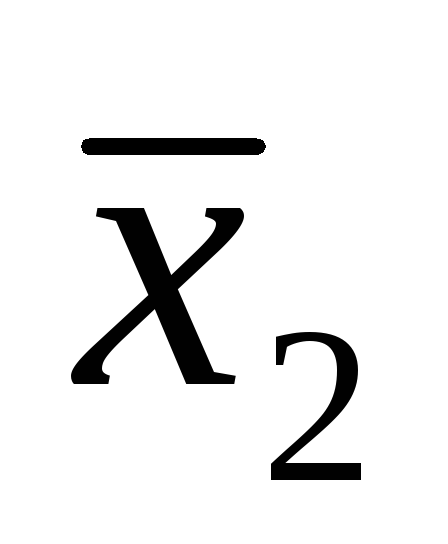 ложно. Таблица истинности представлена
на рис. 8.
ложно. Таблица истинности представлена
на рис. 8.
|
| F= |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Рис. 8. Элемент импликации
Импликация может быть обозначена следующими символами:→, ,.
Элемент (штрих) Шеффера
Обозначение:
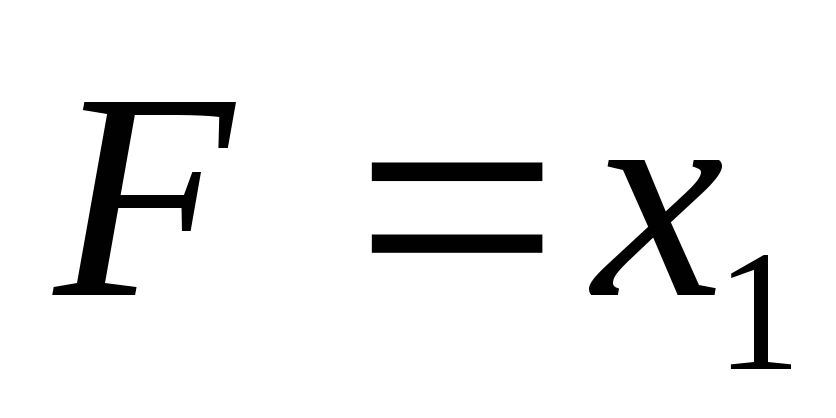
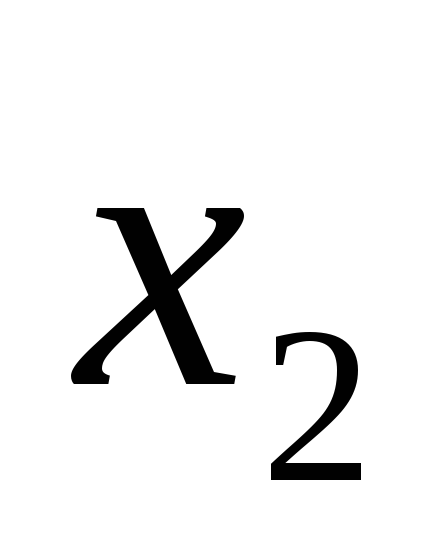 ;
;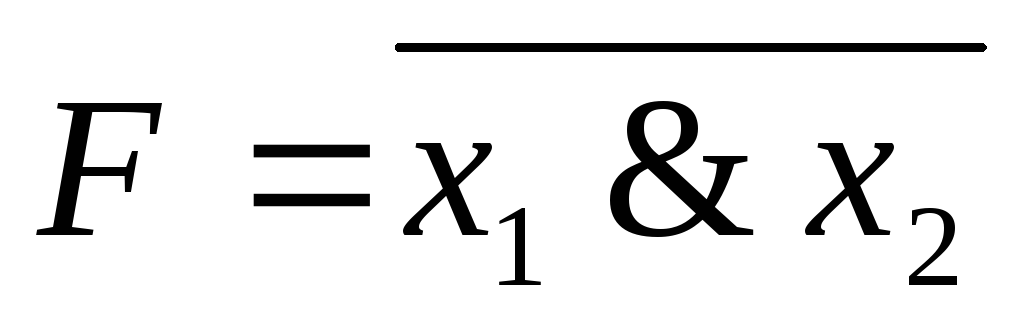 .
.
Другое название этой функции: «И-НЕ».
Высказывание 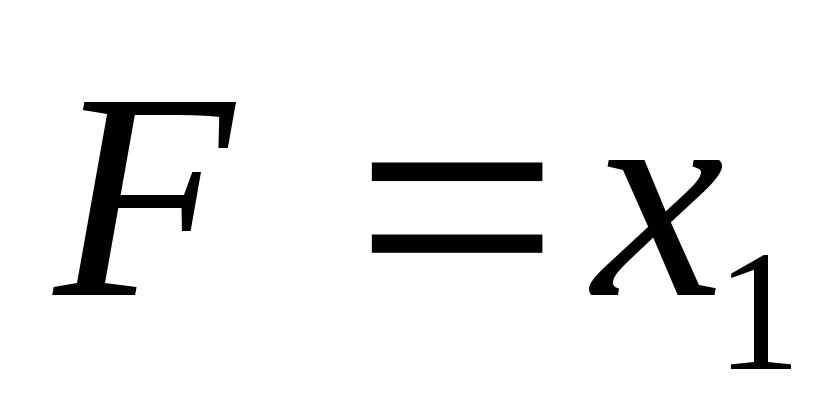
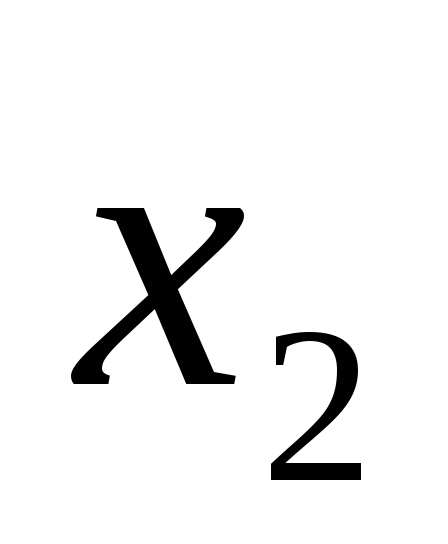 будем считать ложным, когда
будем считать ложным, когда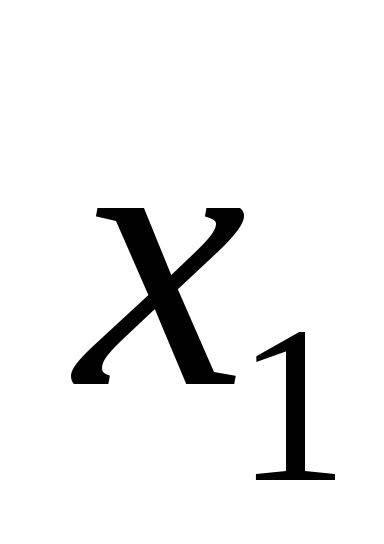 и
и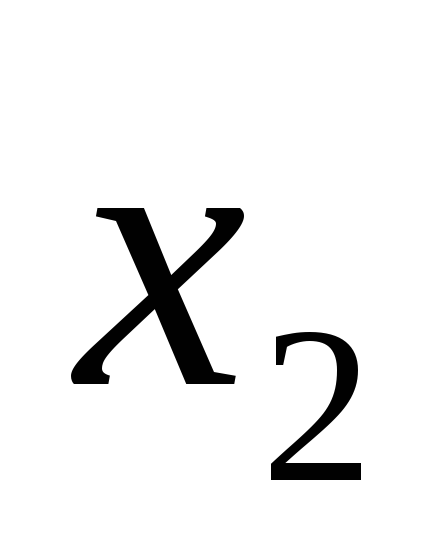 равны единице. Таблица истинности
представлена на рис. 9.
равны единице. Таблица истинности
представлена на рис. 9.
|
|
|
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Рис. 9. Элемент (штрих) Шеффера
Элемент Вебба (стрелка Пирса)
Обозначение:
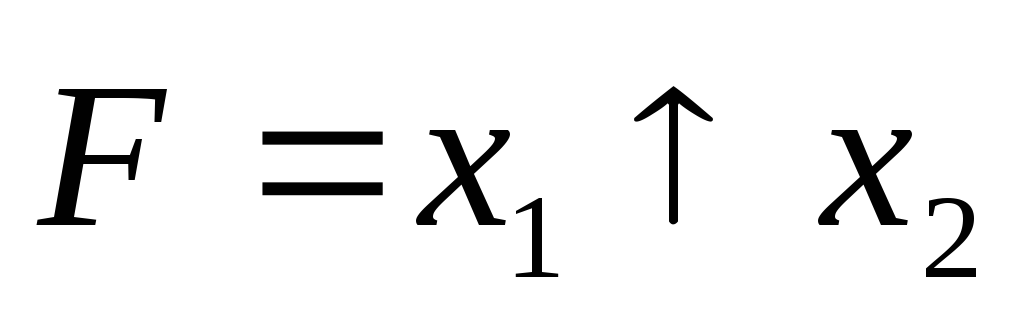 ;
;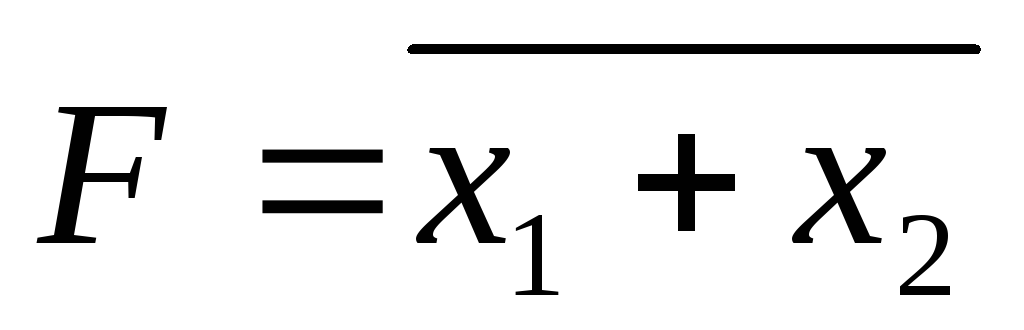 .
.
Высказывание 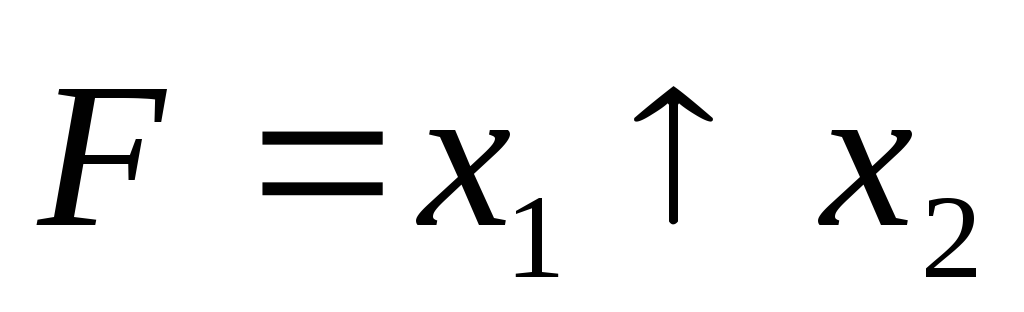 будем считать истинным только тогда,
когда оба операнда
будем считать истинным только тогда,
когда оба операнда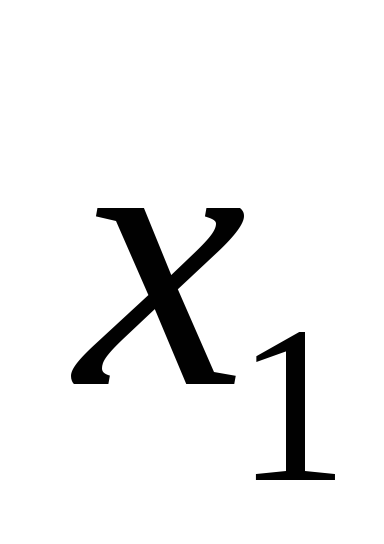 и
и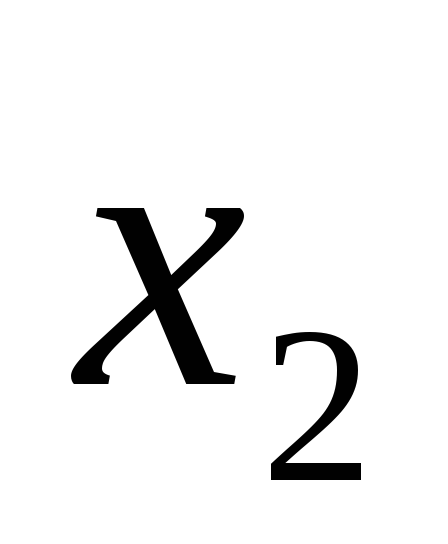 равны нулю. Таблица истинности представлена
на рис.10.
равны нулю. Таблица истинности представлена
на рис.10.
Другое название этой функции: «ИЛИ-НЕ».
Рис. 10. Элемент Вебба (стрелка Пирса)
Сложение по модулю 2.
Обозначение:
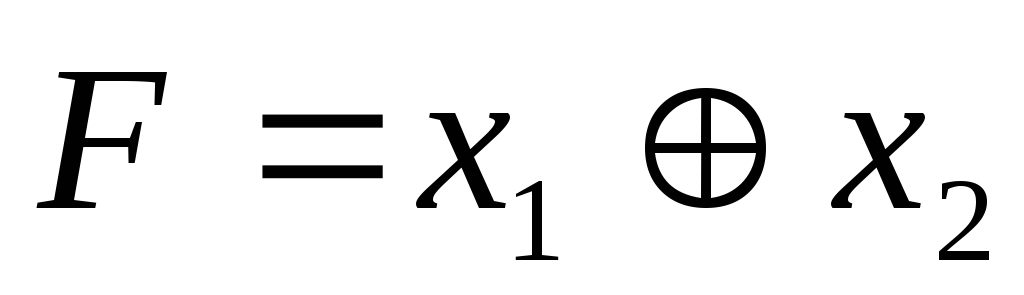 ;
;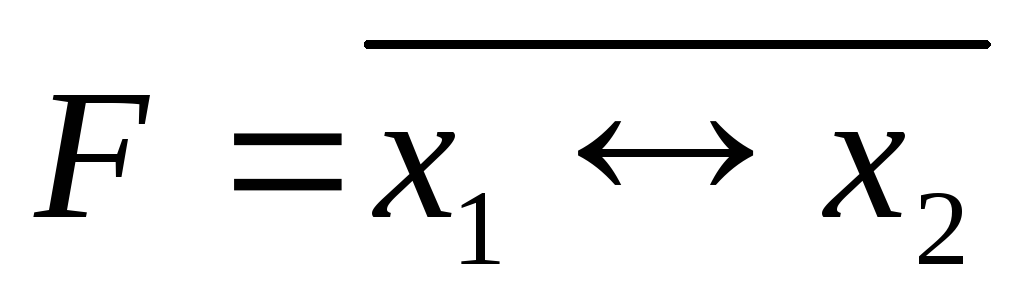 ;
;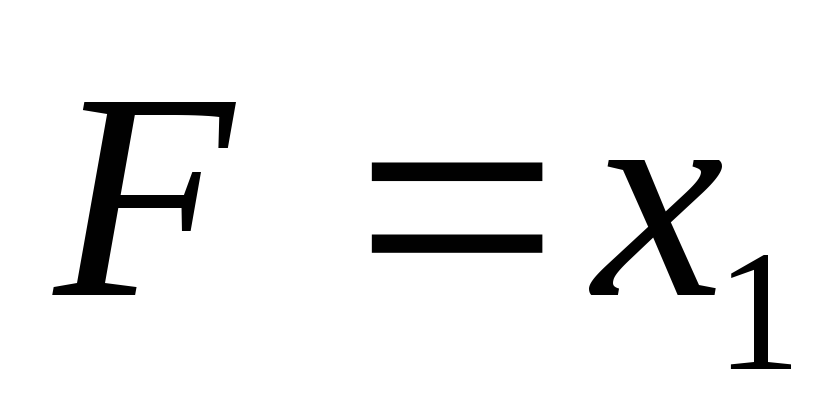 XOR
XOR 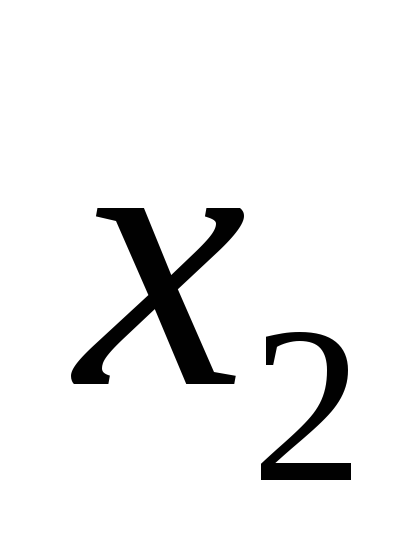 .
.
Высказывание 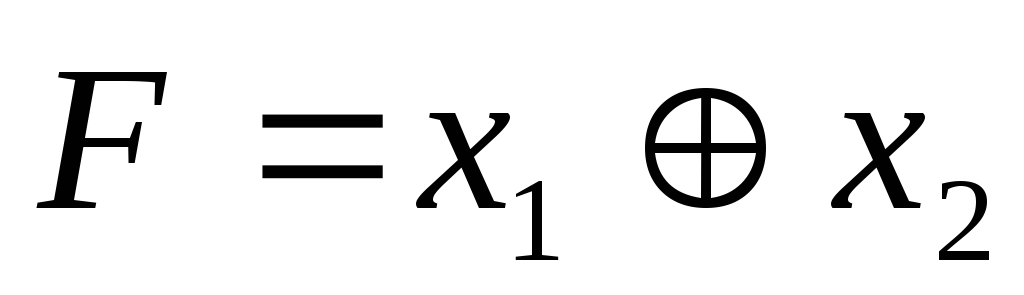 будем считать истинным, если первый
операнд
будем считать истинным, если первый
операнд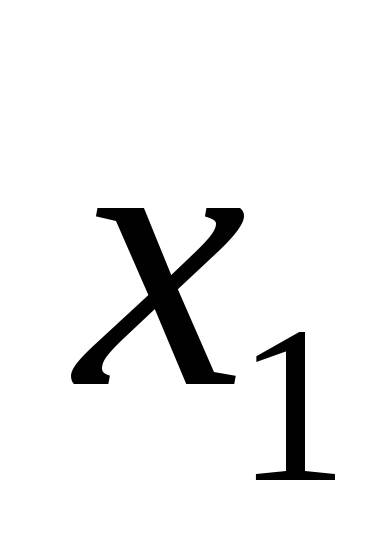 не равен второму операнду
не равен второму операнду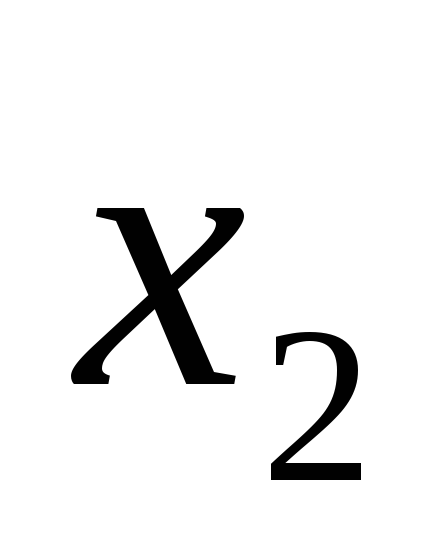 .
Таблица истинности представлена на
рис. 11.
.
Таблица истинности представлена на
рис. 11.
Другие названия этой функции: «исключающее ИЛИ», «логическое ЛИБО», «неравносильность», «неэквивалентность», «логическое сложение», «булево сложение».
Рис. 11. Сложение по модулю 2
Коимпликация
Обозначение:
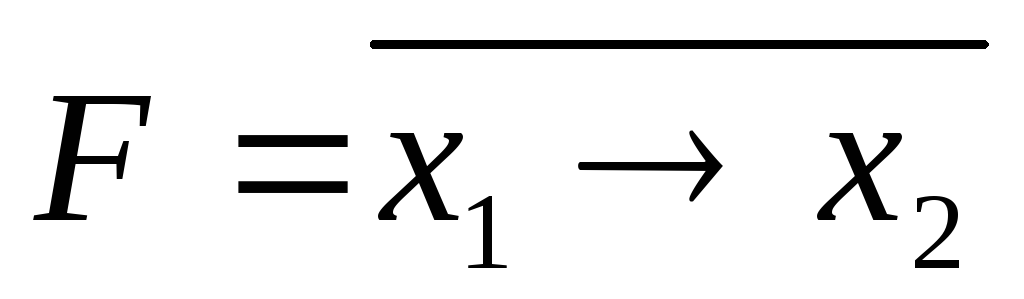 ;
;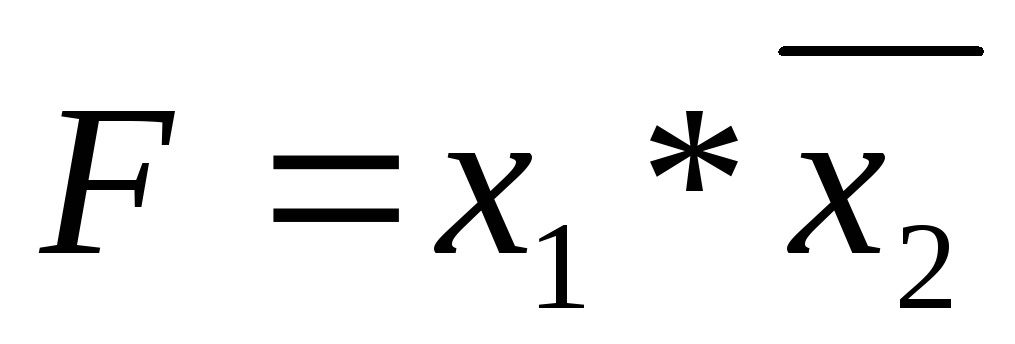 .
.
Высказывание 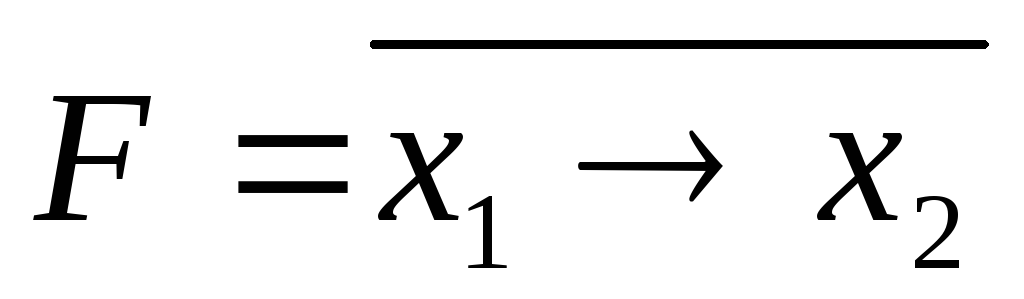 будем считать истинным, если первый
операнд
будем считать истинным, если первый
операнд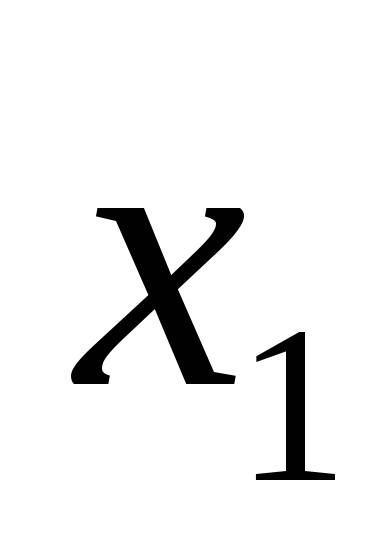 равен 1, а второй операнд
равен 1, а второй операнд 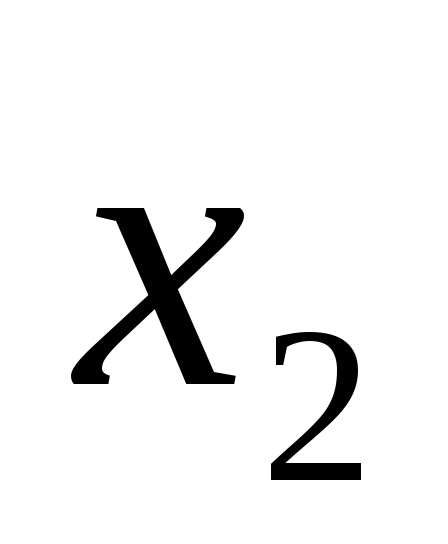 равен 0. Таблица истинности представлена
на рис. 12.
равен 0. Таблица истинности представлена
на рис. 12.
Рис. 12 Таблица истинности функции коимпликация
Приоритет операций в логическом выражении, не содержащем скобок:
О
 трицание.
трицание.Конъюнкция, *, /, div,mod.
Дизъюнкция, +, -.
Операция отношения.
Для усиления операции используются скобки.
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например, ;
- на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и , и , и . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо — с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:
К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
- либо ;
- либо ;
- либо .
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо .
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
Логические функции (ссылка) — Служба поддержки Office
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
Функция | Описание |
|---|---|
|
И |
Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА. |
|
ЛОЖЬ |
Возвращает логическое значение ЛОЖЬ. |
|
ЕСЛИ |
Выполняет проверку условия. |
|
ЕСЛИОШИБКА |
Возвращает введенное значение, если вычисление по формуле вызывает ошибку; в противном случае возвращает результат вычисления. |
|
ЕСНД
|
Возвращает значение, которое задается, если выражение принимает значение #Н/Д. В противном случае возвращает результат выражения. |
|
УСЛОВИЯ
|
Проверяет соответствие одному или нескольким условиям и возвращает значение для первого условия, принимающего значение ИСТИНА. |
|
НЕ |
Меняет логическое значение своего аргумента на противоположное. |
|
ИЛИ |
Возвращает значение ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА. |
|
ПЕРЕКЛЮЧ
|
Сравнивает выражение со списком значений и возвращает результат, соответствующий первому совпадающему значению. Если совпадений не выявлено, может возвращаться указанное значение по умолчанию. |
|
ИСТИНА |
Возвращает логическое значение ИСТИНА. |
|
ИСКЛИЛИ
|
Возвращает логическое исключающее ИЛИ всех аргументов. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
См. также
Функции Excel (по категориям)
Функции Excel (по алфавиту)
1.6.3. Элементарные логические функции и логические элементы
Логические функции, зависящие от одной или двух переменных, называются элементарными. К основным логическим функциям относятся следующие элементарные функции: отрицание; логическое умножение; отрицание от логического умножения; логическое сложение; отрицание от логического сложения; равнозначность; отрицание равнозначности.
Функция отрицания— это логическая функция от одного аргумента, которая принимает значение1, если аргумент равен0, и принимает значение0, если аргумент равен1, и называетсяотрицанием (инверсией)или логической функциейНЕ:
Запись логической функции НЕ
–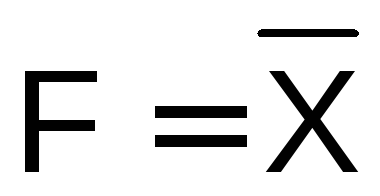 , где черта над переменной–признак инверсии. Логическая функцияНЕот одного аргумента
описывается таблицей истинности:
, где черта над переменной–признак инверсии. Логическая функцияНЕот одного аргумента
описывается таблицей истинности:
Логический элемент «НЕ» (инвертор) реализует операцию отрицания. Если на входе этого логического элемента 0, то на выходе 1, а когда на входе 1, на выходе 0.
Условное обозначение инвертора на структурных схемах приведено на рис/ 1.6.3-1.
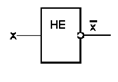
Рис. 1.6.3-1.
Функцией логического умноженияnаргументов называется логическая функция, которая принимает значение1только в том случае, когда все аргументы равны1, а0– во всех остальных случаях.
Функцию логического умножения называют также конъюнкциейили функцией И.
Элементарная функция логического умножения зависит от двух аргументов и описывается следующей таблицей истинности:
X | Y | F |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Запись логической функции И: F=XΛY ; F=X&Y ; F=XY,
где знаки «Λ», «&»,«» – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны.
Логический элемент «И»реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах конъюнкции с двумя входами представлено на рис. 1.6.3-2.
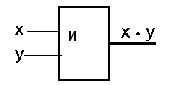
Рис. 1.6.3-2.
Функцией логического сложения n аргументов называется логическая функция, которая принимает значение0только в том случае, когда все аргументы равны0 (т.е. при набореnнулей), и1во всех остальных случаях (т.е. когда хотя бы один аргумент равен1).
Функцию логического сложения называют также дизъюнкцией или логической функциейИЛИ.
Элементарная дизъюнкция зависит от двух аргументов и описывается следующей таблицей истинности:
X | Y | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Запись логической функции ИЛИ: F=XVY ; F=X + Y,где знаки «V», «+»– обозначают операцию логического сложения.
Логический элемент «ИЛИ»реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе элемента «ИЛИ»будет единица, на её выходе также будет единица. Условное обозначение на структурных схемах логического элемента «ИЛИ» с двумя входами представлено на рис. 1.6.3-3.
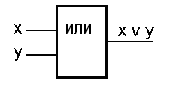
Рис.1.6.3-3.
Функция отрицания от логического умноженияпринимает значение0, когда все аргументы равны1, и1– во всех остальных случаях:
X | Y | F |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Запись
логической функции: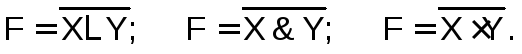
Логический элемент «И–НЕ»состоит из элемента «И»и инвертора и осуществляет отрицание результата функцииИ.Условное обозначение на структурных схемах логического элемента «И–НЕ»с двумя входами представлено на рисунке 1.5.3-4.
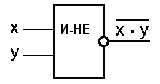
Рис. 1.6.3-4
Функция отрицания от логического сложения принимает значение 1, когда все аргументы равны 0, и значение0 – во всех остальных случаях:
X | Y | F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Запись логической функции: 
Логический элемент «ИЛИ–НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата логической функции «ИЛИ».Условное обозначение на структурных схемах логического элемента «ИЛИ–НЕ» с двумя входами представлено на рис. 1.6.3-5.
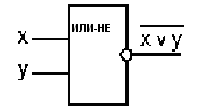
Рис. 1.6.3-5
В сложных выражениях с использованием логических операций И, ИЛИ, НЕсначала выполняются операции отрицанияНЕ, затем операции конъюнкцииИи, в последнюю очередь, операции дизъюнкцииИЛИ.
Для того чтобы изменить указанную последовательность выполнения операций, в выражениях следует использовать скобки.
Например: 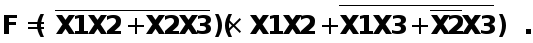
Логические функции
Логические функции
Логическая переменная – это простое высказывание, содержащее только одну мысль. Ее символическое обозначение – латинская буква (A, B, X, Y, …). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).
Логическая функция (составное высказывание) содержит несколько простых высказываний, соединенных между собой с помощью логических операций.
Логические операции – логическое действие.
Если логическую функцию выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить. Значением логического выражения могут быть только ЛОЖЬ или ИСТИНА. При составлении логического выражения необходимо учитывать порядок выполнения логических операций, а именно: действия в скобках; инверсия; конъюнкция; дизъюнкция. В привычных символах — (…), НЕ(), И(), ИЛИ().
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо определить:
количество строк в таблице (вычисляется как 2n, где n – количество переменных) + заголовок,
количество столбцов = количество переменных + количество логических операций,
последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Пример 1
Построим таблицу истинности для выражения (A B) ( A B).
Количество строк = 22 (2-е переменные А и В) + 1(заголовок столбцов) = 5.
Количество столбцов = 2-е переменные (A, B) + 5 логических операций (, , , , ) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
(A B) ( A B)
Построим таблицу:
A | B | A B | A | B | A B | (A B) (A B) |
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Пример 2
Построим таблицу истинности для логического выражения X Y Z.
Количество строк = 23 + 1 = 9.
Количество столбцов = 3-и логические переменные + 3-и логические операции = 6.
Порядок действий: 3 2 1
X Y Z.
Нарисуем и заполним таблицу.
X | Y | Z | Z | Y Z | X Y Z |
0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 1 |
Логические формулы и функции в MS Excel
Пример 3. Введем в ячейку А1 формулу =7>5. Она вернет значение ИСТИНА. Скопируем содержимое A1 в А2 и исправим в А2 формулу: = 3>5. Эта формула вернет значение ЛОЖЬ. Правые части обеих формул представляют собой высказывания, т.е. утверждения, относительно которых можно заключить, верны они или нет. Арифметические формулы высказываниями не являются: они предписывают, как по исходным данным вычислить значение, и вопрос об их истинности или ложности не имеет смысла.
Операции сравнения
> | >= | < | <= | = | <> |
больше | больше или равно | меньше | меньше или равно | равно | не равно |
Обратите
внимание, что символ отношения «больше
или равно» изображается двумя знаками:
>
и =.
Причина в том, что на клавиатуре нет
знака 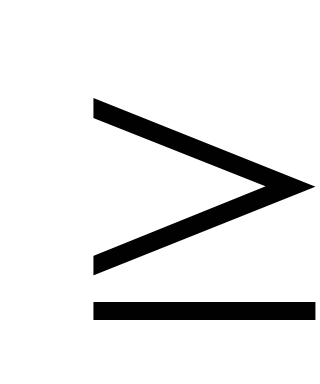 .
.
Имеются логические операции, которые позволяют строить сложные логические выражения. Эти операции реализованы в MS Excel как функции. Вот перечень логических операций и соответствующих им функций MS Excel, расположенных в порядке убывания приоритета.
Название | Обозначение | Функция MS Excel | Арифметический оператор |
Скобки | (…) | (…) | (…) |
Отрицание |
| НЕ | — унарный минус |
Конъюнкция |
| И | * — умножение |
Дизъюнкция |
| ИЛИ | + — сложение |
Здесь можно провести аналогию с арифметическими операторами: отрицанию соответствует унарный минус, конъюнкции — умножение, дизъюнкции — сложение. На самом деле в MS Excel приоритет логических операций не имеет значения, так как они реализованы в виде функций.
У логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Поэтому логические функции можно задать таблицей истинности, где перечислены все возможные значения аргументов и соответствующие им значения функций.
Таблица для функции НЕ имеет вид.
х | НЕ(x) |
ЛОЖЬ | ИСТИНА |
ИСТИНА | ЛОЖЬ |
Таблица для функций И и ИЛИ имеет вид.
x | y | И(x,y) | ИЛИ(x,y) |
ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
ЛОЖЬ | ИСТИНА | ЛОЖЬ | ИСТИНА |
ИСТИНА | ЛОЖЬ | ЛОЖЬ | ИСТИНА |
ИСТИНА | ИСТИНА | ИСТИНА | ИСТИНА |
Функция НЕ может иметь только один аргумент, а функции И и ИЛИ могут иметь два и более аргументов.
Пример 4. В ячейке А6 (с именем z) записано число. Выяснить, принадлежит ли оно отрезку [2, 5].
Решение. Присвоим ячейке А6 имя z. Введем в А6 число 3. Сначала сконструируем логическое выражение, решающее задачу. Для того чтобы z принадлежал отрезку [2, 5], нужно, чтобы одновременно были истинны два условия: x >= 2 и z <= 5.
((z >= 2) и (z <= 5)) В ячейке В6 разместим формулу =И(z>=2;z<=5). В В6 получим значение ИСТИНА.
Пример 5. В ячейке А6 (с именем z) записано число. Выяснить, при надлежит ли оно одному из лучей на числовой оси: (-, 2) или (5, ).
Для того чтобы z принадлежал хотя бы одному из лучей, нужно, чтобы был истинным хотя бы одно из условий: (z < 2) или (z > 5). В ячейке D6 разместим формулу =ИЛИ(z<2;z>5). А6 содержит число 3 поэтому формула возвращает ЛОЖЬ.
На приведенных примерах можно убедиться, что в логических выражениях число 1 ведет себя как ИСТИНА, а число 0 как ЛОЖЬ.
5
Определение логической (булевой) функции
Функция в алгебре высказываний f(x1, x2, …, xn) – это логическая формула, содержащая логические переменные x1, x2, …, xn, связанные между собой логическими операциями. Как аргументы x1, x2, …, xn (независимые переменные), так и сама функция (зависимая переменная) принимают значения 0 или 1. Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Если функция задаётся аналитически, то пишется её имя, затем в круглых скобках перечисляются аргументы функции, после чего пишется знак равно и формула функции (аргументы, соединённые знаками логических операций). Например, функции, заданные аналитически:
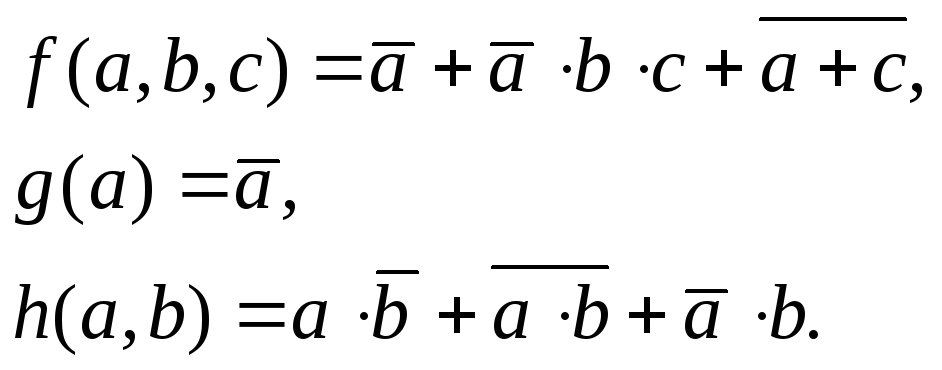
По
формуле логической функции легко
рассчитать ее таблицу истинности.
Необходимо только учитывать порядок
выполнения логических операций
(приоритет) и скобки. Операции
в логическом выражении выполняются
слева направо с учетом скобок. Для уменьшения количества скобок в
формулах вводят «старшинство» для
знаков логических операций. Принято
считать, что знак
дизъюнкции (+) старше знаков импликации,
эквивалентности и строгой дизъюнкции
(→, ↔,  ),
знак конъюнкции (∙) старше всех
перечисленных, а знак инверсии ( ‾ )
старше всех остальных. При наличии
скобок сначала операции выполняются
операции внутри самых внутренних скобок
согласно приоритету, затем во внешних
скобках и т.д.
),
знак конъюнкции (∙) старше всех
перечисленных, а знак инверсии ( ‾ )
старше всех остальных. При наличии
скобок сначала операции выполняются
операции внутри самых внутренних скобок
согласно приоритету, затем во внешних
скобках и т.д.
Таблица истинности логической функции
Построение таблицы истинности логической функции покажем на примере следующей функции:
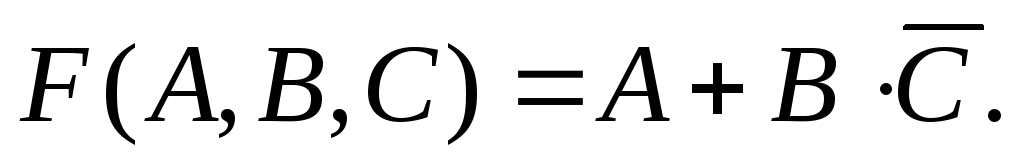
Построение таблицы включает следующие действия:
подсчёт количества аргументов у функции и количество операций, после чего строится таблица с суммарным количеством столбцов. В данном случае количество аргументов три плюс три операции, следовательно, таблица должна включать шесть колонок. Левые колонки отводятся под аргументы функции и обозначаются именами аргументов.
определяется количество строк в таблице по формуле K=2n , где n — количество логических переменных. В данном случае
K = 23= 8.
определяется последовательность выполнения логических операций и остальные столбцы обозначаются выражением с определённой операцией.
Заполняем столбцы с аргументами наборами значений.
Заполняем столбцы с промежуточными формулами и функцией значениями, используя таблицы истинности логических операций.
Аргументы | Промежуточные формулы | Функция | |||
A | B | C |
|
|
|
0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 1 |
Таким образом, для любой функции можно построить таблицу истинности, используя таблицы истинности логических операций.
Законы логики
Если у двух логических функций совпадают таблицы истинности, то есть на всех наборах значений входных переменных они принимают одинаковое значение, то их называют равносильными или эквивалентными. Это обозначается знаком = (равно).
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел будем называть законами:
Переместительный закон (закон коммутативности):
a + b = b + a, a∙b = b ∙a. (4)
Сочетательный закон (закон ассоциативности):
(a + b) + c = a + (b + c), (5)
(a∙ b)∙ c = a∙ (b∙ c). (6)
Закон исключения констант (нуля и единицы):
a +0 = a, A∙1=A. (7)
Распределительный закон (закон дистрибутивности):
(a + b)∙ c = a∙ c + b∙c, (8)
(a + c)∙ (b + c) = a∙b + c, (9)
(a b)∙ c = a∙ c
b)∙ c = a∙ c  b∙c. (10)
b∙c. (10)
Закон противоречия:
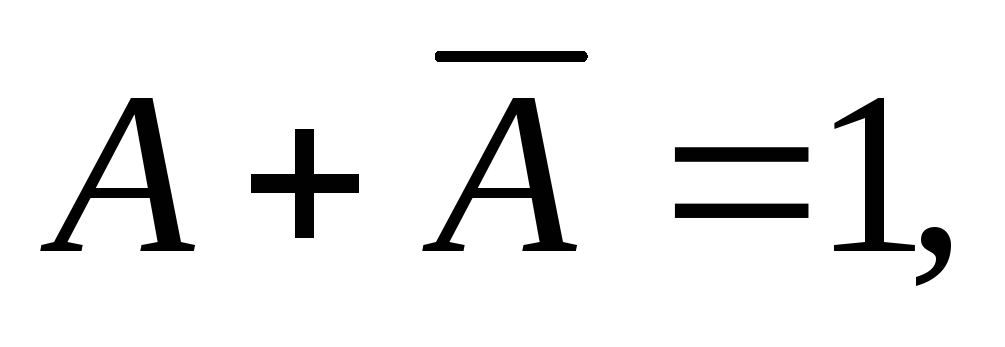
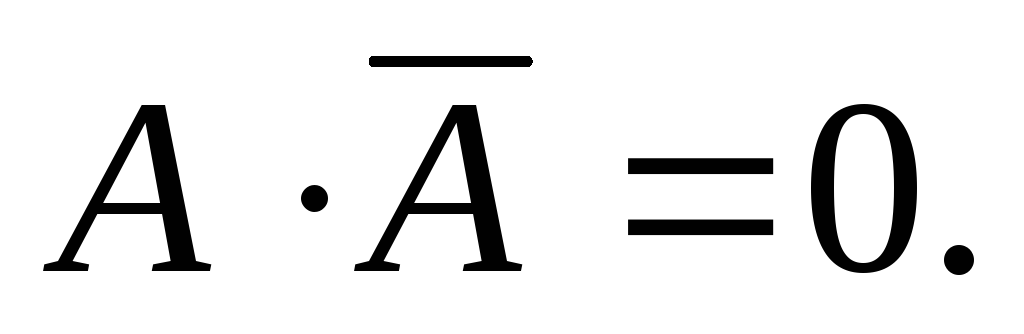 (11)
(11)
Закон равносильности (идемпотентности):
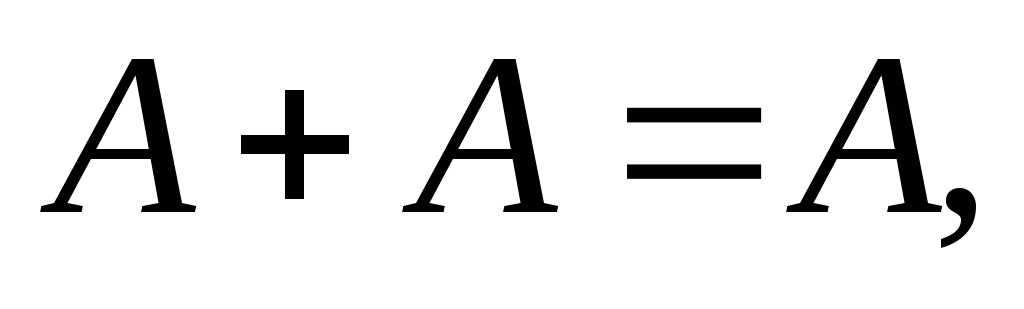
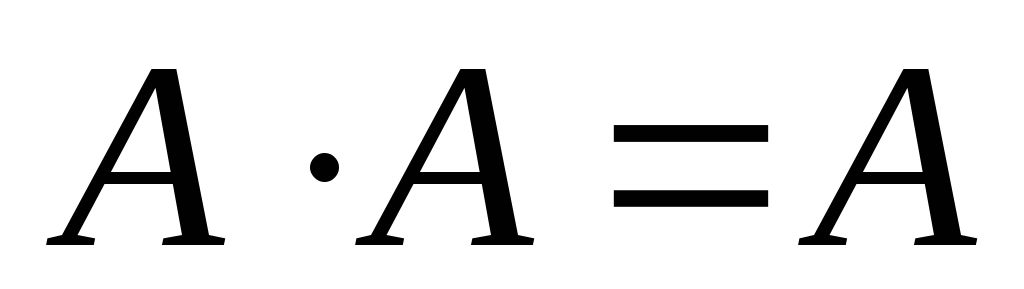 . (12)
. (12)
Закон
двойного отрицания: 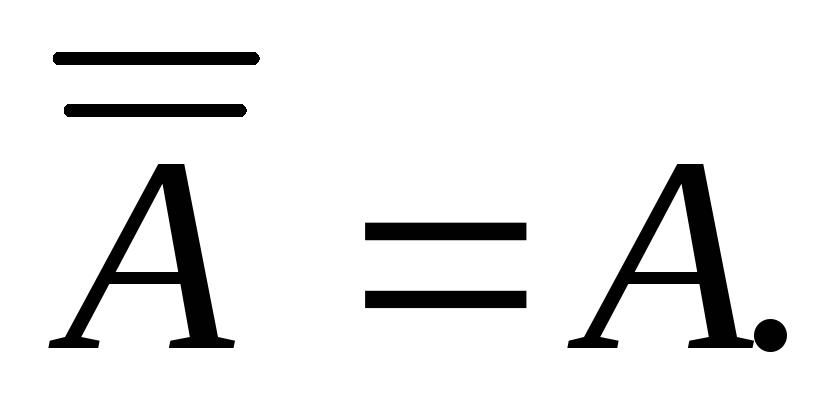 (13)
(13)
Закон инверсии (формулы де Моргана):
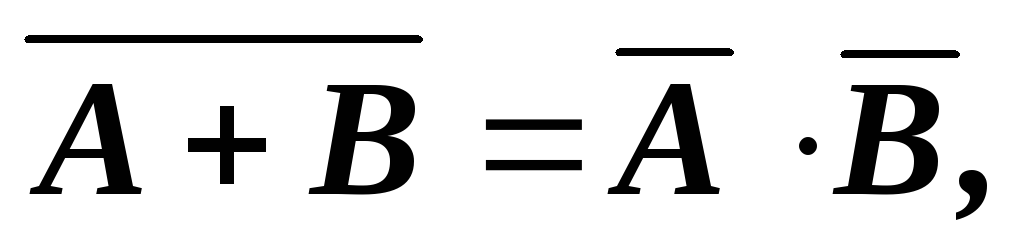 (14)
(14)
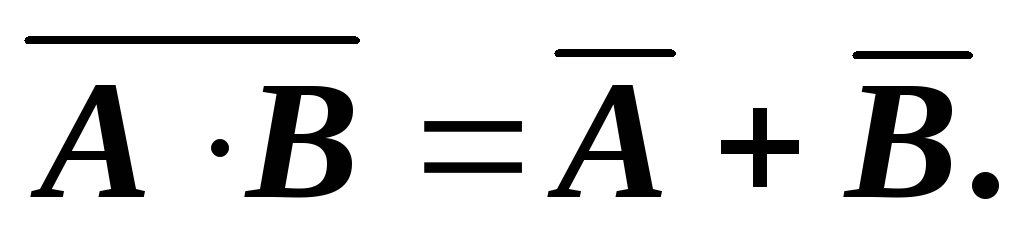 (15)
(15)
Закон поглощения:
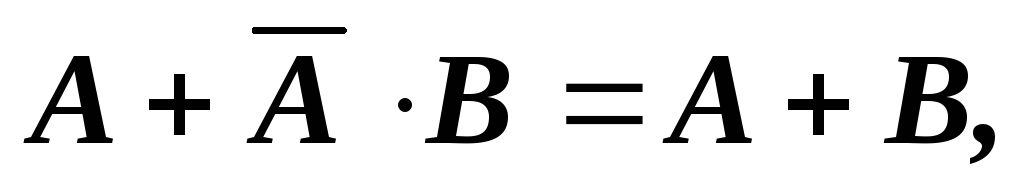 (16)
(16)
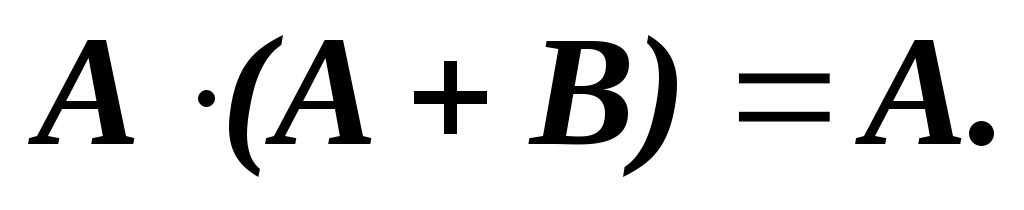 (17)
(17)
Закон склеивания (закон исключения):
 (18)
(18)
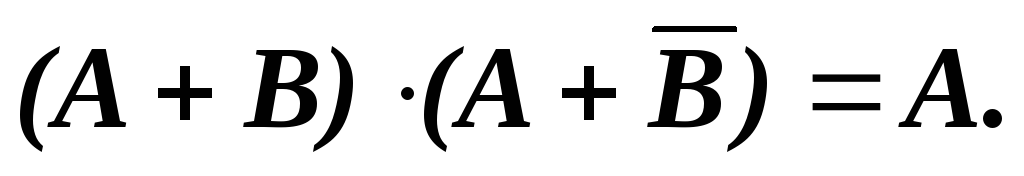 (19)
(19)
Любой из этих законов может быть легко доказан с помощью таблиц истинности.
Докажем первый закон де Моргана (14) с использованием таблиц истинности. Построим таблицы истинности для левой и правой частей закона.
a
b
a+b




0
0
0
1
1
1
1
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
1
1
0
0
0
0
Так
как результирующие столбцы (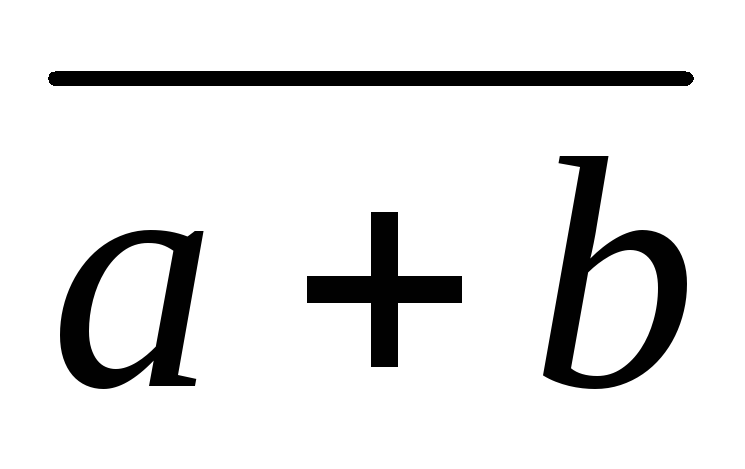 и
и 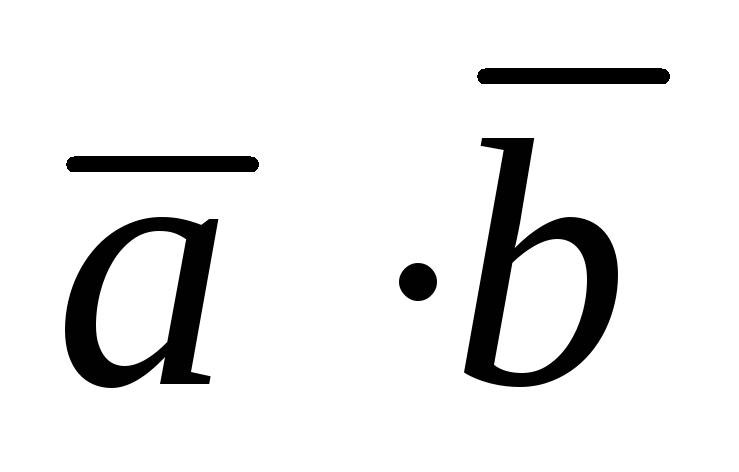 )
совпали,
то формулы, стоящие в левой и правой
частях закона, равносильны.
)
совпали,
то формулы, стоящие в левой и правой
частях закона, равносильны.
Любой из законов алгебры высказываний может быть доказан путем логических рассуждений.
Докажем
ещё один закон поглощения 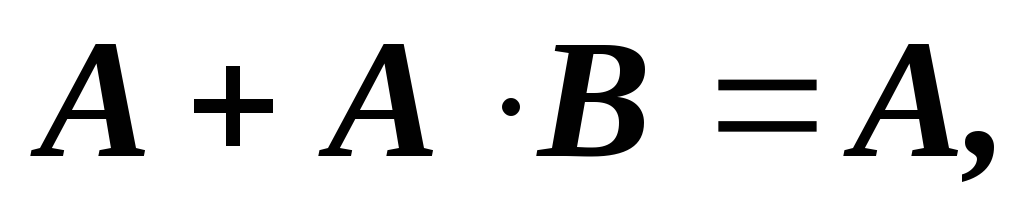 путем логических рассуждений. Для этого
достаточно показать, что если правая
часть истинна, то и левая часть истинна,
и что если левая часть истинна, то и
правая часть истинна.
путем логических рассуждений. Для этого
достаточно показать, что если правая
часть истинна, то и левая часть истинна,
и что если левая часть истинна, то и
правая часть истинна.
Пусть
истинна правая часть, т. е. A =
1, тогда в левой части дизъюнкция 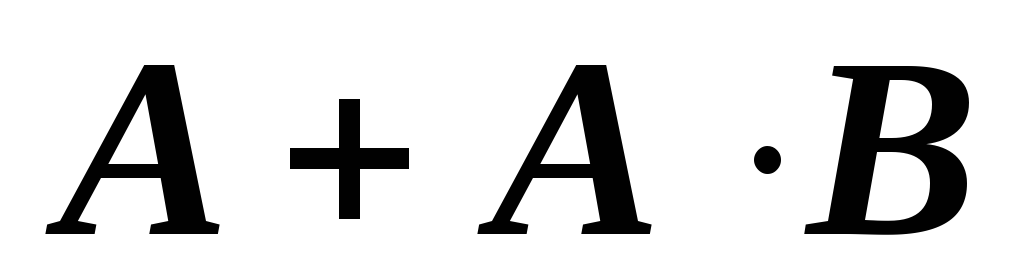 истинна
по определению дизъюнкции. Пусть истинна
левая часть. Тогда по определению
дизъюнкции истинна или формула A, или
формула
истинна
по определению дизъюнкции. Пусть истинна
левая часть. Тогда по определению
дизъюнкции истинна или формула A, или
формула  , или
обе эти формулы одновременно. Если A ложна,
тогда
, или
обе эти формулы одновременно. Если A ложна,
тогда  ложна.
Следовательно, A может
быть только истинной.
ложна.
Следовательно, A может
быть только истинной.
Еще одним способом вывода новых формул являются тождественные преобразования. Например, тот же закон поглощения можно вывести при помощи законов исключения единицы и дистрибутивности:
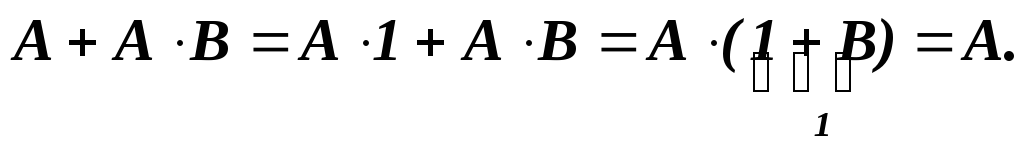
Для операций импликации, эквивалентности и строгой дизъюнкции также может быть сформулирован ряд важных свойств. В частности, каждая из этих операций может быть выражена через конъюнкцию, дизъюнкцию и отрицание. Убедитесь в этом, доказав самостоятельно следующие соотношения:
Представление импликации через конъюнкцию,
дизъюнкцию и инверсию:
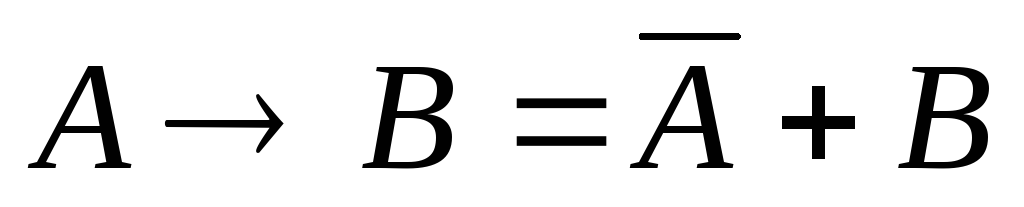 . (20)
. (20)
Представление эквивалентности через
конъюнкцию,
дизъюнкцию и инверсию: 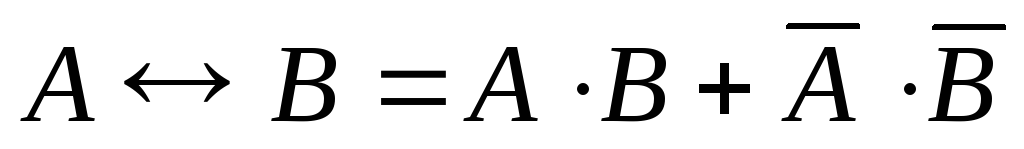 . (21)
. (21)
Представление строгой дизъюнкции через
конъюнкцию, дизъюнкцию и инверсию:
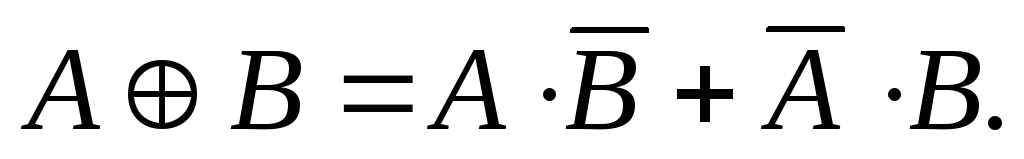 (22)
(22)
Правило
контрапозиции (перевертывания): 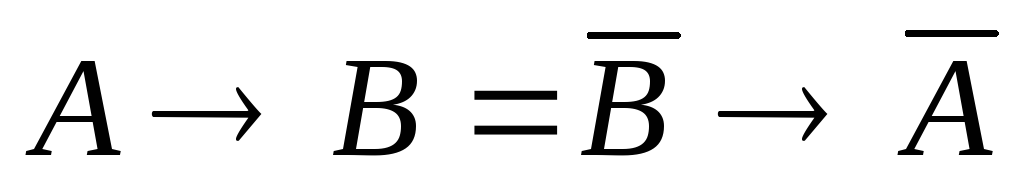 . (23)
. (23)
Свойства импликации:
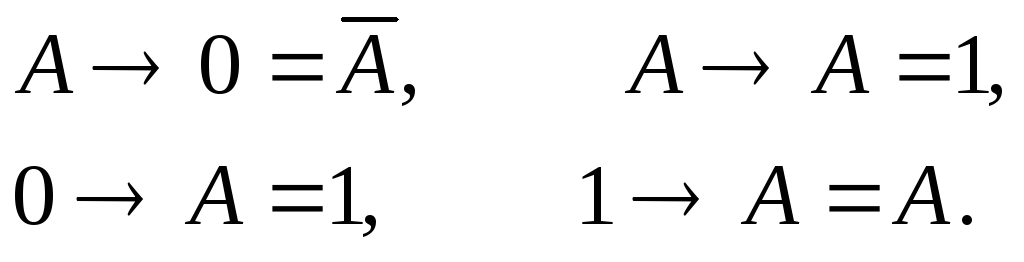 (24)
(24)
Свойства эквивалентности:
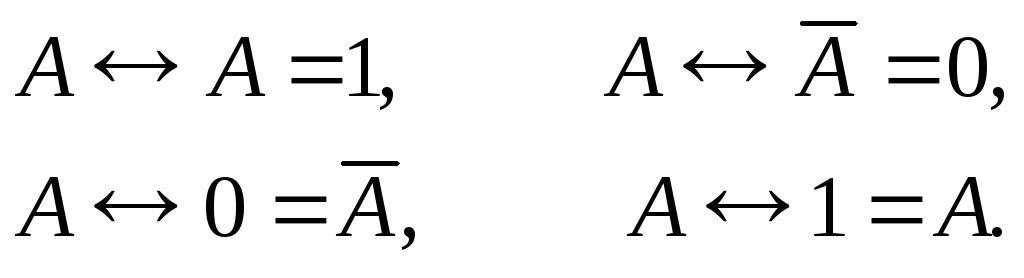 (25)
(25)
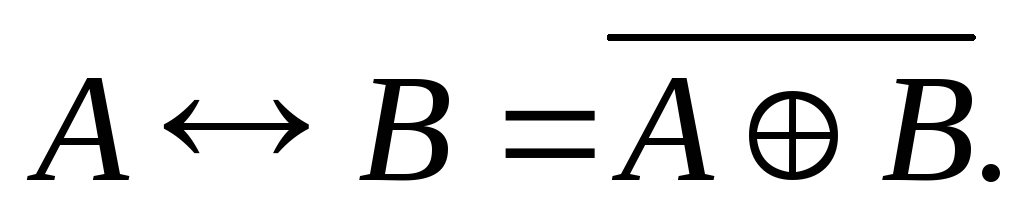 (26)
(26)
Свойства строгой дизъюнкции:
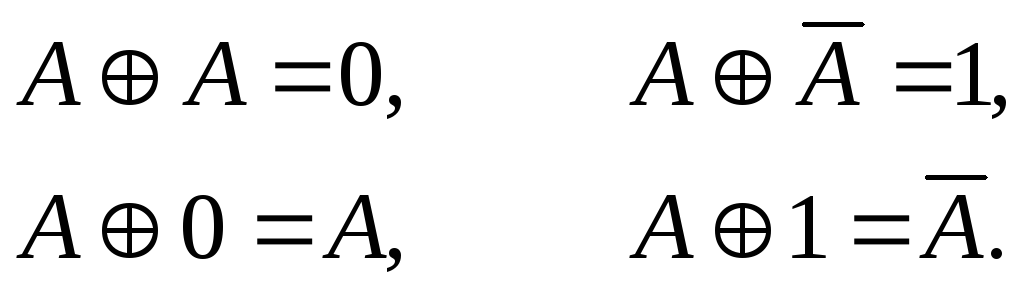 (27)
(27)
Логические функции
Логическая функция (функция алгебры высказываний) f(X1, X2, …, Xn) от n переменных – n-арная операция на множестве [0; 1]. В этой функции логические переменные X1, X2, …, Xn представляют собой высказывания и принимают значения 0 или 1.
Существует 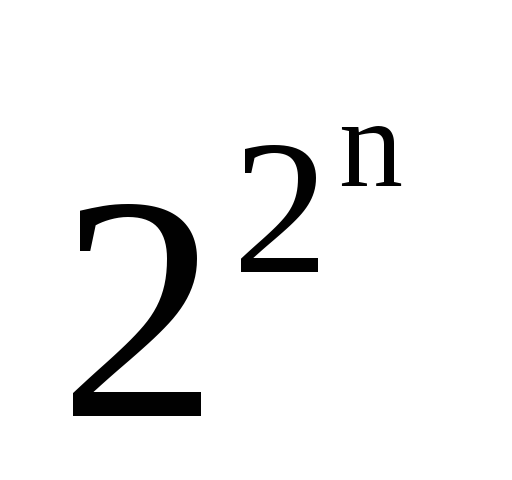 различных логических функций отn
переменных.
различных логических функций отn
переменных.
Логические операции, рассмотренные в предыдущем разделе, можно рассматривать как логические функции от двух переменных.
Набор функций, с помощью которого можно представить (выразить) все логические функции, называется функционально-полным или базисом. Основными базисами являются:
1) булевый базис, состоящий из конъюнкции, дизъюнкции и отрицания;
2) базис NOR, состоящий из стрелки Пирса;
3) базис NAND, включающий штрих Шеффера.Рассмотрим некоторые способы представления логических функций.
Аналитический. Функция задается в виде алгебраического выражения, состоящего из функций одного или нескольких базисов, применяемых к логическим переменным.
Табличный. Функция задается в виде таблицы истинности (соответствия), которая содержит 2n строк (по числу наборов аргументов), n столбцов по числу переменных и один столбец значений функции. В такой таблице каждому набору аргументов соответствует значение функции.
Числовой. Функция задается в виде десятичных (восьмеричных, шестнадцатеричных) эквивалентов номеров тех наборов аргументов, на которых функция принимает значение 1. Нумерация наборов начинается с нуля. Аналогичным образом логическая функция может быть задана по нулевым значениям.
Классификация эвм
По принципу действия
В этом случае критерием является форма представления информации, с которой они работают. Цифровые ВМ – вычислительные машины дискретного действия; работают с информацией, представленной в дискретной, а точнее в цифровой форме.
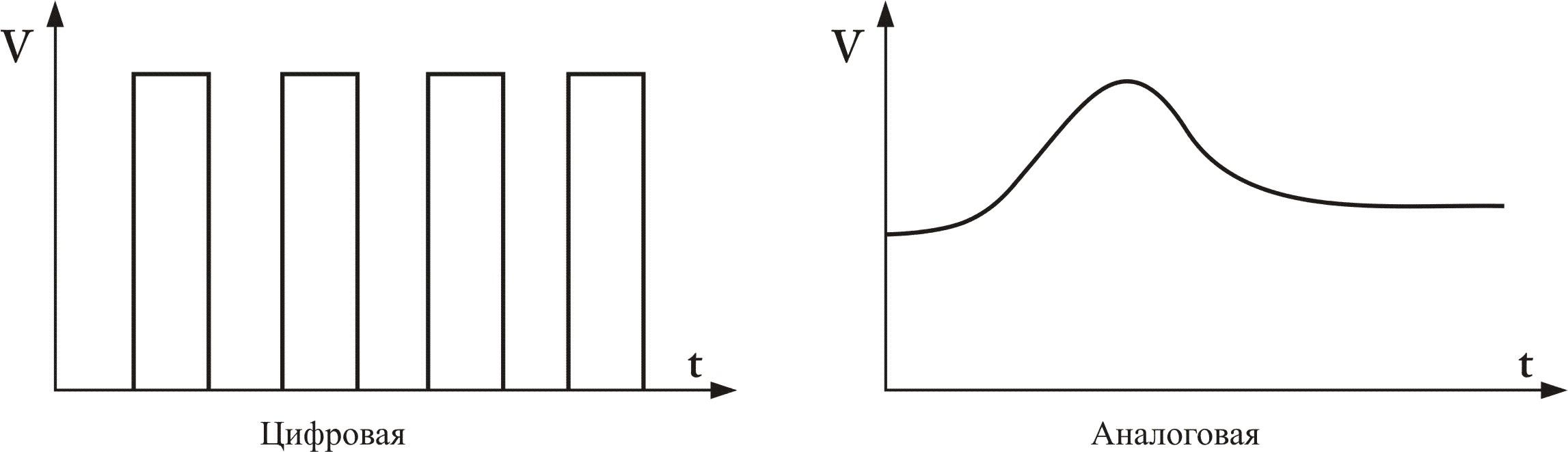
Аналоговые ВМ — вычислительные машины непрерывного действия; работают с информацией, представленной в непрерывной (аналоговой) форме.
По назначению
Универсальные, проблемно-ориентированные, специализированные.
По этапам создания
Разделение ЭВМ на поколения условно, так как поколения сменялись постепенно, поэтому временные границы между поколениями размыты. Поколения ЭВМ разделяют в зависимости от физических элементов или технологии их изготовления, используемые при построении ЭВМ. При сравнении быстродействия ЭВМ под операцией понимают операцию над числами с плавающей точкой.
Поколения ЭВМ
Поколение | Элементная база процес-сора | Макс. емкость ОЗУ, байт | Макс. быстро-действие процес-сора, оп/с | Основные языки програм-мирования | Управление ЭВМ пользователем |
Первое 1951-1954 | электронные лампы | 102 | 104 | Машинный код | Пульт управления и перфокарты |
Второе 1958-1960 | транзисторы | 103 | 106 | Ассемблер | Перфокарты и перфоленты |
Третье 1965-1968 | ИС | 104 | 107 | Процедур-ные языки высокого уровня (ЯВУ) | Алфавитно-цифровой терминал |
Четвертое 1976-1979 | БИС | 105 | 108 | Процедур-ные ЯВУ | Монохромный или графический дисплей, клавиатура |
Четвертое с 1985 | СБИС | 107 | 109 | Процедур-ные ЯВУ | Цветной графический дисплей, клавиатура, «мышь» и др. |
Пятое | усовершенст-вованные СБИС | 108 | 1012 | Языки логического программи-рования | Цветной графический дисплей и устройства голосовой связи |
Первое поколение ЭВМ (1951-1954) строилось на электронных лампах, которые могли быстро переключаться из одного состояния в другое. Лампы имели большие размеры, поэтому ЭВМ первого поколения, состоящие из десятков тысяч ламп, занимали целые этажи и были энергоемки. Программы записывались в ЭВМ с помощью установки перемычек на особом машинном коде.
Второе поколение ЭВМ (1958-1960) строилось на транзисторах – полупроводниковых приборах, которые могли находиться в одном из двух состояний. По сравнению с лампами транзисторы имели малые размеры и потребляемую мощность. Увеличение производительности обеспечивалось за счет более высокой скорости переключения и использованием обрабатывающих устройств, работающих параллельно. Площадь, требующаяся для размещения ЭВМ, уменьшилась до нескольких квадратных метров. Программы записывались на перфокарты – картонные карточки, на которых были выбиты или не выбиты дырочки, кодирующие 0 и 1. Программирование осуществлялось на языке Ассемблер, команды которого затем переводились в машинный код.
Третье поколение ЭВМ (1965-1968) строилось на интегральных схемах (ИС). ИС представляет собой электрическую цепь определенного функционального назначения, которая размещается на кремниевой основе. ИС содержит сотни и тысячи транзисторных элементов, что позволило уменьшить размеры, потребляемую мощность, стоимость и увеличить надежность системы. Помимо Ассемблера, программирование осуществлялось на языках высокого уровня (ЯВУ), имевших большое количество операторов. Каждый оператор объединял несколько команд языка Ассемблер.
Четвертое поколение ЭВМ (1976-по сегодняшний день) строилось на больших интегральных схемах (БИС). БИС содержат не набор нескольких логических элементов, из которых строились затем функциональные узлы компьютера, а целиком функциональные узлы. Примером БИС является микропроцессор. БИС способствовали появлению персональных компьютеров. Увеличение количества транзисторов до миллионов привело к появлению сверхбольших ИС (СБИС).
Пятое поколение ЭВМ существует в теории. Основное требование к ЭВМ – машина должна сама по поставленной цели составить план действий и выполнить его. Такой способ решения задачи называется логическим программированием. Элементная база процессора – СБИС с использованием опто- и криоэлектроники. Оптоэлектроника – раздел электроники, связанный с эффектами взаимодействия оптического излучения с электронами в веществах (главным образом в твердых телах) и использованием этих эффектов для генерации, передачи, хранения, обработки и отображения информации. Криоэлектроника (криогенная электроника) – область науки и техники, занимающаяся применением явлений, имеющих место в твердых телах при температуре ниже 120 К (криогенных температурах) в присутствии электрических, магнитных или электромагнитных полей (явление сверхпроводимости), для создания электронных приборов и устройств.


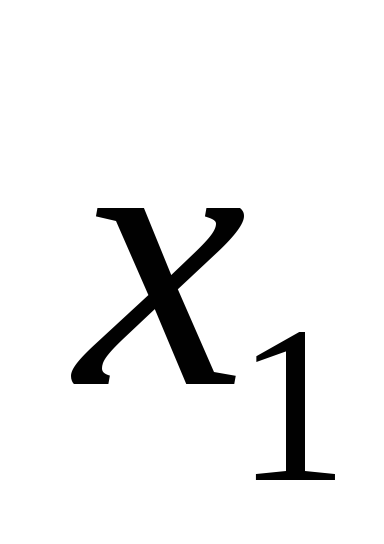
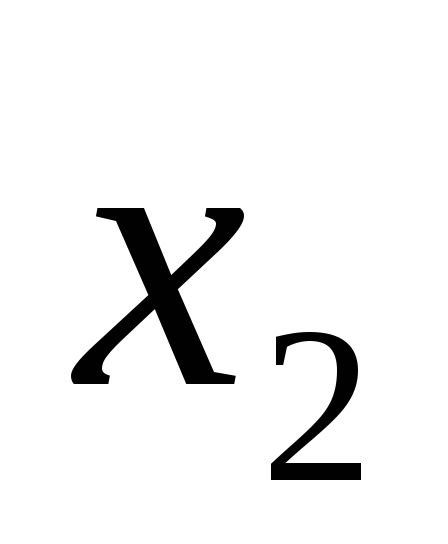
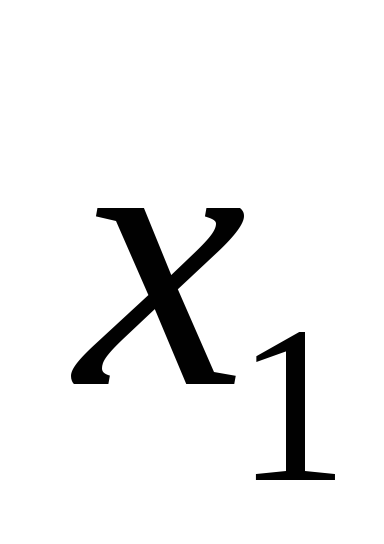
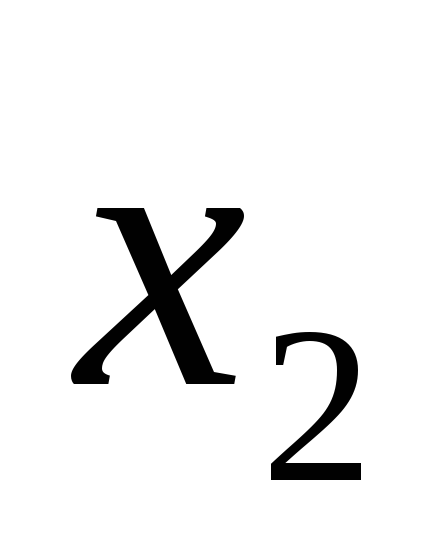
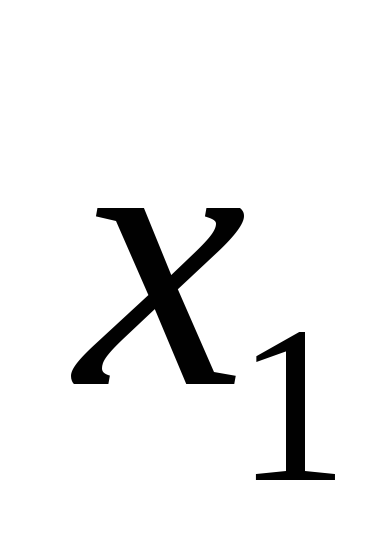
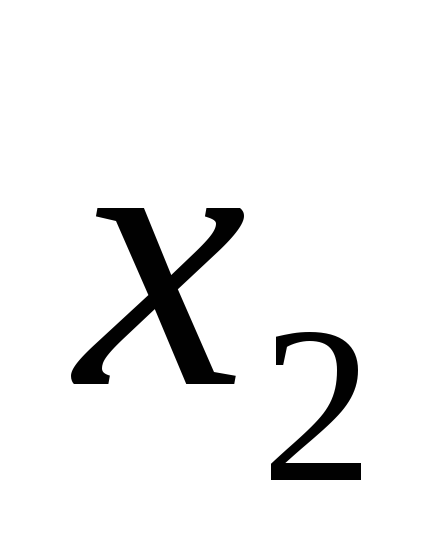
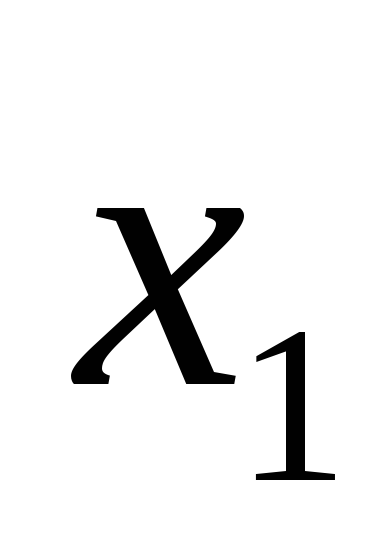 →
→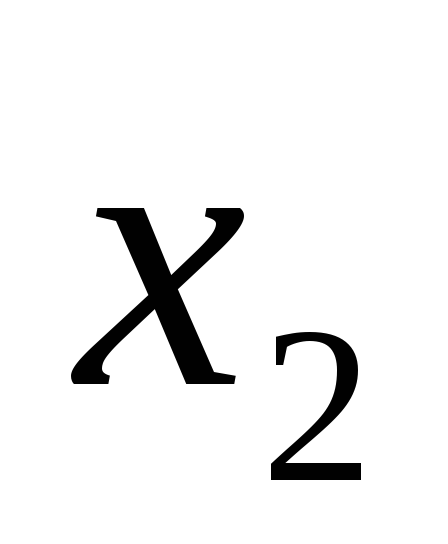
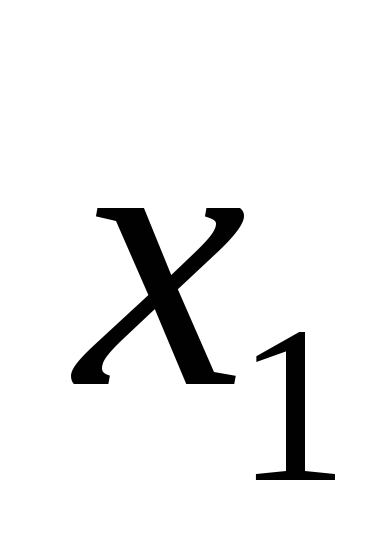
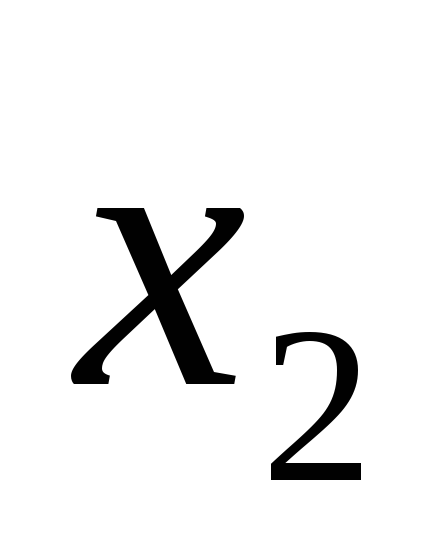
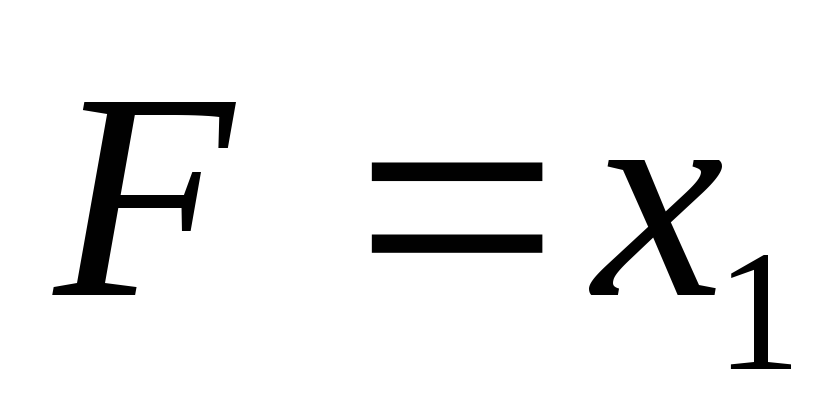
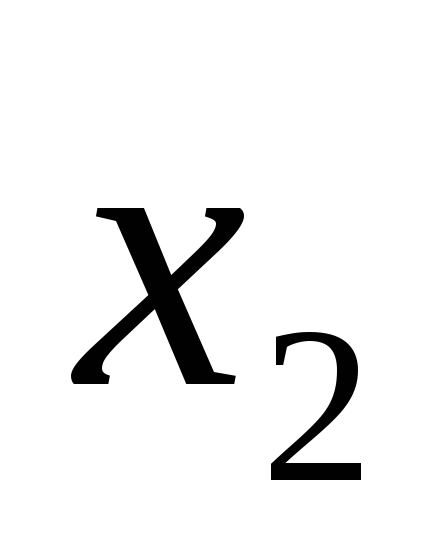
 трицание.
трицание.