ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ: «И,ИЛИ,НЕ»
Всем известна цифровая электроника: компьютеры, телевизоры, DVD и т.д. Сейчас, в нашё время, невозможно представить без сенсорных телефонов и ноутбуков. И поэтому сейчас больше всего начинают изучать цифровую технику, дети в возрасте 7 лет уже играть в компьютерные игры, а первоклассники ходят с сенсорными телефонами. Так что электроника распалась на две части: аналоговую и цифровую. Сегодня мы поговорим о кодах и логических элементов.
Десятичный код
Сейчас появилось много всяких микросхем и микроконтроллеров. Поэтому, чтобы записать мультики, игры, программы в микроконтроллер, надо использовать код. Коды бывают различного вида, например можно записывать в виде римских цифр. Сейчас появилось множество способов, мы рассмотрим только два. Это двоичный или десятичный. Чтобы записать десятичный, требуется десять цифр это 1 2 3 4 5 6 7 8 9 и 0. С помощью этих цифр записываются музыка, игры и прочее. Вот, например 12, нам понадобиться 1 и 2, из десятичного, мы берём 1 и 2, и записываем.
Двоичный код
Есть ещё и двоичный, для двоичного нужно только 0 и 1. Двоичный используется уже много лет, он очень удобен, например чтобы из десятичного кода, число перевести в число двоичного кода, надо из 10-2=8, это число в зависимости что нужно перевести, если из двоичного в десятичный ток надо вычисть это число, а если из десятичного в двоичный ток наоборот, прибавить. Теперь разберёмся и логическими элементами.
Логические элементы
Вот дело подошло к логическим элементам. Начнём пожалуй с элемента «И». Его изображение, а также другие основные элементы, показаны на рисунке далее:
Давайте разберёмся с принципом работы, у цифрового сигнала есть особенность, которая помогает записывать сигнал, это логическая единица и логический ноль. Как это объяснить, да вот так, логический ноль присутствует, если не подано напряжение, или оно очень низкое, а логическая единица, если напряжение среднее или высокое. С помощью этой особенностью можно записывать двоичный код.
Элемент «И» работает не сложно, у него всего два входа и один выход, чтобы была единица на выходе надо подать на все входы единицы, если хоть на одном входе будет ноль, то и на выходе будет ноль. При подаче нуля на обои входы, на выходе будет тоже ноль.
Теперь разберёмся с элементом «ИЛИ», ноль будет присутствовать если на обоих входах будет ноль, на всех остальных случаях всегда будет единица. А элемент «НЕ» очень прост, у него один вход и один выход. Логика его работы очень проста, если на вход подать единицу, то на выходе будет ноль, а если на вход подать ноль, то на выходе будет единица. На этом всё, с вами был Дмитрий Цывцын, желаю удачи!
Алгебра логики. Логические элементы (и, не, или). Дж. Буль.
Для математического описания работы вычислительных устройств, синтеза и анализа схем широко используется алгебра логики. В основе решения логических задач лежит несколько основных логических операций, применяемых в алгебре логики. Алгебра логики — определенная часть математической логики, часто называемая исчислением высказываний.
Под высказываниемпонимается всякое предложение, в котором содержится смысл утверждения (истинности) или отрицания (ложности). Одно и то же высказывание не может быть одновременно истинным и ложным или не истинным и не ложным. Отдельные высказывания можно обозначить заглавными буквами латинского алфавитаА, В, С,…. Если высказывание (суждение) истинно, то, например,А=1. Если С=0, то высказывание С ложно.
Рассматриваются только два значения высказывания: истинное или ложное (1 или 0). Такое условие алгебры логики приводит к соответствию между логическими высказываниями в математической логике и двоичными цифрами в двоичной системе счисления, что позволяет описывать работу схем и блоков машины и проводить их анализ и синтез с помощью алгебры логики.
Основными логическими операциями являются логическое отрицание, логическое умножение, логическое сложение, сложение по модулю 2.
Логическое отрицание (операция НЕ, инверсия).Пусть имеется некоторое высказываниеА.Отрицание этого высказывания обозначаетсяА,которое принято читать:не А.Если высказываниеАистинно(А
Логическое умножение (операция И, конъюнкция).Операцию логического умножения двух переменных А и В обозначают А/\В (принято читать: А и В). Высказывание А/\В истинно только в том случае, если А истинно (А=1) и В истинно (В=1), т.е. А/\В=1. Во всех остальных случаях это высказывание ложно, т. е.А/\В=0. Следовательно, при логическом умножении справедливо следующее правило: 0/\0=0; 0/\1=0; 1/\0=0; 1/\1=1. Правило логического умножения справедливо не только для двух сомножителей, но и для любого их количества, т. е. А/\В/\C/\D/\ …
Логическое сложение (операция ИЛИ, дизъюнкция).Операцию логического сложения двух переменных А и В обозначают А\/В (принято читать: А или В). Высказывание А\/В истинно (А\/В=1) в том случае, если хотя бы одно из переменных А или В истинно (А=1 или В=1). Если же это условие не выполняется, то высказывание ложно (А\/В=0). Таким образом, при логическом сложении справедливо следующее правило: 0\/0=0; 0\/1=1; 1\/0=1; 1\/1=l. Правило логического сложения справедливо не только для двух слагаемых, но и для любого их числа, т. е. A\/B\/C\/D\/ ….
Сложение по модулю 2 (ИЛИ исключающее).Операцию сложения двух переменных А и В по модулю 2 обозначают АВ. Высказывание АВ истинно (AB=l) в том случае, если только одно из переменных А или В истинно (А=1, В=0 или А=0, В=1). Если же это условие не выполняется, то высказывание ложно (АВ=0). Таким образом, сложение по модулю 2 выполняется по такому правилу: 00=0, 01=1; 10=1; 11=0.
На основе рассмотренных логических высказываний можно представить любое сложное высказывание, т. е. любую логическую связь можно выразить посредством логических операций сложения, умножения и отрицания.
В алгебре логики существуют правила, с помощью которых производятся преобразования формул.
Основные правила преобразования следующие:
Если подставить в эти выражения значения 0 и 1 для всех переменных, то можно убедиться в справедливости рассмотренных формул алгебры логики.
При разработке узлов ЭВМ смысл ложных или истинных высказываний A,B,Cво внимание не принимается; аппарат алгебры логики используется для выполнения заданных логических преобразований. Например, арифметические преобразования (сложение, вычитание) задаются в виде совокупности логических преобразований над аргументами.
Selhozpro.Ru » Логические элементы и их электрические аналоги
Из журнала «Радио»
Логических элементов, работающих как самостоятельные цифровые микросхемы малой степени интеграции и как компоненты микросхем более высокой степени интеграции, можно насчитать несколько десятков. Но здесь мы поговорим лишь о четырех из них — о логических элементах И, ИЛИ, НЕ, И-НЕ. Элементы И, ИЛИ и НЕ — основные, а И-НЕ является комбинацией элементов И и НЕ.
Что представляют собой эти «кирпичики» цифровой техники, какова логика их действия? Сразу уточним: напряжение от 0 до 0,4В, т. е. соответствующее уровню логического 0, мы будем называть напряжением низкого уровня, а напряжение более 2,4В, соответствующее уровню логической I,-напряжением высокого уровня. Именно такими уровнями напряжения на входе и выходе логических элементов и других микросхем серии К155 принято характеризовать их логические состояния и работу.
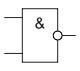
Условное графическое обозначение логического элемента И показано на Рис–1,а. Его условным символом служит знак «&», стоящий внутри прямоугольника; этот знак заменяет союз «и»в английском языке. Слева — два (может быть и больше) логических входа – X1 и X2, справа — один выход Y. Логика действия элемента такова: напряжение высокого уровня появляется на выходе лишь тогда, когда сигналы такого же уровня будут поданы на все его входы
Элемент И — умножение
Разобраться в логике действия логического элемента И поможет его электрический аналог (Рис–1, б), составленный из последовательно соединенных источника питания GB (например, батареи 3336), кнопочных переключателей SB1, SB2 любой конструкции и лампы накаливания HL (МНЗ,5-0,26). Переключатели имитируют электрические сигналы на входе аналога, а нить лампы индицирует уровень сигнала на выходе. Разомкнутое состояние контактов переключателей соответствует напряжению низкого уровня, замкнутое- высокого уровня. Пока контакты кнопок не замкнуты (на обоих входах элемента напряжение низкого уровня), электрическая; цепь аналога разомкнута и лампа, естественно, не светит. Нетрудно сделать другой вывод: лампа накаливания на выходе элемента И включается только после того, как контакты обеих кнопок SB1 и SB2 окажутся замкнутыми В этом и заключается логическая связь между входными и выходными сигналами элемента И.
Теперь взгляните на Рис–1,в. На нем изображены временные диаграммы электрических процессов, дающие достоверное представление о работе логического элемента И. На входе X1 сигнал появляется первым. Как только такой же сигнал будет и на входе Х2, тут же появляется сигнал и на выходе Y, который существует до тех пор, пока на обоих входах имеются сигналы, соответствующие напряжению высокого уровня.
О состоянии и логической связи между входными и выходным сигналами элемента И дает представление так называемая таблица состояний (Рис–1, г), напоминающая таблицу умножения. Глядя на нее, можно сказать, что сигнал высокого уровня на выходе элемента будет только тогда, когда сигналы такого же уровня появятся на обоих его входах. Во всех других случаях на выходе элемента будет напряжение низкого уровня, т. е. соответствующее логическому 0
Элемент ИЛИ
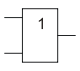
Условный символ логического элемента ИЛИ — цифра 1 внутри прямоугольника (Рис–2, а). У этого элемента, как и у элемента И, может быть два и больше входов. Сигнал на выходе Y, соответствующий напряжению высокого уровня, появляется при подаче такого же сигнала на вход X1, или на вход Х2, или одновременно на оба входа. Чтобы убедиться в таком действии элемента ИЛИ, проведите опыт с его электрическим аналогом (Рис–2, б).
Лампа накаливания HL на выходе аналога будет включаться всякий раз, когда окажутся замкнутыми контакты или кнопки SB1, или SB2, или одновременно обеих (всех) кнопок Закрепить в памяти электрическое свойство элемента ИЛИ помогут временные диаграммы его работы (Рис–2,в) и таблица состояний (Рис–2,г), определяющая логическую связь между входными и выходным сигналами.
Элемент НЕ
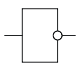
Условный символ логического элемента НЕ — тоже цифра 1 в прямоугольнике Рис–3,а. Но у него один вход и один. выход. Небольшой кружок, которым начинается линия связи выходного сигнала, символизирует логическое отрицание на выходе элемента На языке цифровой техники НЕ означает, что этот элемент является инвертором- электронным устройством, выходной сигнал которого противоположен входному. Иначе говоря, пока на входе элемента НЕ действует сигнал низкого уровня, на его выходе будет сигнал высокого уровня, и наоборот.
Электрический аналог элемента НЕ можно собрать по схеме, представленной на Рис– 3, б. Электромагнитное реле К, срабатывающее при напряжении батарея GB, должно быть выбрано с группой замкнутых контактов. Пока контакты кнопки SB1 разомкнуты, обмотка реле обесточена, его контакты К остаются замкнутыми и, следовательно, лампа HL светит. При нажатии на кнопку ее контакты замыкаются, имитируя появление входного сигнала высокого уровня, в результате чего реле срабатывает. Его контакты, размыкаясь, разрывают цепь питания лампы HL-погасая, она символизирует появление на выходе сигнала низкого уровня. Попробуйте начертить самостоятельно временные диаграммы работы элемента НЕ и составить его таблицу состоянии — они должны получиться такими же, как приведенные на Рис–3, в, г.
Элемент И–НЕ
Как мы уже говорили, логический элемент И-НЕ является комбинацией элементов И и НЕ. Поэтому на его графическом обозначении (Рис–4, а) есть знак «&»и кружок на линии выходного сигнала, символизирующий логическое отрицание. Выход один, а входов два и больше.
Разобраться в принципе действия такого логического элемента цифровой техники вам поможет его электрический аналог, собранный по схеме на Рис–4,б. Электромагнитное реле К, батарея GB и лампа накаливания HL такие же, как в аналоге элемента НЕ. Последовательно с обмоткой реле включите две кнопки (SB1 и SB2), контакты которых будут имитировать входные сигналы. В исходном состоянии, когда контакты кнопок разомкнуты, лампа светит, символизируя сигнал высокого уровня на выходе. Нажмите на одну из кнопок во входной цепи.
Как на это реагирует индикаторная лампа? Она продолжает светить. А если нажать на обе кнопки? В этом случае электрическая цепь, образованная батареей питания обмоткой реле и контактами кнопок, оказывается замкнутой, реле срабатывает и его контакты К, размыкаясь, разрывают вторую цепь аналога-лампа гаснет. Эти опыты позволяют сделать вывод: при сигнале низкого уровня на одном или на всех входах элемента И-НЕ (когда контакты входных кнопок аналога разомкнуты) на выходе действует сигнал высокого уровня, который изменяется на сигнал низкого уровня при появлении таких же сигналов на всех входах элемента (контакты кнопок аналога замкнуты). Такой вывод подтверждается диаграммами работы и таблицей состояний, показанными на Рис–4, в, г. Обратим внимание на следующий факт: если входы элемента И-НЕ соединить вместе и подать на них сигнал высокого уровня, на выходе элемента будет сигнал низкого уровня. И наоборот, при подаче на объединенный вход сигнала низкого уровня на выходе элемента будет сигнал высокого уровня. В этом случае элемент И-НЕ, как, вероятно, вы уже догадались, становится инвертором, т. е. логическим элементом НЕ. Это свойство элемента И-НЕ очень широко используется в приборах и устройствах цифровой техники.
Элемент ИЛИ–НЕ
Элемент исключающий ИЛИ
Автоколебательный мультивибратор
При ёмкости конденсатора С = 1мкФ и изменении R от 0 до 1,5 ком. частота колебаний изменится от 300Гц до 10 кГц.
Ждущий мультивибратор
Изменением ёмкости и сопротивления изменяют длительность вырабатываемых импульсов.
Длительность запускающего импульса должна быть меньше длительности формируемого.
Сопротивление должно быть от 100 Ом до 2,2 к.
Триггер Шмитта
Это спусковое устройство с двумя устойчивыми состояниями. Из одного состояния в другое устройство переходит под действием входного сигнала.
Ещё он преобразует подаваемое на вход переменное напряжение синусоидальной формы в напряжение прямоугольной формы такой же частоты. Срабатывает при определённой амплитуде входного сигнала.
R S — триггер
При 0 на S и 1 на R, триггер находится в единичном состоянии. 1 на S и 0 на R, триггер в нулевом состоянии. Если на оба входа подать 0, на выходах будет 1. Это противоречит логике его действия и считается недопустимым. 1 на обеих входах не изменит первоначального состояния триггера.
D – триггер
D – Вход приёма цифровой информации.
C – Вход тактовых импульсов синхронизации.
0 – на входе R – триггер в нулевом состоянии.
0 – на входе S – триггер в единичном состоянии.
Логика работы D – триггера в режиме приёма информации следующая: если на входе D – 1, то по фронту тактового импульса на входе С – триггер устанавливается в единичное состояние, если на входе D – 0, то по фронту тактового импульса на входе С – триггер устанавливается в нулевое состояние.
На спады синхронизирующих импульсов D – триггер не реагирует. Каждое изменившееся состояние триггера означает запись в его память принятой информации.
Работа D – триггера в счётном режиме.
В счётном режиме триггер делит частоту входного сигнала на 2. Выполняет функцию двоичного счётчика.
J K – триггер
По входам R и S, он работает как RS триггер. Входы J и K – управляющие, каждый из них имеет по три входа объединённые по схеме 3И. С – вход тактовых импульсов. В режиме приёма и хранения информации он служит входом тактовых импульсов, в счётном режиме – информационным входом.
J K – триггер, работает по спаду тактовых импульсов.
Поворотный механизм инкубатора »Логические элементы — это… Что такое Логические элементы?
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
Инвертор, НЕ| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение, ДА
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
2И| ٨ | ||
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)
2ИЛИМнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
2И-НЕМнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
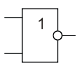2ИЛИ-НЕ| ↓ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
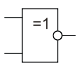ИСКЛ-ИЛИ-НЕ| ↔ | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.
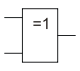ИСКЛ-ИЛИВ англоязычной литературе 2XOR.
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| → | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
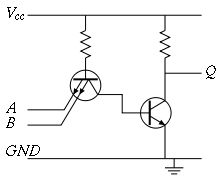Упрощённая схема двухвходового элемента И-НЕ ТТЛ .Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Ссылки
Литература
Универсальные логические элементы
Универсальные логические элементы могут использоваться для выполнения разнообразных операций над своими входными данными. Конкретная операция зависит от того, какие сигналы поданы на управляющие входы. Чтобы синтезировать такой универсальный логический элемент, обычно пользуются СКНФ или СДНФ, как и в синтезе комбинационных логических схем.
Тип логики ТТЛ (транзисторно-транзисторная логика) определяет элементную базу, на которой собран логический элемент, как состоящую преимущественно из транзисторов, причём транзисторы используются и на входе, и на выходе логического элемента (отсюда и название — транзисторно-транзисторная).
Рассмотрим
электрические принципиальные схемы
логического элемента И-НЕ с n входами
– ТТЛ.
На рисунках +U обозначает положительный потенциал источника питания, а -U — отрицательный.
Вызывает некоторый интерес необычный транзистор на входе и схема его включения. Такие многоэмиттерные транзисторы всегда используются на входах логических элементов ТТЛ. Сам транзистор выполняет логическую операцию И. При подаче на один из входов напряжения логического нуля, транзистор открывается и, таким образом, на коллекторе устанавливается напряжение логического 0. Напряжение логической 1 будет на коллекторе только тогда, когда на всех входах будет напряжение логической 1. Подобный транзистор можно рассматривать как много n-p переходов, а соответственно, как много диодов.
Простейший базовый элемент ТТЛ выполняет логическую операцию И-НЕ, в принципе повторяет структуру ДТЛ микросхем и в то же время за счёт использования многоэмиттерного транзистора, объединяет свойства диода и транзисторного усилителя что позволяет увеличить быстродействие, снизить потребляемую мощность и усовершенствовать технологию изготовления микросхемы.
ТТЛ получила широкое распространение в компьютерах, электронных музыкальных инструментах, а также в контрольно-измерительной аппаратуре и автоматике (КИПиА). Благодаря широкому распространению ТТЛ входные и выходные цепи электронного оборудования часто выполняются совместимыми по электрическим характеристикам с ТТЛ. Максимальное напряжение в схемах с ТТЛ может достигать 24В, однако это приводит к большому уровню паразитного сигнала. Достаточно малый уровень паразитного сигнала при сохранении достаточной эффективности достигается при напряжении 5В, поэтому данная цифра и вошла в технический регламент ТТЛ.
Важность ТТЛ заключается в том, что ТТЛ-микросхемы оказались более пригодны для массового производства и при этом превосходили по параметрам ранее выпускавшиеся серии микросхем (резисторно-транзисторная и диодно-транзисторная логика).
В ТТЛ схемах вместо параллельного соединения диодов используется многоэмиттерный транзистор. Физика работы этого логического элемента не отличается от работы диодного логического элемента «2И». Высокий потенциал на выходе многоэмиттерного транзистора получается только в том случае, когда на обоих входах логического элемента (эмиттерах транзистора) присутствует высокий потенциал (то есть нет эмиттерного тока). Принципиальная схема базового логического элемента ТТЛ микросхемы приведена на рисунке 1.
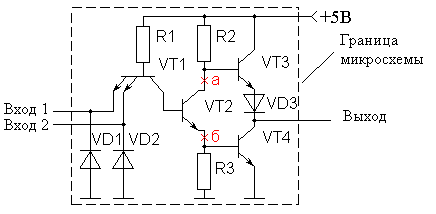Рисунок 1.
Принципиальная схема базового логичиского
элемента ТТЛ микросхемы
Умощняющий усилитель, как и в диодно-транзисторном элементе, инвертирует сигнал на выходе схемы логического элемента. По такой схеме выполнены базовые логические элементы ТТЛ микросхем серий 155, 131, 155 и 531. Схемы «И-НЕ» в этих сериях микросхем обычно имеет обозначение ЛА. Например, схема К531ЛА3 содержит в одном корпусе четыре логических элемента «2И-НЕ». Таблица истинности, реализуемая этой схемой, приведена в таблице 1, а условно-графическое обозначение этих логических элементов приведено на рисунке 2.
Рисунок 2. Условно-графическое обозначение логического элемента «2И-НЕ»
Таблица 1. Таблица истинности схемы, выполняющей логическую функцию «2И-НЕ»
x1 | x2 | F |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
На основе базового логического элемента строится и инвертор. В этом случае на входе схемы используется только один диод. Схема ТТЛ инвертора приведена на рисунке 3.
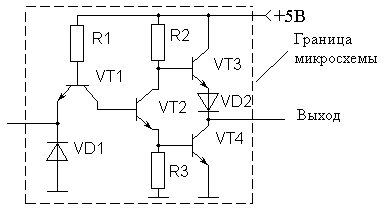Рисунок 3.
Принципиальная схема инвертора ТТЛ
микросхемы
При необходимости объединения нескольких логических элементов «И» по схеме «ИЛИ» (или при реализации логических элементов «ИЛИ») транзисторы VT2 соединяются параллельно в точках «а» и «б», показанных на рисунке 8, а выходной каскад используется один. В результате быстродействие такого, достаточно сложного элемента, получается точно таким же, как и у одиночного логического элемента «2И-НЕ». Принципиальная схема логического элемента «2И-2ИЛИ-НЕ» приведена на рисунке 4.
Рисунок 4.
Принципиальная схема ТТЛ микросхемы
«2И-2ИЛИ-НЕ»
Такие соединения логических элементов широко применяется при реализации цифровых микросхем по произвольной таблице истинности методом СДНФ, а условно-графическое изображение элемента «2И-2ИЛИ-НЕ» приведено на рисунке 5. Такие логические элементы содержатся в отечественных цифровых микросхемах с обозначением ЛР.
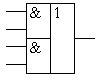Рисунок 5.
Условно-графическое обозначение
логического элемента «2И-2ИЛИ-НЕ»
ТТЛ микросхем
Схемы «ИЛИ-НЕ» в отечественных ТТЛ сериях микросхем средней интеграции имеет обозначение ЛЕ. Например микросхема К1531ЛЕ5 содержит в одном корпусе четыре элемента «2ИЛИ-НЕ». Следует отметить, что в современных микросхемах малой логики стараются в одном корпусе разместить один, в крайнем случае два логических элемента.
Так как в современных схемах ТТЛ и в схемах ДТЛ используется одинаковый выходной усилитель, то и уровни логических сигналов в этих схемах одинаковы. Поэтому часто говорят, что это ТТЛ микросхемы, не уточняя по какой схеме выполнен входной каскад этих микросхем. Тем самым подчеркивается отличие этих микросхем от старых ДТЛ серий микросхем с повышенным напряжением питания. Более того! Появились КМОП микросхемы, совместимые с ТТЛ микросхемами по логическим уровням, например К1564 (иностранный аналог SN74HCT) или К1594 (иностранный аналог SN74АСT).
