Логическая и правовая природа и значение презумпций Текст научной статьи по специальности «Право»

порядке, возмещается государством в полном объеме независимо от вины органа дознания, дознавателя, следователя, прокурора и суда, а вред, причиненный в гражданину в результате частного уголовного преследования, возмещается частным обвинителем в случаях обвинения им заведомо невиновного лица, установленного вступившим в законную силу приговором суда по ст. 306 УК РФ.».

3. Представляется целесообразным изложить п. 1 ч. 2 ст. 133 УПК РФ в следующей редакции: «подсудимый по уголовному делу публичного обвинения, в отношении которого вынесен оправдательный приговор;».

4. Представляется целесообразным дополнить ч. 2 ст. 133 УПК РФ пунктом 1.1 следующего содержания: «подсудимый по уголовному делу частного обвинения, в отношении которого вынесен оправдательный приговор, в случаях вступления в законную силу обвинительного приговора суда в отношении частного обвинителя по обвинению его в совершении преступления, предусмотренного ст. 306 УК РФ.».

5. Часть шестую ст. 318 УПК РФ целесообразно изложить в следующей редакции: «Заявитель предупреждается об уголовной ответственности за заведомо ложный донос в соответствии со ст. 306 УК РФ, а также знакомится с положениями ч. 5 ст. 132 УПК РФ, о чем в заявлении делается отметка, которая удостоверяется подписью заявителя».

С. В. Корнакова

ЛОГИЧЕСКАЯ И ПРАВОВАЯ ПРИРОДА И ЗНАЧЕНИЕ ПРЕЗУМПЦИЙ

Презумпция (от латинского рraesumtio — предположение) — это общее правило, на основании которого заранее постулируется (пре-

зюмируется) какой-то факт1. Первоначально у древних римлян понятие «презумпция» («ргаеБитйо», «ргаеБитеге») означало нечто вперед взять или принять. В широком смысле оно значило: верить, думать, полагать, держаться чего-либо без доказательства, предвидеть, догадываться. «РгаеБитеге» употреблялось у римлян также в значениях: преждевременно употреблять, наперед желать, предвидеть, решиться на что-либо2. В настоящее время используется единственное, обобщенное значение этого понятия — «предположение, признаваемое истинным, пока не доказано обратное»3.

С логической точки зрения презумпции относятся к суждениям популярной индукции, т.е. обобщению через простое перечисление. Более полно и точно индукцию через простое перечисление можно выразить так: индукция посредством перечисления частных случаев, подтверждающих обобщение, пока не встретится случай, противоречащий ему4. Индуктивный переход от знания частных случаев к обобщению не может претендовать на логическую необходимость, поскольку повторяемость признаков может оказаться результатом простого совпадения, поэтому для популярной индукции характерно ослабленное логическое следование — истинные посылки обеспечивают получение не достоверного, а лишь правдоподобного или вероятного заключения. В основе индуктивного метода познания лежит подтверждаемое многовековой практикой положение о проявлении необходимых признаков явлений через их всеобщность и устойчивую повторяемость. Именно эти методологические положения оправдывают логическую состоятельность и эффективность индуктивных выводов в процессе познания.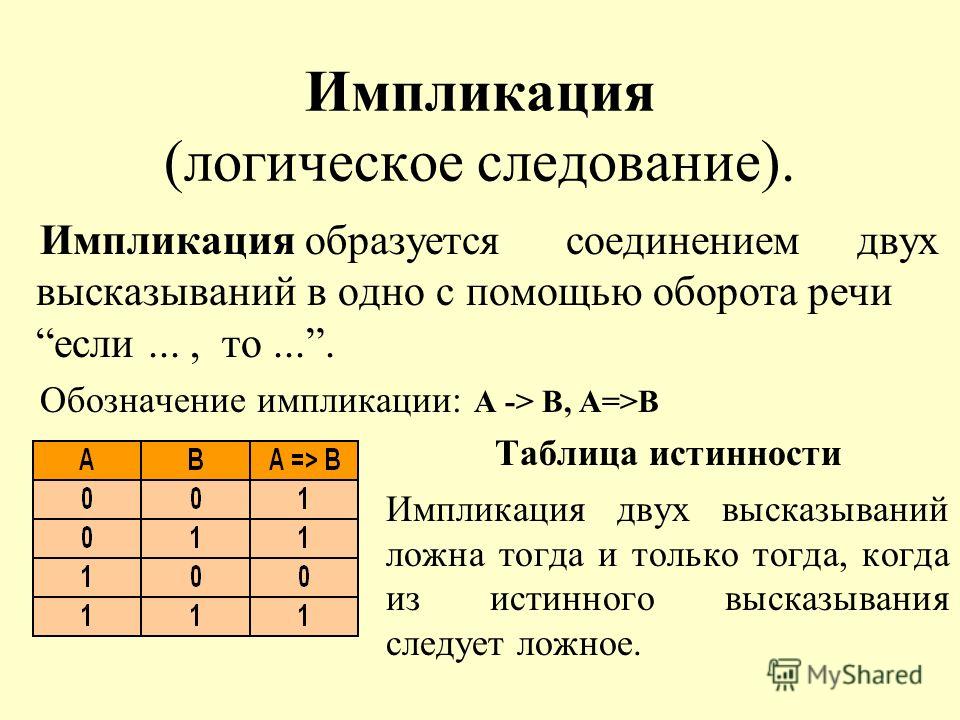

Любая наука, утверждал Э. Гуссерль, опирается на «круг уве-ренностей, выполняющих некую предпосылочную, презумптивную функцию, к которым относятся с давно сложившимся доверием и которые в человеческой жизни до всех потребностей научного обосно-

1 Теория доказательств в советском уголовном процессе / Под ред. Н. В. Жоги-на. — 2-е изд. — М.: Юрид. лит., 1973. — С. 343.

Дормидонтов, Г. Ф. Юридические фикции и презумпции. Классификация явлений юридического быта, относимых к случаям применения фикций / Г. Ф. Дормидонтов. — Казань, 1895. — С. 23.

3 Ожегов, С. И. Словарь русского языка. Изд. 8-е, стереотип. / С. И. Ожегов. -М.: «Сов. энциклопедия», 1970. — С. 573.

4 Рузавин, Г. И. Логика и основы аргументации. Учебник для вузов / Г. И. Руза-вин. — М.: Проект, 2003. — С. 183.

вания приняты в качестве безусловно значимых и практически апробированных»1. В данном определении следует подчеркнуть именно «практическую апробированность» или, другими словами, проверку опытом, эмпирическим путем. Поэтому обоснованность презумпции зависит от обоснованности того эмпирического закона, из которого они выведены. М. С. Строгович указывал, что «эмпирический закон — это «установленная опытным путем постоянная связь явлений, причины которой нам неизвестны или известны не в полной мере», поэтому «эмпирический закон всегда будет иметь приблизительный, вероятный характер»2. Значит, предположение вообще есть вероятное заключение о неизвестном факте, выведенное из общеизвестного на основании опыта, а презумпция — это предположение, основанное на вероятности.

В связи с этим представляется неверным определение фактических презумпций, данное Л. М. Васильевым, по мнению которого, «фактические презумпции в уголовном судопроизводстве — это выработанные общественно-исторической практикой человечества истинные и достоверные знания о развитии природы, общества и мышления, сознательно используемые следователем и судьей в форме дедуктивного движения мысли для исследования обстоятельств, необходимых для осуществления правосудия по уголовным делам»3. Поскольку презумпция — это предположение, а предположение, в свою очередь, означает догадку, предварительную мысль4, то речь не может идти об истинности закрепленного в ней знания и, тем более, о его достоверности. Существенный признак презумпций подчеркивал еще в 1854 году Д. И. Мейер, профессор Казанского университета, автор монографии о фикциях и предположениях: «признание факта существующим по вероятности, что он существует, называется предположением»5. Презумпции закрепляют вероятное знание, до-

1 Цит. по: Ильин, В. В. Теория познания. Введение. Общие проблемы / В. В. Ильин. — М.: Изд-во МГУ, 1993. — С. 70.

2 Строгович, М. С. Логика: учебное пособие для вузов / М. С. Строгович. — М.: Госполитиздат, 1949. — С. 192.

Васильев, Л. М. Фактические презумпции в советском уголовном судопроизводстве. Тексты лекций / Л. М. Васильев. — Кубанский гос. ун-т, 1977. — С.22-23.

4 Ожегов, С. И. Словарь русского языка. — С. 571.

5 Мейер, Д. И. О юридических вымыслах, предположениях, о скрытых и притворных действиях / Д. И. Мейер. — Казань, 1854. — С. 44.

пускающее опровержение, даже высокая степень вероятности которого не дает основания признавать его достоверным.

Несмотря на то, что процесс образования презумпций происходит индуктивным путем, между презумпциями и индуктивными обобщениями имеется существенное различие. Так, в процессе индуктивного обобщения ход мысли можно выразить так: «Насколько нам известно, исключений из данного положения не встречалось, следовательно, оно может иметь общее значение». Обоснованием общего вывода служит незнание противоречащих случаев1, при этом обнаружение хотя бы одного случая, противоречащего обобщению, делает индуктивный вывод несостоятельным. Использование же презумпций, закрепляющих обобщение жизненной практики, предполагает заранее известные случаи, противоречащие этому обобщению, которые могут опровергнуть презумпцию, но понятие «опровержение презумпции» следует понимать в том смысле, что опровергается ее применимость не вообще, а к данному конкретному случаю. Значит, презумпция, в отличие от популярной индукции, не только допускает опровержение, но и не существует без него. Вывод же о том, соответствует ли презюмируемый факт конкретным обстоятельствам в каждом отдельном случае делает субъект познания.

Авторы «Теории доказательств в советском уголовном процессе» подразделяют презумпции, применяемые в доказывании, на два вида: правовые (легальные, законные) и фактические2.

Фактические или общечеловеческие презумпции составляют предположения, которые субъект доказывания делает по своему внутреннему убеждению, выводя из одних фактов заключение о существовании других фактов в соответствии с обстоятельствами дела. Фактические презумпции в большинстве случаев выражают действительно существующее положение вещей, не зависящее от субъекта, поэтому являются объективными по своему содержанию, хотя и не исключают своего опровержения. Д. Мейер, приводит следующее высказывание французского юриста Дома (1753 год) о praesumtiones hominis: «все, что случается естественно и обыкновенно предполагается истинным, и напротив, необыкновенное и неестественное, не будучи доказано, не считается истинным. На этом основано предполо-

1 Михалкин, Н. В. Логика и аргументация в судебной практике: Учебник для вузов / Н. В. Михалкин. — СПб.: Питер, 2004. — С. 126.

2 Теория доказательств в советском уголовном процессе… — С. 344.

жение, что отец любит своих детей, что каждый заботится о своих детях…, что люди действуют сообразно правилам своим и привычкам, что каждый поступает по указаниям рассудка. Никогда затем не следует предполагать, т.е. допускать бездоказательно, что отец ненавидит своих детей, что человек пренебрегает своими интересами, что рассудительный человек совершил действие, недостойное его обычного поведения.»1.

Фактические презумпции основаны на обобщении многовекового опыта предшествующих поколений, поэтому закрепленное в них знание является в высокой степени вероятным, т.е. вероятность истинности такого знания больше вероятности его ложности. Именно этим обосновывается возможность и оправданность использования презюмируемых фактов в процессе доказывания по уголовному делу. Существенным признаком фактических презумпций, таким образом, является их высокая вероятность.

Законным презумпциям в юридической литературе давались различные определения. По справедливому мнению В. И. Каминской, обобщения общественной практики, будучи положенными в основу юридических норм, приобретают правовой характер и с момента обращения их законодателем в правовые нормы по своему значению становятся правовыми презумпциями2.

По определению указанного автора, под правовой презумпцией понимается такое «положение, выраженное прямо или косвенно в правовой норме, которым какой-либо порядок явлений в области отношений, возникающих из человеческого поведения, признается обычным, постоянным, нормальным и не требующим, в силу этого, специальных доказательств»3. В данном определении верно отмечено, что правовые презумпции относятся именно к явлениям «в области отношений, возникающим из человеческого поведения», а в этой области, как ни в какой другой, невозможно установить какие-либо закономерности, поскольку общество тем и отличается от природы, что в нем действуют люди, наделенные сознанием и волей, и ничего подобного нет в природе, где действуют бессознательные силы.

1 Майер, Д. Указ. соч. — С.52-53.

Каминская, В. И. Учение о правовых презумпциях в уголовном процессе / В. И. Каменская. — М.-Л.: Изд-во АН СССР, 1948. — С. 35.

3 Каминская, В. И. Указ. соч. — С. 3.

А. Ф. Клейнман предположения, используемые в сфере действия права, называл юридическими доказательственными презумпциями. Автор справедливо отмечал, что «предположение имеет значение постольку, поскольку закон устанавливает в связи с наличием определенного факта предположение о существовании другого факта. Такая презумпция называется юридической потому, что она установлена нормой права, потому что с ней связаны правовые последствия. Она называется доказательственной презумпцией, так как освобождает сторону от обязанности доказывать презюмируемый факт»1.

Я. Л. Штутин определял презумпцию (законное предположение) как «логический прием, с помощью которого можно вывести существование (несуществование) неизвестного искомого факта из другого достоверно известного факта, если неизвестный искомый факт по предположению, основанному на обобщениях практики, является прямой причиной (следствием) достоверно известного факта и не опровергнут в ходе судебного разбирательства»2.

Данное определение, на мой взгляд, содержит неточность, заключающуюся в том, что «предположение, основанное на обобщении практики», во-первых, не может быть достоверным, и, во-вторых, может являться только наиболее вероятной причиной известного факта, но никак не «прямой», поскольку причина — это явление, порождающее другое явление, и обязательными свойствами причинной связи, кроме последовательности во времени, являются всеобщность, необходимость и однозначность. Использование причинной связи (именно от причины к следствию, но не наоборот) ведет к однозначному, достоверному выводу, имеет принудительный характер, тем самым, исключая предположение.

Верно отражающее природу презумпций определение дано авторами «Теории доказательств в советском уголовном процессе». Презумпция — «общее правило, отображающее устойчивые, неоднократно наблюдаемые связи между фактами, событиями, явлениями, состояниями, свойствами. Применение презумпций состоит в том, что при наличии (установлении) одного из фактов, связь которых выражена презумпцией, делается вывод о существовании другого факта;

1 Советский гражданский процесс / Под. ред. А. Ф. Клейнмана. — М., 1964. -С. 145.

Штутин, Я. Л. Предмет доказывания в гражданском процессе / Я. Л. Штутин. — М.: Юрид. лит., 1951. — С. 94.

последний, таким образом, выводится из презумпции (презюмирует-ся)»1.

Законные презумпции можно определить как предположения, санкционированные нормами права, поэтому обязательные для суда, пока они не опровергнуты надлежащими доказательствами. Практическое значение такого предположения, — справедливо указывал Д. Мейер, — главным образом заключается в том, что факт предполагаемый не нуждается в доказательстве, что потому кем следует должно быть доказано несуществование факта, чтобы устранить юридические последствия, связанные с предполагаемым фактом2, т.е. назначение презумпций состоит в распределении бремени доказывания.

Логический прием индуктивного обобщения, свойственный познавательной деятельности вообще, в сфере действия права приобретает способность вызывать специальные правовые, а не просто познавательные последствия. Следовательно, законные презумпции кроме логического значения, основанного на эмпирическом обобщении взаимосвязи явлений, побуждающем искать наиболее вероятную причину или следствие известного обстоятельства, имеют и правовое значение, заключающееся в способности законных презумпций оказывать влияние на разрешение дела. Эта способность заключается в роли законных презумпций — служить приемом обоснования знания об обстоятельствах уголовного дела, способом перераспределения обязанностей по доказыванию.

Для законных презумпций, таким образом, характерно:

1) они либо прямо санкционированы законом, либо вытекают из его смысла;

2) не исключают своего опровержения;

3) предметом презюмирования являются юридические факты, вызывающие правовые последствия.

Для законных презумпций высокая вероятность закрепленного в них знания не является необходимым признаком. Действительно, нельзя утверждать, что презумпция невиновности, например, основана на высокой степени вероятности невиновности обвиняемого, в большинстве случаев эта презумпция опровергается доказательствами того, что обвиняемые действительно совершили преступление. Необходимость существования этой презумпции основана на том, что

1 Теория судебных доказательств. — С. 343.

2

Мейер, Д. Указ. соч. — С.61.

высшей ценностью для общества в целом и законодателя в частности является человек, его права и свободы, незаконное и необоснованное ограничение которых недопустимо.

Таким образом, значение использования презумпций в процессе уголовно-процессуального доказывания заключается в следующем:

• презумпции выступают способом, облегчающим достижения истины, так как, являясь продуктом многовековой практики, освобождают от необходимости их доказывать вновь;

• создают возможность их использования при оценке аналогичных явлений и ситуаций, поскольку отражают объективно существующие связи и зависимости;

• служат средством обоснования знания об обстоятельствах уголовного дела, способом перераспределения обязанностей по доказыванию.

Для фактических презумпций, как отмечалось, существенным признаком является высокая вероятность закрепленного в них знания, т. е. большее значение имеет логическая природа таких презумпций. Для правовых (законных) презумпций, в отличие от фактических, преобладающей является их правовая, а не логическая природа, т.е. прямая или косвенная закрепленность в правовых нормах, порождающая правовые последствия. Вероятность истинности закрепленного в правовых презумпциях знания может быть меньше вероятности их ложности. Правовые презумпции служат единообразному правовому регулированию, стабильности правопорядка, защите прав граждан, помогают установить рациональный и справедливый порядок доказывания обстоятельств уголовного дела1.

О. М. Смирнов

ЮРИДИЧЕСКОЕ ЗНАЧЕНИЕ ЗАКОНОДАТЕЛЬНОГО ЗАКРЕПЛЕНИЯ ПРИНЦИПОВ РОССИЙСКОГО УГОЛОВНОГО СУДОПРОИЗВОДСТВА

В юридической науке принципы уголовного судопроизводства подверглись основательному рассмотрению.

В науке уголовного процесса приемлемой является точка зрения, согласно которой принципы правосудия — это основополагаю-

1 Теория доказательств в советском уголовном процессе. — С. 345.

1.1. Логическая и математическая символика

Естественные науки / Математический анализ функции одной переменной / 1.1. Логическая и математическая символика

В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение.

Математические символы:

Например, применяя символ «>» к числам  a, b, получим запись «a > b», которая является сокращением для предложения: «число a больше числа b». Если  – обозначения прямых, то запись  есть утверждение, что  параллельна . Запись «xM» означает, что x является элементом множества M.

Наряду с математической символикой в математике широко используется логическая символика, применяемая к высказываниям и предикатам.

Под высказыванием понимается предложение, которое либо только истинно, либо только ложно.

Предикат – это предложение с одной переменной или несколькими переменными. Например, предложение:  «число x больше числа 0» (в символах x > 0) является предикатом от одной переменной x, а предложение: «a + b = c» –  предикат от трех переменных a, b, c.

Предикат при конкретных значениях переменных становится высказыванием, принимая истинное и ложное значение.

Будем обозначать предикаты как функции: Q(x) =«x > 0»,    F(x,b,c) = «x + b = c».

Логические символы:  .

1. Отрицание применяется к одному высказыванию или предикату, соответствует частице «не» и обозначается  .

Например, формула   есть сокращение для предложения: «–3 не больше 0» («неверно, что –3 больше 0»).

2. Конъюнкция применяется к двум высказываниям или предикатам, соответствует союзу «и», обозначается:  А & B   (или

Так формула (–3 > 0) & (2  2 = 4) означает предложение «–3 > 0 и 2  2 = 4», которое, очевидно, ложно.

3. Дизъюнкция применяется к двум высказываниям или предикатам, соответствует союзу «или» (неразделительному) и обозначается AB .

Предложение: «число x принадлежит множеству  или множеству » изображается формулой:.

4. Импликация соответствует союзу «если …, то …» и обозначается: AB.

Так, запись «a > –1 a > 0» есть сокращение для предложения «если

5. Эквиваленция AB соответствует предложению: «A тогда и только тогда, когда B».

Символы  называются кванторами общности и существования, соответственно применяются к предикатам (а не к высказываниям). Квантор  читается, как «любой», «каждый», «все», или с предлогом «для»: «для любого», «для всех» и т.д. Квантор  читается: «существует», «найдется» и др.

Квантор общности применяется к предикату F(x, …), содержащему одну переменную (например,

1. xF(x,…), которая соответствует предложению: «для любого x выполняется F(x, …)» или «все x обладают свойством F(x, …)».

Например: x(x > 0) есть сокращение для фразы: «любое x больше 0», которая является ложным высказыванием.

Предложение: a(a > 0  a > –1) является истинным высказыванием.

2. Квантор существования

Например, истинное высказывание «существует действительное число, квадрат которого равен 2» записывается формулой x(xR & x² = 2). Здесь квантор существования применен к предикату: F(x)=(xR & x² = 2) (напомним, что множество всех действительных чисел обозначается через R).

Если квантор применяется к предикату с одной переменной, то получается высказывание, истинное или ложное. Если квантор применяется к предикату с двумя или большим числом переменных, то получается предикат, в котором переменных на одну меньше. Так, если предикат

Так, предикат  «|sinx| < a»  содержит две переменные x, a. Предикат x (|sinx| < a) зависит от одной переменной a, при  этот предикат обращается в ложное высказывание (|sinx| < ), при а = 2 получаем истинное высказывание x (|sinx| < 2).

Если к предикату x (|sinx| < a) применить квантор существования, то получим формулу: , выражающую истинное высказывание: «функция sinx является ограниченной».

Для некоторых формул введем сокращенную запись.

Так, вместо формулы x(xR & x² = 2)                будем писать:xR(x² = 2),

вместо                       x(x > 0 & x² + 3 = 4)           пишем:            x > 0 (x² + 3 = 4).

Формулу                     x (xR  x²  0)            сократим так:

Будем называть  и т.д. ограниченными кванторами.

Несколько кванторов общности (существования) заменяем на один: вместо  пишем x,y(P(x,y)), вместо  будем писать .

Логические операторы Python с примерами

Улучшить статью

Сохранить статью

• Уровень сложности: Easy
• Последнее обновление: 09 Янв, 2023

Улучшить статью

Сохранить статью

Операторы используются для выполнения операций над значениями и переменными. Это специальные символы, которые выполняют арифметические и логические вычисления. Значение, с которым работает оператор, известно как 9.

Table of Content

• Логические операторы
  • Логический и оператор
  • Логический или оператор
  • Logical Not Operator
• Порядок оценки логических операторов

Logical Operation используется в условных операторах (либо True, либо False). Они выполняют

Таблица истинности для всех комбинаций значений X и Y.

Таблица истинности

Логический оператор И

Логический оператор возвращает значение Истина, если оба операнда имеют значение Истина, в противном случае он возвращает значение Ложь. Example #1:  

Python3

Пример №2:  

Python3

Вывод

 По крайней мере одно число имеет логическое значение как Fal
 

Примечание: Если первое выражение оценивается как ложное при использовании оператора и, то последующие выражения не оцениваются.

Логический оператор ИЛИ

Логический оператор или возвращает значение Истина, если хотя бы один из операндов имеет значение Истина. Пример №1:  

Python3

3 9009 2 
3 9009 2 
 3 9009 33303 
03 03 03 03 9009 33303 0 3 0 3 0 3 9009 3 30. 
Нет числа больше 0
 
    Example #2:   
 Python3 
  
  a   =   10 
  b   =   12 
  c   =   0 
  
  if   a   or   b   or   c: 
         print   (   "Atleast одно число имеет логическое значение как True"   ) 
  else   : 
         print   ( 911144  ) 
  Вывод 
 По крайней мере одно число имеет логическое значение как True
 
  Примечание:  Если первое выражение оценивается как True при использовании оператора или, то последующие выражения не оцениваются.
 Логический оператор "не" 
 Логический оператор "не" работает с одним логическим значением. Если логическое значение равно True, оно возвращает False и наоборот.  Пример:   
 Python3 
  
  a   =   10 
  
  if   not   a: 
         print   (   "Boolean value of a is True"   ) 
  
  if   not   (a   %   3   =   =   0   or   a   %   5   =   =   0   ): 
         print   (   "10 is not divisible by either 3 or 5"   ) 
  else   : 
    Печать   (  "10 делится на 3 или 5"  ) 
 . 
 Порядок вычисления логических операторов 
 В случае нескольких операторов Python всегда вычисляет выражение слева направо. В этом можно убедиться на приведенном ниже примере.  Example:   
 Python3 
  
  def   order(x): 
         print   (   "Method called for value:"   , x) 
         возврат   True   if   x >   0   else   False 
         
  a   =   order 
  b   =   order 
  c   =   order 
  
  if   a(   -   1   )   or   b(   5   )   or   c( ​​  10   ): 
         print   (   "Atleast one of the number is positive"   ) 
  Output 
 Метод вызывается для значения: -1
Метод вызывается для значения: 5
Хотя бы одно из чисел положительное
 

 Статьи по теме
 Следующая
 Побитовые операторы Python
 Что нового
 Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство при просмотре нашего веб-сайта. Используя наш сайт, вы
подтверждаете, что вы прочитали и поняли наши  Политика в отношении файлов cookie  и  Политика конфиденциальности 
 Освоение JavaScript && и || логические операторы | by Nicolas Marcora 
 Это распространенное заблуждение, что использование AND  &&  или OR  || Операторы  всегда должны возвращать  true  или  false  . Это НЕ так, и в этом коротком посте я хотел бы изучить, как цепочка  &&  s и  ||  будут вести себя на самом деле, и как мы можем использовать это в своих интересах.
 Приведение типов 
 Прежде всего, краткое примечание о приведении типов:  true  и  false  являются  булевыми  значениями. Превратить значение в логическое означает взять любое значение, которое НЕ является  истинным  или  ложным , и попытаться преобразовать его в любое из них. В JavaScript вы можете легко проверить результат преобразования любого значения в логическое значение, набрав:  Boolean(value)  . Давайте попробуем в консоли:
 Вы можете видеть, что некоторые значения оцениваются как 9.0113 true  и другие до  false  . Эти значения обычно называют  истинными  и  ложными  значениями. Таким образом, вы можете сказать, что любое значение, которое при преобразовании в логическое значение становится  истинным , является истинным, а любое значение, которое становится  ложным , является ложным.
 Теперь, когда мы разобрались с этим, давайте перейдем к тому, как  &&  и  ||  вести себя.
 Оператор И ( && ) 
 В цепочке из  &&  с, каждое значение будет оцениваться слева направо. Если какое-либо из этих значений окажется  ложным  , это значение будет возвращено, и цепочка не будет продолжена. Если цепочка не разорвется до достижения конца, будет возвращено последнее значение в цепочке.
 Давайте откроем нашу консоль и проверим это:
 Вы это видите? Давайте рассмотрим это шаг за шагом:
  В первом примере  мы проверяем наше первое значение, оно истинно, поэтому мы переходим к следующему значению, которое является ложным, поэтому мы возвращаем его и останавливаемся на этом.
  Во втором примере  происходит то же самое. Мы проверяем первое значение, которое является истинным, мы проверяем второе значение, которое является ложным, поэтому мы возвращаем его и останавливаемся на этом. Обратите внимание, что хотя и существует третье значение, которое на самом деле является истинным, это значение никогда не достигается, потому что перед ним появилось ложное значение, которое разорвало цепочку.
  Третий пример  показывает такое же поведение, только с другим типом ложного значения.
  Последний пример  показывает, что когда все значения в цепочке истинны, возвращается последнее значение в цепочке.
 Оператор ИЛИ ( || ) 
  || Оператор  ведет себя точно так же, как  && , только наоборот! В то время как цепочка  &&  разорвется, если будет найдено ложное значение, цепочка  ||  сломается, когда найдет  истинное значение . И, как и в случае с  &&  s, если нет истинных значений и достигнут конец цепочки, возвращается последнее значение в этой цепочке.
 Давайте также проверим это в консоли:
 Вы можете видеть, что они также следуют одному и тому же шаблону:
  В первом примере  цепочка заканчивается, когда это  истинное  найдено и возвращено.
  Во втором примере  цепочка обрывается, потому что  "Я правдив"  является истинным значением, поэтому цепочка разрывается и возвращается  "Я правдив" .
  В третьем примере , несмотря на то, что ВСЕ значения в цепочке верны, цепочка разрывается после того, как первое значение оказывается правдивым и возвращается, поэтому две другие строки, следующие за ним, никогда не оцениваются.
  В последних двух примерах  вы можете видеть, как, когда все значения в цепочке ложны, возвращается последнее значение в цепочке.
 Внутри оператора if 
 Вот что происходит, когда вы используете эти цепочки внутри оператора  if :
 Получение немного большей функциональности 
 Использование логических операторов таким более практичным способом обычно называется  оценкой короткого замыкания  .
 До сих пор мы видели только такие значения, как строки, undefined, null и оцениваемые объекты. Это уже может быть полезно само по себе, но что, если я скажу вам, что вы также можете помещать функции внутрь этих цепочек?
 Что здесь происходит?
 Сначала проверяется переменная  truely , и, поскольку это непустая строка, она оценивается как  true , и поэтому код переходит к проверке следующего значения… Только это значение является функцией! Итак, функция запускается, и JavaScript оценивает значение , возвращаемое функцией . Таким образом,  truey && doSomeStuff()  в конечном итоге становится  «Я правдивый» && «хороший»  после оценки обоих значений, и  "хороший"  возвращается, потому что это последняя истина в этой цепочке  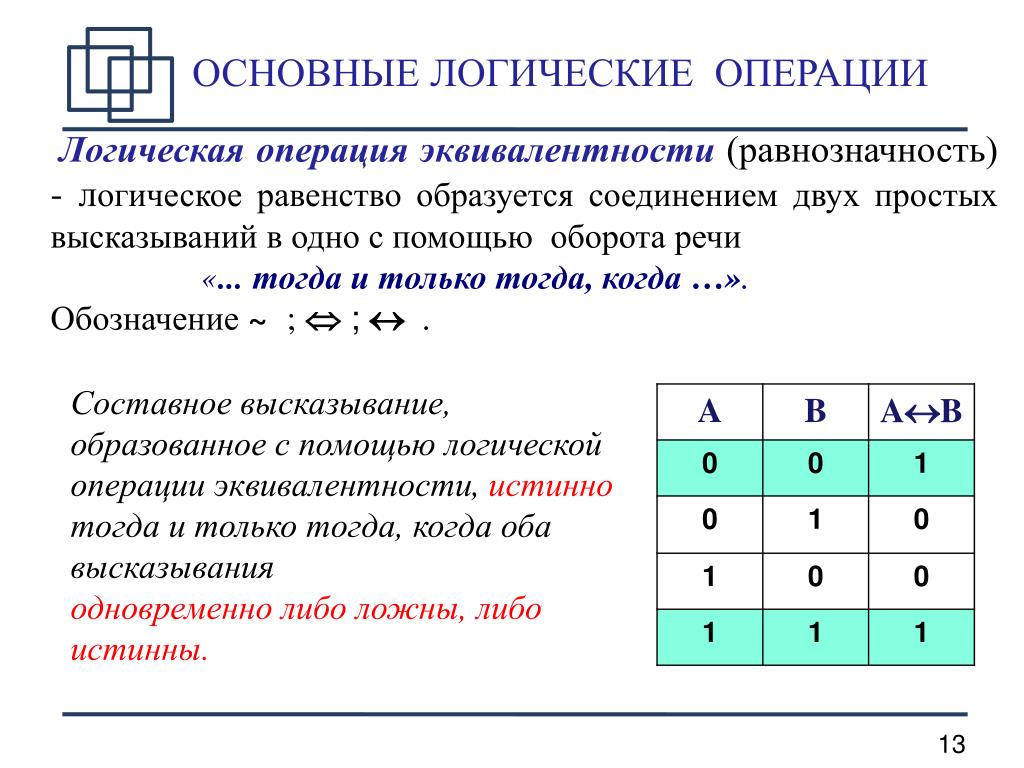&& . Но для того, чтобы получить это значение  "хороший" , функция должна была быть выполнена, и  выполнял действия , зарегистрированные в консоли. Это означает, что когда функция оценивается, она запускается, и любой код, который мы туда вставляем, выполняется. Надеюсь, мы начинаем видеть, как мы можем использовать это в наших интересах! до  true  или  false  , говорящие нам о том, вошел ли пользователь в систему или нет. Теперь мы можем сделать что-то подобное в нашем коде:
 В этом случае нам все равно, что возвращает выражение, но мы хотим выполнить эту функцию   только в том случае, если пользователь зарегистрирован в  . Мы используем это выражение для его побочных эффектов, а не для возвращаемого значения.
 Эта единственная строка будет делать то же самое, что и этот код:
 Но разве это не выглядит намного чище? Я лично думаю, что да!
 Давайте пойдем немного дальше:
 Здесь мы хотим выполнить эту функцию  sendLetter() , но только если пользователь существует, у него есть адрес и в адресе есть первая строка.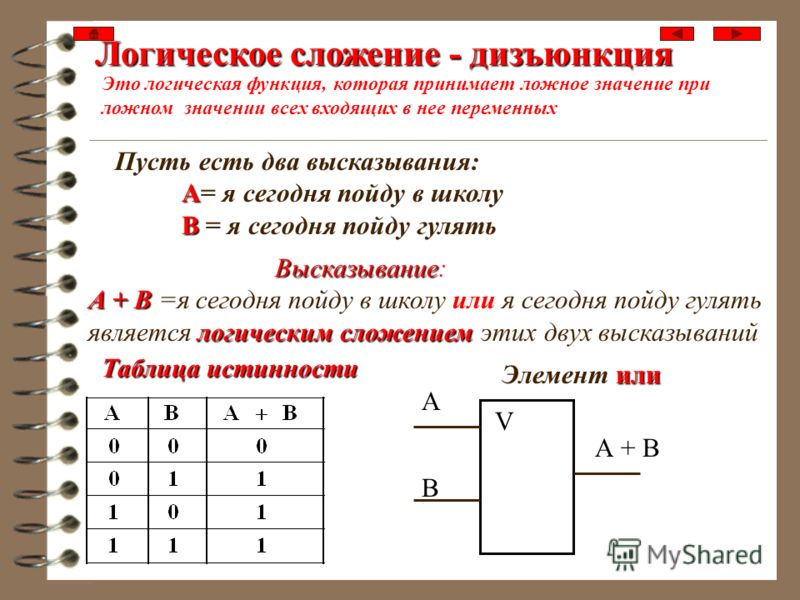 Если в какой-либо точке цепочки значение окажется ложным, то цепочка разорвется и  sendLetter()  вызываться не будет.
 Использование логических операторов в дикой природе 
 Это компонент React. Если вы посмотрите на  строку 8  , вы увидите 9Оператор 0113 &&  используется для включения приветствия h2 пользователю, но только если доступно имя   пользователя.
 Если вы хотите узнать немного больше о React с самого начала, я рекомендую вам взглянуть на мою предыдущую статью: React from Scratch.
 Я нашел эту функцию в официальной кодовой базе React на Github, вы можете найти ее здесь. Он используется для проверки того, является ли объект действительным элементом React, и возвращает  true , если все условия выполнены, или false, если любое из условий равно 9.0113 ложь  и разорвать цепочку.
 Смешивание вещей 
 Хотя не рекомендуется смешивать  &&  и  ||  вместе, я просто хотел указать, что  &&  имеет приоритет над  ||  при вычислении, подобно тому, как умножение  *  имеет приоритет над сложением  +  в математике. Итак:
  'весна' && 'зубная паста || 'зима' && 'конфеты' 
 будут оцениваться как:
  ("весна" && "зубная паста") || («зима» && «конфеты») 
 Другими словами,  &&  будут сгруппированы вместе.
 Предостережение 
 Вполне вероятно, что когда вы впервые начнете изучать JavaScript, вы будете использовать и находить эти операторы только внутри операторов  if , и это совершенно нормально. Но по мере того, как вы начнете продвигаться вперед и читать более сложные базы кода, такие как библиотеки, вы начнете видеть их и использовать чаще, чтобы сделать свой код чище и лаконичнее.
 Все, что в избытке, может быть вредным, поэтому, прежде чем использовать их, всегда думайте, делаете ли вы свой код более легким или сложным для чтения. Читабельность имеет значение!
 Подводя итог 
 Логические операторы  &&  и  ||  очень универсальны и часто неправильно понимаются.