Конъюнкция — это… Что такое Конъюнкция?
Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты:
в инфиксной записи:
- ,
по аналогии с умножением в алгебре знак логического умножения может быть пропущен: ,
в префиксной записи:
- .
Булева алгебра
Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).
Правило: результат равен наименьшему операнду.
Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, , при цифровом обозначении старшинство естественно .
Таблицы истинности:
для бинарной конъюнкции
для тернарной конъюнкции
| X | Y | Z | X Y Z | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | |
| 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции[1].
Многозначная логика
Операция, называемая в двоичной логике конъюнкция, в многозначных логиках называется
Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» имеют смысл только в двоичной логике, а при переходе к многозначным логикам теряют смысл.
Классическая логика
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Схемотехника
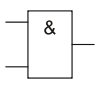 Логический элемент «И»
Логический элемент «И»Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения
- «1» тогда и только тогда, когда на всех входах есть «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе есть «0»
Программирование
В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата или . Например:
if (a & b & c)
{
/* какие-то действия */
};
Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:
a = false; b = true; c = true;
if (a && b && c)
{
/* какие-то действия */
};
Проверка истинности выражения в данном случае остановится после проверки переменной a, т.к. дальнейшее сравнение не имеет смысла.
Результат будет равен , если оба операнда равны (для числовых типов не равны ). В любом другом случае результат будет равен .
При этом применяется стандартное соглашение: если значение левого операнда равно , то значение правого операнда не вычисляется (вместо может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
или выключающую
подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:
if (a != 0 && b / a > 3)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | |
| b = | |
| то | |
| a И b = |
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как , а «ложь» как . При этом часто делают стандартную оговорку о
Примечания
- ↑ 1 2 Словарь по кибернетике /Под редакцией В. С. Михалевича. — 2-е издание — К.: 1989. — 751 с., ISBN 5-88500-008-5
См. также
Логическое умножение — это… Что такое Логическое умножение?
Конъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И».
Это бинарная инфиксная операция, то есть, она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи: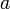 &&
&& 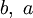
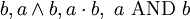 .
.По аналогии с умножением в алгебре знак логического умножения может быть пропущен:
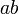 .
.Булева алгебра
В булевой алгебре конъюнкция — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества 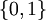 . Результат также принадлежит множеству
. Результат также принадлежит множеству 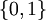
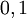 может использоваться любая другая пара подходящих символов, например
может использоваться любая другая пара подходящих символов, например 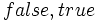 или
или 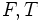 или «ложь», «истина».
или «ложь», «истина».Правило: результат равен 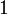
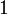 ; во всех остальных случаях результат равен
; во всех остальных случаях результат равен 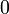 .
.Таблица истинности:
Многозначная логика
В многозначной логике операция конъюнкции может определяться другими способами. Чаще всего применяется схема: 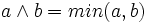 , где
, где ![~a, b \in [0, 1]](/800/600/https/dic.academic.ru/pictures/wiki/files/100/dfbf391a6408e74c7a9b40da50e8fffd.png) . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
Классическая логика
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции: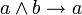
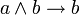
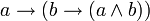
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&».
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата 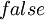 или
или 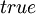 . Например:
. Например:
if (a && b)
{
/* какие-то действия */
};
Результат будет равен 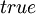 , если оба операнда равны
, если оба операнда равны 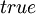 (для числовых типов не равны
(для числовых типов не равны 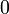 ). В любом другом случае результат будет равен
). В любом другом случае результат будет равен 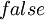 .
.
При этом применяется стандартное соглашение: если значение левого операнда равно 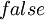 , то значение правого операнда не вычисляется (вместо
, то значение правого операнда не вычисляется (вместо 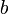 может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет возможность вычисления правого операнда:
может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет возможность вычисления правого операнда:
if (a != 0 && b / a > 3)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 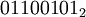 |
| b = | 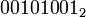 |
| то | |
| a И b = | 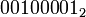 |
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом»…»И» также несет в себе оттенок неопределенного смысла. Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».
См. также
Wikimedia Foundation. 2010.
Исключающее «или» — Википедия
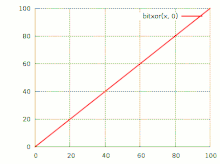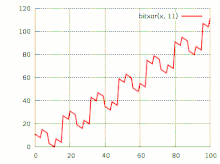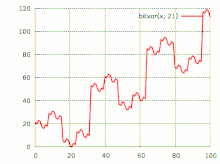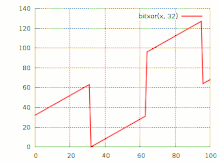 График побитового исключающего «или»
График побитового исключающего «или»Исключа́ющее «или» (сложе́ние по мо́дулю 2, XOR, строгая дизъюнкция, поразрядное дополнение, инвертирование по маске, жегалкинское сложение, логическое вычитание, логи́ческая неравнозна́чность) — булева функция, а также логическая и битовая операция, в случае двух переменных результат выполнения операции истинен тогда и только тогда, когда один из аргументов истинен, а другой — ложен. Для функции трёх (тернарное сложение по модулю 2) и более переменных — результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Сложение по модулю 2 называется «исключающим „или“» и «строгой дизъюнкцией» для отличения от «обычного» (неисключающего) логического «или» — нестрогой логической дизъюнкции. В теории множеств сложению по модулю 2 соответствует операция симметрической разности двух множеств.
Запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более 2 префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:
⊕2(a,b), a{\displaystyle \oplus _{2}(a,b),~a} ^ b, a⊕b,a⊕2b,a+2b,{\displaystyle b,~a\oplus b,a\oplus _{2}b,a+_{2}b,} a ≠ b, a≠b,(a,b)⊕2,a XOR b{\displaystyle a\neq b,(a,b)\oplus _{2},a~XOR~b}
В Юникоде есть символы для сложения по модулю 2: U+22BB ⊻ xor, U+2295 ⊕ circled plus и U+2A27 ⨧ plus sign with subscript two, U+2A52 ⩒ logical or with dot above, а также символ для суммы по модулю 2: U+2A0A ⨊ modulo two sum.
В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true>false{\displaystyle true>false}.
Таблицы истинности:
| a{\displaystyle a} | b{\displaystyle b} | a⊕b{\displaystyle a\oplus b} |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Правило: результат равен 0{\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1{\displaystyle 1}.
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a⊕b⊕c{\displaystyle a\oplus b\oplus c} |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Правило: результат равен 0{\displaystyle 0}, если нет операндов, равных 1{\displaystyle 1}, либо их чётное количество.
В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
- если
a=011001012{\displaystyle a=01100101_{2}}
b=001010012{\displaystyle b=00101001_{2}}
- то
a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}
Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.
Использование побитового исключающего «или» позволяет поменять местами значения целых переменных без использования дополнительной памяти.
В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:
- «результат истинен (равен 1), если A не равно B (A≠B)»;
- «если A не равно B (A≠B), то истина (1)».
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
- A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
- A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).
Операция ⊕{\displaystyle \oplus } исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция ∨{\displaystyle \lor } включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
В квантовых компьютерах аналог операции сложения по модулю 2 — вентиль CNOT.
Логическая ошибка — Википедия
Логическая ошибка — в логике, философии и прочих науках, изучающих познание, ошибка, связанная с нарушением логической правильности умозаключений[1][2]. Ошибочность обусловлена каким-либо логическим недочётом в доказательстве, что делает доказательство в целом неверным.
Формальные ошибки[править | править код]
Подмена тезиса (лат. ignoratio elenchi) — логическая ошибка в доказательстве, состоящая в том, что начав доказывать некоторый тезис, постепенно в ходе доказательства переходят к доказательству другого положения, сходного с тезисом, но имеющего совершенно иное значение.
Использование ложных и недоказанных аргументов, утверждений[править | править код]
Другая логическая ошибка — «предвосхищение основания» (лат. petitio principii). Она заключается в том, что в качестве аргументов используются недоказанные, как правило, произвольно взятые положения: ссылаются на слухи, на ходячие мнения, высказанные кем-то предположения или даже на собственный вымысел, выдавая их за аргументы, якобы обосновывающие тезис. В действительности же доброкачественность таких доводов лишь предвосхищается, но не устанавливается с несомненностью.
Обычно подобные лже-аргументы сопровождаются фразами: «Как абсолютно всем известно…», «Кто же будет спорить с тем, что…», «Аксиомой, не требующей доказательств, является то, что…», «Само собой разумеется, что…», «Каждому известно, что…», дабы рассеять возможные сомнения у простого слушателя.
Особые случаи[править | править код]
- апелляция к личности оппонента, а не к его доводам (argumentum ad hominem)
- переход на личности (ad personam): «Вы глупы и некрасивы, поэтому ваш тезис неверен».
- поиск обстоятельств, якобы заставляющих оппонента выдвигать данный тезис (circumstantiae): «Вы говорите так, потому что хотите произвести впечатление на публику, поэтому ваш тезис неверен».
- указание на то, что оппонент сам поступает вопреки своим доводам: (tu quoque): «Вы сами курите, поэтому ваши доводы о вреде курения неверны».
- нахождение легко критикуемого единомышленника (reductio ad Hitlerum): «Гитлер тоже был вегетарианцем!».
- апелляция к большинству (argumentum ad populum): «Все вокруг считают так, следовательно, это верно».
- апелляция к авторитету (argumentum ad verecundiam): «Это мнение принадлежит авторитету, разве вы его не уважаете?». Используется и в обратную сторону: «Это мнение высказывал Гитлер, Вы что, согласны с Гитлером?»
- апелляция к традиции (argumentum ad antiquitatem): «Так считается с древнейших времен, потому это верно».
- апелляция к милосердию (argumentum ad misericordiam): «Если вы не согласитесь с моим мнением, то разрушите мне всю жизнь».
- апелляция к незнанию; отсутствие доказательств чего-то считается доказательством обратного (argumentum ad ignorantiam): «Привидения существуют, так как никто не доказал, что их нет».
- «аргумент к тошноте» (argumentum ad nauseam), повторение тезиса (возможно, разными людьми) до тех пор, пока противная сторона не потеряет интерес к его оспариванию.
- апелляция к страху или аргумент с позиции силы (argumentum ad baculum[en]): «Если вы не согласитесь, с вами произойдёт что-то плохое».
- выдача желаемого за действительное: «Я хочу, чтобы так было, значит, так и есть».
- апелляция к личному опыту (ad hominem): «Мне это лекарство помогло, значит всем поможет».
Мнимая логическая связь[править | править код]
Логическая уловка, при которой мнимая, желаемая логическая связь выдаётся за истинную (non sequitur).
Ошибка выборки[править | править код]
Систематическая ошибка отбора — ошибка, при которой на основании неподходящей выборки делается вывод о всём множестве (например, по одному примеру судят обо всех), частным случаем такой ошибки является ошибка выжившего.
«После» не значит «вследствие»[править | править код]
«После этого — значит по причине этого» (лат. post hoc ergo propter hoc) — логическая уловка, при которой причинно-следственная связь отождествляется с хронологической, временной: «Если событие X произошло после события Y, значит, событие Y является причиной события X».
Схожей ошибкой является предположение, что совпадение событий во времени означаeт их причинно-следственную связь (лат. сum hoc ergo propter hoc), «Событие X и событие Y происходят одновременно, значит, событие Y является причиной события X». Оба события могут быть следствиями неопределенного количества иных причин.
Корреляция не является причинно-следственной связью[править | править код]
Корреляция между параметрами не является доказательством того, что один из параметров как-то влияет на другой, так как корреляция может быть случайным совпадением, либо следствием влияния на оба параметра третьего, неучтённого параметра. Примером может быть корреляция между количеством фильмов с Николасом Кейджем и смертностью от падения в бассейн[3].
И даже если взаимосвязь параметров доказана, необходимо установить, какой из параметров является причиной, а какой следствием. Так, из взаимосвязи между скоростью вращения мельничного колеса и скоростью ветра не следует, что именно мельницы являются причиной движения воздуха[3].
Доказательство через то же самое[править | править код]
«То же посредством того же», «порочный круг», idem per idem — логическая ошибка, при которой в определение или в доказательство латентно вводится сам доказываемый тезис или определяемое понятие[4].
— Мужчина называется мужчиной потому, что он мужественный.
— Вода называется водой потому, что она водянистая, — вставил Яша Полонский.
- «В чем причина того, что опиум действует усыпляюще? Отвечаю: она в том, что опиум обладает способностью усыплять»
- «Ваш менеджер — придурок, потому что он не умеет думать»
- «Автор ворует чужие идеи, так как он плагиатор»
- «Вода мокрая, так как она влажная»
Приписывание утверждений[править | править код]
Логическая ошибка, которая заключается в приписывании одной стороной другой утверждений, которые на самом деле другая сторона не делала, но которые якобы вытекают из её предыдущих утверждений.
Использование принципиально неопровержимых утверждений[править | править код]
Логическая ошибка, заключающаяся в использовании в качестве аргумента утверждения, которое принципиально невозможно опровергнуть.
Ложная аналогия[править | править код]
Создание аналогии между двумя объектами на основе сходства незначительных признаков при игнорировании значительных или даже принципиальных различий. Например, немецкие учёные К. Фохт и Л. Бюхнер, будучи вульгарными материалистами, утверждали, что «мозг выделяет мысль, как печень выделяет желчь»[5].
Создатель ложной аналогии между объектами затем распространяет нужные ему свойства одного объекта на другой, делая тем самым ложное заключение.
Сверхобобщение[править | править код]
Вывод о явлении в целом, сделанный на основе единичного факта (либо крайне малого количества фактов). Например:
- «Вася опять не убрал свою комнату» → «Все мальчики такие неряхи»;
- «Вчера моя начальница сделала мне необоснованный выговор» → «Все женщины — некомпетентные руководители».
Аристотель в книге «О софистических опровержениях» выделяет шесть видов «софистических опровержений», основанных на неправильном употреблении словесных выражений[6]:
- Одноимённость (омонимия): например, слово «лук» — растение и «лук» — стрелковое оружие.
- Двусмысленность (амфиболия): выражение в целом двусмысленно и может толковаться в обе стороны, например, «день сменяет ночь» или «казнить нельзя помиловать». Амфиболия может основаться и на омонимии, порождая такие выражения как «он прослушал лекцию».
- Соединение (оксюморон): сочетание несочетаемого, противоречащая себе фраза, например, «звонкая тишина», «знойный мороз».
- Разъединение: разделение целого на части и приписывание целому свойств частей. Например, «Пять — это три плюс два, три — нечетное число, два — четное, значит, пять — четное и нечетное число одновременно».
- Ударение или произношение: логические ошибки, построенные на неверном произношении или ударении (например, за́мок и замо́к). Для русского языка эта проблема менее актуальна, чем для греческого.
- Форма выражения: ошибки, связанные с формой выражения — подменой мужского рода женским и наоборот, подменой среднего рода мужским или женским за счет одинаковости окончаний; или подменой качества количеством и наоборот; отождествления результата с процессом, состояния — с действием и т. п.
Эквивокация[править | править код]
Эквивокация — ошибка, заключающаяся в использовании одного и того же слова в разных значениях в одном рассуждении. Частный случай — учетверение терминов.
Например:
- «Все вулканы — горы. Все гейзеры — вулканы. Следовательно, все гейзеры — горы». В первой посылке слово «вулканы» обозначает «горы, из которых изливается огнедышащая магма», а во второй посылке этим же словом «вулканы» обозначено всякое извержение из недр Земли.
- «Он — старый морской волк. Волки живут в лесу. Значит, он живёт в лесу». В первой посылке слово «волк» используется в качестве метафоры, а во второй посылке — в прямом значении.
Связанные концепции
Списки
- ↑ Бирюков Б. В., Васюков В. Л. Логическая ошибка // Новая философская энциклопедия / Ин-т философии РАН; Нац. обществ.-науч. фонд; Предс. научно-ред. совета В. С. Стёпин, заместители предс.: А. А. Гусейнов, Г. Ю. Семигин, уч. секр. А. П. Огурцов. — 2-е изд., испр. и допол. — М.: Мысль, 2010. — ISBN 978-5-244-01115-9.
- ↑ Ошибочное умозаключение // Философский энциклопедический словарь, 2010
- ↑ 1 2 Роман Фишман. Ложные корреляции: как Николас Кейдж влияет на смерть в бассейне // Популярная механика, 26.04.2016
- ↑ Латинско-русский и русско-латинский словарь крылатых слов и выражений on-line // dic.academic.ru, на основе издания Н. Т. Бабичев, Я. М. Боровской. «Словарь латинских крылатых слов». — М.: «Русский язык», 1982 г.; «Русский Язык-Медиа», ISBN 978-5-9576-0309-2; «Дрофа», ISBN 978-5-358-04495-1, 2008 г.
- ↑ Лебедева О.П. Логика: учеб.-метод. пособие. МГИУ, 2008. — 127 с.
- ↑ Аристотель. О софистических опровержениях // Сочинения в 4 томах. — М.: Мысль, 1978. — Т. 2. — С. 687.
Логическое ИЛИ — это… Что такое Логическое ИЛИ?
Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».
Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи: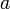 ||
|| 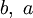 |
| 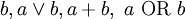 .
.
Булева алгебра
В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен 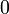 , если оба операнда равны
, если оба операнда равны 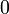 ; во всех остальных случаях результат равен
; во всех остальных случаях результат равен 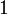 .
.
Многозначная логика
В многозначной логике операция дизъюнкции может определяться другими способами. Чаще всего применяется схема: 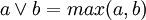 , где
, где ![~a, b \in [0, 1]](/800/600/https/dic.academic.ru/pictures/wiki/files/100/dfbf391a6408e74c7a9b40da50e8fffd.png) . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 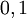 .
.
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространенных вариантов включает 3 аксиомы для дизъюнкции: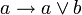
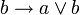
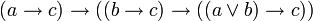
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++ логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|».
Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата 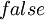 или
или 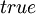 . Например:
. Например:
if (a || b)
{
/* какие-то действия */
};
Результат будет равен 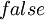 , если оба операнда равны
, если оба операнда равны 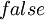 или
или 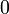 . В любом другом случае результат будет равен
. В любом другом случае результат будет равен 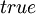 .
.
При этом применяется стандартное соглашение: если значение левого операнда равно 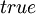 , то значение правого операнда не вычисляется (вместо
, то значение правого операнда не вычисляется (вместо 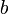 может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
if (a == NULL || a->x == 0)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет разыменования нулевого указателя.
Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 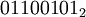 |
| b = | 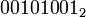 |
| то | |
| a ИЛИ b = | 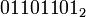 |
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ».
См. также
Wikimedia Foundation. 2010.
Логика в информатике — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 июля 2018; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 июля 2018; проверки требуют 2 правки.Логика в информатике — это направления исследований и отраслей знания, где логика применяется в информатике и искусственном интеллекте. Логика очень эффективна в этих областях[1].
 | Список примеров в этом разделе не основывается на авторитетных источниках, посвящённых непосредственно предмету статьи или её раздела.Добавьте ссылки на источники, предметом рассмотрения которых является тема настоящей статьи (или раздела) в целом, а не отдельные элементы списка. В противном случае раздел может быть удалён. |
Включаются следующие основные применения:
- исследования в логике, вызванные развитием компьютерных наук. Например, аппликативные вычислительные системы, теория вычислений и модели вычислений;
- формальные методы и логика рассуждения о понятиях. Например, семантическая сеть[2], семантическая паутина;
- булева логика и алгебра для разработки аппаратного обеспечения компьютеров;
- решение задач и структурное программирование для разработки прикладных программ и создания сложных систем программного обеспечения
- доказательное программирование — технология разработки алгоритмов и программ с доказательствами правильности алгоритмов;
- фундаментальные понятия и представления для компьютерных наук, которые являются естественной областью для формальной логики. Например, семантика языков программирования[3];
- логика знания и предположения. Например, искусственный интеллект;
- язык Пролог и логическое программирование для создания баз знаний и экспертных систем и исследований в сфере искусственного интеллекта;
- логика для описания пространственного положения и перемещения;
- логика в информационных технологиях. Например, реляционная модель данных, реляционные СУБД, реляционная алгебра, реляционное исчисление[4];
- логика вычислений с объектами. Например, комбинаторная логика, суперкомбинаторы[5];
- логика для компилирования программного кода и его оптимизации. Например, категориальная абстрактная машина;
- логика для эквивалентного преобразования объектов. Например, λ-исчисление;
- переизложение логики и математики в терминах, понятных специалистам в компьютерных науках[6].
Этот список продолжает пополняться.
- ↑ Halpern J.Y., Harper R., Immerman N., Kolaitis Ph.G., Vardi M.Y., and Vianu V. On the unususal effectiveness of logic in computer science. — January, 2001.
- ↑ Roussopoulos N.D. A semantic network model of data bases. — TR No 104, Department of Computer Science, University of Toronto, 1976.
- ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp.~311-372.
- ↑ Codd E. F. Relational Completeness of Data Base Sublanguages. Архивная копия от 18 мая 2008 на Wayback Machine In: R. Rustin (ed.): Database Systems: 65-98, Prentice Hall and IBM Research Report RJ 987, San Jose, California, 1972.
- ↑ Peyton Jones S., Eber J.-M., Seward J. Composing contracts: an adventure in financial engineering. — ICFP 2000
- ↑ Asperti A, and Longo G. Categories, Types and Structures. Category Theory for the working computer scientist. — M.I.T. Press, 1991 (pp. 1-300)
- Вольфенгаген В. Э. Логика. Конспект лекций: техника рассуждений. 2-е изд., дополн. и перераб. — М: АО «Центр ЮрИнфоР», 2004. — 229 с ISBN 5-89158-135-3.
Логическая дизъюнкция — это… Что такое Логическая дизъюнкция?
Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».
Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи: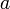 ||
|| 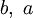 |
| 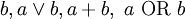 .
.
Булева алгебра
В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен 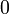 , если оба операнда равны
, если оба операнда равны 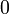 ; во всех остальных случаях результат равен
; во всех остальных случаях результат равен 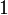 .
.
Многозначная логика
В многозначной логике операция дизъюнкции может определяться другими способами. Чаще всего применяется схема: 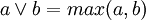 , где
, где ![~a, b \in [0, 1]](/800/600/https/veter.academic.ru/pictures/wiki/files/100/dfbf391a6408e74c7a9b40da50e8fffd.png) . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 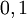 .
.
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространенных вариантов включает 3 аксиомы для дизъюнкции: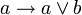
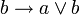
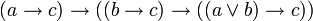
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++ логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|».
Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата 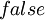 или
или 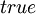 . Например:
. Например:
if (a || b)
{
/* какие-то действия */
};
Результат будет равен 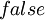 , если оба операнда равны
, если оба операнда равны 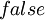 или
или 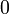 . В любом другом случае результат будет равен
. В любом другом случае результат будет равен 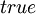 .
.
При этом применяется стандартное соглашение: если значение левого операнда равно 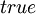 , то значение правого операнда не вычисляется (вместо
, то значение правого операнда не вычисляется (вместо 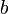 может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
if (a == NULL || a->x == 0)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет разыменования нулевого указателя.
Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 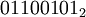 |
| b = | 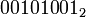 |
| то | |
| a ИЛИ b = | 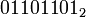 |
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ».
См. также
Wikimedia Foundation. 2010.

