26. Понятие логической функции. Способы задания логических функций.
Логическая функция — это функция логических переменных, которая может принимать только два значения : 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
Способы задания функций алгебры логики АЛ
Логической функцией называется зависимость поведения выходных логических величин от изменения входных логических величин.
Задачей алгебры логики является поиск математического или функционального представления логических функций с целью ее непосредственного использования для управления объектом или процессом.
Имеются различные способы представления логических взаимодействий.
Табличный
способ.
При этом способе функция задается в
виде таблицы
истинности,
представляющей собой совокупность всех
комбинацийвходных переменных (левые
столбцы) и соответствующих им значений
функции (правый столбец).
Таблица истинности содержит 2n строк, n +m столбцов (количество входов n+количество выходовm).
Например: пусть требуется задать функцию двух переменных, т.е. дискретное устройство на два входа и на один выход, следовательно, число столбцов = 2+1, а число строк = 4.
x | y | A |
0 | 0 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
1 | 1 | 1 |
Таблица.
3.2Пример таблицы истинности
Таблицы истинности возможно составить по условиям задания. Задание на управление для выше приведенного примера может выглядеть следующим образом: лампа
Таблицы истинности позволяют автоматизировать поиск искомой логической функции в математическом виде.
Словесно-аналитический способ задания функции алгебры логики.
При этом способе функция задается в виде аналитического выражения.В левой части высказывания указывается действие управляемого привода (или исполнительного устройства), а в правой части- условие, при котором выполняется это действие.
Аналитическое
выражение задается в возможно более
краткой форме. Некоторые подразумеваемые
слова могут опускаться, например, такие
как «кнопка», «нажать», «активен» и
другие. Название датчиков и кнопок
возможно заменять их схемным обозначением.
При этом указание на датчик означает
то, что этот датчик изменил свое состояние
на активное (логическая 1).
Ударение делается на союзы предложения, которые, в большинстве случаев, указывают на логическое действие.
Р ис. 3.3 Пример аналитического задания логической функции
В данном примере описана работа распределителя, с помощью которого производиться управление цилиндром.Электромагнит Y1 включиться (соответственно цилиндр начнет свое движение), если будет нажата кнопка S1
Для поиска несложных логических функций аналитический способ является наиболее простым и быстрым. Однако, этот способ в большей степени основан на интуиции. Поэтому для поиска сложных функций он не используется.
Графические способы.
Для графического описания логических взаимодействий можно использовать разные способы, предлагаемые стандартом IEC 848: шаговая, временная диаграмма, логические функциональные схемы, функциональный план.
При взаимодействии нескольких приводов наиболее наглядным средством установления логических взаимосвязей является
Рис. 3.4 Пример шаговой диаграммы
В шаговой диаграмме различают линии состояния или положения привода (в данном случае это линия, описывающая перемещение цилиндра) и линии управляющих сигналов. Отличием от временной диаграммы является то, вместо временной оси здесь использованы шаги- условные временные отрезки. Длина шага не пропорциональна реальному времени, а связанна с одним действием управляемого объекта. Сигналы взаимодействуют друг с другом (сливание потоков информации) по определенному логическому закону. Каждое логическое действие имеет собственное обозначение. Достоинством шаговой диаграммы является наглядность связей взаимодействия приводов и сигналов управления между собой во времени.
В
ременные
диаграммы важны для изображения динамически
изменяющихся процессов. Горизонтальная
ось является временной. Временные
диаграммы удобны для изображения
динамических процессов, которые быстро
изменяются во времени. Они позволяют
визуально анализировать реакцию выходных
величин на изменение входных.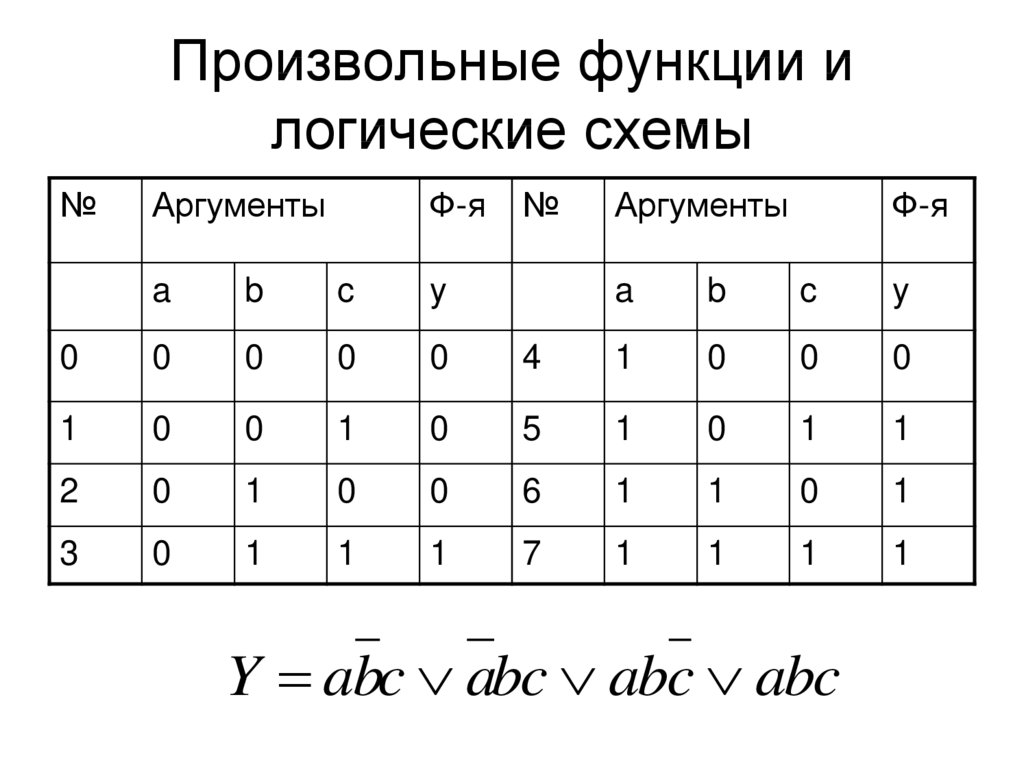
Рис. 3.5 Пример временной диаграммы
Из диаграммы следует, что лампа Н1 «горит» тогда, когда нажата кнопка S1 и не нажата кнопка S2.
Лампа Н2 «горит» тогда, когда нажата кнопка S2 и не нажата кнопка S1.
Логические функциональные блок-схемы состоят из логически связанных между собой отдельных функциональных блоков, которые являются обозначениями элементарных логических функций.
Рис. 3.5 Пример логической функциональной блок-схемы
Логические функциональные блок-схемы обладают всеми достоинствами графического изображения- это наглядность связей логических функциональных блоков. Недостатком данных схем является сложность прослеживания изменения сигналов во времени. Логические функциональные блок-схемы являются одним из самых распространенных языков программирования в промышленности. Напомним, что целью алгебры логики является получение математического или функционального изображения функции.
Функциональный
план является графическим средством
отображения по-шагового управления
процессом.
Весь процесс управления
разбит на отдельные шаги (минимальные
части процесса управления), которые
осуществляются при выполнении определенных
условий. Функциональный план является
языком программирова
ния.
Математическое представление алгебры логики. Элементарные логические действия можно представить с помощью специальных или арифметических символов (AND:, · ;OR: , +; NO:a`), обозначающих логические действия. Используя законы алгебры логики, возможны преобразования математических выражений логических функций.
Булеву функцию можно задать с помощью единичного п – мерного куба (рис. 7).
Рис. 7
Единичным п – мерным кубом называется граф, каждая вершина которого взаимно однозначно соответствует двоичному набору. Две вершины соединены ребром, если соответствующие наборы отличаются только в одном разряде (в одной координате).
На
рис. 7 показаны п-мерные
кубы для булевых функций: двух переменных
(а),
трех переменных (б),
четырех переменных (в).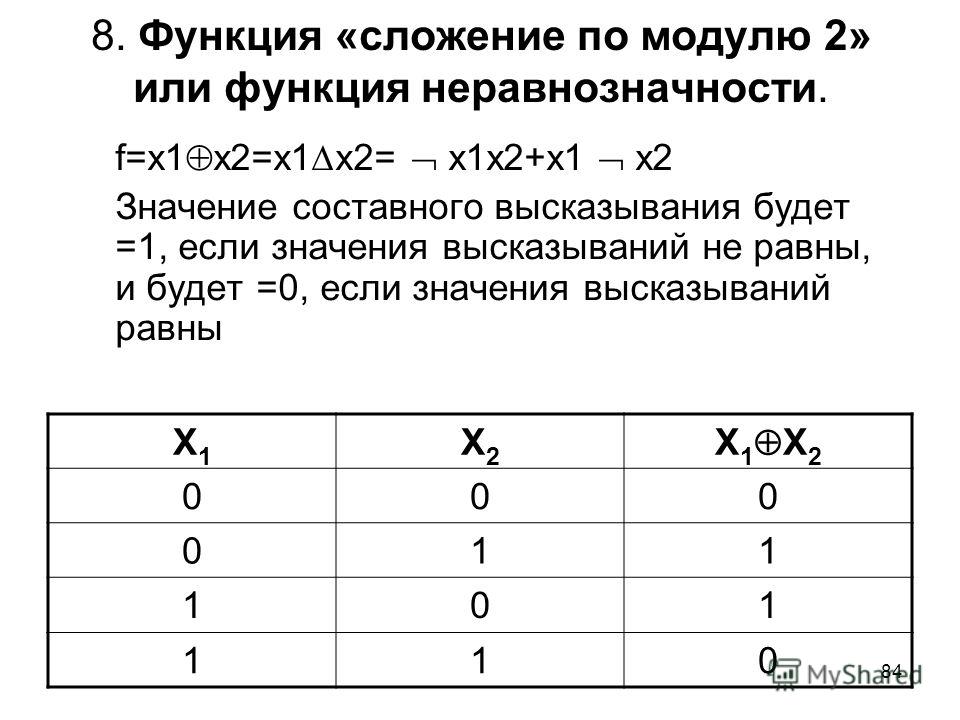
Отметив вершины, в которых булева функция принимает единичные значения, получим геометрическое представление булевой функции. Так функция примет вид:
Рис. 8
Часто для изображения булевых функций двух и трех переменных используют прямоугольную систему координат:
Рис. 9
Изображение булевых функций числа переменных более трех в этом случае невозможен.
В методе минимизации булевых функций Квайна – Мак- Класки используется кубическое представление булевых функций (аналог
Терм максимального ранга принято называть 0-кубом и обозначать К 0. Если два 0-куба из комплекса К 0 различаются только по одной координате, то они образуют куб (отрезок) K 1.
Введение в логику — тест 17
Главная / Образование / Введение в логику / Тест 17
Упражнение 1:
Номер 1
Какое утверждение о логических функциях являются истинными?
Ответ:
 (1) Любая функция, используемая в логике, называется логической  
 (2) Все аргументы логической функции являются логическими переменными, принимающими только два значения, интерпретируемые как истина и ложь  
 (3) Только некоторые аргументы логической функции должны быть логическими переменными, принимающими только два значения, интерпретируемые как истина и ложь  
 (4) Функции бывают логическими и нелогическими 
Номер 2
Какие утверждения о логических функциях являются истинными?
Ответ:
 (1) Любая функция, используемая в математике, является логической функцией  
 (2) Функция является логической, если хотя бы один из ее аргументов является логической переменной, принимающей только два значения, интерпретируемые как истина и ложь  
 (3) Значение логической функции должно быть логической переменной, принимающей только два значения, интерпретируемые как истина и ложь  
 (4) Областью определения логической функции от n переменных является множество кортежей длины n  
Номер 3
Какие утверждения о логических функциях являются истинными?
Ответ:
 (1) Для того чтобы функция была логической достаточно, чтобы все ее аргументы были логическими переменными, принимающими только два значения, интерпретируемые как истина и ложь  
 (2) Кортежи из области определения логической функции от n переменных можно рассматривать как двоичные слова длины n  
 (3) Логические функции должны иметь только один аргумент, принимающий два значения  
 (4) Областью определения логической функции от n переменных является Декартово произведение n множеств (Декартова степень множества {0, 1})  
Номер 4
Какое утверждение логических функциях являются истинными?
Ответ:
 (1) Для того чтобы функция была логической достаточно, чтобы ее значение было логической переменной, принимающей только два значения, интерпретируемые как истина и ложь  
 (2) Областью значений логической функции от n переменных является множество {0, 1}  
 (3) Логические функции должны иметь только два аргумента, принимающие два значения, интерпретируемые как истина и ложь  
 (4) Областью значений логической функции от n переменных является Декартово произведение n множеств (Декартова степень множества {0, 1})  
Номер 5
Какие утверждения о логических функциях являются истинными?
Ответ:
 (1) Для того чтобы функция была логической необходимо и достаточно, чтобы ее значение и все аргументы были логическими переменными, принимающими только два значения, интерпретируемые как истина и ложь  
 (2) Логическая функция – это функция с областью определения, представляющей декартову степень множества {0, 1}, и областью значений, представляющей множество {0, 1}  
 (3) Существует сколь угодно много различных логических функций  
 (4) Конъюнкция и дизъюнкция являются логическими функциями, а отрицание логической функцией не является  
Номер 6
Какие утверждения о логических функциях являются истинными?
Ответ:
 (1) Для того чтобы функция была логической необходимо, но не достаточно, чтобы ее значение и все аргументы были логическими переменными, принимающими только два значения, интерпретируемые как истина и ложь  
 (2) Логическая функция – это функция с областью определения, представляющей декартову степень множества {0, 1}, и областью значений, представляющей множество {0, 1}  
 (3) Существует только конечное число различных логических функций  
 (4) Конъюнкция, дизъюнкция и отрицание являются примерами логических функций  
Упражнение 2:
Номер 1
Сколько существует логических функций от одной переменной?
Ответ:
 (1) 1  
 (2) 2  
 (3) 4  
 (4) сколь угодно много  
Номер 2
Сколько существует логических функций от двух переменных?
Ответ:
 (1) 1  
 (2) 2  
 (3) 4  
 (4) сколь угодно много  
 (5) 16  
Номер 3
Сколько существует логических функций без аргументов?
Ответ:
 (1) 0 
 (2) 1 
 (3) 2 
 (4) таких функций не существует 
 (5) сколь угодно много 
Номер 4
Сколько существует логических функций от четырех переменных?
Ответ:
 (1) таких функций не существует 
 (2) 4 
 (3) 16 
 (4) сколь угодно много 
 (5) 65536 
 (6) 216 
Номер 5
Сколько существует логических функций от трех переменных?
Ответ:
 (1) таких функций не существует 
 (2) 4 
 (3) 16 
 (4) cколь угодно много 
 (5) 65536 
 (6) 256 
Номер 6
Сколько существует логических функций?
Ответ:
 (1) таких функций не существует; 
 (2) 4 
 (3) 16 
 (4) сколь угодно много 
 (5) 65536 
Упражнение 3:
Номер 1
Сколько кортежей в области определения логической функции от одной переменной?
Ответ:
 (1) 1  
 (2) 2  
 (3) 4  
 (4) сколь угодно много  
Номер 2
Сколько кортежей в области определения логической функции от двух переменных?
Ответ:
 (1) 2  
 (2) 4  
 (3) 16  
 (4) сколь угодно много  
Номер 3
Сколько кортежей в области определения логической функции от трех переменных?
Ответ:
 (1) 3 
 (2) 8 
 (3) 9 
 (4) сколь угодно много 
Номер 4
Сколько кортежей в области определения логической функции от четырех переменных?
Ответ:
 (1) 2 
 (2) 4 
 (3) 16 
 (4) сколь угодно много 
Номер 5
Сколько кортежей в области определения логической функции от пяти переменных?
Ответ:
 (1) 25 
 (2) 32 
 (3) 64 
 (4) сколь угодно много 
Номер 6
Сколько кортежей в области определения логической функции от шести переменных?
Ответ:
 (1) 6 
 (2) 36 
 (3) 64 
 (4) сколь угодно много 
Упражнение 4:
Номер 1
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n.Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от одной переменной?
Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от одной переменной?
Ответ:
 2 
Номер 2
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n. Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от двух переменных?
Ответ:
 4 
Номер 3
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n. Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от трех переменных?
Ответ:
 8 
Номер 4
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n.
Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от четырех переменных?
Ответ:
 16 
Номер 5
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n. Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от пяти переменных?
Ответ:
 32 
Номер 6
Число различных логических функций, зависящих от n переменных конечно, но резко возрастает с ростом n. Это число можно представить как 2 в степени k. Чему равна степень k в случае логических функций от шести переменных?
Ответ:
 64 
Упражнение 5:
Номер 1
Какова мощность множества (число его элементов), задающего область определения логической функции от одной переменной?
Ответ:
 2 
Номер 2
Какова мощность множества (число его элементов), задающего область определения логической функции от двух переменных?
Ответ:
 4 
Номер 3
Какова мощность множества (число его элементов), задающего область определения логической функции от трех переменных?
Ответ:
 8 
Номер 4
Какова мощность множества (число его элементов), задающего область определения логической функции от четырех переменных?
Ответ:
 16 
Номер 5
Какова мощность множества (число его элементов), задающего область определения логической функции от пяти переменных?
Ответ:
 32 
Номер 6
Какова мощность множества (число его элементов), задающего область определения логической функции от двух переменных?
Ответ:
 64 
Упражнение 6:
Номер 1
Какая из следующих бинарных логических функций ложна тогда и только тогда, когда ложны оба ее аргумента?
Ответ:
 (1) Конъюнкция 
 (2) Импликация 
 (3) Дизъюнкция 
 (4) Эквивалентность 
 (5) Исключающее ИЛИ 
Номер 2
Какая из следующих бинарных логических функций истинна тогда и только тогда, когда истинны оба ее аргумента?
Ответ:
 (1) Конъюнкция 
 (2) Импликация 
 (3) Дизъюнкция 
 (4) Эквивалентность 
 (5) Исключающее ИЛИ 
Номер 3
Какая из следующих бинарных логических функций ложна тогда и только тогда, когда первый аргумент истинен, а второй ложен?
Ответ:
 (1) Конъюнкция 
 (2) Импликация 
 (3) Дизъюнкция 
 (4) Эквивалентность 
 (5) Исключающее ИЛИ 
Номер 4
Какая из следующих бинарных логических функций ложна тогда и только тогда, когда оба ее аргумента имеют совпадающие значения?
Ответ:
 (1) Конъюнкция 
 (2) Импликация 
 (3) Дизъюнкция 
 (4) Эквивалентность 
 (5) Исключающее ИЛИ 
Номер 5
Какая из следующих бинарных логических функций может быть задана как отрицание функции Эквивалентность?
Ответ:
 (1) Конъюнкция 
 (2) Импликация 
 (3) Дизъюнкция 
 (4) Исключающее ИЛИ 
Номер 6
Какая из следующих бинарных логических функций может быть задана как отрицание функции Исключающее ИЛИ?
Ответ:
 Конъюнкция 
Главная / Образование / Введение в логику / Тест 17
п\) возможные комбинации переменных.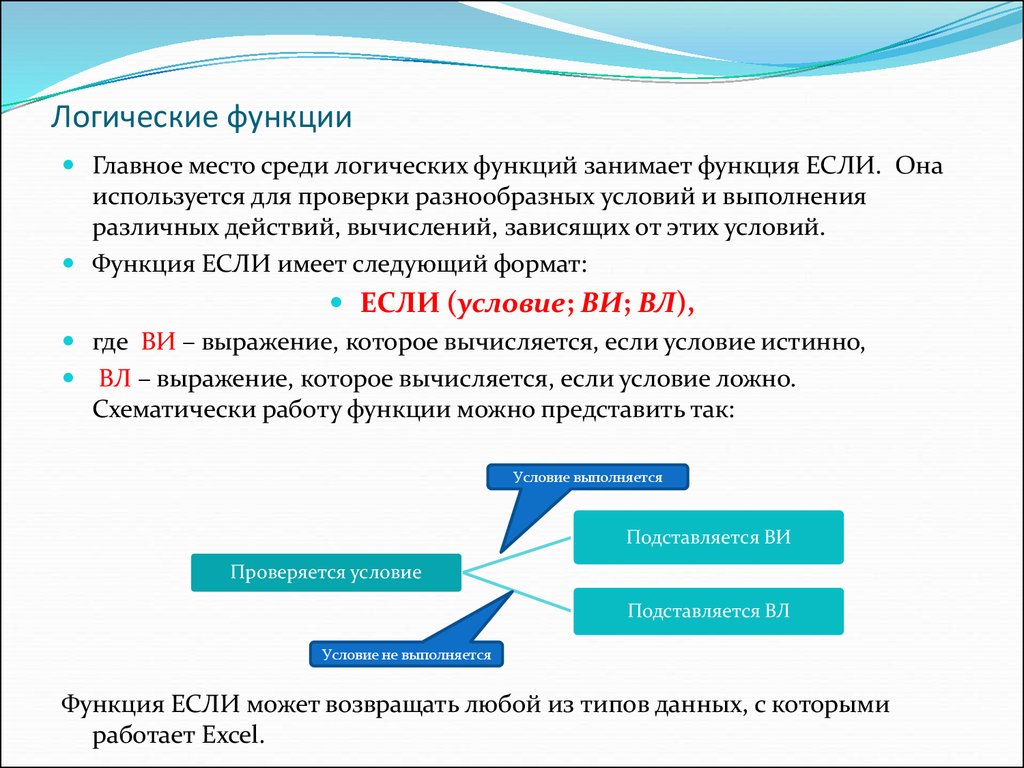
Эти функции будут принимать на выходе только 0 или 1. Вот пример булевой функции: f(a,b,c) = a X b + c. Эти функции реализованы с помощью логических вентилей.Цифровая схема f(a,b,c)
Таблица истинности функции
| б | с | ф(а,б,в) | |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Существует способ реализации функций в канонической форме, минимальной форме функции.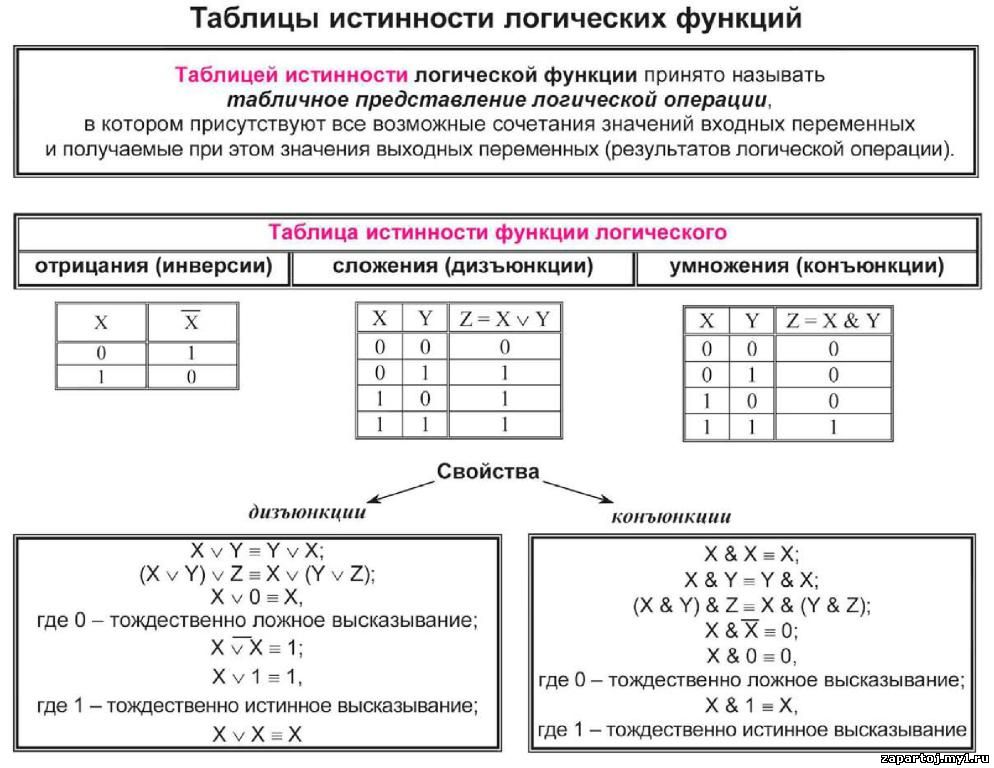
Например, если бы нам пришлось реализовать функцию с таблицей истинности функции f. Сначала мы бы сформировали термы, в которых функция имеет значение 1, с единственной возможной комбинацией для каждого терма. Термин будет равен 1 для одной комбинации записи и 0 для других. Для этого мы будем использовать вентиль И и сделать эту комбинацию со всеми входами, равными 1 в вентиле И. Тогда функция будет суммой всех членов. Таким образом, условия таблицы истинности будут:
Условия ∑
| a | б | в | ф(а,б,в) | Условия ∑ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | !а Х !б Х в |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | !а Х б Х в |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | а Х !б Х в |
| 1 | 1 | 0 | 1 | а Х б Х !с |
| 1 | 1 | 1 | 1 | а Х б Х в |
\[\begin{split}f (a,b,c) &= (!a X !b X c) + (!a X b X c) + (a X !b X c) + (a X b X !c) + (a X b X c) \\ &= !b X c X ( a + !a) + b X c X ( a + !a ) + a X b X !c \\ &= !b X c + b X c + a X b X !c \\ &= с + а Х б Х !с \\ &= (c + a X b) X ( c + !c) = a X b + c\end{split}\]
С помощью законов булевой алгебры делается упрощение для реализации цифровой схемы с меньшим количество ворот.
Есть еще один способ реализовать каноническую функцию, заключающийся в реализации инвертированной функции, а затем снова инвертировании и использовании законов Де Моргана для получения произведения термов. Это двойная форма обобщения. Теперь функция будет произведением терминов, и термины теперь будут иметь значение 0 для одной комбинации входных данных и 1 для каждой другой комбинации.
Условия ∏
| a | б | с | !ф(а,б,в) | Условия | ф(а,б,в) | Условия ∏ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | !а Х !б Х !с | 0 | а+б+в |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | !а Х б Х !с | 0 | а + !б + в |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | а Х !б Х !с | 0 | !а + б + в |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
\[!f (a,b,c) = !a X !b X !c + !a X b X !c + a X !b X !c\]
\[\begin{split }!!f = f &= !( !a X !b X !c + !a X b X !c + a X !b X !c) = !( !a X !b X !c) X !( !a X b X !c) X !( a X !b X !c) \\ &= (a + b + c ) X (a X !b X c) X (!a X b X c) \\\end{split}\]
Работая с терминами, мы получаем основную форму: f = a X b + c.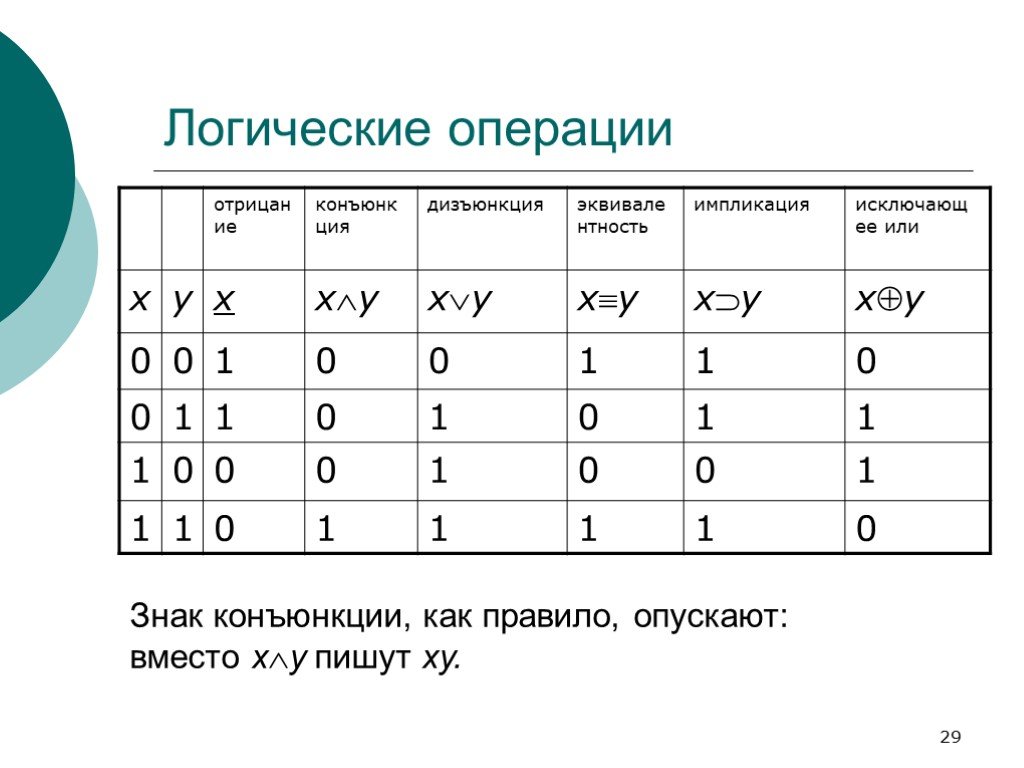
Вывод состоит в том, что есть два способа получить каноническую форму функции, которая представляет собой сумму термов или ее двойственное произведение, являющееся произведением термов.
Логическая функция в Power Apps — Power Platform
Редактировать
Твиттер LinkedIn Фейсбук Электронная почта
- Статья
- 2 минуты на чтение
Преобразует текстовую строку, число или нетипизированное значение в логическое значение.
Описание
Использовать логическое значение для преобразования других типов в логическое значение. Логическим значением является true , false или пусто .
В большинстве случаев приведение типов происходит автоматически, и Булева функция не требует явного использования. Например, If("true", 1, 0) вернет 1, поскольку текстовая строка "true" автоматически преобразуется в логическое значение. Булева функция полезна, когда требуется явное преобразование или при использовании нетипизированного значения.
Синтаксис
Логический ( Строка )
Логический ( StringSingleColumnTable )
- Строка — Обязательный. Строка (строки) для преобразования. Должна быть нечувствительной к регистру версия
"true"или"false". Эти строки не локализованы. пробел и пустая строка также принимаются и преобразуются в пробел . Все остальные текстовые строки возвращают ошибку.
Логическое значение ( Число )
Логическое значение ( NumberSingleColumnTable )
- Число — обязательно. Число (числа) для преобразования.
0преобразуется в false , а все остальные числа преобразуются в true . пустые значения принимаются и преобразуются в пустые .
Число (числа) для преобразования. Булево значение ( Нетипизированный )
- Нетипизированный — Обязательный. Нетипизированное значение для преобразования. Допустимые значения зависят от нетипизированного поставщика. Для JSON , логические значения JSON
true,falseиnullпринимаются, что соответствует значениям true , false и пустым значениям в Power Fx. Все остальные значения вернут ошибку. Значения внутри строки, такие как"true"и"false", не принимаются.
Примеры
Основное использование
| Формула | Описание | Результат |
|---|---|---|
| Логическое значение («истина») | Преобразует текстовую строку "true" в логическое значение. | правда |
| Логическое значение («ложь») | Преобразует текстовую строку "false" в логическое значение. | ложный |
| Логическое значение («ИСТИНА») | Преобразует текстовую строку "TRUE" в логическое значение. | правда |
| Логическое значение («ИСТИНА») | Преобразует текстовую строку "True" в логическое значение. | правда |
| Логический («Правдивый») | Попытка преобразовать текстовую строку "Truthful" в логическое значение, но поскольку это не нечувствительный к регистру вариант true и false , возвращается ошибка. | ошибка (неверный аргумент) |
| Логическое значение (пусто()) | Преобразование пустого значения в логическое значение. | пустой |
| Логический ( 0 ) | Преобразование числа 0 в логическое значение. | ложный |
| Логическое значение( 1 ) | Преобразование числа 1 в логическое значение. | правда |
| Логическое значение ( -1234 ) | Преобразование числа -1234 в логическое значение. | правда |
Использование без типа
| Формула | Описание | Результат |
|---|---|---|
| Логическое значение( ParseJSON( «{ «»bool»»: true }» ).bool ) | Преобразует нетипизированное значение true (логическое значение JSON) в логическое значение. | правда |
Логическое значение( ParseJSON( «{ «»bool»»: null }» ). bool ) | Преобразует нетипизированное значение null (нулевое значение JSON) в логическое значение. | пустой |
| Логическое значение( ParseJSON( «{ «»bool»»: «true» }» ).bool ) | Попытка преобразовать нетипизированное значение "true" (строка JSON) в логическое значение, но поскольку оно не является допустимым логическим значением в JSON, возвращается ошибка. | ошибка (неверный аргумент) |
| Логическое значение( ParseJSON( «[ true, false, null ]» ).bool ) | Попытка преобразовать массив логических значений в таблицу с одним столбцом. Таблицы с одним столбцом не поддерживаются с нетипизированными значениями, вместо этого используется формула ForAll( Table(ParseJSON("[true, false, null]" )), Boolean( ThisRecord.Value ) ) или ForAll( ParseJSON( "[ true, false, null]" ), Boolean( ThisRecord )) . | ошибка (неверный аргумент) |
Таблицы с одним столбцом
| Formula | Описание | Результат |
|---|---|---|
| Логическое значение([«true», «false», Blank()] ) | Преобразует таблицу с одним столбцом текстовых строк в таблицу с одним столбцом логических значений. | [ правда , ложь , пусто ] |
| Логическое значение ([«истина», «фальсификация» ] ) | Преобразует таблицу с одним столбцом текстовых строк в таблицу с одним столбцом логических значений. Поскольку вторая запись в этой таблице не является нечувствительным к регистру вариантом true и false , для этой записи возвращается ошибка. | [ правда , ошибка (недопустимый аргумент) ] |
| Логическое значение ([ 1, 2, 0 ] ) | Преобразует таблицу чисел с одним столбцом в таблицу с одним столбцом логического значения.  |