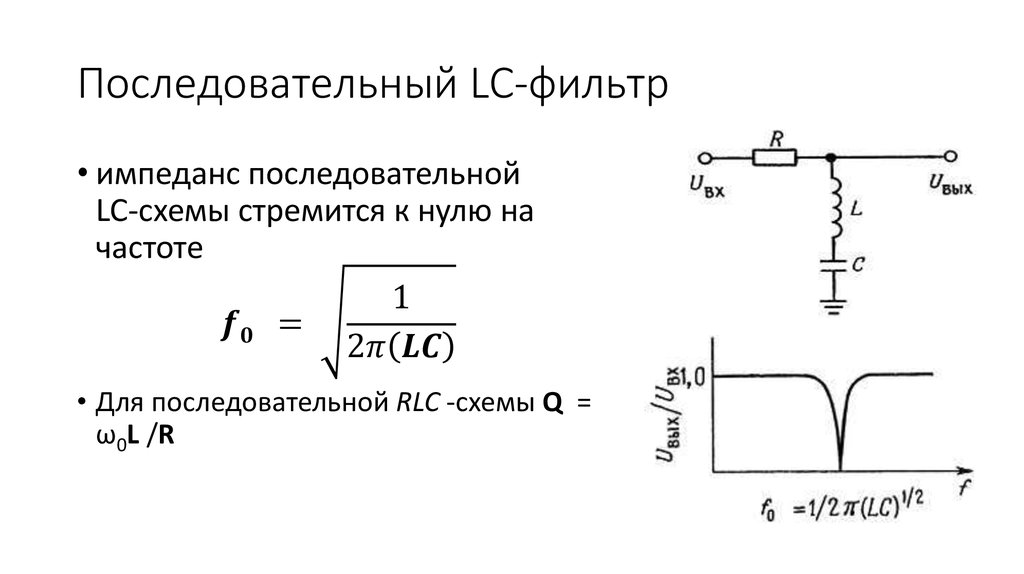
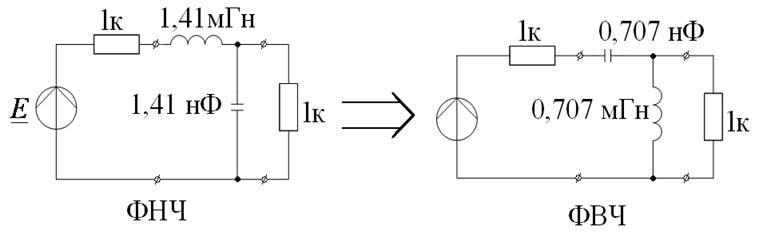
Расчет и реализация пассивных lc – фильтров
Под пассивным фильтром далее подразумевается реактивный четырехполюсник (четырехполюсник без потерь), нагруженный со стороны выходных зажимов на сопротивление нагрузки R2, а со стороны входных — на внутреннее сопротивление генератора R1, как это показано на рис. 2. Рис. 2. Реактивный четырехполюсник с нагрузкой на входе и выходе
При расчете таких фильтров для их описания вводят два коэффициента — коэффициент передачи мощности и коэффициент отражения, определяемые по следующей методике [4], [5].
Максимальная мощность, которая может поступить от источника в нагрузку, равна
(23)
Мощность, поступающая в нагрузку через реактивный четырехполюсник, определяется выражением
(24)
С учетом (23) и (24) коэффициент передачи мощности определяется отношением
Коэффициент отражения определяется как дополнение коэффициента передачи мощности до 1:
(26)
Отсюда следует, что изменение коэффициента отражения в полосе пропускания приводит к изменению затухания на величину
, дБ (27)
Иначе
(28)
В
справочниках по расчету фильтров [7],
[9] используют как максимально допустимый
коэффициент отражения, так и максимальную
неравномерность АЧХ затухания.
Часто вместо коэффициента передачи мощности используется характеристическая функция (j),
(29)
откуда следует, что
(30)
Существует
несколько методов реализации заданной
передаточной функции пассивной цепью.
Наибольшее распространение получили
три основные схемные структуры: лестничные
схемы, мостовые схемы и схемы Дарлингтона
[2], [4], [6]. Тематика курсовой работы
предполагает разработку пассивного LC
-фильтра лестничной структуры, пример
такой схемы приведен в Приложении 1 на
рис. 6. Лестничные схемы обладают важным
преимуществом, вытекающим из следующего
свойства: нуль передачи лестничной цепи
достигается на тех частотах, на которых
полное сопротивление последовательной
ветви или полная проводимость параллельной
ветви равны бесконечности. Из этого
следует, что каждой ветвью обусловлен
нуль передачи (полюс затухания).
Расчет пассивного LC-фильтра лестничной структуры осуществляется в следующей последовательности.
Переход к фильтру-прототипу и определение параметра избирательности фильтра-прототипа.
Выбор типа и порядка фильтра-прототипа.
Определение по таблицам и графикам нормированных параметров фильтра-прототипа.
Преобразование частоты — переход от фильтра-прототипа к ФВЧ или ПФ.
Денормирование параметров элементов фильтра.
Нормирование
частоты можно производить и после
перехода к фильтру-прототипу.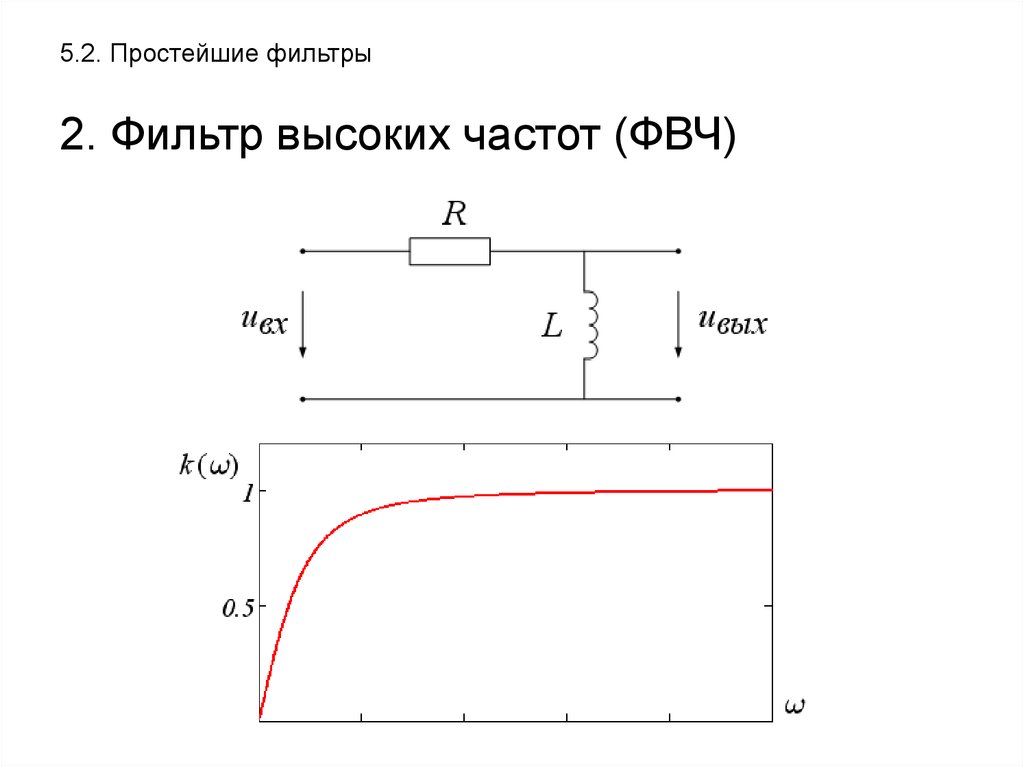
Реализация активных RC-фильтров осуществляется с использованием одного или нескольких активных приборов: транзисторов, зависимых источников и т.п. Наиболее часто применяемым активным прибором является операционный усилитель (ОУ), выполненный в виде интегральной схемы. ОУ представляет собой устройство с двумя входами (инвертирующим и неинвертирующим) и одним выходом, которое обладает большим коэффициентом усиления К0, постоянным в широком диапазоне частот, начиная с нулевой. У идеального ОУ входные сопротивления равны бесконечности, а выходное сопротивление равно нулю. Выходное напряжение ОУ равно
(31)
Условное обозначение и эквивалентная схема ОУ приведены на рис 3.
Рис. 3. Условное обозначение и эквивалентная схема идеального ОУ
Реализация
активных RC -фильтров
может осуществляться в прямой или
каскадной форме.
В первом случае заданная
передаточная функция реализуется
непосредственно как передаточная
функция одного фильтра. Во втором случае
используется каскадное соединение
звеньев, состоящих из активных фильтров
второго порядка и активных или пассивных
фильтров первого порядка с соответствующей
развязкой между каскадами. Такая
реализация позволяет проводить
независимую подстройку каждого звена
фильтра. Каскадные структуры, как
правило, менее чувствительны к изменениям
параметров элементов, чем фильтры прямой
структуры.
Из выражения .(6) следует, что передаточная функция фильтра первого порядка имеет вид
(32)
где M(p)-полиномом первой или нулевой степени.
Для фильтров второго порядка передаточная функция
(33)
В
частности, для фильтров Баттерворта и
Чебышева нижних частот числитель равен а
Каскадная реализация фильтра четного порядка n содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (33). Для фильтра нечетного порядка схема содержит (n-1)/2 звеньев второго порядка и одно звено первого порядка с передаточной функцией типа (32).
Таким образом, основная задача проектирования состоит в реализации передаточной функции второго порядка (33). При этом дополнительно необходимо обеспечить большое входное и малое выходное сопротивление каскада, чтобы избежать применения дополнительных развязывающих каскадов.
Удобным описанием передаточной функции второго порядка является система обобщенных параметров: добротность полюса (нуля)
, (34)
и собственная частота полюса (нуля)
, (35)
Передаточная функция фильтра второго порядка через эти параметры определяется следующим образом:
(36)
Применение
справочников и таблиц для расчета
фильтров предполагает использование
нормированных значений частот полюса
и нуля.
. (37)
Выражение для передаточной функции в форме (37) является основным при расчете фильтров второго порядка.
Рассмотрим общие принципы реализации передаточной функции вида (37) с помощью ОУ, охваченного обратной связью. Пассивная часть схемы представляет собой многополюсник состоящий из резистивных и емкостных элементов (рис. 4).
Р ис. 4. Фильтр на базе ОУ с обратной связью.
Чтобы получать выражение для передаточной функция, составим уравнения, описывающие пассивную часть схемы, используя метод узловых напряжений и матрицу узловых проводимостей:
(38)
.
Полагая,
что в идеальном ОУ входная цепь не
потребляет тока (т.е. I
(39)
Из этого выражения следует, что при большом коэффициенте усиления ОУ передаточная функция активного фильтра определяется только параметрами RC-цепи:
. (40)
Одной из наиболее простых схем, реализующих изложенный выше принцип построения активных фильтров, является схема с многопетлевой обратной связью (рис. 5).
Рис. 5. Активный фильтр с многопетлевой обратной связью.
Составив уравнения по методу узловых напряжений и положив, как и ранее, что входной ток ОУ равен нулю, а выходное напряжение
U3= —K0U2,
после несложных преобразований приходим к следующему выражению для передаточной функции этой схемы:
(41)
При K0 это соотношение принимает вид
.
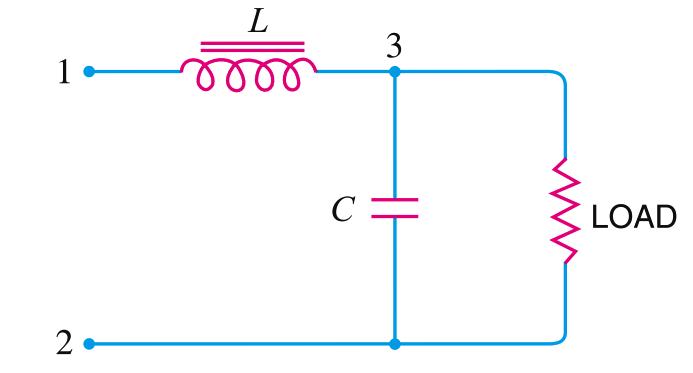(42)
Реализация нужной передаточной функции звена второго порядка сводится, таким образом, к подбору проводимостей элементов, которые могут быть либо резисторами с проводимостью 1/R, либо конденсаторами, с проводимостью, равной pC. В частности из (42) следует, что для реализации ФНЧ необходимо, чтобы проводимости Y1, Y3 и Y4 были резистивными, а Y2, Y5 — емкостными.
Другие
способы реализации звена второго порядка
отличаются структурой RC -цепи и включением ОУ. Так широко
применяются схемы с однопетлевой
обратной связью и неинвертирующим
включением ОУ (фильтры на источнике
напряжения, управляемым напряжением —
ИНУН), схемы, использующие несколько ОУ
(биквадратные фильтры, фильтры на трех
конденсаторах и др). Со способами
реализации этих фильтров можно
ознакомиться в монографиях и справочниках
[3],[4],[8].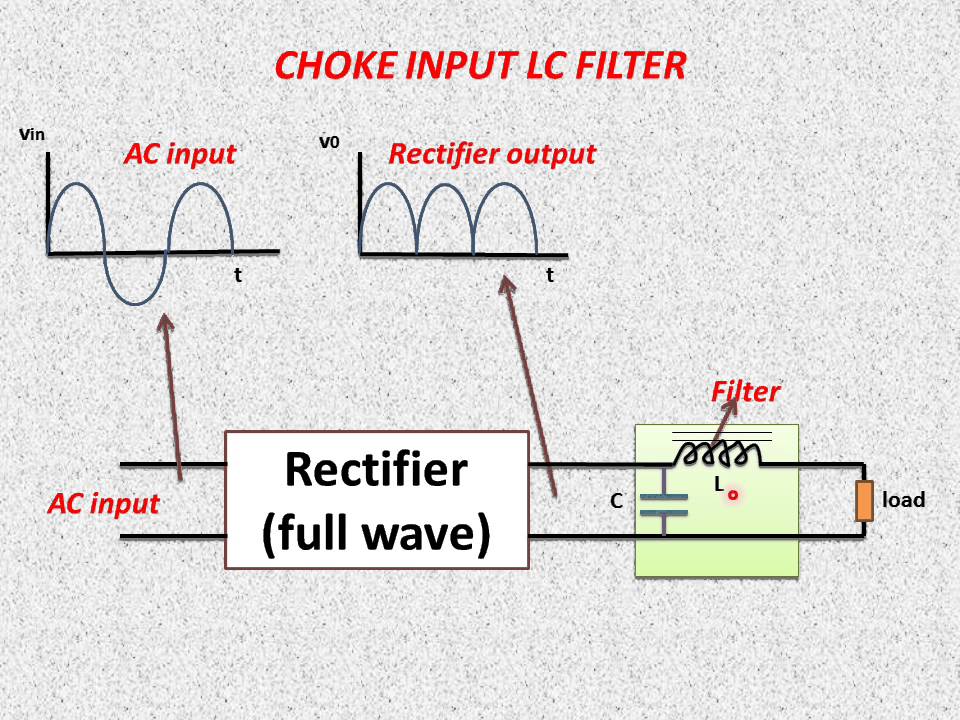
Отметим, что, как правило,
передаточные функции второго порядка
при малых в средних значениях добротности
(менее 20) реализуются с помощью относительно
простых схем. При высоких значениях
добротности (свыше 20) требуются более
сложные схемы [10].
автореферат диссертации по радиотехнике и связи, 05.12.04, диссертация на тему:Анализ и расчет LC фильтров в совершенствовании избирательности судового радиооборудования
Библиография Бессонова, Елена Анатольевна, диссертация по теме Радиотехника, в том числе системы и устройства телевидения
1. Автоматизация проектирования радиоэлектронных средств: Учеб. Пособие для вузов / О.В. Алексеев, A.A. Головков, И.Ю. Пивоваров и др.; Под ред. О.В. Алексеева. — М.:Высшая школа, 2000. — 479 с.
2. Автоматизированная связь с судами / Под ред. К.А. Семенова. JI.Судостроение, 1989. 334 с.
3. Акулынин П.К., Кульбацкий И.А., Кощеев К.Е. Теория связи по проводам. М.: Связьиздат, 1940. — 568 с.
4. Альбац М.Е. Справочник по расчету фильтров и линий задержки.
-М.:ГТИ, 1963.-200 с.
5. Байрашевский A.M., Ничипоренко Н.Т. Судовые радиолокационные системы. М.:Транспорт, 1982. — 317 с.
6. Белецкий А.Ф. Теория линейных электрических цепей. М.:Радио и связь, 1986. — 544 с.
7. Босый Н.Д. Электрические фильтры. УССР.ТИТЛ, 1957. — 516 с.
8. Брауде Г.В. Коррекция телевизионных и импульсных сигналов. -М.: Связь, 1967.
9. Буга H.H., Фалько А.И., Чистяков Н.И. Радиоприемные устройства. М.:Радио и связь, 1986. 320 с.121
10. Васильев В.Я. Графоаналитический метод анализа характеристических параметров электрических фильтров с применением машинной графики.: Дис.кан.техн.наук. Л.:ЛВИМУ, 1986. — 128 с.
11. Великин Я.И., Гельмонт З.Я., Зелях Э.В. Пьезоэлектрические фильтры.- М.:Связь, 1966.-396 с.
12. Венскаускас К.К., Ильин A.A. Принципы построения глобальной морской связи при бедствии и для обеспечения безопасности мореплавания.- М.:ВЮ «Мортехинформреклама», 1988. 104 с.
13. Витков М.Г., Виткова A.A. Численная обусловленность характеристики ослабления некоторых разновидностей фильтров // Электросвязь.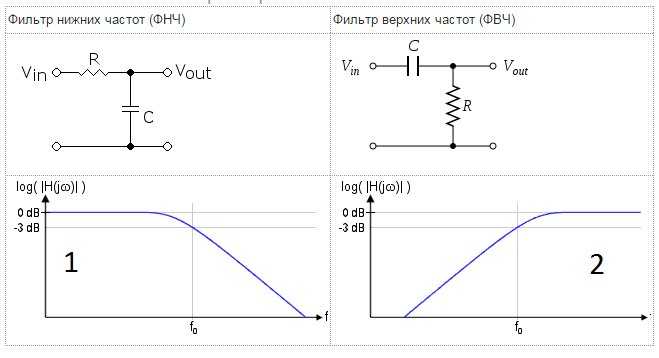
-2000. №5.-С. 36-37.
14. Витков М.Г., Виткова A.A., Горштейн JI.B. Обобщенные полиноминальные полосовые фильтры // Электросвязь. 1999. — №2. — С. 40-42.
15. Гауси М., Лакер К. Активные фильтры с переключаемыми конденсаторами. Пер. с англ. / Под ред. В.И. Капустина. М.:Радио и связь, 1986. -166 с.
16. Гехер К. Теория чувствительности и допусков электронных цепей. / Пер. с англ. Под ред. Ю.Х. Хотунцева. М.:Советское радио, 1973. -200 с.
17. Глобальная морская система связи при бедствии и для обеспечения безопасности. / Под ред. Ю.С. Ацерова. М.:Транспорт, 1989. — 62 с.
18. Головин О.В. Радиоприемные устройства. М.: Высшая школа, 1997. -384 с.
19. Голубев В.И., Окогот В.А., Полищук Я.В. Схемы дискретной перестройки резонансной частоты колебательного контура // Электросвязь.- 1969. -№5.-С. 41-46.
20. Голубев В.Н. Эффективная избирательность радиоприемных устройств. М.:Связь, 1978. — 240 с.
21. Зааль Р. Справочник по расчету фильтров. / Пер. с нем.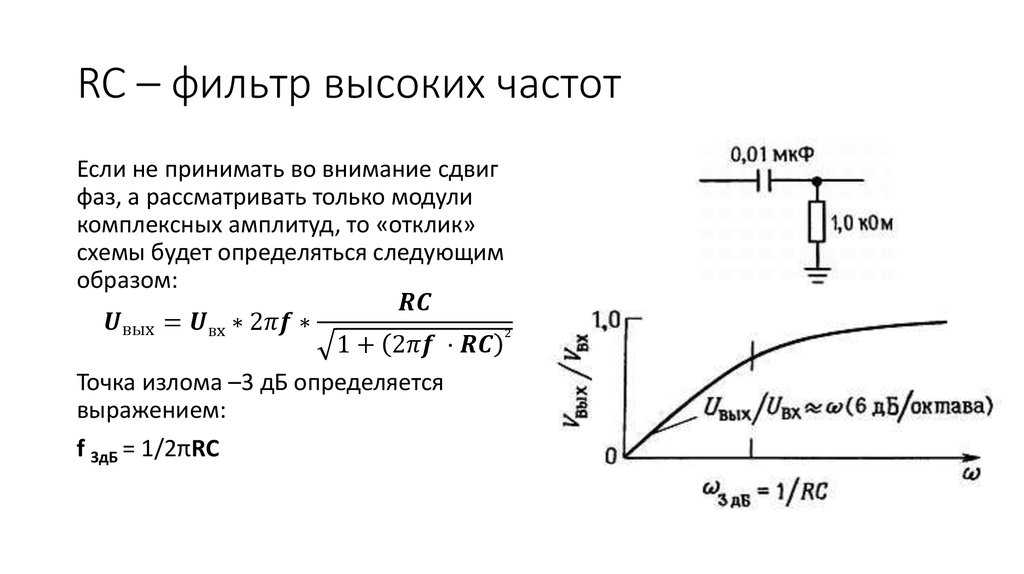
Под ред. H.H. Слепова. М.:Радио и связь, 1983. — 752 с.122
22. Знаменский А. Е., Попов Е.С. Перестраиваемые электрические фильтры. М.:Связь, 1979.- 129 с.
23. Знаменский А.Е., Теплюк И.Н. Активные RC фильтры. — М.:Связь, 1970.
24. Карлащук И.К. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. М.:Солон-Р, 2000. — 512 с.
25. Кильдишева О.Э., Лондон С.Е., Раутиан В.Г. Высокоселективные LC фильтры гармоник радиопередающих устройств // Электросвязь. -2000. №5. — С. 33-35.
26. Коган С.С. Теория и расчет фильтров для установок дальней связи. -М.:Связьиздат, 1950. 170 с.
27. Короткое A.C. Микроэлектронные аналоговые фильтры на преобразователях импеданса. СПб.:Наука, 1999.- 416 с.
28. Коротков A.C. Синтез полосовых фильтров на переключаемых конденсаторах // Радиотехника. 1999. — №8. — С. 17-21.
29. Лабутин В.К. Частотно-избирательные цепи с электронной настройкой. М.:Энергия, 1966.
30. Лаврентьев М.А., Шабат Б.
В. Методы теории функций комплексного переменного. М.:Гостехиздат, 1951. 607 с.
31. Ланнэ A.A. Оптимальный синтез линейных электронных схем. -М.:Связь, 1978.-336 с.
32. Лапшин Б.А. Новая теория и расчет фильтров и трансформаторов на отрезках передающих линий. СПб.:Наука, 1998. — 179 с.
33. Ларионов О.М. Исследование и разработка выходных трактов ключевых гираторов с улучшенным спектральным составом выходного напряжения. / Автореф.дис.кан.техн.наук. СПб.:СПбГУТ, 2000. — 17 с.
34. Лосев А.К. Теория и расчет электромеханических фильтров. М.:Связь, 1965.-264 с.
35. Лосев А.К. Теория линейных электрических цепей: Учеб. Для вузов. -М.:Высшая школа, 1987. 512 с.123
36. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.- М.:Высшая школа, 1990.
37. Моле Дж. X. Расчет электрических фильтров для аппаратуры связи. -М.:Госэнергоиздат, 1963. 332 с.
38. Никанкин В.К, Никанкин К.В. Техническое обслуживание радиооборудования ГМССБ: Учебное пособие для учебно-тренажерных центров Глобальной морской системы связи при бедствии (ГМССБ GMDSS).
— СПб.:ГМА им. адм. С.О. Макарова, 2000. 144 с.
39. Обломов А.Ф., Токарев JT.A., Момот Е.Г. Вопросы избирательности радиопремников. М.:Энергия, 1965. — 140 с.
40. Общесоюзные нормы на ширину полосы частот и внеполосные спектры излучений радиопередающих устройств гражданского назначения. -М.:Связь, 1976.-64 с.
41. Орлов B.C., Бондаренко B.C. Фильтры на поверхностных акустических волнах. М.:Радио и связь, 1984, 273 с.
42. Попов В.П. Основы теории цепей. М.:Высшая школа, 2000. — 576 с.
43. Правила по оборудованию морских судов. СПб.¡Морской регистр судоходства, 1999.
44. Применение пакета программ Microwave Harmonica: Методические указания. / Сост.: A.A. Головков, В.Ю.Приходько. СПб.:СПбГЭТУ, 1998.-32 с.
45. Проектирование радиопередающих устройств с применением ЭВМ. / Под ред. О.В. Алексеева. М.:Радио и связь, 1987. — 392 с.
46. Проектрирование радиопередатчиков. / Под ред. В.В. Шахгильдяна. -М.:Радио и связь, 2000. 654 с.
47. Пшесмыцкий О.
Проектирование электрических лестничных фильтров. Пер. с польского. М.:Связь, 1968.
48. Радиоприемное устройство: Техническое описание, инструкция по эксплуатации, схемы электрические принципиальные. Cn6.:MCS, 2000.124
49. Самарский A.A., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. М. .Наука. Физматлит, 1997. — 320 с.
50. Семенов К.А. Анализ линейных электрических цепей методом круговых диаграмм. Л.:Энергия, 1979. — 112 с.
51. Семенов К.А. Критическая добротности и оптимизация параметров фильтров верхних частот типа ш // Радиотехника. 1994. — №11. — С. 9394.
52. Семенов К.А. Круговые диаграммы для расчета собственного затухания электрических фильтров. М.:Морской транспорт, 1958. — 195 с.
53. Семенов К.А. О затухании фильтров нижних и верхних частот типа т на частоте среза // Электросвязь. 1956. — №7. — С. 59-61.
54. Семенов К.А., Бессонова Е.А. Анализ затухания фильтров нижних и верхних частот типа m // Радиотехника. 1999.
— №12. — С. 87-89.
55. Семенов К.А., Бессонова Е.А. Полосовой фильтр, обеспечивающий наибольшую избирательность в системах радиосвязи. / Морские информационные технологии: Сб. Научн. Статей. Выпуск 1. Под ред. А.Е. Сазонова. -СПб.:РГПУ им. А.И. Герцена, 2001. С. 94-100.
56. Семенов К.А., Васильев В.Я. Обобщенный графоаналитический расчет фильтров с применением машинной графики // Радиотехника. 1985. -№12.
57. Семенов К.А., Каплин Е.А., Кузьмин Б.И., Рябышкин В.Н. Состояние и перспективы развития морской радиосвязи // Электросвязь. 1998. -№8.-С. 9-12.125
58. Семенов К.А., Кузьмин Б.И., Бессонова Е.А. Системы и средства морской радиосвязи на выставке «Нева-99» // Электросвязь. 1999. — №12. -С. 67.
59. Семенов К.А., Рябышкин В.Н., Кузьмин Б.И. Современная судовая радиосвязь на морском флоте // Электросвязь. 1998. — №8. — С. 12-15.
60. Сергеев В.В Развитие теории энергетических функций реактивных четырехполюсников и ее приложение к анализу и синтезу LC-фильтров.
/ Автореферат дис.докт.техн.наук. СПб.:СПбГУТ, 2000. — 31 с.
61. Симонов Ю.Л. Усилители промежуточной частоты. М.:Советское радио, 1973.-383 с.
62. Смит Ф. Круговые диаграммы в радиоэлектронике. / Пер. с англ. М.Н. Бергера, Б.Ю. Капилевича. М.:Связь, 1976. — 144 с.
63. Собенин Я.А. Расчет полиномиальных фильтров. М.Связьиздат, 1963.-208 с.
64. Справочник по расчету фильтров с учетом потерь / Пер. с нем. под ред. К.А.Сильвинской М.:Связь, 1972. 200 с.
65. Справочник по судовому оборудованию радиосвязи и радионавигации. / Под ред. К.А. Семенова. Л.Судостроение, 1979. — 336 с.
66. Судовые радиоприемные устройства / К.А. Семенов, Г.М. Крылов, Б.И. Кузьмин, В.А. Марков. М.:Транспорт, 1984. — 382 с.
67. Ханзел Г. Справочник по расчету фильтров. / Пер. с англ. Под ред. А.Е. Знаменского. М.Советское радио, 1974. — 288 с.
68. Христиан Э., Эйзенман Е. Таблицы и графики по расчету фильтров. / Пер. с англ. Под ред. А.Ф. Белецкого. М.Связь, 1975. -408 с.
69. Хьюлсман Л.П. Активные фильтры: Пер. с англ. / Под ред. И.Н. Теп-люка. М.:Мир, 1972. — 516 с.
70. Шенберг М.М. Графики для расчета фильтров по характеристическим параметрам // Радиотехника. 1956. — т. 11. — №11.
71. Ши Т.Е. Четырехполюсники и электрические фильтры. М.Связьтехиздат, 1934. 367 с.126
72. Balakrishnan A.V. Matched filters for multiple processes // JRE Trans Inform Theory. -1961. V. 7. — №1.
73. Cauer W. Theorie der linearen Wechselstromschattungen, 2 Aulf, Akademie-Verlag, Berlin, 1954.
74. Epprecht G.W. A new circle-diagram for transformation in line technique // Arch. Electr. Übertragung. June. — 1958. — V. 12. — №6.
75. Gordon J.P. A circle diagram for optical resonators // Bell system Technical J.-V. 43.- 1964.-July. №4.
76. Have R.G., Lightfoot F.M. Matced filter for low and medium date rate communications // JREE. V. 7. 1963. — Oct. — №9.
77. IMO GMDSS Handbook. IMO, London, 1995.
78. Jones W.L. Design of tunable filters of near constant bandwidth // Electronic Letters.
1965. — V. 1. — №6.
79. Kurzrok R.M. Additional consideration in comb-line band-pass filters interstage coupling // IEEE Trans. 1967. — V. MTT-15. — April. — P. 262-263.
80. Levy R.A. A comb-line band-pass elliptic filters// IEEE Trans. 1971. — V. MTT-19. — №1. — P. 26-29.
81. Lichtenfeld K. Method for simplifying filter design // Electronics. 1960. — V. 33. -№21.
82. Nicolson B.F. The practical design of interdigital and comb-line filters // The Radio and Electronic Engineer. 1967. — July. — P. 39-52.
83. Schumacher T. Direct coupled ganged tuned band-pass filters // The Microwave Journal. 1964. — July. — №7. — P. 48-52.
84. Serenade Design Environment. Ansoft New Jersy, USA, 1999.
85. Thungwist D. Circle diagram applied to monopulse // JRE. Trans. Commun. Syst. V. GS-10. — 1962. — September. — №3.
86. Zobel O.J. Extensions to the theory and design of electric wave-filters, Bell Syst. Techn. Journ., Vol. 10.11, April 1931.
87. Zverev A.
J. Handbook of filter synthesis. John Wiley. New-York, 1967. -521 p.127
– фильтры LC, L и PI
В предыдущей статье мы обсудили основы согласования импеданса и способы использования согласующего трансформатора импеданса. Помимо использования согласующего трансформатора импеданса, разработчики могут также использовать схемы фильтра импеданса на выходе ВЧ-усилителя, которые могут использоваться как схема фильтрации, а также как схема согласования импеданса. Существует много типов схем фильтров, которые можно использовать для согласования импеданса, наиболее распространенные из них обсуждаются в этой статье.
Согласование LC-фильтра Различные LC-фильтры могут использоваться для согласования импедансов и обеспечения фильтрации. Фильтрация особенно важна на выходе ВЧ усилителей мощности , поскольку они генерируют много нежелательных гармоник, которые необходимо отфильтровать перед тем, как они будут переданы антенной, поскольку они могут вызывать помехи и передавать на частотах, отличных от разрешенных станцией.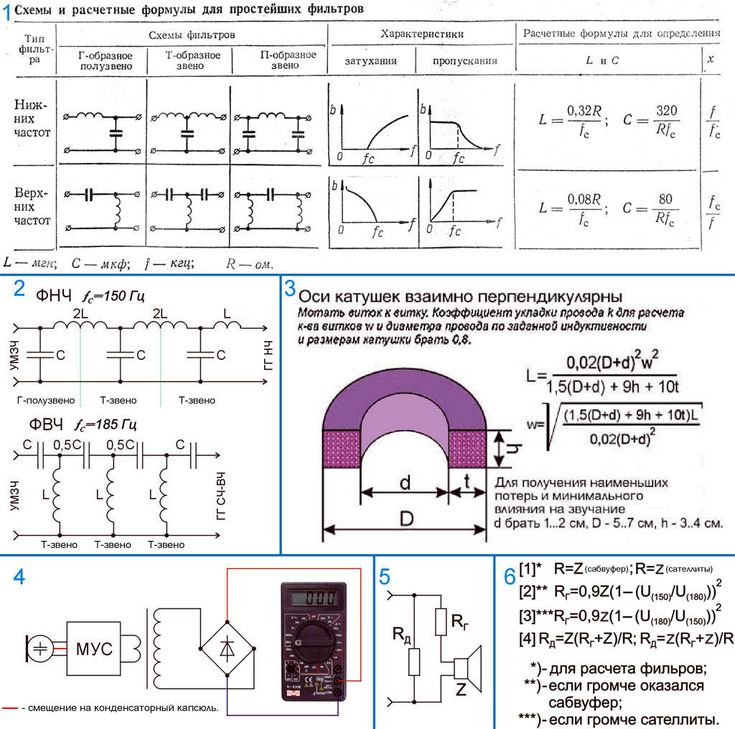
для передачи может быть незаконным. Мы рассмотрим низкочастотные LC-фильтры , потому что усилители мощности радиоприемника генерируют только гармоники, а гармонические сигналы всегда являются целым кратным базовых сигналов, поэтому они всегда имеют более высокие частоты, чем базовый сигнал — вот почему мы используем фильтры нижних частот, они пропустить желаемый сигнал, избавившись от гармоник. При проектировании LC-фильтров мы будем говорить о сопротивлении источника и сопротивлении нагрузки, а не об импедансе, потому что, если нагрузка или источник имеют некоторую последовательную или параллельную индуктивность или емкость и, следовательно, нерезистивный импеданс, расчеты становятся намного сложнее. В этом случае лучше всего использовать калькулятор PI filter или L filter. В большинстве случаев, таких как интегральные схемы, правильно изготовленные и настроенные антенны, телевизионные и радиоприемники, передатчики и т. д., выходное/входное сопротивление = сопротивление.
Коэффициент добротности
Каждый LC-фильтр имеет параметр, известный как добротность , в фильтрах нижних и верхних частот он определяет крутизну частотной характеристики. Фильтр с низкой добротностью будет очень широкополосным и не будет отфильтровывать нежелательные частоты так же хорошо, как фильтр с высокой добротностью. Высокодобротный фильтр будет отфильтровывать нежелательные частоты, но у него будет резонансный пик, поэтому он также будет действовать как полосовой фильтр. Высокая добротность иногда снижает эффективность.
Фильтры L Фильтры L представляют собой простейшую форму фильтров LC. Они состоят из конденсатора и катушки индуктивности, соединенных аналогично RC-фильтрам, причем катушка индуктивности заменяет резистор. Их можно использовать для согласования импеданса, который выше или ниже импеданса источника. В каждом L-фильтре есть только одна комбинация L и C, которая может согласовать заданное входное сопротивление с заданным выходным сопротивлением.
Например, чтобы согласовать нагрузку 50 Ом с нагрузкой 100 Ом на частоте 14 МГц, нам понадобится катушка индуктивности 560 нГн с конденсатором 114 пФ — это единственная комбинация, которая может обеспечить согласование на этой частоте с этими сопротивлениями. Их добротность, а значит и качество фильтра равняется
√((R A /R B )-1)=Q
Где R A — больший импеданс, RL — меньший импеданс, а Q — добротность при соответствующей подключенной нагрузке.
В нашем случае нагруженный Q будет равен √((100/50)-1) = √(2-1) = √1 = 1. Если бы мы хотели больше или меньше фильтрации (разные Q), мы бы нужен фильтр PI, где Q полностью регулируется, и вы можете иметь различные комбинации L и C, которые могут дать вам требуемое согласование на заданной частоте, каждая с другой Q.
Чтобы рассчитать значения компонентов фильтра L, нам нужны три вещи: выходное сопротивление источника, сопротивление нагрузки и частота работы.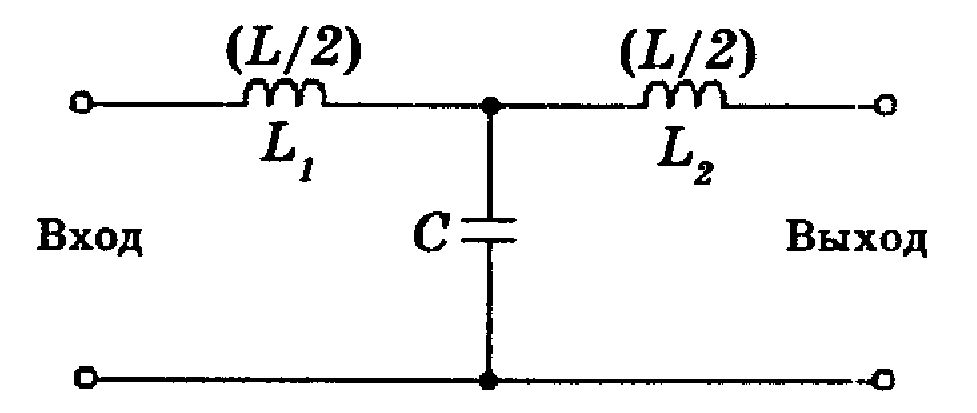
Например, выходное сопротивление источника будет 3000 Ом, сопротивление нагрузки 50 Ом, а частота 14 МГц. Поскольку сопротивление нашего источника больше, чем сопротивление нагрузки, мы будем использовать фильтр «b»
. Сначала нам нужно рассчитать реактивные сопротивления двух компонентов L-фильтра, затем мы можем рассчитать индуктивность и емкость на основе реактивного сопротивления и частота использования:
X L =√(R S *(R L -R S )) X L =√(50 Ом*(3000 Ом-50 Ом) X L =√(50 Ом*(3000 Ом-50 Ом) X L =√(50 Ом*2950 Ом) X L =√(50 Ом*2950 Ом) X L =√147500 Ом 2 X L =384,1 Ом
Мы используем калькулятор реактивного сопротивления, чтобы определить индуктивность, которая имеет реактивное сопротивление 384,1 Ом на частоте 14 МГц
L=4,37 мкГн X C = (R S *R L )/X L Х С =(50 Ом*3000 Ом)/384,1 Ом X C =150000 Ом 2 /384,1 Ом X C =390,6 Ом
Мы используем калькулятор реактивного сопротивления, чтобы определить индуктивность, которая имеет реактивное сопротивление 390,6 Ом при 14 МГц
C= 29,1 пФ
Как вы можете видеть, частотная характеристика фильтра представляет собой фильтр нижних частот с резонансным пиком на частоте 14 МГц, резонансный пик вызван фильтром, имеющим высокую добротность, если добротность была ниже, фильтр был бы lowpass без пика.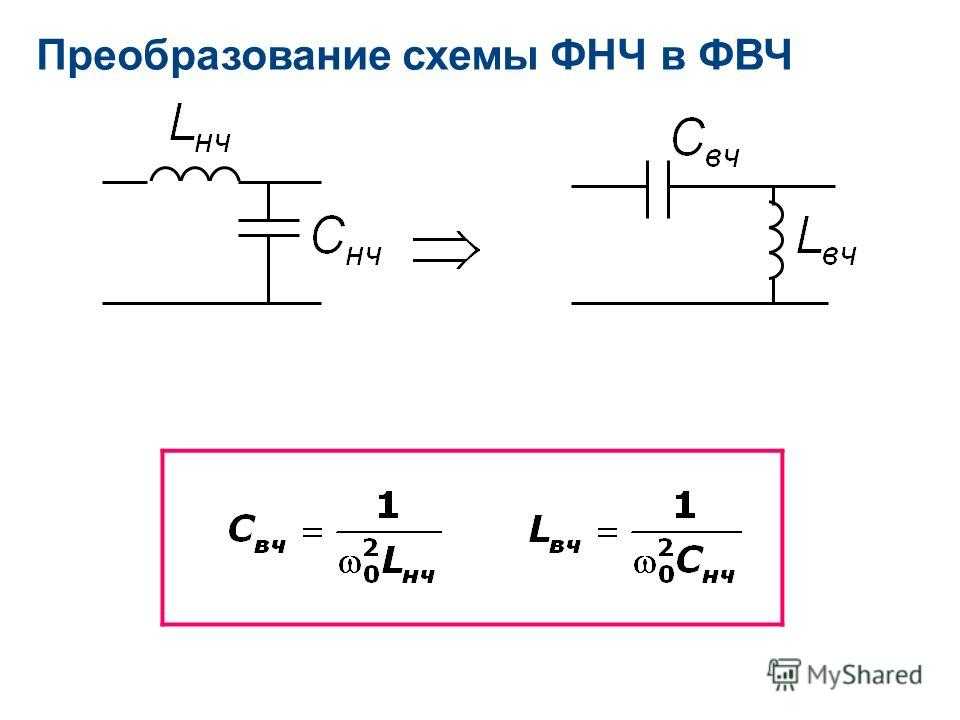
Если бы мы хотели другую добротность, чтобы фильтр был более широкополосным, нам пришлось бы использовать PI-фильтр, поскольку добротность L-фильтра зависит от сопротивления источника и сопротивления нагрузки. Если мы используем эту схему для согласования выходного импеданса лампы или транзистора, нам нужно будет вычесть выходную емкость на землю из конденсатора фильтра, потому что они параллельны. Если мы используем транзистор с емкостью коллектор-эмиттер (она же выходная емкость) 10 пФ, емкость C должна быть 190,1 пФ вместо 29,1 пФ.
Фильтр ПИ представляет собой универсальную согласующую схему, состоящую из 3 реактивных элементов, обычно двух конденсаторов и одной катушки индуктивности. В отличие от L-фильтра, где только одна комбинация L и C давала требуемое согласование импеданса на заданной частоте, фильтр PI позволяет использовать несколько комбинаций C1, C2 и L для достижения желаемого согласования импеданса, каждая комбинация имеет разную добротность.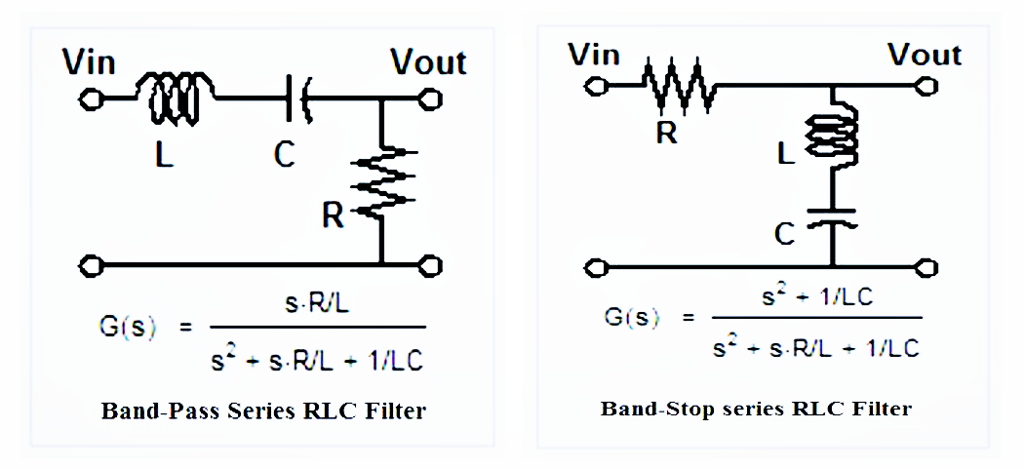
ПИ-фильтры чаще используются в приложениях, где требуется настройка на различные сопротивления нагрузки или даже сложные импедансы, например, в ВЧ-усилителях мощности, поскольку их отношение входного и выходного импеданса (r i ) определяется отношением квадратов конденсаторов, поэтому при настройке на другой импеданс катушка может остаться прежней, при этом настраиваются только конденсаторы. C1 и C2 в ВЧ усилителях мощности часто являются переменными.
(C1/C2)²=r i
Когда нам нужен более широкополосный фильтр , мы используем Q немного выше Q crit , когда нам нужен более резкий фильтр, например, на выходе RF усилитель мощности мы используем Q, который намного больше, чем Q crit , но ниже 10, так как чем выше добротность фильтра, тем ниже эффективность. Типичная добротность ПИ-фильтров в выходных ВЧ-каскадах равна 7, но это значение может варьироваться.
Q crit =√(R A /R B -1)
Где: R A — большее из двух сопротивлений (источника или нагрузки), а R B — меньшее сопротивление.
В целом ПИ-фильтр при более высокой добротности можно рассматривать, пренебрегая согласованием импедансов, как параллельный резонансный контур, составленный из катушки L и конденсатора С с емкостью, равной:
C=(C1*C2)/(C1+C2)
Этот резонансный контур должен резонировать на частоте, на которой будет использоваться фильтр.
Для расчета значений компонентов фильтра PI нам нужны четыре вещи: выходное сопротивление источника, сопротивление нагрузки, рабочая частота и добротность.
Например, нам нужно согласовать источник 8 Ом с источником 75 Ом. нагрузка с Q 7.
R A — большее из двух сопротивлений (источника или нагрузки), а R B — меньшее сопротивление.
Х С1 =R А /Q X C1 =75 Ом/7 X C1 =10,7 Ом
Мы используем калькулятор реактивного сопротивления для определения емкости, которая имеет реактивное сопротивление 10,7 Ом на частоте 7 МГц
С1=2,12 нФ X L =(Q*R A +(R A *R B /X C2 ))/(Q 2 +1) X L =(7*75 Ом+(75 Ом*8 Ом/3,59 Ом))/7 2 +1 X L =(575 Ом+(600 Ом 2 /3,59 Ом))/50 X L =(575 Ом+(167 Ом))/50 Х L =742 Ом/50 X L = 14,84 Ом
Мы используем калькулятор реактивного сопротивления, чтобы определить индуктивность, имеющую реактивное сопротивление 14,84 Ом на частоте 7 МГц
L=340 нГн X C2 =R B *√((R A /R B )/(Q 2 +1-(R A /R B )) X C2 =8 Ом*√((75 Ом/8 Ом)/(Q 2 +1-(75 Ом/8 Ом))) X C2 =8 Ом*√(9,38/(49+1-3,38)) X C2 =8 Ом*√(9,38/46,62) X C2 =8 Ом*√0,2 X C2 =8 Ом*0,45 Х С2 =3,59 Ом
Мы используем калькулятор реактивного сопротивления для определения емкости, которая имеет реактивное сопротивление 3,59 Ом на частоте 7 МГц
C2=6,3 нФ
Как и в случае L-фильтра, если наше выходное устройство имеет какую-либо выходную емкость (пластина-катод для ламп, коллектор-эмиттер для BJT, часто просто выходная емкость для MOSFET, ламп и BJT), мы необходимо вычесть его из C1, потому что эта емкость подключена к нему параллельно.
Если бы мы использовали транзистор IRF510 с выходной емкостью 180 пФ, в качестве устройства вывода мощности С1 потребовалось бы 6,3-0,18 нФ, то есть 6,17 нФ. Если бы мы использовали несколько транзисторов параллельно, чтобы получить более высокую выходную мощность, емкости суммировались бы.
Для 3 IRF510 это будет 6,3 нФ-0,18 нФ*3 = 6,3 нФ-0,54 нФ, то есть 5,76 нФ вместо 6,3 нФ.
Другие LC-цепи, используемые для согласования импедансовСуществует множество различных LC-цепей, используемых для согласования импедансов, таких как Т-фильтры , специальные согласующие схемы для транзисторных усилителей мощности или PI-L-фильтры (PI фильтр с дополнительным индуктором).
Калькулятор фильтра нижних частот
Если вам нужно убрать высокие частоты из вашего сигнала, вы можете использовать фильтры нижних частот: рассчитайте частоту среза наиболее распространенных схем фильтрации.
Прочтите нашу короткую статью; вы узнаете:
- Что такое ФНЧ;
- Как рассчитать частоту среза RC-фильтра;
- Расчет фильтра нижних частот RL;
- Активные фильтры: уравнения для ФНЧ с операционным усилителем.
Что такое фильтр нижних частот? Почему мы рассчитываем частоту среза фильтра нижних частот?
Фильтр нижних частот представляет собой универсальное многофункциональное устройство, имеющее множество применений. Мы можем подытожить их как две стороны одной медали: вы берете то, что предпочитаете.
- Фильтр нижних частот срезает высокие частоты в сигнале ; или
- Фильтр нижних частот сохраняет низкие частоты модуляции .
Единого описания таких устройств не существует: в нашем калькуляторе ФНЧ мы будем иметь дело с четырьмя наиболее распространенными:
- Фильтр RC ;
- Фильтр LC ;
- Инвертирующий фильтр на ОУ ; и
- Неинвертирующий фильтр на ОУ .
Несмотря на то, что их конструкция сильно различается, мы можем легко рассчитать частоту среза в фильтрах нижних частот, не слишком углубляясь в физику и математику.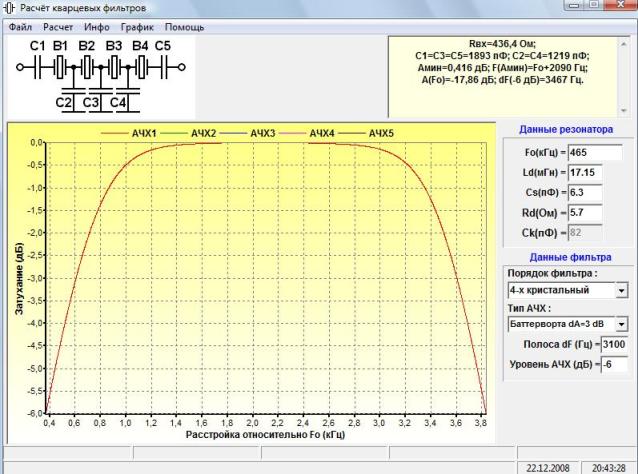
Фильтры нижних частот необходимы во многих областях, связанных с сигналами. Например, когда вы проектируете громкоговоритель , необходимо разделить сигнал на частотные полосы: узнайте больше на нашем калькуляторе кроссовера.
Фильтр нижних частот RC: расчеты и пояснения
Вы, вероятно, уже сталкивались с RC-фильтрами: это самые распространенные и понятные фильтры нижних частот. Мы сделали для них целый инструмент: калькулятор RC-цепи!
RC означает резистор и конденсатор : для работы нашего фильтра нужны только эти два пассивных компонента. Сопротивление включено последовательно как с нагрузкой, так и с конденсатором, и мы получаем сигнал с двух концов конденсатора. Вот схема:
Импеданс (величина, почти аналогичная сопротивлению) конденсатора сильно зависит от частоты сигнала , резко падая для высоких частот. В этой области спектра конденсатор действует как замкнутая цепь.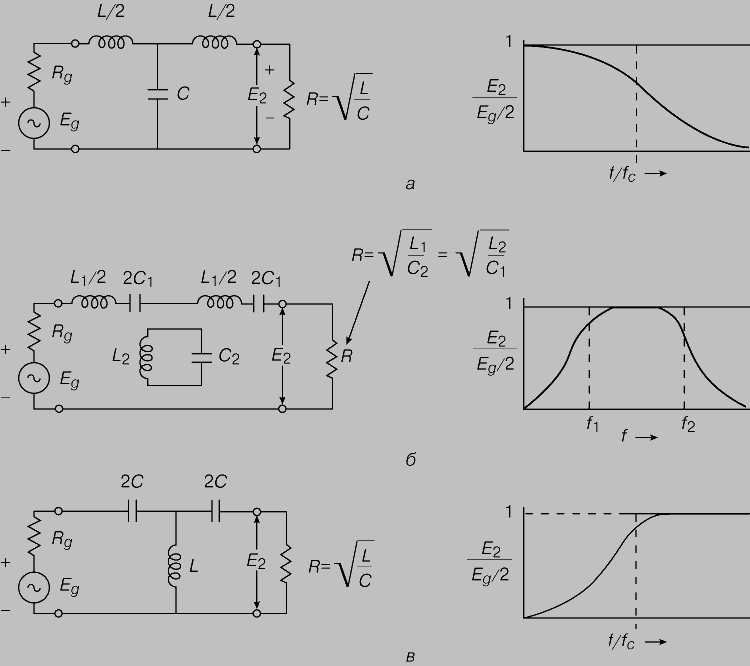
В то время как высокие частоты проходят через компонент, высокий импеданс на низких частотах выталкивает последние на параллель, где мы их улавливаем.
Рассчитываем частоту среза RC-фильтра, проходящего через характерное время RC-цепи :
τ=R⋅C\tau = R\cdot Cτ=R⋅C
Прямым обращением уравнения и добавлением постоянного члена:
fc=12⋅π⋅τ= 12⋅π⋅R⋅Cf _{\text{c}} = \frac{1}{2\cdot \pi \cdot \tau}=\frac{1}{2\cdot \pi \cdot R\cdot C} fc=2⋅π⋅τ1=2⋅π⋅R⋅C1
Рассчитать фильтр нижних частот LC
Следующим фильтром нижних частот в нашем калькуляторе является фильтр RL. Здесь мы заменяем конденсатор катушкой индуктивности . Поведение этого фильтра мало чем отличается от RC-фильтра; вычисляем частоту среза ФНЧ RL по формуле:
fc=R2⋅π⋅Lf_{\text{c}} = \frac{R}{2\cdot \pi\cdot L}fc=2⋅π⋅LR
Мы показываем схему для RL фильтр на картинке ниже. Как видите, положение элементов изменилось: катушка индуктивности ведет себя противоположно конденсатору, увеличивая импеданс с частотой.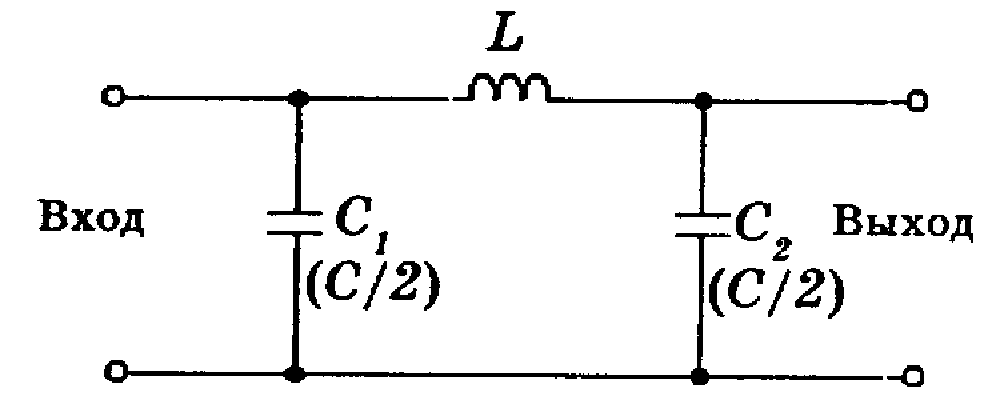
Индуктор блокирует высокие частоты, в то время как низкие частоты проходят без помех.
Наиболее совершенным фильтром нижних частот является фильтр RLC. В этой схеме присутствуют все три элемента. Его описание, однако, выходит за рамки нашего калькулятора ФНЧ: мы подробно рассказывали о нем на нашем 9-м курсе.0003 Калькулятор схемы RLC
Активные фильтры нижних частот: формулы для фильтров операционных усилителей
Активные фильтры нижних частот включают компоненты с их источником питания. Добавление внешнего источника позволяет нам усилить сигнал на выходе схемы.
Инвертирующий фильтр нижних частот на операционном усилителе: формула и объяснение коэффициента усиления0003 Резистор обратной связи
RfR _{\text{f}}Rf.Резистор обратной связи вместе с включенным параллельно конденсатором определяет частоту среза ФНЧ: вычисляем ее по формуле, уже виденной в калькуляторе ФНЧ RC.
fc=12⋅π⋅Rf⋅Cf_{\text{c}} = \frac{1}{2\cdot \pi\cdot R_{\text{f}}\cdot C}fc=2⋅π ⋅Rf⋅C1
Коэффициент усиления ( усиление ) операционного усилителя зависит от номинала резисторов, сходящихся на его входе:
G=-RfRiG = -\frac{R_{\text{f}}}{R_{\text{i}}}G=-RiRf
Мы используем значение коэффициента усиления для расчета выходной сигнал с формулой:
vout=G⋅vinv_{\text{out}} = G\cdot v_{\text{in}}vout=G⋅vin
Обратите внимание на знак минус ? Операционный усилитель инвертирует сигнал на 180°180\градус180° в противофазе.
