Кварцевый резонатор принцип работы

На самом деле, кварц  – это один из самых распространенных минералов  в земной коре. Если полупроводниковые радиокомпоненты в основном делают из кремния, то кварц также состоит из кремния, но в связке с кислородом. Его формула SiO2.

Выглядит он примерно вот так:

Кварцевый резонатор

Резонатор – (от лат. resono –  звучу в ответ, откликаюсь) – это система, которая способна совершать колебания с максимальной амплитудой, то есть резонировать, при воздействии внешней силы определенной частоты и формы. 

Кварцевые резонаторы выглядят в основном вот так:

 

Что такое обертоны

Обертоны, или как еще их называют, моды или гармоники – это кратные частоты, выше основной частоты кварца.

С помощью фильтров гасят основную частоту кварца и выделяют обертон.

В кварцевом резонаторе в режиме обертонов используют нечетные обертоны.

Если основная частота кварца F – это первый обертон, то его рабочие обертоны будут как 3F, 5F, 7F, 9F.   Стоит также отметить, что амплитуда обертона убывает с ростом его частоты, поэтому далее 9 обертона смысла брать уже нет, так как выделять амплитуду маленького сигнала очень трудно.

Обозначение кварца на схеме

Кварц является диэлектриком. А что будет если тонкий диэлектрик разместить между двумя металлическими пластинами? Получится конденсатор! Конденсатор получается очень маленькой емкости, так что замерить его емкость вряд ли получится. Зато не стали мудрить со схемотехническим обозначением кварца, и на схемах его показывают как прямоугольный кусочек кристалла, заключенный между двумя пластинками конденсатора:

Принцип работы кварца

Для того, чтобы понять принцип работы кварцевого резонатора, надо рассмотреть его эквивалентную схему:

С – это собственно емкость между обкладками конденсатора. То есть если убрать кристалл кварца, то останутся две пластины и их выводы. Именно они и обладают этой емкостью.

С1 – это динамическая емкость самого кристалла. Динамическая – это значит проявляется при работе кварца. Ее значение несколько фемтоФарад. Фемто – это 10-15 !

L1 – это динамическая индуктивность кристалла. Она может достигать несколько тысяч Генри!

R1 – динамическое сопротивление, при работе кварца может достигать от нескольких Ом и до нескольких КилоОм

Можно заметить, что С1, L1 и R1 образуют последовательный колебательный контур, который обладает своей резонансной частотой.

Принцип работы кварцевого резонатора такой: если к обкладкам кварцевого резонатора подвести переменное напряжение, то  его пластинка начнет колебаться с частотой подведенного напряжения.

Если подведенная частота  будет совпадать с собственной резонансной частотой колебания кварца, то наступит резонанс.

Напряжение на обкладка кварца резко возрастает. В этом случае кварцевый резонатор ведет себя, как настроенный на определенную частоту колебательный контур с очень высокой добротностью.

Каждый кварц имеет разные частоты последовательного и параллельного резонанса.

Если мы видим на кварце вот такую надпись

это говорит нам о том, что на частоте последовательного резонанса мы можем возбудить этот кварц на частоте 8 Мегагерц.

В основном кварц работает на частоте последовательного резонанса.

Здесь также есть еще одно правило: если частота маркируется в целых числах в Килогерцах – это работа на основной гармонике, а если в Мегагерцах через запятую – это обертонная гармоника.

Например: РГ-05-18000кГц – резонатор для работы на основной частоте, а РГ-05-27,465МГц – для работы на 3-ем обертоне.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.


Кварцевые резонаторы | ООО Пьезотрон

Конструктивно пьезоэлектрический резонатор состоит из пьезокристаллического элемента (кварца, ниобата или танталата лития, лангасита или других пьезоэлектриков), на который нанесена плёнка металла (чаще всего серебра или никеля), держателя, в котором крепится пьезокристаллический элемент, и корпуса с выводами, в котором размещён держатель с закреплённым в нём пьезокристаллическим элементом. Диапазон частот используемых в настоящее время пьезоэлектрических резонаторов на объёмных волнах находится в пределах от нескольких килогерц до нескольких сотен мегагерц.

Историческая справка

Пьезоэлектрический резонатор был изобретён американским учёным У. Кэди в 1920 г. Начиная с первой половины 20-го века пьезоэлектрические кварцевые резонаторы нашли широкое применение в радиосвязи для стабилизации частоты генераторов электромагнитных колебаний. При включении резонатора между выходом и входом лампового усилителя возникает цепь положительной обратной связи и осуществляется возбуждение на частоте собственных колебаний резонатора. При этом стабильность частоты генератора определяется прежде всего добротностью пьезоэлектрического резонатора. Кварцевые резонаторы имеют добротность в тысячи и десятки тысяч раз большую, чем добротность колебательных контуров, которые ранее использовались в генераторах электромагнитных колебаний. В соответствующее число раз повышается стабильность частоты генераторов при использовании в них пьезоэлектрических резонаторов.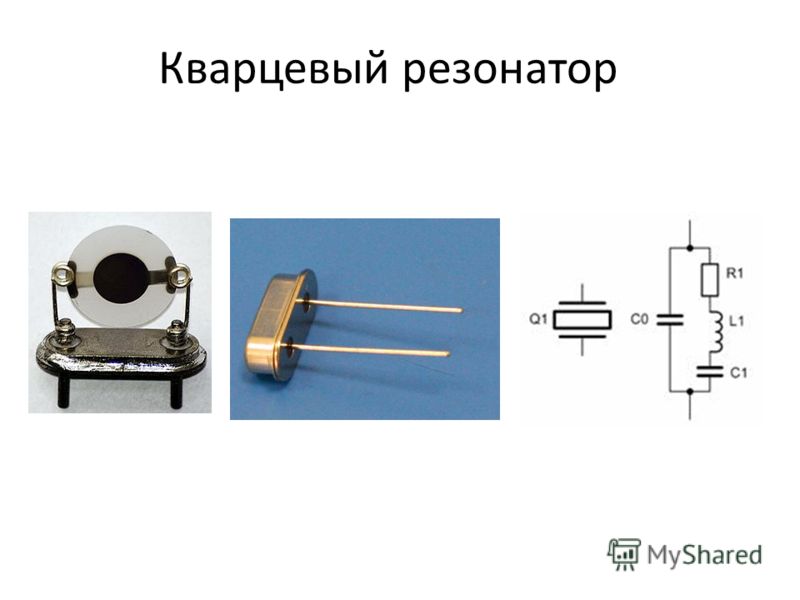

Стабильность частоты генераторов на колебательных контурах не может быть лучше 1·10^-3~1·10^-4, в то время как использование пьезоэлектрических резонаторов даже не самого лучшего качества позволяет увеличить стабильность частоты до 1·10^-7~1·10^-8.

Эквивалентная электрическая схема резонатора

Колебательную систему резонатора можно представить в виде последовательно расположенных сопротивления

R_k, динамических индуктивности L_k и ёмкости C_k и параллельно подключённой статической ёмкости C₀.

На частоте последовательного резонанса, при котором динамические сопротивления, возникающие на L_k и C_k, компенсируют друг друга, пьезоэлектрический резонатор работает как активное сопротивление R_k. В соответствии с формулой Томсона частота последовательного резонанса равна

При этом добротность можно представить в виде выражения

Основные параметры пьезоэлектрических резонаторов

Помимо добротности и динамического сопротивления к важнейшим параметрам пьезоэлектрических резонаторов относятся точность настройки по частоте, температурная стабильность частоты, долговременная и кратковременная стабильности частоты.

Точность настройки резонаторов по частоте в зависимости от предъявляемых требований может находиться в пределах от ±0,5·10^-6 до ±20·10^-6 и более.

Температурная зависимость частоты наиболее широко используемых кварцевых резонаторов среза AT графически представляет собой так называемую кубическую параболу с перегибом (точкой симметрии параболы) при +27°С. Для интервала температур -60 ~ +85°С температурная нестабильность может находиться в пределах ±30·10

-6. При выборе рабочей температуры термостатируемого генератора вблизи температуры экстремума кубической параболы температурная нестабильность частоты резонатора может находиться в пределах (3-5)·10^-9/1°C.

Долговременная стабильность частоты пьезоэлектрических резонаторов зависит прежде всего от совершенства технологических процессов их изготовления. Для резонаторов широкого применения долговременная стабильность частоты находится в пределах (5-10)·10^-6 за год.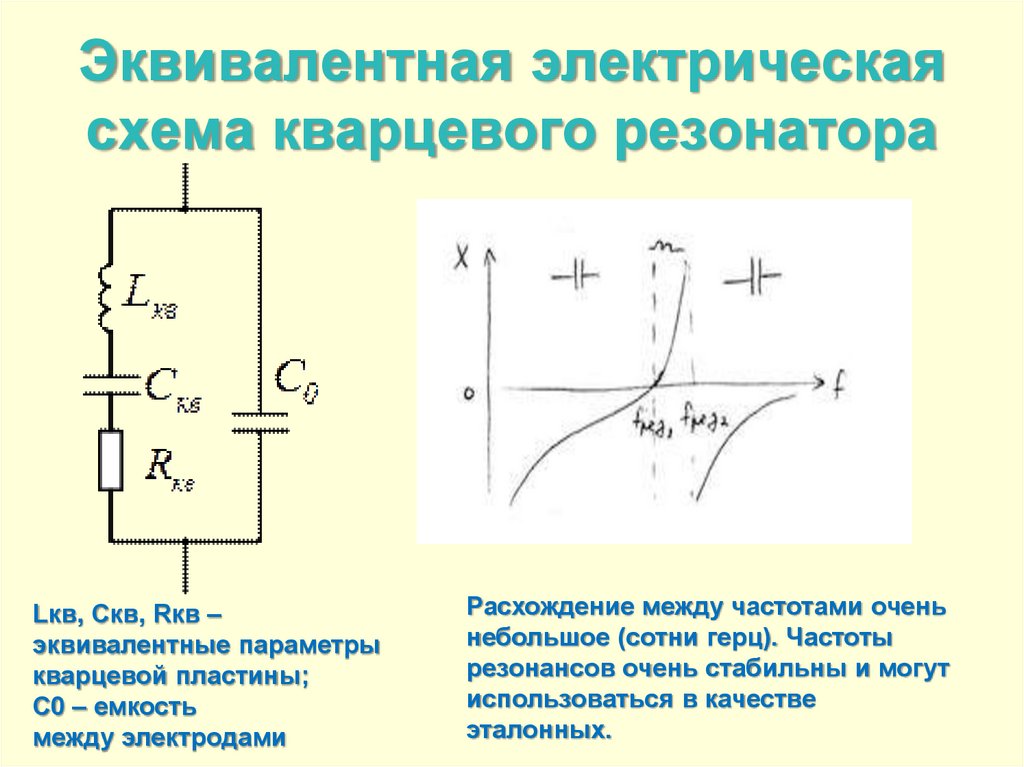

Прецизионные кварцевые резонаторы могут обеспечить стабильность (1-3)·10^-8 за год.

Кратковременная стабильность частоты относится к выходным характеристикам генераторов. Но она также зависит от качества резонаторов, в первую очередь от добротности. Кратковременная стабильность может измеряться за определённые промежутки времени (1с, 1мс, 10с и т.д.). Например, к обычным генераторам могут предъявляться требования к кратковременной нестабильности 1·10^-9 за 1мс.

Немаловажным параметром резонаторов является соотношение динамической (С_k) и статической ёмкостей (С₀

), поскольку от этого параметра зависит величина перестройки частоты генераторов с помощью реактивных элементов. Данный параметр для резонаторов одной частоты зависит от площади возбуждающих электродов и номера механической гармоники, на которой возбуждается резонатор. Частоту кварцевых резонаторов среза AT можно представить в виде формулы

F = n/2t C₆₆/ρ ,

 где   n — номер механической гармоники;
          t — толщина пьезоэлемента;
          C₆₆ — модуль упругости среза AT;
          ρ — плотность кварца.

Отношение C₀ к C_k с переходом с первой (основной) на третью механическую гармонику увеличивается в 9 раз, на пятую механическую гармонику – в 25 раз, то есть пропорционально квадрату номера механической гармоники. При этом диапазон перестройки частоты генераторов с увеличением номера механической гармоники уменьшается в той же степени. Таким образом, использование резонаторов с возбуждением на том или ином номере механической гармоники зависит от сочетания требований к пределам перестройки, с одной стороны, и, с другой стороны, от требований к долговременной стабильности, поскольку последняя при прочих равных условиях улучшается при увеличении номера механической гармоники. При этом необходимо учитывать влияние уровня возбуждения резонатора на параметры и долговременную стабильность частоты.

Как запускаются кварцевые генераторы?

Уровень шума генератора XTAL без питания можно приблизительно вычислить; в этой схеме, даже при отсутствии питания, резистор 1 кОм создает широкополосный случайный электрический шум:

^{смоделируйте эту схему — схема создана с помощью CircuitLab}

Предположим, что Rnoise 1 кОм, который создает среднеквадратичное напряжение 4 нановольта на корень_Герц полосы пропускания.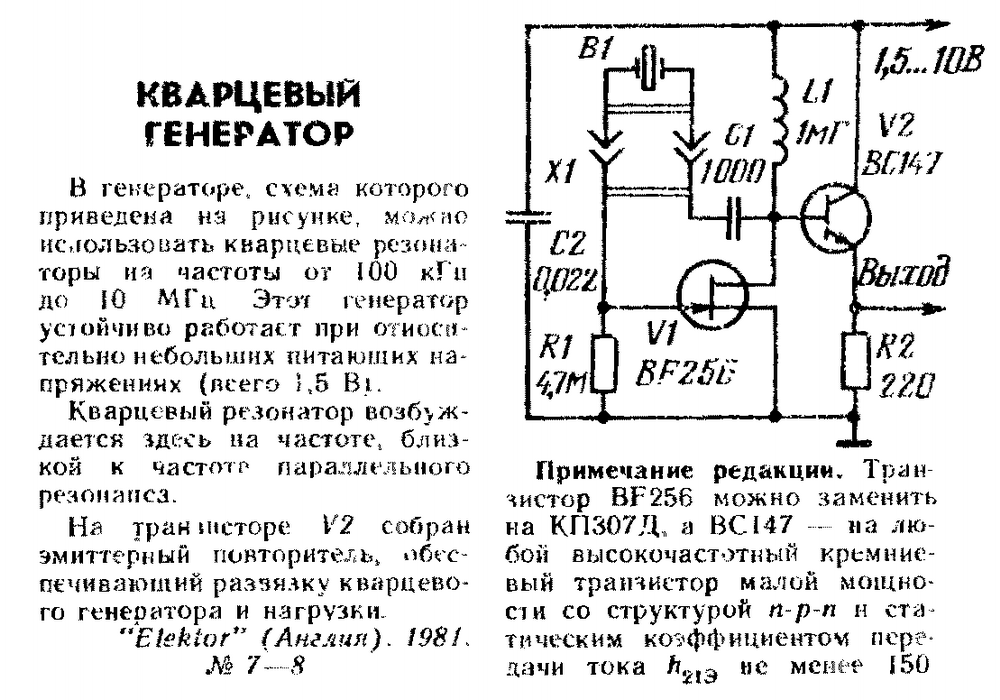 Мощность шума линейно увеличивается с полосой пропускания; таким образом, шумовое напряжение увеличивается на квадратный корень ширины полосы пропускания. Полоса пропускания 10 Гц дает 4 нВ * sqrt (10) = 4 * 3,1 = 12,4 нановольта RMS. Этот кристалл с частотой 8 МГц, вероятно, имеет добротность 80 000 или полосу пропускания 100 Гц. Шумовое напряжение будет 4 нВ * sqrt (100) = 4 нВ * 10 = 40 нановольт.

Можем ли мы смоделировать это?

Что происходит в этой симуляции?

1) изучите нижний левый график «общая характеристика усиления/фазы» и обратите внимание на кривую КРАСНОГО цвета имеет провал в фазе, но эта фаза НЕ ДОСТИГАЕТ -180 градусов, таким образом, Баркгаузен не удовлетворен; требуется еще 5 (ПЯТЬ) градусов фазового сдвига. Отсюда вставка резисторов в кварцевые генераторы, чтобы обеспечить больший фазовый сдвиг.

2) что такое Q? Я предполагал 80000. Какова вычисляемая добротность без учета 1000 Ом в источнике напряжения «Датчик»? Изучите центральные значения «определения каскада импеданса» и обратите внимание на кварцевую схему и значения компонентов.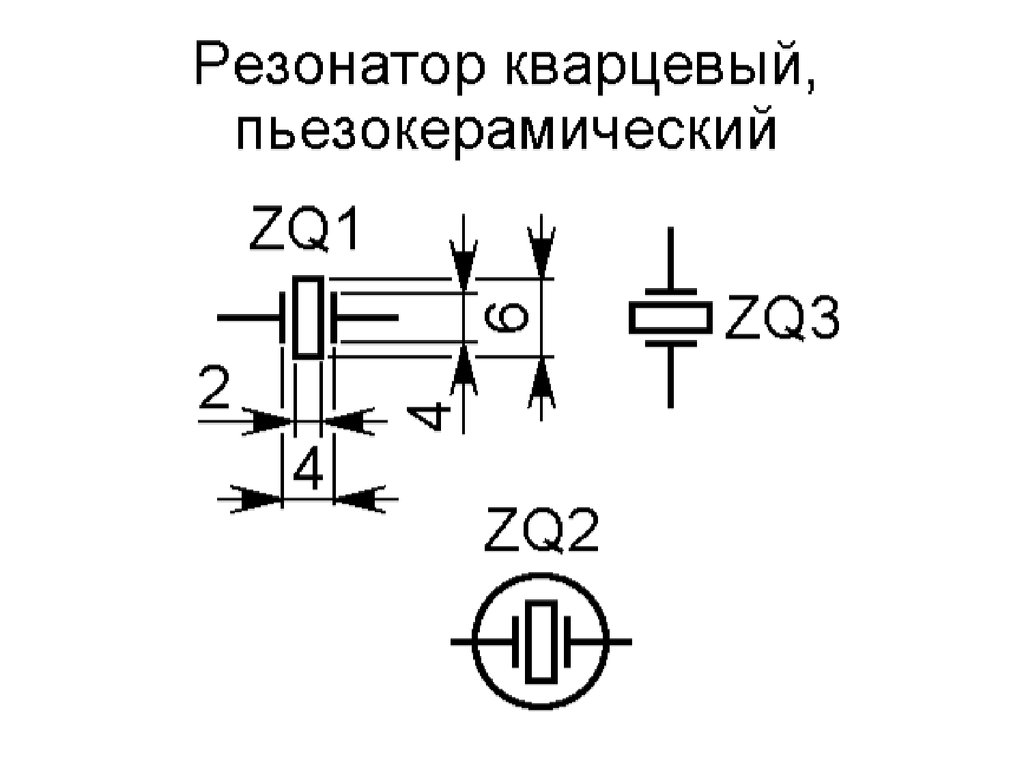 Катушка индуктивности 0,01 Генри. Реактивное сопротивление на частоте 8 МГц равно 2 * 3,14 * 8 000 000 * 0,01 (2 * Pi * F * L) = 500 000 Ом для XL. Элемент с потерями (модель потерь подвижного кварца) 100 Ом.

Таким образом, Q составляет всего 500 000/100, или 5 000.

3) Теперь о выходном шуме (обычно это случайный шум при запуске, используемый усилителем/транзистором/MOSFET с активным элементом). Два напряжения показаны двумя кривыми — оранжевой и красной — на нижнем правом графике «тепловой шум (среднеквадратичное значение)». Красная кривая, шум от 1 кОм в стимуле (крайний левый этап «S0» в моделировании), достигает пика при 14 нановольт RMS. Оранжевая кривая для этапа 1 «S1», шум от 100 Ом в меню Crystal «определение каскада импеданса» достигает пика при среднеквадратичном значении 22 нановольта.

Общий смоделированный случайный шум на частоте 8 МГц представляет собой RSS 14 нВ и 22 НВ, или около 30 нановольт RMS.

Каков минимальный уровень шума вашего осциллографа? Область применения ШИРОКОПОЛОСНАЯ. Предположим, что дигитайзер использует Cвыборку 5 пФ; используя Vnoise = sqrt(K * T /C), и зная, что 10 пФ производят среднеквадратичное значение шума ровно 20 микровольт при 290 градусах Кельвина (+17C), 5 пФ вносит 20 * 1,414 = 28 микровольт среднеквадратичного шума.

Дайте пол осциллографа 28 микровольт, 30 нановольт кристалла UNPOWERED не могут быть измерены.

==============================

Ответ на первый комментарий «Как добавление резисторов увеличивает фазовый сдвиг?? »

^{симулировать эту схему}

Вот еще один метод обеспечения фазового сдвига

^{симулировать эту схему На частоте 40 МГц реактивное сопротивление 10 пФ составляет ~400 Ом; реактивное сопротивление 3 пФ равно -j1200 Ом. Большая часть циркулирующей энергии вашей сети PI_network будет проходить через структуры ESD и превращаться в тепло. Кроме того, емкость обратного смещения диода ESD составляет НЕЛИНЕЙНЫЙ .}

осциллятор — Частота, с которой может работать кварцевый кристалл

спросил 1 год, 11 месяцев назад

Изменено 1 год, 11 месяцев назад

Просмотрено 226 раз

\$\начало группы\$

Я так понимаю, что при попадании сигнала приложенного напряжения на кристалл кварца он механически вибрирует. Теперь предположим, что напряжение составляет 1 кГц, а кварцевый кристалл — 32,728 кГц, выдержит ли кварцевый кристалл это? Следует ли также, что частота приложенного не должна превышать частоту кварцевого кристалла? Спасибо.

• генератор
• кристалл
• резонанс

\$\конечная группа\$

3

\$\начало группы\$

За исключением резонансной частоты, кварцевый кристалл не будет механически реагировать на входную частоту. Поэтому он не будет поврежден. Только на резонансной частоте или очень близкой к ней амплитуда колебаний кристалла будет значительной. Если входное напряжение будет слишком высоким, амплитуда колебаний кристалла может превысить его механическую прочность, и тогда он может быть поврежден. Очень высокая механическая добротность кристалла предотвращает это на частотах вне резонанса.

\$\конечная группа\$

1

\$\начало группы\$

Все это можно в значительной степени смоделировать. Возьмем эквивалентную схему кристалла 10,000000 МГц: —

Затем, если вы начертите импеданс кристалла, вы получите ответ, который в значительной степени выглядит как довольно высокий импеданс везде, кроме тех мест, где он резонирует: —

отклик импеданса выше от 9от 0,99 МГц до 10,01 МГц.

Таким образом, если вы приложите напряжение на последовательной резонансной частоте (10,000000 МГц), вы можете разрушить устройство, потому что оно (пример) имеет импеданс всего 20 Ом, и обычно требуется только (плюс-минус) от нескольких десятков до нескольких сотни микроватт, чтобы привести к выходу из строя многих кристаллов.