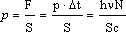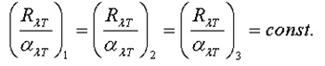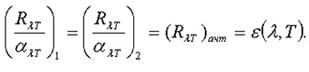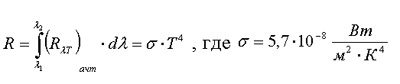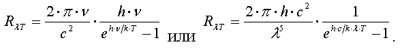Закон Кирхгофа
Введем некоторые характеристики теплового излучения.
Поток энергии (любых частот), испускаемый единицей поверхности излучающего тела в единицу времени во всех направлениях (в пределах телесного угла 4π), называется энергетической светимостью тела (R) [R] = Вт/м2.
Излучение состоит из волн различной частоты (ν). Обозначим поток энергии, испускаемой единицей поверхности тела в интервале частот от ν до ν + dν, через dRν. Тогда при данной температуре
| , |
где — спектральная плотность энергетической светимости, или лучеиспускательная способность тела.
Опыт показывает, что лучеиспускательная способность тела
Зная лучеиспускательную способность, можно вычислить энергетическую светимость:
| (1.2.1) |
Пусть на элементарную площадку поверхности тела падает поток лучистой энергии , обусловленный электромагнитными волнами, частоты которых заключены в интервале dν. Часть этого потока будет поглощаться телом. Безразмерная величина
| (1.2.2) |
Тело, для которого и меньше единицы для всех частот, называется серым телом (это тоже идеализация).
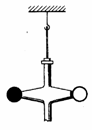
Между испускательной и поглощательной способностью тела существует определенная связь. Мысленно проведем следующий эксперимент (рис. 1.1).
Рис. 1.1
Пусть внутри замкнутой оболочки находятся три тела. Тела находятся в вакууме, следовательно обмен энергией может происходить только за счет излучения. Опыт показывает, что такая система через некоторое время придет в состояние теплового равновесия (все тела и оболочка будут иметь одну и ту же температуру).
В таком состоянии тело, обладающее большей лучеиспускательной способностью, теряет в единицу времени и больше энергии, но , следовательно это тело должно обладать и большей поглощающей способностью:
| . |
| Кирхгоф Густав Роберт (1824–1887) – немецкий физик. Работы посвящены электричеству, механике, гидродинамике, математической физике, оптике, гидродинамике. Построил общую теорию движения тока в проводниках. Развил строгую теорию дифракции. Установил один из основных законов теплового излучения, согласно которому отношение испускательной способности тела к поглощательной не зависит от природы излучающего тела (закон Кирхгофа). |
Густав Кирхгоф в 1856 году сформулировал закон и предложил модель абсолютно черного тела.
Отношение лучеиспускательной к поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты и температуры.
| , | (1.2.3) |
где – универсальная функция Кирхгофа.
Эта функция имеет универсальный, или абсолютный, характер.
Сами величины и , взятые отдельно, могут изменяться чрезвычайно сильно при переходе от одного тела к другому, но их отношение постоянно для всех тел (при данной частоте и температуре).
Для абсолютно черного тела , следовательно, для него , т.е. универсальная функция Кирхгофа есть не что иное, как лучеиспускательная способность абсолютно черного тела.
Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощающую способность , но только в ограниченном интервале частот. Однако полость с малым отверстием очень близка по своим свойствам к абсолютно черному телу. Луч, попавший внутрь, после многократных отражений обязательно поглощается, причём луч любой частоты (рис. 1.2).
Рис. 1.2
Лучеиспускательная способность такого устройства (полости) очень близка к f(ν,T). Таким образом, если стенки полости поддерживаются при температуре T, то из отверстия выходит излучение весьма близкое по спектральному составу к излучению абсолютно черного тела при той же температуре.
Разлагая это излучение в спектр, можно найти экспериментальный вид функции
Рис. 1.3
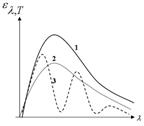
Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре.
Эти кривые одинаковы для всех тел.
Кривые похожи на функцию распределения молекул по скоростям. Но там площади, охватываемые кривыми, постоянны, а здесь с увеличением температуры площадь существенно увеличивается. Это говорит о том, что энергетическая совместимость сильно зависит от температуры. Максимум излучения (излучательной способности) с увеличением температуры смещается
Закон Кирхгофа. @
Кирхгоф (1859 г.) нашел количественную связь излучательной и поглощательной способности: отношение излучательной и поглощательной способности не зависит от природы тела и является универсальной функцией частоты и температуры, одинаковой для всех тел:
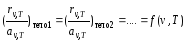 ,
,
где функция f(ν,T) называется универсальной функцией Кирхгофа. Этот закон следует из того, что для теплового равновесия количества поглощаемой и излучаемой телом энергии должны быть равны для всех диапазонов частот:
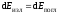 .
.
Это равенство можно переписать
в следующем виде: 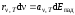 ,
откуда следует
,
откуда следует
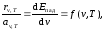
где f(ν,T)-
общая для всех тел функция, характеризующая
распределение энергии по частотам в
падающем на тела тепловом излучении.
Закон справедлив для любого тела, в том
числе и для абсолютно черного. Поскольку
его поглощательная способность равна
единице, то из закона следует 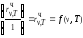
Законы теплового излучения. Формулы Рэлея-Джинса и Планка.
Фотоэффект. Виды фотоэффекта. Внешний фотоэлектрический эффект. Уравнение Эйнштейна для внешнего фотоэффекта. Законы фотоэффекта. Квантовая теория фотоэффекта.
Фотоэффе́кт— это испусканиеэлектроноввеществом под действиемсвета(и, вообще говоря, любогоэлектромагнитного излучения). В конденсированныхвеществах(твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
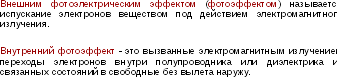

Законы фотоэффекта:
Формулировка
Согласно 2-му закону фотоэффекта,максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-й закон фотоэффекта:для каждого
вещества существует красная граница
фотоэффекта, то есть минимальная частота
света 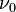 (или
максимальная длина волныλ0),
при которой ещё возможен фотоэффект, и
если
(или
максимальная длина волныλ0),
при которой ещё возможен фотоэффект, и
если 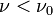

Квантовая теория фотоэффекта
В 1905 г. Эйнштейн, опираясь на работы М. Планка по излучению (гл. 11), предложил совершенно новую теорию фотоэффекта. По Эйнштейну, световой поток представляет собой поток «атомов света», названных Эйнштейном фотонами; каждый фотон обладает энергией
E=hv (10.4)
и импульсом
p=E/c
При этом отдельный фотон поглощается отдельным электроном, и электрон приобретает возможность покинуть металл, если его энергия превышает «работу выхода» из металла, характеризуемую разностью потенциалов UK.Применяя закон сохранения
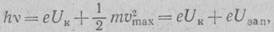 (10.5)
(10.5)
Где 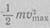 —
максимальная кинетическая энергия
вылетевшего электрона. За счет
взаимодействия с окружающими частицами
электрон может вылететь с меньшей
энергией, поэтому кривая (см. рис. 10.2)
имеет пологий спад.
—
максимальная кинетическая энергия
вылетевшего электрона. За счет
взаимодействия с окружающими частицами
электрон может вылететь с меньшей
энергией, поэтому кривая (см. рис. 10.2)
имеет пологий спад.
Из уравнения (10.5) следует, что существует минимальная частота света,, необходимая для фотоэффекта:
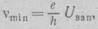
т. е. фотоэффект имеет «красную, границу»
Закон Столетова (10.1) означает, что число освободившихся электронов пропорционально числу падающих фотонов, имеющих определенную вероятность поглотиться в данном веществе; Коэффициент пропорциональности меньше единицы, так как не каждый электрон, поглотивший свет, обязательно покинет металл; он может до вылета отдать избыток энергии соседним частицам. Таким образом, фотоэффект получает полное объяснение, но с совершенно новой точки зрения.
Нужно отметить, что Эйнштейн не пользовался законом сохранения импульса. Вероятно, это связано с. неясностью механизма ‘ взаимодействия электрона с металлом до вылета из последнего. Но следует указать, что импульс фотона (ν≈5 x 10uГц) равен:
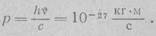
Импульс вылетевшего электрона (при задерживающем потенциале U=1 В) достигает значения:
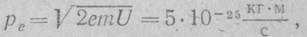
что на два-три порядка превышает импульс фотона.
Экспериментальные подтверждения квантовых свойств света. Эффект Комптона. Давление света. Корпускулярные свойства фотонов. Масса, импульс и энергия фотонов.
Эффект Комптона(Комптон-эффект) — неупругоерассеяниефотоновна свободныхэлектронах. Эффект сопровождается изменениемчастотыфотонов, часть энергии которых после рассеяния передается электронам.
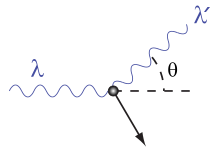

Иллюстрация к эффекту Комптона
При рассеянии фотонана покоящемсяэлектронечастоты фотона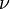 и
и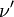 (до
и после рассеяния соответственно)
связаны соотношением:
(до
и после рассеяния соответственно)
связаны соотношением:
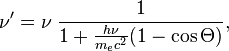
где 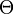 —
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
—
угол рассеяния (угол между направлениями
распространения фотона до и после
рассеяния).
Перейдя к длинам волн:
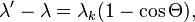
где 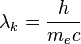 —комптоновская
длина волныэлектрона, равная
—комптоновская
длина волныэлектрона, равная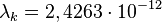 м.
м.
Если свет представляет собой поток фотонов, то каждый фотон, попадая в регистрирующий прибор (глаз, фотоэлемент), должен вызывать то или иное действие независимо от других фотонов. Это же означает, что при регистрации слабых световых потоков должны наблюдаться флуктуации их интенсивности. Эти флуктуации слабых потоков видимого света действительно наблюдались С. И. Вавиловым. Наблюдения проводились визуально. Глаз, адаптированный к темноте, обладает довольно резким порогом зрительного ощущения, т. е. воспринимает свет, интенсивность которого не меньше некоторого порога. Для света с l = 525 нм порог зрительного ощущения соответствует у разных людей примерно 100-400 фотонам, падающим на сетчатку за 1 с. С. И. Вавилов наблюдал периодически повторяющиеся вспышки света одинаковой длительности. С уменьшением светового потока некоторые вспышки уже не воспринимались глазом, причем чем слабее был световой поток, тем больше было пропусков вспышек. Это объясняется флуктуациями интенсивности света, т. е. число фотонов оказывалось по случайным причинам меньше порогового значения. Таким образом, опыт Вавилова явился наглядным подтверждением квантовых свойств света.
Давление света |
|
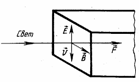
В 1873 г. Дж.Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу:свет должен оказывать давление на препятствие(благодаря действию силы Лоренца; на рисункеv- направление скорости электронов под действием электрической составляющей электромагнитной волны). | |
Квантовая теория света объясняет
световое давление как результат
передачи фотонами своего импульса
атомам или молекулам вещества. Пусть
на поверхность абсолютно черного тела
площадью Sперпендикулярно к ней ежесекундно
падаетNфотонов: |
|
При падении света на зеркальную поверхность удар фотона считают абсолютно упругим, поэтому изменение импульса и давление в 2 раза больше, чем при падении на черную поверхность (удар неупругий). | |
Это давление оказалось ~4.10-6Па. ПредсказаниеДж.Максвеллом существования светового давления было экспериментально подтвержденоП.Н.Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Теория и эксперимент совпали. Опыты П. Н. Лебедева — экспериментальное доказательство факта: фотоны обладают импульсом |

ТОП 10: |
Тепловое излучение — это электромагнитное излучение, которое возникает за счет энергии вращательного и колебательного движения атомов и молекул в составе вещества. Тепловое излучение характерно для всех тел, которые имеют температуру, превышающую температуру абсолютного нуля. — коэффициент поглощения — отношение поглощенной телом энергии к падающей энергии. Так, если на тело падает излучение потока dФпад, то одна его часть отражается от поверхности тела — dФотр , другая часть проходит в тело и частично превращается в теплоту dФпогл, а третья часть после нескольких внутренних отражений — проходит через тело наружу dФпр : α = dФпогл/dФпад. Законы теплового излучения 1. Закон Кирхгофа. Тепловое излучение является равновесным — сколько энергии излучается телом, столь ее им и поглощается. Для трех тел, находящихся в замкнутой полости можно записать:
Указанное соотношение будет верным и тогда, когда одно из тел будет АЧ:
Т.к. для АЧТ αλT.
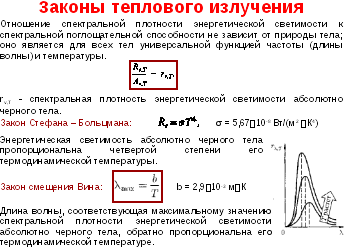
Вопрос15. Тепловое излучение. Закон Стефана-Больцмана.
Чтобы понять, как действует этот закон, представьте себе атом, излучающий свет в недрах Солнца. Свет тут же поглощается другим атомом, излучается им повторно — и таким образом передается по цепочке от атома к атому, благодаря чему вся система находится в состоянии энергетического равновесия. В равновесном состоянии свет строго определенной частоты поглощается одним атомом в одном месте одновременно с испусканием света той же частоты другим атомом в другом месте. В результате интенсивность света каждой длины волны спектра остается неизменной. Температура внутри Солнца падает по мере удаления от его центра. Поэтому, по мере движения по направлению к поверхности, спектр светового излучения оказывается соответствующим более высоким температурам, чем температура окружающий среды. В результате, при повторном излучении, согласно закону Стефана—Больцмана, оно будет происходить на более низких энергиях и частотах, но при этом, в силу закона сохранения энергии, будет излучаться большее число фотонов. Таким образом, к моменту достижения им поверхности спектральное распределение будет соответствовать температуре поверхности Солнца (около 5 800 К), а не температуре в центре Солнца (около 15 000 000 К). Энергия, поступившая к поверхности Солнца (или к поверхности любого горячего объекта), покидает его в виде излучения. Закон Стефана—Больцмана как раз и говорит нам, какова излученная энергия. Вопрос 16. Распределение энергии в спектре абсолютно черного тела. Закон Вина. Моделью абсолютно черного тела является замкнутая полость с небольшим отверстием О. Луч света, попавший внутрь такой полости через отверстие, многократно отражается от непрозрачных стенок, каждый раз испытывая частичное поглощение, в результате чего интенсивность вышедшего из отверстия излучения оказывается практически равной нулю. Опыт показывает, что независимо от материала стенок такая полость обладает поглощательной способностью А(ν,T) близкой к единице, если размер отверстия меньше 0,1 диаметра полости. Немецкий физик Вильгельм Вин в 1893 году сформулировал закон, который определяет положение максимума спектральной плотности энергетической светимости тела в спектре излучения АЧТ в зависимости от температуры. Согласно закону, длина волны λmax, на которую приходится максимум спектральной плотности энергетической светимости АЧТ, обратно пропорционален его абсолютной температуре Т: λmax = в/t, где в = 2,9*10-3 м·К- постоянная Вина.
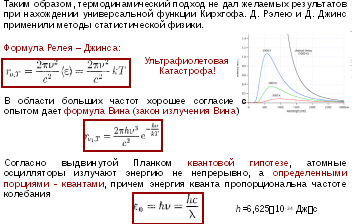
Представленные законы не позволяли теоретически найти уравнения распределения спектральной плотности энергетической светимости по длинам волн. Труды Релея и Джинса, в которых ученые исследовали спектральный состав излучения АЧТ на основе законов классической физики, привели к принципиальным трудностям, названных ультрафиолетовой катастрофой. В диапазоне УФ-волн энергетическая светимость АЧТ должна была достигать бесконечности, хотя в опытах она уменьшалась к нулю. Эти результаты противоречили закону сохранения энергии. Вопрос 17.Квантовая гипотеза и формула Планка. 4. Теория Планка. Немецкий ученый в 1900 году выдвинул гипотезу о том, что тела излучают не непрерывно, а отдельными порциями — квантами. Энергия кванта пропорциональна частоте излучения: E = hν = h·c/λ , где h = 6,63*10-34 Дж·с постоянная Планка.
Эта формула находится в соответствии с опытными данными во всем интервале длин волн при всех температурах. |
Законы теплового излучения Закон Кирхгофа
Реальное тело находится в состоянии термодинамического равновесия с окружающей средой. Следовательно, если какое-то тело больше излучает, то оно должно и больше поглощать энергии для того, чтобы его температура не изменялась, и, соответственно, наоборот.
Таким образом, испускательная способность тела и его поглощательная способность связаны между собой.
Немецкий физик Г. Кирхгоф, опираясь на второй закон термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между испускательной и поглощательной способностью тел: отношение испускательной способности тела (спектральной плотности энергетической светимости) к его поглощательной способности (коэффициент поглощения) есть величина постоянная, не зависящая от природы тела (закон Кирхгофа):
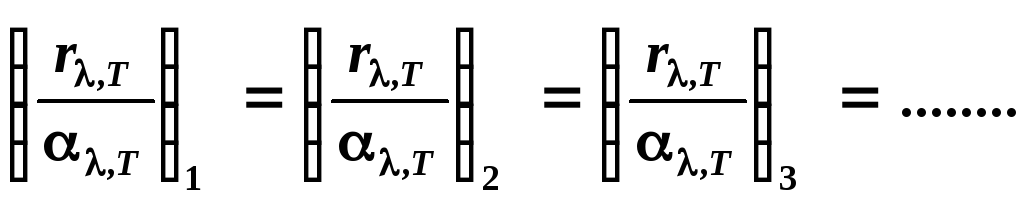 (4)
(4)
Соотношение
(4) справедливо для всех тел, в том числе
и для абсолютно чёрных ( ),
для которых поглощательная способность
равна единице, т.е.
),
для которых поглощательная способность
равна единице, т.е. 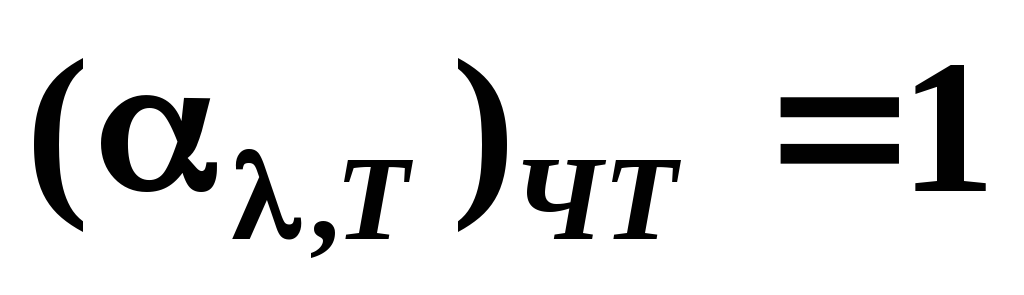 .
Поэтому можно записать:
.
Поэтому можно записать:
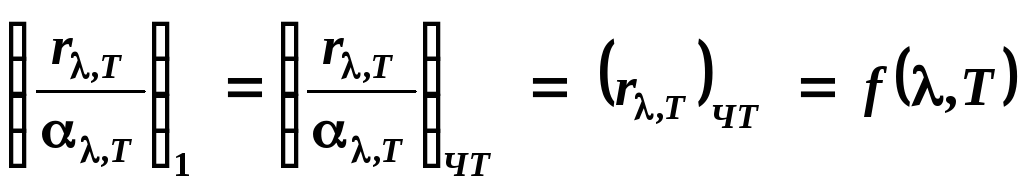 ,
,
где 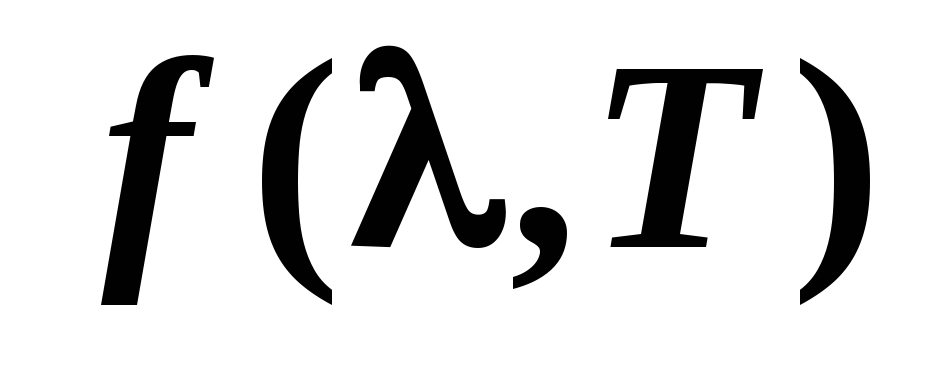 называется универсальной функцией
Кирхгофа.
называется универсальной функцией
Кирхгофа.
И тогда закон Кирхгофа примет вид:
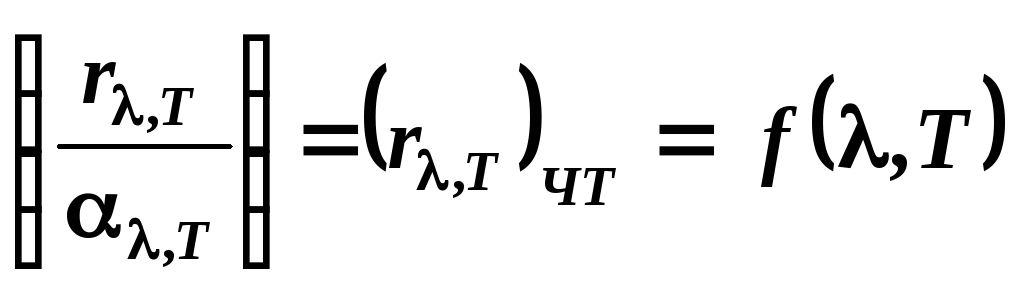 .
.
Отношение испускательной способности к поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией длины волны и температуры, равной спектральной плотности энергетической светимости абсолютно черного тела.
Отсюда
следует, в частности, что лучеиспускательная
способность реальных тел всегда меньше
лучеиспускательной способности абсолютно
черного тела (поскольку 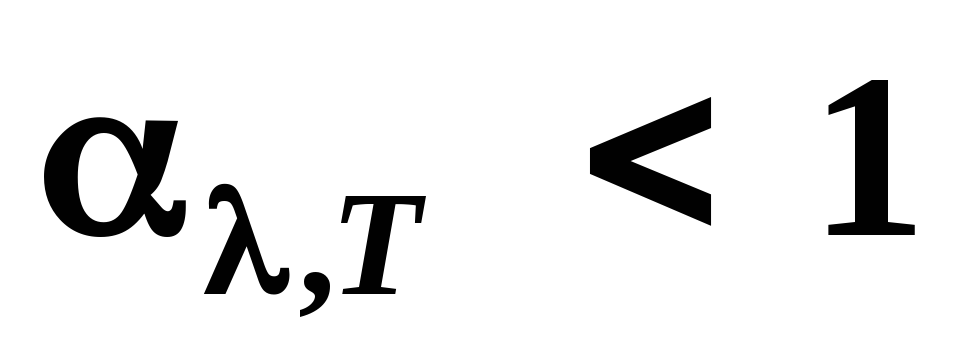 ).
).
Закон Стефана-Больцмана
Австрийские физики Й. Стефан и Л. Больцман, анализируя экспериментальные данные и применяя термодинамический метод, установили зависимость энергетической светимости абсолютно чёрного тела от температуры: энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры.
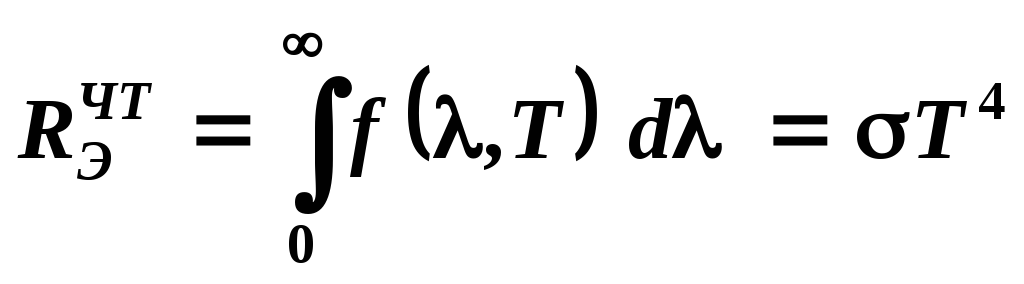 .
(5)
.
(5)
Этот
закон носит название закона Стефана-Больцмана.
Здесь 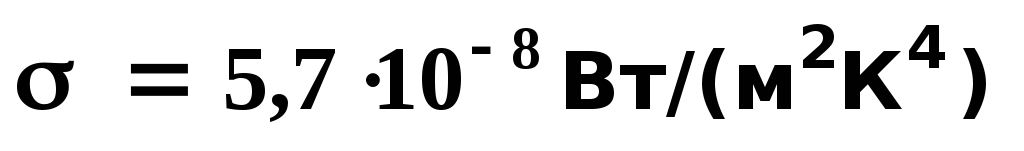 – постоянная Стефана-Больцмана.
– постоянная Стефана-Больцмана.
Энергетическая светимость реальных тел всегда меньше, чем абсолютно чёрных, поэтому для реальных тел закон Стефана-Больцмана выглядит так:
 ,
,
где  – коэффициент, показывающий, какую
часть излучения чёрного тела составляет
излучение реального тела, т.е. степень
черноты тела (
– коэффициент, показывающий, какую
часть излучения чёрного тела составляет
излучение реального тела, т.е. степень
черноты тела (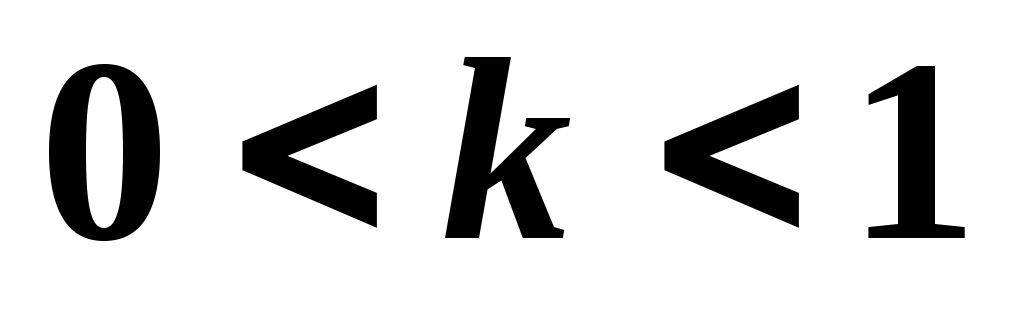 ).
).
Законы Вина
Закон смещения Вина.
Немецкий
физик В.Вин, опираясь на законы термо-
и электродинамики, установил зависимость
длины волны 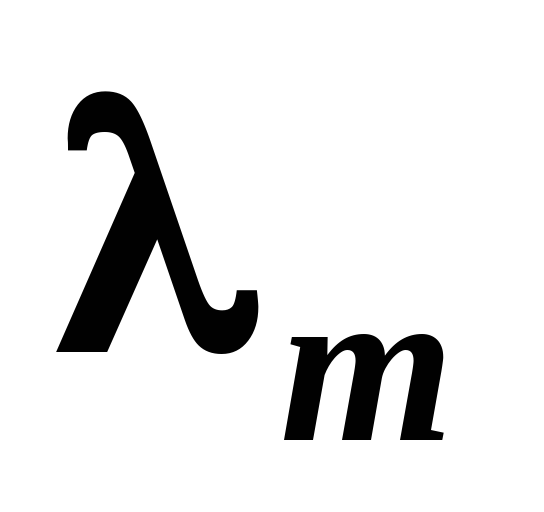 ,
соответствующей максимуму функции
,
соответствующей максимуму функции 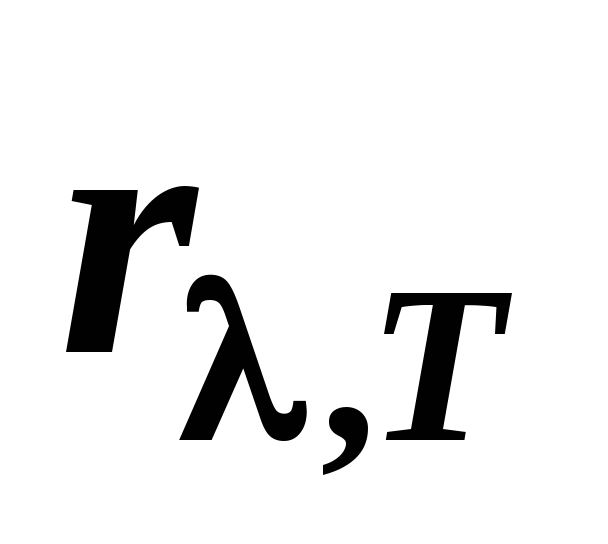 ,
от температуры
,
от температуры  : длина
волны, соответствующая максимальному
значению спектральной плотности
энергетической светимости чёрного
тела, обратно пропорциональна его
термодинамической температуре:
: длина
волны, соответствующая максимальному
значению спектральной плотности
энергетической светимости чёрного
тела, обратно пропорциональна его
термодинамической температуре:
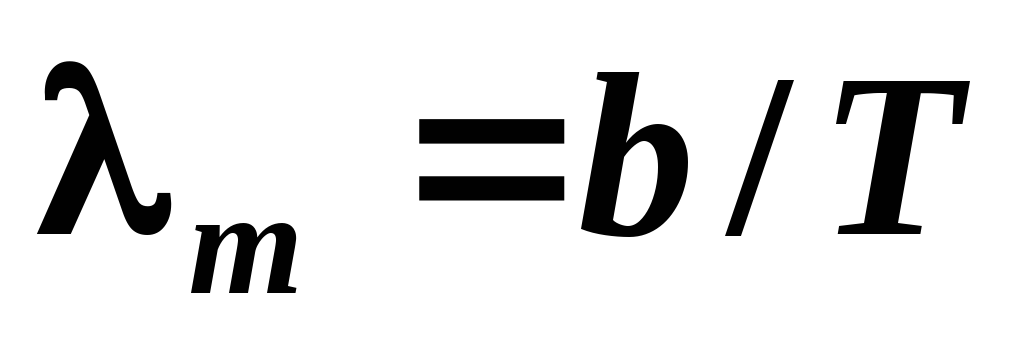 ,
(6)
,
(6)
где 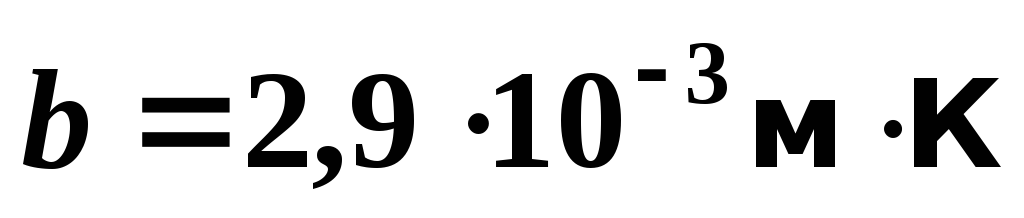 – постоянная Вина, полученная
экспериментально.
– постоянная Вина, полученная
экспериментально.
Из
выражения (6) следует, что по мере
возрастания температуры положение
максимума функции 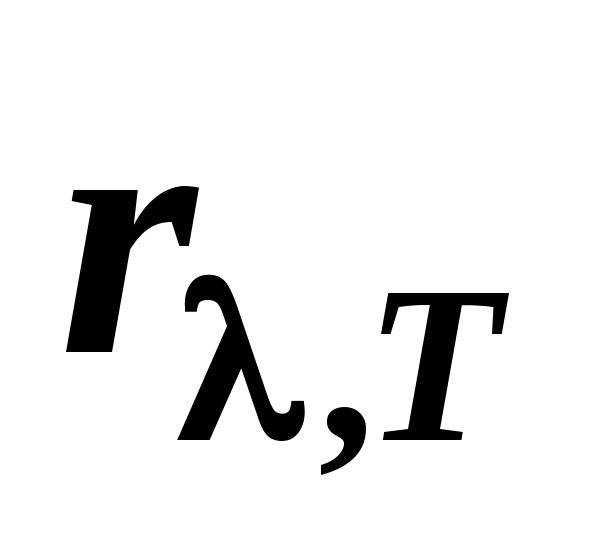 смещается в область коротких длин волн.
Поэтому уравнение (6) называется законом
смещения (см.
рис.1).
смещается в область коротких длин волн.
Поэтому уравнение (6) называется законом
смещения (см.
рис.1).
2) Максимальное значение плотности энергетической светимости чёрного тела пропорционально пятой степени абсолютной температуры:
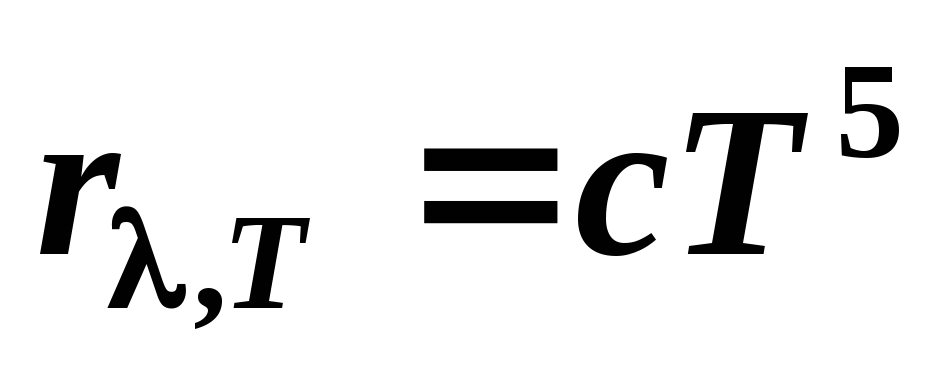 ,
,
где 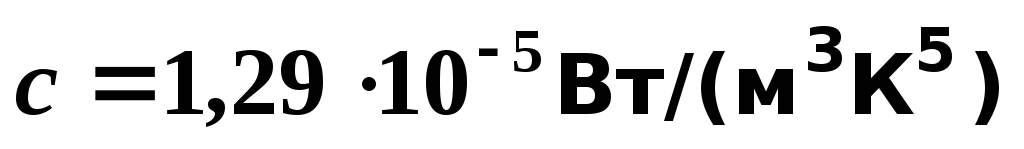 – постоянная, значение которой определено
экспериментально.
– постоянная, значение которой определено
экспериментально.
Закон излучения Кирхгофа | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Закон излучения Кирхгофа — отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же.
По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него (Поглощательная способность тела) . Поэтому функция совпадает с испускательной способностью
В формуле мы использовали :
— Испускательная способность тела
— Поглощательная способность тела
— Функция Кирхгофа
1. Тепловое излучение. Основные характеристики теплового излучения. Абсолютно черное тело. Закон Кирхгофа
Электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела, называется тепловым излучением. Оно определяется температурой и оптическими свойствами тела.
Основные характеристики теплового излучения:
1) Энергетическая светимость Me [Вт/м2] – количество энергии, излучаемой за единицу времени по всем направлениям с единицы площади поверхности тела во всем диапазоне длин волн.
2) Спектральная плотность энергетической светимости Mλ,T [Вт/м3] – количество энергии, излучаемой за единицу времени по всем направлениям с единицы площади поверхности тела в единичном диапазоне длин волн.
Энергетическая светимость и спектральная плотность энергетической светимости связаны следующим образом:
Mλ,T = dMe/dλ;
Me = 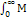 λ,T dλ .
λ,T dλ .
Тело, которое при всех температурах полностью поглощает все падающее на него излучение во всем диапазоне длин волн, называется абсолютно черным. Спектральный коэффициент поглощения абсолютно черного тела равен единице для всех длин волн, т.е.: aλ,T = aT = 1.
Спектральная плотность энергетической светимости Mλ,T и коэффициент поглощения aλ,T любого тела связаны соотношением, называемым законом Кирхгофа: в состоянии теплового равновесия отношение спектральной плотности энергетической светимости к спектральному коэффициенту поглощения не зависит от природы тела и является для всех тел одной и той же универсальной функцией, равной спектральной плотности энергетической светимости абсолютно черного тела: (Mλ,T /aλ,T)1 = (Mλ,T /aλ,T)2 = Moλ,T .
Следствия из закона Кирхгофа:
1) Всякое тело при данной температуре излучает преимущественно лучи тех же длин волн, которые сильнее всего поглощает.
2) Из всех тел при одной и той же температуре абсолютно черное тело обладает наибольшей спектральной плотностью энергетической светимости для любой длины волны излучения.
2. Законы излучения абсолютно черного тела (Стефана – Больцмана и Вина). Гипотеза и формула Планка для абсолютно черного тела
1) Закон Стефана – Больцмана: Энергетическая светимость абсолютно черного тела пропорциональна четвертой степени абсолютной температуры: M0e = σT4, где σ = 5,67 · 10-8 Вт/(м2 · К4) – постоянная Стефана – Больцмана.
2) Закон смещения Вина: длина волны λ’, на которую приходится максимум излучения в спектре абсолютно черного тела, обратно пропорциональна абсолютной температуре: λ’ = b/T, где
b = 2,9 · 10-3 м·К.Теоретически излучение абсолютно черного тела было исследовано и рассчитано Планком в 1900 году, который впервые предположил, что энергия испускается в виде отдельных порций: постулат Планка. Постулат Планка: ε = hv, где
h = 6,626 · 10-34 Дж·с – постоянная Планка.
Формула Планка для расчета спектральной плотности энергетической светимости абсолютно черного тела имеет вид: Moλ,T = 2πhc2/λ5 · 1/exp(hc/λkT)-1, где c = 3·108 м/с – скорость света в вакууме, k = 1,38·10-23 Дж/К – постоянная Больцмана.
3. Фотоны. Энергия, масса и импульс фотона
Фотон – элементарная частица, квант электромагнитного излучения.
Энергия фотона: ε = hv, где h = 6,626 · 10-34 Дж·с – постоянная Планка.
Масса фотона: m = h·v/c2. Эта формула получается из формул
ε = hv и ε = m·c2. Масса, определяемая формулой m = h·v/c2, является массой движущегося фотона. Фотон не имеет массы покоя (m0 = 0), так как он не может существовать в состоянии покоя.
Импульс фотона: Все фотоны движутся со скоростью с = 3·108 м/с. Очевидно импульс фотона P = m·c, откуда следует, что
P = h·v/c = h/λ.
Правило Прево. Законы Кирхгофа, Стефана-Больцмана, Вина
При тепловом равновесии выполняется правило Прево: если два тела поглощают разные количества энергии, то и излучение у них должно быть различным. Так, нагревая кристалл кварца и кусок стали до высокой температуры, наблюдаем яркое каление стали, кристалл же кварца совсем не светится. Таким образом, обнаруживается большая способность к излучению тел, хорошо поглощающих.
Тогда закон Кирхгофа запишется в следующем виде: 1. Тепловое излучение является равновесным — сколько энергии излучается телом, столь ее им и поглощается. Для трех тел, находящихся в замкнутой полости можно записать:
2. Указанное соотношение будет верным и тогда, когда одно из тел будет АЧ:
2. Указанное соотношение будет верным и тогда, когда одно из тел будет АЧ:
Т.к. для АЧТ αλT=1
т.е. отношение излучательной способности тела к его поглощательной способности является одинаковым для всех тел.
Это закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.
Следствия из закона Кирхгофа:
1. Спектральная энергетическая светимость АЧТ является универсальной функцией длины волны и температуры тела.
2. Спектральная энергетическая светимость АЧТ наибольшая.
3. Спектральная энергетическая светимость произвольного тела равна произведению его коэффициента поглощения на спектральную энергетическую светимость абсолютно черного тела.
4. Любое тело при данной температуре излучает волны той же длины волны, которое оно поглощает при данной температуре.
т.е. отношение излучательной способности тела к его поглощательной способности является одинаковым для всех тел.
Это закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.
Следствия из закона Кирхгофа:
1. Спектральная энергетическая светимость АЧТ является универсальной функцией длины волны и температуры тела.
2. Спектральная энергетическая светимость АЧТ наибольшая.
3. Спектральная энергетическая светимость произвольного тела равна произведению его коэффициента поглощения на спектральную энергетическую светимость абсолютно черного тела.
4. Любое тело при данной температуре излучает волны той же длины волны, которое оно поглощает при данной температуре.
ε(λ,T)=rλТ — физический смысл универсальной функции Кирхгофа — универсальная функция Кирхгофа — испускательная способность абсолютно черного тела.
Систематическое изучение спектров ряда элементов позволило Кирхгофу и Бунзену установить однозначную связь между спектрами поглощения и излучения газов и индивидуальностью соответствующих атомов. Так был предложен спектральный анализ, с помощью которого можно выявить вещества, концентрация которых составляет 0,1*10-9
Систематическое изучение спектров ряда элементов позволило Кирхгофу и Бунзену установить однозначную связь между спектрами поглощения и излучения газов и индивидуальностью соответствующих атомов. Так был предложен спектральный анализ, с помощью которого можно выявить вещества, концентрация которых составляет 0,1*10-9
Закон Вина
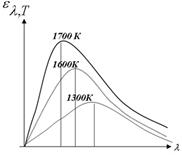
Изучение распределения светимости для разных длин волн при разных температурах (рис 4) дало следующие результаты:
1. Спектр излучения сплошной
2.Излучательная способность резче уменьшается в сторону коротких волн
3.Максимум излучательной способности с ростом температуры смещается в сторону более коротких волн.4. Площадь, ограниченная каждой кривой и осью абсцисс, определяет полную энергию, испускаемую единицей поверхности за единицу времени, т.е. Rэ .
Тщательное количественное исследование кривых позволило установить соотношение
названное законом смещения Вина: длина волны λmax, на которую приходиться максимум излучательной способности rλ , обратно пропорциональна его абсолютной температуре. По современным данным, постоянная Вина b = 2,898·10-3м·К.Но все эти законы чисто эмпирические,следствия обобщения опытных данных, теоретическое обоснование было дано Планком.


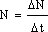 .Каждый фотон обладает импульсом
.Каждый фотон обладает импульсом .
Полный импульс, получаемый
поверхностью тела, равен
.
Полный импульс, получаемый
поверхностью тела, равен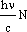 .
Световое давление:
.
Световое давление: