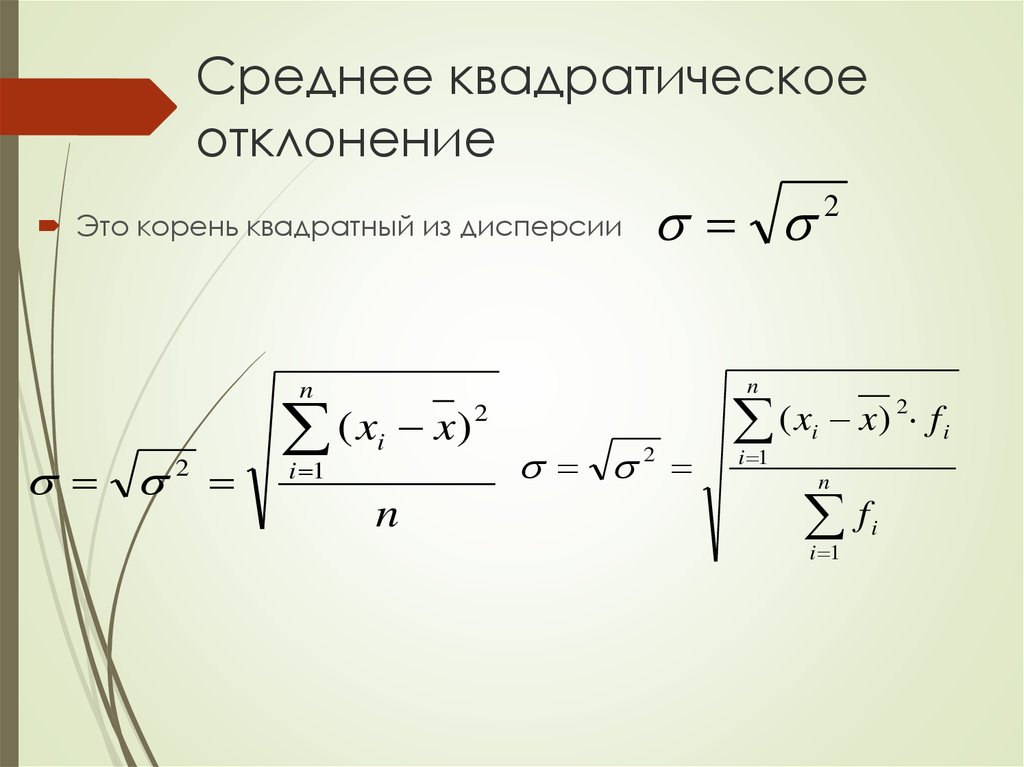
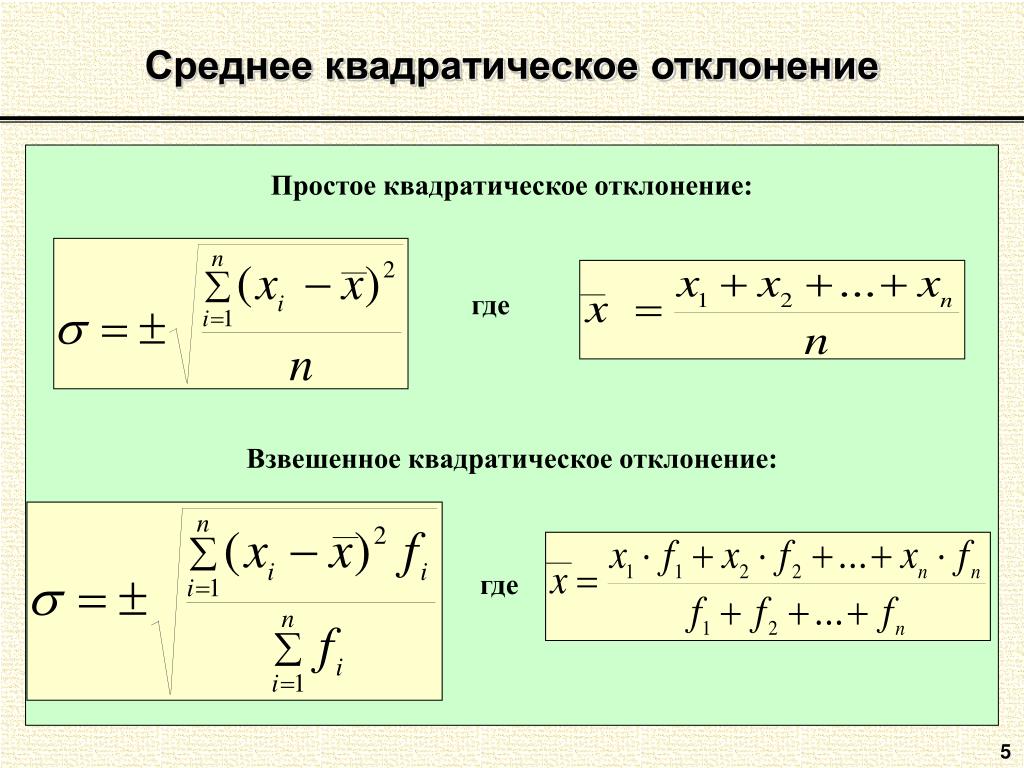
Разбираем формулы среднеквадратического отклонения и дисперсии в Excel | Методы анализа
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
|
10 |
14 |
Сморите пример расчета здесь: среднеквадратическое отклонние и дисперсия
Для этого временного ряда i=1, n=10, ,
Рассмотрим формулу среднего значения:
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего.
=90/(10-1)=10
6. Среднеквадратическое отклонение равно = корень(10)=3,2
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Скачать файл с примером
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Скачать файл с примером
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.

- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Добавить комментарий
Относительное среднее квадратическое отклонение. Среднеквадратическое отклонение
Х i — случайные (текущие) величины;
X̅ – среднее значение случайных величин по выборке, рассчитывается по формуле:
Итак, дисперсия — это средний квадрат отклонений . То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат , складывается и затем делится на количество значений в данной совокупности.
Разница между отдельным значением и средней отражает меру отклонения.
Разгадка магического слова «дисперсия» заключается всего в этих трех словах: средний – квадрат – отклонений.
Среднее квадратичное отклонение (СКО)
Извлекая из дисперсии квадратный корень, получаем, так называемое «среднеквадратичное отклонение». Встречаются названия «стандартное отклонение» или «сигма» (от названия греческой буквы
Итак, дисперсия – это сигма в квадрате, или – среднее квадратичное отклонение в квадрате.
Среднеквадратичное отклонение, очевидно, также характеризует меру рассеивания данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета). Размах вариации – это разница между крайними значениями. Среднеквадратичное отклонение, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.
Размах вариации – это разница между крайними значениями. Среднеквадратичное отклонение, как мера неопределенности, также участвует во многих статистических расчетах. С ее помощью устанавливают степень точности различных оценок и прогнозов. Если вариация очень большая, то стандартное отклонение тоже получится большим, следовательно, и прогноз будет неточным, что выразится, к примеру, в очень широких доверительных интервалах.
Поэтому в методах статистической обработки данных в оценках объектов недвижимости в зависимости от необходимой точности поставленной задачи используют правило двух или трех сигм.
Для сравнения правила двух сигм и правила трех сигм используем формулу Лапласа:
Ф — Ф ,
где Ф(x) – функция Лапласа;
Минимальное значение
β = максимальное значение
s = значение сигмы (среднее квадратичное отклонение)
a = среднее значение
В этом случае используется частный вид формулы Лапласа когда границы α и β значений случайной величины X равно отстоят от центра распределения a = M(X) на некоторую величину d: a = a-d, b = a+d. Или
(1)
Формула (1) определяет вероятность заданного отклонения d случайной величины X с нормальным законом распределения от ее математического ожидания М(X) = a.
Если в формуле (1) принять последовательно d = 2s и d = 3s, то получим:
(2),
(3). Или
(1)
Формула (1) определяет вероятность заданного отклонения d случайной величины X с нормальным законом распределения от ее математического ожидания М(X) = a.
Если в формуле (1) принять последовательно d = 2s и d = 3s, то получим:
(2),
(3). |
Правило двух сигм
Почти достоверно (с доверительной вероятностью 0,954) можно утверждать, что все значения случайной величины X с нормальным законом распределения отклоняются от ее математического ожидания M(X) = a на величину, не большую 2s (двух средних квадратических отклонений). Доверительной вероятностью (Pд) называют вероятность событий, которые условно принимаются за достоверные (их вероятность близка к 1).
Проиллюстрируем правило двух сигм геометрически. На рис. 6 изображена кривая Гаусса с центром распределения а. Площадь, ограниченная всей кривой и осью Оx, равна 1 (100%), а площадь криволинейной трапеции между абсциссами а–2s и а+2s, согласно правилу двух сигм, равна 0,954 (95,4% от всей площади).
Вероятность условно невозможных значений называют уровнем значимости случайной величины. Уровень значимости связан с доверительной вероятностью формулой:
где q – уровень значимости, выраженный в процентах.
Правило трех сигм
При решении вопросов, требующих большей надежности, когда доверительную вероятность (Pд) принимают равной 0,997 (точнее — 0,9973), вместо правила двух сигм, согласно формуле (3), используют правило
Согласно правилу трех сигм при доверительной вероятности 0,9973 критической областью будет область значений признака вне интервала (а-3s, а+3s). Уровень значимости составляет 0,27%.
Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. Т.е. выборка высокоточная.
Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий, можно считать практически невозможными. Т.е. выборка высокоточная.
В этом и состоит сущность правила трех сигм:
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения (СКО).
На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
Уровень значимости принимают в зависимости от дозволенной степени риска и поставленной задачи. Для оценки недвижимости обычно принимается менее точная выборка, следуя правилу двух сигм.
Для расчетов средней геометрической простой используется формула:
Геометрическая взвешенная
Для определения средней геометрической взвешенной применяется формула:
редние
диаметры колес, труб, средние стороны
квадратов определяются при помощи
средней квадратической.
Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:
Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.
Квадратическая простая
Средняя квадратическая простая вычисляется по формуле:
Квадратическая взвешенная
Средняя квадратическая взвешенная равна:
22. Абсолютные показатели вариации включают:
размах вариации
среднее линейное отклонение
дисперсию
среднее квадратическое отклонение
Размах вариации (r)
Размах вариации — это разность между максимальным и минимальным значениями признака
Он
показывает пределы, в которых изменяется
величина признака в изучаемой совокупности.
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. Решение: размах вариации = 9 — 2 = 7 лет.
Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат
Среднее линейное и квадратическое отклонение
Среднее линейное отклонение — этосредняя арифметическая из абсолютных отклонений отдельных значений признака от средней.
Среднее линейное отклонение простое:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В нашем примере: лет;
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
Среднее
линейное отклонение в силу его условности
применяется на практике сравнительно
редко (в частности, для характеристики
выполнения договорных обязательств по
равномерности поставки; в анализе
качества продукции с учетом технологических
особенностей производства).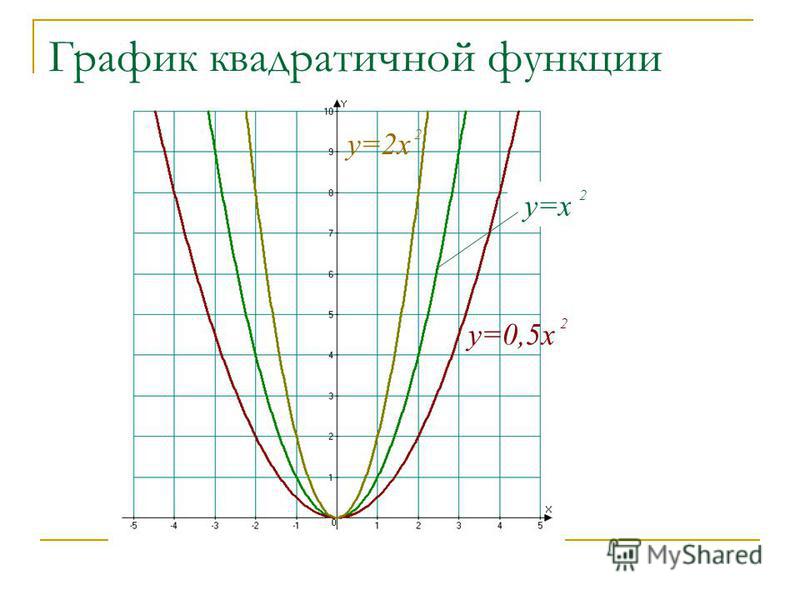
Среднее квадратическое отклонение
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака отсредней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.
Среднее
квадратическое отклонение, являясь
основной абсолютной мерой вариации,
используется при определении значений
ординат кривой нормального распределения,
в расчетах, связанных с организацией
выборочного наблюдения и установлением
точности выборочных характеристик, а
также при оценке границ вариации признака
в однородной совокупности.
Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.
Максимальное и минимальное значение
Среднее линейное отклонение
Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от в анализируемой совокупности данных. Математическая формула имеет вид:
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n
В Эксель эта функция называется СРОТКЛ .
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».
Дисперсия
{module 111}
Возможно, не все знают, что такое , поэтому поясню, — это мера, характеризующая разброс данных вокруг математического ожидания. Однако в распоряжении обычно есть только выборка, поэтому используют следующую формулу дисперсии:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅ – среднее арифметическое по выборке,
n – количество значений в анализируемой совокупности данных.
Соответствующая функция Excel — ДИСП.Г . При анализе относительно небольших выборок (примерно до 30-ти наблюдений) следует использовать , которая рассчитывается по следующей формуле.
Отличие, как видно, только в знаменателе. В Excel для расчета выборочной несмещенной дисперсии есть функция ДИСП.В .
Выбираем нужный вариант (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.
Среднеквадратичное отклонение
Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:
по генеральной совокупности
по выборке
Можно просто извлечь корень из дисперсии, но в Excel
для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН. Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации , который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое . Формула коэффициента вариации проста:
Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
Для этого в строке формул пишем:
СТАНДОТКЛОН.Г()/СРЗНАЧ()
В скобках указывается диапазон данных. При необходимости используют среднее квадратичное отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «Главная»:
Изменить формат также можно, выбрав из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
Полезное свойство.
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.
Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние , среднеквадрати́чное отклоне́ние , квадрати́чное отклоне́ние ; близкие термины: станда́ртное отклоне́ние , станда́ртный разбро́с ) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания . {n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}
{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .
В соответствии с ГОСТ Р 8.736-2011 среднеквадратическое отклонение считается по второй формуле данного раздела. Пожалуйста, сверьте результаты.
Правило трёх сигм
Правило трёх сигм ( 3 σ {\displaystyle 3\sigma } ) — практически все значения нормально распределённой случайной величины лежат в интервале (x ¯ − 3 σ ; x ¯ + 3 σ) {\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x ¯ {\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).
Если же истинная величина
x
¯
{\displaystyle {\bar {x}}}
неизвестна, то следует пользоваться не
σ
{\displaystyle \sigma }
, а s . Таким образом, правило трёх сигм преобразуется в правило трёх s .
Таким образом, правило трёх сигм преобразуется в правило трёх s .
Интерпретация величины среднеквадратического отклонения
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить. отождествляется с риском портфеля.
Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить. отождествляется с риском портфеля.
Климат
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.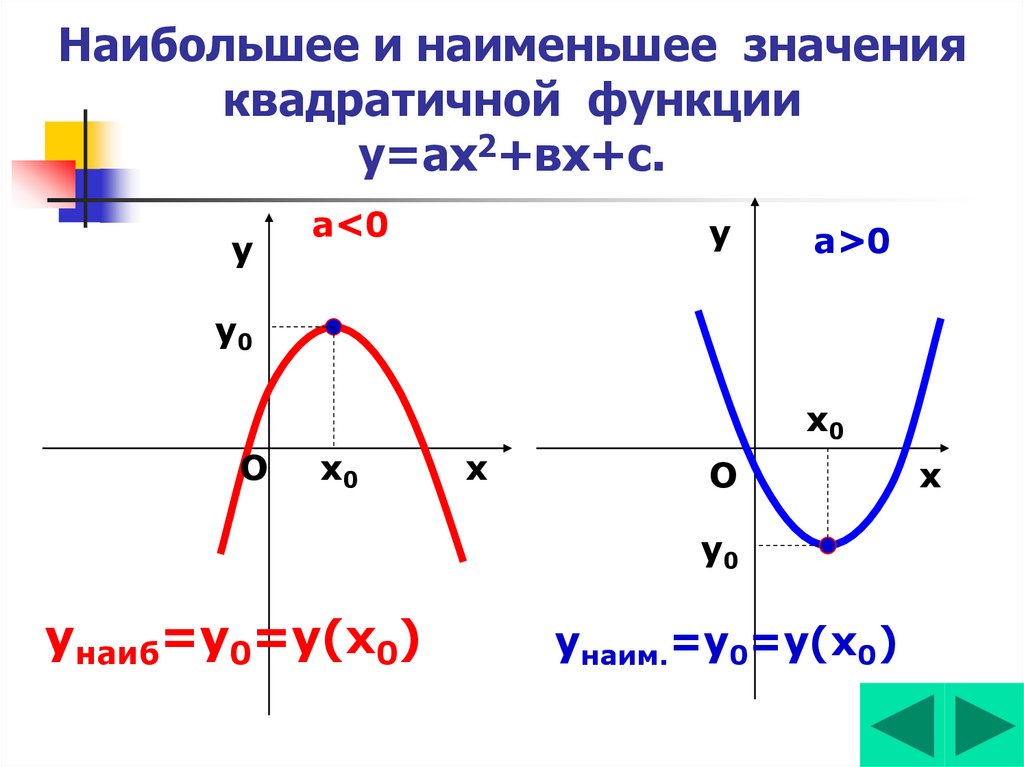
Спорт
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Приближенный метод оценки колеблемости вариационного ряда — определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного признака в пределах вариационного ряда является среднее квадратическое отклонение (σ — сигма) . Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.
Основной общепринятой мерой колеблемости количественного признака в пределах вариационного ряда является среднее квадратическое отклонение (σ — сигма) . Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.
Методика расчета среднего квадратического отклонения включает следующие этапы:
1. Находят среднюю арифметическую величину (Μ).
2. Определяют отклонения отдельных вариант от средней арифметической (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех отклонений равняется нулю.
3. Возводят каждое отклонение в квадрат d 2 .
4. Перемножают квадраты отклонений на соответствующие частоты d 2 *p.
5. Находят сумму произведений å(d 2 *p)
6. Вычисляют среднее квадратическое отклонение по формуле:
При n больше 30,или при n меньше либо равно 30, где n — число всех вариант.
Значение среднего квадратичного отклонения:
1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.
Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.
2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.
Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.
Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат — частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.
Установлено, что при нормальном распределении признака:
68,3% значений вариант находится в пределах М±1s
95,5% значений вариант находится в пределах М±2s
99,7% значений вариант находится в пределах М±3s
3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М±1s обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1s указывает на отклонение изучаемого параметра от нормы.
4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды
5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.
Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv) , представляющий собой относительную величину: процентное отношение среднего квадратического отклонения к средней арифметической.
Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение — именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv) , представляющий собой относительную величину: процентное отношение среднего квадратического отклонения к средней арифметической.
Коэффициент вариации вычисляется по формуле:
Чем выше коэффициент вариации, тем большая изменчивость данного ряда. Считают, что коэффициент вариации свыше 30 % свидетельствует о качественной неоднородности совокупности.
Квадратичные функции
Квадратичные функции
|
Содержание : Эта страница соответствует § 3. 1 (стр.
244) текста.
1 (стр.
244) текста.
Предполагаемые проблемы из текста:
р. 251 #1-8, 10, 11, 15, 16, 18, 19, 21, 23, 24, 30, 33, 37, 38, 75
Графики
Стандартная форма
приложений
Графики
А квадратичная функция имеет вид f(x) = ax 2 + bx + c , где a , b и c — это числа, где a не равны нулю.
График квадратичной функции представляет собой кривую, называемую параболой . Параболы могут раскрываться вверх или вниз и различаются по «ширине» или «крутизне», но все они имеют одинаковую основную форму «U». На рисунке ниже показаны три графика, и все они являются параболами.
Все параболы симметричны относительно линии, называемой осью симметрии . Парабола пересекается
его ось симметрии в точке, называемой вершиной параболы.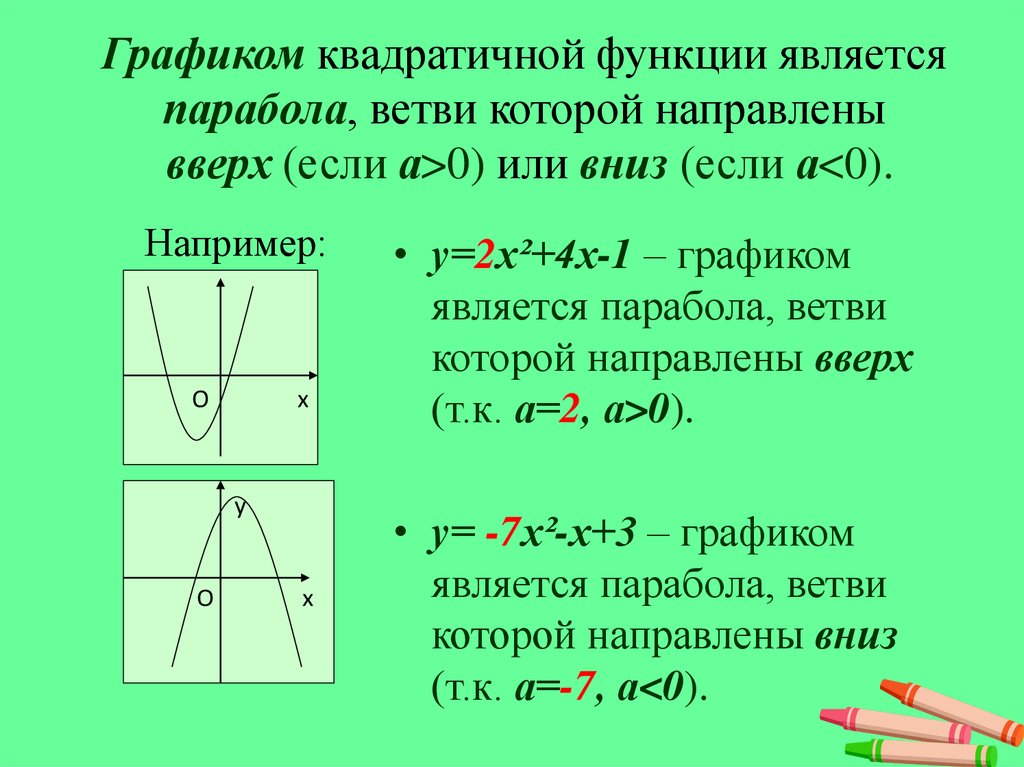
Вы знаете, что две точки определяют прямую. Это означает, что если вам даны любые две точки на плоскости, то существует одна и только одна линия, содержащая обе точки. Аналогичное утверждение можно сделать о точках и квадратичных функции.
Даны три точки на плоскости, которые имеют разные первые координаты и не лежат на одной прямой. одну квадратичную функцию f, график которой содержит все три точки. Апплет ниже иллюстрирует этот факт. График содержит три точки и параболу, проходящую через все три. Соответствующая функция показана в тексте поле под графиком. Если перетащить любую из точек, то функция и парабола обновятся.
Многие квадратичные функции можно легко изобразить вручную, используя методы растяжения/сжатия и сдвига. (перевод) парабола y = x 2 . (См. раздел об управлении графики.)
Пример 1 .
Нарисуйте график y = x 2 /2. Начиная с графика y = x 2 , мы уменьшаем его в множитель из одной половины.
Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем 5 единиц вниз.
Упражнение 1 :
(a) Нарисуйте график y = (x + 2) 2 — 3. Ответ
(b) Нарисуйте график y = -(x — 5) 2 + 3. Ответ
Вернуться к содержанию
Стандартная форма
Функции в частях (a) и (b) упражнения 1 являются примерами квадратичных функций в стандартной форме . Когда квадратичная функция имеет стандартную форму, ее график легко начертить, отражая, сдвигая и растяжение/сжатие параболы y = x 2 .
Говорят, что квадратичная функция f(x) = a(x — h) 2 + k, не равная нулю, имеет стандартную форму . Если а положительное, то график открывается вверх, а если а отрицательное, то открывается вниз.
линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).
Любая квадратичная функция может быть переписана в стандартной форме с помощью , дополняющего квадрат . (см. раздел о решая уравнения алгебраически, чтобы просмотреть завершение квадрата.) Шаги, которые мы используем в этом разделе для заполнения квадрата, будут выглядеть немного иначе, потому что наш главный цель здесь не решение уравнения.
Обратите внимание, что, когда квадратичная функция находится в стандартной форме, также легко найти ее нули по квадратному корню. принцип.
Пример 3 .
Запишите функцию f(x) = x 2 — 6x + 7 в стандартной форме. Нарисуйте график функции f и найдите ее нули. и вершина.
f(x) = x 2 — 6x + 7.
= (x 2 — 6x )+ 7. Сгруппируйте x 2 и х членов и затем завершите квадрат на этих условиях.
= (х 2 — 6х + 9 — 9) + 7.
Нам нужно прибавить 9, потому что это квадрат половины коэффициента x, (-6/2) 2 = 9. Когда мы решали уравнение, мы просто прибавляли 9 к обеим частям уравнения. В этой настройке мы добавляем и вычитаем 9 так что мы не меняем функцию.
= (х 2 — 6x + 9) — 9 + 7. Мы видим, что x 2 — 6x + 9 — полный квадрат, а именно (x — 3) 2 .
f(x) = (x — 3) 2 — 2. Это стандартная форма .
Из этого результата легко найти вершину графа функции f (3, -2).
Чтобы найти нули f, мы приравняем f к 0 и найдем x.
(х — 3) 2 — 2 = 0,
(х — 3) 2 = 2.
(х — 3) = ± квадратный сантиметр (2).
х = 3 ± квадрат (2).
Чтобы начертить график f, сдвинем график y = x 2 на три единицы вправо и на две единицы вниз.
Если коэффициент при х 2 не равен 1, то мы должны вынести этот коэффициент из х 2 и х терминов, прежде чем продолжить.
Пример 4 .
Запишите f(x) = -2x 2 + 2x + 3 в стандартной форме и найдите вершину графика f.
f(x) = -2x 2 + 2x + 3.
= (-2x 2 + 2x) + 3.
= -2(х 2 — х) + 3.
= -2(х 2 — х + 1/4 — 1/4) + 3.
Мы прибавляем и вычитаем 1/4, потому что (-1/2) 2 = 1/4, а -1 — коэффициент при x.
= -2(х 2 — х + 1/4) -2(-1/4) + 3.
Обратите внимание, что все в скобках умножается на -2, поэтому, когда мы удаляем -1/4 из скобок, мы надо умножить на -2.
= -2(х — 1/2) 2 + 1/2 + 3.
= -2(х — 1/2) 2 + 7/2.
Вершина — это точка (1/2, 7/2). Поскольку график открывается вниз (-2 < 0), вершина является самой высокой точкой на графике.
Упражнение 2 :
Запишите f(x) = 3x 2 + 12x + 8 в стандартной форме. Нарисуйте график функции f, найдите его вершину и найдите нули f. Ответ
Альтернативный метод нахождения вершины
В некоторых случаях завершение квадрата — не самый простой способ найти вершину параболы. Если график квадратичная функция имеет две точки пересечения с х, тогда линия симметрии — это вертикальная линия, проходящая через середину x-перехватов.
Х-пересечения на графике выше находятся в точках -5 и 3. Линия симметрии проходит через -1, что является средним
из -5 и 3. (-5 + 3)/2 = -2/2 = -1. Как только мы знаем, что линия симметрии равна x = -1, мы знаем первую координату
вершины равно -1. Вторую координату вершины можно найти, вычислив функцию при x = -1.
Вторую координату вершины можно найти, вычислив функцию при x = -1.
Пример 5 .
Найдите вершину графика функции f(x) = (x + 9)(х — 5).
Поскольку формула для f факторизуется, нули легко найти: -9 и 5.
Среднее значение нулей равно (-9 + 5)/2 = -4/2 = -2. Итак, линия симметрии равна x = -2, а первая координата вершины равно -2.
Вторая координата вершины: f(-2) = (-2 + 9)(-2 — 5) = 7*(-7) = -49.
Следовательно, вершина графика функции f равна (-2, -49).
Вернуться к содержанию
Приложения
Пример 6 .
Владелец ранчо имеет 600 метров забора, чтобы оградить прямоугольный загон с другим забором, разделяющим его посередине. как на схеме ниже.
Как показано на схеме, четыре горизонтальные секции забора будут иметь длину по x метров, а три каждая вертикальная секция будет иметь длину y метров.
Цель владельца ранчо — использовать весь забор и ограждать как можно большую площадь .
Каждый из двух прямоугольников имеет площадь xy, поэтому у нас есть
общая площадь: A = 2xy.
Мы мало что можем сделать с величиной А, пока она выражается как произведение двух переменных. Однако, тот факт, что у нас есть только 1200 метров забора, приводит к уравнению, которому x и y должны удовлетворять.
3у + 4х = 1200,
3г = 1200 — 4х.
г = 400 — 4x/3.
Теперь у нас есть выражение y как функция x, и мы можем подставить это выражение вместо y в формулу для общего район А.
А = 2xy = 2x (400 -4x/3).
Нам нужно найти значение x, при котором A будет как можно больше. A является квадратичной функцией x, и график открывается вниз, поэтому самая высокая точка на графике A является вершиной. Поскольку A факторизуется, самый простой способ найти вершина состоит в том, чтобы найти x-перехваты и среднее значение.
2x (400 -4x/3) = 0,
2x = 0 или 400 -4x/3 = 0.
х = 0 или 400 = 4х/3.
х = 0 или 1200 = 4х.
х = 0 или 300 = х.
Следовательно, линия симметрии графика A равна x = 150, среднее значение 0 и 300.
Теперь, когда мы знаем значение x, соответствующее наибольшей площади, мы можем найти значение y, вернувшись назад. к уравнению, связывающему x и y.
у = 400 — 4х/3 = 400 -4(150)/3 = 200.
Вернуться к содержанию
|
Квадратные уравнения
Пример квадратного уравнения :
Функция создает красивые кривые, подобные этой:
Имя
Название Quadratic происходит от «quad», что означает квадрат, потому что переменная возводится в квадрат (например, x 2 ).
Его также называют «уравнением степени 2» (из-за «2» на x )
Стандартная форма
Стандартная форма квадратного уравнения выглядит следующим образом:
- a , b и c — известные значения. не может быть 0.
- « x » — это переменная или неизвестная (мы пока этого не знаем).
Вот несколько примеров:
| 2x 2 + 5x + 3 = 0 | В этом a=2 , b=5 и c=3 | |
| х 2 — 3х = 0 | Это немного сложнее:
| |
| 5x — 3 = 0 | Ой! Это , а не квадратное уравнение: отсутствует x 2 (другими словами a=0 , что означает, что оно не может быть квадратным) |
Поиграй с этим
Поиграйте с «Проводником квадратных уравнений», чтобы увидеть:
- график функции и
- решений (называемых «корнями»).
Скрытые квадратные уравнения!
Как мы видели ранее, Стандартная форма квадратного уравнения равна
.топор 2 + Ьх + с = 0
Но иногда квадратное уравнение выглядит не так!
Например:
| Замаскированный | В стандартной форме | а, б и в | |
|---|---|---|---|
| х 2 = 3x — 1 | Переместить все термины в левую часть | х 2 − 3x + 1 = 0 | а=1, б=-3, с=1 |
| 2(ш 2 — 2ш) = 5 | Развернуть (раскрыть скобки), и сдвинуть 5 влево | 2w 2 − 4w − 5 = 0 | а=2, б=-4, с=-5 |
| z(z−1) = 3 | Разверните и переместите 3 влево | z 2 — z — 3 = 0 | а=1, б=-1, с=-3 |
Как их решить?
« решений » квадратного уравнения, где равно нулю .
Их еще называют « корни «, или иногда « нули »
Обычно есть 2 решения (как показано на этом графике).
И есть несколько способов найти решения:
Мы можем разложить квадратное уравнение на множители (найти, на что умножить, чтобы получить квадратное уравнение)
Или мы можем завершить квадрат
Или мы можем использовать специальную квадратичную формулу :
Просто подставьте значения a, b и c и выполните вычисления.
Сейчас мы рассмотрим этот метод более подробно.
О квадратичной формуле
Плюс/Минус
Во-первых, что это за плюс/минус, который выглядит как ± ?
± означает, что есть ДВА ответа:
х = −b + √(b 2 − 4ac) 2a
х = −b − √(b 2 − 4ac) 2a
Вот пример с двумя ответами:
Но так получается не всегда!
- Представьте, что кривая «просто касается» оси x.

- Или представьте, что кривая такая высотой , что она даже не пересекает ось x!
Здесь нам поможет «Дискриминант»…
Дискриминант
Видите ли вы b 2 − 4ac в приведенной выше формуле? Он называется Дискриминантом , потому что он может «различать» возможные типы ответов:
- когда b 2 − 4ac положительно, мы получаем два действительных решения
- когда он равен нулю, мы получаем только ОДНО действительное решение (оба ответа одинаковы)
- когда он отрицательный, мы получаем пару Комплексных решений
Комплексные решения? Давайте поговорим о них после того, как увидим, как пользоваться формулой.
Использование квадратичной формулы
Просто подставьте значения a, b и c в квадратную формулу и выполните вычисления.
Пример: решить 5x
2 + 6x + 1 = 0Коэффициенты: a = 5, b = 6, c = 1
Квадратичная формула: x = −b ± √(b 2 − 4ac) 2a
Поставьте a, b и c: x = −6 ± √(6 2 − 4×5×1) 2×5
Решить:x = −6 ± √(36−20) 10
х = −6 ± √(16) 10
х = −6 ± 4 10
x = −0,2 или −1
Ответ: x = −0,2 или x = −1
или We See.
| Чек -0,2 : | 5×( −0,2 ) 2 + 6×( −0,2 ) + 1 = 5×(0,04) + 6×(−0,2) + 1 = 0,2 = 1,2 + 1 | |
| Чек -1 : | 5×( −1 ) 2 + 6×( −1 ) + 1 = 5×(1) + 6×(−1) + 1 = 5 − 6 + 1 = 0 |
Вспоминая формулу
Добрый читатель предложил спеть ее под «Pop Goes the Weasel»:
| ♫ | «х равно минус b | ♫ | «Вокруг тутового куста | |
| плюс-минус квадратный корень | Обезьяна погналась за лаской | |||
| b-квадрат минус четыре a c | Обезьяна думала, что все это забава | |||
| ВСЕ более двух дюймов | Поп! идет ласка» |
Попробуйте спеть ее несколько раз, и она застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х = −b ± √(b 2 − 4ac) 2а
«Отрицательный мальчик думал «да» или «нет» о походе на вечеринку,
на вечеринке он разговаривал с квадратным мальчиком, но не с 4 классными цыпочками.
Все было кончено в 2 часа ночи. »
Комплексные решения?
Когда Дискриминант (значение b 2 − 4ac ) отрицателен, мы получаем пару Комплексных решений… что это значит?
Это означает, что наш ответ будет включать воображаемые числа. Ух ты!
Пример: решить 5x
2 + 2x + 1 = 0Коэффициенты равны : a=5, b=2, c=1
Обратите внимание, что дискриминант отрицательный:b 2 − 4ac = 2 2 − 4×5×1
= −16
Используйте квадратичную формулу : x = -2 ± √(-16) 10
√(−16) = 4 i
(где i — мнимое число √−1)
Итак: x = −2 ± 4 i 10
Ответ: x = −0,2 ± 0,4 i
График не пересекает ось x.


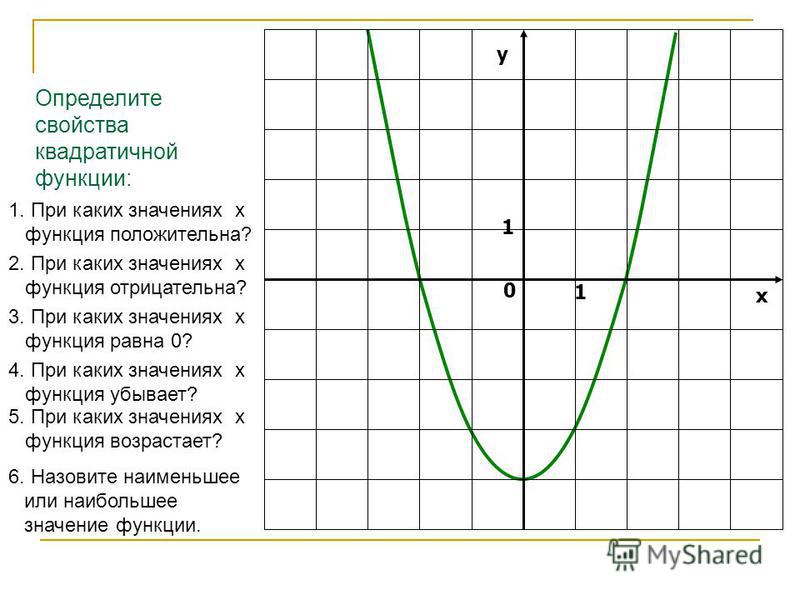 Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем
5 единиц вниз.
Это означает, что для каждой точки на графике y = x 92 — 5. Начнем с графика y = x 2 , сдвинем вправо на 4 единицы, затем
5 единиц вниз. линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).
линия симметрии — вертикальная линия x = h, а вершина — точка (h,k).