Векторная алгебра описывает способы выполнения различных операций над векторами, в том числе сложение, вычитание, разные типы перемножения. Здесь приводится лишь часть этого раздела математики, непосредственно относящаяся к задачам, наиболее часто возникающим в физической и инженерной практике. Понятие вектора В геометрическом смысле вектор — это направленный отрезок, определяемый точками своего начала и конца. Ограничения В силу специфики сайта векторные операции рассматриваются для наиболее частого случая — трёхмерного пространства, описываемого в декартовой системе координат (три взаимно ортогональные оси отсчёта). Для пространств меньшей мерности (двухмерной плоскости и одномерной прямой) обычно достаточно обнулить «неиспользуемые» координаты. Пространства большей мерности не рассматриваются, поскольку до сих пор являются физической экзотикой. Для работы с ними следует изучить курс векторной алгебры более серьёзно. В связи с малой практической востребованностью не рассматривается выполнение операций над векторами в полярных и других недекартовых системах координат. Не рассматривается и матричное исчисление, поскольку для трёхмерного пространства алгебраическая форма векторных операций является достаточно простой и удобной, хотя и не столь универсальной. Кроме того, матричное исчисление требует довольно специфического подхода, что затрудняет его применение теми, кто с прежде с матрицами не сталкивался. Основные понятияРассмотрим основные понятия, используемые на этой странице. Проекции и координаты вектора Любой трёхмерный вектор можно спроецировать на три взаимно перпендикулярные оси отсчёта, пересекающиеся в одной точке (декартовы оси координат). Выбор точки отсчёта и положение осей (базис системы координат) теоретически непринципиален, но на практике обычно выбирается так, чтобы как можно большее число участвующих в расчёте векторов было направлено вдоль какой-либо из осей координат — это упрощает вычисления. Каждый вектор можно охарактеризовать координатами двух точек — его начала и конца, — либо проекциями на оси координат и координатами точки привязки (обычно точкой привязки является начало вектора, но иногда бывает удобнее использовать в этом качестве его конец). В физике чаще применяется второй подход. В этом случае в трёхмерном пространстве вектор a Некоторые определения Модулем вектора |a| в геометрии называется его длина, а в физике — абсолютное значение направленной величины (т.е. значение, измеренное вдоль направления её действия). Среди всевозможных взаимных ориентаций векторов выделяют коллинеарные и ортогональные вектора. Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направлеными строго в противоположные стороны. Ортогональными называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны. Понятие равных векторов менее однозначно. Иногда под этим понимают любые сонаправленные вектора одного размера, расположение точки привязки которых безразлично и может быть в любом месте пространства. Более строгое определение подразумевает и совпадение точек привязки. В физике под «равенством векторов» обычно имеют в виду первый случай (величины и направления одинаковы, положение точки привязки произвольно). Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления. Иногда нулевой вектор трактуют как всенаправленный, хотя в строгом смысле это не так. Операции над векторамиСложение векторовВ алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака: сx = ax + bx ;сy = ay + by ; сz = az + bz . Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). Вычитание векторовВычитание векторов с = a – b можно представить как сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак: сy = ay – by ; сz = az – bz . Умножение вектора на числоПри умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число: bx = k · ax ;by = k · ay ; bz = k · az .  В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи. Операция умножения на число является коммутативной a · k = k · a (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет нулевой вектор, говорить о направлении которого некорректно. Операция умножения на число является дистрибутивной k · (a + b) = k · a + k · b (произведение суммы векторов на число равно сумме произведений слагаемых на это же число). Скалярное произведение векторовРезультатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними. Вычисление скалярного произведенияВ алгебраической форме скалярное произведение d = a · b вычисляется как d = ax · bx + ay · by + az · bz .Свойства скалярного произведенияКоммутативность: a · b = b · a . Дистрибутивность: Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) . Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора). Векторное произведение векторов
Результатом векторного перемножения двух векторов a и b является вектор c, длина которого равна произведению их модулей, умноженному на синус угла между ними, а сам вектор ориентирован таким образом, что перпендикулярен обоим исходным векторам, и тройка a b c является правой. Вычисление векторного произведенияВ алгебраической форме векторное произведение c = [a × b] в правой системе координат вычисляется как сx = ay · bz – az · by ;сy = az · bx – ax · bz ; сz = ax · by – ay · bx . В левой системе координат знаки слагаемых меняются на противоположные. В физике обычно подразумевается, что точки привязки всех перемножаемых векторов и результирующего вектора совпадают (и вектора-сомножители, и результат их векторного произведения действуют в одной и той же точке пространства). Свойства векторного произведенияАнтикоммутативность: [a × b] = –[b × a] . Дистрибутивность: [a × (b + c)] = [a × b] + [a × c] . Сочетательность относительно скалярного множителя: k · [a × b] = [(k · a) × b] = [a × (k · b)] . Смешанное произведение: a · [b × c] = [a × b] · c . Векторный квадрат вектора всегда является нулевым вектором: [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора). ♦ | |
| последняя правка 27.01.2011 21:01:52 |
вектор в квадрате равен
Вы искали вектор в квадрате равен? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вектор скалярный, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор в квадрате равен».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор в квадрате равен,вектор скалярный,вектора скалярные,векторное и скалярное произведение,векторное и скалярное произведение векторов,векторы скалярные,возведение вектора в квадрат,как найти скалярное произведение,как найти скалярное произведение векторов формула,как скалярное произведение векторов находить,квадрат вектора,найти скалярное произведение,примеры скалярное произведение векторов,скалярное,скалярное и векторное произведение векторов,скалярное произведение,скалярное произведение вектора на самого себя,скалярное произведение вектора самого на себя,скалярное произведение векторное произведение,скалярное произведение векторов,скалярное произведение векторов в координатах,скалярное произведение векторов в координатах формула,скалярное произведение векторов в пространстве,скалярное произведение векторов и векторное произведение векторов,скалярное произведение векторов по координатам,скалярное произведение векторов по координатам векторов,скалярное произведение векторов примеры,скалярное произведение векторов формула,скалярное произведение векторов формула в координатах,скалярное произведение векторов формулы,скалярное произведение векторов через координаты,скалярное произведение векторов через координаты формула,скалярное произведение двух векторов,скалярное произведение и векторное,скалярное произведение как найти,скалярное произведение формула,скалярное произведение через координаты векторов,скалярное умножение,скалярное умножение векторов,скалярные вектора,скалярные векторы,скалярные произведения векторов,скалярный вектор,скалярный квадрат,скалярный квадрат вектора,скалярный квадрат вектора как найти,скалярный квадрат вектора равен квадрату его длины,умножение векторов скалярное,умножение скалярное,формула скалярного произведения,формула скалярного произведения векторов,формула скалярное произведение векторов в координатах,формулы скалярного произведения,формулы скалярного произведения векторов,формулы скалярное произведение векторов,чему равен скалярный квадрат вектора,чему равно скалярное произведение векторов.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор в квадрате равен,вектор скалярный,вектора скалярные,векторное и скалярное произведение,векторное и скалярное произведение векторов,векторы скалярные,возведение вектора в квадрат,как найти скалярное произведение,как найти скалярное произведение векторов формула,как скалярное произведение векторов находить,квадрат вектора,найти скалярное произведение,примеры скалярное произведение векторов,скалярное,скалярное и векторное произведение векторов,скалярное произведение,скалярное произведение вектора на самого себя,скалярное произведение вектора самого на себя,скалярное произведение векторное произведение,скалярное произведение векторов,скалярное произведение векторов в координатах,скалярное произведение векторов в координатах формула,скалярное произведение векторов в пространстве,скалярное произведение векторов и векторное произведение векторов,скалярное произведение векторов по координатам,скалярное произведение векторов по координатам векторов,скалярное произведение векторов примеры,скалярное произведение векторов формула,скалярное произведение векторов формула в координатах,скалярное произведение векторов формулы,скалярное произведение векторов через координаты,скалярное произведение векторов через координаты формула,скалярное произведение двух векторов,скалярное произведение и векторное,скалярное произведение как найти,скалярное произведение формула,скалярное произведение через координаты векторов,скалярное умножение,скалярное умножение векторов,скалярные вектора,скалярные векторы,скалярные произведения векторов,скалярный вектор,скалярный квадрат,скалярный квадрат вектора,скалярный квадрат вектора как найти,скалярный квадрат вектора равен квадрату его длины,умножение векторов скалярное,умножение скалярное,формула скалярного произведения,формула скалярного произведения векторов,формула скалярное произведение векторов в координатах,формулы скалярного произведения,формулы скалярного произведения векторов,формулы скалярное произведение векторов,чему равен скалярный квадрат вектора,чему равно скалярное произведение векторов. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор в квадрате равен. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вектора скалярные).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор в квадрате равен. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вектора скалярные).
Решить задачу вектор в квадрате равен вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Кросс-произведение-квадрат
Изменено 7 лет, 6 месяцев назад
Просмотрено 5к раз
$\begingroup$
Недавно я где-то видел следующее выражение:
$$\frac{1}{2} \left\| \frac{\vec{u}}{9} \times \frac{\vec{u} + \vec{v}}{9} \right\| + \frac{1}{2} \left\| \ гидроразрыва {\ vec {и} + \ vec {v}} {92\| {162}$?
- перекрестное произведение
$\endgroup$
6
$\begingroup$
Ответ, который вы видели, был правильным.
Прежде всего, векторное произведение ассоциативно, т. е. $(\vec{u}+\vec{v})\times\vec{w} = (\vec{u}\times\vec{w})+ (\vec{v}\times\vec{w})$. То же самое верно и для левой стороны. Более того, векторное произведение является линейным, т. е. $(\lambda \vec{u}) \times (\mu \vec{v}) = \lambda\mu (\vec{u} \times \vec{v})$ . Наконец, напомним, что для любого вектора $\vec{u}$ имеем $\vec{u} \times \vec{u} = \vec{0}$.
Мы можем применить эти правила, чтобы упростить задачу:
$$\frac{1}{2}\left\|\frac{\vec{u}}{9} \times \frac{\vec{u} +\vec{v}}{9}\право\| = \frac{1}{2}\left\|\frac{\vec{u} \times \vec{v}}{81}\right\|$$
$$\frac{1}{2} \left\|\frac{\vec{u}+\vec{v}}{9} \times \frac{\vec{v}}{9}\right\| = \frac{1}{2}\left\|\frac{\vec{u} \times \vec{v}}{81}\right\|$$
Сложив это вместе, мы получим:
$ $\frac{1}{2}\left\|\frac{\vec{u} \times \vec{v}}{81}\right\|+\frac{1}{2}\left\|\ frac{\vec{u} \times \vec{v}}{81}\right\|=\left\|\frac{\vec{u} \times \vec{v}}{81}\right\| $$
$\endgroup$
$\begingroup$
Обратите внимание, что $u \times (u + v) = (u\times u) + (u \times v) = 0 + (u \times v) = u\times v$, поскольку векторное произведение является дистрибутивным по сложение, а векторное произведение вектора само по себе является нулевым вектором ($0$ — это нулевой вектор). Точно так же мы получаем $(u+v) \times v = u \times v$ (на этот раз с использованием «дистрибутивности справа»). Следовательно,
Точно так же мы получаем $(u+v) \times v = u \times v$ (на этот раз с использованием «дистрибутивности справа»). Следовательно,
\begin{align} \frac{1}{2} \left\| \ frac {\ vec {u}} {9} \ times \ frac {\ vec {u} + \ vec {v}} {9} \право\| + \frac{1}{2} \left\| \frac{\vec{u} + \vec{v}}{9}\times \frac{\vec{v}}{9} \right\| & = \frac{1}{2 \times 9 \times 9} \|u \times (u+v)\| + \frac{1}{2 \times 9 \times 9} \|(u+v) \times v\| \\ & = \frac{\|u\times v\|}{81} \end{выравнивание}
$\endgroup$
$\begingroup$
Вы не поняли перекрестное произведение $\times$. Это не обычное умножение, и одно из свойств, которым оно подчиняется, это $$\vec{u}\times\vec{u} = 0$$
См. http://en.wikipedia.org/wiki/Cross_product для введение.
Изменить : Также обратите внимание, что взятие нормы вектора, обозначенного $\lVert\vec{u}\rVert$, не является линейным, поэтому $$\lVert\vec{u}\rVert + \lVert \vec{v}\rVert \neq \lVert\vec{u} + \vec{v}\rVert$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 93\) — вектор, перпендикулярный
как с по , так и с по .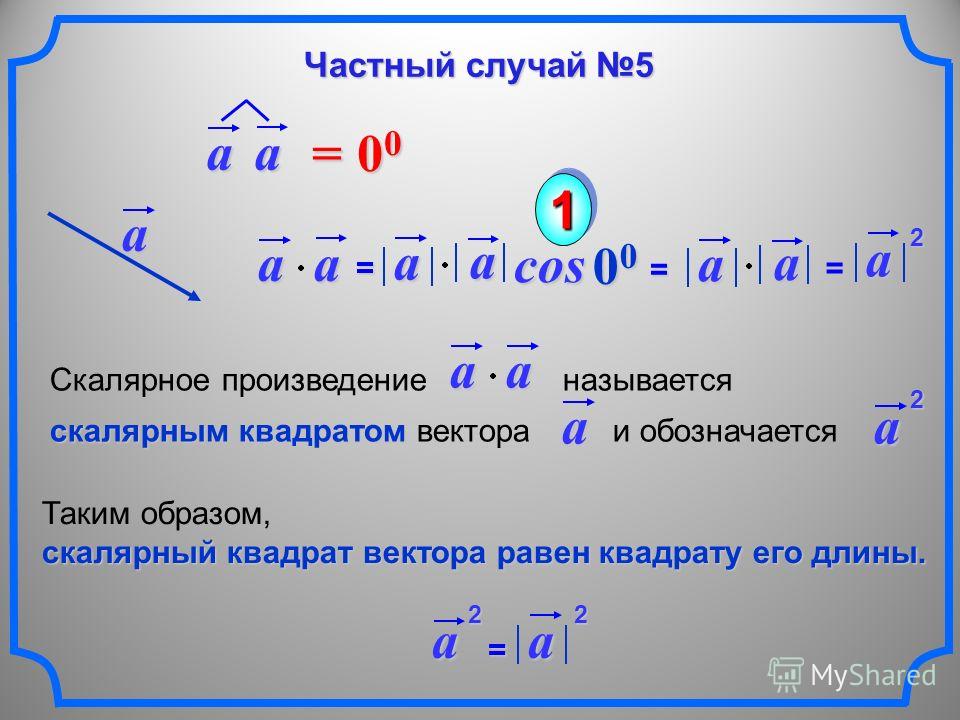 Если a и b являются массивами векторов, то векторы
определяются последней осью a и b по умолчанию, и эти оси
может иметь размеры 2 или 3. Если размер a или b равен
2 предполагается, что третья компонента входного вектора равна нулю, а
перекрестный продукт рассчитывается соответственно. В случаях, когда оба входных вектора
имеют размерность 2, возвращается z-компонент векторного произведения.
Если a и b являются массивами векторов, то векторы
определяются последней осью a и b по умолчанию, и эти оси
может иметь размеры 2 или 3. Если размер a или b равен
2 предполагается, что третья компонента входного вектора равна нулю, а
перекрестный продукт рассчитывается соответственно. В случаях, когда оба входных вектора
имеют размерность 2, возвращается z-компонент векторного произведения.
- Параметры
- a array_like
Компоненты первого вектора(ов).
- b array_like
Компоненты второго вектора(ов).
- axisa int, необязательный
Ось a , определяющая вектор(ы). По умолчанию последняя ось.
- axisb int, необязательный
Ось b , определяющая вектор(ы). По умолчанию последняя ось.
- axisc int, необязательный
Ось c , содержащая вектор(ы) векторного произведения.
 Игнорируется, если
оба входных вектора имеют размерность 2, так как возврат является скалярным.
По умолчанию последняя ось.
Игнорируется, если
оба входных вектора имеют размерность 2, так как возврат является скалярным.
По умолчанию последняя ось.- ось int, опционально
Если определено, ось a , b и c , которая определяет вектор(ы) и перекрестный продукт (ы). Переопределяет ось a , ось b и ось c .
- Возвращает
- c ndarray
Векторное перекрестное произведение.
- Поднимает
- ValueError
Когда размерность вектора(ов) в a и/или b не соответствует равно 2 или 3.
См. также
-
внутренний внутренний продукт
-
внешний Внешний продукт.
-
ix_ Создание индексных массивов.
Примечания
Новое в версии 1. 9.0.
9.0.
Поддерживает полную трансляцию входов.
Примеры
Векторное перекрестное произведение.
>>> х = [1, 2, 3] >>> у = [4, 5, 6] >>> нп.кросс(х, у) массив([-3, 6, -3])
Один вектор размерностью 2.
>>> х = [1, 2] >>> у = [4, 5, 6] >>> нп.кросс(х, у) массив([12, -6, -3])
Эквивалент:
>>> х = [1, 2, 0] >>> у = [4, 5, 6] >>> нп.кросс(х, у) массив([12, -6, -3])
Оба вектора размерностью 2.
>>> х = [1,2] >>> у = [4,5] >>> нп.кросс(х, у) массив(-3)
Множественные векторные векторные произведения. Обратите внимание, что направление креста вектор произведения определяется правилом правой руки .
>>> x = np.array([[1,2,3], [4,5,6]])
>>> y = np.array([[4,5,6], [1,2,3]])
>>> нп.кросс(х, у)
массив([[-3, 6, -3],
[ 3, -6, 3]])
Ориентацию c можно изменить с помощью ключевого слова axisc .
>>> np.cross(x, y, axisc=0)
массив([[-3, 3],
[6, -6],
[-3, 3]])
Измените определение вектора x и y , используя ось a и ось b .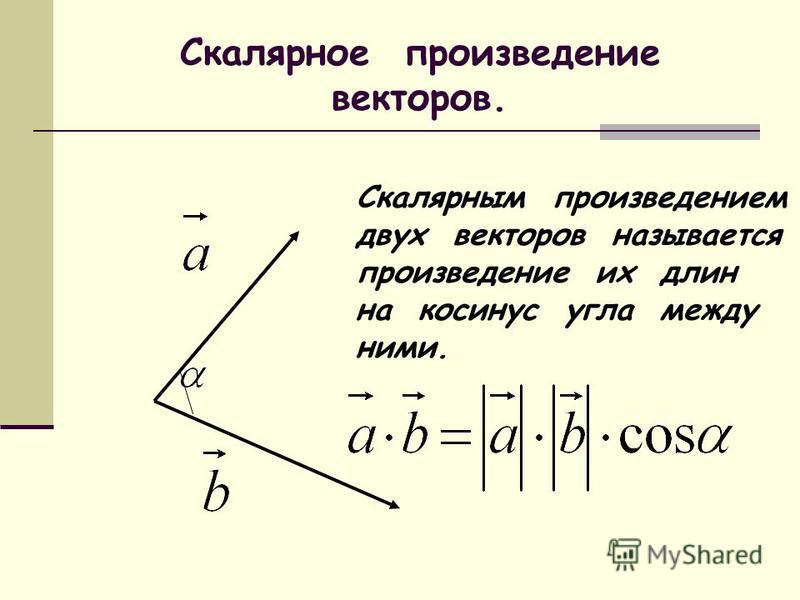





 В ортогональной системе координат модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
В ортогональной системе координат модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.




 Игнорируется, если
оба входных вектора имеют размерность 2, так как возврат является скалярным.
По умолчанию последняя ось.
Игнорируется, если
оба входных вектора имеют размерность 2, так как возврат является скалярным.
По умолчанию последняя ось.