Про системы счисления / Хабр
Что же это, чёрт возьми, такое, как работают нули-единицы, и кто и зачем это вообще придумал.
Начинаю серию статей с простым объяснением всяких фундаментальных вещей с иллюстрациями. Школьнику, которого учитель информатики заставляет переводить числа туда-сюда, а он вообще не врубается, что происходит. Дизайнеру, который не знает, что значит цвет #FFDD00. Тем, кто всё знает, но не против ещё раз укрепить модель.
В статье всё замаскировано под исторические события. Это фикция, я не знаю историю, поэтому придумал свою, чтобы было проще рассказывать.
Жил-был древний человек.
И были у него овцы.
И решил он однажды посчитать, сколько у него овец. Но считать ещё не умел.
Древний человек придумал оставлять засечки на камне. Одна засечка — одна овца. Когда рождается овца, человек рисовал засечку, когда умирала — стирал.
И жил так прекрасно древний человек, пока не поумнел и не решил узнать что-нибудь об окружающем его мире. И захотел он посчитать количество звёзд на небе — тем же способом.
И захотел он посчитать количество звёзд на небе — тем же способом.
И умер.
Это, конечно, такой естественный отбор был. Человек должен с копьём на кабана охотиться, а не звёзды считать.
Потом были древние римляне. Их было много, поэтому, очевидно, были те, кто поумнее, и все остальные. Последние охотились на кабана с копьём, а умные считали добычу и столкнулись с той же проблемой, что и древний человек.
И они подумали: «а давайте нарисуем ещё больше разных закорючек, и они будут кратко обозначать большие числа».
И придумали, что эти закорючки будут такими:
V = IIIII,
X = VV,
L = XXXXX,
C = LL,
D = CCCCC,
M = DD.
Ещё они придумали хитрые правила, чтобы, например, вместо VIIII писать IX, но для простоты повествования мы про эти правила забудем.
И смогли римляне посчитать, что средняя продолжительность жизни — лет L, а звёзд на небе видно примерно MMD. Им этого хватало.
Но время шло, и человечеству понадобилось записывать всё большие числа. Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.
Латинского алфавита, чтобы придумать ещё больше обозначений, не хватило бы, да и не очень это было удобно.
И нашёлся один умный человек, который придумал такую сложную и непонятную систему, что я не удивлюсь, если его за это потом сожгли.
Заметьте, что во всех предыдущих способах записи закорючки (цифры), стоящие рядом, просто складываются. Если древний человек написал II, это значит «I засечка и ещё I засечка». Если римлянин написал VII, это значит буквально IIIII + I + I, то есть IIIIIII.
Умный человек (горе ему) придумал вот что:
Пусть у нас будет сколько-то закорючек, например, X (здесь и дальше X — римская цифра, а не «неизвестное»). Позвал знакомого араба, сказал ему: «придумай мне X закорючек». Араб почесал репу и нарисовал: 0123456789.
Пусть 0 означает «ничего», а каждая следующая цифра сама по себе означает число, больше предыдущего на 1.
А дальше вообще отвал башки.
Пусть чем раньше в числе стоит цифра, тем большую «значимость» она имеет.
 3 и так далее.
3 и так далее.Немного терминологии, чтобы привязать знания к реальности.
Система счисления — это способ записывать количество какими-то чёрточками. Способ подсчёта овец древним человеком — система счисления. Запись чисел с помощью V, X и M римлянами — система счисления. Новый и прогрессивный способ, придуманный умным человеком, — тоже.
Непозиционная система счисления — та, где от положения цифры её значение не меняется. Древний человек придумал именно такую систему — I всегда значит I.
Позиционная система счисления — та, где, наоборот, положение цифры влияет на её значение. Такую систему изобрёл умный человек. Например, в числе 456 цифра 4 означает 400, а в числе 546 — всего 40.
Основание системы счисления — общее количество закорючек (цифр) в ней. Умный человек придумал систему счисления с основанием X (в этой системе, в свою очередь, X записывается как 10).
Разряд — положение цифры в числе.
Что будет, если изменить основание системы счисления, например, на 2?
В целом, то же самое, только: — цифры остались всего две — можем придумать любые, но для удобства обычно берут символы из нашей системы счисления.
 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10.Выходит, 1010 в двоичной системе счисления обозначает такое же количество, какое 10 — в нашей, десятичной.
Двоичная система удобна, потому что в ней достаточно иметь всего две возможные позиции в каждом из разрядов — «ток течёт» или «ток не течёт», «палец загнут» или «палец выпрямлен».
Например, загибая пальцы рук, можно посчитать от 00000 00000 до 11111 11111, если принять левый мизинец за старший разряд, а правый мизинец — за младший, нулевой. Получается, в переводе на десятичную систему счисления на пальцах можно посчитать от нуля до 1023.
Первое, на что я хочу обратить внимание, — основание системы счисления в этой же системе всегда записывается как «10». В двоичной системе счисления число 2 записывается как «10», потому что 1 * 2 + 0 = 2. В шестнадцатеричной системе счисления число 16 записывается как «10», потому что 1 * 16 + 0 = 16. Ну вы поняли.
В связи с этим есть мем:
Инопланетянин говорит, что камней «10», потому что использует систему счисления с основанием 4 по-нашему.
 В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.Кстати, про шестнадцатеричную систему счисления. Десять привычных нам цифр уже есть, а где ещё шесть взять? Да давайте просто возьмём ещё шесть букв. После 9 идёт A, потом B, потом C, D, E, F, и только потом — 10. Получается, что последние цифробуквы шестнадцатеричной системы счисления переводятся в десятичную так:
A = 10,
B = 11,
C = 12,
D = 13,
E = 14,
F = 15.И последнее на сегодня — для дизайнеров. Что означает запись #FFDD00 для цвета? Наверняка вы знаете, что каждый пиксель на экране состоит из трёх лампочек — красного, зелёного и синего цвета, а все остальные цвета получаются смешиванием этих трёх в разной пропорции.
Каждая из лампочек может светить с условной яркостью от 0 до 255. #FFDD00 — это три числа: FF, DD и 00, где каждое число обозначает яркость каждой лампочки.
FF = 15 * 16 + 15 = 255.

DD = 13 * 16 + 13 = 221.
00 = 0.Получается, красная лампочка включена на все 255, зелёная на 221, а синяя полностью выключена.
#FFFFFF — все лампочки горят на максимум и дают белый цвет. #000000 — все выключены, чёрный цвет.
Вот так, короче.
Следующая статья будет (наверное) про то, что такое, чёрт возьми, электричество, сила тока, чем она отличается от напряжения, что такое заряд, сопротивление и потенциал.
Подписывайтесь на меня в Твиттере: https://twitter.com/adam_arutyunov
А ещё есть канал — «Адам Арутюнов поднимается до мидла». В нём — вы не поверите. t.me/cdarr
5.1. Когда была изобретена позиционная система счисления?. Великая смута. Конец Империи
5.1. Когда была изобретена позиционная система счисления?
Сегодня считается, что позиционная система записи чисел была изобретена в Индии «очень давно» [821], с. 88. И затем заимствована арабами, которые наконец-то и принесли ее в средневековую Европу. Именно в Европе «арабские цифры» послужили толчком к быстрому развитию математики и вычислений во второй половине XVI — начале XVII века.
 В 1585 году были уже изобретены десятичные дроби [821], с. 119. Историк математики Д.Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.
В 1585 году были уже изобретены десятичные дроби [821], с. 119. Историк математики Д.Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.Подчеркнем, что как десятичные дроби, так и логарифмы могли появиться лишь ПОСЛЕ ВВЕДЕНИЯ ПОЗИЦИОННОЙ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем ВСКОРЕ после, поскольку, коль скоро позиционная система счисления была внедрена, изобретение дробей и логарифмов уже не заключало в себе особой сложности. В самом деле, рассмотрим вопрос об изобретении десятичных дробей. Если мы имеем позиционную систему счисления, то перемещение любой цифры на один разряд вверх «повышает ее вес», то есть вклад этой цифры в значение записанного в позиционной системе числа, в десять раз. Для целых чисел самым младшим разрядом является разряд единиц.

Чуть более сложным, но тоже не представляющим из себя принципиальных затруднений является изобретение ДЕСЯТИЧНЫХ ЛОГАРИФМОВ — опять-таки на основе десятичной позиционной системы счисления. Дело в том, что целая часть десятичного логарифма это ДЛИНА ЗАПИСИ ЧИСЛА в позиционной десятичной системе, уменьшенная на единицу. Не трудно заметить — и это, скорее всего, было достаточно быстро сделано, — что при умножении двух натуральных чисел длины их записей, в общем-то, складываются (с точностью до единицы, которую иногда приходится вычитать).

Следовательно, от появления идеи позиционного десятичного счисления до создания десятичных дробей и логарифмов не могло пройти очень много времени.
 А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.
А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.Но сегодня нас хотят убедить, что в западноевропейском обществе такие далекие от математики люди, как, например, художники, свободно пользовались позиционной десятичной системой счисления уже в XV веке и даже в более ранние эпохи. Не говоря уж об индусах, которые якобы пользовались этой системой аж в 500 году до н. э. (!) [755], с. 20. Правда, как потом рассказывает нам та же скалигеровская история науки, «древние» индусы почему-то «забыли» об этих своих выдающихся математических открытиях. Но, по счастью, успели рассказать о них арабам. Которые и донесли этот светоч «древнейших знаний» до необразованной Европы.

По нашему мнению, нарисованная историками картина неестественна и даже нелепа. Определить примерную дату изобретения позиционной десятичной системы счисления можно по бурному развитию и внедрению этой идеи, которое началось лишь в конце XVI века [821]. Следовательно, сама идея возникла где-то в середине XVI века, а не в глубокой древности. Нельзя отделять идею от ее прямых и ОЧЕВИДНЫХ следствий СОТНЯМИ и даже ТЫСЯЧАМИ лет. Поэтому все те «древне»-вавилонские, «древне»-индийские, «древне»-арабские и вообще «очень-очень древние» тексты, в которых использована идея позиционного десятичного счисления, не могли появиться ранее XVI века.

Это в полной мере относится и к якобы «древнейшей» КЛИНОПИСИ Двуречья. Сегодня нам говорят, будто «древние шумеры» еще в ТРЕТЬЕМ ТЫСЯЧЕЛЕТИИ ДО Н. Э. широко пользовались позиционной системой [821], с. 40. А якобы за ДВЕ ТЫСЯЧИ ЛЕТ ДО Н. Э. они уже свободно решают линейные и квадратные уравнения с двумя неизвестными. Д.Л. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» [821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н. Э. «древние шумеры» производят вычисления «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работ уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
По нашему мнению, все эти «древне»-шумерские математические высоты были достигнуты лишь в XVI–XVII или даже в ВОСЕМНАДЦАТОМ веках НАШЕЙ ЭРЫ.


Данный текст является ознакомительным фрагментом.
ГЛАВА 10 КОГДА БЫЛА СОЗДАНА АНТИГИТЛЕРОВСКАЯ КОАЛИЦИЯ?
11.14. Когда и как была создана китайская история
11.14. Когда и как была создана китайская история Как, кем и когда была написана «древняя китайская история»? Оказывается, что в XVII–XVIII веках, при манжурах, в Китае происходила какая-то исключительно бурная деятельность ПО НАПИСАНИЮ КИТАЙСКОЙ ИСТОРИИ [151].

5.1. Когда изобрели позиционную систему счисления
5.1. Когда изобрели позиционную систему счисления Сегодня считается, что позиционная система записи чисел изобретена в Индии «очень давно» [821], с. 88. И затем была заимствована арабами, которые, наконец-то, и принесли ее в средневековую Европу. Именно в Европе «арабские
Когда была катастрофа?
Когда была катастрофа? Воспоминания об отдаленном потопе и о сопровождавших его гибельных землетрясениях поддерживались последующими катастрофами местного порядка. Так, около 1450 года до н. э. произошел прорыв вод Атлантического океана в Средиземное море, уровень
Когда была установлена Пасхалия
Когда была установлена Пасхалия Приведем резюме исследования Г.
 В. Носовского [6 тЗ], гл. 2. Речь идет о двух важнейших вехах исторической хронологии – датировках Рождества Христова и Первого Вселенского собора в Никее, часто называемого Никейским собором. На этих датах в
В. Носовского [6 тЗ], гл. 2. Речь идет о двух важнейших вехах исторической хронологии – датировках Рождества Христова и Первого Вселенского собора в Никее, часто называемого Никейским собором. На этих датах вXXIV. День, когда была уничтожена империя
XXIV. День, когда была уничтожена империя Атауальпе, тринадцатому Инке, правителю десятимиллионной империи, под началом которого находится четвертьмиллионная армия, противостоят 177 авантюристов, прибывших из Европы. В ходе предыдущих экспедиций эти люди пытались найти
Когда Албания была Кавказской
Когда Албания была Кавказской Порой мне кажется, из недосказанности соткан мир… Прочитав иные монографии, видишь, будто он такой же, как платье голого короля, что нахваливали в сказке Андерсена прожженные мошенники… Почему нет? Иные исторические события абсолютно
Когда книга была уже написана… (Необходимое послесловие)
Когда книга была уже написана… (Необходимое послесловие) Действительно, жарким летом 2007 года, когда работа над данным текстом была, в целом, завершена, к автору пришла еще одна, только что опубликованная книга, вплотную примыкающая к рассматривавшимся выше проблемам.
 Как
Как• 2. Медный век – время, когда Империя была еще в Египте
• 2. Медный век – время, когда Империя была еще в Египте Историки не могут прийти к однозначному мнению, где и когда человек впервые открыл медь. «Где произошло впервые применение меди для изготовления из нее орудий и других изделий, а равно изобретение бронзы – трудно
• 4. Когда была изобретена бронза?
• 4. Когда была изобретена бронза? Сегодня считается, что бронза (сплав меди с оловом) была известна с древнейших времен. А медный век историки часто называют «бронзовым веком». Если верить скалигеровским датировкам, то в «античности» якобы было изготовлено огромное
Когда Албания была кавказской
Когда Албания была кавказской Порой мне кажется, из недосказанности соткан мир… Прочитав иные монографии, видишь, будто он такой же, как платье голого короля, что нахваливали в сказке Андерсена прожженные мошенники… Почему нет? Иные исторические события абсолютно
Кто изобрел числа? | Вандополис
МАТЕМАТИКА — Числа
Задумывались ли вы когда-нибудь.
 ..
..- Кто изобрел числа?
- Кто из известных математиков помог разработать числа?
- Какое влияние числа оказали на развивающиеся общества?
Теги:
Просмотреть все теги
- История,
- Математика,
- Один,
- Номер,
- Подсчет,
- Математика,
- Доисторический,
- Резьба,
- Кость,
- Кость Ишанго,
- Африка,
- Фибула,
- Бабуин,
- Счетная метка,
- Общество,
- Торговля,
- Город,
- Шумер,
- Месопотамия,
- Ирак,
- Письмо,
- Дополнение,
- Вычитание,
- арабский,
- Цифра, 9Система 0007,
- Индия,
- Математик,
- Брахмагупта,
- Арьябхат,
- Египетский,
- Измерение,
- Пирамида,
- Геометрия,
- История,
- Математика,
- Один,
- Номер,
- Подсчет,
- Математика,
- Доисторический,
- Резьба,
- Кость,
- Кость Ишанго,
- Африка,
- Фибула,
- Бабуин,
- Счетная метка,
- Общество,
- Торговля,
- Город,
- Шумер,
- Месопотамия,
- Ирак,
- Письмо,
- Дополнение,
- Вычитание,
- арабский,
- Цифра, Система
- ,
- Индия,
- Математик,
- Брахмагупта,
- Арьябхат,
- Египетский,
- Измерение,
- Пирамида,
- Геометрия
- Можете ли вы поверить, что некоторые из самых старых свидетельств чисел были найдены на кости? Зайдите в Интернет, чтобы проверить страницу «Математическое сокровище: кость Ишанго», чтобы узнать больше об этом интересном артефакте. Если бы вы нашли эту кость, поняли бы вы, что на ней изображено и насколько она важна?
- Вы ежедневно сильно полагаетесь на цифры? Вы можете быть удивлены! Попробуйте идти так долго, как только сможете, не используя никаких цифр.
 Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни!
Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни! - Вы знакомы с обычной системой счисления с основанием 10, в которой используются числа от 0 до 9., но знаете ли вы, что существует множество других систем счисления, таких как основание 8, основание 2 и даже основание 16? Ознакомьтесь с онлайн-системами счисления, чтобы узнать, как работают эти другие интересные системы счисления!
- https://www.deseretnews.com/article/865560110/A-brief-history-of-numbers-and-counting-Part-1-Mathematics-advanced-with-civilization.html
- http://www.smithsonianmag.com/innovation/how-humans-invented-numbersand-how-numbers-resized-our-world-180962485/
- http://www.
 whoinvented.org/who-invented-numbers/
whoinvented.org/who-invented-numbers/ - идея
- сейф
- простой
- общество
- объяснить
- бабуин
- тайна
- представьте себе
- выделить
- произошло
- доказательство
- авансы
- цивилизаций
- важность
- расчеты
- математика
- разработка
- технологический
Сегодняшнее чудо дня было вдохновлено Сарой из Леандера, штат Техас. Сара Уондерс , “ Откуда взялись наши числа 1-9? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара!
Сара Уондерс , “ Откуда взялись наши числа 1-9? «Спасибо, что ДУМАЕТЕ вместе с нами, Сара!
Один плюс один равно двум. В одной минуте 60 секунд. Шестьдесят минут равны одному часу. В одних сутках 24 часа. Один год состоит из 365 дней. Все это основные факты, которые мы знаем наизусть, но они подчеркивают важность одной вещи: цифр.
Можете ли вы представить мир без чисел? Можно с уверенностью сказать, что общество, каким мы его знаем сегодня, никогда бы не развилось без чисел. Научные и технические достижения, на которых построено общество, зависят от математики, которая, в свою очередь, зависит от чисел.
Несмотря на их важность, развитие чисел остается по большей части загадкой. Это потому, что первые древние доисторические люди, которые, вероятно, разработали простые методы счета, не оставили никаких записей, чтобы объяснить себя.
Здравый смысл и древние свидетельства указывают на то, что числа и счет начались с единицы. Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.
Хотя они, вероятно, не называли это «единицей», доисторические люди, вероятно, считали единицами и отслеживали, вырезая линии на кости.
Доказательства того, что это произошло 20 000 лет назад, можно найти на древнем артефакте, известном как Кость Ишанго. Найденная в Африке в 1960 году кость Ишанго (малоберцовая кость бабуина) имеет серию линий, которые выглядят как то, что мы сегодня назвали бы «счетными метками».
Отслеживание небольшого количества предметов с подсчетными метками было достаточно для отдельных лиц и небольших групп. Однако по мере того, как общества начали формироваться и расти, торговля стала более сложной, требуя развития чисел для выполнения простых математических расчетов.
Историки считают, что числа и счет расширились за пределы единицы около 4000 г. до н.э. в Шумере, который располагался в южной Месопотамии на территории нынешнего южного Ирака. Шумеру, одной из первых цивилизаций, в которой появились города, которые были центрами торговли, понадобились новые методы подсчета и ведения записей.
Пока в Шумере разрабатывались новые системы счисления и счета, также разрабатывались основы арифметики и письма. Отслеживание продаваемых товаров требовало письма и базовых операций сложения и вычитания в дополнение к расширенной системе счисления и счета.
Все эти основополагающие идеи развивались одновременно с ростом городов и расцветом торговли. Некоторые историки считают, что некоторые из этих идей независимо развивались и в других регионах мира.
Например, арабская система счисления, с которой мы все сегодня знакомы, обычно приписывается двум математикам из древней Индии: Брахмагупте из 6 века до н.э. и Арьябхат с 5 по век до н.э.
В конце концов, числа стали необходимы не только для подсчета вещей. Мы можем поблагодарить древних египтян за то, что они совершили скачок от использования чисел для счета к использованию их для измерения вещей. Историки считают, что их использование чисел для измерения позволило древним египтянам построить пирамиды и заложить основу для передовых математических концепций, таких как геометрия.
Common Core, Научные стандарты следующего поколения и Национальный совет по социальным исследованиям.»> Стандарты: CCRA.L.3, CCRA.L.6, CCRA.R.1, CCRA.R.2, CCRA.R.4, CCRA.R.10, CCRA.SL.1, CCRA.W.2, CCRA .W.4, CCRA.W.9, CCRA.L.1, CCRA.L.2
Интересно, что дальше?
Завтрашнее чудо дня имеет катастрофический финал!
Попробуйте
Вы готовы считать? Не забудьте проверить следующие действия с другом или членом семьи:
Чудесные источники
Получили?
Проверьте свои знанияWonder Contributors
Благодарим:
Алексис из Кентукки, Тревор и Сара
за ответы на вопросы по сегодняшней теме Wonder!
Удивляйтесь вместе с нами!
Что вас интересует?
Wonder Words
Примите участие в конкурсе Wonder Word
Оцените это чудо
Поделись этим чудом
×ПОЛУЧАЙТЕ СВОЕ ЧУДО ЕЖЕДНЕВНО
Подпишитесь на Wonderopolis и получайте Wonder of the Day® по электронной почте или SMS
Присоединяйтесь к Buzz
Не пропустите наши специальные предложения, подарки и рекламные акции. Узнай первым!
Узнай первым!
Поделитесь со всем миром
Расскажите всем о Вандополисе и его чудесах.
Поделиться Wonderopolis
Wonderopolis Widget
Хотите делиться информацией о Wonderopolis® каждый день? Хотите добавить немного чуда на свой сайт? Помогите распространить чудо семейного обучения вместе.
Добавить виджет
Ты понял!
Продолжить
Не совсем!
Попробуйте еще раз
Краткая история чисел: как были изобретены числа от 0 до 9
Вы когда-нибудь задумывались, как впервые появились числа?
Используя всего десять символов (0 – 9), мы можем записать любое мыслимое рациональное число. Но почему мы используем эти десять символов? И почему их 10?
Как это ни странно нам сейчас кажется, но было время, когда числа, какими мы их знаем, просто не были придуманы.
Как древние люди вели счет
Ранние люди в эпоху палеолита, вероятно, считали животных и другие предметы быта, вырезая метки на стенах пещер, костях, дереве или камне. Каждая итоговая отметка соответствовала единице, а каждая пятая отметка учитывалась, чтобы отслеживать результаты.
Эта система хороша для небольших чисел, но она не работает с большими числами — попробуйте написать 27 890, используя счетные метки.
Символы для чисел, разработанные ранними цивилизациямиПо мере развития ранних цивилизаций они придумывали различные способы записи чисел. Многие из этих систем, в том числе греческие, египетские и еврейские цифры, по сути, были расширениями счетных меток. Использовался ряд различных символов для представления больших значений. Например, в древнеегипетской системе свернутая веревка представляла 100, а водяная лилия — 1000.
Каждый символ повторялся столько раз, сколько необходимо, и все они складывались вместе, поэтому в древнеегипетской системе 300 отображалось как три свернутые веревки.
Но даже с этой системой это все еще был громоздкий метод записи больших чисел.
Позиционная запись: более простой способ записи больших чисел
У всех ранних систем счисления есть одна общая черта. Они требуют, чтобы кто-то записал много символов для записи одного числа и создал новые символы для каждого большего числа.
Позиционная система позволяет повторно использовать одни и те же символы, присваивая символам разные значения в зависимости от их положения в последовательности.
Несколько цивилизаций разработали позиционные обозначения независимо друг от друга, в том числе вавилоняне, китайцы и ацтеки.
К седьмому веку индийские математики усовершенствовали десятичную (или десятичную) позиционную систему, которая могла представлять любое число всего десятью уникальными символами. В течение следующих нескольких столетий арабские купцы, ученые и завоеватели начали распространять его в Европе.
Ключевым достижением этой конкретной системы (которая также была независимо разработана майя) было число 0.


 3 и так далее.
3 и так далее.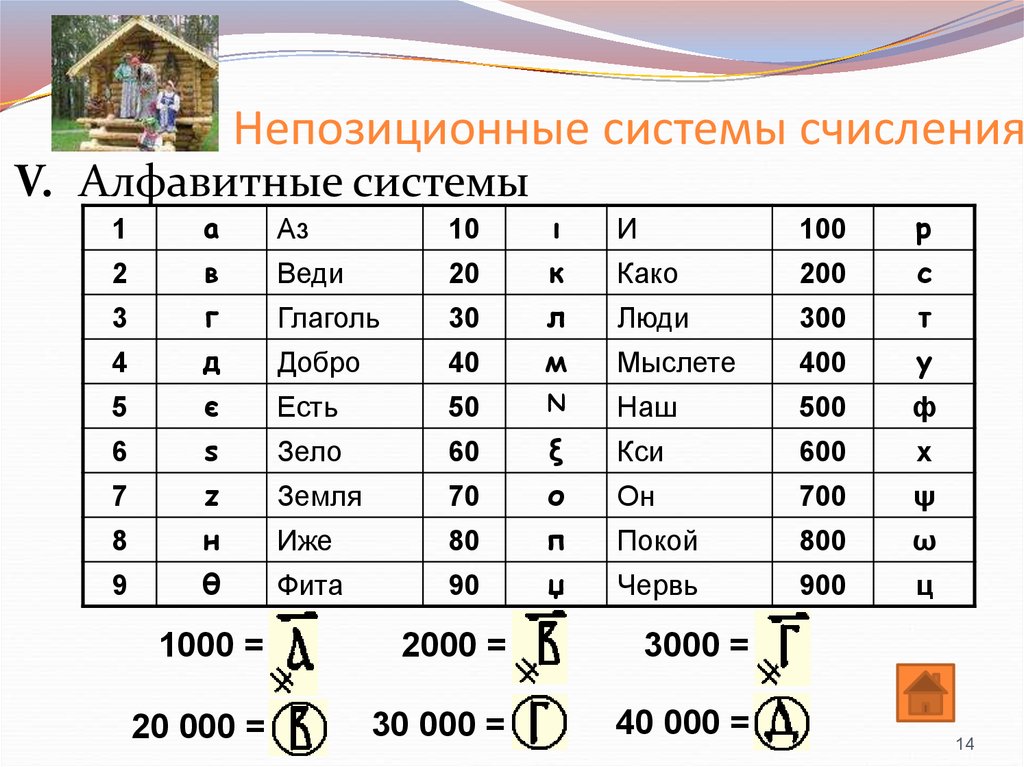 3 = 0 + 2 + 0 + 8 = 10.
3 = 0 + 2 + 0 + 8 = 10. В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.
В его системе счисления наше «4» записывается как раз как «10». А что такое «4», инопланетянин вообще не знает, потому что у него цифры 0, 1, 2 и 3.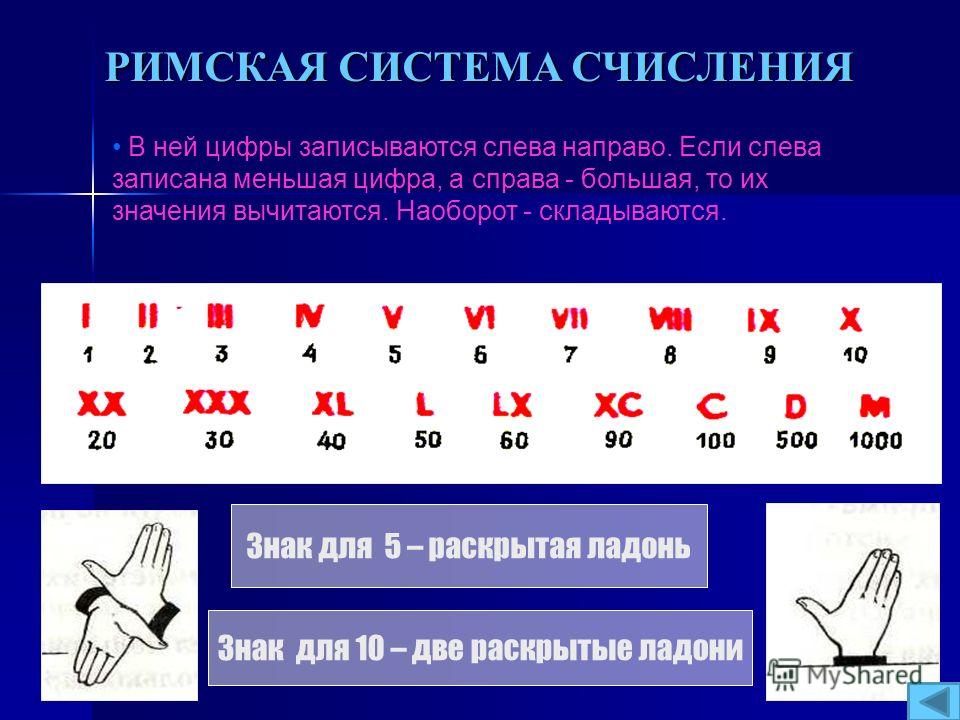
 В 1585 году были уже изобретены десятичные дроби [821], с. 119. Историк математики Д.Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.
В 1585 году были уже изобретены десятичные дроби [821], с. 119. Историк математики Д.Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.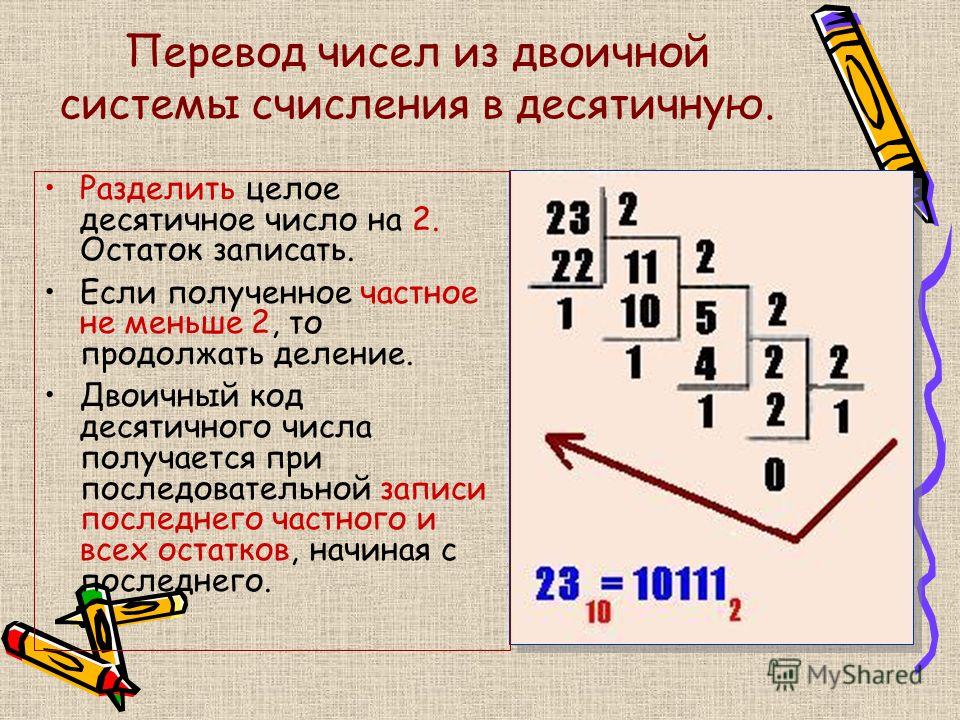

 А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.
А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и т. п.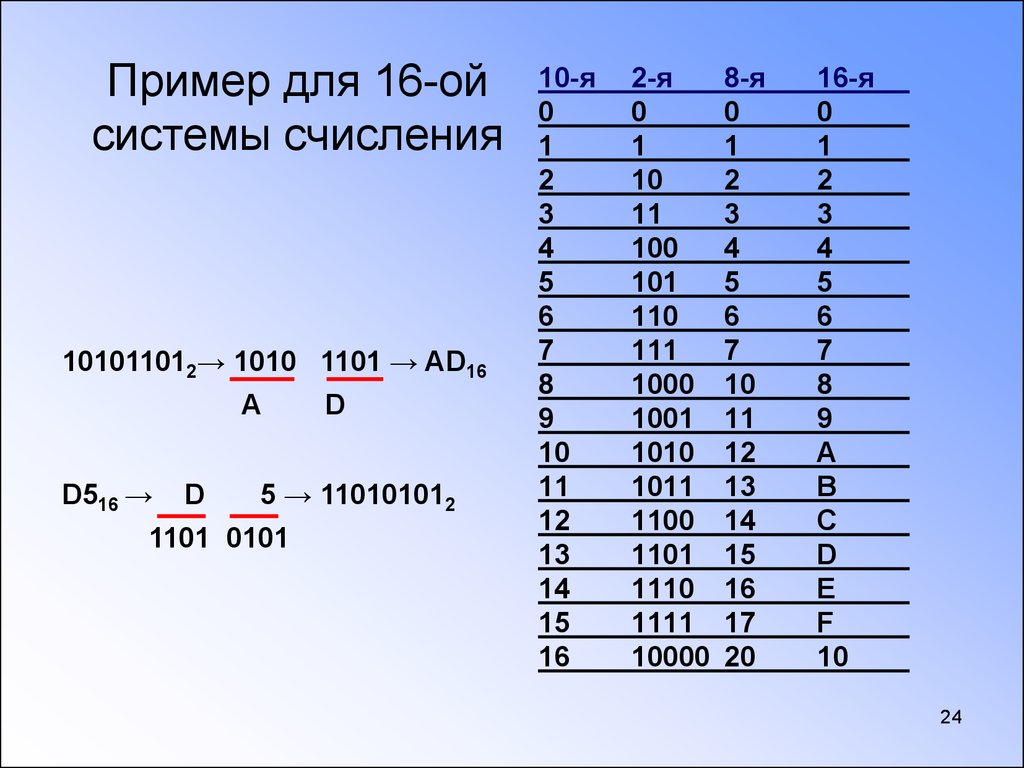




 В. Носовского [6 тЗ], гл. 2. Речь идет о двух важнейших вехах исторической хронологии – датировках Рождества Христова и Первого Вселенского собора в Никее, часто называемого Никейским собором. На этих датах в
В. Носовского [6 тЗ], гл. 2. Речь идет о двух важнейших вехах исторической хронологии – датировках Рождества Христова и Первого Вселенского собора в Никее, часто называемого Никейским собором. На этих датах в Как
Как ..
.. Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни!
Это означает отсутствие телевидения, так как вам нужны цифры, чтобы выбрать правильный канал. Вы также не можете бросить закуску в микроволновую печь, так как вам понадобятся числа, чтобы запрограммировать ее на приготовление в течение определенного времени. Как еще появляются числа? Как только вы начнете думать об этом, вы будете поражены тем, как переплетены числа в вашей повседневной жизни! whoinvented.org/who-invented-numbers/
whoinvented.org/who-invented-numbers/